Abstract
In this paper, a workflow for creating advanced aerodynamics design dashboards is proposed. A CAD modeler is directly linked to the CFD simulation results so that the designer can explore in real time, assisted by virtual reality (VR), how shape parameters affect the aerodynamics and choose the optimal combination to optimize performance. In this way, the time required for the conception of a new component can be drastically reduced because, even at the preliminary stage, the designer has all the necessary information to make more thoughtful choices. Thus, this work sets a highly ambitious and innovative goal: to create a smart design dashboard where every shape parameter is directly and in real-time linked to the results of the high-fidelity analyses. The OPAM (Open Parametric Aircraft Model), a simplified model of the Boeing 787, was considered as a case study. CAD parameterization and mesh morphing were combined to generate the design points (DPs), while Reduced Order Models (ROMs) were developed to link the results of the CFD analyses to the chosen parameterization. The ROMs were exported as FMUs (Functional Mockup Units) to be easily managed in any environment. Finally, a VR design dashboard was created in the Unity environment, enabling the interaction with the geometric model in order to observe in a fully immersive and intuitive environment how each shape parameter affects the physics involved. The MetaQuest 3 headset has been selected for these tests. Thus, the use of VR for a design platform represents another innovative aspect of this work.
1. Introduction
Digitization, machine learning, and AI (Artificial Intelligence) techniques [1,2,3,4], along with the increasing computational and management availability of big data [5], are revolutionizing every area of engineering. The availability of HPC (High Performance Computing) infrastructure and the increasing reliability of software for high-fidelity simulations make it possible to greatly reduce the time required to collect and store data.
HPC evolution [6,7,8,9] has revolutionized the field of CFD, enabling faster and more accurate simulations. The implementation of parallel computing has allowed the maximum utilization of computational resources, distributing workloads over multiple processors. In particular, the use of GPUs [10,11] (Graphics Processing Units) has shown significant performance advantages due to their ability to perform a large number of operations in parallel. GPUs are designed to handle large-scale parallel computing operations, making them ideal for CFD simulations. Unlike traditional CPUs, which are optimized to execute a series of instructions sequentially, GPUs can perform thousands of operations simultaneously. This makes them particularly effective for the intensive numerical calculations required in CFD simulations.
The integration of GPUs into HPC systems has opened up new possibilities for CFD simulations, allowing increasingly complex problems to be tackled with greater precision and in less time. The future of CFD computing in parallel with the use of GPUs promises further advances, with the development of new hardware architectures and algorithms optimized to make the most of GPU capabilities.
The development of HPC is leading to two trends: on the one hand, increasingly complex (dynamic analysis of critical maneuvers, fluid-structure coupling, higher velocities, etc.) [12,13,14,15] and precise (denser computational meshes) analyses can be tackled [16]. On the other hand, large datasets for optimization algorithms can be obtained in reasonable times. It is evident how having this computing power, without an automatic method for generating these datasets, greatly reduces the potential. Many steps forward have been made on both the automatic generation of CAD, and thus mesh [17,18,19,20], and on the mesh-morphing techniques [21,22,23,24]. In general, it is evident that the automation of the creation process of each design point is indispensable.
The development of synthetic data must be accompanied by the development of techniques for managing this big data. From this point of view, the trend is the application of machine learning and AI techniques to create smarter metamodels with which to interact in real time.
ROMs are one of the most promising techniques in CFD [25,26]. These models simplify complex problems by reducing the number of variables and the size of the system while still maintaining good accuracy. Another key aspect is the ability to easily interact with these models. FMU [27] is a free standard that defines a container and interface for exchanging models. This standard is supported by over 200 tools and is maintained as a project of the Modelica Association. It allows the integration of models developed with different simulation tools, facilitating collaboration between teams and organizations using different software. Thanks to standardization, models can be easily exchanged and reused, reducing development time and costs. The standard is suitable for the simulation of complex systems, allowing large models to be handled efficiently.
Finally, increasingly advanced applications are being developed that take advantage of VR [28] viewers to have a more immersive and intuitive experience and to have a greater understanding of the physics involved in the problem being studied.
All these new approaches and methods converge in this study in the creation of a design dashboard in which the CAD model is directly linked to the CFD results, so in real time and VR, it is possible to design an aircraft, monitoring the effect of each variation on aerodynamics. The entire workflow is automatic, and the CFD analyses are run in an HPC environment. ROMs are built from CFD analysis, and it allows real-time interaction. FMU is the standard used for data exchange for MATLAB and VR interface. The innovative aspects of this work are:
- Development of a fully automated workflow that connects CAD and mesh: The proposed approach is highly innovative, combining the benefits of mesh morphing and parametric CAD. The parameterization is defined at the CAD level, and the CAD modifications are encoded in a way that can be used to deform the mesh. This ensures excellent geometry control while minimizing computation times.
- Use of ROMs and FMUs: These techniques make CFD analysis results available in real time in any environment.
- Integration of VR: Virtual reality is employed to create an interactive dashboard where the user, using their hands or sliders, can adjust the geometry and visualize in real time how the aerodynamics change, both in terms of scalar values and field quantities.
This paper is organized as follows:
- In this paragraph, a quick introduction is given on the state of the art for the topics addressed, and the structure of the paper is outlined;
- In Section 2, a theoretical background is provided, and the tools used are presented;
- In Section 3, the stage case and the OPAM project are presented;
- In Section 4, we focus on the method used, a hybrid workflow that exploits CAD-based parameterization and a mesh morphing technique;
- In Section 5, several dashboards are shown in which the results are deployed. In particular, the MATLAB and VR dashboards are shown;
- In Section 6, the testcase is shown.
2. Theoretical Background
In this section, an overview of the background theories and technologies adopted in this study is provided.
2.1. Mesh Morphing and Radial Basis Functions (RBFs)
Mesh morphing [21,22,23,24] consists of defining a mathematical law that controls the deformation of the mesh. In particular, several studies have pointed out that RBFs are very flexible and interesting tools to deform the mesh. The idea is to define source points and apply a known displacement to them. RBFs are used to map the deformation defined on the mesh nodes using a proximity criterion. The interpolation quality and its behavior depend on the chosen RBFs.
A linear system with an order equal to the number of introduced source points must be solved to calculate the coefficients. Once these unknown coefficients are determined, the motion of any arbitrary point, whether inside or outside the domain (interpolation/extrapolation), is represented as the sum of the radial contributions from each source point, provided the point falls within the influence domain. An interpolation function, consisting of a radial basis and a polynomial, is defined as follows:
The minimal degree of the polynomial depends on the choice of the basis function. A unique interpolant exists if the basis function is conditionally positive definite. If the basis functions are conditionally positive definite of order m = 2, a linear polynomial can be used:
The values for the coefficients of RBF and the coefficients of the linear polynomial can be obtained by solving the following system:
where are the known values at the source points. is the interpolation matrix defined by calculating all the radial interactions between source points, and is the constraint matrix.
The radial basis function is a meshless method. Only the grid points are moved, regardless of the connected elements, making it suitable for parallel implementation.
2.2. Design of Experiment and Response Surface
Design of Experiment (DOE) is a widely adopted statistical approach used to plan experiments and analyze the relationship between the input and output variables of a system. The aim of this methodology is to maximize the information gain while minimizing the number of experiments required, thereby optimizing the use of resources. In simulations, DOE helps identify the most influential factors, their interactions, and their effects on outputs. Traditional DOE methods require optimal sampling strategies to obtain the maximum information about this system. Full Factorial (FF) [29], Central Composite Design (CCD) [30], and Latin Hypercube Sampling (LHS) are well established sampling algorithms.
Response Surface Methodology (RSM) [31,32,33,34,35,36] is an extension of DOE that focuses on modeling output responses determined by a set of input parameters. It involves using various mathematical techniques to model a response surface that approximates the relationship between input and output variables to create a continuous response over the design space. The main methods used to implement response surfaces include Neural Networks (NN) [31], Polynomial Functions [32], Kriging [33], Genetic Aggregation (GA) [34,36], Non-Parametric Regression [35], and RBF.
In this study, the GARS (Genetic Aggregation Response Surface) method was used to find the correlations between input and scalar output. In fact, this method is very robust and accurate, and it is widely used in the literature [34,36]. The GARS method employs genetic algorithms to determine an optimal combination of multiple response surfaces, ensuring that the aggregated model captures the essential characteristics of the provided data. It iteratively refines parameters to enhance accuracy. Initially, a population of potential solutions is generated and evaluated based on fitness criteria. Through successive generations, individuals with higher fitness are selected and undergo crossover and mutation, producing offspring solutions. The process continues until convergence, yielding optimized weights for the response surface. This iterative approach efficiently navigates the solution space, improving the accuracy of weight evaluation for enhanced model performance.
Mathematically, the algorithm can be expressed as follows:
where
- G(x) is the aggregated response surface,
- Ri(x) are the individual response surfaces,
- wi are the optimized weights.
The weights are evaluated by integrating a Multi-Objective Genetic Algorithm (MOGA) [37] to meet the optimization objective requirements. A specific RS function can take various forms, and its ability to fit the data depends on the type of problem and the simulation model used.
2.3. Reduced Order Models
Proper Orthogonal Decomposition (POD) [37,38,39,40,41,42] is a powerful technique widely utilized for extracting crucial features from high-dimensional datasets. In scientific applications, it has proven effective in reducing computational costs by establishing low-order models that faithfully replicate the original system’s behavior.
One of the most effective methods used alongside POD is singular value decomposition (SVD) [41], which compresses the dataset into a small number of modes. These modes correspond to the dominant features of the system’s behavior and are derived from the covariance matrix diagonalization of the dataset. Each DP of the dataset is a snapshot. Given that M is the matrix composed of the learning data where each column represents the values of an individual snapshot, the SVD matrix can be expressed as follows:
where
- is a diagonal matrix composed of σi, the singular values of matrix .
- and are matrices such that = and = .
- are the learning solution vectors (learning snapshots i).
The field solution in the design space can then be approximated as a linear combination of r modes:
r is a critical parameter that balances accuracy and compression while excluding noise. It is worth noticing that in Equation (6), each snapshot is approximated by spanning the retained modes using the retained components of the companion column of resulting from the SVD as new modal coordinates in the reduced space coordinates.
Once the POD modes have been obtained, it is possible to define a ROM, which is a low-dimensional mathematical representation of the system preserving the essential features of the original problem. A static ROM is trained by adopting GARS to represent the variation of the outputs according to the inputs. Each snapshot results from a state of the input x, where the x vector is defined in the input space (it usually comprises physical input parameters, such as speed, load, and pressure, and geometrical input parameters, such as diameter, hole, and thickness) and can be represented in the reduced space by the retained components of the companion column of resulting from the SVD. The GARS method could be used to represent the variation in each natural coordinate in the response space, i.e., each component of s is individually trained by a specific RS to capture its variation with respect to the input x; however, this is impractical as the size of s could be high (up to many millions of dof). The POD compressed version of the data is used instead of the full one. In the compressed space, the coordinates are the weights of the modes ; the size of the vector is usually smaller than one of the problem natural coordinates and is lower than the number of snapshots used, typically a small fraction. The GARS training happens on the weights, i.e., using the parameters x corresponding to each snapshot as scalar inputs to train the companion-retained components of , as computed for POD generation. This approach allows to map the input space x in the reduced space according to (7), where the dependence of a generic (unseen) new input state x is now represented. The full dataset for a new input state is recovered by a simple span of the modes using the new GARS-evaluated coefficients as weights for the new, unseen input.
In this study, we use the parameters of a CAD editor as input, which allows to update the geometrical model onto a new shape according to a complex non-linear process. For each new geometrical shape, a snapshot is generated by adopting mesh morphing and providing the data to train both the geometrical ROM and both the CFD results. It results in a real-time connection of each parameter (defined in CAD) to the shape and results of the CFD analyses. Alongside the full field data (i.e., the natural coordinates of each snapshot), we collect global scalar results (as drag and lift), which are not compressed by POD but are used together with the reduced coordinates to train the ROM. Therefore, with sufficiently comprehensive CAD parameterization, the ROM approach, so defined, provides an interactive design tool where all quantities of interest, both scalar and field, can be monitored effectively reaching the new unseen state in a very short time.
2.4. Functional Mock-Up Interface
A functional mock-up unit (FMU) is a standard component designed to facilitate the integration of heterogeneous models according to the Functional Mock-up Interface (FMI). FMUs are modular and reusable components that implement standardized interfaces for the simulation of numerical models, facilitating interoperability between different modeling tools. Developed as part of the European Modelica project and formalized under the FMI standard, FMUs are employed in a wide range of applications [43,44,45,46], including automotive, aerospace, energy, and robotics. An FMU is a self-contained functional unit that includes both a mathematical model and a communication interface. It is distributed as a zip file containing an XML description of the model, a binary executable file (which implements the mathematical model), and configuration data. There are two main types of FMUs:
- Model Exchange (ME): Allows the exchange of models described as systems of differential or algebraic equations. This type of FMU is integrated directly into the host simulator.
- Co-Simulation (CS): Includes an internal solver, enabling the FMU to run the simulation autonomously while communicating with other models or simulations through standardized interfaces.
FMUs can be generated to make ROMs reusable. In our approach, we encapsulate the ROM and the global results into FMUs. We adopt three types of FMUs to manage the geometrical model, the field results, and the global results. FMUs are intended to manipulate the sets of scalar quantities, and in our implementation, we receive the new state to be represented in the parametric space as input (each individual parameter as a scalar CAD input), and the state of the system in the reduced coordinate system as output, as in (7). The evaluation happens in real time and allows to calculate the full state from the corresponding FMUs: geometry, field results, and global results. As far as the portability of the modes (large fields of data) is concerned, instead of accessing the data from the FMUs directly, we have the ability to write the full field (i.e., a complete span of the modes) on file. This is not efficient for interactivity, and so we adopt the solution to dump the modes on file from the FMU and then load them on the device (i.e., the GPU of the VR or the one of the laptop).
3. Reference Case
The GMGW (Geometry and Mesh Generation Workshops) aimed to identify suitable improvements and best practices for generating more accurate and reliable meshes. For the second GMGW [47], a parametric aircraft model inspired by the Boeing 787-800 Dreamliner, a twin-engine civilian aircraft for medium- to long-haul routes, was provided [48]. The simplified model (see Figure 1, left) is based on 53 parameters and scaled approximately 1:300 relative to the B787. The entire aircraft body is composed of spheres, cylinders, cones, and ruled surfaces. Cross-sections for the ruled surfaces are either NACA 4-series airfoils or super-ellipses. Full details on the generation of wings, fuselage, and other parts of the aircraft can be found in [48]. As a CAD editor, ESP (Engineering Sketch Pad), an open-source editor developed by the Massachusetts Institute of Technology, was used [49].

Figure 1.
OPAM baseline geometry (a) and the structured mesh used in [50] (b).
The workshop challenge involved starting with a parametric CAD model and developing an automatic meshing procedure that maintains mesh quality for each DP. In this study, a different perspective was taken to address the challenge. Instead of generating a new mesh for each DP, the CAD modifications were transferred to the existing mesh, deforming the baseline mesh accordingly. This innovative and creative approach offers several computational advantages. Notably, it makes the workflow well-suited for generating ROMs, where it is crucial to keep the mesh topology unchanged, and provides a significant step forward compared to the mesh-morphing-based approach presented at GMGW [50], adding the full automation of the process according to the CAD parametrization.
The focus of the OPAM-1 challenge was automatic mesh creation. In fact, the ESP tool is fully scriptable, so once the parametric model is defined, each CAD variant can be generated with a Python script. Having also a procedure for automatic mesh creation makes the workflow very attractive, greatly reducing the time to prepare the CFD analysis. Several studies [17,18,19,51,52] have been conducted in this regard, demonstrating the possibility of automating the mesh creation process. However, some critical issues remain. The processes used are often not fully automated and always require a preliminary step in which the parts that form the aircraft are described and grouped and the reference dimensions for the problem are set. In addition, the mesh creation phase remains a fairly computationally expensive phase. Finally, even after automating the mesh creation process, it remains very difficult to ensure that the mesh is iso-topological (a key aspect of creating ROMs).
Another approach is mesh-morphing, which involves using the same mesh while defining parameters at the mesh level; it was used for the OPAM-1 testcase [50], emphasizing its flexibility by showing its effectiveness in large geometric variations. The mesh used for this testcase and the variations considered are shown in Figure 1b and Figure 2.
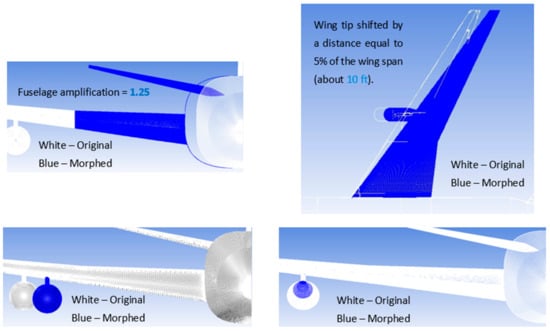
Figure 2.
Shape parameters defined using mesh morphing in [50].
The main advantages of this approach are related to the fact that the same computational grid is always used, so there is no re-meshing noise, the mesh topology does not change (crucial for ROM generation), the convergence of the CFD analysis is faster, and in general, the CFD model update takes less time. In particular, comparing the time required for the two studies [50,51], even considering the different facility used, mesh morphing is very advantageous. Conversely, the main limitation is related to the setup. In fact, to obtain these shape variations, complex setups are required, there is often a limit on the maximum amplifications to ensure a good mesh quality, and the shape variations must be iso-topological. In addition, in some cases, it is difficult to define the displacements of source points when there is a more complex shape change and the fundamental operations (rigid displacements, scaling, offsets, etc.) are not captured with sufficient accuracy (specifically in [50], post-morphing STL surface projections are required to preserve the geometry).
4. Hybrid Workflow
The main innovative aspect of this study lies in the parameterization and the algorithm used to create each DP in the DOE. A hybrid method was employed [53,54], combining the advantages of mesh morphing and parametric CAD. Specifically, the parameters are defined in a Python script that generates the CAD. Each CAD variant is then compared with the baseline, creating a cloud of points that spans from the initial state to the new CAD. This point cloud is used as an RBF field to transfer information from the CAD level to the mesh level. Finally, the mesh is deformed, and a CFD simulation is conducted for each DP. Figure 3 illustrates the workflow followed in this study. To generate the baseline mesh, a convergence analysis is necessary, progressively refining the mesh to find a trade-off between very dense meshes that are slow and coarser meshes. This starting point remains essential for this workflow as well. Once the baseline is generated, the other DP morphs the already created mesh, so it is only necessary to monitor the mesh quality to prevent highly distorted cells. From this perspective, RBFs are an excellent solution, as they help preserve mesh quality.

Figure 3.
Hybrid workflow.
The proposed method has the advantages of both the previously described methods. In fact, CAD-based parameterization is preserved, which provides excellent control over the final shape, but mesh morphing is used to update the baseline mesh onto the desired variant. This hybrid workflow, in addition to being a very attractive alternative to more established approaches, makes it possible to create ROMs from a parametric CAD model, thus allowing CFD information to be transferred to CAD editors to create smarter design platforms and reduce the time required for design. This workflow is applied to the OPAM-1 testcase; however, the method is general and can be extended to any model, not necessarily limited to the aeronautical domain. The starting point is a parametric CAD model. This workflow can be applied to any iso-topological parametric CAD model.
4.1. Parametric CAD
For the generation of parametric CAD, the open-source CAD editor ESP was employed [49]. The workflow demonstrates remarkable flexibility and is easily customizable for integration with various CAD editors. Trials have been conducted using diverse tools, including CadQuery 2.4.0 [55,56], JPAD [57], AxCent [58], and Rhino 7 [59].
ESP is a browser-based design software designed for creating, modifying, and generating three-dimensional solid models. It uses OpenCascade 7.7 [60] as the engine for geometry generation and reads input ASCII files containing parameters, invoking the necessary functions to generate the CAD. In this case, scripting the modification of these ASCII files is needed. ESP has a graphical interface but can also be run in batch mode.
4.2. CAD–Mesh Connection
One of the critical points in the workflow is the transfer of information from CAD to the mesh. This requires a routine to encode the shape variation defined in the geometry, making it usable for mesh deformation. To facilitate this, a tool based on the OpenCascade geometrical modeler [61] was developed to create a point cloud on the surface of the baseline geometry and a series of corresponding points on the CAD variant.
Several challenges arise in this operation. A fundamental aspect is the recognition of homologous surfaces and edges. Using scriptable CAD editors offers a significant advantage in this regard. The same operations are executed sequentially by changing the input parameters, ensuring that the order of the generated surfaces and edges remains consistent. For the successful coupling of homologous entities on different CADs, it is essential that the CADs are iso-topological, so that the homologous points on the homologous surfaces and edges can be defined. We adopt an evolution of the approach proposed in [62]: the surfaces of the baseline geometry are covered with a regular grid of points in the two-dimensional U-V space, and similarly, the edges are covered with a set of one-dimensional points evenly spaced. The final position of the points on the edges is imposed by prescribing the same parametric positions; the final positions of the points inside the surfaces are obtained by transforming the U-V parametric position of each node according to a 2D RBF deformation defined by the surface parametric position of the points on the edges in the original and deformed shape. Since the number of points is the same between the two clouds, the grids can be put into one-to-one correspondence. Additionally, managing the interface zone between two surfaces is crucial. To ensure a good mesh quality and proper overlap of the deformed mesh with the corresponding geometry, points on edges and surfaces are independently defined, and a buffer is provided between them; surface interior points that are within a buffer distance to the edges are removed. The interior point spacing is constant both in the u and v directions and computed at the center of each surface, imposing individually a du and a dv that produces the desired spacing in the 3D space. This approach does not require an external meshing tool and allows to obtain good-quality, uniformly spaced clouds suitable for RBF mesh morphing in 3D.
Once the two-point clouds are created, they can be used to drive surface mesh morphing by adopting the positions of the cloud on the baseline geometry as source points and the difference between the updated cloud and the baseline as the prescribed field. The approach is summarized in Figure 4, where a CAD variation of a simple wing is shown; in Figure 5, where the CAD-based source points extracted from edges and surfaces are shown; in Figure 6 (top), where the two final clouds adopted to drive the surface morphing are shown; and in Figure 6 (bottom), where the deformed mesh is represented. The resulting surface mesh matching with the target b-rep shape is represented in Figure 7, where the morphed mesh is superimposed to the CAD and the projection of its point onto the CAD is shown.

Figure 4.
Example of NACA profiles (baseline—(left) and deformed—(right)).
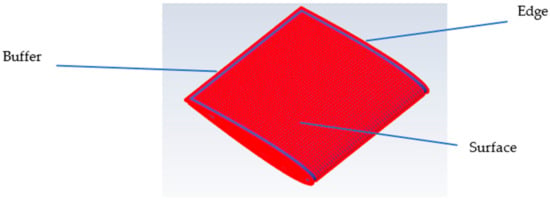
Figure 5.
Cloud of points generated on the baseline.

Figure 6.
Comparison of points on the baseline (red) and on the deformed geometry (green) (top). Deformed mesh controlled by the source points (bottom).

Figure 7.
Comparison of deformed mesh and updated CAD (top). Comparison of deformed mesh and updated CAD; green points have deviation under 0.01 mm (bottom).
4.3. RBF Volume Mesh Morphing
In order to complete the proposed workflow, we need to propagate the shape variation known at surfaces into the volume. To warp the full volume where the CFD mesh is defined, the mesh morphing technique based on RBFs was utilized to update each DP. Specifically, the point clouds computed at surfaces were translated into an RBF field, which is used as source points in an RBF problem. This process effectively transfers the parameterization defined at the CAD level to the mesh level. It is worth considering that with respect to the workflow proposed in [54], where all the nodes of the CFD mesh are used to control the morphed shape by combining simple operations, the new proposed approach relies on a smaller cloud of uniformly spaced RBF points. The ability of the RBF to smoothly interpolate the data allows to control the fine-spaced CFD mesh according to the RBF defined on a coarser one. The effectiveness can be easily verified by projecting the deformed mesh onto the corresponding CAD to assess the achieved tolerance. For the example case shown, Figure 7 illustrates how all points of the deformed mesh projected onto the deformed CAD have a deviation smaller than the tolerance (0.01 mm) and therefore are displayed as green points.
5. Design Dashboard
Once the workflow for generating a single DP was defined, a procedure was defined to perform the following tasks:
- Create the dataset;
- Create a metamodel that provides the necessary information in real-time as the considered CAD-based parameters vary;
- Define interactive handles to be positioned in the 3D scene;
- Visualize everything in real-time on the MATLAB dashboard and on the Meta Quest 3 headset in VR;
- Enable real-time interaction with the model by creating sliders or handles.
In Figure 8, the complete workflow is shown. The first step is to create the dataset. In this study, a DOE was conducted using the LHS algorithm [63]. For each DP, various types of data were saved:
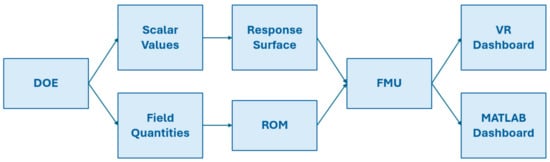
Figure 8.
The entire workflow.
- Global scalar quantities of interest (drag, lift, and efficiency);
- Coordinates x, y, and z of each surface node;
- CFD results at the x, y, and z coordinates (pressure values).
An RS was then constructed to correlate the input parameters with the scalar values of interest, i.e., the global parameters and the weights of the retained modes of each ROM, as detailed in Section 2.3. All metamodels were exported as FMUs [64] to be read in the Unity and MATLAB environments where the design dashboard was created.
Once the FMUs are exported, a model is available that allows for real-time evaluation of scalar and field quantities. It can be used to sample the parameter domain and to correlate input and output parameters.
The MATLAB dashboard is controlled by associating an interactive slider with each input parameter; the graphical one is controlled by defining specific handles and how the handles are related to the input parameters of the model. A proper positioning and connection of the handles with the input parameters allows to gain very realistic interactivity.
5.1. Matlab Dashboard
The FMUs were imported into the MATLAB–Simulink environment to create an optimization dashboard that allows real-time evaluation of both field quantities and scalar quantities. This approach enables multi-level optimization: the scalar quantities provide an idea of the overall behavior, while the 2D and 3D contours help contextualize the results, understand the physics involved, exclude certain solutions, or choose more interesting ones.
5.1.1. FMU Import
The first step is the import of the FMUs. This is performed in Simulink using the dedicated block. For the RS, a single FMU is imported, which encapsulates the law correlating the scalar input and output of interest. For the ROM, two different FMUs are imported:
- One controls the generation of modes, which is executed only once, and the modes are stored as vectors.
- The other controls the generation of weights, containing the RS that outputs the weights for each n-tuple of inputs (Figure 9).
 Figure 9. FMU imported onto Simulink.
Figure 9. FMU imported onto Simulink.
Once the weights and modes are known, a simple linear combination is sufficient to obtain the field quantity of interest. This approach, i.e., separating modes and weights, allows for real-time response. The modes are stored in memory and evaluated only once, and the linear combination does not require significant computation time.
5.1.2. Optimization Dashboard
The collected data are managed by a MATLAB script that enables optimization at various levels. Scalar values can be used to guide optimization and identify a global optimum using response surfaces. At this stage, the MOGA algorithm has been used to explore the parameter space and identify optimal solutions. In the case of multi-objective optimization, it is possible to identify a Pareto front that encompasses the best solutions. Once potential targets have been identified, the ROMs are used to select the optimal solution. Real-time parameter exploration allows for observation of the influence of parameters on aircraft aerodynamics. This approach facilitates a more robust and informed optimization process because it provides a clear understanding of the physics involved and the contribution of each parameter. By also analyzing the 3D contours or 2D Cp profiles, it is possible to discard design points that, despite improving efficiency, lead to greater flow instability.
5.2. VR Graphical Dashboard
Using the graphical dashboard, the user can see the deformation of the mesh and the pressure values for all the combinations of the available parameters in an interactive UI and/or in a virtual reality environment, in which the interaction is managed using a digital representation of the user’s hands.
The dashboard has been developed using Unity Engine by leveraging the latest features offered by its VR packages. It consists of three main modules: the import module, the visualization module, and the interaction module.
5.2.1. Import Module
The import module is responsible for managing the reading of the data needed by the visualization module. The data needed are as follows:
- Baseline 3D mesh (STL file)
- FMUs containing transformations from input parameters to mode coefficients
- Mode matrix of the mesh ROM (CSV file)
- Pressure ROM modes matrix (CSV file)
The baseline 3D mesh is imported using a custom format that stores the collection of 3D vertices and the collection of triangle indices. As the connectivity of the mesh is not known because FMUs store cloud of points, at import time, the number of vertices is first checked to be sure that FMU data are compatible with the mesh, and then the connectivity between the mesh and the cloud is reconstructed with a fast search algorithm. We used a NNS (Nearest Neighbor Search) algorithm based on a k-d tree with k = 3.
5.2.2. Visualization Module
The visualization module is responsible for managing the rendering of the imported data in real-time, both for the mesh deformation and texturing. The mesh texturing is used to represent the pressure values.
The diagram below (Figure 10) shows what happens in each frame when the user updates one or more of the available parameters.
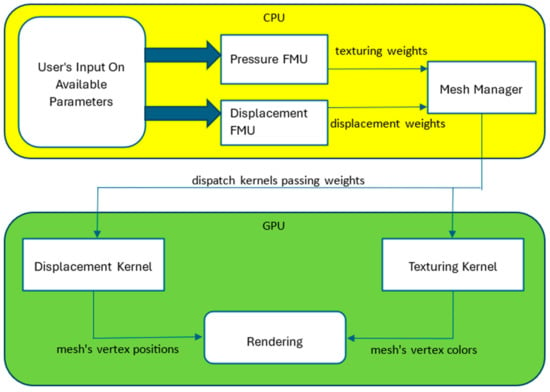
Figure 10.
The diagram showing what happens in each frame when the user updates one or more of the available parameters.
All the necessary calculations, except those of the FMU weight retrieval, are performed on the GPU so that the data structures that contain the results are passed directly to the rendering pipeline.
The displacement and the texturing kernel are initialized with their respective modes so that the final vertex positions and colors can be computed as a weighted sum of those modes.
The color of the single pixel is computed using the interpolated value generated during the rasterization phase of the rendering pipeline.
5.2.3. Interaction Module
The interaction module is responsible for managing the user’s interactions with the virtual environment. Its VR implementation is based on Unity’s VR Interaction Toolkit. The main purpose of this module is to allow the user to modify the value of the parameters using a 3D user interface and/or 3D handles.
As soon as the user modifies one of the parameter’s values, the new value is propagated to the visualization module to update the mesh displacement and texture, as shown in the previous paragraph.
6. Design Example According to the Proposed Workflow
This paragraph presents the complete workflow applied to the case of OPAM-1, described in Section 3. Six parameters affecting the wings were selected, and the hybrid workflow was used to generate each DP. The entire workflow outlined in Figure 8 is fully automated, allowing for the generation of DPs ready to be run on any CFD solver. Therefore, it can be seen as a more computationally efficient alternative to traditional automatic mesh-generation tools. The described workflow was used to generate the dataset. For each DP, the surface node coordinates and the surface pressure values, drag, lift, and efficiency values were saved to be used as snapshots. The node coordinates of each DP’s surface mesh and the pressure values were used to create ROMs, while scalar values were interpolated to obtain a response surface.
In the final dashboard, these datasets can be utilized across multiple levels. Specifically, the response surfaces can be used to identify the optimal solution. Within the best identified DP, field quantities (specifically pressure fields) can be examined to gain deeper insights into the physics involved. Real-time exploration around the selected DP allows for the discovery of potentially more interesting solutions. Additionally, extracting pressure coefficient profiles at any section provides confirmation of the findings.
6.1. CFD Model of OPAM
As mentioned in previous paragraphs, the OPAM case study was chosen. The geometry can be quickly updated with the provided comprehensive parametrization, comprising 53 parameters describing every part of the aircraft.
The first step was to define the baseline and create the CFD mesh of the initial geometry. Table 1 outlines the main characteristics of the mesh, and Figure 11 provides some details of the mosaic mesh. Symmetry was leveraged to reduce the computational domain.

Table 1.
Details of CFD Mesh.
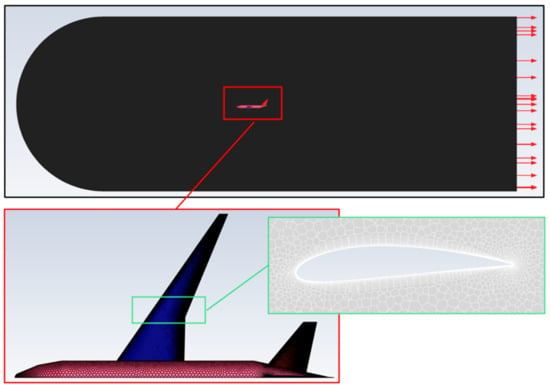
Figure 11.
CFD Mesh.
The following main options are configured:
- Steady-state simulation;
- Density-based solver;
- k-omega SST turbulence model;
- Air as an ideal gas with the Sutherland viscosity law;
- Boundary conditions:
- ○
- Inlet [pressure-far-field]: Mach equal to 0.7 inclined by α = 0°.
- ○
- Outlet [pressure-outlet]: Pressure and temperature standard (101,325 Pa, 298 K).
- ○
- Side [pressure-far-field]: Same conditions as the Inlet.
- ○
- Symmetry [symmetry]: Symmetry plane.
- ○
- Plane [wall].
The implicit Roe-FDS formulation with second-order discretization was employed.
6.2. Parameters and DOE
Out of the 53 model parameters, the 6 parameters summarized in Table 2 were chosen to modify the wing shape while maintaining a constant wing area. Variations were made in the aspect ratio, leading edge sweep, setting angle, and camber ratio at the break and tip. The range of parameters was chosen around the baseline to create a sufficiently challenging deformation for testing the workflow while remaining physically reasonable. For example, an excessive aspect ratio, although potentially improving performance, would result in an overly long wing, making the structure unstable. Future tests could be conducted by expanding the range of certain parameters and considering an extended number of parameters and ranges. In Figure 12, the effect of the first two parameters, i.e., the variation of the aspect ratio and the sweep angle, can be appreciated. The effect of the remaining four local parameters acting on the wing profile can be appreciated by examining Figure 13, Figure 14, Figure 15 and Figure 16. A DOE consisting of 66 DPs was generated using the LHS. The number of design points (DP) was set, starting from a reasonable initial value and increasing the number of analyses until sufficiently accurate models were obtained. The goal is to achieve a trade-off between the result accuracy and computational time.

Table 2.
Range and baseline value for each parameter.

Figure 12.
Blue baseline, red DP66, green DP65.

Figure 13.
Design Point 66 with chord at 0.5 and 0.75 compared to the baseline (black line).

Figure 14.
Alphab = −5 with chord at 0.25, 0.5, and 0.75 compared to the baseline (black line).

Figure 15.
Caberb effect: Caberb = 0.06 with chord at 0.25, 0.5, and 0.75 compared to the baseline (black line).

Figure 16.
Effect of alpha_t (−6) and camber_t (0.02) at the tip compared to the baseline (pink).
Specifically, DP 65 and 66 are highlighted, as they represent the extreme values of the parameters within their respective ranges when compared to the baseline configuration:
- DP65: 8, 33, −5, 0.02, −10, 0.02
- DP66: 10, 37, −1, 0.06, −6, 0.06
In this phase, it was verified that the mesh quality did not degrade. Specifically, DP 65 exhibited the lowest mesh quality. The relevant values of the minimum orthogonal quality for certain DPs are reported in Table 3. To gain a better idea of how the mesh is updated when undergoing a consistent change, a cut of the volume mesh at two sections along the wing span is represented in Figure 13, Figure 14, Figure 15 and Figure 16.

Table 3.
Mesh Quality.
Finally, it was verified that there is indeed a good correspondence between the CAD and mesh for each DP. Figure 17 shows a comparison between the mesh and CAD for DP 65, where the maximum deviation has been observed. It can be observed that the CAD and the surface mesh perfectly overlap. In Figure 18, the comparison between the surface mesh and the corresponding CAD is shown. For the reported DP, there is a deviation ranging from −0.09 mm to 0.07 mm. The green areas indicate points with deviation under the tolerance (0.01 mm).
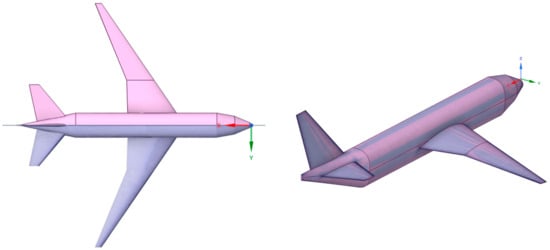
Figure 17.
Comparison of CAD and mesh for DP 65.
Figure 18.
Deviation of the mesh from the deformed CAD for DP 65.
6.3. Response Surface
FMUs are used to interpolate scalar quantities, such as drag and lift. In the figures and tables below (Figure 19, Figure 20, Figure 21 and Figure 22, Table 4 and Table 5), the main results about precision of the RSs are reported. In the Appendix A, the complete DOE with input and output parameters has been included. A total of 60% of the points are used for training, 20% as a validation set, and the remaining 20% as a test set. The Response Surfaces are very accurate both in terms of RMS and the R parameter. The obtained values are presented in the following tables and graphs. A good fit is the result of a quality dataset. In fact, LHS allows for a good representation of the parameter space, while the choice of the number of DP, as mentioned earlier, is crucial to ensure sufficiently comprehensive sampling.
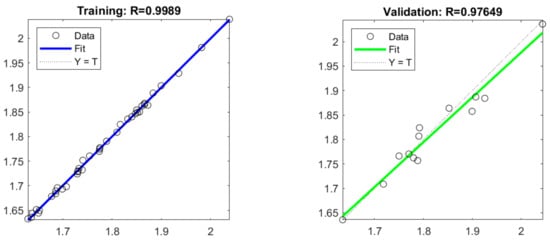
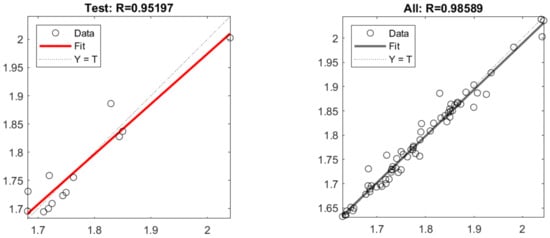
Figure 19.
R value for drag evaluation.
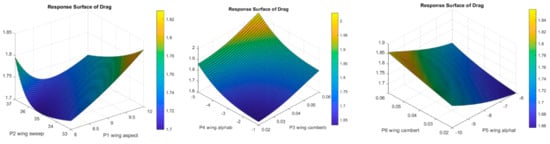
Figure 20.
Response surfaces for drag evaluation.
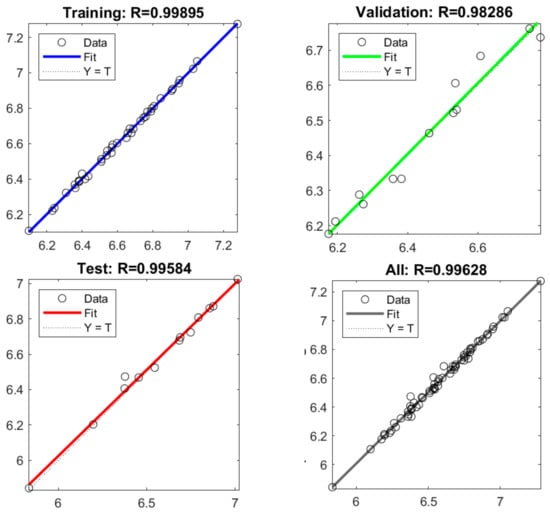
Figure 21.
R value for lift evaluation.
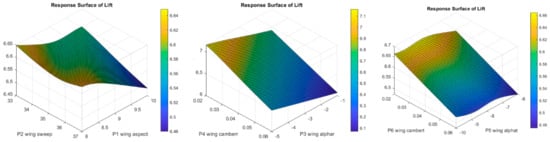
Figure 22.
Response surfaces for lift evaluation.

Table 4.
Performance of FMUs for drag evaluation.

Table 5.
Performance of FMUs for lift evaluation.
Finally, the response surfaces for drag and lift are shown for pairs of input parameters.
6.4. Mesh ROM
The ROM of the geometry allows real-time evaluation of node positions for any aircraft configuration, i.e., for any combination of selected parameters. Specifically, all nodes of the wing, the part of interest for monitoring, were selected. A model was trained to assess how each parameter affects the final geometry. Six modes were selected, and 50% of the DPs were used for training. The error of the ROM evaluated by the software is less than 0.48%. In particular, the DP in the test set where the error is maximum (0.48%) is reported. The blue points (Figure 23) represent those of the CFD mesh, while the red points are the corresponding points evaluated with the ROM. Excellent overlap is observed both globally and locally (profiles at 0.25, 0.5, and 0.75 chord positions are specifically shown). The absolute error plot for the three coordinates is shown in Figure 24, while Figure 25 shows the percentual error defined as follows:
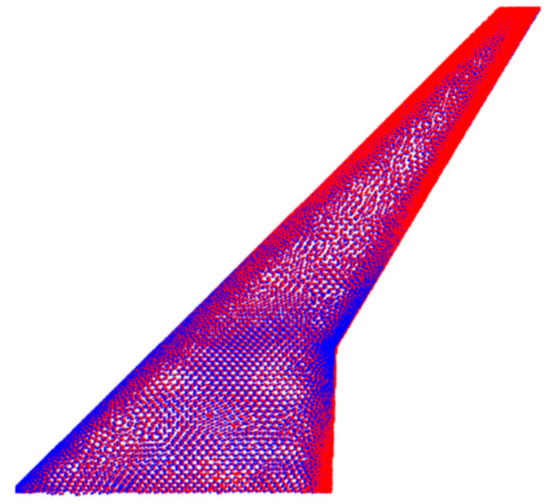

Figure 23.
The blue points represent those of the CFD mesh, while the red points depict the corresponding points evaluated with the ROM for the profiles at 0.25, 0.5, and 0.75 chord positions.
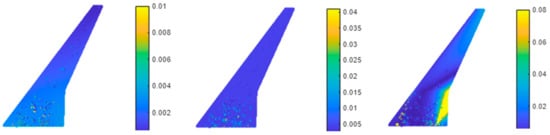
Figure 24.
Relative error for coordinates x, y and z.
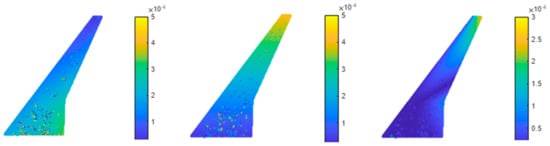
Figure 25.
Absolute error [m] for coordinates x, y, and z.
6.5. Pressure ROM
The ROM of the pressure allows real-time evaluation of pressure values (or associated quantities, like Cp) for any combination of selected parameters. All wing nodes, the part of interest for monitoring, were selected. A model was trained to assess the influence of each parameter on the final geometry. Five modes were selected (Figure 26), and 50% of the DPs were used for training. The error of the ROM evaluated by the software is less than 5.1%. Again, a comparison was made between the values predicted by the ROM and those computed by CFD for the DP in the test set with maximum error (5.1%). A good correspondence is observed (Figure 27, Figure 28 and Figure 29). The maximum pointwise error is around 10% (Figure 28). To improve performance, it would be necessary to increase the number of considered modes and expand the training dataset. However, the level of accuracy is considered acceptable. In fact, the error becomes significant only in the peak pressure regions, while the overall trend, which is useful for making both qualitative and quantitative considerations, is captured very well. Additionally, the DP of the test set with the maximum error has been reported.
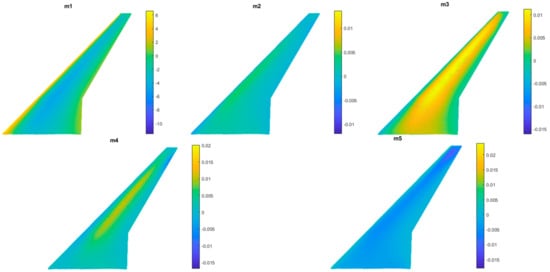
Figure 26.
Pressure ROM Modes.
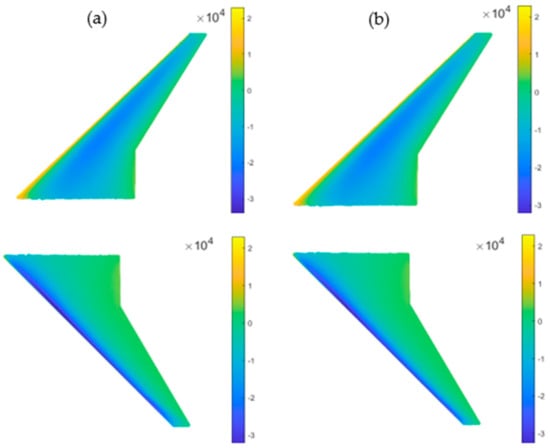
Figure 27.
Comparison of pressure: CFD (a) vs. ROM (b) for the DP with max error in the test set.
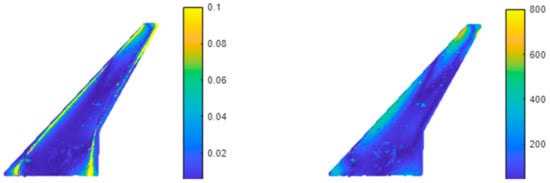
Figure 28.
Percentual error (left) and absolute error [Pa] (right) for the DP in the test set with maximum error.
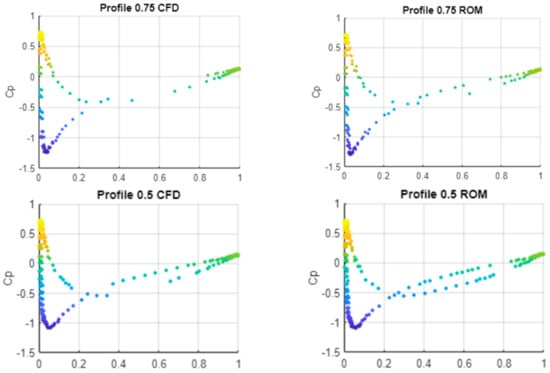
Figure 29.
CP profile on the chord at 0.75 and 0.5; comparison between CFD and ROM for the DP in the test set with maximum error.
6.6. Optimization Results
The collected data are managed by a MATLAB script that enables optimization at various levels. Scalar values can be used to guide optimization and identify a global optimum using response surfaces. Real-time parameter exploration allows observation of their influence on aircraft aerodynamics. This approach facilitates a more robust and informed optimization process because it provides a clear understanding of the physics involved and the contribution of each parameter. For example, it allows for discarding DPs that, despite improving efficiency, lead to greater flow instability.
Using this approach, an optimal point (see Table 6) was identified that significantly improves performance (see Table 7). In particular, it can be observed that the flow is better guided, and there is less separation at the trailing edge. By examining the pressure contour, the efficiency also improves due to the dual effect of increased pressure on the lower surface (enhancing efficiency) and on the upper surface due to reduced separation (lowering drag). Figure 30 shows a comparison between the baseline and optimized geometries. A comparison between the CFD results and predictions from the ROM is given in Figure 31, where pressure contours are compared; Figure 32, where velocity pathlines are compared; and in Figure 33, where original and optimized configurations are compared.

Table 6.
Range and optimized value for each parameter.

Table 7.
Comparison of baseline and optimized shape.
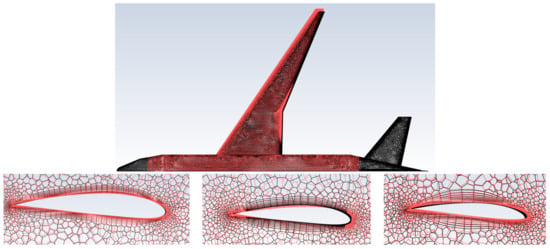
Figure 30.
Comparison of baseline (black) and optimized (red) mesh.
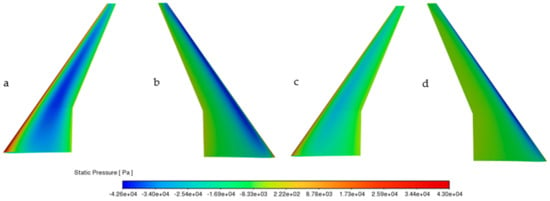
Figure 31.
Comparison of pressure contours: baseline-upper (a), baseline-lower (b), optimized-upper (c) and optimized lower surface (d).
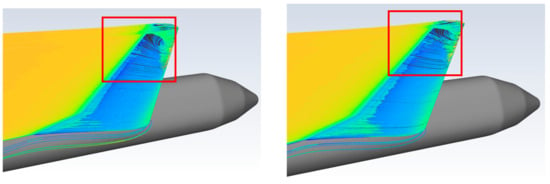
Figure 32.
Comparison of velocity pathlines: baseline (left) and optimized (right).
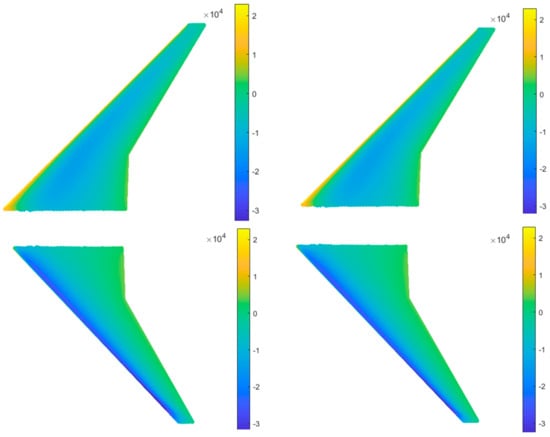
Figure 33.
Comparison of CFD (left) and ROM (right) on the front and rear ends of the wing for the optimized point.
6.7. VR Dashboard
The generated Reduced Order Models have been loaded into the interactive virtual reality dashboard. The Meta Quest 3 headset has been used to explore in real time how the CAD-based parameters affect the aerodynamics of the aircraft in a fully immersive environment.
As described in the previous sections, the data need to be prepared for import into the viewer. The modes for the geometry and for the pressure are loaded into the GPU memory at initialization (see Figure 10). The FMUs are loaded into the CPU and allow for the updated weights of the modes (both geometry and results) to be obtained in almost real-time. The achieved visualization performance was stable at 60 frames per second, resulting in a very good immersive experience. The parameter menu is activated by making the left-hand palm face towards the camera.
The users can interact with the model in two ways: using sliders (Figure 34) or with a smaller model of the aircraft (Figure 35). The sliders can be interacted with by using the index finger (Figure 34). Simply “grabbing” a slider with the index and thumb and dragging it updates the parameter value, which in turn updates the geometry and the pressure field.
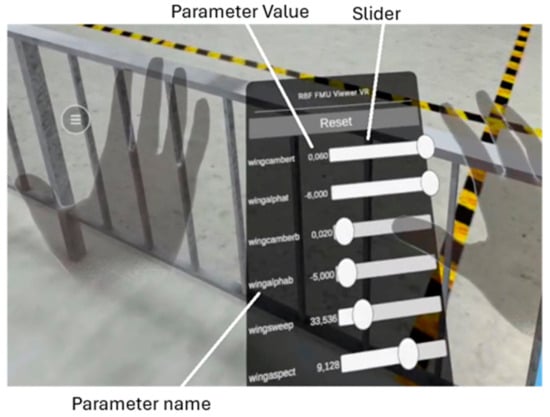
Figure 34.
Slider interface.
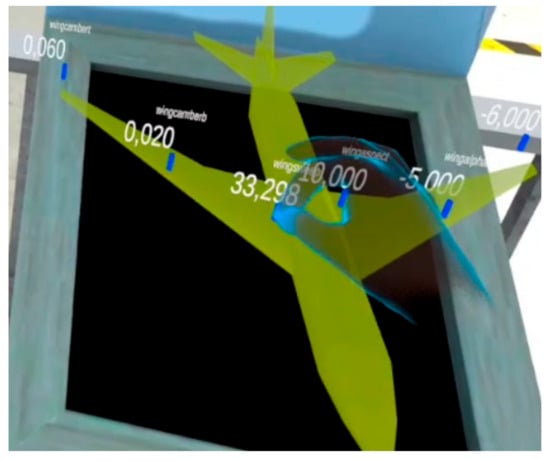
Figure 35.
Three-dimensional interactive handles used to modify in real-time the values of the parameters.
It is also possible to interact with a smaller model, with handles positioned at the points where the parameters act, or with the sliders (Figure 35). The handles have a fixed range of movement and can be manipulated by dragging them using the index finger and thumb. Moving the handles within the predefined range updates both the smaller model and the larger model with the pressure field. The VR App has been developed formatting numbers according to the European decimal separator, i.e., a comma instead of a point.
The real-time results are displayed on the full model. An aircraft hangar setting (Figure 36) was used to make the experience even more realistic and immersive.


Figure 36.
Full plane in the hangar with CFD results.
7. Conclusions
In this paper, a workflow has been demonstrated to connect the CAD-based parameterization with the CFD analysis results, creating an advanced design dashboard for real-time and VR applications. Designers can explore the parameter space in mixed reality to identify the optimal design by observing both scalar outputs, such as Cd or Cl, and field quantities, like 3D pressure fields or 2D Cp profiles across various chords.
A specific workflow was developed to transfer the CAD-based parameterization to the mesh level. This approach proved highly effective as it preserves the mesh topology and maintains its quality. The mesh quality is monitored by evaluating the Minimal Orthogonal Quality for each DP. Table 3 shows the Minimal Orthogonal Quality for some points of the DOE (including the most critical ones). It can be observed that it remains within acceptable limits even for very significant shape variations. This method overcomes the main limitations of other conventional approaches. In fact, it allows the mesh and CAD to remain connected at all times, offering a computationally efficient solution to the problem of automatic mesh generation. CAD and mesh are almost perfectly overlapping. This aspect is evaluated by projecting the mesh onto the corresponding CAD surface. As shown in Figure 7 and Figure 18, the distance between the mesh points and the CAD surfaces is always very small.
ROMs were used to create metamodels for real-time interaction, allowing visualization of the field quantities of interest. This method is robust and sufficiently accurate. Specifically, two ROMs are required: one for the mesh and one for the pressure field. The ROM error is always less than 5%, while the maximum pointwise error is 10% for the pressure field. The results were considered sufficiently accurate, but greater precision could be achieved by increasing the number of modes and DPs. Future studies will likely explore these scenarios to further improve the accuracy of the reduced-order models.
Finally, the ROMs were imported into the MetaQuest3 viewer. The result is a platform where the CAD editor is directly linked to the CFD results. Mixed reality adds interactivity, ease of data visualization, immersion, and the ability to share information and insights. Figure 34, Figure 35 and Figure 36 show previews of the real-time dashboard: the user can interact with the geometric model through sliders or by moving knobs on the airplane model, and the geometry and aerodynamics are updated in real time.
Future developments will involve exploring larger datasets and evaluating a greater number of parameters for more complex geometries and meshes. Additionally, ROMs can be used to evaluate other field quantities, such as velocity, to visualize other entities like streamlines in mixed reality.
Author Contributions
Conceptualization, A.L. and M.E.B.; methodology, A.L. and M.E.B.; software, A.L.; validation, A.L.; formal analysis, A.L.; investigation, A.L. and M.E.B.; resources, A.L.; data curation, A.L.; writing—original draft preparation, A.L.; writing—review and editing, M.E.B.; supervision, M.E.B.; project administration, M.E.B. All authors have read and agreed to the published version of the manuscript.
Funding
The study was partially supported by the Project “Digital Twin for Advanced Design in the Aerospace Industry” (“DigiPaD”) awarded with a cascade call of the Project ECS 0000024 Rome Technopole,—CUP E49J24002850003, NRP Mission 4 Component 2 Investment 1.5, Funded by the European Union—NextGenerationEU.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The authors gratefully acknowledge the support provided by the DigiPAD project, led by RBF Morph. The RBF Morph team has been instrumental in enabling this study, with special thanks to Marco Camponeschi for his valuable contributions to the VR implementation, and Giorgio Urso for his expertise in CAD automated mesh morphing.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Below is the complete DOE with the corresponding values for each input and output parameter:
| #DP | aspectr | sweep | alphab | camberb | alphat | cambert | Lift [N] | Drag [N] | Lift/Drag |
| 1 | 9.700 | 33.021 | −2.302 | 0.045 | −6.337 | 0.050 | 6.383 | 1.792 | 3.562 |
| 2 | 9.941 | 33.428 | −3.810 | 0.020 | −6.580 | 0.040 | 7.015 | 1.739 | 4.033 |
| 3 | 8.136 | 35.129 | −1.572 | 0.021 | −7.861 | 0.045 | 6.731 | 1.635 | 4.117 |
| 4 | 8.949 | 35.638 | −1.836 | 0.030 | −6.507 | 0.051 | 6.543 | 1.653 | 3.959 |
| 5 | 9.013 | 34.722 | −4.870 | 0.025 | −8.735 | 0.042 | 7.052 | 1.907 | 3.698 |
| 6 | 8.685 | 33.522 | −1.562 | 0.049 | −8.776 | 0.034 | 6.358 | 1.754 | 3.624 |
| 7 | 8.078 | 36.778 | −2.319 | 0.051 | −6.089 | 0.032 | 6.383 | 1.682 | 3.795 |
| 8 | 8.284 | 33.172 | −2.963 | 0.053 | −8.622 | 0.044 | 6.435 | 1.832 | 3.513 |
| 9 | 9.971 | 34.480 | −1.994 | 0.057 | −9.389 | 0.031 | 6.197 | 1.840 | 3.368 |
| 10 | 8.191 | 35.461 | −3.364 | 0.044 | −7.060 | 0.022 | 6.659 | 1.677 | 3.970 |
| 11 | 8.485 | 35.536 | −3.817 | 0.023 | −7.711 | 0.024 | 7.029 | 1.707 | 4.117 |
| 12 | 8.123 | 36.126 | −4.892 | 0.033 | −9.217 | 0.026 | 6.952 | 1.866 | 3.726 |
| 13 | 8.988 | 35.387 | −2.247 | 0.054 | −9.113 | 0.025 | 6.362 | 1.775 | 3.585 |
| 14 | 9.346 | 34.625 | −1.026 | 0.033 | −9.370 | 0.021 | 6.540 | 1.686 | 3.880 |
| 15 | 8.905 | 35.924 | −1.303 | 0.043 | −7.117 | 0.057 | 6.262 | 1.725 | 3.630 |
| 16 | 9.765 | 35.087 | −3.306 | 0.041 | −8.467 | 0.023 | 6.651 | 1.750 | 3.801 |
| 17 | 9.502 | 33.747 | −2.705 | 0.026 | −8.856 | 0.024 | 6.877 | 1.710 | 4.021 |
| 18 | 9.571 | 34.327 | −2.814 | 0.052 | −7.243 | 0.056 | 6.274 | 1.829 | 3.430 |
| 19 | 9.824 | 33.568 | −2.104 | 0.038 | −7.410 | 0.046 | 6.461 | 1.720 | 3.756 |
| 20 | 8.793 | 33.789 | −3.676 | 0.059 | −7.522 | 0.034 | 6.383 | 1.873 | 3.409 |
| 21 | 9.327 | 36.202 | −4.361 | 0.039 | −7.928 | 0.048 | 6.690 | 1.856 | 3.605 |
| 22 | 8.433 | 34.508 | −4.529 | 0.037 | −6.255 | 0.043 | 6.793 | 1.770 | 3.837 |
| 23 | 9.661 | 34.085 | −4.395 | 0.056 | −6.927 | 0.026 | 6.455 | 1.900 | 3.398 |
| 24 | 8.642 | 34.894 | −4.038 | 0.045 | −9.467 | 0.029 | 6.685 | 1.852 | 3.610 |
| 25 | 9.603 | 35.340 | −1.101 | 0.046 | −7.174 | 0.041 | 6.194 | 1.731 | 3.579 |
| 26 | 8.364 | 36.374 | −3.705 | 0.047 | −9.877 | 0.033 | 6.598 | 1.844 | 3.578 |
| 27 | 9.907 | 35.717 | −4.772 | 0.048 | −7.639 | 0.035 | 6.573 | 1.935 | 3.397 |
| 28 | 9.653 | 36.106 | −3.208 | 0.048 | −8.266 | 0.045 | 6.418 | 1.817 | 3.532 |
| 29 | 8.729 | 35.309 | −1.720 | 0.034 | −9.528 | 0.044 | 6.567 | 1.718 | 3.822 |
| 30 | 8.246 | 33.836 | −3.112 | 0.028 | −9.301 | 0.059 | 6.795 | 1.788 | 3.800 |
| 31 | 8.444 | 36.624 | −4.585 | 0.055 | −6.665 | 0.052 | 6.377 | 1.982 | 3.218 |
| 32 | 8.536 | 33.264 | −1.156 | 0.024 | −8.401 | 0.038 | 6.671 | 1.651 | 4.041 |
| 33 | 9.310 | 34.394 | −2.930 | 0.025 | −6.202 | 0.027 | 6.845 | 1.647 | 4.157 |
| 34 | 8.928 | 35.052 | −2.791 | 0.060 | −6.172 | 0.040 | 6.232 | 1.789 | 3.483 |
| 35 | 8.340 | 33.961 | −1.671 | 0.035 | −6.424 | 0.025 | 6.568 | 1.629 | 4.031 |
| 36 | 9.782 | 36.663 | −1.443 | 0.052 | −8.521 | 0.037 | 6.175 | 1.774 | 3.481 |
| 37 | 9.413 | 34.773 | −1.803 | 0.058 | −8.078 | 0.055 | 6.099 | 1.852 | 3.292 |
| 38 | 9.244 | 36.269 | −3.560 | 0.031 | −6.494 | 0.036 | 6.778 | 1.689 | 4.013 |
| 39 | 8.515 | 34.170 | −2.589 | 0.041 | −9.772 | 0.056 | 6.539 | 1.810 | 3.613 |
| 40 | 9.156 | 36.058 | −3.889 | 0.057 | −8.011 | 0.036 | 6.375 | 1.899 | 3.356 |
| 41 | 8.058 | 35.620 | −3.468 | 0.058 | −9.156 | 0.049 | 6.359 | 1.866 | 3.407 |
| 42 | 8.008 | 34.219 | −4.259 | 0.030 | −8.248 | 0.035 | 6.947 | 1.780 | 3.904 |
| 43 | 9.261 | 34.277 | −2.056 | 0.040 | −7.568 | 0.028 | 6.509 | 1.686 | 3.861 |
| 44 | 9.099 | 33.089 | −3.175 | 0.036 | −9.733 | 0.032 | 6.759 | 1.791 | 3.775 |
| 45 | 9.380 | 33.655 | −4.644 | 0.050 | −9.062 | 0.039 | 6.536 | 2.044 | 3.198 |
| 46 | 9.090 | 33.918 | −3.392 | 0.031 | −6.990 | 0.048 | 6.748 | 1.730 | 3.902 |
| 47 | 8.617 | 34.853 | −4.082 | 0.027 | −6.711 | 0.060 | 6.857 | 1.775 | 3.863 |
| 48 | 8.379 | 36.450 | −2.161 | 0.037 | −8.681 | 0.058 | 6.509 | 1.733 | 3.756 |
| 49 | 8.182 | 33.346 | −2.541 | 0.042 | −7.960 | 0.046 | 6.546 | 1.730 | 3.783 |
| 50 | 9.444 | 35.212 | −4.704 | 0.040 | −6.041 | 0.054 | 6.679 | 1.850 | 3.610 |
| 51 | 9.873 | 35.975 | −1.350 | 0.028 | −6.773 | 0.030 | 6.530 | 1.636 | 3.991 |
| 52 | 9.482 | 35.828 | −2.385 | 0.027 | −9.973 | 0.038 | 6.749 | 1.744 | 3.869 |
| 53 | 9.142 | 36.502 | −2.668 | 0.021 | −7.804 | 0.052 | 6.790 | 1.699 | 3.996 |
| 54 | 8.708 | 36.877 | −3.011 | 0.032 | −7.263 | 0.042 | 6.690 | 1.683 | 3.976 |
| 55 | 8.830 | 36.951 | −1.898 | 0.022 | −8.175 | 0.029 | 6.770 | 1.638 | 4.132 |
| 56 | 8.759 | 34.061 | −4.990 | 0.046 | −8.318 | 0.050 | 6.608 | 2.040 | 3.239 |
| 57 | 9.549 | 36.824 | −4.439 | 0.039 | −8.989 | 0.030 | 6.747 | 1.861 | 3.626 |
| 58 | 9.719 | 34.999 | −3.574 | 0.023 | −9.855 | 0.053 | 6.907 | 1.850 | 3.733 |
| 59 | 8.253 | 34.685 | −1.392 | 0.050 | −6.854 | 0.054 | 6.243 | 1.750 | 3.568 |
| 60 | 9.215 | 33.453 | −3.942 | 0.053 | −9.604 | 0.055 | 6.400 | 2.038 | 3.140 |
| 61 | 9.877 | 36.418 | −4.197 | 0.029 | −8.916 | 0.058 | 6.807 | 1.883 | 3.614 |
| 62 | 8.580 | 35.800 | −2.439 | 0.055 | −7.326 | 0.020 | 6.382 | 1.719 | 3.713 |
| 63 | 9.043 | 36.727 | −1.248 | 0.044 | −9.660 | 0.047 | 6.310 | 1.763 | 3.579 |
| 64 | 8.857 | 33.207 | −4.163 | 0.034 | −7.466 | 0.022 | 6.913 | 1.741 | 3.971 |
| 65 | 8.000 | 33.000 | −5.000 | 0.020 | −10.000 | 0.020 | 7.280 | 1.925 | 3.781 |
| 66 | 10.000 | 37.000 | −1.000 | 0.060 | −6.000 | 0.060 | 5.834 | 1.848 | 3.158 |
References
- Prusak, I.; Torlo, D.; Nonino, M.; Rozza, G. An optimisation based domain decomposition reduced order model for parameter dependent non stationary fluid dynamics problems. Comput. Math. Appl. 2024, 166, 253–268. [Google Scholar] [CrossRef]
- Geronzi, L.; Martinez, A.; Rochette, M.; Yan, K.; Bel-Brunon, A.; Haigron, P.; Escrig, P.; Tomasi, J.; Daniel, M.; Lalande, A.; et al. Computer-aided shape features extraction and regression models for predicting the ascending aortic aneurysm growth rate. Comput. Biol. Med. 2023, 162, 107052. [Google Scholar] [CrossRef]
- Kwon, T.W.; Kim, H.G.; Lee, J.S.; Jeong, C.H.; Choi, Y.C.; Ha, M.Y. AI-Enhanced design of excavator engine room cooling system using computational fluid dynamics and artificial neural networks. Case Stud. Therm. Eng. 2024, 54, 103959. [Google Scholar] [CrossRef]
- Miao, X.; Wang, Z.; Ren, S.; Zhang, L.; Li, H.; Dong, L.; Chen, D.; Hu, C. Intelligent mesh refinement based on U-NET for high-fidelity CFD simulation in numerical reactor. Nucl. Eng. Des. 2023, 411, 112411. [Google Scholar] [CrossRef]
- Mumuni, A.; Mumuni, F. Automated data processing and feature engineering for deep learning and big data applications: A survey. J. Inf. Intell. 2024, in press. [Google Scholar] [CrossRef]
- Jamshed, S. Using HPC for Computational Fluid Dynamics, Shamoon Jamshed; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar] [CrossRef]
- Neau, H.; Ansart, R.; Baudry, C.; Fournier, Y.; Mérigoux, N.; Koren, C.; Laviéville, J.; Renon, N.; Simonin, O. HPC challenges and opportunities of industrial-scale reactive fluidized bed simulation using meshes of several billion cells on the route of Exascale. Powder Technol. 2024, 444, 120018. [Google Scholar] [CrossRef]
- Shang, Z. Impact of mesh partitioning methods in CFD for large scale parallel computing. Comput. Fluids 2014, 103, 1–5. [Google Scholar] [CrossRef]
- Koch, M.; Arlandini, C.; Antonopoulos, G.; Baretta, A.; Beaujean, P.; Bex, G.J.; Biancolini, M.E.; Celi, S.; Costa, E.; Drescher, L.; et al. HPC in the medical field: Overview and current examples. Technol. Health Care 2023, 31, 1509–1523. [Google Scholar] [CrossRef] [PubMed]
- Di Pierro, B.; Hank, S. CPU and GPU parallel efficiency of ARM based single board computing cluster for CFD applications. Comput. Fluids 2024, 272, 106187. [Google Scholar] [CrossRef]
- Ghioldi, F.; Piscaglia, F. Acceleration of supersonic/hypersonic reactive CFD simulations via heterogeneous CPU-GPU supercomputing. Comput. Fluids 2023, 266, 106041. [Google Scholar] [CrossRef]
- Voß, A.; Klimmek, T. Parametric aeroelastic modeling, maneuver loads analysis using CFD methods and structural design of a fighter aircraft. Aerosp. Sci. Technol. 2023, 136, 108231. [Google Scholar] [CrossRef]
- Zhang, L.; Chang, X.; Ma, R.; Zhao, Z.; Wang, N. A CFD-based numerical virtual flight simulator and its application in control law design of a maneuverable missile model. Chin. J. Aeronaut. 2019, 32, 2577–2591. [Google Scholar] [CrossRef]
- Viviani, A.; Aprovitola, A.; Pezzella, G.; Rainone, C. CFD design capabilities for next generation high-speed aircraft. Acta Astronaut. 2021, 178, 143–158. [Google Scholar] [CrossRef]
- Rozov, V.; Stuhlpfarrer, M.; Fernández Osma, M.; Breitsamter, C. Engine Modeling for Small-Disturbance-CFD Related to Aircraft Flutter Investigations. J. Fluids Struct. 2020, 96, 103045. [Google Scholar] [CrossRef]
- Nielsen, E.J.; Diskin, B. High-performance aerodynamic computations for aerospace applications. Parallel Comput. 2017, 64, 20–32. [Google Scholar] [CrossRef]
- Chawner, J.R.; Taylor, N.J. Progress in Geometry Modeling and Mesh Generation Toward the CFD Vision 2030. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Hanke, J. Geometry Preparation and Mesh Generation Using Simcenter STAR-CCM+ for 4th AIAA CFD High Lift Prediction Workshop. In Proceedings of the AIAA 2022, Chicago, IL, USA, 27 June–1 July 2022. [Google Scholar] [CrossRef]
- Chawner, J.R.; Michal, T.R.; Slotnick, J.P.; Rumsey, C.L. Summary of the 1st AIAA Geometry and Mesh Generation Workshop (GMGW-1) and Future Plans. In Proceedings of the AIAA 2018, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar] [CrossRef]
- Gandhi, V.; Joe, J.; Dannenhoffer, J.F.; Dalir, H. Rapid design generation and multifidelity analysis of aircraft structures. Aerosp. Sci. Technol. 2021, 112, 106612. [Google Scholar] [CrossRef]
- Biancolini, M.E.; Viola, I.M.; Riotte, M. Sails trim optimisation using CFD and RBF mesh morphing. Comput. Fluids 2014, 93, 46–60. [Google Scholar] [CrossRef]
- Gagliardi, F.; Giannakoglou, K.C. A two–step radial basis function-based CFD mesh displacement tool. Adv. Eng. Softw. 2019, 128, 86–97. [Google Scholar] [CrossRef]
- Immonen, E. A parametric morphing method for generating structured meshes for marine free surface flow applications with plane symmetry. J. Comput. Des. Eng. 2019, 6, 348–353. [Google Scholar] [CrossRef]
- Eguea, J.P.; Bravo-Mosquera, P.D.; Catalano, F.M. Camber morphing winglet influence on aircraft drag breakdown and tip vortex structure. Aerosp. Sci. Technol. 2021, 119, 107148. [Google Scholar] [CrossRef]
- Zilong, L.; Ping, H. Accelerating unsteady aerodynamic simulations using predictive reduced-order modeling. Aerosp. Sci. Technol. 2023, 139, 108412. [Google Scholar] [CrossRef]
- Vergari, L.; Cammi, A.; Lorenzi, S. Reduced order modeling approach for parametrized thermal-hydraulics problems: Inclusion of the energy equation in the POD-FV-ROM method. Prog. Nucl. Energy 2020, 118, 103071. [Google Scholar] [CrossRef]
- Negri, E.; Fumagalli, L.; Cimino, C.; Macchi, M. FMU-supported simulation for CPS Digital Twin. Procedia Manuf. 2019, 28, 201–206. [Google Scholar] [CrossRef]
- Glujic, D.; Vukelic, G.; Bernecic, D.; Vizentin, G.; Ogrizovic, D. Coupling CFD and VR for advanced firefighting training in a virtual ship engine room. Results Eng. 2024, 24, 103025. [Google Scholar] [CrossRef]
- Capetillo, A.; Ibarra, F. Multiphase injector modelling for automotive SCR systems: A full factorial design of experiment and optimization. Comput. Math. Appl. 2017, 74, 188–200. [Google Scholar] [CrossRef]
- Wang, J.; Khan, S.A.; Yasmin, S.; Alam, M.M.; Liu, H.; Farooq, U.; Akgül, A.; Hassan, A.M. Central composite design (CCD)-Response surface methodology (RSM) for modeling and simulation of MWCNT-water nanofluid inside hexagonal cavity: Application to electronic cooling. Case Stud. Therm. Eng. 2023, 50, 103488. [Google Scholar] [CrossRef]
- Akbar, N.S.; Zamir, T.; Akram, J.; Noor, T.; Muhammad, T. Simulation of hybrid boiling nano fluid flow with convective boundary conditions through a porous stretching sheet through Levenberg Marquardt artificial neural networks approach. Int. J. Heat Mass Transf. 2024, 228, 125615. [Google Scholar] [CrossRef]
- Song, W.; Andy, J.K. Surrogate-Based Aerodynamic Shape Optimization of a Civil Aircraft Engine Nacelle. AIAA J. 2007, 45, 2565–2574. [Google Scholar] [CrossRef]
- Li, T.Z.; Yang, X.L. An efficient uniform design for Kriging-based response surface method and its application. Comput. Geotech. 2019, 109, 12–22. [Google Scholar] [CrossRef]
- Xuan-Binh Lam, D. Multidisciplinary design optimization for aircraft wing using response surface method, genetic algorithm, and simulated annealing. J. Sci. Technol. Civ. Eng. 2019, 14, 28–41. [Google Scholar] [CrossRef]
- Coppedè, A.; Gaggero, S.; Vernengo, G.; Villa, D. Hydrodynamic shape optimization by high fidelity CFD solver and Gaussian process based response surface method. Appl. Ocean Res. 2019, 90, 101841. [Google Scholar] [CrossRef]
- Ge, Y.; He, Q.; Lin, Y.; Yuan, W.; Chen, J.; Huang, S.-M. Multi-objective optimization of a mini-channel heat sink with non-uniform fins using genetic algorithm in coupling with CFD models. Appl. Therm. Eng. 2022, 207, 11812. [Google Scholar] [CrossRef]
- Bisighini, B.; Aguirre, M.; Biancolini, M.E.; Trovalusci, F.; Perrin, D.; Avril, S.; Pierrat, B. Machine learning and reduced order modelling for the simulation of braided stent deployment. Front. Physiol. 2023, 14, 1148540. [Google Scholar] [CrossRef]
- Fresca, S.; Manzoni, A. POD-DL-ROM: Enhancing deep learning-based reduced order models for nonlinear parametrized PDEs by proper orthogonal decomposition. Comput. Methods Appl. Mech. Eng. 2022, 338, 114181. [Google Scholar] [CrossRef]
- Lorenzi, S.; Cammi, A.; Luzzi, L.; Rozza, G. POD-Galerkin method for finite volume approximation of Navier–Stokes and RANS equations. Comput. Methods Appl. Mech. Eng. 2016, 311, 151–179. [Google Scholar] [CrossRef]
- Santolamazza, A.; Groth, C.; Introna, V.; Porziani, S.; Scarpitta, F.; Urso, G.; Valentini, P.P.; Costa, E.; Ferrante, E.; Sorrentino, S.; et al. A Digital Shadow cloud-based application to enhance quality control in manufacturing. IFAC-PapersOnLine 2020, 53, 10579–10584. [Google Scholar] [CrossRef]
- Yan, Z.; Gong, J.; Louste, C.; Wu, J.; Fang, J. Modal analysis of EHD jets through the SVD-based POD technique. J. Electrost. 2023, 126, 103858. [Google Scholar] [CrossRef]
- Mifsud, M.; Vendl, A.; Hansen, L.-U.; Görtz, S. Fusing wind-tunnel measurements and CFD data using constrained gappy proper orthogonal decomposition. Aerosp. Sci. Technol. 2019, 86, 312–326. [Google Scholar] [CrossRef]
- Casella, F.; Leva, A. Modelling and Simulation of Thermal Power Generation Systems with Modelica: 20 Years of Experience with the ThermoPower Library. IFAC-PapersOnLine 2024, 58, 227–234. [Google Scholar] [CrossRef]
- Masoom, A.; Guironnet, A.; Zeghaida, A.A.; Ould-Bachir, T.; Mahseredjian, J. Modelica-based simulation of electromagnetic transients using Dynaωo: Current status and perspectives. Electr. Power Syst. Res. 2021, 197, 107340. [Google Scholar] [CrossRef]
- D’Amelio, E.L.; Bascetta, L.; Cucci, D.A.; Matteucci, M.; Bardaro, G. A Modelica simulator to support the development of the control system of an autonomous All-Terrain mobile robot. IFAC-PapersOnLine 2015, 48, 274–279. [Google Scholar] [CrossRef]
- Hinkelman, K.; Wang, J.; Zuo, W.; Gautier, A.; Wetter, M.; Fan, C.; Long, N. Modelica-based modeling and simulation of district cooling systems: A case study. Appl. Energy 2022, 311, 118654. [Google Scholar] [CrossRef]
- Woeber, C.; Masters, J.S.; McDaniel, D.R. Summary of Exascale and Remeshing Efforts for the Second Geometry and Mesh Generation Workshop. In Proceedings of the AIAA 2019, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Dannenhoffer, J.F. Analysis of GMGW2 Case 3: Design Variations. In Proceedings of the AIAA 2019, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Haimes, R.; Drela, M. On The Construction of Aircraft Conceptual Designs. In Proceedings of the AIAA 2012, Garden Grove, CA, USA, 19–21 June 2012. [Google Scholar] [CrossRef]
- Cella, U.; Biancolini, M.E. RBF Morph. 2019. Available online: https://www.rbf-morph.com/wp-content/uploads/2019/02/GMGW2-Case3-Wade.pdf (accessed on 1 November 2024).
- Karman, S.; Wyman, N. Automatic Unstructured Mesh Generation with Geometry Attribution. In Proceedings of the AIAA 2019, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Chan, W.M.; Pandyay, S.A.; Haimes, R. Automation of Overset Structured Surface Mesh Generation on Complex Geometries. In Proceedings of the AIAA 2019, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Magri, G.; Lopez, A.; Della Barba, F. Ottimizzazione Aerodinamica di un Velivolo Mediante CAD Parametrico e Mesh Morphing. Master’s Thesis, Univeristy of Padova, Padua, Italy, 2023. [Google Scholar]
- Gagliardi, F.; Giannakoglou, K.C. RBF-based morphing of B-Rep models for use in aerodynamic shape optimization. Adv. Eng. Softw. 2019, 138, 102724. [Google Scholar] [CrossRef]
- Cadquery Documentation. Available online: https://cadquery.readthedocs.io/en/latest/ (accessed on 26 December 2024).
- Viisainen, J.V.; Yu, F.; Codolini, A.; Chen, S.; Harper, L.T.; Sutcliffe, M.P.F. Rapidly predicting the effect of tool geometry on the wrinkling of biaxial NCFs during composites manufacturing using a deep learning surrogate model. Compos. Part B Eng. 2023, 253, 110536. [Google Scholar] [CrossRef]
- Automatic modeling of aircraft external geometries for preliminary design workflows. Aerosp. Sci. Technol. 2020, 98, 105667. [CrossRef]
- Guo, S.; Duan, F.; Tang, H.; Lim, S.C.; Yip, M.S. Multi-objective optimization for centrifugal compressor of mini turbojet engine. Aerosp. Sci. Technol. 2014, 39, 414–425. [Google Scholar] [CrossRef]
- Goldbach, A.-K.; Lázaro, C. CAD-integrated parametric design and analysis of lightweight shell structures. Structures 2024, 64, 106566. [Google Scholar] [CrossRef]
- Available online: https://dev.opencascade.org/doc/overview/html/ (accessed on 26 December 2024).
- Available online: https://www.opencascade.com/products/cad-builder/ (accessed on 26 December 2024).
- Sieger, D.; Menzel, S.; Botsch, M. On Shape Deformation Techniques for Simulation-Based Design Optimization. In New Challenges in Grid Generation and Adaptivity for Scientific Computing; SEMA SIMAI Springer Series; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Iordanis, I.; Koukouvinos, C.; Silou, I. On the efficacy of conditioned and progressive Latin hypercube sampling in supervised machine learning. Appl. Numer. Math. 2024, 208, 256–270. [Google Scholar] [CrossRef]
- Guilbaud, T.; Fiorina, C.; Lorenzi, S.; Scolaro, A.; Carminati, F.; Maire, D.; Pautz, A. Investigating the Functional Mock-up Interface as a Coupling Framework for the multi-fidelity analysis of nuclear reactors. Prog. Nucl. Energy 2024, 169, 105022. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).