Abstract
Accurate liver segmentation from computed tomography (CT) scans is essential for liver cancer diagnosis and liver surgery planning. Convolutional neural network (CNN)-based models have limited segmentation performance due to their localized receptive fields. Hybrid models incorporating CNNs and transformers that can capture long-range dependencies have shown promising performance in liver segmentation with the cost of high model complexity. Therefore, a new network architecture named G-UNETR++ is proposed to improve accuracy in liver segmentation with moderate model complexity. Two gradient-based encoders that take the second-order partial derivatives (the first two elements from the last column of the Hessian matrix of a CT scan) as inputs are proposed to learn the 3D geometric features such as the boundaries between different organs and tissues. In addition, a hybrid loss function that combines dice loss, cross-entropy loss, and Hausdorff distance loss is designed to address class imbalance and improve segmentation performance in challenging cases. The proposed method was evaluated on three public datasets, the Liver Tumor Segmentation (LiTS) dataset, the 3D Image Reconstruction for Comparison of Algorithms Database (3D-IRCADb), and the Segmentation of the Liver Competition 2007 (Sliver07) dataset, and achieved 97.38%, 97.50%, and 97.32% in terms of the dice similarity coefficient for liver segmentation on the three datasets, respectively. The proposed method outperformed the other state-of-the-art models on the three datasets, which demonstrated the strong effectiveness, robustness, and generalizability of the proposed method in liver segmentation.
1. Introduction
Liver segmentation is essential for liver cancer diagnosis and liver surgery planning. Liver cancer is one of the leading causes of cancer-related deaths worldwide [1]. Computed tomography (CT) images are commonly used by physicians for the detection of lesions. Before liver lesion analysis, the fast, accurate, and automatic segmentation of the liver region from CT images is required.
Conventional methods such as region growing [2], level-set [3], and deformable models [4] commonly depend on the manual identification of seed points or regions [5,6] and the interactive setting of parameters [7] and have limited capabilities of feature representation [8]. Deep learning techniques, especially U-Net [9] and its variants, have shown promising performance in liver segmentation [10]. A U-Net-like model generally consists of an encoder for learning global contextual representations and a decoder for decoding the learned representations to a pixel- or voxel-wise segmentation [11,12]. Convolutional neural network (CNN)-based U-Net models have limited performance in segmentation due to their localized receptive fields [13].
Graph convolutional networks (GCNs) that combine CNN and graph theory have been developed and showed promising results for various applications, such as classification [14,15] and segmentation [16]. For the first time, Khoshkhabar et al. [16] proposed a network comprising four Chebyshev graph convolution layers and a fully connected layer for the segmentation of the liver and liver tumors. Though their model showed high accuracy (99.1%) in liver segmentation, the dice score (91.1%) they reported still needs to be improved.
Transformer-based U-Net models have shown exceptional performance because of their capabilities of learning long-range dependencies [11]. Various hybrid models that incorporate CNN and a transformer have been proposed. Some of the models [12,17] utilize a transformer-based encoder and a CNN-based decoder, while others [18,19] apply the hybrid design for both the encoder and decoder. Zhou et al.’s study [19] achieved the highest accuracy in liver segmentation with the cost of high model complexity in terms of number of parameters and floating point operations per second (FLOPs). Lastly, Shaker et al. [20] proposed a novel efficient paired attention (EPA) block in their hybrid hierarchical model named UNETR++ by applying both spatial and channel attention to reduce model complexity, but slightly sacrificed accuracy in liver segmentation. Table 1 summarizes the accuracy (dice score: DSC) of liver segmentation and complexity of these transformer-based hybrid models over the public Synapse dataset [21].

Table 1.
Accuracy and complexity of transformer-based U-Net models.
To address the aforementioned issues, we propose a gradient-enhanced hybrid hierarchical model, named G-UNETR++, that strives to achieve better accuracy with a moderate model complexity similar to TransUNet [17] or UNETR [12]. Based on UNETR++, we add another two gradient-based encoders that take the second-order partial derivatives (the first two elements from the last column of the Hessian matrix of a CT scan) as the input to learn the 3D geometric features such as the boundaries between different organs and tissues. We carefully design the gradient-based encoders to maintain a moderate model complexity while improving liver segmentation accuracy. Furthermore, we design a hybrid loss function that incorporates dice loss, cross-entropy (CE) loss, and Hausdorff distance (HD) loss to address class imbalance and improve the segmentation of challenging cases to further improve liver segmentation accuracy. The contributions of this study can be summarized as follows:
- We introduce a new network architecture named G-UNETR++ to improve accuracy in liver segmentation with moderate model complexity.
- We propose gradient-based encoders to learn the 3D geometric features such as the boundaries between different organs and tissues.
- We design a novel hybrid loss function that combines dice loss, CE loss, and HD loss to address class imbalance and improve segmentation in challenging cases.
2. Related Work
This section provides a comprehensive review of existing studies categorized into three groups including CNN-based, transformer-based, and hybrid architectures for medical image segmentation. The strengths and weaknesses of these studies are introduced.
2.1. CNN-Based Segmentation Networks
U-Net, originally designed based on CNN for 2D biomedical image segmentation, has become a fundamental network for medical image segmentation and been extended for 3D medical image segmentation [22,23,24,25,26]. Çiçek et al. [22] extended the U-Net architecture by replacing all 2D operations with 3D ones for volumetric segmentation. Inspired by U-Net, Milletari et al. [25] proposed a network based on volumetric convolutions for 3D image segmentation. Roth et al. [26] proposed a multi-class 3D fully convolutional network (FCN) for multi-organ segmentation from CT scans. They proposed a two-stage, coarse-to-fine approach that improved segmentation accuracy by 7.5% per organ in terms of dice score. However, CNN-based models suffer from localized receptive fields, limiting their ability to capture long-range spatial dependencies [7]. This shortcoming hinders their effectiveness in learning the global context for the complex medical image analysis tasks.
2.2. Transformer-Based Segmentation Networks
Since the introduction of Vision Transformer (ViT) [27], models that apply the self-attention mechanism in transformers, especially pure transformer-based networks [28,29] without convolutions, have been proposed for medical image segmentation. These models showed promising results thanks to their ability to encode long-range dependencies to learn global relationships among the sequence of image patches by self-attention operation [20]. Cao et al. [28] proposed a U-Net-like pure transformer that applies a hierarchical ViT with shifted windows as the encoder and decoder with skip connections for multi-organ and cardiac segmentation tasks. They reported that their model showed excellent performance and generalization ability. However, their model can only process 2D medical images, not 3D ones. Karimi et al. [29] proposed a convolution-free network using transformers for 3D medical image segmentation. Their method first splits a given 3D image block into 3 × 3 × 3 or 5 × 5 × 5 3D patches, computes a 1D embedding for each patch, and then predicts the segmentation map for the center patch using self-attention between the patch embeddings. They reported that their model showed better performance than the state-of-the-art CNN models over three datasets. However, pure transformer-based models suffer from capturing local features and are data-hungry [30].
2.3. Hybrid Segmentation Networks
Hybrid architectures that combine convolution and self-attention operations have recently shown better performance than pure CNN- or transformer-based architectures in medical image segmentation. Chen et al. [17] introduced TransUNet, which combines transformers and CNN in their U-Net-like architecture for 2D medical image segmentation. Their model consists of a CNN-Transformer hybrid model as the encoder where CNN is first used for generating a feature map from the input image, then the transformer encodes tokenized image patches from the feature map to extract global contexts, and finally a CNN-based decoder that upsamples the encoded features combined with the high-resolution CNN feature maps to enable precise localization. Valanarasu et al. [31] introduced MedT, which consists of a transformer-based encoder and a CNN-based decoder. To overcome the requirement of large-scale datasets by transformer-based models for proper training, they proposed a gated axial-attention model by introducing an additional control mechanism in the self-attention module to train their model properly, even with small-scale datasets in medical imaging applications. Xie et al. [32] proposed a hybrid architecture that consists of a CNN-based encoder to extract feature representations, an efficient deformable transformer-based encoder to model the long-range dependency from the extracted feature maps, and a CNN-based decoder for segmentation. They claimed that their deformable transformer reduces computational and spatial complexities and therefore enables the processing of multi-scale and high-resolution feature maps. Wang et al. [33] proposed a similar architecture to TransUNet but in a 3D version for brain tumor segmentation on 3D MRI images. Zhou et al. [34] introduced MCFA-UNet, a 3D segmentation network based on the U-Net architecture, to solve the problem of edge detail feature loss due to insufficient feature extraction from existing methods. Their model consists of a multi-scale feature cascaded attention module to extract multi-scale feature information, an attention-gate mechanism to fuse different levels of feature information, and the deep supervision learning method to optimize segmentation in the decoding process. Hatamizadeh et al. [12] introduced UNETR, a U-Net-like architecture consisting of a stack of transformers as the encoder to extract feature representations of different layers in the transformer and then merged this with a CNN-based decoder through skip connections to predict the final segmentation. Zhou et al. [19] introduced nnFormer, a 3D U-Net-like architecture that exploits the combination of interleaved convolution and self-attention operations and introduces a local and global volume-based self-attention mechanism to learn volume representations. In terms of segmentation performance, nnFormer outperformed UNETR, although nnFormer is much more complex than UNETR in terms of the number of parameters and FLOPs. Recently, Shaker et al. [20] introduced UNETR++, a 3D medical segmentation approach that incorporates a novel EPA block that efficiently learns spatial and channel-wise features using a pair of inter-dependent branches based on spatial and channel attention. UNETR++ showed a higher accuracy than UNETR but a slightly lower accuracy than nnFormer in liver segmentation. However, UNETR++ is less complex than both UNETR and nnFormer. Inspired by UNETR++, we introduce G-UNETR++ to further improve accuracy in liver segmentation with a moderate model complexity similar to UNETR.
3. Methods
In this section, we first introduce the entire architecture of the proposed G-UNETR++ model. Then, we describe the technical details of the proposed gradient-enhanced encoders. Lastly, we explain the proposed hybrid loss function.
3.1. Architecture
Figure 1 shows the architecture of the proposed G-UNETR++, consisting of a hierarchical encoder–decoder structure with skip connections between the encoder and decoder, followed by convolutional blocks to generate segmentation results, based on the recently introduced UNETR++ [20]. Instead of a single encoder in UNETR++, we added another two gradient-based encoders in parallel. In our G-UNETR++ architecture, each encoder consists of four stages. In the first stage, patch embedding is performed to divide volumetric input into 3D non-overlapping patches, followed by the EPA block in UNETR++. In the patching embedding step, the volumetric input is divided into 3D patches , where (P1, P2, P3) is the resolution of each patch and denotes the length of the sequence. The 3D patches are then projected into C_1 channel dimensions to obtain a feature map. The same patch resolution (4, 4, 2) as in UNETR++ is used in our G-UNETR++. For each of the remaining three stages, downsampling non-overlapping convolution layers are used to decrease the resolution by a factor of two, followed by the EPA block. In each of the four stages, the outputs of the three EPA blocks from the three parallel encoders are added.
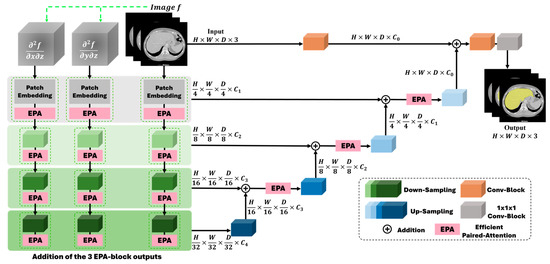
Figure 1.
Architecture of G-UNETR++ consisting of a hierarchical encoder–decoder structure with skip connections between the encoder and decoder, followed by convolutional blocks to generate segmentation results.
The EPA block consists of two attention modules, spatial and channel attention, to learn enriched spatial–channel feature representations from both spatial and channel dimensions. The two attention modules share the keys and queries but use different value layers to generate feature representations more effectively and efficiently. A more detailed description of the EPA block can be found in UNETR++ [20]. Like the encoder, the decoder is structured into four stages as well. Each stage comprises an upsampling layer with deconvolution to increase the resolution of the feature representations by a factor of two, followed by the EPA block. For the last decoding stage, no EPA block is included. For each stage, a skip connection is used to connect the encoder and decoder to merge the feature maps at different resolutions to recover the spatial information lost in the downsampling procedures to obtain more accurate segmentation results. Between the two stages in the decoder, the number of channels is decreased by a factor of two. In the last decoding stage, the output of the previous decoding stage is fused with the convolutional feature representations from the encoder to recover spatial information. Then, the fused outputs are fed to a 3 × 3 × 3 and a 1 × 1 × 1 convolutional block to obtain the voxel-wise segmentation results.
3.2. Gradient-Enhanced Encoder Scheme
Unlike previous studies [8,35,36,37,38,39,40,41], we propose a novel gradient-enhanced encoder scheme to additionally learn geometric features by adding two gradient-based encoders in parallel to the encoder in the UNETR++ framework, as shown in Figure 2. The proposed gradient-based encoders take the second-order partial derivatives and as their inputs, respectively, to learn 3D geometric features such as the boundaries between different organs and tissues especially along the z-axis, where denotes a CT scan image and x, y, and z represent the coordinates of a voxel in the image. The two second-order partial derivatives are the first two elements of the last column of the Hessian matrix of a CT scan. The Hessian matrix of a CT scan is calculated as follows:
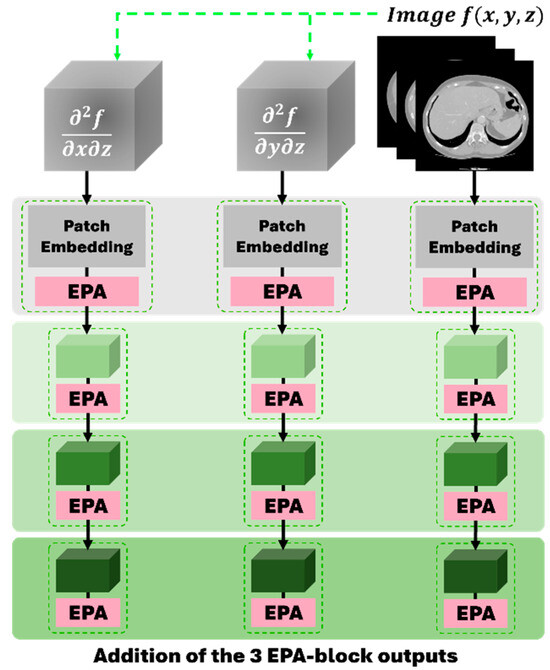
Figure 2.
The proposed gradient-enhanced encoder scheme, consisting of two proposed gradient-based encoders (left and middle) and the encoder in the UNETR++ framework (right).
The two second-order partial derivatives are computed as follows. First, we compute the first-order partial derivatives for each 2D CT slice along the x- and y-axes. Then, we calculate the second-order partial derivatives for each 2D CT slice along the z-axis, as shown in Equations (2) and (3), respectively:
where S represents a CT slice and N and M are the height and width of the slice, respectively. Then, by stacking the second-order partial derivatives of all the CT slices, we obtain and , respectively. Like the encoder in UNETR++, our gradient-based encoders also have a four-stage encoding procedure in order to learn the 3D geometric features.
As shown in Figure 3, the proposed gradient-enhanced encoders take the two second-order partial derivatives that enhance the local curvature and edge information of the anatomical structures in medical images as the input and then learn these features in a hierarchical manner. Across different stages of the encoding process, the gradient-enhanced encoders are able to preserve important structural details. This hierarchical approach ensures that the geometric information crucial for segmentation remains discernible, preserving the fine details necessary for distinguishing the liver from its adjacent structures.
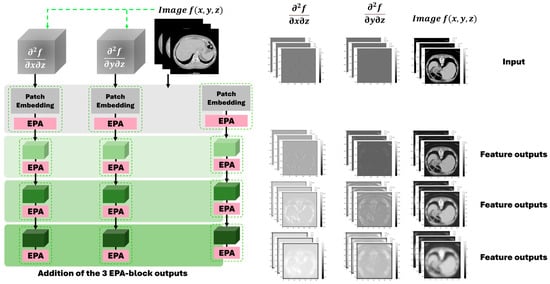
Figure 3.
The proposed gradient-enhanced encoder scheme and the output examples of feature maps from different encoders across different stages of the encoding process following the U-Net structure.
3.3. Loss Function
To address class imbalance and improve the segmentation of challenging cases, we propose a novel hybrid loss function that incorporates CE loss, dice loss, and HD [42] loss.
CE measures the difference between two probability distributions for a given random variable or set of events. It is widely used for object classification and works well for segmentation because segmentation is a voxel-level classification. CE loss is defined as follows:
where represents the ground truth, and denotes the prediction probability when . The dice coefficient is widely used to measure the similarity between two images in computer vision. Dice loss is defined as follows:
where N denotes the number of all predicted voxels, indicates the prediction probability at voxel , and refers to the ground truth at voxel . HD is used to measure the distance between two sets of points and therefore allows the measurement of localization similarity. HD loss is defined as follows:
where denotes the ground truth, and indicates the predicted binary segmentation with a threshold of 0.5. Then, the proposed total loss function in this study is defined as follows:
where , , and are the weights of dice loss, CE loss, and HD loss, respectively. In this study, . We incorporate the deep supervision technique [43,44] into our decoder for better training efficiency. The hybrid loss function is designed to work synergistically with the gradient-enhanced encoder scheme. The gradient-enhanced encoders extract fine-grained boundary details and structural features, aligning well with the objectives of the hybrid loss function. HD loss especially focuses on boundary precision, benefiting from the boundary features learned by the gradient-enhanced encoders. Dice loss ensures global shape consistency, and CE loss improves voxel-level accuracy. By leveraging both global and local features, the hybrid loss function can effectively address the class imbalance problem and improve the segmentation performance of challenging cases.
4. Experiments and Results
4.1. Datasets
Three different public datasets are included in this study: the Liver Tumor Segmentation (LiTS) dataset, the 3D Image Reconstruction for Comparison of Algorithms Database (3D-IRCADb), and the Segmentation of the Liver Competition 2007 (Sliver07) dataset. The LiTS dataset is the most widely used dataset for liver and tumor segmentation, including a training set of 131 CT scans and a test set of 70 CT scans, ranging from 42 to 1026 CT slices in each scan with a resolution of pixels for each CT slice and a slice spacing ranging from 0.45 mm to 6.0 mm. Four radiologists from six clinical centers manually labeled the training set. The labels for the test set are not available. The 3D-IRCADb dataset is a more challenging dataset, including more complex data on the liver and tumors with low contrast and an overlap between the liver and tumor regions for some cases. The 3D-IRCADb-01 dataset consists of CT scans with the ground truth of 10 male and 10 female patients. The 3D-IRCADb-02 dataset consists of two CT scans with the ground truth of the chest and abdomen. The resolution of each CT slice is pixels with a slice thickness from 1 mm to 4 mm. The range of the number of slices for each scan is from 74 to 260 slices with a pixel spacing varied from 0.57 mm to 0.87 mm. The Sliver07 dataset, which is the most challenging dataset, contains 20 CT scans with ground truth. Most of the scans contain diseased livers with cysts and tumors. The resolution of each CT slice is pixels with a slice thickness from 1 mm to 3 mm. The range of the number of slices for each scan is from 64 to 394 slices, with a pixel spacing varied from 0.58 mm to 0.82 mm. We derived 131, 20, and 20 CT scans with ground truth from the LiTS dataset, 3D-IRCADb dataset, and Sliver07 dataset, respectively. Figure 4 shows two example CT images from each of the three datasets, respectively.
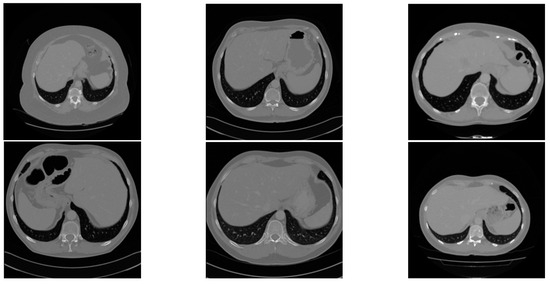
Figure 4.
Two example CT images from the LiTS dataset (left), Sliver07 dataset (middle), and the 3D-IRCADb dataset (right), respectively.
4.2. Data Preprocessing and Augmentation
We randomly split the 131 CT scans from the LiTS dataset into 91 for training, 20 for validation, and 20 CT scans for testing our proposed G-UNETR++. The 20 CT datasets from 3D-IRCADb and the other 20 CT datasets from Sliver07 are used for cross-validation to assess the robustness and generalization of the proposed method. The Hounsfield unit values of all the datasets are adjusted to the range of [−200, 200] to enhance the contrast between the liver and other tissues and remove irrelevant tissues. Figure 5 shows the original CT slice and the preprocessed CT slice. We resize the CT slices from to to reduce computational cost. The same data augmentation operations used in UNETR++, such as rotation, scaling, mirroring, and intensity shifting, are applied in our method.
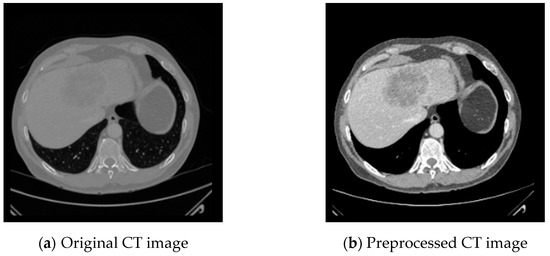
Figure 5.
CT image preprocessing to enhance the contract between the liver and other tissues and remove irrelevant tissues by adjusting the Hounsfield unit values to the range of [−200, 200].
4.3. Post-Processing
To further improve the performance of liver segmentation. We applied the connected components algorithm and the median filter to remove noises. The connected components algorithm labels contiguous regions of the segmented volume and isolates the largest connected component, corresponding to the liver. This process is particularly effective in addressing false positives that often occur near the edges of the liver or in regions with similar intensity values. By identifying and retaining only the largest connected region, the algorithm ensures that the segmentation remains focused on the target organ. Then, the median filter is applied to refine the segmentation by smoothing out high-frequency noises and irregularities. Unlike other smoothing techniques, the median filter preserves the edges of the anatomical structures, ensuring that the boundaries of the liver remain intact while removing noises. The combination of the connected components algorithm and the median filter effectively enhances the segmentation by eliminating irrelevant structures and improving both the reliability and accuracy of the output. Figure 6 shows that noises are removed after post-processing to improve liver segmentation accuracy.
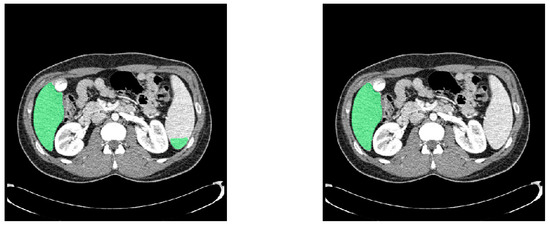
Figure 6.
Comparison of liver segmentation results in green before (left) and after (right) post-processing.
4.4. Experimental Environment and Parameters
The experiments were performed on an Ubuntu 18.04 operating system workstation with a Xeon w3-2435 processor, 128 GB of memory, and two NVIDIA RTX 3090 GPUs (24 GB each). The proposed G-UNETR++ was implemented using PyTorch. Five-fold cross-validation was used for training our model. Adam optimizer [45] was used to optimize the loss function. The initial learning rate was set to . The learning rate decay strategy in this study was the same as used in nnFormer [19]. The model was trained with 1000 epochs with a batch size of 64. L2 regularization with a factor of was applied to avoid overfitting during training.
4.5. Evaluation Metrics
To extensively evaluate the performance of the proposed G-UNETR++, we used various metrics, including the dice similarity coefficient (DSC), volumetric overlap error (VOE), relative absolute volume difference (RAVD), average symmetric surface distance (ASSD), and maximum symmetric surface distance (MSSD).
DSC is commonly used to measure the overlapping similarity between the predicted output (B) and the ground truth (A). The range of DSC is from 0 to 1, with a higher value indicating a more accurate prediction. DSC is defined as follows:
Another metric based on overlap is the Jaccard index that measures the degree of agreement between the predicted output and the ground truth as the ratio of the intersection over the union between the predicted output and the ground truth. VOE is the corresponding error measure of the Jaccard index, defined as follows:
RAVD is the relative coefficient of the non-overlapping parts between the predicted output and the ground truth, ranging from 0 to 1, with a smaller value indicating a more accurate prediction. RAVD is defined as follows:
ASSD measures the average distance between the predicted output and the ground truth, with 0 mm indicating a perfect segmentation. The shortest distance of a voxel to the set of surface voxels of is defined as follows:
where denotes the Euclidean distance between and . ASSD is defined as follows:
MSSD, also known as HD, is computed by the maximum distance between the surface voxels of the predicted output and the ground truth, with 0 mm indicating a perfect segmentation. MSSD is defined as follows:
Other metrics including accuracy, precision, recall, and F1-score were used to further evaluate the proposed model. Their calculation formulas are defined as follows [46]:
where TP, TN, FP, and FN represent the confusion matrix’s true positive, true negative, false positive, and false negative values.
4.6. Segmentation Results of the Proposed Model
The segmentation results of the proposed model over different datasets with various metrics are shown in Table 2. As presented in the table, these metrics demonstrate the high performance of our proposed framework in liver segmentation.

Table 2.
Performance of the proposed G-UNETR++ for liver segmentation.
To further validate our model, we assessed the areas under the curve (AUC) derived from the precision–recall curves on the proposed G-UNETR++ network. As shown in Figure 7, the AUC for the most challenging dataset, Sliver07, ranged from 0.99158 to 0.998752, which demonstrates the high effectiveness of the proposed model.
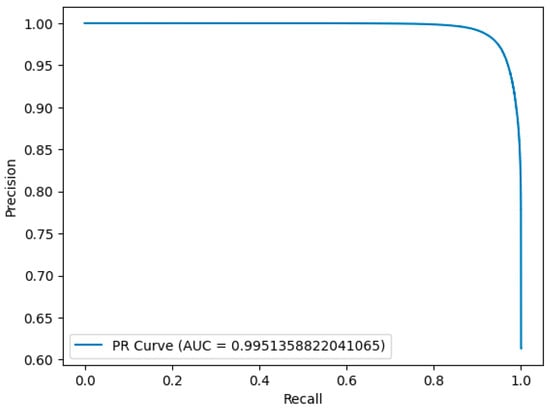
Figure 7.
Precision–recall curve analysis for liver segmentation over one example in the most challenging dataset, Sliver07.
4.7. Ablation Study
Comprehensive ablation studies on the LiTS dataset were conducted to evaluate the effectiveness of the proposed G-UNETR++ for liver segmentation. We evaluated the effectiveness of the proposed gradient-enhanced encoders (G-Encoders) for liver segmentation. Table 3 shows the result of the ablation study of G-UNETR++, which indicates that the proposed G-Encoders effectively improve the performance of liver segmentation. To evaluate the effectiveness of the proposed loss function, we trained our G-UNETR++ with dice loss + CE loss and the proposed loss, respectively. Table 4 shows that the proposed loss function is effective in improving the performance of liver segmentation. Lastly, we evaluated the effectiveness of the proposed post-processing method for liver segmentation. Table 5 shows that after post-processing, the performance of liver segmentation has been improved.

Table 3.
Ablation study for the proposed method on LiTS dataset.

Table 4.
Ablation study for loss function over the proposed G-UNETR++ on LiTS dataset.

Table 5.
Ablation study for post-processing over the proposed G-UNETR++ on LiTS dataset.
4.8. Comparison of Models
We compared our proposed G-UNETR++ with various state-of-the-art methods to evaluate its effectiveness, robustness, and generalization on the LiTS, Sliver07, and 3D-IRCADb datasets. Table 6 shows the comparison results of the proposed method with nine state-of-the-art methods on the LiTS dataset. The proposed method outperformed all the other methods in terms of DSC, VOE, ASSD, and MSSD. The proposed method achieved a maximum improvement of 3% in the main DSC evaluation metric. For VOE, ASSD, and MSSD, the proposed method outperformed the other methods by 0.39~4.91%, 0.38~1.66 mm, and 3.11~27.40 mm, respectively. Table 7 shows the comparison results of the proposed method with three state-of-the-art methods on the Sliver07 dataset. The proposed method achieved the best performance in terms of DSC, VOE, ASSD, and MSSD. For DSC, VOE, ASSD, and MSSD, the proposed method outperformed the other methods by 0.47~2.32%, 0.98~4.12%, 0.42~2.09 mm, and 5.46~40.81 mm, respectively. Table 8 shows the comparison results of the proposed method with eight state-of-the-art methods on the 3D-IRCADb dataset. The proposed method achieved the best in terms of DSC, VOE, and ASSD, and the second best in terms of MSSD. For DSC, VOE, and ASSD, the proposed method outperformed the other methods by 0.09~2.30%, 0.29~4.85%, and 0.17~2.62 mm, respectively. The results showed that the proposed method achieved excellent segmentation performance, even on both non-training datasets (Sliver07 and 3D-IRCADb datasets). Therefore, the proposed method showed strong effectiveness, robustness, and generalizability for accurate liver segmentation using CT scans. Figure 8 shows segmentation results of the proposed method over the three different datasets with one example from each dataset. As shown in Figure 8, the green region represents the ground truth, and the red line represents the liver boundary from our segmentation results. Even for the challenging cases with tumors, our segmentation results were perfectly aligned with the ground truth.

Table 6.
Comparison of different models on LiTS dataset.

Table 7.
Comparison of different models on Sliver07 dataset.

Table 8.
Comparison of different models on 3D-IRCADb dataset.
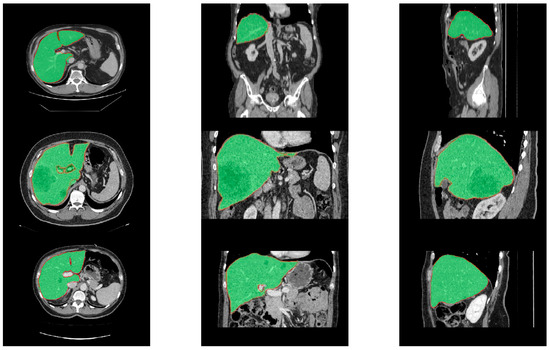
Figure 8.
Segmentation results of the proposed method over the LiTS (upper row), Sliver07 (middle row), and 3D-IRCADb (bottom row) datasets with one example from each dataset in different views (left: axial, middle: coronal, and right: sagittal). The green regions represent the ground truth, surrounded by red lines representing the segmentation results of our proposed method.
5. Discussion and Conclusions
In this study, we propose G-UNETR++, an effective hybrid segmentation network for accurate liver segmentation using CT scans. We introduce gradient-enhanced encoders (G-Encoders) for learning 3D geometric features to achieve better performance in liver segmentation. To evaluate the performance of the proposed method, comprehensive ablation studies on the LiTS dataset were conducted. The results of the ablation studies showed that our G-Encoder, the proposed loss function, and our post-processing method are effective for liver segmentation.
To further evaluate the performance of the proposed method, we compared our method with other state-of-the-art methods on the LiTS dataset. The comparison results showed that our method was superior to the other methods, achieving a DSC of 0.9738 for liver segmentation. To evaluate the generalizability of the proposed method, we tested our method with the other two non-training datasets, Sliver07 and 3D-IRACDb. The results showed that our method was superior to other methods, achieving DSC scores of 0.9732 and 0.9750 on the two datasets, respectively. These results demonstrated that our method shows strong generalizability over the different datasets collected under different conditions for liver segmentation.
Though the proposed G-UNETR++ achieved higher accuracy in liver segmentation than the baseline model UNETR++, the two proposed G-Encoders increased the complexity level of our model in terms of the number of parameters (97.73M) and FLOPs (73.12G), compared with the number of parameters (42.96M) and FLOPs (47.98G) of UNETR++. However, our model achieved a 1% higher dice score than UNETR++ for liver segmentation. With a similar complexity level to TransUNet and UNETR, our model achieved a 3% higher dice score. From this aspect, the increase in the complexity level is worthwhile. Still, future research is needed to reduce the complexity level of G-UNETR++. One potential direction is to employ a multi-resolution approach for the second-order partial derivatives computation. Instead of calculating the second-order partial derivatives for the entire input volume, this method focuses only on important regions of interest (ROI). Such a strategy will significantly reduce computational costs and memory usage, making the model more efficient without compromising segmentation accuracy. Another direction lies in adaptively activating gradient-enhanced encoders based on the complexity of the input data. The model can selectively enable or disable certain encoder stages by analyzing the gradient change rates across the input volume. This adaptive mechanism will optimize resource allocation, ensuring that the computational effort is focused only on the required stages, thus striking a better balance between efficiency and performance. These approaches will offer promising paths to further enhance the practicality and scalability of G-UNETR++, particularly for deployment in resource-constrained environments.
During our model development stage, we found that false positive and false negative errors appeared. False positive errors usually occur between the liver and its adjacent organs such as the stomach, spleen, and heart due to the overlap between their intensity values. To address this issue, we applied the connected components algorithm and the median filter to reduce false positive errors. To deal with false negative errors that usually occur within some small regions near the tumor boundaries, we proposed our hybrid loss function, especially by including HD loss to enhance boundary delineation by focusing on spatial accuracy at the edges of segmented regions. The hybrid loss improved liver segmentation accuracy.
The proposed G-UNETR++ showed significant generalizability over datasets from different sources for liver segmentation. Future research will be conducted to apply the proposed model for the segmentation of other organs, such as brain tumors and multiple organs from the abdomen, for not only CT scans, but also MRI scans.
In conclusion, the proposed G-UNETR++ is effective for liver segmentation using CT scans with high accuracy, robustness, and generalizability with a moderate complexity level. Future studies will focus on further reducing the complexity level and broadening the applications of our model.
Author Contributions
Conceptualization, S.L., K.H. and X.Y.; methodology, S.L., K.H. and X.Y.; software, S.L., K.H. and H.S.; validation, S.L., K.H., H.S. and X.Y.; formal analysis, S.L. and K.H.; investigation, S.L., K.H., H.S. and X.Y.; resources, X.Y., J.D.Y., H.C.Y. and H.Y.; data curation, S.L., H.P. and J.D.Y.; writing—original draft preparation, S.L., K.H., H.S., H.P., S.K., J.K. and X.Y.; writing—review and editing, S.L., K.H., H.P., S.K., J.K., X.Y. and H.Y.; visualization, S.L., K.H. and X.Y.; supervision, X.Y. and H.Y.; project administration, S.L., X.Y. and H.Y.; funding acquisition, X.Y., J.D.Y., H.C.Y. and H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by No. 202300720001 of the Handong Global University Research Grants, Fund of Biomedical Research Institute, Jeonbuk National University Hospital, and a grant from the Mid-Career Researcher Program through the National Research Foundation (NRF) of Korea (2022R1A2C1013198).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The LiTS dataset is available at https://competitions.codalab.org/competitions/17094 (accessed on 30 October 2024). The 3D-IRCADb dataset is available at https://www.ircad.fr/research/data-sets/liver-segmentation-3d-ircadb-01 (accessed on 30 October 2024). The Sliver07 dataset is available at https://sliver07.grand-challenge.org (accessed on 30 October 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Sung, H.; Ferlay, J.; Siegel, R.L.; Laversanne, M.; Soerjomataram, I.; Jemal, A.; Bray, F. Global cancer statistics 2020: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA Cancer J. Clin. 2021, 71, 209–249. [Google Scholar] [CrossRef]
- Lu, X.; Wu, J.; Ren, X.; Zhang, B.; Li, Y. The study and application of the improved region growing algorithm for liver segmentation. Optik 2014, 125, 2142–2147. [Google Scholar] [CrossRef]
- Yang, X.; Yu, H.; Choi, Y.; Lee, W.; Wang, B.; Yang, J.; Hwang, H.; Kim, J.H.; Song, J.; Cho, B.H.; et al. A hybrid semi-automatic method for liver segmentation based on level-set methods using multiple seed points. Comput. Methods Programs Biomed. 2014, 113, 69–79. [Google Scholar] [CrossRef]
- Lu, D.; Wu, Y.; Harris, G.; Cai, W. Iterative mesh transformation for 3D segmentation of livers with cancers in CT images. Comput. Med. Imaging Graph. 2015, 43, 1–14. [Google Scholar] [CrossRef][Green Version]
- Dawant, B.M.; Li, R.; Lennon, B.; Li, S. Semi-automatic segmentation of the liver and its evaluation on the MICCAI 2007 grand challenge data set. In Proceedings of the MICCAI 2007 Workshop: 3D Segmentation in the Clinic: A Grand Challenge, Brisbane, Australia, 29 October 2007; pp. 215–221. [Google Scholar]
- Hermoye, L.; Laamari-Azjal, I.; Cao, Z.; Annet, L.; Lerut, J.; Dawant, B.M.; Van Beers, B.E. Liver segmentation in living liver transplant donors: Comparison of semiautomatic and manual methods. Radiology 2005, 234, 171–178. [Google Scholar] [CrossRef] [PubMed]
- Jiang, L.; Ou, J.; Liu, R.; Zou, Y.; Xie, T.; Xiao, H.; Bai, T. RMAU-Net: Residual Multi-Scale Attention U-Net for liver and tumor segmentation in CT images. Comput. Biol. Med. 2023, 158, 106838. [Google Scholar] [CrossRef]
- Chen, Y.; Zheng, C.; Zhou, T.; Feng, L.; Liu, L.; Zeng, Q.; Wang, G. A deep residual attention-based U-Net with a biplane joint method for liver segmentation from CT scans. Comput. Biol. Med. 2023, 152, 106421. [Google Scholar] [CrossRef] [PubMed]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the Medical Image Computing and Computer-Assisted Intervention MICCAI International Conference, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Gul, S.; Khan, M.S.; Bibi, A.; Khandakar, A.; Ayari, M.A.; Chowdhury, M.E.H. Deep learning techniques for liver and liver tumor segmentation: A review. Comput. Biol. Med. 2022, 147, 105620. [Google Scholar] [CrossRef]
- Yu, X.; Yang, Q.; Zhou, Y.; Cai, L.Y.; Gao, R.; Lee, H.H.; Li, T.; Bao, S.; Xu, Z.; Lasko, T.A.; et al. UNesT: Local spatial representation learning with hierarchical transformer for efficient medical segmentation. Med. Image Anal. 2023, 90, 102939. [Google Scholar] [CrossRef]
- Hatamizadeh, A.; Tang, Y.; Nath, V.; Yang, D.; Myronenko, A.; Landman, B.; Roth, H.R.; Xu, D. UNETR: Transformers for 3d medical image segmentation. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 3–8 January 2022; pp. 574–584. [Google Scholar]
- Hu, H.; Zhang, Z.; Xie, Z.; Lin, S. Local relation networks for image recognition. In Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Republic of Korea, 27 October–2 November 2019; pp. 3464–3473. [Google Scholar]
- Mohajelin, F.; Sheykhivand, S.; Shabani, A.; Danishvar, M.; Danishvar, S.; Lahijan, L.Z. Automatic recognition of multiple emotional classes from EEG signals through the use of graph theory and convolutional neural networks. Sensors 2024, 24, 5883. [Google Scholar] [CrossRef]
- Ardabili, S.Z.; Bahmani, S.; Lahijan, L.Z.; Khaleghi, N.; Sheykhivand, S.; Danishvar, S. A novel approach for automatic detection of driver fatigue using EEG signals based on graph convolutional networks. Sensors 2024, 24, 364. [Google Scholar] [CrossRef]
- Khoshkhabar, M.; Meshgini, S.; Afrouzian, R.; Danishvar, S. Automatic liver tumor segmentation from CT images using graph convolutional network. Sensors 2023, 23, 7561. [Google Scholar] [CrossRef]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. Transunet: Transformers make strong encoders for medical image segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar]
- Hatamizadeh, A.; Nath, V.; Tang, Y.; Yang, D.; Roth, H.; Xu, D. Swin UNETR: Swin transformers for semantic segmentation of brain tumors in MRI images. arXiv 2022, arXiv:2201.01266. [Google Scholar]
- Zhou, H.-Y.; Guo, J.; Zhang, Y.; Yu, L.; Wang, L.; Yu, Y. nnFormer: Interleaved transformer for volumetric segmentation. arXiv 2021, arXiv:2109.03201. [Google Scholar]
- Shaker, A.M.; Maaz, M.; Rasheed, H.; Khan, S.; Yang, M.-H.; Khan, F.S. UNETR++: Delving into efficient and accurate 3D medical image segmentation. IEEE Trans. Med. Imaging 2024, 43, 3377–3390. [Google Scholar] [CrossRef]
- Landman, B.; Xu, Z.; Igelsias, J.E.; Styner, M.; Langerak, T.R.; Klein, A. 2015 MICCAI multi-atlas labeling beyond the cranial vault workshop and challenge. In Proceedings of the MICCAI Multi-Atlas Labeling Beyond Cranial Vault—Workshop Challenge, Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Çiçek, Ö.; Abdulkadir, A.; Lienkamp, S.S.; Brox, T.; Ronneberger, O. 3D U-Net: Learning dense volumetric segmentation from sparse annotation. In Proceedings of the International Conference on Medical Image Computing and Computer Assisted Intervention, Athens, Greece, 17–21 October 2016; pp. 424–432. [Google Scholar]
- Dou, Q.; Chen, H.; Jin, Y.; Yu, L.; Qin, J.; Heng, P.-A. 3D deeply supervised network for automatic liver segmentation from CT volumes. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Athens, Greece, 17–21 October 2016; pp. 149–157. [Google Scholar]
- Gibson, E.; Giganti, F.; Hu, Y.; Bonmati, E.; Bandula, S.; Gurusamy, K.; Davidson, B.; Pereira, S.P.; Clarkson, M.J.; Barratt, D.C. Automatic multi-organ segmentation on abdominal CT with dense V-networks. IEEE Trans. Med. Imaging 2018, 37, 1822–1834. [Google Scholar] [CrossRef]
- Milletari, F.; Navab, N.; Ahmadi, S.-A. V-Net: Fully convolutional neural networks for volumetric medical image segmentation. In Proceedings of the 2016 4th International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 565–571. [Google Scholar]
- Roth, H.R.; Oda, H.; Hayashi, Y.; Oda, M.; Shimizu, N.; Fujiwara, M.; Misawa, K.; Mori, K. Hierarchical 3D fully convolutional networks for multi-organ segmentation. arXiv 2017, arXiv:1704.06382. [Google Scholar]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2021, arXiv:2010.11929. [Google Scholar]
- Cao, H.; Wang, Y.; Chen, J.; Jiang, D.; Zhang, X.; Tian, Q.; Wang, M. Swin-Unet: U-Net-like pure transformer for medical image segmentation. arXiv 2021, arXiv:2105.05537. [Google Scholar]
- Karimi, D.; Vasylechko, S.D.; Gholipour, A. Convolution-free medical image segmentation using transformers. arXiv 2021, arXiv:2102.13645. [Google Scholar]
- Khan, A.; Rauf, Z.; Sohail, A.; Rehman, A.; Asif, H.M.; Asif, A.; Farooq, U. A survey of the vision transformers and its CNN-transformer based variants. arXiv 2023, arXiv:2305.09880. [Google Scholar]
- Valanarasu, J.M.J.; Oza, P.; Hacihaliloglu, I.; Patel, V.M. Medical transformer: Gated axial-attention for medical image segmentation. In Proceedings of the 24th International Conference on Medical Image Computing and Computer-Assisted Intervention, Strasbourg, France, 27 September–1 October 2021; pp. 36–46. [Google Scholar]
- Xie, Y.; Zhang, J.; Shen, C.; Xia, Y. CoTr: Efficiently bridging CNN and transformer for 3D medical image segmentation. In Proceedings of the 24th International Conference on Medical Image Computing and Computer-Assisted Intervention, Strasbourg, France, 27 September–1 October 2021; pp. 171–180. [Google Scholar]
- Wang, W.; Chen, C.; Ding, M.; Yu, H.; Zha, S.; Li, J. TransBTS: Multimodal brain tumor segmentation using transformer. In Proceedings of the 24th International Conference on Medical Image Computing and Computer-Assisted Intervention, Strasbourg, France, 27 September–1 October 2021; pp. 109–119. [Google Scholar]
- Zhou, Y.; Kong, Q.; Zhu, Y.; Su, Z. MCFA-UNet: Multiscale cascaded feature attention U-Net for liver segmentation. IRBM 2023, 44, 100789. [Google Scholar] [CrossRef]
- Guo, X.; Schwartz, L.H.; Zhao, B. Automatic liver segmentation by integrating fully convolutional networks into active contour models. Med. Phys. 2019, 46, 4455–4469. [Google Scholar] [CrossRef] [PubMed]
- Song, L.; Wang, H.; Wang, Z.J. Bridging the gap between 2D and 3D contexts in CT volume for liver and tumor segmentation. IEEE J. Biomed. Health Inform. 2021, 25, 3450–3459. [Google Scholar] [CrossRef] [PubMed]
- Lei, T.; Wang, R.; Zhang, Y.; Wan, Y.; Liu, C.; Nandi, A.K. DefED-Net: Deformable encoder-decoder network for liver and liver tumor segmentation. IEEE Trans. Radiat. Plasma Med. Sci. 2022, 6, 68–78. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, F.; Wang, Y.; Zheng, C. Hybrid-attention densely connected U-Net with GAP for extracting livers from CT volumes. Med. Phys. 2022, 49, 1015–1033. [Google Scholar] [CrossRef]
- Kushnure, D.T.; Talbar, S.N. HFRU-Net: High-level feature fusion and recalibration UNet for automatic liver and tumor segmentation in CT images. Comput. Methods Programs Biomed. 2022, 213, 106501. [Google Scholar] [CrossRef]
- Li, R.; Xu, L.; Xie, K.; Song, J.; Ma, X.; Chang, L.; Yan, Q. DHT-Net: Dynamic hierarchical transformer network for liver and tumor Segmentation. IEEE J. Biomed. Health Inform. 2023, 27, 3443–3454. [Google Scholar] [CrossRef]
- Zhu, J.; Liu, Z.; Gao, W.; Fu, Y. CotepRes-Net: An efficient U-Net based deep learning method of liver segmentation from Computed Tomography images. Biomed. Signal Process. Control 2024, 88, 105660. [Google Scholar] [CrossRef]
- Karimi, D.; Salcudean, S.E. Reducing the Hausdorff distance in medical image segmentation with convolutional neural networks. IEEE Trans. Med. Imaging 2020, 39, 499–513. [Google Scholar] [CrossRef]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. Unet++: A nested u-net architecture for medical image segmentation. arXiv 2018, arXiv:1807.10165. [Google Scholar]
- Lee, C.-Y.; Xie, S.; Gallagher, P.; Zhang, Z.; Tu, Z. Deeply-supervised nets. arXiv 2014, arXiv:1409.5185. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2017, arXiv:1412.6980. [Google Scholar]
- Chibuike, O.; Yang, X. Convolutional Neural Network–Vision Transformer Architecture with Gated Control Mechanism and Multi-Scale Fusion for Enhanced Pulmonary Disease Classification. Diagnostics 2024, 14, 2790. [Google Scholar] [CrossRef] [PubMed]
- Fan, T.; Wang, G.; Li, Y.; Wang, H. MA-Net: A multi-scale attention network for liver and tumor segmentation. IEEE Access 2020, 8, 179656–179665. [Google Scholar] [CrossRef]
- Sakboonyara, B.; Taeprasartsit, P. U-Net and mean-shift histogram for efficient liver segmentation from CT images. In Proceedings of the 11th International Conference on Knowledge and Smart Technology (KST), Phuket, Thailand, 23–26 January 2019; pp. 51–56. [Google Scholar]
- Seo, H.; Huang, C.; Bassenne, M.; Xiao, R.; Xing, L. Modified U-Net (mU-Net) with incorporation of object-dependent high level features for improved liver and liver-tumor segmentation in CT images. IEEE Trans. Med. Imaging 2020, 39, 1316–1325. [Google Scholar] [CrossRef]
- Budak, Ü.; Guo, Y.; Tanyildizi, E.; Şengür, A. Cascaded deep convolutional encoder-decoder neural networks for efficient liver tumor segmentation. Med. Hypotheses 2020, 134, 109431. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).