Simulation Study of Deep Belief Network-Based Rice Transplanter Navigation Deviation Pattern Identification and Adaptive Control
Abstract
1. Introduction
- (1)
- A rice transplanter navigation control simulation platform is designed. Simulating the state interference error during rice transplanter navigation operations provides a reliable and real experimental platform for subsequent research.
- (2)
- A deviation pattern identification method was designed. Based on the Deep Belief Network (DBN), three models were trained and implemented in two phases for real-time identification of deviation patterns.
- (3)
- An adaptive control method is designed. Based on the preview model, the optimal preview distance is adjusted in real time and the deviation is suppressed effectively.
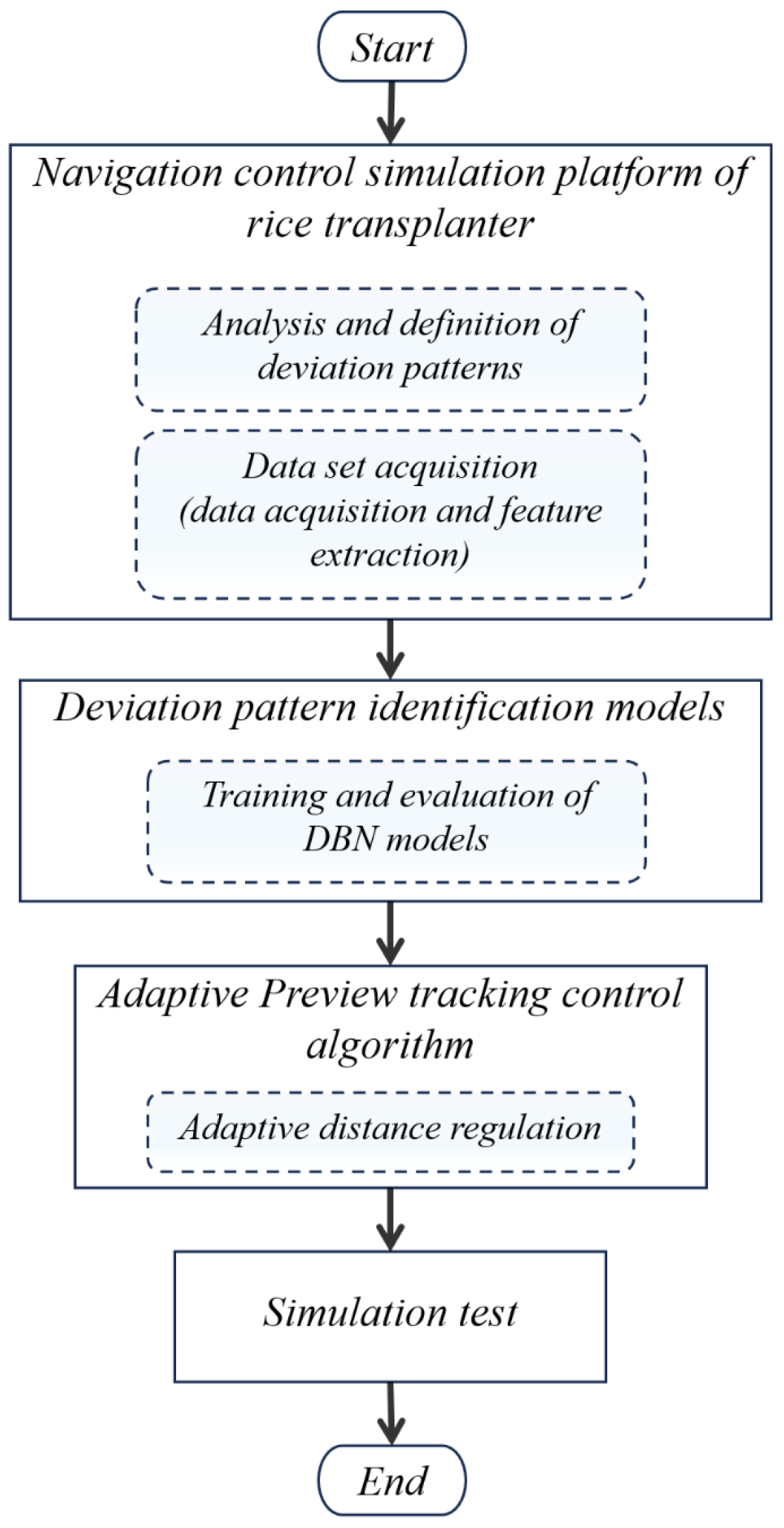
2. Materials and Methods
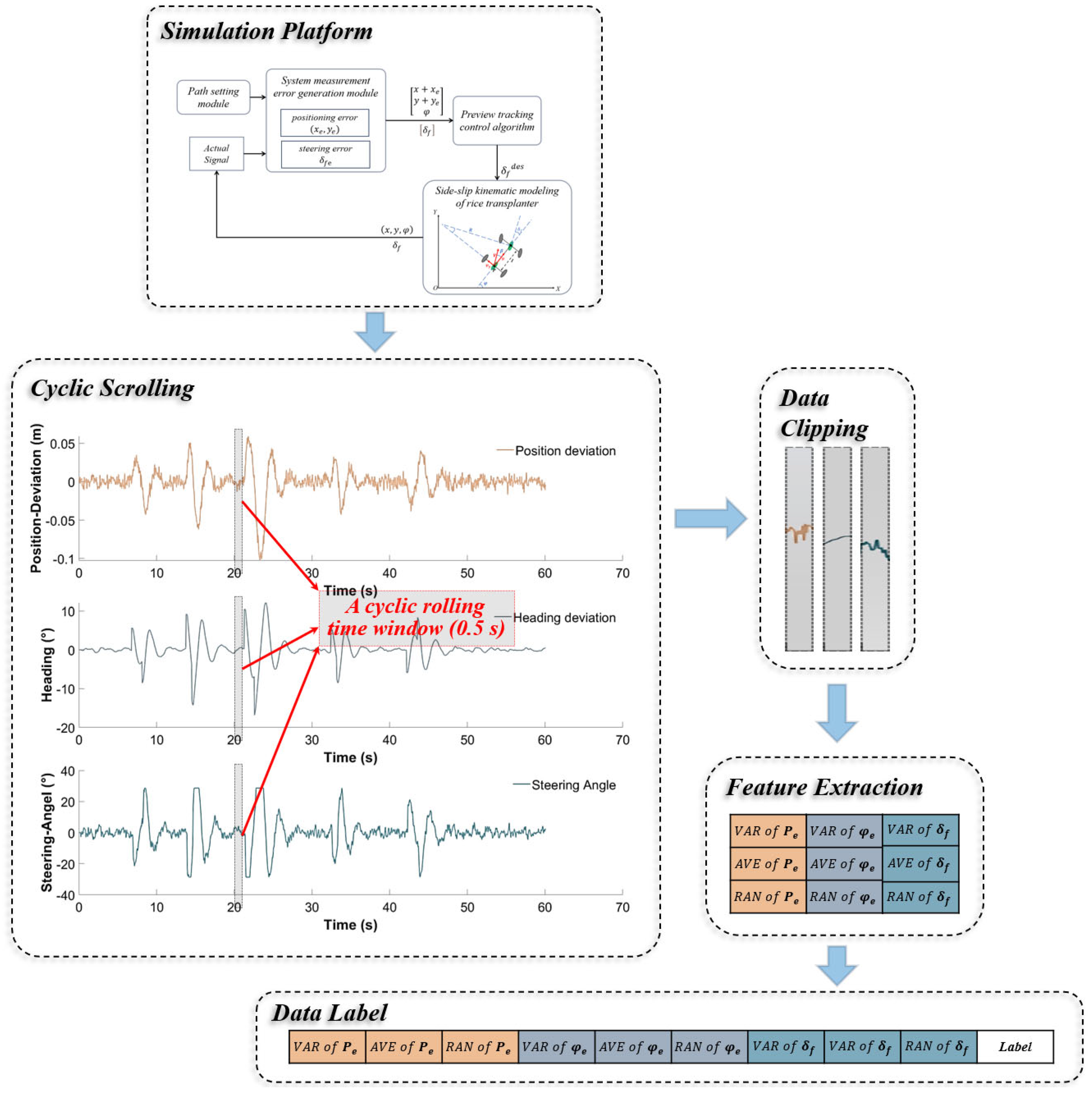
2.1. Simulation Platform of Rice Transplanter Navigation Control
2.1.1. Sideslip Kinematic Modelling of Rice Transplanter
2.1.2. Design of Preview Tracking Algorithm Based on Small Angle Linearization
2.1.3. Systematic Measurement Error Generation Module
- (1)
- Positioning measurement error
- (2)
- Steering control error
2.1.4. Navigation Path Setting Module
- (1)
- Enter the measured position of the rice transplanter control point and its heading angle .
- (2)
- Set the target heading angle , forward speed , and extend the navigation line from the starting point.
- (3)
- Calculate the heading angle deviation between and , and the position deviation between and , and output and .
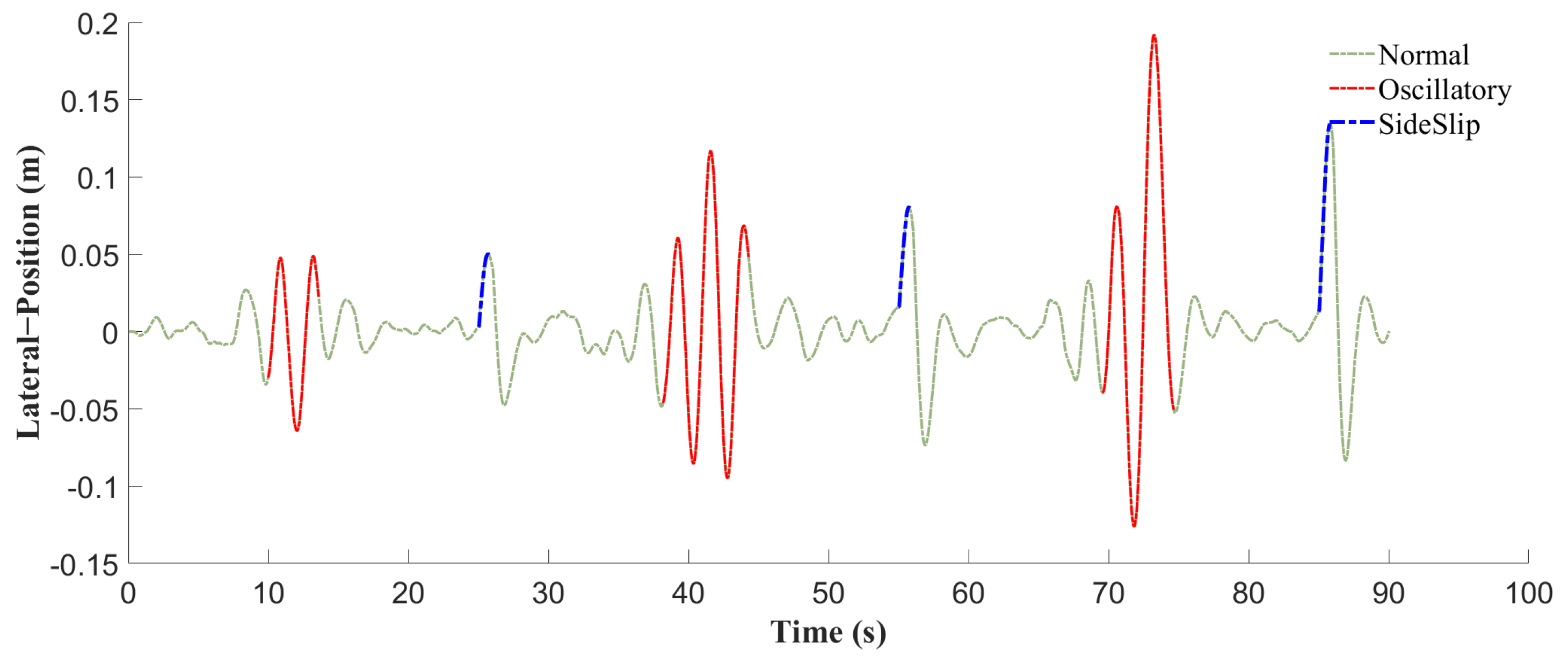
2.2. Definition and Analysis of Path-Tracking Deviation Pattern
2.2.1. Definition of Path-Tracking Deviation Patterns
- Classification of abnormal states
- 2.
- Classification of degree of oscillation
- 3.
- Classification of Degree of Sideslip
2.2.2. Key Characteristic Variables of Path-Tracking Deviation Patterns
- Key characterization variables in oscillation states
- 2.
- Key characterization variables in sideslip states
2.3. DBN-Based Path-Tracking Deviation Pattern Identification Model and Dataset Preparation
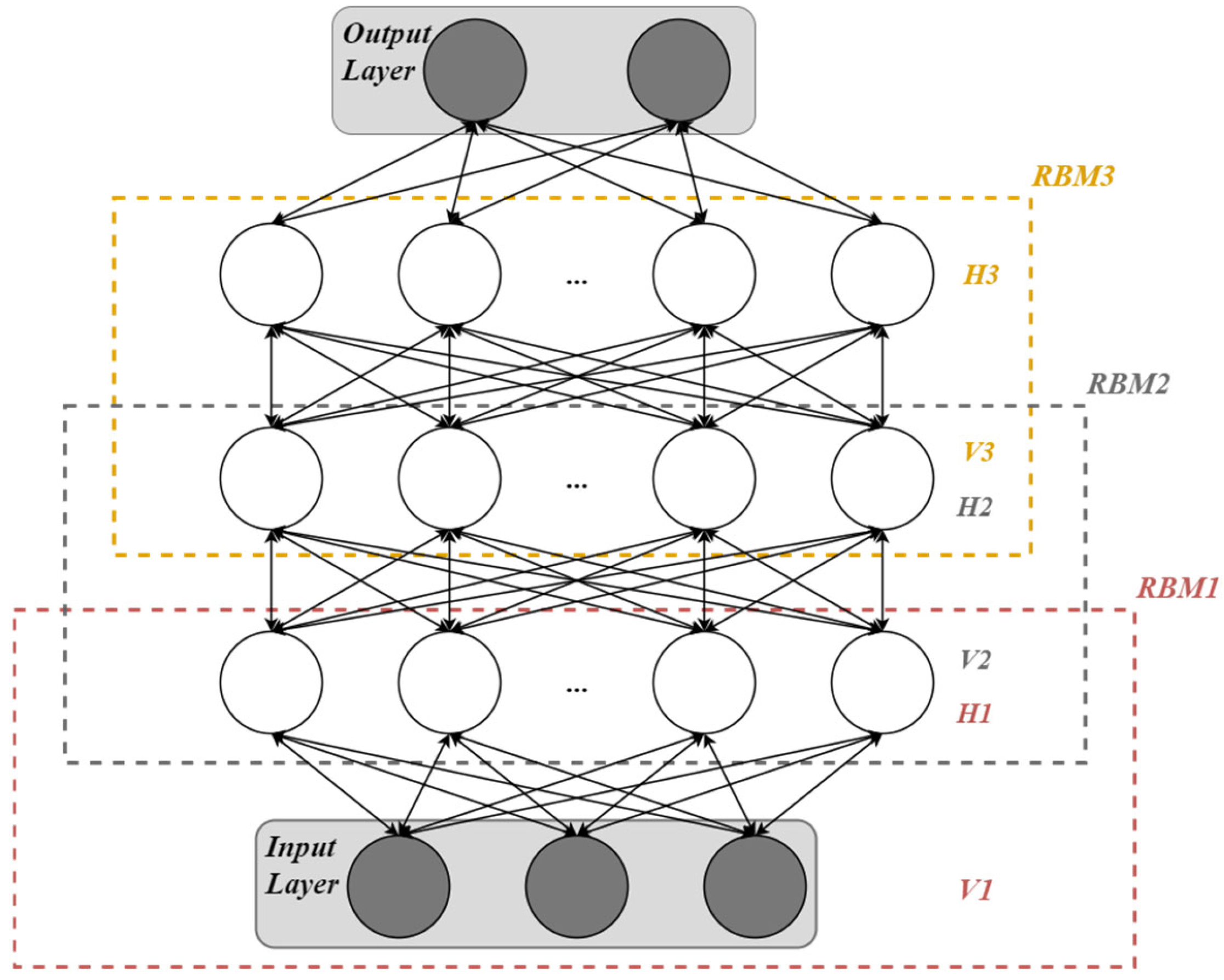
2.3.1. Training of DBN
- Structure of DBN
- 2.
- Unsupervised pre-training process
- 3.
- Supervised reverse fine-tuning process
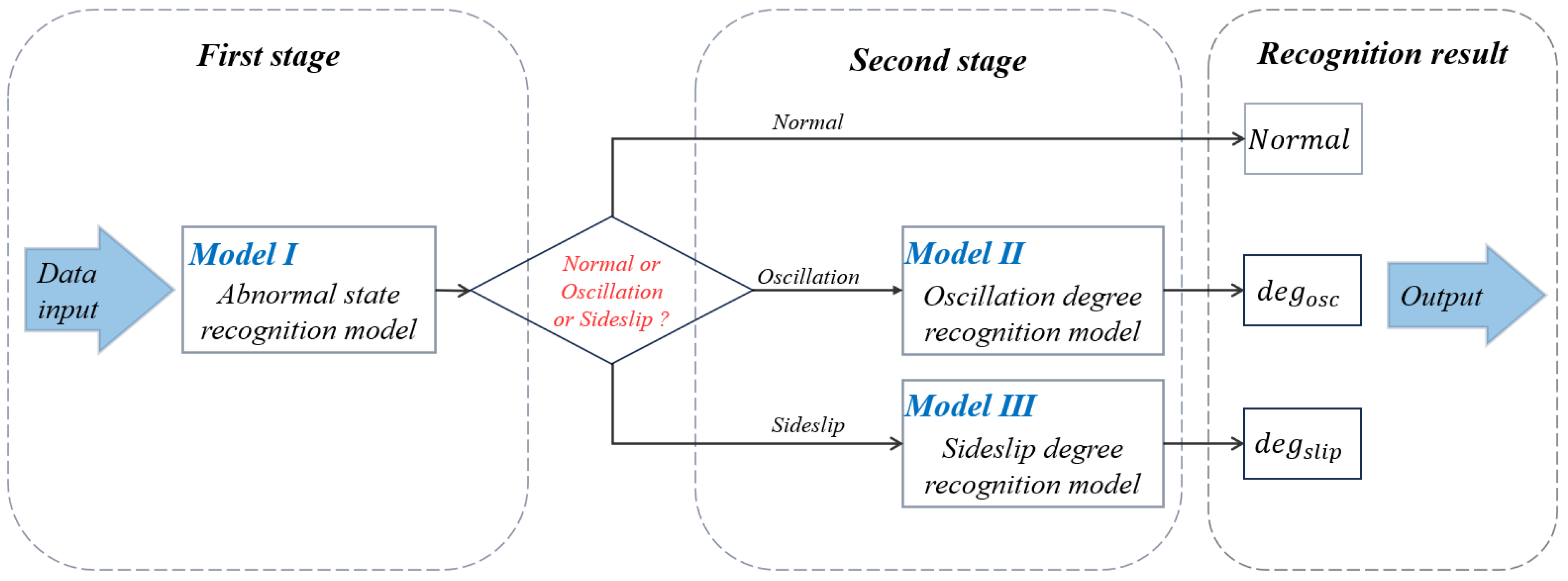
2.3.2. Design of the Deviation Pattern Identification Model
2.3.3. Data Acquisition and Feature Extraction
- (1)
- Traversing the raw data curves of the navigation key feature variables (position deviation , heading deviation , and steering angle ) using a circular scrolling time window (0.5 s in length);
- (2)
- According to the path-tracking deviation pattern defined in Section 2.2.1, the data curves under the corresponding time window are intercepted, split, reorganized, and labeled for classification in the form of arrays.
- (3)
- Extract the mean, variance, and extreme deviation of the raw data curve slices, save the data to the workspace in the MATLAB platform, and finally export and save it as a .xlsx file.
2.3.4. Dataset Segmentation
2.4. Design of Adaptive Preview Control Algorithm
- (1)
- The main regulator calculates the basic preview distance to ensure stable control of the system under undisturbed conditions;
- (2)
- The sub-regulator calculates the preview distance adjustment value to ensure that the system quickly suppresses deviation under disturbing conditions.
2.4.1. Design of the Main Regulator
2.4.2. Design of the Sub-Regulator
- Definition of sub-regulator
- 2.
- Setting constraints
- 3.
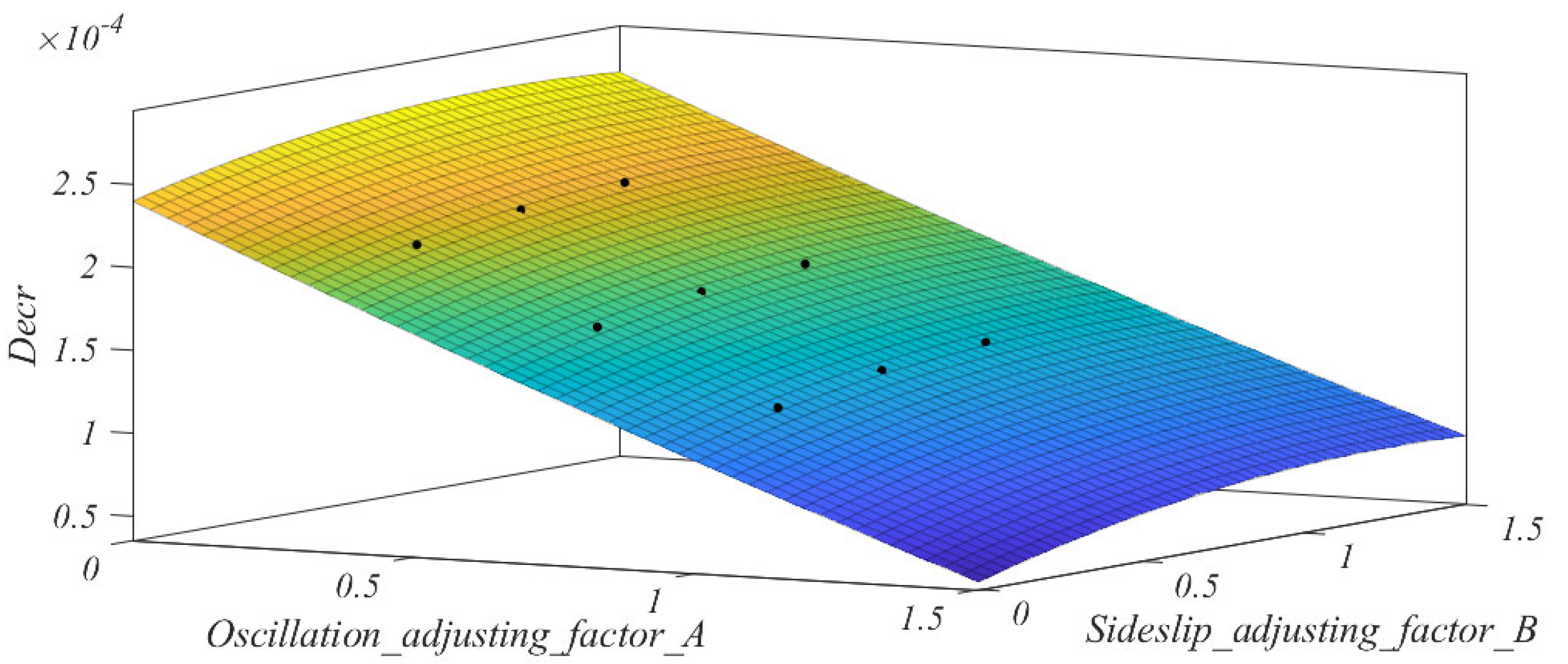
- Optimal adjustment factor test
- (1)
- At a , the control curve is set up as shown in Figure 10. Specifically, on the basis of the main regulator (the sub-regulator does not intervene), three degrees of oscillations are induced by narrowing the preview distance, and three degrees of sideslip are induced by applying different degrees of lateral velocity. The overall variance of the control curves .
- (2)
- Set and as multiple groups of level factors (value range 0~1), intervene the sub-regulator on the basis of the main regulator, i.e., add the preview distance adjustment value as shown in Equation (23), carry out the simulation test with different adjustment coefficients, and obtain the overall variance of each tracking curve.
- (3)
- The declining variance of each tracking curve is used as an evaluation index, as shown in Equation (25).
3. Results and Analysis
3.1. Path-Tracking Deviation Pattern Identification Test
3.1.1. Test Preparation
- Evaluation Index
- 2.
- Parameters of DBN
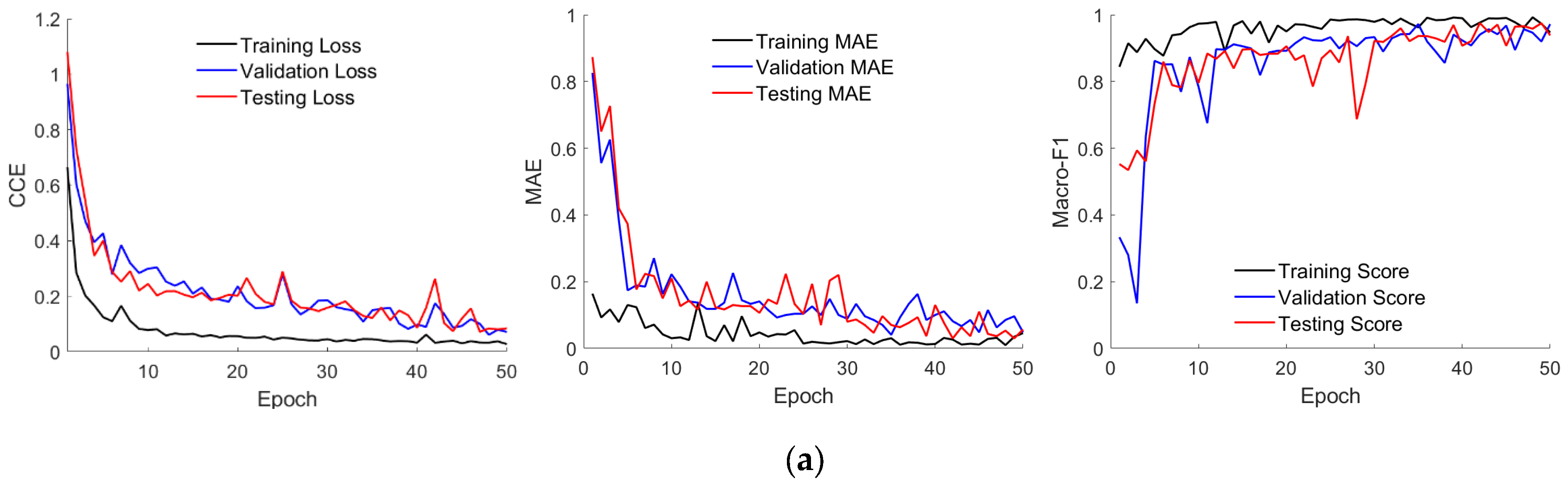
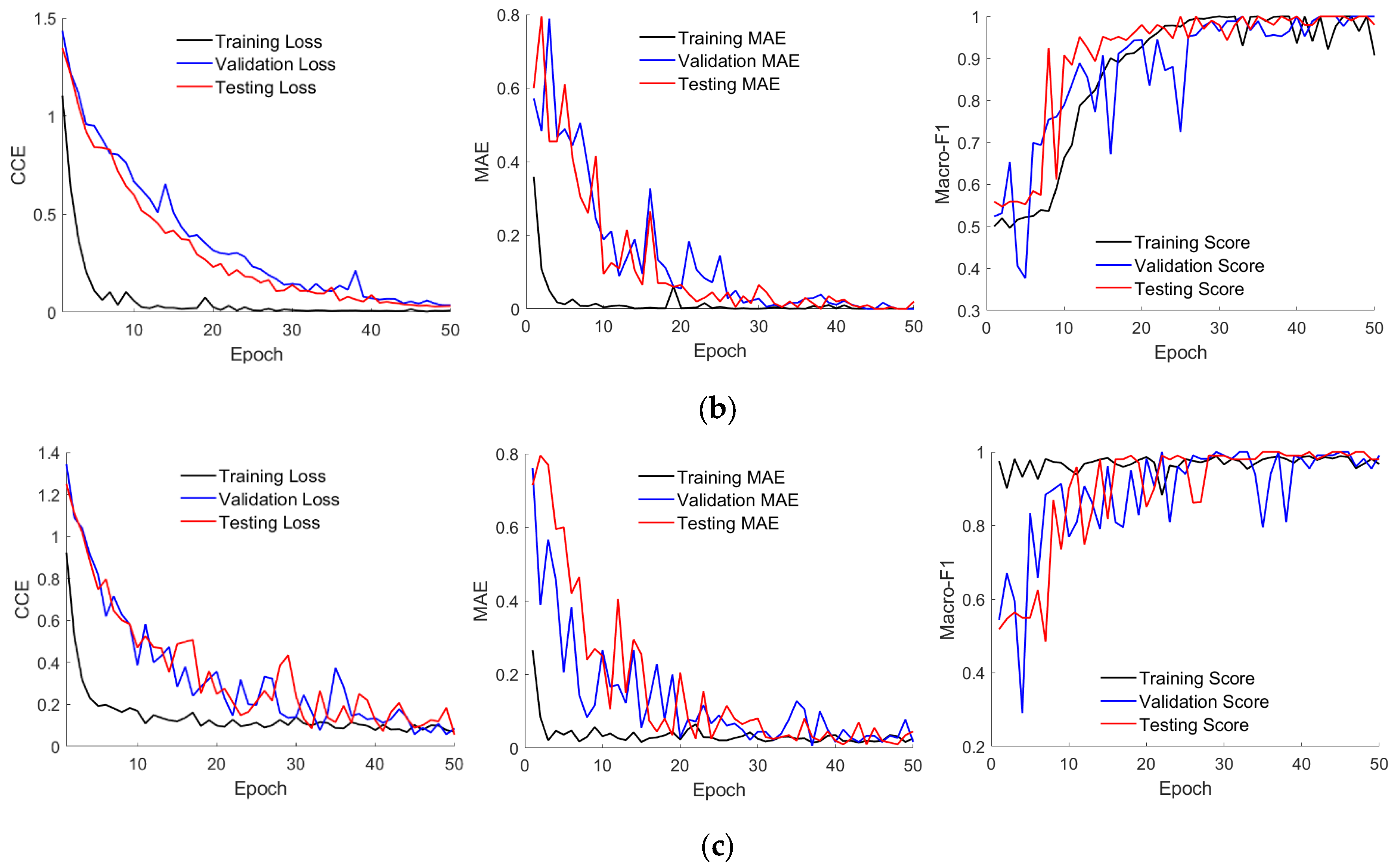
3.1.2. Performance Testing of Models
- DBN performance tests
- (1)
- Comparing the feature learning ability of the three models in the face of different data samples through a single training;
- (2)
- Observing the prediction performance of the three models on different datasets after multiple training and testing by using a 10-fold cross-validation test.
- 2.
- Comparative validation tests of different deep learning methods
- 3.
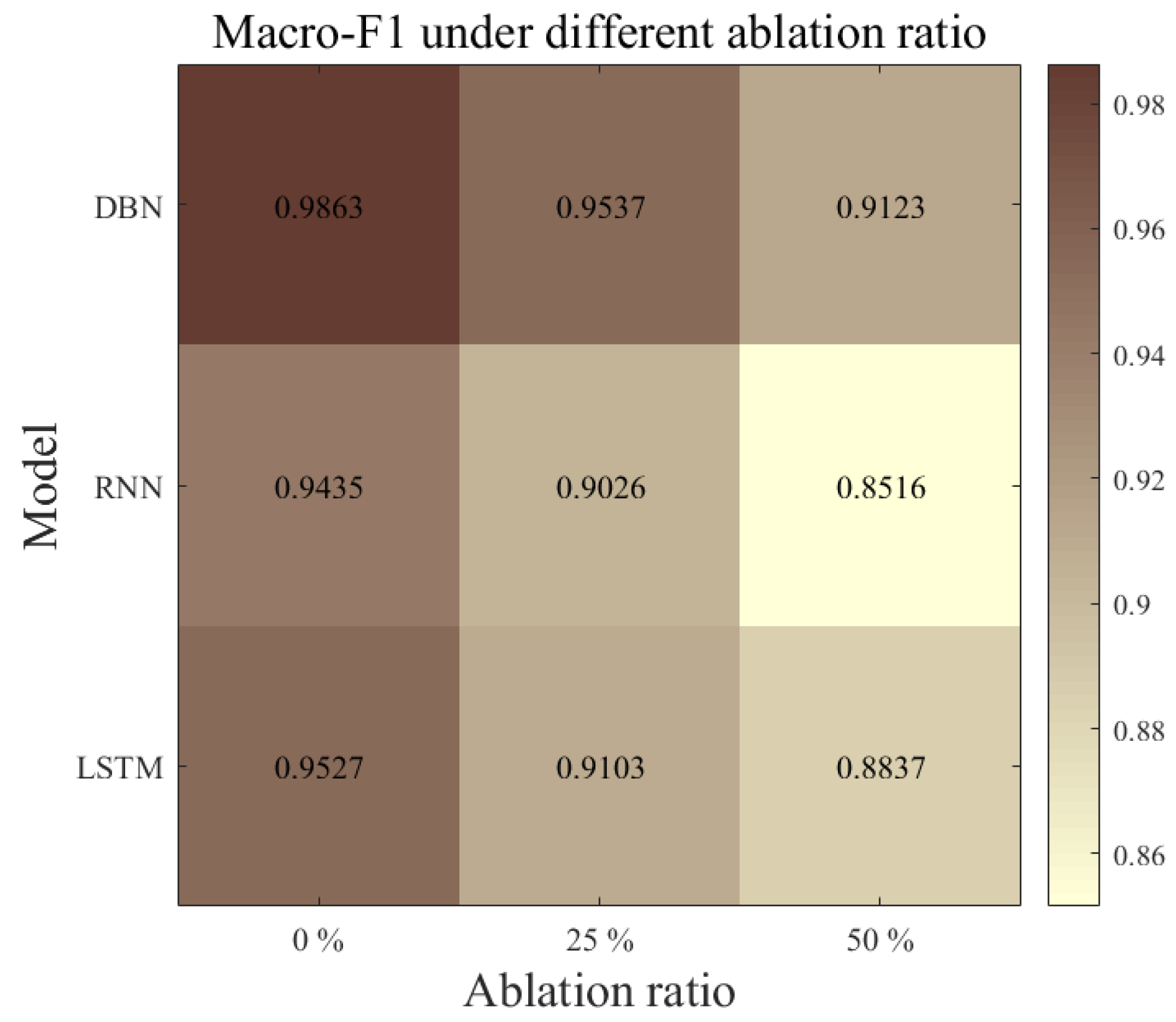
- An ablation study of different deep learning methods
3.2. Simulation Test of Adaptive Control Method Based on Deviation Pattern Identification
3.2.1. Experimental Design
- Test conditions
- 2.
- Control strategy
- 3.
- Test group setup
3.2.2. Test Results
4. Discussion
4.1. Conclusions
4.2. Outlook
- (1)
- In the navigation control scenario of the non-straight path, the deviation pattern of the rice transplanter is more complicated, which is a considerable challenge for feature extraction and pattern identification.
- (2)
- In the DBN model training, the training process and performance of Model Three on the identification of the degree of sideslip deviation are still a bit different compared with the other two models, and the reasons for the analysis are roughly as follows: ① The complexity of the data features is higher; ② the setting of the training parameters of the model is not good. The model performance can be optimized by adding the optimization algorithm to find the suitable training parameters.
- (3)
- The steering control lag time of the main controller mentioned in this study is difficult to obtain, and a more in-depth study based on the lag time will be carried out subsequently.
- (4)
- For the above research, we will subsequently construct a complete and efficient adaptive pre-aiming control algorithm in a rice transplanter navigation system through hardware development, model deployment, and algorithm transplantation and test the performance of the algorithm in real products.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wei, W.; Xiao, M.; Duan, W.; Wang, H.; Zhu, Y.; Zhai, C.; Geng, G. Research Progress on Autonomous Operation Technology for Agricultural Equipment in Large Fields. Agriculture 2024, 14, 1473. [Google Scholar] [CrossRef]
- Yao, Z.; Zhao, C.; Zhang, T. Agricultural machinery automatic navigation technology. iScience 2024, 27, 108714. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Wang, Y.; Chen, Y.; Jin, C.; Du, J. Development of autonomous navigation controller for agricultural vehicles. Int. J. Agric. Biol. Eng. 2020, 13, 70–76. [Google Scholar] [CrossRef]
- Rankin, A.L.; Crane, C.D., III; Armstrong, D.G., II. Evaluating a PID, pure pursuit, and weighted steering controller for an autonomous land vehicle. In Mobile Robots XII, Proceedings of the Intelligent Systems and Advanced Manufacturing, Pittsburgh, PA, USA, 14–17 October 1997; Gage, D.W., Ed.; SPIE: Bellingham, WA, USA, 1998; pp. 1–12. [Google Scholar] [CrossRef]
- Snider, J.M. Automatic Steering Methods for Autonomous Automobile Path Tracking; Technical Report, no. CMU-RITR-09-08; Robotics Institute: Pittsburgh, PA, USA, 2009. [Google Scholar]
- Corno, M.; Panzani, G.; Roselli, F.; Giorelli, M.; Azzolini, D.; Savaresi, S.M. An LPV Approach to Autonomous Vehicle Path Tracking in the Presence of Steering Actuation Nonlinearities. IEEE Trans. Contr. Syst. Technol. 2021, 29, 1766–1774. [Google Scholar] [CrossRef]
- Qin, Z.; Chen, L.; Hu, M.; Chen, X. A Lateral and Longitudinal Dynamics Control Framework of Autonomous Vehicles Based on Multi-Parameter Joint Estimation. IEEE Trans. Veh. Technol. 2022, 71, 5837–5852. [Google Scholar] [CrossRef]
- Liu, H.; Sun, J.; Cheng, K.W.E. A Two-Layer Model Predictive Path-Tracking Control With Curvature Adaptive Method for High-Speed Autonomous Driving. IEEE Access 2023, 11, 89228–89239. [Google Scholar] [CrossRef]
- Liu, W.; Hua, M.; Deng, Z.; Meng, Z.; Huang, Y.; Hu, C.; Song, S.; Gao, L.; Liu, C.; Shuai, B.; et al. A Systematic Survey of Control Techniques and Applications in Connected and Automated Vehicles. IEEE Internet Things J. 2023, 10, 21892–21916. [Google Scholar] [CrossRef]
- Xia, Q.; Chen, P.; Xu, G.; Sun, H.; Li, L.; Yu, G. Adaptive Path-Tracking Controller Embedded With Reinforcement Learning and Preview Model for Autonomous Driving. IEEE Trans. Veh. Technol. 2024, 1–15. [Google Scholar] [CrossRef]
- Hazem, Z.B.; Bingül, Z. A comparative study of anti-swing radial basis neural-fuzzy LQR controller for multi-degree-of-freedom rotary pendulum systems. Neural Comput. Appl. 2023, 35, 17397–17413. [Google Scholar] [CrossRef]
- Wu, X.; Fang, P.; Liu, X.; Liu, M.; Huang, P.; Duan, X.; Huang, D.; Liu, Z. AM-UNet: Field Ridge Segmentation of Paddy Field Images Based on an Improved MultiResUNet Network. Agriculture 2024, 14, 637. [Google Scholar] [CrossRef]
- Mahendran, N.; Vincent, P.M.D.R. Deep belief network-based approach for detecting Alzheimer’s disease using the multi-omics data. Comput. Struct. Biotechnol. J. 2023, 21, 1651–1660. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Tan, Z.; Sheng, W.; Liu, Z.; Wu, X.; Ma, L.; Li, Z. Identification of Groundwater Contamination Sources Based on a Deep Belief Neural Network. Water 2024, 16, 2449. [Google Scholar] [CrossRef]
- Han, X.; Kim, H.-J.; Jeon, C.W.; Moon, H.C.; Kim, J.H.; Yi, S.Y. Application of a 3D tractor-driving simulator for slip estimation-based path-tracking control of auto-guided tillage operation. Biosyst. Eng. 2019, 178, 70–85. [Google Scholar] [CrossRef]
- Han, X.-Z.; Kim, H.-J.; Moon, H.-C.; Woo, H.-J.; Kim, J.-H.; Kim, Y.-J. Development of a Path Generation and Tracking Algorithm for a Korean Auto-guidance Tillage Tractor. J. Biosyst. Eng. 2013, 38, 1–8. [Google Scholar] [CrossRef]
- Han, X.Z.; Kim, H.J.; Kim, J.Y.; Yi, S.Y.; Moon, H.C.; Kim, J.H.; Kim, Y.J. Path-tracking simulation and field tests for an auto-guidance tillage tractor for a paddy field. Comput. Electron. Agric. 2015, 112, 161–171. [Google Scholar] [CrossRef]
- Yang, Y.; Li, Y.; Wen, X.; Zhang, G.; Ma, Q.; Cheng, S.; Qi, J.; Xu, L.; Chen, L. An optimal goal point determination algorithm for automatic navigation of agricultural machinery: Improving the tracking accuracy of the Pure Pursuit algorithm. Comput. Electron. Agric. 2022, 194, 106760. [Google Scholar] [CrossRef]
- Wang, H.; Wang, G.; Luo, X.; Zhang, Z.; Gao, Y.; He, J.; Yue, B. Path Tracking Control Method of Agricultural Machine Navigation based on Aiming Pursuit Model. Trans. Chin. Soc. Agric. Eng. Trans. CSAE 2019, 35, 11–19. [Google Scholar] [CrossRef]
- Na’aim, M.Z.B.M.; Manaf, M.B.A. Establishment of control points using GNSS-RTK technique. E3S Web Conf. 2024, 479, 02001. [Google Scholar] [CrossRef]
- Wang, S.; Dong, X.; Liu, G.; Gao, M.; Xiao, G.; Zhao, W.; Lv, D. GNSS RTK/UWB/DBA Fusion Positioning Method and Its Performance Evaluation. Remote Sens. 2022, 14, 5928. [Google Scholar] [CrossRef]
- He, J.; Zhu, J.; Luo, X.; Zhang, Z.; Hu, L.; Gao, Y. Design of Steering Control System for Rice Transplanter Equipped with Steering Wheel-like Motor. Trans. Chin. Soc. Agric. Eng. Trans. CSAE 2019, 35, 10–17. [Google Scholar] [CrossRef]
- Wang, H.; Hu, J.; Gao, L. Compensation Model for Measurement Error of Wheel Turning Angle in Agricultural Vehicle Guidance. Trans. Chin. Soc. Agric. Mach. 2014, 45, 33–37. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, G.; Luo, X.; He, J.; Wang, J.; Wang, H. Detection Method of Steering Wheel Angle for Tractor Automatic Driving. Trans. Chin. Soc. Agric. Mach. 2019, 50, 352–357. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef] [PubMed]
- Le Roux, N.; Bengio, Y. Representational Power of Restricted Boltzmann Machines and Deep Belief Networks. Neural Comput. 2008, 20, 1631–1649. [Google Scholar] [CrossRef]
- Chu, H.; Pei, H.; Si, X.-S.; Du, D.-B.; Pang, Z.-N.; Wang, X. A Prognostic Model Based on DBN and Diffusion Process for Degrading Bearing. IEEE Trans. Ind. Electron. 2020, 67, 8767–8777. [Google Scholar] [CrossRef]
- Sherstinsky, A. Fundamentals of Recurrent Neural Network (RNN) and Long Short-Term Memory (LSTM) network. Phys. D Nonlinear Phenom. 2020, 404, 132306. [Google Scholar] [CrossRef]
- Wang, L.; Chen, Z.; Zhu, W. An improved pure pursuit path tracking control method based on heading error rate. Ind. Robot. 2022, 49, 973–980. [Google Scholar] [CrossRef]


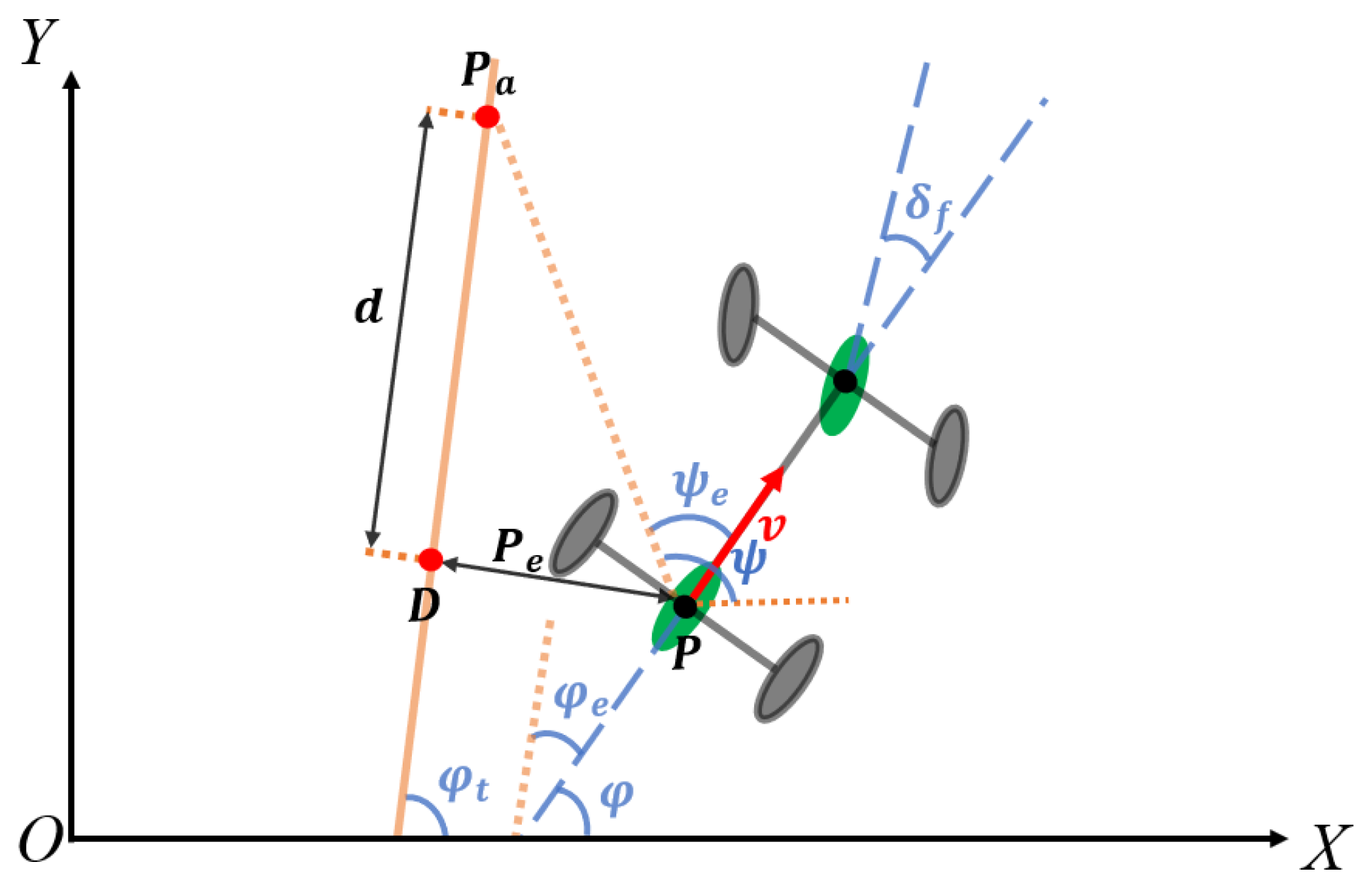



| Symbol | Description | Symbol | Description |
|---|---|---|---|
| Position of control point | Vehicle heading angle | ||
| Forward velocity | Steering angle | ||
| Lateral velocity | Wheelbase length | ||
| Sideslip angle | Turning radius |
| Symbol | Description | Symbol | Description |
|---|---|---|---|
| Target heading angle | Preview distance | ||
| preview point | Position deviation | ||
| Preview heading angle | Deviation to target heading angle | ||
| Deviation to preview heading angle |
| Abnormal State | Classification Criteria | Label |
|---|---|---|
| Normal | 1 | |
| Oscillation | 2 | |
| Sideslip | 3 |
| Degree of Oscillation | Classification Criteria | Label |
|---|---|---|
| Mild | 1 | |
| Moderate | 2 | |
| Severe | 3 |
| Degree of Sideslip | Classification Criteria | Label |
|---|---|---|
| Mild | 1 | |
| Moderate | 2 | |
| Severe | 3 |
| Model | Input | Output | Description |
|---|---|---|---|
| I | State Variable Characterization Dataset | Normal or Oscillation or Sideslip | Identify abnormal states (The division rules are shown in Table 3) |
| II | Degree of Oscillation | Identify the degree of Oscillation (The division rules are shown in Table 4) | |
| III | Degree of Sideslip | Identify the degree of sideslip (The division rules are shown in Table 5) |
| Dataset | Percentage | Actual Number |
|---|---|---|
| Training | 90%·90% | 2430 |
| Validation | 90%·10% | 270 |
| Testing | 10% | 300 |
| Full Data | 100% | 3000 |
| Index | (m/s) | (m) | (s) | (m) |
|---|---|---|---|---|
| 1 | 0.90 | 0.04 | 0.18 | 0.25 |
| 2 | 1.35 | 0.04 | 0.18 | 0.35 |
| 3 | 0.90 | 0.08 | 0.18 | 0.40 |
| 4 | 1.35 | 0.08 | 0.18 | 0.45 |
| 5 | 0.90 | 0.04 | 0.42 | 0.65 |
| 6 | 1.35 | 0.04 | 0.42 | 0.90 |
| 7 | 0.90 | 0.08 | 0.42 | 0.75 |
| 8 | 1.35 | 0.08 | 0.42 | 1.00 |
| 9 | 0.75 | 0.06 | 0.30 | 0.45 |
| 10 | 1.50 | 0.06 | 0.30 | 0.65 |
| 11 | 1.13 | 0.02 | 0.30 | 0.45 |
| 12 | 1.13 | 0.10 | 0.30 | 0.65 |
| 13 | 1.13 | 0.06 | 0.10 | 0.30 |
| 14 | 1.13 | 0.06 | 0.50 | 1.05 |
| 15 | 1.13 | 0.06 | 0.30 | 0.55 |
| Index | Coefficient | /m2 | /m2 | |
|---|---|---|---|---|
| 1 | 0.96 | 0.96 | 0.001125 | 0.000140 |
| 2 | 0.96 | 0.64 | 0.001131 | 0.000134 |
| 3 | 0.96 | 0.32 | 0.001143 | 0.000123 |
| 4 | 0.64 | 0.96 | 0.001084 | 0.000181 |
| 5 | 0.64 | 0.64 | 0.001090 | 0.000175 |
| 6 | 0.64 | 0.32 | 0.001100 | 0.000165 |
| 7 | 0.32 | 0.96 | 0.001041 | 0.000224 |
| 8 | 0.32 | 0.64 | 0.001047 | 0.000218 |
| 9 | 0.32 | 0.32 | 0.001057 | 0.000208 |
| Parameters | Value | Description |
|---|---|---|
| 9 | Number of nodes in the input layer, corresponds to the number of features | |
| 100 | Number of nodes in the hidden layer 1 | |
| 100 | Number of nodes in the hidden layer 2 | |
| 10 | Batch size of pre-training | |
| Learning rate of pre-training | ||
| 100 | Epoch of pre-training | |
| 0.999 | Learning rate scale factor of pre-training | |
| 10 | Batch size of reverse fine-tuning | |
| 0.50 | Learning rate of reverse fine-tuning | |
| 50 | Epoch of reverse fine-tuning | |
| 0.999 | Learning rate scale factor of reverse fine-tuning | |
| 3 | Number of nodes in the output layer corresponds to the number of categories |
| Dataset | MAE | Macro-F1/% | Accuracy/% | Time/s |
|---|---|---|---|---|
| Training | 0.0193 | 98.38 | 98.84 | 0.00809 |
| Validation | 0.0156 | 98.67 | 99.02 | 0.00208 |
| Testing | 0.0330 | 97.29 | 98.13 | 0.00151 |
| Dataset | MAE | Macro-F1/% | Accuracy/% | Time/s |
|---|---|---|---|---|
| Training | 0.0026 | 99.93 | 99.74 | 0.00869 |
| Validation | 0.0056 | 100 | 99.44 | 0.00266 |
| Testing | 0.0035 | 100 | 99.65 | 0.00242 |
| Dataset | MAE | Macro-F1/% | Accuracy/% | Time/s |
|---|---|---|---|---|
| Training | 0.0245 | 97.35 | 97.55 | 0.00641 |
| Validation | 0.0361 | 95.97 | 96.39 | 0.00194 |
| Testing | 0.0285 | 94.84 | 97.15 | 0.00178 |
| Indicator | Model | DBN | RNN | LSTM |
|---|---|---|---|---|
| MAE | I | 0.0236 | 0.0967 | 0.0758 |
| II | 0.0038 | 0.0235 | 0.0186 | |
| III | 0.0274 | 0.1694 | 0.0657 | |
| Macro-F1/% | I | 98.56 | 93.57 | 94.58 |
| II | 99.85 | 96.96 | 98.50 | |
| III | 95.34 | 90.36 | 93.67 | |
| Accuracy/% | I | 99.02 | 92.46 | 92.35 |
| II | 99.58 | 96.81 | 98.34 | |
| III | 97.44 | 89.42 | 92.66 |
| A | B | Experimental Purpose | |
|---|---|---|---|
| Adaptive preview distance | 0.288 | 0.992 | Dynamic preview distance, when a deviation is identified, until the deviation is over. |
| Static preview distance | NaN | NaN | Static preview distance: 1 m. |
| Maximum Absolute Lateral Deviation/m | Mean Absolute Lateral Deviation/m | Root Mean Square Lateral Deviation/m | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 0~30 s | 30~60 s | 60~90 s | 0~30 s | 30~60 s | 60~90 s | 0~30 s | 30~60 s | 60~90 s | |
| Static preview distance | 0.0642 | 0.117 | 0.192 | 0.0121 | 0.0232 | 0.0271 | 0.0189 | 0.0346 | 0.0476 |
| Adaptive preview distance | 0.0660 | 0.0713 | 0.115 | 0.0114 | 0.0146 | 0.0158 | 0.0178 | 0.0205 | 0.0265 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, X.; Fang, P.; Xiong, N.; Liu, M.; Wu, X.; Fu, L.; Liu, Z. Simulation Study of Deep Belief Network-Based Rice Transplanter Navigation Deviation Pattern Identification and Adaptive Control. Appl. Sci. 2025, 15, 790. https://doi.org/10.3390/app15020790
Duan X, Fang P, Xiong N, Liu M, Wu X, Fu L, Liu Z. Simulation Study of Deep Belief Network-Based Rice Transplanter Navigation Deviation Pattern Identification and Adaptive Control. Applied Sciences. 2025; 15(2):790. https://doi.org/10.3390/app15020790
Chicago/Turabian StyleDuan, Xianhao, Peng Fang, Neng Xiong, Muhua Liu, Xulong Wu, Li Fu, and Zhaopeng Liu. 2025. "Simulation Study of Deep Belief Network-Based Rice Transplanter Navigation Deviation Pattern Identification and Adaptive Control" Applied Sciences 15, no. 2: 790. https://doi.org/10.3390/app15020790
APA StyleDuan, X., Fang, P., Xiong, N., Liu, M., Wu, X., Fu, L., & Liu, Z. (2025). Simulation Study of Deep Belief Network-Based Rice Transplanter Navigation Deviation Pattern Identification and Adaptive Control. Applied Sciences, 15(2), 790. https://doi.org/10.3390/app15020790





