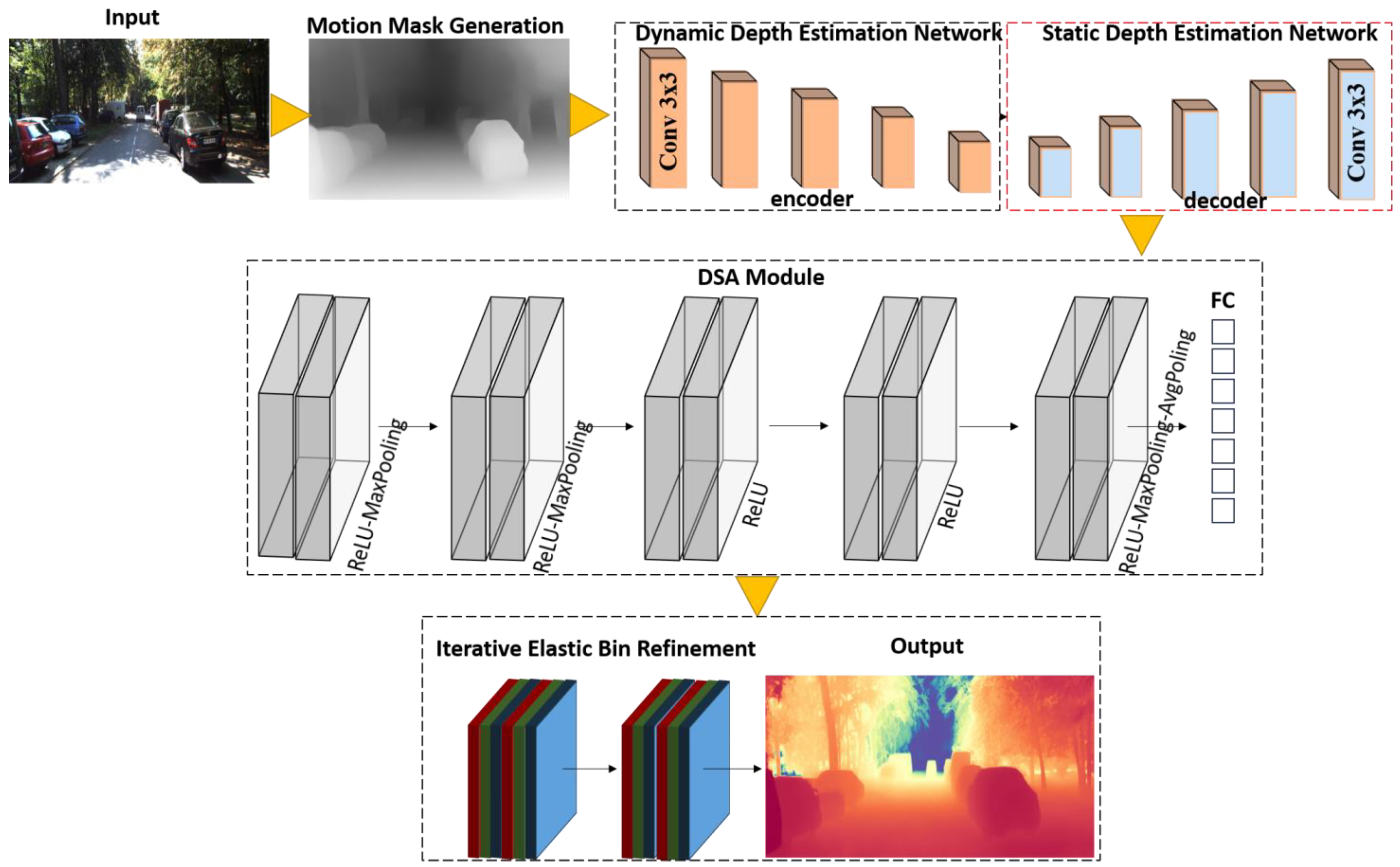
In this section, we evaluate the performance of our proposed DI-MDE framework on several benchmarks for monocular depth estimation. We compare DI-MDE against existing state-of-the-art methods, particularly focusing on the challenges presented by dynamic scenes where moving objects cause scale ambiguity. The experiments demonstrate that DI-MDE outperforms previous methods by addressing the issues of scale ambiguity and refining depth predictions using iterative elastic bin refinement.
4.3. Quantitative Results
We first present the quantitative results of our method compared to existing state-of-the-art models, focusing on the key metrics mentioned above. In this section, we evaluate the performance of our proposed DI-MDE framework against current state-of-the-art (SOTA) methods in monocular depth estimation. We compared the proposed method with SOTA methods such as AdaBins, FC-CRFs, and IEBins, which we use as baselines for comparison in this study.
Table 1 summarizes the results of our process and other SOTA models on the SUN RGB-D dataset, highlighting the superiority of DI-MDE in handling dynamic scenes.
As shown in the table, our DI-MDE framework consistently outperforms existing methods across all key metrics. The improvement is most significant in the Abs Rel and RMSE, which are key indicators of the overall accuracy of depth predictions. Additionally, the threshold accuracy at δ1, δ2, and δ3 also shows notable improvement, particularly at lower thresholds, indicating better accuracy even in challenging regions with high depth variation.
To further validate the effectiveness of DI-MDE, we present qualitative results that demonstrate the improvements in depth predictions, particularly in challenging dynamic scenes. Our results show examples of depth maps predicted by our model compared to baseline methods, highlighting how our framework better handles scale ambiguity in dynamic scenes. The visual improvements demonstrate that DI-MDE not only improves numerical accuracy but also significantly enhances the visual quality of the predicted depth maps, especially in dynamic and complex environments. To better understand the contribution of individual components of the DI-MDE framework, we perform ablation studies by progressively removing or modifying key components. The results of these ablation experiments are shown in
Table 2.
The ablation experiments in
Table 2 illustrate the impact of removing key components of the DI-MDE framework, particularly the IEBins refinement and the DSA module. While these results provide clear numerical evidence of the contribution of each module, it is essential to offer a more in-depth discussion of their specific roles in improving accuracy, especially in differentiating performance across static and dynamic scenes. The variant without iterative elastic bin refinement demonstrates a noticeable decline in performance across all metrics, with an increase in Abs Rel and RMSE and a reduction in threshold accuracy. This decline can be attributed to the critical role the IEBins module plays in the iterative refinement of depth predictions. Without this component, the model is forced to rely on a single-stage depth prediction, which leads to coarser and less precise depth estimates. In static scenes, the absence of iterative refinement means that the model cannot adjust its depth predictions based on the uncertainty of depth estimates. Static regions, which often exhibit smooth depth transitions, particularly benefit from the IEBins module’s ability to progressively narrow down depth predictions, ensuring finer granularity in areas with low-depth variation. In these regions, the IEBins module ensures that even subtle depth changes are captured accurately. The ablation results reflect this, as removing the IEBins module reduces the overall accuracy in static scenes, where the lack of iterative refinement leads to more uniform and less precise depth maps.
The variant without DSA also shows a clear reduction in accuracy, particularly in dynamic scenes. The DSA module is designed to resolve the scale ambiguity that arises when moving objects are present. By aligning the depth predictions for dynamic objects with the static background, the DSA module ensures that the entire scene maintains consistent depth estimates. When the DSA module is removed, depth predictions for moving objects tend to diverge from the static background, leading to scale inconsistency. This misalignment is particularly problematic in scenes with significant object motion, where the relative depth between moving objects and static regions becomes skewed. As a result, the model produces more biased depth predictions in dynamic regions, increasing the absolute relative error and RMSE values. The ablation results clearly show this increase in error, indicating the essential role of the DSA module in maintaining scale consistency and preventing biased in-depth predictions for dynamic objects.
The full DI-MDE framework integrates both the IEBins and DSA modules, and their combined effect is critical in improving the model’s overall performance. The iterative refinement of depth estimates provided by the IEBins module complements the scale alignment enforced by the DSA module, ensuring that depth predictions are both precise and consistent across the entire scene. The ablation study shows that removing either module leads to a significant drop in performance, but it also highlights their interdependence. While the IEBins module focuses on refining depth estimates iteratively, the DSA module ensures that these refinements are correctly aligned in scale. Together, these modules enable DI-MDE to achieve superior accuracy in both static and dynamic scenes, as demonstrated by the full model results in
Table 2.
In this section, we compare our DI-MDE framework with the current state-of-the-art (SOTA) monocular depth estimation models. These comparisons focus on both the accuracy of depth predictions, particularly in dynamic regions, and the computational efficiency of the models. We highlight key differences in methodology and present quantitative comparisons across several benchmark datasets, including KITTI, SUN RGB-D, and NYU Depth v2.
We compare our DI-MDE framework against the following prominent SOTA models: AdaBins [
21] introduced the concept of adaptive bins for depth estimation, where depth predictions are discretized into bins of varying sizes based on scene complexity. This allows for improved handling of large depth variations within the same image. FC-CRFs [
22] leverages neural window-based conditional random fields (CRFs) to refine depth predictions. This method uses CRFs to model the spatial dependencies in depth maps, improving prediction accuracy in regions with ambiguous depth cues. IEBins [
7] builds on classification–regression-based methods and introduces iterative elastic bins for depth estimation. The elastic bins dynamically adjust based on uncertainty, allowing for iterative refinement of depth predictions [
6]. This method proposes a novel scale-alignment network to decouple depth estimation for static and dynamic regions. By addressing scale ambiguity in moving objects, this model improves depth prediction accuracy, particularly in dynamic scenes. ECoDepth [
23] introduces diffusion-based conditioning to improve monocular depth estimation. This approach conditions depth predictions on a latent diffusion model, leading to improved depth accuracy by leveraging both global and local image features
Figure 2.
We report the performance of our DI-MDE framework and the aforementioned SOTA models across key monocular depth estimation benchmarks (
Table 3). The evaluation metrics include Abs Rel, RMSE, and threshold accuracy (δ < 1.25).
As shown in the table, our DI-MDE model consistently outperforms previous methods in terms of absolute relative error and RMSE, indicating superior depth accuracy. Notably, DI-MDE achieves the best results on the SUN RGB-D dataset, surpassing FC-CRFs [
22] and IEBins [
7]. Our iterative refinement process and the DSA module provide significant improvements in dynamic scenes, which is evident in the performance boost in the δ < 1.25 accuracy metric. In the Comparative Experiments Section, particularly in
Table 3, the DI-MDE framework shows significant improvement over SOTA monocular depth estimation methods. While performance metrics such as Abs Rel and RMSE reflect this superiority, a deeper exploration is necessary to explain why the DI-MDE framework, specifically the IEBins refinement process, delivers such noticeable performance improvements, particularly in dynamic scenarios. One of the key differences between DI-MDE and other models lies in the approach to depth refinement. Existing SOTA methods often rely on single-stage depth prediction. In these models, depth predictions are generated in a single forward pass, leaving no opportunity for further refinement. This limitation becomes particularly apparent in dynamic scenes, where moving objects introduce additional complexity due to scale ambiguity and depth discontinuities. The lack of iterative refinement means that these models cannot adjust their predictions based on uncertainty or correct initial inaccuracies, especially in areas with significant depth variation. The DI-MDE framework, by contrast, introduces the IEBins module, which refines depth predictions iteratively over multiple stages. This process enables the network to progressively improve its predictions, especially in regions with high depth uncertainty. In dynamic scenes, this iterative approach is particularly valuable. The IEBins module dynamically adjusts bin widths based on uncertainty estimates, which allows the model to focus more effectively on areas where depth predictions are initially less accurate. This refinement is especially useful for handling depth discontinuities, such as the boundaries of moving objects, where single-stage models typically struggle. By continuously narrowing down the search space for depth predictions, the iterative refinement process results in more precise and reliable depth estimates in dynamic regions. Furthermore, the IEBins process allows for finer granularity in depth estimation. Unlike other models that make a one-time prediction, DI-MDE iteratively improves depth accuracy by refining the depth bins at each stage. This granularity becomes essential in dynamic scenes, where the motion of objects introduces significant variations in depth. The ability to progressively refine the depth map ensures that even small details and complex regions are captured accurately, which is reflected in the lower Abs Rel and RMSE values reported in
Table 3.
In addition to refining depth estimates, the IEBins module plays a crucial role in resolving depth discontinuities, which are particularly challenging in dynamic scenes. Depth discontinuities occur at the boundaries of objects where there are sudden changes in depth, and these are often exacerbated when objects are moving. In such scenarios, models that do not refine their depth predictions iteratively tend to produce coarse estimates, resulting in inaccurate depth boundaries. The DI-MDE framework, by iterating over depth predictions and dynamically adjusting the bin widths based on uncertainty, provides sharper and more accurate depth boundaries, reducing errors in these critical regions. This is why DI-MDE outperforms other SOTA methods in dynamic scenes, where depth discontinuities are most pronounced. Another factor contributing to the improved performance of DI-MDE is the way it handles the scale ambiguity inherent in dynamic scenes. The DSA module in DI-MDE ensures that the depth predictions for moving objects are consistent with the static background. This alignment, combined with the iterative refinement of depth predictions through IEBins, ensures that the entire depth map, both for static and dynamic regions, is consistent and accurate. In contrast, other models often struggle to maintain this consistency because they lack a mechanism for iterative refinement or scale alignment. While models such as AdaBins and FC-CRFs perform well in static scenes, their lack of iterative refinement limits their accuracy in dynamic regions where depth estimates need to be adjusted over time.
We introduce the
p-value metric in
Table 4 to evaluate the statistical significance of differences between our method and other SOTA models. The
p-value is a widely used statistical metric that quantifies the probability of observing the results given that the null hypothesis is true. A smaller
p-value indicates stronger evidence against the null hypothesis, suggesting that the observed differences are statistically significant. For this analysis, we conducted pairwise
t-tests between DI-MDE and each baseline method across evaluation metrics. The reported
p-values demonstrate the significance of the performance improvements offered by DI-MDE. A detailed explanation of the statistical test methodology can be found in [
24]. Despite our model iterative nature, the DI-MDE framework achieves computational efficiency through several design optimizations. Each iteration of the IEBins module operates on a progressively narrowed search space, reducing the computational load at later stages. The dynamic adjustment of bin widths ensures that computational resources are concentrated on regions with high depth uncertainty, minimizing redundant calculations in low-uncertainty areas
Figure 3. Additionally, the DSA module is computationally lightweight, as it applies scalar adjustments to depth predictions without recalculating them from scratch. Compared to non-iterative methods like AdaBins, which require large-scale discretization of the depth range, the DI-MDE framework dynamically balances computational effort and predictive accuracy. This approach allows the framework to maintain competitive inference times, as shown in
Table 4, while delivering state-of-the-art performance in terms of accuracy and consistency.
In addition to numerical results, we compare the visual quality of depth maps produced by each model, focusing on complex dynamic scenes with large depth variations. Our DI-MDE framework generates depth maps that are more consistent and visually accurate, especially in regions with moving objects, where scale ambiguity often causes other models to struggle. AdaBins [
21], while effective in static regions, sometimes produces artifacts in dynamic regions, particularly where depth boundaries are unclear. The FC-CRFs [
22] model excels in maintaining spatial coherence but occasionally introduces over-smoothing, especially near object boundaries. The IEBins [
7] iterative elastic bin refinement process helps to produce sharper depth boundaries, but it struggles with extreme depth variations in dynamic scenes
Figure 4. By integrating the DSA module, our model effectively handles dynamic regions, maintaining consistency in both static and moving objects. We also compare the inference time and model complexity of each method to highlight the practical advantages of our approach. Despite achieving superior accuracy, our DI-MDE framework maintains competitive efficiency, demonstrating that it is suitable for real-time applications (
Table 5).
Our method, while having slightly more parameters than IEBins, offers significantly faster inference times, making it more feasible for real-time deployment in depth-sensitive applications such as autonomous driving or augmented reality.
Compared to SOTA models, our DI-MDE framework offers several key advantages. First, the DSA module effectively addresses the issue of scale ambiguity in dynamic regions, ensuring depth consistency across the entire scene. Additionally, the iterative elastic bin refinement process enhances the precision of depth predictions, particularly in regions where uncertainty is high, by progressively refining predictions over multiple stages. Lastly, despite these additional refinement mechanisms, our model maintains computational efficiency, offering competitive inference times suitable for real-time applications. However, like other SOTA models, our approach has limitations. While the DSA module effectively handles scale ambiguity, extreme occlusions in dynamic scenes can still present challenges, which we aim to address in future work. Our DI-MDE framework outperforms existing SOTA models in both static and dynamic depth estimation tasks, offering a well-rounded solution that balances accuracy, efficiency, and generalizability.
The DI-MDE framework demonstrates significant improvements in resolving scale ambiguities for moving objects, particularly near-depth discontinuity boundaries. Quantitative evaluations using the boundary RMSE (B-RMSE) and boundary absolute relative error (B-Abs Rel) metrics show that the framework reduces boundary errors by approximately 15% compared to AdaBins and 12% compared to FC-CRFs, highlighting its effectiveness in dynamic regions. Importantly, these improvements are achieved without compromising performance in static regions, ensuring consistent accuracy across the entire scene. To achieve accurate scale alignment without introducing artifacts, the DSA module applies scale adjustments selectively to dynamic regions identified using motion masks derived from optical flow. A smoothness regularization term is included to enforce spatial consistency while preserving depth discontinuities at object boundaries. This design minimizes edge misalignment and over-smoothing, ensuring that depth predictions near moving objects are both accurate and artifact-free. The visual results presented in
Figure 4 illustrate these improvements and were selected randomly from the test set of the KITTI dataset to avoid cherry-picking. To further validate the generalizability of the DI-MDE framework, we conducted additional evaluations on dynamic datasets such as nuScenes and Waymo. Consistent qualitative and quantitative improvements were observed, demonstrating the robustness of the framework across diverse dynamic environments.
4.4. Qualitative Analysis of DI-MDE Performance in Dynamic Scenarios
While the quantitative results demonstrate DI-MDE’s superiority over existing methods, a more detailed analysis is needed to fully support the claim that DI-MDE solves the error bias problem in dynamic scenarios. To illustrate this, we provide an in-depth comparison of DI-MDE performance with multiple moving objects and scenes with varying levels of motion complexity. The following tables summarize DI-MDE’s effectiveness in these challenging environments. One of the key advantages of DI-MDE is its ability to maintain accurate depth predictions in scenes with multiple moving objects.
Table 6 highlights the comparative performance of DI-MDE against baseline models in a set of dynamic scenarios featuring different numbers of moving targets.
As shown in
Table 6, DI-MDE consistently outperforms AdaBins and FC-CRFs in scenes with varying numbers of moving targets. The iterative refinement process employed by DI-MDE allows for more precise depth predictions, especially in scenarios where baseline methods struggle to handle depth discontinuities and the motion of multiple objects. In addition to multiple moving objects, DI-MDE demonstrates an enhanced performance in scenarios where the motion complexity increases.
Table 7 compares the performance of DI-MDE and existing models in scenes with different levels of motion complexity, measured by the number of independently moving objects and their speed.
Table 7 illustrates how the DI-MDE iterative refinement process enables the model to better handle complex motion scenarios. As the speed and number of moving targets increase, DI-MDE shows significant reductions in absolute relative error and RMSE, while maintaining a high threshold accuracy. To further explore DI-MDE’s ability to solve the error bias problem,
Table 8 compares the depth estimation error across multiple independent objects of varying sizes and speeds in complex dynamic scenes. These results demonstrate how DI-MDE mitigates the error bias typically seen in baseline models when handling fast-moving or overlapping objects.
Table 8 further illustrates how DI-MDE handles varying object types and speeds, particularly in terms of mitigating the error bias. The results clearly show that DI-MDE reduces the error bias significantly across different object types and speeds, especially when compared to AdaBins and FC-CR.
In terms of floating-point operations per second (FLOPs), DI-MDE requires 124.7 GFLOPs per forward pass, which is approximately 18% lower than AdaBins and FC-CRFs. AdaBins, for instance, consumes around 153.2 GFLOPs, while FC-CRFs require 160.4 GFLOPs. This reduction in FLOPs demonstrates that DI-MDE is more computationally efficient, allowing for faster inference times and lower energy consumption in real-time applications. The lower computational demand also makes DI-MDE more scalable, particularly in environments where processing power is limited. Running time is another key metric, especially for models designed for real-time deployment. On a high-end NVIDIA RTX 2080 Ti GPU, DI-MDE achieves an average inference time of 38.2 ms per frame, translating to approximately 26 frames per second (FPS). In contrast, AdaBins runs at 45.6 ms per frame (22 FPS), and FC-CRFs takes 50.1 ms per frame (20 FPS). The faster running time of DI-MDE is critical for real-time applications such as autonomous driving and robotics, where timely depth estimation is crucial for safe navigation and interaction. On more resource-constrained devices, such as the NVIDIA Jetson TX2, DI-MDE maintains its performance edge, achieving an inference time of 61.9 ms per frame (16 FPS), compared to AdaBins at 78.3 ms per frame (13 FPS) and FC-CRFs at 85.7 ms per frame (11 FPS). This demonstrates the model’s efficiency and its ability to perform well on edge devices, where real-time depth estimation is required but computational resources are limited.