Inversion of Mechanical Parameters of Tunnel Surrounding Rock Based on Improved GWO-BP Neural Network
Abstract
1. Introduction
2. Methods
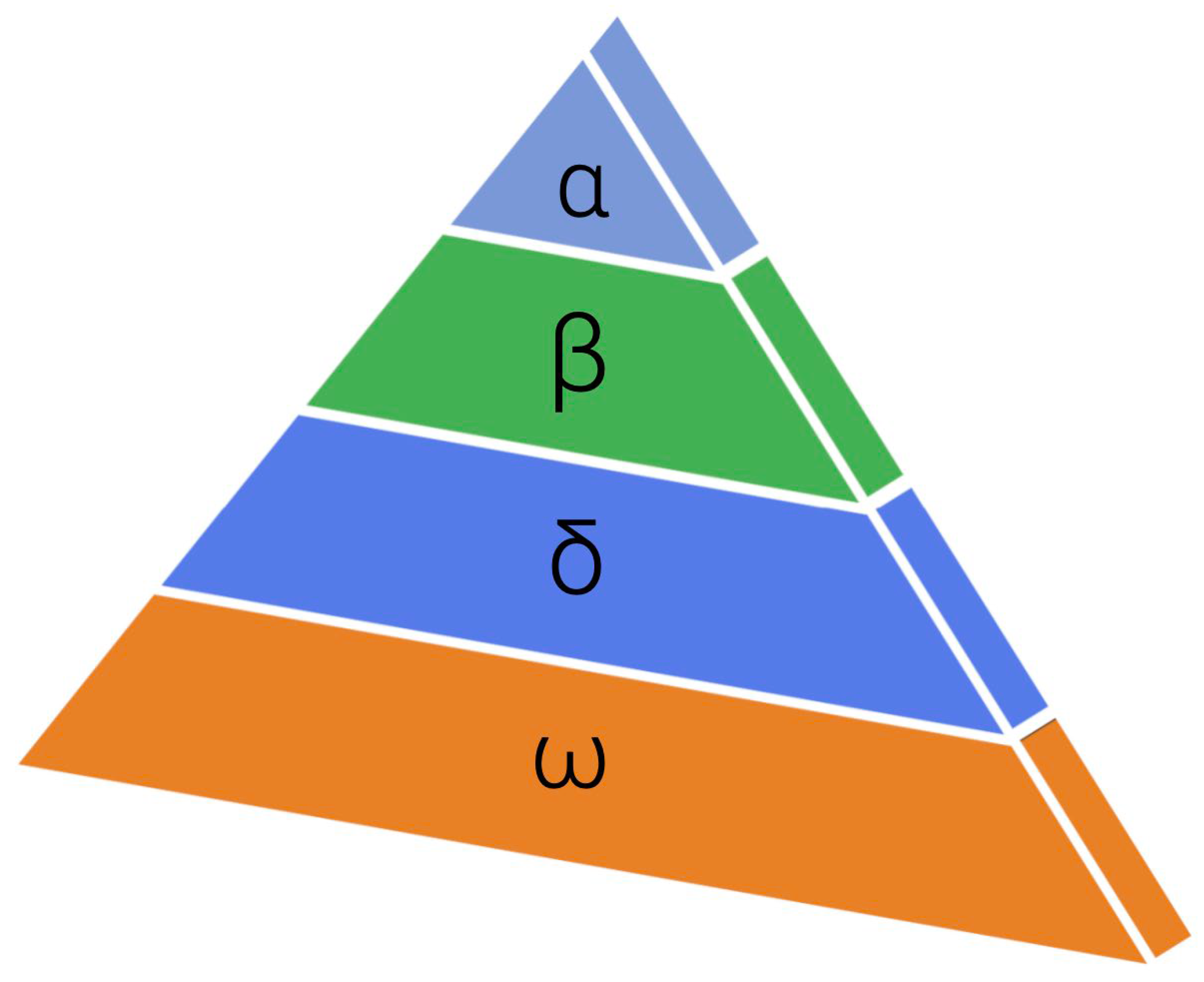
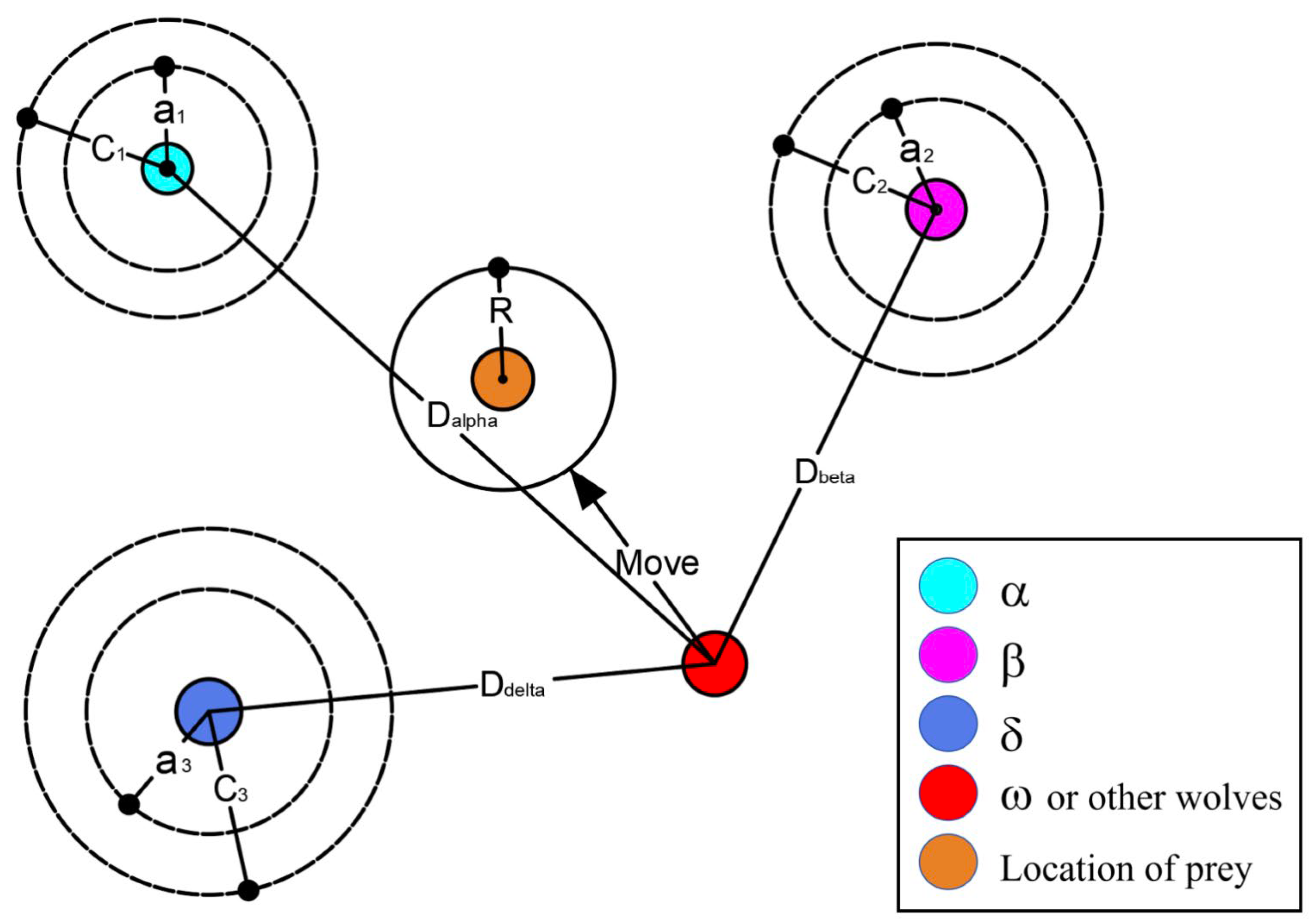
2.1. Principles of GWO
2.2. Improved Grey Wolf Optimizer (IGWO)
- Population Initialization Stage
- 2.
- Position Vector Update Stage
- 3.
- Enhancements to Step Size and Leadership Influence
2.2.1. The Integration of Cubic Chaotic Mapping and Reverse Learning Strategies
- 4.
- Diversification of the Initial Population
- 5.
- Elitization of the Initial Population
- Initial Population Creation
- Chaotic and Reverse Transformations
- Elite Population Formation
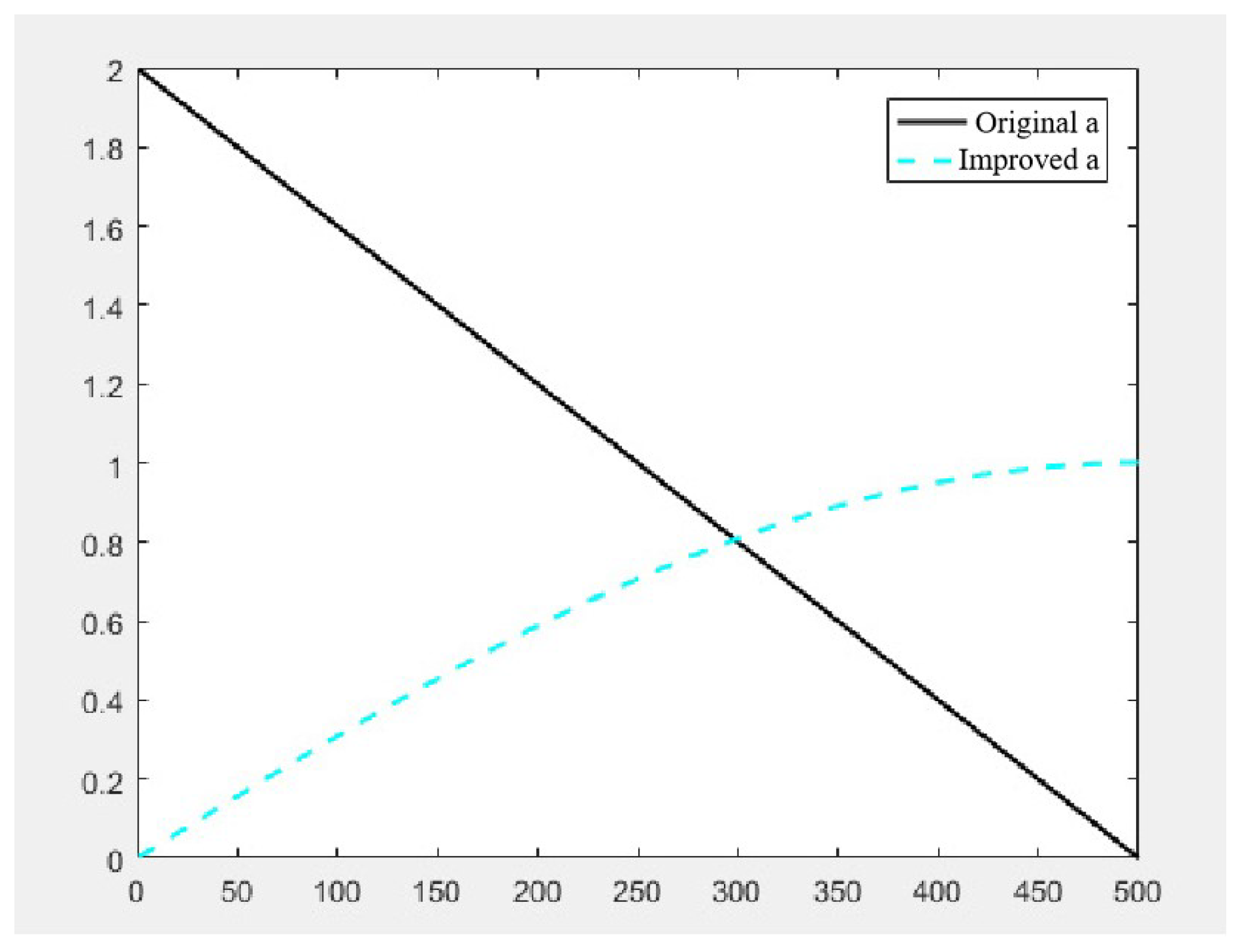
2.2.2. Nonlinear Convergence Factor
2.2.3. Adjusting the Position Update Mechanism
- 6.
- Incorporating Step Size Proportional Weight
- 7.
- Enhancing the Significance of Position Updates by the Alpha Wolf
3. Implementation
3.1. Evaluating the Enhanced Algorithm Through Tests and Simulations
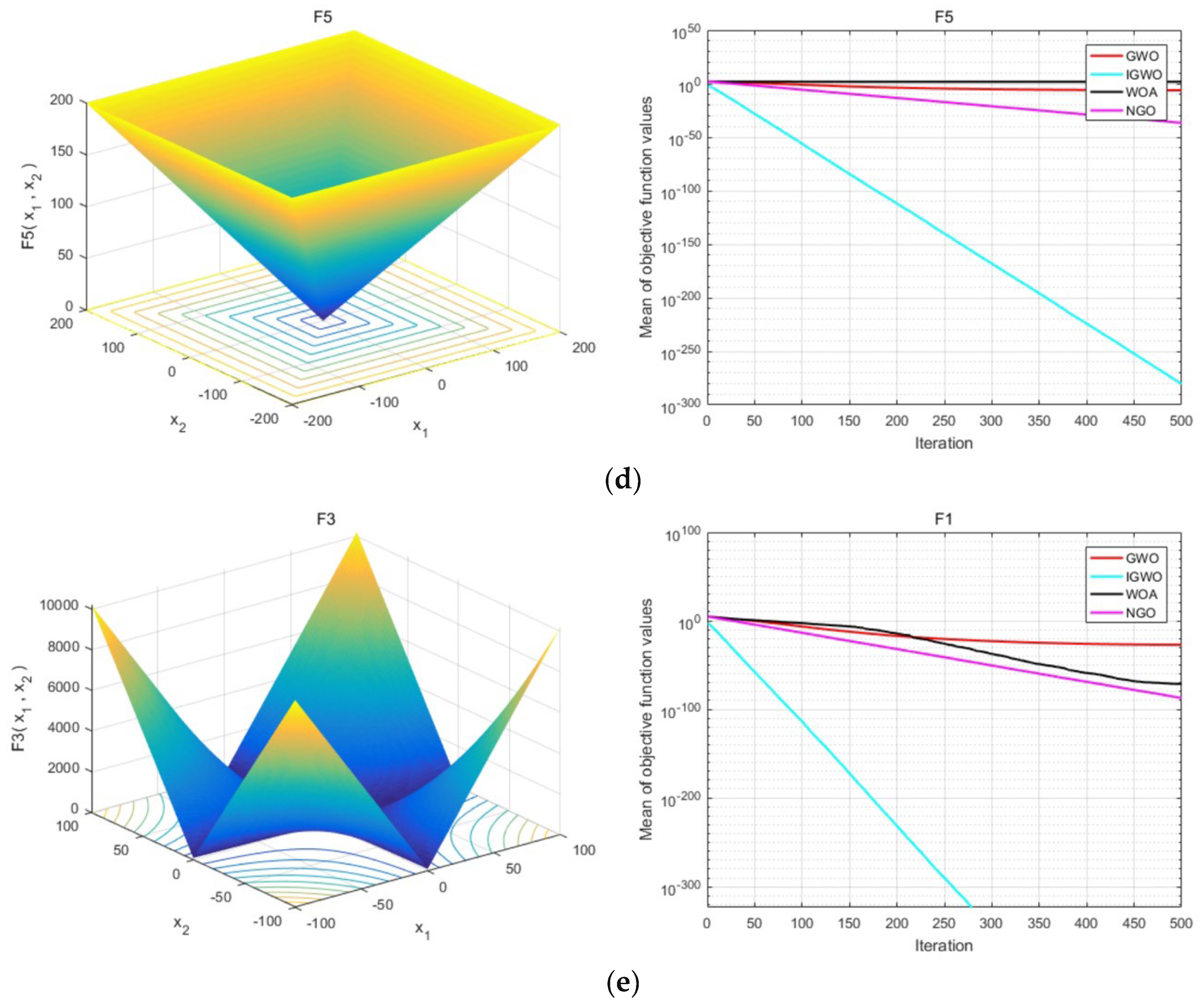
3.1.1. Benchmark Functions
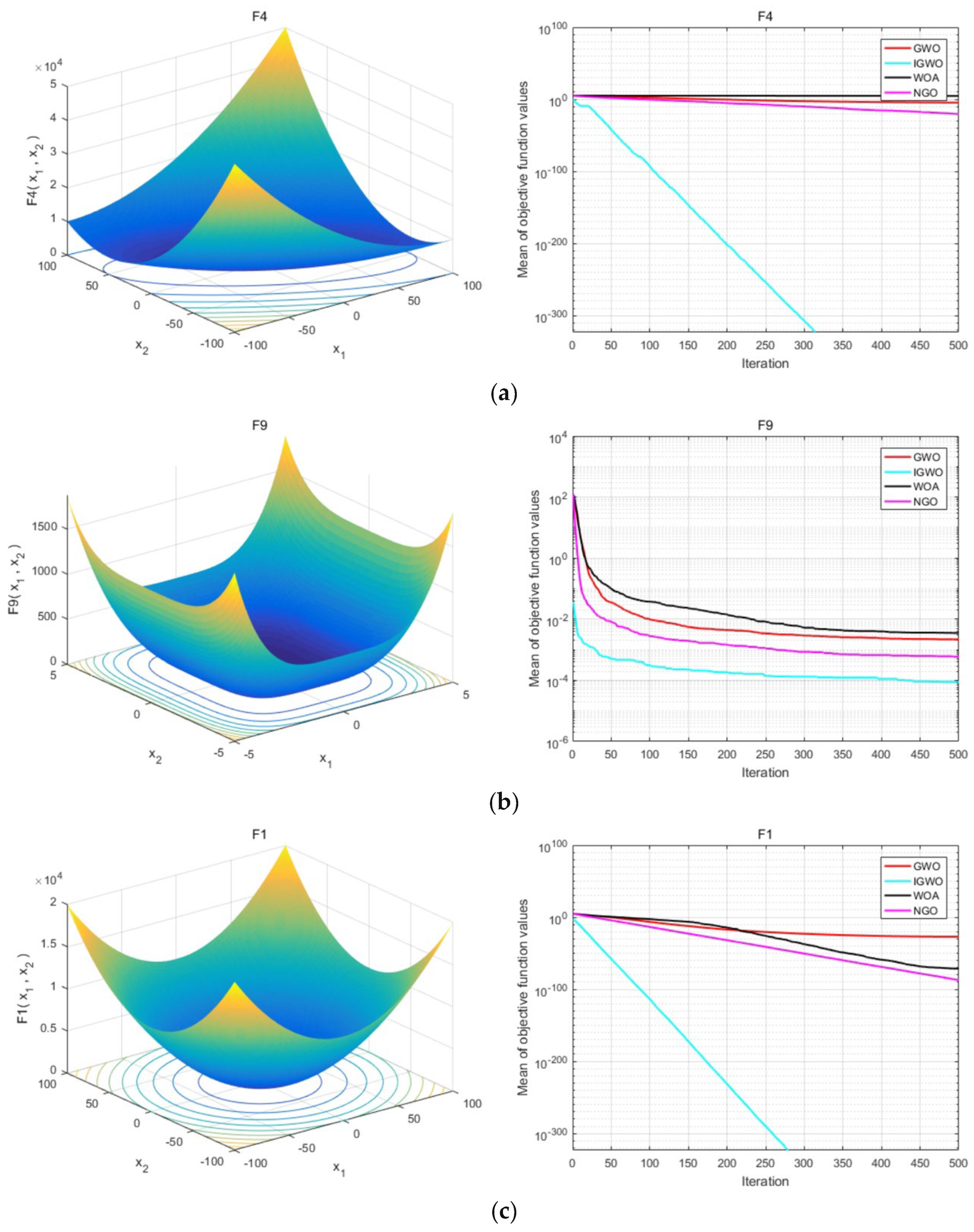
3.1.2. Evaluating IGWO Against Competing Algorithms
- 8.
- The IGWO algorithm outperforms the basic GWO, WOA, and NGO algorithms in terms of both accuracy and robustness, as evidenced by its mean values and standard deviations across all test functions.
- 9.
- In dealing with unimodal functions (), the IGWO achieves global optimums or near-optimums more efficiently than its counterparts.
- 10.
- When tackling multimodal functions (), the IGWO successfully navigates away from local optima to secure superior solutions, especially apparent in its performance on the Rastrigin () and Griewank () functions where it, alongside NGO, reaches the global optimum with minimal standard deviation. In contrast, the basic GWO is notably prone to settling at local optima.
- 11.
- Overall, the IGWO algorithm’s results across various test functions attest to its excellent versatility and adaptability, showcasing its effectiveness in addressing optimization challenges of varying types and complexities.
4. Experiments and Analyses
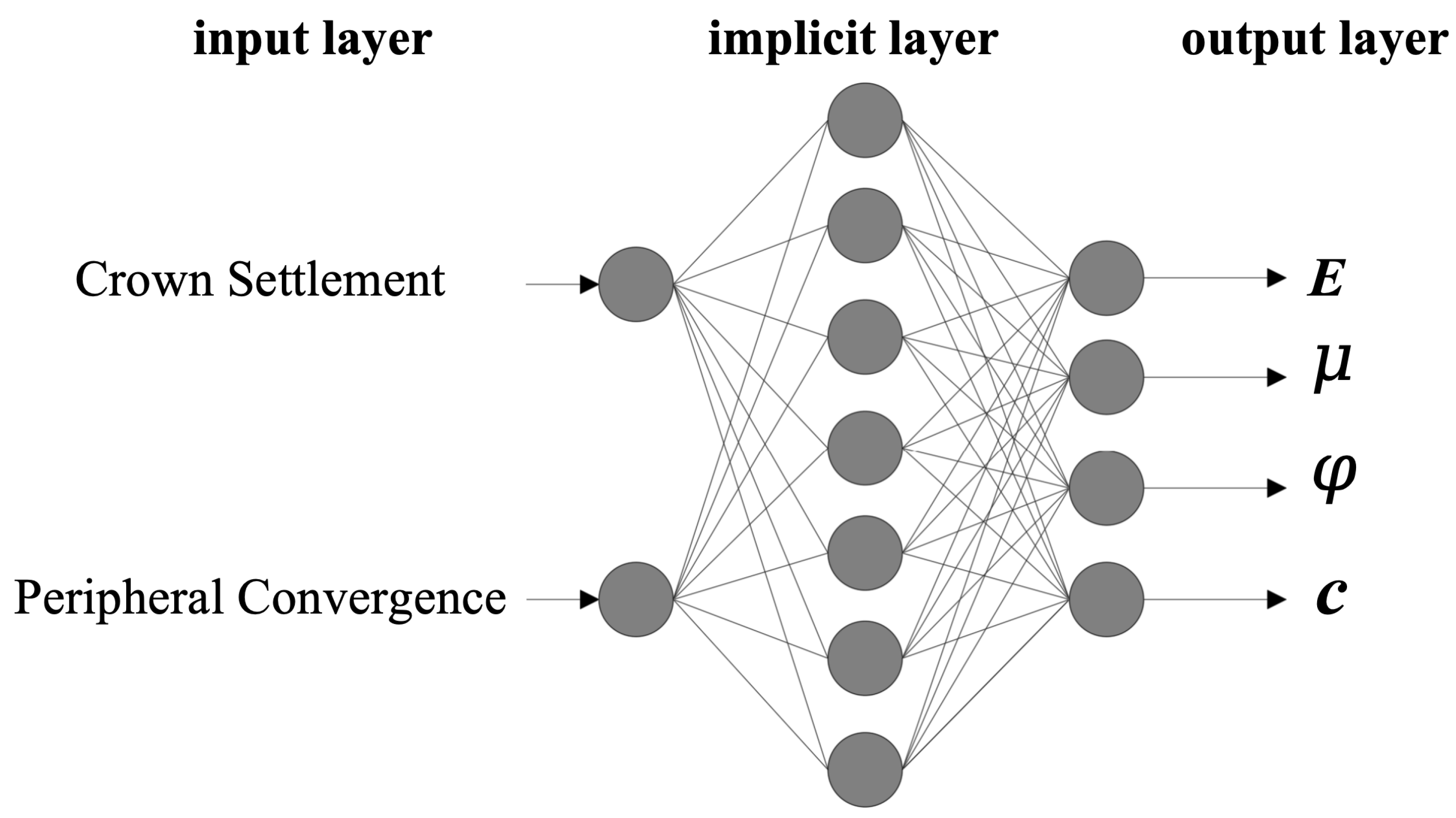
4.1. Inverse Analysis of Tunnel Surrounding Rock Mechanical Parameters Based on IGWO-BP
4.2. Forward Verification
4.2.1. Project Overview
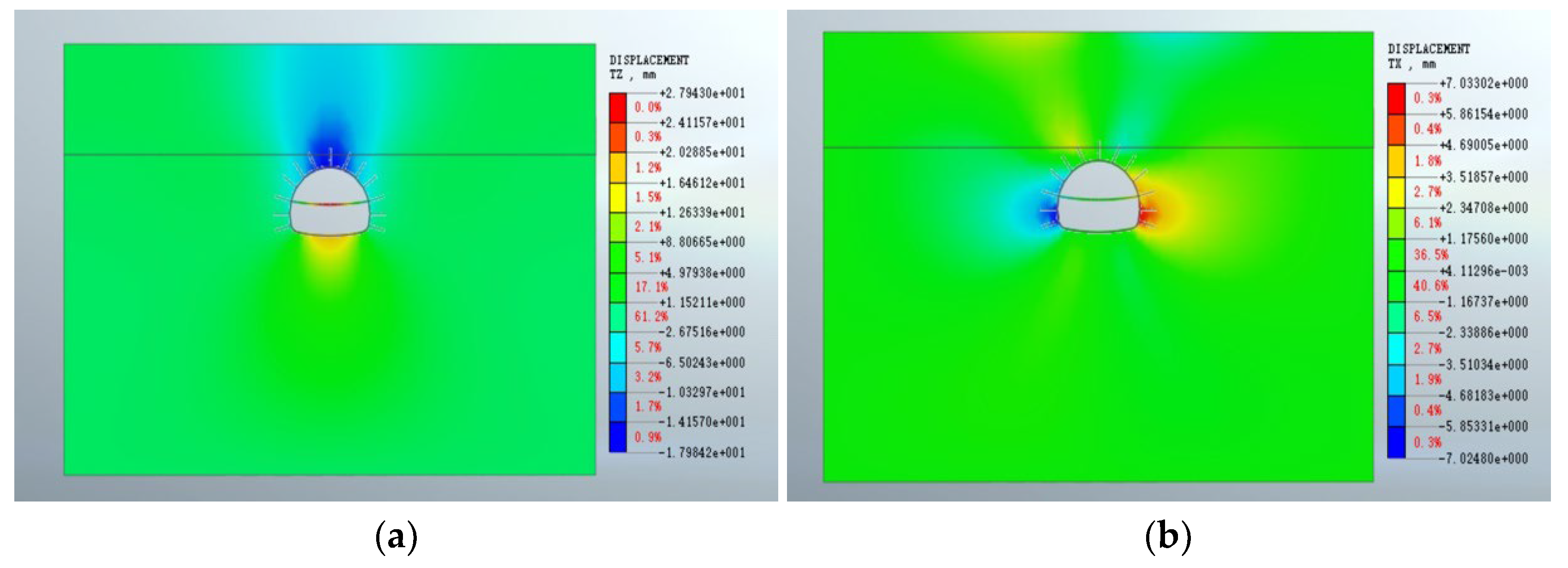
4.2.2. Developing the Tunnel Model
5. Conclusions
- 12.
- This research thoroughly analyzes the limitations of the Grey Wolf Algorithm and proposes an enhanced version, the Improved Grey Wolf Optimization (IGWO). This upgraded algorithm leverages cubic chaotic mapping and a refraction reverse learning strategy for optimizing the initial population, significantly improving data diversity and uniqueness. Moreover, by substituting the traditional linear convergence factor with a nonlinear one and introducing new parameters such as step size ratio weight and leading wolf weight, the algorithm notably enhances its ability to balance local and global search capabilities. This enhancement not only allows for a more effective escape from local optima but also substantially improves optimization efficiency and accuracy.
- 13.
- In applying this to surrounding rock parameter inversion, the study utilizes an IGWO-optimized BP neural network model, incorporating orthogonal analysis methods to devise 25 numerical simulation experiments. These experiments, which take vault settlement and peripheral convergence data as inputs and output the mechanical parameters of surrounding rock, establish a reverse analysis model. The IGWO-BP neural network model’s effectiveness and accuracy in inverting surrounding rock parameters are confirmed by inverse analysis of actual data from YK37 + 330, achieving relative errors of 5.02% in vault settlement and 4.15% in peripheral convergence. These results highlight the model’s precision and practicality.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Davarpanah, S.M.; Sharifzadeh, M.; Sattarvand, J.; Narimani, S. Evaluation of building displacement induced by EPB tunneling through GPS-GNSS monitoring system and back analysis technique (Tabriz Subway Twin Tunnels). Civ. Eng. J. 2016, 2, 270–285. [Google Scholar] [CrossRef]
- Deng, H.-S.; Fu, H.-L.; Shi, Y.; Zhao, Y.-Y.; Hou, W.-Z. Countermeasures against large deformation of deep-buried soft rock tunnels in areas with high geostress: A case study. Tunn. Undergr. Space Technol. 2022, 119, 104238. [Google Scholar] [CrossRef]
- Ferrero, A.M.; Migliazza, M.; Segalini, A.; Gullì, D. In situ stress measurements interpretations in large underground marble quarry by 3D modeling. Int. J. Rock Mech. Min. Sci. 2013, 60, 103–113. [Google Scholar] [CrossRef][Green Version]
- Kirsten, H. Determination of rock mass elastic moduli by back analysis of deformation measurements. Explor. Rock Eng. 1976, 1, 165–172. [Google Scholar]
- Sakurai, S.; Abe, S. A design approach to dimensioning underground openings. In Proceedings of the 3nd International Conference on Numerical Methods in Geomechanics, Aachen, Germany, 2–6 April 1979. [Google Scholar]
- Gioda, G.; Maier, G. Direct search solution of an inverse problem in elastoplasticity: Identification of cohesion, friction angle and in situ stress by pressure tunnel tests. Int. J. Numer. Methods Eng. 1980, 15, 1823–1848. [Google Scholar] [CrossRef]
- Sakurai, S.; Takeuchi, K. Back analysis of measured displacements of tunnels. Rock Mech. Rock Eng. 1983, 16, 173–180. [Google Scholar] [CrossRef]
- Yang, Z.; Liu, Z. The elementary applications of back-analysis from displacements in designs of underground engineering. Undergr. Eng. 1981, 2, 20–24. [Google Scholar] [CrossRef]
- Guo, H.Z.; Ma, Q.C.; Xue, X.C.; Wang, D. The analytical method of the initial stress field for rock masses. Chin. J. Geotech. Eng. 1983, 5, 64–75. (In Chinese) [Google Scholar]
- Feng, X.; Zhang, Z.; Yang, C.X.; Lin, Y.M. Study on genetic neural network method of displacement back analysis. Chin. J. Rock Mech. Eng. 1999, 18, 529–633. [Google Scholar]
- Ravandi, E.G.; Rahmannejad, R.; Monfared, A.E.; Ravandi, E.G. Application of numerical modeling and genetic programming to estimate rock mass modulus of deformation. Int. J. Min. Sci. Technol. 2013, 23, 733–737. [Google Scholar] [CrossRef]
- Miro, S.; König, M.; Hartmann, D.; Schanz, T. A probabilistic analysis of subsoil parameters uncertainty impacts on tunnel-induced ground movements with a back-analysis study. Comput. Geotech. 2015, 68, 38–53. [Google Scholar] [CrossRef]
- Gao, W.; Chen, D.; Dai, S.; Wang, X. Back analysis for mechanical parameters of surrounding rock for underground roadways based on new neural network. Eng. Comput. 2018, 34, 25–36. [Google Scholar] [CrossRef]
- Wan, Z.; Huang, Y.; Zhu, Z.; Wang, T.; Jing, J.; Xiao, L. Back analysis on mechanical parameters of RCC dam during operation period in alpine region. Water Conserv. Hydropower Technol. 2017, 48, 50–55. [Google Scholar]
- Zhuang, D.; Ma, K.; Tang, C.; Liang, Z.; Wang, K.; Wang, Z. Mechanical parameter inversion in tunnel engineering using support vector regression optimized by multi-strategy artificial fish swarm algorithm. Tunn. Undergr. Space Technol. 2019, 83, 425–436. [Google Scholar] [CrossRef]
- Liu, J.; Weng, X.J.; Zhang, L.S.; Zhang, L.Z. Inversion of mechanical parameters of tunnel surrounding rock based on GA-BP neural network. Chin. J. J. Highw. Transp. Res. Dev. 2020, 37, 90–96. [Google Scholar]
- Cui, J.; Wu, S.; Cheng, H.; Kui, G.; Zhang, H.; Hu, M.; He, P. Composite interpretability optimization ensemble learning inversion surrounding rock mechanical parameters and support optimization in soft rock tunnels. Comput. Geotech. 2024, 165, 105877. [Google Scholar] [CrossRef]
- Zhao, H.; Feng, X. Study on genetic-support vector machine in displacement back analysis. Chin. J. Rock Mech. Eng. 2003, 22, 1618–1622. [Google Scholar]
- Zhou, G.; Sun, Y.; Jia, P. Application of genetic algorithm based BP neural network to parameter inversion of surrounding rock and deformation prediction. Mod. Tunn. Technol. 2018, 55, 107–113. [Google Scholar]
- Gao, W. Back analysis algorithm in geotechnical engineering based on particle swarm optimization. Yantu Lixue Rock Soil Mech. 2006, 27, 795–798. [Google Scholar]
- Kai, W.; Qian, S.; Song, M.E. A model of PSO-LSSVM and its application to displacement back analysis. Rock Soil Mech. 2009, 30, 1109–1114. [Google Scholar]
- Qi, Z.; Jiang, Q.H.; Zhou, C.B.; Xiang, B.Y.; Shao, J.D. A new slope displacement back analysis method based on v-SVR and MVPSO algorithm and its application. Chin. J. Rock Mech. Eng. 2013, 32, 1185–1196. [Google Scholar]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.Z.; Mirjalili, S.M. Evolutionary population dynamics and grey wolf optimizer. Neural Comput. Appl. 2015, 26, 1257–1263. [Google Scholar] [CrossRef]
- Gholizadeh, S. Optimal design of double layer grids considering nonlinear behaviour by sequential grey wolf algorithm. J. Optim. Civ. Eng. 2015, 5, 511–523. [Google Scholar]
- Jayabarathi, T.; Raghunathan, T.; Adarsh, B.; Suganthan, P.N. Economic dispatch using hybrid grey wolf optimizer. Energy 2016, 111, 630–641. [Google Scholar] [CrossRef]
- Heidari, A.A.; Pahlavani, P. An efficient modified grey wolf optimizer with Lévy flight for optimization tasks. Appl. Soft Comput. 2017, 60, 115–134. [Google Scholar] [CrossRef]
- Kumar, V.; Kumar, D. An astrophysics-inspired grey wolf algorithm for numerical optimization and its application to engineering design problems. Adv. Eng. Softw. 2017, 112, 231–254. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, H.; Han, T.; Zhou, H.; Li, C. A grey wolf optimizer using Gaussian estimation of distribution and its application in the multi-UAV multi-target urban tracking problem. Appl. Soft Comput. 2019, 78, 240–260. [Google Scholar] [CrossRef]
- Kamboj, V.K. A novel hybrid PSO–GWO approach for unit commitment problem. Neural Comput. Appl. 2016, 27, 1643–1655. [Google Scholar] [CrossRef]
- Turabieh, H. A hybrid ANN-GWO algorithm for prediction of heart disease. Am. J. Oper. Res. 2016, 6, 136–146. [Google Scholar] [CrossRef]
- Zhang, X.; Kang, Q.; Cheng, J.; Wang, X. A novel hybrid algorithm based on biogeography-based optimization and grey wolf optimizer. Appl. Soft Comput. 2018, 67, 197–214. [Google Scholar] [CrossRef]
- Padhy, S.; Panda, S.; Mahapatra, S. A modified GWO technique based cascade PI-PD controller for AGC of power systems in presence of plug in electric vehicles. Eng. Sci. Technol. Int. J. 2017, 20, 427–442. [Google Scholar] [CrossRef]
- Moscato, P. On evolution, search, optimization, genetic algorithms and martial arts: Towards memetic algorithms. Caltech Concurr. Comput. Program C3P Rep. 1989, 826, 37. [Google Scholar]
- Wang, D.; Tan, D.; Liu, L. Particle swarm optimization algorithm: An overview. Soft Comput. 2018, 22, 387–408. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Price, K.V. Differential evolution. In Handbook of Optimization: From Classical to Modern Approach; Springer: Berlin/Heidelberg, Germany, 2013; pp. 187–214. [Google Scholar]
- Song, H.M.; Sulaiman, M.H.; Mohamed, M.R. An application of grey wolf optimizer for solving combined economic emission dispatch problems. Int. Rev. Model. Simul. 2014, 7, 838–844. [Google Scholar]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Dehghani, M.; Hubálovský, Š.; Trojovský, P. Northern goshawk optimization: A new swarm-based algorithm for solving optimization problems. IEEE Access 2021, 9, 162059–162080. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, L.; Wang, M.; Yang, H. Mechanical response and failure characteristics of tunnels subjected to reverse faulting with nonuniform displacement: Theoretical and numerical investigation. Eng. Fail. Anal. 2024, 156, 107809. [Google Scholar] [CrossRef]
- Song, Z.; Yang, Z.; Huo, R.; Zhang, Y. Inversion analysis method for tunnel and underground space engineering: A short review. Appl. Sci. 2023, 13, 5454. [Google Scholar] [CrossRef]


| Function Name | Function Expression | Search Range | fmin |
|---|---|---|---|
| Schwefel 1.2 | [−100, 100] | 0 | |
| Quartic | [−1.28, 1.28] | 0 | |
| Sphere | [−100, 100] | 0 | |
| Schwefel 2.21 | [−100, 100] | 0 | |
| Schwefel 2.22 | [−10, 10] | 0 | |
| Schwefel 2.26 | [−500, 500] | −12,569.5 | |
| Rastrigin | [−5.12, 5.12] | 0 | |
| Ackley | [−32, 32] | 0 | |
| Griewank | [−50, 50] | 0 | |
| Goldstein Price | [−2, 2] | 3 |
| Function | GWO | WOA | NGO | IGWO | |
|---|---|---|---|---|---|
| f1 | Mean | 3.9762 × 10−6 | 47,898.1385 | 1.1477 × 10−22 | 0 |
| Standard Deviation | 9.4465 × 10−6 | 10,779.6838 | 4.0563 × 10−22 | 0 | |
| f2 | Mean | 0.0019989 | 0.0035984 | 0.00070632 | 7.1205 × 10−5 |
| Standard Deviation | 0.0012469 | 0.0054488 | 0.00030836 | 6.8094 × 10−5 | |
| f3 | Mean | 1.0125 × 10−27 | 2.3525 × 10−72 | 7.7076 × 10−88 | 0 |
| Standard Deviation | 1.5709 × 10−27 | 1.2881 × 10−71 | 1.2394 × 10−87 | 0 | |
| f4 | Mean | 6.7115 × 10−7 | 38.1611 | 1.2477 × 10−37 | 3.1068 × 10−279 |
| Standard Deviation | 4.8223 × 10−7 | 29.044 | 1.023 × 10−37 | 0 | |
| f5 | Mean | 1.06 × 10−16 | 6.8394 × 10−52 | 1.2728 × 10−45 | 7.4703 × 10−305 |
| Standard Deviation | 8.6006 × 10−17 | 2.2572 × 10−51 | 1.3106 × 10−45 | 0 | |
| f6 | Mean | −5818.9213 | −10,324.6818 | −7637.5386 | −3466.9346 |
| Standard Deviation | 795.4492 | 1763.6363 | 613.4378 | 118.4035 | |
| f7 | Mean | 1.176 | 0 | 0 | 0 |
| Standard Deviation | 2.3394 | 0 | 0 | 0 | |
| f8 | Mean | 1.019 × 10−13 | 4.6777 × 10−15 | 6.6909 × 10−15 | 8.8818 × 10−16 |
| Standard Deviation | 1.694 × 10−14 | 2.9405 × 10−15 | 1.7413 × 10−15 | 0 | |
| f9 | Mean | 0.0022384 | 0.010723 | 0 | 0 |
| Standard Deviation | 0.006078 | 0.040847 | 0 | 0 | |
| f10 | Mean | 5.7 | 3 | 3 | 599.8247 |
| Standard Deviation | 14.7885 | 8.3808 × 10−5 | 1.2802 × 10−15 | 0.019301 |
| Test Number | Output Vector | Input Vector | ||||
|---|---|---|---|---|---|---|
| kPa | GPa | Crown Settlement | Peripheral Convergence | |||
| 1 | 80 | 20 | 200 | 0.32 | 17.82 | 8.44 |
| 2 | 80 | 22 | 250 | 0.34 | 14.28 | 6.74 |
| 3 | 80 | 24 | 300 | 0.36 | 11.78 | 5.58 |
| 4 | 80 | 26 | 350 | 0.38 | 9.98 | 4.74 |
| 5 | 80 | 28 | 400 | 0.40 | 12.23 | 6.84 |
| 6 | 110 | 20 | 250 | 0.36 | 10.14 | 5.62 |
| 7 | 110 | 22 | 300 | 0.38 | 8.61 | 4.63 |
| 8 | 110 | 24 | 350 | 0.40 | 7.46 | 4.08 |
| 9 | 110 | 26 | 400 | 0.32 | 10.18 | 6.78 |
| 10 | 110 | 28 | 200 | 0.34 | 8.42 | 5.07 |
| 11 | 140 | 20 | 300 | 0.40 | 7.19 | 4.33 |
| 12 | 140 | 22 | 350 | 0.32 | 6.29 | 3.76 |
| 13 | 140 | 24 | 400 | 0.34 | 8.38 | 6.30 |
| 14 | 140 | 26 | 200 | 0.36 | 7.25 | 5.16 |
| 15 | 140 | 28 | 250 | 0.38 | 6.37 | 4.06 |
| 16 | 170 | 20 | 350 | 0.34 | 5.68 | 3.54 |
| 17 | 170 | 22 | 400 | 0.36 | 7.58 | 5.99 |
| 18 | 170 | 24 | 200 | 0.38 | 6.66 | 4.97 |
| 19 | 170 | 26 | 250 | 0.40 | 5.98 | 4.26 |
| 20 | 170 | 28 | 300 | 0.32 | 5.30 | 3.42 |
| 21 | 200 | 20 | 400 | 0.38 | 7.11 | 5.81 |
| 22 | 200 | 22 | 200 | 0.40 | 6.32 | 4.82 |
| 23 | 200 | 24 | 250 | 0.32 | 5.72 | 4.18 |
| 24 | 200 | 26 | 300 | 0.34 | 5.24 | 3.66 |
| 25 | 200 | 28 | 350 | 0.32 | 17.82 | 8.44 |
| Material | GPa | kPa | Unit Weight/kN/m3 | ||
|---|---|---|---|---|---|
| First Soil Layer | 0.4 | 0.35 | 50 | 20 | 20 |
| Second Soil Layer | —— * | 20 | |||
| Anchor Bolts/ Steel Arches | 210 | 0.3 | - | - | 78.5 |
| Shotcrete | 28 | 0.2 | - | - | 24 |
| Pile Number | Monitoring Items | Measured Values/mm | Calculated Values/mm | Error/% | Inversion Parameters | |||
|---|---|---|---|---|---|---|---|---|
| GPa | kPa | |||||||
| YK37 + 330 | Crown Settlement | 17.12 | 17.98 | 5.02 | 0.32 | 0.26 | 156.14 | 28.52 |
| Peripheral Convergence | 6.74 | 7.02 | 4.15 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Chen, Q.; Zhou, W.; Huang, X. Inversion of Mechanical Parameters of Tunnel Surrounding Rock Based on Improved GWO-BP Neural Network. Appl. Sci. 2025, 15, 537. https://doi.org/10.3390/app15020537
Zhang C, Chen Q, Zhou W, Huang X. Inversion of Mechanical Parameters of Tunnel Surrounding Rock Based on Improved GWO-BP Neural Network. Applied Sciences. 2025; 15(2):537. https://doi.org/10.3390/app15020537
Chicago/Turabian StyleZhang, Chen, Qiunan Chen, Wenbing Zhou, and Xiaocheng Huang. 2025. "Inversion of Mechanical Parameters of Tunnel Surrounding Rock Based on Improved GWO-BP Neural Network" Applied Sciences 15, no. 2: 537. https://doi.org/10.3390/app15020537
APA StyleZhang, C., Chen, Q., Zhou, W., & Huang, X. (2025). Inversion of Mechanical Parameters of Tunnel Surrounding Rock Based on Improved GWO-BP Neural Network. Applied Sciences, 15(2), 537. https://doi.org/10.3390/app15020537







