Abstract
Conducting research on the dynamic behavior of root–soil systems is crucial for accurately assessing the seismic response of ecological slopes, thereby providing a scientific foundation for the development of appropriate seismic design measures. Documentation of the improvement of soil dynamics through vegetation root systems is insufficient in the current research. This study utilizes resonance column tests to explore how root systems influence the dynamic properties of clayey soil and to uncover the mechanisms behind this enhancement. The results indicate that both root distribution and mass density have a significant impact on the soil’s dynamic shear modulus and damping ratio. When roots are distributed in the upper part of the soil, the dynamic shear modulus and damping ratio of the soil are higher than in cases of even distribution or concentration in the lower part. The dynamic shear modulus initially increases and then decreases with the increase in root mass density, reaching its peak at a root mass density of 1.5% g·cm−3. The damping ratio is influenced by both root mass density and confining pressure, with different critical root mass densities observed under varying confining pressures. The maximum enhancement in dynamic shear modulus is 27.6%, achieved at a 3% root mass density, with a peak damping ratio of 5.39%. Variations in both dynamic shear modulus and damping ratio with shear strain follow the Hardin–Drnevich hyperbolic curve.
1. Introduction
In recent decades, rapid development has been witnessed in critical infrastructure sectors such as highways, railways, and bridges in China. However, as a consequence, a significant number of exposed engineering slopes have been formed, making them highly susceptible to various geological hazards. As a response to this issue, vegetation-based ecological protection has emerged as an essential approach for mitigating engineering slope disasters and preserving the ecological environment, thus becoming a current research focus within the field of geotechnical engineering [1,2,3]. Vegetation-based ecological slopes are defined as measures adopted on slope surfaces, including grass planting and tree plantation, aiming to stabilize and protect the soil on the surface and prevent the occurrence of natural disasters such as soil erosion [4] and landslides [5]. Additionally, environmental beautification and the promotion of ecosystem restoration are also achieved through these measures [6].
The soil damping ratio, as a critical indicator of the energy dissipation capacity of soil under dynamic loading, holds extensive research value in the field of geotechnical engineering. Particularly in slope protection engineering, the soil damping ratio directly affects the stability and response characteristics of slopes under dynamic loads such as earthquakes and vibrations. In the 1960s and 1970s, extensive research was conducted on the damping ratio and shear modulus of soils by scholars such as Seed [7] and Hardin et al. [8,9]. It was observed that the damping ratio of soils tends to increase with the increase in shear strain amplitude. The experimental results of the dynamic stress–strain relationship of soil were analyzed and summarized by Chen et al. [10]. It was recommended to use the plasticity index to describe the empirical curve of the relationship between damping ratio and shear strain. However, it has been found that using a single parameter (such as plasticity index) to describe the damping ratio attenuation curve does not match the actual working load conditions (soil usually bears multiple complex dynamic loads, such as earthquakes, mechanical vibrations, and traffic loads).
The dynamic shear modulus and damping characteristics of red sandstone [11,12] and tailings [13,14] were investigated by researchers, yielding valuable research findings. Park D et al. [15] proposed empirical G/G max and D curves for the dynamic properties of cohesive core materials by analyzing the shear modulus and damping ratio curves of dam cores. Zhao et al. [16] conducted experimental research on the dynamic properties of fiber-modified soil, revealing that a fiber content of 0.2% resulted in minimal damage and maximum dynamic strength and elastic modulus for the modified soil samples. Collins KM et al. [17] conducted a dynamic analysis of gravel based on shear modulus and damping ratio, deriving a fitted relationship between optimal damping ratio and shear modulus. Li et al. [18] performed large-scale dynamic triaxial tests on rice husk ash-modified soil, analyzing the effects of the rice husk ash content, dynamic stress amplitude, and reinforcement method on the axial cumulative deformation, dynamic stress–strain curve, and dynamic elastic modulus. Tang et al. [19] investigated the improvement in the dynamic performance of loess in the Xining area before and after reinforcement using bidirectional geogrids.
The mechanism by which grass roots reinforce soil primarily involves two aspects: directly enhancing soil structure through physical interaction and regulating soil moisture and matric suction, while indirectly improving soil shear strength. Their combined effect significantly increases soil strength and stability. Most studies consider the tensile strength of roots as a direct measure of apparent root cohesion in slope soils [20].
Regarding the dynamic characteristics of root–soil composites, R. Sonnenberg et al. [21] controlled the growth of willows to provide different root systems and distribution characteristics. Using centrifuge model experiments for stability back-analysis, they found that roots provided only a limited amount of reinforcement. In contrast, when compared with measured root characteristics and commonly used root reinforcement models, roots were found to provide significant reinforcement. Therefore, further research is needed on the effective reinforcement of soil kernels by root systems. The presence of roots has been demonstrated by several studies to enhance the damping ratio and shear strength of soil. For instance, experimental and numerical investigations were conducted by Chenari et al. [22], in which metal wires were substituted for plant roots, resulting in an observed increase in the damping ratio with both shear displacement and root density. The performance of root-reinforced soil under cyclic loading was explored through triaxial cyclic loading tests conducted by Yan et al. [23], revealing improvements in the soil’s shear strength attributable to the presence of roots. Furthermore, experiments conducted by Liu et al. [24] revealed that roots possess a remarkable capacity to enhance soil resistance against liquefaction, with cross-placed roots exhibiting superior reinforcement effects. However, due to the complexity of soil and the difficulty in representing the three-dimensional distribution of roots with precise mathematical models, as well as the challenges in quantitatively capturing root–soil dynamic interactions), the influence of plant root content on soil dynamic properties remains in its early exploratory stage. As a result, a mass ratio methodology is proposed in this study to ascertain root content and dynamic characteristic tests on red clay with integrated roots prevalent in southern regions of China were conducted. By incorporating considerations such as root mass density and distribution, the temporal variations of the dynamic shear modulus and damping ratio of root–clay composites are elucidated by this investigation. These research findings provide valuable insights to inform the design of anti-seismic and anti-vibration measures for ecological slope protection along southern railway subgrades.
2. Experimental Materials with Tested Material
2.1. Experimental Materials
The test soil was obtained from the red clay of the railway embankment slope near Zhuzhou West Station in Hunan, China, as illustrated in Figure 1. The particle size distribution curve of the soil is presented in Figure 2. The physical parameters of the soil are detailed in Table 1. The soil particle gradation curve is relatively smooth without significant abrupt changes (the particle sizes at cumulative passing rates of 60%, 30%, and 10% are d60 = 1.0214, d30 = 0.3520, and d10 = 0.0955, respectively). The uniformity coefficient (Cu) is 10.70, and the curvature coefficient (Cc) is 1.27, indicating that it is well-graded soil [25].

Figure 1.
Clay in Zhuzhou city.
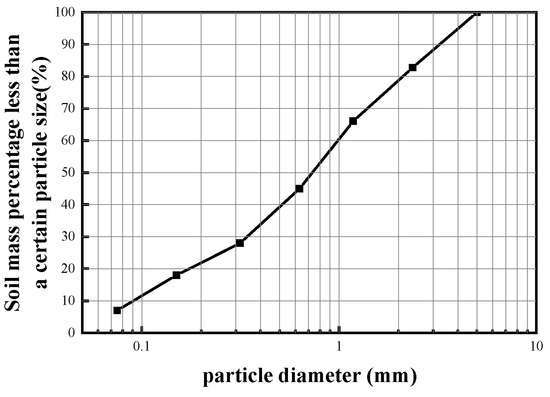
Figure 2.
Particle size grading curve of soil.

Table 1.
Physical parameters of soil.
The experiment employed the root systems of Cynodon dactylon, using grass roots with a diameter of 0.5–1 mm and maintaining the length of the grass roots between 8 mm and 10 mm. To quantify the number of roots added to the soil, we introduced the concept of root mass density.
The following terms are defined as follows: represents the root mass density, stands for the total mass of roots within the soil sample, and V signifies the volume of the soil sample.
2.2. Tested Equipment
For this experiment, the GDSRCA resonant column testing system, developed by the British company GDS, was utilized. The testing system includes a computer, a data acquisition unit, a backpressure controller, software-driven components, and signal amplifiers as detailed in reference [26], depicted in Figure 3. The resonant column testing utilizes an electromagnetic drive system to generate sinusoidal vibrations. In torsional experiments, four pairs of coils are connected in series to generate torque acting on the soil specimen. Due to the influence of the magnetic field, the drive disk undergoes oscillatory motion. Adjusting the frequency and amplitude of the applied voltage enables the identification of the resonant frequency of the specimen. The amplitude can be detected by scanning the frequency applied using an accelerometer positioned on the drive disk.

Figure 3.
Resonance column test system.
2.3. Experimental Procedure
To investigate the influence of plant roots in the 1–5 m clay layer on the dynamic properties of soil, three different confining pressures (100 kPa, 200 kPa, and 300 kPa) were applied. The root mass density of clay is generally low, ranging between 0 and 0.03 [27]. Therefore, the dynamic shear modulus and damping ratio of clay were tested under five different root mass density conditions (0%, 1%, 1.5%, 2%, 2.5%, and 3%).
The experimental plant selected was Cynodon dactylon, a common local herbaceous plant. It is a widely distributed grass species native to tropical and subtropical regions, including Africa, Asia, and southern Europe. It is now widely cultivated globally, especially in warm climates such as the southern United States, China, India, and Australia. Its chemical composition is primarily cellulose and minerals, with fiber components mainly consisting of cellulose, hemicellulose, and lignin. Due to its strong drought resistance, it is often used for slope protection and soil and water conservation [28].
The resonant column specimens were cylindrical, with a diameter of 50 mm and a height of 100 mm. Due to specimen size limitations, Cynodon dactylon roots with a diameter of 0.5–1 mm and a length of 8–10 mm were selected. The specimen soil was dried at 108 °C for 8 h and then prepared with a dry density of 1.65 and a water content of 12%. To thoroughly mix Cynodon dactylon roots with the soil, the soil and roots were evenly divided into five portions by weight, as required by the standard [25]. The mixture was layered into the mold in 20 mm layers, as shown in Figure 4.

Figure 4.
Test specimen.
In the installation process of the resonant column test, it is crucial to start by covering the specimen with latex film and securing it onto the base of the resonant column, ensuring airtightness. Next, place the top cap, install the drive system, and connect the drive disk to the specimen’s top cap. Install the accelerometer, connect the coils, and safeguard the coil wires. Mount the top disk/LVDT on the top of the resonant column. After completing the installation of all components, double-check the magnet positions in the coils and make necessary adjustments to ensure the safety of all wires. Lastly, install the glass cover to complete the assembly of the entire testing apparatus. Careful execution of this process, involving detailed operations and precise adjustments, is crucial for ensuring the accuracy and reliability of the experiment, as depicted in Figure 5. In the preliminary experiments, fine-grained soils such as clay exhibited significant damping effects at low frequencies (<30 Hz), but the damping ratio gradually stabilized as the frequency increased. Testing in the 30 Hz to 150 Hz range captures the damping trend of clay while also providing stable damping ratio data. The testing conditions included undrained and unconsolidated soil samples subjected to applied confining pressures. Upon reaching a stable confining pressure, the twist resonance test was conducted using GDS RCA (v 1.0.0) software. In the test, an input voltage was applied, and a frequency sweep was performed within the range of 30–150 Hz. This procedure provided data on resonance voltage amplitude and resonance frequency, allowing for the calculation of parameters such as dynamic shear modulus based on these values. After completing the twist resonance test, the testing apparatus automatically transitioned to the damping test mode, with the resonance frequency as a parameter for the damping test. These steps were repeated until all the necessary tests were completed, as outlined in reference [29].

Figure 5.
Procedure of test.
3. Experimental Results Analysis
3.1. Influence of Plant Root Systems on Soil Shear Modulus
Torsional resonance testing provides resonance frequency and resonance voltage of the specimen. The following formulas can be employed to calculate shear wave velocity, shear modulus, shear strain, and other relevant parameters [29].
Rotational inertia:
Fundamental equation for fixed–free resonant column:
Shear wave velocity calculated according to the following formula:
Shear modulus can be calculated from shear wave velocity according to the following formula:
In the provided expressions, the variables represent key parameters in the context of the experiment. d stands for the outer diameter of the solid specimen, m denotes the mass of the specimen, signifies the rotational inertia of the soil sample, represents the rotational inertia of the column drive system, is the natural resonance frequency of the specimen obtained from the resonant column test, indicates the height of the specimen, and represents the bulk density. These variables play crucial roles in characterizing and analyzing various aspects of the experimental setup and outcomes.
Under the influence of dynamic loading, the dynamic shear modulus is a crucial dynamic parameter characterizing soil behavior. It serves as a key indicator for describing the stress–strain relationship within the soil [30]. In this study, the dynamic shear modulus test results were fitted using the Hardin–Drnevich hyperbolic model. The hyperbolic formula [8] is as follows:
In the equation, the following terms are defined as follows: denotes the maximum dynamic shear modulus, represents shear strain, and is the reference shear strain.
3.1.1. Different Root Distribution Patterns
Different root distribution patterns in the soil are shown to yield varying maximum dynamic shear moduli and dynamic shear modulus–shear strain curves, as illustrated in Figure 6 and Figure 7. At confining pressures of 100 kPa and 200 kPa, the dynamic shear modulus–shear strain curves for upper root distribution are consistently positioned above those for uniform root distribution and lower root distribution. At a confining pressure of 300 kPa, the dynamic shear moduli for the three root distribution patterns exhibit remarkable similarity. This phenomenon arises from the electromagnetic drive system, which calculates shear modulus by generating sinusoidal torque. When roots are exclusively in the upper section of the specimen, the upper soil shows greater stiffness and strength, resulting in the specimen exhibiting more substantial restorative forces and shorter vibration cycles under dynamic excitation. Consequently, this increases the resonance frequency and dynamic shear modulus. Thus, under lower confining pressures, the upper root distribution pattern is advantageous in enhancing the soil’s dynamic shear modulus. In practice, this aligns with scenarios where roots are mainly distributed at the surface of the embankment in the upper portion of the soil, contributing to an improved soil dynamic shear modulus and reduced dynamic strain amplitudes.
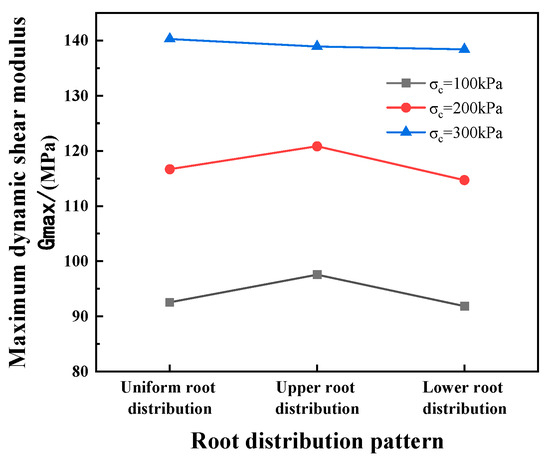
Figure 6.
The maximum dynamic shear modulus of soil with different root distribution patterns.
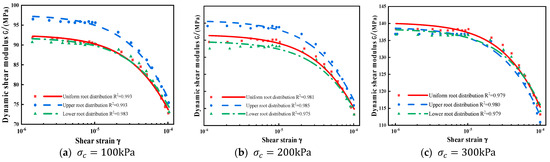
Figure 7.
G ~ γ relationship curves for soil with different root distribution patterns.
3.1.2. Different Root Mass Density
The maximum dynamic shear modulus and the dynamic shear modulus–shear strain curves for soils with different root mass densities are presented in Figure 8 and Figure 9, respectively. These graphs reveal that the dynamic shear modulus of all soil specimens amended with roots surpasses that of the native soil. Several factors contribute to this occurrence. Firstly, plant root systems interconnect soil particles, thereby increasing the internal cohesion within the soil [31]. The conceptual diagram of soil–root interaction is shown in Figure 10. Additionally, root systems introduce frictional forces at the interface between the roots and the soil, enhancing the roughness and surface area inside the soil, thereby amplifying inter-particle friction. This effectively enhances the shear strength of the soil [32,33,34]. Secondly, the presence of root systems can restrict soil deformations, especially for smaller-scale deformations. Roots constrain the displacement of soil particles, slowing the rate of deformation and enhancing the soil’s rigidity [35,36]. Thirdly, the distribution of root systems can create a network-like structure within the soil, resembling an “anchoring” effect. This network enhances the overall structural integrity of the soil [37]. When the soil experiences shear stress, the presence of root systems impedes the sliding of soil particles along the shear planes, resisting shear deformation. This obstruction makes shear deformation in the soil more challenging, leading to an increased dynamic shear modulus [3,38]. In summary, plant root systems have the capacity to significantly enhance the dynamic shear modulus of the soil.
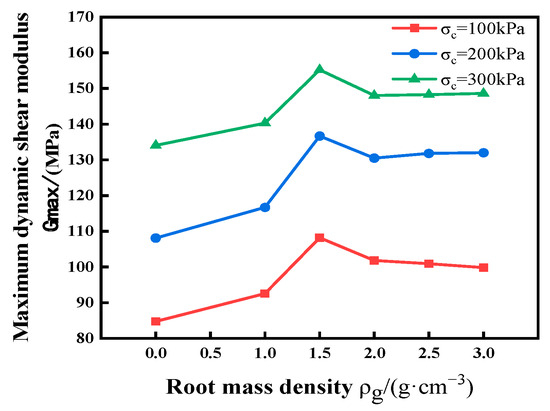
Figure 8.
The maximum dynamic shear modulus of soil with different root mass densities.
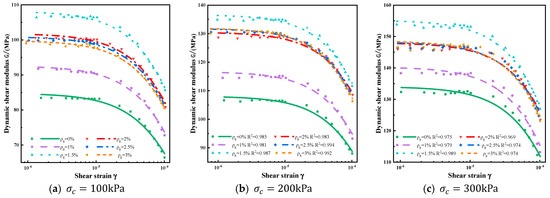
Figure 9.
G ~ γ relationship curves for soil with different root mass densities.
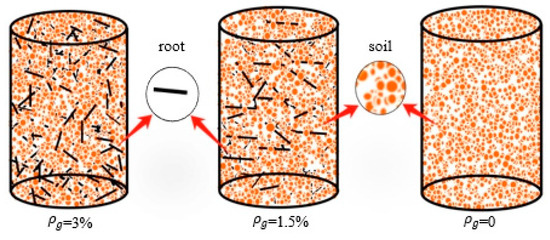
Figure 10.
Conceptual diagram of root–soil interaction.
At three different confining pressures, the dynamic shear modulus gradually increases within the range of 0–1.5% root mass density. The dynamic shear modulus peaks at a root mass density of 1.5% , after which it begins to decrease. For root mass densities of 2% , 2.5% , and 3% , the dynamic shear modulus in root-reinforced soil remains relatively stable. This signifies that the inclusion of plant root systems can enhance the soil’s dynamic shear modulus. Within a specific range of root mass density, an increased reinforcement effect is observed, and plant roots can impede soil shear deformation. However, when the root content surpasses the optimal root mass density, the increase in the network structure reduces the contact area between soil particles, resulting in reduced cohesion. Moreover, the internal friction in the soil increases with higher root density, which can resist relative particle displacement and elevate the dynamic shear modulus. However, this increase in cohesion and shear resistance tends to saturate as root density rises. Additionally, the presence of roots reduces the specimen’s porosity, increasing the overall compactness of the soil and, consequently, enhancing the dynamic shear modulus. Nonetheless, when root content exceeds the optimal root mass density, the increasing root mass density leads to a relative decrease in soil quality, resulting in a reduced rate of change in the dynamic shear modulus, which eventually stabilizes at a certain value.
With an increase in confining pressure, the overlap of the dynamic shear modulus–shear strain curves for root mass densities of 2%, 2.5%, and 3% improves. At a confining pressure of 300 kPa, the overall curves become virtually indistinguishable. This indicates that with increasing confining pressure, the dynamic shear modulus curves for high root mass densities gradually converge. At 300 kPa of confining pressure, there is little differentiation among the dynamic shear modulus curves for high root mass densities. The influence of plant root systems on soil dynamic shear modulus weakens as confining pressure increases. This phenomenon primarily results from the fact that as the confining pressure increases, the arrangement of soil particles, roots, and the interstitial space becomes denser. This decrease in porosity heightens the cohesion and frictional forces between soil particles and roots. Consequently, the impact of the roots diminishes, reducing their effect on the dynamic shear modulus of the specimen.
3.1.3. Shear Modulus Fitting Results of the Hardin–Drnevich Hyperbolic Model
The dynamic shear modulus fitting parameters of the Hardin–Drnevich hyperbolic model are shown in Table 2. As observed in the table, the maximum dynamic shear modulus for samples with added plant root systems consistently surpasses that of samples without plant roots. The maximum dynamic shear modulus can be enhanced by up to 27.6% (, ), underscoring the capacity of plant root systems to elevate the soil’s dynamic shear modulus. The correlation coefficients obtained are all greater than 0.97, indicating a robust fit of the regression curves to the observed values. The findings in this table offer valuable insights for seismic design involving root-reinforced soil.

Table 2.
Hardin–Drnevich hyperbolic model’s dynamic shear modulus fitting parameters.
3.2. Influence of Plant Root Systems on Soil Damping Ratio
The viscous damping ratio obtained from the resonant column test is derived from the free vibration decay curve. This curve is obtained by the accelerometer installed on the resonant column drive disk. A sine wave is applied to the soil, and after ceasing the excitation, the results of free vibration are measured. The decrement of the logarithmic curve can be calculated based on the logarithm of the continuous cycle amplitude ratio. The viscous damping ratio is then computed using the logarithmic decrement according to the following formula:
In this study, the relationship between damping ratio and shear strain was fitted using the Hardin–Drnevich hyperbolic model. The hyperbolic formula [8] is as follows:
In the equation, represents the shear strain, stands for the reference shear strain, denotes the damping ratio, and signifies the maximum damping ratio.
3.2.1. Different Root Distribution Patterns
The maximum damping ratio and the damping ratio–shear strain curves for different root distribution patterns are depicted in Figure 11 and Figure 12, respectively. The figures reveal that, under all three confining pressures, the damping ratio of soil with roots distributed in the upper part exceeds that of soil with roots uniformly distributed or distributed in the lower part. This observation can be attributed to the introduction of roots into the soil, enhancing the stiffness of the specimen. Soil with roots in the upper part exhibits greater stiffness in the upper portion and reduced stiffness in the lower section, while soil with roots in the lower part displays diminished stiffness in the upper portion and elevated stiffness in the lower segment. The heightened upper stiffness results in a more rigid and swift response of the vibration system to vibrations, leading to a heightened rate of energy dissipation and, consequently, an increased damping ratio. Conversely, increased lower stiffness yields a softer and slower response of the vibration system, resulting in a comparatively reduced rate of energy dissipation and a diminished damping ratio. Furthermore, soil with roots in the lower part is typically constrained by the upper soil, restricting the transfer of vibrational energy, which contributes to a relatively lower damping ratio. Therefore, placing roots in the upper part of the soil proves advantageous for elevating the soil’s damping ratio and facilitating energy dissipation. This aligns with practical scenarios where roots are predominantly distributed on the surface of embankments, which corresponds to the upper part of the soil and fosters energy dissipation.
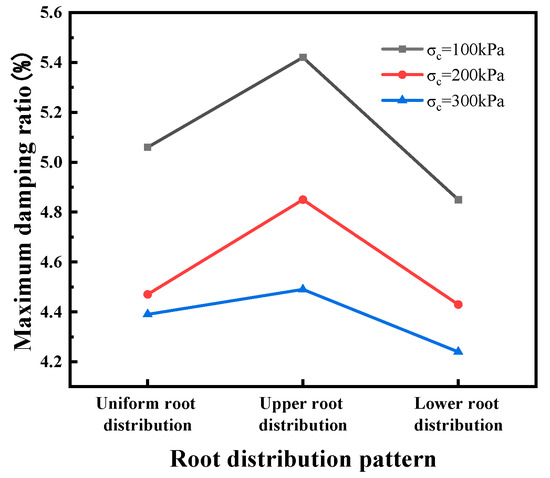
Figure 11.
The maximum damping ratio of soil with different root distribution patterns.
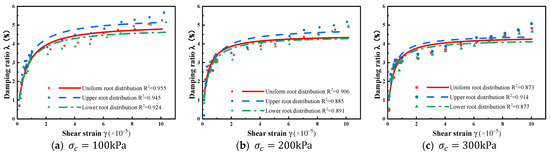
Figure 12.
λ ~ γ relationship curves for soil with different root distribution patterns.
3.2.2. Different Root Mass Density
The maximum damping ratio and the damping ratio–shear strain curves for soils with different root mass densities are illustrated in Figure 13 and Figure 14. It is evident from these figures that under a confining pressure of 100 kPa, the maximum damping ratio () was 5.36% when the root mass density was 0. As the root mass density increased to 1.5% , the damping ratio decreased to 4.92%, reaching the minimum critical value. Further increasing the root mass density caused the damping ratio to rise, reaching 5.39% at a root mass density of 3% . Under confining pressures of 200 kPa and 300 kPa, the relationship between the damping ratio and root mass density followed the same trend as under 100 kPa, showing an initial decrease followed by an increase. Specifically, the damping ratio decreased from = 4.76% at = 0 and = 4.46 at = 0 to the minimum critical values of = 4.44% at = 2% and = 4.18% at = 2.5% . When the root mass density reached 3% , the maximum damping ratio increased to 4.8% and 4.27%, respectively. Notably, under 100 kPa and 200 kPa confining pressures, the maximum damping ratio of samples with a 3% root mass density consistently surpasses that of samples with 0% root mass density. This can be attributed to the fact that the inclusion of roots in the samples enhances the soil’s ductility, facilitating energy dissipation and resulting in an elevated damping ratio. Simultaneously, it leads to a denser soil structure, increasing the contact area between soil particles and between soil particles and roots. However, this is not conducive to energy dissipation and results in a lower damping ratio. Simultaneously, it leads to a denser soil structure, increasing the contact area between soil particles and between soil particles and roots. However, this is not conducive to energy dissipation and results in a lower damping ratio. Beyond this point, roots predominantly enhance the soil’s ductility, leading to an increased damping ratio. In summary, the damping ratio initially decreases and then increases with an increase in root mass density. In practical slope scenarios, the growth of plant roots tends to loosen the surface soil, reducing the compactness of the soil on the slope’s surface. Angers DA et al. [39] previously concluded that during the growth process of roots, large pores may form through the soil, but these pores are local and beneficial. While roots enhance the soil’s ductility, their effect on reducing soil compaction is favorable for energy dissipation.
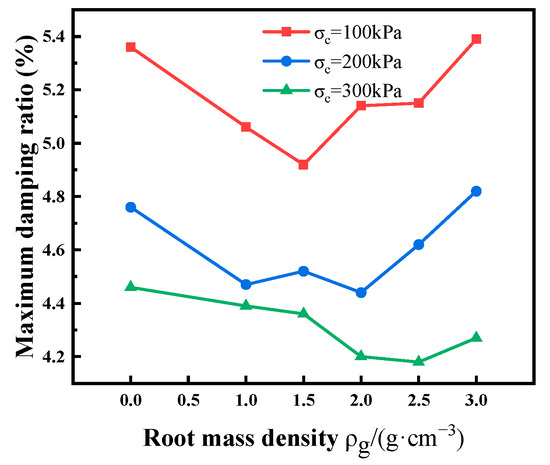
Figure 13.
The maximum damping ratio of soil with different root mass densities.
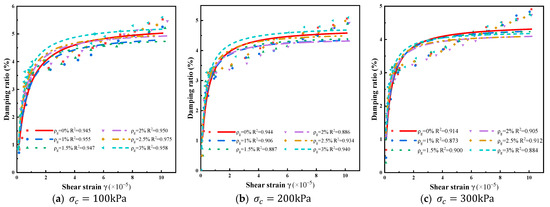
Figure 14.
λ ~ γ relationship curves for soil with different root mass densities.
3.2.3. Damping Ratio Fitting Results of the Hardin–Drnevich Hyperbolic Model
The fitting parameters for the Hardin–Drnevich hyperbolic model for damping ratio are presented in Table 3, respectively. The obtained correlation coefficients are all greater than or equal to 0.87, indicating a good fit of the regression curves to the observed values. These results can be valuable for seismic design considerations involving root-reinforced soil.

Table 3.
Hardin–Drnevich hyperbolic model’s damping ratio fitting parameters.
3.3. Reinforcement Mechanism of Roots
The root systems of plants play a crucial role in fortifying the soil and augmenting its mechanical properties. In the field of mechanics, WU [40,41] developed a soil mechanics model for evaluating the effectiveness of vertical root systems in slope protection based on the Mohr–Coulomb strength criteria. However, some scholars argue that the WU model overestimates the reinforcement effect of roots on soil. Pollen believes this is mainly because the WU model assumes the simultaneous fracture of all roots, with full tensile strength exerted at the fracture point [42], which is inconsistent with reality. In one study, Pollen applied the fiber bundle continuous fracture theory, widely used in the materials industry, proposed a progressive failure mode for roots, and subsequently developed the FBM (fiber-bundle model). However, during the actual failure process, factors such as soil properties, root diameter, root growth direction, and friction between roots and soil can influence the soil reinforcement effect of roots, and these factors are not considered in the FBM model. Therefore, to address these issues, Schwarz et al. introduced the RBM (root bundle model) [43], which considers the total pull resistance of root bundles as a function of displacement, represented as the sum of the pull resistance of individual roots [43,44].
where is the pullout force of a root belonging to diameter class , N is the number of diameter classes, and n is the number of roots present in the bundle of diameter class . is calculated for each root diameter class using the single root pullout model.
The variation of the bundle pullout force as a function of the displacement can be expressed with the following differential equation:
where and are displacements at two different loads.
Growing plant roots release thick substances like root mucilage with adhesive properties, effectively binding soil particles. The presence of polysaccharides and organic acids in root mucilage forms gel-like bonds, enhancing soil cohesion and shear resistance. Root activities lead to biological cementation, establishing a gel-like structure among soil particles and fortifying cohesive forces within the soil. Other than bolstering the overall stability of the soil, this structural enhancement acts as a preventive measure against water and wind erosion.
Plant root systems give rise to the development of a root network. Efficiently binding soil particles, this network enhances the soil’s cohesion. During dynamic loading, this binding effect becomes more pronounced, resisting the relative displacement of soil particles induced by external vibrations. This elevation enhances the overall stiffness and strength of the soil. Additionally, this process increases the dynamic shear modulus of the soil, making it more stable under dynamic loading. The established root network positively influences the damping characteristics of the soil, slowing the propagation speed of vibrations within the soil and increasing the damping level. The reinforcing impact of plant root systems effectively mitigates the vibrational response of the soil, providing a more reliable safeguard for the soil and associated structures.
4. Conclusions
Prior studies have primarily concentrated on investigating the dynamic impact of root distribution patterns on soil. In this study, resonance column tests were conducted on clay with different root distribution patterns and root mass densities, leading to the following key conclusions:
- The upper root distribution significantly increased the dynamic shear modulus of the soil under confining pressures of 100–200 kPa, demonstrating greater stiffness and strength, which enhanced dynamic soil properties and reduced dynamic strain amplitude.
- Plant roots improved the dynamic shear modulus of soil, with the effect varying according to root mass density. The dynamic shear modulus peaked at a root mass density of 1.5% , then stabilized. Increased confining pressure reduced the influence of high root mass density, with the relationship curve gradually converging. This indicates that optimizing root distribution and density can effectively enhance soil dynamic properties.
- The upper root distribution significantly increased the soil damping ratio, enhancing energy dissipation capacity due to increased upper stiffness and accelerated vibration response. In contrast, the lower root distribution exhibited a lower damping ratio due to confinement effects. This suggests that placing roots in the upper soil layer can improve dynamic soil stability, consistent with the root distribution characteristics on embankment surfaces.
- The damping ratio decreased initially and then increased with rising root mass density, with critical values observed at each confining pressure (1.5% for 100 kPa, 2% for 200 kPa, and 2.5% for 300 kPa). At a low density, roots enhanced soil compaction and reduced the damping ratio, while at a high density, they improved ductility and increased energy dissipation. Optimizing root mass density can help improve the dynamic properties of slope soils.
Author Contributions
Methodology, Q.S.; validation, Q.S., C.T. and C.Z.; formal analysis, Q.S., C.T. and C.Z.; investigation Y.M.; resources, Q.S.; data curation, C.T. and C.Z.; writing—original draft preparation, C.Z.; writing—review and editing, C.T. and Q.S.; supervision, Y.M.; project administration, Q.S. and Y.M.; funding acquisition, Q.S. All authors have read and agreed to the published version of the manuscript.
Funding
This study was supported by the National Science Foundation of China (No. 51878185; No. 2019YFC1509805) and the Scientific Research Project of Hunan Provincial Department of Education (24C0978).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors upon request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Gong, C.; Ni, D.; Liu, Y.; Li, Y.; Huang, Q.; Tian, Y.; Zhang, H. Herbaceous Vegetation in Slope Stabilization: A Comparative Review of Mechanisms, Advantages, and Practical Applications. Sustainability 2024, 16, 7620. [Google Scholar] [CrossRef]
- Löbmann, M.T.; Geitner, C.; Wellstein, C.; Zerbe, S. The influence of herbaceous vegetation on slope stability—A review. Earth-Sci. Rev. 2020, 209, 103328. [Google Scholar] [CrossRef]
- Bordoloi, S.; Ng, C.W. The effects of vegetation traits and their stability functions in bio-engineered slopes: A perspective review. Eng. Geol. 2020, 275, 105742. [Google Scholar] [CrossRef]
- Zhu, Y.G.; Wang, C.; Liu, Z.Q. Effects of rainfall and vegetation cover on soil erosion railway bed slope. Bull. Soil Water Conserv. 2021, 41, 8–14. [Google Scholar]
- Yang, Z.G.; Xi, W.F.; Shi, Z.T.; Yang, Z.Q.; Xiao, B. Study on the relationship between landslide creep and vegetation cover in mountainous areas with complex vegetation. Sci. Surv. Mapp. 2023, 48, 157–165+175. [Google Scholar]
- Zhou, Y.; Ma, W. Plant roots in the active zone improving the performance of ecological reinforced soil retaining walls. Bull. Eng. Geol. Environ. 2023, 82, 414. [Google Scholar] [CrossRef]
- Seed, H.B. Soil moduli and damping factors for dynamic response analyses. J. Terramech. 1972, 8, 109. [Google Scholar] [CrossRef]
- Hardin, B.O.; Drnevich, V.P. Shear modulus and damping in soils: Design equations and curves. J. Soil Mech. Found. Div. 1972, 98, 667–692. [Google Scholar] [CrossRef]
- Zhong, X.G.; Zeng, X.; Rose, J.G. Shear modulus and damping ratio of rubber-modified asphalt mixes and unsaturated subgrade soils. J. Mater. Civ. Eng. 2002, 14, 496–502. [Google Scholar] [CrossRef]
- Chen, G.; Xie, J.; Zhang, K. The empirical evaluation of soil moduli and damping ratio for dynamic analysis. Earthq. Eng. Eng. Dyn. 1995, 15, 73–84. [Google Scholar]
- Wang, H.; He, M.; Zhu, J.; Guo, S.; Chen, Y.; Li, N. Experimental investigation of linear damping characteristics on granite and red sandstone under dynamic cyclic loading. Eur. J. Environ. Civ. Eng. 2022, 26, 5259–5278. [Google Scholar] [CrossRef]
- Yang, B.; He, M.; Zhang, Z.; Zhu, J.; Chen, Y. Experimental investigation and empirical model on damping properties of rock under multistage cyclic loading. Soil Dyn. Earthq. Eng. 2022, 163, 107557. [Google Scholar] [CrossRef]
- Wang, W.; Cao, G.; Li, Y.; Zhou, Y.; Lu, T.; Wang, Y.; Zheng, B. Experimental study of dynamic characteristics of tailings with different reconsolidation degrees after liquefaction. Front. Earth Sci. 2022, 10, 876401. [Google Scholar] [CrossRef]
- Zhang, Q.; Yin, G.; Wei, Z.; Fan, X.; Wang, W.; Nie, W. An experimental study of the mechanical features of layered structures in dam tailings from macroscopic and microscopic points of view. Eng. Geol. 2015, 195, 142–154. [Google Scholar] [CrossRef]
- Park, D.; Kishida, T. Shear modulus reduction and daming ratio curves for earth core materials of dams. Can. Geotech. J. 2019, 56, 14–22. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, Y.; Ling, X.; Gong, W.; Li, G.; Su, L. Dynamic behavior of natural sand soils and fiber reinforced soils in heavy-haul railway embankment under multistage cyclic loading. Transp. Geotech. 2021, 28, 100507. [Google Scholar] [CrossRef]
- Zhao, J.; Bai, X.; Xie, M.; Zheng, J. Experimental study on dynamic response characteristics of small-spaced reinforced soil under cvclic loading. J. Civ. Environ. Eng. 2023, 45, 125–133. [Google Scholar]
- Rollins, K.M.; Evans, M.D.; Diehl, N.B.; III, W.D. Shear modulus and daming relationships for gravels. J. Geotech. Geoenviron. Eng. 1998, 124, 396–405. [Google Scholar] [CrossRef]
- Tang, F.C.; Zhang, W.Y.; Tang, X.; Liu, C.K. Study on the dynamic characteristics of geogrid reinforced loess under cyclic loading. Water Resour. Hydropow. Eng. 2024, 55, 148–161. [Google Scholar]
- Vahedifard, F.; Abdollahi, M.; Leshchinsky, B.A.; Stark, T.D.; Sadegh, M.; AghaKouchak, A. Interdependencies between wildfire—Induced alterations in soil properties, near—Surface processes, and geohazards. Earth Space Sci. 2024, 11, e2023EA003498. [Google Scholar] [CrossRef]
- Sonnenberg, R.; Bransby, M.F.; Hallett, P.D.; Bengough, A.G.; Mickovski, S.B.; Davies, M.C.R. Centrifuge modelling of soil slopes reinforced with vegetation. Can. Geotech. J. 2010, 47, 1415–1430. [Google Scholar] [CrossRef]
- Chenari, R.J.; Pishkhani, S.S.; Fard, M.K.; Sosahab, J.S. Experimental and numerical investigation of dynamic properties of soil stabilized by Young Vetiver. Riv. Ital. Di Geotec. 2018, 52, 49–58. [Google Scholar]
- Yan, Z. Dynamic experimental study on remolded soil and plant-root reinforced soil under cyclic load. Port Waterw. Eng. 2021, 2021, 186–191. [Google Scholar]
- Liu, S.; Li, J.; Ji, X.; Fang, Y. Influence of root distribution patterns on soil dynamic characteristics. Sci Rep. 2022, 12, 13448. [Google Scholar] [CrossRef] [PubMed]
- GB/T 50123; Ministry of Water Resources of the People’s Republic of China. Standard for Geotechnical Testing Method. China Planning Press: Beijing, China, 2019; pp. 41–125.
- Peng, Q.F. Study on the Influence of Particle Shape and Average Particle Size Ratio on the Dynamic Characteristics of Rubber-Sand Mixtures. Master’s Thesis, Hunan University of Technology, Zhuzhou, China, 2021. [Google Scholar]
- Eshel, A.; Beeckman, T. (Eds.) Plant Roots: The Hidden Half; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Agnihotri, L.S.V. Estimating the genetic relationship in various warm season turfgrass genotypes using RAPD and ISSR markers. Natl. Acad. Sci. Lett. 2018, 41, 197–201. [Google Scholar] [CrossRef]
- Ahn, S.; Ryou, J.-E.; Ahn, K.; Lee, C.; Lee, J.-D.; Jung, J. Evaluation of dynamic properties of sodium-alginate-reinforced soil using a resonant-column test. Materials 2021, 14, 2743. [Google Scholar] [CrossRef]
- Lu, Z.C.; Yang, Z.G.; Liu, J.M.; Lv, J.H.; Zhang, Q.; Ling, X.Z. Low-Temperature dynamic triaxial testing of frozen expansive soil-rubber(ESR) mixtures. J. Eng. Geol. 2021, 29, 1312–1319. [Google Scholar]
- White, R.G.; Kirkegaard, J.A. The distribution and abundance of wheat roots in a dense, structured subsoil–implications for water uptake. Plant Cell Environ. 2010, 33, 133–148. [Google Scholar] [CrossRef] [PubMed]
- Foresta, V.; Capobianco, V.; Cascini, L. Influence of grass roots on shear strength of pyroclastic soils. Can. Geotech. J. 2020, 57, 1320–1334. [Google Scholar] [CrossRef]
- Fan, C.C.; Su, C.F. Role of roots in the shear strength of root-reinforced soils with high moisture content. Ecol. Eng. 2008, 33, 157–166. [Google Scholar] [CrossRef]
- Baets, D.S.; Poesen, J.; Reubens, B.; Wemans, K.; De Baerdemaeker, J.; Muys, B. Root tensile strength and root distribution of typical Mediterranean plant species and their contribution to soil shear strength. Plant Soil 2008, 305, 207–226. [Google Scholar] [CrossRef]
- Meijer, G.J.; Muir Wood, D.; Knappett, J.A.; Bengough, G.A.; Liang, T. Analysis of coupled axial and lateral deformation of roots in soil. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 684–707. [Google Scholar] [CrossRef]
- Fan, C.C.; Su, C.F. Effect of soil moisture content on the deformation behaviour of root-reinforced soils subjected to shear. Plant Soil 2009, 324, 57–69. [Google Scholar] [CrossRef]
- Gao, W.; Hodgkinson, L.K.; Watts, C.W.; Ashton, R.W.; Shen, J.; Ren, T.; Dodd, I.C.; Binley, A.; Phillips, A.L.; Hedden, P. Deep roots and soil structure. Plant Cell Environ. 2016, 39, 1662–1668. [Google Scholar] [CrossRef]
- Ghestem, M.; Veylon, G.; Bernard, A.; Vanel, Q.; Stokes, A. Influence of plant root system morphology and architectural traits on soil shear resistance. Plant Soil 2014, 377, 43–61. [Google Scholar] [CrossRef]
- Angers, D.A.; Caron, J. Plant-induced changes in soil structure: Processes and feedbacks. Bioge-Ochemistry 1998, 42, 55–72. [Google Scholar]
- Wu, T.H.; McKinnell, W.P., III; Swanston, D.N. Strength of tree roots and landslides on Prince of Wales Island, Alaska. Can. Geotech. J. 1979, 16, 19–33. [Google Scholar] [CrossRef]
- Wu, T.H.; McOmber, R.M.; Erb, R.T.; Beal, P.E. Study of soil-root interaction. J. Geotech. Eng. 1988, 114, 1351–1375. [Google Scholar] [CrossRef]
- Pollen, N.; Simon, A. Estimating the mechanical effects of riparian vegetation on stream bank stability using a fiber bundle model. Water Resour Res. 2005, 41, W07025. [Google Scholar] [CrossRef]
- Schwarz, M.; Cohen, D.; Or, D. Root-soil mechanical interactions during pullout and failure of root bundles. J. Geophys. Res. Earth Surf. 2010, 35, 354–361. [Google Scholar]
- Schwarz, M.; Lehmann, P.; Or, D. Quantifying lateral root reinforcement in steep slopes—From a bundle of roots to tree stands. Earth Surf Process Landf. 2010, 35, 354–367. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).