Vibration Control of Passenger Aircraft Active Landing Gear Using Neural Network-Based Fuzzy Inference System

Abstract

Runway surface roughness is recognized as a principal cause of passenger aircraft vibration during taxiing, adversely affecting ride comfort, safety, and even human health. Effective mitigation of such vibrations is therefore essential for improving passenger experience and operational reliability. Previous studies have investigated passive, semi-active, and intelligent controllers such as PID, H∞, and ANFIS; however, the comprehensive application of a robust adaptive neuro-fuzzy inference system (RANFIS) to active landing-gear control has not yet been addressed. The novelty of this work lies in combining robustness with adaptive learning of fuzzy rules and neural network parameters, thereby filling this critical gap in the literature. To investigate this, a six-degrees-of-freedom aircraft dynamic model was developed, and three controllers were comparatively evaluated: model-based neural network (MBNN), adaptive neuro-fuzzy inference system (ANFIS), and the proposed RANFIS. Performance was assessed in terms of rise time, settling time, peak value, and steady-state error under stochastic runway excitations. Simulation results show that while MBNN and ANFIS provide satisfactory control, RANFIS achieved superior performance, reducing vibration peaks to ≤0.3–1.0 cm, shortening settling times to <1.5 s, and decreasing steady-state errors to <0.05 cm. These findings confirm that RANFIS offers a more effective solution for enhancing comfort, safety, and structural durability in next-generation active landing-gear systems.

1. Introduction

With advancing technology, people’s expectations from vehicles are increasing, with safety and comfort at the forefront. Runway roughness is a primary source of discomfort and safety issues during taxi, takeoff, and landing. Consequently, research has accelerated to minimize vibration and ensure a comfortable journey. Landing gear is used in aircraft to isolate vibrations, and these systems are commonly classified into three categories: passive, semi-active, and active. Among them, passive landing gear is the simplest configuration, employing spring and damping elements. Because the spring and damper parameters are fixed, passive systems are generally less effective at reducing vibrations than the other approaches. Active landing gear augments the spring–damper with an actuator, enabling force input to the system and thereby offering improved control performance.

Sancak and Güçlü [1] studied a fighter-aircraft landing-gear system with a semi-active suspension using a magnetorheological (MR) damper to reduce vibrations caused by runway roughness during taxiing. They designed PID and fuzzy-logic controllers to regulate the voltage applied to the MR damper. Gharapurkar et al. [2] used an H-infinity (H∞) approach for the semi-active control of aircraft landing-gear systems. Hualin et al. [3] mitigated vibrations transmitted to the fuselage by combining PID control with fuzzy logic in their controller design. In another study, a nonlinear model predictive control (NMPC) algorithm was developed for semi-active landing-gear control under various ground conditions, using a genetic algorithm as the optimization engine [4]. Liu and Shi [5] investigated damping-control design, simulation, and vibration testing for semi-active landing gear, including the design of MR dampers used in the gear; compared with passive control, the MR solution was shown to be effective.

Runway-induced vibration can reduce a pilot’s ability to control the aircraft and create safety risks before takeoff and after landing. In addition, passenger and crew comfort are adversely affected by vibrations transmitted to the airframe. Yazıcı and Sever [6] implemented active control of an oleo-pneumatic active landing-gear system and simulated the aircraft response to random runway irregularities during taxiing. Sivakumar and Haran [7] compared the dynamic responses of passive and active landing gear while taxiing. Wang et al. [8] used a PID controller for vibration control of an active landing-gear system, deriving a mathematical model for runway-roughness-induced aircraft vibrations and showing that active control substantially reduced vertical displacements due to impact loads and runway disturbances. Zapateiro et al. [9] applied adaptive backstepping with H∞ performance to achieve satisfactory damping in active and semi-active landing gear.

Within artificial-intelligence-based control, ANFIS and its derivatives are strong candidates for vibration suppression and predictive decision support in complex nonlinear systems. Recent ANFIS-based studies on flying platforms and flexible structures support the broad validity of the method; furthermore, ANFIS-based prediction of runway-friction degradation in aviation demonstrates a bridge to operational integration [10]. In parallel, the potential of neuro-fuzzy and other neuro-control architectures to manage landing-gear vibrations and angular variables has been demonstrated under various conditions. For example, Yıldırım and Durmuşoğlu [11] controlled vibrations occurring in the landing-gear mechanism during landing using a proposed intelligent method. Hou et al. [12] developed roughness models for asphalt and concrete runways that consider structural properties, and systematically investigated taxiing/takeoff/landing vibrations on a multi-body 6-DOF aircraft model using the pseudo-excitation method and spatial-frequency instantaneous frequency response function techniques, as well as the effects of stochastic structural parameters via Monte Carlo analysis.

Recent contributions further highlight the growing importance of advanced intelligent controllers for vibration suppression in aerospace systems. Moutsopoulou et al. [13] presented a comprehensive review of intelligent control techniques for structural-vibration mitigation, emphasizing their applicability to aeronautical systems. Wu [14] demonstrated the potential of adaptive neuro-fuzzy strategies for robust control of unmanned aerial vehicles during taxiing, while Nunes et al. [15] applied nonlinear model predictive control to vibration suppression and trajectory tracking in eVTOL platforms, showing the competitive edge of intelligent approaches over classical methods. Similarly, Long and Le [16] introduced type-2 fuzzy and reservoir-computing concepts for robust landing and vibration control. Collectively, these studies confirm the trend toward neuro-fuzzy, learning-based, and hybrid intelligent designs as viable solutions to the stochastic and nonlinear nature of aircraft–ground interactions. Building upon this body of work, the present study focuses on a robust adaptive neuro-fuzzy inference system (RANFIS) to advance passenger comfort and landing-gear safety.

All the aforementioned studies have made notable contributions to landing-gear control. Nevertheless, the comprehensive application of a neural-network-based fuzzy inference system (NN-FIS) to achieve both robust and optimal control of an active landing-gear system has not been fully addressed. This identifiable gap underscores the necessity of the present research. Given the adaptive and self-learning capabilities of ANFIS, it offers a promising framework for maintaining optimal performance under uncertainties induced by runway roughness. In this study, we derive the dynamic equations of an active landing-gear system to analyze its vibration response to stochastic runway excitations. Based on these equations, we propose a robust adaptive neural-based fuzzy inference system (RANFIS) to mitigate vibrations during taxiing. The central research question is whether RANFIS can effectively suppress vibrations in an active landing-gear system under stochastic runway excitations, thereby enhancing passenger comfort and improving landing-gear performance compared with conventional intelligent controllers. Simulation results demonstrate that, relative to such approaches, the proposed controller significantly reduces displacement responses induced by runway irregularities. Consequently, passenger and crew comfort are enhanced, while the durability and operational performance of the landing-gear system are improved.

The remainder of the paper is organized as follows. Section 2 presents the complete aircraft model along with the derived dynamic equations. Section 3 introduces the proposed intelligent control framework. Section 4 provides comparative simulation results under various runway conditions. Section 5 concludes the study with a summary of findings and a discussion of future research directions.

2. Mathematical Model of Full Aircraft with Active Landing-Gear System

Today, commercial passenger aircraft typically employ nose landing gear equipped with passive oleo-pneumatic shock absorbers, commonly modeled as nonlinear spring–damper elements. While these passive elements dissipate part of the vibrational energy induced by runway roughness, they cannot fully suppress the dynamic responses transmitted to the airframe. In this study, we augment the conventional passive suspension architecture by incorporating active control components. The passive shock-absorber characteristics are retained, while additional control forces are generated through hydraulic actuators arranged in parallel. Actuator forces are regulated in real time by the proposed intelligent control algorithms. Consequently, the mathematical model captures both the purely passive configuration and the actively controlled configuration, enabling a direct comparison of vibration reduction and the resulting improvements in passenger comfort.

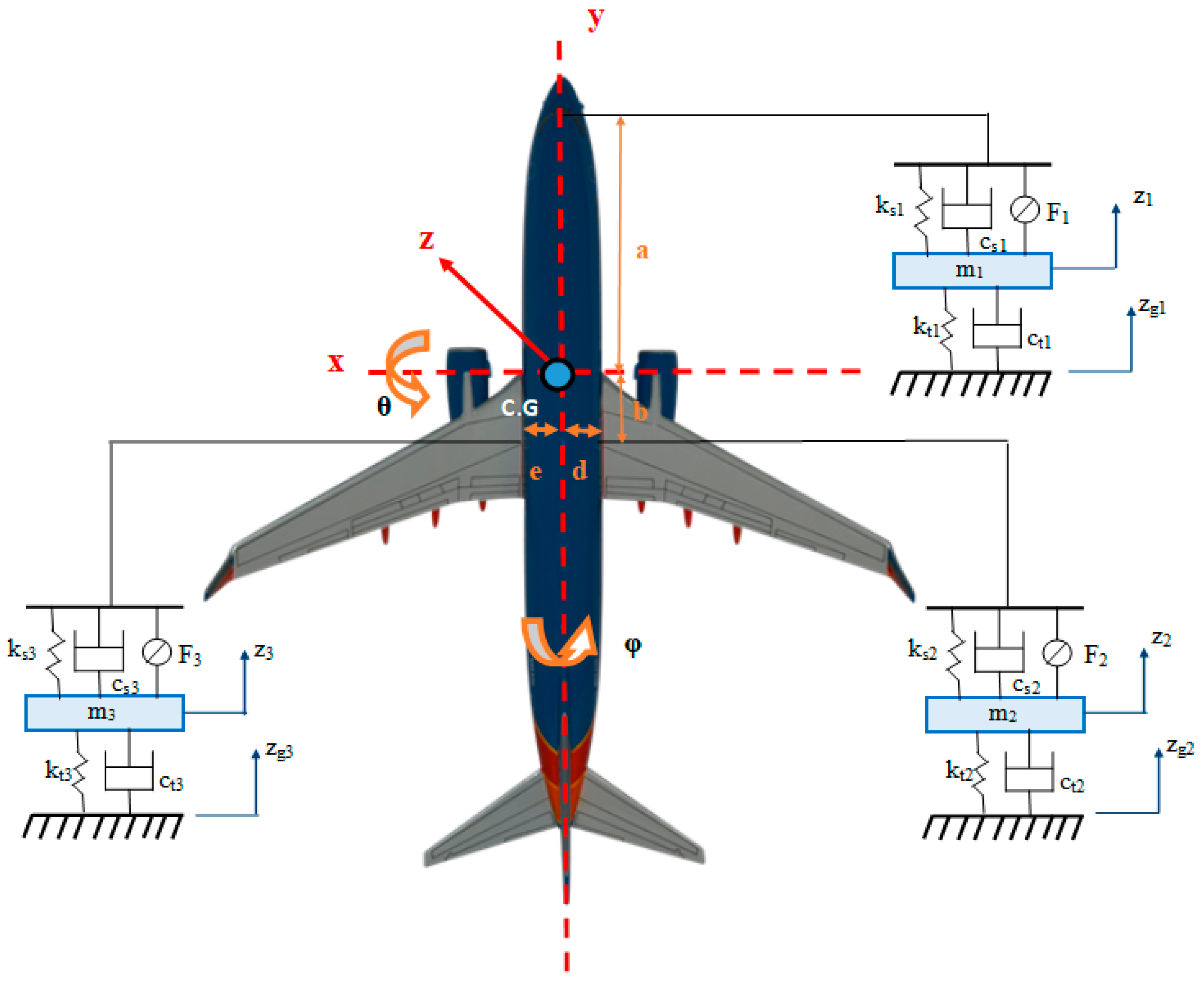
In the full aircraft model, the fuselage body or sprung mass is free to roll and pitch. The sprung mass is attached to the three unsprung masses (nose, left and right main landing gears) and they move vertically concerning the sprung mass [7]. The mathematical model of the full 6-degree-of-freedom aircraft model with an active damper is given in Figure 1. In this model, z, θ, and φ are the vertical displacement, pitch and roll movements of the fuselage, z₁, z₂ and z₃ nose, left and right main landing-gear displacements, a; distance of the nose landing gear from the aircraft’s center of gravity, b; the distance of the center of gravity from the main landing gears, d; distance from the center of gravity of the left main landing gear, e; shows the distance of the right main landing gear to the center of gravity. It should be noted that the model is defined with respect to the static equilibrium configuration, in which the weight of the aircraft is balanced by the static deflections of the landing-gear elements. Accordingly, the vibration responses presented represent deviations from this equilibrium state, ensuring that the analysis is performed around realistic operating points.

Using Newton’s second law of motion, the dynamic equations describing the motion of the active landing gear are written as [7].

For the vertical motion of the fuselage,

$$M\ddot{z}+k_{s1}p+k_{s2}q+k_{s3}r+c_{s1}\dot{p}+c_{s2}\dot{q}+c_{s3}\dot{r}+F_1=0$$

(1)

where

$$p=z-a\theta -h\phi -z_1$$

$$q=z+b\theta -d\phi -z_2$$

$$r=z+b\theta +e\phi -z_3$$

$$h=d-e$$

i.e.,

$$\begin{gathered} M\ddot{z}+k_{s1}\left(z-a\theta -h\phi -z_1\right)+k_{s2}\left(z+b\theta -d\phi -z_2\right)+k_{s3}\left(z+b\theta +e\phi -z_3\right) \\ +c_{s1}(\dot{z}-a\dot{\theta }-h\dot{\phi }-\dot{z_1})+c_{s2}(\dot{z}+b\dot{\theta }-d\dot{\phi }-\dot{z_2})+c_{s3}(\dot{z}+b\dot{\theta }+e\dot{\phi }-\dot{z_3})+F_1=0 \end{gathered}$$

(2)

In this equation, k_s1 is the nose landing-gear stiffness rate, k_s2 is the left main landing-gear stiffness rate and k_s3 is the right main landing-gear stiffness rate. c_s1, c_s2, and c_s3 represent the nose landing gear, left landing-gear and right landing-gear damping rates. M denotes the fuselage mass and F₁ denotes the active control force of the nose landing gear.

For the pitch motion of the fuselage,

$$I_{yy}\ddot{\theta }-k_{s1}pa+k_{s2}qb+k_{s3}rb-c_{s1}\dot{p}a+c_{s2}\dot{q}b+c_{s3}\dot{r}b+F_2=0$$

(3)

where I_yy is the mass moment of inertia about y-axis and F₂ is the active control force of the left main landing gear.

For the roll motion of the fuselage,

$$I_{xx}\ddot{\phi }-k_{s1}ph+k_{s2}qd+k_{s3}re-c_{s1}\dot{p}h-c_{s2}\dot{q}d+c_{s3}\dot{r}e+F_3=0$$

(4)

where I_xx is the mass moment of inertia about x-axis and F₃ is the active control force of the right main landing gear.

For the motion of the nose landing gear,

$$m_1\ddot{z_1}-k_{s1}p-c_{s1}\dot{p}+k_{t1}\left(z_1-z_{g1}\right)+c_{t1}\left(\dot{z}-\dot{z}{g}_1\right)-F_1=0$$

(5)

where m₁ represents the nose landing-gear unsprung mass, z_g1 represents the runway disturbance input for the nose landing-gear wheel, k_t1 denotes the nose landing-gear tyre stiffness and c_t1 denotes the nose landing-gear tyre damping rate.

For the motion of the left main landing gear,

$$m_2\ddot{z_2}-k_{s2}q-c_{s2}\dot{q}-k_{t2}\left(z_2-z_{g2}\right)+c_{t2}\left(\dot{z_2}-\dot{z}{g}_2\right)-F_2=0$$

(6)

where m₂ represents the left main landing-gear unsprung mass, z_g2 represents the runway disturbance input for the left main landing-gear wheel, k_t2 denotes the left main landing-gear tyre stiffness and c_t2 denotes the left main landing-gear tyre damping rate.

For the motion of the right main landing gear,

$$m_3\ddot{z_3}-k_{s3}r-c_{s3}\dot{r}+k_{t3}\left(z_3-z_{g3}\right)+c_{t3}\left(\dot{z_3}-\dot{z}{g}_3\right)-F_3=0$$

(7)

where m₃ represents the right main landing-gear unsprung mass, z_g3 represents the runway disturbance input for the right main landing-gear wheel, k_t3 denotes the right main landing-gear tyre stiffness and c_t3 denotes the right main landing-gear tyre damping rate.

The above equations of motion can be written in matrix form as

$$\left[M\right]\left\{\ddot{z}\right\}+\left[C\right]\left\{\dot{z}\right\}+\left[K\right]\left\{z\right\}=\left\{F\right\}$$

(8)

where [M] is the mass matrix denoted by

$$M=\left[\begin{array}{cccccc}M& 0& 0& 0& 0& 0\\ 0& I_{yy}& 0& 0& 0& 0\\ 0& 0& I_{xx}& 0& 0& 0\\ 0& 0& 0& m_1& 0& 0\\ 0& 0& 0& 0& m_2& 0\\ 0& 0& 0& 0& 0& m_3\end{array}\right]$$

(9)

[C] is the damping matrix denoted by

$$C=\left[\begin{array}{cccccc}H1& H2& H3& -c_{s1}& -c_{s2}& -c_{s3}\\ H2& H4& H5& a{c}_{s1}& -b{c}_{s2}& -b{c}_{s3}\\ H3& H5& H6& h{c}_{s1}& d{c}_{s2}& -e{c}_{s3}\\ -c_{s1}& a{c}_{s1}& h{c}_{s1}& c_{s1}+c_{t1}& 0& 0\\ -c_{s2}& -b{c}_{s2}& d{c}_{s2}& 0& c_{s2}+c_{t2}& 0\\ -c_{s3}& -b{c}_{s3}& -e{c}_{s3}& 0& 0& c_{s3}+c_{t3}\end{array}\right]$$

(10)

where

$$H1=c_{s1}+c_{s2}+c_{s3}$$

$$H2=-{ac}_{s1}+{bc}_{s2}+{bc}_{s3}$$

$$H3=-{hc}_{s1}-{dc}_{s2}+{ec}_{s3}$$

$$H4=a^2{c}_{s1}+b^2{c}_{s2}+b^2{c}_{s3}$$

$$H5={hac}_{s1}-{dbc}_{s2}+{ebc}_{s3}$$

$$H6=h^2{c}_{s1}+d^2{c}_{s2}+e^2{c}_{s3}$$

[K] is the stiffness matrix denoted by

$$K=\left[\begin{array}{cccccc}P1& P2& P3& {-ks}_1& {-ks}_2& {-ks}_3\\ P2& P4& P5& {ak}_{s1}& -{bk}_{s2}& {-bk}_{s3}\\ P3& P5& P6& {hk}_{s1}& {dk}_{s2}& -{ek}_{s3}\\ {-ks}_1& {ak}_{s1}& {hk}_{s1}& k_{s1}+k_{t1}& 0& 0\\ {-ks}_2& -{bk}_{s2}& {dk}_{s2}& 0& k_{s2}+k_{t2}& 0\\ {-ks}_3& {-bk}_{s3}& -{ek}_{s3}& 0& 0& k_{s3}+k_{t3}\end{array}\right]$$

(11)

where

$$P1=k_{s1}+k_{s2}+k_{s3}$$

$$P2=-{ak}_{s1}+{bk}_{s2}+{bk}_{s3}$$

$$P3=-{hk}_{s1}-{dk}_{s2}+{ek}_{s3}$$

$$P4=a^2{k}_{s1}+b^2{k}_{s2}+b^2{k}_{s3}$$

$$P5={hak}_{s1}-{dbk}_{s2}+{ebk}_{s3}$$

$$P6=h^2{k}_{s1}+d^2{k}_{s2}+e^2{k}_{s3}$$

{z} is the displacement vector denoted by

$$\left\{z\right\}=\left\{\begin{array}{c}z\\ \theta \\ \phi \\ z_1\\ z_2\\ z_3\end{array}\right\}$$

(12)

{F} is the force vector denoted by

$$\left\{F\right\}=\left\{\begin{array}{c}-F_1\\ -F_2\\ -F_3\\ k_{t1}{z}_{g1}+c_{t1}\dot{z}{g}_1+F_1\\ k_{t2}{z}_{g2}+c_{t2}\dot{z}{g}_2+F_2\\ k_{t3}{z}_{g3}+c_{t3}\dot{z}{g}_3+F_3\end{array}\right\}$$

(13)

The main equation can be written as

$$\left\{\ddot{z}\right\}={\left[M\right]}^{-1}\left\{F\right\}-{\left[M\right]}^{-1}\left[C\right]\left\{\dot{u}\right\}-{\left[M\right]}^{-1}\left[K\right]\left\{u\right\}$$

(14)

In the simulation conducted to analyze the behavior of an airliner’s active landing gear under the influence of runway surface roughness, B737-800 model aircraft (Boeing 737-800, Boeing Commercial Airplanes, Washington, DC, USA), one of the most preferred aircraft models by airlines, was used as a reference. In the analysis, it is assumed that 80% of the aircraft’s fuselage mass is transferred to the main landing gear and 20% to the nose landing gear. The reference parameters for the aircraft are given in

Table 1. Full aircraft parameters.

Parameter	Value	Units
M	78,472	kg
m1	578	kg
m2 = m3	1150	kg
ks1	58,027	N/m
ks2 = ks3	996,531	N/m
cs1	131,500	Ns/m
cs2 = cs3	572,500	Ns/m
kt1	1,996,300	N/m
kt2 = kt3	2,812,900	N/m
ct1	131,500	Ns/m
ct2 = ct3	572,500	Ns/m
Ixx	3,394,953	Kg·m2
Iyy	1,866,711	Kg·m2
a	14.6	m
b	1	m
d	2.86	m
e	2.86	m

[12].

3. Control Systems

This study employs three distinct control strategies to manage the vibrations experienced in the referenced passenger aircraft during taxiing. These are: a model-based neural network controller, an adaptive neuro-fuzzy inference systems controller, and a robust adaptive neuro-fuzzy inference systems control system.

Table 2. Training parameters for neural network-based control structures.

Parameter	Value
η: Learning rate	0.2
α: Momentum term	0.15
g(·): Activation function	Sigmoid
N: Iteration number	3,000,000
nI: Input layer neurons	2
nO: Output layer neurons	1
nH: Hidden layer neurons	20

shows the training settings for controller structures that use neural networks. The sub-sections give explanations of these control structures.

As summarized in Table 2, the dataset was divided into 70% training and 30% validation subsets. The training set was used to update the network parameters, while validation ensured generalization. Overfitting was prevented by applying early stopping when the validation error did not improve within 15 consecutive epochs, and by analyzing training-validation error convergence. Cross-validation with rotated data partitions further confirmed that the models retained robustness. These procedures were consistently applied across MBNN, ANFIS, and RANFIS to enable a fair comparison.

3.1. Model-Based Neural Network (MBNN) Controller

Model-based neural networks can provide more accurate prediction and control performance with less data compared to purely data-driven methods. Additionally, its ability to generalize, which inherently incorporates system dynamics, is higher. This network structure combines the system’s analytical model and experimental data. The input layer contains system variables, the hidden layers contain nonlinear activation functions and unknown dynamics, and the output layer contains the system response [17,18]. In the learning process, the error function was updated using the backpropagation algorithm for network weights, drawing from both the measured data and model-based constraints. Figure 2 presents the model-based neural network control scheme. Here, the figure consists of 4 blocks. These are listed as the full aircraft model, neural network controller, reference model, and neural network model.

MBNN is designed to control the displacements of the full aircraft model. It was composed of a second-degree linear reference model and a neural network. The law equation for the proposed controller is given below.

$$u\left(t\right)={\sum }_{j=1}^8\left(\left({\displaystyle \frac{2}{\left(1+e^{-2\left[\sum _{j=1}^8\left[x_d\left(t\right)w_{1j}+x_a\left(t\right)w_{2j}\left(t\right)\right]+1\right]}\right)-1}}\right)w_{j1}\left(t\right)+1\right)$$

(15)

where u(t) is the signal of the neural network controller, and x_d(t) is the desired displacement input of the full aircraft model for the neural controller.w_1j(t) is the weight matrices between first input layer neuron and in the hidden layer neurons. w_2j(t) is the weight matrices between second input layer neuron and in the hidden layer neurons. x_a(t) is dispalcement input of the full aircraft model for neural controller.

3.2. Adaptive Network-Based Fuzzy İnference System (ANFIS) Controller

ANFIS is a hybrid structure that combines the rule-based inference mechanism of fuzzy logic with the learning ability of artificial neural networks. The system optimizes the parameters of membership functions and the rule base using input-output data. In the educational process, a hybrid learning approach is generally preferred, where the backpropagation algorithm and the least squares method are used together. Thus, both linear and nonlinear dynamics can be modeled and controlled with higher accuracy. The standard architecture of an ANFIS is illustrated in Figure 3, where a circle denotes a fixed node and a square indicates an adaptable node [19].

To facilitate understanding, it employed two inputs, designated as x₁ and x₂, and a single output, referred to as z, to elucidate the architecture of the fuzzy inference system [20]. Should the rule base comprise two fuzzy if–then rules, such as

Rule 1: If x₁ is A₁ and x₂ is B₁ then z₁ = p₁x₁ + q₁x₂ + r₁

(16)

Rule 1: If x₁ is A₂ and x₂ is B₂ then z₂ = p₂x₁ + q₂x₂ + r₂

(17)

In this context, A_i and B_i represent fuzzy membership sets, while q_i denotes the quantity of membership functions. The design parameter, r_i, is established during the training process. The structure of a six-layer ANFIS is illustrated in Figure 3. The ANFIS architecture is composed of six distinct layers:

Layer 1.

This is the input layer, which defines full aircraft model displacement and desired displacement.

Layer 2.

Each node in this tier is an adaptive node characterized by a specific fuzzy membership function. For two inputs, the outputs of the node are:

$$L_i^1=\mu A_i\left(x\right), i=\mathrm{1,2}$$

(18)

$$L_i^1=\mu B_i\left(x\right), i=\mathrm{1,2}$$

(19)

In this context, μA_i and μB_i represent membership functions. Typically, μA(x) and μB(x) are chosen to exhibit a bell shape, characterized by a maximum value and a minimum value of 0, similar to the generalized bell function.

$$\mu A_i\left(x\right)={\displaystyle \frac{1}{1+\left[{\left(\frac{x-c_i}{a_i}\right)}^2\right]b_i}}$$

(20)

The values {a_i, b_i, ci} represent the parameter set.

Layer 3.

Each node in the third layer is a circular node designated as “η” which multiplies all incoming signals and transmits the resultant product.

$$w_i=\mu A_i\left(x\right)\mu B_i\left(x\right) (i=1,2\dots )$$

(21)

The output of each node in the second layer signifies the activation intensity of the corresponding rule.

Layer 4.

Each node in the fourth layer is a circular node designated as “Ɲ” the output of the ith node is the ratio of the firing strength of the ith rule to the total firing strength of all rules.

$$\overline{w_i}={\displaystyle \frac{w_i}{w_1+w_2}} (i=1,2\dots )$$

(22)

Layer 5.

In this layer, each node i possesses the following function:

$$L_i^5=\overline{w_i}{f}_i=\overline{w_i}(p_i{x}_1+q_i{x}_2+r_i)$$

(23)

with $\overline{w_i}$ being the normalized firing strength derived from Layer 3.

Layer 6.

The sole node in the sixth layer is a circular node designated as “Σ”. It calculates total outputs as the summation of all input signals.

$$L_i^6=\sum \overline{w_i}{f}_i={\displaystyle \frac{\sum w_i{f}_i}{\sum w_i}}$$

(24)

ANFIS has a more flexible structure than classical fuzzy logic systems because both the premise and consequent parameters can be adjusted simultaneously. The most important aspect of this approach is the hybrid learning algorithm that combines backpropagation-based gradient descent with the least squares method when constructing the fuzzy inference mechanism. Thus, the model can more effectively represent linear and nonlinear complex dynamics, improving control performance.

3.3. Robust Adaptive Network-Based Fuzzy İnference (RANFIS) Control Structure

The RANFIS controller is a hybrid structure that combines the learning capabilities of an artificial neural network-based fuzzy inference system with robust control principles. This system demonstrates resilience against uncertainties and parameter variations, while enabling more precise modeling of nonlinear dynamics by adapting both premise and consequent parameters [20]. The mathematical representation of the force in the robust control system is provided by the subsequent equation:

$$u\left(t\right)=\sum {\displaystyle \frac{\overline{w_i} (p_i{x}_1+q_i{x}_2+r_i)}{w_i}}$$

(25)

In this context, r and b represent the parameters of the robust controller, which are empirically determined to be r = 30 and b = 0.0015. Figure 4 illustrates the schematic depiction of the proposed neural-based control system concept. The backpropagation algorithm is employed to modify the weights of the neural network. For the six-degree-of-freedom aircraft model, the controllers receive as inputs the pitch angle (θ), roll angle (φ), vertical fuselage displacement (z), and relative gear displacements (z₁, z₂, z₃). The control outputs are actuator forces applied in parallel with the oleo-pneumatic struts. In the ANFIS framework, a first-order Sugeno-type fuzzy inference system with Gaussian membership functions is adopted. The rule base is updated online through a hybrid learning procedure combining least-squares estimation and gradient descent. The RANFIS controller builds upon this structure by introducing robustness parameters (r,br, br,b) into the adaptive law, thereby enhancing tolerance against modeling errors and random disturbances. This design allows the controller to achieve rapid transient suppression while maintaining robustness under stochastic runway excitation.

Back Propagation Neural Network (BPNN)

BPNN is the most commonly used method for updating the weights of neural networks. In forward propagation, the network output and task-specific loss are calculated; in backpropagation, gradients are derived using the chain rule, and weights are updated with a gradient descent-based optimizer. The weights connecting the input layer to the hidden layer are modified as follows:

$$\Delta W_{ij}\left(t\right)=-\eta {\displaystyle \frac{\partial E_2\left(t\right)}{\partial W_{ij}\left(t\right)}}+\alpha \Delta W_{ij}(t-1)$$

(26)

The weights connecting the hidden layer to the output layer are modified according to the subsequent equation;

$$\Delta W_{jk}\left(t\right)=-\eta {\displaystyle \frac{\partial E_1\left(t\right)}{\partial W_{jk}\left(t\right)}}+\alpha \Delta jk(t-1)$$

(27)

where η represents the learning rate, and α denotes the momentum term. E₂(t) represents the propagation error between the hidden layer and the output layer. E₁(t) represents the error between the experimental and neural network output signals [21].

4. Simulation Results

This section presents the simulation results obtained for the control of vibrations experienced by the passenger aircraft during taxiing. In the study, the taxi speed was fixed at 55 km/h, and a random road profile was used to represent the irregularities encountered by the aircraft landing gear. The random runway profile used in the simulations was generated in accordance with the ISO 8608 standard [22], with a reference spatial frequency of n₀ = 0.1 m⁻¹ and a roughness coefficient of G_q(n₀) = 256 × 10⁻⁶ m³, corresponding to a Class C surface condition that represents typical airport taxiway roughness. As part of the analyzes, the vertical displacements of the nose landing gear, left rear landing gear, right rear landing gear, and the aircraft fuselage were evaluated. These dynamic behaviors were examined using three different control approaches: Model-based Neural Network Controller (MBNN), Adaptive Neural Network-based Fuzzy Inference System (ANFIS), and the proposed Robust Adaptive Neural Network-based Fuzzy Inference Controller (RANFIS). To evaluate the effectiveness of the proposed control approaches, basic control system performance parameters such as peak value, peak time, rise time, settling time, and steady-state error were calculated. The findings obtained comparatively demonstrate the effectiveness of different control structures in vibration control.

Figure 5 shows the MBNN-based approach, which exhibits high-amplitude oscillations with a peak value of approximately ±0.003 rad and a steady-state error of 0.008 rad. Due to a settling time exceeding 5 s, it demonstrates unstable behavior. The ANFIS method, on the other hand, showed better performance with a peak value of ±0.002 rad and an error of 0.004 rad, but the settling time of approximately 3.5 s indicates that the vibrations could not be completely suppressed. In contrast, the RANFIS approach achieved the highest success with a low peak value of ±0.001 rad, a rise time of less than 0.1 s, and a settling time of less than 1 s; it reduced the steady-state error to a negligible level and perfectly tracked the desired reference response.

When the simulation findings obtained from the roll direction in Figure 6 are evaluated with numerical performance parameters, the differences between the methods become clearly apparent. The MBNN-based control approach produced the highest overshoot value with a peak value of approximately 0.0032 rad, and despite a rise time of around 0.5 s and a peak time of 0.8 s, it exhibited a settling time longer than 5 s. Additionally, the fact that it leaves a steady-state error of approximately 15% indicates that this method exhibits inadequate control performance in the roll direction. The ANFIS method, on the other hand, reduced the peak value to 0.002 rad, with a rise time of 0.4 s, a peak time of around 0.7 s, and stabilization achieved within approximately 3.5 s. The reduction in the steady-state error to 7% proves that this represents a significant improvement compared to the MBNN. On the other hand, the robust adaptive neuro-fuzzy inference system (RANFIS) method reached a minimum peak value of 0.001 rad, providing a rapid response with a rise time of only 0.3 s and a peak time of 0.5 s. The system settling and becoming stable within approximately 1.2 s, and the steady-state error dropping to a level of 1–2%, clearly demonstrates the superiority of this method in suppressing vibrations in the roll direction.

The simulation results obtained for the vertical displacement shown in Figure 7 clearly reveal the performance differences between the methods. The MBNN-based method produced a peak value of approximately 3.5 cm, with a rise time of 0.6 s, a peak time around 0.9 s, and a settling time exceeding 5 s. Additionally, the steady-state error remaining around 12% indicates that this method is insufficient for vibration control. It can be seen that with the ANFIS approach, the peak value decreased to 2.2 cm, the rise time was around 0.4 s, and the settling time was approximately 3.5 s. The steady-state error remained within the range of 6–7%, representing a significant improvement over the previous method. In contrast, the robust adaptive neuro-fuzzy inference system (RANFIS) method showed the most successful performance, with a peak value of 1.0 cm, a rise time of 0.3 s, and a settling time of only 1.5 s. With the steady-state error dropping below 2%, the RANFIS method has emerged as the clear most effective solution for vertical displacement control.

As shown in Figure 8, the MBNN method produced high-amplitude oscillations; the peak value was 7.0 cm, the peak time was 8.3 s, the rise time was 0.50 s, the settling time was over 5.0 s, and the steady-state error was −0.6 cm. With ANFIS, the peak value was 4.2 cm, the peak time was 9.0 s, the rise time was 0.35 s, the settling time was 3.2 s, and the steady-state error was −1.0 cm. RANFIS, on the other hand, tracked the reference almost flawlessly; the peak value was obtained as 0.25 cm, the peak time as 0.35 s, the rise time as 0.20 s, the settling time as 0.90 s, and the steady-state error as less than 0.05 cm. These metrics clearly show that RANFIS provides a significantly superior control performance in terms of vibration suppression and comfort in the nose landing gear.

As seen in Figure 9, for the vertical displacement of the right rear landing gear, the MBNN produced a significant overshoot with a peak value of approximately 7.8 cm, showing a rise of 0.55 s and a peak time around 0.90 s; the settling time exceeds 5 s, and the steady-state error remains at approximately −0.8 cm negative offset. In ANFIS, the peak value decreases to around 6 cm; the rise time is approximately 0.40 s, the peak time is around 0.70 s; the settling time is in the range of 3 s, and the steady-state error is approximately −1.0 cm. RANFIS, on the other hand, follows the reference almost flawlessly in practice: the peak is below 0.3 cm, the rise is around 0.22 s, the peak time is 0.35 s, the settling time is less than 1.1 s, and the steady-state error is below 0.05 cm, close to zero. Considering that the rear landing gear carries the majority of the aircraft’s load, this table confirms RANFIS’s clear leadership in terms of energy damping capacity and comfort metrics.

In Figure 10, the response of the aircraft’s left main landing-gear active suspension system to a random road roughness input signal is shown. MBNN is struggling to maintain control under high energy; the peak value is approximately 7.2 cm, the rise time is 0.55 s, the peak time is 0.95 s, the settling time is over 5 s, and the steady-state error is −0.7 cm. ANFIS slightly reduces the amplitudes; the peak value is 5.8 cm, the rise time is 0.42 s, the peak time is 0.72 s, the settling time is 3.1 s, and the steady-state error is −0.9 cm. The RANFIS reference is practically flawless in practice; the peak value is 0.28 cm, the rise time is 0.21 s, the peak time is 0.33 s, the settling time is less than 1 s, and the steady-state error is below 0.05 cm. In short, RANFIS makes a clear difference in both peak management and rapid settling under high load conditions on the main landing gear.

The performance parameters of the applied control systems are given in

Table 3. The performance parameters of the applied control systems.

Signal	Control Structure	Peak Value	Rise Time(s)	Settling Time(s)	Steady-State Error
Pitch θ (×10−3 rad)	MBNN	3.0	0.25	>5.0	0.80
	ANFIS	2.0	0.20	3.5	0.40
	RANFIS	0.10	0.10	<1.0	~0.00
Roll ϕ (×10−3 rad)	MBNN	3.2	0.50	>5.0	0.45
	ANFIS	2.0	0.40	3.5	0.21
	RANFIS	1.0	0.30	1.2	0.02
Fuselage vertical z (cm)	MBNN	3.5	0.60	>5.0	0.30
	ANFIS	2.2	0.40	3.5	0.15
	RANFIS	1.0	0.30	1.5	0.03
Nose gear z1 − zg1 (cm)	MBNN	7.0	0.50	>5.0	−0.60
	ANFIS	4.2	0.35	3.2	−1.00
	RANFIS	0.25	0.20	0.90	<0.05
Right main gear z2 − zg2 (cm)	MBNN	7.8	0.55	>5.0	−0.80
	ANFIS	6.0	0.40	3.0	−1.00
	RANFIS	0.30	0.22	1.1	<0.05
Left main gear z3 − zg3 (cm)	MBNN	7.2	0.55	>5.0	−0.70
	ANFIS	5.8	0.42	3.1	−0.90
	RANFIS	0.28	0.21	<1.0	<0.05

. Across all axis and landing-gear positions, RANFIS significantly outperforms the others with the lowest peak value, shortest settling time, and negligible steady-state error; ANFIS provides moderate improvement, while MBNN falls short in terms of comfort and tracking accuracy with high peaks and long settling times. Considering that the main landing gear carries the majority of the aircraft’s load, the improvement brought by RANFIS is particularly noticeable and operationally critical, especially in the rear gear.

5. Conclusions and Discussion

This study compared three controllers (MBNN, ANFIS, RANFIS) for suppressing body pitch–roll angles and body/landing-gear vertical displacements at a taxi speed of 55 km/h under a random runway profile. Performance was evaluated via rise time, settling time, peak value, and steady-state error. RANFIS consistently provided the smallest peaks, the shortest settling times (<1–1.5 s), and near-zero steady-state errors (<0.05 cm). Attitude deviations dropped to the sub-milliradian range, while fuselage and gear peak displacements fell to ≤0.3–1.0 cm. Improvements were most pronounced at the main gears (~80% of load), where ANFIS-level centimeter peaks were reduced to ≤0.3 cm and settling was shortened by a factor of 2–3. While ANFIS improved over MBNN, it could not fully suppress oscillations and offsets; MBNN produced the largest overshoot and the longest settling.

RANFIS’s advantage stems from combining robustness with adaptive rule/parameter updates, a combination well suited to the load-dependent gear–body interactions during taxiing. The observed reductions translate into tangible gains in passenger comfort, reduced fatigue loads on gear components, and improved steering/braking stability. Operationally, a RANFIS-class controller supports compliance with ride-quality envelopes and reduced suspension wear.

The present findings are consistent with recent research highlighting the value of intelligent and hybrid controllers for aeronautical vibration suppression. For example, adaptive fuzzy and neuro-fuzzy designs have been reported to improve landing-gear dynamics under stochastic runway conditions [14]. Model predictive and nonlinear robust strategies have also been tested in flexible aircraft and eVTOL platforms, achieving improved vibration attenuation but often at higher computational cost [15]. More recent contributions on type-2 fuzzy and reinforcement learning-based controllers further support the shift toward adaptive intelligent designs [16]. The RANFIS framework extends this literature by demonstrating a hybrid robust-adaptive scheme capable of superior suppression under random runway excitation.

The results are simulation-based; actuator time/speed limits, servo dynamics, and measurement noise are idealized. A single taxi speed and runway spectrum were used; crosswind, braking/turning maneuvers, and thermal effects were excluded. In addition, all state variables were initialized at equilibrium positions (zero pitch/roll angles and zero vertical displacements), with random runway excitation introduced as the only disturbance. While this choice ensures comparability across controllers, alternative initialization schemes (e.g., perturbed initial attitudes or pre-loaded suspension states) may influence transient peaks and settling behavior. Likewise, simplifying modeling assumptions—such as symmetric gear parameters and idealized actuator dynamics—reduce computational complexity but may affect quantitative accuracy. These factors do not alter the comparative superiority of RANFIS but are important for assessing reproducibility and robustness. Future work will therefore include sensitivity analyses under varied initialization strategies and alternative modeling assumptions.

The results are simulation-based. A single taxi speed and runway spectrum were used; crosswind, braking/turning maneuvers, and thermal effects were excluded. All state variables were initialized at equilibrium (zero pitch/roll and vertical displacements), with runway excitation as the only disturbance; measurement noise was idealized. Simplifying assumptions—such as symmetric gear parameters and idealized actuator/servo dynamics—reduce model complexity but may affect quantitative accuracy. Actuator time/speed limits, bandwidth, and saturation constraints were not modeled; forces were applied directly in the governing equations to isolate controller differences among MBNN, ANFIS, and RANFIS. These caveats align with broader uncertainty/reproducibility concerns in vibration simulations [23,24] and motivate sensitivity analyses and uncertainty quantification, alongside a hardware-in-the-loop (HIL) extension that explicitly models actuator dynamics and saturation.

Finally, international standards such as ISO 2631-1 [25] (whole-body vibration), ICAO Annex 14 [26] (aerodrome design), and FAA AC 25-7D [27] (ride quality) provide benchmarks for evaluating taxiing comfort and safety. The observed reductions are consistent with maintaining these limits. Critically, this study contributes by establishing a reproducible benchmark for robust-adaptive intelligent control of landing-gear systems, showing that significant vibration suppression can be achieved without excessive computational cost, and by providing a foundation for future system integration.

In future work, HIL experiments will be conducted to validate the proposed control strategy under real-world conditions, providing a critical step toward experimental verification and eventual application in next-generation active landing-gear systems.