Forced Vibration Analysis of a Hydroelastic System with an FGM Plate, Viscous Fluid, and Rigid Wall Using a Discrete Analytical Method
Abstract
1. Introduction
2. Materials and Methods
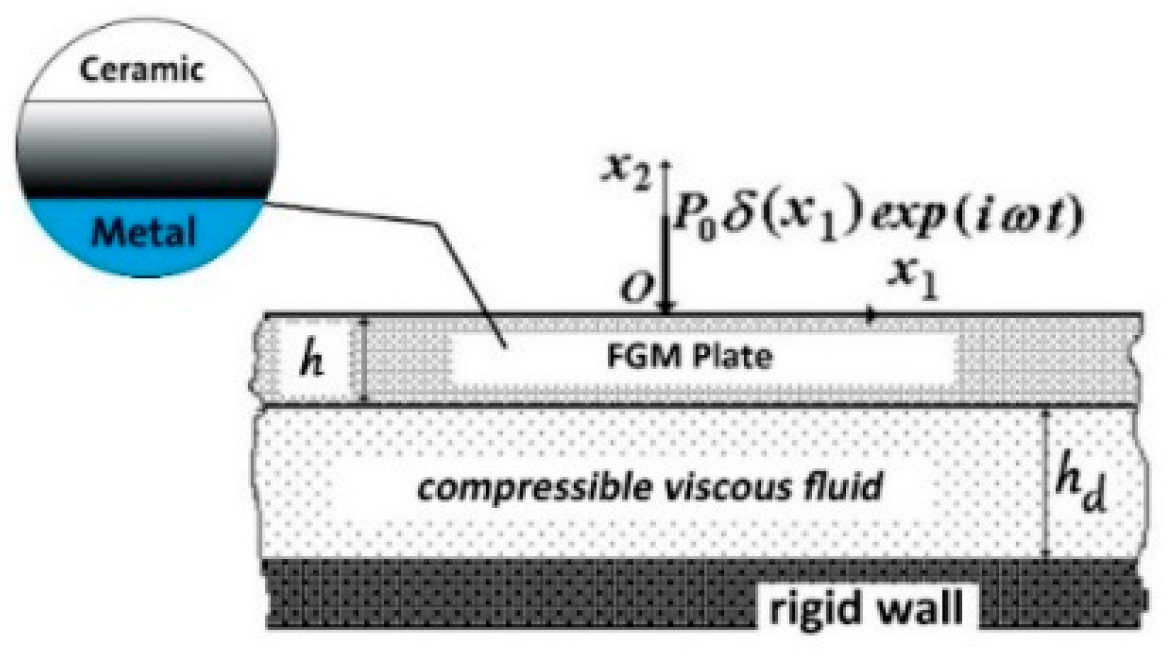
2.1. Description of the Hydroelastic System
2.2. Mathematical Model of the Plate Motion
2.3. Governing Field Equations for the Fluid Flow
2.4. Solution Method: Discrete Analytical Approach
3. Numerical Applications and Results
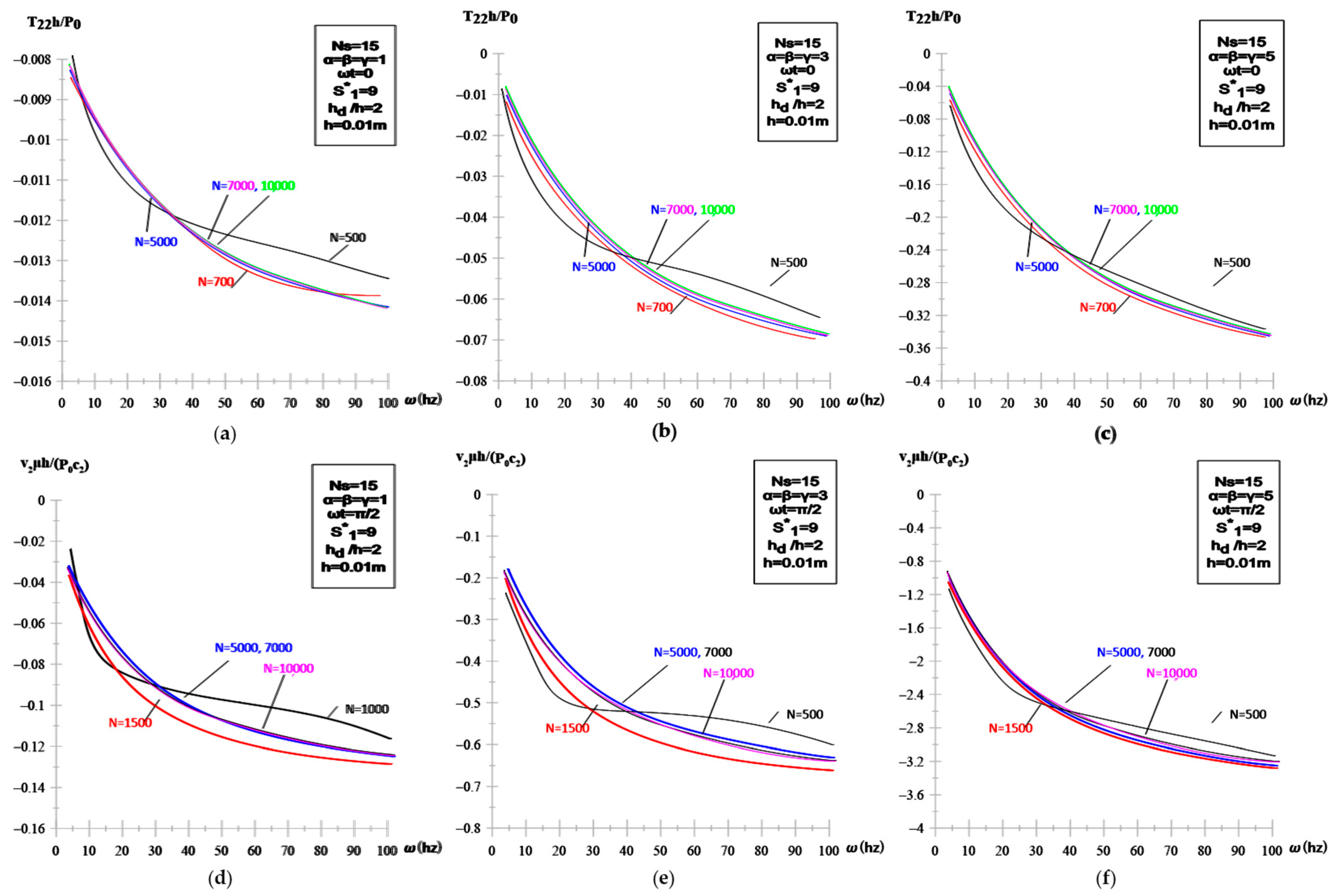
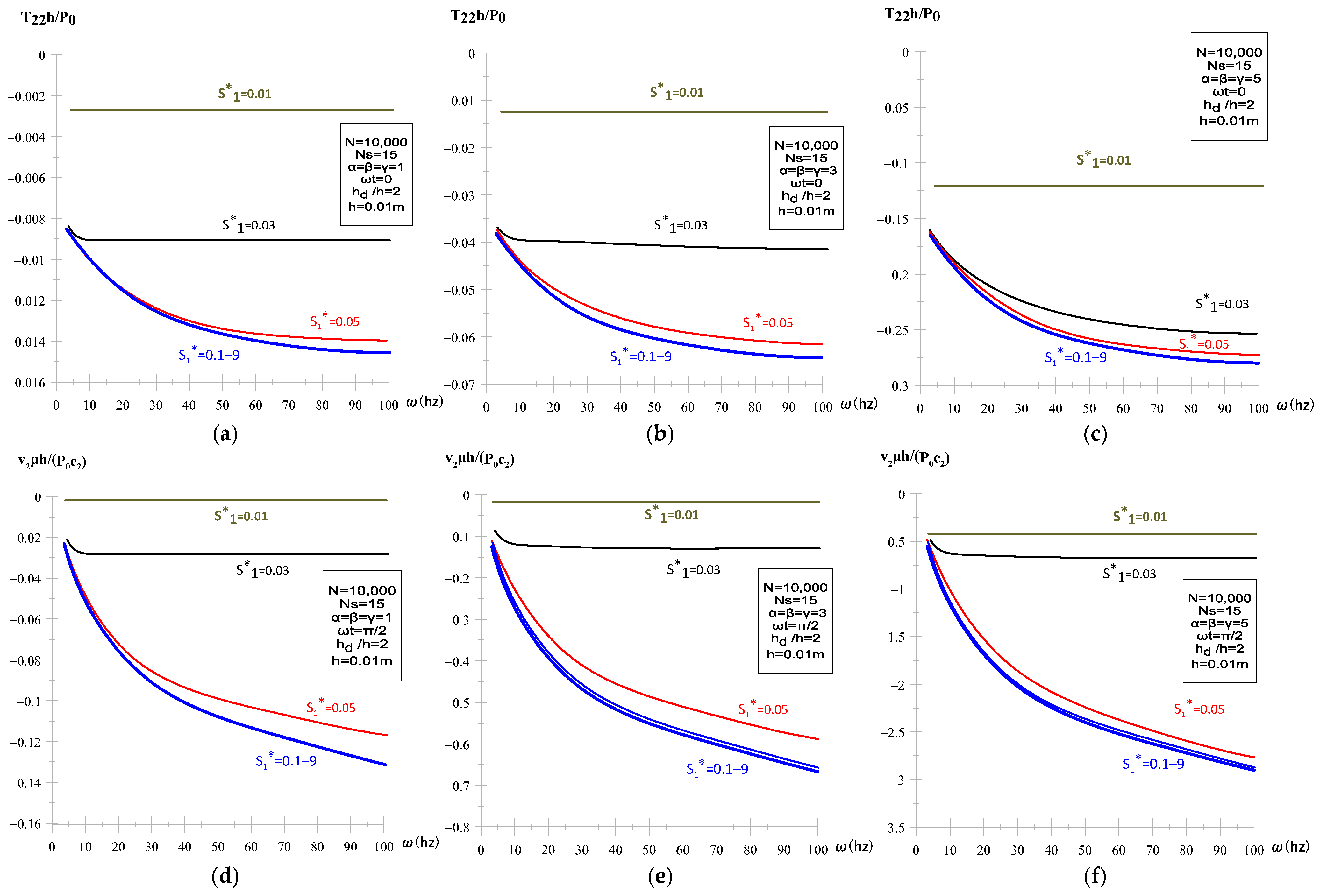
3.1. Convergence of the Numerical Algorithm
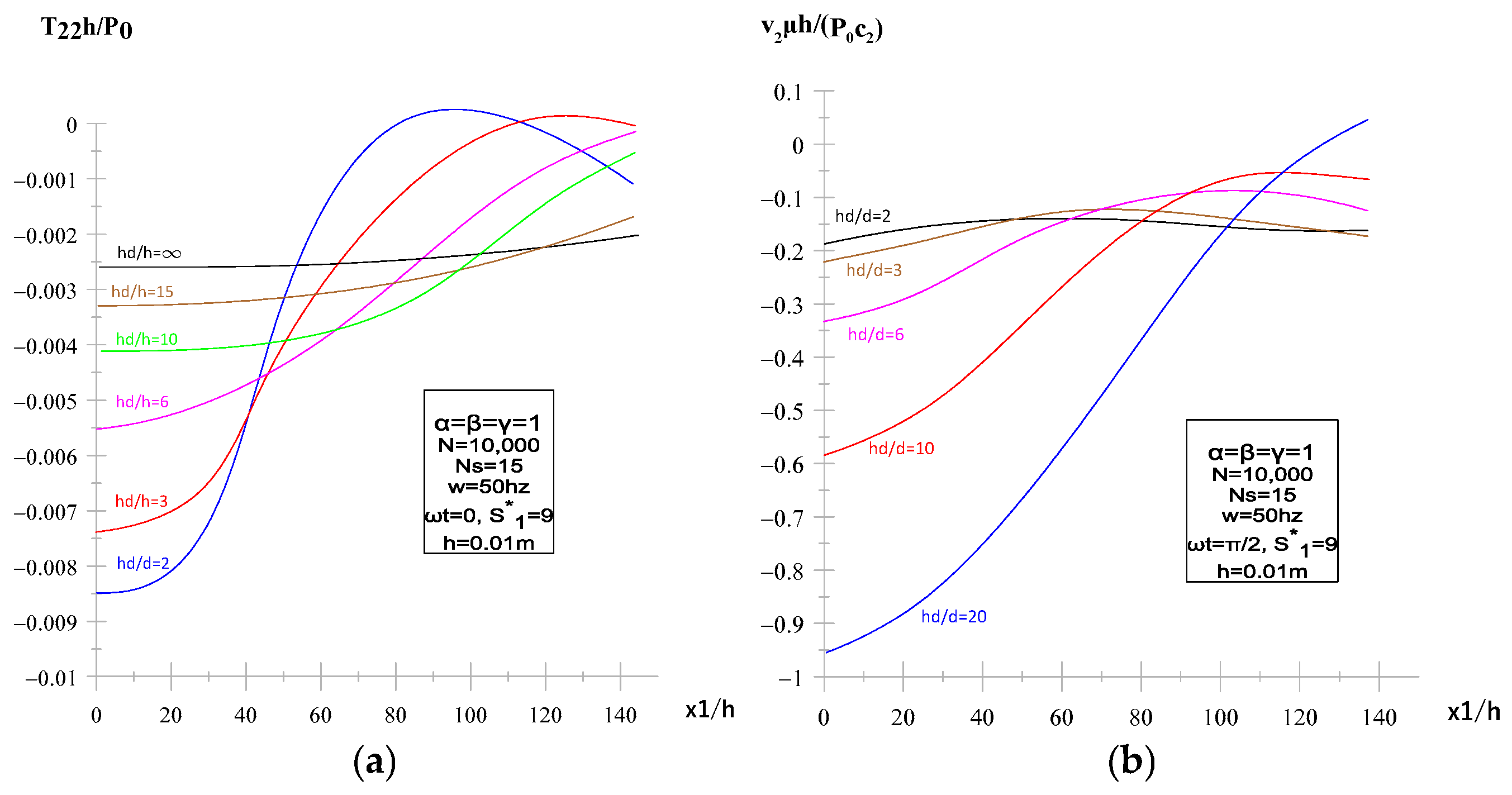
3.2. Effect of Fluid Depth Ratio and Plate Thickness
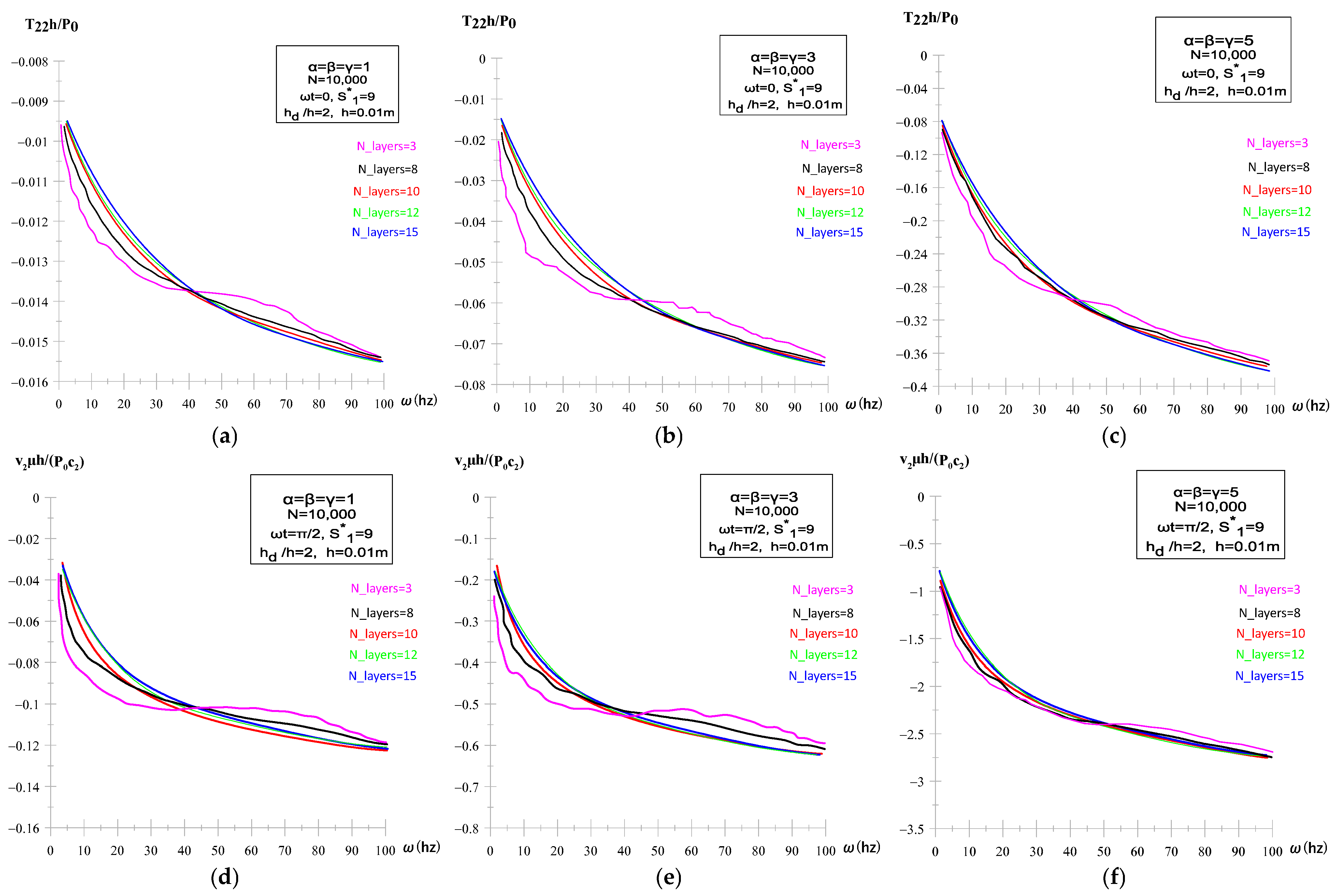
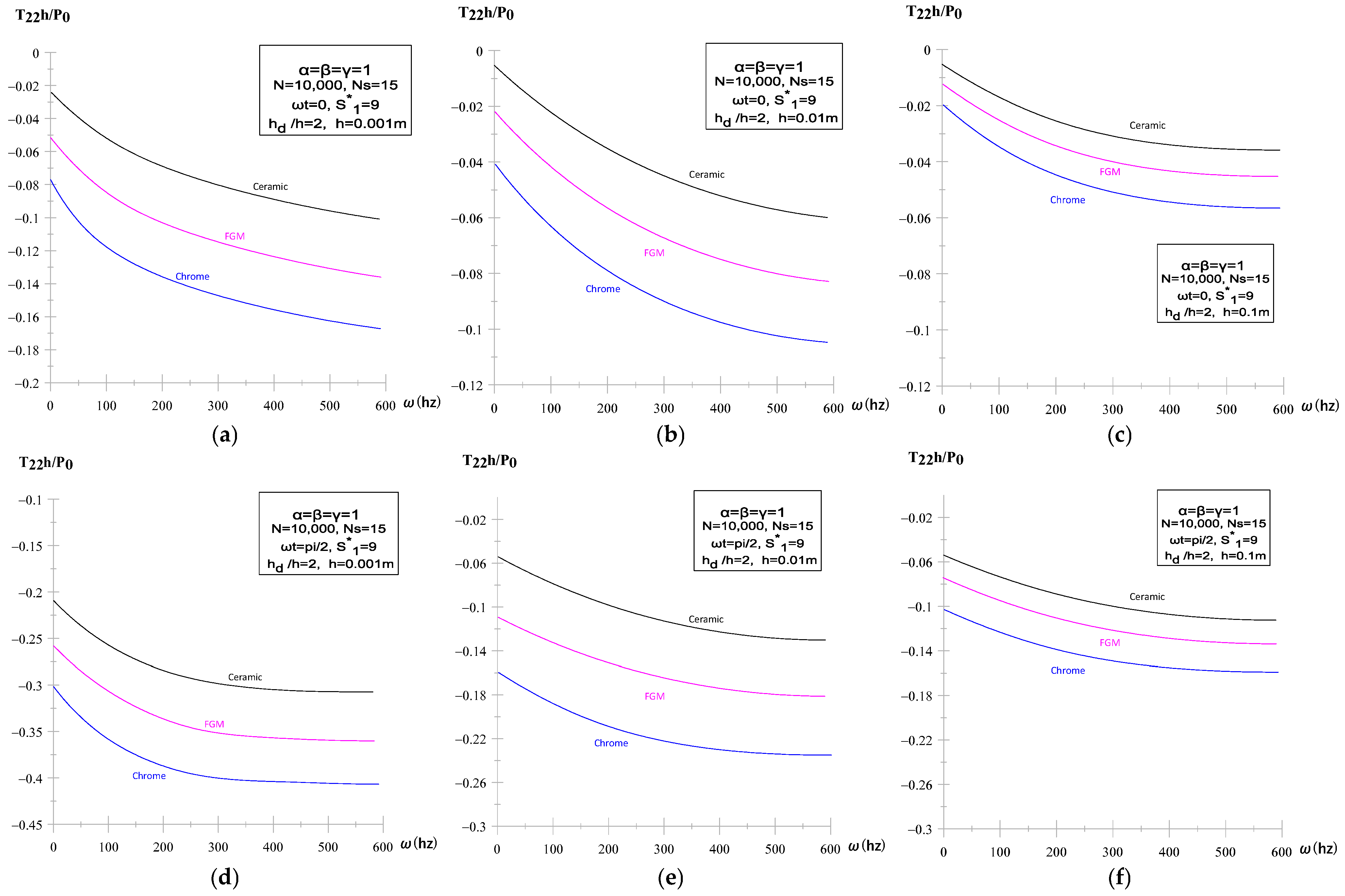
3.3. Influence of Gradation Index and Excitation Phase
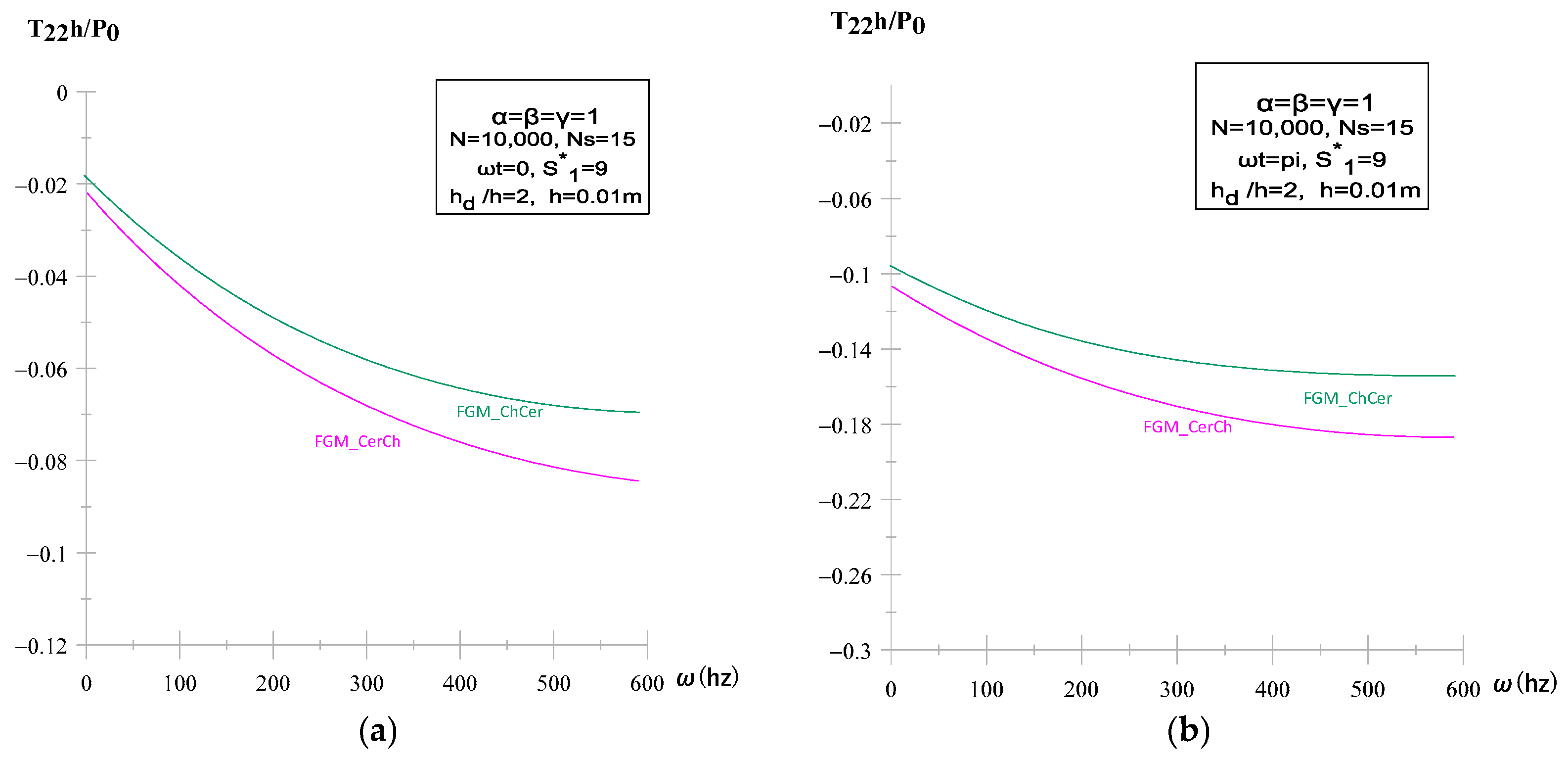
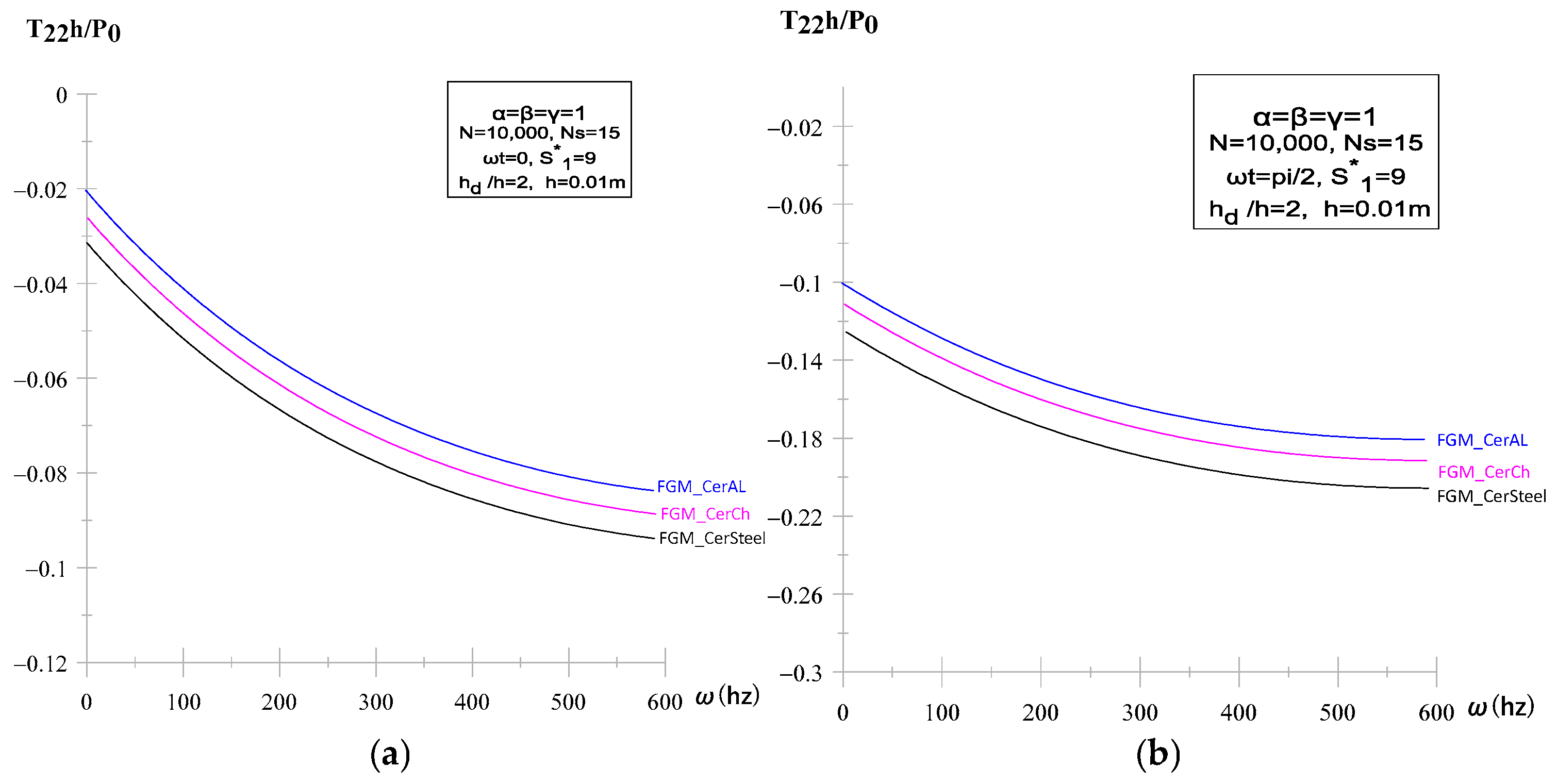
3.4. Effect of Gradation Direction and Metal Type
3.5. Summary of Main Numerical Findings
4. Conclusions
- *
- Extending forced vibration analysis to FGM plates in viscous, compressible, and confined fluid domains.
- *
- Demonstrating how gradation index, material type, and orientation systematically influence hydroelastic stresses and velocities.
- *
- Establishing the discrete analytical method as a reliable tool for analyzing complex FGM–fluid interactions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lamb, H. Axisymmetric vibration of circular plates in contact with water. Proc. R. Soc. Lond. A 1921, 98, 205–216. [Google Scholar]
- Fu, Y.; Price, W.G. Interactions between a partially or totally immersed vibrating cantilever plate and surrounding fluid. J. Sound. Vib. 1987, 118, 495–513. [Google Scholar] [CrossRef]
- Bagno, A.M.; Guz, A.N.; Shchuruk, G.I. Influence of fluid viscosity on waves in an initially deformed compressible elastic layer interacting with a fluid medium. Int. Appl. Mech. 1994, 30, 643–649. [Google Scholar] [CrossRef]
- Bagno, A.M.; Guz, A.N. Elastic waves in prestressed bodies interacting with fluid (Survey). Int. Appl. Mech. 1997, 33, 435–465. [Google Scholar] [CrossRef]
- Amabili, M. Effect of finite fluid depth on the hydroelastic vibrations of circular and annular plates. J. Sound. Vib. 1996, 191, 909–925. [Google Scholar] [CrossRef]
- Jeong, K.-H.; Kim, K.-J. Hydroelastic vibration of a circular plate submerged in a bounded compressible fluid. J. Sound. Vib. 2005, 283, 153–172. [Google Scholar] [CrossRef]
- Chapman, C.J.; Sorokin, S.V. The forced vibration of an elastic plate under significant fluid loading. J. Sound. Vib. 2005, 281, 719–741. [Google Scholar] [CrossRef]
- Graham, W.R. Analytical approximations for the modal acoustic impedances of simply supported rectangular plates. J. Acoust. Soc. Am. 2007, 122, 719–730. [Google Scholar] [CrossRef]
- Atkinson, C.; de Lara, M.M. The frequency response of a rectangular cantilever plate vibrating in a viscous fluid. J. Sound. Vib. 2007, 300, 352–367. [Google Scholar] [CrossRef]
- Ayela, C.; Nicu, L. Micromachined piezoelectric membranes with high nominal quality factors in Newtonian liquid: A Lamb’s model validation at the microscale. Sens. Actuators A Phys. 2007, 123, 860–868. [Google Scholar] [CrossRef]
- Kozlovsky, Y. Vibration of plates in contact with viscous fluid: Extension of Lamb’s model. J. Sound. Vib. 2009, 326, 332–339. [Google Scholar] [CrossRef]
- Askari, M.; Ghaffarzadeh, H.; Ghannad, M. Hydroelastic vibration of circular plates in contact with fluid. Appl. Math. Model. 2013, 37, 2574–2587. [Google Scholar]
- Khorshidi, K.; Malekzadeh, P. Hydroelastic vibration of functionally graded rectangular plates in fluid domains. Compos. Struct. 2015, 127, 74–83. [Google Scholar]
- Canales, F.; Ritto, T.G.; Rochinha, F.A. On the hydroelastic response of elastic plates in compressible fluid domains. J. Fluids Struct. 2018, 81, 160–173. [Google Scholar]
- Li, Y.; Liu, B.; Li, X. Free vibration of FGM Mindlin plates partially submerged in incompressible fluid. Thin-Walled Struct. 2022, 178, 109420. [Google Scholar]
- Ardıç, H.; Güler, M.A. Hydroelastic vibration analysis of FGM Mindlin plates in viscous fluids via isogeometric methods. Ocean. Eng. 2025, 290, 120955. [Google Scholar]
- Akbarov, S.D.; Ismailov, M.I.; Kepceoğlu, A. Forced vibration of a pre-stressed elastic plate interacting with compressible viscous fluid in rigid-wall confinement. Mech. Adv. Mater. Struct. 2017, 24, 1–15. [Google Scholar]
- Farsani, R.E.; Malekzadeh, P.; Alibeigloo, A. Free vibration analysis of porous functionally graded plates in contact with fluid. Ocean. Eng. 2021, 232, 109120. [Google Scholar] [CrossRef]
- Farsani, R.E.; Malekzadeh, P.; Alibeigloo, A. Hydroelastic analysis of variable-thickness porous FGM plates in fluid tanks. Appl. Math. Model. 2022, 103, 556–573. [Google Scholar]
- Pham, T.; Do, T.; Bui, T. Thermal vibration of multidirectional porous FGM plates interacting with fluid. Eur. J. Mech. A Solids 2024, 103, 105183. [Google Scholar]
- Murari, R.; Kumar, V.; Sharma, R. Vortex-induced vibrations of functionally graded auxetic plates in fluid environments. Compos. Part. B Eng. 2024, 266, 112012. [Google Scholar]
- Kurpa, L.; Drach, I.; Tserkovnyuk, O. Free vibration analysis of porous FGM plates using the R-functions method. Compos. Struct. 2024, 317, 117276. [Google Scholar]
- Norouzi, A.; Ghadiri, M.; Asemi, K. Fluid–structure interaction in nonlinear plates under flow: A review. Arch. Appl. Mech. 2023, 93, 1461–1483. [Google Scholar]
- Birman, V.; Byrd, L.W. Modeling and analysis of functionally graded materials and structures. Appl. Mech. Rev. 2019, 62, 1–25. [Google Scholar]
- Guz, A.N. Dynamics of Compressible Viscous Fluid; Cambridge Scientific Publishers: Cambridge, UK, 2009. [Google Scholar]
- Akbarov, S.D.; Ismailov, M.I. The forced vibration of the system consisting of an elastic plate, compressible viscous fluid and rigid wall. J. Vib. Control 2015, 23, 1809–1827. [Google Scholar] [CrossRef]
- Guz, A.N. Elastic Waves in Bodies with Initial (Residual) Stresses; A.C.K.: Kiev, Ukraine, 2004. [Google Scholar]
- Cao, X.; Jin, F.; Jeon, I. Calculation of propagation properties of Lamb waves in a functionally graded material (FGM) plate by power series technique. NDT E Int. 2011, 44, 84–92. [Google Scholar] [CrossRef]
- Kuzeci, Z.E.; Akbarov, S.D. Vibration of a Two-Layer “Metal+PZT” Plate Contacting with Viscous Fluid. Comput. Mater. Contin. 2023, 74, 4341–4350. [Google Scholar] [CrossRef]



| Material/Fluid | (GPa) | Lamé (GPa) | Density (kg/m3) | (GPa) | Poisson’s Ratio | Dynamic Viscosity (kg/m.s) | Reference Density (kg/m3) | Sound Speed (m/s) |
|---|---|---|---|---|---|---|---|---|
| Plate(Cr) | 102.5 | 74.2 | 7190 | 248.5 | 0.21 | — | ||
| Ceramic | 118.1 | 138 | 3900 | 300 | 0.27 | |||
| Fluid (Glycerin) | 1.393 | 1260 | 1927 |
| Parameter Studied | Range/Cases | Notes | ||
|---|---|---|---|---|
| Number of sublayers Ns | 3–15 | Converges after Ns ≥ 12 | Converges with stress results | Low Ns gives oscillations |
| Intervals N | 500–10,000 | Stable for N ≥ 7000 | Same trend | Spectral resolution critical |
| Integration parameter | 0.01–9 | Stable for ≥ 0.1 | Matches stress convergence | Small β causes oscillations |
| Fluid depth ratio | 0.2–15 | ↑ → ↓ stresses | ↑ → ↑ velocities | Shallow fluid amplifies stresses |
| Plate thickness (h) | 0.001–0.1 m | Thin → ↑ stresses | Thin → ↑ velocities | Thick plates give more stabilization |
| Gradation index | 1, 3, 5 | Higher n → ↓ stresses | Higher n → smoother profiles | Ceramic-rich improves stiffness |
| Gradation direction | Cer→Metal vs. Metal→Cer | Cer→Metal → ↓ stresses | Metal at interface → ↑ stresses | Interface material dominates |
| Metallic phase | Cr, Steel, Al | Cr > Steel > Al (stress level) | Same ordering | Due to stiffness + density |
| Excitation phase | 0 vs. | → ↓ amplitudes | → smoother velocity | Phase shifts damp interaction |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alrubaye, M.M.; Akbarov, S.D. Forced Vibration Analysis of a Hydroelastic System with an FGM Plate, Viscous Fluid, and Rigid Wall Using a Discrete Analytical Method. Appl. Sci. 2025, 15, 10854. https://doi.org/10.3390/app151910854
Alrubaye MM, Akbarov SD. Forced Vibration Analysis of a Hydroelastic System with an FGM Plate, Viscous Fluid, and Rigid Wall Using a Discrete Analytical Method. Applied Sciences. 2025; 15(19):10854. https://doi.org/10.3390/app151910854
Chicago/Turabian StyleAlrubaye, Mohammed M., and Surkay D. Akbarov. 2025. "Forced Vibration Analysis of a Hydroelastic System with an FGM Plate, Viscous Fluid, and Rigid Wall Using a Discrete Analytical Method" Applied Sciences 15, no. 19: 10854. https://doi.org/10.3390/app151910854
APA StyleAlrubaye, M. M., & Akbarov, S. D. (2025). Forced Vibration Analysis of a Hydroelastic System with an FGM Plate, Viscous Fluid, and Rigid Wall Using a Discrete Analytical Method. Applied Sciences, 15(19), 10854. https://doi.org/10.3390/app151910854






