Real-Time Global Velocity Profile Calculation for Eco-Driving on Long-Distance Highways Using Variable-Step Spatial Segmentation
Abstract
1. Introduction
- Loss of road topology information: If the segment length is excessively large, important geographical features, such as steep gradients within short intervals, may be overlooked. For instance, when using a 500 m step size, a steep slope within a 200 m section may be averaged with flat regions, which would lead to inaccurate representation of the actual slope. Such inaccuracies can result in critical errors when deriving fuel-optimal velocity profiles.
- Computational inefficiency: Conversely, if a very short step size is chosen to capture fine variations in road geometry, the number of segments grows exponentially over the entire route. This dramatically increases the computational burden of optimization algorithms such as DP or nonlinear programming (NLP), thereby hindering real-time applicability. Such inefficiencies become even more pronounced on long-haul freight routes.
- Difficulty in real-time re-optimization: In practice, unexpected events, such as changes in traffic conditions or route adjustments, necessitate rapid re-computation of the optimal velocity profile. However, under a fixed-step framework, such events increase the problem size substantially, whereby the recalculation times become too long to satisfy real-time requirements.
2. Longitudinal Dynamic Model
2.1. Longitudinal Vehicle Dynamics
2.2. Re-Parameterization of Independent Variables
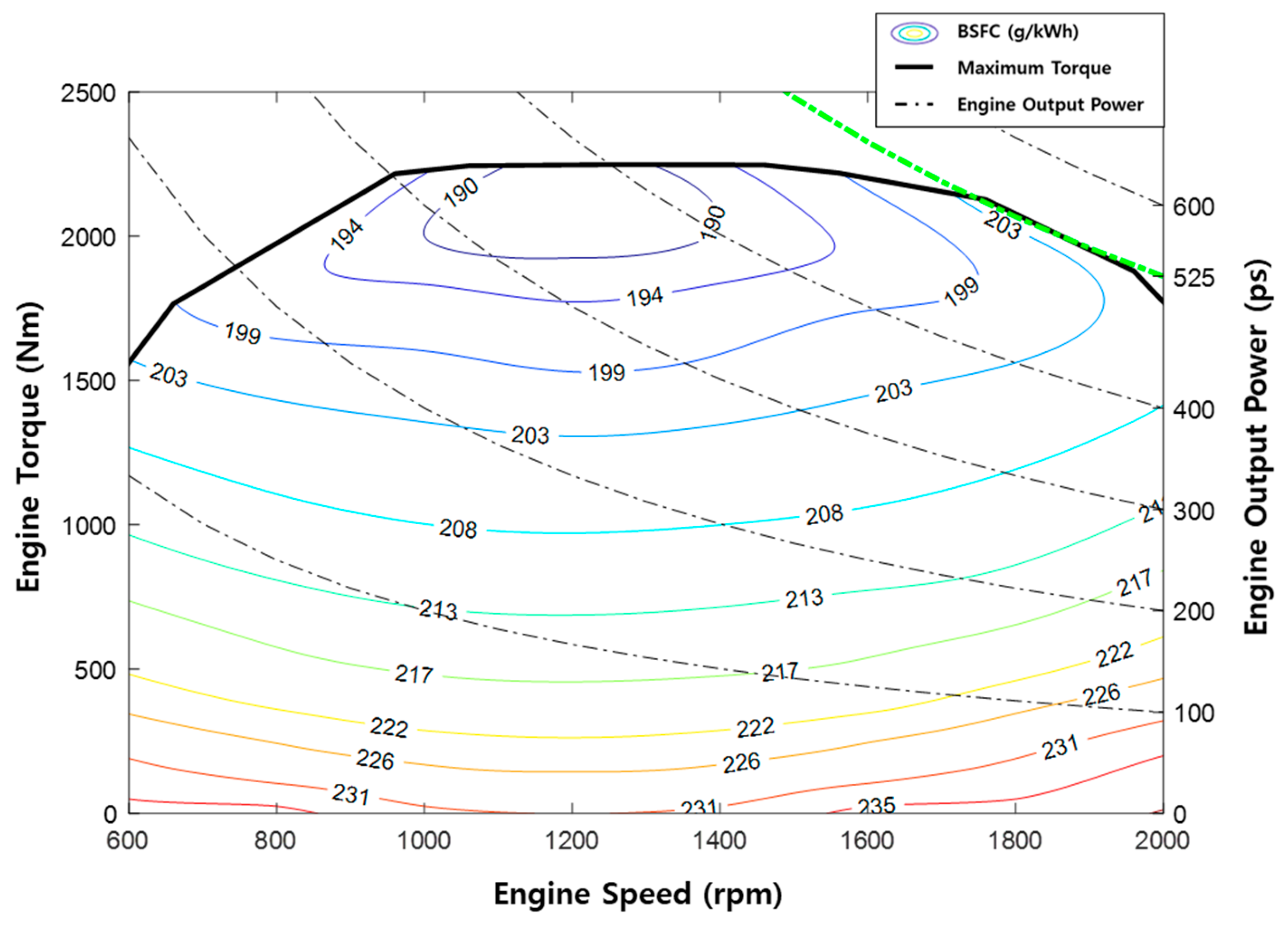
2.3. Engine Model
2.4. Transmission System
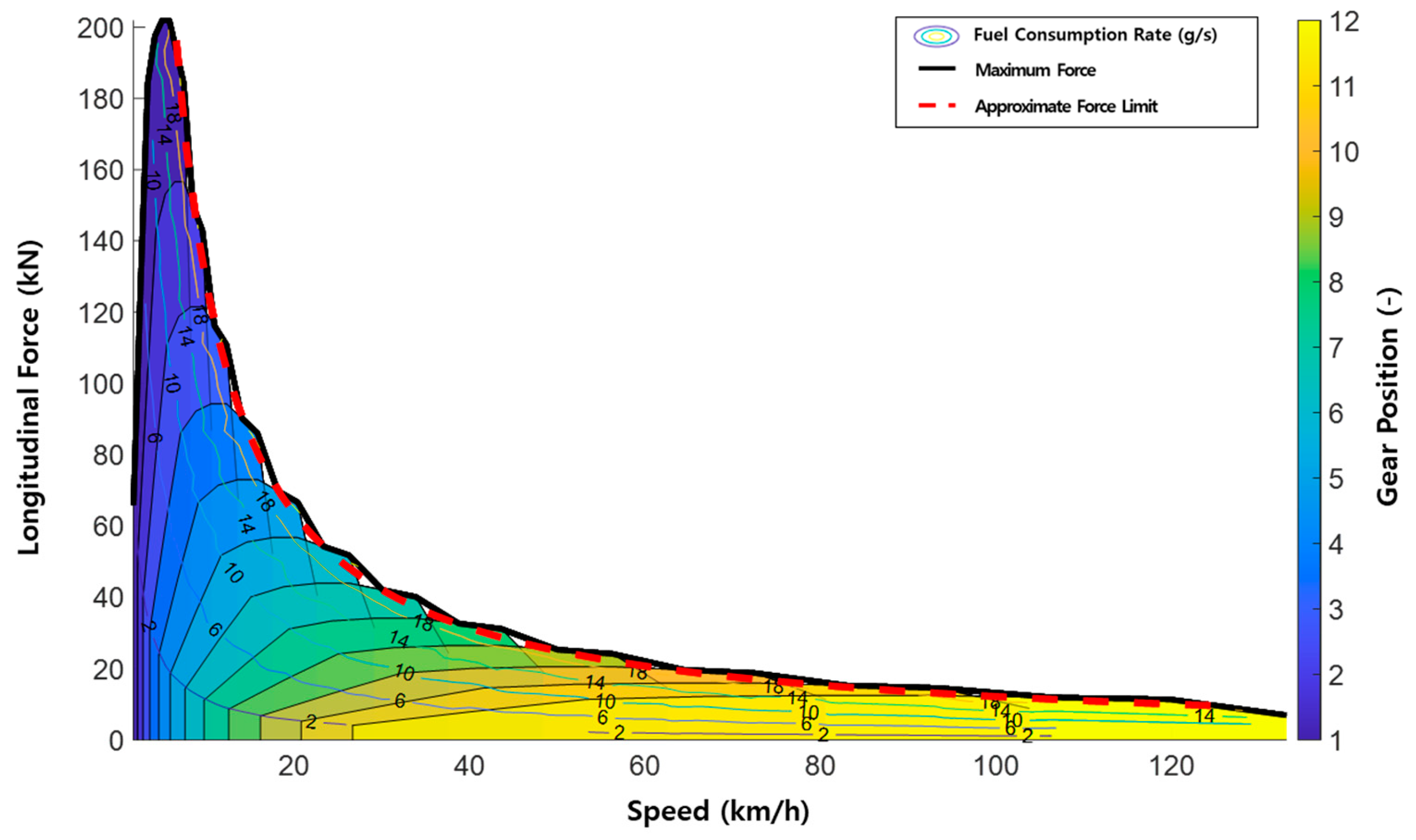
2.5. Driving Performance and Maximum Force Approximation
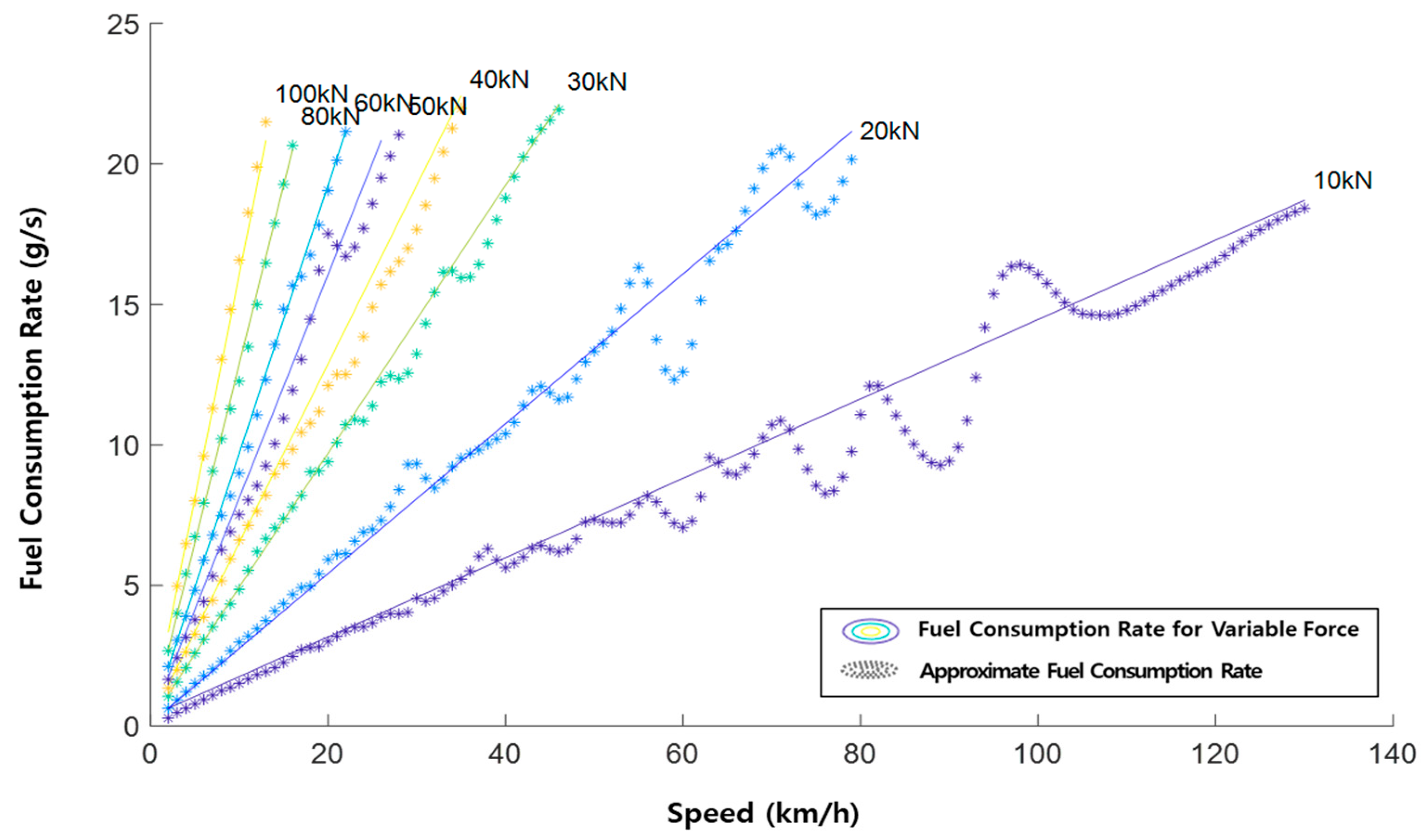
2.6. Fuel Consumption Model
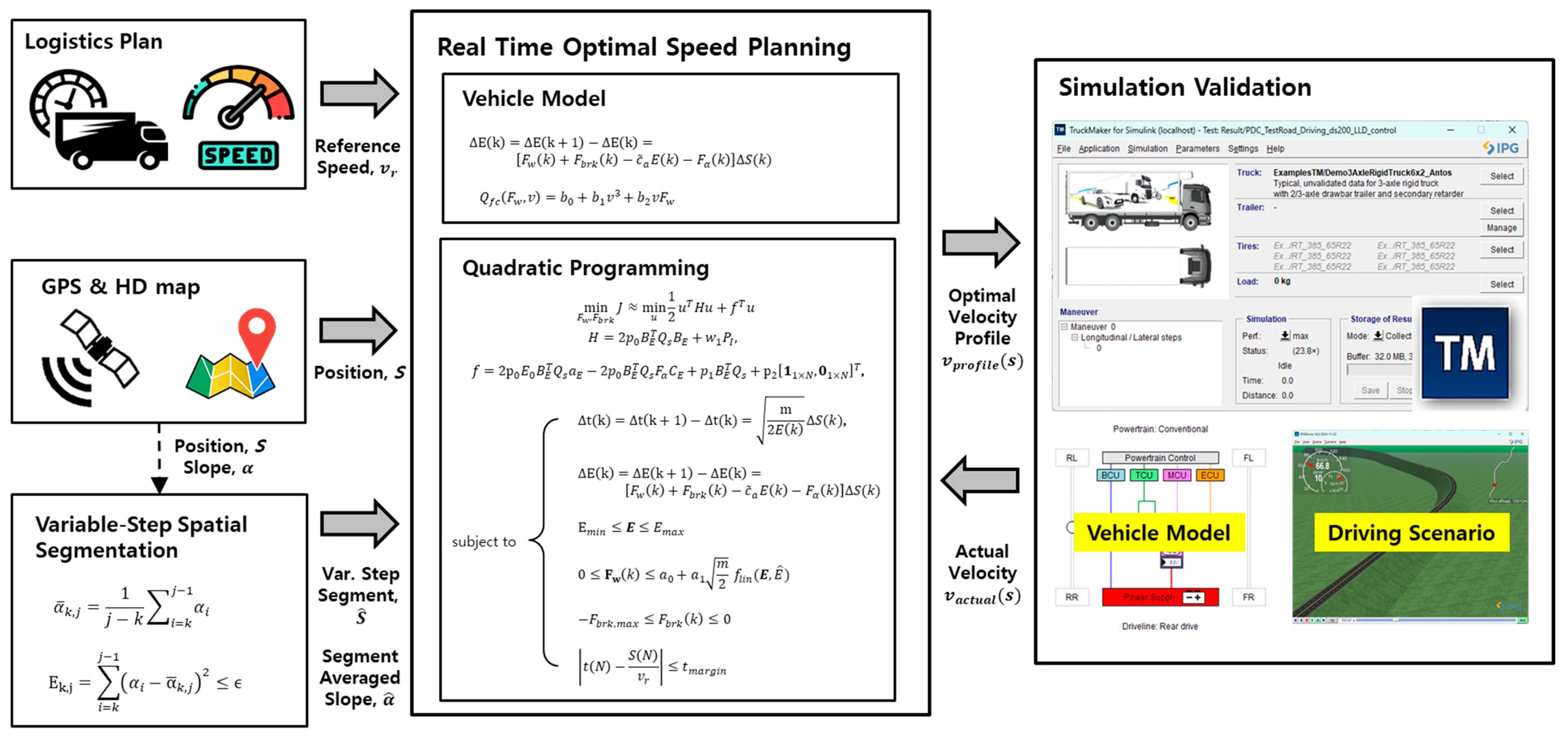
3. Optimal Model for Eco-Driving
3.1. Problem Formulation
3.2. Variable-Step Spatial Segmentation
3.2.1. Notation
- : finely sampled distance vector at 20 m intervals;
- : slope vector between consecutive distance vectors;
- : number of distance sample datapoints;
- : slope error threshold;
- : variable-step segment index set;
- k: current segment start index;
- j: candidate segment end index;
- : variable-step spatial segment set;
- : segment-averaged slope set.
3.2.2. Error Criterion
3.2.3. Algorithm
| Algorithm 1: Spatial Segmentation based on Sum of Squared Errors | ||
| 1: | ||
| 2: | ||
| 3: | ||
| 4: | ▷ List of Segment Start Indices | |
| 5: | ||
| 6: | ||
| 7: | ||
| 8: | ||
| 9: | ▷ Segment-Averaged Slope | |
| 10: | ▷ Sum of Squared Errors | |
| 11: | ▷ End criteria | |
| 12: | ||
| 13: | else | |
| 14: | ||
| 15: | end if | |
| 16: | end while | |
| 17: | ▷ Append Segment End Index | |
| 18: | ▷ Update k | |
| 19: | end while | |
| 20: | ▷ Number of Segments | |
| 21: | for m=1 to M do | |
| 22: | ||
| 23: | ||
| 24: | ||
| 25: | ||
| 26: | end for | |
| 27: | ▷ Cumulative Sum of Segment Distances | |
| 28: | return | |
3.3. QP Reformulation
3.3.1. Objective Function Approximation for QP
3.3.2. Constraints Approximation for QP
- Kinetic Energy Constraints
- Wheel Traction Force Constraints
- Braking Force Constraints
- Final Travel Time Constraint
3.3.3. Acceleration Penalty for Ride Comfort
4. Simulation Results
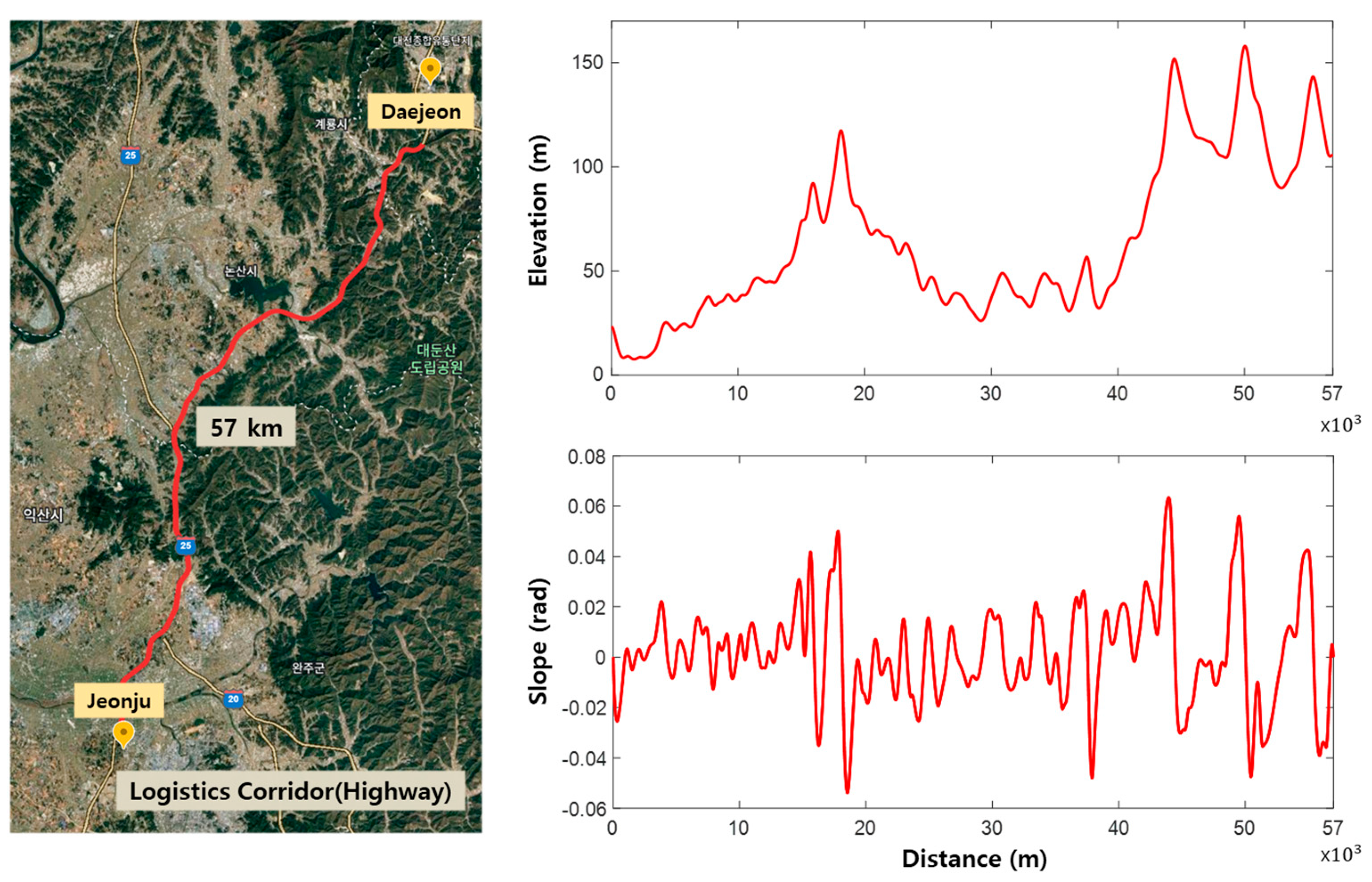
4.1. Driving Scenario
4.2. Comparison of Spatial Segmentation
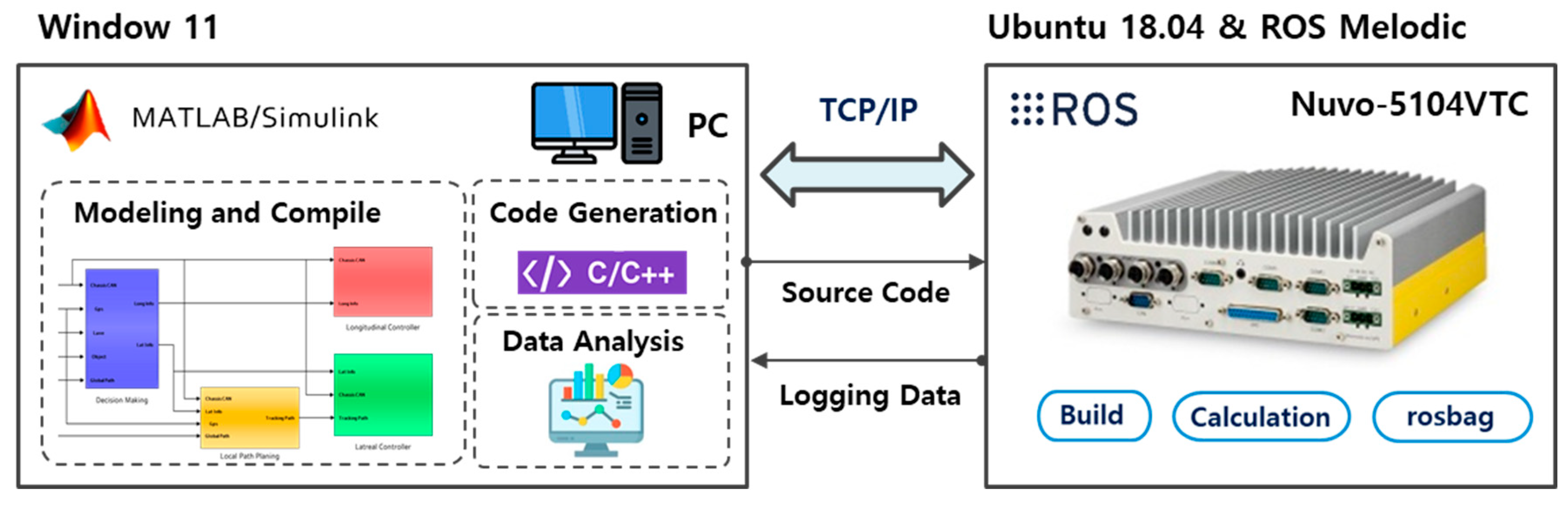
4.3. Simulation Environment
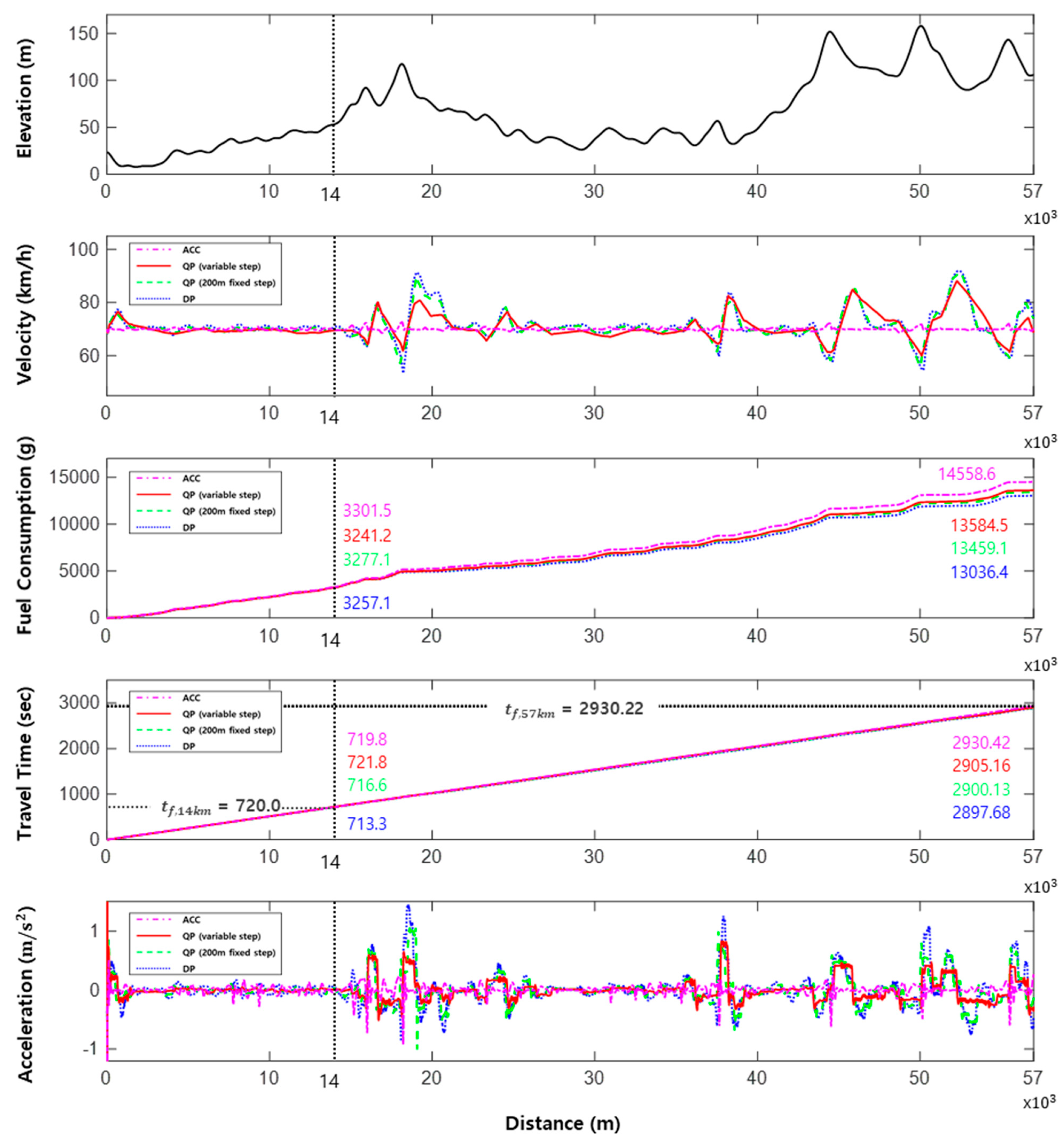
4.4. Simulation Results and Discussion
4.4.1. Results Under Curb-Weight Condition
4.4.2. Results Under Fully Loaded Condition
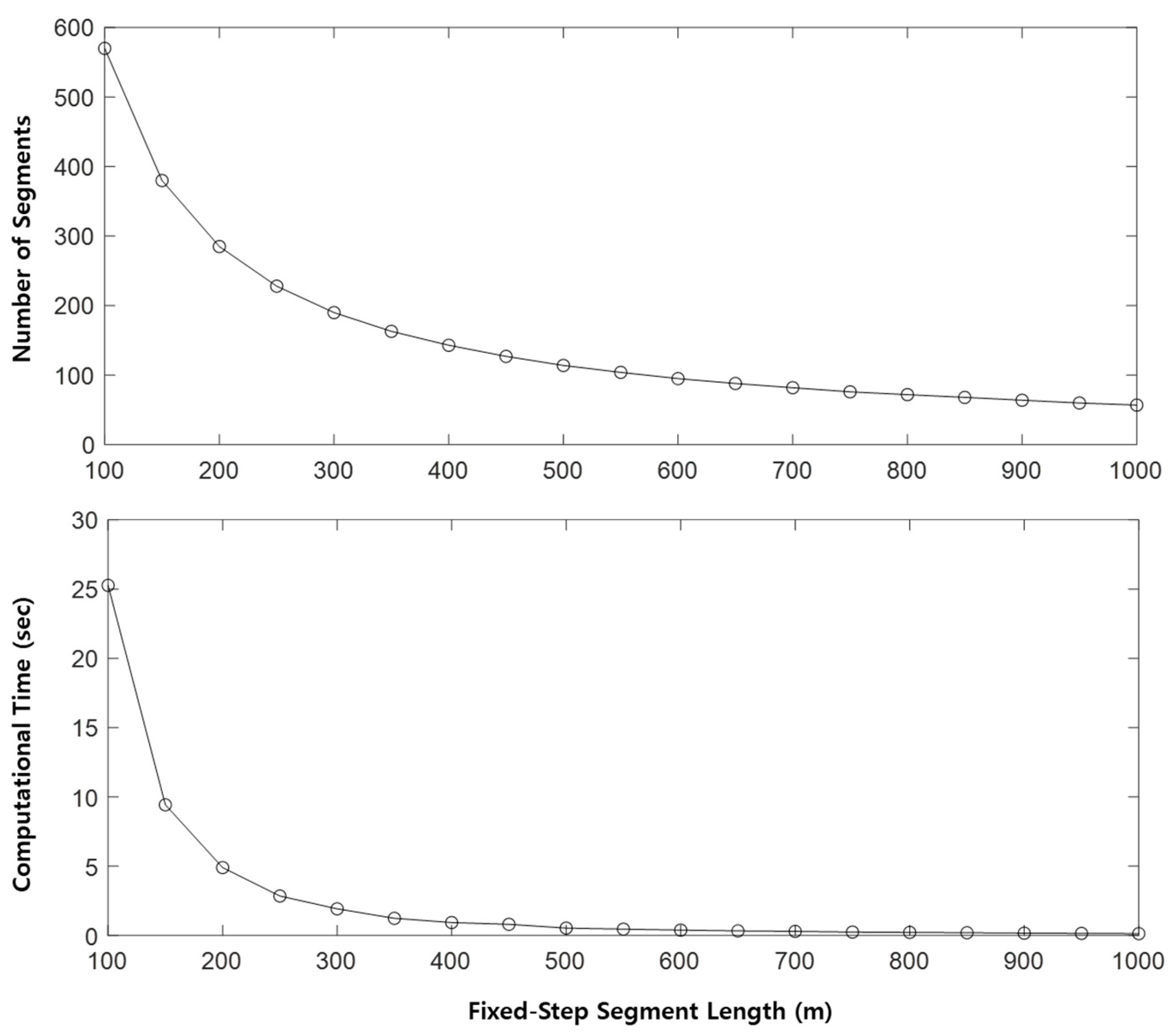
4.4.3. Computation Time
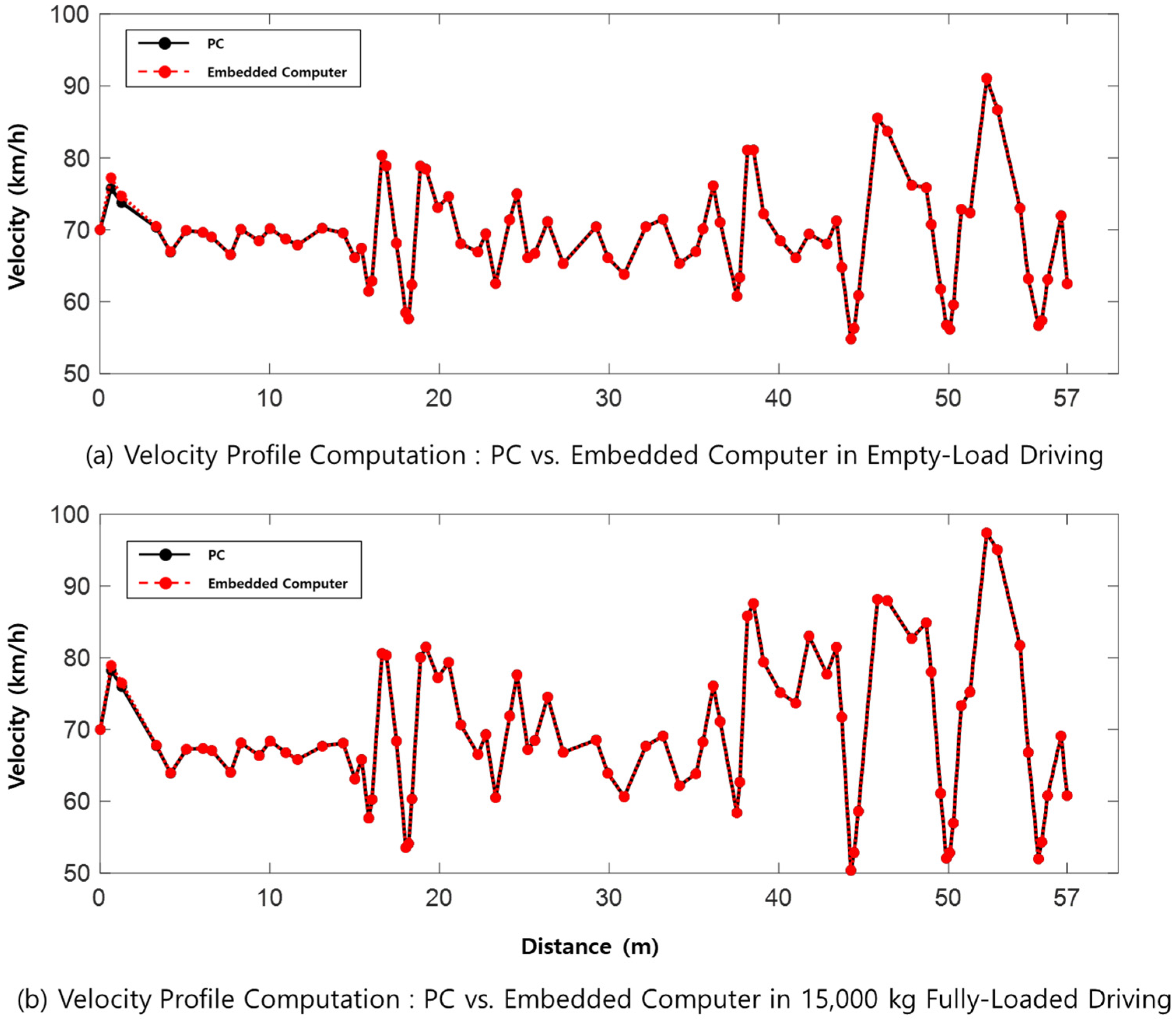
4.4.4. Experimental Result
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- IPCC Sixth Assessment Report. Available online: https://www.ipcc.ch/report/ar6/wg3/ (accessed on 31 August 2025).
- International Energy Agency (IEA). Trucks and Buses. Available online: https://www.iea.org/energy-system/transport/trucks-and-buses (accessed on 31 August 2025).
- Trucksales. Mercedes Benz Predictive Powertrain Control (PPC) Review. Available online: https://www.trucksales.com.au/editorial/details/mercedes-benz-predictive-powertrain-control-ppc-review-145985/ (accessed on 31 August 2025).
- Held, M. Fuel-Efficient Look-Ahead Control for Heavy-duty Vehicles with Varying Velocity Demands; KTH Royal Institute of Technology: Stockholm, Sweden, 2020. [Google Scholar]
- Daimler Truck AG. Available online: https://www.daimlertruck.com/en/newsroom/pressrelease/predictive-powertrain-control-ppc-10-questions-and-answers-about-the-predictive-cruise-control-from-mercedes-benz-trucks-46682406 (accessed on 31 August 2025).
- Federal Highway Administration (FHWA), U.S. Department of Transportation. Available online: https://www.federalregister.gov/documents/2017/01/18/2017-00681/national-performance-management-measures-assessing-performance-of-the-national-highway-system (accessed on 31 August 2025).
- FDOT. Travel Time Reliability 101. Available online: https://fdotwww.blob.core.windows.net/sitefinity/docs/default-source/planning/fto/reliability/reliability-101.pdf (accessed on 31 August 2025).
- Federal Highway Administration (FHWA), U.S. Department of Transportation. Available online: https://ops.fhwa.dot.gov/publications/tt_reliability/brochure/ (accessed on 31 August 2025).
- Federal Motor Carrier Safety Administration (FMCSA), U.S. Department of Transportation. Available online: https://www.fmcsa.dot.gov/sites/fmcsa.dot.gov/files/docs/Development_of_a_North_American_Standard_for_Protection_Against_Shifting_and_Falling_Cargo_508CLN.pdf (accessed on 31 August 2025).
- Federal Motor Carrier Safety Administration (FMCSA), U.S. Department of Transportation. Available online: https://www.federalregister.gov/documents/2000/12/18/00-31919/development-of-a-north-american-standard-for-protection-against-shifting-and-falling-cargo (accessed on 31 August 2025).
- Xu, C.; Geyer, S.; Fathy, H.K. Formulation and comparison of two real-time predictive gear shift algorithms for connected/automated heavy-duty vehicles. IEEE Trans. Veh. Technol. 2019, 68, 7498–7510. [Google Scholar] [CrossRef]
- Li, S.; Yang, L.; Gao, Z. Efficient real-time control design for automatic train regulation of metro loop lines. IEEE Trans. Intell. Transp. Syst. 2018, 20, 485–496. [Google Scholar] [CrossRef]
- Zhang, J.; Jin, H. Optimized calculation of the economic speed profile for slope driving: Based on iterative dynamic programming. IEEE Trans. Intell. Transp. Syst. 2020, 23, 3313–3323. [Google Scholar] [CrossRef]
- Honda, K.; Yonetani, R.; Nishimura, M.; Kozuno, T. When to replan? An adaptive replanning strategy for autonomous navigation using deep reinforcement learning. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; IEEE: Yokohama, Japan, 2024; pp. 6650–6656. [Google Scholar]
- Lee, Y.; Lee, D.Y.; Lee, S.H.; Kim, Y. A comparative study on model predictive control design for highway car-following scenarios: Space-domain and time-domain model. IEEE Access 2021, 9, 162291–162305. [Google Scholar]
- Bellman, R. Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1957; p. 39. [Google Scholar]
- Hellström, E.; Ivarsson, M.; Åslund, J.; Nielsen, L. Look-ahead control for heavy trucks to minimize trip time and fuel consumption. Control. Eng. Pract. 2009, 17, 245–254. [Google Scholar]
- Hellström, E. Look-Ahead Control of Heavy Trucks Utilizing Road Topography; Linkopings Universitet: Linköping, Sweden, 2007. [Google Scholar]
- Pulvirenti, L.; Tresca, L.; Rolando, L.; Millo, F. Eco-driving optimization based on variable grid dynamic programming and vehicle connectivity in a real-world scenario. Energies 2023, 16, 4121. [Google Scholar]
- Shiledar, A.; Gupta, S.; Spano, M.; Villani, M.; Canova, M.; Rizzoni, G. Real-time eco-driving of a connected and automated fuel cell electric truck using approximate dynamic programming. In Proceedings of the 2024 American Control Conference (ACC), Toronto, ON, Canada, 10–12 July 2024; IEEE: Toronto, ON, Canada, 2024; pp. 2989–2994. [Google Scholar]
- Spano, M.; Shiledar, A.; Gupta, S.; Villani, M.; Misul, D.; Canova, M.; Rizzoni, G. Performance Evaluation of an Eco-Driving Controller for Fuel Cell Electric Trucks in Real-World Driving conditions; SAE Technical Paper; SAE: Warrendale, PA, USA, 2024. [Google Scholar]
- Hamednia, A.; Murgovski, N.; Fredriksson, J. Predictive velocity control in a hilly terrain over a long look-ahead horizon. IFAC-Pap. 2018, 51, 485–492. [Google Scholar]
- Hamednia, A.; Sharma, N.K.; Murgovski, N.; Fredriksson, J. Computationally efficient algorithm for eco-driving over long look-ahead horizons. IEEE Trans. Intell. Transp. Syst. 2021, 23, 6556–6570. [Google Scholar] [CrossRef]
- Zhang, Y.; Qu, X.; Tong, L. Optimal eco-driving control of autonomous and electric trucks in adaptation to highway topography: Energy minimization and battery life extension. IEEE Trans. Transp. Electrif. 2022, 8, 2149–2163. [Google Scholar]
- Li, X.; Lv, T.; Yue, H.; Liu, S.; Na, X.; Chen, H.; Gao, B. Predictive cruise control algorithm design for commercial vehicle energy saving based on quadratic programming. In International Conference on Energy Storage and Intelligent Vehicles; Springer: Berlin/Heidelberg, Germany, 2022; pp. 1076–1088. [Google Scholar]
- Watling, D.P.; Connors, R.D.; Chen, H. Fuel-optimal truck path and speed profile in dynamic conditions: An exact algorithm. Eur. J. Oper. Res. 2023, 306, 1456–1472. [Google Scholar] [CrossRef]
- Shimizu, Y.; Horibe, T.; Watanabe, F.; Kato, S. Jerk constrained velocity planning for an autonomous vehicle: Linear programming approach. In Proceedings of the 2022 International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; IEEE: Philadelphia, PA, USA, 2022; pp. 5814–5820. [Google Scholar]
- Koch, A.; Nicoletti, L.; Herrmann, T.; Lienkamp, M. Implementation and analyses of an eco-driving algorithm for different battery electric powertrain topologies based on a split loss integration approach. Energies 2022, 15, 5396. [Google Scholar] [CrossRef]
- Albert, A. Regression and the Moore–Penrose Pseudoinverse. In Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1972; Volume 94. [Google Scholar]
- Popp, K.; Schiehlen, W. Ground Vehicle Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Rajamani, R. Vehicle Dynamics and Control; Springer: New York, NY, USA, 2006. [Google Scholar]
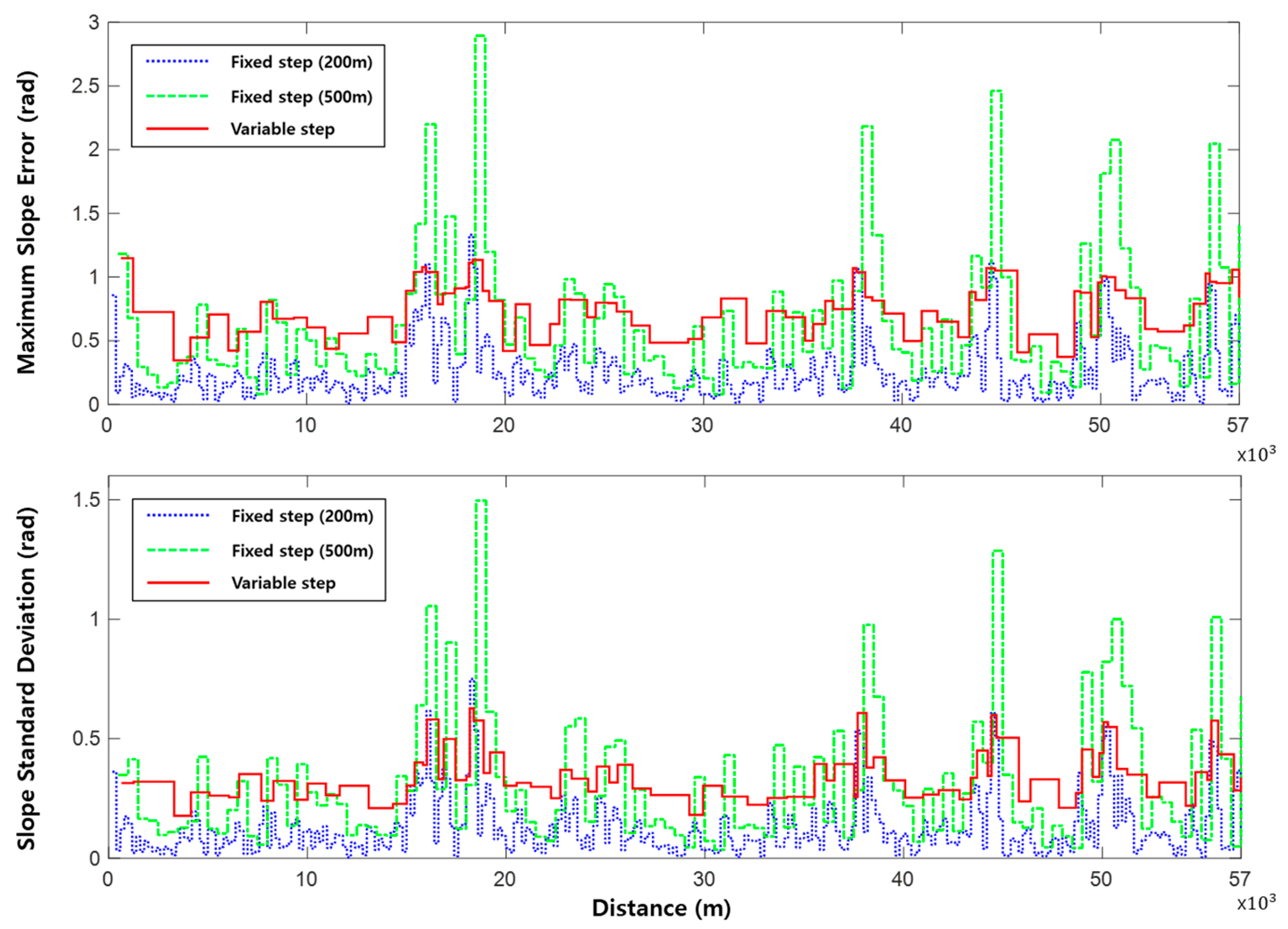
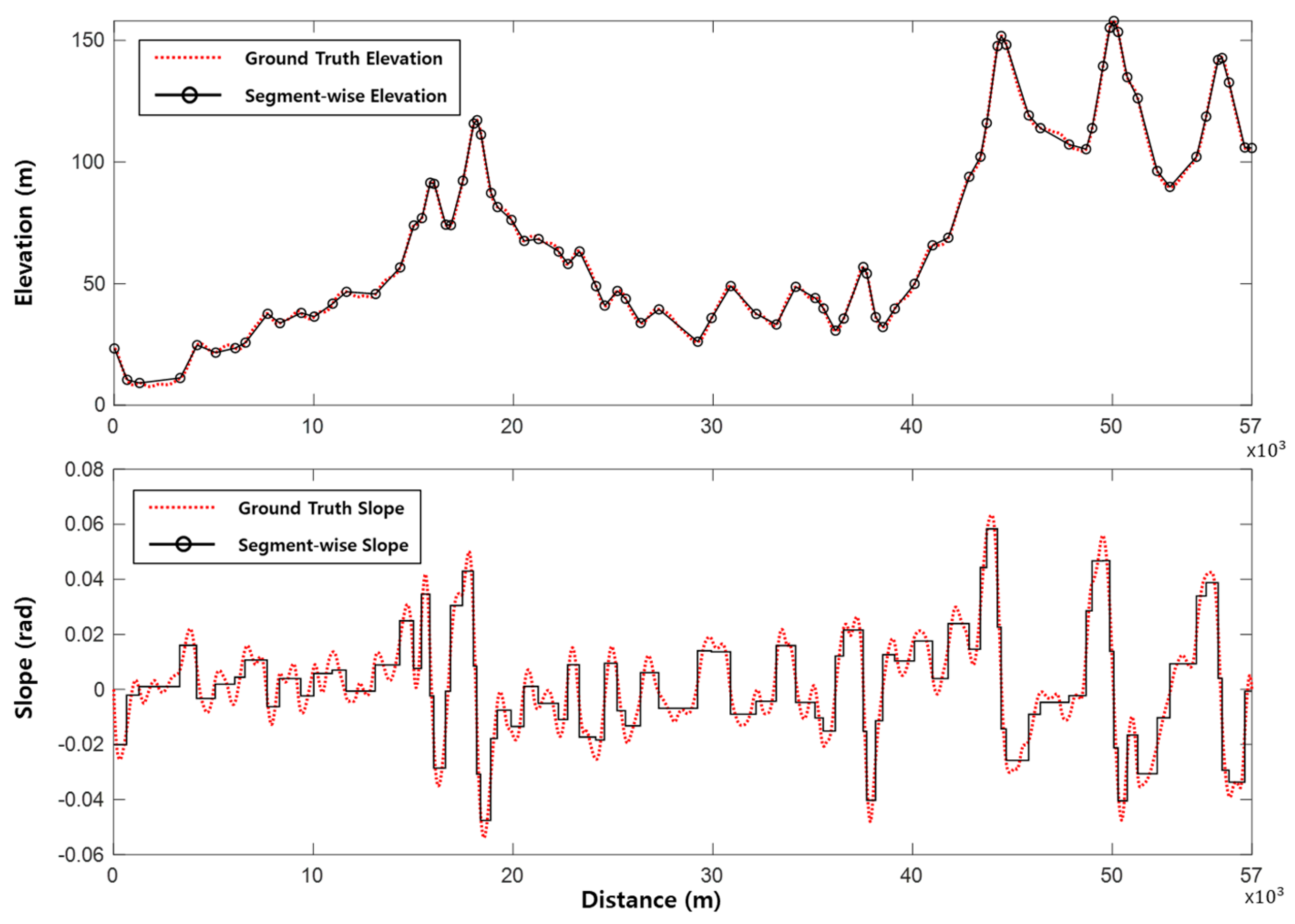

| Segmentation Method | Segment Count | Constraint Count | RMSE (Rad) |
|---|---|---|---|
| Fixed step (200 m) | 285 | 1712 | 0.0031 |
| Fixed step (500 m) | 114 | 686 | 0.0072 |
| Variable step | 83 | 500 | 0.0053 |
| Category | Symbol | Parameter | Value |
|---|---|---|---|
| Vehicle parameters | m | Mass | 25,200 kg |
| g | Gravitational acceleration | ||
| Air density | |||
| Drag coefficient | 0.41 | ||
| Frontal area | |||
| Rolling coefficient | 0.00939 | ||
| Wheel radius | 0.51 m | ||
| Track width | 2.6 m | ||
| h | Height of the c.g. | 1.435 m | |
| Model parameters | Slope error threshold | 0.001 | |
| On-time margin | 3% | ||
| Minimum velocity | 50 km/h | ||
| Maximum velocity | 100 km/h | ||
| Reference velocity | 70 km/h | ||
| Penalty 1 (ride comfort) | 10 |
| Terrain | Algorithm | Average Velocity (km/h) | (s) | Fuel Consumption Rate (L/100 km) | Fuel-Saving Rate (%) |
|---|---|---|---|---|---|
| Plain | ACC | 70.02 | −0.2 | 29.48 | – |
| QP (variable step) | 69.83 | 1.8 | 28.94 | 1.83 | |
| QP (200 m fixed step) | 70.33 | −3.4 | 29.26 | 0.74 | |
| DP | 70.65 | −6.7 | 29.08 | 1.34 | |
| Mixed (plain + hilly) | ACC | 70.00 | 0.2 | 31.93 | – |
| QP (variable step) | 70.61 | −25.06 | 29.79 | 6.69 | |
| QP (200 m fixed step) | 70.73 | −30.09 | 29.51 | 7.55 | |
| DP | 70.79 | −32.54 | 28.58 | 10.45 |
| Terrain | Algorithm | Average Velocity (km/h) | (s) | Fuel Consumption Rate (L/100 km) | Fuel-Saving Rate (%) |
|---|---|---|---|---|---|
| Plain | ACC | 70.02 | −0.2 | 40.98 | – |
| QP (variable step) | 68.20 | 19 | 39.52 | 3.58 | |
| QP (200 m fixed step) | 69.73 | 2.8 | 40.12 | 2.11 | |
| DP | 69.86 | 1.4 | 39.96 | 2.50 | |
| Mixed (plain + hilly) | ACC | 69.95 | 1.98 | 44.99 | – |
| QP (variable step) | 70.26 | −10.72 | 40.48 | 10.00 | |
| QP (200 m fixed step) | 70.45 | −18.42 | 40.42 | 10.16 | |
| DP | 70.46 | −19.12 | 38.69 | 13.99 |
| Segment Length (m) | Segment Count | Computation Time (s) |
|---|---|---|
| 100 | 570 | 25.27 |
| 200 | 285 | 4.90 |
| 300 | 190 | 1.92 |
| 400 | 143 | 0.93 |
| 500 | 114 | 0.53 |
| 600 | 95 | 0.39 |
| 700 | 82 | 0.29 |
| 800 | 72 | 0.22 |
| 900 | 64 | 0.16 |
| 1000 | 57 | 0.13 |
| Segment Length (m) | Segment Count | Computation Time (s) | |
|---|---|---|---|
| PC | Embedded Computer | ||
| 100 | 570 | 25.27 | - |
| 200 | 285 | 4.90 | 14.38 |
| 300 | 190 | 1.92 | 4.23 |
| 400 | 143 | 0.93 | 1.97 |
| 500 | 114 | 0.53 | 0.98 |
| 600 | 95 | 0.39 | 0.62 |
| 700 | 82 | 0.29 | 0.37 |
| 800 | 72 | 0.22 | 0.26 |
| 900 | 64 | 0.16 | 0.19 |
| 1000 | 57 | 0.13 | 0.13 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoo, J.; Ha, Y.; Moon, S.; Kim, J.; Yoo, J. Real-Time Global Velocity Profile Calculation for Eco-Driving on Long-Distance Highways Using Variable-Step Spatial Segmentation. Appl. Sci. 2025, 15, 10811. https://doi.org/10.3390/app151910811
Yoo J, Ha Y, Moon S, Kim J, Yoo J. Real-Time Global Velocity Profile Calculation for Eco-Driving on Long-Distance Highways Using Variable-Step Spatial Segmentation. Applied Sciences. 2025; 15(19):10811. https://doi.org/10.3390/app151910811
Chicago/Turabian StyleYoo, Jaeyeon, Yunchul Ha, Seongjoon Moon, Jeesu Kim, and Jinwoo Yoo. 2025. "Real-Time Global Velocity Profile Calculation for Eco-Driving on Long-Distance Highways Using Variable-Step Spatial Segmentation" Applied Sciences 15, no. 19: 10811. https://doi.org/10.3390/app151910811
APA StyleYoo, J., Ha, Y., Moon, S., Kim, J., & Yoo, J. (2025). Real-Time Global Velocity Profile Calculation for Eco-Driving on Long-Distance Highways Using Variable-Step Spatial Segmentation. Applied Sciences, 15(19), 10811. https://doi.org/10.3390/app151910811







