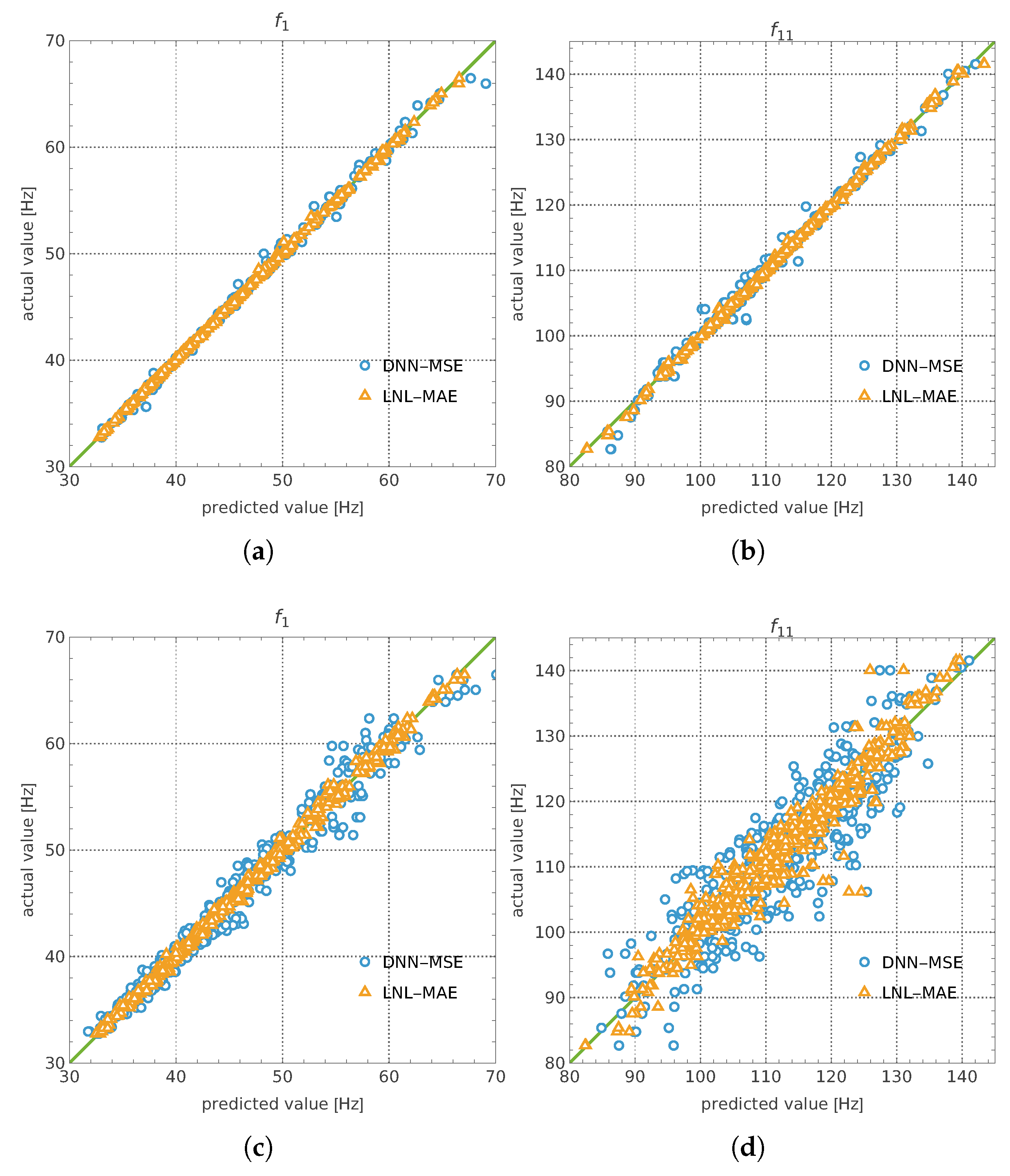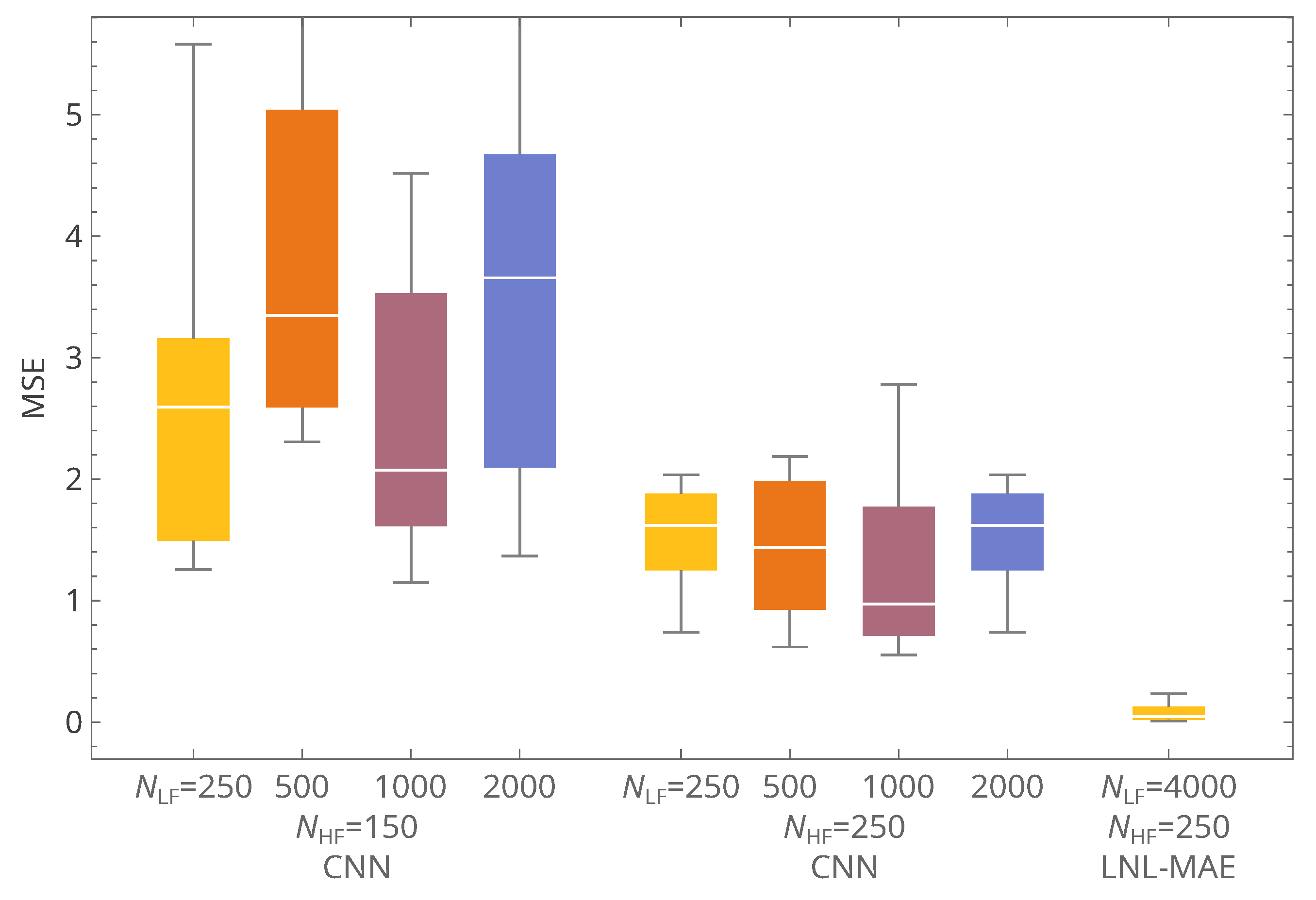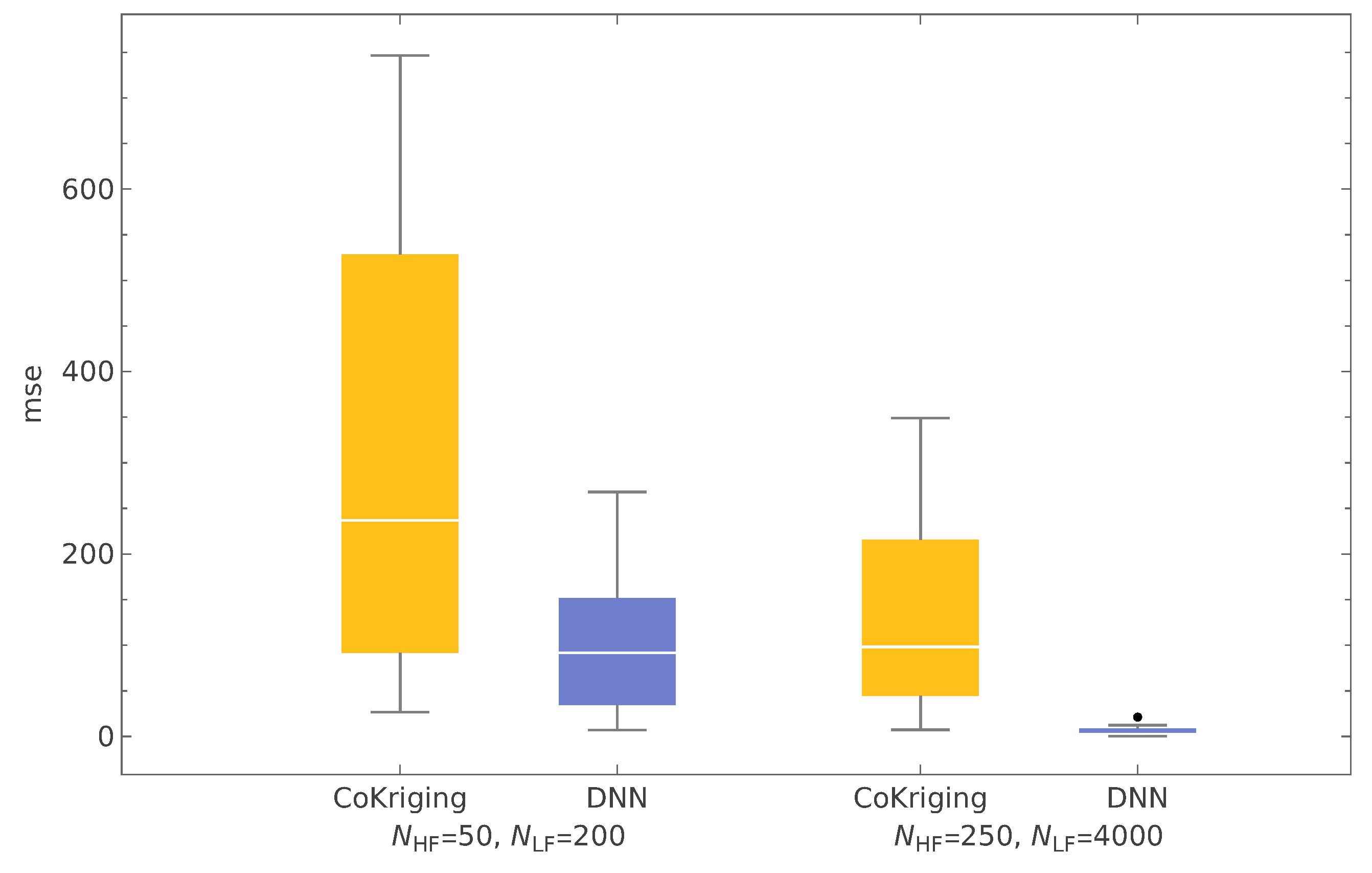2.1. The Structure
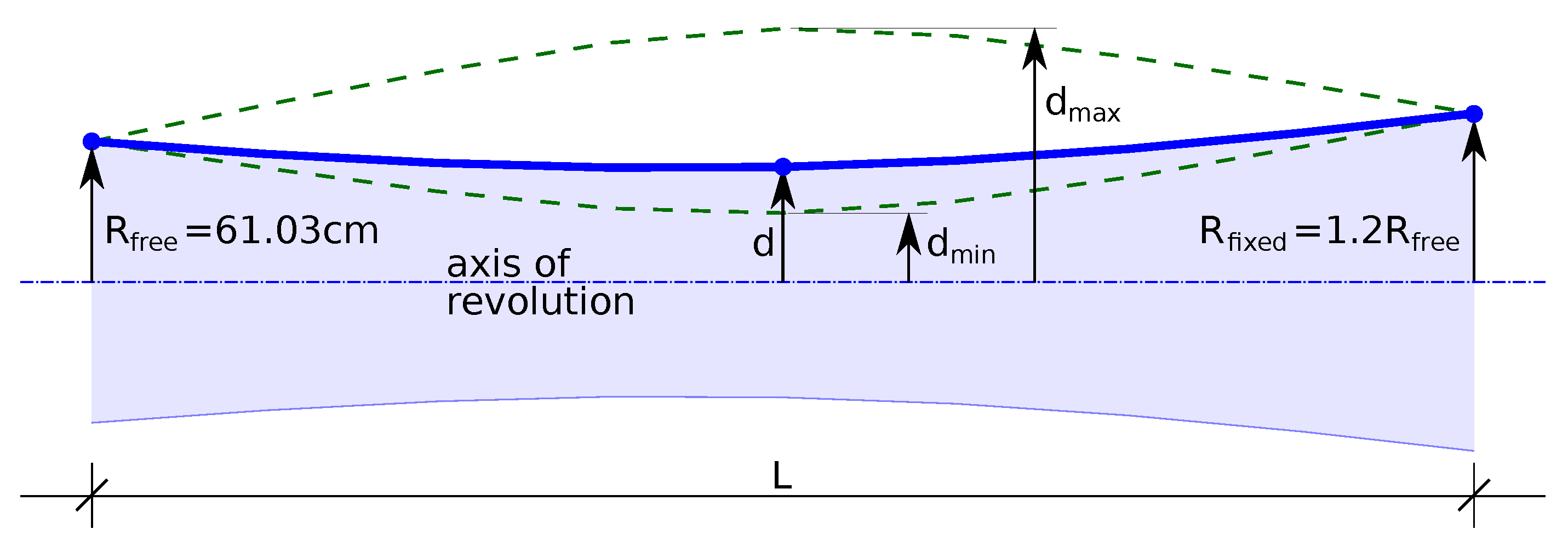
The finite element model adopts an axisymmetric layered-shell formulation: a two-dimensional meridional profile (
Figure 1) is revolved to form a shell of revolution, and the laminate response is computed using classical lamination theory [
32]. The reference geometry is a hyperboloid of revolution whose mid-surface is controlled by a single scalar “depth’’ parameter
d,
, that modulates the curvature reversal at the waist, permitting both convex and concave variants within one family (
Figure 2);
d is treated as a continuous design variable during optimization. The constant geometric parameters are fixed as
m,
cm, and
. The boundary conditions are the edge at
is fully clamped (all displacements constrained), while the opposite edge at
is free.
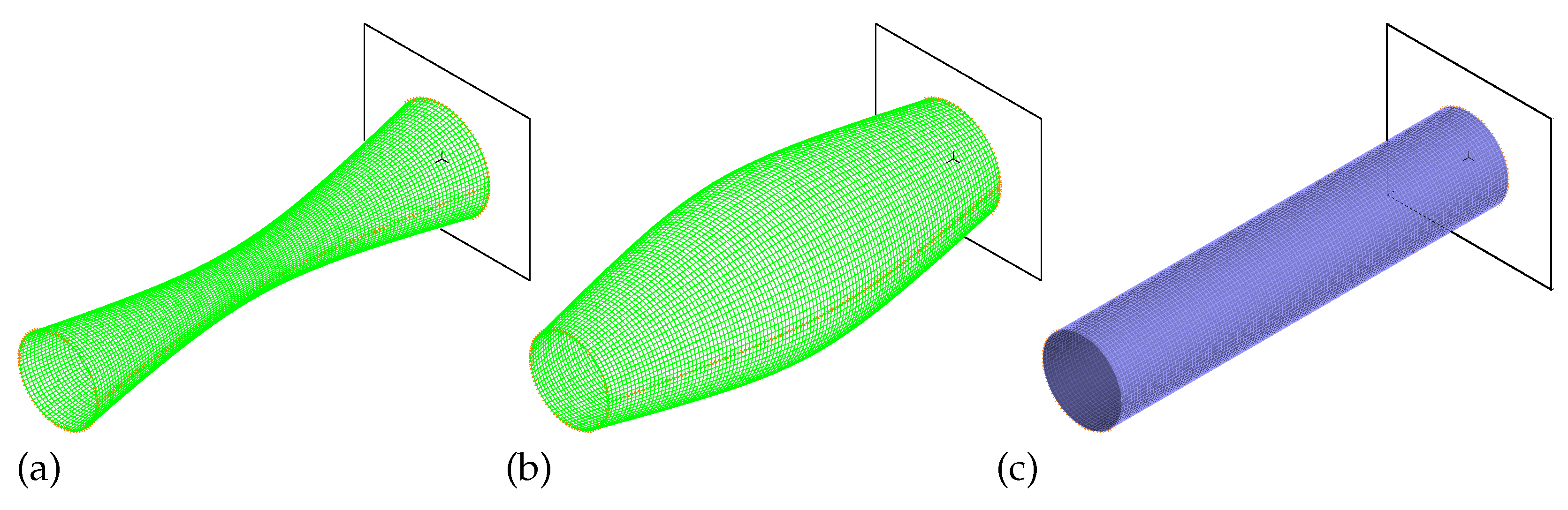
Competing cylindrical (
Figure 2c) and conical baselines were examined at an earlier stage; here, we focus on the hyperboloidal profile due to its richer curvature control and the resulting flexibility in shaping global and local stiffness.
The shell has constant total thickness
cm with a fixed eight-ply layup, with each ply of thickness
. The stacking sequence is denoted as
, where each ply angle
is discretized in
steps over
and treated as a decision variable. Material assignment is optimized at the ply level: for each lamina
i, a categorical variable
selects either one of two fiber-reinforced composites (CFRP, GFRP) or a theoretical tFRP defined by property values averaged from CFRP and GFRP. A summary of the adopted properties is given in
Table 1 (cf. [
37]).
The resulting 17-component design vector
combines one geometric parameter with eight angle variables and eight material choices. In the analysis, each lamina inherits orthotropic properties according to
, and the model captures the stiffness trade-offs among mass, strength, and cost while remaining compact enough for surrogate-assisted multi-objective optimization.
The selection of design variables and simulation models applied in this study follows from our earlier systematic analyses. In particular, lamination angles were adopted as primary variables since they have the strongest impact on stiffness and dynamic properties; in earlier works, they were treated as continuous variables, but it was shown that discretizations finer than
increase computational complexity without providing noticeable improvements [
38]. Similarly, different numbers of layers were examined (from 4 to 32), and it was demonstrated that increasing the number beyond 8–16 does not improve the optimized objective functions, while it substantially enlarges the design space [
38]. Therefore, in the present work, eight layers and a
step were chosen as rational compromises between accuracy and efficiency. The introduction of the geometric parameter
d and material selection (CFRP, GFRP, tFRP) in [
31] was an intentional step to test the proposed procedure in more complex optimization tasks, including geometry and cost optimization, and to study their influence on objectives such as frequency band width and material cost.
2.2. Finite Element Model
Two finite element discretizations are employed that differ solely in target mesh density. In both cases, the structure is modeled with four-node MITC4 multilayer shell elements consistent with first-order shear-deformation kinematics [
39]. The nominal finite-element size (maximum edge length of an approximately square element) is denoted by
h. For the reference, high-fidelity model
we take
cm, acknowledging small spatial variations along the circumferential and meridional directions. A coarser companion model,
5, is built with
cm.
The finite element simulations were performed using the commercial software ADINA 9.8 [
39]. All analyses were carried out in the implicit eigenvalue setting (modal analysis). The high-fidelity model
employed a
mesh, resulting in approximately 1,202,000 degrees of freedom, and required on average 888.36 s of CPU time per run. The
model used a
mesh with 48,400 degrees of freedom and an average CPU time of 59.02 s. Wall-clock times were not reported because they were not representative under varying thread availability and system load conditions. All computations were executed on a workstation equipped with an AMD EPYC
TM 7443P processor (24 CPU cores, base clock 2.85 GHz, maximum boost clock 4.0 GHz) and 256 GB of RAM.
The two levels serve distinct purposes.
provides the high-fidelity baseline used both for validation and for generating a pseudo-experimental target, whereas
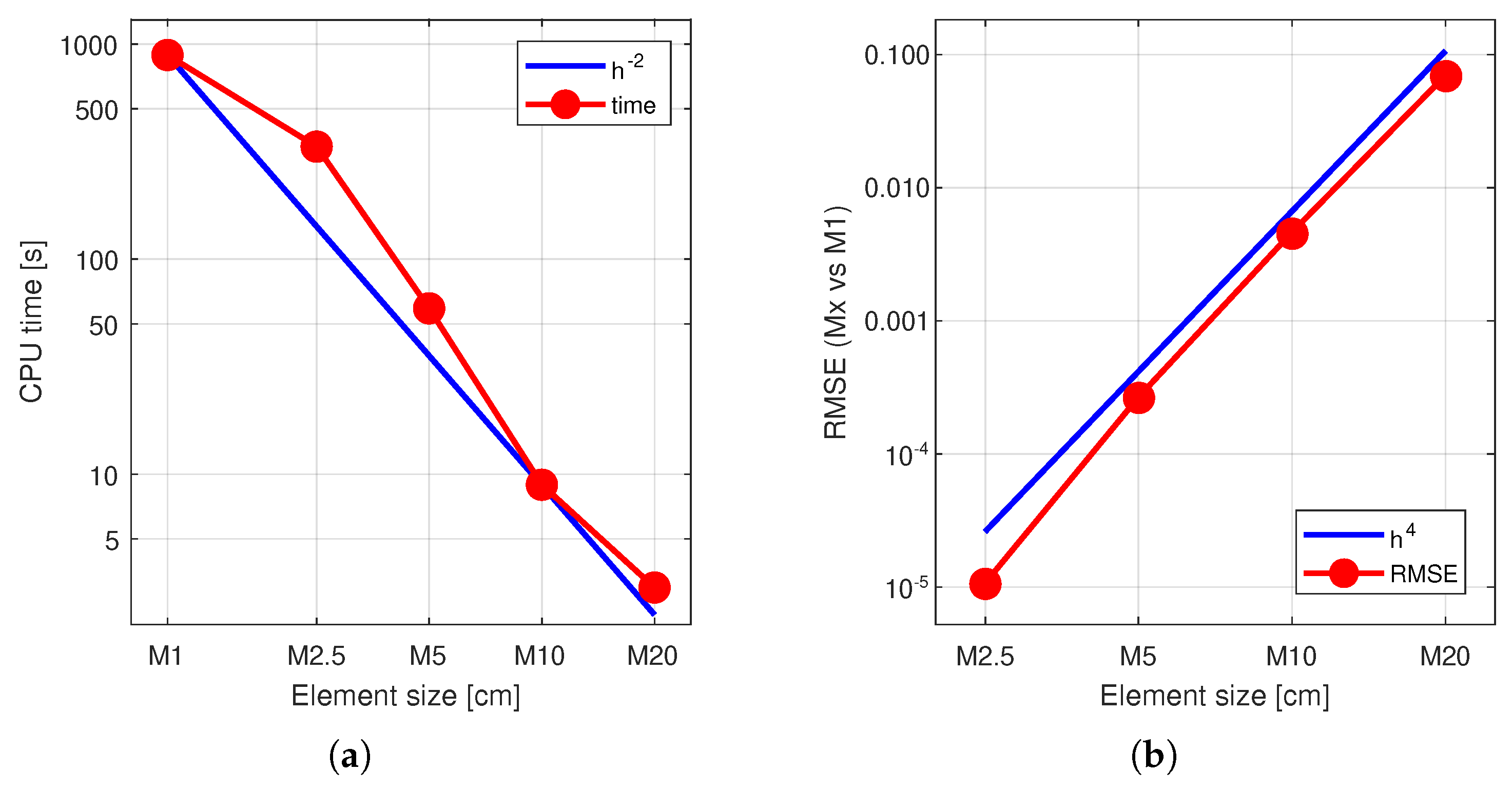
5 supplies inexpensive additional samples to enlarge the training corpus of the surrogate. Because
5 elements are four times larger, the 2D mesh cardinality drops approximately by a factor of
, yielding a commensurate reduction in solution time (see
Figure 3a). This comes at the cost of accuracy: in our setting, eigenfrequency errors grow on the order of
when moving from
to
5 (see
Figure 3b), a degradation explicitly handled by the downstream learning and optimization steps [
28].
To emulate laboratory measurements and modeling discrepancies, we transform the vector of natural frequencies computed with
,
, through a smooth nonlinear mapping,
and use
as the pseudo-experimental target.
Unlike the common practice of stacking the lowest modes in ascending order, the frequency vector here is composed only of entries associated with preselected mode shapes. Following mode-shape identification, we retain the eleven most diagnostically relevant patterns and assemble
accordingly [
38]. In the identification procedure, each computed mode shape was examined and classified into one of several groups (circumferential, bending, torsional, or axial), each characterized by specific circumferential and axial modal indices. The frequency vector was then constructed exclusively from the eleven modes selected as representative. This targeted selection improves surrogate learnability and, in turn, the convergence behavior of the optimization [
38]. A key advantage of this approach is that it preserves full continuity of the network outputs, since each entry corresponds to a fixed vibration mode rather than to an arbitrarily ordered frequency. The resulting increase in approximation accuracy stems from avoiding mode-shape crossing: a phenomenon in which, within a frequency-ordered list, eigenfrequencies associated with different physical modes exchange positions (for example, a bending-mode frequency may overtake a circumferential-mode frequency). By eliminating this ambiguity, the surrogate network can learn stable input–output relationships across the design space. The neural approximation of the pseudo-experimental mapping is denoted
.
Finally, we stress that is not derived from physical testing; it is a controlled device to inject plausible model–test discrepancies into a fully numerical workflow. This enables sensitivity to measurement-like distortions while respecting the practical limits on feasible experimental campaigns.
The rationale behind the selection of the fidelity levels is as follows. The high-fidelity model was first established through a standard finite element mesh-convergence study, which confirmed that its discretization accuracy provides a reliable reference for modal frequencies. With respect to computational scaling, increasing the element size by a factor of k reduces the total number of elements approximately by , leading to a quadratic decrease in CPU time. Conversely, the discretization error in the natural frequencies grows approximately with , as reflected by the root mean square error (RMSE) relative to .
The choice of as the low-fidelity model was therefore a deliberate compromise: it provides a substantial reduction in computational time (roughly one-sixteenth of the cost) while maintaining an error level that remains acceptable for use in multi-fidelity learning. For still coarser meshes (e.g., ), the additional time savings would no longer compensate for the rapid growth in modal frequency errors. In fact, under such coarse discretization, the analytic mode-shape identification method employed in this study could not be applied consistently, since the mode shapes become too distorted to classify reliably.
In summary, was chosen as the high-fidelity reference following standard mesh-convergence procedures, while represents a balanced compromise between efficiency and accuracy. This design ensures that the auxiliary network in Variant 1 is trained on low-fidelity data that are both computationally inexpensive and sufficiently correlated with the reference solution, enabling effective multi-fidelity refinement.
2.3. Optimization Problem
The design task targets resonance avoidance and affordability in a single, coherent framework. Structural resonance arises when an external excitation aligns with one of the system’s natural frequencies, amplifying response and potentially precipitating damage. When the dominant excitation is known a priori, the spectrum can be shaped to create a guard band around that frequency by displacing all relevant eigenfrequencies away from it during design. In our setting, the nominal excitation is fixed at
(other values are possible and have been used in prior studies) (see [
28,
31,
38,
40]).
Let
denote the 17-parameter design vector introduced earlier (see Equation (
1)), and let
be the curated index set of eleven mode shapes used throughout the study. Denote by
the corresponding collection of natural frequencies predicted by the analysis chain (i.e., the FE model and, where applicable, the pseudo-experimental mapping and/or surrogate). The first objective enforces a gap around the excitation frequency by maximizing the absolute distance from
to the nearest natural frequency, either lower or higher, that appears among the selected modes. In minimization form:
The second objective captures material expenditure. With constant total thickness and equal ply thicknesses, each lamina occupies approximately the same volume
, where
is the volume of the whole structure induced by the geometry parameter
d. Let
be the unit cost (per volume) of the material assigned to ply
i (from
Table 1). The cost objective is then
The multi-objective problem refers to identifying designs that simultaneously minimize both objectives,
subject to the variable domains specified earlier for geometry, ply orientations, and plywise material choices. The solution set is a Pareto front of non-dominated trade-offs. To explore this front, we employ NSGA-II [
3], which is well suited to mixed discrete–continuous design spaces and rugged, multi-modal response landscapes.
2.4. Pareto-Front Evaluation and Quality Indicators
Visual inspection of Pareto fronts is informative when the sets differ markedly in shape or extent; however, when discrepancies are subtle, plotting alone can be inconclusive. In such cases, quantitative indicators are necessary to compare convergence to the true front and the distribution of solutions along it. Numerous indicators exist, emphasizing different aspects of quality—cardinality, convergence, spread, or combined effects. See overviews and taxonomies in [
41,
42]. In line with prior evidence on their utility and interpretability, we adopt hypervolume-based assessment and introduce a normalized variant called the relative hypervolume indicator.
For a minimization problem with objective vector
and a finite approximation
A of a Pareto set, the (Lebesgue) hypervolume indicator
measures the area dominated by
A with respect to a reference point
that is (componentwise) worse than all points under consideration [
35]. Formally,
where
denotes planar Lebesgue measure and
intervals are oriented so that
. Larger values indicate better coverage (i.e., closer and more extensive approximation of the Pareto front) [
43].
Building on Equation (
6), we evaluate each approximate front
A against a common reference that approximates the (unknown) True Pareto Front (TPF). Since a closed-form TPF is unavailable in this problem class, we construct a high-quality proxy by taking the nondominated envelope of allfronts obtained across methods and repeated runs, and use it as TPF for scoring. We then define the relative hypervolume indicator as
which satisfies
provided that
A is dominated by (or equal to) TPF with respect to the same
. To mitigate scale effects, objectives are consistently normalized before hypervolume computation, and a single reference point
, worse than all normalized envelope points, is used for all comparisons.
For completeness, we note that a wide range of Pareto-front indicators has been proposed, emphasizing different aspects of convergence and diversity [
41,
42]. In the present study, however, we restrict attention to hypervolume and its relative form as these measures proved sufficient to capture the quality differences relevant to the optimization problems considered.
2.5. Surrogate Models and Optimization Workflow
The central idea behind surrogate models (SM) is to curb the computational burden of optimization by replacing expensive high-fidelity evaluations (e.g., the Finite Element Method, FEM) with a fast learned approximator trained on a limited dataset [
2,
4,
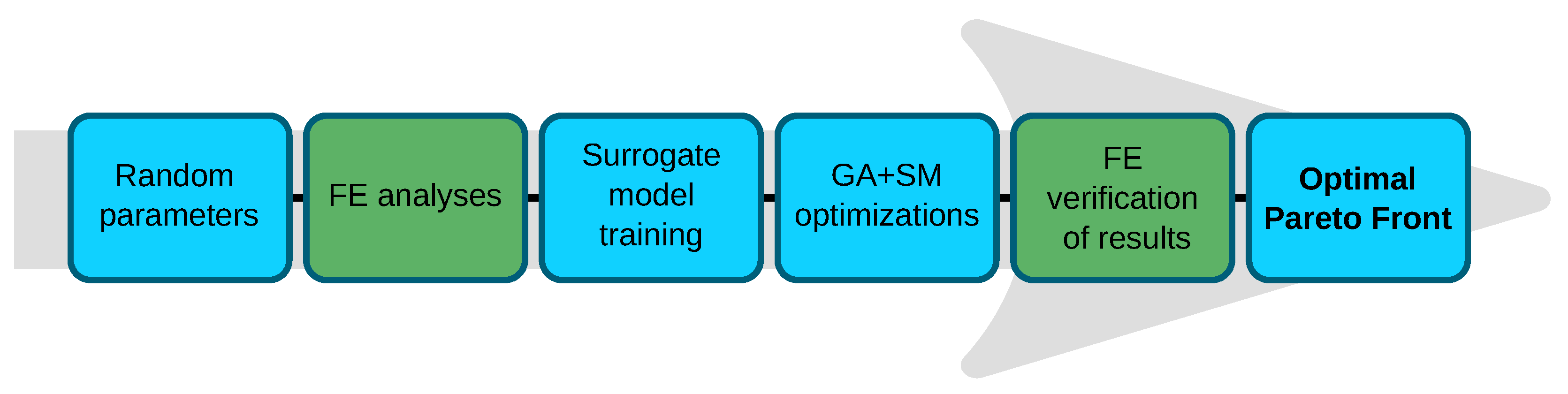
6]. In this study, we consider the canonical pipeline in which a deep neural network surrogate is trained on FEM-generated samples, subsequently queried by a genetic algorithm during the search over design variables, and finally validated against FEM for the candidate solutions, see
Figure 4.
While this approach substantially accelerates the optimization phase, it does not eliminate computational costs; instead, the load shifts to preparing training data and fitting the SM. Our goal is to develop a framework that also reduces the effort at this stage. Moreover, the same workflow can be adopted when experimental measurements are available for structures of the same class as those optimized here. In both scenarios, the number of expensive observations (laboratory tests or high-fidelity FEM simulations) must be minimized while retaining sufficient fidelity for decision-making. The stages that dominate the computational load—dataset preparation and SM training—are highlighted in green in
Figure 4. In this article, we focus specifically on this pre-optimization segment; approaches to lowering the computational burden of the post-optimization FEM-based verification have been presented in the authors’ earlier work [
28].
To that end, we construct the SM with two information sources of different fidelity (a multi-fidelity design).In its simplest form, these are (i) a small set of high-fidelity (HF) data produced by a detailed FEM or by laboratory experiments (when available) and (ii) a large set of low-fidelity (LF) data from a simplified, fast FEM. In this work, we use the two FEM models introduced earlier:
(HF) and
5 (LF). Appropriately corrected and aligned LF information supports broad exploration of the design space, whereas judiciously chosen HF samples correct systematic discrepancies and calibrate uncertainty [
20,
25]. Within deep learning, we exploit cross-fidelity correlations—e.g., staged training, and stacked models—as demonstrated in aerodynamic and electromagnetic applications [
15,
16,
17,
18,
19]. Additionally,
is used to generate pseudo-experimental targets via the nonlinear mapping of natural frequencies defined by Equation (
2), enabling realistic model–test discrepancies to be emulated in a fully numerical workflow.
2.5.1. Variant 0—HF-Only, Single-Fidelity Baseline
A single deep neural network surrogate is trained exclusively on high-fidelity (
) data: each training pair consists of the design vector and its pseudo-experimental response obtained by applying the mapping in Equation (
2) to the
frequencies. No low-fidelity (
5) data are used. During optimization, the genetic algorithm queries only this surrogate to evaluate the frequency objective (no FEM calls), while the cost objective is computed analytically. This is a classical reference approach (see
Figure 5).
The primary (and, in Variant 0, the only) network
maps the design vector to the eleven pseudo-experimental target frequencies,
where
denotes the transformed
frequencies defined by Equation (
2). The training set thus comprises pairs
, and the surrogate’s outputs are used directly to evaluate
during GA search.
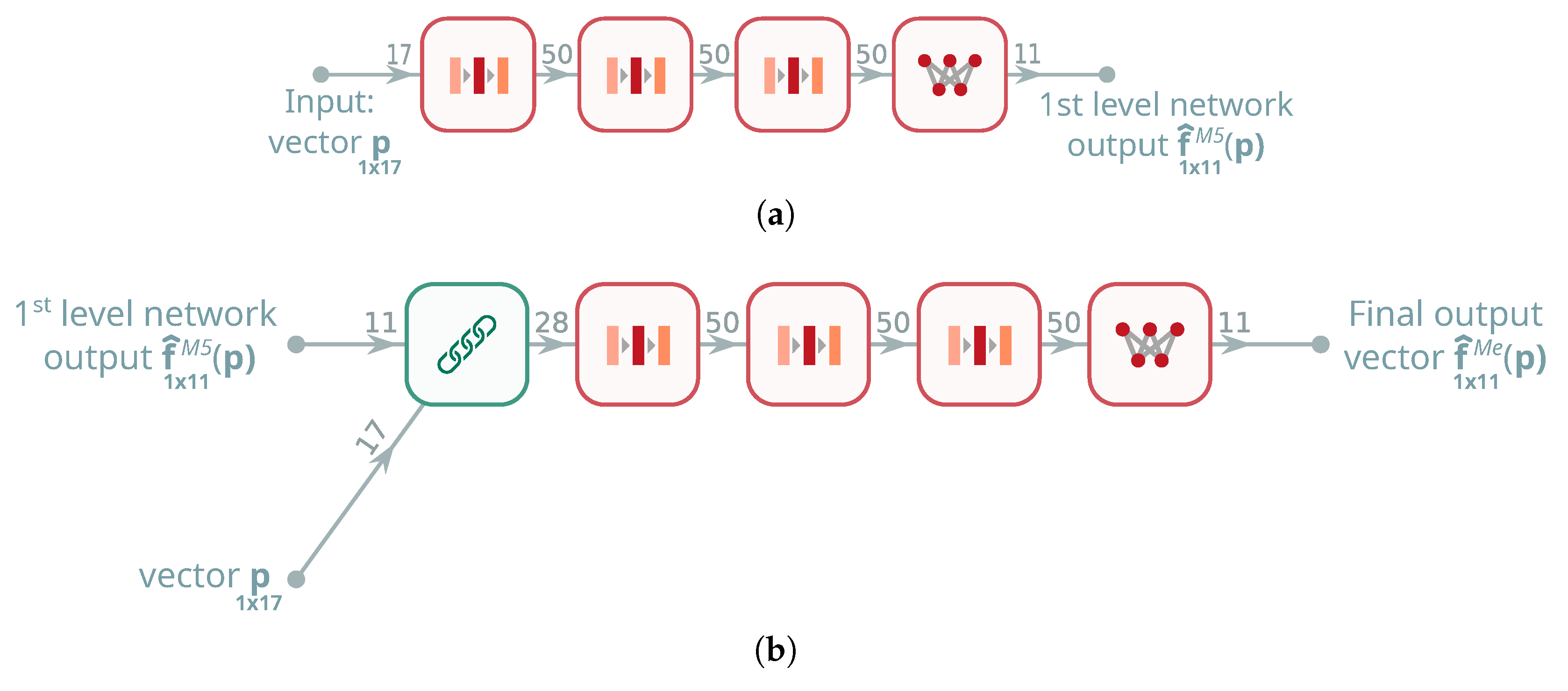
2.5.2. Variant 1—MF-Trained, Auxiliary Refinement + SF Primary Evaluator
Learning data are drawn from both fidelities: a limited HF set (
, pseudo-experimental targets available via Equation (
2)) and a large LF set (
5). Two surrogates play different roles:
Auxiliary network
(see
Figure 6) is trained before optimization to refine LF outputs toward HF quality. It ingests (during training) a triplet consisting of the design vector and paired simulator responses,
where the third argument (pseudo-experimental response,
) acts as a teacher signal used only during training to stabilize the LF
HF correction. At inference time, the teacher branch is dropped, and
uses only
to synthesize HF-like predictions
. Applying
to a large LF-only corpus yields a dense set of refined pseudo-experimental labels, thereby assembling a large training set without repeated HF simulations.
Primary network
(used during optimization;the same as in Variant 0) (see
Figure 5) is then trained offline on the union of scarce true HF/pseudo-experimental pairs and abundant refined pseudo-experimental pairs
. In the application phase, the GA queries only
to evaluate the frequency objective (no FEM calls are made), exactly as in Variant 0, but with a model trained on a MF-enhanced dataset—delivering substantial computational savings while retaining HF-level fidelity where it matters.
Two architectural realizations of the primary network were examined (
Figure 6a,b). The first (
Figure 6a, hereafter DNN) is a conventional fully connected multilayer deep neural network, and this baseline leverages depth to capture cross-feature interactions while remaining simple and robust.
The second design (
Figure 6b, hereafter LNL) explicitly separates linear and nonlinear processing within each block to better model mappings that decompose into an additive linear trend plus a nonlinear residual. This decomposition strengthens the network’s ability to represent responses that are well approximated by a linear component modulated by a structured nonlinear correction (e.g., stiffness-weighted trends with geometry- and angle-dependent residuals).
For completeness, a third variant was considered in which the
and
transformations are realized by two separate subnetworks
and
operating in parallel on different inputs (
Figure 6c, hereafter 2NETS), with predictions combined additively only at the output:
Although conceptually appealing, this configuration did not yield consistent advantages under the fixed training budget and is therefore reported only for completeness.
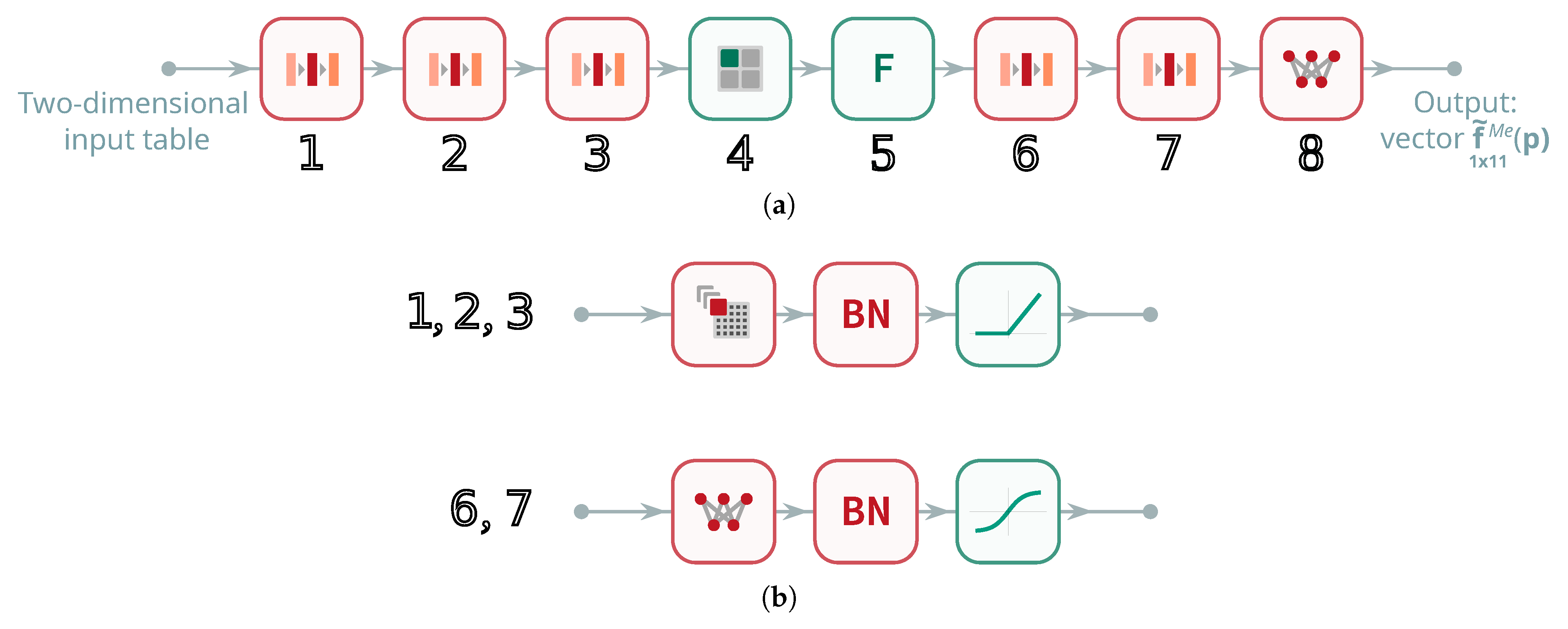
In addition to the DNN, LNL, and 2NETS configurations, a convolutional neural network (CNN) was also tested (
Figure 7). The CNN replaces the fully connected layers with convolutional blocks designed to capture local correlations between input features. While such architectures are highly effective in image processing tasks, their advantage is less pronounced for tabular, mixed-type input vectors such as those considered here. In practice, the CNN exhibited consistently weaker accuracy than both the DNN and LNL architectures and was therefore not pursued further in the optimization studies.
The input data to the CNN are organized as two-dimensional tables. In each i-th input table, where , there are four meta-columns: , , , and , with a total number of rows. For the first two columns, and , the tabular values in the j-th row are and , respectively, where . With regard to the last two columns, the values and remain constant across all rows in the i-th table.
2.5.3. Variant 2—Cascaded HF Emulator + Pseudo-Experimental Mapper (Two-Network Ensemble)
During optimization, the evaluator is a pair of neural networks queried in sequence, with no FEM calls in the loop (
Figure 8). The first network
takes the design vector
and returns a vector of eleven pseudo-
5 frequencies,
i.e., it emulates the low-fidelity model
5. The second network
receives both the design vector and the output of
and predicts the pseudo-experimental targets,
where
is defined by the mapping in Equation (
2). Training proceeds in two steps with teacher forcing: (i) fit
on LF data to approximate
; and (ii) fit
on pairs
to approximate
.
At application time, the GA uses only the neural ensemble to evaluate ; the cost remains analytic. This cascade preserves the structure “LF → pseudo-experiment,” improves data efficiency, and cleanly separates modeling roles, while acknowledging and controlling potential error propagation from the first to the second stage.
2.6. Rationale and Computational Footprint
The three variants are designed to disentangle accuracy–cost trade-offs under strict limits on high-fidelity (HF) evaluations. Let
and
denote the numbers of HF (
and in consequence
e(
)) and low-fidelity (LF,
5) simulations used to train the surrogate(s). With the
5 element size four times larger than
, one LF run costs approximately
of an HF run, while its discretization error grows on the order of
[
28]. We therefore report an HF-equivalent training cost:
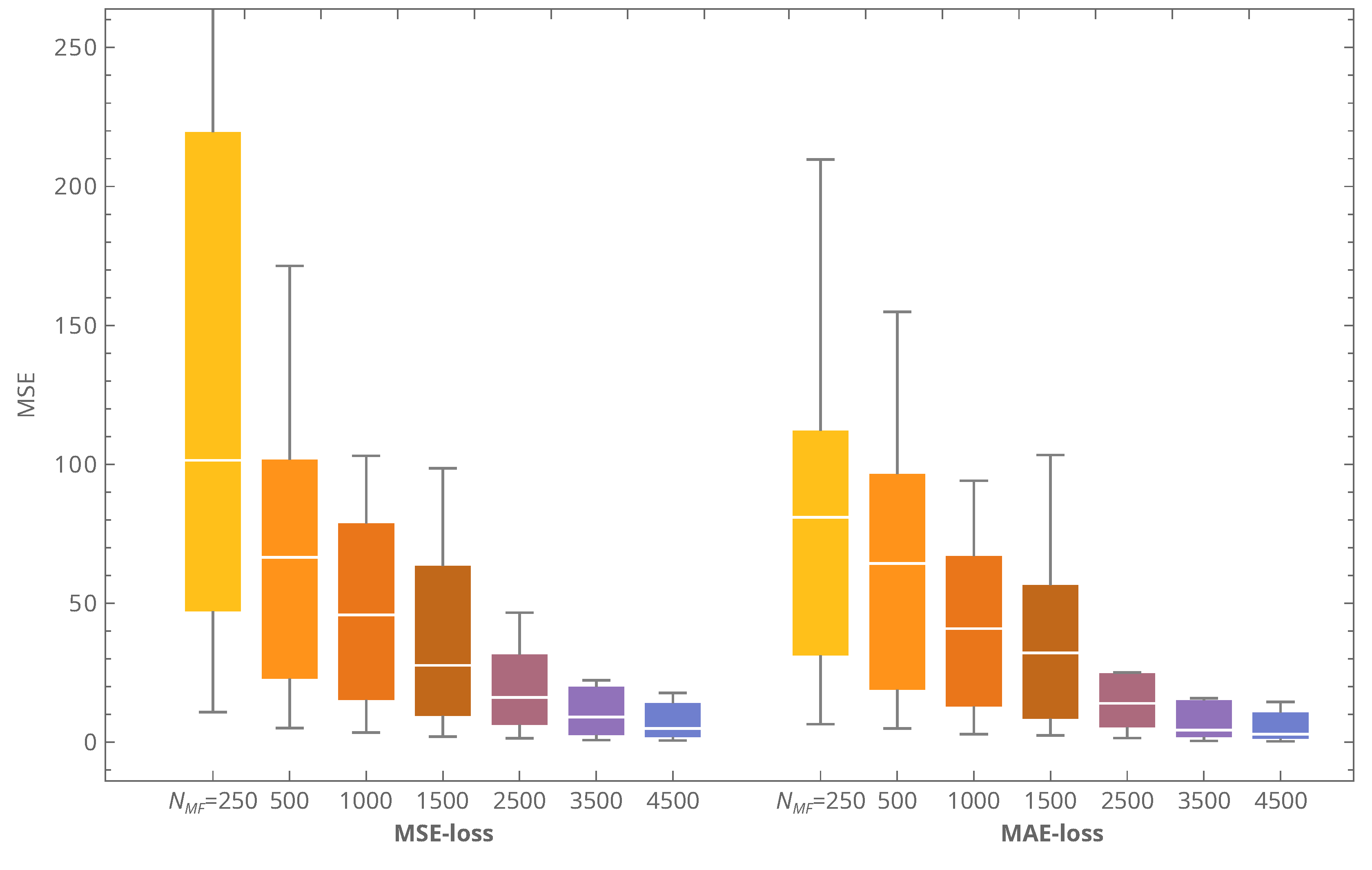
The adopted dataset sizes and fidelity ratios were also justified in prior research. A heuristic rule was proposed, namely, that the number of training patterns (in thousands) should be approximately one-fourth to one-fifth of the number of design variables [
38], which, for the current 17 variables, corresponds to about 4000 low-fidelity samples. In later works, we demonstrated that supplementing these with about 250 high-fidelity samples ensures a good balance between accuracy and cost [
28,
29]. The choice of the high-fidelity finite element mesh was validated by convergence analyses [
38], while the low-fidelity mesh was selected based on the error–time trade-off.
Variant 0 (HF-only) requires a dense HF dataset to generalize over the 17-dimensional design space. In line with prior experience, several thousand samples are needed; to fix ideas, set
, which gives
. Using the per-run CPU time of the HF model reported in
Section 2.2, one HF-equivalent unit corresponds to
s of CPU time. Thus, a budget of
amounts to
days of CPU time.
Variant 1 (MF-trained, auxiliary refinement) replaces most HF labels with refined LF labels produced by the auxiliary network. Using, for illustration,
paired with
(with 250 LF samples co-located with the HF designs) yields
i.e., an order-of-magnitude reduction in HF-equivalent cost. Although raw LF errors scale unfavorably with mesh coarsening, the refinement learned by the auxiliary network suppresses this bias before training the primary evaluator. On the same CPU-time scale,
entails
days of HF-equivalent simulation time for pattern generation.
Variant 2 (cascaded emulator + mapper) distributes learning across two networks: an LF-trained emulator and an HF-trained mapper to pseudo-experimental targets. Its HF-equivalent cost follows Equation (
12) with the budgets assigned to the two stages. Matching the illustrative budgets of Variant 1 leads to a comparable
, while allowing even larger
at negligible HF-equivalent overhead to reduce variance. The cascade preserves the LF
structure at inference, offering a complementary accuracy–cost trade-off relative to the offline-refinement route. Accordingly, with
, the HF-equivalent simulation time for dataset generation is again
days.
In addition to simulation time, one must account for network training and testing. With three NVIDIA A30 GPUs acceleration (each NVIDIA A30 with one GA100 graphics processor unit, 24 GB memory, 1440 MHz, 3584 shading and 224 tensor cores) (NVIDIA, Santa Clara, CA, USA), the times per run were as follows: Variant 0—a single network trained in ≈5 min; repeated 30 times, this totals h. Variant 1—two networks, auxiliary min and primary min per repeat; for 30 repeats, ≈3.25 h. Variant 2—identical training profile to Variant 1, i.e., ≈3.25 h for 30 repeats. The sole exception concerns models trained with an arcsinh-based loss, for which convergence was several times slower than with MSE/MAE under the same stopping criteria. After adopting surrogates, the GA optimization time became negligible relative to FEM simulation time. A final FEM-based verification of the returned designs added a comparable overhead across all settings; the verification stage required h.
Because the FEM simulations were executed exclusively on CPUs, whereas the neural-network training/testing was executed exclusively on a GPU, adding “CPU time” and “GPU time” into a single total is neither justified nor meaningful. We therefore report them separately (HF-equivalent CPU time for dataset generation and GPU wall time for network training). If, despite this caveat, one wished to approximate a single aggregate, the CPU time should first be normalized by the number of concurrently used threads (≈20 in our runs) to obtain a comparable per-device wall time; however, such an aggregate would still have limited interpretability.
In summary, the variants benchmark (i) a classical HF-only baseline,(ii) an MF pipeline that converts abundant LF into pseudo-HF labels for a single evaluator, and (iii) an MF cascade that factors the mapping and can exploit vast LF corpora—each eliminating FEM calls during optimization but differing in where computational effort is spent and how LF information is leveraged.
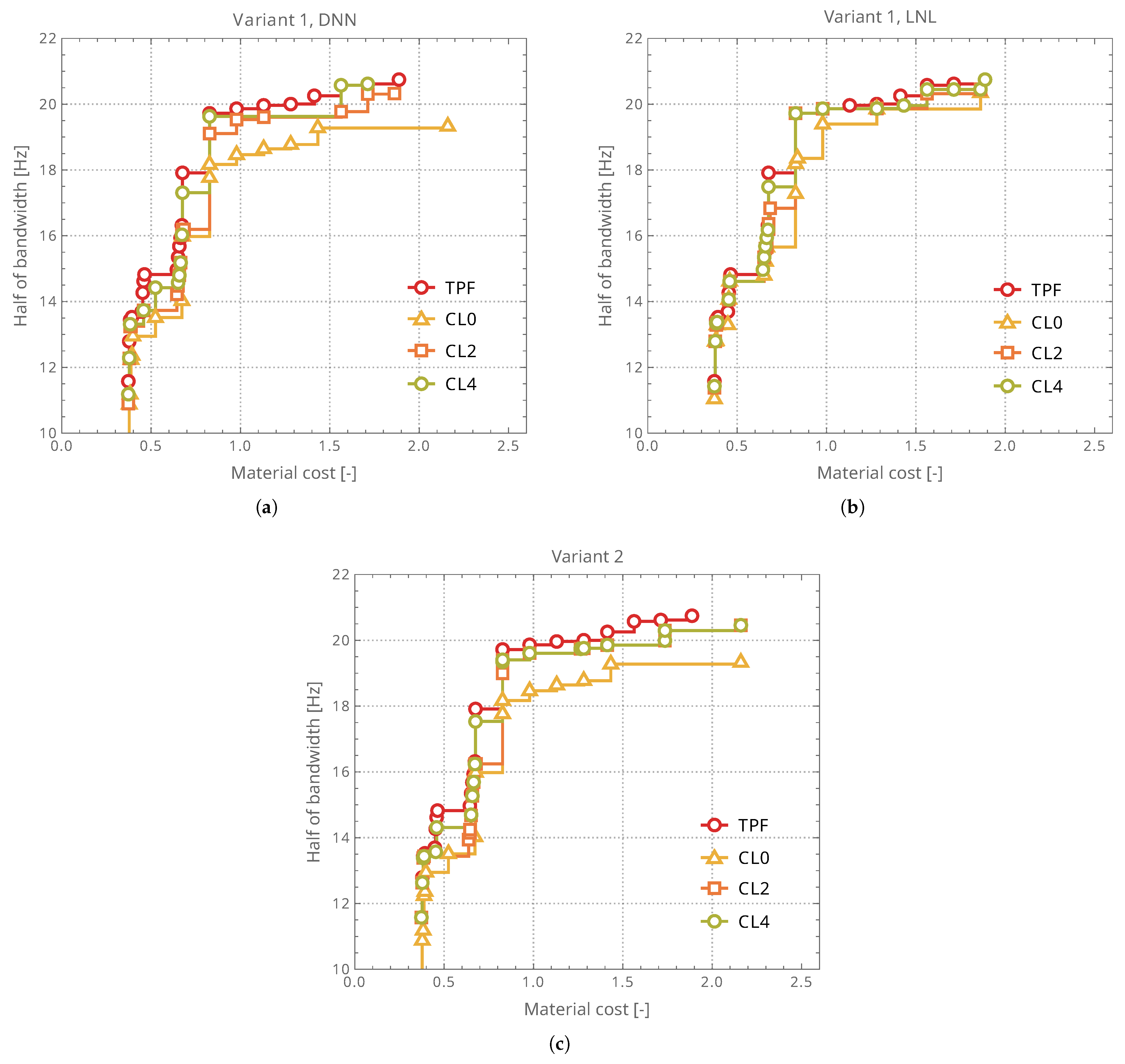
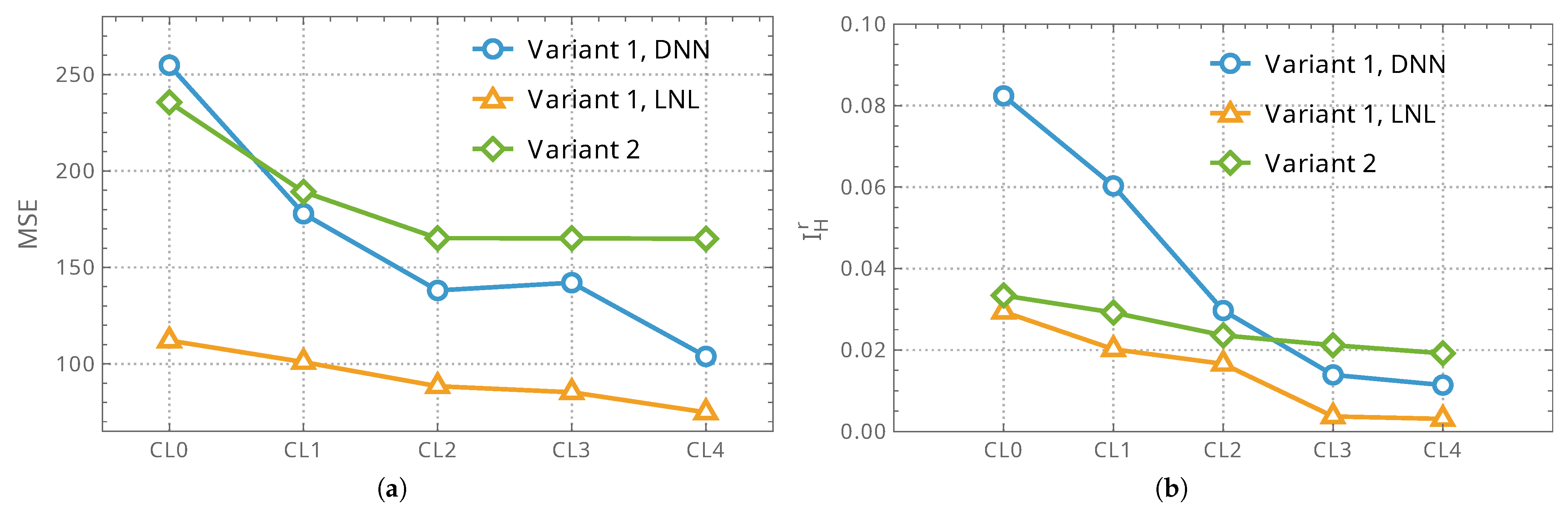
In the present hyperboloidal shell setting (see
Figure 2a–c), relying solely on Variant 0 is not only computationally onerous but also degrades surrogate accuracy: the SM validation error (MSE) is two orders of magnitude larger than for an otherwise comparable cylindrical case (see
Figure 2d). Two factors are dominant. First, the design space is higher-dimensional (17 versus 16 variables), which raises sample complexity and demands substantially more HF labels to achieve the same generalization level; the additional variable is a geometric descriptor—the hyperboloid depth parameter
d—absent in the cylindrical baseline. Second, accurate identification and tracking of the target mode shapes across designs is markedly harder for the hyperboloid: curvature reversal and stronger meridional coupling induce modal veering and near-degeneracies, making the mapping from FE eigenpairs to the fixed set of eleven target modes more error-prone. Even rare misassignments (label noise) propagate into the surrogate’s loss, inflate MSE, and reduce fidelity near the resonance-avoidance band.
Recognizing these limitations, we treat the hyperboloidal case as a deliberately stringent benchmark and leverage the MF strategies (Variants 1–2) to counteract both issues: they reduce the HF labeling burden while using LF-informed refinement/cascades to stabilize learning under label noise and heightened nonlinearity. This choice tests whether multi-fidelity design—not mere model capacity—can restore predictive accuracy and, in turn, improve Pareto-front quality at a fraction of the HF-equivalent cost.
We analyzed three surrogate configurations, summarized in
Table 2. All variants predict the vector of selected natural frequencies used in
; the cost
is evaluated analytically from material choices and geometry; hence, it is not surrogated. The backbone family, optimizer, and training budget are kept identical across variants; only the data sources and training protocols differ.
2.7. Neural Networks Applied
Deep neural networks are used as the surrogate backbone because they efficiently approximate highly nonlinear mappings from the mixed discrete–continuous design vector to the eleven target frequencies while remaining inexpensive at query time [
13,
14]. Inputs comprise standardized continuous features (geometry and ply angles) and one-hot encodings for plywise material choices; depending on the variant, auxiliary signals are concatenated, so the effective input dimensionality is either 17 (design only), 28 (design+
). Hidden layers employ nonlinear activations, and the output head is linear to predict all eleven frequencies jointly, allowing the model to exploit cross-output correlations. Regularization includes weight decay, dropout, and batch normalization; optimization uses mini-batches with gradient clipping and an early-stopping criterion on a held-out validation split.
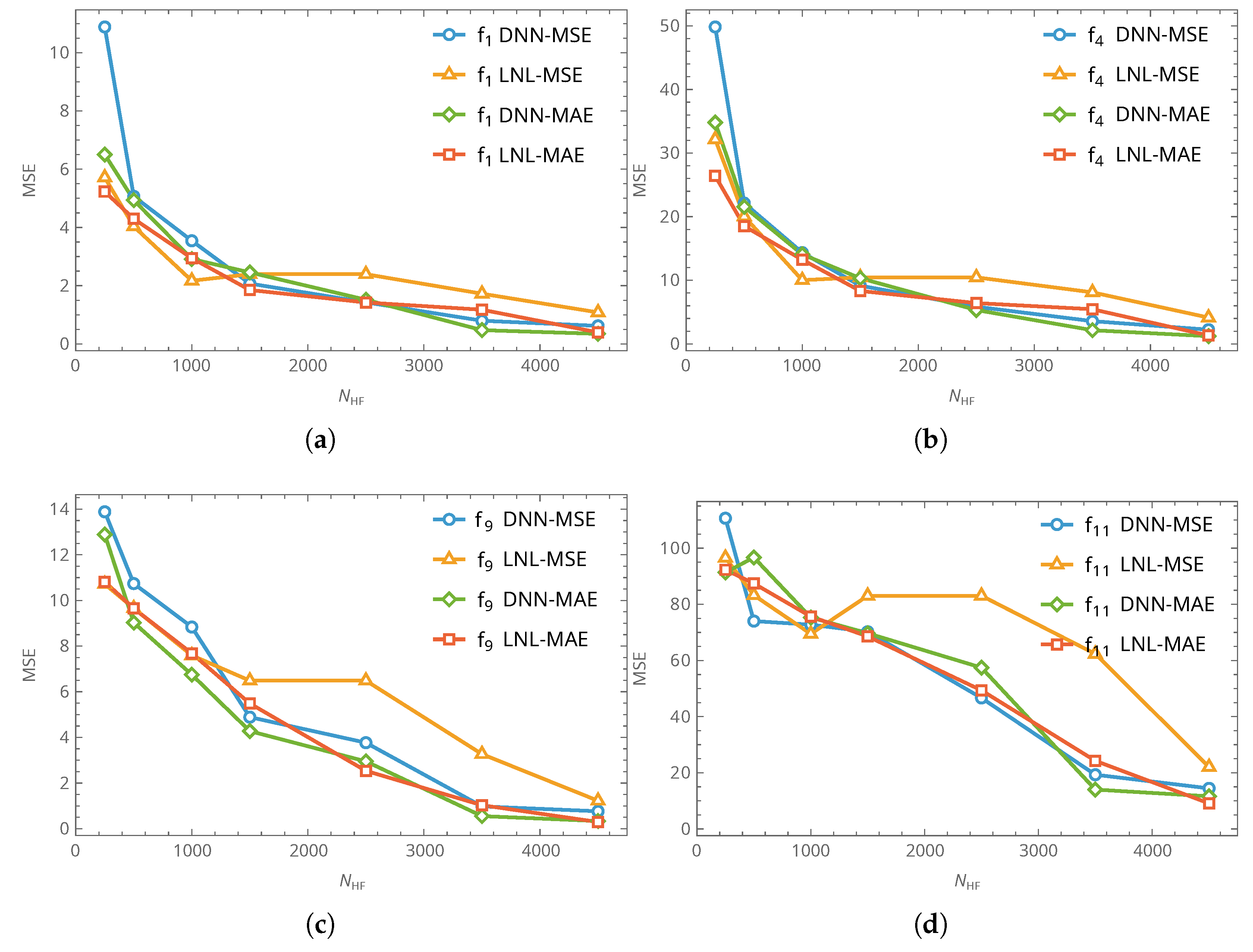
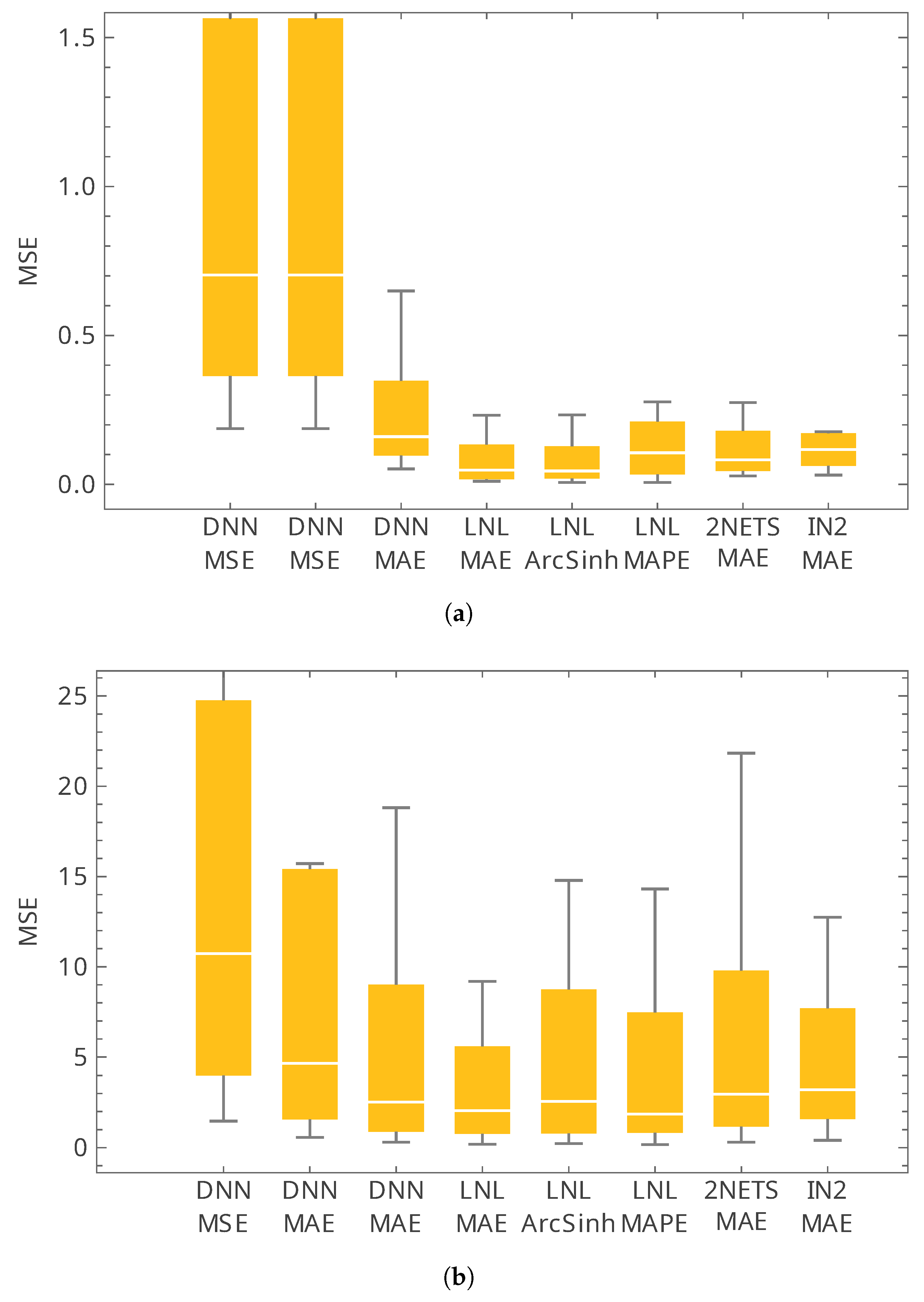
To avoid biasing results toward a specific architecture or optimizer, we performed a controlled hyperparameter sweep covering network depth (4–8 layers), width (20–100 units per layer), and three optimizers (ADAM, RMSProp, and SGD), together with several activation functions (ReLU, tanh, and sigmoid; softmax was considered only in auxiliary classification branches when applicable). For the loss, we compared MSE and MAE with more robust alternatives, namely the mean absolute percentage error (MAPE) and an error metric based on the inverse hyperbolic sine transformation (ArcSinh-based error), in order to accommodate scale differences across modes. Overall, performance differences were found to depend primarily on the fidelity strategy (single- vs. multi-fidelity data usage and network coupling) rather than on incidental architectural or optimizer choices.
The details of the examined approaches are summarized in
Table 3.
2.8. Non-Dominated Sorting Genetic Algorithm II in Brief
The Non-Dominated Sorting Genetic Algorithm II is a population-based, elitist evolutionary method widely used for multi-objective optimization [
3]. It maintains a set of candidate solutions and iteratively improves both convergence to, and coverage of, the Pareto front by combining fast non-dominated sorting with a crowding-distance diversity measure.
The algorithm begins by sampling an initial population
of size
N from the decision space
and evaluating the corresponding objective vectors
. At each generation
t, an offspring set
of size
N is created using tournament selection guided by Pareto rank and crowding distance, followed by simulated binary crossover and polynomial mutation or related operators [
44]. The objective values of
are then evaluated and combined with the parent population to form
. Fast non-dominated sorting is applied to
to identify fronts
, and crowding distance is used within each front to estimate local solution density [
3]. The next population
is filled with entire fronts in order of rank until the size limit is reached; if the last front does not fit, the most widely spaced solutions are selected based on crowding distance.
This process repeats until the generation budget or another stopping criterion is met, and the first front
of the final population is returned as an approximation of the Pareto-optimal set [
45]. By jointly addressing convergence (toward Pareto optimality) and diversity (distribution along the front), with an overall sorting complexity of
for
M objectives [
3], NSGA-II provides a robust default for mixed discrete–continuous design spaces and rugged, multi-modal response landscapes.
 computing a weighted affine sum, followed by batch normalization
computing a weighted affine sum, followed by batch normalization  and a pointwise activation
and a pointwise activation  . Note: block 4
. Note: block 4  in (a,b) and component
in (a,b) and component  in (c) are standard single hidden layers that perform only a weighted affine sum (no activation).
in (c) are standard single hidden layers that perform only a weighted affine sum (no activation).
 computing a weighted affine sum, followed by batch normalization
computing a weighted affine sum, followed by batch normalization  and a pointwise activation
and a pointwise activation  . Note: block 4
. Note: block 4  in (a,b) and component
in (a,b) and component  in (c) are standard single hidden layers that perform only a weighted affine sum (no activation).
in (c) are standard single hidden layers that perform only a weighted affine sum (no activation).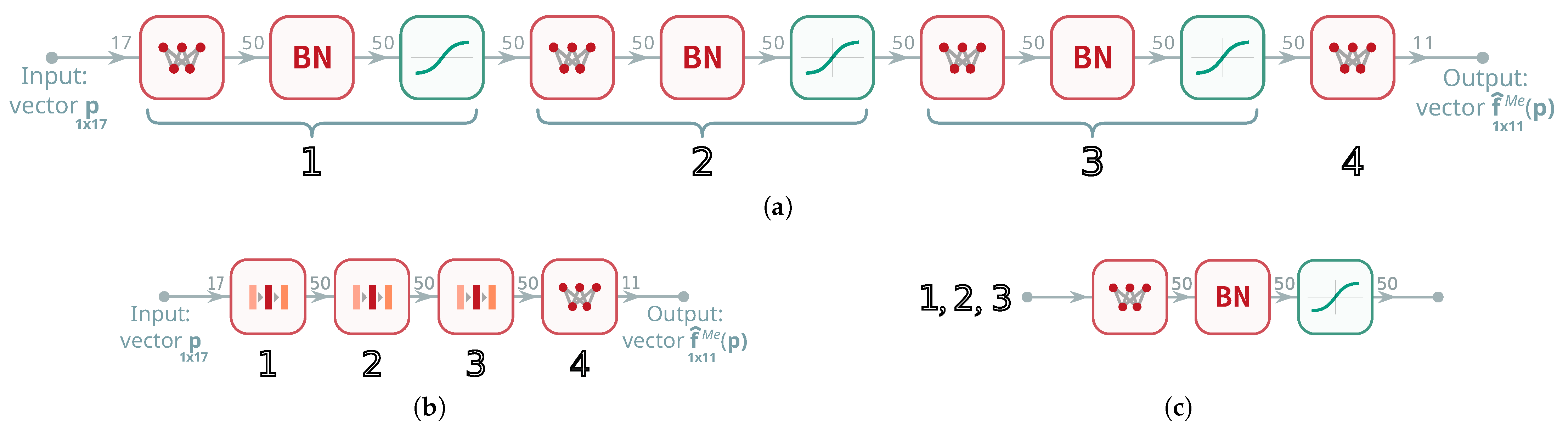
 is a concatenation block;
is a concatenation block;  is an addition block.
is an addition block.
 is a concatenation block;
is a concatenation block;  is an addition block.
is an addition block.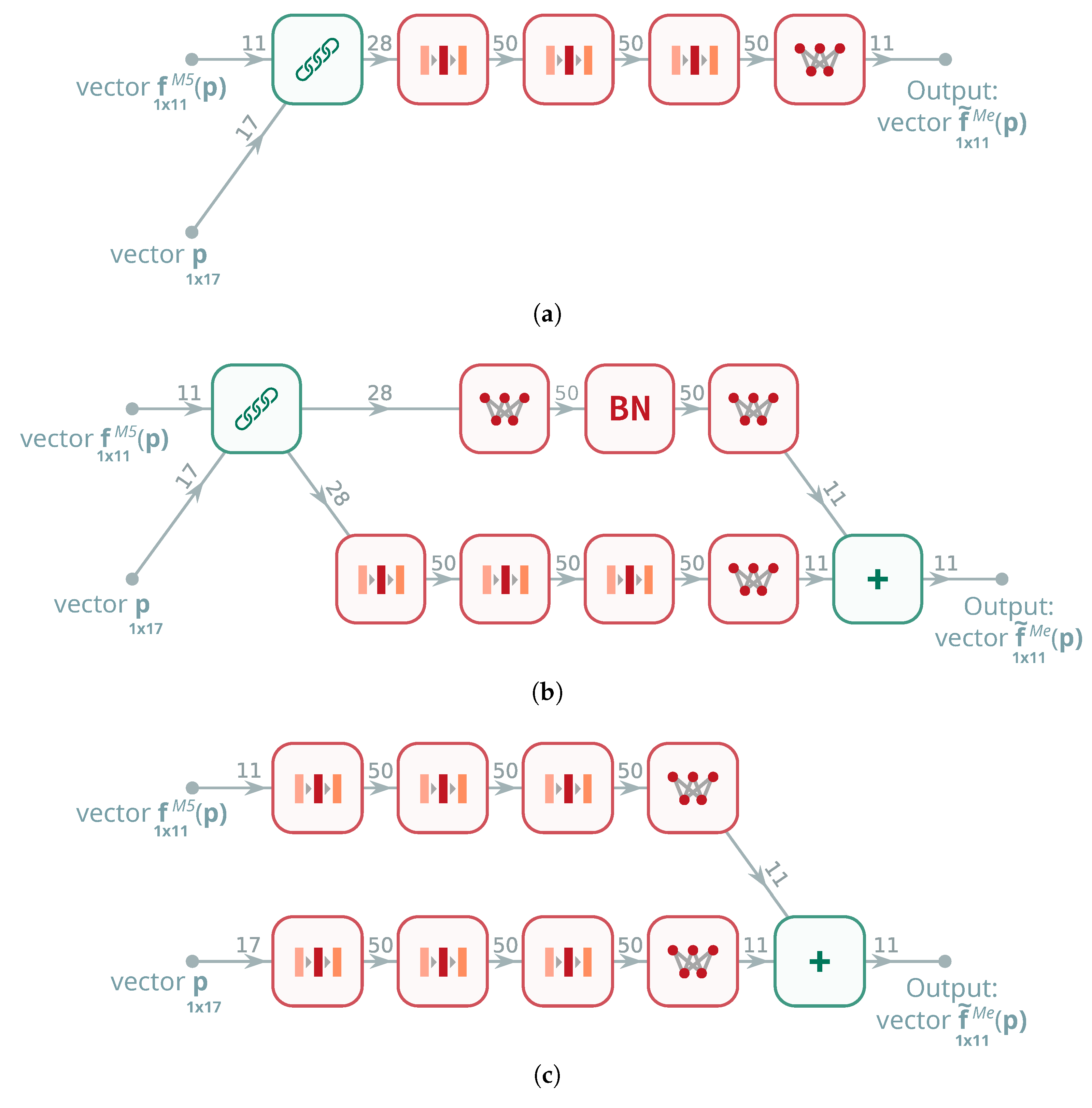
 convolutional layers (blocks 1–3) extract local features from the input, while the subsequent blocks perform feature reduction and mapping:
convolutional layers (blocks 1–3) extract local features from the input, while the subsequent blocks perform feature reduction and mapping:  block 4 corresponds to a pooling layer and
block 4 corresponds to a pooling layer and  block 5 to a flattening layer, which then feed into dense layers (6 and 7) producing refined pseudo-experimental predictions.
block 5 to a flattening layer, which then feed into dense layers (6 and 7) producing refined pseudo-experimental predictions.
 convolutional layers (blocks 1–3) extract local features from the input, while the subsequent blocks perform feature reduction and mapping:
convolutional layers (blocks 1–3) extract local features from the input, while the subsequent blocks perform feature reduction and mapping:  block 4 corresponds to a pooling layer and
block 4 corresponds to a pooling layer and  block 5 to a flattening layer, which then feed into dense layers (6 and 7) producing refined pseudo-experimental predictions.
block 5 to a flattening layer, which then feed into dense layers (6 and 7) producing refined pseudo-experimental predictions.