Abstract
Adverse weather events have a negative impact on the productivity of construction site activities. Understanding these effects is essential for developing realistic construction schedules. The influence of weather is shaped by both environmental factors (climate, geography, topography) and construction-related aspects such as technologies, materials, equipment, and site exposure. This paper proposes a model to quantify the influence of adverse weather by estimating monthly intervals of expected days with reduced construction productivity, based on data regarding specific weather events, including precipitation, wind, extreme temperatures, snow cover, fog, and high humidity. Data analysis employs the inclusion–exclusion principle, a combinatorial technique, alongside confidence interval estimation, a standard statistical approach. The model was applied in three Croatian cities to demonstrate its practicality and accuracy. Contractors with extensive on-site experience reviewed the results, providing insights into weather-sensitive activities and organizational practices.
1. Introduction
One of the characteristics of the construction projects is working outdoors, which implies sensitivity to the weather [1,2]. Weather can negatively influence the execution of construction activities [3,4], affecting workforce output, supplier performance, and material durability, which in turn may prolong project duration and generate financial risks [5]. Due to its substantial impact, weather represents a key factor shaping construction productivity [6]. Productivity, expressed as the ratio of outputs (e.g., quantity) to inputs (e.g., labor hours) in a given activity [7], plays a decisive role in the successful delivery of construction projects, directly determining the achievement of targeted timeframes and budgets [8,9]. As a central concern for managers, investors, and researchers alike, construction productivity significantly contributes to the gap between planned investments and actual costs [6]. Improving productivity enhances resource utilization, economic value, and the quality of deliverables [10,11].
Construction workers are constantly exposed to a variety of outdoor weather factors, which affect their thermal comfort, health, and productivity [12]. Adverse weather conditions reduce output, cause project delays and financial losses, and provide legitimate grounds for deadline extensions [13]. The extent to which weather variables impact construction activities depends on the technologies, equipment, materials, and procedures applied; the exposure of the site; the frequency of unusual weather; and the regional or national definition of average conditions [14]. Operations conducted under adverse weather inevitably incur productivity losses, with their magnitude influenced by both the type of activity and the level of protection provided [15]. These effects also vary considerably by geographic location [3,16,17].
Adverse weather, an unavoidable reality for contractors, often compels work under unfavorable conditions, yet adequate planning for such challenges is frequently lacking [18]. Understanding the role of weather in construction progress is therefore essential for effective planning and successful project delivery [19]. Projects can mitigate risks from weather conditions if relevant weather information is incorporated during the planning phase [20]. Proper decision-making at the planning stage can substantially reduce project time, cost, and effort [21]. Decision-makers must model weather events to predict their impact on construction tasks [16,22]. Quantifying the weather impact is valuable to contractors for preparing realistic timetables, cost estimates, and reliable bids [17,23]. Determining the impact of weather on labor productivity and health enables more accurate project preparation and the implementation of appropriate measures to enhance worker comfort and efficiency at the construction site [10]. However, when calculating the duration of activities, contractors mostly ignore the impact of adverse weather conditions, which results in an incorrect estimate of the project duration [24]. This is largely because tender periods are often too short and essential site-specific data are frequently unavailable at that phase [13].
The aim of this paper is to propose a model for processing data on adverse weather events in order to obtain monthly intervals with mathematically expected days of reduced productivity (compared to optimal, desired, or usual productivity) due to unfavorable weather impacts. It provides a flexible and scalable framework applicable to diverse climatic conditions and project locations, using data on adverse weather events (such as precipitation, wind, extreme temperatures, snow cover, fog, and high humidity) obtained from the relevant national meteorological service. The data processing involves the application of combinatorics and statistics. The proposed model is intended to be used by construction contractors during the preparation phase and in the development of realistic time schedules for construction work. To demonstrate its applicability, the model was applied in three Croatian cities: Rijeka, Krk, and Pazin. The results of its application are the mathematically expected days of reduced productivity for each month of the year due to unfavorable weather impacts. These results were evaluated by contractors with many years of experience managing construction sites in those cities. The research model presented in this paper builds upon the work of Šopić and Car-Pušić [25].
2. Literature Review
2.1. Impact of Adverse Weather Events on Construction
Adverse weather causes delays in about 45% of construction projects across the globe [16]. The most common adverse weather events leading to work stoppages, productivity losses, cost overruns, and project delays in construction are precipitation (heavy rainfall or snowfall), extreme temperatures (high and low), and intense winds [16,17,19,26,27]. Among these, rainfall and extreme temperatures are considered the most impactful weather difficulties [5]. Different types of construction work are affected by weather in different ways, since each involves distinct materials and equipment [27].
Any form of precipitation (rain or snow) hampers productivity, with a noticeable decline occurring even under light rain or snow compared to optimum dry conditions [8]. Many construction activities are highly sensitive to rainfall, which can disrupt progress while it is raining and continue to affect construction work for several days afterward [5,28]. Light rainfall (below 4 mm per 12 h) can reduce labor productivity by as much as 40%, whereas heavy snowfall may lower it by 35%, regardless of whether it coincides with scheduled work tasks [16]. Productivity generally decreases when precipitation exceeds 10 mm [27]. Exterior painting and asphalt paving are canceled at precipitation ≥1 mm, earthworks and concrete works at ≥ 10 mm, and steelworks at ≥30 mm [14].
Extreme temperatures, whether hot or cold, exert physical and psychological effects on construction workers, thereby diminishing their productivity [29]. Physiologically, exposure to hot weather can cause heat stress or stroke, whereas cold temperatures may result in tissue damage or numbness in extremities, all of which may psychologically affect a worker to the point of demoralization and reduced productivity [15,30]. Productivity remains largely unaffected between 10 °C and 20 °C, but drops significantly at temperatures exceeding 25 °C or falling below 0 °C [19]. For each 1 °C increase above 28 °C, worker productivity can drop by up to 57% [16]. Concrete works and asphalt paving are canceled when the minimum temperature is ≤0 °C, earthworks, steelworks, and exterior painting are canceled when the mean temperature is ≤0 °C, and at temperatures ≥40 °C, concrete works, steelworks, and asphalt paving are canceled [14]. Work must stop entirely when temperatures fall below −23.3 °C or rise above 43.3 °C, since efficient construction operations are not feasible under such conditions [31].
High wind speeds can cause work stoppages, reduce productivity, and negatively affect construction methods, labor, materials, and equipment [30,32,33]. The influence of strong winds also requires securing loose materials and may pose risks to workers from wind-blown debris [16]. Wind speeds of 8.94 m/s (32.2 km/h) or higher may reduce labor productivity by 30–40%, particularly in activities involving structural steel work, curtain wall installation, roofing, exterior painting, and other weather-exposed tasks [34]. When wind speeds exceed 9.72 m/s (35 km/h), crane operations become slower and less precise, and must stop completely if winds rise above 13.89 m/s (50 km/h) [35]. Concrete works, formwork/scaffolding, steelworks, and exterior painting are canceled at wind speeds ≥15.43 m/s (55.56 km/h), while earthworks and asphalt paving are generally not affected by wind at this level [14]. High wind speeds elevate the risk of accidents, often preventing workers from using scaffolding in accordance with safety regulations [16]. Some outdoor construction activities are less sensitive to wind effects.
Since weather thresholds affecting construction activities depend on the type and characteristics of the activity, as well as on materials, equipment, and the degree of exposure to atmospheric conditions, it is nearly impossible to define rigid limits beyond which on-site work cannot be performed [3,27]. Therefore, weather thresholds must be adjusted to the project-specific conditions and the working environment [34].
2.2. Research on Multiple Adverse Weather Events in Construction
The following section presents some of the significant studies conducted in recent years. All of the referenced studies highlight the significant impact of adverse weather events, particularly precipitation, strong winds, and extremely cold or hot days, on construction productivity and project duration, with weather factors being integrated into various models and methods to enable more accurate project planning, reduce delays, and improve on-site safety.
Ballesteros-Pérez et al. [13] developed a holistic model that enables practitioners to incorporate weather data into forecasting project durations, enhancing construction productivity, and supporting the resolution of contract claims. The model was tested through a case study involving the construction of two buildings located in different regions of Spain. The findings indicated that neglecting the impact of weather can extend project duration by 5–20% beyond the planned schedule. Nonetheless, the model has certain limitations, such as the omission of covariances between climatic factors influencing productivity and the insufficient consideration of the human dimension in response to extreme weather events.
Marzoughi et al. [5] proposed a decision support (DS) framework designed to incorporate weather-related factors in order to improve the estimation of project duration. They pointed out that their framework integrates various multivariate statistical tools and multicriteria decision-making approaches to achieve its objective. A model is also implemented based on the proposed framework. The major limitations of this study include the generic nature of the proposed decision support framework. Additionally, the study faces challenges such as the lack of model validation that could account for multiple construction projects with varying complexities or types, the unavailability of some necessary databases, and difficulties in obtaining expert input for the knowledge base.
Ballesteros-Pérez et al. [14] presented a method for processing a country’s historical weather data into a set of weather delay maps for some representative standard construction activities. They emphasized that their method allows a planner to anticipate how much longer a project activity will take to complete as a consequence of the weather. Some of the limitation include the awareness that allowing increased activity durations (due to weather) might lead to lower productivity levels. The accuracy of the method relies on having data from numerous weather stations, which may not be available in countries with fewer or newer stations. While their method is simple and customizable for many applications, it may be overly simplified for projects with more complex conditions.
Larsson and Rudberg [17] developed a discrete event simulation (DES) model for the analysis of weather impact on project duration. They emphasized that the simulation results indicate the following: weather has a significant impact on project duration and must be considered when planning operations; substantial differences between weather seasons can influence the timing of project start-up; and factors such as building height and threshold values for different crane types must be considered when planning lifting operations. The limitation of the model primarily indicates that the presented results are valid for concrete wall construction under Swedish climate conditions, particularly in the Stockholm region.
Larsson and Rudberg [19] conducted an in-depth study on the effects of different weather conditions on the productivity of typical concrete work tasks, highlighting that their research examines how practitioners, such as site managers, estimate these effects. Their study employs a questionnaire survey method, using pairwise comparisons of different weather factors within the Analytical Hierarchy Process (AHP). Some limitations of the study include that productivity reduction estimates do not account for interdependencies between weather factors and that the presented results are subject to uncertainties related to the quality of responses provided by respondents.
Hwang et al. [12] conducted a study using an outdoor thermal comfort index to examine how various factors (such as temperature, wind speed, humidity, radiant temperature, and clothing) affect accident rates. The primary aim of the study was to investigate the relationship between construction accidents and outdoor thermal comfort for construction workers, considering both the frequency and probability of accidents. Their results indicated that the probability of an accident was highest at a physiological equivalent temperature (PET) of 34.7 °C. A limitation of the study is that it only considered projects commissioned by public institutions, which may not capture the characteristics of private construction projects.
Previous research clearly confirms that adverse weather events significantly affect labor productivity, the duration and costs of construction projects, as well as safety on construction sites. It has been shown that extreme temperatures, precipitation, and strong winds can lead to reduced efficiency, or even complete work stoppages. Most existing studies aim to quantify this impact and assist in better schedule planning and risk assessment. However, limitations of current research include narrow applicability to specific regions or types of construction activities, as well as limited verification and/or validation under real-world conditions. There is a need for more accurate, flexible, and verified/validated tools that would enable broader and more precise practical application, regardless of location or project type. Despite the recognized importance, most contractors still insufficiently consider the impact of weather on construction during the planning phase of construction work, which results in underestimated timelines and increased costs.
3. Model Development for Quantifying the Impact of Adverse Weather on Construction Productivity
The research presented in this paper consists of three main steps. Figure 1 presents the overall research workflow. The first step involves the development of the model for quantifying the impact of adverse weather on construction productivity, which is divided into two parts. The first part includes the collection of data on adverse weather events, while the second part focuses on the processing of these data. Data processing involves the application of the inclusion–exclusion principle (a combinatorics technique) and confidence interval estimation (a statistical test). Applying the model results in monthly intervals with mathematically expected days of reduced construction productivity (compared to optimal, desired, or usual productivity) due to unfavorable weather impacts.
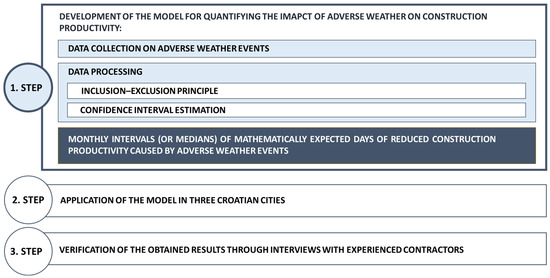
Figure 1.
Research workflow.
The second step of the research workflow is devoted to demonstrating the practical use of the developed model. For this purpose, it was applied in three Croatian cities: Rijeka, Krk, and Pazin. As a result, monthly estimates of low-productivity days were obtained for each city.
The third step includes the verification of the obtained results, which was carried out using the interview research method. The respondents were contractors with many years of experience in construction site management.
One contribution of the research is the proposal of the model for quantifying the impact of adverse weather on construction productivity while the second contribution includes its application in three Croatian cities: Rijeka, Krk, and Pazin. Based on its application, mathematically expected days of reduced productivity for each month of the year due to unfavorable weather impacts were obtained, which can be used in developing more accurate time schedules for construction work in those cities.
Figure 2 provides a more detailed overview of the first step, namely the model for quantifying the impact of adverse weather on construction productivity. The following Section 3.1 and Section 3.2 explain the individual elements of the model in detail.
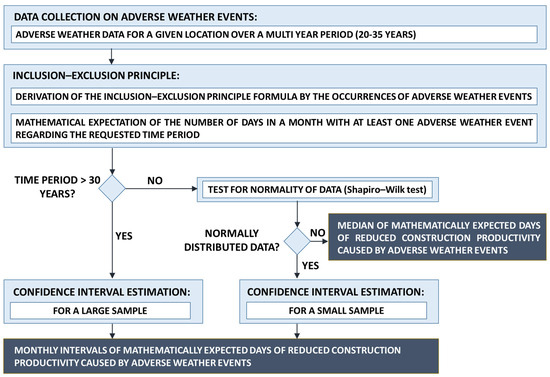
Figure 2.
Overview of the research first step.
The novelty of the proposed model lies in the integration of the inclusion–exclusion principle with statistical confidence interval estimation, representing a unique methodological approach in this context. Unlike many existing models that are limited to specific weather types or regions, this model offers a flexible and scalable framework applicable across a wide range of climatic conditions and project locations. Additionally, it provides mathematically expected days of reduced productivity for each month, offering a more precise and reliable tool for planning construction schedules in varying weather conditions.
3.1. Data Collection on Adverse Weather Events
Adverse weather events (precipitation, wind, cold, heat, snow cover, fog, high humidity, etc.) data should be obtained from the relevant national meteorological service for the area in which the model for quantifying the impact of adverse weather on construction productivity is intended to be applied.
The requested data should be presented as the total number of days per month for each specific adverse weather event. It is necessary to obtain weather data for a multi-year period (e.g., about 25 years), as recommended by Radujković et al. [36]. A generally acceptable range is 20 to 35 years. These weather data will serve as input for applying the principle of inclusion–exclusion. By applying the inclusion–exclusion principle, the mathematically expected number of days with reduced productivity due to unfavorable weather impacts is obtained. These values are then subjected to confidence interval estimation.
While natural hazards such as earthquakes, floods, volcanic eruptions, typhoons (hurricanes, cyclones), tornadoes, and landslides can cause severe disruptions or even destruction, this study focuses on adverse weather events (precipitation, wind, cold, heat, snow cover, fog, high humidity, etc.) that occur more regularly and whose impact on construction productivity can be quantified.
3.2. Data Processing
3.2.1. The Principle of Inclusion–Exclusion (PIE)
The inclusion–exclusion principle (PIE) is among the most basic techniques of combinatorics [37]. In the past, it has been known by various names, such as the cross-classification principle, and has been used by many mathematicians over the centuries [38]. The inclusion–exclusion principle represents one of the algebraic tools because of the possibility to reduce a combinatorial problem to a relatively routine algebraic calculation [39]. The underlying method of the inclusion–exclusion principle involves initially overcounting elements, followed by successive corrections to adjust for the overcounting, iterating this process as necessary [40]. This approach is particularly useful for determining the number of elements in the union of overlapping sets [41]. Applying the inclusion–exclusion principle, whether explicitly or implicitly, requires two essential components: a universe of objects (a set that generally includes more than just the elements of interest) and a corresponding set of properties (characteristics that the objects in the universe may or may not possess) [39].
Basic inclusion–exclusion principle by given finite sets A and B [42]:
This idea extends to three sets, A, B, and C [38]:
In general, let A1, A2, …, An be sets, then the inclusion–exclusion principle can be applied as follows [43]:
Weather involves the interplay of various events, including wind, rain, cold, etc., which, contrary to common assumptions, are not clearly correlated in terms of their occurrence [13]. Multiple adverse weather events can occur on the same day. In this context, the inclusion–exclusion principle provides the mathematically expected number of days in a given month with at least one adverse weather-related event. For instance, if three adverse weather events are recorded in a given month, the formula for the mathematically expected number of days in that month with at least one adverse weather-related event can be expressed as follows [44]:
where
- a—number of days in a given month with precipitation (≥10 mm);
- b—number of days in a given month with stormy winds;
- c—number of days in a given month with cold days (Tmin < 0 °C);
- d—total number of days in a given month.
The expression is the mathematical expectation of the number of days that are rainy, windy, and cold, while the expressions , , are the mathematical expectations of the number of days that are rainy and windy, rainy and cold, and windy and cold. Formula (4) refers to the most common situation in which cold days (Tmin < 0 °C) and hot days (Tmax ≥ 30 °C) do not occur within the same month. In the same way, instead of cold days, hot days during the warm part of the year can be included.
However, if four adverse weather events are recorded in a given month, for instance, rainy, windy, and cold days, as well as days with snow cover, the formula would take the following form:
where
- a—number of days in a given month with precipitation (≥10 mm);
- b—number of days in a given month with stormy winds;
- c—number of days in a given month with cold days (Tmin < 0 °C);
- e—number of days in a given month with snow cover;
- d—total number of days in a given month.
Furthermore, if five adverse weather events are recorded in a given month, such as rainy, windy, cold, as well as days with snow cover and foggy days, the formula would be as follows:
where
- a—number of days in a given month with precipitation (≥10 mm);
- b—number of days in a given month with stormy winds;
- c—number of days in a given month with cold days (Tmin < 0 °C);
- e—number of days in a given month with snow cover;
- f—number of days in a given month with fog;
- d—total number of days in a given month.
In the formulas above, expressions such as represent the mathematical expectation of the number of days in a month with two adverse weather events; expressions such as represent the mathematical expectation of the number of days with three events; expressions such as refer to four events; and expressions such as to five events. In other words, in each month, several adverse weather events may occur, and more than one can appear on the same day. The application of the inclusion–exclusion principle takes this into account and provides the mathematical expectation of the number of days in a month with at least one adverse weather event.
In this paper, formulas based on the inclusion–exclusion principle are presented for three, four, and five adverse weather events. The formulas can also be extended to cases involving six or more adverse weather events. This application of the inclusion–exclusion principle provides significant flexibility regarding the number of adverse weather events occurring at a given location and considered in relation to their impact on construction activities. Thus, the inclusion–exclusion principle serves as a powerful mathematical tool for achieving a more realistic assessment of the effects of adverse weather on construction works.
3.2.2. Confidence Interval Estimation
A population is a huge collection of individuals, and a sample is a group of individuals drawn from a population [45]. We use sample data to generalize about an unknown population [46].
The confidence interval estimation provides a range of values that best represents the population [47]. It is constructed from sample data, within which the population parameter is likely to occur at a specified probability, known as the level of confidence [48]. Values that bound the confidence interval are confidence limits [49]. The confidence limits are the two numbers that form endpoints of the confidence interval [50].
The confidence level represents the probability that the population parameter is contained within the confidence interval and is conventionally set at 95%, although alternative levels such as 90%, 99%, and 99.9% are also in common use [51]. More precisely, the most common percentage used is 95%, but if more confidence is needed, 99% is typically used, whereas if less confidence is required, 90% is typically used [52].
When you hear an “interval estimate with 95% confidence”, or simply, a “95% confidence interval estimate”, it indicates that if all possible samples of the same size n were drawn, approximately 95% of them would contain the population parameter within the interval, while about 5% would not [52]. The correct interpretation of a 95% confidence interval is that there is a 95% probability that the interval calculated from the sample contains the population mean, not that the population mean has a 95% probability of lying within the interval, as the population mean is a fixed value while the interval varies across samples [49].
Interval width is considered precision. Precision and confidence level are inversely proportional. The larger the interval, the better the chance of trapping a true parameter value; however, the larger the confidence interval, the less meaningful it is [53].
When the sample size is small (n ≤ 30) and the data have a normal distribution, we use the t-test, which employs a t-distribution [54]. The most commonly used method for assessing whether data from a small sample follow a normal distribution is the Shapiro–Wilk test. The t-distribution, also known as Student’s t-distribution, was developed by William Sealey Gosset, at the beginning of the 20th century [55].
For a sample of size n (n ≤ 30) drawn from a normally distributed dataset with unknown population standard deviation (σ), the confidence interval can be expressed as follows [50,53]:
where
- —sample mean;
- —interval width;
- —quantiles of Student’s t-distribution with (n − 1) degrees of freedom (df) for an area of α/2 in the upper (right) tail;
- s—sample standard deviation;
- n—sample size;
- α—significance level (for a confidence level of 1 − α).
The shape of Student’s t-distribution depends on its degrees of freedom (df) [46]. The degrees of freedom (df) are defined as (n − 1), where n represents the sample size [56]. As the sample size increases, the corresponding degrees of freedom also grow, causing the t-distribution to increasingly resemble the standard normal distribution [50]. The approximation is found to be quite close for n > 30. Therefore, by a large sample, we are generally referring to n > 30. For larger samples, testing for normality is generally not required.
The expression for the confidence interval of a large sample (n > 30) is [50,53]:
where
- – sample mean;
- —interval width;
- —the Z-score corresponding to the desired confidence level (for example, 1.96 for a 95% confidence level);
- σ—population standard deviation (or the sample standard deviation if the population standard deviation σ is unknown);
- n—sample size;
- α—significance level (for a confidence level of 1 – α).
4. Model Application to Selected Cities (Rijeka, Krk, Pazin)
Data on adverse weather events were requested from the Croatian Meteorological and Hydrological Service (DHMZ), the national meteorological service responsible for meteorological observations and climate-related information in Croatia. The data were provided as the total number of days per month with recorded occurrences of each specific adverse weather event over a multi-year period.
The model was applied in three Croatian cities: Rijeka, Krk, and Pazin. Regarding the selected locations, the adverse weather events considered included precipitation (≥10 mm), stormy winds, cold days (Tmin < 0 °C), and hot days (Tmax ≥ 30 °C). These thresholds generally reduce construction productivity for the selected cities, which was confirmed by experienced contractors through interviews conducted for the verification of this research. Defining strict limits beyond which work cannot be performed, however, depends on project-specific requirements, materials, equipment, degree of exposure to atmospheric conditions, and comprehensive site-specific information, as previously mentioned through the literature review.
The air temperature is measured at a height of 2 m above the ground, the speed and direction of the wind are carried out at a height of 10 m above the ground, and the wind strength is determined by observation. Cold days refer to those days when the minimum temperature is <0°C, while hot days are when the maximum daily temperature is ≥30 °C. A stormy wind refers to the maximum daily wind gust ≥ 17.2 m/s (61.92 km/h) or wind strength ≥ 8 Bf. In the case of precipitation, the precipitation’s amount, type, intensity, and characteristics are measured and determined. These thresholds, definitions, and measurement procedures are based on the standards of the DHMZ.
In Croatia, in the case of exceeding the deadline for the execution of works due to weather problems, contractors may request appropriate confirmations from the DHMZ organization to justify the delay. Such data are charged according to the official price list.
4.1. Data Collection of Adverse Weather Events for Rijeka, Krk, and Pazin
The model was applied in three Croatian cities: Rijeka, Krk, and Pazin. Rijeka and Krk are located in the Primorje-Gorski Kotar County, while Pazin is located in the Istria County. Rijeka is the seat of the Primorje-Gorski Kotar County, the largest Croatian port, and one of the strongest Croatian transport and industrial centers. Krk is the largest city on the island of Krk, the most populated Croatian island, and is known as a tourist destination and port. Pazin is a city in central Istria, the largest Croatian peninsula, and the seat of Istria County.
DHMZ provided data on adverse weather events for Rijeka, Krk, and Pazin from 1999 to 2022. The dataset included precipitation (≥10 mm), stormy winds, cold days (Tmin < 0 °C), and hot days (Tmax ≥ 30 °C), expressed as the total number of days per month for each specific adverse weather event. In these cities, precipitation events (≥10 mm) are predominantly associated with rainfall, while the occurrence of snow-covered days is quite rare.
Statistically, the data for all three cities formed small samples. During the observed period, and considering the occurrence of cold days (Tmin < 0 °C) and hot days (Tmax ≥ 30 °C), only cold days were recorded from October to April, whereas only hot days were recorded from May to September. This pattern can be observed in the figures presented in this section. Consequently, for each individual month, only three out of the four considered adverse weather events are relevant to study.
Figure 3 shows the distribution of the total number of days with precipitation (≥10 mm) per year for Rijeka, Krk, and Pazin from 1999 to 2022. In Rijeka, the highest number of days with precipitation occurred in 2010 (63 days), while the lowest was in 2011 (29 days). In Krk, the highest number of days with precipitation occurred in 2014 (56 days), while the lowest was in 2015 (20 days). In Pazin, the highest number of days with precipitation occurred in 2014 (62 days), while the lowest was in 2003 (25 days).
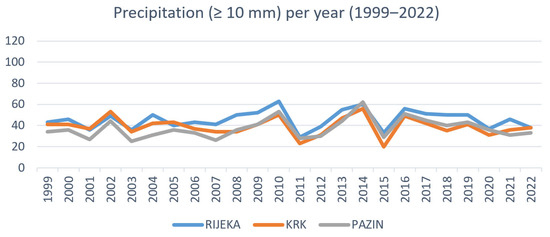
Figure 3.
Distribution of the total number of days with precipitation per year.
Figure 4 shows the distribution of the number of days with precipitation (≥10 mm) for each month from 1999 to 2022 for Rijeka, Krk, and Pazin. In Rijeka, the highest number of days with precipitation (more than 100 days) occurred in September (123 days), October (112 days), November (131 days), and December (117 days), while the lowest number of days (less than 60 days) occurred in June (57 days) and July (49 days). In Krk, the highest number of days with precipitation (more than 100 days) occurred in September (115 days), November (124 days), and December (105 days), while the lowest number of days (less than 60 days) occurred in April (50 days), June (45 days), and July (35 days). In Pazin, the highest number of days with precipitation (more than 100 days) occurred in November (111 days), while the lowest number of days (less than 60 days) occurred in January (56 days) and July (51 days).
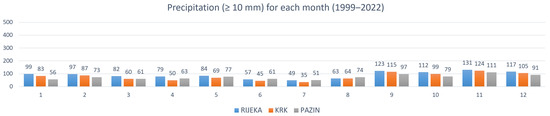
Figure 4.
Distribution of the number of days with precipitation for each month from 1999 to 2022.
Figure 5 provides a comparative overview of the total number of days with precipitation (≥10 mm) from 1999 to 2022 for Rijeka, Krk, and Pazin. It can be observed that Rijeka had the highest number of days with precipitation (a total of 1093 days), followed by Krk (with 936 days) and Pazin (with 894 days).
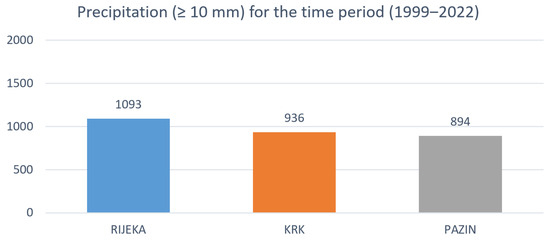
Figure 5.
Comparative overview of the total number of days with precipitation from 1999 to 2022.
Figure 6 shows the distribution of the total number of days with stormy winds per year for Rijeka, Krk, and Pazin from 1999 to 2022. In Rijeka, the highest number of days with stormy winds occurred in 2003 (29 days), while the lowest was in 2021 (1 day). In Krk, the highest number of days with stormy winds occurred in 2008 (5 days), while in many years, no stormy wind days were recorded (from 2002 to 2003, from 2006 to 2007, from 2009 to 2016, and from 2018 to 2022). In Pazin, the highest number of days with stormy winds occurred in 2019 (9 days), while in 1999, 2000, 2011, and 2014, no stormy wind days were recorded. On average, stormy winds occur 14 days per year in Rijeka, while Krk and Pazin are not particularly windy.
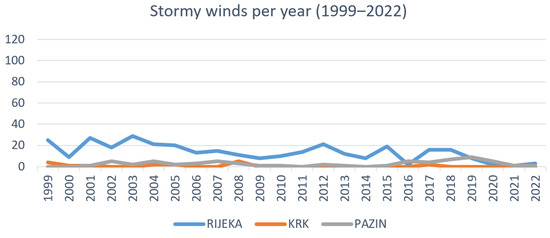
Figure 6.
Distribution of the total number of days with stormy winds per year.
Figure 7 shows the distribution of the number of days with stormy winds for each month from 1999 to 2022 for Rijeka, Krk, and Pazin. In Rijeka, the highest number of days with stormy winds (more than 30 days) occurred in January (45 days), February (52 days), March (38 days), November (45 days), and December (45 days), while the lowest number of days (less than 10 days) occurred in June (9 days) and August (8 days). In Krk, the highest number of days with stormy winds occurred in January (4 days), November (4 days), and December (6 days), while from March to May and from July to October, no days with stormy winds were recorded (0 days). In Pazin, the highest number of days with stormy winds occurred in March (12 days) and November (11 days), while in April, no days with stormy winds were recorded (0 days).
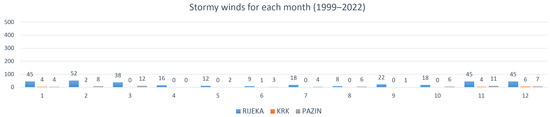
Figure 7.
Distribution of the number of days with stormy winds for each month from 1999 to 2022.
Figure 8 provides a comparative overview of the total number of days with stormy winds from 1999 to 2022 for Rijeka, Krk, and Pazin. It can be observed that Rijeka had the highest number of days with stormy winds (a total of 328 days), followed by Pazin (with 64 days) and Krk (with 17 days).
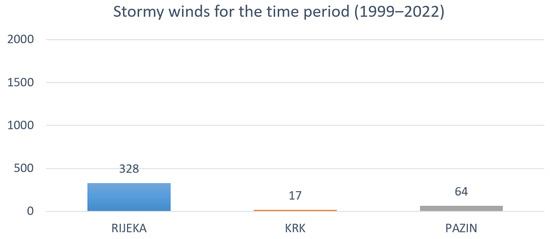
Figure 8.
Comparative overview of the total number of days with stormy winds from 1999 to 2022.
Figure 9 shows the distribution of the total number of cold days (Tmin < 0 °C) per year for Rijeka, Krk, and Pazin from 1999 to 2022. In Rijeka, the highest number of cold days occurred in 2005 (30 days), while the lowest was in 2020 (3 days). In Krk, the highest number of cold days occurred in 2005 (71 days), while the lowest was in 2020 (2 days). In Pazin, the highest number of cold days occurred in 2005 (105 days), while the lowest was in 2014 (32 days).
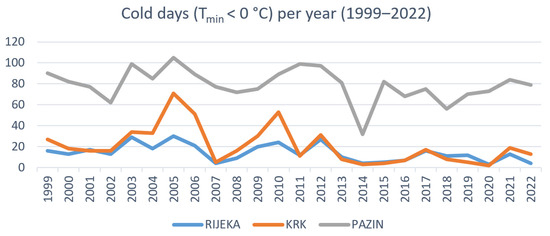
Figure 9.
Distribution of the total number of cold days per year.
Figure 10 shows the distribution of the number of cold days (Tmin < 0 °C) for each month from 1999 to 2022 for Rijeka, Krk, and Pazin. In Rijeka, the highest number of cold days (more than 100 days) occurred in January (132 days) and February (102 days). In Krk, the highest number of cold days (more than 100 days) occurred in January (190 days) and February (137 days). In Pazin, the highest number of cold days (more than 100 days) occurred in January (495 days), February (411 days), March (293 days), November (180 days), and December (406 days). For all three cities, no cold days were recorded from May to September (0 days). Therefore, cold days occurred exclusively from October to April.
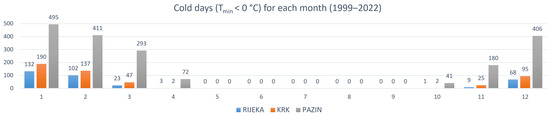
Figure 10.
Distribution of the number of cold days for each month from 1999 to 2022.
Figure 11 provides a comparative overview of the total number of cold days (Tmin < 0 °C) from 1999 to 2022 for Rijeka, Krk, and Pazin. It can be observed that Pazin had the highest number of cold days (a total of 1898 days), followed by Krk (with 498 days) and Rijeka (with 338 days).
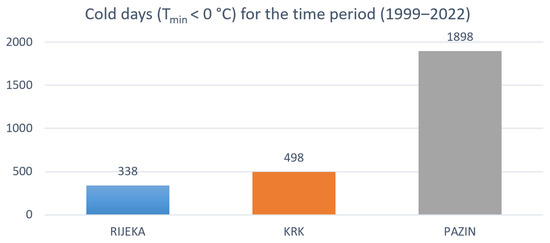
Figure 11.
Comparative overview of the total number of cold days from 1999 to 2022.
Figure 12 shows the distribution of the total number of hot days (Tmax ≥ 30 °C) per year for Rijeka, Krk, and Pazin from 1999 to 2022. In Rijeka, the highest number of hot days occurred in 2003 (74 days), while the lowest number was in 2014 (17 days). In Krk, the highest number of hot days occurred in 2003 (77 days), while the lowest was in 2014 (21 days). In Pazin, the highest number of hot days occurred in 2012 (68 days), while the lowest was in 2014 (13 days).
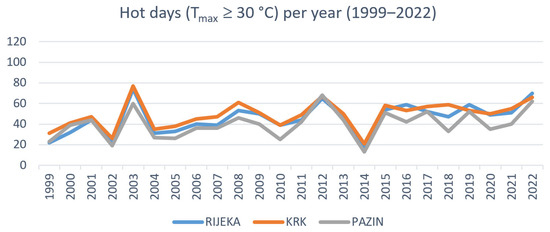
Figure 12.
Distribution of the total number of hot days per year.
Figure 13 shows the distribution of the number of hot days (Tmax ≥ 30 °C) for each month from 1999 to 2022 for Rijeka, Krk, and Pazin. In Rijeka, the highest number of hot days (more than 300 days) occurred in July (422 days) and August (392 days). In Krk, the highest number of hot days (more than 300 days) occurred in July (457 days) and August (419 days). In Pazin, the highest number of hot days (more than 300 days) occurred in July (374 days) and August (344 days). For all three cities, no hot days were recorded from October to April (0 days). Therefore, hot days occurred exclusively from May to September.
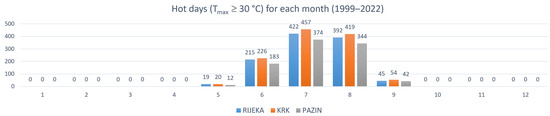
Figure 13.
Distribution of the number of hot days for each month from 1999 to 2022.
Figure 14 provides a comparative overview of the total number of hot days (Tmax ≥ 30 °C) from 1999 to 2022 for Rijeka, Krk, and Pazin. It can be observed that Krk had the highest number of hot days (a total of 1176 days), followed by Rijeka (with 1093 days) and Pazin (with 955 days).
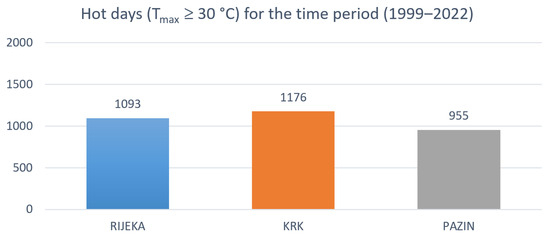
Figure 14.
Comparative overview of the total number of hot days from 1999 to 2022.
4.2. Data Processing for Rijeka, Krk, and Pazin
4.2.1. Applying the Principle of Inclusion–Exclusion (PIE)
For all three cities, considering the occurrence of cold days (Tmin < 0 °C) and hot days (Tmax ≥ 30 °C), only cold days were recorded from October to April, while only hot days were recorded from May to September. In other words, cold and hot days did not occur in the same month. The occurrence of cold days excluded the possibility of hot days, and vice versa. It would therefore be incorrect to assume their simultaneous occurrence within a single month. Accordingly, the inclusion–exclusion principle should be applied such that, for each month of the year, in addition to precipitation and strong winds, either cold days or hot days are considered. Thus, for each month, out of the four considered adverse weather events, three can be included in the analysis.
Moreover, multiple adverse weather events may occur on the same day (like precipitation and strong wind, or precipitation, strong wind, and cold days, etc.). DHMZ data were provided as the total number of days per month for each specific adverse weather event (e.g., number of days with precipitation, number of days with strong wind, number of cold days, and number of hot days). Consequently, the total number of days affected by adverse weather in a month cannot be obtained by simply summing these values, as some days may include multiple simultaneous events.
The inclusion–exclusion principle accounts for the fact that multiple adverse weather events can occur on the same day. Applying this principle yields the mathematically expected number of days in a month with at least one adverse weather event. This mathematically expected number of days in a month with at least one adverse weather event also represents days with reduced productivity on construction sites (compared to optimal, desired, or usual productivity) due to unfavorable weather impacts, which was confirmed by experienced contractors through interviews conducted for the verification of this research.
The inclusion–exclusion principle was applied for each month of the year during the period from 1999 to 2022 for Rijeka, Krk, and Pazin. As a result, the mathematically expected days of reduced productivity due to unfavorable weather impacts were obtained. Table 1, Table 2 and Table 3 present data for Rijeka, Krk, and Pazin, respectively, for the month of January, showing the number of days with precipitation, strong wind, and cold days during the period from 1999 to 2022. Each table includes a separate, color-highlighted, column displaying the results obtained by applying the inclusion–exclusion principle. The data generated in this way were used for further analysis, specifically for the application of confidence interval estimation. Separate tables have been created for each month, and data for the remaining months are available from the authors upon request, with a justification of the need.

Table 1.
Overview of adverse weather days and color-highlighted results of applying the inclusion–exclusion principle for Rijeka in January (1999–2022).

Table 2.
Overview of adverse weather days and color-highlighted results of applying the inclusion–exclusion principle for Krk in January (1999–2022).

Table 3.
Overview of adverse weather days and color-highlighted results of applying the inclusion–exclusion principle for Pazin in January (1999–2022).
4.2.2. Applying Confidence Interval Estimation
Using the inclusion–exclusion principle, samples of mathematically expected days with at least one adverse weather event, i.e., reduced construction site productivity (compared to optimal, desired, or usual productivity) due to unfavorable weather impacts were generated for each month (according to the period from 1999 to 2022). The generated samples represented small samples, for which the normality of data distribution was tested. To test for normality, the Shapiro–Wilk test was applied at a 5% significance level, using the Real Statistics add-in for Excel. The Shapiro–Wilk test generates a p-value (a numerical measure), which is used to determine whether the assumption of a normal distribution holds. If the p-value is less than 0.05 (the 5% significance level), the data do not follow a normal distribution, while a p-value greater than 0.05 indicates that the data do follow a normal distribution (Shapiro–Wilk test, normal: yes/no).
For all samples with normally distributed data, confidence interval estimation was applied at a 95% confidence level (1 − α = 0.95, α = 0.05). By applying this test, a corresponding monthly interval was obtained, allowing the conclusion that, with 95% probability, the interval contains the actual number of days in that month with at least one adverse weather event, i.e., reduced construction site productivity (compared to optimal, desired, or usual productivity) due to unfavorable weather impacts. For all samples in which the data were not normally distributed, the median of the sample was used as the representative number of low-productivity days in the month, as the median is commonly applied for non-normally distributed data.
Thus, for Rijeka, Krk, and Pazin, by applying confidence interval estimation (to data calculated using the inclusion–exclusion principle), monthly intervals were obtained which, with 95% probability, contain the actual number of days with reduced construction site productivity. Table 4, Table 5 and Table 6 present the descriptive statistics and the confidence interval estimates for Rijeka, Krk, and Pazin. In each table, the columns containing the confidence interval estimates are highlighted in color to distinguish them from other data. Since the interval values are expressed in decimal form and represent days, they were rounded to the nearest whole number for easier interpretation. Table 7, therefore, provides an overview of the mathematically expected number of days with reduced construction site productivity (compared to optimal, expected, or usual productivity) due to unfavorable weather impacts. For months in which the data did not follow a normal distribution, the sample median was used as the representative number of low-productivity days. To distinguish results more clearly, values for each city are highlighted in distinct colors.

Table 4.
Descriptive statistics and color-highlighted confidence interval estimation for Rijeka (1999–2022).

Table 5.
Descriptive statistics and color-highlighted confidence interval estimation for Krk (1999–2022).

Table 6.
Descriptive statistics and color-highlighted confidence interval estimation for Pazin (1999–2022).

Table 7.
Overview of mathematically expected days with reduced productivity due to adverse weather.
The monthly intervals (and medians), as presented in Table 7, are recommended for use in Rijeka, Krk, and Pazin during the preparation of construction schedules. When planning weather-sensitive activities, an appropriate number of days with reduced productivity due to unfavorable weather should be included to ensure that the schedule realistically reflects such impacts. The extent of productivity reduction depends on several factors, including the type and complexity of the project, workers’ experience and capabilities, the sensitivity of equipment to weather, material supply and site logistics, the nature of construction activities, work organization and scheduling, personal protective equipment, available technical resources on site, and other similar factors. Inevitably, some days on the construction site will result in zero productivity or complete work stoppages due to extremely adverse weather conditions. Completely ignoring the impacts of adverse weather when preparing a construction schedule is incorrect. Doing so increases the risk of delays and may lead to unattainable deadlines.
5. Results Verification
The research results, obtained through the application of the inclusion–exclusion principle and confidence interval estimation, were verified using the interview research method. The respondents were six contractors with extensive experience in managing construction sites in Rijeka, Krk, and Pazin, all employed by leading construction companies in Croatia and the surrounding region. Their on-site professional experience ranged from 5 to over 20 years: two had 5–10 years, another two 10–15 years, one 15–20 years, and one more than 20 years of experience.
The interviews were conducted individually in a “one-on-one” format, using both synchronous and traditional “face-to-face” communication. The interviews followed a semi-structured approach, with some pre-prepared questions guiding the discussion. At the beginning of each interview, the research was briefly explained, after which the respondents shared their answers, opinions, and perspectives in an open, discussion-based format.
The prepared questions were divided into two main discussion topics. The first topic focused on identifying the types of construction work most sensitive to adverse weather and examining how companies organize their activities in response. The second topic involved evaluating the mathematically expected days of reduced productivity due to unfavorable weather impacts, identifying the weather events with the most significant negative influence on construction productivity, and determining the months in which the greatest productivity decline is expected.
5.1. Contractors’ Experiences with Adverse Weather in Construction
The respondents shared their experiences regarding the challenges of carrying out construction work under adverse weather events. They emphasized that adverse weather significantly impacts outdoor construction activities such as earthworks, concrete work, masonry, insulation, roofing, façade installation, and asphalt paving, while indoor activities are generally less affected. According to their responses, unfavorable weather impacts can disrupt, delay, or otherwise complicate the proper execution of construction tasks in various ways.
Precipitation (≥10 mm) reduces worker productivity and hinders the execution of earthworks, concreting, asphalting, masonry of load-bearing walls, external waterproofing, and façade installation. Additionally, due to precipitation, materials used or installed can become slippery, making handling them properly and safely more difficult. Prolonged exposure to precipitation and cold can weaken workers’ immune systems, increasing the risk of colds and other illnesses.
Strong winds can compromise the stability of scaffolding and tower cranes. During strong winds, lifting and transporting loads with cranes becomes more difficult, as does performing roofing work. Furthermore, strong winds increase the risk of workers losing balance, which is especially dangerous when working at heights. They also stir up dust, which disrupts workers and complicates the execution of tasks.
Cold days (Tmin < 0 °C) slow down the execution of certain activities. Concreting, asphalting, masonry of load-bearing walls, external waterproofing, and earthworks become more difficult and, in some cases, may need to be temporarily halted. Water in fresh concrete and binding agents can freeze, asphalt cools too quickly, and waterproofing materials cannot be properly applied to cold surfaces. When the ground is frozen, earthworks are generally postponed. During cold days, special additives and techniques must be used to minimize negative effects. It is crucial to provide workers with adequate warm clothing, footwear, and personal protective equipment designed for cold weather. Additionally, workers need frequent breaks in heated areas.
Hot days (Tmax ≥ 30 °C) adversely affect the quality of concrete, binders, adhesives, and coatings. The evaporation of water and solvents accelerates drying. Therefore, special additives and appropriate techniques must be applied to mitigate the negative effects. Worker exposure to high temperatures increases the risk of dehydration, fatigue, and exhaustion. Asphalting generates extreme heat, placing considerable physical strain on workers and greatly increasing the risk of exhaustion. It is essential to ensure that workers take frequent breaks in cooler areas and maintain proper hydration on hot days (Tmax ≥ 30 °C).
The respondents also shared insights into company practices during adverse weather, including the treatment of hourly wage rates for construction workers. Under such conditions, workers usually arrive at the construction site in the morning and wait in containers to see if the weather will improve. During this waiting period on the construction site, workers’ hourly wage is typically reduced (commonly by 20–30% of their usual rate), reflecting the hours they spend waiting (and not working) due to adverse weather. If a company has multiple active construction sites and external work cannot be performed at one site, workers may be sent to another site where indoor work is being carried out, as long as this decision does not disrupt the work organization at the other site or cause an overload of workers.
5.2. Weather Events with the Greatest Impact on Productivity and Productivity Loss Periods
All respondents agreed that it is unrealistic to expect optimal productivity every day. Furthermore, they all agreed that when developing a construction time schedule, it is necessary to account for appropriate time contingencies due to adverse weather events. However, they emphasized that in practice, such contingencies are often not implemented.
Obtaining weather data from the DHMZ is subject to fees based on the official price list. Contractors typically request these data only when necessary to justify delays during construction, rather than during the planning or scheduling phases, using them primarily as supporting evidence when significant delays occur.
Figure 15 shows the distribution of responses regarding which adverse weather events cause the greatest difficulties in construction work. Respondents were allowed to list one or more adverse weather events. In Rijeka, the most disruptive weather event was precipitation (42%), followed by stormy wind (33%), cold days (17%), and hot days (8%). In Krk, where wind is less prevalent, the main challenges were attributed to precipitation (57%) and cold days (43%). Additionally, due to its status as a tourist destination, earthworks and structural construction works are typically banned during the summer months (usually from 15 June to 15 September). In Pazin, the most disruptive weather event was cold days (50%), followed by precipitation (30%), stormy wind (10%), and hot days (10%).
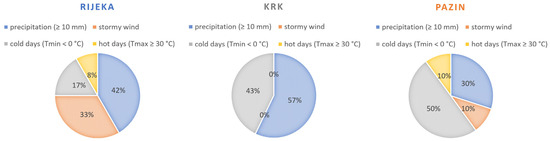
Figure 15.
Distribution of responses regarding which adverse weather events cause the greatest difficulties in construction work.
Figure 16 shows the distribution of responses regarding the months most affected by adverse weather in construction work. Respondents were allowed to list one or more months. In Rijeka, the months most affected by adverse weather (≥50% of responses) were January (83%), February (83%), December (67%), and November (50%). Of the other months, March stands out (33%). To a lesser extent (<20% of responses), respondents mentioned April (17%), July (17%), August (17%), September (17%), and October (17%). In Krk, the months most affected by adverse weather (≥50% of responses) were January (83%), February (67%), December (67%), and November (50%). To a lesser extent (<20% of responses), September was mentioned (17%). In Pazin, the months most affected by adverse weather (≥50% of responses) were January (83%), February (83%), December (83%), March (67%), and November (67%). To a lesser extent (<20% of responses), October was mentioned (17%).
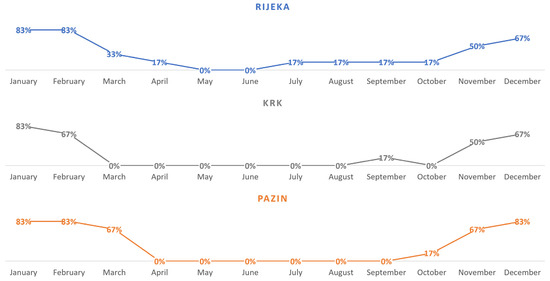
Figure 16.
Distribution of responses regarding the months most affected by adverse weather in construction work.
The interview results align well with the data provided by DHMZ for the selected locations, confirming the reliability of the collected expert opinions (i.e., contractors). Differences in the distribution of adverse weather events among the three cities reflect local climate characteristics. In Rijeka, construction productivity is most hampered by precipitation and stormy winds; in Krk, by precipitation and cold days; and in Pazin, by cold days and precipitation. A clear seasonal pattern emerges, with the winter months, particularly January, February, and December, being the most disruptive for construction activities. This has direct implications for realistic project planning and scheduling. In addition, local circumstances, such as summer restrictions on earthworks and structural construction in Krk due to tourism, further affect the feasibility of work. The summer period is also often scheduled for worker vacations, which can balance out the loss of productivity on construction sites caused by high temperatures. Taken together, these findings highlight the importance of integrating weather data into construction planning to optimize scheduling and resource allocation.
The respondents confirmed the accuracy of the results presented in Table 7. The reliability of these results is supported by the fact that they are based on actual data on adverse weather events and on productivity-reducing thresholds identified in the literature. However, while Table 7 provides a solid basis for developing construction schedules for sites in Rijeka, Krk, and Pazin, it is also necessary to account for project-specific factors, including the type and characteristics of activities, the materials and equipment used, and the degree of exposure to atmospheric conditions.
6. Conclusions
In this paper, an original model for quantifying the impact of adverse weather on construction productivity, combining the combinatorial inclusion–exclusion principle with statistical confidence interval estimation, is presented. The model simultaneously accounts for multiple adverse weather events. It was applied in three Croatian cities (Rijeka, Krk, and Pazin), demonstrating its flexibility and practical applicability. The results are expressed as mathematically expected days of reduced productivity per month, reflecting the effects of adverse weather, which can significantly improve the accuracy of construction schedule planning. The findings were further verified through interviews with experienced contractors, confirming the model’s usability and reliability.
However, while the model provides the mathematically expected days of reduced productivity, it does not specify the magnitude of the productivity reduction (e.g., by 25%, 50%, 75%, etc.). Determining the appropriate degree of productivity loss is therefore the responsibility of the person preparing the construction schedule, who must consider the specific site conditions and the nature of the work.
One of the limitations of the model is the time-consuming processing required due to the large volume of data. In addition, weather data may be incomplete, for example, if measurements for certain months are missing. To verify the model results, interviews with experienced contractors were conducted. This method also has limitations, including the possibility of subjective responses, misinterpretation of questions, insufficiently detailed or vague answers, and the influence of the respondent’s personality on their responses.
This research lays the groundwork for the further development of tools that integrate weather-related events into construction project planning, helping to reduce delays and improve productivity on construction sites. Future studies could focus on testing alternative analytical techniques, exploring different approaches to model verification and validation, and expanding the model to other locations and project types. Such efforts would enhance the model’s practical relevance and broaden its applicability under diverse environmental conditions.
Author Contributions
Conceptualization, M.Š., A.V. and I.M.; methodology, M.Š.; software, M.Š. and A.V.; validation, M.Š. and I.M.; formal analysis, M.Š., A.V. and I.M.; investigation, M.Š. and A.V.; resources, M.Š.; data curation, M.Š. and A.V.; writing—original draft preparation, M.Š.; writing—review and editing, M.Š.; visualization, M.Š.; supervision, M.Š. and I.M.; project administration, M.Š. and I.M.; funding acquisition, M.Š. and I.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been fully supported by the University of Rijeka under project number uniri-mladi-tehnic-23-47 (UNIRI projects for young scientists 2023, project leader: Martina Šopić) and under project number uniri-iskusni-tehnic-23-65 (UNIRI projects for experienced scientists 2023, project leader: Ivan Marović).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- El-Rayes, K.; Moselhi, O. Impact of rainfall on the productivity of highway construction. J. Constr. Eng. Manag. 2001, 127, 125–131. [Google Scholar] [CrossRef]
- Alshebani, M.N.; Wedawatta, G. Making the construction industry resilient to extreme weather: Lessons from construction in hot weather conditions. Procedia Econ. Financ. 2014, 18, 635–642. [Google Scholar] [CrossRef]
- Ballesteros-Pérez, P.; del Campo-Hitschfeld, M.L.; González-Naranjo, M.A.; González-Cruz, M.C. Climate and construction delays: Case study in Chile. Eng. Constr. Archit. Manag. 2015, 22, 596–621. [Google Scholar] [CrossRef]
- Marzouk, M.; Hamdy, A. Quantifying weather impact on formwork shuttering and removal operation using system dynamics. KSCE J. Civ. Eng. 2013, 17, 620–626. [Google Scholar] [CrossRef]
- Marzoughi, F.; Arthanari, T.; Askarany, D. A decision support framework for estimating project duration under the impact of weather. Autom. Constr. 2018, 87, 287–296. [Google Scholar] [CrossRef]
- Liu, X.; Song, Y.; Yi, W.; Wang, X.; Zhu, J. Comparing the random forest with the generalized additive model to evaluate the impacts of outdoor ambient environmental factors on scaffolding construction productivity. J. Constr. Eng. Manag. 2018, 144, 04018037. [Google Scholar] [CrossRef]
- Moohialdin, A.S.M.; Lamari, F.; Miska, M.; Trigunarsyah, B. Construction worker productivity in hot and humid weather conditions: A review of measurement methods at task, crew and project levels. Eng. Constr. Archit. Manag. 2020, 27, 83–108. [Google Scholar] [CrossRef]
- Moselhi, O.; Khan, Z. Analysis of labour productivity of formwork operations in building construction. Constr. Innov. 2010, 10, 286–303. [Google Scholar] [CrossRef]
- Tijanić, K.; Šopić, M.; Marović, I.; Car-Pušić, D. Analysis of the construction machinery work efficiency as a factor of the earthworks sustainability. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Philadelphia, PA, USA, 2019; Volume 222, p. 012009. [Google Scholar]
- Al Refaie, A.M.; Alashwal, A.M.; Abdul-Samad, Z.; Salleh, H. Weather and labor productivity in construction: A literature review and taxonomy of studies. Int. J. Product. Perform. Manag. 2021, 70, 941–957. [Google Scholar] [CrossRef]
- Šopić, M.; Bogdan, A.; Marović, I. Efficiency versus Effectiveness in Earthworks Based on Time Study Analysis. In Proceedings of the 15th International OTMC Conference and 6th IPMA Senet Conference: Smart Built Environment Through Digital Transformation, Zagreb, Croatia, 21–24 September 2022; pp. 336–353. [Google Scholar]
- Hwang, J.; Jeong, J.; Lee, M.; Jeong, J.; Lee, J. Establishment of outdoor thermal comfort index groups for quantifying climate impact on construction accidents. Sustain. Cities Soc. 2023, 91, 104431. [Google Scholar] [CrossRef]
- Ballesteros-Pérez, P.; Rojas-Céspedes, Y.A.; Hughes, W.; Kabiri, S.; Pellicer, E.; Mora-Melià, D.; del Campo-Hitschfeld, M.L. Weather-wise: A weather-aware planning tool for improving construction productivity and dealing with claims. Autom. Constr. 2017, 84, 81–95. [Google Scholar] [CrossRef]
- Ballesteros-Pérez, P.; Smith, S.T.; Lloyd-Papworth, J.G.; Cooke, P. Incorporating the effect of weather in construction scheduling and management with sine wave curves: Application in the United Kingdom. Constr. Manag. Econ. 2018, 36, 666–682. [Google Scholar] [CrossRef]
- Koehn, E.; Brown, G. Climatic effects on construction. J. Constr. Eng. Manag. 1985, 111, 129–137. [Google Scholar] [CrossRef]
- Schuldt, S.J.; Nicholson, M.R.; Adams, Y.A.; Delorit, J.D. Weather-related construction delays in a changing climate: A systematic state-of-the-art review. Sustainability 2021, 13, 2861. [Google Scholar] [CrossRef]
- Larsson, R.; Rudberg, M. Impact of weather conditions on in situ concrete wall operations using a simulation-based approach. J. Constr. Eng. Manag. 2019, 145, 05019009. [Google Scholar] [CrossRef]
- Thomas, H.R.; Ellis, R.D., Jr. Fundamental principles of weather mitigation. Pract. Period. Struct. Des. Constr. 2009, 14, 29–35. [Google Scholar] [CrossRef]
- Larsson, R.; Rudberg, M. Effects of weather conditions on concrete work task productivity—A questionnaire survey. Constr. Innov. 2023, 23, 306–321. [Google Scholar] [CrossRef]
- Jang, M.H.; Yoon, Y.S.; Suh, S.W.; Ko, S.J. Method of using weather information for support to manage building construction projects. In Proceedings of the AEI 2008: Building Integration Solutions, Denver, CO, USA, 24–27 September 2008; pp. 1–10. [Google Scholar]
- Mirahadi, F.; Zayed, T. Simulation-based construction productivity forecast using neural-network-driven fuzzy reasoning. Autom. Constr. 2016, 65, 102–115. [Google Scholar] [CrossRef]
- Gudac, I.; Marović, I.; Hanak, T. Sustainable optimization of winter road maintenance services under real-time information. Procedia Eng. 2014, 85, 183–192. [Google Scholar] [CrossRef]
- Moselhi, O.; Gong, D.; El-Rayes, K. Estimating weather impact on the duration of construction activities. Can. J. Civ. Eng. 1997, 24, 359–366. [Google Scholar] [CrossRef]
- Senouci, A.; Al-Abbasi, M.; Eldin, N.N. Impact of weather conditions on construction labour productivity in Qatar. Middle East J. Manag. 2018, 5, 34–49. [Google Scholar] [CrossRef]
- Šopić, M.; Car-Pušić, D. Statistička obrada podataka o vremenskim neprilikama u svrhu određivanja mjesečnog intervala s matematički očekivanim danima zastoja pri radu gradilišta na području grada Rijeke. Zb. Rad. (Građevinski Fak. Sveučilišta U Rijeci) 2018, 21, 67–85. [Google Scholar] [CrossRef]
- Shahin, A.; AbouRizk, S.M.; Mohamed, Y. Modeling weather-sensitive construction activity using simulation. J. Constr. Eng. Manag. 2011, 137, 238–246. [Google Scholar] [CrossRef]
- Jung, M.; Park, M.; Lee, H.S.; Kim, H. Weather-delay simulation model based on vertical weather profile for high-rise building construction. J. Constr. Eng. Manag. 2016, 142, 04016007. [Google Scholar] [CrossRef]
- Mohamed, S.; Srinavin, K. Forecasting labor productivity changes in construction using the PMV index. Int. J. Ind. Ergon. 2005, 35, 345–351. [Google Scholar] [CrossRef]
- Shan, Y.; Goodrum, P.M. Integration of building information modeling and critical path method schedules to simulate the impact of temperature and humidity at the project level. Buildings 2014, 4, 295–319. [Google Scholar] [CrossRef]
- Ibbs, W.; Sun, X. Weather’s effect on construction labor productivity. J. Leg. Aff. Disput. Resolut. Eng. Constr. 2017, 9, 04517002. [Google Scholar] [CrossRef]
- Nguyen, L.D.; Kneppers, J.; García de Soto, B.; Ibbs, W. Analysis of adverse weather for excusable delays. J. Constr. Eng. Manag. 2010, 136, 1258–1267. [Google Scholar] [CrossRef]
- Mohamed, E.; Jafari, P.; Chehouri, A.; AbouRizk, S. Simulation-based approach for lookahead scheduling of onshore wind projects subject to weather risk. Sustainability 2021, 13, 10060. [Google Scholar] [CrossRef]
- Marović, I.; Sušanj, I.; Ožanić, N. Development of ANN model for wind speed prediction as a support for early warning system. Complexity 2017, 2017, 3418145. [Google Scholar] [CrossRef]
- Apipattanavis, S.; Sabol, K.; Molenaar, K.R.; Rajagopalan, B.; Xi, Y.; Blackard, B.; Patil, S. Integrated framework for quantifying and predicting weather-related highway construction delays. J. Constr. Eng. Manag. 2010, 136, 1160–1168. [Google Scholar] [CrossRef]
- Shahin, A.; AbouRizk, S.M.; Mohamed, Y.; Fernando, S. Simulation modeling of weather-sensitive tunnelling construction activities subject to cold weather. Can. J. Civ. Eng. 2014, 41, 48–55. [Google Scholar] [CrossRef]
- Radujković, M.; Burcar Dunović, I.; Dolaček Alduk, Z.; Nahod, M.; Vukomanović, M. Organizacija Građenja; Udžbenici Sveučilišta u Zagrebu: Zagreb, Hrvatska, 2015. [Google Scholar]
- Sane, S.S. Combinatorial Techniques; Springer: Berlin/Heidelberg, Germany, 2013; Volume 65. [Google Scholar]
- Wilson, R.; Watkins, J.J. (Eds.) Combinatorics: Ancient & Modern; OUP Oxford: Oxford, UK, 2013. [Google Scholar]
- Mazur, D.R. Combinatorics: A Guided Tour; American Mathematical Society: Providence, RI, USA, 2020; Volume 55. [Google Scholar]
- Flajolet, P.; Sedgewick, R. Analytic Combinatorics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Andreescu, T.; Feng, Z. A Path to Combinatorics for Undergraduates: Counting Strategies; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ferland, K. Discrete Mathematics and Applications; Chapman and Hall/CRC: London, UK, 2017. [Google Scholar]
- Soberón, P. Problem-Solving Methods in Combinatorics; Birkhäuser/Springer Basel AG: Basel, Switzerland, 2013. [Google Scholar]
- Lipschutz, S.; Lipson, M. Probability. Schaum’s Outlines, 2nd ed.; McGraw-Hill: New York, NY, USA, 2000. [Google Scholar]
- Schmuller, J. Statistical Analysis with R for Dummies; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2017. [Google Scholar]
- Boyd, R. Introductory Statistics, 4th ed.; Creative Commons: San Francisco, CA, USA, 2021. [Google Scholar]
- Donnelly, R.A. The Complete Idiot’s Guide to Statistics, 2nd ed.; Penguin Group Inc.: New York, NY, USA, 2007. [Google Scholar]
- Lind, D.A.; Marchal, W.G.; Wathen, S.A. Basic Statistics for Business & Economics; McGraw-Hill Companies Inc.: New York, NY, USA, 2006. [Google Scholar]
- Pagano, R.R. Understanding Statistics in the Behavioral Sciences, 10th ed.; Cengage Learning: Wadsworth, OH, USA; Belmont, CA, USA, 2013. [Google Scholar]
- Wackerly, D.D.; Mendenhall, W.; Scheaffer, R.L. Mathematical Statistics with Applications, 7th ed.; Thomson Higher Education: Belmont, CA, USA, 2008. [Google Scholar]
- Siegel, A.F.; Wagner, M.R. Practical Business Statistics, 6th ed.; Elsevier Inc.: Oxford, UK, 2012. [Google Scholar]
- Levine, D.M.; Stephan, D.F. Even You Can Learn Statistics: A Guide for Everyone Who Has Ever Been Afraid of Statistics, 2nd ed.; Pearson Education Inc.: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Rohatgi, V.K.; Saleh, A.M.E. An Introduction to Probability and Statistics, 2nd ed.; John Wiley & Sons Inc.: Montreal, QC, Canada, 2001. [Google Scholar]
- Lee, C.F.; Lee, J.; Chang, J.R.; Tai, T. Essentials of Excel, Excel VBA, SAS and Minitab for Statistical and Financial Analyses; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Jackson, S.L. Research Methods and Statistics: A Critical Thinking Approach, 3rd ed.; Cengage Learning: Wadsworth, OH, USA; Belmont, CA, USA, 2009. [Google Scholar]
- Schmuller, J. Statistical Analysis with Excel for Dummies, 3rd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).