Effect of Crease-Weakening Schemes on the Structural Performance of Lightweight Foldable Columns Based on the Pillow Box Pattern
Abstract
1. Introduction
1.1. Origami-Inspired Architectural Structures
1.2. Crease-Weakening Schemes
1.3. Research Contribution
2. Materials and Methods
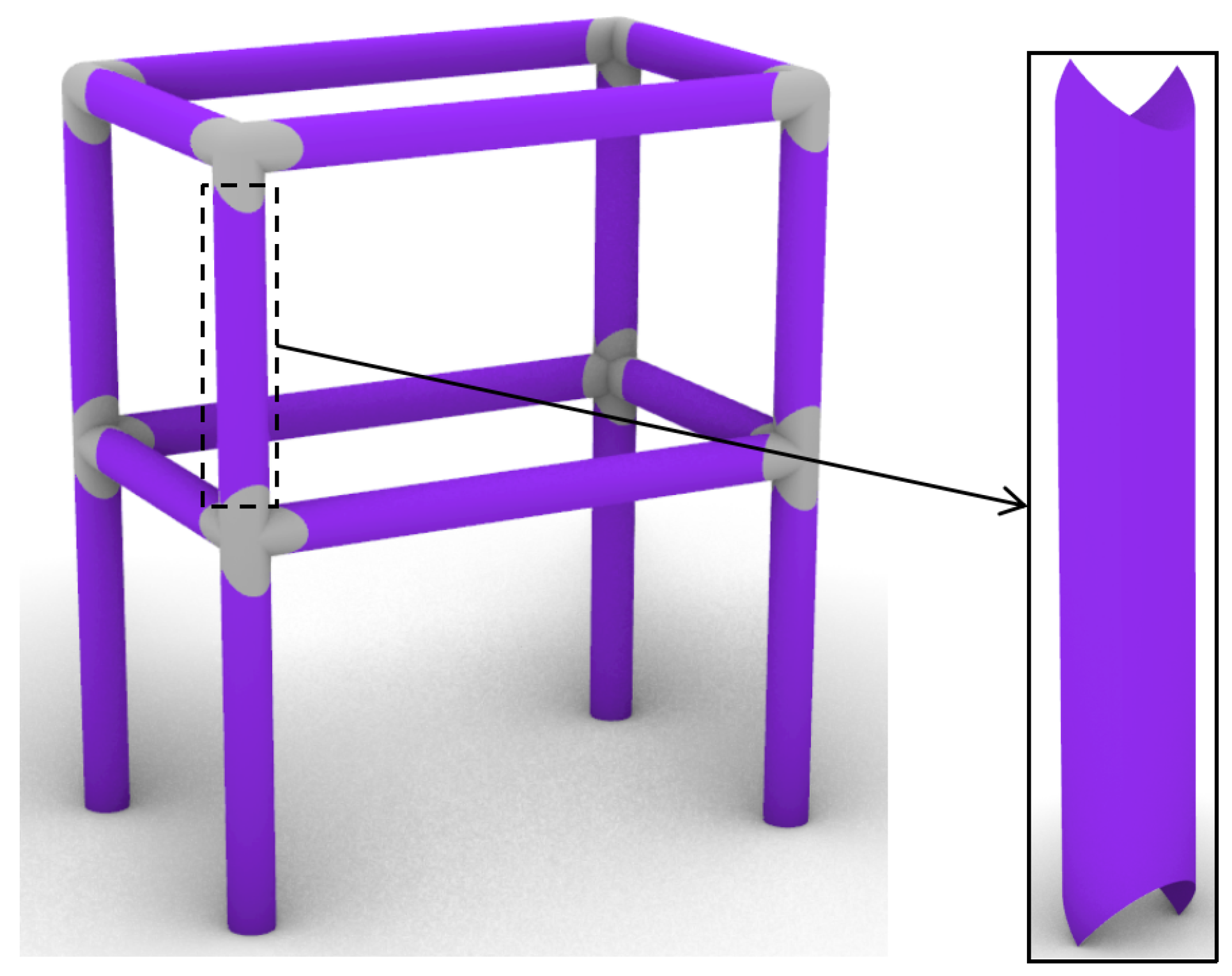
2.1. Structural Concept and Geometric Design
2.1.1. Modular Unit Configuration
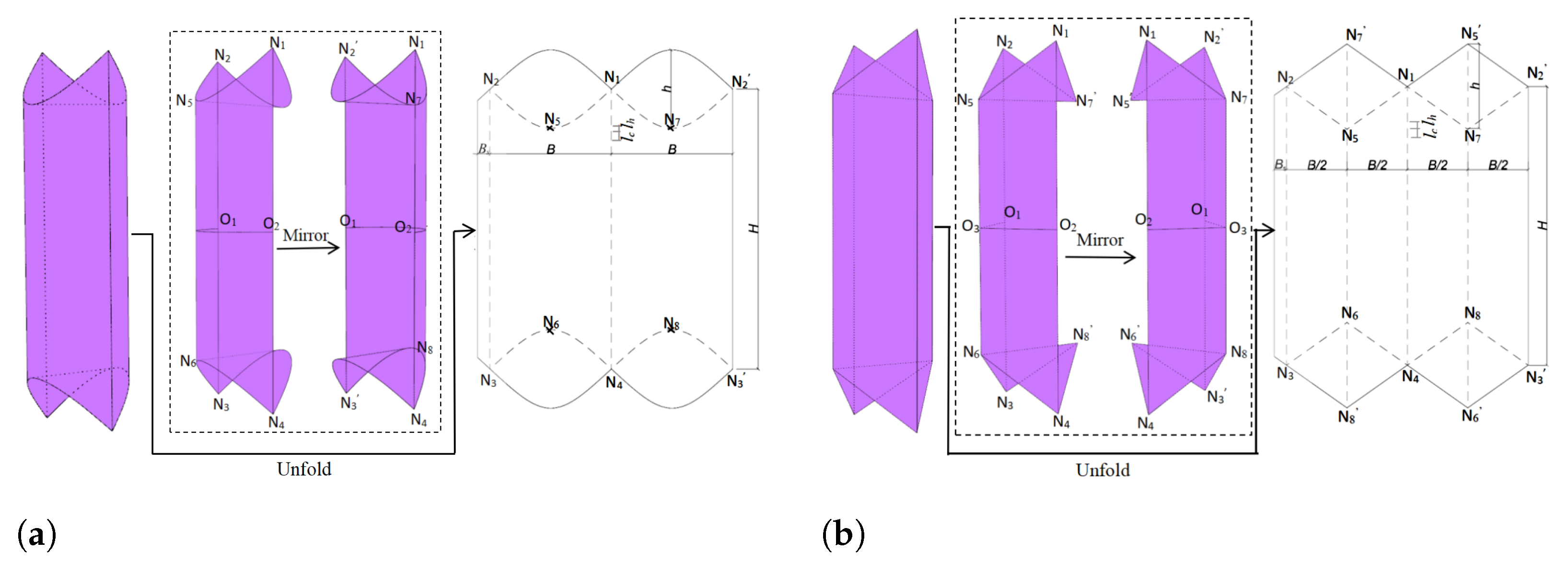
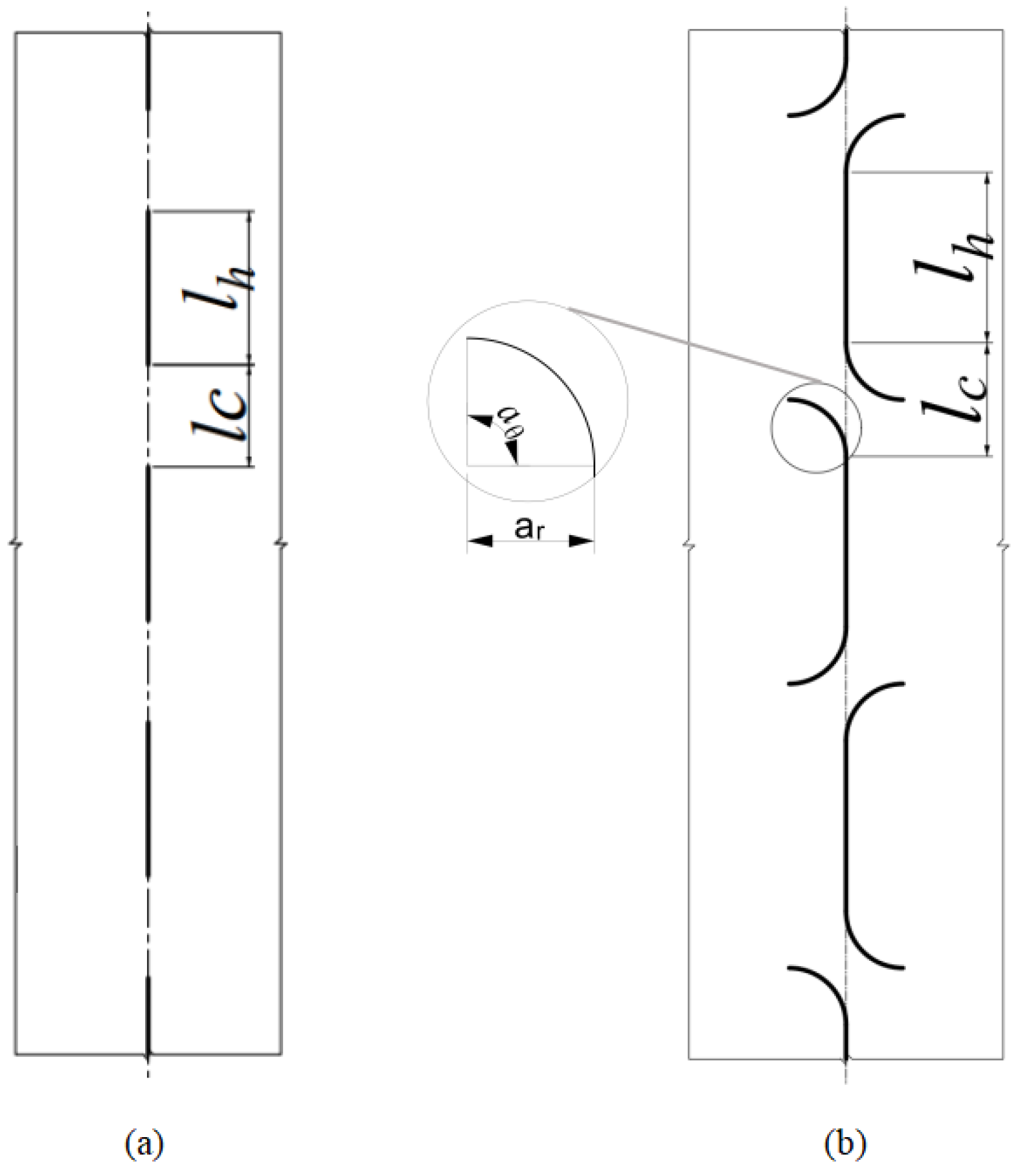
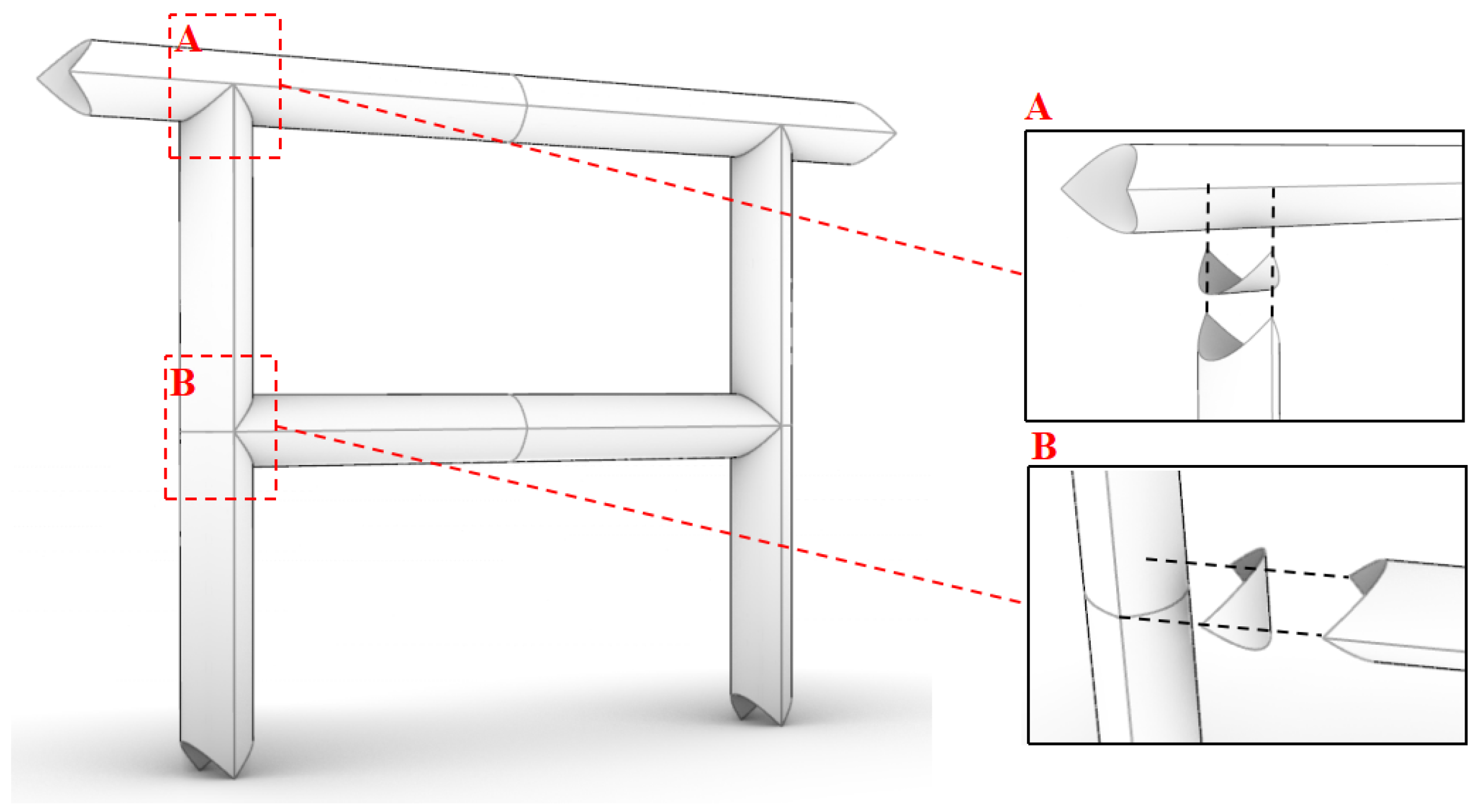
2.1.2. Crease Design
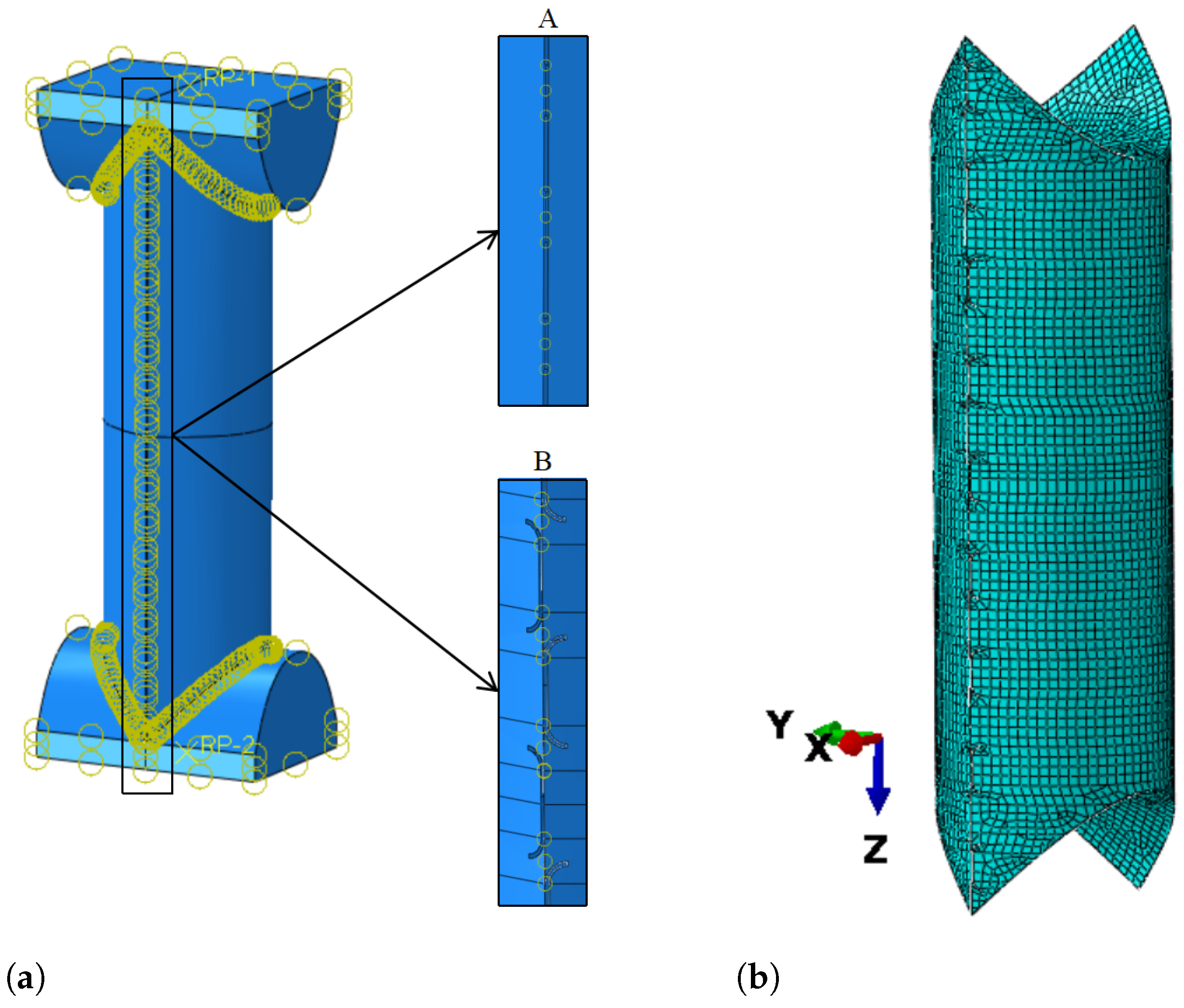
2.2. Validation of Crease Fabrication and Simulation
2.2.1. Experiment
2.2.2. Numerical Model
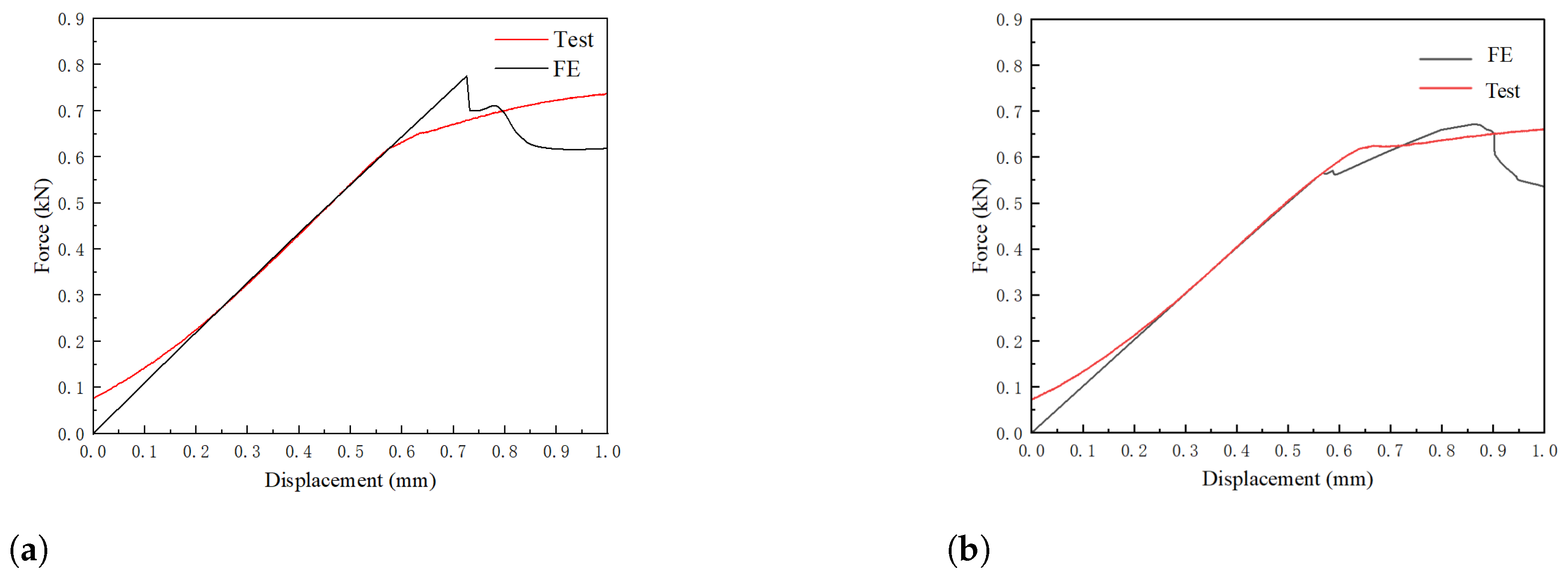
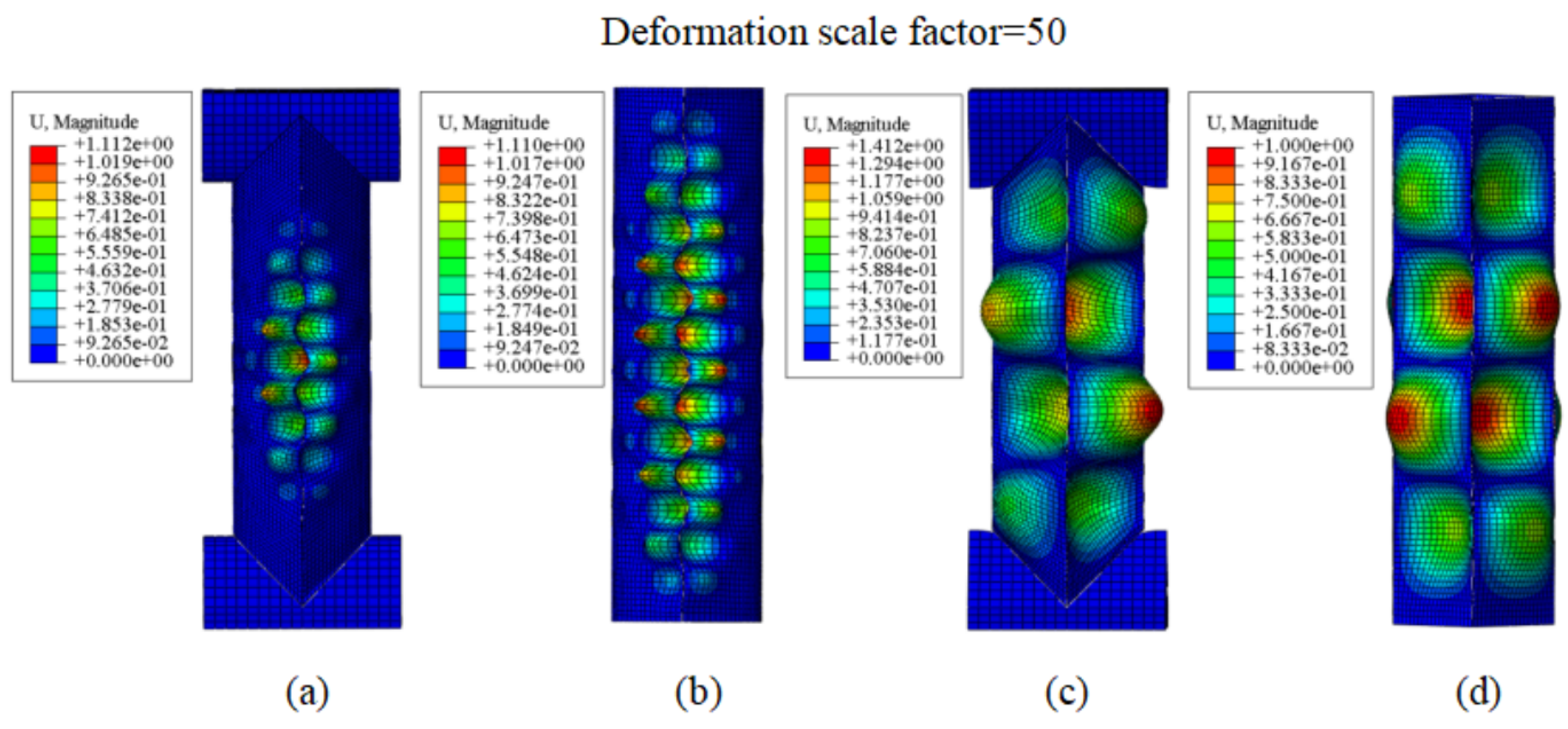
2.2.3. Results
3. Numerical Analysis
3.1. Numerical Model
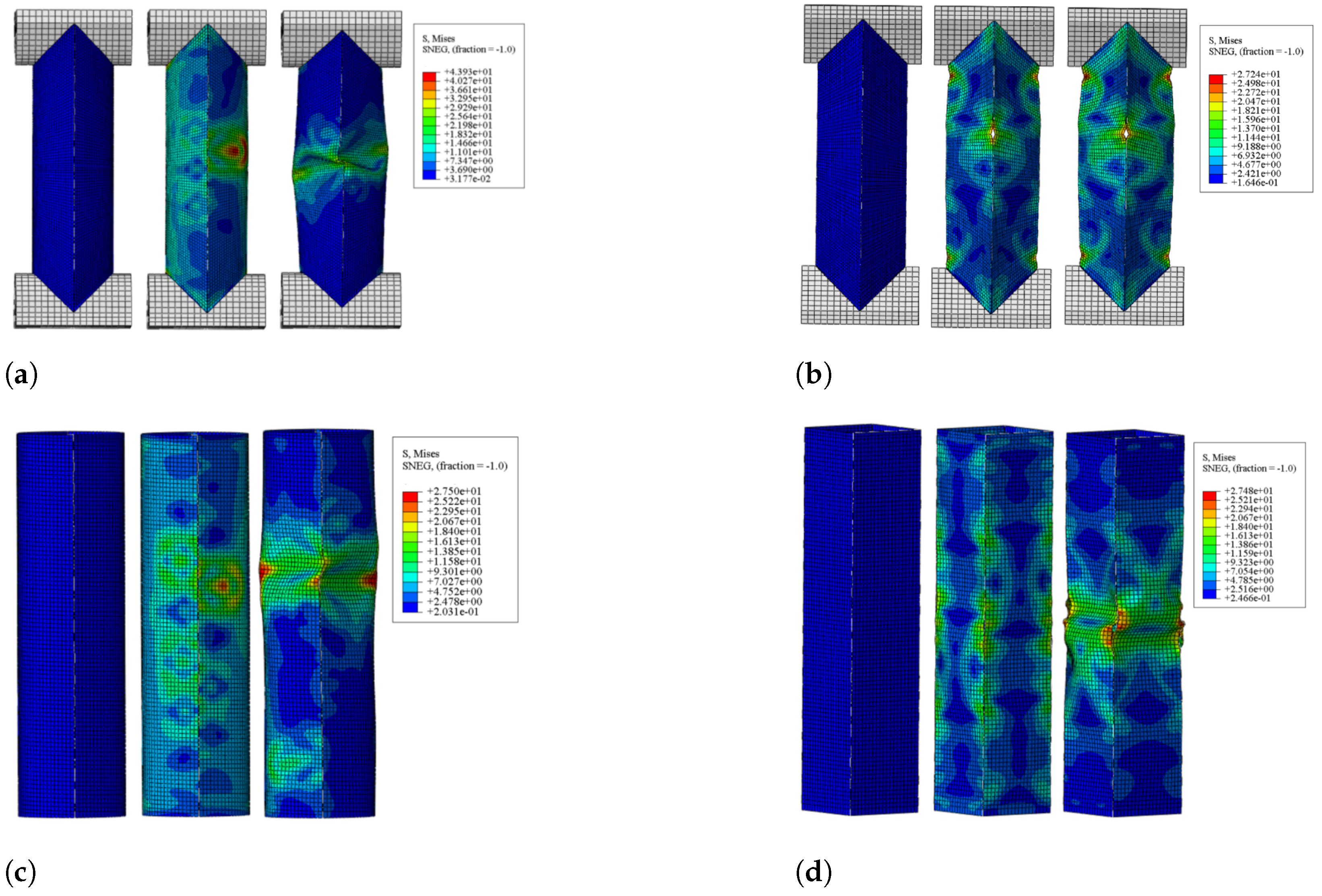
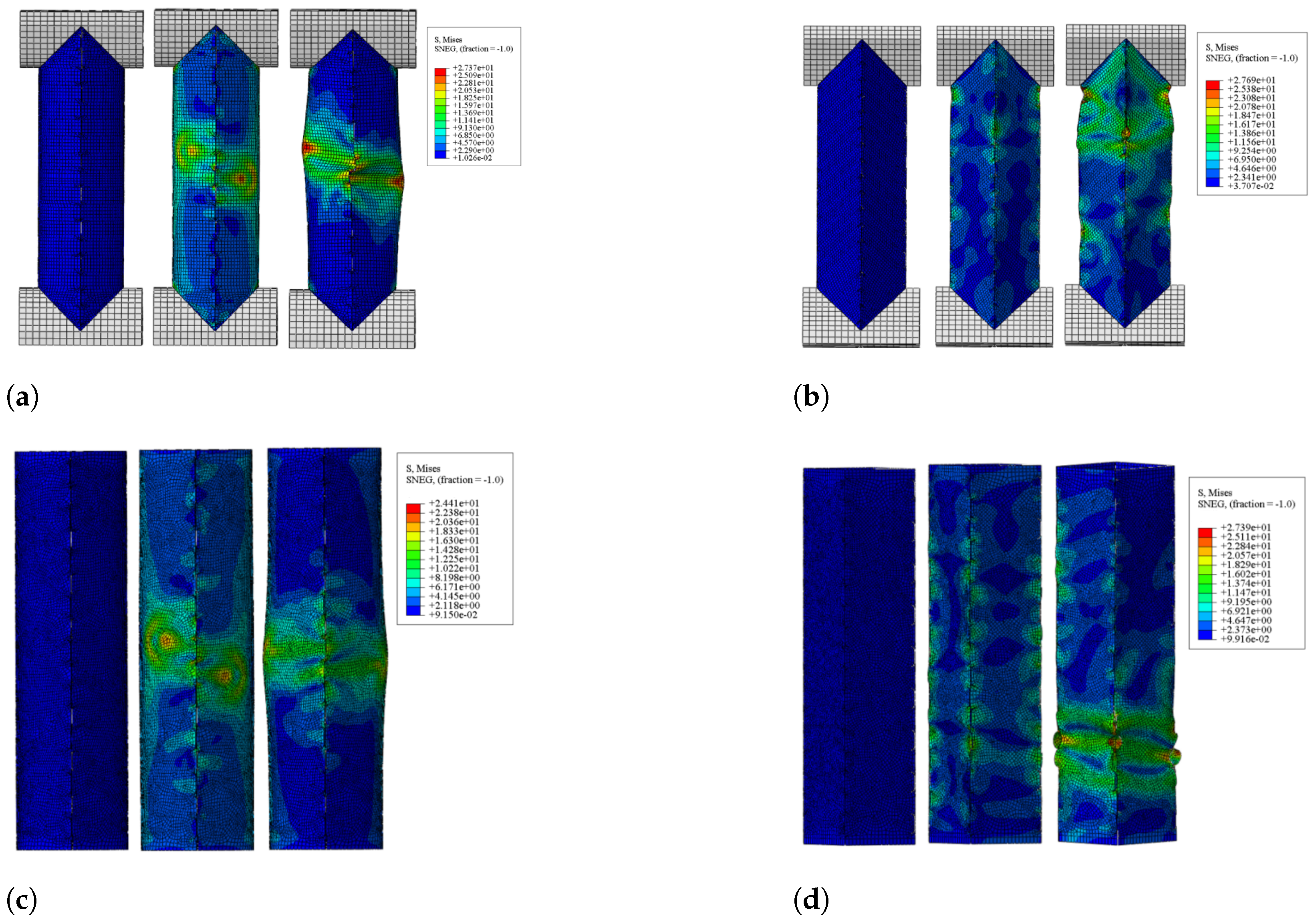
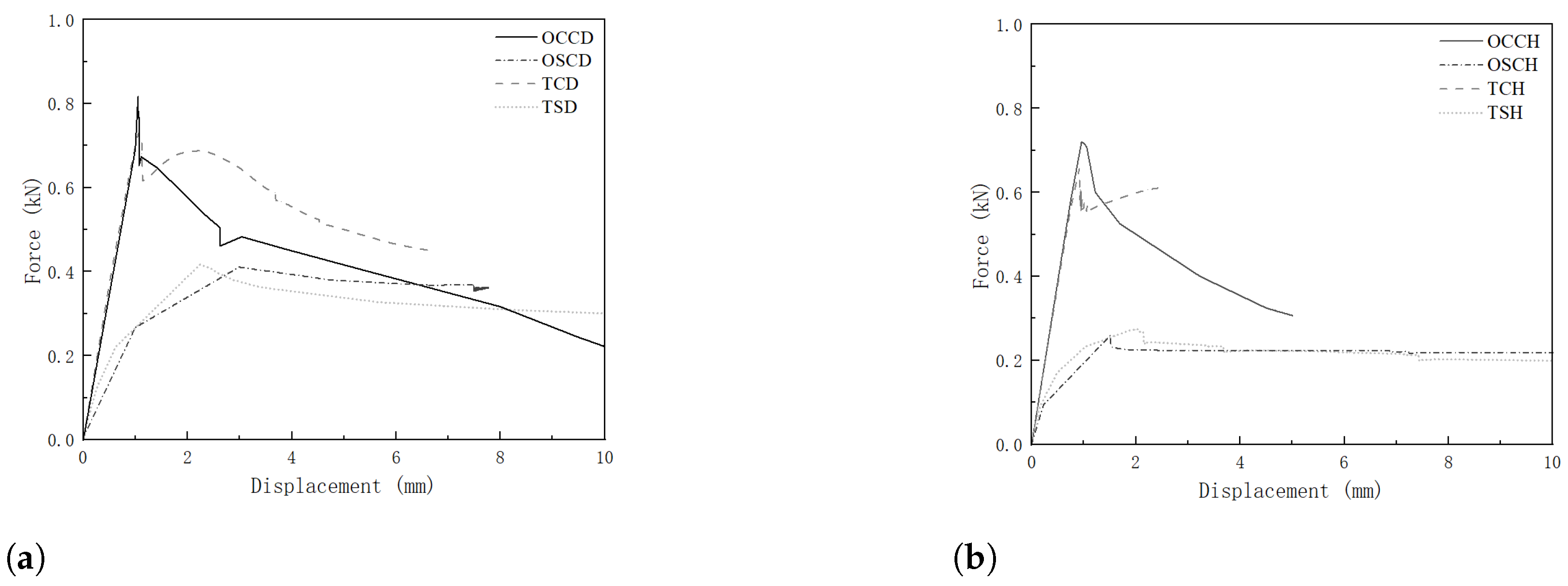
3.2. Numerical Results
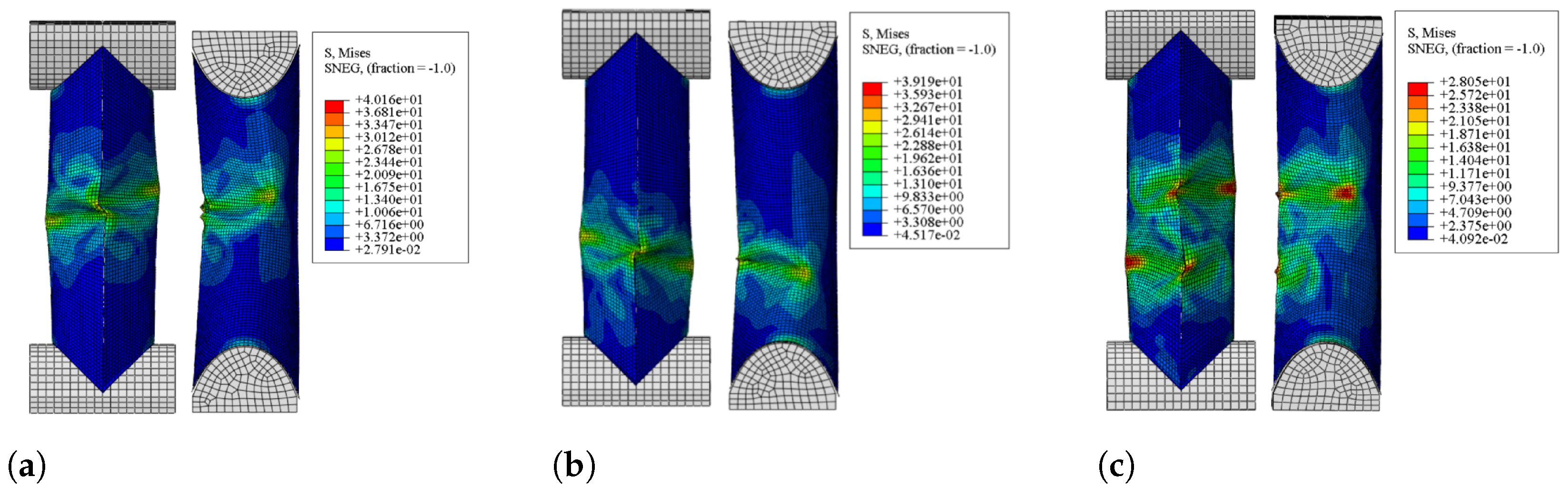
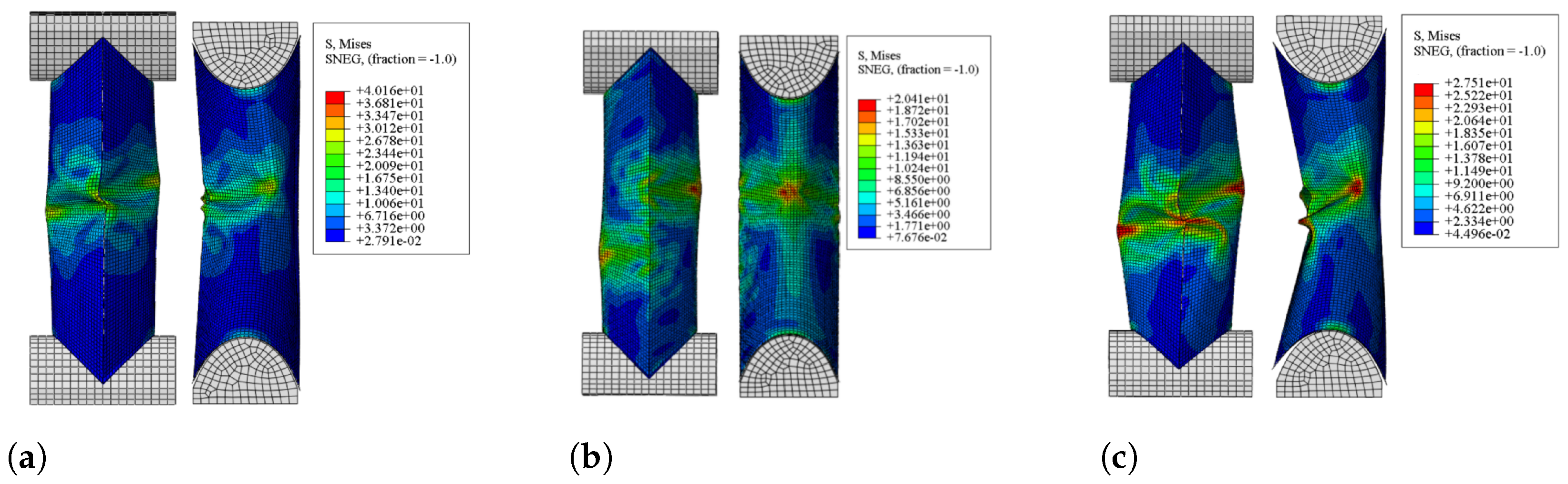
4. Influence of Design Parameters on Mechanical Response
4.1. Porosity
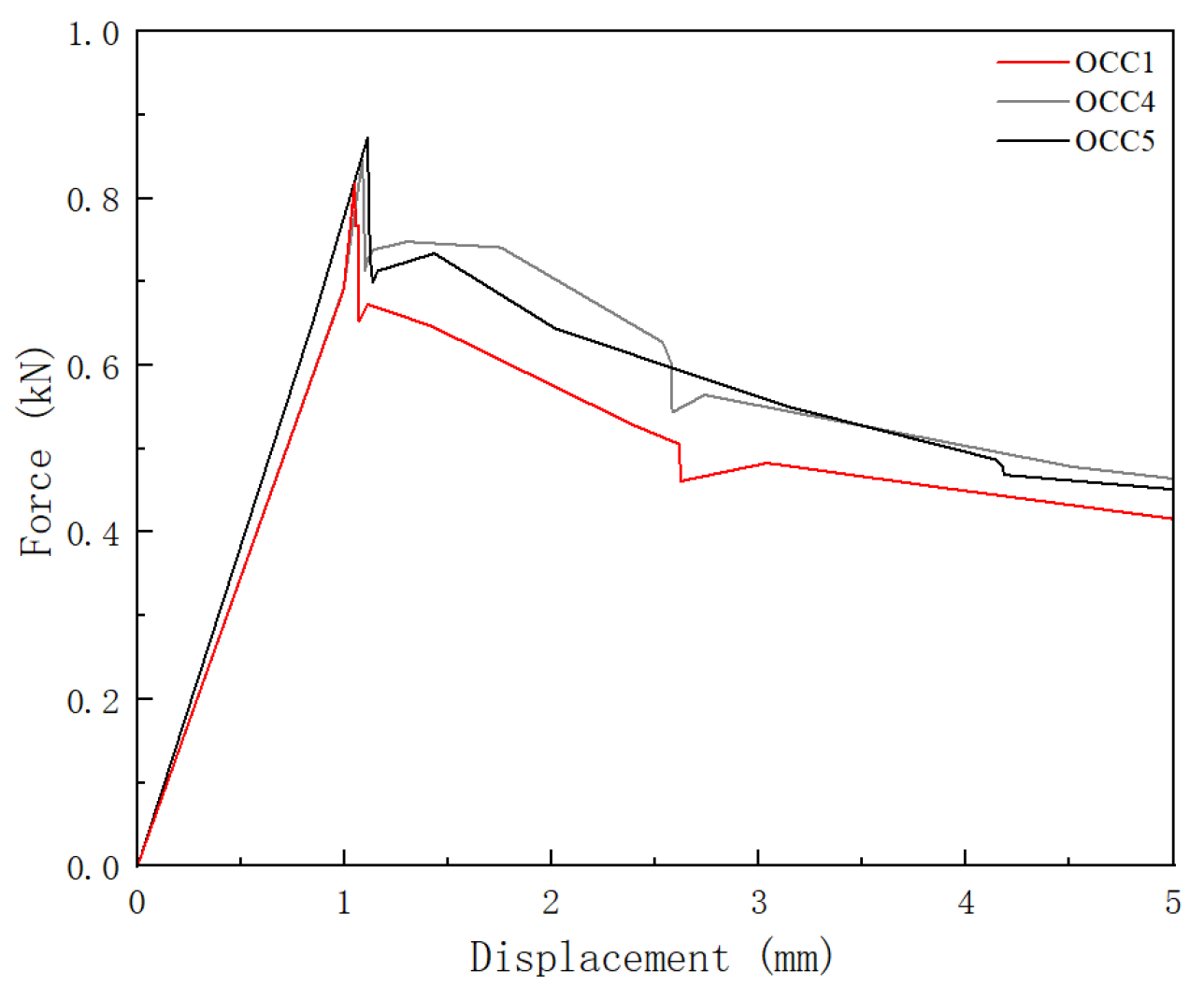
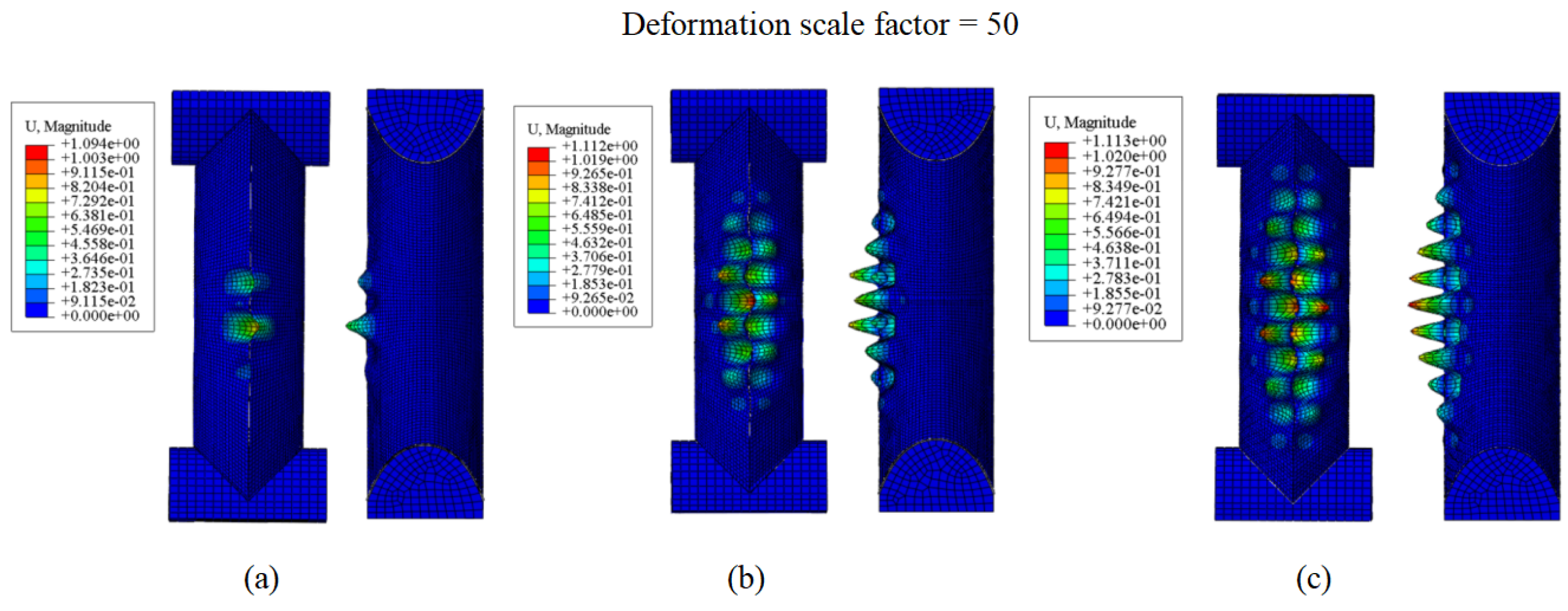
4.2. Number of Crease Units n
5. Discussion
5.1. Parameter Analysis
5.2. Comparison of Pillow Box Column and Tubular Column
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Huang, Z.; Chen, Z.; Zhu, L.; Ye, L.; Liu, Q. Implementation of parametric modeling to design Miura origami-inspired canopy toward adaptive urban habitat. Archit. Struct. Constr. 2024, 4, 113–122. [Google Scholar] [CrossRef]
- Melançon, D.; Bertoldi, K.; Garcia-Mora, C.J.; Hoberman, C.; Gorissen, B. Multistable inflatable origami structures at the metre scale. Nature 2021, 592, 545–550. [Google Scholar] [CrossRef] [PubMed]
- Tachi, T. Rigid-Foldable Thick Origami. J. Mech. Des. 2010, 132, 011005. [Google Scholar] [CrossRef]
- Ando, K.; Izumi, B.; Shigematsu, M.; Tamai, H.; Matsuo, J.; Mizuta, Y.; Miyata, T.; Sadanobu, J.; Suto, K.; Tachi, T. Lightweight rigidly foldable canopy using composite materials. SN Appl. Sci. 2020, 2, 1994. [Google Scholar] [CrossRef]
- Norman, M.; Arjomandi, K. Origami Applications in Structural Engineering: A Look at Temporary Shelters. In Proceedings of the 2nd World Congress on Civil, Structural, and Environmental Engineering (CSEE’17), Barcelona, Spain, 2–4 April 2017; Volume 130, pp. 2371–2452. [Google Scholar]
- Acevedo, S. Paper Architecture Inspired in Origami and Emergency Temporary Architecture: Challenges and Potentials in This Implementation. In Proceedings of the 3rd Annual International Conference on Architecture and Civil Engineering (ACE 2015), Singapore, 13–14 April 2015; pp. 1–5. [Google Scholar]
- Durney, M.W.; Pendley, A.D. Precision-Folded, High Strength, Fatigue-Resistant Structures and Sheet Therefor. U.S. Patent US8377566B2, 19 February 2013. [Google Scholar]
- Marasciuolo, N.; Tommasi, D.D.; Trentadue, F.; Vitucci, G. Tailored multiscale instabilities in a grid metamaterial. Extrem. Mech. Lett. 2025, 75, 102284. [Google Scholar] [CrossRef]
- Ghandi, M. Designing Affordable, Portable, and Flexible Shelter for the Homeless and the Refugees. In Proceedings of ECAADe 2018: Computing for a Better Tomorrow; eCAADe and Faculty of Civil Engineering, Architecture and Environmental Engineering, Lodz University of Technology: Łódź, Poland, 2018; Volume 1. [Google Scholar]
- Tumbeva, M.; Wang, Y.; Sowar, M.; Dascanio, A.; Thrall, A. Quilt pattern inspired engineering: Efficient manufacturing of shelter topologies. Autom. Constr. 2016, 63, 57–65. [Google Scholar] [CrossRef]
- Thrall, A.; Quaglia, C. Accordion shelters: A historical review of origami-like deployable shelters developed by the US military. Eng. Struct. 2014, 59, 686–692. [Google Scholar] [CrossRef]
- Martínez-Martín, F.; Thrall, A. Honeycomb core sandwich panels for origami-inspired deployable shelters: Multi-objective optimization for minimum weight and maximum energy efficiency. Eng. Struct. 2014, 69, 158–167. [Google Scholar] [CrossRef]
- Lee, T.; Gattas, J. Geometric design and construction of structurally stabilized accordion shelters. J. Mech. Robot. 2016, 8, 031009. [Google Scholar] [CrossRef]
- Tepavčević, B.; Stojaković, V.; Mitov, D. Mass Customization of Deployable Origami-based Structures. In Blucher Design Proceedings; Editora Blucher: Porto, Portugal, 2019; pp. 163–170. [Google Scholar] [CrossRef]
- Micheletti, A.; Giannetti, I.; Mattei, G.; Alessandro, T. Kinematic and static design of rigid origami structures: Application to modular yoshimura patterns. J. Archit. Eng. 2022, 28, 04022009. [Google Scholar] [CrossRef]
- Koschitz, D. Curved-Crease Paperfolding Shell. In Proceedings of the IASS Annual Symposium: Origami Folded Systems, Barcelona, Spain, 7–10 October 2019; pp. 1–8. [Google Scholar]
- Martín-Pastor, A.; García-Alvarado, R. Developable Wooden Surfaces for Lightweight Architecture: Bio-Dune Pavilion. In Digital Wood Design: Innovative Technologies Representing Architectural Design; Bianconi, F., Filippucci, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 1481–1500. [Google Scholar]
- Fayyad, I. Mapping Rectangles to Cylinders: Waste-Conscious Constructions of Curved Structural Surfaces. Technol. Archit. Des. 2023, 7, 53–66. [Google Scholar] [CrossRef]
- Zhu, Y.; Filipov, E.T. Large-scale modular and uniformly thick origami-inspired adaptable and load-carrying structures. Nat. Commun. 2024, 15, 2353. [Google Scholar] [CrossRef]
- Nagy, L.; Rhode-Barbarigos, L.; Adriaenssens, S.; Kilian, A. Conceptual design of a single-crease origami-arc inspired movable footbridge structure. Int. J. Space Struct. 2015, 30, 75–84. [Google Scholar] [CrossRef]
- Maleczek, R.; Bernhard, M.; Maderebner, R.; Preisinger, C. Fold and Snap–Flatpacking a Wooden Beam. In Proceedings of the IASS 2024 Symposium: Redefining the Art of Structural Design, Zurich, Switzerland, 26–30 August 2024. [Google Scholar]
- Woodruff, S.R.; You, Z.; Gattas, J.M. Curved creases redistribute global bending stiffness in corrugations: Theory and experimentation. J. Mech. Mater. Struct. 2020, 15, 215–230. [Google Scholar] [CrossRef]
- Lee, M.; Abu-Saleem, M.; Tachi, T.; Gattas, J.M. A Lightweight Building Construction System Using Curved-Crease Origami Blocks. In Proceedings of the International Meeting on Origami in Science, Mathematics and Education (OSME), Melbourne, Australia, 16–18 July 2024. [Google Scholar]
- Brancart, S.; Vergauwen, A.; Roovers, K.; den Bremt, D.V.; Laet, L.D.; Temmerman, N.D. Undulatus: Design and Fabrication of a Self-Interlocking Modular Shell Structure Based on Curved-Line Folding. In Proceedings of the IASS Annual Symposia, Amsterdam, The Netherlands, 17–20 August 2015; pp. 1–12. [Google Scholar]
- Filz, G.H.; Kumrić, I. Z-snap Pavilion: Advanced Fabrication and Assembly of Self-Locking, Bending Active Modules into a Semi-Double-Layer, shell-like structure. In Proceedings of the IASS Annual Symposia, Hamburg, Germany, 25–28 September 2017; pp. 1–8. [Google Scholar]
- Körner, A.; Eshraghi, V.; Zolfaghari, A.; Haghighi, L.A.; Kalantari, M.; Knippers, J. Arch(k)inetic–Curved-Line Folding for Elastic, Adaptive Building Envelopes. In Proceedings of the IASS Annual Symposia, Boston, MA, USA, 16–20 July 2018; pp. 1–8. [Google Scholar]
- Bukauskas, A.; Koronaki, A.; Lee, T.-U.; Ott, D.; Al Asali, M.W.; Jalia, A.; Bashford, T.; Gatóo, A.; Newman, J.; Gattas, J.M.; et al. Curved-crease origami face shields for infection control. PLoS ONE 2021, 16, e0245737. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Liu, X.; Qiu, X.; Zhou, Y.; Liu, Y.; Fu, W.; Guo, X.; Qian, Z.; Du, K.; Cai, J. Comparative folding/unfolding performance of notch-type compliant joints. Case Stud. Constr. Mater. 2023, 18, e01760. [Google Scholar] [CrossRef]
- Raducanu, D.; Cojocaru, V.D.; Raducanu, V.A.; Nocivin, A.; Serban, N.; Cinca, I.; Cojocaru, E.M.; Moldovan, L.; Trisca-Rusu, C.; Balkan, I.V. Design and Optimization of a Curved-Crease-Folding Process Applied to a Light Metallic Structure. Processes 2021, 9, 1110. [Google Scholar] [CrossRef]
- Ma, J. Thin-Walled Tubes with Pre-Folded Origami Patterns as Energy Absorption Devices. Ph.D. Thesis, University of Oxford, Oxford, UK, 2011. [Google Scholar]
- Song, J.; Chen, Y.; Lu, G. Axial crushing of thin-walled structures with origami patterns. Thin-Walled Struct. 2012, 54, 65–71. [Google Scholar] [CrossRef]
- Zhang, B.; Men, C.; Kong, Y.; Lv, Z.; Li, C.; Hu, D. Quasi-Static Compression Response and Energy Absorption of CNTF/EP Origami Thin-Walled Tubes. Adv. Mater. Interfaces 2025, 12, 2400826. [Google Scholar] [CrossRef]
- Shi, Q.; Shi, X.; Gattas, J.M.; Kitipornchai, S. Folded assembly methods for thin-walled steel structures. Thin-Walled Struct. 2021, 160, 107372. [Google Scholar] [CrossRef]
- Ablat, M.A.; Alafaghani, A.; Sun, J.Q.; Qattawi, A. Experimental Evaluation of Tension and Shear Responses of Material Discontinuities in Origami-Based Sheet Metal Bending. J. Manuf. Sci. Eng. 2018, 140, 071016. [Google Scholar] [CrossRef]
- Ablat, M.A.; Qattawi, A. Finite Element Analysis of Origami-Based Sheet Metal Folding Process. J. Eng. Mater. Technol. 2018, 140, 031008. [Google Scholar] [CrossRef]
- Jeong, D.; Lee, K. Design and analysis of an origami-based three-finger manipulator. Robotica 2018, 36, 261–274. [Google Scholar] [CrossRef]
- Bai, Y.; Nardi, D.C.; Zhou, X.; Picón, R.A.; Flórez-López, J. A new comprehensive model of damage for flexural subassemblies prone to fatigue. Comput. Struct. 2021, 256, 106639. [Google Scholar] [CrossRef]
- Wagner, M.A.; Huang, J.-L.; Okle, P.; Paik, J.; Spolenak, R. Hinges for origami-inspired structures by multimaterial additive manufacturing. Mater. Des. 2020, 191, 108643. [Google Scholar] [CrossRef]
- Moshtaghzadeh, M. Prediction of fatigue life of a flexible foldable origami antenna with Kresling pattern. Eng. Struct. 2022, 251, 113399. [Google Scholar] [CrossRef]
- Moshtaghzadeh, M.; Bakhtiari, A.; Izadpanahi, E.; Mardanpour, P. Artificial Neural Network for the prediction of fatigue life of a flexible foldable origami antenna with Kresling pattern. Thin-Walled Struct. 2022, 174, 109160. [Google Scholar] [CrossRef]
- Ablat, M.A.; Qattawi, A. Investigating the design and process parameters of folded perforated sheet metal. Int. J. Adv. Manuf. Technol. 2019, 102, 615–633. [Google Scholar] [CrossRef]
- Shi, Q.; Heitzmann, M.T.; Gattas, J.M. Nonlinear rotational stiffness and clash prevention in perforated steel fold lines. Eng. Struct. 2020, 209, 110218. [Google Scholar] [CrossRef]
- Nasrollahi, V.; Arezoo, B. Prediction of springback in sheet metal components with holes on the bending area, using experiments, finite element and neural networks. Mater. Des. 2011, 32, 695–705. [Google Scholar] [CrossRef]
- Nikhare, C.P.; Kotkunde, N.; Singh, S.K. Effect of material discontinuity on springback in sheet metal bending. J. Mater. Eng. Perform. 2013, 22, 3445–3452. [Google Scholar] [CrossRef]
- Hwang, H.-Y. Effects of perforated crease line design on mechanical behaviors of origami structures. Int. J. Solids Struct. 2021, 230–231, 111158. [Google Scholar] [CrossRef]
- Chen, Y.; Shi, P.; Bai, Y.; Li, J.; Feng, J.; Sareh, P. Engineered origami crease perforations for optimal mechanical performance and fatigue life. Thin-Walled Struct. 2024, 185, 110572. [Google Scholar] [CrossRef]
- Mitani, J. Pillow Box Design. arXiv 2024, arXiv:2410.17593. [Google Scholar] [CrossRef]
- Lee, T.U.; You, Z.; Gattas, J.M. Elastica Surface Generation of Curved-Crease Origami. Int. J. Solids Struct. 2018, 136–137, 13–27. [Google Scholar] [CrossRef]
- Howe, D.V.; Dimeska, A. Polypropylene, Isotactic. In Polymer Data Handbook; Mark, J.E., Ed.; Oxford University Press: Oxford, UK, 2009; pp. 971–978. [Google Scholar]
- Weerasekara, L.; Mallikarachchi, C. Effect of Crease Curvature on Bending Stiffness in Curved Crease Origami. In Proceedings of the 2024 Moratuwa Engineering Research Conference (MERCon), Moratuwa, Sri Lanka, 8–10 August 2024; IEEE: New York, NY, USA, 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, Y.; Zhou, Y.; Kim, S.; Feng, J.; Cai, J. Numerical analysis on buckling-control of slender tube inspired by origami. Int. J. Non-Linear Mech. 2025, 171, 105025. [Google Scholar] [CrossRef]
- Ma, J.; You, Z. Energy absorption of thin-walled beams with a pre-folded origami pattern. Thin-Walled Struct. 2013, 73, 198–206. [Google Scholar] [CrossRef]








| Metric | PPC1T1D | PPC1T1H |
|---|---|---|
| Peak Force (kN) | ||
| Test | 0.76 | 0.66 |
| FEA | 0.77 | 0.67 |
| Difference (%) | 1.32 | 1.52 |
| Stiffness (kN/mm) | ||
| Test | 1.04 | 0.98 |
| FEA | 1.07 | 1.00 |
| Difference (%) | 2.88 | 2.04 |
| Specimen | h/mm | /mm | (°) |
|---|---|---|---|
| OCC-D | 126 | \ | \ |
| OSC-D | 138 | \ | \ |
| TCC-D | 126 | \ | \ |
| TSC-D | 138 | \ | \ |
| OCC-H | 126 | 5 | 90 |
| OSC-H | 138 | 5 | 90 |
| TCC-H | 126 | 5 | 90 |
| TSC-H | 138 | 5 | 90 |
| Sample | Peak Force (kN) | Stiffness (kN/mm) |
|---|---|---|
| OCC-D | 0.817 | 0.74 |
| OCC-H | 0.720 | 0.76 |
| Sample | (mm) | (mm) | n | ||
|---|---|---|---|---|---|
| OCC1 (OCC-D) | 0.6 | 10 | 15 | 1.50 | 18 |
| OCC2 | 0.6 | 6 | 9 | 1.50 | 30 |
| OCC3 | 0.6 | 20 | 30 | 1.50 | 9 |
| OCC4 | 0.4 | 15 | 10 | 0.67 | 18 |
| OCC5 | 0.5 | 12.5 | 12.5 | 1.00 | 18 |
| Sample | Peak Load (kN) | Stiffness (kN/mm) | |
|---|---|---|---|
| OCC1 | 0.6 | 0.82 | 0.74 |
| OCC4 | 0.4 | 0.85 | 0.74 |
| OCC5 | 0.5 | 0.87 | 0.78 |
| Sample | n | Peak Load (kN) | Stiffness (kN/mm) |
|---|---|---|---|
| OCC1 | 18 | 0.82 | 0.74 |
| OCC2 | 36 | 0.90 | 0.69 |
| OCC3 | 9 | 0.75 | 0.78 |
| Sample | OCC3 | OCC1 | OCC2 |
|---|---|---|---|
| Eigenvalue | 779.0 | 1086.3 | 1175.8 |
| Sample | Peak Force (kN) | Stiffness (kN/mm) |
|---|---|---|
| OCC-D | 0.817 | 0.74 |
| TCC-D | 0.728 | 0.64 |
| OSC-D | 0.411 | 0.27 |
| TSC-D | 0.417 | 0.34 |
| OCC-H | 0.720 | 0.76 |
| TCC-H | 0.656 | 0.73 |
| OSC-H | 0.260 | 0.41 |
| TSC-H | 0.274 | 0.35 |
| Sample | OCC-D | TCC-D | OSC-D | TSC-D | OCC-H | TCC-H | OSC-H | TSC-H |
|---|---|---|---|---|---|---|---|---|
| Eigenvalue | 1086.3 | 1044.5 | 93.8 | 92.4 | 810.4 | 760.2 | 57.7 | 86.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Gattas, J.M.; Feng, J. Effect of Crease-Weakening Schemes on the Structural Performance of Lightweight Foldable Columns Based on the Pillow Box Pattern. Appl. Sci. 2025, 15, 10756. https://doi.org/10.3390/app151910756
Zhang Q, Gattas JM, Feng J. Effect of Crease-Weakening Schemes on the Structural Performance of Lightweight Foldable Columns Based on the Pillow Box Pattern. Applied Sciences. 2025; 15(19):10756. https://doi.org/10.3390/app151910756
Chicago/Turabian StyleZhang, Qingyun, Joseph M. Gattas, and Jian Feng. 2025. "Effect of Crease-Weakening Schemes on the Structural Performance of Lightweight Foldable Columns Based on the Pillow Box Pattern" Applied Sciences 15, no. 19: 10756. https://doi.org/10.3390/app151910756
APA StyleZhang, Q., Gattas, J. M., & Feng, J. (2025). Effect of Crease-Weakening Schemes on the Structural Performance of Lightweight Foldable Columns Based on the Pillow Box Pattern. Applied Sciences, 15(19), 10756. https://doi.org/10.3390/app151910756






