Abstract
This study compared two physiological modeling approaches, the Peronnet-Thibault (P-T) model and the Minimal Power (MP) model, to identify key parameters representing individual physiological characteristics and to explore their applications in running training. Model parameters were estimated using nonlinear least squares fitting, and predictive performance was evaluated by the mean absolute error (MAE). Results from the World Running Records (WRR) indicated that the MP model generally outperformed the P-T model in linking running performance with physiological variables, demonstrating greater capability in extracting physiological parameters. Further validation using the British Runner Records (BRR) showed that the MP model achieved MAE values of 3.02% for males and 3.47% for females, reflecting strong generalization to real running performance. Furthermore, descriptive analyses of the relationships between MP model parameters and running performance further support its potential value in personalized training and performance prediction.
1. Introduction
With the accelerated pace of life and increased health awareness, running has become a common way to improve fitness and health due to its simplicity and efficiency. Technological advances and the popularity of wearable devices have gradually made running more specialized and data-driven, enabling the collection of physiological and performance-related data such as heart rate, , and cadence [1,2]. In recent years, running performance analysis based on physiological parameters has gradually become a hot research topic. By integrating the athlete’s physiological state, training data, researchers try to reveal the relationship between physiological parameters and running performance, to provide theoretical support for personalized training and optimization of runners’ performance [3,4].
Over the past century, researchers have proposed a variety of models to predict running performance. Kennelly demonstrated a relationship between time (T) and distance (d), with , based on competition data from animals and humans [5]. However, for distances between 100 m and 50 miles, the relative error can reach up to 9%. Hill [6] proposed the hyperbolic power model, which reveals the maximum power output that athletes can maintain under different durations and lays a theoretical foundation for the correlation between performance and metabolism, and Keller [7,8] introduced the optimal control theory to simulate the speed distribution during a race through the variational method. Ward-Smith [9], based on the first law of thermodynamics, developed an energy consumption model from the perspective of mechanical work and energy output. This model integrates aerobic and anaerobic energy supply mechanisms, incorporating processes such as energy conversion, storage, heat dissipation, and resistance overcoming, to explain energy utilization and speed changes in high-intensity competitions.
However, these models did not adequately capture the relationship between physiological parameters and athletic performance, prompting the development of new models. Daniels [10] proposed the VDOT model to quantify an athlete’s aerobic capacity and running economy, thereby enabling the prediction of race performance across different distances. However, it depends on precise values of maximal oxygen uptake (), which limits the model’s applicability. Peronnet and Thibault proposed a model that incorporates physiological parameters derived from the aerobic and anaerobic energy supply mechanisms, in order to link them with actual running performance and establish a balance between energy input and output [11]. Alvarez-Ramirez [12] introduced additional time scales into the P-T model to improve its predictive performance; however, this enhancement involves more parameters, which increases the model’s complexity and reduces its practicality. Emig et al. proposed a Minimum Power Consumption model to divide metabolic phases on a time scale, analyze the relationship between maximum average power, additional power demand and instantaneous power, and introduce an endurance index to improve performance prediction [13]. Subsequently, Emig and co-workers [14] validated the predictive accuracy of the model and further explored the evolution of world records and physiological parameters to refine the models of physiological mechanisms for running performance prediction. Physiological parameters (e.g., maximal oxygen uptake, aerobic endurance, etc.) employed in model construction can be used to develop personalized training programs aimed at optimizing athlete performance under varying physiological conditions.
In this study, we first systematically compare two physiologically based models, the Peronnet-Thibault (P-T) model and the Minimum Power Consumption (MP) model, to identify key parameters that are more representative of an individual’s physical performance characteristics. To evaluate the applicability of the MP model to real-world running, we fitted the model using the personal best records of British runners, and confirmed through prediction results its effectiveness in capturing individual physiological parameters under real conditions. In addition, the study also attempted to explore the association between the model parameters and actual running performance, and further analyzed the distribution characteristics of these parameters in the population and their representativeness. By revealing the variability of physiological abilities among individuals, it aims to provide a theoretical basis and data support for achieving personalized and scientific training.
2. Method
2.1. The Peronnet-Thibault Model
During running, the energy required by the body is supplied by two main systems: the aerobic system and the anaerobic system. The aerobic system supplies energy steadily through oxidative processes, while the anaerobic system releases energy rapidly through lactate metabolism and glycolysis during high-intensity exercise. Based on this physiological mechanism, the Peronnet-Thibault (P-T) Model calculates the power generated by the aerobic and anaerobic systems separately and integrates the two to obtain the total power output of the human body for different durations, which is used to simulate the energy expenditure and exercise performance during running. The average power in the model is obtained based on a combination of theoretical derivation and empirical observation, and is expressed as the sum of the average aerobic power () and the average anaerobic power (), as follows:
where denotes the total energy currently available for anaerobic metabolism, is the basal power, is the difference between peak and basal power (). Two constants are introduced to characterize the dynamics of the energy systems. () characterizes the time constant of aerobic metabolism, reflecting the time scale over which aerobic power gradually increases due to the lag between cardiopulmonary circulation and mitochondrial oxidative reactions [15,16], while () represents the time constant of anaerobic metabolism, describing the timescale over which anaerobic energy supply declines exponentially due to limited energy reserves and the accumulation of metabolic by-products [11].
The time () for which elite endurance athletes maintain maximum aerobic power () is finite, usually about 420 s [17,18,19]. For running races with durations equal to or less than that time, peak power () is approximately equal to , whereas for races with durations greater than that time, decreases linearly with as time increases [20] and the magnitude of this decrease is expressed as . This decline occurs because, as the contribution of anaerobic metabolism diminishes over time, the limited capacity of the aerobic system cannot fully compensate for the loss, resulting in a progressive reduction in the power output. Thus, the parameter can be expressed as
Peronnet and Thibault proposed that it can be assumed that the total anaerobic metabolic energy () can be used in its entirety for any race longer than 120 s to 150 s [11], but shorter than in duration. Beyond , the anaerobic metabolic energy () gradually decays as the duration of the run continues to increase, where [21]
On the other hand, the actual average output power () required to run at a given speed () can be calculated by the formula proposed by di Prampero [22]
where represents body surface area, represents body mass (set at 70 kg for males and 50 kg for females, with corresponding of 1.8 for males and 1.6 for females), and denotes running distance. Therefore, based on the energy balance between input and output and the relationship between speed, time, and distance, the P-T model can be concluded as
Consequently, based on these three parameters (, and ), a P-T model was constructed as shown in Equation (5). The ability of an athlete to use the anaerobic pathway to generate energy during a brief period of high-intensity activity is represented by total anaerobic energy (). The higher the value of parameter , the more explosive the athlete is in the anaerobic environment. The maximum amount of energy that an athlete can produce in an aerobic environment is referred to as maximum aerobic power (). The magnitude of directly affects an athlete’s endurance capacity during prolonged exercise. In the P-T model, the degree of aerobic endurance is represented by the magnitude of aerobic energy expenditure (). More specifically, a higher value of the parameter indicates that the athlete has greater aerobic endurance and is more effective in maintaining a high level of power output throughout the competition.
Furthermore, these three parameters interact differently depending on the race duration relative to . When , the outcome is primarily determined by anaerobic metabolism, and a larger enhances the athlete’s capability in short-distance, high-intensity efforts. When , aerobic metabolism predominates, with a larger and a higher improving the performance of long-distance. By considering these effects and interactions, the P-T model bridges the gap between theory and practice.
2.2. The Minimum Power Consumption Model
The Minimum Power (MP) Model was proposed by Emig et al. [13,14,23] to eliminate extraneous normalization parameters from the model through the lens of relative power. The model defines relative power () as the ratio of actual power output () to aerobic power reserve (). By using velocity () as a parameter to quantify power, running economy () is then derived. The relationship between power and velocity further simplifies the equation so that running economy can be expressed as
where the minimum velocity corresponding to the production of maximum aerobic power () is referred to as the crossover velocity () [24]. And denotes the base power, and denotes the output power at an average speed ().
To construct a running performance prediction model , it is necessary to know the best time () a runner can run at a given power. The maximum average power () that can be sustained for a duration is used to quantify this information. In addition, the instantaneous power () consumed by the runner during a race of duration is defined. Since during the actual race the runner will become fatigued, this will result in the instantaneous power being greater than the maximum average power, which needs to be compensated by supplementing with additional energy, which is known as supplemental power (). Since different distances involve different energy mechanisms and different energy systems produce energy in different ways, different amounts of supplemental power need to be provided over different time frames. Therefore, to determine the supplementary power’s, a time scale () should be introduced to distinguish between short and long distances. This means that the supplementary power can be expressed as
To build the model, Emig et al. [13]. proposed a relation that states that the average of the instantaneous power is equal to the sum of the supplementary power and the maximum average power () over a duration . This is expressed as
On this basis, they made a key conjecture that the instantaneous power utilized at a certain moment is equal to the maximum average power utilized for the remaining time () [25]. It can be expressed as
Through this relationship, at different periods can be expressed as
By solving this equation inversely and combining it with the relationship between power and speed, the expression for the variation of time with speed can be obtained, based on which the expression is simplified by the introduction of two new variables, the endurance indices for long and short distances, , and . Thus, the time that running can be sustained under a given power condition is expressed as
Using the relationship between speed, distance, and time (), we may estimate the duration of a run at a specific distance (), that is
The equation is expressed as the real branch of the Lambert W-function [26], defined as the inverse of the function . This branch provides an analytical solution to equations of the form , which naturally arise in the derivation of . Thus, the selection of is a natural choice for obtaining a closed-form solution.
The expression denotes the Minimum Power Consumption (MP) model, which is based on four key parameters: crossover velocity (), crossover time (), long distance endurance index (), and short distance endurance index (). As a model of important physiological parameters, the model provides a systematic framework for a comprehensive assessment of an athlete’s competitive level. Among them, parameter is a key index to measure the aerobic metabolic capacity and endurance level of athletes; parameter refers to the time for which an athlete is able to sustain maximal aerobic power, reflecting the aerobic endurance as well as the ability to maintain high-intensity output during the competition. In addition, parameters and are used to characterise athletes’ endurance at different distances. The higher and lower correlate with better endurance and running performance. The model specifies long-distance running endurance as , whereas short-distance running endurance as . mainly measures the stability of athletes’ performance under prolonged, high-continuous loading conditions; whereas focuses more on the athletes’ ability to produce output during short, high-intensity exercise, reflecting in particular their anaerobic metabolism level and explosive power.
Combining these four parameters, the generalized running model can comprehensively reflect the physiological characteristics of athletes in various distance running events. The model provides a scientific and systematic assessment tool for understanding key physiological mechanisms such as endurance and aerobic capacity, helps to analyze physiological differences between individuals and supports the development of personalized training plans.
2.3. Data Resource
In this study, we used two main data sources:
- (1)
- World Running Records (WRR): The dataset is derived directly from the authoritative IAAF Handbook [27], which provides us with running world records for nine different distances ranging from the 1000-m sprint to the full marathon, with records for males ranging from 1918 to 2023 and for females ranging from 1984 to 2023. This choice attempts to fully cover a wide range of results in terms of short-distance explosive power and long-distance endurance, in addition to guaranteeing the validity and authenticity of the data.
- (2)
- British Runners Records (BRR): To delve deeper into the performance characteristics of the average runner, we have selected data from the BRR database from a widely used online resource (http://www.thepowerof10.info/ (accessed on 15 March 2024)) [28]. We focus on the analysis of five representative race distances—5 km (5 K), 10 km (10 K), 10 miles (10 M), half marathon (HM) and full marathon (Mar). Based on this, we select for runners who had raced at all five distances to construct an exhaustive dataset of 2079 UK runners. The dataset is relatively gender balanced, with 38.3% female and 61.7% male.
2.4. Calculating Model Parameters
The P-T model and the MP model rely on a set of independent parameters that are used to characterize physiological information about an individual. These parameters can be estimated by fitting a given set of exercise performance data derived from exercise performed at maximum intensity. To calculate the model parameters, a nonlinear least squares method [29] was used to fit the WRR data for a range of distances between 1000 m and 10,000 m to minimize the difference between actual race times () and predicted times (). Specifically, the objective of fitting using the least squares method was to minimize the residual sum of squares (RSS).
To analyze the distributional properties of the parameters in more detail and to assess their validity in characterizing individual endurance levels and aerobic capacity, we collected personal bests from BRR dataset at four different race distances (5 K, 10 K, 10 M, and HM), and fit the data to the distances using a unified nonlinear least squares method [29].
2.5. Error Assessment
To evaluate the predictive performance of the model, we employed three commonly used metrics: Mean Absolute Error (MAE), Variance (Var), and Standard Deviation (Std). MAE measures the average magnitude of the prediction errors and is defined as:
where is the true value, is the predicted value, and n is the number of samples.
The Var is used to describe the degree of dispersion of the prediction error and is defined as:
The Std is the square root of the Var and is used to indicate the magnitude of fluctuations in the prediction error:
3. Results
3.1. Key Physiological Parameters for Accurate Running Performance Modeling
To verify the ability of the model to capture the key physiological parameters, we calculated the relative error between the predicted time and the actual finish time based on the WRR dataset (see Figure 1A,B). This study uses the magnitude of the prediction error as an indirect measure of the accuracy of estimating physiological parameters in the model. The smaller the error, the more the parameters extracted by the model truly reflect the physiological characteristics of the runners, thus indicating a higher physiological explanatory power.
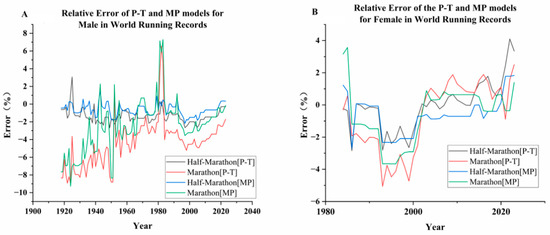
Figure 1.
Relative errors of the male (A) and female (B) for Half-Marathon and Marathon in the World Running Records for the P-T and MP models.
The results showed that despite some fluctuations in the prediction of half-marathon and marathon performance by the two models, the prediction errors have decreased significantly since 2000, reflecting the continuous optimization of the models in the estimation of physiological parameters. Specifically, for male runners (Figure 1A), the relative error of the P-T model decreased from −2% to −0.28% for the half marathon and from −4.53% to −1.71% for the full marathon, while the relative error of the MP model also improved from −1.5% to 0.33% for the half marathon and from −3.23% to −0.14% for the full marathon. Similar trends were observed for female runners (Figure 1B). These trends suggest that both models are effective in extracting and estimating key physiological parameters that reflect the physiological characteristics of runners. Among them, the MP model was more advantageous in parameter extraction.
In addition, the results indicate that prediction error decreases over time, likely due to two factors: improvements in athletes’ technical levels, training methods, tactical strategies, and physiological adaptability, which lead to more stable performance; and the evolving physiological parameters in the model, which increasingly align with actual athletic demands, thereby enhancing prediction accuracy.
To more clearly compare the differences in parameter estimation capabilities between the two models, we further analyzed MAE, Var and Std, and the results are shown in Figure 2. For male runners (Figure 2A), the MAE of the P-T model was HM 1.46% and Mar 4.69% respectively, while the MAE of the MP model was HM 0.79% and Mar 3.08% respectively. For female runners (Figure 2B), the MAE of the P-T model was HM 1.05% and Mar 1.85% respectively, while the MAE of the MP model was HM 1.00% and Mar 1.42% respectively. Since the errors of the two models on Var and Std did not show significant differences, we calculated the 95% confidence interval and conducted the Wilcoxon signed-rank test to examine the significance of the MAE difference. The relevant results are plotted in Figure 3.
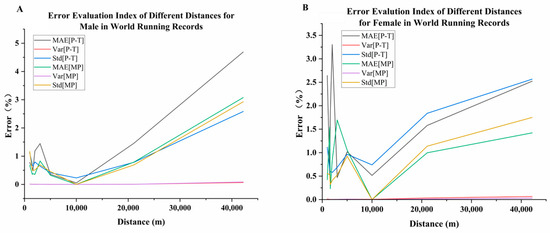
Figure 2.
Mean absolute error (MAE), variance (Var), and standard deviation (Std) of the male (A) and female (B) in the P-T and MP models at various distances for each year in the WRR data.
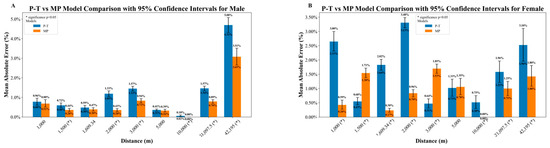
Figure 3.
Comparison of mean absolute errors (MAEs) between P-T and MP models for male (A) and female (B) runners, with 95% bootstrap confidence intervals. Wilcoxon signed-rank tests were performed to assess the statistical significance of differences (p < 0.05, indicated by *).
The results indicate a significant difference in prediction error between the two models for HM and Mar distances. For male marathon runners, although the MP model exhibits a wider 95% confidence interval, it achieves a lower MAE compared to the P-T model. For female runners, the MP model shows both a narrower confidence interval and a lower MAE. This may be because marathon running involves a broader range of influencing factors and greater variability, including differences in race conditions, pacing strategies, and individual physiological and psychological responses. With the evolution of training techniques and physiological parameters, the MP model has become increasingly aligned with actual marathon performance, resulting in a lower MAE but a wider confidence interval for male runners. For female runners, who began competitive participation later and whose technical development is relatively more mature, the confidence intervals are generally narrower overall.
3.2. Evaluating Physiological Parameters for Prediction Accuracy in Real-World
To extend the application to real-world running performance and capture the physiological characteristics of individuals, we used the BRR dataset to investigate the prediction accuracy of the model parameters in real-world scenarios. Using the same methodology, we selected a set of individuals’ best running performances (5 K, 10 K, 10 M, HM) for fitting and calculated the model parameters according to Equation (12). Then, these parameters were used to predict the performance of different distance events and compared with the actual performance to evaluate the performance of the model parameters in real scenarios, and the results are shown in Figure 4. The results show that the relative errors of the predictions are mainly concentrated in the range of ±5% and show a high degree of consistency across gender and distance events. These results fully demonstrate that the MP model performs well in terms of prediction accuracy and stability, and can effectively extract the physiological characteristics of individuals. However, further validation across broader populations and conditions is necessary to confirm the generalizability of these findings.
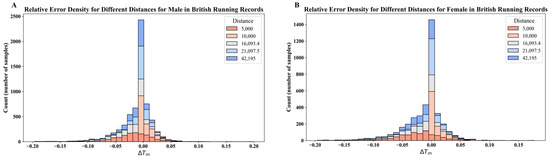
Figure 4.
Stacked histograms showing the distribution of relative prediction errors for male (A) and female (B) athletes at different distances in the BRR dataset, based on the Minimum Power (MP) model. Different colors represent different race distances, as indicated in the legend. The vertical axis represents the numbe of samples of errors within each interval (width = 0.01), and the horizontal axis represents the relative error ().
We calculated the MAE, Var, and Std for both male and female runners to comprehensively evaluate the prediction accuracy of the MP model on the British runner dataset. The results are presented in Table 1. For male runners, the MAE of the MP model at the Mar distance is 3.02%, whereas for female runners it is 3.47%, indicating that the MP model achieves high accuracy in full marathon predictions.

Table 1.
Error evaluation indicators of various distances on the British runner dataset.
To further compare gender differences across various distances, we calculated the 95% confidence interval of the MAE, as shown in the Figure 5. The results demonstrate that, overall, the predictive performance for male runners is superior to that for female runners. However, at the 10 M, the prediction error for male runners is slightly higher than that for female runners. Additionally, the confidence interval for female runners is generally wider, indicating greater uncertainty in their prediction results.
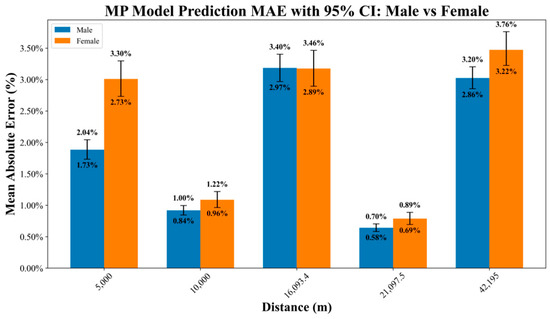
Figure 5.
Gender and distance comparison of the prediction error (MAE) of the MP model and the 95% confidence interval. The figure shows the mean absolute error and its confidence interval for male and female runners at different distances to visually compare the prediction performance of the MP model under different gender and distance conditions.
Var, Std, and confidence interval analyses further indicated that, although the predictive accuracy of the MP model varied across distances, both Var and Std remained relatively low. Moreover, the differences between the upper and lower bounds of the 95% confidence intervals were small, demonstrating the model’s stable and robust predictive performance. These results suggest that the physiological parameters of MP model are highly applicable in practical settings, effectively capturing runners’ physiological characteristics and providing strong support for individualized training programs. Notably, confidence intervals for female athletes were generally wider than those for male athletes, reflecting greater variability in prediction performance between genders.
3.3. Analyzing the Impact of Physiological Parameters on Running Performance
This section was based on BRR data from 5 km (5 K) to half-marathon (HM) races and aimed to systematically analyze the correlation between running performance and various parameters. Figure 6 shows the probability densities of , , , and , and the BRR dataset for males and females.
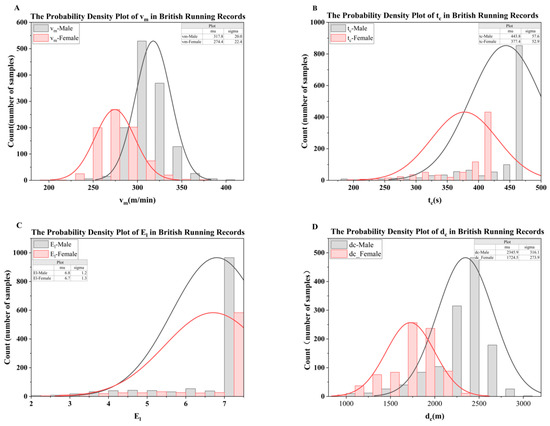
Figure 6.
Probability density distributions of the physiological parameters (A), (B), (C), and (D) in the BRR dataset. Grey and pink colors represent male and female athletes, respectively.
It is worth noting that male and female athletes exhibited clear differences in several endurance-related metrics. The time to maintain maximal aerobic power () averaged 444 s for males, compared to 377 s for females, a difference consistent with males’ ability to sustain higher levels of aerobic capacity for longer periods [30]. The crossover velocity () to maintain maximal aerobic power averaged 317 m/min for males, which was significantly higher than the 274 m/min for females, a difference consistent with males’ greater pacing capacity during high-intensity exercise [31]. At the same time, the mean crossover distance () of males was 2346 m, which was significantly higher than that of females (1725 m), further verifying the advantage of males in prolonged aerobic power maintenance. Finally, the mean long distance endurance () of males was 6.8, slightly higher than that of females (6.7), which may be attributable to the effects of long-term endurance training [32]. These findings indicate that the model parameters not only capture performance differences between genders but also possess clear physiological significance related to endurance levels and aerobic capabilities.
The parameters and exhibit a normal distribution, suggesting not only their balanced presence in the population but also their fundamental role in influencing running performance. In contrast, the distributions of and are right-skewed, indicating that most runners concentrate in the higher range, which reflects a generally strong ability to sustain maximum aerobic power. This skewness may also point to inter-individual variability in endurance capacity. In addition, based on the relationship among , , and , under the condition that dc is relatively fixed, and have an inverse relationship. This indicates that faster runners reach their endurance limit in a shorter time, while slower runners can maintain it for a longer period, thereby reflecting the differences in various running strategies and physiological characteristics. Overall, these results reflect the consistency between the model parameters and their underlying physiological implications, suggesting that MP parameters can be effectively utilized to guide training strategies and performance optimization.
To further analyze the relationship between marathon performance and endurance (), crossover velocity (), and crossover time (), and to reveal the role of physiological traits in the MP model of running performance, the present study plotted the distribution of each parameter concerning running performance based on Equation (14).
As shown in Figure 7, the dashed line is plotted according to Equation (17), and the dotted line indicates the theoretical marathon running performance () corresponding to the combination of long-distance endurance level () and crossover velocity () under the condition of fixed crossover time ( = 420 s). The corresponding values are labelled on the left side of each curve, and the scatter in the figure indicates the measurements of actual runners.
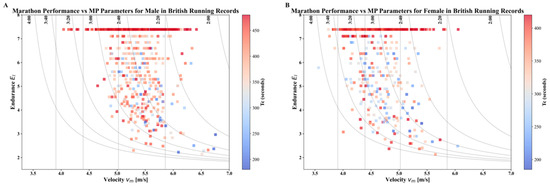
Figure 7.
The relationship between the MP model parameters and the Marathon results of male (A) and female (B) athletes in the BRR dataset.
4. Discussion
4.1. From World Records to Real-World Data
In this study, we first compared the parameter estimation capabilities of the two models through world record data to evaluate the differences in their predictive performance. The relevant conclusions are consistent with the existing studies [11,23], supporting that the MP model has better physiological explanatory power in terms of gender and different race distances. The results (Figure 3) show that the prediction error of the MP model is higher than the P-T model in some cases. Specifically, for female runners, the P-T model performed better at 1500 m and 3000 m. At the 5000 m, the models showed minimal differences, with the P-T model performing slightly better.
This difference may be attributed to the difference in modelling concepts between the two models: the MP model focuses more on maximizing the physiological function of runners and emphasizes the optimization of physiological parameters to enhance endurance performance, whereas the P-T model mainly focuses on the quantification of energy expenditure during running. Female athletes’ is concentrated mainly within the 2000–2500 m range, where . At distances close to (2000 m), performance depends on both and , with a notable anaerobic contribution. Because the MP model relies on relatively stable physiological parameters, it more accurately captures this aerobic–anaerobic balance, leading to superior predictions. In contrast, at shorter (1500 m) or longer (3000 m) distances, performance is more strongly affected by competition strategies, instantaneous energy expenditure, and variability in anaerobic metabolism. These dynamic processes align more closely with the P-T model’s strengths, giving it an advantage. At 5000 m and beyond, aerobic energy supply becomes dominant and stabilizes, thereby minimizing performance differences between the two models.
Furthermore, women performed better than men in Mar prediction, which might be related to their later start in participating in elite competition, referring specifically to a shorter history of engagement at the elite level, as well as to improvements brought about by training methods and technical advancements [33,34].
In further analysis, we evaluate the MP model’s ability to describe physiological parameters in real-world scenarios more comprehensively. Overall, the MP model has a relatively high fitting accuracy for items at different distances, and the prediction errors are mostly concentrated within ±5%, demonstrating good stability and consistency. The results indicates that the physiological parameters relied on by the MP model can not only effectively capture the changes in sports performance, but also stably reflect the physiological demand characteristics of athletes in different events. Therefore, this set of physiological parameters has strong practical applicability and the ability to express physiological information, providing a solid foundation for scientific and personalized training and performance prediction.
Although the prediction error of the MP model on the BRR dataset is slightly higher, its performance on the WRR dataset is still excellent, especially showing high accuracy when predicting the achievements of world-class athletes. The primary reason for the higher prediction errors in the BRR dataset lies in the combination of its data characteristics and individual variability. The BRR dataset exclusively includes each athlete’s personal best performances, which aligns with the model’s principles. However, athletes exhibit significant variations in physical attributes, training habits, and specialized capabilities. Furthermore, different race distances demand distinct requirements for endurance, speed, technique, and strength. Athletes typically undergo specialized training for specific distances, achieving peak performance at those distances while potentially performing relatively weaker at others. This performance variability stemming from individual differences and specialized training causes substantial fluctuations in an athlete’s BRR data across different distances, thereby increasing prediction errors. In contrast, the WRR data extracts the best annual performances at each distance, better reflecting the physiological characteristics of human physical limits, resulting in relatively smaller errors.
These results also indicates that the MP model can effectively capture the influence of athletes’ physiological parameters on training and competition performance. Although the BRR dataset contains more individual differences and external variables, resulting in prediction errors, the MP model can still capture the physiological information of runners very well. This indicates that physiological parameters play a crucial role in the development and expression of running performance. It can not only improve the prediction accuracy of the performance of high-level athletes, but also provide a solid theoretical basis for the performance analysis in the real world.
4.2. Differences in Physiological Parameters on Running Performance
We find some interesting phenomena from Figure 7. From the perspective of cross-sectional analysis, even though some runners possess strong endurance, they are unable to maintain a sufficiently fast pace due to insufficient crossover velocity (), which limits the overall competitive performance; while certain runners with higher also have difficulty in sustaining high-intensity output for a long period if they lack sufficient endurance support. This phenomenon stems from the fact that as running speed increases, the energy supply mechanism gradually transforms from aerobic to anaerobic metabolism [25,35,36]. If a runner exceeds the aerobic threshold prematurely, leading to early lactate accumulation and fatigue, the duration of his high-intensity exercise will be drastically shortened, thus affecting the overall performance [37,38]. Longitudinal analyses further showed that under the same conditions of , runners with lower endurance still struggled to achieve better performance, which highlighted the key role of endurance in maintaining high-intensity output [39,40]. Therefore, in addition to increasing the threshold of , emphasis should be placed on improving the time to maintain aerobic power and enhancing the individual’s ability to sustain a high level of performance during a race through systematic and targeted endurance training [41]. Such training modalities may include tempo runs, intervals, and threshold pace run, which are well-known methods for improving aerobic power maintenance and endurance capacity [42,43].
Furthermore, this study assessed the effects of long-distance endurance index (), crossover velocity (), and crossover time () on running performance by analysing the performance of runners of different genders across a wide range of running distances (see Figure 6). The results showed significant differences in the distribution of and between male and female runners: male runners tended to concentrate their at a higher value, whereas females concentrated at a lower value. This difference may be related to differences in the composition of muscle fiber types between the sexes [44]. Males typically have a higher proportion of fast muscle fibers [45,46], which are capable of generating greater muscle contraction and explosiveness in a short period, helping to maintain higher exercise speeds [47,48]; in addition, males also show a greater ability to maintain MAP for a longer duration compared with females. In comparison, women have a higher proportion of slow muscle fibers with good fatigue resistance and higher mitochondrial density, which makes them more suitable for aerobic endurance exercise of low to moderate intensity and longer duration [48,49]. However, at near-maximal intensity output, females have a relatively weaker sustaining capacity, which may be limited by factors such as cardiorespiratory fitness, oxygen-carrying capacity of the blood, and efficiency of muscle oxygen metabolism [50,51,52]. Furthermore, muscle fiber composition is influenced not only by sex but also modulated by training history, age, and genetic factors [32,53]. Long-term specialized training alters the proportion of muscle fiber types; aging affects the quantity and function of fast-twitch fibers; and genetic factors exert a fundamental influence on muscle fiber distribution. These physiological differences and inter-individual variations partially explain the characteristic distribution of running performance across genders.
Moreover, physiological studies have indicated that females have certain advantages in terms of fatigue resistance, fat oxidation efficiency, and hormone regulation during prolonged exercise [30,54]. For example, women are more inclined to utilize fat as an energy source, thereby conserving glycogen and delaying fatigue, and therefore often perform better in endurance events [55,56]. However, the average endurance of male runners was slightly higher than that of the females, ostensibly suggesting a slight male advantage in delaying fatigue and maintaining athletic performance. This may be due to the fact that the results were derived from the personal bests of a large number of runners. The sample size of males was significantly larger than that of females, which may have resulted in biased statistical results for high-level male runners. Therefore, gender differences in endurance may be more complex and need further analysis in conjunction with a more balanced sample and multiple physiological indicators, such as maximal oxygen uptake (), lactate clearance rate, and muscle fiber composition.
4.3. Personalized Training Based on Physiological Parameters
As shown in Figure 7, the measured data points in the scatterplot reveal several key phenomena:
- (1)
- Runners with lower crossover speeds tend to perform poorly at the same endurance level;
- (2)
- Runners with insufficient endurance levels also have difficulty in achieving the desired performance at the same crossover speed;
- (3)
- Even if the values of parameter and are similar, they deviate from the theoretical performance if the is shorter.
These results suggest that , , and are the core variables determining the performance of running, and they interact with each other, and the absence of any one of them may lead to the limitation of athletic performance.
This relationship reveals a core principle: the pathway to improved athletic performance is not homogenized, but depends on targeted strengthening of the individual’s weakest physiological link. For example, an athlete with a high but a low will have a strong start but a significant deceleration in the back end. Traditional uniform intensity training may not be effective in improving their shortcomings. An assessment based on this model would explicitly design high-intensity interval training to improve lactate tolerance (to improve ), rather than continuing to increase aerobic power training (to improve ) [57], which is already a strength. Similarly, athletes in long-distance events with significantly lower values should focus on strengthening their aerobic base endurance training [58,59].
4.4. Limitations and Future Work
Although the MP model constructed in this study holds significant reference value for capturing physiological parameter characteristics, it still has certain limitations. First, the model does not account for key environmental factors such as weather and altitude, which may affect prediction accuracy. Second, the training dataset exhibits gender imbalance, potentially limiting the model’s adaptability to individuals of different sexes. Furthermore, while this approach reflects physiological potential under ideal conditions, it inadequately accounts for dynamic changes in current physical condition, training levels, and other physiological factors. Due to data constraints, this study analyzes only peak performances across various distances. Future research can focus on physiological parameters themselves, moving beyond their role as mere predictive tools. This involves integrating environmental factors, constructing gender-balanced high-quality datasets, and incorporating samples from the top 10% of performers. Such approaches will deepen exploration of the model’s applicability in terms of stability and average performance, thereby enhancing its responsiveness and adaptability to individual variations.
5. Conclusions
Physiological parameters are key indicators of an individual’s physical condition and exercise capacity, and can reveal the physiological responses of athletes under different exercise intensities. Through the study of these parameters, we can better understand the physiological characteristics of athletes, so as to optimize training plans and competition strategies.
First, this paper compares the performance of the P-T model and the MP model in reflecting the physiological characteristics of runners based on WRR. The results show that the physiological parameters of the MP model can more effectively characterize the physiological characteristics of athletes. To further verify the physiological interpretability of the parameters in the MP model in the real world, we used the BRR dataset. It was found that the physiological parameters of the MP model could accurately reveal the physiological characteristics in the real-world running, which helped to better understand the endurance level and maximum aerobic capacity of individuals.
Further analysis revealed that the physiological parameters of the MP model offer valuable guidance for training. Specifically, can be used to determine the optimal intensity for speed and endurance training; can inform the design and monitoring of high-intensity interval training; and can support the development of strategies to improve fatigue resistance, refine training techniques, and enhance energy management. Additionally, intervention studies and longitudinal tracking could validate and further optimize these parameter-driven training programs.
Author Contributions
Z.Z.: Conceptualization, Methodology, Data curation, Formal analysis, Writing original manuscript preparation; C.L.: Methodology, Investigation, Visualization; W.C.: Supervision, Data curation; Y.S.: Supervision, writing—Reviewing and Editing; B.P. (Corresponding Author): Writing—Reviewing and Editing, Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Fundamental Research Funds for the Central Universities of China, No. 2023GCZX003 (Research on the Nonlinear Accurate Measurement Systems of Exercise Loads).
Data Availability Statement
Data available from the corresponding author upon request.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Kaewkannate, K.; Kim, S. A comparison of wearable fitness devices. BMC Public Health 2016, 16, 433. [Google Scholar] [CrossRef]
- Moore, I.S.; Willy, R.W. Use of wearables: Tracking and retraining in endurance runners. Curr. Sports Med. Rep. 2019, 18, 437–444. [Google Scholar] [CrossRef] [PubMed]
- LaCaille, R.A.; Masters, K.S.; Heath, E.M. Effects of cognitive strategy and exercise setting on running performance, perceived exertion, affect, and satisfaction. Psychol. Sport Exerc. 2004, 5, 461–476. [Google Scholar] [CrossRef]
- El Helou, N.; Tafflet, M.; Berthelot, G.; Tolaini, J.; Marc, A.; Guillaume, M.; Hausswirth, C.; Toussaint, J.-F. Impact of environmental parameters on marathon running performance. PLoS ONE 2012, 7, e37407. [Google Scholar] [CrossRef]
- Kennelly, A.E. An approximate law of fatigue in the speeds of racing animals. Proc. Am. Acad. Arts Sci. 1906, 42, 275–331. [Google Scholar]
- Hill, A.V. The physiological basis of athletic records. Sci. Mon. 1925, 21, 409–428. [Google Scholar] [CrossRef]
- Keller, J.B. A theory of competitive running. Phys. Today 1973, 26, 43–47. [Google Scholar] [CrossRef]
- Keller, J.B. Optimal velocity in a race. Am. Math. Mon. 1974, 81, 474–480. [Google Scholar] [CrossRef]
- Ward-Smith, A. A mathematical theory of running, based on the first law of thermodynamics, and its application to the performance of world-class athletes. J. Biomech. 1985, 18, 337–349. [Google Scholar] [CrossRef]
- Daniels, J. Daniels’ Running Formula; Human Kinetics: Champaign, IL, USA, 2013. [Google Scholar]
- Péronnet, F.; Thibault, G. Mathematical analysis of running performance and world running records. J. Appl. Physiol. 1989, 67, 453–465. [Google Scholar] [CrossRef]
- Alvarez-Ramirez, J. An improved Peronnet-Thibault mathematical model of human running performance. Eur. J. Appl. Physiol. 2002, 86, 517–525. [Google Scholar] [CrossRef] [PubMed]
- Mulligan, M.; Adam, G.; Emig, T. A minimal power model for human running performance. PLoS ONE 2018, 13, e0206645. [Google Scholar] [CrossRef] [PubMed]
- Emig, T.; Peltonen, J. Human running performance from real-world big data. Nat. Commun. 2020, 11, 4936. [Google Scholar] [CrossRef] [PubMed]
- Linnersson, D. Dynamics of pulmonary gas exchange and heart rate changes at start and end of exercise. Acta Physiol. Scand. Suppl. 1974, 415, 1–68. [Google Scholar]
- Hagberg, J.; Nagle, F.; Carlson, J. Transient O2 uptake response at the onset of exercise. J. Appl. Physiol. 1978, 44, 90–92. [Google Scholar] [CrossRef]
- Costill, D.L. Energetics of marathon running. Med. Sci. Sports 1969, 1, 81–86. [Google Scholar] [CrossRef]
- Londeree, B.R. The use of laboratory test results with long distance runners. Sports Med. 1986, 3, 201–213. [Google Scholar] [CrossRef]
- Kawai, M.; Candau, R. Muscle contraction and supplying ATP to muscle cells. In Exercise Physiology: From a Cellular to an Integrative Approach; IOS Press: Amsterdam, The Netherlands, 2010; pp. 3–25. [Google Scholar]
- Péronnet, F.; Thibault, G.; Rhodes, E.C.; McKenzie, D.C. Correlation between ventilatory threshold and endurance capability in marathon runners. Med. Sci. Sports Exerc. 1987, 19, 610–615. [Google Scholar] [CrossRef]
- Gollnick, P.D.; Hermansen, L. Biochemical adaptations to exercise anaerobic metabolism. Exerc. Sport Sci. Rev. 1973, 1, 1–44. [Google Scholar] [CrossRef]
- Di Prampero, P.E. Energetics of muscular exercise. Rev. Physiol. Biochem. Pharmacol. 2005, 89, 143–222. [Google Scholar]
- Emig, T.; Adam, G. Evolution of world running record performances for men and women: Physiological characteristics. Front. Physiol. 2024, 15, 1372092. [Google Scholar] [CrossRef]
- Billat, V.; Morton, R.; Blondel, N.; Berthoin, S.; Bocquet, V.; Koralsztein, J.; Barstow, T. Oxygen kinetics and modelling of time to exhaustion whilst running at various velocities at maximal oxygen uptake. Eur. J. Appl. Physiol. 2000, 82, 178–187. [Google Scholar] [CrossRef]
- Billat, V.; Hamard, L.; Koralsztein, J.P.; Morton, R.H. Differential modeling of anaerobic and aerobic metabolism in the 800-m and 1500-m run. J. Appl. Physiol. 2009, 107, 478–487. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Butler, M. IAAF World Athletics Championships, Doha 2019: Statistics Handbook; IAAF Communications Department: Monaco, Monaco, 2019. [Google Scholar]
- Athletics, B. The Power of 10. Available online: http://www.thepowerof10.info/rankings (accessed on 15 March 2024).
- Kundu, S.; Ubhaya, V. Fitting a least squares piecewise linear continuous curve in two dimensions. Comput. Math. Appl. 2001, 41, 1033–1041. [Google Scholar] [CrossRef]
- Santisteban, K.J.; Lovering, A.T.; Halliwill, J.R.; Minson, C.T. Sex differences in VO2max and the impact on endurance-exercise performance. Int. J. Environ. Res. Public Health 2022, 19, 4946. [Google Scholar] [CrossRef] [PubMed]
- Lewis, D.A.; Kamon, E.; Hodgson, J.L. Physiological differences between genders implications for sports conditioning. Sports Med. 1986, 3, 357–369. [Google Scholar] [CrossRef] [PubMed]
- Plotkin, D.L.; Roberts, M.D.; Haun, C.T.; Schoenfeld, B.J. Muscle fiber type transitions with exercise training: Shifting perspectives. Sports 2021, 9, 127. [Google Scholar] [CrossRef]
- Besson, T.; Macchi, R.; Rossi, J.; Morio, C.Y.; Kunimasa, Y.; Nicol, C.; Vercruyssen, F.; Millet, G.Y. Sex differences in endurance running. Sports Med. 2022, 52, 1235–1257. [Google Scholar] [CrossRef]
- Cheuvront, S.N.; Carter, R.; DeRuisseau, K.C.; Moffatt, R.J. Running performance differences between men and women: An update. Sports Med. 2005, 35, 1017–1024. [Google Scholar] [CrossRef]
- Lacour, J.; Padilla-Magunacelaya, S.; Barthélémy, J.; Dormois, D. The energetics of middle-distance running. Eur. J. Appl. Physiol. Occup. Physiol. 1990, 60, 38–43. [Google Scholar] [CrossRef] [PubMed]
- Jaiyesimi, B.G.; Afolalu, S.A.; Snow, M.N.; Babalola, G.E.; Ikumapayi, O.M.; Jaiyesimi, K.F.; David, D.D. Dynamics of Energy Cost of Performance during Sprint and Long-Distance Running. In Proceedings of the 2024 IEEE 5th International Conference on Electro-Computing Technologies for Humanity (NIGERCON), Ado Ekiti, Nigeria, 26–28 November 2024; IEEE: Ado Ekiti, Nigeria, 2024. [Google Scholar]
- Coyle, E.F. Integration of the physiological factors determining endurance performance ability. Exerc. Sport Sci. Rev. 1995, 23, 25–64. [Google Scholar] [CrossRef]
- Kindermann, W.; Simon, G.; Keul, J. The significance of the aerobic-anaerobic transition for the determination of work load intensities during endurance training. Eur. J. Appl. Physiol. Occup. Physiol. 1979, 42, 25–34. [Google Scholar] [CrossRef]
- Morton, R.H.; Hodgson, D.J. The relationship between power output and endurance: A brief review. Eur. J. Appl. Physiol. Occup. Physiol. 1996, 73, 491–502. [Google Scholar] [CrossRef]
- Midgley, A.; Mc Naughton, L. Time at or near VO2max during continuous and intermittent running: A review with special reference to considerations for the optimisation of training protocols to elicit the longest time at or near VO2max. J. Sports Med. Phys. Fit. 2006, 46, 1–14. [Google Scholar]
- Hottenrott, K.; Ludyga, S.; Schulze, S. Effects of high intensity training and continuous endurance training on aerobic capacity and body composition in recreationally active runners. J. Sports Sci. Med. 2012, 11, 483. [Google Scholar] [PubMed]
- Casado, A.; Foster, C.; Bakken, M.; Tjelta, L.I. Does lactate-guided threshold interval training within a high-volume low-intensity approach represent the “next step” in the evolution of distance running training? Int. J. Environ. Res. Public Health 2023, 20, 3782. [Google Scholar] [CrossRef]
- Li, F.; Nassis, G.P.; Shi, Y.; Han, G.; Zhang, X.; Gao, B.; Ding, H. Concurrent complex and endurance training for recreational marathon runners: Effects on neuromuscular and running performance. Eur. J. Sport Sci. 2021, 21, 1243–1253. [Google Scholar] [CrossRef]
- Nuzzo, J.L. Sex differences in skeletal muscle fiber types: A meta-analysis. Clin. Anat. 2024, 37, 81–91. [Google Scholar] [CrossRef]
- García-Ramos, A.; Feriche, B.; Calderón, C.; Iglesias, X.; Barrero, A.; Chaverri, D.; Schuller, T.; Rodríguez, F.A. Training load quantification in elite swimmers using a modified version of the training impulse method. Eur. J. Sport Sci. 2015, 15, 85–93. [Google Scholar] [CrossRef]
- Haizlip, K.; Harrison, B.; Leinwand, L. Sex-based differences in skeletal muscle kinetics and fiber-type composition. Physiology 2015, 30, 30–39. [Google Scholar] [CrossRef] [PubMed]
- Nuzzo, J.L. Narrative review of sex differences in muscle strength, endurance, activation, size, fiber type, and strength training participation rates, preferences, motivations, injuries, and neuromuscular adaptations. J. Strength Cond. Res. 2023, 37, 494–536. [Google Scholar] [CrossRef]
- Hopwood, H.J.; Bellinger, P.M.; Compton, H.R.; Bourne, M.N.; Minahan, C. The relevance of muscle fiber type to physical characteristics and performance in team-sport athletes. Int. J. Sports Physiol. Perform. 2023, 18, 223–230. [Google Scholar] [CrossRef] [PubMed]
- Raue, U.; Begue, G.; Minchev, K.; Jemiolo, B.; Gries, K.J.; Chambers, T.; Rubenstein, A.; Zaslavsky, E.; Sealfon, S.C.; Trappe, T. Fast and slow muscle fiber transcriptome dynamics with lifelong endurance exercise. J. Appl. Physiol. 2024, 136, 244–261. [Google Scholar] [CrossRef]
- Edman, S.; Flockhart, M.; Larsen, F.J.; Apró, W. Need for speed: Human fast-twitch mitochondria favor power over efficiency. Mol. Metab. 2024, 79, 101854. [Google Scholar] [CrossRef]
- Bahrami, F.; Fathi, M.; Ahmadvand, H.; Pajohi, N. Endurance training changes the expression of miR-1 and miR-133 and predicted genes in slow and fast twitch muscles. Arch. Gerontol. Geriatr. 2023, 108, 104929. [Google Scholar] [CrossRef]
- Diaz-Canestro, C.; Pentz, B.; Sehgal, A.; Montero, D. Sex differences in cardiorespiratory fitness are explained by blood volume and oxygen carrying capacity. Cardiovasc. Res. 2022, 118, 334–343. [Google Scholar] [CrossRef]
- Gallagher, D.; Heymsfield, S.B. Muscle distribution: Variations with body weight, gender, and age. Appl. Radiat. Isot. 1998, 49, 733–734. [Google Scholar] [CrossRef]
- Peterson, L.R.; Soto, P.F.; Herrero, P.; Schechtman, K.B.; Dence, C.; Gropler, R.J. Sex differences in myocardial oxygen and glucose metabolism. J. Nucl. Cardiol. 2007, 14, 573–581. [Google Scholar] [CrossRef]
- Le Mat, F.; Géry, M.; Besson, T.; Ferdynus, C.; Bouscaren, N.; Millet, G.Y. Running endurance in women compared to men: Retrospective analysis of matched real-world big data. Sports Med. 2023, 53, 917–926. [Google Scholar] [CrossRef] [PubMed]
- Tiller, N.B.; Elliott-Sale, K.J.; Knechtle, B.; Wilson, P.B.; Roberts, J.D.; Millet, G.Y. Do sex differences in physiology confer a female advantage in ultra-endurance sport? Sports Med. 2021, 51, 895–915. [Google Scholar] [CrossRef]
- Spurway, N. Aerobic exercise, anaerobic exercise and the lactate threshold. Br. Med. Bull. 1992, 48, 569–591. [Google Scholar] [CrossRef] [PubMed]
- Midgley, A.W.; McNaughton, L.R.; Jones, A.M. Training to enhance the physiological determinants of long-distance running performance: Can valid recommendations be given to runners and coaches based on current scientific knowledge? Sports Med. 2007, 37, 857–880. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, L.M.; Lopez, R.M.; Klau, J.F.; Casa, D.J.; Kraemer, W.J.; Maresh, C.M. The effects of resistance training on endurance distance running performance among highly trained runners: A systematic review. J. Strength Cond. Res. 2008, 22, 2036–2044. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).