A Finite-Element Model of Seated Human Body Representing the Distribution of Static Pressures and Dynamic Forces over a Rigid Seat During Vertical Vibration for Sitting Postures with Various Thigh Contact
Abstract
1. Introduction
- The static pressure distribution at the body–seat interface;
- The overall vertical in-line and fore-and-aft cross-axis apparent masses of the human body under vertical vibration;
- The localised vertical in-line and fore-and-aft cross-axis apparent masses measured at the ischial tuberosities, the middle thighs, and the front thighs.
2. Measurement of Static Pressure Distribution and Dynamic Forces over the Seat
2.1. Equipment and Stimuli
2.2. Analysis of Static Pressure Distribution
2.3. Definition of Overall and Localised Apparent Masses
3. Finite-Element Model of the Seated Human Body
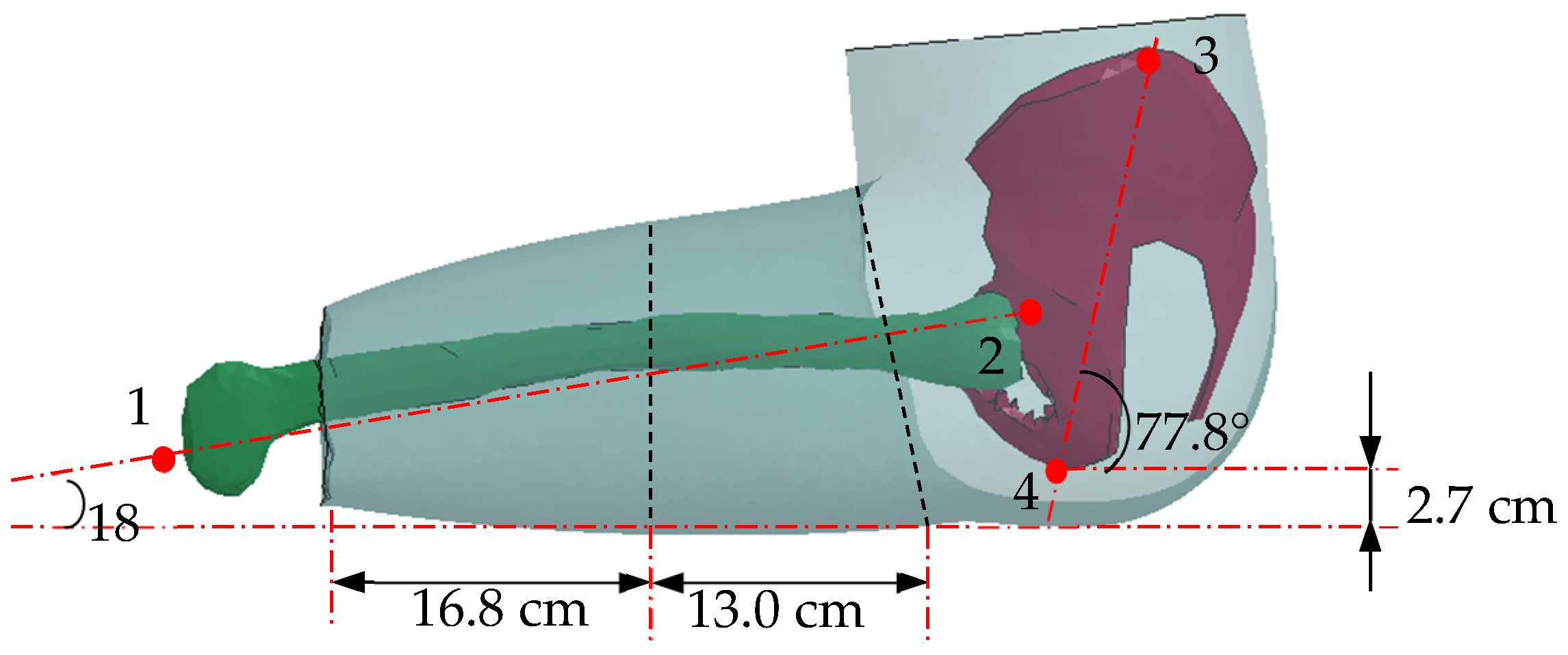
3.1. Structure of the Model
3.2. Viscoelastic Material
3.3. Modelling of Sitting Postures with Different Tight Contact with the Seat
4. Results
4.1. Static Pressure
4.2. Overall and Localised Apparent Masses
5. Discussion
5.1. Measured and Modelled Static Pressure and Apparent Masses
5.2. Model Structure and Complexity
5.3. Material Properties
5.4. Implications for Prediction of Overall Sitting Comfort
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ebe, K.; Griffin, M.J. Quantitative prediction of overall seat discomfort. Ergonomics 2000, 43, 791–806. [Google Scholar] [CrossRef] [PubMed]
- Ebe, K.; Griffin, M.J. Factors affecting static seat cushion comfort. Ergonomics 2001, 44, 901–921. [Google Scholar] [CrossRef] [PubMed]
- Porter, J.M.; Gyi, D.E.; Tait, H.A. Interface pressure data and the prediction of driver discomfort in road trials. Appl. Ergon. 2003, 34, 207–214. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lantoine, P.; Lecocq, M.; Bougard, C.; Dousset, E.; Marqueste, T.; Bourdin, C.; Allègre, J.-M.; Bauvineau, L.; Mesure, S. Car seat impact on driver’s sitting behavior and perceived discomfort during prolonged real driving on varied road types. PLoS ONE 2021, 16, e0259934. [Google Scholar] [CrossRef]
- Hirao, A.; Naito, S.; Yamazaki, N. Pressure sensitivity of buttock and thigh as a key factor for understanding of sitting comfort. Appl. Sci. 2022, 12, 7363. [Google Scholar] [CrossRef]
- Wu, X.; Rakheja, S.; Boileau, P.-É. Study of human–seat interface pressure distribution under vertical vibration. Int. J. Ind. Ergon. 1998, 21, 433–449. [Google Scholar] [CrossRef]
- Hinz, B.; Rützel, S.; Blüthner, R.; Menzel, G.; Wölfel, H.P.; Seidel, H. Apparent mass of seated man—First determination with a soft seat and dynamic seat pressure distributions. J. Sound Vib. 2006, 298, 704–724. [Google Scholar] [CrossRef]
- Mirakhorlo, M.; Kluft, N.; Shyrokau, B.; Happee, R. Effects of seat back height and posture on 3D vibration transmission to pelvis, trunk and head. Int. J. Ind. Ergon. 2022, 91, 103327. [Google Scholar] [CrossRef]
- Dewangan, K.; Rakheja, S.; Marcotte, P.; Shahmir, A. Effects of elastic seats on seated body apparent mass responses to vertical whole body vibration. Ergonomics 2015, 58, 1175–1190. [Google Scholar] [CrossRef]
- Liu, C.; Griffin, M.J. Measuring vibration-induced variations in pressures between the human body and a seat. Int. J. Ind. Ergon. 2018, 67, 274–282. [Google Scholar] [CrossRef]
- Tufano, S.; Griffin, M.J. Nonlinearity in the vertical transmissibility of seating: The role of the human body apparent mass and seat dynamic stiffness. Veh. Syst. Dyn. 2013, 51, 122–138. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, P.; Liang, S. Apparent mass of the seated human body during vertical vibration in the frequency range 2–100 Hz. Ergonomics 2020, 63, 1150–1163. [Google Scholar] [CrossRef] [PubMed]
- Amari, M.; Perrin, N. Whole-body vibration exposure in unfavourable seated postures: Apparent mass and seat-to-head transmissibility measurements in the fore-and-aft, lateral, and vertical directions. Ergonomics 2023, 66, 136–151. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Qiu, Y.; Griffin, M.J. Dynamic forces over the interface between a seated human body and a rigid seat during vertical whole-body vibration. J. Biomech. 2017, 61, 176–182. [Google Scholar] [CrossRef]
- Liu, C.; Qiu, Y. Nonlinearity in the localised apparent masses of the seated human body exposed to vertical vibration. Mech. Syst. Signal Process. 2020, 135, 106394. [Google Scholar] [CrossRef]
- Verver, M.; Van, H.J.; Oomens, C.; Wismans, J.S.H.M.; Baaijens, F.P.T. A finite element model of the human buttocks for prediction of seat pressure distributions. Comput. Methods Biomech. Biomed. Eng. 2004, 7, 193–203. [Google Scholar] [CrossRef]
- Siefert, A.; Pankoke, S.; Wölfel, H.-P. Virtual optimisation of car passenger seats: Simulation of static and dynamic effects on drivers’ seating comfort. Int. J. Ind. Ergon. 2008, 38, 410–424. [Google Scholar] [CrossRef]
- Makhsous, M.; Lin, F.; Cichowski, A.; Cheng, I.; Fasanati, C.; Grant, T.; Hendrix, R.W. Use of MRI images to measure tissue thickness over the ischial tuberosity at different hip flexion. Clin. Anat. 2011, 24, 638–645. [Google Scholar] [CrossRef]
- Dong, R.; He, L.; Du, W.; Cao, Z.-K.; Huang, Z.-L. Effect of sitting posture and seat on biodynamic responses of internal human body simulated by finite element modeling of body-seat system. J. Sound Vib. 2019, 438, 543–554. [Google Scholar] [CrossRef]
- Liu, Y.; Zhong, X.; Ghebreiyesus, W.; Ji, J.; Xi, F. Analysis and modeling of human seat interaction with a focus on the upper body and backrest using biomechanics and contact mechanics. Work 2021, 68, S161–S182. [Google Scholar] [CrossRef]
- Yadav, S.K.; Huang, C.; Mo, F.; Li, J.; Chen, J.; Xiao, Z. Analysis of seat cushion comfort by employing a finite element buttock model as a supplement to pressure measurement. Int. J. Ind. Ergon. 2021, 86, 103211. [Google Scholar] [CrossRef]
- Kitazaki, S.; Griffin, M.J. A modal analysis of whole-body vertical vibration, using a finite element model of the human body. J. Sound Vib. 1997, 200, 83–103. [Google Scholar] [CrossRef]
- Wei, L.; Griffin, M.J. Mathematical models for the apparent mass of the seated human body exposed to vertical vibration. J. Sound Vib. 1998, 212, 855–874. [Google Scholar] [CrossRef]
- Cho, Y.; Yoon, Y. Biomechanical model of human on seat with backrest for evaluating ride quality. Int. J. Ind. Ergon. 2001, 27, 331–345. [Google Scholar] [CrossRef]
- Matsumoto, Y.; Griffin, M.J. Modelling the dynamic mechanisms associated with the principal resonance of the seated human body. Clin. Biomech. 2001, 16, S31–S44. [Google Scholar] [CrossRef]
- Yoshimura, T.; Nakai, K.; Tamaoki, G. Multi-body dynamics modelling of seated human body under exposure to whole-body vibration. Ind. Health 2005, 43, 441–447. [Google Scholar] [CrossRef]
- Rakheja, S.; Stiharu, I.; Zhang, H.; Boileau, P. Seated occupant interactions with seat backrest and pan, and biodynamic responses under vertical vibration. J. Sound Vib. 2006, 298, 651–671. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, K.; Liu, Y.; Guo, Q.; Wen, Y.; Feng, Z. Nonlinear dynamic modeling and body injuries analysis of human/seat system under vertical impact. Int. J. Ind. Ergon. 2023, 95, 103450. [Google Scholar] [CrossRef]
- Zheng, G.; Qiu, Y.; Griffin, M.J. An analytic model of the in-line and cross-axis apparent mass of the seated human body exposed to vertical vibration with and without a backrest. J. Sound Vib. 2011, 330, 6509–6525. [Google Scholar] [CrossRef]
- Bhardawaj, S.; Sharma, R.C.; Sharma, S.K.; Rao, L.G.; Vashist, A. Modeling of biomechanical human body model for seat to head transmissibility analysis. Noise Vib. Worldw. 2023, 54, 62–74. [Google Scholar] [CrossRef]
- Liu, C.; Qiu, Y.; Griffin, M.J. Finite element modelling of human-seat interactions: Vertical in-line and fore-and-aft cross-axis apparent mass when sitting on a rigid seat without backrest and exposed to vertical vibration. Ergonomics 2015, 58, 1207–1219. [Google Scholar] [CrossRef]
- Kim, E.; Fard, M.; Kato, K. A seated human model for predicting the coupled human-seat transmissibility exposed to fore-aft whole-body vibration. Appl. Ergon. 2020, 84, 102929. [Google Scholar] [CrossRef]
- Liu, C. Localised Biodynamic Responses of the Seated Human Body During Excitation by Vertical Vibration. Ph.D. Thesis, University of Southampton, Southampton, UK, 2016. [Google Scholar]
- Ansys, I. LS-DYNA Keyword User’s Manual; Ansys Inc.: Canonsburg, PA, USA, 2024. [Google Scholar]
- Drake, R.L.; Vogl, W.; Mitchell, A.W.M. Gray’s Anatomy for Students, 4th ed.; Elsevier: London, UK, 2019. [Google Scholar]
- Ebe, K.; Griffin, M.J. Qualitative models of seat discomfort including static and dynamic factors. Ergonomics 2000, 43, 771–790. [Google Scholar] [CrossRef]
- GB/T 10000-2023; Human Dimensions of Chinese Adults. China Standards Press: Beijing, China, 2023.
- Li, Y.; Dang, S.; Li, W.; Chai, Y. Free and forced vibration analysis of two-dimensional linear elastic solids using the finite element methods enriched by interpolation cover functions. Mathematics 2022, 10, 456. [Google Scholar] [CrossRef]
- Lone, A.S.; Harmain, G.; Jameel, A. Modeling of contact interfaces by penalty based enriched finite element method. Mech. Adv. Mater. Struct. 2023, 30, 1485–1503. [Google Scholar] [CrossRef]
- Dell’Accio, F.; Guessab, A.; Nudo, F. New quadratic and cubic polynomial enrichments of the Crouzeix–Raviart finite element. Comput. Math. Appl. 2024, 170, 204–212. [Google Scholar] [CrossRef]

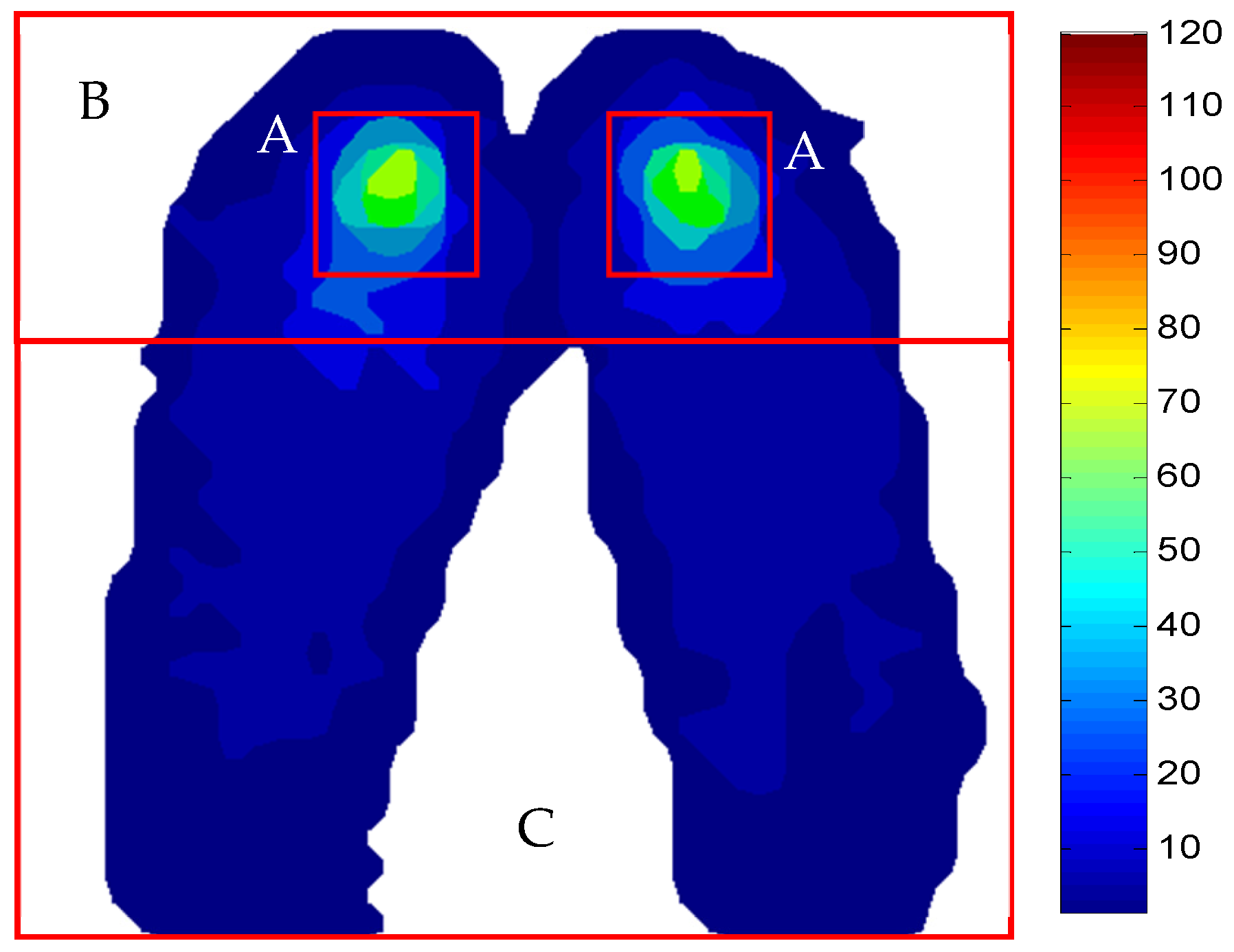


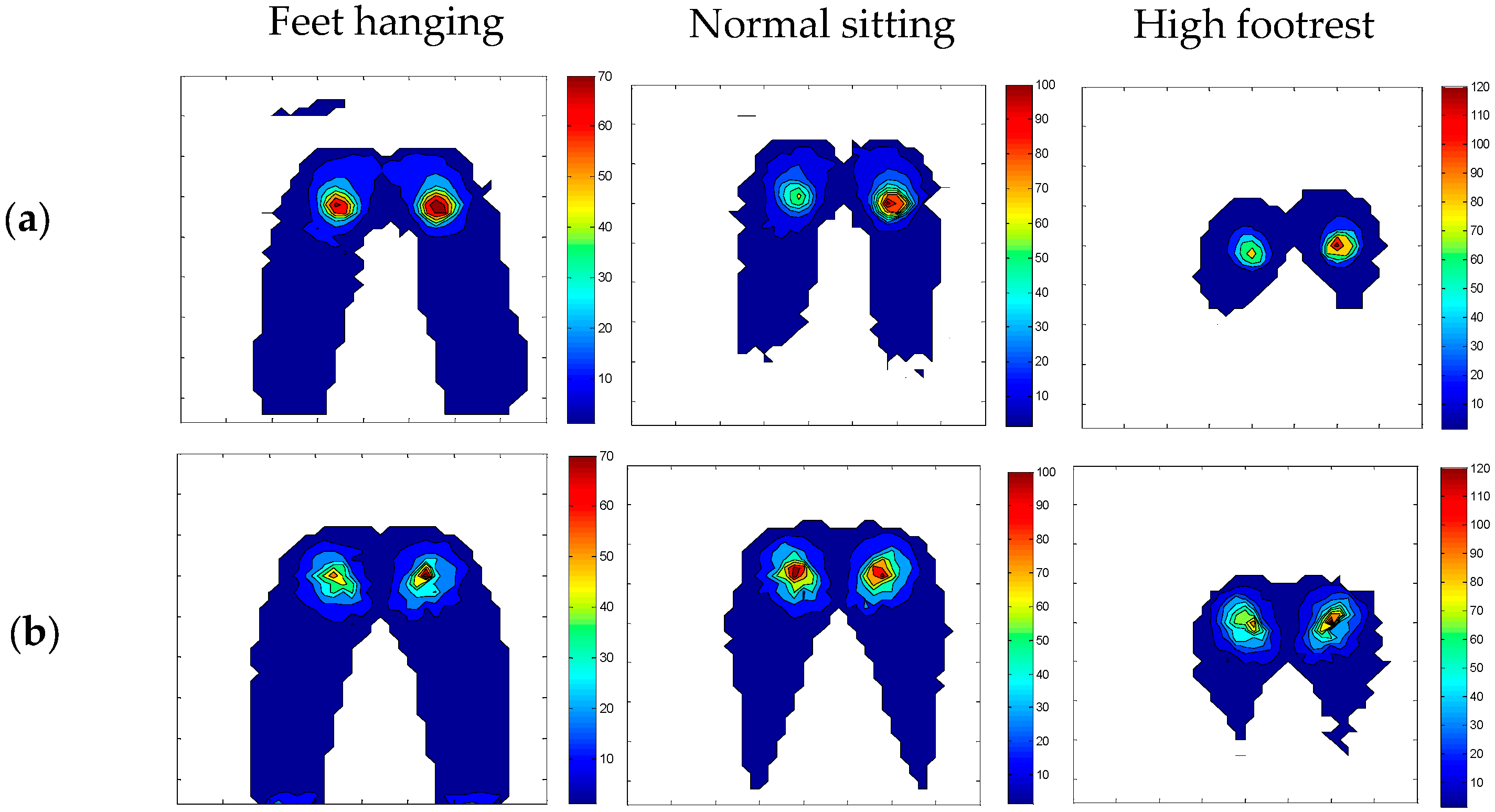
 measurement;
measurement;  model.
model.
 measurement;
measurement;  model.
model.
 model;
model;  measurement (Line styles are identical in subsequent figures).
measurement (Line styles are identical in subsequent figures).
 model;
model;  measurement (Line styles are identical in subsequent figures).
measurement (Line styles are identical in subsequent figures).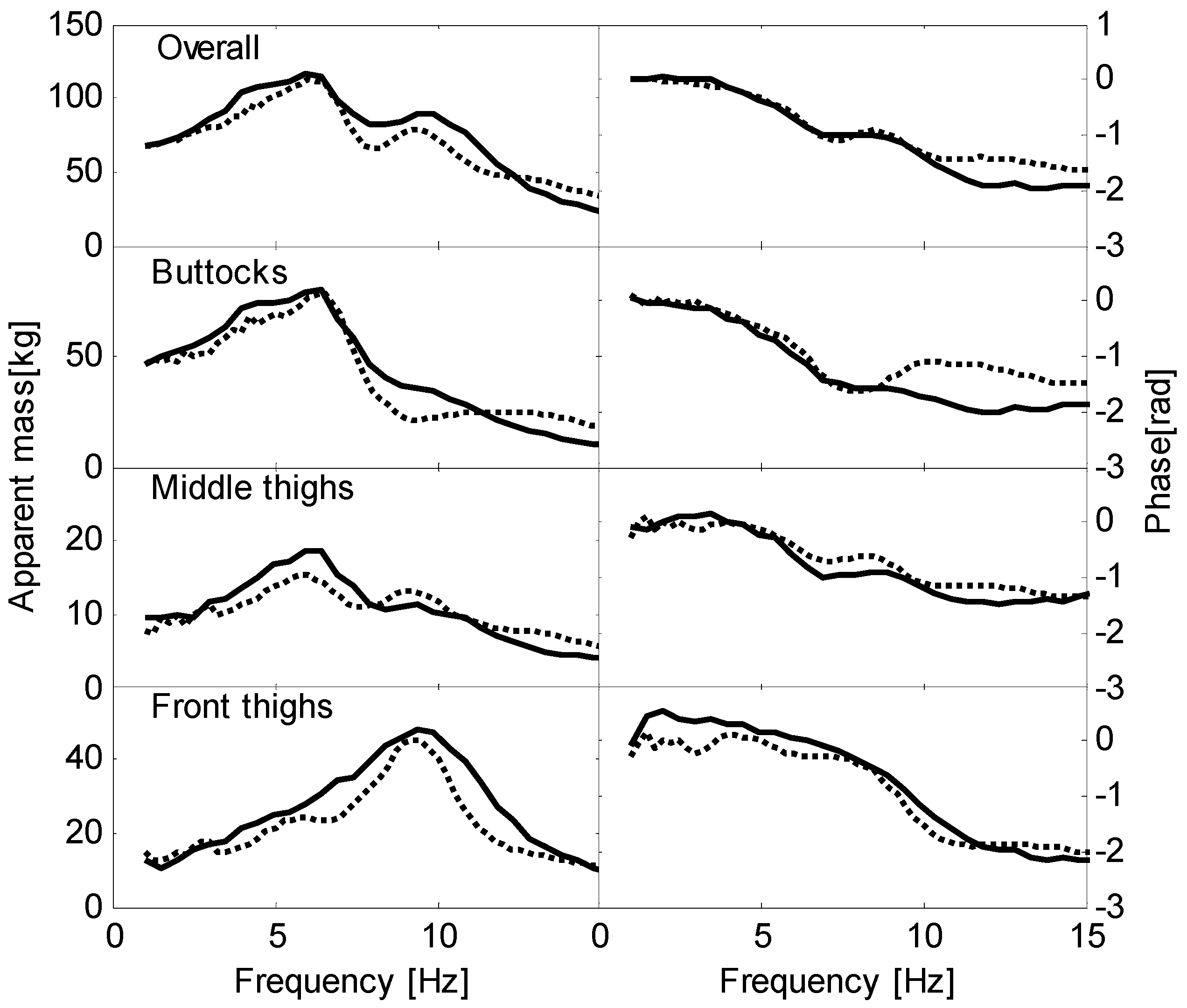




| Anthropometric Dimensions | Measurement | Model |
|---|---|---|
| Total mass [kg] | 63.5 | 63.5 |
| Stature [cm] | 170.0 | 170.0 |
| Sitting height [cm] | 90.0 | 90.0 |
| Circumference of front thigh [cm] | 38.4 | 37.4 |
| Circumference of middle thigh [cm] | 50.3 | 49.1 |
| Circumference of rear thigh [cm] | 58.5 | 57.1 |
| Width of front thigh [cm] | 11.5 | 12.1 |
| Width of middle thigh [cm] | 15.4 | 15.5 |
| Width of rear thigh [cm] | 20.3 | 17.1 |
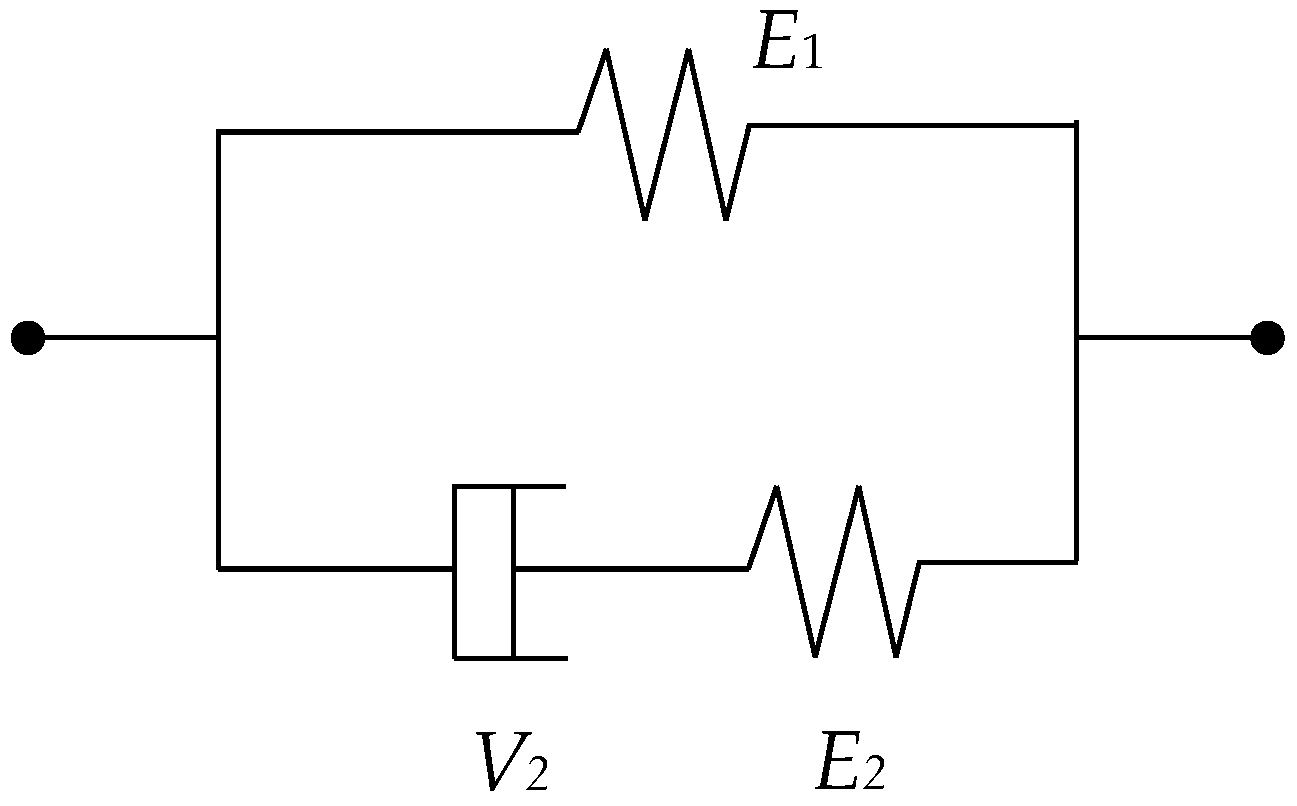
| Density (kg/m3) | E1 (MPa) | N1 | E2 (MPa) | V2 | N2 | Poisson’s Ratio | |
|---|---|---|---|---|---|---|---|
| Buttocks and middle thighs | 1085 | 0.001 | 3.6 | 0.5 | 6.0 × 10−4 | 0 | 0.45 |
| Front thighs | 1085 | 0.001 | 3.6 | 0.5 | 6.0 × 10−3 | 0 | 0.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yin, W.; Liu, S.; Liang, J.; Liu, C.; Qiu, Y.; Zheng, X.; Sun, L.; Huang, S. A Finite-Element Model of Seated Human Body Representing the Distribution of Static Pressures and Dynamic Forces over a Rigid Seat During Vertical Vibration for Sitting Postures with Various Thigh Contact. Appl. Sci. 2025, 15, 10716. https://doi.org/10.3390/app151910716
Yin W, Liu S, Liang J, Liu C, Qiu Y, Zheng X, Sun L, Huang S. A Finite-Element Model of Seated Human Body Representing the Distribution of Static Pressures and Dynamic Forces over a Rigid Seat During Vertical Vibration for Sitting Postures with Various Thigh Contact. Applied Sciences. 2025; 15(19):10716. https://doi.org/10.3390/app151910716
Chicago/Turabian StyleYin, Weitan, Shaoqing Liu, Jianying Liang, Chi Liu, Yi Qiu, Xu Zheng, Linfeng Sun, and Shan Huang. 2025. "A Finite-Element Model of Seated Human Body Representing the Distribution of Static Pressures and Dynamic Forces over a Rigid Seat During Vertical Vibration for Sitting Postures with Various Thigh Contact" Applied Sciences 15, no. 19: 10716. https://doi.org/10.3390/app151910716
APA StyleYin, W., Liu, S., Liang, J., Liu, C., Qiu, Y., Zheng, X., Sun, L., & Huang, S. (2025). A Finite-Element Model of Seated Human Body Representing the Distribution of Static Pressures and Dynamic Forces over a Rigid Seat During Vertical Vibration for Sitting Postures with Various Thigh Contact. Applied Sciences, 15(19), 10716. https://doi.org/10.3390/app151910716







