A Scalable Two-Level Deep Reinforcement Learning Framework for Joint WIP Control and Job Sequencing in Flow Shops

Abstract

Effective production control requires aligning strategic planning with real-time execution under dynamic and stochastic conditions. This study proposes a scalable dual-agent Deep Reinforcement Learning (DRL) framework for the joint optimisation of Work-In-Process (WIP) control and job sequencing in flow-shop environments. A strategic DQN agent regulates global WIP to meet throughput targets, while a tactical DQN agent adaptively selects dispatching rules at the machine level on an event-driven basis. Parameter sharing in the tactical agent ensures inherent scalability, overcoming the combinatorial complexity of multi-machine scheduling. The agents coordinate indirectly via a shared simulation environment, learning to balance global stability with local responsiveness. The framework is validated through a discrete-event simulation integrating agent-based modelling, demonstrating consistent performance across multiple production scales (5–15 machines) and process time variabilities. Results show that the approach matches or surpasses analytical benchmarks and outperforms static rule-based strategies, highlighting its robustness, adaptability, and potential as a foundation for future Hierarchical Reinforcement Learning applications in manufacturing.

1. Introduction

Effective production control is vital for maintaining operational efficiency, particularly within the dynamic conditions and fluctuating demand patterns characteristic of contemporary markets [1,2]. The ability to adaptively manage the performance of production lines is crucial for responsiveness and sustaining a competitive advantage [3,4]. While traditional control methods have limitations in handling the complexity of modern manufacturing, Industry 4.0 technologies, especially Artificial Intelligence (AI) [5], offer promising solutions [6,7]. Deep Reinforcement Learning (DRL), a subset of AI, has emerged as a powerful technique for enhancing decision-making in complex production system tasks like scheduling and control, often outperforming traditional heuristics and even metaheuristics in terms of solution quality and computational speed in dynamic settings [7]. In parallel, modelling approaches such as digital twin and multi-method simulation have been increasingly employed to create realistic test-beds for training AI-driven controllers in manufacturing [8,9,10].

One critical aspect of production control is managing Work-In-Process (WIP). Traditional approaches like Constant Work-In-Process (CONWIP) offer robust flow management under stable conditions [11] but struggle with the inherent dynamism of modern systems due to their static nature [12,13] and the fact that they are valid only under specific circumstances. Recent research, including work by Vespoli et al. and other preliminary investigations [14,15], has shown the potential of DRL, specifically Deep Q-Networks (DQN), to dynamically adjust WIP levels in response to real-time system states, thereby improving adaptability and maintaining target throughput even under varying processing times [15].

Simultaneously, effective job sequencing through dynamic dispatching rule selection is crucial for optimising performance metrics. Relying on a single, static dispatching rule is often insufficient, as the optimal rule frequently depends on the current system state and objectives [7]. Prior work has explored using DRL to dynamically select dispatching rules, demonstrating the benefits of adaptive sequencing strategies [16].

However, the state-of-the-art, as highlighted in recent reviews [7], often addresses WIP control and dynamic scheduling as separate problems. While DRL has been applied extensively to various scheduling problems (flow shop, job shop, etc.) and, more recently, to adaptive WIP control [15], there remains a gap in integrating these two critical control functions within a unified and scalable adaptive framework. Recent studies have also shown the potential of integrating AI with simulation-based frameworks to support decision-making in supply chain and manufacturing contexts [10,17], yet these approaches still tend to focus on isolated tasks rather than integrated control.

Optimising WIP levels and sequencing rules in tandem is inherently challenging due to their strong interdependence. A major obstacle to a fully integrated approach lies in the curse of dimensionality: in dispatching, the number of possible rule combinations increases exponentially with the number of machines, inflating both the action and state spaces. Learning an effective dispatching policy from scratch under such conditions requires extensive exploration and incurs substantial computational effort and convergence time [18]. When these functions are addressed in isolation, a common approach in the literature, there is a heightened risk of sub-optimal outcomes, as sequencing decisions that appear locally efficient may undermine global throughput objectives.

This paper addresses this gap by proposing a novel DRL framework structured as a two-level, dual-agent architecture that is inherently scalable. We decouple the problem into two distinct but interconnected roles: (i) a high-level strategic agent determines the overall system load by dynamically adjusting WIP levels to meet global throughput (TH) targets; (ii) a low-level tactical agent makes real-time, event-driven sequencing decisions. This tactical agent, built on a parameter-sharing DQN architecture, is invoked only when a machine completes a task and requires a new instruction. This design reduces the action space complexity from exponential to constant, enabling the framework to scale effectively to extensive production systems.

The key to our approach is that the agents are implicitly coordinating. They learn through a shared simulation environment and complementary reward structures, allowing them to master the complex trade-offs between global stability and local efficiency without direct communication. This work extends our previous explorations [14,16], which addressed these problems in isolation, into a unified, robust, and scalable architecture where a powerful control policy can emerge from the interaction of specialized agents. To validate this, we develop a tailored state-action-reward system and employ a multi-method simulation model combining Discrete Event Simulation (DES) and Agent-Based Modelling. This creates a realistic test-bed to train the agents and evaluate their emergent coordination across various scenarios, including different system sizes and processing time variabilities.

To guide the reader, the remainder of this paper is structured as follows. Section 2 introduces the methodology, including the WIP–throughput dynamics based on Factory Physics, the challenge of dynamic job sequencing, the role of DRL in sequential decision-making, and a review of related works. Section 3 presents the proposed two-level DRL framework for joint production control, detailing the event-driven dispatching agent with parameter sharing, the hierarchical control problem formulation, and the design of state, action, and reward spaces, as well as the specific roles of the strategic and tactical agents. Section 4 describes the experimental methodology, including the simulation environment, benchmarking setup, and training protocol. Moreover Section 5 reports the experimental results across scalability, robustness, adaptive dispatching, and training analysis. Section 6 discusses the implications and limitations of the findings, and Section 7 concludes the paper.

The main contributions of this study can be summarised as follows:

(i)

We design an event-driven, scalable tactical agent with an action space of constant size, independent of the number of machines in the system.

(ii)

We develop a reward function grounded in Factory Physics principles, explicitly balancing throughput and stability considerations.

(iii)

We conduct an extensive experimental evaluation on flow-shop systems with 5, 10, and 15 machines, including a variability analysis to test robustness under different stochastic conditions.

(iv)

We demonstrate the capability of adaptive dispatching-rule selection to achieve alternative throughput objectives, showing how global and local goals can be jointly optimised.

2. Methodology

Controlling WIP is crucial to ensuring efficiency and productivity in production processes and resource management systems. Various methods exist for managing and controlling WIP, ranging from traditional static approaches to advanced RL and DRL methods.

Traditional static methods, such as the CONWIP system, utilise fixed rules to maintain a consistent level of WIP throughout the production process. These systems are valued for their simplicity and effectiveness in stable environments, but often lack the flexibility to respond dynamically to changes in demand or operational disruptions. However, dynamic methods, particularly those based on RL and DRL, offer the capability to adapt in real-time to varying production conditions.

Our research builds upon established principles from production control theory and recent advances in artificial intelligence. The section provides the necessary background on the core concepts that underpin our proposed framework: the fundamental dynamics of flow shops as described by Factory Physics, the role of dispatching rules, and the mechanics of Deep Reinforcement Learning.

2.1. WIP-Throughput Dynamics and Factory Physics

The relationship between WIP, throughput (TH), and cycle time (CT) is fundamental to understanding and controlling any production system. The fundamental work of Hopp and Spearman in “Factory Physics” provides a quantitative foundation for this relationship [19]. Their analysis of pull systems, particularly CONWIP, led to the formulation of the Practical Worst Case (PWC) model, a robust analytical benchmark for systems operating under significant variability [20]. The PWC model, summarized in

Table 1. Relationship in Hopp and Spearman [19] “Factory Physics”.

Performance Scenario	Cycle Time	Throughput
Best Case	$C{T}_{min}=T_0$ if   $w<W_0$	$T{H}_{max}={\displaystyle \frac{w}{T_0}}$ if   $w<W_0$
	$C{T}_{min}={\displaystyle \frac{w}{r_b}}$ otherwise	$T{H}_{max}=r_b$ otherwise
Worst Case	$C{T}_{max}=w{T}_0$	$T{H}_{min}={\displaystyle \frac{1}{T_0}}$
Practical Worst Case (PWC)	$C{T}_{PWC}=T_0+{\displaystyle \frac{w-1}{r_b}}$	$T{H}_{PWC}={\displaystyle \frac{w{r}_b}{W_0+w-1}}$

, establishes the expected performance of a production line with exponentially distributed processing times. It links key performance indicators using system parameters: Raw Processing Time $T_0$, the average total processing time for a job, summed across all workstations. Bottleneck Rate $r_b$, the production rate of the slowest workstation, which dictates the maximum possible system throughput. Critical WIP $W_0$, the theoretical WIP level $W_0=r_b\ast T_0$ at which a deterministic system achieves maximum throughput and minimum cycle time. Current WIP w, the number of jobs currently in the system.

While the PWC framework provides an invaluable theoretical baseline, it is a static analytical model, not an active control strategy. It describes expected behaviour under fixed conditions but does not offer a mechanism to dynamically adjust control parameters in response to real-time system state changes.

Our work is inspired by these fundamental laws; we do not use the PWC model for direct control, but rather leverage its principles to design the reward functions and state representation for our DRL agents. This approach grounds the agents’ learning process in established manufacturing physics, enabling them to implicitly understand the system’s underlying dynamics.

2.2. The Challenge of Dynamic Job Sequencing

While system-level WIP policies set the overall production volume, dispatching rules govern the execution sequence of jobs at individual workstations. These rules are simple heuristics used to prioritize jobs waiting in a queue. Common examples include First-In, First-Out (FIFO), processes jobs in their order of arrival. It is fair and simple but can be inefficient if long jobs block shorter ones. Shortest Processing Time (SPT), prioritizes jobs that require the least amount of processing time. This rule is known to minimize mean job flow time but may lead to the starvation of longer jobs. Longest Processing Time (LPT), prioritizes jobs with the longest processing time, often used to improve machine utilization. The core challenge in modern manufacturing is that the effectiveness of any single dispatching rule is highly state-dependent.

The optimal rule changes continuously based on factors like current queue lengths, the processing time distribution of waiting jobs, and the overall system state dictated by the WIP control policy. As highlighted by Salatiello et al. [21], relying on a single, static rule is therefore inherently suboptimal in dynamic and stochastic environments. This creates a complex, sequential decision problem: which rule should be active at which machine, and at what time? Answering this question requires a control strategy that can dynamically select the most appropriate rule in real-time. This is precisely the type of adaptive, context-aware decision-making for which DRL is exceptionally well-suited.

2.3. Deep Reinforcement Learning for Sequential Decision-Making

RL is a paradigm of machine learning where an agent learns to make optimal decisions by interacting with an environment. The agent receives feedback in the form of rewards and learns a policy—a mapping from states to actions—that maximizes a cumulative reward signal over time. This makes RL particularly well-suited for solving complex, dynamic optimization problems like those found in manufacturing. Our work employs Deep Q-Networks (DQN), a DRL algorithm developed by Mnih et al. [22]. DQN leverages deep neural networks to handle high-dimensional state spaces, making it possible to apply RL to complex, real-world problems. The core characteristics of DQN that are critical for our application are as follows:

• The agent learns directly from trial-and-error interaction with the environment (in our case, the simulation model) without needing an explicit mathematical model of its dynamics. This is essential for complex systems where such models are intractable.
• DQN learns a state-action value function, or Q-function, Q(s, a), which estimates the expected long-term reward of taking action a in state s. The optimal policy is then implicitly defined by choosing the action with the highest Q-value in any given state.
• The agent can learn about the optimal policy while following a different, more exploratory policy (e.g., $ϵ$-greedy [23]). This is achieved by storing past experiences—tuples of (state, action, reward, next state)—in a replay buffer, which improves sample efficiency and stabilizes the learning process.

The learning objective in Q-learning is to find a Q-function that satisfies the Bellman optimality equation. For a given transition, the Q-value is updated based on the immediate reward r and the discounted maximum Q-value of the next state $s^{\prime }$:

$$Q(s,a)\leftarrow (1-\alpha )Q(s,a)+\alpha \left[r(s,a)+\gamma \underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime })\right]$$

(1)

where $\gamma$ is the discount factor balancing immediate and future rewards, and $\alpha$ is the learning rate. DQN approximates the Q-function using a neural network with parameters $\theta$, denoted Q(s, a; θ). The network is trained by minimizing the mean squared error between the predicted Q-value and a target value y, which is calculated using a separate, periodically updated target network with parameters ${\theta }^{-}$ to stabilize training:

$$L\left(\theta \right)=\mathbb{E}\left[{\left(y-Q(s,a;\theta )\right)}^2\right],\mathrm{where}y=r+\gamma \underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime };{\theta }^{-})$$

(2)

By leveraging these techniques, DQN provides a powerful and flexible algorithm for learning effective control policies in environments with large, continuous state spaces and discrete action spaces, which directly matches the requirements of our production control problem.

2.4. Related Works in DRL for Manufacturing Control

DRL has been increasingly applied to solve complex decision-making problems in manufacturing. Beyond the well-studied streams of dynamic scheduling/dispatching and (more recently) adaptive WIP control, a growing body of work investigates integrated planning–scheduling frameworks with hierarchical or multi-agent RL. These contributions strengthen the case for coordination across time scales, but they are typically tailored to flexible/line-less settings (mobile robots, layout reconfiguration) rather than conventional flow-shops with WIP as an explicit control lever.

A significant body of work has concentrated on optimizing job sequencing. For instance, Luo et al. [24] and Park et al. [25] developed DRL agents that dynamically select dispatching rules in job shop environments, outperforming static heuristics. Similarly, Wang et al. [26] and Li et al. [27] explored advanced DRL architectures for assembly and parallel machine scheduling, achieving notable improvements in local performance metrics such as earliness or flow time. While powerful, these approaches treat WIP management as an external factor or a secondary constraint, rather than an active control variable.

A separate, emerging stream addresses adaptive WIP regulation. Traditional release mechanisms such as Workload Control (WLC) [28] or POLCA [29] already emphasized load-dependent release, but in static form. Our strategic agent can be viewed as a generalization of these mechanisms: instead of fixed cards or workload thresholds, it learns to regulate WIP adaptively to achieve throughput targets. Vespoli et al. [15] show that a single DRL agent can effectively manage system-wide WIP levels in a flow shop, stabilizing throughput under high variability. Our strategic agent can be seen as a generalization of this concept, learning a dynamic job release policy not tied to a fixed card count, thereby offering greater flexibility.

Related efforts using digital twins (e.g., Xia et al. [30]; Müller-Zhang et al. [31]) facilitate DRL-based control, but typically focus on micro-level parameters or segment the control problem rather than unifying WIP and sequencing logic.

Recent integrated frameworks demonstrate hierarchical/multi-agent coordination but in problem settings orthogonal to ours. Wang et al. propose a demand-driven hierarchical planner–scheduler for flexible smart manufacturing with mobile, multi-skilled robots, using a property-infused MADDPG to couple an outer planning loop and an inner scheduling loop [32]. Their focus is integrated capacity/configuration and robot assignment under disruptions, not WIP governance in flow-shops. Kaven et al. tackle online, integrated layout planning and scheduling in line-less mobile assembly systems via a cooperative, asynchronous MARL approach based on PPO, with an encoder–decoder that scales to variable-sized system states [33].

While powerful, these solutions address a different problem: optimizing the physical configuration and routing of resources. They are not directly transferable to conventional flow shops where the line is fixed and system-wide material flow, governed by WIP, is the dominant control lever.

Despite progress on dynamic dispatching, adaptive WIP control and, recent, hierarchical or multi-agent integration in flexible systems, there remains a lack of frameworks that jointly and concurrently optimize WIP levels and job sequencing in flow-shops, with scalability guaranteed as the number of machines grows. These levers are interdependent: WIP determines local queue states, while dispatching policies determine WIP consumption rates. Decoupling them, as common in prior work, risks suboptimal coordination.

We address this gap with a two-level, dual-agent architecture that learns (i) a strategic WIP policy and (ii) a tactical, event-driven sequencing policy via parameter sharing. Unlike hyper-heuristic designs where WIP is handled separately [34], our approach embeds dynamic sequencing into the same control loop that regulates WIP, yielding scalable coordination in conventional flow-shops.

From a methodological perspective, the DRL literature also provides extensions to vanilla DQN: Double-DQN, Dueling-DQN, and Prioritized Experience Replay (PER) [35] mitigate overestimation and sample inefficiency, while recurrent variants such as DRQN explicitly address partial observability in sequential tasks [36]. Here we adopt standard DQN to isolate the contribution of the dual-agent decomposition itself.

The preceding review, crystallized in

Table 2. Argumentative comparison of DRL-based manufacturing control approaches.

Reference	Primary Control Lever(s)	Scalability Strategy	Action Space Growth	Key Focus and Limitations
Focus on Sequencing/Dispatching
Luo et al. [24]	Sequencing (Rule Selection)	Centralized DQN/Double DQN	Constant	Adaptive dispatching; WIP is secondary.
Park et al. [25]	Sequencing (Rule Selection)	Digital twin integration	Constant	Flexible dispatching; no adaptive WIP regulation.
Wang et al. [26]	Sequencing (Assembly Scheduling)	Dual Q-learning for local/global objectives	Grows with jobs/operations	Due-date adherence; WIP is static.
Li et al. [27]	Sequencing (Parallel Machines)	Innovative state/action design	Grows with jobs	Machine-level scheduling only.
Focus on WIP Control
Vespoli et al. [15]	WIP Control (Adaptive CONWIP)	System-level single agent	Constant	Adaptive job release; sequencing is fixed.
Focus on Integrated Control in Flexible/Reconfigurable Systems
Panzer et al. [34]	Sequencing (Hyper-heuristic)	Modular policy learning	Constant	Reconfigurable systems; WIP handled externally.
Wang et al. [32]	Integrated (Planning, Robot Scheduling)	Hierarchical MARL (P-MADDPG)	Increases with tasks/robots	Coordination in flexible manufacturing (robotics).
Kaven et al. [33]	Integrated (Layout, Scheduling)	Cooperative MARL with encoder-decoder	State-dependent (variable)	Online layout/routing for line-less assembly.
Focus on DRL-driven Simulation & Segmented Control
Xia et al. [30]	Micro-level Parameters	Digital twin training	Task-dependent	Real-time adaptability for micro-tasks.
Müller-Zhang et al. [31]	Planning	Segmentation by lot size	Varies by scale	No unified WIP-control mechanism.
This Work	Integrated (WIP + Sequencing)	Hierarchical dual-agent; parameter sharing	Constant	Scalable joint control for conventional flow shops.

, reveals a distinct research gap. The literature is largely partitioned into three streams: (i) approaches that optimize the sequencing lever but treat WIP as a static external factor; (ii) those that manage the WIP control lever but rely on fixed sequencing rules; and (iii) advanced hierarchical frameworks that target different control levers (e.g., layout, robot routing) for flexible, non-conventional production systems. Consequently, there is a lack of frameworks that jointly and concurrently optimize system-level WIP and machine-level sequencing in conventional flow shops. Furthermore, a critical challenge highlighted in our comparison is scalability. Many integrated approaches exhibit an action space that grows with the system size (e.g., with the number of jobs or robots), limiting their applicability. There is a clear need for an architecture that can manage the strong interdependence between WIP and sequencing while maintaining a constant action space growth, thus ensuring scalability. To address this gap, this paper proposes a two-level, dual-agent architecture. It is specifically designed to manage this interdependence through a strategic WIP agent and a tactical sequencing agent, whose parameter-sharing design guarantees a constant-size action space, delivering a truly scalable solution for conventional flow shops.

3. A Two-Level DRL Framework for Joint Production Control

3.1. System Model and Assumptions

The control framework proposed in this study is designed for a conventional flow shop production system. To establish a clear and reproducible basis for our model, we define the following system characteristics and operational assumptions:

• An infinite backlog of jobs is assumed to be perpetually available. This allows the strategic agent to control the release of new jobs into the system at any time, focusing the problem on internal flow regulation (at the push-pull boundary) rather than on managing stochastic external arrivals.
• The buffers located between consecutive machines are assumed to have unlimited capacity. Consequently, a machine is never blocked because the downstream buffer is full. This assumption isolates the system’s performance dynamics to queuing and processing variability.
• All machines are considered perfectly reliable and are not subject to breakdowns, maintenance periods, or sequence-dependent setup times. This simplification allows the analysis to focus squarely on the core challenges of WIP control and dynamic sequencing.
• All machines in the flow shop are functionally identical and share the same average processing rate. While individual job processing times are stochastic, there is no designated bottleneck station by design.
• When a dispatching decision is triggered at a machine, the processing times of all jobs currently waiting in its input buffer are known. This is a standard assumption in the scheduling literature and is a prerequisite for implementing dispatching rules such as Shortest Processing Time (SPT) and Longest Processing Time (LPT).

To establish a robust benchmark relative to the literature, we adopt the CONWIP approach as our control mechanism. CONWIP facilitates a quantitative modelling of throughput, one of the key performance indicators, by regulating the allowable WIP level within the production system. This method builds on the work of Hopp and Spearman [19], whose PWC framework provides a rigorous basis for understanding the interrelations among throughput, cycle time, and WIP under uncertainty.

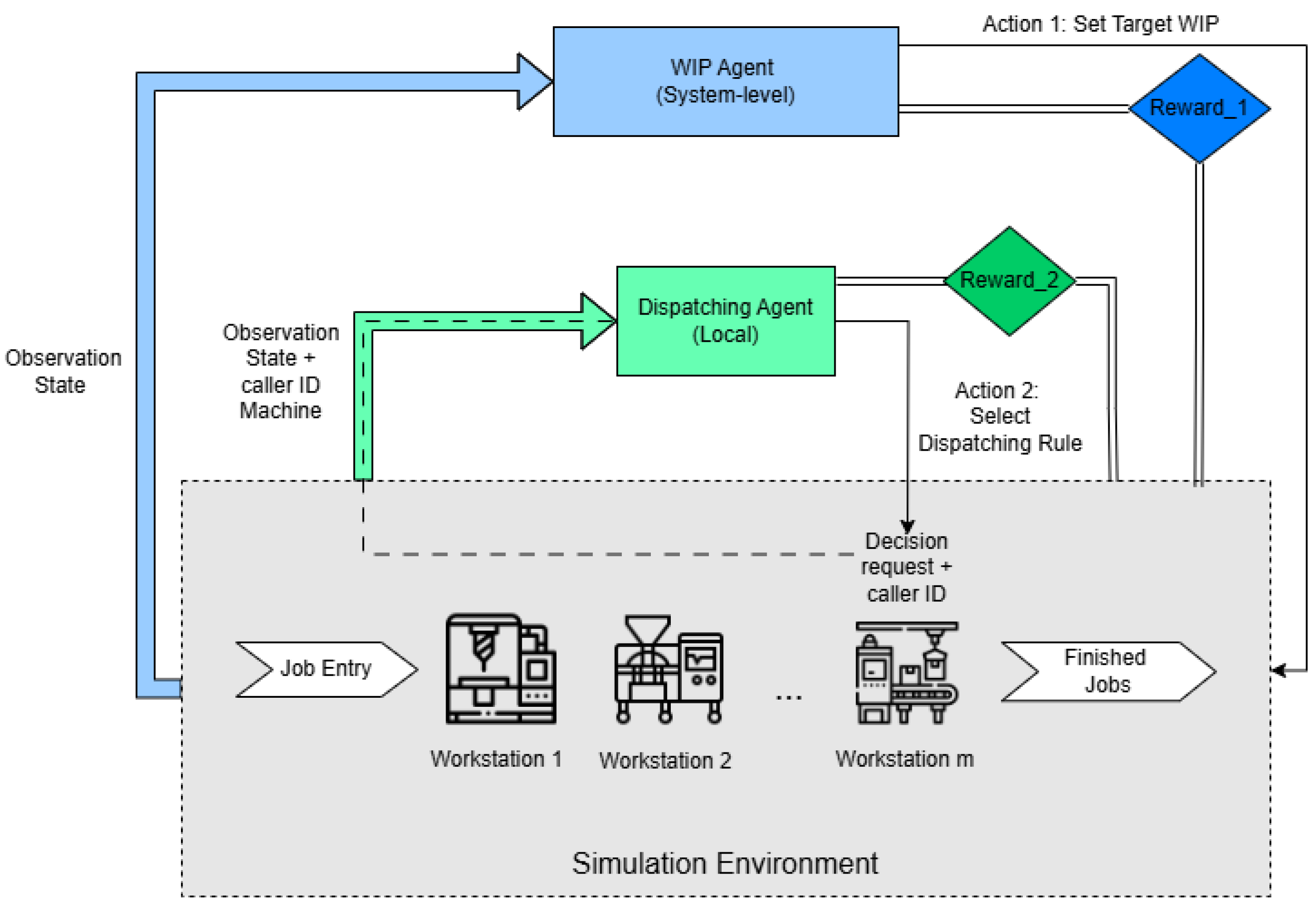
Our main innovation consists of a coordinated DRL architecture in which two agents perform complementary but interdependent functions, as illustrated in Figure 1. Instead of treating WIP control and job scheduling as isolated tasks, our framework integrates them into a hierarchical structure that is both robust and scalable. The key components of our approach are as follows:

• A strategic WIP control agent, which operates at the system level to dynamically regulate the number of jobs in the production line, aiming to meet global throughput targets.
• A tactical dispatching agent, which makes real-time, local sequencing decisions for each machine, aiming to optimize material flow efficiency.

Each agent operates within a shared simulation environment and relies on a state representation enriched with both global and local production features. Inspired by the principles of the PWC framework, their respective reward structures encourage aligned decisions that improve both system-level flow and station-level efficiency. The strategic agent’s actions (setting the WIP level) directly alter the state of the system, influencing the queue lengths and workload observed by the tactical agent. In turn, the tactical agent’s decisions on job sequencing affect how quickly WIP is consumed, which impacts the overall system throughput and provides feedback to the strategic agent. This structure creates a natural hierarchy where global strategy guides local tactics.

A critical innovation of our framework lies in the design of the tactical dispatching agent, which ensures the entire system is scalable. Instead of a monolithic agent that decides on a policy for all machines simultaneously—an approach that suffers from an exponentially growing action space—our tactical agent is event-driven and employs a parameter-sharing architecture.

3.2. Event-Driven Dispatching with Parameter Sharing

The tactical dispatching agent is not activated at fixed time intervals. Instead, it is triggered (or “called”) by a specific event: a machine completes processing a job and its input buffer is not empty. At this moment, a decision is needed on which job to process next. This event-driven mechanism ensures that decisions are made precisely when and where they are required.

To handle these decisions scalable, we use a single DQN agent trained with parameter sharing. The architecture works as follows:

• Action Space: When invoked for a specific machine, the agent’s task is to select one dispatching rule from a predefined set: FIFO, SPT, or LPT. The action space is therefore a discrete set of size 3, which is constant and independent of the number of machines in the system. This design choice completely avoids the curse of dimensionality.
• State (Observation) Space: A DQN is trained to make decisions for any machine. When a decision is required for machine i, the agent receives a state vector that includes both local and global information. This state representation is largely consistent with the one described but is augmented with a machine identifier (e.g., a caller encoded vector representing machine i). This allows the single policy network to learn context-specific actions, tailoring its decision to the particular machine that triggered the event.
• Policy Learning: By training a single network on experiences gathered from all machines, the agent learns a generalized policy. It learns to map a given machine’s local state and the system’s global state to the most effective dispatching rule for that specific context.

By integrating dynamic WIP management with this scalable, adaptive dispatching rule selection, we present an innovative solution that enhances production efficiency and flexibility in stochastic manufacturing environments. This approach not only achieves target throughput more consistently but also provides the agility and scalability required by modern, complex flow-shop systems.

3.3. Modelling the Hierarchical Control Problem

The hierarchical control problem is modelled as a Partially Observable Markov Decision Process (POMDP). This formalism is appropriate primarily due to the nature of the tactical agent’s decision-making process. As this agent is event-driven and shared across all machines, its observation at any given decision point is inherently partial: it receives a detailed snapshot of the local state for the machine requesting a decision, alongside a summary of the global system state, rather than a continuous and complete view of all simultaneous machine-level dynamics.

While the environment is formally a POMDP, we employ a standard feed-forward DQN for our agent. This choice is justified because the observation, despite being a snapshot, is engineered to be sufficiently rich to approximate the Markov property for the immediate task. Furthermore, by training a single policy network on experiences gathered from all machines over time, the DQN learns to generalize and infer the underlying system dynamics from the aggregated set of partial observations stored in its replay buffer.

The agents interact with a multi-method simulation environment, which incorporates both Discrete Event Simulation (DES) and agent-based modelling to provide a realistic test-bed for training and evaluation.

The specific configuration of the state representation (observation space), action spaces, and reward functions presented here builds upon and expands our initial investigations [14,16], with crucial refinements to ensure scalability and robustness.

3.3.1. State Space

Both agents observe the state of the shared environment, but they attend to different aspects of it. The global observation vector captures the current condition of the flow shop. For a system with m machines, the full state vector is structured as follows:

• Queue Sizes: A vector of m values [${\mathbf{S}}_0,\dots ,{\mathbf{S}}_{m-1}$] representing the number of jobs waiting at each machine.
• Queue Statistics (Standard Deviation and CV): Two vectors of size m each, [${\mathbf{S}}_m,\dots ,{\mathbf{S}}_{2m-1}$] and [${\mathbf{S}}_{2m},\dots ,{\mathbf{S}}_{3m-1}$], recording the standard deviation and coefficient of variation of processing times for jobs in each queue. These metrics inform agents about local variability.
• Machine Utilizations: A vector of m values [${\mathbf{S}}_{3m},\dots ,{\mathbf{S}}_{4m-1}$] measuring the estimated utilization of each machine.
• Global Performance Metrics: Two scalar values, $S_{4m}$ and $S_{4m+1}$. $S_{4m}$ is the normalized mean error of the system’s throughput relative to its target. $S_{4m+1}$ is a binary feasibility flag indicating if system constraints (e.g., WIP caps) are met.

The strategic WIP control agent observes the entire state vector, with a focus on global metrics like $S_{4m}$ and $S_{4m+1}$ to make its decisions.

The tactical dispatching agent, being event-driven and shared across machines, requires an augmented state representation. When this agent is “called” to make a decision for machine i, its input vector includes the global state information relevant to local decisions (e.g., queue sizes and utilizations) and, critically, a machine identifier. This identifier, a caller encoded vector of size m, informs the single DQN policy which machine it is currently making a decision for. The global performance metrics ($S_{4m}$, $S_{4m+1}$) are excluded from its observation, as its task is focused on local flow efficiency.

3.3.2. Action Space

The action spaces are decoupled according to the agents’ roles:

• WIP Control (Strategic Agent): The action space is a discrete set of 41 possible adjustments to the system-wide WIP level (e.g., releasing 0 to 40 new jobs). This agent is invoked at regular, longer time intervals to set the overall production strategy.
• Job Sequencing (Tactical Agent): This agent’s action space is designed for scalability. When invoked for a machine i, it selects an action from a small, discrete set of dispatching rules: {FIFO, SPT, LPT}. The action space thus has a constant size of 3, regardless of the number of machines in the system. This avoids the exponential complexity of $3^m$ associated with centralized, simultaneous rule assignment and is the key to the framework’s scalability.

3.3.3. Reward Functions

Each agent is guided by a distinct reward function tailored to its objective, ensuring that they learn complementary, synergistic behaviours.

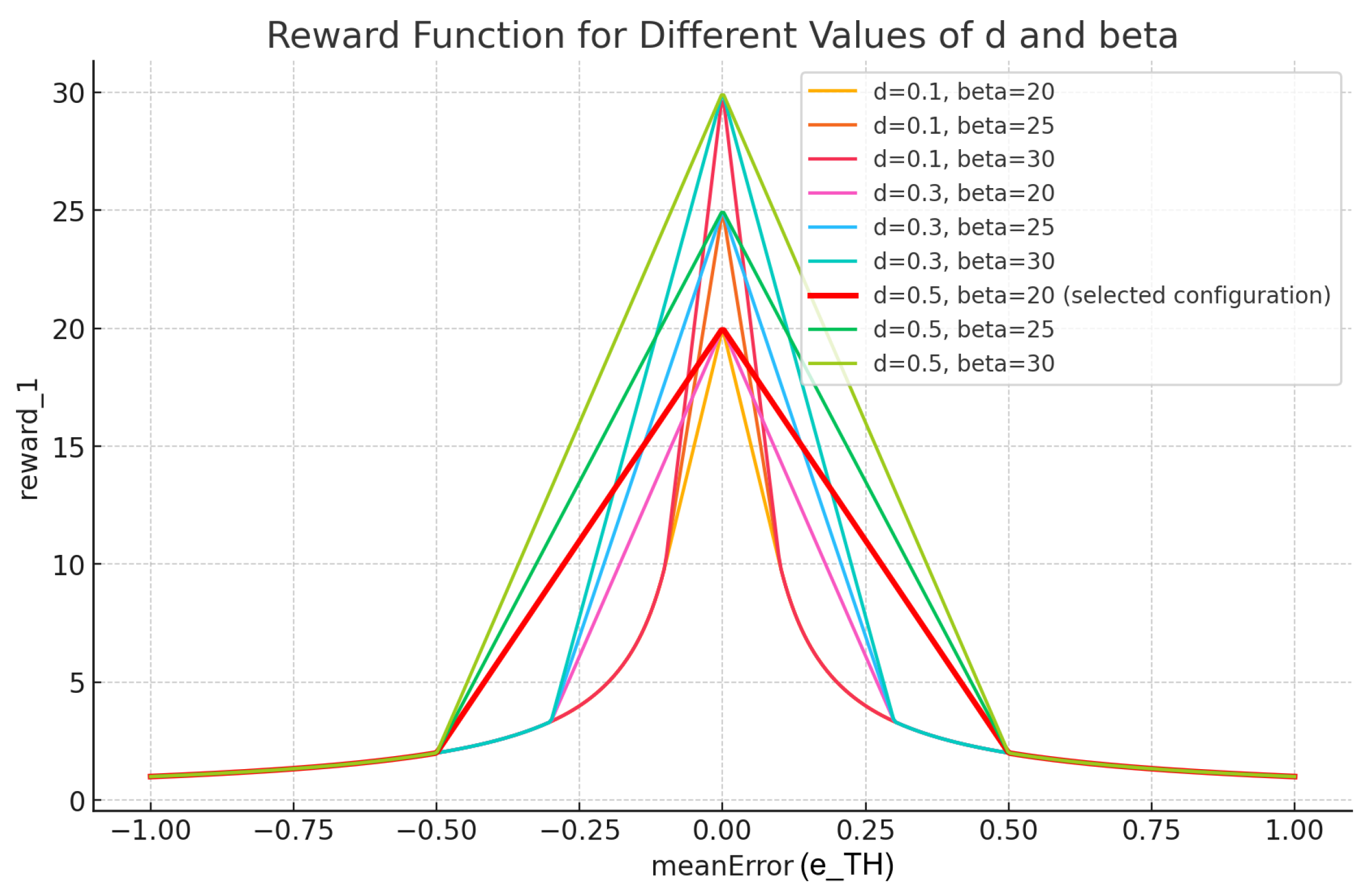
• Reward for WIP Control Agent: The system-level agent receives a reward based on how closely the system’s throughput matches the target. This reward, defined in Equation (3), penalizes deviations from the desired throughput, using a tolerance band d and a scaling coefficient $\beta$ to provide smooth gradients near the target and strong penalties for poor performance. This incentivizes the agent to maintain global stability.
• Reward for Dispatching Agent: The station-level agent is rewarded based on its impact on local throughput. This reward, defined in Equation (5), is a logarithmic function of the throughput observed over a recent time window. It promotes efficient job sequencing up to the bottleneck rate $r_b$, without encouraging instability. The normalization by ${\mathrm{score}}_{\max }$ ensures comparability across different system states.

Together, these complementary reward structures allow the system to coordinate high-level throughput regulation and low-level sequencing decisions, leading to emergent global optimization behaviour in complex flow-shop scenarios.

3.4. Strategic Agent: System-Level WIP Regulation

Within the coordinated dual-agent architecture, the strategic agent is responsible for regulating the overall system load. Its primary role is to maintain an efficient production flow and meet a global throughput target by dynamically adjusting the Work-In-Process (WIP) level. At regular intervals, this agent selects an action from a discrete set of 41 possible choices, which correspond to releasing between 0 and 40 new jobs into the system. This decision directly influences the long-term operational state of the production line.

The strategic agent is guided by a custom reward function that evaluates how closely the system’s actual throughput aligns with the target. Specifically, the agent is rewarded based on the absolute deviation, defined as $e_{TH}=TH-T{H}_{\mathrm{target}}$. The closer this error is to zero, the higher the reward, directly encouraging actions that minimize the deviation. The reward function is defined by a piecewise structure (Equation (3)) with a parameter d representing a tolerance threshold.

• When the error is outside the threshold ($|e_{TH}|>d$), the reward is inversely proportional to the error, strongly penalizing poor control.
• When the error is within the threshold, a linear expression modulated by a constant $\beta$ provides smoother gradients, ensuring stable learning near the optimal policy.

This design consistently incentivizes the agent to minimise error while avoiding reward discontinuities.

$$rewar{d}_1=\{\begin{array}{cc}{\displaystyle \frac{1}{|e_{TH}|}},\hfill & \mathrm{if}|e_{TH}|>d\\ \left({\displaystyle \frac{1}{d}}-\beta \right)·{\displaystyle \frac{|e_{TH}|}{d}}+\beta ,\hfill & \mathrm{if}|e_{TH}|\le d\end{array}$$

(3)

As illustrated in Figure 2, this function balances robust penalties with fine-grained feedback. Based on a pre-experimental tuning campaign [14], the parameters d and $\beta$ were selected. The tolerance threshold $d=0.5$ defines a $\pm 50\%$ band around the target throughput. This relatively wide threshold was selected to mitigate the impact of minor stochastic fluctuations, while empirical tests confirmed that it remained sufficiently narrow to allow genuine control errors to be detected. The slope coefficient $\beta =20$ was chosen to maintain sufficient gradient near the target while avoiding excessively steep updates that could destabilise learning.

This tuning was conducted over 10 preliminary training runs in the $m=5$ machine scenario, monitoring convergence stability and reward variance. The selected values provided a compromise between fast convergence and robustness to throughput variability.

3.5. Tactical Agent: Event-Driven Local Sequencing

The tactical agent is responsible for optimizing local material flow by making real-time job sequencing decisions. As highlighted in the literature [37,38], no single dispatching rule is optimal across all contexts. Our agent addresses this by dynamically selecting the most appropriate rule based on the current system state.

Crucially, this agent operates on an event-driven basis. It is triggered only when a machine completes a job and needs to select the next one from its queue.

At this decision point, the agent chooses one of three widely used dispatching rules: FIFO, SPT, or LPT. This set was deliberately selected to span distinct and complementary scheduling behaviours.

• FIFO as a neutral, fairness-oriented baseline that preserves arrival order;
• SPT as a throughput-oriented rule known to minimise mean flow time in many stochastic settings;
• LPT as a utilisation-oriented rule that can reduce idle time in specific bottleneck scenarios.

Covering these three archetypes ensures that the agent is exposed to markedly different control logics, enabling the learning process to capture trade-offs between stability, responsiveness, and utilisation without over-complicating the action space.

Limiting the action set also serves a practical purpose: it keeps the tactical agent’s decision space constant and compact, which is essential for the scalability objective of this study. Expanding the set to a large number of similar heuristics would increase training complexity and potentially dilute policy learning [37,38], without proportionate gains in representativeness. As shown in previous works on adaptive dispatching [37,38], even a small, well-chosen portfolio of rules can approximate or surpass the performance of larger rule sets in dynamic environments.

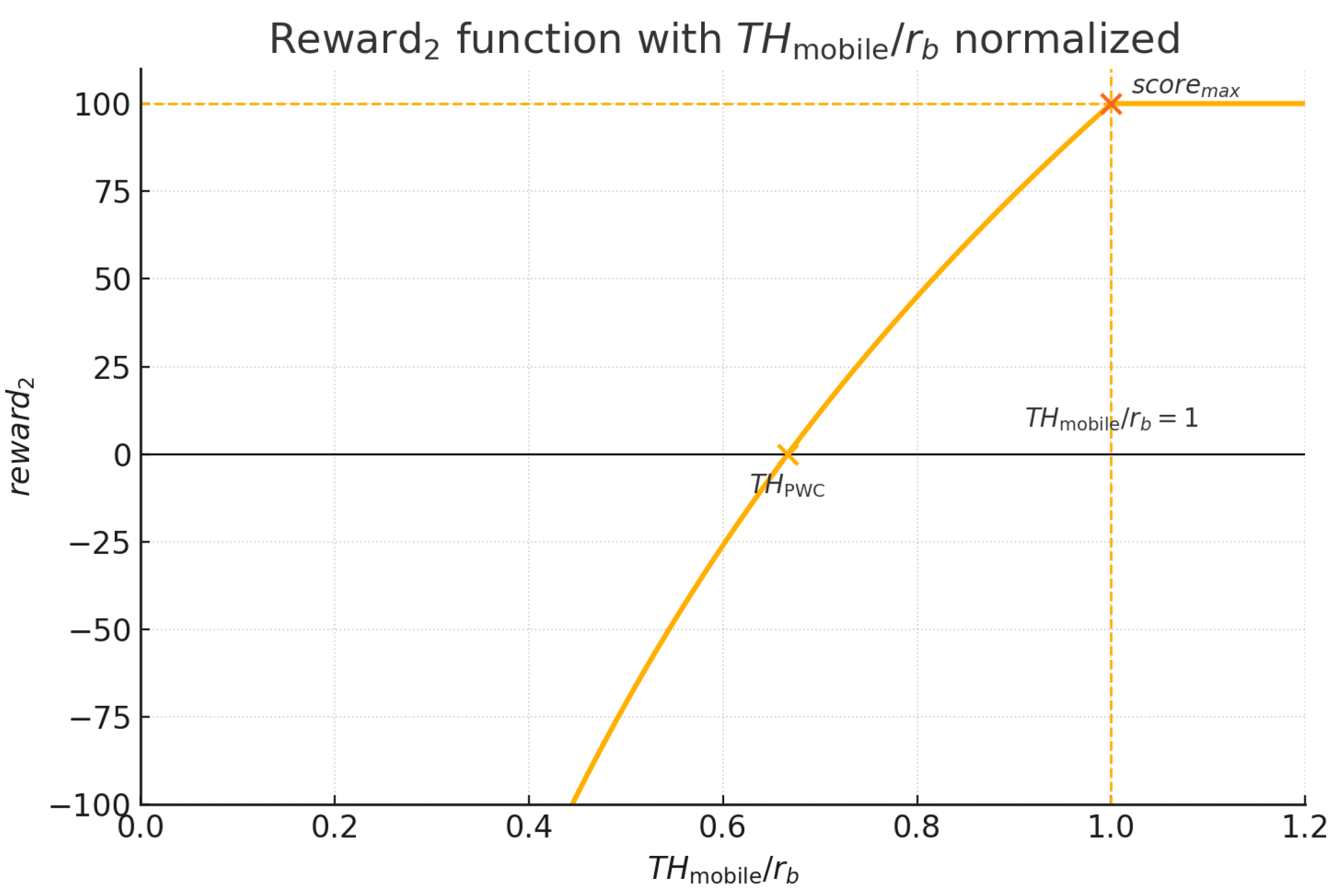
The tactical agent’s reward function is designed to promote local throughput efficiency. It monitors the mobile throughput of the system, defined as

$$T{H}_{mobile}={\displaystyle \frac{N}{{\Delta }_t}}$$

(4)

where N is the number of jobs completed in a sliding window of ${\Delta }_t=240$ min (equivalent to half a working shift). This measure provides a responsive evaluation of sequencing performance. The sliding window $\Delta t=240$ min corresponds to half of a standard working shift in many industrial contexts, allowing the reward to reflect medium-term sequencing effects without being dominated by transient noise. The cap parameter $scor{e}_{max}=100$ normalises reward magnitudes to a scale consistent with the strategic agent, facilitating balanced policy learning.

The choice of using the bottleneck rate $r_b$ as an upper bound in the logarithmic term ensures that the agent is incentivised to approach but not overshoot the stable capacity of the system, in line with established production control principles.

To further enhance the scalability of the approach to systems with multiple machines and different capacity profiles, $T{H}_{\mathrm{mobile}}$ is normalised by $r_b$. This transformation, shown in Equation (6), allows the reward curve to be expressed in a dimensionless form, making it invariant to absolute throughput values. As a result, the same learning architecture and hyperparameters can be applied consistently across scenarios with different bottleneck capacities, without requiring manual recalibration of reward scaling.

The corresponding reward function, $rewar{d}_2$, is defined in Equation (5) and showed in Figure 3. It assigns logarithmically increasing rewards for improvements in $T{H}_{mobile}$ (or its normalised counterpart) up to the bottleneck rate $r_b$. This encourages the agent to maximize throughput without inducing instability. Once $T{H}_{mobile}>r_b$, the reward is capped at a fixed value $scor{e}_{max}$ to avoid unrealistic incentives. To clarify, the logarithmic terms in Equations (5) and (6) are applied only to dimensionless and strictly positive arguments. In the normalized formulation, the factor $\frac{T{H}_{\mathrm{mobile}}}{r_b}$ represents throughput expressed as a fraction of the $r_b$, while $\frac{W_0+W-1}{W}$ is a positive scaling coefficient depending on the current WIP state. Their product is therefore dimensionless and non-negative under the constraint $\frac{T{H}_{\mathrm{mobile}}}{r_b}\in [0,1]$, which ensures that the logarithm is always well defined. The denominator, $log\left({\left(\frac{W_0+W-1}{W}\right)}^{1/scor{e}_{max}}\right)$, acts as a normalization factor that bounds the reward within $[0,scor{e}_{max}]$. This design guarantees both dimensional consistency and mathematical validity while preserving interpretability in terms of throughput regulation.

$$rewar{d}_2=\{\begin{array}{cc}{\displaystyle \frac{log\left(\frac{W_0+W-1}{W·r_b}·T{H}_{mobile}\right)}{log\left({\left(\frac{W_0+W-1}{W}\right)}^{\frac{1}{scor{e}_{max}}}\right)}},\hfill & \mathrm{if}T{H}_{mobile}\in [0,r_b]\\ scor{e}_{max},\hfill & \mathrm{if}T{H}_{mobile}\in (r_b,\infty )\end{array}$$

(5)

$$rewar{d}_{2normalized}=\{\begin{array}{cc}{\displaystyle \frac{log\left(\frac{W_0+W-1}{W}·\frac{T{H}_{\mathrm{mobile}}}{r_b}\right)}{log\left({\left(\frac{W_0+W-1}{W}\right)}^{\frac{1}{scor{e}_{max}}}\right)}},\hfill & \mathrm{if}{\displaystyle \frac{T{H}_{\mathrm{mobile}}}{r_b}}\in [0,1]\\ scor{e}_{max},\hfill & \mathrm{if}{\displaystyle \frac{T{H}_{\mathrm{mobile}}}{r_b}}\in (1,\infty )\end{array}$$

(6)

In Equation (5), $W_0$ is the critical WIP and W is the current WIP. This reward structure ensures the tactical agent learns sequencing policies that promote efficient flow without destabilizing the system.

3.6. Computational Complexity and Scalability Analysis

A fundamental claim of our framework is its scalability, which is rooted in its computational efficiency. This section provides a formal analysis of the computational complexity, focusing on the online inference phase, which is critical for real-time decision-making. Let m denote the number of machines in the Flow Shop.

Inference involves a forward pass through a DQN to select an action given the current state. The complexity is determined by the size of the network’s input layer and its fixed architecture.

• Strategic WIP Agent: This agent observes the entire state vector. As described in Section 3.3.1, its input vector is composed of Queue Sizes (m values), Queue Statistics ($2m$ values), Machine Utilizations (m values), and Global Performance Metrics (2 values). The total input vector size is therefore $4m+2$. Since the computational cost of a forward pass in a neural network is dominated by the matrix operations involving the input layer, the inference complexity for the strategic agent is linear with respect to the number of machines, or $\mathcal{O}\left(m\right)$.
• Tactical Dispatching Agent: This agent’s scalability is achieved through parameter sharing and a carefully curated state representation. When invoked for a decision at machine i, its observation space excludes the two global performance metrics but includes a machine identifier. Specifically, its input vector consists of Queue Sizes (m), Queue Statistics ($2m$), Machine Utilizations (m), and a caller-encoded vector representing the machine identifier (m). The total input vector size is thus $5m$. Consequently, the inference complexity for a single dispatching decision also remains linear, $\mathcal{O}\left(m\right)$.

Crucially, the framework’s architecture avoids the combinatorial explosion typical of multi-machine scheduling. By using an event-driven mechanism where a single agent makes one decision at a time (with a constant action space of size 3), we transform an inherently exponential problem into a linear one. A naive, centralized approach that simultaneously selects one of three rules for all m machines would face an action space of size $3^m$ and an exponential complexity of $\mathcal{O}\left(3^m\right)$. In contrast, our method’s linear complexity, $\mathcal{O}\left(m\right)$, ensures its applicability to large-scale systems. This theoretical result is validated by our empirical findings (Section 5.4), where inference times were consistently under 1 ms, well within the strict requirements for real-time control. During the offline training phase, the complexity of a single backpropagation update is proportional to the number of network parameters. As the size of the input layer—and thus the number of parameters in the first hidden layer—grows linearly with m, the training complexity per step is also $\mathcal{O}\left(m\right)$. While larger systems may require more training episodes to converge, the fundamental computational cost per learning step remains efficiently scalable.

4. Experimental Setting and Results

4.1. Simulation Environment and DRL Framework Integration

The experimental environment was developed in AnyLogic, a simulation platform supporting multi-method modelling. We leveraged this capability to create a high-fidelity representation of the flow shop:

• Discrete Event Simulation (DES): The overall process flow, including job creation, movement between workstations, and queuing dynamics, was modelled using a DES paradigm. This ensures a precise and robust handling of event-driven interactions and resource contentions.
• Agent-Based Modelling (ABM): Individual entities like ‛Jobs‛ and ‛Machines‛ were implemented as agents. This allowed for the encapsulation of specific behaviours, attributes (e.g., processing times), and decision logic at a granular level.

This hybrid approach provides a realistic test-bed, combining the systemic rigour of DES with the localized intelligence of ABM.

For the Reinforcement Learning components, we used the rl4j library, which is based on Deeplearning4j in Java. A key contribution of our work setup is the tight, integration between the AnyLogic simulation and the rl4j framework. This allowed us to perform the entire DRL training cycle—where agents observe states, take actions within the simulation, and receive rewards—directly inside the AnyLogic platform. This setup streamlines the experimental workflow, eliminating the need for complex co-simulation setups or model exports, and facilitates rapid prototyping and validation.

4.2. Production Scenarios and Benchmarking

Our core production scenario is a CONWIP-governed flow shop. The experimental campaign was designed to test the performance, scalability, and robustness of our dual-agent framework under various conditions:

• Scalability Analysis: We tested the framework on systems of increasing size, specifically configurations with 5, 10, and 15 machines. This was crucial to validate the effectiveness of our scalable, event-driven dispatching agent.
• Robustness to Variability: Beyond the baseline scenario with exponentially distributed processing times (which aligns with the PWC benchmark), we explored the system’s resilience to different levels of variability. We used a Gamma distribution for processing times and varied its shape parameter $\alpha$. Scenarios ranged from highly stochastic ($\alpha <1$) to nearly deterministic ($\alpha >1$), covering a wide spectrum of realistic manufacturing environments.
• Benchmark Comparison: The performance of our DRL agent was consistently benchmarked against traditional static policies. This included comparing its throughput and cycle times against the analytical PWC model and evaluating its dispatching choices against fixed rules like FIFO and SPT.

The choice of benchmarks was guided by the study’s primary objectives: to evaluate the scalability and coordination capability of the proposed dual-agent architecture against strong, widely recognised baselines.

For WIP control, the PWC model [11,19] was adopted as it provides a theoretical throughput reference under stochastic processing times and is a standard analytical benchmark in production control research. Although PWC is a static model, its conservative nature makes it a rigorous baseline for assessing improvements from dynamic, adaptive policies.

For sequencing, fixed dispatching rules were chosen as they represent the prevailing industrial practice in flow-shop control and are commonly used in adaptive dispatching literature [37,38] as reference points for evaluating new decision-making mechanisms.

More complex metaheuristic or hybrid methods were deliberately excluded from the comparative set, as their integration would require significantly different optimisation timescales and objectives, potentially obscuring the specific contribution of the dual-agent DRL architecture. The present scope is to validate the proposed coordination mechanism against strong, interpretable baselines; extending the comparison to other optimisation paradigms is a direction for future work.

To ensure statistical reliability, each experimental scenario was replicated R times ($R=10$ for the main experiments), with independent random seeds controlling processing time generation, considering the job were always available in the queues. Mean values are reported for all performance metrics, and standard deviations are included for variability-sensitive measures such as throughput error and WIP.

We evaluate the following:

• Throughput error: $e_{TH}=TH-T{H}_{\mathrm{target}}$; we report mean and standard deviation across replications.
• WIP: time-averaged number of jobs in system; we report mean and standard deviation.

The PWC reference curves are obtained from Table 1 using the scenario-specific $(T_0,r_b,W_0)$, with W swept over the operating range.

The number of replications was chosen to balance statistical confidence with computational cost, following common practice in simulation-based production control studies [39].

4.3. Hyperparameters and Training Protocol

The dual agents in our framework, the strategic ${\pi }_{WIP}$ and the tactical ${\pi }_{SEQ}$, are trained concurrently, each learning its policy via the Deep Q-learning algorithm. Each agent maintains its own separate replay buffer and Q-network, allowing them to learn from experiences tailored to their specific tasks and timescales. The entire training process is orchestrated within the simulation as described in Algorithm 1, which details the main interaction loop, while Algorithms 2 and 3 describe the specific decision-making and learning logic for each agent.

Algorithm 1 Main Training Loop.

1: Initialize Environment E, Agents ${\pi }_{WIP},{\pi }_{SEQ}$, Replay Buffers $B_{WIP},B_{SEQ}$ 2: for episode = 1 to max_episodes do 3:     $s_{current}\leftarrow E.reset\left(\right)$ 4:     $t_{next\_WIP\_decision}\leftarrow T_{WIP}$ 5:     while E is running do 6:         $event,t_{event}\leftarrow E.getNextEvent\left(\right)$ 7:         if $event$ is MachineFreed(i) then 8:            $\mathrm{P}\mathrm{R}\mathrm{O}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{T}\mathrm{A}\mathrm{C}\mathrm{T}\mathrm{I}\mathrm{C}\mathrm{A}\mathrm{L}\mathrm{D}\mathrm{E}\mathrm{C}\mathrm{I}\mathrm{S}\mathrm{I}\mathrm{O}\mathrm{N}(E,{\pi }_{SEQ},B_{SEQ},s_{current},i)$ 9:         end if 10:         if $t_{event}\ge t_{next\_WIP\_decision}$ then 11:            $\mathrm{P}\mathrm{R}\mathrm{O}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{S}\mathrm{T}\mathrm{R}\mathrm{A}\mathrm{T}\mathrm{E}\mathrm{G}\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{E}\mathrm{C}\mathrm{I}\mathrm{S}\mathrm{I}\mathrm{O}\mathrm{N}(E,{\pi }_{WIP},B_{WIP},s_{current})$ 12:            $t_{next\_WIP\_decision}\leftarrow t_{next\_WIP\_decision}+T_{WIP}$ 13:         end if 14:         $s_{current}\leftarrow E.getState\left(\right)$ 15:     end while 16: end for

Algorithm 2 Strategic Agent Logic: $\mathrm{P}\mathrm{R}\mathrm{O}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{S}\mathrm{T}\mathrm{R}\mathrm{A}\mathrm{T}\mathrm{E}\mathrm{G}\mathrm{I}\mathrm{C}\mathrm{D}\mathrm{E}\mathrm{C}\mathrm{I}\mathrm{S}\mathrm{I}\mathrm{O}\mathrm{N}$

Require: Environment E, Agent ${\pi }_{WIP}$, Buffer $B_{WIP}$, State s

1: Choose action $a_{WIP}\in \{0,\dots ,40\}$ from s using $ϵ$-greedy policy on ${\pi }_{WIP}$    2: Execute $a_{WIP}$ in E by releasing jobs    3: $r_{WIP}\leftarrow E.getReward1\left(\right)$    4: $s^{\prime }\leftarrow E.getState\left(\right)$    5: Store transition $(s,a_{WIP},r_{WIP},s^{\prime })$ in $B_{WIP}$    6: Sample minibatch from $B_{WIP}$ and perform a gradient descent step on ${\pi }_{WIP}$

Algorithm 3 Tactical Agent Logic: $\mathrm{P}\mathrm{R}\mathrm{O}\mathrm{C}\mathrm{E}\mathrm{S}\mathrm{S}\mathrm{T}\mathrm{A}\mathrm{C}\mathrm{T}\mathrm{I}\mathrm{C}\mathrm{A}\mathrm{L}\mathrm{D}\mathrm{E}\mathrm{C}\mathrm{I}\mathrm{S}\mathrm{I}\mathrm{O}\mathrm{N}$

Require: Environment E, Agent ${\pi }_{SEQ}$, Buffer $B_{SEQ}$, State s, Machine ID i

1: $s_{aug}\leftarrow s\oplus \mathrm{caller}\left(i\right)$▹ Augment state with machine ID    2: Choose action $a_{SEQ}\in \left\{\mathrm{FIFO},\mathrm{SPT},\mathrm{LPT}\right\}$ from $s_{aug}$ using $ϵ$-greedy policy on ${\pi }_{SEQ}$    3: Execute $a_{SEQ}$ in E by setting the rule for machine i    4: $r_{SEQ}\leftarrow E.getReward2\left(\right)$    5: $s_{aug}^{\prime }\leftarrow E.getState\left(\right)\oplus \mathrm{caller}\left(i\right)$    6: Store transition $(s_{aug},a_{SEQ},r_{SEQ},s_{aug}^{\prime })$ in $B_{SEQ}$    7: Sample minibatch from $B_{SEQ}$ and perform a gradient descent step on ${\pi }_{SEQ}$

Prior to the main experimental campaign, all reward parameters (d, $\beta$, $\Delta t$, $scor{e}_{max}$) were tuned in a pilot study to balance responsiveness, stability, and interpretability. This process involved testing small grids of candidate values and selecting those that maximised policy stability (low variance in throughput error) and convergence speed, while maintaining a clear operational meaning (e.g., $\Delta t$ tied to industrial shift duration). This ensures that the reward shaping is both empirically grounded and practically interpretable.

The training loop is driven by the simulation clock. The strategic agent acts on a fixed time-based schedule ($T_{WIP}$), making high-level decisions about the system’s WIP level. In contrast, the tactical agent is event-driven, reacting instantly to ‛MachineFreed‛ events to make local sequencing decisions. This dual-timescale, hybrid activation mechanism allows the system to balance long-term strategic planning with real-time tactical adaptation.

The agents’ Q-functions are approximated using a neural network with two hidden layers of 300 nodes each. The choice of hyperparameters is critical for successful training and was informed by both established practices in DRL literature [40,41] and a preliminary tuning phase.

• Optimizer and Learning Rate: We used the Adam optimizer, a standard choice for DRL applications, with a learning rate of $0.001$.
• Regularization: To prevent overfitting and improve generalization, L2 regularization with a factor of $0.005$ was applied to the network weights.
• Discount Factor ($\gamma$): A value of $0.99$ was used to encourage the agents to prioritize long-term rewards, promoting far-sighted policies.
• Exploration Strategy ($ϵ$-greedy): The exploration rate $ϵ$ was linearly annealed from an initial value to a minimum value. This annealing process occurred over the final 10% of the total training steps to ensure a smooth transition from an initial exploratory phase to a final exploitative phase.
• TD-Error Clipping: To stabilize the learning process, the Temporal-Difference (TD) error used in the backpropagation step was clipped, preventing excessively large updates to the network weights.

Each training run was conducted for a total of 1 million simulation steps. To ensure the agents learned policies that are robust to changing conditions, the target throughput for the strategic agent was changed every 250,000 steps.

For completeness, the full hyperparameter configuration is reported in

Table 3. Hyperparameter settings for the dual-agent DQN framework.

Hyperparameter	Value
Neural network architecture	2 hidden layers, 300 units each, ReLU activations
Optimizer	Adam ($\alpha =0.001$)
Discount factor ($\gamma$)	0.99
Batch size	128
Replay buffer size	$1.0\times {10}^5$ transitions per agent, FIFO sampling
Target network update interval	1000 steps (hard update)
Exploration strategy	$ϵ$-greedy, $ϵ:1.0\to 0.1$ linearly over $9\times {10}^5$ steps
TD-error clipping	$[-1,1]$
Gradient clipping	Global norm capped at 10
Algorithmic variants	Double DQN enabled; Dueling and PER not used
Training steps	$1.0\times {10}^6$ per run
Random seeds	10 independent runs with held-out seeds for evaluation

. The settings follow established practices in deep reinforcement learning and were confirmed in preliminary pilot runs to ensure stable convergence. We explicitly indicate batch size, replay buffer setup, target network update interval, $ϵ$-schedule, activations, clipping, and reproducibility details, as requested by the reviewers.

It is important to distinguish between the training phase and the evaluation phase. During training, both agents update their networks online using $ϵ$-greedy exploration and replay buffers, while throughput targets for the strategic agent are periodically shifted (every 250,000 steps) to promote robustness. In contrast, all results reported in Section 4 are obtained in a separate evaluation phase, where the network weights are frozen, exploration is disabled ($ϵ=0$), and policies are tested on held-out random seeds not seen during training. Each evaluation episode begins with a short warm-up period to allow the system to reach a steady state before measurements are collected over a fixed test window. This separation ensures that performance metrics reflect the learned policies under stable conditions rather than transient fluctuations during learning.

5. Experimental Results

This section presents the empirical validation of the proposed dual-agent DRL framework. Its performance is evaluated across three critical dimensions: scalability against an analytical benchmark, robustness to process stochasticity, and the adaptiveness of its emergent dispatching policy. Results for the second and third experimental sets are reported only for the 5-machine configuration, as preliminary analyses showed that the 10- and 15-machine cases exhibited analogous trends and relative performances. Each experiment was replicated R times ($R=10$) with independent random seeds controlling processing time generation, ensuring statistical reliability. Mean values are reported for all metrics, with standard deviations explicitly shown for variability-sensitive measures such as throughput error and WIP.

To ensure the reliability of our simulation results, we adopted the following protocol. To mitigate initialization bias, where the system’s initial empty-and-idle state can skew performance metrics, a warm-up period was implemented at the start of each evaluation run. The length of this period was determined during preliminary testing by visually inspecting the time series of key output variables, such as WIP and throughput. Data collection for the evaluation window only began after these variables were observed to have reached a stable, stationary behaviour, indicating that the simulation had achieved a statistical steady state. This procedure ensures that the reported performance metrics are representative of the system’s long-term operational behaviour. For each experimental scenario, we conducted $R=10$ independent runs using different random number seeds. This method yields independent observations of the system’s performance, allowing for a valid assessment of its stochastic behaviour. Performance metrics are reported as the sample mean across the 10 replications. To provide insight into the robustness of the learned policy, we accompany these means with the sample standard deviation (STD). The standard deviation here quantifies the variability of the performance metric across different stochastic replications. While formal confidence intervals on the mean would be a standard alternative, the reported standard deviation serves to illustrate the consistency of the agent’s performance. The clear and consistent trends observed in the mean values across all tested scenarios support the primary conclusions of this paper.

5.1. Scalability and Performance Against an Analytical Benchmark

A primary objective of this study was to develop a control framework that is both effective and scalable to complex, multi-stage production lines. To assess this capability, we benchmarked the performance of our DRL agent against the well-established Practical Worst Case (PWC) model for flow shops of 5, 10, and 15 machines. The PWC model provides a strong theoretical upper bound on throughput for systems with stochastic processing times.

It is important to note that the PWC analytical benchmark is known to be tightest under the assumption of exponentially distributed processing times (which corresponds to the Gamma distribution with shape parameter $\alpha =1$ in our robustness analysis). For other distributions, it serves as a robust, though potentially more conservative, point of reference.

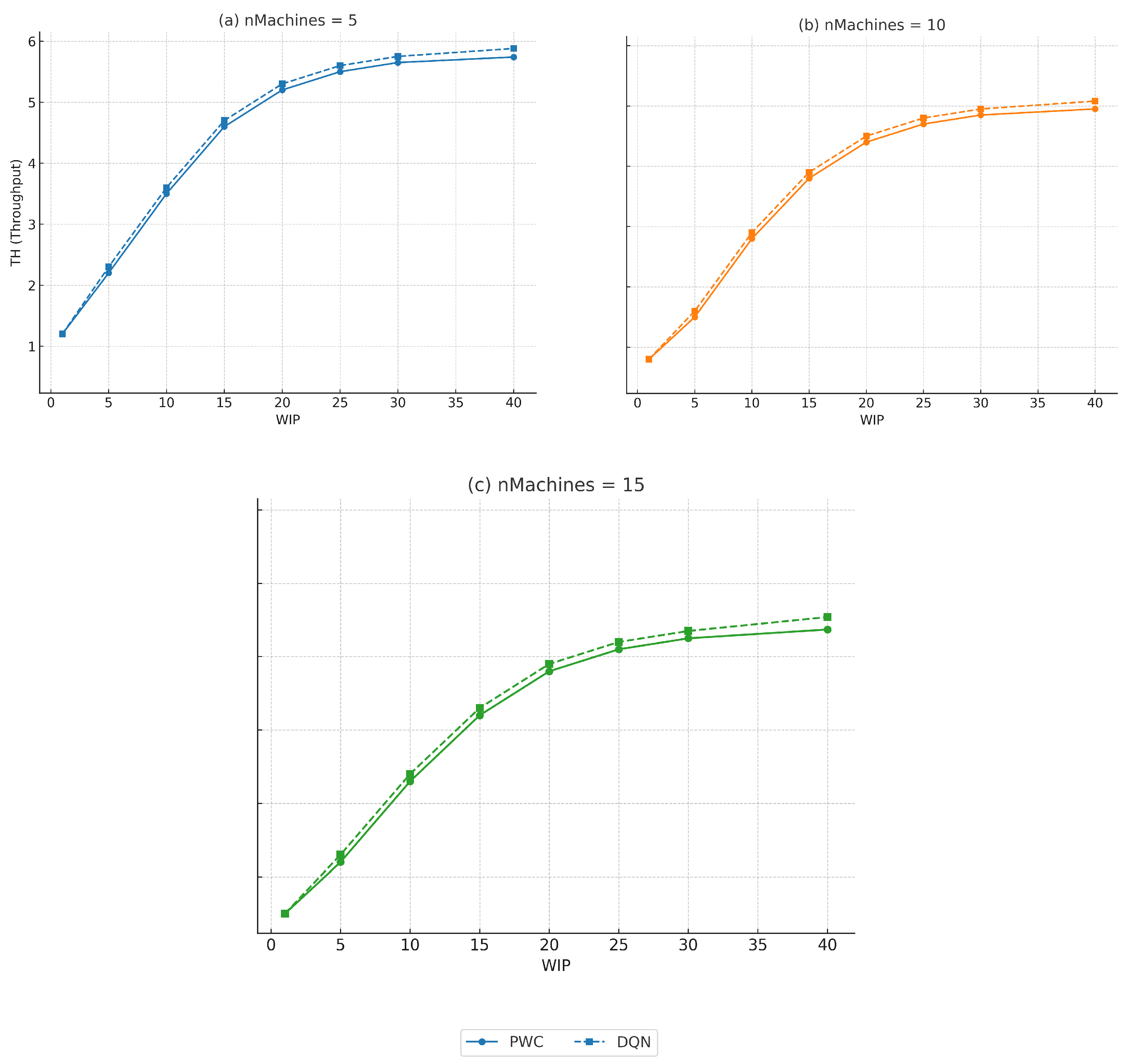
Figure 4 presents a comparative analysis between the theoretical benchmarks obtained from the PWC model and the empirical performance achieved by the proposed DQN-based control strategy. For each configuration—(a) $n=5$, (b) $n=10$, and (c) $n=15$ machines—throughput ($TH$) is plotted as a function of Work-In-Process ($WIP$). The PWC curves exhibit the expected diminishing returns as $WIP$ increases, eventually converging towards a saturation plateau.

Table 4. Maximum throughput (TH) comparison between the PWC benchmark and the proposed DQN-based approach. DQN results are reported as the mean and standard deviation (in parentheses) over 10 replications.

Machines (m)	THPWC	THDQN (STD)	Improvement (%)
5	5.74	5.88 (0.18)	+2.44%
10	4.95	5.08 (0.15)	+2.63%
15	4.37	4.54 (0.19)	+3.89%

summarises the maximum throughput values and the relative improvements achieved by the proposed approach compared with the PWC benchmark. In all configurations, the DQN-based agent matches or slightly outperforms the PWC reference. However, for higher $WIP$ values, the curves converge towards the same saturation limit, indicating that beyond this point there is little to gain from adopting either method.

The results yield several key insights:

• Across all system scales, the proposed DQN-based agent consistently achieves throughput levels that closely match or, in some cases, slightly exceed the PWC benchmark. This confirms the agent’s capability to learn highly effective, near-optimal control policies that approach theoretical performance limits.
• The framework demonstrates robust scalability: performance remains stable as the system size increases from 5 to 15 machines. This validates the architectural design, where event-driven agents with parameter sharing maintain decision-making complexity independent of system size, effectively mitigating the curse of dimensionality.
• In smaller and more agile systems (n = 5), the proposed approach occasionally surpasses the PWC benchmark. This advantage arises from the agent’s ability to make rapid, state-dependent decisions, which are not captured by the static and conservative assumptions of analytical models.
• For higher $WIP$ levels, however, the performance gap between the proposed method and the PWC benchmark becomes negligible, as both approaches converge towards the system’s capacity-driven plateau.

It is important to emphasise that outperforming the PWC model is not the intended claim of this study. The PWC serves as a strong analytical reference rather than a competing optimisation algorithm. The fact that the proposed framework approaches, and occasionally slightly exceeds, the PWC throughput under specific configurations highlights its capability to exploit state-dependent adaptation effectively. Furthermore, the observed improvements over static dispatching rules demonstrate the benefit of embedding sequencing decisions within the same adaptive control loop as WIP regulation, without the need to introduce more complex metaheuristics to validate the core coordination concept.

The comparative analysis presented in Figure 4 and summarised in Table 4 provides important insights into the operational behaviour of the system under different control strategies. At moderate $WIP$ levels, the proposed DQN-based approach consistently matches or outperforms the PWC benchmark, demonstrating its capability to learn effective, near-optimal policies that leverage system dynamics more efficiently than static analytical models. This effect is particularly evident in smaller and more agile systems (n = 5), where the agent’s rapid, state-dependent decisions occasionally allow it to slightly surpass the theoretical limits predicted by the PWC benchmark.

However, as $WIP$ increases, both approaches exhibit a progressive reduction in marginal throughput gains, eventually converging towards a shared saturation plateau. This convergence highlights an intrinsic property of the system: once the effective bottleneck capacity is reached, adding additional $WIP$ does not yield meaningful improvements in throughput, regardless of the control strategy employed. From a practical perspective, this implies that investing computational resources into more sophisticated optimisation policies may provide limited benefits when the system operates near its theoretical limits.

Overall, these findings confirm that the proposed framework achieves near-optimal performance while maintaining robust scalability. Significant advantages are obtained particularly in low-to-moderate $WIP$ regimes, where adaptive and intelligent decision-making yields the greatest operational benefits.

It is also worth noting that, for the subsequent experimental analyses, results are presented exclusively for the 5-machine configuration. Preliminary investigations confirmed that the trends observed in 10- and 15-machine systems closely mirror those of the 5-machine case, with consistent relative performances across all tested policies. Therefore, focusing on the 5-machine configuration is sufficient to capture the key behavioural patterns without introducing redundant information.

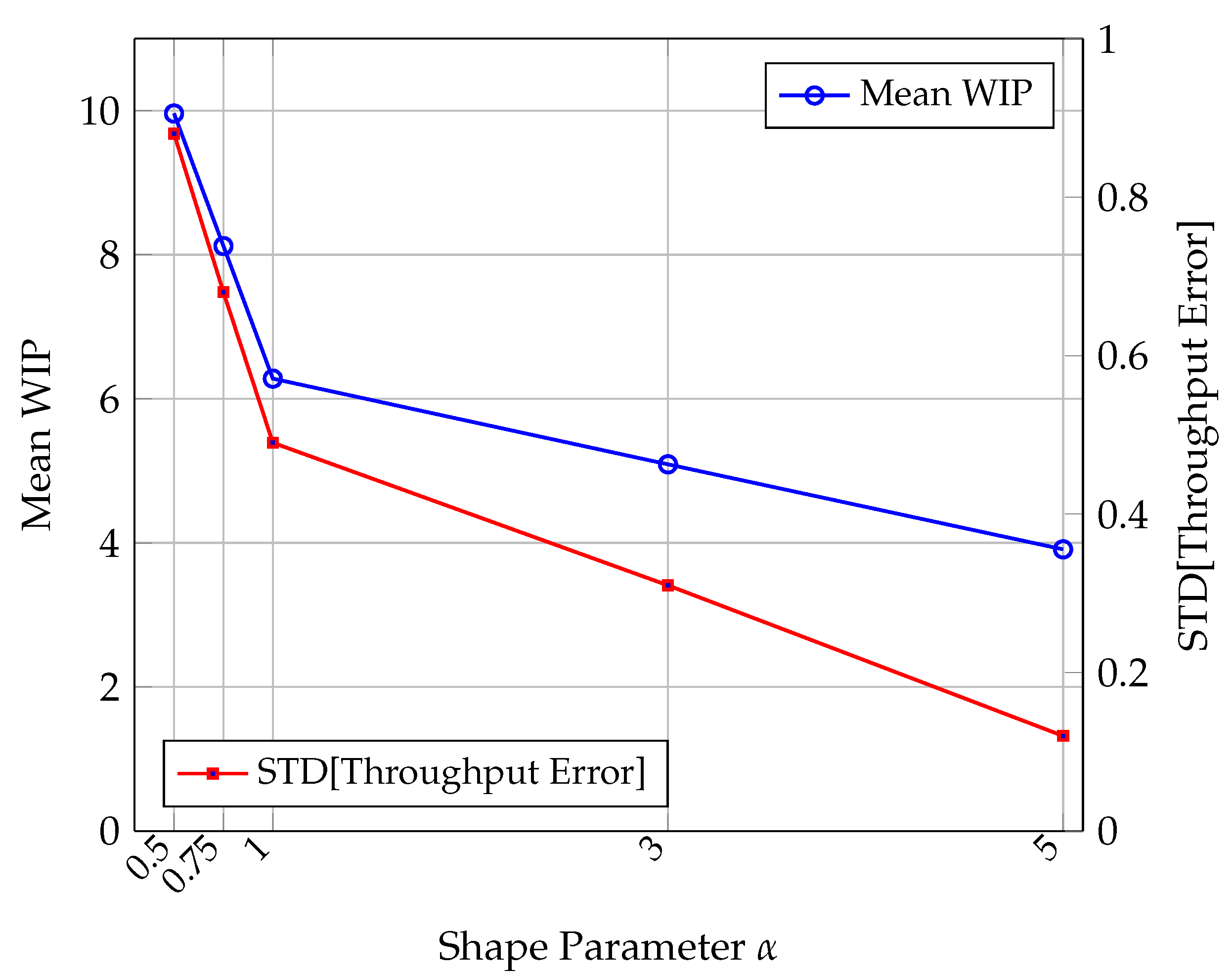
5.2. Robustness to Process Time Variability

Real-world manufacturing systems are subject to varying degrees of stochasticity. To assess robustness, the proposed framework was tested under a fixed throughput target ($T{H}_{\mathrm{target}}\approx 0.6·r_b$, where $r_b$ is the bottleneck rate [42]) while systematically varying process time variability. Processing times followed a Gamma distribution, with the shape parameter $\alpha \in 0.5,0.75,1,3,5$. Low $\alpha$ values ($\alpha <1$) correspond to high-variance, heavy-tailed distributions typical of custom manufacturing, whereas high $\alpha$ values ($\alpha >1$) approximate near-deterministic conditions found in standardized assembly lines.

The results, summarised in

Table 5. System performance with a fixed target ($T{H}_{\mathrm{target}}=0.6·r_b$) under varying process time variability.

Shape Parameter ($\mathit{\alpha }$)	Mean WIP	STD [Throughput Error]
0.50	9.96	0.88
0.75	8.12	0.68
1.0	6.28	0.49
3.0	5.09	0.31
5.0	3.91	0.12

and visualised in Figure 5, highlight two clear adaptive behaviours. First, as process times become more predictable (higher $\alpha$), the agent consistently achieves the target throughput with substantially lower WIP—decreasing from 9.96 in the high-variability case ($\alpha =0.5$) to 3.91 in the near-deterministic case ($\alpha =5$). This reflects a lean-oriented control policy that avoids excess job accumulation when predictability allows tighter flow regulation.

Second, throughput stability improves markedly: the standard deviation of the throughput error falls from 0.88 to 0.12 across the $\alpha$ range. So, this is the variability of the performance metric across different stochastic realizations (i.e., different random seeds). This decline, also visible in the red curve of Figure 5, indicates that the agent not only meets the target more accurately but also maintains performance consistency under predictable conditions. Notably, the coefficient of variation (CV) for throughput error remained below 15% in all cases, confirming robust control across different stochastic regimes.

Overall, these findings demonstrate that the learned policy generalises effectively to different variability conditions, adapting WIP control and sequencing behaviour to maintain both efficiency and stability.

5.3. Analysis of the Adaptive Dispatching Policy

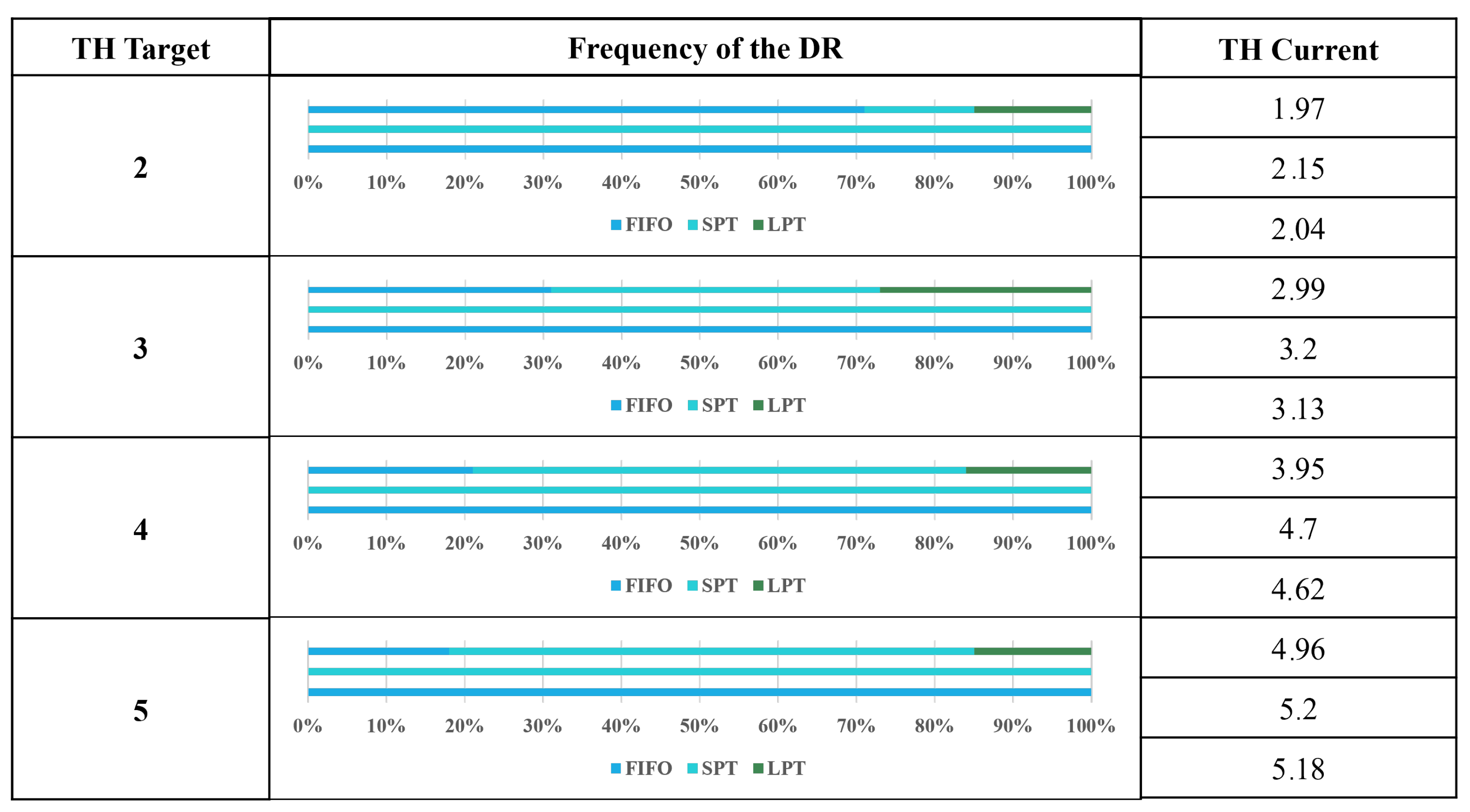
We analysed the dynamic selection of dispatching rules under varying throughput (TH) targets, comparing the agent’s learned policy with the static baselines. Figure 6 summarises the results: the first column lists the TH target for each scenario; the central panel displays horizontal stacked bars indicating the relative frequency with which each rule (FIFO, SPT, LPT) was selected by the DQN agent; and the right column (“TH current”) reports the mean throughput achieved by the static FIFO, static SPT, and proposed DQN-based policy, averaged over all replications. This structure allows a direct visual comparison between the agent’s adaptive rule-selection behaviour and the performance of fixed-rule benchmarks across different production targets.

At low targets (e.g., 2 and 3), the agent predominantly selects FIFO, prioritising stability and predictable flow. As targets increase (e.g., 4 and 5), the policy shifts decisively toward SPT, maximising throughput. LPT is rarely selected, reflecting its limited utility in this configuration. This emergent behaviour highlights the principal advantage of a learned policy over static rule-based systems. The DRL agent develops an adaptive strategy, selecting the most appropriate dispatching rule based on global performance objectives, thereby enabling a more responsive and efficient control of the production line.

Importantly, this strategic shift is not merely behavioural but translates into measurable performance gains. For instance, in high-TH scenarios (targets 4 and 5), the increased selection of SPT coincided with mean throughput improvements of approximately 19% and 4.8%, respectively, compared to FIFO under the same conditions, while maintaining comparable WIP levels. This correlation reinforces that the agent’s rule-switching policy directly supports the achievement of throughput objectives rather than being an artefact of stochastic variation.

5.4. Training Time and Learning Curves

The proposed dual-agent framework was trained on a workstation equipped with an Intel^® Core™ Ultra 7 155H processor (3.80 GHz) and 32 GB of RAM, supported by an NVIDIA RTX 3080 GPU. The strategic WIP-control agent (${\pi }_{\mathrm{WIP}}$) was trained for 250 episodes, each representing a complete run of the simulation under a fixed throughput target. The tactical dispatching agent (${\pi }_{\mathrm{SEQ}}$), being event-driven, was trained for 100 episodes, each comprising a variable number of sequencing decisions determined by shop-floor events.

To enable a direct visual comparison between the agents, the learning curves are expressed as Training Progress (%), where 0% corresponds to the beginning of training and 100% to the completion of the respective episode budget. This normalisation accounts for the distinct activation frequencies of the two agents: the strategic agent operates on a periodic, time-driven schedule, whereas the tactical agent is invoked only upon ’MachineFreed’ events.

Figure 7 presents the evolution of the mean episodic reward for both agents. The vertical scales are consistent with the respective reward functions: for the strategic agent, the reward is capped at $\beta =20$ (Equation (3)); for the tactical agent, the reward grows logarithmically with ${\displaystyle \frac{T{H}_{\mathrm{mobile}}}{r_b}}$ and saturates at $scor{e}_{max}=100$ (Equations (5) and (6)).

Both curves follow a characteristic DRL learning trajectory: a rapid initial increase corresponding to the acquisition of baseline-effective policies, followed by a slower convergence towards a plateau. The WIP-control agent reached its maximum reward band ($\approx \beta$) within roughly 70% of its training budget, maintaining only minor oscillations thereafter. The tactical agent, which starts from lower initial rewards due to randomised sequencing, exhibited a steeper relative improvement and approached $scor{e}_{max}$ by the end of training. Residual oscillations in both curves are attributable to the $ϵ$-greedy exploration mechanism and stochastic variability in processing times.

Convergence was defined as a change of less than 1% in the moving average reward (window size = 25 episodes) over consecutive windows. Under this criterion, ${\pi }_{\mathrm{WIP}}$ converged in approximately 180 episodes and ${\pi }_{\mathrm{SEQ}}$ in around 75 episodes. The corresponding wall-clock training times were approximately 1 h 30 min for the WIP-control agent and 1 h for the tactical agent. Once trained, both agents produced control decisions in under 1 ms per inference step, confirming their suitability for real-time deployment.

6. Discussion and Limitations

This section synthesizes the key findings of our study, discusses their practical implications and limitations, and outlines a roadmap for future research.

Our central finding is that a coordinated, dual-agent DRL framework can learn to effectively manage the trade-off between global WIP levels and local sequencing efficiency. The framework’s performance, which consistently matches or slightly exceeds the PWC benchmark, warrants a nuanced interpretation. The PWC model provides a robust analytical reference, particularly tight under the assumption of exponential processing times. The ability of our DRL agent to occasionally surpass this benchmark does not violate theoretical principles but rather highlights the limitations of a static model. The PWC’s assumptions are inherently conservative; our DRL agent, by contrast, learns a dynamic, state-contingent policy. It can, for instance, opportunistically switch to SPT when queues are long to rapidly clear congestion, an adaptive behaviour not captured by the PWC’s static analysis. This demonstrates the value of data-driven, real-time adaptation in exploiting favourable system dynamics.

A key limitation of this study is its reliance on a purely simulated environment for validation. While simulation was essential for controlled experimentation, scalability testing, and safe DRL training, the transition to a physical environment presents additional challenges and requires a structured approach. The proposed framework’s effectiveness in a real-world setting would depend on overcoming factors such as sensor noise, data latency from MES/SCADA systems, and handling modelled disturbances like machine breakdowns or material shortages. A practical roadmap for implementation would follow a phased approach:

• The first step would involve integrating the trained DRL agents with a digital twin fed by real-time data from a production line. In this case, the agents would generate decisions without executing them, allowing for a risk-free comparison of their proposed actions against the actual decisions made on the shop floor. This phase would validate the agent’s responsiveness to real-world dynamics and help fine-tune the state representation.
• Following successful validation, the framework could be deployed on a small-scale, non-critical production cell or a hardware-in-the-loop (HIL) testbed. This would allow for assessing the agent’s interaction with physical hardware and control systems, providing critical insights into control latencies and execution fidelity.
• Finally, a gradual, full-scale deployment could be undertaken. An important aspect would be to enable mechanisms for online or periodic retraining of the agents to allow them to adapt to long-term shifts in production patterns or system characteristics.

Beyond the simulation-to-reality gap, it is important to acknowledge other limitations which represent threats to the external validity of our findings. Our model relies on several simplifying assumptions, such as unlimited buffers and no machine breakdowns. While this was necessary to isolate the core control problem, these factors are critical in real-world systems and their absence limits the direct generalizability of our quantitative results. The tactical agent’s action set was intentionally limited to three archetypal rules {FIFO, SPT, LPT}. While this was sufficient to demonstrate the value of adaptive selection, a real-world system might benefit from a broader or more specialized set of dispatching rules. Our evaluation focused on throughput- and WIP-based metrics. The learned policy may not be optimal for other important objectives, such as minimizing tardiness or meeting specific due dates.

The limitations identified above naturally lead to a prioritized roadmap for future work. The most critical next step is to incorporate more realistic system features, such as machine failures, setup times, and finite buffers. Training the agents to handle these disruptions is essential for practical deployment. Extending the framework to handle due-date-related objectives (e.g., minimizing mean tardiness) is a key priority. This would likely involve modifying the state space to include due-date information and redesigning the reward functions accordingly. An ablation study comparing our standard DQN baseline against more advanced architectures would be valuable. Specifically, testing a Deep Recurrent Q-Network (DRQN) could formally address the partial observability and potentially improve policy performance.

7. Conclusions

This work presented a novel and scalable dual-agent DQN architecture for the coordinated control of WIP and job sequencing in flow-shop environments. By explicitly separating global and local decision-making, the framework integrates a strategic agent—responsible for regulating system-wide WIP to meet global throughput targets—and a tactical agent that dynamically selects the most suitable dispatching rule in response to evolving shop-floor conditions. This design not only ensures high adaptability under stochastic dynamics but also mitigates the curse of dimensionality through event-driven, parameter-sharing mechanisms that preserve scalability as the number of machines increases.

Empirical validation confirmed the framework’s effectiveness across three key dimensions: scalability, robustness, and adaptiveness. The proposed architecture maintained near-optimal throughput across 5-, 10-, and 15-machine configurations, closely matching or slightly surpassing the PWC analytical benchmark without performance degradation as the system scaled. The learned policies adapted effectively to varying levels of process time variability (Gamma-distributed), consistently meeting throughput targets while reducing WIP under more predictable conditions. Furthermore, the tactical agent developed a state-dependent rule-selection strategy, achieving measurable throughput gains over static dispatching baselines while maintaining comparable WIP levels.

The integration of DQN with Discrete Event Simulation (DES) and Agent-Based Modelling provided a realistic and controllable training environment, reinforcing the framework’s practical applicability. By normalising throughput in the reward structure, the proposed approach remains inherently scalable to larger and more complex production systems without redesigning the learning process.

Future work will explore extensions to more complex shop-floor configurations (e.g., hybrid flow-shops, job-shops), relaxation of simplifying assumptions, and the adoption of Hierarchical Reinforcement Learning (HRL) for interpretable multi-level control. In this vision, WIP control acts as the global regulator of job inflow, while dispatching rules serve as local flow managers at each workstation. Coordinating these “valves” adaptively is key to avoiding inefficiencies such as job accumulation or machine starvation.

Given its scalability, robustness, and synergy with Industry 4.0 technologies, the proposed framework offers strong potential for industries facing high variability, demand uncertainty, and operational complexity—such as automotive, electronics, and consumer goods manufacturing—where conventional control methods often fall short.