Evaluation and Correction of Systematic Motion Errors in a Compact Three-Wheeled Omnidirectional Platform Based on Servomotors
Abstract
1. Introduction
New Contribution
2. Materials and Methods
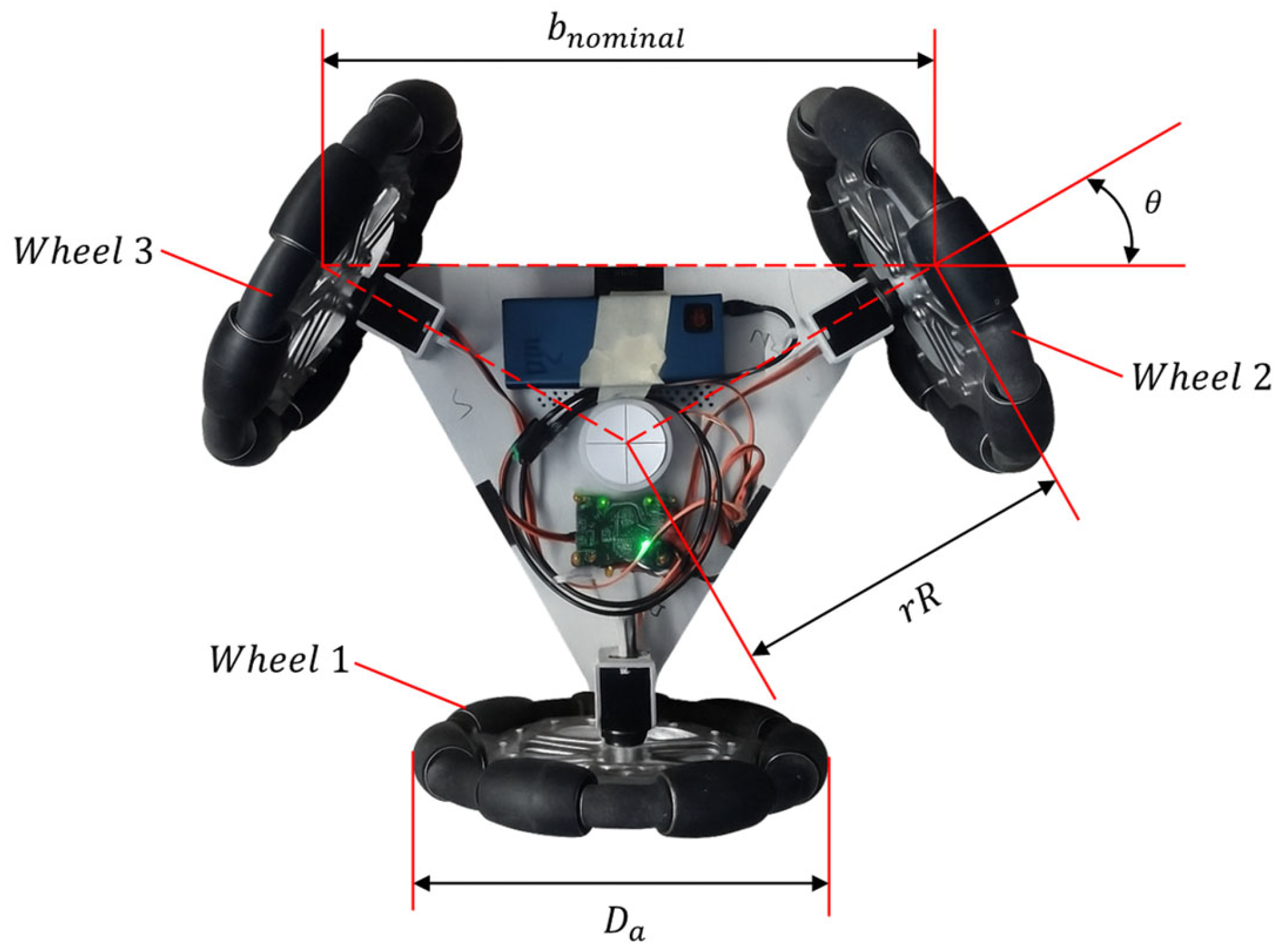
2.1. TRIA-BOT Omnidirectional Platform
2.1.1. Omnidirectional Wheels
2.1.2. Digital Servomotors
2.1.3. The 3D-Printed Platform Base
2.1.4. Power Bank
2.1.5. Platform Controller
2.1.6. Motion Commands
- General time–motion command. Represented as , where (in m/s) is the linear velocity of the omnidirectional platform, (in degrees) is the angular orientation of the displacement, (in rad/s) is the angular velocity of rotation with respect to the center of the platform, and (in s) is the duration for which the command is executed by the platform.
- Rotation command. Represented as R, where (in degrees) defines the rotation angle, and (in rad/s) specifies the angular velocity of the platform during rotation.
2.2. Reference UMBmark Calibration Procedure
2.2.1. Reference Bidirectional Square Path for Differential-Drive Platforms
2.2.2. Calibration Parameters for a Differential-Drive Platform
2.2.3. Calibration Parameters for a Three-Wheeled Omnidirectional Platform
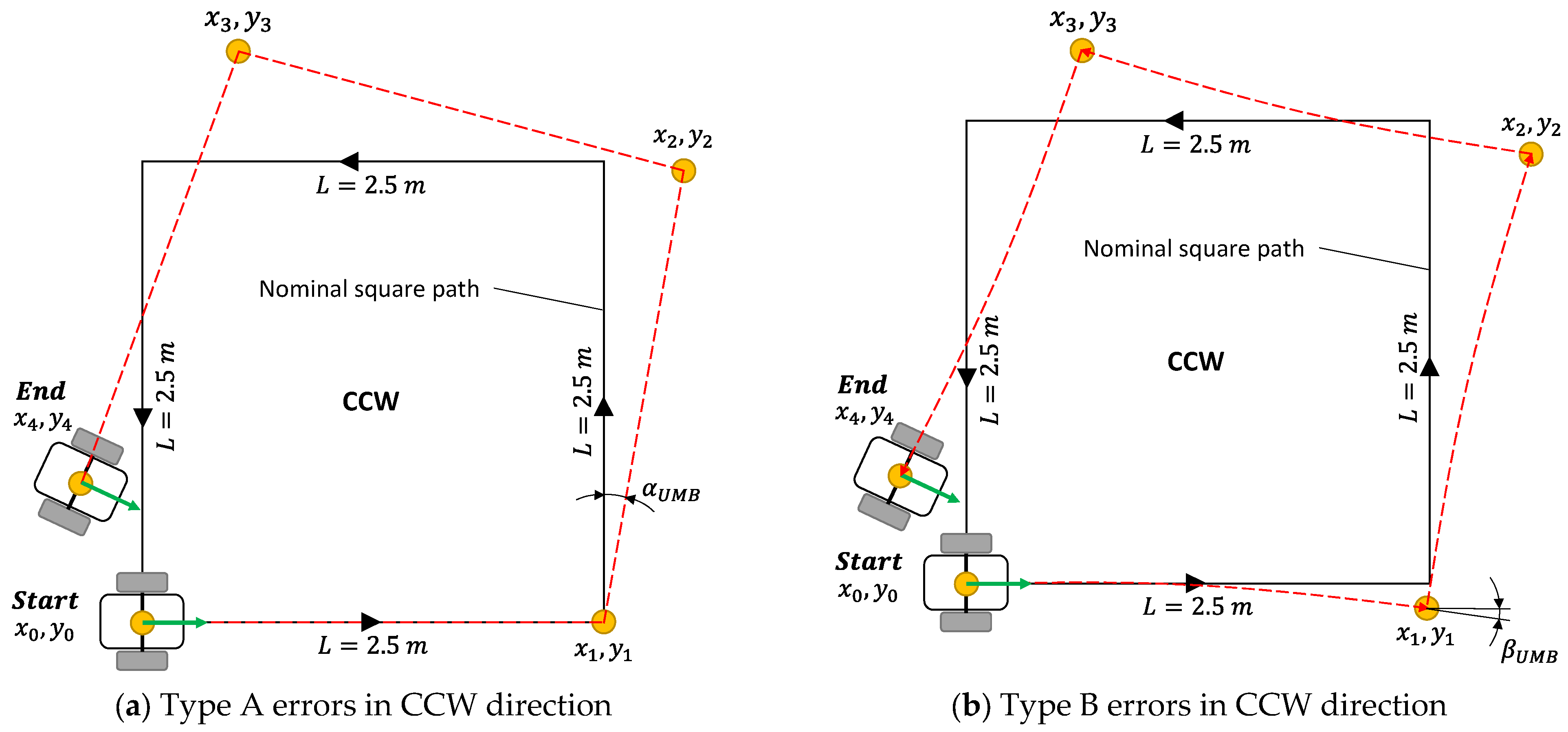
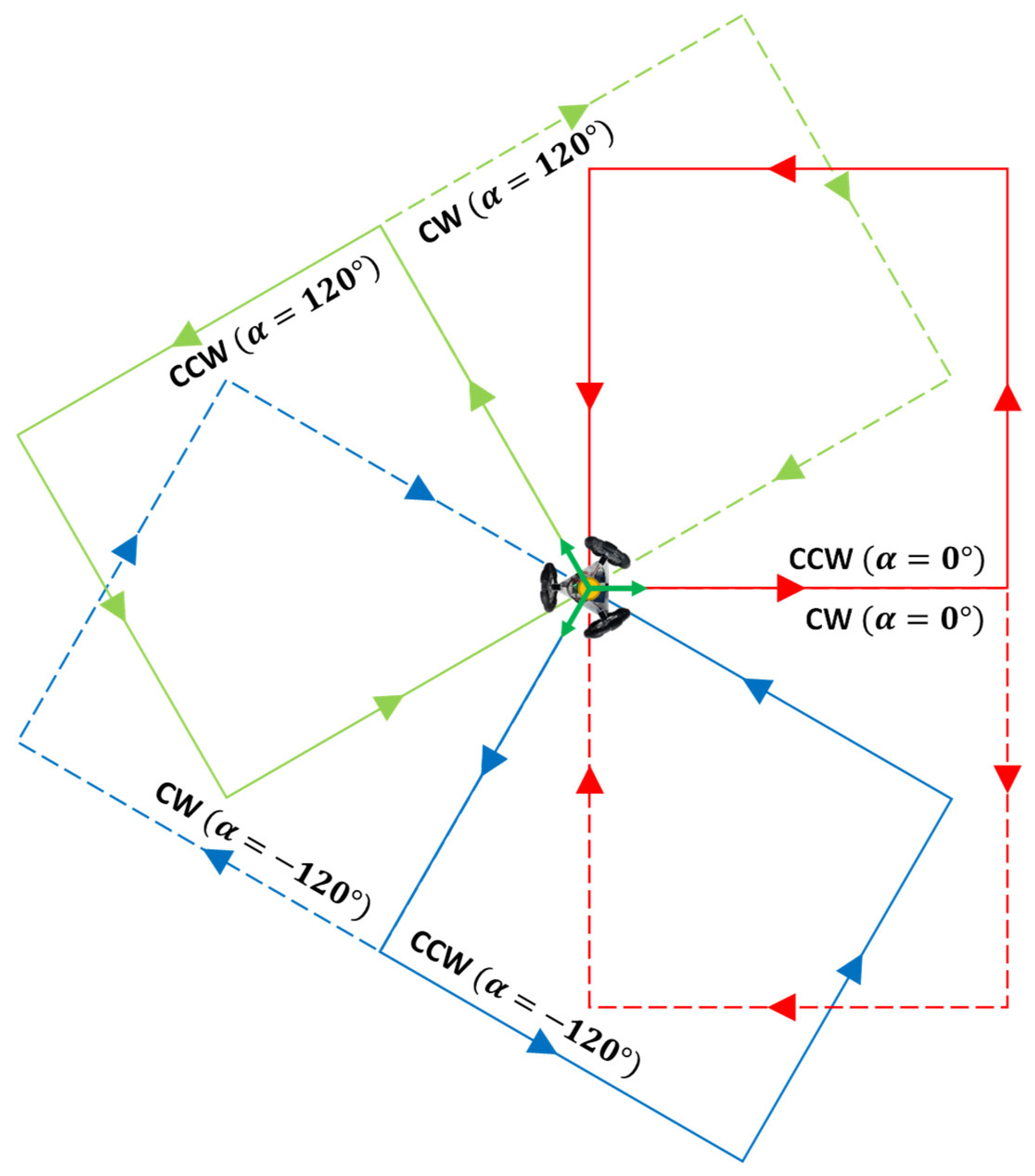
2.2.4. Bidirectional Square Paths for a Three-Wheeled Omnidirectional Platform
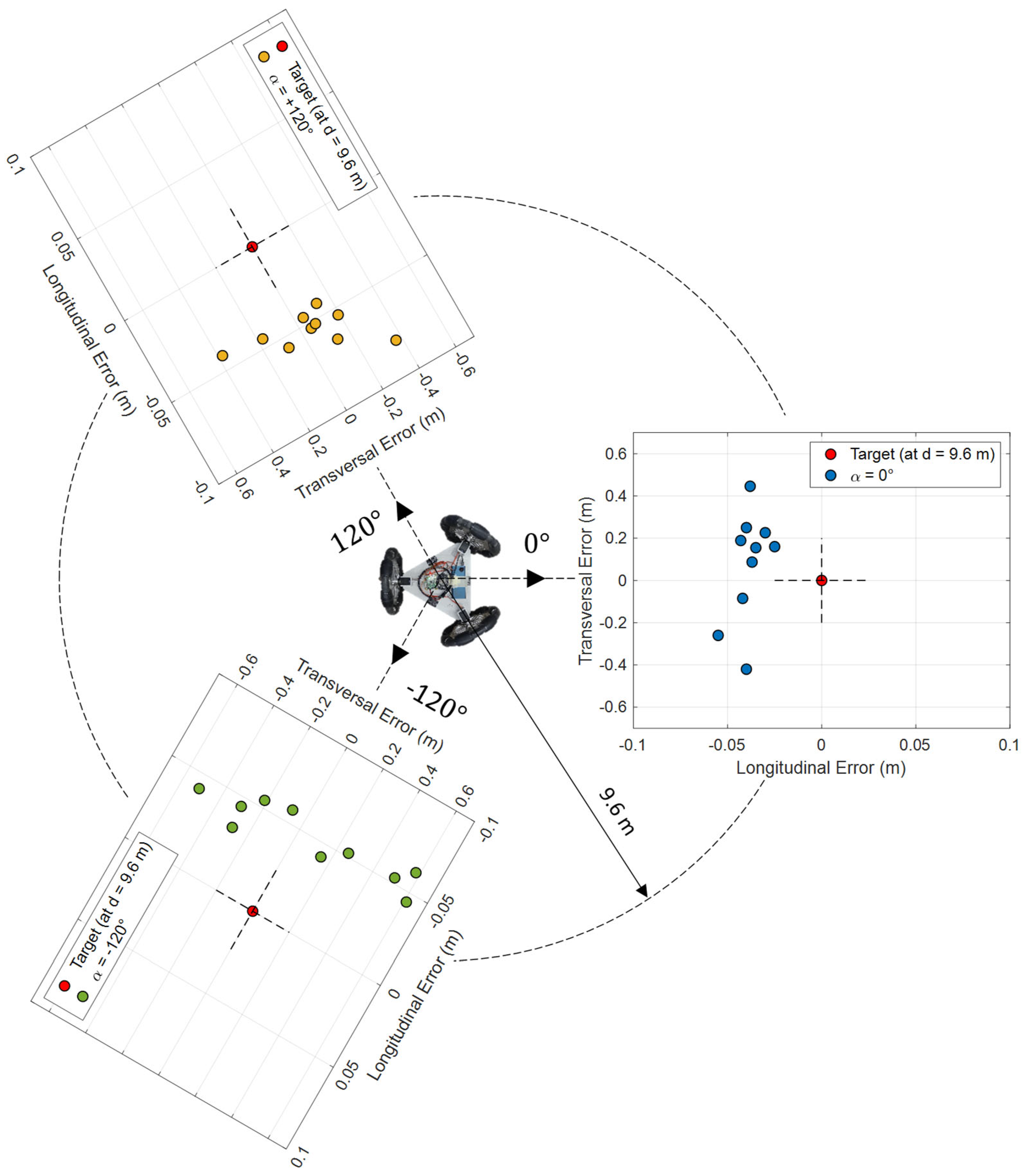
2.2.5. UMBmark Trajectory Experiment
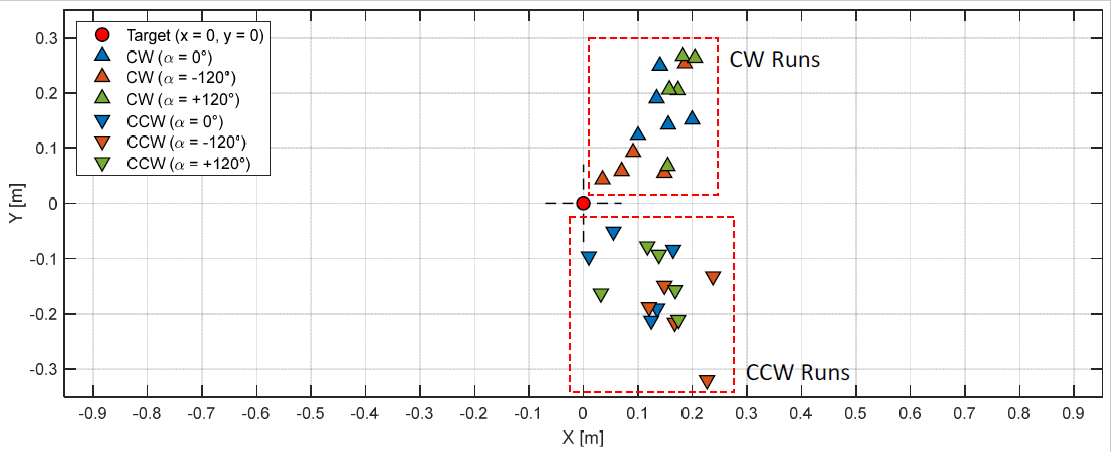
2.2.6. UMBmark Trajectory Results
3. Correction of Systematic Rotation Errors
3.1. UMBmark Rotation Calibration
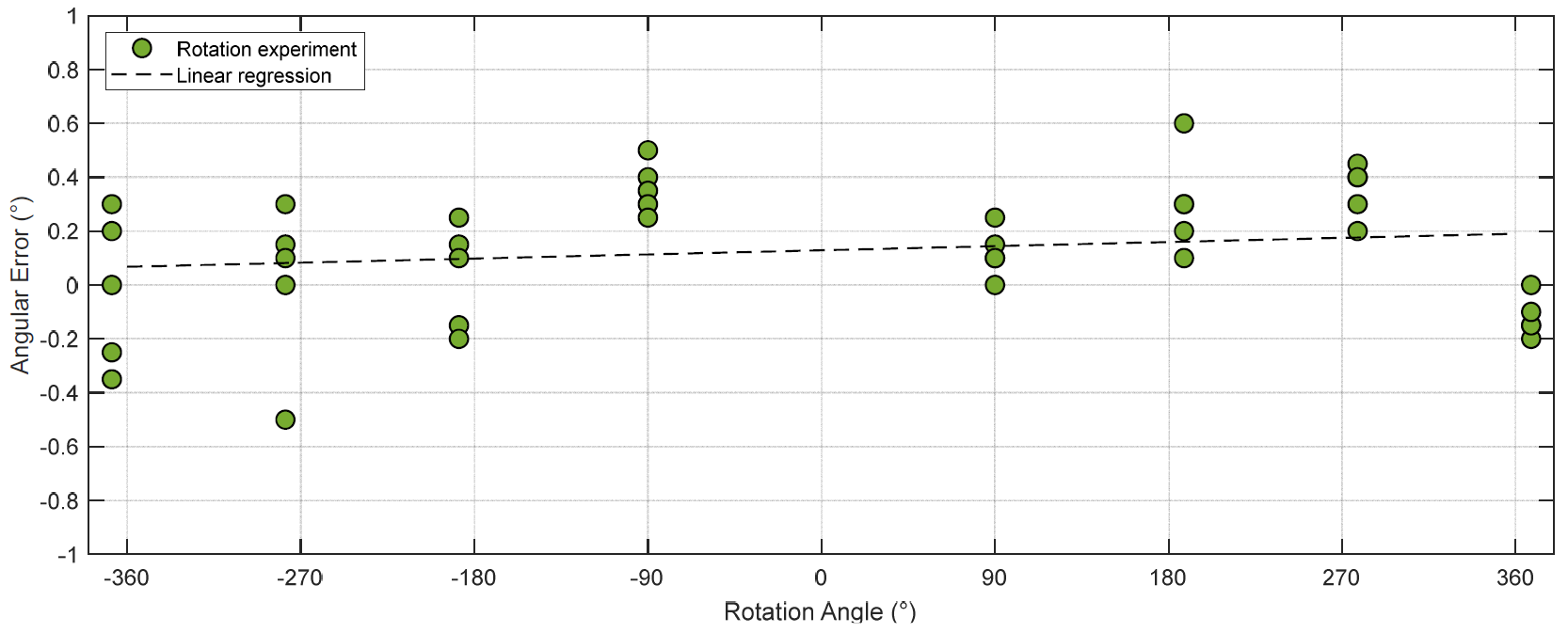
3.2. Direct Rotation Calibration
4. Correction of Forward Displacement Errors
4.1. UMBmark Forward Displacement Calibration
4.2. Direct Forward Displacement Calibration
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sesmero, C.P.; Buonocore, L.R.; Di Castro, M. Omnidirectional Robotic Platform for Surveillance of Particle Accelerator Environments with Limited Space Areas. Appl. Sci. 2021, 11, 6631. [Google Scholar] [CrossRef]
- Tavakoli, M.; Viegas, C.; Marques, L.; Pires, J.N.; de Almeida, A.T. OmniClimbers: Omni-Directional Magnetic Wheeled Climbing Robots for Inspection of Ferromagnetic Structures. Robot. Auton. Syst. 2013, 61, 997–1007. [Google Scholar] [CrossRef]
- Song, H.; Wu, Y.; Wu, Y.; Zhou, G.; Luo, C. Two-Vehicle Coordination System for Omnidirectional Transportation Based on Image Processing and Deviation Prediction. J. Control Autom. Electr. Syst. 2021, 32, 875–883. [Google Scholar] [CrossRef]
- Orozco-Magdaleno, E.C.; Gómez-Bravo, F.; Castillo-Castañeda, E.; Carbone, G. Evaluation of Locomotion Performances for a Mecanum-Wheeled Hybrid Hexapod Robot. IEEE/ASME Trans. Mechatron. 2021, 26, 1657–1667. [Google Scholar] [CrossRef]
- Palacín, J.; Clotet, E.; Martínez, D.; Martínez, D.; Moreno, J. Extending the Application of an Assistant Personal Robot as a Walk-Helper Tool. Robotics 2019, 8, 27. [Google Scholar] [CrossRef]
- Gao, Z.Q.; Chen, H.B.; Du, Y.P.; Wei, L. Design and Development of an Omni-Directional Mobile Robot for Logistics. Appl. Mech. Mater. 2014, 602–605, 1006–1010. [Google Scholar] [CrossRef]
- Levratti, A.; Riggio, G.; Fantuzzi, C.; De Vuono, A.; Secchi, C. TIREBOT: A Collaborative Robot for the Tire Workshop. Robot. Comput.-Integr. Manuf. 2019, 57, 129–137. [Google Scholar] [CrossRef]
- Raczl, S.-G.; Crenganis, M.; Barsan, A.; Adrian, M. Omnidirectional Autonomous Mobile Robot With Mecanum Wheel. In Proceedings of the International Student Innovation and Scientific Research Exhibition, Sibiu, Romania, 1 April 2019. [Google Scholar]
- Li, Y.; Dai, S.; Zhao, L.; Yan, X.; Shi, Y. Topological Design Methods for Mecanum Wheel Configurations of an Omnidirectional Mobile Robot. Symmetry 2019, 11, 1268. [Google Scholar] [CrossRef]
- Almasri, E.; Uyguroğlu, M.K. Modeling and Trajectory Planning Optimization for the Symmetrical Multiwheeled Omnidirectional Mobile Robot. Symmetry 2021, 13, 1033. [Google Scholar] [CrossRef]
- Mohanraj, A.P.; Elango, A.; Reddy, M.C. Front and Back Movement Analysis of a Triangle-Structured Three-Wheeled Omnidirectional Mobile Robot by Varying the Angles between Two Selected Wheels. Sci. World J. 2016, 2016, 7612945. [Google Scholar] [CrossRef]
- Yan, G.-R.; Zhang, H.-B. A New Kind of Wheel-Model All Directional Moving Mechanism. J. Harbin Inst. Technol. 2001, 33, 854–857. [Google Scholar]
- Salih, J.E.M.; Rizon, M.; Yaacob, S.; Adom, A.H.; Mamat, M.R. Designing Omni-Directional Mobile Robot with Mecanum Wheel. Am. J. Appl. Sci. 2006, 3, 1831–1835. [Google Scholar] [CrossRef]
- Rey, R.; Cobano, J.A.; Corzetto, M.; Merino, L.; Alvito, P.; Caballero, F. A Novel Robot Co-Worker System for Paint Factories without the Need of Existing Robotic Infrastructure. Robot. Comput. Integr. Manuf. 2021, 70, 102122. [Google Scholar] [CrossRef]
- Huang, Y.; Meng, R.; Yu, J.; Zhao, Z.; Zhang, X. Practical Obstacle-Overcoming Robot with a Heterogeneous Sensing System: Design and Experiments. Machines 2022, 10, 289. [Google Scholar] [CrossRef]
- Tian, P.; Zhang, Y.N.; Zhang, J.; Yan, N.M.; Zeng, W. Research on Simulation of Motion Compensation for 8×8 Omnidirectional Platform Based on Back Propagation Network. Appl. Mech. Mater. 2013, 299, 44–47. [Google Scholar] [CrossRef]
- Borenstein, J.; Everett, H.R.; Feng, L. Where Am I? Sensors and Methods for Mobile Robot Positioning; University of Michigan: Ann Arbor, MI, USA, 1996. [Google Scholar]
- Borenstein, J.; Everett, H.R.; Feng, L.; Wehe, D. Mobile Robot Positioning: Sensors and Techniques. J. Robot. Syst. 1997, 14, 231–249. [Google Scholar] [CrossRef]
- Abbas, T.; Arif, M.; Ahmed, W. Measurement and Correction of Systematic Odometry Errors Caused by Kinematics Imperfections in Mobile Robots. In Proceedings of the 2006 SICE-ICASE International Joint Conference, Busan, Republic of Korea, 18 October 2006. [Google Scholar]
- Gargiulo, A.M.; di Stefano, I.; Genova, A. Model-Based Slippage Estimation to Enhance Planetary Rover Localization with Wheel Odometry. Appl. Sci. 2021, 11, 5490. [Google Scholar] [CrossRef]
- Borenstein, J.; Feng, L. Measurement and Correction of Systematic Odometry Errors in Mobile Robots. IEEE Trans. Robot. Autom. 1996, 12, 869–880. [Google Scholar] [CrossRef]
- Lee, K.; Jung, C.; Chung, W. Accurate Calibration of Kinematic Parameters for Two Wheel Differential Mobile Robots. J. Mech. Sci. Technol. 2011, 25, 1603–1611. [Google Scholar] [CrossRef]
- Wang, D.; Xu, M.; Chen, Y.; Zhong, H.; Zhu, Y.; Wang, Z.; Gao, L. Positioning Method of Four-Wheel-Steering Mobile Robots Based on Improved UMBmark of Michigan Benchmark Algorithm. J. Adv. Comput. Intell. Intell. Inform. 2023, 27, 135–142. [Google Scholar] [CrossRef]
- Sousa, R.B.; Petry, M.R.; Moreira, A.P. Evolution of Odometry Calibration Methods for Ground Mobile Robots. In Proceedings of the 2020 IEEE International Conference on Autonomous Robot Systems and Competitions (ICARSC), Ponta Delgada, Portugal, 15 April 2020. [Google Scholar]
- Tomasi, D.L.; Todt, E. Rotational Odometry Calibration for Differential Robot Platforms. In Proceedings of the 2017 Latin American Robotics Symposium (LARS) and 2017 Brazilian Symposium on Robotics (SBR), Curitiba, Brazil, 8–11 November 2017. [Google Scholar]
- Bostani, A.; Vakili, A.; Denidni, T.A. A Novel Method to Measure and Correct the Odometry Errors in Mobile Robots. In Proceedings of the 2008 Canadian Conference on Electrical and Computer Engineering, Niagara Falls, ON, Canada, 4–7 May 2008. [Google Scholar]
- Ivanjko, E.; Komšić, I.; Petrović, I. Simple Off-Line Odometry Calibration of Differential Drive Mobile Robots. In Proceedings of the 16th International Workshop on Robotics in Alpe-Adria-Danube Region, Ljubljana, Slovenia, 7 June 2007. [Google Scholar]
- Jung, C.; Chung, W. Calibration of Kinematic Parameters for Two Wheel Differential Mobile Robots by Using Experimental Heading Errors. Int. J. Adv. Robot. Syst. 2011, 8, 68. [Google Scholar] [CrossRef]
- Antonelli, G.; Chiaverini, S.; Fusco, G. A Calibration Method for Odometry of Mobile Robots Based on the Least-Squares Technique: Theory and Experimental Validation. IEEE Trans. Robot. 2005, 21, 994–1004. [Google Scholar] [CrossRef]
- Mondal, S.; Yun, Y.; Chung, W.K. Terminal Iterative Learning Control for Calibrating Systematic Odometry Errors in Mobile Robots. In Proceedings of the 2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Montreal, QC, Canada, 6–9 July 2010. [Google Scholar]
- De Giorgi, C.; De Palma, D.; Parlangeli, G. Online Odometry Calibration for Differential Drive Mobile Robots in Low Traction Conditions with Slippage. Robotics 2024, 13, 7. [Google Scholar] [CrossRef]
- Censi, A.; Franchi, A.; Marchionni, L.; Oriolo, G. Simultaneous Calibration of Odometry and Sensor Parameters for Mobile Robots. IEEE Trans. Robot. 2013, 29, 475–492. [Google Scholar] [CrossRef]
- Cantelli, L.; Ligama, S.; Muscato, G.; Spina, D. Auto-Calibration Methods of Kinematic Parameters and Magnetometer Offset for the Localization of a Tracked Mobile Robot. Robotics 2016, 5, 23. [Google Scholar] [CrossRef]
- Maddahi, Y.; Maddahi, A.; Sepehri, N. Calibration of Omnidirectional Wheeled Mobile Robots: Method and Experiments. Robotica 2013, 31, 969–980. [Google Scholar] [CrossRef]
- Lin, P.; Liu, D.; Yang, D.; Zou, Q.; Du, Y.; Cong, M. Calibration for Odometry of Omnidirectional Mobile Robots Based on Kinematic Correction. In Proceedings of the 2019 14th International Conference on Computer Science & Education (ICCSE), Toronto, ON, Canada, 19 August 2019. [Google Scholar]
- Savaee, E.; Hanzaki, R.A. A New Algorithm for Calibration of an Omni-Directional Wheeled Mobile Robot Based on Effective Kinematic Parameters Estimation. J. Intell. Robot. Syst. 2021, 101, 28. [Google Scholar] [CrossRef]
- Palacín, J.; Rubies, E.; Clotet, E. Systematic Odometry Error Evaluation and Correction in a Human-Sized Three-Wheeled Omnidirectional Mobile Robot Using Flower-Shaped Calibration Trajectories. Appl. Sci. 2022, 12, 2606. [Google Scholar] [CrossRef]
- Sousa, R.B.; Petry, M.R.; Costa, P.G.; Moreira, A.P. OptiOdom: A Generic Approach for Odometry Calibration of Wheeled Mobile Robots. J. Intell. Robot. Syst. 2022, 105, 39. [Google Scholar] [CrossRef]
- Palacín, J.; Rubies, E.; Bitriá, R.; Clotet, E. Non-Parametric Calibration of the Inverse Kinematic Matrix of a Three-Wheeled Omnidirectional Mobile Robot Based on Genetic Algorithms. Appl. Sci. 2023, 13, 1053. [Google Scholar] [CrossRef]
- Moreno, J.; Clotet, E.; Lupiañez, R.; Tresanchez, M.; Martínez, D.; Pallejà, T.; Casanovas, J.; Palacín, J. Design, Implementation and Validation of the Three-Wheel Holonomic Motion System of the Assistant Personal Robot (APR). Sensors 2016, 16, 1658. [Google Scholar] [CrossRef]









| Orientations | ||||
|---|---|---|---|---|
| 0.1458 | 0.0936 | 0.1714 | −0.1266 | |
| 0.1060 | 0.1800 | 0.1002 | −0.201 | |
| 0.1742 | 0.1258 | 0.2014 | −0.1404 |
| Orientations | ||
|---|---|---|
| −1.3716 | −1.7074 | |
| −1.6386 | −1.7257 | |
| −1.7188 | −1.9583 |
| Orientations | |||
|---|---|---|---|
| −0.2991 | −0.2566 | −0.2778 | |
| −0.4239 | −0.5775 | −0.5007 | |
| −0.2773 | −0.3495 | −0.3134 |
| Orientations | ||||
|---|---|---|---|---|
| −515.46 | 0.99921 | 0.29913 | 0.29890 | |
| 286.04 | 1.00142 | 0.29880 | 0.29923 | |
| −457.04 | 0.99911 | 0.29915 | 0.29888 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martínez, D.; Rubies, E.; Bitriá, R.; Palacín, J. Evaluation and Correction of Systematic Motion Errors in a Compact Three-Wheeled Omnidirectional Platform Based on Servomotors. Appl. Sci. 2025, 15, 10700. https://doi.org/10.3390/app151910700
Martínez D, Rubies E, Bitriá R, Palacín J. Evaluation and Correction of Systematic Motion Errors in a Compact Three-Wheeled Omnidirectional Platform Based on Servomotors. Applied Sciences. 2025; 15(19):10700. https://doi.org/10.3390/app151910700
Chicago/Turabian StyleMartínez, David, Elena Rubies, Ricard Bitriá, and Jordi Palacín. 2025. "Evaluation and Correction of Systematic Motion Errors in a Compact Three-Wheeled Omnidirectional Platform Based on Servomotors" Applied Sciences 15, no. 19: 10700. https://doi.org/10.3390/app151910700
APA StyleMartínez, D., Rubies, E., Bitriá, R., & Palacín, J. (2025). Evaluation and Correction of Systematic Motion Errors in a Compact Three-Wheeled Omnidirectional Platform Based on Servomotors. Applied Sciences, 15(19), 10700. https://doi.org/10.3390/app151910700







