Design and Experimental Process of Vertical Roller Potato–Stem Separation Device

Featured Application

This study designed a compact vertical roller potato–stem separation device by determining the physical properties and separation conditions of potatoes and their stems. It effectively addresses the issue of poor potato–stem separation performance in small-scale potato harvesters. The results of this research have been implemented in Shandong Province, China, and are being promoted continuously. The small-scale potato harvesters equipped with this device are able to adapt to the fragmented potato-planting patterns in the region, achieving flexible and high-performance harvesting operations for potatoes.

Abstract

In order to solve the problem encountered by traditional potato–stem separation devices, that is, they cannot meet the requirements when installed in small-scale harvesters, a new type of vertical differential roller potato–stem separation device was developed. The device features a compact structure and simultaneously possesses both separating and conveying functions. Through the analysis of the separation force between potato and stem, the structure and parameters of the separation device were determined. The simulation and the field test of the potato–stem separation process were carried out with the vertical differential roller speed, the vertical differential roller gap width and the conveyor chain speed as the influencing factors. The simulation test analysed the influence law of different working parameters on the performance of potato–stem separation. The field test revealed the order of the effects of various factors on the impurity rate and skin-breaking rate, concluding that the optimal combination of operational parameters was a vertical differential roller rotational speed of 6 s⁻¹, a vertical differential roller gap width of 7 mm, and a conveyor chain speed of 1.4 m·s⁻¹. This experiment fills the research gap in the study of potato–stem separation devices suitable for small-scale potato harvesters and promotes the development of compact potato harvesters.

1. Introduction

Potatoes are a favoured staple foodstuff because of their drought tolerance, stable high yields and wide utility [1,2]. In recent years, the world’s potato acreage has reached 20 million ha, and potato crops are grown in more than 150 countries around the world, making it the fourth most important food crop after wheat, rice, and maize [3]. Potato–stem separation is an important part of the mechanised potato-harvesting process. The performance quality of the device will have a direct impact on the quality of the potato harvest.

In order to reduce the rate of potato damage and skin breakage, to avoid the occurrence of stem entanglement and blockages, and to improve the performance of potato–stem separation, global enterprises and researchers focusing on potato–stem separation devices have carried out a lot of research and improvement. However, due to commercial sensitivities, published research is limited, so the technical characteristics of harvesters used in many developed, large-scale potato production areas can only be analysed by directly referring to the potato–stem separation device installed on representative potato harvesters. For example, the large-scale and multi-stage potato harvesters of Grimme (Hunteburg, Germany) and AVR (Roeselare, the Kingdom of Belgium) are usually equipped with elastic picking roller and lifting separation devices [4]. The elastic picking roller separation device uses the blocking effect of flexible rods to guide the stems into the gap between the elastic picking roller and the conveyor chain. The two rotate in opposite phases and use friction to break the stems and pull them away from the potato tubers. Then, the potato tubers pass through the gap between the flexible rods and fall onto the conveyor chain. The advantage of this type of device is that it can effectively separate potatoes from stems and also remove residual film and weeds. The disadvantage is that when there is an excess of the potato–soil–stem mixture, the device is prone to clogging, which in turn leads to a reduction in the harvesting quality of the potato harvester [5]. The device also has strict location requirements for installation, and must be installed at the junction of adjacent two-stage conveyor chains with a height difference. The lifting separation device separates potatoes and stems through the speed difference between the stem lifter and the conveyor chain. The device’s stem lifters are usually made of flexible annular steel cables connected to bars, forming a highly flexible flow grid structure, which greatly improves potato–stem separation performance. However, due to the need to add additional stem lifters, the structure of the device is relatively complex and requires considerable installation space.

Due to the severe fragmentation of potato fields, scholars in China have conducted extensive research on small-scale potato harvesters, including the potato–stem separation devices applied in these harvesters. These devices are essentially simplified and miniaturised elastic picking roller separation devices that function by removing stems from the potato tubers through the compression and friction action between the stem-picking drum and the conveying chain rods. However, these devices must also be installed at the junction of two adjacent conveying chains in the potato harvester, which necessitates that the harvester be equipped with dual or multiple levels of conveying chains [4,6,7,8]. Consequently, the further miniaturisation of potato harvesters has been constrained.

In many systems around the world, including those in China, field sizes are small and fragmented and large-scale potato harvesters are unable to enter the fields for operation. Therefore, a more flexible small-scale single-stage potato harvester can effectively meet the fragmented production model of small-scale potato farming [9,10,11]. However, the various types of potato–stem separation devices introduced in the previous text cannot be applied to this type of potato harvester [12]. Therefore, a potato–stem separation device suitable for small-scale single-stage potato harvesters urgently needs to be developed.

To address this, this study establishes the motion and force models of potato plants during the transportation and separation process, clarifying the conditions for achieving stem separation and lateral transportation of potatoes based on mechanical parameter measurements of potato plants, and subsequently designing a vertical roller potato–stem separation device. The device utilises a completely new structure that facilitates both the removal of stems and the transportation of potatoes simultaneously. It overcomes the shortcomings of the current elastic picking roller separation device, which requires the use of a multi-stage conveyor system, as well as the complexities and space requirements of the lifting separation device.

2. Materials and Methods

2.1. Force Analysis of Potato–Stem Separation

2.1.1. Force Analysis of Stem

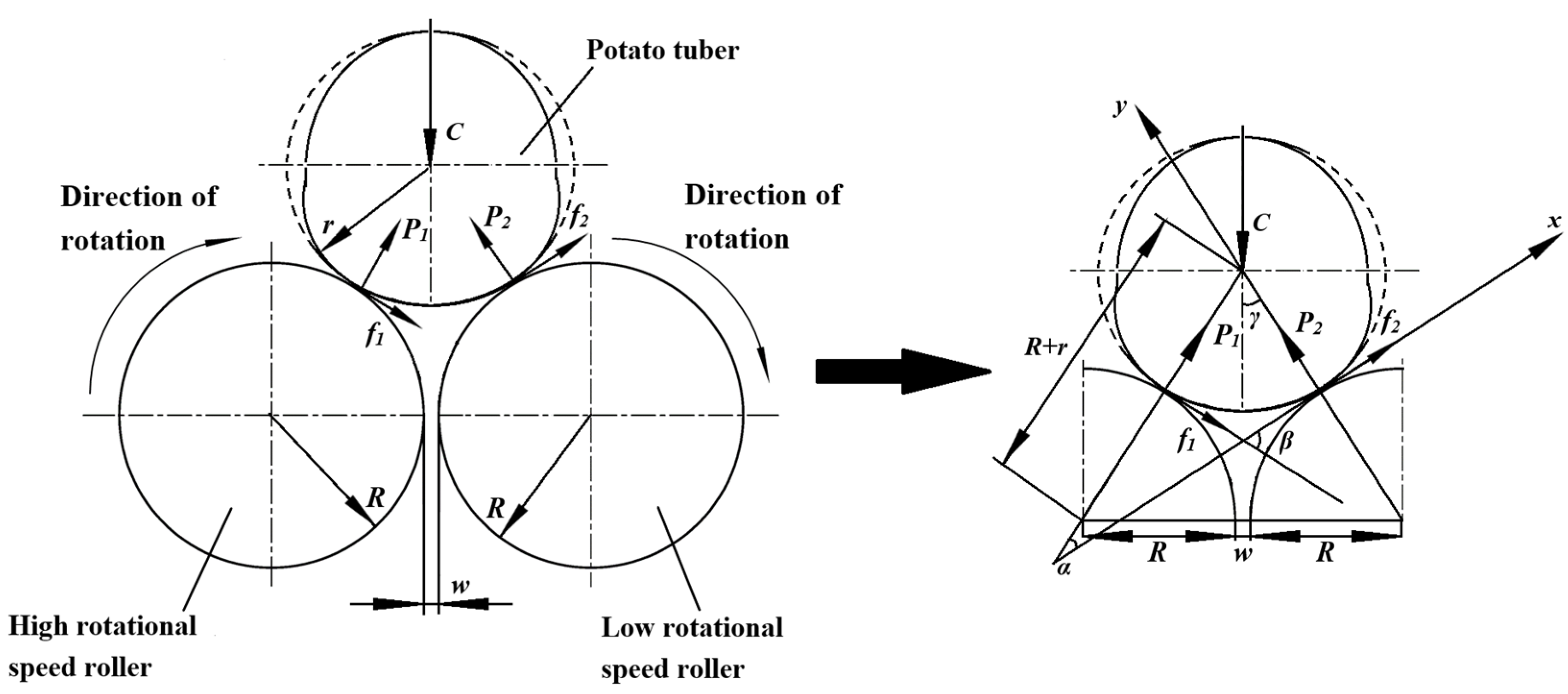
Since the width of the gap between the vertical differential rollers is smaller than the diameter of the potato stem, when the stem enters the gap between the two adjacent rollers, its radial direction will be subjected to squeezing force from both rollers, and therefore, deformation occurs. At the same time, the stem is also subjected to friction in the opposite direction exerted by the two adjacent vertical differential rollers because they are covered with rubber, and there is a difference in rotational speed between them. The simplified force analysis diagram of the potato stem during the separation process is shown in Figure 1.

After being squeezed by adjacent differential rollers, the diameter of the stem changes from D to d, and the change in diameter Δd can be expressed as:

$$\Delta d=D-d$$

(1)

The Δd value is positively correlated with the squeeze force N it receives, but due to the multi-layered composite structure of potato stems, the correlation between Δd and N cannot be expressed by a formula and can only be determined through experiments.

During the squeezing process, potato stems are subjected to frictional forces exerted by the differential rollers on both sides. The stem has a tendency to move in the opposite direction of the roller, so the stem is subjected to the static friction applied by the high-speed roller, and its value can be calculated by Equation (2):

$$T=N·{\mu }_0$$

(2)

where T is the friction force (N) exerted on potato stems by high-speed vertical differential rollers; N is the squeeze force (N) on potato stems by vertical differential rollers; and μ₀ is the static friction factor between the potato stem and rubber.

At the same time, there is sliding between the stem and the low-speed vertical differential roller, and the sliding direction is opposite to the direction of the roller, so the stem will be subjected to the dynamic friction exerted by the low-speed roller, the value of which can be calculated by Equation (3):

$$T^{\prime }=N·\mu$$

(3)

where T′ is the friction force (N) exerted on potato stems by low-speed vertical differential rollers, and μ is the dynamic friction factor between potato stem and rubber.

Due to the fact that μ₀ > μ, the frictional forces acting on both sides of the potato stems are different. Therefore, the total tensile force F exerted on the potato stem can be calculated as:

$$F=T-T^{\prime }$$

(4)

In Equation (4), T, applied by the high-speed differential roller, is greater than T′, applied by the low-speed differential roller, so F is always >0. This indicates that the total tensile force received by the potato stem is always directed towards the rear of the differential roller, so the stem will be clamped by adjacent differential rollers and transported backwards.

As the stem and the connected potato tuber continue to move backwards, the tuber will come into contact with two adjacent differential rollers (Figure 1b). As the diameter of the tuber is much larger than the gap width of the vertical differential rollers, the potato cannot enter the rollers.

At this point, the stolon between the stem and the potato tuber will tighten, generating a tensile force T″, which is also the breaking force of the stolon. When the total tension force F on the stem is greater than the stolon breaking force T″, the potato tuber and the stem will be separated. Therefore, the conditions for potato stem separation can be summarised by Equation (5):

$$N·\left({\mu }_0- \mu \right)>T^{″}$$

(5)

2.1.2. Force Analysis of Potato Tuber

There are relative motions between the potato tuber and the differential rollers when the two come into contact, so the potato will be subjected to pressure and friction from the differential rollers and guided to the discharge port on the side of the conveyor chain. The force analysis diagram of the potato during the separation process is shown in Figure 2 and establishes a coordinate system with the contact point between the potato and the right differential roller as the origin, the common tangent between the two as the x-axis, and the normal as the y-axis.

The resultant force F_x exerted on the potato in the direction of the x-axis can be calculated by Equation (6):

$$F_x=f_2+P_1\mathit{cos}\alpha +f_1\mathit{cos}\beta -C\mathit{sin}\gamma$$

(6)

where P₁ is the support force (N) of the left roller for the potato; f₁ is the frictional force (N) between the left roller and the potato; f₂ is the friction force (N) between the right roller and potato; C is the pushing force (N) of the conveyor chain on the potato; α is the angle (°) between the line connecting the left roller and the potato envelope circular centre and the x-axis; β is the angle (°) between the frictional force between the left roller and potato and the x-axis; and γ is the angle (°) between the pushing force of the conveyor chain on the potato and the y-axis.

The resultant force F_y exerted on the potato in the direction of the y-axis can be calculated by Equation (7):

$$F_y=P_2+P_1\mathit{sin}\alpha -f_1\mathit{sin}\beta -C\mathit{cos}\gamma$$

(7)

where P₂ is the support force (N) of the low-speed differential roller for the potato.

The relationship between P₁, P₂ and f₁, f₂ can be expressed as:

$$f_1=P_1·{\mu }^{\prime }$$

(8)

$$f_2=P_2·{\mu }^{\prime }$$

(9)

where μ′ is the dynamic friction factor between the rubber and potato tuber.

According to geometric analysis, α, β, γ can be expressed as:

$$\alpha ={\displaystyle \frac{\pi }{2}}-2\gamma$$

(10)

$$\beta =2\gamma$$

(11)

$$\tan \gamma ={\displaystyle \frac{2R+w}{\sqrt{4r^2+8Rr-w^2-4Rw}}}$$

(12)

where R is the radius (mm) of the differential roller; r is the radius (mm) of the equivalent envelope circle of the potato tuber; and w is the gap width (mm) of adjacent differential rollers.

According to motion analysis, for the tuber to be transported laterally and not to be damaged by the pressure of the differential rollers, the received force must point in the positive direction of the x-axis. Based on this, the condition for the effective conveyance of the potato can be obtained as follows:

$$F_x>0$$

(13)

$$F_y=0$$

(14)

According to Equations (6)–(11), the following inequality can be derived:

$$\left(P_1+P_2\right)\left({\mu }^{\prime }-\mathit{tan}\gamma \right)+2P_1\mathit{tan}\gamma {\left(\mathit{sin}\gamma \right)}^2+P_1\mathit{sin}2\gamma >0$$

(15)

According to geometric relationships, the γ angle must be between 0° and 90°. Therefore, when μ′ > tan γ, all three terms on the left side of Inequality 15 are greater than zero, and the inequality must hold. Therefore, based on Equation (12), it can be concluded that for the condition for Inequality 15 to hold, the condition for the potato to be transported laterally is:

$${\mu }^{\prime }>{\displaystyle \frac{2R+w}{\sqrt{4r^2+8Rr-w^2-4Rw}}}$$

(16)

2.2. Determination of Mechanical Parameters of Stem and Potato

2.2.1. Determination of Separation Forces Between Tubers and Stems

The potato is attached to the stem by a stolon, and when the stolon breaks, the potato is separated from the stem. In order to determine the tensile force required to achieve potato–stem separation, the breaking force of the stolon is determined by means of a tensile test. The material used in this test is the “Dutch V7” variety of potatoes. The sample was collected on the day of harvest in Dongguo Town, Tengzhou City, Shandong Province, China. The local soil type is cinnamon soil. On the day of sample collection, the moisture content of potato stem samples was 72.46%, the moisture content of soil was 25.04%, and the weather conditions were clear and dry. A potato with stolon and stem was placed horizontally on the test bench, and one end of the potato was fixed with a test clamp. A digital push-pull gauge (WDF-100 push-pull gauge, Weidu Electronics Co., Ltd., Wenzhou, China) was used to hold the stem at the other end of the stolon as shown in Figure 3. The gauge was pulled slowly until the stolon broke, at which time the pull force shown by the gauge was recorded as the pull force required for potato–stem separation.

2.2.2. Determination of the Breaking Force of Stems Under Compound Load

The separation device applies pressure to deform the stem through the gap between adjacent rollers and removes the stem from the potato by the friction generated from the rotation. In this process, if the stem breaks first, the potato is still attached to the remnant stem. In this case, the residual stem needs to be redirected to the gap between the rollers for a second removal attempt, which increases the operational load of the potato–stem separation, and is very likely to cause a blockage in the device. Therefore, by investigating the relationship between the radial pressure on the stem and the resulting deformation, and by determining the tensile strength of the extruded stem, it is possible to determine the breaking order of the stem and potato stolon, to avoid stem breakage and repetitive segregation [13,14].

In this study, the type of TA.XTPLUS texture tester (British Stable Micro System, Godalming, Surrey, UK) is used to determine the pressure-deformation characteristics of potato stems. This type of texture tester is a single-column solution for texture analysis and materials property testing, measuring up to 50 kg in force with a minimum speed of 0.01 mm·s⁻¹, which can be programmed to conduct almost any mechanical test. The potato stem samples were compressed along the radial direction at a loading rate of 0.2 mm·s⁻¹ by the texture tester until the layers of tissue ruptured and failed, as shown in Figure 4.

After the radial pressure-deformation test, potato stems with radial compression deformations of 2 mm, 4 mm and 6 mm were prepared and their tensile strengths were determined. Considering that this part of the stem has a shorter length, a consistent diameter, a uniform internal texture, and a gentle curvature, we regard its tensile strength as a constant value, rather than one that varies along its length. In this study, the TA.XTPLUS texture tester was also used to determine the stretching and fracture characteristics of potato stems. The stem samples were stretched along the axial direction at a loading rate of 0.2 mm·s⁻¹ until fracture failure, as shown in Figure 5.

2.2.3. Determination of the Dynamic Friction Factor Between Potato and Rubber

The dynamic friction factor between the potato tuber and the rubber surface of the differential roller is a key parameter required for analysing the movement process of potatoes. The dynamic friction factor needs to be indirectly calculated by analysing the force on the measured object in the sliding state. In this test, a J0207 electric spark dot timer (Bohsan Cultural Supplies Co., Ltd., Taizhou, China) was fixed at the end of the inclined rubber plate, and the plate was adjusted to the angle of 53°, as shown in Figure 6a. At this angle, the potato tuber will slide down due to unbalanced force. Then, a hook was fixed at one end of the potato tuber’s long axis direction, and a paper tape was passed through the dot timer and connected to the hook, as shown in Figure 6b. Finally, the potato tuber was placed on the upper surface of the inclined rubber plate, and the timer was started when the potato was released. The relationship between displacement and time for the potato tuber during the sliding process was recorded by the marked points on the paper tape, as shown in Figure 6c.

During the sliding process, the potato tuber was subjected to its own gravity and the frictional resistance generated by the inclined rubber plate. Due to the gravity component being greater than the sliding resistance, the potato tuber slid at an accelerating rate. The acceleration of the potato tuber was calculated by measuring the total distance between 10 consecutive recording points on the paper tape, as well as the distances between the first 5 and last 5 recording points. The equation of the acceleration can be expressed as:

$$\left(S_2-S_1\right)\times {10}^{-3}=a{t}^2$$

(17)

where S₁ is the total distance (mm) of the first 5 recording points; S₂ is the total distance (mm) of the last 5 recording points; a is the sliding acceleration (m·s⁻²) of the potato tuber; and t is the dot time (s) for 5 consecutive recording points. The dot timer used in this study had a time interval of 0.02 s between adjacent recording points, so t = 0.1 s.

By analysing the force on the potato tuber accelerating downward on the inclined plate, Equation (18) can be obtained:

$$mg\mathit{sin}\theta -{\mu }^{\prime }mg\mathit{cos}\theta =ma$$

(18)

where m is the potato tuber quality (kg); g is the gravitational acceleration (m·s⁻²); θ is the angle (°) of the inclined plate, which is 53° in this test; and μ′ is the dynamic friction factor between the rubber and potato tuber.

The formula for the dynamic friction factor can be obtained as:

$${\mu }^{\prime }=\mathit{tan}\theta -{\displaystyle \frac{\left(S_2-S_1\right)\times {10}^{-3}}{g{t}^2\mathit{cos}\theta }}$$

(19)

2.2.4. Determination of the Static and Dynamic Friction Factors Between Stem and Rubber

Due to the small contact area between the individual stem and the inclined plate, and the tendency for it to easily roll off the inclined surface, it is necessary to group multiple segments of the stem together when determining the factors of friction between the stem and rubber, as shown in Figure 7. This method can effectively increase the contact area between the stem and the inclined plate, thereby preventing the occurrence of individual stems rolling off.

Unlike the method for determining the dynamic factor of friction, the measurement of the static factor of friction does not require the use of a spark dot timer. First, place the stems on the inclined plate, then slowly raise the fixed clamp connected to one end of the inclined plate on the iron frame. As the angle of inclination of the inclined plate increases, promptly stop raising the fixed clamp when the stems begin to slide and record the inclination angle at that moment. The equation of the static friction factor between the stem and the rubber can be expressed as:

$${\mu }_0=\tan \theta$$

(20)

where θ is the angle (°) of the inclined plate; and μ₀ is the static friction factor between potato stem and rubber.

The method for determining the dynamic friction factor between the stem and rubber is consistent with the process described in Section 2.2.3, and will therefore not be further elaborated upon.

2.3. Simulation Design

The potato–stem separation device proposed in this study is a new structure that has not been adopted in existing mechanised potato harvesting schemes. Even with theoretical calculations, the actual effectiveness of the device still remains uncertain. To verify that this newly developed potato–stem separation device has the capability for potato–stem separation, and to provide researchers with a certain understanding of the operational performance of the device under different parameters, a single-factor simulation experiment needs to be conducted prior to processing and field testing of the device. In the EDEM 2020 software, the method of particle filling allows for the precise reconstruction of irregular and flexible potato plant models. By setting the inter-particle bonding strength and the contact characteristics between the particles and the solid model, it accurately reflects the fracture of the stem and the transportation process of the potatoes. Therefore, this study employs DEM rather than FEM for the simulation research.

2.3.1. Modelling of the Vertical Differential Roller Potato–Stem Separation Device on a Potato Harvester

According to the research results in Section 3.1.2 and Section 3.1.4, the average diameter of the potato stem samples was measured to be 9.5 mm before the test, and the static friction factor between the stem and the rubber (μ₀) was 1.175 and the dynamic friction factor (μ) was 1.032. According to the research result in Section 3.1.2, when the compression deformation of the potato stem reached 2 mm, the average pressure was 88.89 N; when the compression deformation reached 4 mm, the average pressure was 312.85 N; and when the compression deformation reached 6 mm, the average pressure was 380.73 N. By substituting the aforementioned data into Equations (2)–(4), it can be calculated that the total tensile force on the stem was 12.71 N at a differential roller gap width of 7.5 mm (compression deformation of 2 mm), 44.74 N at a differential roller gap width of 5.5 mm (compression deformation of 4 mm), and 54.44 N at a differential roller gap width of 3.5 mm (compression deformation of 6 mm). It can be seen that when the gap width of the differential rollers is within this range, the tension force on the stem is greater than the connecting force between the potato and the stem and is smaller than the breaking force of the stem, which is in line with the requirements of potato–stem separation. Considering the machining accuracy of the machine and the slight deformation of the rubber roller under stress, the rounded width levels of 3 mm, 5 mm and 7 mm were set in the subsequent experiments to investigate the effects of different gap widths on the performance of potato–stem separation. In addition, a level of 9 mm was added to the experiment as a comparison, to analyse the performance of the potato–stem separation device under more extreme operating conditions.

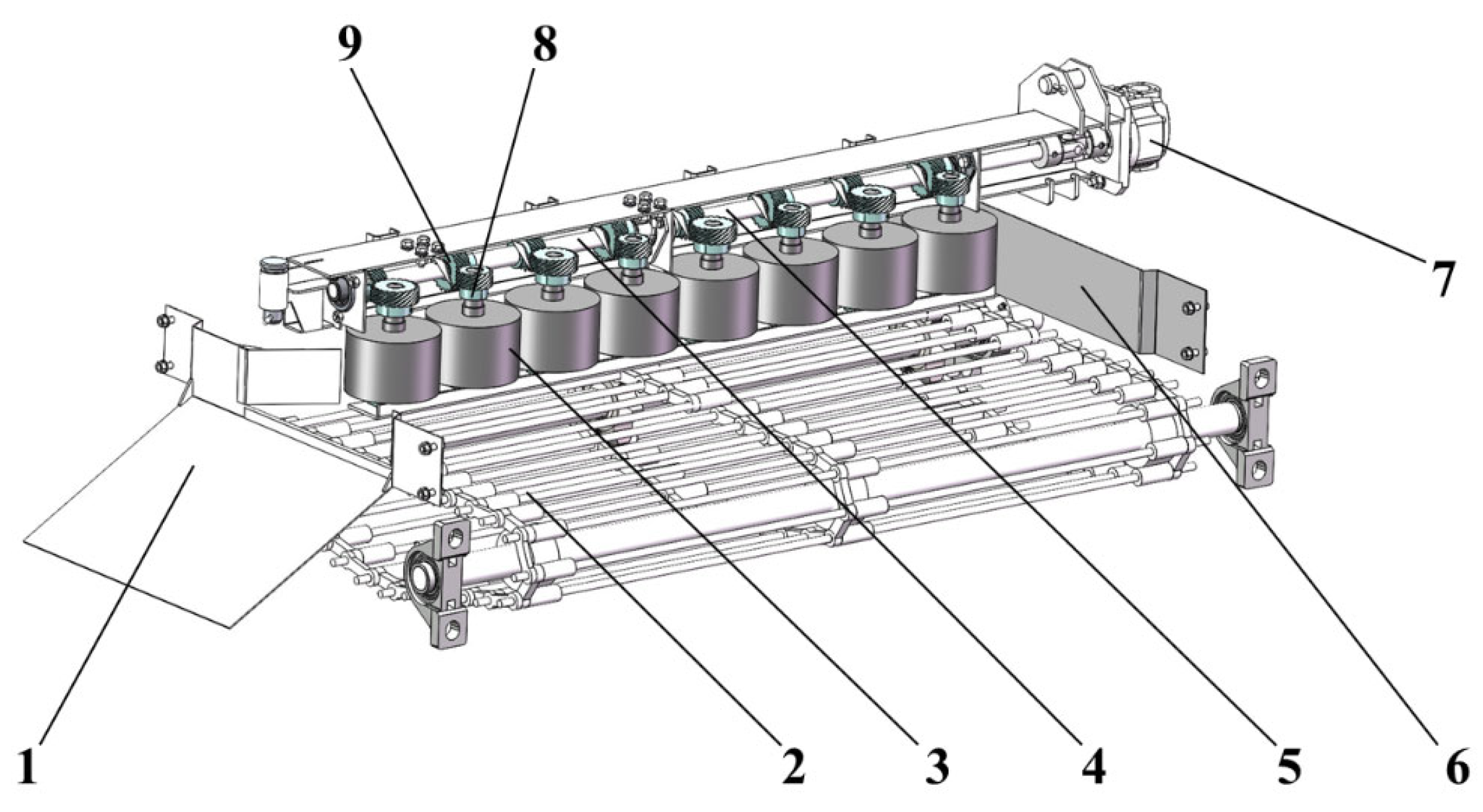
A model of the vertical differential roller potato–stem separation device is shown in Figure 8. Other structural parameters of the device were determined based on the actual installation space of the test prototype, and the data are summarised in

Table 1. Structural parameters of vertical differential roller potato–stem separation device.

Item	Parameter
Number of vertical differential rollers	8
Diameter of vertical differential rollers (mm)	120
The gap width of vertical differential rollers (mm)	3/5/7/9
Conveyor chain width (mm)	1050
Conveyor chain bar spacing (mm)	40

. Substituting the dynamic friction factor between the potato and rubber measured in Section 2.2, the relevant structural data and size data of the potato varieties at the experimental site test the inequality given by Equation (16), which can make it hold. Therefore, the separation device developed by this study can ensure that potatoes can be transported laterally and will not be damaged by the pressure of the differential rollers.

The potato–stem separation device was installed above the end of the conveyor chain, consisting of a hydraulic motor, a driving shaft, a driven shaft, eight driving helical gears, eight driven helical gears, and eight vertical differential rollers. The hydraulic motor, driving shaft, and driven shaft are connected by couplings, so that the motor can drive the shafts to rotate together. There are four driving helical gears, each fitted on the driving shaft and the driven shaft, which meshed with the driven helical gears fitted on the shaft end of the differential rollers, thereby converting the horizontal rotational motion of the shaft into the vertical rotational motion of the rollers. There is a certain gap between adjacent differential rollers.

During the operation, the potato harvester excavates and gathers the potato–stem–soil mixture at the front end of the conveyor chain. The mixture is separated from the soil by the vibration of the conveyor chain, while the potatoes and stems are transported to the end of the conveyor chain and come into contact with differential rollers.

Under the rotation of the differential rollers, potatoes are guided to the discharge port on the side of the conveyor chain and placed in the field through the slide. The stems are guided into the gaps between the differential rollers and subjected to compression and friction applied by the rollers, thus being removed from the potatoes and discharged behind the potato harvester.

Based on the determined structural parameters, a simplified model of the device was built using the EDEM software (Altair Engineering, Troy, MI, USA). The simulation process was greatly simplified by the fact that the drive could be applied directly to the differential roller and the conveyor chain bar in the EDEM software, thus eliminating the need for additional modelling of the drive device. In order to effectively collect the separated potato and stem discrete meta-model, baffles and receiving boxes were added to the side and bottom of the potato–stem separation device model to avoid the particle loss caused by the model moving outside the model calculation range during the simulation process [15]. The completed simulation model of the vertical differential roller potato–stem separation device is shown in Figure 9.

2.3.2. Modelling of a Discrete Meta-Model of the Potato Stem Complex

In accordance with the average size of potatoes and their stems at the experimental site, the potato stem complex model was firstly established in SolidWorks 2024 (Dassault Systèmes, Vélizy-Villacoublay, France), in which the length of the potato model was 65 mm, the width was 55 mm, the thickness was 45 mm; and the diameter of the potato stem model was 9 mm, with a length range of 65–75 mm and a lateral width range of 45–55 mm.

The model was saved as ‘.stl’ and imported into EDEM software for particle filling. The particles were connected by Heretz–Mindlin with bonding key, the radius of the particles was set to 3.5 mm, and the contact radius was set to 4 mm [16]. The parameters of the bonding key were as shown in

Table 2. Bonding parameters.

Item	Parameter
Normal bond stiffness (N·m−3)	9.0 × 107
Tangential bond stiffness(N·m−3)	9.0 × 107
Normal critical stress (Pa)	5.0 × 109
Tangential critical stress (Pa)	5.0 × 109

, and the particle model of the potato stem complex after filling is shown in Figure 10. Under this combination of parameters, the average breaking force of the potato stolon was 6.487 N, obtained by performing the tensile simulation test in EDEM, which is similar to the data measured in the real tensile test of Section 3.1.1. This shows that the particle model of the potato and stem is in line with the actual situation.

2.3.3. One-Factor Simulation Experimental Design

In order to restore the contact mechanism between the potato and the stem and mechanical structures in the actual operation process, the materials of the rollers and conveyor chain bars were defined as ‘rubber’ and ‘Q235’, respectively, and the material of the potato stem complex particle model was defined as ‘potato stem’, with the material parameters shown in

Table 3. Material parameters.

Item	Rubber	Q235	Potato Stem
Poisson’s ratio	0.49	0.30	0.28
Density (kg·m−3)	1200	7865	1034
Modulus of elasticity (Pa)	1.50 × 107	2.05 × 1011	1.24 × 107
Source	Fan et al., 2023 [17]	Liu et al., 2024 [18]	Fan et al., 2023 [17]

. The contact parameters between potato stem-Q235 and potato stem-rubber were set separately as shown in

Table 4. Contact parameters.

Item	Potato Stem-Q235	Potato Stem-Rubber
Factor of restitution	0.465	0.30
Factor of static friction	0.570	1.18
Factor of rolling friction	0.100	0.70
Source	Zhou et al., 2023 [19]	Fan et al., 2023 [17]

. The influence of each factor on the performance of potato–stem separation was further investigated by EDEM discrete element simulation, taking the high-speed differential roller speed, the gap width of adjacent differential rollers, and the conveyor chain speed as the influencing factors, with the proportion of the mass of unseparated stems as the evaluation indexes.

The potato–stem separation device developed in this study consists of a conveyor chain and multiple differential vertical rollers. There are interactions between the rotation speed of the differential roller, the line speed of the conveyor chain and the gap width of differential rollers. The rotation speed of the differential roller and the line speed of the conveyor chain jointly affect the contact time between the potato and its stem with the differential roller, that is, the duration of the separation process of potato and stem, which determines the separation performance of the device to a certain extent. The rotation speed of the differential roller and the gap width of differential rollers jointly affect the stress of the potato stem, which also determines the separation performance of the device to a certain extent. The above three parameters are limited by the drive system and the structural dimensions of the test platform. In order to ensure the rigour and authenticity of the study, four representative levels were selected for each operating parameter within the standard operating condition of the potato harvester.

In order to analyse the influence of the speed of the vertical differential roller on the separation performance, the gap width of adjacent rollers was set to 7 mm, and the speed of the conveyor chain was set to 1.4 m·s⁻¹. As the speed of the drive motor increases, the torque it provides gradually decreases. To prevent blockage caused by the drop in torque, we selected four levels at equal intervals within the effective working speed range of the motor. After the reduction in speed through the gear mechanism, the comparative tests were carried out under four working conditions of 2 s⁻¹, 4 s⁻¹, 6 s⁻¹, and 8 s⁻¹ for the speed of the high-speed roller. Due to the staggered use of 20-tooth and 15-tooth helical gears to drive the differential rollers, the rotation speed difference between the high-speed and low-speed differential rollers was a fixed value of 1.78. From this, it can be calculated that the corresponding low-speed rollers rotate at speeds of 1.125 s⁻¹, 2.25 s⁻¹, 3.375 s⁻¹, and 4.5 s⁻¹.

In order to analyse the influence of the gap width of adjacent differential rollers on the separation performance, the speed of the high-speed roller was set at 6 s⁻¹, and the speed of the conveyor chain was set at 1.4 m·s⁻¹. Considering the machining accuracy and the deformation of the vertical rollers during the compression of the stems, we rounded the gap width data. Gap widths of 3 mm, 5 mm, and 7 mm corresponded to radial compression deformation values of 6 mm, 4 mm, and 2 mm for the stems, respectively. Additionally, we introduced a gap width of 9 mm to study the performance of the separation device under more extreme operating conditions. The comparative tests were carried out for four working conditions, i.e., the gap widths of adjacent rollers were 3 mm, 5 mm, 7 mm, and 9 mm.

In order to analyse the influence of the conveyor chain speed on the separation performance, the speed of the high-speed roller was set to 6 s⁻¹, and the gap width of the adjacent rollers was set to 7 mm. The prototype used in this experiment features four operational gears, with each gear corresponding to a specific linear speed of the conveying chain. The comparative tests were carried out for four conditions of the conveyor chain speeds of 1.2 m·s⁻¹, 1.4 m·s⁻¹, 1.6 m·s⁻¹ and 1.8 m·s⁻¹.

There were 25 models of the potato stem complex generated for each simulation test, and the operational performance of the potato–stem separation device was evaluated at the end of the simulation by counting the ratio of the mass of the unseparated stems to the total mass of the separated potato stem mixture under the current operating parameters.

2.4. Field Experiment Design

2.4.1. Experimental Device

The prototype used in this test was a self-propelled potato harvester developed by Jiangsu University, and the vertical differential roller potato–stem separation device was installed at the end of the conveyor chain of the machine, as shown in Figure 11.

The field experiment was conducted in the following year after sample collection in Dongguo Town, Tengzhou City, Shandong Province, China. During the experiment, the weather was clear and dry, with a soil moisture content of 27.73%. The potato variety used was “Dutch V7”, and the local soil type was cinnamon soil. The experiment was carried out within the jurisdiction of a single grower to ensure uniform water and fertiliser conditions as well as planting practices for all potato plants. The aforementioned conditions were highly consistent with those at the time of sample collection, thereby minimising deviations between the mechanical parameters of the potato plants and the measured values. During the test, the linear speed of the conveyor chain, the rotational speed of the differential rollers and the gap width of the adjacent differential rollers could be adjusted, so as to perform single-factor and multi-factor interaction tests, in order to study the effect of these factors on the rate of impurity and skin breakage in potatoes. In each set of tests, the potato-harvesting tester was operated across two rows and travelled for 20 m, during which time the removed potato stems were excluded from the rear of the machine, while the separated potatoes were guided to an outlet on the side of the machine and dropped onto a tarpaulin laid on the side rows. The rate of impurity and skin breakage can be obtained by measuring the proportion of the mass of stems on the tarpaulin to the total mass of the material, and the proportion of the mass of skin-broken potatoes to the total mass of all potatoes [20]. In order to improve the statistical reliability of the experimental results, each set of tests was repeated three times, and the impurity and skin-breaking rate results presented are the average values of the three repetitions.

2.4.2. One-Factor Experimental Design

In order to analyse the influence of the vertical differential roller speed on the impurity rate and skin-breaking rate, the gap width of adjacent differential rollers was set to 7 mm, the conveyor chain speed was set to 1.4 m·s⁻¹, and the comparison test was carried out for the four working conditions of high-speed rollers at 2 s⁻¹, 4 s⁻¹, 6 s⁻¹, and 8 s⁻¹.

In order to analyse the influence of the gap width of adjacent differential rollers on the impurity rate and skin-breaking rate, the speed of the high-speed roller was set at 6 s⁻¹, the speed of the conveyor chain was set at 1.4 m·s⁻¹, and comparative tests were carried out under four working conditions, i.e., the gap widths of adjacent differential rollers were 3 mm, 5 mm, 7 mm, and 9 mm.

In order to analyse the influence of conveyor line speed on the impurity rate and skin-breaking rate, the speed of the high-speed differential roller was set at 6 s⁻¹, the gap width of adjacent differential rollers was set at 7 mm, and comparative tests were carried out for the four conditions of conveyor line speeds of 1.2 m·s⁻¹, 1.4 m·s⁻¹, 1.6 m·s⁻¹, and 1.8 m·s⁻¹.

2.4.3. Multifactorial Experimental Design

After eliminating the less effective parameters from the single-factor experiments, we utilised the remaining parameters to design the multifactorial experiments, which can reduce the workload of the multifactorial experiments and enhance the efficiency of parameter optimisation. The Box–Behnken design response surface test in the Design-Expert v13 software (Stat-Ease, Minneapolis, MN, USA) was used to conduct a 17-group field test with three factors and three levels, using the high-speed vertical differential roller speed A, the gap width of adjacent rollers B, and the conveyor chain speed C as the influencing factors, and the potato impurity content and skin-breaking rate as the test indexes. In the test, the speeds of the high-speed roller were set to 4 s⁻¹, 6 s⁻¹, and 8 s⁻¹, the gap widths of the rollers were set to 5 mm, 7 mm, and 9 mm, and the speeds of the conveyor chain were set to 1.2 m·s⁻¹, 1.4 m·s⁻¹, and 1.6 m·s⁻¹, respectively.

3. Results

3.1. Determination Results

3.1.1. Separation Forces Between Tubers and Stems

A total of 20 sets of pulling force tests were conducted in this study, and the statistical data are shown in

Table 5. Connection force data of stem and potato tubers.

Number	Max Connection Force/N
1	4.08
2	5.21
3	6.23
4	4.93
5	6.33
6	6.20
7	7.59
8	7.18
9	7.03
10	5.20
11	6.99
12	10.16
13	9.12
14	7.89
15	4.31
16	5.04
17	9.62
18	4.18
19	5.91
20	9.81
Average	6.651
Standard deviation	1.907
95% Confidence Interval	(5.76, 7.54)

, resulting in an average pulling force of 6.651 N required for the separation.

3.1.2. Breaking Force of Stems Under Compound Load

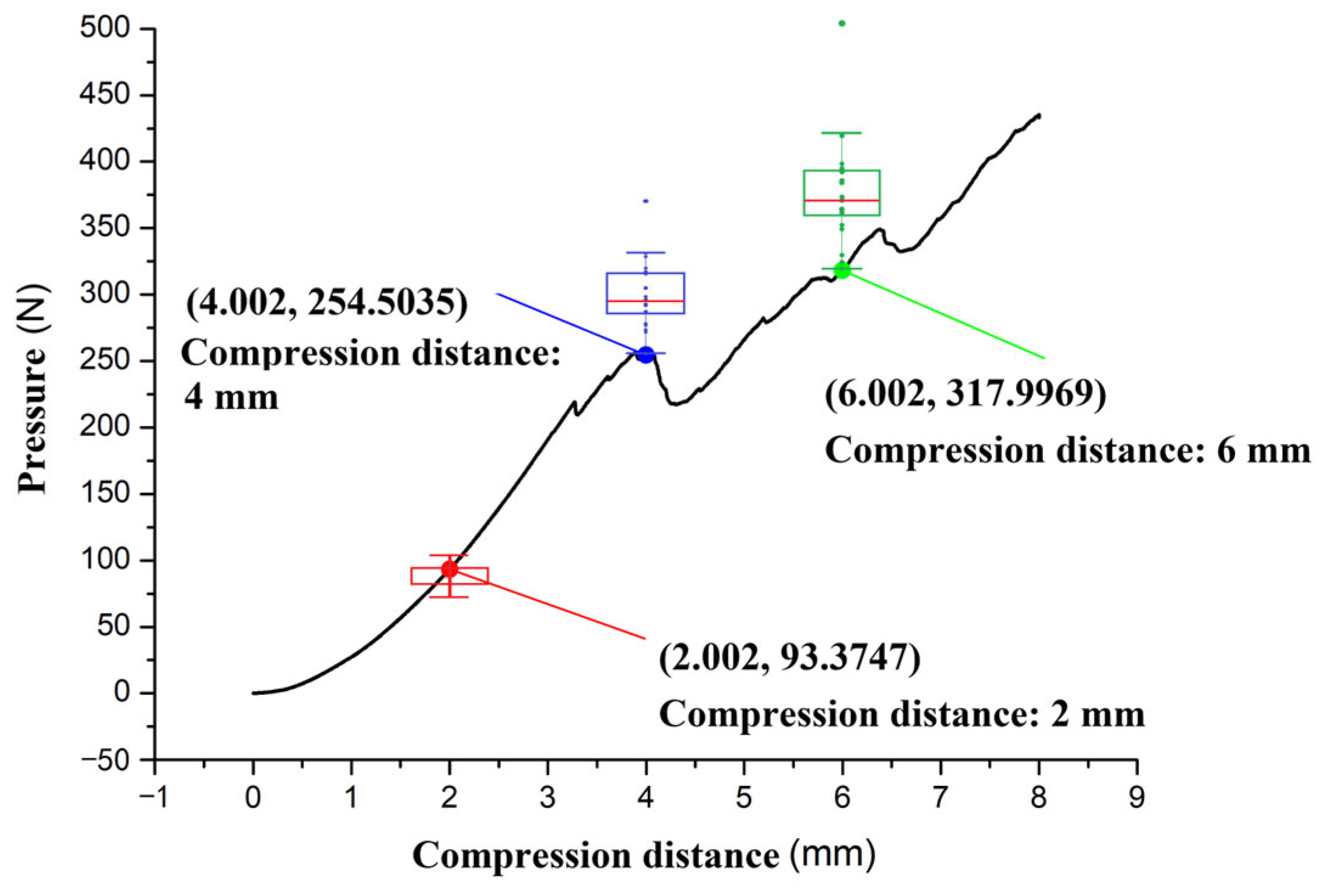
After measurement, the average diameter of these 20 sets of stems was found to be 9.5 mm. Then, a total of 20 sets of radial pressure deformation tests were carried out. By analysing the output of the force-displacement curves from the mass spectrometer, it can be seen that the compression force gradually increases with the increase in compression displacement and shows multiple peaks when in the process of increasing (Figure 12). When the compression distance is 2 mm, the distribution of pressure forces is relatively uniform, with no outliers, showing a slight right-skewed normal distribution. When the compression distance is 4 mm, the distribution of the pressure force is relatively uniform, exhibiting a slightly right-skewed normal distribution, but there is a noticeable outlier with a significantly large value. When the compression distance is 6 mm, the pressure force approximately follows a normal distribution, centred around the average, but the data distribution exhibits a wide range and a high degree of dispersion. The reason is that the potato stem is distributed from outside to inside with skin, bast fibre tissue, xylem and thin-walled tissue in turn [21]. With the gradual rupture and failure of each layer of the tissue, its radial compression force shows a fluctuation phenomenon. Twenty sets of force-displacement curves were analysed, and the points on the curves whose transverse coordinates were the target compression deformation were selected to obtain the corresponding radial compression force of the main stem. The statistical pressure data shows that when the compression deformation of the potato stem reached 2 mm, the average pressure was 88.89 N; when the compression deformation reached 4 mm, the average pressure was 312.85 N; and when the compression deformation reached 6 mm, the average pressure was 380.73 N. Based on the above data and the friction factor between the potato stem and the rubber, disclosed in existing research [14], it can be concluded that the inequality in Equation (5) holds.

After the radial pressure-deformation test, 10 sets of tensile tests were carried out using samples of potato stems, each with radial compression deformations of 2 mm, 4 mm, and 6 mm. After compression, the potato stem was torn and fractured under the stretching of the texture instrument. By analysing the force-displacement curve, it can be seen that the tensile force gradually increased with the increase in the tensile displacement, and multiple peaks were presented in the process of improvement, as shown in Figure 13. The reason for this is the successive fracture and failure of the various tissues within the stem during the stretching process, resulting in a fluctuating tensile force. When the potato stem sample wholly breaks, the value of the tensile force will decrease sharply, and the peak value of the tensile force before it breaks will be the maximum breaking force of the stem. The maximum breaking force and maximum tensile deformation data are shown in

Table 6. Maximum breaking force of potato stems.

Number	Max Breaking Force/N (2 mm of Compression)	Max Breaking Force/N (4 mm of Compression)	Max Breaking Force/N (6 mm of Compression)
1	158.40	157.17	123.50
2	200.49	176.09	129.22
3	151.48	142.19	134.76
4	148.56	160.19	95.65
5	191.85	159.74	144.13
6	173.87	143.97	126.34
7	172.79	183.78	116.63
8	167.86	173.69	90.19
9	186.86	137.83	92.22
10	164.13	177.96	113.12
Average	171.629	161.261	116.576
Standard deviation	17.204	16.303	18.656
95% Confidence Interval	(159.34, 183.92)	(149.62, 172.90)	(103.25, 129.90)

. By analysing the data, it can be seen that the maximum breaking force of the potato stem with a radial compression deformation value of 4 mm did not decrease significantly when compared to that of a stem with a value of 2 mm, so the radial compression of 2–4 mm could not effectively damage the internal tissue of the stem; thus, when the radial compression deformation reaches 6 mm, the degree of the internal tissue rupture and failure of the potato stem is greatly increased, and then the maximum breaking force of the stem decreases significantly. The maximum breaking force corresponding to a deformation of 2 mm exhibits a slight right-skewed normal distribution, while the maximum breaking force corresponding to a deformation of 4 mm shows a slight left-skewed normal distribution. In contrast, the maximum breaking force for a deformation of 6 mm presents a significant left skew and a bimodal tendency. The distribution of the maximum breaking force is characterised by considerable dispersion, which is a result of the randomness inherent in plant growth.

Based on the data above, the overall breaking force of the stem is much higher than the connection force between stem and potato tuber regardless of the load condition, which means the stem will not break first during the process of potato–stem separation.

3.1.3. Dynamic Friction Factor Between Potato and Rubber

In total, 10 sets of dynamic friction tests between the potato and rubber were conducted, and the distance between the recording points and the corresponding dynamic friction factor for each set of tests were recorded in

Table 7. Recording point distance and dynamic friction factors.

Number	Distance from the First 5 Points/mm	Distance from the Last 5 Points/mm	Dynamic Friction Factor
1	41	73	0.80
2	40	83	0.62
3	39	86	0.55
4	37	74	0.72
5	43	88	0.58
6	38	71	0.78
7	39	75	0.73
8	42	83	0.65
9	41	85	0.60
10	45	82	0.72
Average	40.500	80.000	0.675
Standard deviation	2.415	6.128	0.087
95% Confidence Interval	(38.78, 42.22)	(75.62, 84.38)	(0.61, 0.74)

, resulting in an average dynamic friction factor between the potato and rubber of 0.675.

3.1.4. Static and Dynamic Friction Factors Between Stem and Rubber

In total, 10 sets of static friction tests between stem and rubber were conducted, and the sliding angle of the stem and the corresponding static friction factors for each set of tests were recorded in

Table 8. Recorded sliding angle and static friction factors.

Number	Sliding Angle/°	Static Friction Factor
1	50	1.19
2	51	1.23
3	48	1.11
4	49	1.15
5	50	1.19
6	47	1.07
7	49	1.15
8	52	1.28
9	50	1.19
10	50	1.19
Average	49.6	1.175
Standard deviation	1.430	0.059
95% Confidence Interval	(48.58, 50.62)	(1.13, 1.22)

, resulting in an average static friction factor between the stem and rubber of 1.175.

Also, 10 sets of dynamic friction tests between the stem and rubber were conducted, and the distance between the recording points and the corresponding dynamic friction factor for each set of the tests were recorded in

Table 9. Recorded point distance and dynamic friction factors.

Number	Distance from the First 5 Points/mm	Distance from the Last 5 Points/mm	Dynamic Friction Factor
1	35	57	0.97
2	35	54	1.02
3	33	49	1.07
4	38	54	1.07
5	39	53	1.10
6	31	52	0.98
7	28	47	1.02
8	40	61	0.98
9	42	60	1.03
10	36	51	1.08
Average	35.7	53.8	1.032
Standard deviation	4.270	4.491	0.046
95% Confidence Interval	(32.65, 38.75)	(50.59, 57.01)	(1.00, 1.06)

, resulting in an average dynamic friction between the stem and rubber of 1.032.

3.2. Analysis of One-Factor Simulation

In the simulation process, first of all, the conveyor chain bar will generate a certain number of potato stem complex particle models, and to be stable after the accumulation of the particle model, the conveyor chain begins to drive the potato stem complex at a certain speed toward the vertical differential rollers which are installed side-by-side. Under the removing action of the rollers, the stem is separated from the potato and falls into the receiving box behind the rollers. At the same time, the potato comes into contact with the rotating differential rollers, and is guided to the receiving box on the side of the conveyor chain. The simulation process of potato–stem separation is shown in Figure 14.

Results of the one-factor simulation experiments are shown in

Table 10. Results of one-factor simulation experiments.

Number	Experimental Factors			Percentage of Unseparated Stem Mass (%)
	Speed of High-Speed Vertical Differential Roller (s−1)	Gap Width of Vertical Differential Rollers (mm)	Line Speed of the Conveyor Chain (m·s−1)
1	2	7	1.4	8.45
2	4	7	1.4	7.65
3	6	7	1.4	4.13
4	8	7	1.4	4.32
5	6	3	1.4	12.28
6	6	5	1.4	6.33
7	6	7	1.4	4.13
8	6	9	1.4	11.96
9	6	7	1.2	3.63
10	6	7	1.4	4.13
11	6	7	1.6	4.05
12	6	7	1.8	6.20

. The data show that when the speed of the high-speed vertical differential roller is increased from 4 s⁻¹ to 6 s⁻¹, the proportion of the mass of unseparated stems decreases considerably. From observing the separation process, it can be seen that when the speed of the high-speed roller is 6 s⁻¹ or above, the potato stem is more likely to enter into the gaps between the adjacent rollers, so as to achieve the removal of more stems in the same period of time. With the increase in the gap width of the rollers, the proportion of the mass of unseparated stems decreases and then increases, the reason for this is that when the gap width is too small, it is difficult for the stems to enter the gap between the adjacent rollers, so they pile up on the outer side of the rollers and are transported to the side of the receiving box, together with the potatoes. When the gap width is too large, some of the stems are unable to contact the two adjacent rollers at the same time, and cannot be subjected to the squeezing and friction provided by the rollers, and thus are difficult to remove from the potatoes. As the line speed of the conveyor chain increases, the proportion of the mass of unseparated stems shows, to a certain extent, a gradually increasing trend, because the faster the line speed, the faster the transfer process of the potato–stem mixture, and the shorter the time used for separating the potatoes from the stems, so that some of the stems are transferred together with the potatoes to the side of the receiving box before they are removed.

3.3. Analysis of Field Experiment Results

3.3.1. Analysis of One-Factor Field Experiments

The results of the one-factor field experiments are shown in

Table 11. Results of one-factor field experiments.

Number	Experimental Factors			Impurity Rate Y1 (%)	Skin-Breaking Rate Y2 (%)
	Speed of High-Speed Vertical Differential Roller A (s−1)	Gap Width of Vertical Differential Rollers B (mm)	Line Speed of the Conveyor Chain C (m·s−1)
1	2	7	1.4	3.2	3.9
2	4	7	1.4	2.8	3.3
3	6	7	1.4	2.1	1.4
4	8	7	1.4	2.6	2.4
5	6	3	1.4	3.6	1.9
6	6	5	1.4	2.2	1.4
7	6	7	1.4	2.1	1.4
8	6	9	1.4	3.1	1.5
9	6	7	1.2	1.2	1.1
10	6	7	1.4	2.1	1.4
11	6	7	1.6	3.1	2.1
12	6	7	1.8	3.5	2.5

. By comparing the results of groups 1 to 4 (only the roller speed has been adjusted) from the field experiments and simulation tests, it can be calculated that the unseparated stem mass from the simulation test results are on average 3.46% higher than the impurity rate from the field experiment results. And the Pearson correlation coefficient for the two sets of data is 0.879, indicating a very strong correlation between them. By comparing the results of groups 5 to 8 (only the gap width has been adjusted) of the tests, it can be calculated that the unseparated stem mass is on average 5.93% higher than the impurity rate. And the Pearson correlation coefficient for the two sets of data is 0.955, also indicating a very strong correlation between them. By comparing the results of groups 9 to 12 (only the line speed has been adjusted) of the tests, it can be calculated that the unseparated stem mass is on average 2.03% higher than the impurity rate. And the Pearson correlation coefficient for the two sets of data is 0.758, indicating a strong correlation between them.

From the above comparison, it can be seen that the results of the simulation tests are all higher than those of the field experiments. In particular, the experimental results related to the parameter group associated with the vertical rollers exhibited the greatest differences. The reasons for this phenomenon include two aspects: EDEM software has limitations in accurately replicating the actual working process of mechanical structures, such as its inability to simulate the flexible deformation produced when the rollers compress potato stems; and there are differences between the modelling of potato plants and their actual conditions, primarily due to low-position cutting of potato plants in the field before harvest, resulting in a stem length remaining on the potato that is shorter than what is modelled in EDEM. At the same time, the Pearson correlation coefficient between the simulated data and the field experiment data reached either a strong or very strong correlation. This suggests a high consistency in their trends of variation, demonstrating that the simulation model can reflect the actual working process of the separation device to a certain extent. The differences between simulation tests and field experiments may be further diminished, which indicates that it is essential to employ the method of DEM-MBD coupled simulation in future research.

By comparing the impurity rate and skin-breaking rate of differential rollers under different speeds of vertical differential rollers, it can be seen that with the increase in speed, the impurity rate and skin-breaking rate of potatoes show a trend that decreases and then increases. When the speed of the high-speed differential roller reaches 6 s⁻¹, the impurity rate and skin-breaking rate of potatoes are at the lowest value. The reason for the above phenomenon is that when the vertical differential rollers rotate too fast, the stems are removed from the potatoes more quickly, thus making it easier to break the skin of the potatoes. At the same time, when the speed of the rollers is too fast, the entanglement of the stems with the roller body is significant, and some of the stems are rolled back into the conveyor chain by the roller body, thus increasing the impurity rate. When the differential roller speed is slow, the potato stem separation efficiency is low, and the impurity rate is therefore higher, and at the same time, due to the accumulation of the blocking phenomenon, the potato skin-breaking rate is also higher.

By comparing the impurity rate and skin-breaking rate of the potato–stem separation device with different gap widths of vertical differential rollers, it can be seen that when the gap widths are 3 mm and 9 mm, the potato impurity rate is higher because the 3 mm gap is too small, making it difficult for the stems to pass through the rollers and accumulate on the conveyor chain. Afterwards they are guided together with the potatoes to the outlet. When the gap width of the adjacent vertical differential rollers is 9 mm, the contact area between rollers and stems is reduced, and the pressure on the stems is limited to provide sufficient friction to remove the stems. If the gap width between rollers is too large or too small, it will produce a certain degree of increase in skin-breaking rate. When the gap is too large, the contact area between potatoes and rollers increases, making it more easy for stems to be squeezed between the two adjacent rollers. When the gap is too small, it is difficult for the stem to pass through the rollers, and the blockage from the accumulation of potato skins can easily cause pressure injuries.

By comparing the impurity rate and skin-breaking rate of the device at different line speeds of the conveyor chain, it can be seen that the impurity rate and skin-breaking rate of potatoes increases with the rise in the conveyor chain line speed, and the impurity rate and skin-breaking rate of the potatoes are lowest when the line speed is 1.2 m·s⁻¹. The reason for this phenomenon is that when the conveyor chain line speed is high, the potato–stem separation device workload increases. It cannot separate a large amount of the potato–stem mixture in a short time, and the collision force between potatoes and the rollers during high-speed movement is greater, so the rates of impurity and skin-breaking are higher.

3.3.2. Analysis of Multifactorial Field Experiments

The field response surface test arrangement as well as the test results are shown in

Table 12. Results of multifactorial field experiments.

Number	Experimental Factors			Impurity Rate Y1 (%)	Skin-Breaking Rate Y2 (%)
	Speed of High-Speed Vertical Differential Roller A (s−1)	Gap Width of Vertical Differential Rollers B (mm)	Line Speed of the Conveyor Chain C (m·s−1)
1	4	7	1.2	2.1	1.4
2	6	9	1.6	2.3	1.6
3	4	7	1.6	1.6	0.9
4	8	9	1.4	3.2	1.5
5	8	7	1.2	2.0	0.7
6	4	9	1.4	2.5	0.8
7	6	5	1.2	1.2	1.7
8	8	5	1.4	2.6	1.5
9	6	7	1.4	1.5	1.3
10	6	7	1.4	1.4	1.4
11	8	7	1.6	3.5	2.0
12	4	5	1.4	1.3	1.6
13	6	7	1.4	1.6	1.2
14	6	7	1.4	1.7	1.4
15	6	5	1.6	2.6	2.2
16	6	9	1.2	2.9	1.6
17	6	7	1.4	1.6	1.2

. Quadratic polynomial regression was fitted to the test data counted in the table using Design-Expert software to establish a second-order regression model for the speed of the high-speed vertical differential rollers, the gap width of the rollers, and the line speed of the conveyor chain; additionally, the established model was subjected to an analysis of variance. The analysis of variance for impurity rate is shown in

Table 13. Analysis of variance for impurity rate.

Source	Sum of Squares	Degree of Freedom	Mean Square Sum	F	p1
Model	7.65	9	0.8497	72.54	<0.0001
A	1.81	1	1.81	154.09	<0.0001
B	1.28	1	1.28	109.27	<0.0001
C	0.4050	1	0.4050	34.57	0.0006
AB	0.0900	1	0.0900	7.68	0.0276
AC	1.0000	1	1.0000	85.37	<0.0001
BC	1.0000	1	1.0000	71.18	<0.0001
A2	0.8338	1	0.8338	56.08	<0.0001
B2	0.6569	1	0.6569	32.70	0.0001
C2	0.3664	1	0.3664	31.28	0.0008
Residuals	0.0820	7	0.0117
Out-of-the-way items	0.0300	3	0.0100	0.7692	0.5682
Error	0.0520	4	0.0130
Total	7.73	16

¹ Note: p < 0.01 indicates that the item is extremely significant; p < 0.05 indicates that the item is significant.

, and the analysis of variance for the skin-breaking rate is shown in

Table 14. Analysis of variance for skin-breaking rate.

Source	Sum of Squares	Degree of Freedom	Mean Square Sum	F	p 1
Model	2.36	9	0.2622	31.92	<0.0001
A	0.1250	1	0.1250	15.22	0.0059
B	0.2813	1	0.2813	34.24	0.0006
C	0.2113	1	0.2113	25.72	0.0014
AB	0.1600	1	0.1600	19.48	0.0031
AC	0.8100	1	0.8100	98.61	<0.0001
BC	0.0625	1	0.0625	7.61	0.0282
A2	0.2375	1	0.2375	28.91	0.0010
B2	0.3480	1	0.3480	42.37	0.0003
C2	0.1480	1	0.1480	18.02	0.0038
Residuals	0.0575	7	0.0082
Out-of-the-way items	0.0175	3	0.0058	0.5833	0.6569
Error	0.0400	4	0.0100
Total	2.42	16

¹ Note: p < 0.01 indicates that the item is extremely significant; p < 0.05 indicates that the item is significant.

.

Through the analysis, it can be seen that influencing factor A (the high-speed vertical differential roller’s speed) significantly affects the impurity rate, and influencing factor B (the gap width of rollers), and influencing factor C (line speed of conveyor chain) also significantly affect the impurity rate. The effect of the interaction term is extremely significant, and the effect of the secondary term is extremely significant as well. The order of the influence of each factor on the impurity rate is A (high-speed vertical differential roller’s speed) > B (the gap width of rollers) > C (line speed of the conveyor chain). Excluding the insignificant terms in the analysis of variance, the regression equation between the impurity rate and the significant factors was obtained as:

$$\begin{array}{ll}Impurity Rate=& 1.56+0.4750A+0.4000B+0.2250C-0.1500AB\\ & +0.5000AC-0.5000BC+0.4450A^2-0.3950B^2\\ & +0.2950C^2\end{array}$$

(21)

The effect of these three factors on the skin-breaking rate is extremely significant, and the effect of the interaction term as well as the secondary term is extremely significant too. The order of the influence of each factor on the impurity rate is B (the gap width of rollers) > C (line speed of the conveyor chain) > A (high-speed vertical differential roller’s speed). Excluding the insignificant terms in the analysis of variance, the regression equation between the skin-breaking rate and the significant factors was obtained as:

$$\begin{array}{ll}Skin-breaking& Rate\\ & =1.30+0.1250A-0.1875B+0.1625C+0.2000AB\\ & +0.4500AC-0.1250BC-0.2375A^2+0.2875B^2\\ & +0.1875C^2\end{array}$$

(22)

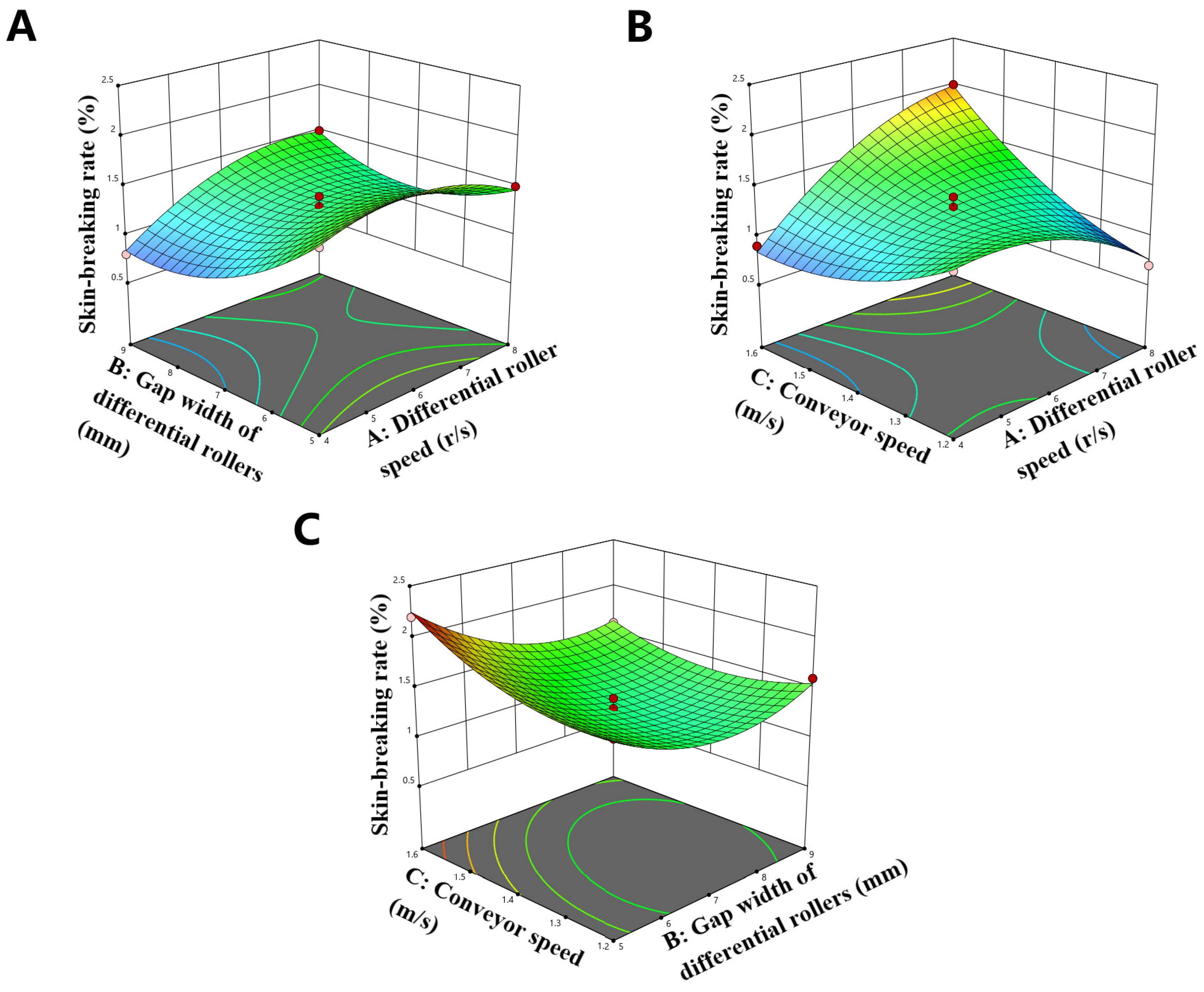
Using the response surface method, one of the factors was fixed at the intermediate level, and the interaction between the other two factors was analysed for the effects on the potato impurity rate Y1 and skin-breaking rate Y2. Figure 15 shows the influence law of any two of the three factors interacting on the impurity rate of the potato, and Figure 16 shows the pattern of the influence law of any two of the three factors interacting on the skin-breaking rate of potato.

As can be seen from Figure 15, the impurity rate first reduced and then increased with the increase in the gap width of vertical differential rollers. When the gap width was too large, the pressure exerted on the stem by the rollers was reduced, resulting in difficulties removing the stems. When the gap width was too small, the roller body was not easily entangled with the stem and was prone to blocking. The impurity rate first reduced and then increased with the increase in the speed of the vertical differential rollers. When the speed was too high, the roller body was less likely to entangle the stems. It also made the potatoes collide with the high-speed rollers and damaged the potato skin. When the speed was too low, the separation rate of potatoes and stems was reduced, making it easier for blockages to occur, increasing the impurity rate. The impurity rate reduced with the increase in the line speed of the conveyor chain. As the linear speed of the stem will be the same as the line speed of the conveyor chain, the stem and the roller body are quickly entangled during the high-speed movement, which makes the separation efficiency increase.

As can be seen from Figure 16, the skin-breaking rate first reduced and then increased with the increase in the gap width between vertical differential rollers. When the gap width was too large, the potato was easy to squeeze between the two adjacent rollers, resulting in skin breakage. When the gap width was too small, stems were quickly removed by the rollers, thus breaking the potato skin. The skin-breaking rate increased with the increase in the speed of vertical differential rollers. The roller collided with potatoes through the process, which easily led to skin breakage. The skin-breaking rate was first reduced and then increased with the line speed of the conveyor chain. When the line speed was too low, the speed of the potato was low as well, and the collision time with the high-speed roller increased, making the skin-breaking rate increase. When the line speed was too high, the speed of the potato was high as well, and collided with the roller at a high speed, leading to a higher skin-breaking rate.

In order to find the best combination of test levels, the regression model was solved using the optimisation module in the Design-Expert 13 software, and the constraints were determined on the basis of the working conditions and operational requirements of the vertical differential roller on the potato–stem separation device:

$$\left\{\begin{array}{c}min{Y}_1\left(A,B,C\right)\\ min{Y}_2\left(A,B,C\right)\\ \left\{\begin{array}{c}4 \mathrm{r}·{\mathrm{s}}^{-1}\le A\le 8 \mathrm{r}·{\mathrm{s}}^{-1}\\ 5 \mathrm{m}\mathrm{m}\le B\le 9 \mathrm{m}\mathrm{m}\\ 1.2 \mathrm{m}·{\mathrm{s}}^{-1}\le C\le 1.6 \mathrm{m}·{\mathrm{s}}^{-1}\end{array}\right.\end{array}\right.$$

(23)

The optimisation goals to minimise the impurity rate and skin-breaking rate was set, while the value ranges of roller speed, gap width, and line speed were determined on the basis of the working conditions and operational requirements of the vertical differential roller on the potato–stem separation device. The Design-Expert 13 software defined the satisfaction function with the goal of minimising impurity rates and skin breakage rates, and subsequently established an overall satisfaction function. The software then employed numerical search algorithms to continuously attempt various combinations within the ranges of roller speed, gap width, and line speed, in order to predict the impurity rate and skin-breaking rate corresponding to each combination, ultimately identifying a parameter combination that maximises overall satisfaction value.

Through the optimised solution, the best performance of potato–stem separation is obtained when the rotational speed of the high-speed vertical differential roller is 6 s⁻¹, the gap width of rollers is 7 mm, and the line speed of the conveyor chain is 1.4 m·s⁻¹. According to the results of the field experiments, the potato impurity rate was 1.56%, and the skin-breaking rate was 1.30%.

4. Discussion

The existing elastic picking roller potato–stem separation device is equipped with a picking roller with rubber attached to the surface, which is used to apply friction and squeezing pressure to the potato stems, thereby achieving the winding and removal of the stems. This provides an example of a successful application for the theoretical basis of this study. In this study, a new type of differential vertical roller potato–stem separation device was developed, and was installed above the end of the conveyor chain and driven by a separate hydraulic motor or electric motor. During the process of guiding potatoes to the side discharge port of the harvester, multiple differential rollers applied pressure and friction to the potato stems, and removed them from the potato tuber. The device has a compact structure and does not require installation at the junction between multi-stage conveyor chains. The continuous operation of differential rollers and conveyor chains ensures that potatoes and stems always remain in a flowing state. Therefore, compared with the existing elastic picking roller type of potato–stem separation devices, the vertical differential roller potato–stem separation device developed by this study has the advantages of a simple structure, strong universality, and no blockages, which can effectively solve the problem of poor potato–stem separation performance in small-scale single-stage potato harvesters.

According to the results of the one-factor field experiments, there was consistency in the variation in potato impurity rate and skin-breaking rate, in which A (the speed of the high-speed vertical differential roller) and B (the gap width of the vertical differential rollers) were too high or too low to have a negative impact on the impurity rate and skin-breaking rate, and C (the line speed of the conveyor chain) could effectively reduce the impurity rate and skin-breaking rate if it was maintained at a low level. According to the results of multifactorial field experiments, the effects of the three influencing factors and their interactions on the potato impurity rate and skin-breaking rate are very significant. Although there is an order of influence between the three parameters, there is no notable disparity. Combined with the field experiment results and the actual potato production requirements, the operating parameters of the separation device should be reasonably selected during the operation process. In the process of potato harvesting, the weight of the skin-breaking rate is higher than the impurity rate. In order to ensure a certain harvesting efficiency, C (the line speed of the conveyor chain) can be appropriately increased under the premise that A (the speed of the high-speed vertical differential roller) and B (the gap width of the vertical differential rollers) are controlled at a medium level to meet the needs of potato production.

Compared to other devices of similar specifications, the vertical roller potato–stem separation device developed in this study has lower requirements for installation position and space, does not require a conveyor chain junction structure, and can adapt to different conveyor chain widths by changing the number of vertical rollers, thus demonstrating greater adaptability. The device is equipped with both transfer and separation functions, and there are no obstructive structures similar to flexible rods along the conveyance path, effectively preventing clogging issues. The impurity rate, skin breakage rate, and efficiency of this device are on par with existing separation devices, meeting the standards required by the potato production industry.

It should be noted that the results of this test only reflect the working performance of the device under the conditions of potato varieties and harvesting models in Tengzhou City, Shandong Province, China. Due to the differences in size, connectivity, and other characteristics among various potato plant varieties, different operational combinations of parameters such as the gap width, the speed ratio, the diameter and the rotational speed of the rollers are required. Due to differences in the input quantity and soil texture under different harvesting modes, different operational combinations for parameters such as the width and line speed of conveyor chain, diameter and rotational speed of rollers are required. Therefore, it is evident that the current experimental results are relatively limited. In order to enhance the applicability of the separation device, the investigation of different potato varieties and harvesting modes is required, as well as the establishment of a more refined simulation model, thus a more extensively optimised experiment should be conducted in the future.

5. Conclusions

In this paper, a new type of compact and multifunctional vertical roller potato–stem separation device was developed. The structure and parameters of the device were designed by determining the physical and mechanical parameters of the potato stems, combined with the force analysis of the stems in the separation process. Simulation tests of potato–stem separation were carried out using the discrete element method to investigate the influence law of different working parameters on the performance of potato–stem separation, and to verify that the designed device can achieve the working purpose. The correctness of the simulation results was verified and the optimum combination of operating parameters of the device was determined through one-factor and multi-factor potato–stem separation tests in the field. The device overcomes the shortcomings of stringent requirements for installation location and necessary space of the current separation device. The study fills the research gap in the study of potato–stem separation devices suitable for small-scale potato harvesters and promoted the development of small-scale potato harvesters to a certain extent. The following conclusions can be drawn from the above study:

(1)

Simulation test results show that the designed vertical differential rollers on potato–stem separation devices can complete the separation of potato and stem. When the speed of high-speed vertical differential roller reaches 6 s⁻¹ and above, the proportion of unseparated stem mass is relatively low. With the improvement of the gap width of differential rollers, the proportion of unseparated stem mass shows a trend of initially decreasing and then increasing. With the increase in the line speed of the conveyor chain, the proportion of unseparated stem mass gradually rises. With the increase in conveyor chain speed, the proportion of unseparated stem mass gradually increases.

(2)

Field test results show that the influence of each working parameter on the potato impurity rate is in the following order: differential rollers’ speed > differential rollers’ gap width > conveyor chains’ line speed; the influence on potato skin-breaking rate is in the following order: differential rollers’ gap width > conveyor chain’s line speed > differential rollers’ speed. When the speed of high-speed vertical differential roller speed is 6 s⁻¹, the gap width of differential rollers is 7 mm, and the line speed of the conveyor chain is 1.4 m·s⁻¹, the device has the best performance of potato–stem separation.

The variety of potato species is rich, and the distribution of planting areas is extensive, leading to significant differences in potato production modes among different varieties and regions. Therefore, the working efficiency and operational performance of this apparatus under various conditions still needs to be determined. This manuscript also lacks studies on the other operational performances related to potato tubers such as conveying efficiency and loss rate. In addition, the rudimentary structure of the experimental prototype limited the investigation of the quality performance of the separation device under various structural and operational parameter combinations. Due to limitations of time, regional and experimental prototypes, the data, and conclusions presented in this paper are limited. In response to the shortcomings of this paper, the following outlook is proposed:

(1)

Conduct a broader measurement of the physical and mechanical properties of different potato plant varieties while fully considering the differences in various harvesting environments, such as soil texture and moisture content. Optimise device design through theoretical calculations, simulation and bench testing, and validate feasibility through field experiments. Subsequently, enhance the adaptability of the devices.

(2)

Establish a larger number of potato models of varying sizes, and combine them with a soil discrete element model, thus replicating the force and motion characteristics of potato tubers in the separation and conveying process under real harvesting conditions. Further deepen the study of the movement and stress conditions of potato tubers during the conveying and separating processes.

(3)

Adopt a more refined experimental platform to investigate the operational performance of the separation device under a wider range of structural and operational parameter combinations. Additionally, integrate multiple sensors to construct an automated feedback regulation system to enable the device to adapt to different harvesting environments.