Prediction of the Injury Severity of Accidents at Work: A New Approach to Analysis of Already Existing Statistical Data
Abstract
1. Introduction
2. Related Works
3. Material and Methods
3.1. Subject of the Analyses
3.2. The Predicted Variables
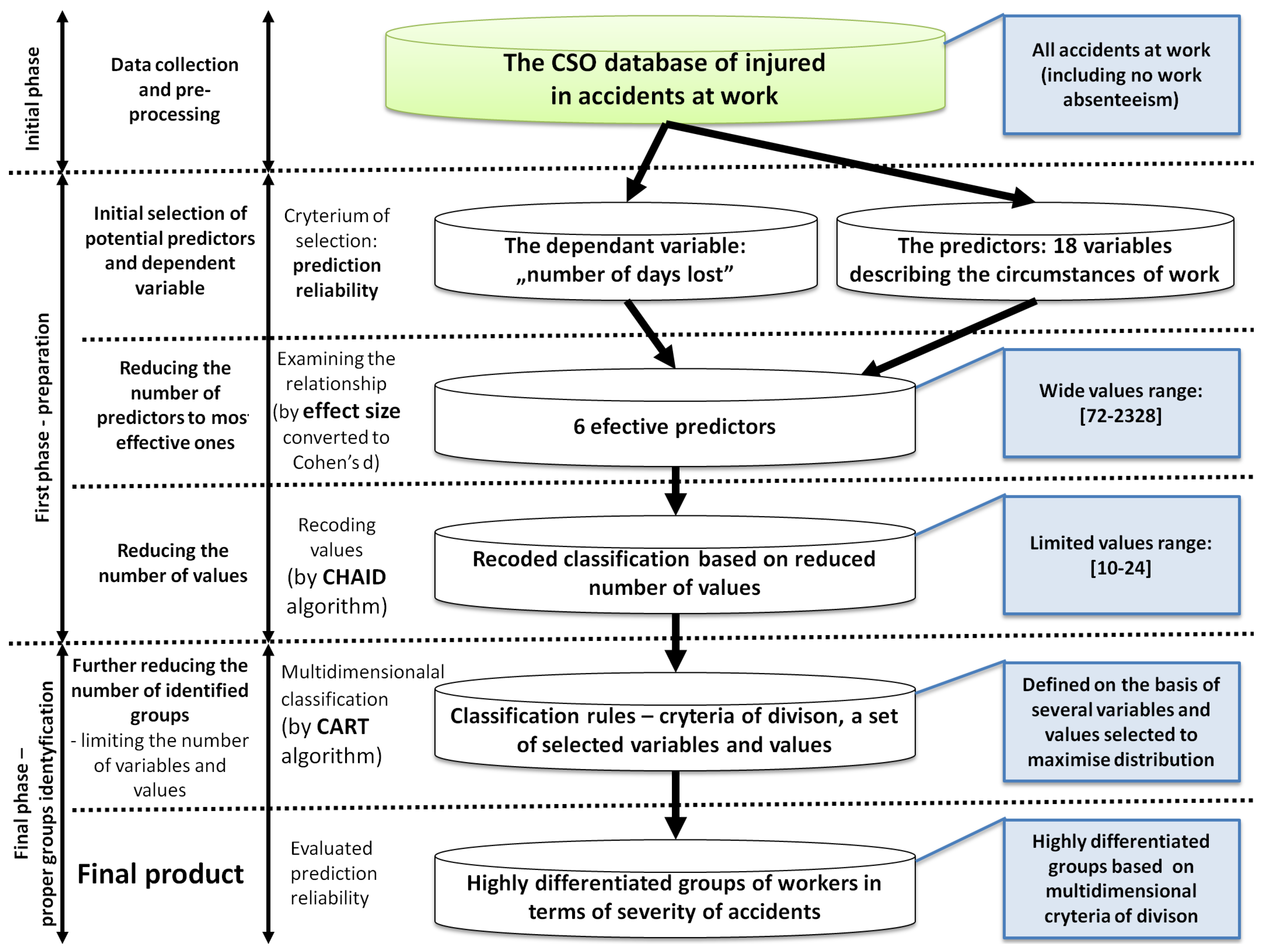
3.3. Methodology
3.3.1. The Initial Phase
3.3.2. The First Phase—Preparation
- Selecting the most effective predictors of severity from the variables describing accident circumstances;
- Transforming selected predictors by limiting the range of their values to ensure that the identified groups were sufficiently large.
3.3.3. The Final Phase—Group Identification
- p is the number of classes of the response attribute;
- n(j|t) represents the number of records in node t that belong to class j;
- n(t) is the total number of records in node t.
4. Results
4.1. Data Preparation
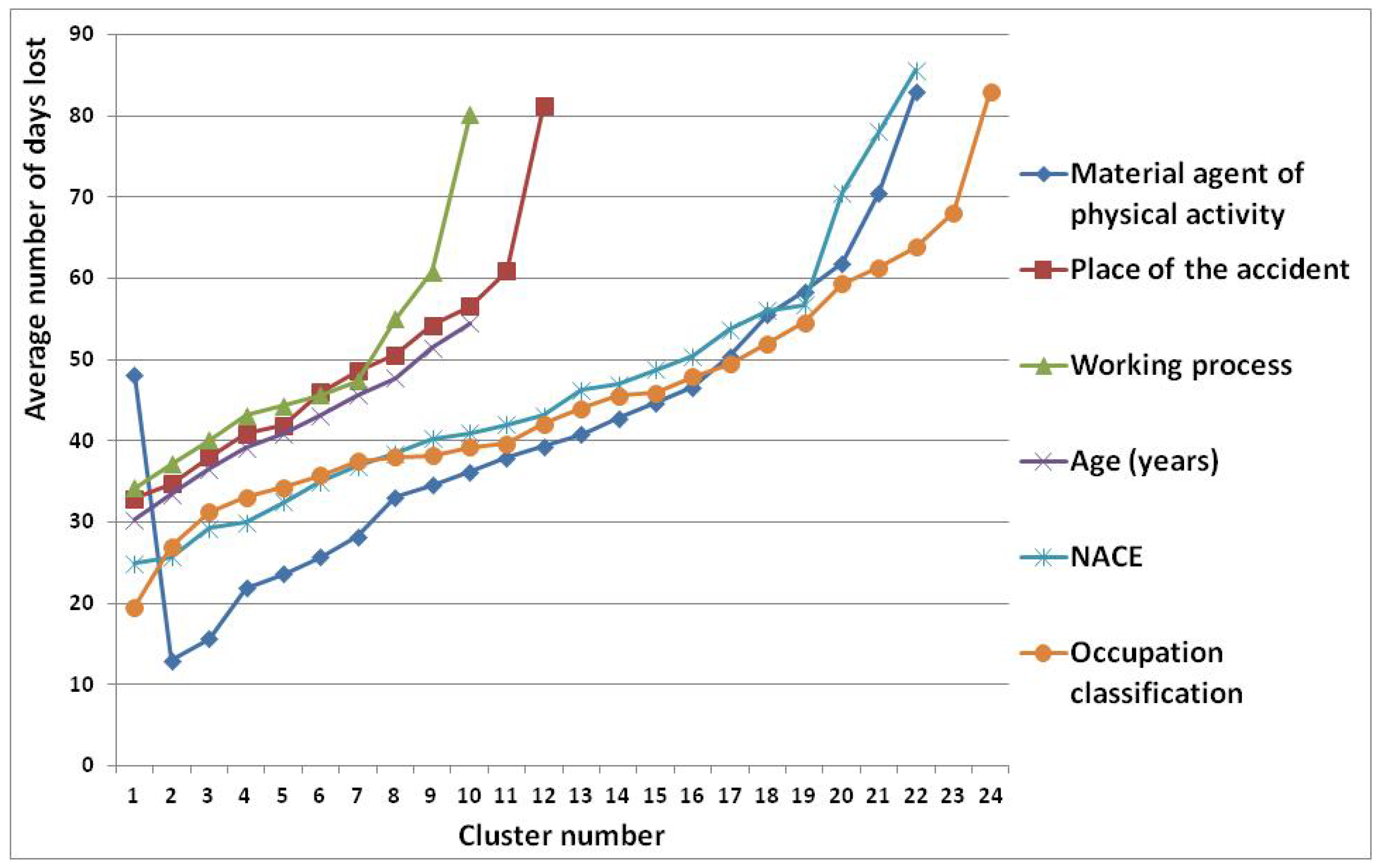
4.1.1. Reducing the Number of Predictors
4.1.2. Reducing the Number of Values—The Development of a New Classification
- Occupation classification
- 2.
- Material agent of physical activity
- 3.
- NACE—economic activity
- 4.
- Place of accident
- 5.
- Working process
- 6.
- Age in years
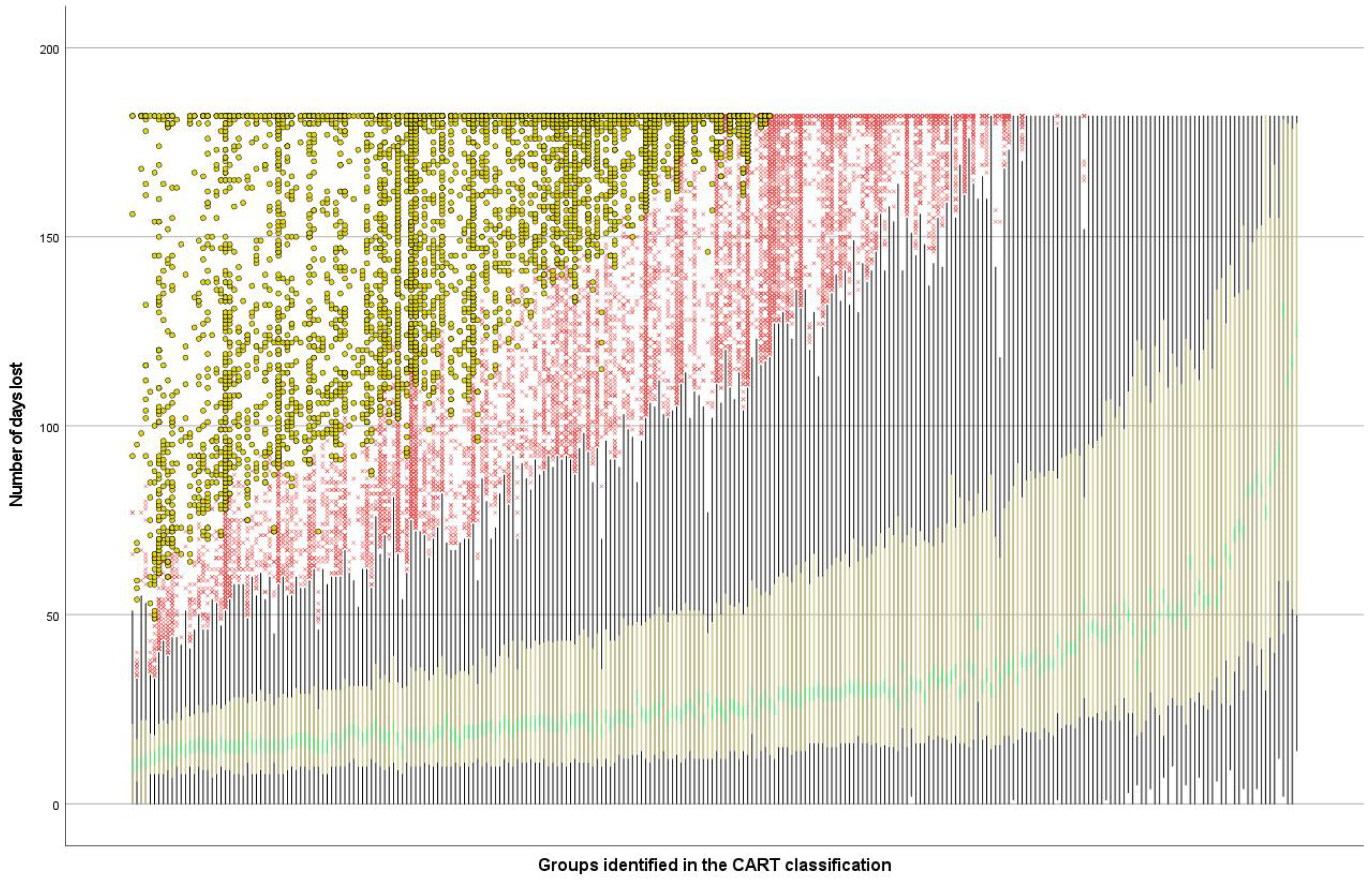
4.2. Final Group Identification
- The highest accident-related absence (mining): The highest absence (over 75 days) was primarily identified in professions and economic activities (NACE) related to various types of mining—both underground and open pit—especially hard coal, but also, less frequently, metal ore mining and, slightly more often, oil and natural gas extraction. Moreover, this group also includes some economic activities, with a little shorter absence duration, related to the construction of specific civil engineering structures, service supporting land transportation, the distribution of electricity, the production and supply of hot water, and very few forestry-related services. Occupation: The professions performed in this group were clearly related to economic activities, and therefore included all types of mine workers (unskilled and skilled, supervisors, engineers, mechanics and operators of mining, drilling and loading equipment and machines), as well as professions used in mining, such as ironworkers (metalworkers), various steel and railway structure assemblers, and construction workers like bricklayers, assistants, and painters. This group also included, but less frequently and with shorter absences, lumberjacks/tree fellers and carpenters. Place of accident: As expected, places of accidents were mainly underground mines and quarries, open-pit mines, public transport areas, places of production, factories, workshops, and construction sites. Process: The most common working process in this group, by far, was mining and earthworks. Next in order was the factor that occurred in every group—movement, including means of transport. The third encompassed all manual works like setting up, installing, mounting, dismantling, taking apart, etc. Lastly, production and processing accounted for the remaining portion, bringing the total to over 80% of the working processes overall. Material agent: The most common material agents of physical activity were underground facilities, tunnels, walkways, movable structures, and surfaces above ground level. What makes this group particularly unique is the significantly lower frequency of the most common material agent—“Floors and other fixed horizontal surfaces at ground level”—which appears very often in every other group. In contrast, various objects commonly used in mining, such as manually transported or moved loads, portable or mobile machines for extracting materials or earthworks, constructions materials, debris and other fragmented materials, rail vehicles, stationary machines for extracting materials or earthworks, mechanized hand tools for drilling, screwing, bolting, and stationary conveyors, continuous motion transport devices and systems and their equipment, were much more common. Age: This group also included older workers, as the mean age was 49 years old (almost 8 years more than other groups) with a standard deviation 8.6. It is worth noting that when the accident was in any way related to mining, it led to a significantly longer absence.
- High accident absence (mobile machines): A long-lasting, but not the highest, absence (less than 75 but over 50 days) was specific to (NACE) road transport, chosen construction and industrial processing, forestry, and animal breading (especially freight and passenger transport by road; construction of roads, motorways, buildings, civil and water projects, installations and power lines; collection, treatment, and supply of water; forestry activities; poultry breeding; private security activities; industrial cleaning activities; installation of industrial machinery and equipment; production of specific products like meat, metal, and specific metal products—structures, parts, and machines—lead, zinc, and tin, builders’ carpentry and concrete, milk and cheese, wood and sawmill, paper, chemical products, bread, pastry, and processing fruits and vegetables). Material agent: What is also characteristic of this length of absence is that the most common material agents of activities were heavy vehicles, such as trucks, buses, and coaches (less frequently rail and other vehicles); stationary or mobile cranes and lifting devises; stationary continuous or vertical motion transport devices (conveyor belts, escalators, elevators, buckets, hoist), their loads, transport equipment, and accessories; machines and devices for forming by pressing, crushing, and rolling; sawing; preparing materials by grinding, separating, and mixing; packing; and construction machinery (portable or mobile). Age: the age of injured persons in this group was much higher than the average age (almost 50 and over).
- Medium accident absence (retail and production sites): This was still relatively high but slightly below the average absence (about 30–49 days) and was specific to a much wider range of economic activities (NACE), which can be divided into several main sectors: manufacturing (includes the production of various goods, e.g., furniture, plastic, rubber, metal products; specialized products such as agricultural machinery, motor vehicles, electronics, doors, and windows; and food manufacturing like beverage and seafood); wholesale trade, retail sale, and services (repair and maintenance of vehicles and machinery); transport and logistics (postal services, passenger rail transport); healthcare and social care (health services, nursing home care). Place of accident: What is specific to this group is that the most common locations of accidents were industrial production sites (factories, workshops, and, less frequently, storages area, as well as maintenance and repair areas). Occupation: The occupation of injured persons in this group was also very diversified and included various types of manufacturing machine operators and mechanics, metalworking labourers (welders, lathe/milling operators), carpenters, car drivers and forklift operators, municipal/city guards, waste loaders, various machine and equipment assemblers, window fitters, and unskilled labourers in simple jobs such as packers, cleaners, and household workers. Material agent: Apart from “solid horizontal surfaces at ground level (floors)”, the most common material agents were manually moved loads and other materials, objects, products, packaging, and machines and vehicle parts. Frequently occurring factors were also light vehicles for transporting goods or passengers; large and small construction materials (girders, beams, bricks, tiles, etc.); various types of stationary machines and devices (mostly for cutting, milling, sawing, forming, joining); mechanized hand tools (for drilling, screwing, bolting); and warehouse accessories (racks, shelves, pallets). Age: In this group, the age was lower than the average age (31 years). However, if the age was higher than the average but other group selection criteria were still met, the post-accident absence was higher than the average.
- Low-duration absence (health care/food processing): The groups with the lowest duration of absence were primarily related to (NACE) health care (hospital activates, general and specialised medical practice). In cases where the accident location was a healthcare facility, the primary material agents (material agent) involved were sharp and cutting instruments used in surgery and medical procedures (needlestick injuries and cuts), with injured employees being medical workers. It is worth noting that post-accident absences tend to be slightly longer when accidents involve the use of non-medical cutting tools (e.g., scissors) or kitchen and household tools. Such accidents are more common in restaurants, food production (e.g., meat processing), and retail rather than in medical facilities. When the injured person in such accidents is a food processing worker (e.g., butchers, fish processing workers, and related jobs) or a worker performing elementary tasks in the industry, such as a housekeeper, an office cleaner, then the duration of absence is little longer. Similarly, if the injured person is a shop assistant (especially in food sales), a cook, or a kitchen helper, the absence duration is extended even more (this group also includes warehouse workers with cut injuries and postmen bitten by pets).
4.3. Evaluation Procedure—Prediction Reliability Metrics
- Exact values—numeric predictions with precision to one day of absence (on the basis of median, mean, and 5% trimmed mean);
- Three-class categorization—up to 1 month, from 32 to 45 days, more than 45 days;
- Second-class categorization—up to 1 month, more than 1 month.
- (i)
- Exact value predictions: Here, the model was treated as a regression model. Predictive performance was assessed using standard regression metrics: MAE (Mean Absolute Error), MSE (Mean Squared Error), RMSE (Root Mean Squared Error), and R2 (Coefficient of Determination).
- (ii)
- Categorical predictions: In addition, the numeric range of the target variable was discretized into three and two categories, and in these scenarios, performance was measured using accuracy, precision, recall, F1-score, and G-mean [4,46,47,48]. Precision, recall, and F1-score were computed per class and then macro-averaged to ensure equal treatment of all classes. G-mean was calculated as the geometric mean of class-wise recalls.
- Accuracy—defined as the ratio of the correctly predicted observations to the total number of observations. It is expressed by the following equation:
- Precision—defined as the ratio of correctly predicted observations under a particular class to the total number of predicted observations under a similar class. It is expressed by the following equation:
- Recall—defined as the ratio of correctly predicted observations under a particular class to all actual observations in that class. It is expressed by the following equation:
- F1-score—a metric calculated from the recall and precision by denoting the relative importance of recall versus precision, which in the conducted analysis was taken as 1. It is expressed by the following equation:
- G-mean—defined as the geometric mean of precision and recall. It is expressed by the following equation:
5. Discussion
5.1. Theoretical Implications
5.2. Practical Implications
5.3. Model Assumptions and Comparisons
5.4. Model Limitations
5.5. Future Work
6. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Available online: https://ec.europa.eu/eurostat/databrowser/view/hsw_ph3_01/default/table?lang=en&category=hlth.hsw.hsw_acc_work.hsw_ph3 (accessed on 22 March 2024).
- Leppink, N. Socio-economic costs of work-related injuries and illnesses: Building synergies between Occupational Safety and Health and Productivity. In Proceedings of the INAIL Seminar on «The Costs of Non-Safety», Bologna, Italy, 14 October 2015. [Google Scholar]
- Tixier, A.J.-P.; Hallowell, M.R.; Rajagopalan, B.; Bowman, D. Automated content analysis for construction safety: A natural language processing system to extract precursors and outcomes from unstructured injury reports. Automat. Constr. 2016, 62, 45–56. [Google Scholar] [CrossRef]
- Sarkar, S.; Pramanik, A.; Maiti, J.; Reniers, G. Predicting and analyzing injury severity: A machine learning-based approach using class-imbalanced proactive and reactive data. Saf. Sci. 2020, 125, 104616. [Google Scholar] [CrossRef]
- Hallowell, M.R.; Alexander, D.; Gambatese, J.A. Energy-based safety risk assessment: Does magnitude and intensity of energy predict injury severity? Construct. Manage. Econ. 2017, 35, 64–77. [Google Scholar] [CrossRef]
- Eurostat European Commission. Methodologies & Working papers. In European Statistics on Accidents at Work (ESAW): Summary Methodology; Eurostat Methodologies & Working papers; Office of the European Union: Brussels, Belgium, 2013. [Google Scholar]
- European Commission. Directorate-General for Employment. In Social Affairs and Inclusion, Guidance on Risk Assessment at Work; European Commission: Luxembourg, 1996. [Google Scholar]
- Matías, J.M.; Rivas, T.; Martín, J.E. A machine learning methodology for the analysis of workplace accidents. Int. J. Comput. Math. 2008, 85, 559–578. [Google Scholar] [CrossRef]
- Sarkar, S.; Patel, A.; Madaan, S.; Maiti, J. Prediction of occupational accidents using decision tree approach. In Proceedings of the 2016 IEEE Annual India Conference (INDICON), Bangalore, India, 16–18 December 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Sarkar, S.; Vinay, S.; Raj, R.; Maiti, J.; Mitra, P. Application of optimized machine learning techniques for prediction of occupational accidents. Comput. Oper. Res. 2019, 106, 210–224. [Google Scholar] [CrossRef]
- Chang, L.; Wang, H. Analysis of traffic injury severity: An application of non-parametric classification tree techniques. Accid. Anal. Prev. 2006, 38, 1019–1027. [Google Scholar] [CrossRef] [PubMed]
- Cheng, C.; Leu, S.; Cheng, Y.; Wu, T.; Lin, C. Applying data mining techniques to explore factors contributing to occupational injuries in Taiwan’s construction industry. Accid. Anal. Prev. 2012, 48, 214–222. [Google Scholar] [CrossRef]
- Lukacova, A.; Babic, F.; Paralic, J. Building the prediction model from the aviation incident data. In Proceedings of the 2014 IEEE 12th International Symposium on Applied Machine Intelligence and Informatics (SAMI), Herl’any, Slovakia, 23–25 January 2014; pp. 365–369. [Google Scholar]
- Mistikoglu, G.; Gerek, I.; Erdis, E.; Usmen, P.M.; Cakan, H.; Kazan, E. Decision tree analysis of construction fall accidents involving roofers. Expert Syst. Appl. 2015, 42, 2256–2263. [Google Scholar] [CrossRef]
- He, X.; Chen, W.; Nie, B.; Zhang, M. Classification technique for danger classes of coal and gas outburst in deep coal mines. Saf. Sci. 2010, 48, 173–178. [Google Scholar] [CrossRef]
- Yi, W.; Chan, A.P.C.; Wang, X.; Wang, J. Automation in construction develop- ment of an early-warning system for site work in hot and humid environments: A case study. Autom. Constr. 2016, 62, 101–113. [Google Scholar] [CrossRef]
- Sánchez, A.S.; Fernández, P.R.; Lasheras, F.S.; Juez, F.J.D.C.; Nieto, P.J.G. Prediction of work-related accidents according to working conditions using support vector machines. Appl. Math. Comput. 2011, 218, 3539–3552. [Google Scholar] [CrossRef]
- Rivas, T.; Paz, M.; Martín, J.E.; Matías, J.M.; García, J.F.; Taboada, J. Explaining and predicting workplace accidents using data-mining techniques. Reliab. Eng. Syst. Saf. 2011, 96, 739–747. [Google Scholar] [CrossRef]
- Sanmiquel, L.; Rossell, J.M.; Vintro, C. Study of Spanish mining accidents using data mining techniques. Saf. Sci. 2015, 75, 49–55. [Google Scholar] [CrossRef]
- Christopher, A.B.A.; Appavu, S. Data mining approaches for aircraft accidents prediction: An empirical study on Turkey airline. In Proceedings of the 2013 International Conference on Emerging Trends in Computing, Communication and Nanotechnology (ICE-CCN), Tirunelveli, India, 25–26 March 2013; pp. 739–745. [Google Scholar]
- Gürbüz, F.; Özbakir, L.; Yapici, H. Classification rule discovery for the aviation incidents resulted in fatality. Knowl. Based Syst. 2009, 22, 622–632. [Google Scholar] [CrossRef]
- Butka, P.; Pócs, J.; Pócsová, J.; Sarnovský, M. Multiple Data Tables Processing via One-Sided Concept Lattices. In Advances in Intelligent Systems and Computing; Springer: Berlin/Heidelberg, Germany, 2013; Volume 183, pp. 89–98. [Google Scholar]
- Butka, P.; Pocs, J.; Pocsova, J. Use of Concept Lattices for Data Tables with Different Types of Attributes. J. Inf. Organ. Sci. 2012, 36, 1–12. [Google Scholar]
- Nazeri, Z. Application of Aviation Safety Data Mining Workbench at American Airlines; The MITRE Corporation: Bedford, MA, USA, 2003. [Google Scholar]
- Viademonte, S.; Burstein, F.; Dahni, R.; Williams, S. Discovering Knowledge from Meteorological Databases: A Meteorological Aviation Forecast Study. In Data Warehousing and Knowledge Discovery; Kambayashi, Y., Winiwarter, W., Arikawa, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 61–70. [Google Scholar]
- Luo, X.; Li, X.; Goh, Y.M.; Song, X.; Liu, Q. Application of machine learning technology for occupational accident severity prediction in the case of construction collapse accidents. Saf. Sci. 2023, 163, 106138. [Google Scholar] [CrossRef]
- Kumar, L.S.; Burns, G.N. Determinants of safety outcomes in organizations: Exploring ONET data to predict occupational accident rates. Pers. Psychol. 2024, 77, 555–594. [Google Scholar] [CrossRef]
- Rahman, M.M.; Hossain, A.; Sikder, M.A. Machine learning applications in industry safety: Analysis and prediction of industrial accidents. In Proceedings of the 2024 International Conference on Smart Systems for Applications in Electrical Sciences (ICSSES), Tumakuru, India, 3–4 May 2024; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, R.; Hu, X.; Hou, J.; Li, X. Application of machine learning techniques for predicting the consequences of construction accidents in China. Process Saf. Environ. Prot. 2021, 145, 293–302. [Google Scholar] [CrossRef]
- Das, S.; Khanwelkar, D.R.; Maiti, J. A semi-automated coding scheme for occupational injury data: An approach using Bayesian decision support system. Expert Syst. Appl. 2024, 237, 121610. [Google Scholar] [CrossRef]
- Choi, J.; Gu, B.; Chin, S.; Lee, J.-S. Machine learning predictive model based on national data for fatal accidents of construction workers. Autom. Constr. 2020, 110, 102974. [Google Scholar] [CrossRef]
- Khairuddin, M.Z.F.; Hui, P.L.; Hasikin, K.; Razak, N.A.A.; Lai, K.W.; Saudi, A.S.M.; Ibrahim, S.S. Occupational injury risk mitigation: Machine learning approach and feature optimization for smart workplace surveillance. Int. J. Environ. Res. Public Health 2022, 19, 13962. [Google Scholar] [CrossRef]
- European Parliament; Council of the European Union. Regulation (EC) No 1338/2008 of the European Parliament and of the Council of 16 December 2008 on Community Statistics on Public Health and Health and Safety at Work (Text with EEA Relevance); European Union: Brussels, Belgium, 2008. [Google Scholar]
- European Council. Council Directive (1989) 89/391/EEC—OSH ‘Framework Directive’. Official Journal of the European Communities, 1989, No. L 183/1–8. Available online: http://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:31989L0391&from=EN (accessed on 13 October 2022).
- Implementing Commission Regulation (EU). Commission Regulation (EU) No 349/2011 of 11 April 2011 Implementing Regulation (EC) No 1338/2008 of the European Parliament and of the Council on Community Statistics on Public Health and Health and Safety at Work, as Regards Statistics on Accidents at work Text with EEA Relevance; European Union: Brussels, Belgium, 2011; p. 3. [Google Scholar]
- CSO (GUS). Accidents at Work in 2019; CSO (GUS): Warsaw, Poland, 2020.
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Erlbaum: Hillsdale, NJ, USA, 1988. [Google Scholar]
- Rosenthal, R. Parametric Measures of Effect Size. In The Handbook of Research Synthesis; Cooper, H., Hedges, L.V., Eds.; Sage: New York, NY, USA, 1994; pp. 231–244. [Google Scholar]
- Lenhard, W.; Lenhard, A. Calculation of Effect Sizes; Psychometrica: Dettelbach, Germany, 2016; Available online: https://www.psychometrica.de/effect_size.html (accessed on 26 September 2025).
- Borenstein. Effect sizes for continuous data. In The Handbook of Research Synthesis and Meta Analysis; Cooper, H., Hedges, L.V., Valentine, J.C., Eds.; Russell Sage Foundation: New York, NY, USA, 2009; pp. 221–237. [Google Scholar]
- Kass, G.V. An Exploratory Technique for Investigating Large Quantities of Categorical Data. Journal of the Royal Statistical Society. Ser. C (Appl. Stat.) 1980, 29, 119–127. [Google Scholar] [CrossRef]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.I. Classification and Regression Trees; Wadsworth: Belmont, CA, USA, 1984. [Google Scholar]
- Breiman, L. Random forest. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Han, J.; Pei, J.; Kamber, M. Data Mining: Concepts and Techniques; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Zacharis, N.Z. Classification and regression trees (cart) for predictive modeling in blended learning. Int. J. Intell. Syst. Appl. 2018, 3, 1–9. [Google Scholar] [CrossRef]
- Bennin, K.E.; Keung, J.; Phannachitta, P.; Monden, A.; Mensah, S. Mahakil: Diversity based oversampling approach to alleviate the class imbalance issue in software defect prediction. IEEE Trans. Softw. Eng. 2018, 44, 534–550. [Google Scholar] [CrossRef]
- Douzas, G.; Bacao, F.; Last, F. Improving imbalanced learning through a heuristic oversampling method based on k-means and smote. Inf. Sci. 2018, 465, 1–20. [Google Scholar] [CrossRef]
- Poh, C.Q.X.; Ubeynarayana, C.U.; Goh, Y.M. Safety leading indicators for construction sites: A machine learning approach. Automat. Constr. 2018, 93, 375–386. [Google Scholar] [CrossRef]
- Sarkar, S.; Maiti, J. Machine learning in occupational accident analysis: A review using science mapping approach with citation network analysis. Saf. Sci. 2020, 131, 104900. [Google Scholar] [CrossRef]
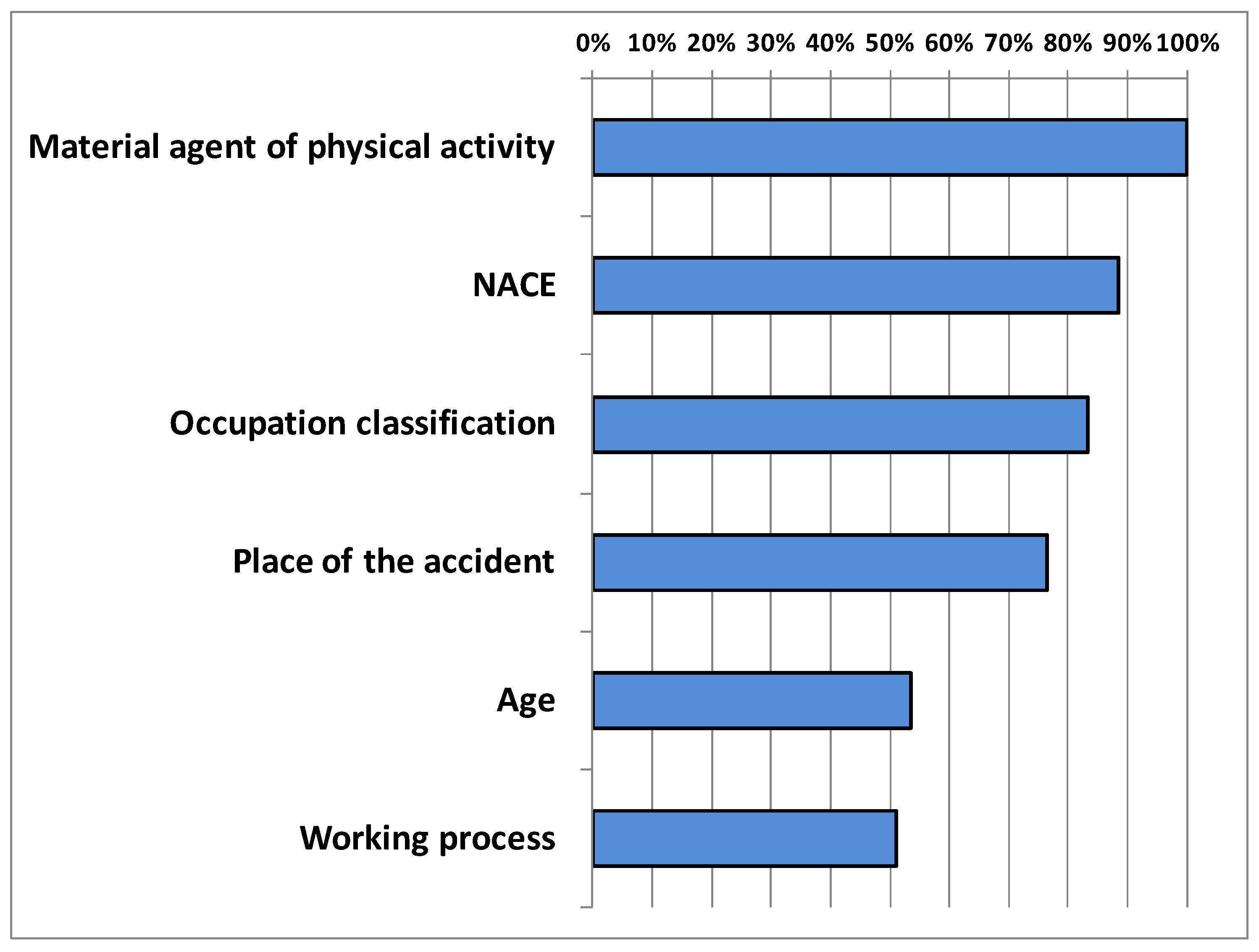
| Variable | Conversion to Cohen’s d |
|---|---|
| Occupation classification | 0.4825 |
| Material agent of physical activity | 0.4442 |
| NACE | 0.4291 |
| Place of accident | 0.3577 |
| Working process | 0.3203 |
| Age in years | 0.3201 |
| Variable | Number of Values Before Recoding | Number of Values After Recoding | Conversion to Cohen’s d Before | Conversion to Cohen’s d After |
|---|---|---|---|---|
| Occupation classification (O) | 2328 | 24 | 0.4825 | 0.3809 |
| Material agent of physical activity (M) | 154 | 22 | 0.4442 | 0.4291 |
| NACE (N) | 598 | 22 | 0.4291 | 0.4135 |
| Place of accident (P) | 49 | 12 | 0.3577 | 0.3577 |
| Working process (W) | 30 | 10 | 0.3203 | 0.3203 |
| Age in years (A) | 72 | 10 | 0.3201 | 0.3136 |
| Rule | Freq. | Est. nr. of Days Lost |
|---|---|---|
| WHERE (N = 19 OR N = 24 OR N = 13 OR N = 15 OR N = 21 OR N = 20 OR N = 4 OR N = 12 OR N = 11 OR N = 22) AND (N = 19 OR N = 24 OR N = 13) AND ((P IS NULL) OR P <> 6 AND P <> 3 AND P <> 9 AND P <> 2 AND P <> 8 AND P <> 12 AND P <> 1 AND P <> 7 AND P <> 5 AND P <> 10) AND ((A IS NULL) OR A <> 3 AND A <> 2 AND A <> 1) AND (A = 7 OR A = 9 OR A = 10 OR A = 8 OR A = 6) AND (M = 11 OR M = 13 OR M = 12 OR M = 16 OR M = 1 OR M = 14 OR M = 19 OR M = 8) AND ((O IS NULL) OR O <> 4 AND O <> 10 AND O <> 12 AND O <> 13 AND O <> 17) | 243 | 113 |
| WHERE (N = 19 OR N = 24 OR N = 13 OR N = 15 OR N = 21 OR N = 20 OR N = 4 OR N = 12 OR N = 11 OR N = 22) AND (N = 19 OR N = 24 OR N = 13) AND (P = 6 OR P = 3 OR P = 9 OR P = 2 OR P = 8 OR P = 12 OR P = 1 OR P = 7 OR P = 5 OR P = 10) AND ((A IS NULL) OR A <> 3 AND A <> 4 AND A <> 2 AND A <> 5 AND A <> 1) AND ((M IS NULL) OR M <> 11 AND M <> 3 AND M <> 13 AND M <> 17 AND M <> 16 AND M <> 5 AND M <> 18 AND M <> 7) AND ((O IS NULL) OR O <> 14 AND O <> 16 AND O <> 1 AND O <> 15 AND O <> 5 AND O <> 7 AND O <> 3 AND O <> 17 AND O <> 19) AND ((M IS NULL) OR M <> 10 AND M <> 4 AND M <> 2 AND M <> 20 AND M <> 8) AND ((A IS NULL) OR A <> 6) AND ((O IS NULL) OR O <> 4 AND O <> 12 AND O <> 2 AND O <> 23) | 122 | 111 |
| WHERE (N = 19 OR N = 24 OR N = 13 OR N = 15 OR N = 21 OR N = 20 OR N = 4 OR N = 12 OR N = 11 OR N = 22) AND (N = 19 OR N = 24 OR N = 13) AND ((P IS NULL) OR P <> 6 AND P <> 3 AND P <> 9 AND P <> 2 AND P <> 8 AND P <> 12 AND P <> 1 AND P <> 7 AND P <> 5 AND P <> 10) AND ((A IS NULL) OR A <> 3 AND A <> 2 AND A <> 1) AND ((A IS NULL) OR A <> 7 AND A <> 9 AND A <> 10 AND A <> 8 AND A <> 6) AND ((M IS NULL) OR M <> 11 AND M <> 3 AND M <> 6 AND M <> 4 AND M <> 7 AND M <> 14 AND M <> 20) AND ((O IS NULL) OR O <> 6 AND O <> 16 AND O <> 1 AND O <> 15 AND O <> 5 AND O <> 2) AND ((M IS NULL) OR M <> 10 AND M <> 13 AND M <> 17 AND M <> 1 AND M <> 8) AND (W = 2 OR W = 4) | 106 | 97 |
| WHERE (N = 19 OR N = 24 OR N = 13 OR N = 15 OR N = 21 OR N = 20 OR N = 4 OR N = 12 OR N = 11 OR N = 22) AND (N = 19 OR N = 24 OR N = 13) AND ((P IS NULL) OR P <> 6 AND P <> 3 AND P <> 9 AND P <> 2 AND P <> 8 AND P <> 12 AND P <> 1 AND P <> 7 AND P <> 5 AND P <> 10) AND ((A IS NULL) OR A <> 3 AND A <> 2 AND A <> 1) AND (A = 7 OR A = 9 OR A = 10 OR A = 8 OR A = 6) AND ((M IS NULL) OR M <> 11 AND M <> 13 AND M <> 12 AND M <> 16 AND M <> 1 AND M <> 14 AND M <> 19 AND M <> 8) AND ((M IS NULL) OR M <> 10 AND M <> 9 AND M <> 17 AND M <> 5 AND M <> 7 AND M <> 2) | 791 | 94 |
| WHERE (N = 19 OR N = 24 OR N = 13 OR N = 15 OR N = 21 OR N = 20 OR N = 4 OR N = 12 OR N = 11 OR N = 22) AND (N = 19 OR N = 24 OR N = 13) AND ((P IS NULL) OR P <> 6 AND P <> 3 AND P <> 9 AND P <> 2 AND P <> 8 AND P <> 12 AND P <> 1 AND P <> 7 AND P <> 5 AND P <> 10) AND ((A IS NULL) OR A <> 3 AND A <> 2 AND A <> 1) AND ((A IS NULL) OR A <> 7 AND A <> 9 AND A <> 10 AND A <> 8 AND A <> 6) AND (M = 11 OR M = 3 OR M = 6 OR M = 4 OR M = 7 OR M = 14 OR M = 20) | 732 | 92 |
| WHERE (N = 19 OR N = 24 OR N = 13 OR N = 15 OR N = 21 OR N = 20 OR N = 4 OR N = 12 OR N = 11 OR N = 22) AND ((N IS NULL) OR N <> 19 AND N <> 24 AND N <> 13) AND ((A IS NULL) OR A <> 7 AND A <> 9 AND A <> 10 AND A <> 8) AND ((M IS NULL) OR M <> 15 AND M <> 21 AND M <> 6 AND M <> 4 AND M <> 9 AND M <> 1 AND M <> 14 AND M <> 19 AND M <> 20) AND ((M IS NULL) OR M <> 11 AND M <> 3 AND M <> 22 AND M <> 17 AND M <> 5 AND M <> 7 AND M <> 8) AND (A = 6 OR A = 5) AND ((P IS NULL) OR P <> 6 AND P <> 8 AND P <> 12 AND P <> 11 AND P <> 10) AND (O = 6 OR O = 9 OR O = 8 OR O = 18 OR O = 15 OR O = 5 OR O = 2 OR O = 7 OR O = 3 OR O = 13 OR O = 11 OR O = 22 OR O = 20) AND ((W IS NULL) OR W <> 8 AND W <> 1) | 2091 | 42.4 |
| WHERE ((N IS NULL) OR N <> 19 AND N <> 24 AND N <> 13 AND N <> 15 AND N <> 21 AND N <> 20 AND N <> 4 AND N <> 12 AND N <> 11 AND N <> 22) AND ((M IS NULL) OR M <> 10 AND M <> 11 AND M <> 3 AND M <> 15 AND M <> 22 AND M <> 17 AND M <> 5 AND M <> 7 AND M <> 8) AND ((A IS NULL) OR A <> 3 AND A <> 4 AND A <> 2 AND A <> 5 AND A <> 1) AND (O = 14 OR O = 8 OR O = 24 OR O = 21 OR O = 15 OR O = 2 OR O = 7 OR O = 3 OR O = 11 OR O = 20) AND ((N IS NULL) OR N <> 3 AND N <> 2 AND N <> 1 AND N <> 25 AND N <> 16 AND N <> 17 AND N <> 14) AND ((A IS NULL) OR A <> 9 AND A <> 10) AND ((P IS NULL) OR P <> 4) AND (M = 13 OR M = 12 OR M = 16 OR M = 18) AND ((P IS NULL) OR P <> 3 AND P <> 2 AND P <> 7 AND P <> 5) | 1055 | 42.3 |
| WHERE (N = 19 OR N = 24 OR N = 13 OR N = 15 OR N = 21 OR N = 20 OR N = 4 OR N = 12 OR N = 11 OR N = 22) AND ((N IS NULL) OR N <> 19 AND N <> 24 AND N <> 13) AND ((A IS NULL) OR A <> 7 AND A <> 9 AND A <> 10 AND A <> 8) AND ((M IS NULL) OR M <> 15 AND M <> 21 AND M <> 6 AND M <> 4 AND M <> 9 AND M <> 1 AND M <> 14 AND M <> 19 AND M <> 20) AND ((M IS NULL) OR M <> 11 AND M <> 3 AND M <> 22 AND M <> 17 AND M <> 5 AND M <> 7 AND M <> 8) AND ((A IS NULL) OR A <> 6 AND A <> 5) AND ((O IS NULL) OR O <> 14 AND O <> 8 AND O <> 24 AND O <> 15 AND O <> 5 AND O <> 2 AND O <> 7 AND O <> 3 AND O <> 13 AND O <> 11 AND O <> 19 AND O <> 20 AND O <> 23) AND ((A IS NULL) OR A <> 2 AND A <> 1) AND ((P IS NULL) OR P <> 4 AND P <> 11) | 4210 | 42.2 |
| WHERE ((N IS NULL) OR N <> 19 AND N <> 24 AND N <> 13 AND N <> 15 AND N <> 21 AND N <> 20 AND N <> 4 AND N <> 12 AND N <> 11 AND N <> 22) AND (M = 10 OR M = 11 OR M = 3 OR M = 15 OR M = 22 OR M = 17 OR M = 5 OR M = 7 OR M = 8) AND (M = 15 OR M = 22 OR M = 17 OR M = 5 OR M = 7 OR M = 8) AND ((M IS NULL) OR M <> 15 AND M <> 22) AND (O = 6 OR O = 4 OR O = 9 OR O = 1 OR O = 10 OR O = 12 OR O = 5 OR O = 13 OR O = 17 OR O = 22 OR O = 23) AND (A = 7 OR A = 9 OR A = 10 OR A = 8) AND ((N IS NULL) OR N <> 5 AND N <> 3 AND N <> 2 AND N <> 25 AND N <> 23 AND N <> 17 AND N <> 18 AND N <> 14) AND (M = 5 OR M = 8) | 397 | 41.8 |
| WHERE ((N IS NULL) OR N <> 19 AND N <> 24 AND N <> 13 AND N <> 15 AND N <> 21 AND N <> 20 AND N <> 4 AND N <> 12 AND N <> 11 AND N <> 22) AND ((M IS NULL) OR M <> 10 AND M <> 11 AND M <> 3 AND M <> 15 AND M <> 22 AND M <> 17 AND M <> 5 AND M <> 7 AND M <> 8) AND ((A IS NULL) OR A <> 3 AND A <> 4 AND A <> 2 AND A <> 5 AND A <> 1) AND (O = 14 OR O = 8 OR O = 24 OR O = 21 OR O = 15 OR O = 2 OR O = 7 OR O = 3 OR O = 11 OR O = 20) AND (N = 3 OR N = 2 OR N = 1 OR N = 25 OR N = 16 OR N = 17 OR N = 14) AND ((A IS NULL) OR A <> 7 AND A <> 6) AND ((M IS NULL) OR M <> 14 AND M <> 19 AND M <> 20) AND (M = 13 OR M = 21 OR M = 12 OR M = 4) AND ((P IS NULL) OR P <> 12 AND P <> 1 AND P <> 4 AND P <> 7 AND P <> 10) | 1482 | 41.1 |
| WHERE ((N IS NULL) OR N <> 19 AND N <> 24 AND N <> 13 AND N <> 15 AND N <> 21 AND N <> 20 AND N <> 4 AND N <> 12 AND N <> 11 AND N <> 22) AND (M = 10 OR M = 11 OR M = 3 OR M = 15 OR M = 22 OR M = 17 OR M = 5 OR M = 7 OR M = 8) AND (M = 15 OR M = 22 OR M = 17 OR M = 5 OR M = 7 OR M = 8) AND ((M IS NULL) OR M <> 15 AND M <> 22) AND ((O IS NULL) OR O <> 6 AND O <> 4 AND O <> 9 AND O <> 1 AND O <> 10 AND O <> 12 AND O <> 5 AND O <> 13 AND O <> 17 AND O <> 22 AND O <> 23) AND ((A IS NULL) OR A <> 7 AND A <> 9 AND A <> 10 AND A <> 8 AND A <> 5) AND ((N IS NULL) OR N <> 25 AND N <> 23 AND N <> 17 AND N <> 14) AND (O = 16 OR O = 2) AND ((A IS NULL) OR A <> 4 AND A <> 6) | 1162 | 18.5 |
| WHERE ((N IS NULL) OR N <> 19 AND N <> 24 AND N <> 13 AND N <> 15 AND N <> 21 AND N <> 20 AND N <> 4 AND N <> 12 AND N <> 11 AND N <> 22) AND (M = 10 OR M = 11 OR M = 3 OR M = 15 OR M = 22 OR M = 17 OR M = 5 OR M = 7 OR M = 8) AND (M = 15 OR M = 22 OR M = 17 OR M = 5 OR M = 7 OR M = 8) AND ((M IS NULL) OR M <> 15 AND M <> 22) AND ((O IS NULL) OR O <> 6 AND O <> 4 AND O <> 9 AND O <> 1 AND O <> 10 AND O <> 12 AND O <> 5 AND O <> 13 AND O <> 17 AND O <> 22 AND O <> 23) AND ((A IS NULL) OR A <> 7 AND A <> 9 AND A <> 10 AND A <> 8 AND A <> 5) AND ((N IS NULL) OR N <> 25 AND N <> 23 AND N <> 17 AND N <> 14) AND ((O IS NULL) OR O <> 16 AND O <> 2) AND ((P IS NULL) OR P <> 2 AND P <> 1 AND P <> 4 AND P <> 7 AND P <> 10); | 1827 | 17.9 |
| WHERE ((N IS NULL) OR N <> 19 AND N <> 24 AND N <> 13 AND N <> 15 AND N <> 21 AND N <> 20 AND N <> 4 AND N <> 12 AND N <> 11 AND N <> 22) AND (M = 10 OR M = 11 OR M = 3 OR M = 15 OR M = 22 OR M = 17 OR M = 5 OR M = 7 OR M = 8) AND (M = 15 OR M = 22 OR M = 17 OR M = 5 OR M = 7 OR M = 8) AND (M = 15 OR M = 22) AND ((W IS NULL) OR W <> 5 AND W <> 2 AND W <> 4) AND (M = 22) | 1158 | 15.2 |
| WHERE ((N IS NULL) OR N <> 19 AND N <> 24 AND N <> 13 AND N <> 15 AND N <> 21 AND N <> 20 AND N <> 4 AND N <> 12 AND N <> 11 AND N <> 22) AND (M = 10 OR M = 11 OR M = 3 OR M = 15 OR M = 22 OR M = 17 OR M = 5 OR M = 7 OR M = 8) AND (M = 15 OR M = 22 OR M = 17 OR M = 5 OR M = 7 OR M = 8) AND (M = 15 OR M = 22) AND ((W IS NULL) OR W <> 5 AND W <> 2 AND W <> 4) AND ((M IS NULL) OR M <> 22) AND (A = 10 OR A = 8 OR A = 4 OR A = 2 OR A = 6) | 2120 | 13.3 |
| WHERE ((N IS NULL) OR N <> 19 AND N <> 24 AND N <> 13 AND N <> 15 AND N <> 21 AND N <> 20 AND N <> 4 AND N <> 12 AND N <> 11 AND N <> 22) AND (M = 10 OR M = 11 OR M = 3 OR M = 15 OR M = 22 OR M = 17 OR M = 5 OR M = 7 OR M = 8) AND (M = 15 OR M = 22 OR M = 17 OR M = 5 OR M = 7 OR M = 8) AND (M = 15 OR M = 22) AND ((W IS NULL) OR W <> 5 AND W <> 2 AND W <> 4) AND ((M IS NULL) OR M <> 22) AND ((A IS NULL) OR A <> 10 AND A <> 8 AND A <> 4 AND A <> 2 AND A <> 6) | 2208 | 11.9 |
| Prediction | |||||
|---|---|---|---|---|---|
| Observed | A | B | … | N | |
| A | EAA | EAB | EA… | EAN | |
| B | EBA | EBB | EB… | EBN | |
| … | E…A | E…B | E… … | E…N | |
| N | ENA | ENB | EN… | ENN | |
| Scenario | Eta Square | Cohen’s d | R | R2 | MAE | MSE | RMSE | Accuracy | Precision (macro) | Recall (macro) | F1 (macro) | G-mean | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. Exact values | Training model (1 + 2 year) | 0.1 | 0.68 | 0.322 | 0.1 | 31.9 | 1956 | 44.2 | 2.02% | - | - | - | - |
| Test model (year 3) | 0.92 | 0.64 | 0.288 | 0.08 | 32.1 | 1977 | 44.5 | 2% | - | - | - | - | |
| Final model (3 years) | 0.1 | 0.67 | 0.318 | 0.1 | 31.9 | 1954 | 44.2 | 2.04% | - | - | - | - | |
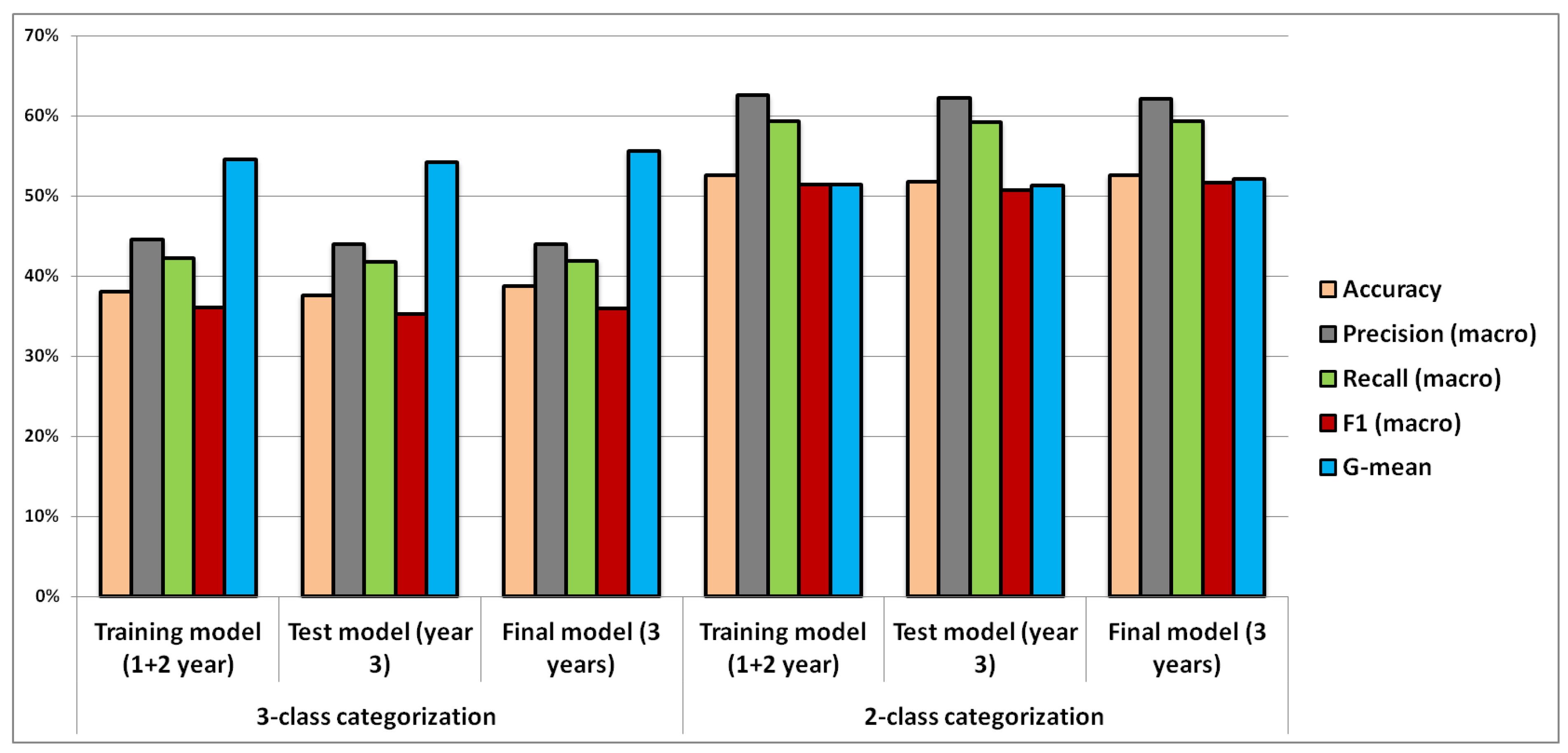
| 2. 3-class categorization | Training model (1 + 2 year) | - | - | - | - | - | - | - | 38.0% | 44.5% | 42.2% | 36.0% | 54.5% |
| Test model (year 3) | - | - | - | - | - | - | - | 37.6% | 44.0% | 41.8% | 35.2% | 54.2% | |
| Final model (3 years) | - | - | - | - | - | - | - | 38.7% | 43.9% | 41.9% | 35.9% | 55.6% | |
| 3. 2-class categorization | Training model (1 + 2 year) | - | - | - | - | - | - | - | 52.6% | 62.5% | 59.3% | 51.4% | 51.4% |
| Test model (year 3) | - | - | - | - | - | - | - | 51.7% | 62.2% | 59.2% | 50.7% | 51.3% | |
| Final model (3 years) | - | - | - | - | - | - | - | 52.6% | 62.1% | 59.3% | 51.6% | 52.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ordysiński, S. Prediction of the Injury Severity of Accidents at Work: A New Approach to Analysis of Already Existing Statistical Data. Appl. Sci. 2025, 15, 10666. https://doi.org/10.3390/app151910666
Ordysiński S. Prediction of the Injury Severity of Accidents at Work: A New Approach to Analysis of Already Existing Statistical Data. Applied Sciences. 2025; 15(19):10666. https://doi.org/10.3390/app151910666
Chicago/Turabian StyleOrdysiński, Szymon. 2025. "Prediction of the Injury Severity of Accidents at Work: A New Approach to Analysis of Already Existing Statistical Data" Applied Sciences 15, no. 19: 10666. https://doi.org/10.3390/app151910666
APA StyleOrdysiński, S. (2025). Prediction of the Injury Severity of Accidents at Work: A New Approach to Analysis of Already Existing Statistical Data. Applied Sciences, 15(19), 10666. https://doi.org/10.3390/app151910666






