A DH-KSVD Algorithm for Efficient Compression of Shock Wave Data

Abstract

To address low training efficiency and poor reconstruction in traditional K Singular Value Decomposition (KSVD) for compressive sensing of shock wave signals, this study proposes an improved algorithm, DH-KSVD, integrating dynamic pruning and hybrid coding. The dynamic pruning mechanism eliminates redundant atoms according to their contributions and adaptive thresholds, while incorporating residual features to enhance dictionary compactness and training efficiency. The hybrid sparse constraint integrates the sparsity of ${\ell }_0$-Orthogonal Matching Pursuit (OMP) with the noise robustness of ${\ell }_1$-Least Absolute Shrinkage and Selection Operator (LASSO), dynamically adjusting their relative weights to enhance both coding quality and reconstruction stability. Experiments on typical shock wave datasets show that, compared with Discrete Cosine Transform (DCT), KSVD, and feature-based segmented dictionary methods (termed CC-KSVD), DH-KSVD reduces average training time by 46.4%, 31%, and 13.7%, respectively. At a Compression Ratio (CR) of 0.7, the Root Mean Square Error (RMSE) decreases by 67.1%, 65.7%, and 36.2%, while the Peak Signal-to-Noise Ratio (PSNR) increases by 35.5%, 39.8%, and 11.8%, respectively. The proposed algorithm markedly improves training efficiency and achieves lower RMSE and higher PSNR under high compression ratios, providing an effective solution for compressing long-duration, transient shock wave signals.

1. Introduction

The pressure of shock waves generated by explosions constitutes a critical parameter for evaluating the destructive potential of weapons; consequently, precise measurement of these shock waves is of considerable importance [1,2]. Shock wave signals are characterized by transience, pronounced non-stationarity, and substantial energy fluctuations [3,4], thereby necessitating sampling rates in the megahertz range to faithfully capture critical physical features including the rising edge, peak, and decay. In specialized contexts such as maritime destructive experiments, a single explosion lasting only a few seconds can yield millions to tens of millions of data points, while multi-channel synchronous monitoring further amplifies the exponential increase in data volume. Moreover, in light of the inherent limitations of wireless transmission bandwidth at sea and the potential hazard of rapid vessel sinking, efficient data compression emerges as an indispensable prerequisite.

Current data compression methods are primarily categorized into two types: lossless compression and lossy compression [5]. The selection between these methods should be determined according to the specific application context, balancing fidelity with compression efficiency. Presently, widely utilized lossless compression algorithms, including Huffman coding [6], arithmetic coding [7], and Lempel–Ziv–Welch (LZW) dictionary coding [8], are capable of reducing data volume without any loss of original information. However, they are primarily based on modeling redundant characters or symbol frequencies and are suitable for data with stable structures or discrete values. For continuous real-valued data, such as shock wave signals, which exhibit significant non-stationarity, rapid fluctuations, and intricate spectral structures, lossless compression algorithms frequently encounter difficulties in attaining optimal compression. In contrast, lossy compression methods that focus on feature preservation exhibit greater potential. Among these, Compressive Sensing (CS) theory [9,10] offers a novel framework for efficiently reconstructing signals at sampling rates below the Nyquist rate, assuming that the signal possesses a sparse representation in a specific sparse basis or dictionary. The reconstruction performance is highly contingent upon the quality of the sparse representation basis design. Early sparse dictionaries primarily employed analytical construction methods, such as Gabor functions [11] and wavelet bases [12], which utilize fixed basis function libraries, while these methods offer high computational efficiency, their predefined basis functions constrain their capacity to effectively capture the complex feature structures inherent in shock wave signals.

To tackle this challenge, researchers have proposed adaptive dictionary learning approaches, among which the K Singular Value Decomposition (KSVD) algorithm is the most representative. This approach iteratively optimizes dictionary atoms and sparse coefficients, allowing the dictionary to adaptively capture the dominant feature patterns within training samples. It has been extensively applied in domains such as image classification [13,14] and video denoising [15,16,17]. Although the KSVD algorithm demonstrates strong performance in sparse representation, it remains constrained by high computational complexity and limited robustness. The existing studies have predominantly concentrated on the sparse coding stage. For instance, reference [18] proposed an adaptive sparsity estimation strategy, whereas reference [19] utilized segmented orthogonal matching pursuit to accelerate the solution of underdetermined equations, thereby enhancing training efficiency. However, these approaches exhibit unstable sparsity estimation in high-noise environments and are typically confined to optimizing the coding process, while neglecting the joint optimization of the dictionary update stage. Consequently, achieving a balance among sparsity, training efficiency, and reconstruction accuracy remains challenging. Reference [20] enhanced discriminative capability by jointly optimizing dictionary representation capabilities and classifier performance, but its computational complexity is high and it is highly dependent on labels. Reference [21] proposed a method based on signal feature segmentation training and dictionary concatenation, which reduced dictionary size and training time via classification learning; nevertheless, its performance relies heavily on prior sparsity knowledge and classification accuracy. In high-noise environments, sparsity estimation is unstable, affecting reconstruction quality.

The main contributions of this paper are summarized as follows:

• A dynamic pruning mechanism is introduced to evaluate the importance of atoms based on their contribution. By adaptively removing redundant atoms while supplementing residual features, the compactness of the dictionary is enhanced and training efficiency is improved.
• A hybrid sparse coding strategy is designed to integrate the strict sparsity of ${\ell }_0$-based Orthogonal Matching Pursuit (OMP) with the noise robustness of ${\ell }_1$-based Least Absolute Shrinkage and Selection Operator (LASSO), dynamically balancing their weights to improve coding quality and reconstruction stability.
• The proposed DH-KSVD algorithm achieves superior performance in both training efficiency and reconstruction accuracy under more aggressive compression, especially in noisy environments, offering an effective solution for transient signal compression such as shock waves.

The remainder of this paper is organized as follows: Section 2 presents the theoretical background, including the characteristics of shock wave signals and the fundamentals of CS and KSVD. Section 3 details the proposed DH-KSVD algorithm, including the dynamic pruning mechanism, hybrid sparse constraint strategy, and its integration into the CS framework. Section 4 provides experimental results and comparative analysis, including ablation studies and performance evaluation under various conditions. Section 5 discusses the advantages and limitations of the proposed method, along with insights into potential future research directions. Finally, Section 6 concludes the paper.

2. Theoretical Analysis

2.1. Shock Wave Characteristics

Shock wave signals constitute a representative class of transient, nonstationary signals, typically generated by violent events such as explosions, high-speed impacts, supersonic flight, and structural damage. These signals exhibit distinctive physical properties and temporal characteristics. In the time domain, shock wave signals manifest abrupt, short-lived high-amplitude responses, with waveforms characterized by steep rising edges, extremely brief durations, and rapidly decaying tails, thereby producing a strongly nonstationary structure [22]. In the frequency domain, these signals encompass abundant high-frequency components, with a broad spectral range typically extending from tens of hertz to several hundreds of kilohertz. Additionally, such signals are often accompanied by nonlinear effects and noise disturbances, exhibiting high complexity. To accurately capture the fine-grained characteristics of shock waves, engineering practices commonly employ oversampling strategies with sampling frequencies far surpassing the Nyquist criterion. Although this approach enables complete signal reconstruction, it produces substantial redundant data, particularly in scenarios involving high channel density, multi-dimensional acquisition, or remote transmission, thereby markedly increasing the costs of acquisition, storage, and processing. Traditional compression methods such as DCT and wavelet transform can reduce some redundancy, but they lack adaptability to shock waves, which are highly time-varying and exhibit local sudden changes, often resulting in limited compression rates and significant reconstruction distortions. However, CS theory offers a new approach to achieving compression at the acquisition end without relying on high-density sampling points, thereby providing a feasible theoretical and practical path for compressing shock wave signals.

2.2. Compressive Sensing Theory

CS constitutes a theoretical framework that simultaneously performs compression and modeling during the signal acquisition stage, thereby overcoming the constraints imposed by the traditional Nyquist sampling theorem. It enables efficient signal acquisition and reconstruction from a limited number of random observations, provided that the signal exhibits sparsity within a specific transform domain. For shock wave signals characterized by sparse spectra and pronounced locality, CS can substantially reduce sampling rates and storage overhead. Nevertheless, its application encounters two principal challenges: constructing sparse bases that align with the signal structure to ensure reconstruction accuracy, and efficiently and robustly estimating sparse coefficients in underdetermined systems.

The mathematical model of CS can be expressed as

$$y=\mathbf{\Phi }x=\mathbf{\Phi }\mathbf{\Psi }\theta =\mathbf{A}\theta$$

(1)

where $x\in {\mathbb{R}}^N$ represents the original signal, $\mathbf{\Psi }\in {\mathbb{R}}^{N\times K}$ is the sparse representation dictionary, and $\theta \in {\mathbb{R}}^K$ is the sparse coefficient vector. When $\theta$ satisfies both ${\parallel \theta \parallel }_0=K$ and $K\ll N$, the signal is said to exhibit K-sparsity under the dictionary. ${\parallel ·\parallel }_0$ denotes the number of non-zero elements in the vector, used to measure sparsity. $\mathbf{\Phi }\in {\mathbb{R}}^{M\times N}$ is the measurement matrix, y is the observation vector, $M\ll N$ indicates that the number of observations is far below the original dimension, and $\mathbf{A}=\mathbf{\Phi }\mathbf{\Psi }\in {\mathbb{R}}^{M\times K}$ is the equivalent perception matrix. The key to the entire system is whether signal x can be represented in sparse form under the dictionary, and how to recover the sparse coefficients $\theta$ from y under the underdetermined condition of $M\ll N$, thereby reconstructing the original signal $x=\mathbf{\Psi }\theta$.

Under the CS model, the essence of signal reconstruction is to solve sparse optimization problems, which can be formally expressed as

$$\underset{\theta }{min}{\parallel \theta \parallel }_0\mathrm{s}.\mathrm{t}.y=\mathbf{A}\theta$$

(2)

Since solving the ${\ell }_0$-norm is NP-hard, an approximate optimization form is typically used:

$$\underset{\theta }{min}{\parallel \theta \parallel }_1\mathrm{s}.\mathrm{t}.y=\mathbf{A}\theta$$

(3)

When considering noise conditions, the error margin $\epsilon$ is introduced to obtain the following form:

$$\underset{\theta }{min}{\parallel \theta \parallel }_1\mathrm{s}.\mathrm{t}.{\parallel y=\mathbf{A}\theta \parallel }_2^2\le \epsilon$$

(4)

Common solution methods include Basis Pursuit (BP), Matching Pursuit (MP), OMP [23], LASSO [24], etc. In traditional OMP, the selection of sparse supports is constructed gradually through a greedy strategy, i.e., in each step, the dictionary atoms most relevant to the current residual are selected, and the support set is updated. OMP can effectively identify atoms that are highly correlated with the signal, but in the presence of noise or dictionary redundancy, it may select redundant atoms, leading to unstable sparsity coefficients. Therefore, to further optimize the distribution of sparsity coefficients, a LASSO optimization stage can be introduced based on the sparse support set obtained by OMP. LASSO utilizes the convex relaxation property of the ${\ell }_1$ norm to further optimize the coefficient distribution when the sparse support is known, suppressing noise effects while avoiding overfitting.

In practical applications, the quality of sparse representation, measured by sparsity level, reconstruction accuracy, and adaptability to local signal structures, is the key bottleneck constraining the compression efficiency of shock wave signals. Although predefined bases such as wavelets and discrete cosines have a certain degree of sparsity, they cannot effectively capture local structural features for sudden signals such as shock waves, resulting in poor sparse representation quality and affecting compression and reconstruction performance. Therefore, reliance solely on predefined transform domains is inadequate to fully exploit the sparse potential of shock wave signals.

To address this challenge, researchers have proposed data-driven sparse modeling methods, which involve learning to construct an adaptive dictionary $\mathbf{D}$ from training data to replace the predefined sparse basis $\mathbf{\Phi }$, thereby maximizing sparse representation capabilities. Compared to fixed bases, data-driven dictionaries offer greater flexibility and expressive power, making them particularly suitable for modeling complex, time-varying signals like shock waves.

2.3. KSVD Sparse Model

KSVD is one of the most commonly used dictionary learning algorithms today. It belongs to the iterative dictionary learning method, whose goal is to learn a dictionary $\mathbf{D}=[d_1,d_2,\dots ,d_L]\in {\mathbb{R}}^{d\times L}$ and a sparse coding matrix $\mathbf{\Theta }=[{\theta }_1,{\theta }_2,\dots ,{\theta }_N]\in {\mathbb{R}}^{d\times N}$ under the condition of a given training sample matrix $\mathbf{X}=[X_1,X_2,\dots ,X_N]\in {\mathbb{R}}^{d\times N}$, so that each sample $X_i$ can be sparsely represented under $\mathbf{D}$ as

$$X_i\approx \mathbf{D}{\theta }_i\mathrm{with}{∥{\theta }_i∥}_0\le T_0$$

(5)

where $T_0$ is the preset upper limit of sparsity. The optimization objective function of KSVD is

$$\underset{\mathbf{D},\mathbf{\Theta }}{min}{∥\mathbf{X}-\mathbf{D}\mathbf{\Theta }∥}_F^2\mathrm{s}.\mathrm{t}.\forall i,{∥{\theta }_i∥}_0\le T_0\mathrm{for}i=1,2,\dots ,N$$

(6)

KSVD employs an alternating minimization strategy comprising two iterative stages: fixing the dictionary to solve for sparse coefficients, followed by fixing the sparse coefficients to update the dictionary. First, the dictionary $\mathbf{D}$ is initialized, and algorithms such as OMP are applied to perform sparse coding on all samples, thereby obtaining the sparse coefficients ${\theta }_i$ under the current dictionary, as shown in Equation (7).

$${\theta }_i=arg\underset{\theta }{min}{∥X_i-\mathbf{D}\theta ∥}_2^2\mathrm{s}.\mathrm{t}.{∥\theta ∥}_0\le T_0$$

(7)

During the dictionary update phase, the KSVD algorithm updates each atom $d_k$ and its corresponding sparse coefficients in a column-wise manner. Let ${\omega }_k=\{i\mid {\theta }_{k,i}\ne 0\}$ be the set of sample indices that use atom $d_k$. The residual matrix is then constructed to remove the contribution of atom $d_k$: ${\mathbf{E}}_k=\mathbf{X}-{\sum }_{\begin{array}{c}j\ne k\end{array}}{d}_j{\theta }_j$. Then extract the submatrix ${\mathbf{E}}_k^{\omega }$ under the support, perform SVD on the residuals: ${\mathbf{E}}_k^{\omega }=\mathbf{U}\mathbf{S}{\mathbf{V}}^T$. Set $d_k=\mathbf{U}(:,1)$, and update the corresponding sparse coefficient to ${\theta }_{k,\omega }=\mathbf{S}(1,1)·\mathbf{V}{(:,1)}^T$. Repeating these steps for each iteration ultimately yields the optimal representation dictionary $\mathbf{D}$. In this work, the dictionary is constructed to pursue a better linear representation of the signal, thereby attaining lower sparsity and facilitating the subsequent CS coding and reconstruction process.

3. Improved Algorithm DH-KSVD

3.1. Dynamic Dictionary Pruning Mechanism

In traditional KSVD algorithms, although the fixed dictionary structure guarantees the stability of sparse representations, efficiency issues become especially prominent when handling signals with abrupt local changes, such as shock waves. A substantial number of atoms are seldom activated during signal reconstruction, or are highly redundant with other atoms, thus consuming considerable computational resources while providing marginal improvements in reconstruction performance. To address this issue, this study introduces a dynamic pruning mechanism. By establishing a multi-dimensional atom evaluation system, the mechanism quantifies the usage efficiency and feature uniqueness of atoms, eliminating redundant or inefficient atoms to enable adaptive and lightweight dictionary optimization. Equation (8) defines the comprehensive contribution assessment function for the j-th atom, which integrates the representation strength and usage frequency of atoms to quantify their contributions to signal reconstruction.

$$C_j=\sum _{l=1}^L\left|{\widehat{\theta }}_l\left(j\right)\right|+\partial \sum _{l=1}^L\Pi \left({\widehat{\theta }}_l\left(j\right)\ne 0\right)$$

(8)

In this equation, ${\widehat{\theta }}_l\left(j\right)$ denotes the sparsity coefficient of the j-th atom in the l-th training sample, L represents the total number of training samples, and ∂ is a tuning parameter that balances the weights of representation strength and usage frequency. The first term quantifies the overall representation strength of the atom across all samples, whereas the second term enumerates the number of samples in which it is activated, thereby reflecting its usage frequency.

After evaluating the comprehensive contributions of atoms, an adaptive threshold strategy is employed for pruning, as illustrated in the following equation:

$$\mathrm{Prune}\left(d_j\right)=\Pi \left(C_j<\tau \left(1+\gamma ·\mathrm{Uniq}\left(d_j\right)\right)·\underset{k}{max}{C}_k\right)$$

(9)

Pruning conditions compare the composite contribution $C_j$ of an atom against a dynamic value determined jointly by the base pruning threshold $\tau$ and the maximum contribution ${max}_k{C}_k$ in the current dictionary, thereby mitigating instability caused by scale variations. Building upon this, the uniqueness metric $\mathrm{Uniq}\left(d_j\right)$ is introduced as a regulating factor, with its influence intensity controlled by the parameter $\gamma$. For atoms exhibiting high uniqueness, even when their comprehensive contribution is low, the pruning strictness should be appropriately relaxed to prevent the removal of key features.

The uniqueness of an atom is evaluated by computing its similarity to other atoms, as defined by the following equation:

$$\mathrm{Uniq}\left(d_j\right)=1-\underset{k\ne j}{max}{\displaystyle \frac{|d_j{d}_k|}{\parallel d_j{\parallel }_2{\parallel d_k\parallel }_2}}$$

(10)

This equation evaluates the maximum correlation between an atom $d_j$ and the other atoms in the dictionary. A higher degree of similarity corresponds to a lower level of uniqueness. In this manner, atoms possessing unique representational capacity within the dictionary can be identified and afforded special protection during pruning, thereby preventing a decline in the dictionary’s representational capability as a consequence of pruning. To further enhance the stability of the pruning process, a sliding window mechanism was introduced, in which pruning operations were executed every five iterations and the statistics within the window were updated prior to each pruning step. This sliding window design ensures that pruning decisions are informed not only by the current iteration but also by the recent usage patterns of atoms, thereby mitigating misjudgments of their long-term value caused by short-term fluctuations.

Although the dynamic pruning mechanism enhances efficiency, it still carries the risk of over-pruning or inadvertently eliminating key atoms. To address this issue, a dynamic expansion mechanism was devised to introduce new atoms when necessary, thereby restoring the integrity of the dictionary. The core concept is to generate new atoms through the analysis of signal residuals when the reconstruction error increases markedly or when the dictionary contains too few atoms. Specifically, the following equation is employed to select new atoms:

$$d_{\mathrm{new}}=arg\underset{d\in {\mathbf{D}}_{\mathrm{candidate}}}{min}\sum _{l=1}^L{∥X_l-{\mathbf{D}}_{\mathrm{current}}{\widehat{\theta }}_l-d{\widehat{\theta }}_l\left(d\right)∥}^2$$

(11)

where ${\mathbf{D}}_{\mathrm{candidate}}$ is a set of candidate atoms composed of residual signals that cannot be fully represented by the current dictionary ${\mathbf{D}}_{\mathrm{current}}$. The construction process is as follows: first, calculate the reconstruction error $R_l=X_l-D_{\mathrm{current}}{\theta }_l$ for all training samples $X_l$ in the current dictionary $D_{\mathrm{current}}$. Subsequently, the residuals corresponding to the top 10% of samples with the largest reconstruction errors are selected as the initial residual set. This set undergoes normalization processing, and typical residual patterns are extracted via K-means clustering. The resulting cluster centers are ultimately designated as the candidate atom set $D_{\mathrm{candidate}}$. Finally, using Equation (11), a new atom $d_{\mathrm{new}}$ capable of maximally reducing the overall reconstruction error is selected for addition to the dictionary. This strategy ensures that new atoms originate from structural residuals that the system has long been unable to represent effectively, rather than random noise or transient perturbations. Simultaneously, the clustering operation enhances the representativeness and stability of candidate atoms. Furthermore, to prevent new atoms from being highly correlated with existing ones, which could increase dictionary coherence or cause collapse, we introduce a uniqueness screening mechanism during candidate atom incorporation. This mechanism requires that new atoms must exhibit a maximum correlation below 0.95 with all existing atoms in the dictionary. Those failing this criterion are discarded outright to preserve dictionary diversity and prevent cumulative coherence.

In addition, to avoid insufficient pruning or unstable pruning strategies, a dynamic adjustment mechanism is introduced to adjust the pruning threshold based on the performance of the current dictionary, as shown in the following equation:

$${\tau }_{\mathrm{new}}={\tau }_{\mathrm{old}}+\alpha \left({\mathrm{Error}}_{\mathrm{current}}-{\mathrm{Error}}_{\mathrm{target}}\right)$$

(12)

where ${\tau }_{\mathrm{old}}$ represents the current base threshold, $\alpha$ denotes the learning rate, which controls the step size or speed of adjusting the pruning threshold $\tau$ to ensure the adjustment process is neither too abrupt nor too slow. ${\mathrm{Error}}_{\mathrm{current}}$ is the current average reconstruction error, representing the average distortion level after applying sparse coding to a set of signals using the current dictionary. ${\mathrm{Error}}_{\mathrm{target}}$ is the target error, representing the minimum reconstruction error level to be achieved. This mechanism enables automatic adjustment of pruning strictness when reconstruction error deviates from the target, thereby achieving a dynamic balance between dictionary size and expressive capability. The specific equation for ${\mathrm{Error}}_{\mathrm{current}}$ is

$${\mathrm{Error}}_{\mathrm{current}}={\displaystyle \frac{1}{N·L}}\sum _{l=1}^L{\parallel X_l-D_{\mathrm{current}}{\theta }_l\parallel }^2$$

(13)

When an atom remains inactive for several consecutive iterations, the system prioritizes its pruning; conversely, when the usage frequency of an atom increases substantially, the system postpones its pruning to preserve its potential contribution to signal representation.

3.2. Hybrid Sparse Constraint Strategy

In sparse coding, traditional methods such as OMP and LASSO each offer distinct advantages, yet are accompanied by inherent limitations. The OMP algorithm excels in delivering accurate sparse representations by progressively selecting the most relevant dictionary atoms to approximate signals. However, it is susceptible to overfitting when exposed to noise interference or dictionary redundancy, resulting in insufficient sparsity or increased reconstruction error. LASSO improves the model’s robustness to noise through the incorporation of an ${\ell }_1$ regularization term; however, the sparsity of its solution is typically contingent on the selection of the regularization parameter, and in some instances, precise control over sparsity cannot be assured. Therefore, to strike a balance between the accuracy and robustness of sparse representation, this study proposes a hybrid sparse constraint strategy that integrates the strengths of OMP and LASSO, thereby constructing a hierarchical optimization framework. The first stage utilizes the OMP algorithm for initial sparse selection, identifying the most relevant set of atoms in the signal representation. In contrast, the second stage formulates a LASSO optimization problem within this sparse subspace to further refine the coefficients, mitigate noise effects, and improve overall stability.

First, we define the sparse representation model of the signal $X\in {\mathbb{R}}^n$ as follows:

$$X_i=\mathbf{D}{\theta }_i+\epsilon$$

(14)

where $\mathbf{D}\in {\mathbb{R}}^{n\times K}$ denotes a known overcomplete dictionary, $\theta \in {\mathbb{R}}^K$ represents a sparse coefficient vector, and $\epsilon$ accounts for additive noise.

In the first stage, the OMP algorithm is employed to identify the sparse support set $\Lambda \subseteq \{1,2,\dots ,K\}$ of the signal and obtain the initial sparse coefficient estimate ${\theta }_{\mathrm{OMP}}$. In the second stage, a sub-dictionary ${\mathbf{D}}_{\Lambda }$ is constructed based on the support set $\Lambda$, and the LASSO problem is subsequently solved within this subspace. In the specific implementation, the support selection process of OMP can be formalized through the following iterative steps:

Initialize the residual $r_0=X$ and the support set ${\Lambda }_0=\varphi$.

For each iteration:

$$\begin{array}{c} j_i=arg\underset{j}{max}\left|d_j{r}_{i-1}\right|\hfill \end{array}$$

(15)

$$\begin{array}{c}{\Lambda }_i={\Lambda }_{i-1}\cup \left\{j_i\right\}\hfill \end{array}$$

(16)

$$\begin{array}{c} {\theta }_i=arg\underset{\theta }{min}{∥X-{\mathbf{D}}_{{\Lambda }_i}\theta ∥}_2^2\hfill \end{array}$$

(17)

$$\begin{array}{c}ri=X-{\mathbf{D}}_{{\Lambda }_i}{\theta }_i\hfill \end{array}$$

(18)

where $d_i$ denotes the j-th column of dictionary $\mathbf{D}$, and X is the least-squares solution o ${\theta }_i$ on the support set ${\Lambda }_i$. Equation (15) specifies that during the i-th iteration, an atom $d_i$ most relevant to the current residual $r_{i-1}$ is selected from the dictionary $\mathbf{D}$. Specifically, this is achieved by calculating the absolute value of the inner product between each atom $d_i$ in the dictionary and the current residual $r_{i-1}$, and selecting the index $j_i$ of the atom yielding the maximum absolute inner product value. This ensures that the atom that most closely matches the current residual is chosen at each iteration. The newly selected atom index $j_i$ is added to the support set ${\Lambda }_i$, as shown in Equation (16). Solving the least-squares problem on the current support set ${\Lambda }_i$ yields the sparse coefficient vector ${\theta }_i$, where $\mathbf{D}$ denotes the sub-dictionary composed of atoms from ${\Lambda }_i$. Finally, the residual $r_i$ is updated using the new sparse coefficients ${\theta }_i$.

OMP selects the most relevant atoms by maximizing the inner product between the dictionary atoms and the residuals, and updates the coefficients using the least squares method. Upon completion of the OMP stage, the LASSO optimization phase begins. To further improve the robustness of the sparse representation, the coefficients on the support set $\Lambda$ are optimized through regularization:

$${\widehat{\theta }}_{\Lambda }=arg\underset{{\theta }_{\Lambda }}{min}{\displaystyle \frac{1}{2}}{∥X-{\mathbf{D}}_{\Lambda }{\theta }_{\Lambda }∥}_2^2+\lambda {∥{\theta }_{\Lambda }∥}_1$$

(19)

where ${\mathbf{D}}_{\Lambda }$ is a subset of columns corresponding to the support set $\Lambda$ in dictionary $\mathbf{D}$, and ${\theta }_{\Lambda }$ denotes the corresponding sparse coefficient subset, $\lambda$ is the regularization parameter, used to control sparsity. Through this hierarchical strategy, the introduction of LASSO not only retains the sparse support determined in the OMP stage, but also further compresses the coefficients via ${\ell }_1$ regularization, suppressing noise effects and improving overall stability.

To dynamically adjust regularization parameter $\lambda$ based on signal noise levels and dictionary redundancy, a noise level estimation and dynamic adjustment mechanism is introduced. First, the noise level is estimated using the median absolute deviation (MAD):

$$\widehat{\sigma }={\displaystyle \frac{\mathrm{MAD}\left(r\right)}{0.6745}}$$

(20)

MAD(r) denotes the median absolute deviation of the final residual vector r computed during the OMP phase. 0.6745 is a constant used to make MAD equal to the standard deviation under a Gaussian distribution. The regularization parameter $\lambda$ is dynamically adjusted based on the estimated noise level $\widehat{\sigma }$ and dictionary size Q:

$$\lambda =\beta ·\widehat{\sigma }·\sqrt{2logQ}$$

(21)

where $\beta$ is an empirical adjustment coefficient, typically ranging between 0.5 and 1.0. $\sqrt{2logQ}$ is a factor related to the dictionary size that accounts for the impact of dictionary redundancy on regularization strength. As the dictionary size increases, the likelihood of selecting erroneous atoms also rises, necessitating stronger regularization to suppress this effect. This strategy enables the adaptive adjustment of regularization strength based on the signal-to-noise ratio, thereby ensuring the stability of sparse coding across various noise environments.

3.3. Algorithm Description of DH-KSVD

The DH-KSVD algorithm comprises four distinct stages: parameter initialization, hybrid sparse coding, dictionary updating, and dynamic pruning. Prior to the algorithm’s initiation, the input variables encompass the training sample matrix ${\mathbf{X}}_{N\times L}$, the initial dictionary ${\mathbf{D}}_{N\times ds}$, the pruning threshold $\tau$, learning rate $\alpha$, adjustment parameters ∂, $\gamma$ and the maximum number of iterations ${max}_{iter}$. For each iteration, the parameters are initialized, an empty set ${\Lambda }_0$ is defined to store the currently selected atom indices, and the initial sparse coefficient matrix $\widehat{\theta }$ and atom frequency matrix F are set to zero matrices, respectively.

Consider the i-th iteration as an example; first, perform mixed sparse coding to find the optimal sparse representation of the signal. For each sample $X_l$, select the atoms from the dictionary that are most relevant to the current residual. Specifically, the inner product between each atom and the residual is calculated, and add the atom index j corresponding to the maximum value to the set of selected atoms $\Lambda$. The coefficients ${\widehat{\theta }}_{\Lambda }$ of these selected atoms are solved using least squares, and the residual r is updated. After obtaining the preliminary sparse representation, the coefficients $\widehat{\theta }$ are further optimized to ensure not only accurate data fitting but also high sparsity and robustness to noise. The sparse coefficient matrix $\widehat{\theta }$ and the atom frequency matrix F reflect the results of the current iteration.

During the dictionary update phase, for each atom corresponding to a non-zero coefficient, calculate its corresponding error matrix $E_n$ and update the atom using SVD. Dynamic pruning is employed to preserve the effectiveness and compactness of the dictionary. The decision to remove an atom is based on its contribution to the reconstructed signal $C_j$ and its uniqueness index $\mathrm{Uniq}\left(d_j\right)$. If an atom’s contribution falls below the threshold $\tau$ plus the weighted sum of its uniqueness metric, the atom is removed from the dictionary. The algorithm also incorporates a dynamic expansion mechanism that automatically adds new atoms to the dictionary when the reconstruction error is high. Simultaneously, it adaptively adjusts the pruning threshold $\tau$ and regularization parameter $\lambda$ based on the current error level to optimize algorithmic performance. After each iteration, the current residual $E\left(i\right)$ is evaluated to determine whether it is smaller than the residual from the previous iteration $E(i-1)$. If the condition is satisfied, the optimal dictionary ${\mathbf{D}}_{Min}$ is updated. When the number of iterations i reaches ${max}_{iter}$, the iteration process terminates.

The steps of the DH-KSVD algorithm are shown in Algorithm 1.

Algorithm 1 DH-KSVD algorithm

Input:${\mathbf{X}}_{N\times L}$, ${\mathbf{D}}_{N\times ds}$, ∂, $\tau$, $\alpha$, $\gamma$, $\lambda$, Q, ${\max }_{\mathrm{iter}}$ Output:${\mathbf{D}}_{Min}$, $\widehat{\theta }$  1: Initialization: $i=1$, $r_0=\mathbf{X}$, ${\Lambda }_0=\varphi$, $F=0_{ds\times 1}$, $n=1$  2: while $i\le {\max }_{\mathrm{iter}}$ do  3:     Hybrid Sparse Coding (OMP+LASSO):  4:     for $l=1$ to L do  5:         OMP Stage: ${\Lambda }_0=\varphi$, $r=X_l$  6:         $j_i=arg\underset{j}{max}\left|d_j{r}_{i-1}\right|$, ${\Lambda }_i={\Lambda }_{i-1}\cup \left\{j_i\right\}$, ${\theta }_i=arg\underset{\theta }{min}{\parallel X_l-{\mathbf{D}}_{{\Lambda }_i}\theta \parallel }_2^2$, $r_i=X_l-{\mathbf{D}}_{{\Lambda }_i}{\theta }_i$  7:         LASSO Stage: ${\widehat{\theta }}_{\Lambda }=arg\underset{{\theta }_{\Lambda }}{min}{\displaystyle \frac{1}{2}}\parallel X_l-{\mathbf{D}}_{\Lambda }{\theta }_{\Lambda }{\parallel }_2^2+\lambda {\parallel {\theta }_{\Lambda }\parallel }_1$  8:         Update $\widehat{\theta }$ and atomic frequency $F_j\leftarrow F_j+1$ for $j\in \Lambda$  9:     end for 10:     Dictionary Update: 11:     SVD Update: 12:     for $n=1$ to $ds$ do 13:         ${\omega }_n=\left\{i\right|{\widehat{\theta }}_n\left(i\right)\ne 0\}$, $E_n=\mathbf{X}\left({\omega }_n\right)-\sum _{j\ne n}{\mathbf{D}}_j{\widehat{\theta }}_j\left({\omega }_n\right)$, $[U,\Sigma ,V]=\mathrm{SVD}\left(E_n\right)$,       ${\mathbf{D}}_n=U_1$, ${\widehat{\theta }}_n\left({\omega }_n\right)=\Sigma (1,1)V_1^T$ 14:     end for 15:     Dynamic Pruning (execute every five iterations): 16:     for $j=1$ to $ds$ do 17:         Contribution Calculation: $C_j={\displaystyle \sum _{l=1}^L}\left|{\widehat{\theta }}_j\left(l\right)\right|+\partial F_j$, $\forall j\in \{1,\dots ,ds\}$ 18:         Uniqueness Evaluation: $\mathrm{Uniq}\left(d_j\right)=1-\underset{k\ne j}{max}{\displaystyle \frac{|d_j{d}_k|}{\parallel d_j{\parallel }_2{\parallel d_k\parallel }_2}}$ 19:         Prune Condition: Remove $d_j$ if $C_j<\tau (1+\gamma ·\mathrm{Uniq}\left(d_j\right))·\underset{k}{max}{C}_k$ 20:     end for 21:     Dynamic Expansion: 22:     ${\mathrm{Error}}_{\mathrm{current}}$: $E\left(i\right)={\displaystyle \frac{1}{N·L}}{\displaystyle \sum _{l=1}^L}{\parallel X_l-\mathbf{D}{\widehat{\theta }}_l\parallel }_2^2$ 23:     Add new atom: $d_{\mathrm{new}}=arg\underset{d}{min}{\displaystyle \sum _{l=1}^L}{∥X_l-\mathbf{D}{\widehat{\theta }}_l-d{\widehat{\theta }}_l\left(d\right)∥}^2$ 24:     Parameter Adaptive Adjustment: ${\tau }_{\mathrm{new}}={\tau }_{\mathrm{old}}+\alpha \left({\mathrm{Error}}_{\mathrm{current}}-{\mathrm{Error}}_{\mathrm{target}}\right)$ 25:     Estimate noise level: $\widehat{\sigma }={\displaystyle \frac{\mathrm{MAD}\left(r\right)}{0.6745}}$ 26:     Adjust regularization parameter: $\lambda =\beta ·\widehat{\sigma }·\sqrt{2logQ}$ 27:     Residual and Termination: 28:     if $E\left(i\right)<E(i-1)$ then 29:         set ${\mathbf{D}}_{Min}=\mathbf{D}$, $i=i+1$ 30:     end if 31: end while

3.4. Application of DH-KSVD in CS Framework

3.4.1. A Compressed Sensing Framework Based on DH-KSVD

The CS framework based on DH-KSVD, as depicted in Figure 1, comprises three key components: diction ary training, data compression, and signal reconstruction.

In the CS framework, the application of DH-KSVD is initiated during the dictionary training phase. Given the substantial volume of actual signal data, it is impractical to use the entire signal directly for dictionary learning. Therefore, the original signal must first be divided into blocks. According to Equation (22), the signal is divided into several signal blocks of appropriate length, which serve as training samples for redundant dictionary learning. Subsequently, an improved KSVD algorithm is employed to iteratively optimize the dictionary. In each iteration, a hybrid sparse coding strategy combining OMP and LASSO is used to obtain the sparse representations of each signal block, and the dictionary atoms are updated via SVD. This process not only ensures the dictionary’s efficient representation of local features, but also achieves adaptive optimization of the dictionary structure through dynamic pruning and expansion mechanisms, thereby enhancing its sparsity performance.

Upon completion of dictionary training, the data compression phase begins. Using the learned redundant dictionary $\mathbf{D}$, sparse decomposition is performed on each block of the original signal to obtain sparse coefficient vectors. Subsequently, these sparse or compressible signals are subjected to low-dimensional projection using the measurement matrix $\mathbf{\Phi }$, thereby achieving compressed sampling of the signals. The compressed measurement values reduce the data dimension, facilitating efficient transmission in bandwidth-constrained wireless sensor networks. This compression process does not require full knowledge of the original signal’s information; instead, it relies on a small number of measurements to preserve the signal’s key structural features, thereby effectively reducing communication overhead and conserving energy consumption.

When performing signal reconstruction at the management node, after receiving the compressed measurement data, the known dictionary $\mathbf{D}$ and measurement matrix $\mathbf{\Phi }$ are used to solve the underdetermined linear system via a sparse reconstruction algorithm, thereby recovering the sparse coefficients $\theta$ for each signal block. Subsequently, these coefficients are multiplied by the dictionary to reconstruct the corresponding signal segments. Finally, all reconstructed signal blocks are concatenated and reshaped according to Equation (23) to restore the complete signal with the same length as the original signal. This reconstruction process fully utilizes the sparse prior of the signal under the learned dictionary to achieve high-precision signal recovery, thereby balancing the efficiency and reconstruction performance of DH-KSVD within the CS framework.

$${\mathbf{X}}_{n\times t}=\left[\begin{array}{cccc}{x}_1& x_{n+1}& \dots & x_{(t-1)n+1}\\ x_2& x_{n+2}& \dots & x_{(t-1)n+2}\\ ⋮& ⋮& \ddots & ⋮\\ x_n& x_{2n}& \dots & x_{tn}\end{array}\right]$$

(22)

$$x_{tn\times 1}=\mathrm{reshape}(X(:,1),X(:,2),\dots ,X(:,t))={[x_1,x_2,\dots ,x_{tn}]}^T$$

(23)

3.4.2. Algorithm Complexity Analysis

To theoretically evaluate the computational efficiency of the DH-KSVD algorithm, an asymptotic analysis of its time complexity during training and encoding phases is conducted. The overall complexity of the algorithm is primarily determined by three core components: hybrid sparse coding, dictionary updating, and dynamic pruning.

During the training phase, the computational cost per iteration is as follows: first, the mixed sparse coding stage processes each of the L training samples sequentially. The OMP stage constructs the sparse support set by greedily selecting atoms, with a complexity of $O(Q·N·L)$, where Q is the number of dictionary atoms and N is the signal dimension. Subsequently, the LASSO phase performs coefficient optimization on the support set selected by OMP, with a complexity of approximately $O(T_0^3+T_0^{2}N)$, where $T_0$ denotes the sparsity factor. Although higher than pure OMP, it significantly improves noise robustness. Secondly, during the dictionary update phase, KSVD performs singular value decomposition (SVD) on each atom, with a complexity of $O\left(N\right|{\omega }_k{|}^2)$, where $|{\omega }_k|$ is the number of samples using that atom. Finally, the dynamic pruning mechanism executes periodically after several iterations, with a complexity of $O(Q^2·N+Q·L)$ for evaluating atomic contributions and uniqueness. Overall, the asymptotic time complexity of a single iteration of DH-KSVD is on the same order as traditional KSVD, approximately $O(Q·N·L+Q·N·|{\omega }_k{|}^2)$. However, thanks to the dynamic pruning mechanism, redundant atoms are progressively eliminated during iteration, resulting in the effective number of atoms $Q_{\mathrm{eff}}$ being significantly smaller than the initial number Q. Consequently, the computational load of the algorithm decreases substantially during actual execution, particularly in later iterations. This provides the theoretical basis for its significantly reduced training time. During the encoding phase, the complexity of sparse representation for a single signal block is similar to that of the sparse coding phase in training, being $O(Q·N+T_0^3)$, ensuring the efficiency of the data compression process.

4. Experimental Results and Analysis

4.1. Experimental Conditions Setting

Explosion tests were performed using a piezoelectric sensor with a range of 50 psi, and shock wave signals were collected at a sampling rate of 2 MSa/s. Each test duration was 6 s, generating 24 MB of data. However, the key physical characteristics of shock waves are primarily manifested during the millisecond-scale main pulse process, which includes rapid rise time, peak overpressure, and positive pressure duration. To evaluate the dictionary training efficiency and reconstruction performance of the proposed DH-KSVD algorithm within the CS framework, this study extracts 4096 consecutive sampling points containing the complete main pulse process from the original shock wave signal as the analysis unit, corresponding to a time window of 2.048 ms. A total of 150 independent datasets were collected to ensure diversity in explosion distance and environmental conditions. The datasets were divided into 120 training sets and 30 test sets through hierarchical random sampling. The training sets were employed for dictionary learning and algorithm parameter optimization, while the test sets were used to assess the algorithm’s reconstruction performance and generalization ability.

In evaluating the algorithm’s performance, the average iteration time (${\overline{T}}_{iter}$), Compression Ratio ($CR$), Root Mean Square Error ($RMSE$), and Peak Signal-to-Noise Ratio ($PSNR$) were chosen as the evaluation metrics.

${\overline{T}}_{iter}$ is defined as the time required to perform a maximum of 1000 dictionary iteration training steps.

$CR$ is defined as

$$CR={\displaystyle \frac{N-M}{N}}$$

(24)

where N represents the original data volume and M represents the number of measured values obtained by downsampling the original signal using measurement matrix $\mathbf{\Phi }$. A higher CR implies that less data is retained after compression, indicating a greater degree of compression.

$RMSE$ is employed to quantify the degree of difference between the reconstructed signal and the original signal, while $PSNR$ reflects the quality of the reconstructed signal, measured in dB. The higher the $PSNR$, the better the quality of the reconstruction. The definitions are provided as follows:

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{(x_i-{\widehat{x}}_i)}^2}$$

(25)

$$PSNR=10lg\left({\displaystyle \frac{x_{\max }^2}{\frac{1}{N}{\displaystyle \sum _{i=1}^N}{(x_i-{\widehat{x}}_i)}^2}}\right)$$

(26)

where x represents the original signal, $\widehat{x}$ denotes the reconstructed signal, and $x_{\max }$ represents the maximum component of vector x.

All experiments were conducted on a laptop with an 11th Gen Intel(R) Core(TM) i7-1165G7 CPU @ 2.80 GHz, 16 GB RAM, and Windows 10. The code was implemented in Python 3.9 using NumPy 1.21.0, SciPy 1.7.0, and scikit-learn 0.24.2.

4.2. Algorithm Performance Analysis

To comprehensively evaluate the performance of the proposed DH-KSVD algorithm, this study compares it with the DCT, traditional KSVD, and CC-KSVD algorithms [21] under identical experimental conditions. All 150 sets of experimental data underwent the same preprocessing workflow: each set of 4096-point one-dimensional shock wave signals is processed segmentally according to Equation (22), divided into 32 consecutive non-overlapping sub-segments of length 128, forming a training sample matrix of size 128 × 32. This segmentation strategy addresses the highly non-stationary nature of shockwave signals: their amplitude, frequency, and energy undergo drastic changes within extremely short time intervals. Direct sparse modeling of the entire signal segment poses challenges, as a single dictionary struggles to simultaneously capture distinctly different local features such as rising edges, peaks, and decay phases, often resulting in inefficient representation. By segmenting the signal into shorter chunks, local approximations can be made to be stationary. This allows the dictionary to focus on learning recurring key waveform patterns, thereby enhancing the accuracy and learning efficiency of sparse representations.

In addition to standardized data preprocessing, the following key parameters require initial configuration:

The dictionary learning process for all algorithms is terminated upon reaching a maximum of 1000 iterations.

The measurement matrix $\mathbf{\Phi }$ was constructed using a Gaussian random matrix.

The initial dictionary size is set to 128 × 256, meaning the dictionary initially contains 256 atoms. The dictionary’s 128 rows correspond to the signal fragment length, ensuring each atom resides in the same $R^{128}$ space as its signal fragment for direct linear sparse reconstruction. The column count of 256 represents the initial number of atoms, forming an overcomplete dictionary (redundancy ratio of 2:1). Moderately overfitted dictionaries enhance the flexibility and reconstruction accuracy of sparse representations, particularly in dynamic pruning algorithms such as DH-KSVD. A larger initial dictionary provides a rich pool of candidate atoms, facilitating the selection of high-contribution, highly independent atoms to achieve superior sparse models. Conversely, an overly small initial dictionary suffers from insufficient diversity.

The sparsity upper bound $T_0$ was set to 12 in accordance with the fundamental requirement of compressed sensing theory, which stipulates $M\gtrsim C{T}_{0}lgN$ for stable reconstruction. This choice balances the trade-off between representation accuracy and computational efficiency: an excessively small $T_0$ (e.g., <8) compromises the fidelity of the reconstructed signal, while an excessively large $T_0$ (e.g., >16) increases computational complexity and may lead to overfitting.

Additionally, the parameter initialization for the DH-KSVD algorithm is shown in

Table 1. Parameter initialization for the DH-KSVD algorithm.

Hyperparameter	Value	Description
$\tau$	0.25	Base threshold for atom pruning.
$\alpha$	0.1	Controls step size for adjusting $\tau$ based on reconstruction error.
∂	0.6	Weight for usage frequency in contribution score (higher values emphasize frequently used atoms).
$\gamma$	0.2	Balances atom uniqueness in pruning decision; helps avoid removing rare but informative atoms.
$\lambda$	0.01	Automatically adjusted within [0.005, 0.02] based on estimated noise level during training.

.

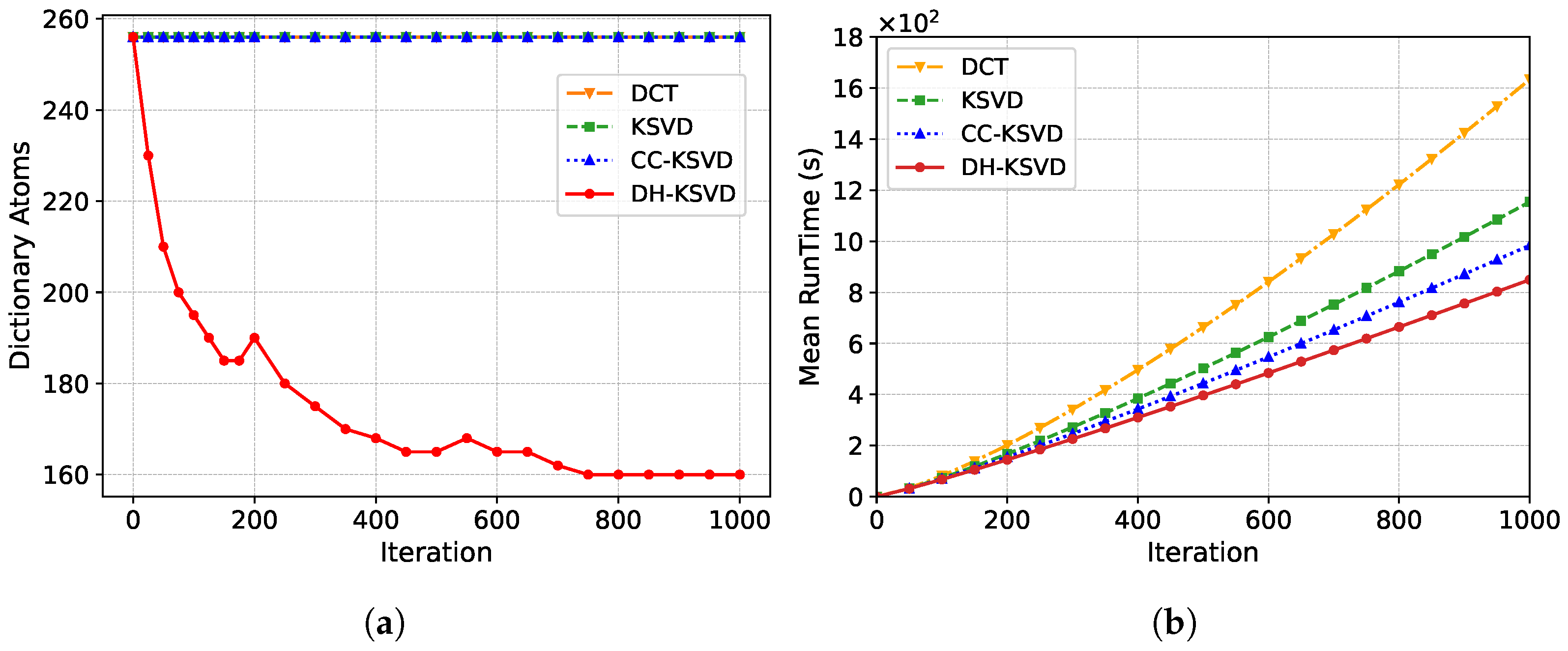
4.2.1. Efficiency Analysis of Training Dictionary

To evaluate the improvement in dictionary training efficiency achieved by the dictionary pruning mechanism, 120 training samples were used in the dictionary learning stage. All algorithms used a uniform initial dictionary size of 128 × 256, $T_0$ is 12, the maximum number of iterations was set to 1000. The experiment was conducted 200 times using Monte Carlo simulation. In each simulation, the initial dictionary $\mathbf{D}$ is randomly initialized from a standard normal distribution. Training samples are selected from the complete dataset via stratified random sampling, comprising 120 signal groups to ensure representative distributions of typical shock waveforms across all categories in each experiment. The average values of all performance indicators were taken as the final results to effectively suppress random deviations arising from initialization and sample selection.

The changes in the number of dictionaries throughout the iteration process are shown in Figure 2a. In the early stages of iteration, the dictionary has not yet fully adapted to the training data, resulting in a large number of ineffective or redundant atoms. At this stage, inefficient atoms are rapidly removed to accelerate the optimization of the dictionary structure. As the iteration progresses, the dictionary gradually approaches the optimal representation, and the pruning intensity is reduced to avoid deleting critical atoms, resulting in a more refined dictionary structure. Ultimately, the dictionary converges, and the number of atoms stabilizes, marking the completion of the optimization process and forming a compact and efficient sparse representation dictionary. Based on the analysis of the change in iteration time with the number of iterations in Figure 2b, compared to the fixed dictionary atom counts of the other three algorithms, the average training time of the DH-KSVD dictionary was reduced by 46.4%, 31%, and 13.7% compared to DCT, KSVD, and CC-KSVD, respectively.

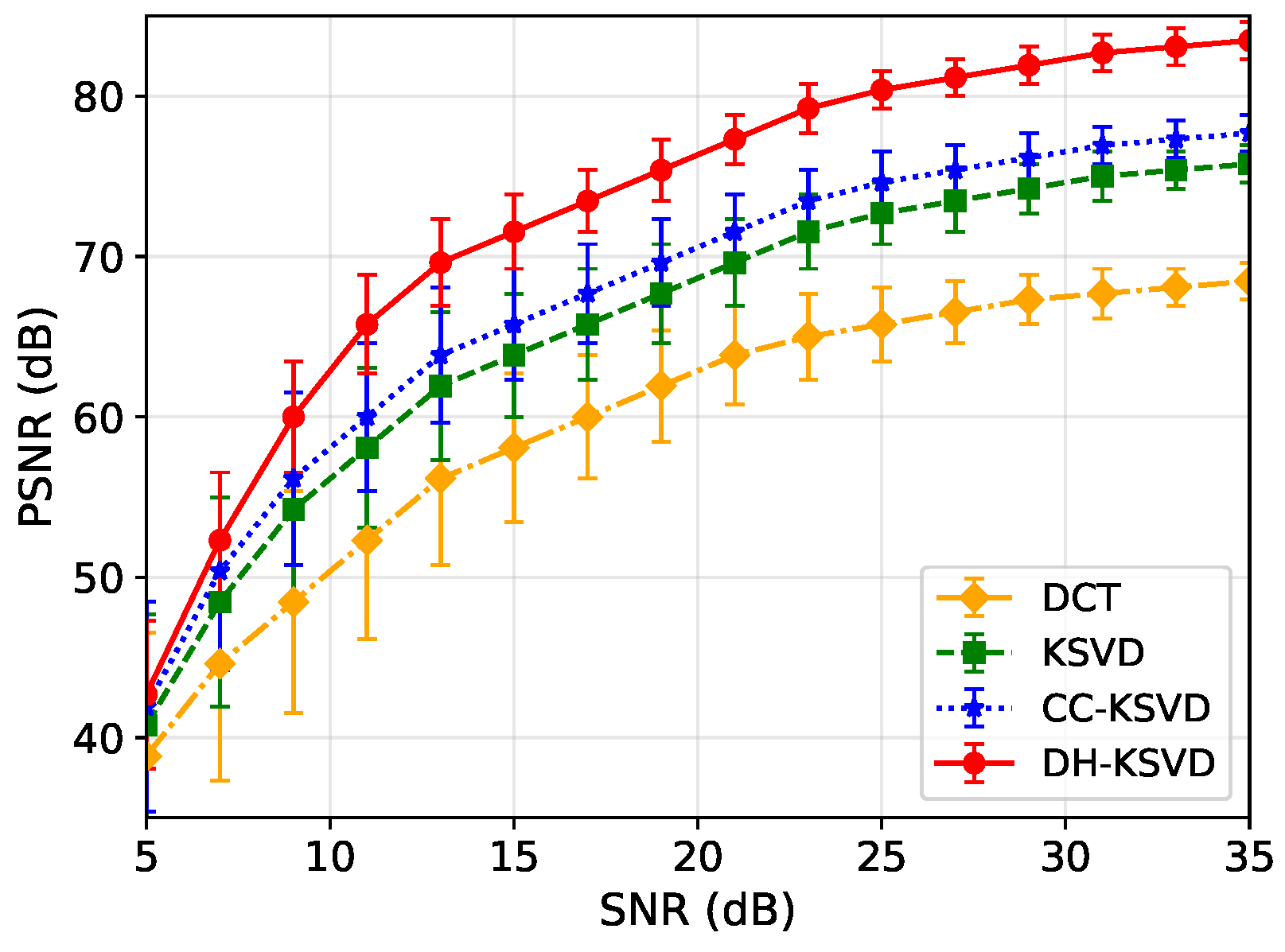
4.2.2. Robustness Analysis of Algorithms

To assess the improvement in robustness of the algorithm in noisy environments under the mixed sparse constraint strategy, signal reconstruction experiments were conducted on 30 test sets with varying Signal-to-Noise Ratios ($SNR$) by adding Additive White Gaussian Noise (AWGN) to each test set at a CR of 0.7. In the experiment, noise was injected after the measurement process, i.e., the observation model was

$$y=\mathbf{\Phi }x+\mathbf{n},\mathbf{n}\sim \mathcal{N}(0,{\sigma }^2\mathbf{I})$$

(27)

where x is the original signal, $\mathbf{\Phi }$ is the measurement matrix, y is the noisy observation vector, and n is independent and identically distributed Gaussian noise. The noise variance ${\sigma }^2$ is adjusted based on the preset $SNR$, defined as the ratio of signal power to noise power in the measurement vector, i.e.,

$$SNR=10{log}_{10}\left({\displaystyle \frac{{\parallel \mathbf{\Phi }x\parallel }^2}{{\parallel \mathbf{n}\parallel }^2}}\right).$$

(28)

This setting ensures comparability of performance across different noise levels and aligns with the physical context of real-world systems where noise primarily originates from measurement equipment or transmission channels. For each experimental group, the $PSNR$ of reconstruction results is computed and averaged based on 200 independent Monte Carlo trials (each including a randomly generated measurement matrix $\mathbf{\Phi }$ and independent noise realizations) to enhance statistical reliability.

As shown in Figure 3, the average $PSNR$ of all algorithms increased with increasing $SNR$, indicating that lower noise levels contribute to enhanced reconstruction quality. Meanwhile, the error bars in the figure represent ±1 standard deviation, reflecting fluctuations in reconstruction performance. It can be observed that in the low-$SNR$ region, i.e., high-noise environments, the DH-KSVD algorithm not only achieves a significantly higher average PSNR than the other three algorithms but also exhibits shorter error bars, indicating lower performance variability and stronger noise resistance. Specifically, when $SNR$ ranges from 5 to 10 dB, the average $PSNR$ of DH-KSVD is 3 to 11 dB higher than that of the traditional KSVD algorithm, thereby fully validating its superior performance in reconstructing noisy signals.

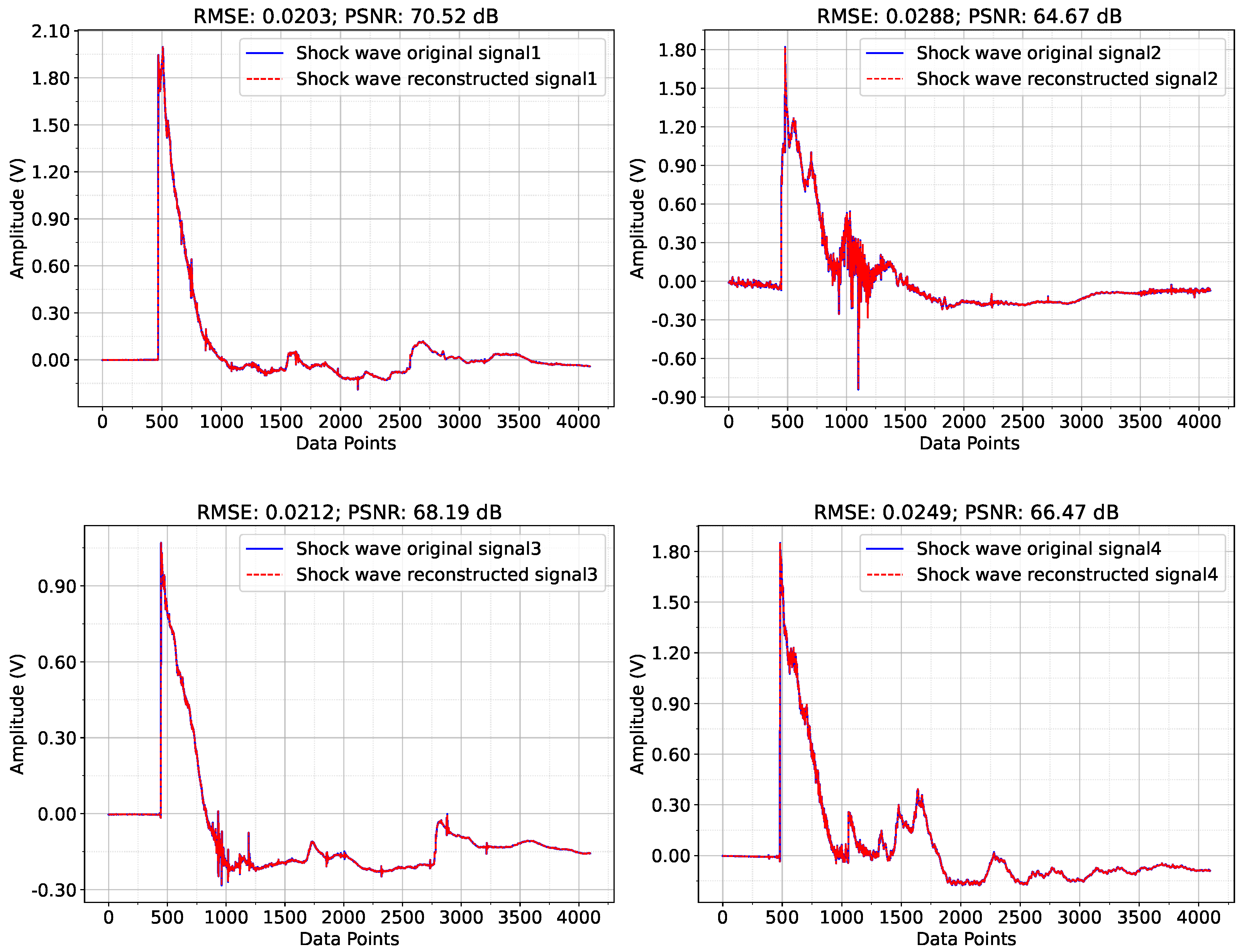
4.2.3. Performance Analysis of CS Reconstruction Algorithm

To validate the reconstruction performance of the proposed DH-KSVD algorithm within the CS framework, this study systematically evaluates its performance across different $CR$s and compares it with the DCT, traditional KSVD, and CC-KSVD algorithms, as depicted in Figure 4. $CR$ is progressively increased from 0.1 to 0.9. For each $CR$, 200 independent samples and reconstructions are performed on 30 independent test set signals using a random Gaussian observation matrix. The random Gaussian measurement matrix $\mathbf{\Phi }\in {\mathbb{R}}^{M\times N}$ has elements following a $\mathcal{N}\left(0,1/M\right)$ distribution. Each Monte Carlo trial employs a brand-new, independently sampled measurement matrix. The test set signals are selected from the complete dataset via stratified random sampling, comprising 30 signal groups. The final performance metrics are the average of all repeated experiments to reduce the impact of randomness. The evaluation metrics include $RMSE$ and $PSNR$, where a lower $RMSE$ and higher $PSNR$ indicate better reconstruction accuracy.

The results from different $CR$s show that the $RMSE$ of DH-KSVD is lower than that of DCT, KSVD, and CC-KSVD, while the $PSNR$ is higher than the other three categories, confirming the effectiveness of the proposed algorithm. The results indicate that the DH-KSVD algorithm maintains a low $RMSE$ and high $PSNR$ regardless of whether the CR is low or high. Specifically, at a CR of 0.7, the $RMSE$ of the DH-KSVD algorithm is reduced by approximately 67.1%, 65.7%, and 36.2% compared to DCT, KSVD, and CC-KSVD, respectively, while the $PSNR$ is improved by 35.5%, 39.8%, and 11.8%, respectively. These quantitative metrics confirm the proposed algorithm’s advantages in the efficient compression and reconstruction of shock wave signals and its potential for application within the CS framework.

Figure 5, shows the reconstruction results of four randomly selected signals from the test set under a CR of 0.7. As shown in the figure, the reconstruction errors of the four signal groups are all relatively low, with $RMSE$ values ranging from 0.0203 to 0.0288 and $PSNR$ values exceeding 64 dB for all cases. This indicates that the DH-KSVD algorithm achieves good reconstruction accuracy, high signal fidelity, and low error under a $CR$ of 0.7.

4.3. Ablation Experiment

To demonstrate the effectiveness of each improvement module, ablation experiments were conducted in this study. The proposed DH-KSVD integrates two key components: (i) a Dynamic Dictionary Pruning mechanism (D) that adaptively removes redundant atoms during dictionary learning to enhance compactness and training efficiency; and (ii) a Hybrid Sparse Coding strategy (H) that combines ${\ell }_0$-OMP and ${\ell }_1$-LASSO to improve coding robustness and reconstruction accuracy. For the ablation analysis, KSVD-A incorporates only the D module into the standard KSVD framework, retaining the conventional ${\ell }_0$-OMP sparse coding while enabling dynamic dictionary pruning. This variant evaluates the impact of dictionary compactness on training efficiency. KSVD-B integrates only the H module, replacing the single ${\ell }_0$-OMP coding with the hybrid ${\ell }_0$-OMP + ${\ell }_1$-LASSO strategy, but without applying dictionary pruning. This allows us to assess the contribution of enhanced sparse coding to reconstruction performance. DH-KSVD combines both D and H modules, representing the full proposed algorithm.

In the KSVD-A algorithm, the pruning threshold $\tau$ is initialized to 0.05 and subsequently updated adaptively via Equation (12). In KSVD-B, the regularization parameter $\lambda$ is initialized to 0.01 and adjusted adaptively based on the residual norm of each iteration using Equation (21).

Table 2. Ablation experiments of each improved module in DH-KSVD (CR = 0.7).

Model	D	H	${\overline{\mathit{T}}}_{\mathbf{iter}}$ (s)	RMSE	PSNR (dB)
KSVD	✕	✕	$11.71\times {10}^2\pm 8.5$	$0.0802\pm 0.0015$	$42.79\pm 0.32$
KSVD-A	✓	✕	$8.26\times {10}^2\pm 4.2$	$0.0790\pm 0.0012$	$45.88\pm 0.28$
KSVD-B	✕	✓	$12.24\times {10}^2\pm 6.8$	$0.0289\pm 0.0008$	$60.90\pm 0.15$
DH-KSVD	✓	✓	$8.20\times {10}^2\pm 3.9$	$0.0228\pm 0.0008$	$61.87\pm 0.12$

shows the ablation experiment results of DH-KSVD, indicating that gradually introducing the improved module can significantly improve dictionary training efficiency and compression reconstruction performance, where ✕ denotes the module is disabled and ✓ denotes it is enabled. After incorporating the dictionary pruning mechanism into KSVD-A, the dictionary training time was significantly reduced, decreasing by approximately 30% compared to traditional KSVD. Moreover, the standard deviation of timing decreased from ±8.5 s to ±4.2 s, with a significantly reduced fluctuation range. This not only demonstrates that the dynamic pruning mechanism effectively reduces redundant atoms and enhances the compactness of the dictionary, but also reflects that this strategy enhances the stability of the training process. This indicates that the dynamic pruning mechanism effectively enhances the compactness and training efficiency of the dictionary. KSVD-B significantly improves reconstruction quality by adopting a hybrid sparse coding strategy, with a substantial reduction in $RMSE$ and a significant increase in $PSNR$. However, training time increases slightly, and the standard deviation is marginally higher than KSVD. This is due to the fact that the hybrid coding strategy demands additional computational resources during optimization to balance sparsity and robustness, resulting in slightly greater fluctuations in runtime. When the two improved modules were combined in DH-KSVD, the dictionary training time was reduced by 31% compared to traditional KSVD, $RMSE$ decreased by 65.7%, and $PSNR$ improved by 39.8%. Moreover, the smallest standard deviation in time indicates that the pruning mechanism effectively suppresses computational fluctuations. The $RMSE$ standard deviation is only ±0.0008, demonstrating exceptionally high reconstruction stability. The $PSNR$ standard deviation of ±0.12 dB is the best among all models, indicating not only high reconstruction quality but also high reproducibility. This comprehensively validates the effectiveness of the modules working in tandem to both enhance dictionary training efficiency and achieve high-quality signal reconstruction within the CS framework.

5. Discussion

The proposed DH-KSVD algorithm significantly enhances dictionary training efficiency and signal reconstruction accuracy when compressing shock wave data within the CS framework. The integration of a dynamic pruning mechanism with a hybrid sparse coding strategy effectively addresses key limitations of traditional KSVD algorithms. The following sections explore the implications, limitations, and potential future directions revealed by this research.

Implications of the proposed method:

• Enhanced efficiency and practicality for transient signal compression: the core of the DH-KSVD algorithm lies in its “offline training, online compression” paradigm. The dictionary learning process itself is computationally intensive and performed offline, while the resulting highly compact and expressive dictionary enables efficient online compression on resource-constrained edge devices. This design makes the method particularly suitable for practical applications such as destructive testing at sea, where megahertz-level sampling generates massive data volumes but transmission bandwidth and storage space are extremely limited. Compared to the KSVD algorithm, dictionary training time is significantly reduced (by 31%), while maintaining excellent reconstruction quality even at high compression ratios. This directly enhances the feasibility of long-term, multi-channel shock wave monitoring.
• Robustness in noisy environments: the hybrid sparse constraint strategy combines the precise atom selection of ${\ell }_0$-OMP with the noise-resistant coefficient optimization of ${\ell }_1$-LASSO, endowing the DH-KSVD algorithm with enhanced resistance to noise interference. Experimental results confirm that the DH-KSVD algorithm consistently achieves higher $PSNR$ values compared to various benchmark algorithms, demonstrating particularly outstanding performance in low-$SNR$ scenarios. This robustness is crucial for shock wave measurements, which are frequently impacted by environmental and system noise contamination.

Limitations and future research:

• The performance comparisons in this work are conducted within the traditional sparse representation framework. A valuable future direction is to benchmark DH-KSVD against modern reconstruction paradigms, such as reweighted-${\ell }_1$ or deep-learning-based methods, to further validate its generalization capability and robustness across diverse signal conditions.
• The current version of the DH-KSVD algorithm is designed to handle additive noise but does not explicitly address the challenge of missing samples or structurally corrupted data, which is a common issue in harsh acquisition environments. Future work will therefore focus on enhancing the framework’s resilience to such forms of data imperfection. Promising research directions include the integration of robust regression techniques capable of decomposing a signal into clean and sparse error components, as well as the development of preprocessing strategies based on data imputation or inpainting to effectively compensate for packet loss or sensor failures.
• Although the online compression stage is designed for efficient operation, further optimization is needed to achieve real-time processing on low-power embedded platforms. Future work will focus on the co-design of algorithms and hardware, exploring strategies such as dictionary quantization and fixed-point computation implementation. This approach will maximize the algorithm’s practical value in extreme edge computing scenarios.
• The values of hyperparameters and were determined through systematic analysis on an independent validation set. Although the proposed thresholding method has demonstrated effectiveness in the current task, optimal threshold selection remains a challenging and highly context-dependent problem. Future research will explore and integrate adaptive thresholding techniques from other signal processing domains. For instance, threshold determination for RD-HR maps in High-Frequency Surface Wave Radar systems presents a similar challenge, where recent data-driven strategies including geometry-based and experimentally derived adaptive algorithms [25,26] offer promising extensions to the current framework. Incorporating such approaches is expected to enhance the method’s robustness, automation capability, and applicability across diverse scenarios.

6. Conclusions

This study proposes a DH-KSVD algorithm that incorporates dynamic pruning and hybrid coding to address the challenges of low dictionary training efficiency and poor signal reconstruction quality in traditional methods within the CS framework. By introducing a dynamic pruning mechanism to optimize the dictionary structure, the algorithm significantly enhances computational efficiency while improving the compactness of the dictionary. Additionally, a hybrid sparse constraint strategy, combining the advantages of ${\ell }_0$-OMP and ${\ell }_1$-LASSO, is employed to improve coding quality and enhance reconstruction stability. Experimental results show that the average dictionary training time of DH-KSVD is significantly shorter than that of DCT, KSVD, and CC-KSVD, and it can significantly reduce $RMSE$ and improve $PSNR$ under high $CR$s. Furthermore, ablation experiments further validate the effectiveness of each improved module, demonstrating that the dynamic pruning mechanism and hybrid sparse coding strategy are crucial for enhancing the overall algorithm performance. Overall, the DH-KSVD algorithm demonstrates outstanding performance in both computational efficiency and reconstruction quality, particularly exhibiting stronger robustness and higher reconstruction accuracy when processing noisy signals. This provides an efficient and reliable solution for the data compression of shock wave signals, offering significant practical application value.