Experimental Study and Engineering Application of Concrete-Encased Reinforcement for Mine Pillars
Abstract
1. Introduction
2. Experimental Plan
2.1. Preparation of the Test Samples
2.2. Testing Method for the Test Samples
3. Results of the Uniaxial Compression Tests on the Test Samples
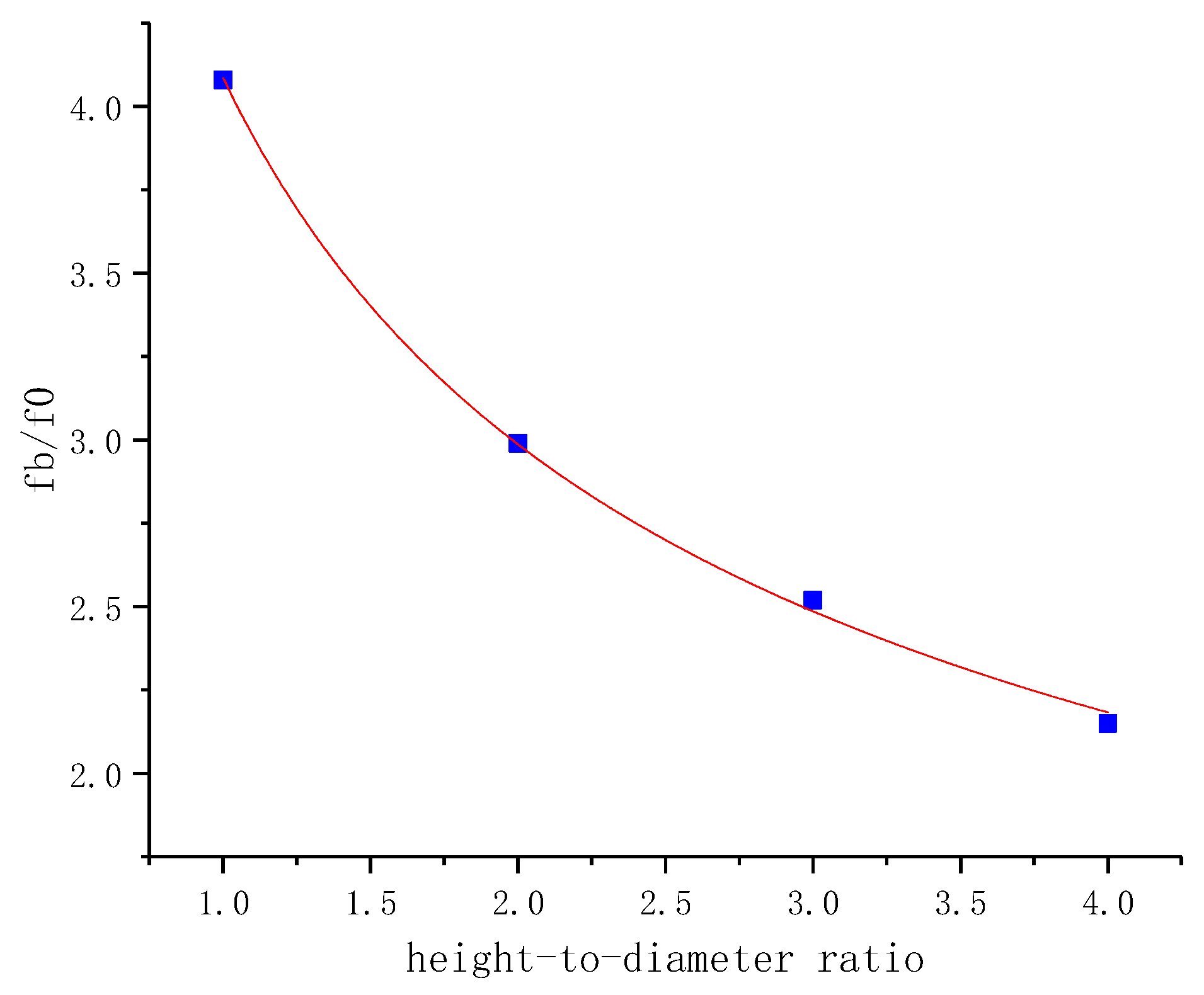
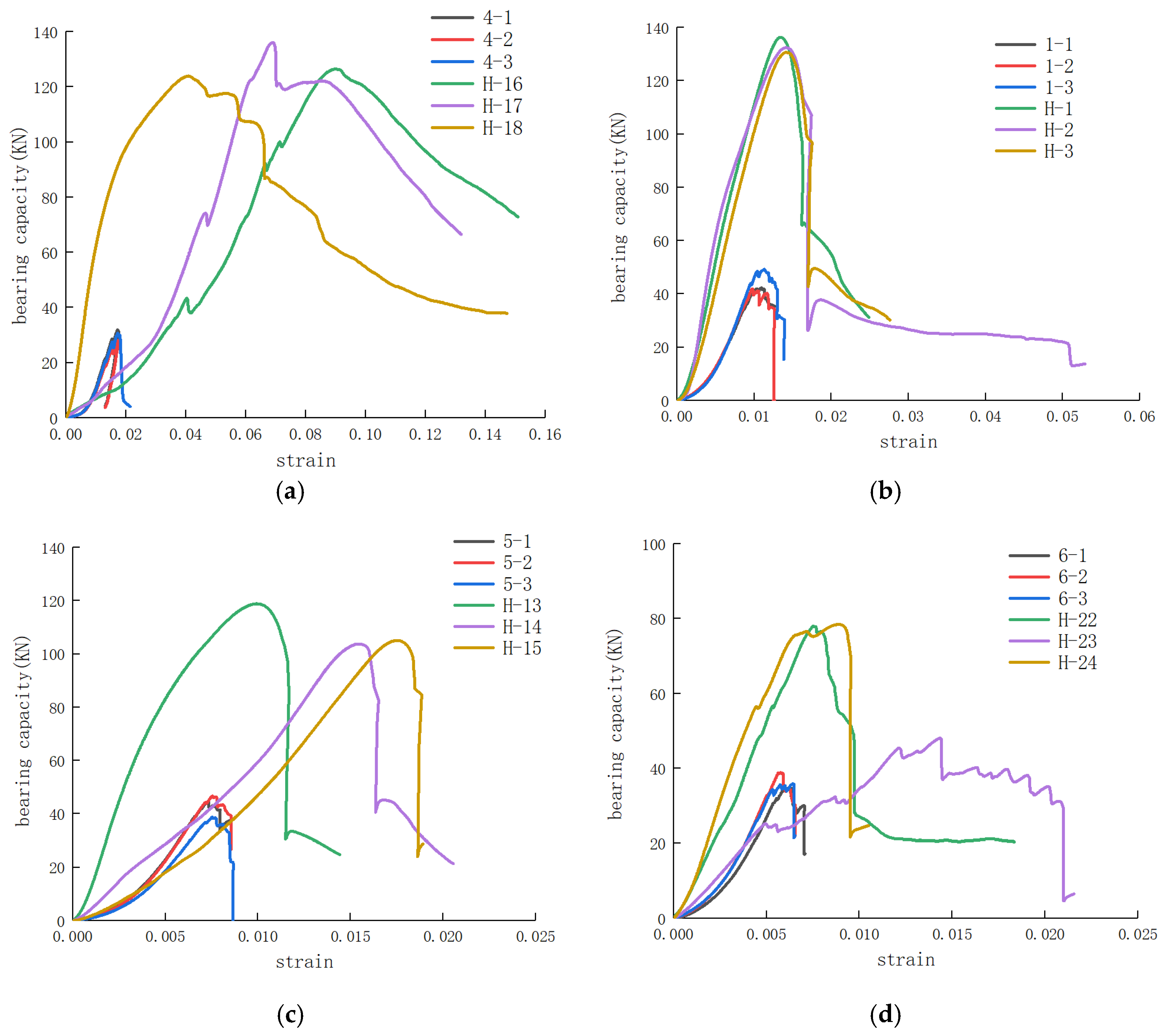
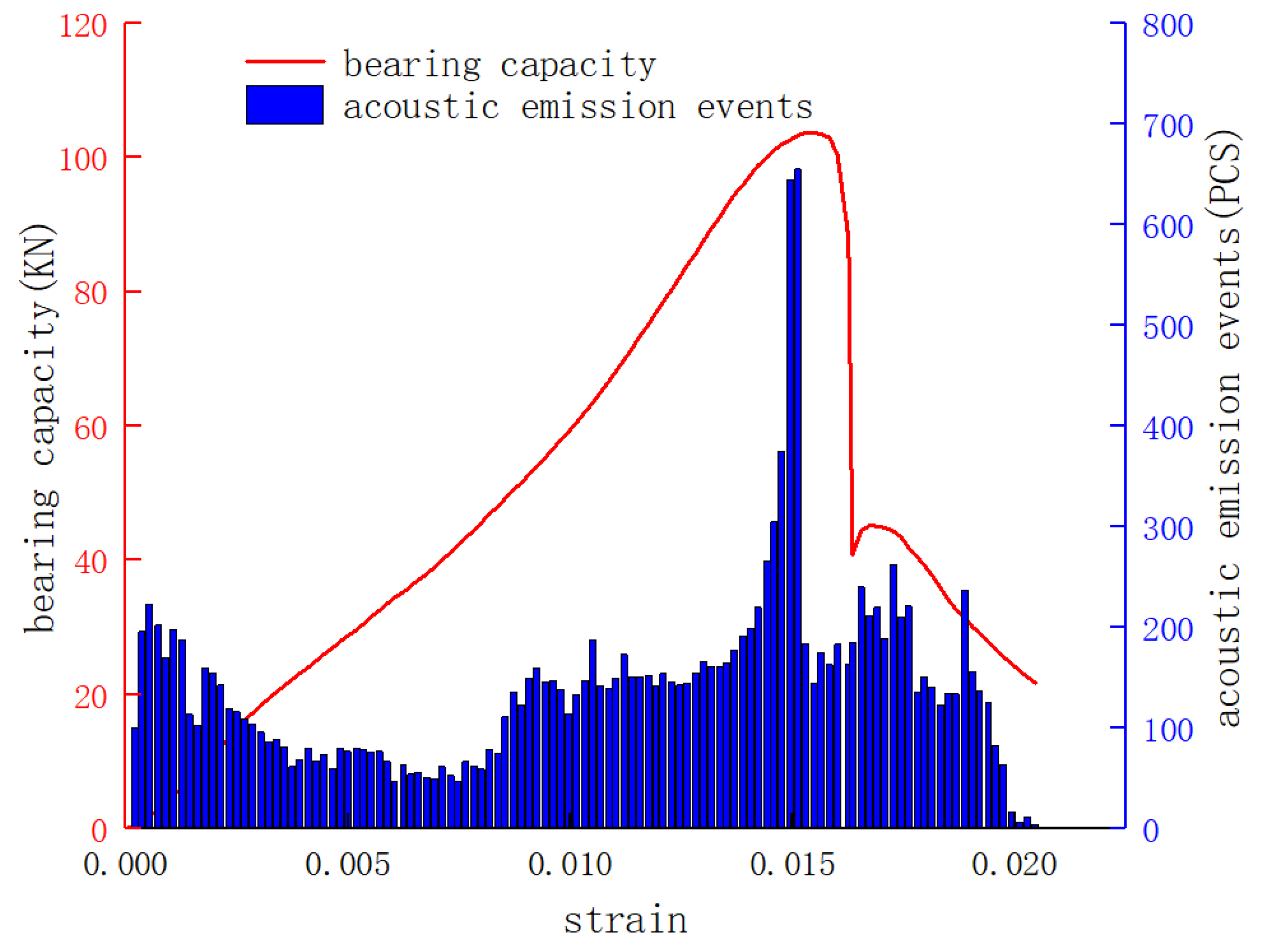
3.1. Uniaxial Compression Tests on Test Samples of Different Sizes
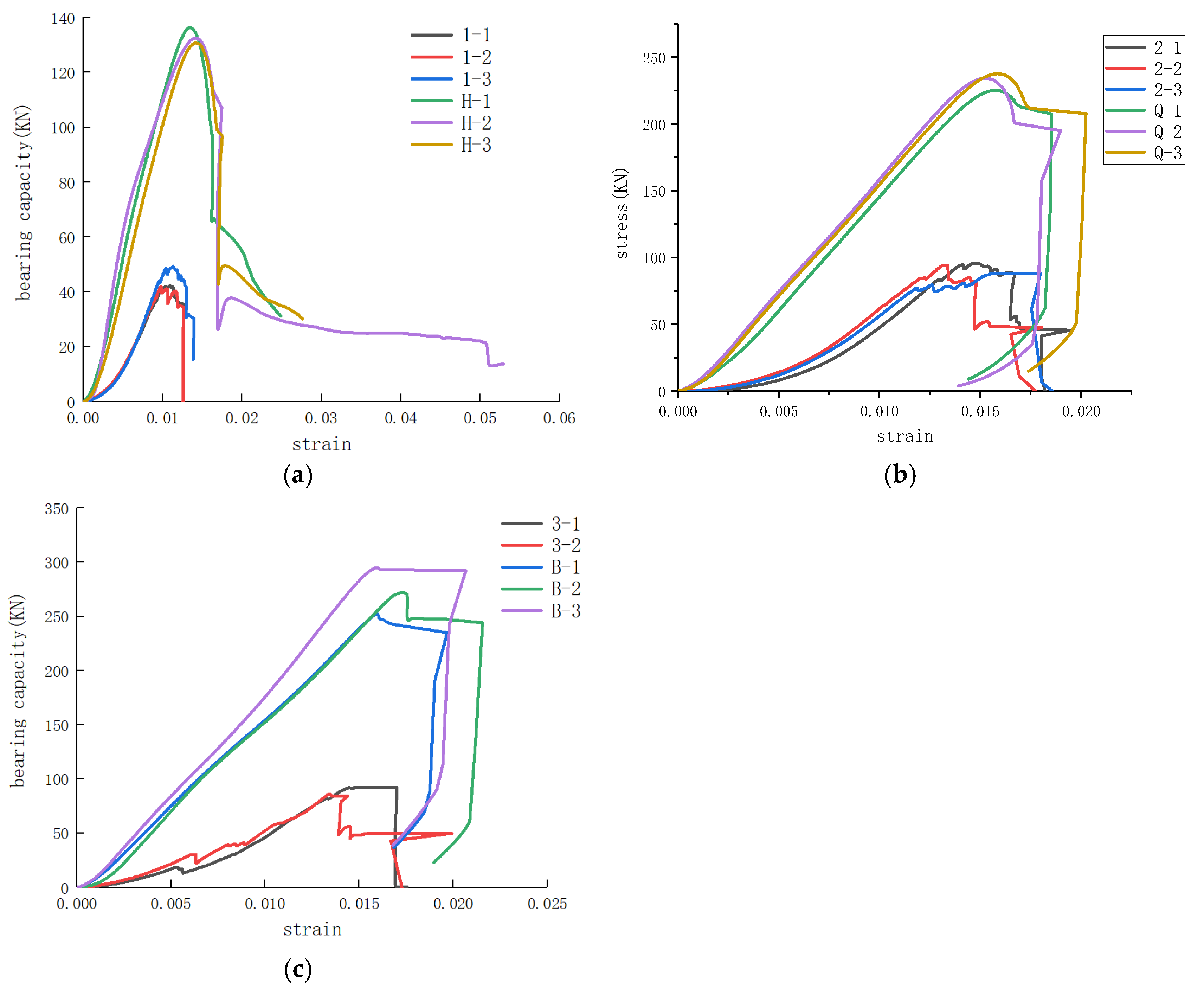
3.2. Uniaxial Compression Tests on Rock Specimens with Different Strengths
| Rock Sample | Rock Type | (kN) | (kN) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| H-1 | red sandstone | 44.49 | 0.0107 | 136.31 | 0.0135 | 3.06 | 2.99 | 1.26 | 1.32 |
| H-2 | red sandstone | 44.49 | 0.0107 | 132.41 | 0.0147 | 2.98 | 1.37 | ||
| H-3 | red sandstone | 44.49 | 0.0107 | 130.74 | 0.0141 | 2.94 | 1.32 | ||
| Q-1 | green sandstone | 92.79 | 0.0145 | 225.28 | 0.0200 | 2.43 | 2.50 | 1.38 | 1.18 |
| Q-2 | green sandstone | 92.79 | 0.0145 | 234.18 | 0.0155 | 2.52 | 1.07 | ||
| Q-3 | green sandstone | 92.79 | 0.0145 | 237.54 | 0.0159 | 2.56 | 1.10 | ||
| B-1 | white sandstone | 118.03 | 0.0151 | 252.30 | 0.0160 | 2.14 | 2.32 | 1.06 | 1.18 |
| B-2 | white sandstone | 118.03 | 0.0151 | 272.12 | 0.0214 | 2.31 | 1.42 | ||
| B-3 | white sandstone | 118.03 | 0.0151 | 294.59 | 0.0159 | 2.50 | 1.05 | ||
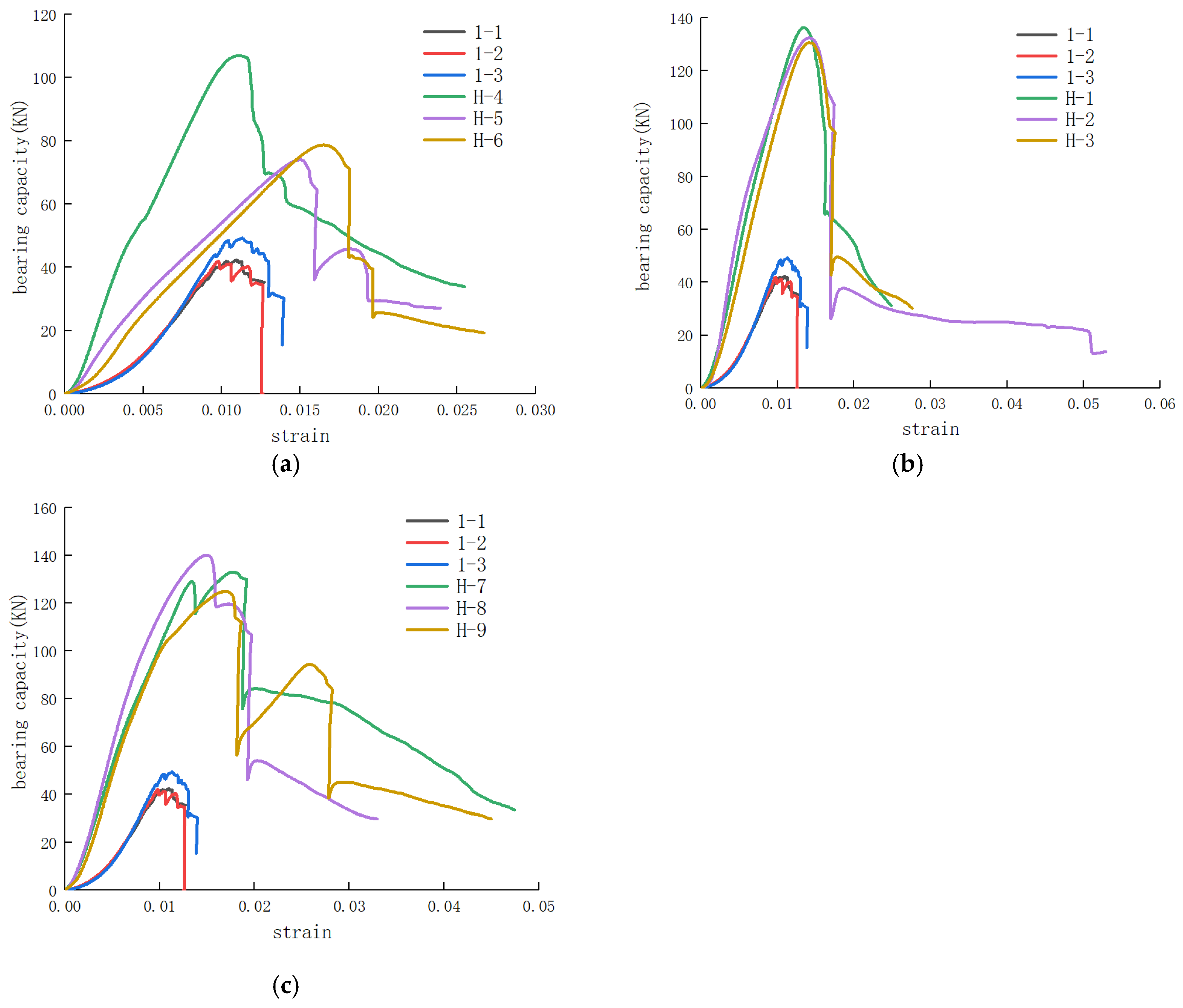
3.3. Uniaxial Compression Tests on Samples with Different Encasing Materials
| Rock Sample | Encasing Material | (KN) | (KN) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| H-4 | M5 mortar | 44.49 | 0.0107 | 106.87 | 0.0111 | 2.40 | 1.94 | 1.04 | 1.33 |
| H-5 | M5 mortar | 44.49 | 0.0107 | 74.00 | 0.0149 | 1.66 | 1.39 | ||
| H-6 | M5 mortar | 44.49 | 0.0107 | 78.71 | 0.0166 | 1.77 | 1.55 | ||
| H-1 | M10 mortar | 44.49 | 0.0107 | 136.31 | 0.0135 | 3.06 | 2.99 | 1.26 | 1.32 |
| H-2 | M10 mortar | 44.49 | 0.0107 | 132.41 | 0.0147 | 2.98 | 1.37 | ||
| H-3 | M10 mortar | 44.49 | 0.0107 | 130.74 | 0.0141 | 2.94 | 1.32 | ||
| H-7 | M10 reinforced mortar | 44.49 | 0.0107 | 133.02 | 0.0177 | 2.99 | 2.98 | 1.65 | 1.54 |
| H-8 | M10 reinforced mortar | 44.49 | 0.0107 | 140.07 | 0.0150 | 3.15 | 1.40 | ||
| H-9 | M10 reinforced mortar | 44.49 | 0.0107 | 124.89 | 0.0168 | 2.81 | 1.57 | ||
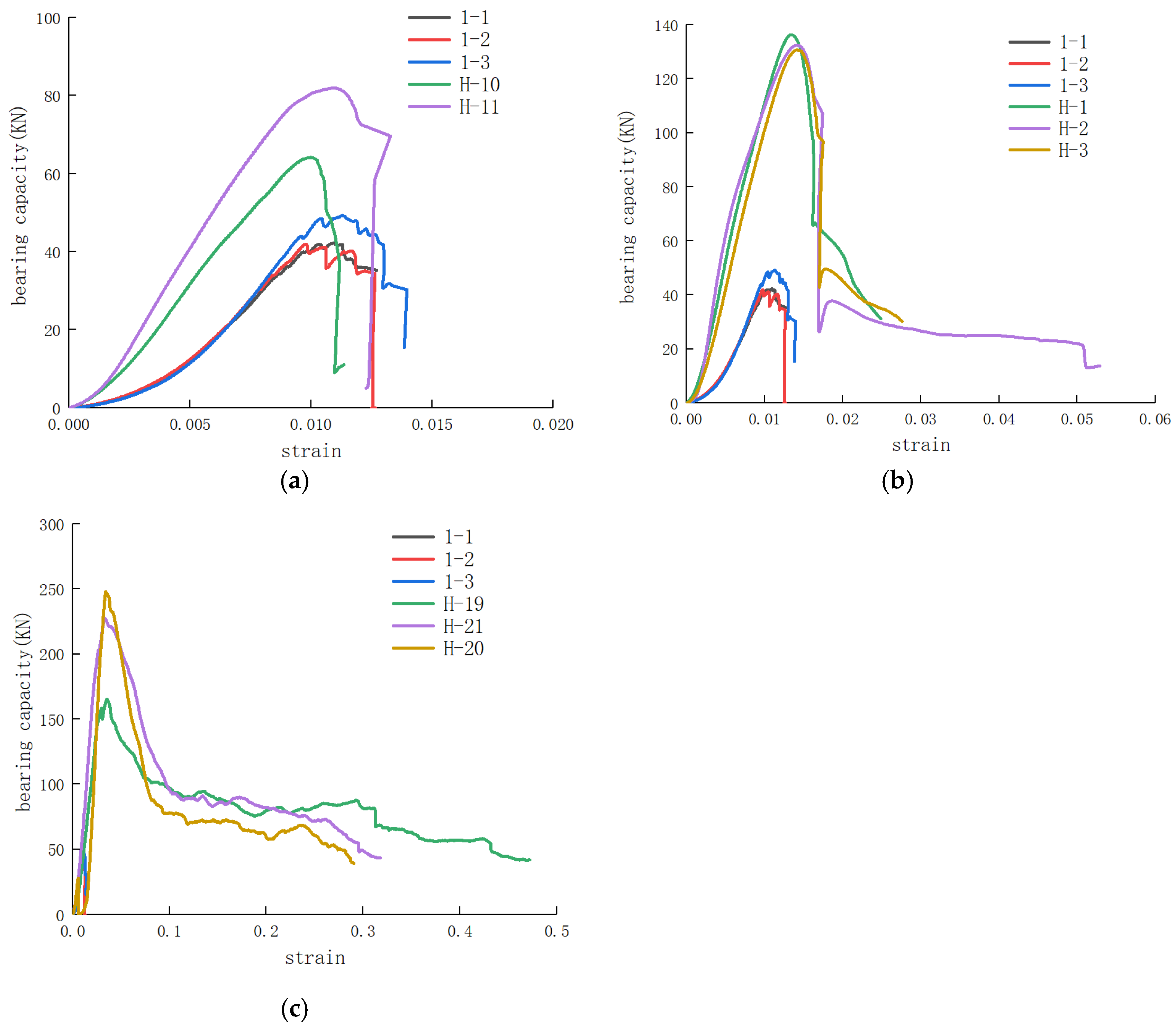
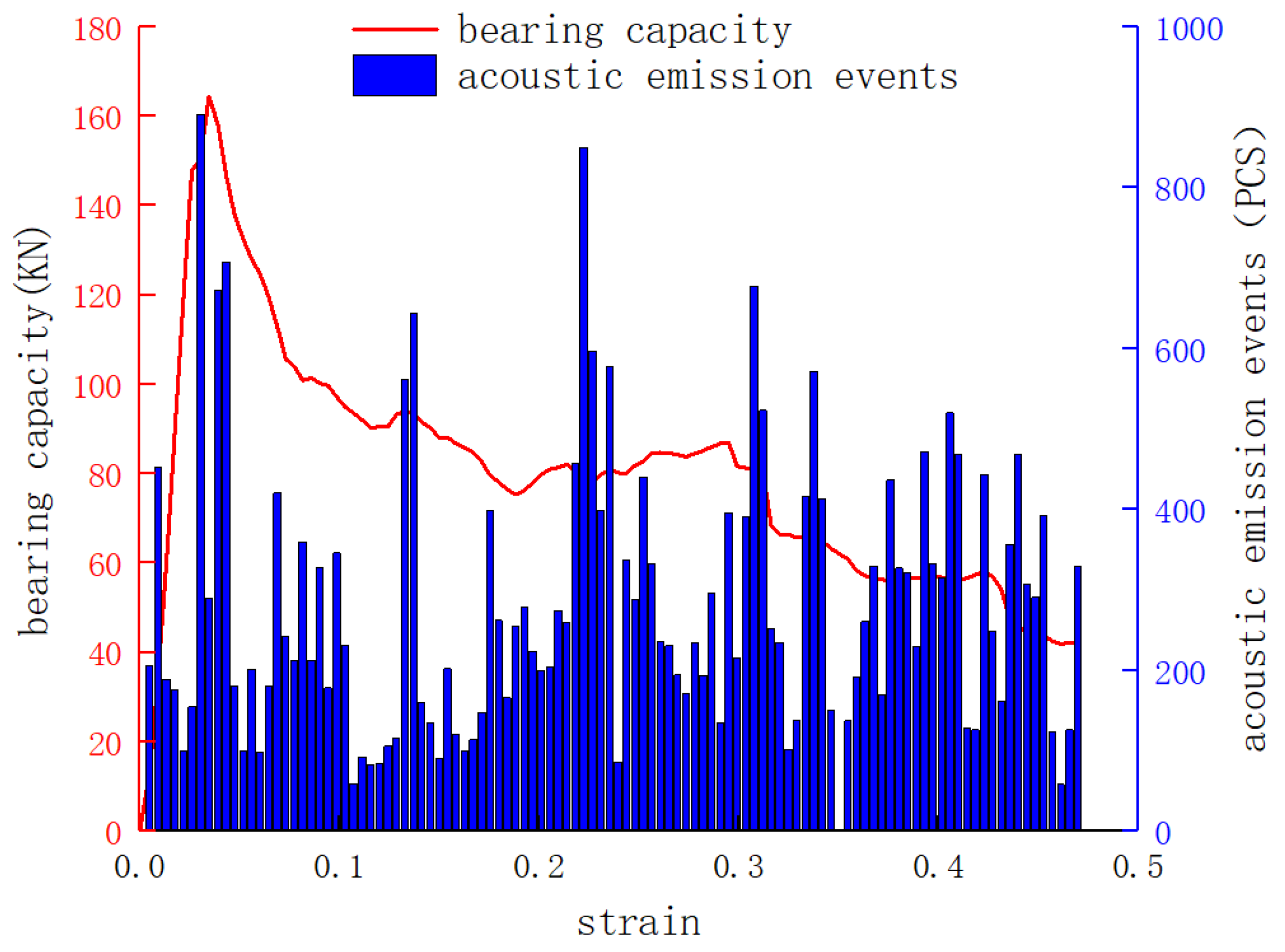
3.4. Uniaxial Compression Tests on Samples with Different Encasing Thicknesses
4. Analysis of the Deformation and Failure Characteristics of the Samples and the Reinforcement Mechanism
4.1. Analysis of the Sample Deformation and Failure Characteristics
4.1.1. Failure Modes of Rock Specimens of Different Sizes
4.1.2. Failure Modes of Rock Specimens with Different Strengths
4.1.3. Failure Modes of Specimens with Different Encasing Materials
4.1.4. Failure Modes of Specimens with Different Encasing Thicknesses
4.2. Sensitivity Analysis of Influencing Factors of Reinforcement Effect
4.3. Analysis of the Reinforcement Mechanism for the Encased Test Specimens
5. Engineering Application
6. Conclusions
- (1)
- Mortar encapsulation significantly enhances the bearing capacity and axial peak strain of rock specimens. Specimens with smaller height-to-diameter ratios demonstrate more substantial bearing capacity improvement, indicating better reinforcement effectiveness. The bearing capacity enhancement ratio follows a power function relationship with the height-to-diameter ratio. Rocks with lower strength exhibit greater bearing capacity improvement after encapsulation, resulting in superior reinforcement effect. Both increased encapsulation material strength and greater encapsulation thickness lead to notable improvement in bearing capacity and enhanced reinforcement effectiveness.
- (2)
- Orthogonal range analysis was employed to evaluate the sensitivity of four influencing factors: rock size, rock strength, encapsulation material, and encapsulation thickness. The results indicate that the primary-to-secondary order of factors affecting the reinforcement effectiveness is encapsulation thickness > rock height-to-diameter ratio > encapsulation material > rock strength.
- (3)
- Compared to unwrapped specimens, encapsulated rock specimens transition from overall failure to fragmentation failure modes. The encapsulated specimens absorb more external energy and demonstrate significantly improved load-bearing capacity. With increasing encapsulation strength and thickness, the specimens exhibit tendencies toward plastic deformation failure. The mortar-encapsulated rock specimen can be considered as a parallel composite structure of rock and mortar layers. This composite system not only gains additional load-bearing capacity from the mortar layer but also shows substantially enhanced inherent load-bearing capacity of the rock itself due to the confining pressure provided by the encapsulation. The inherent load-bearing capacity of the rock specimen increases significantly with both the strength and thickness of the encapsulation material.
- (4)
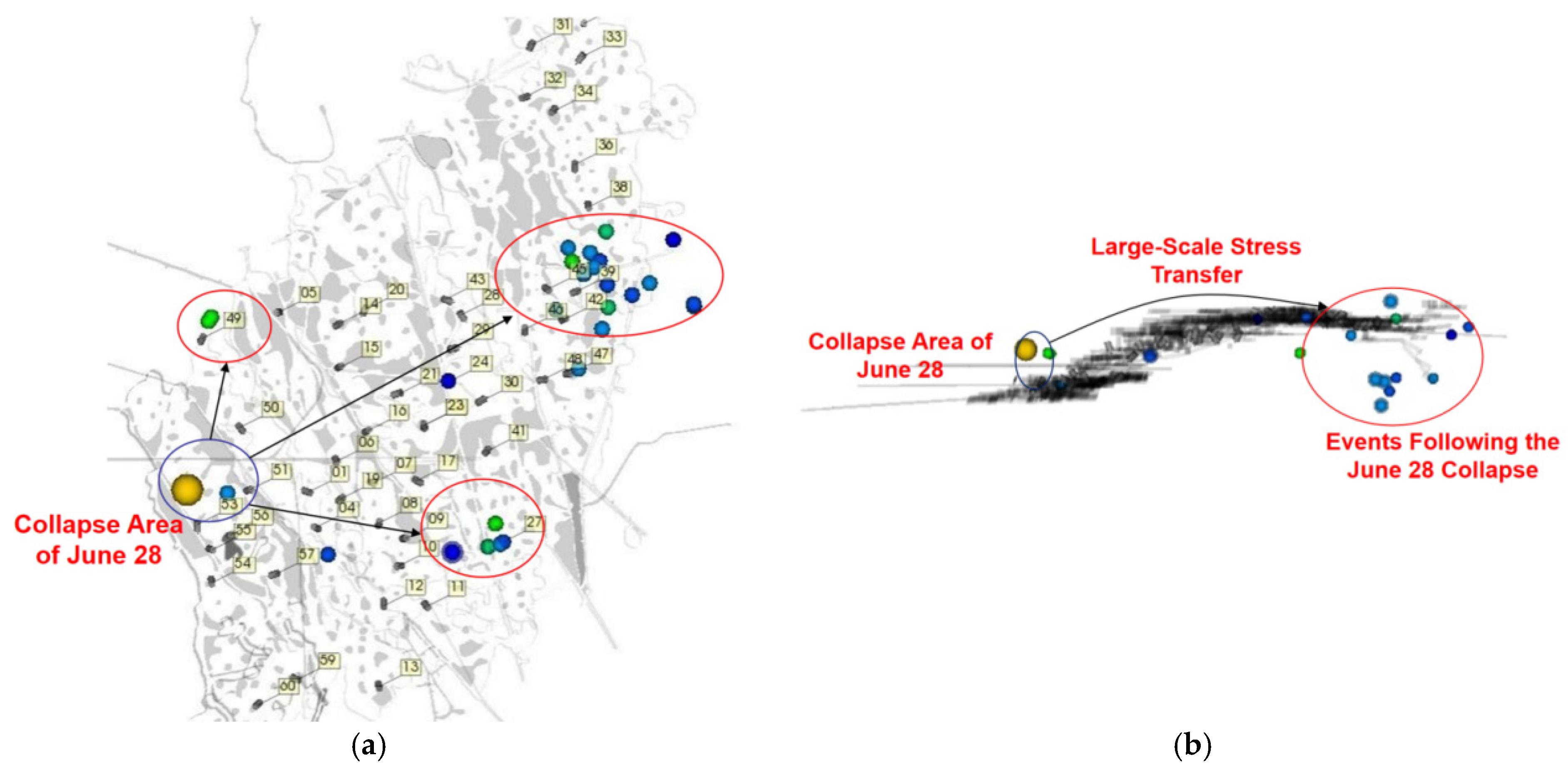
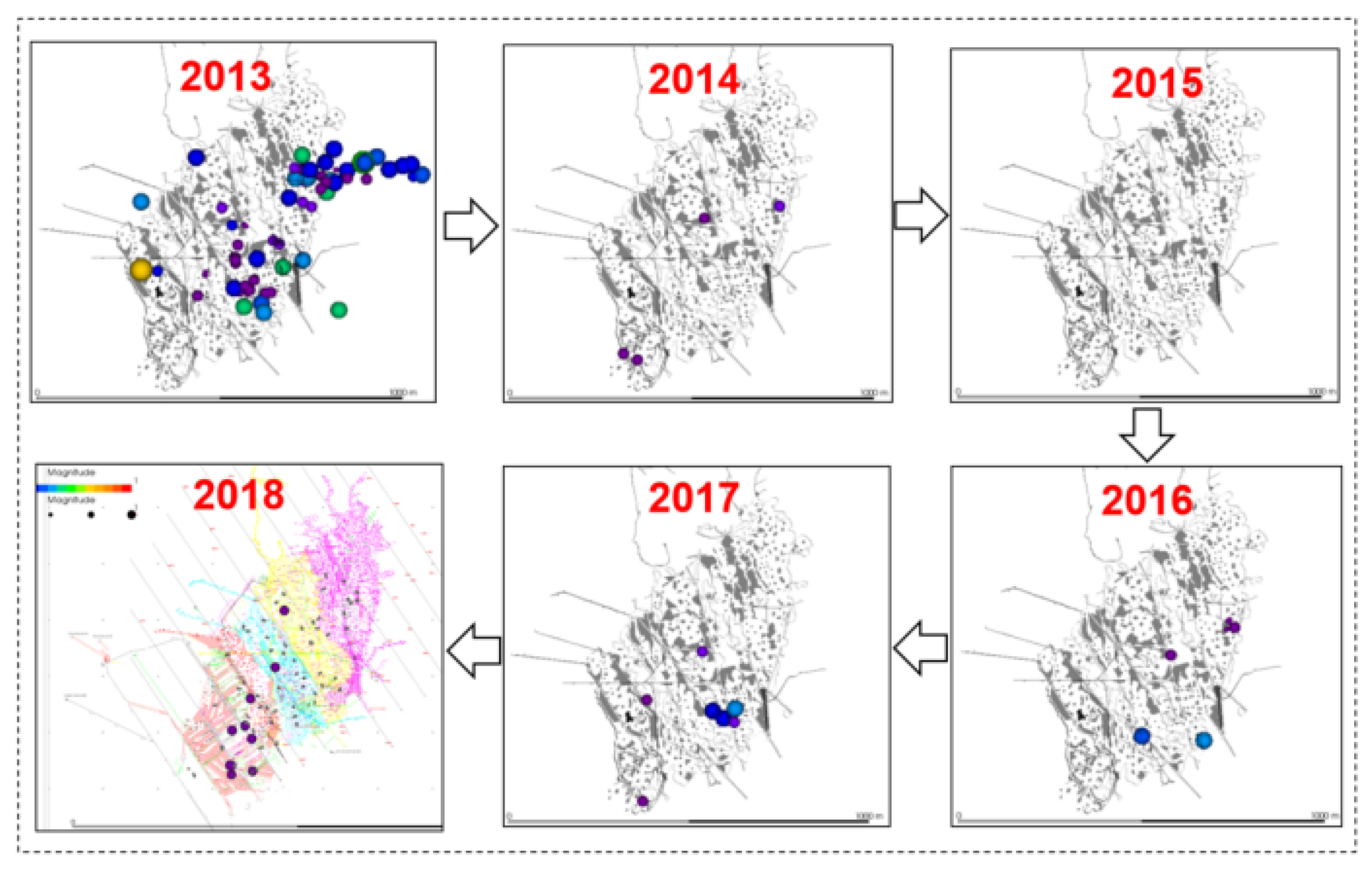
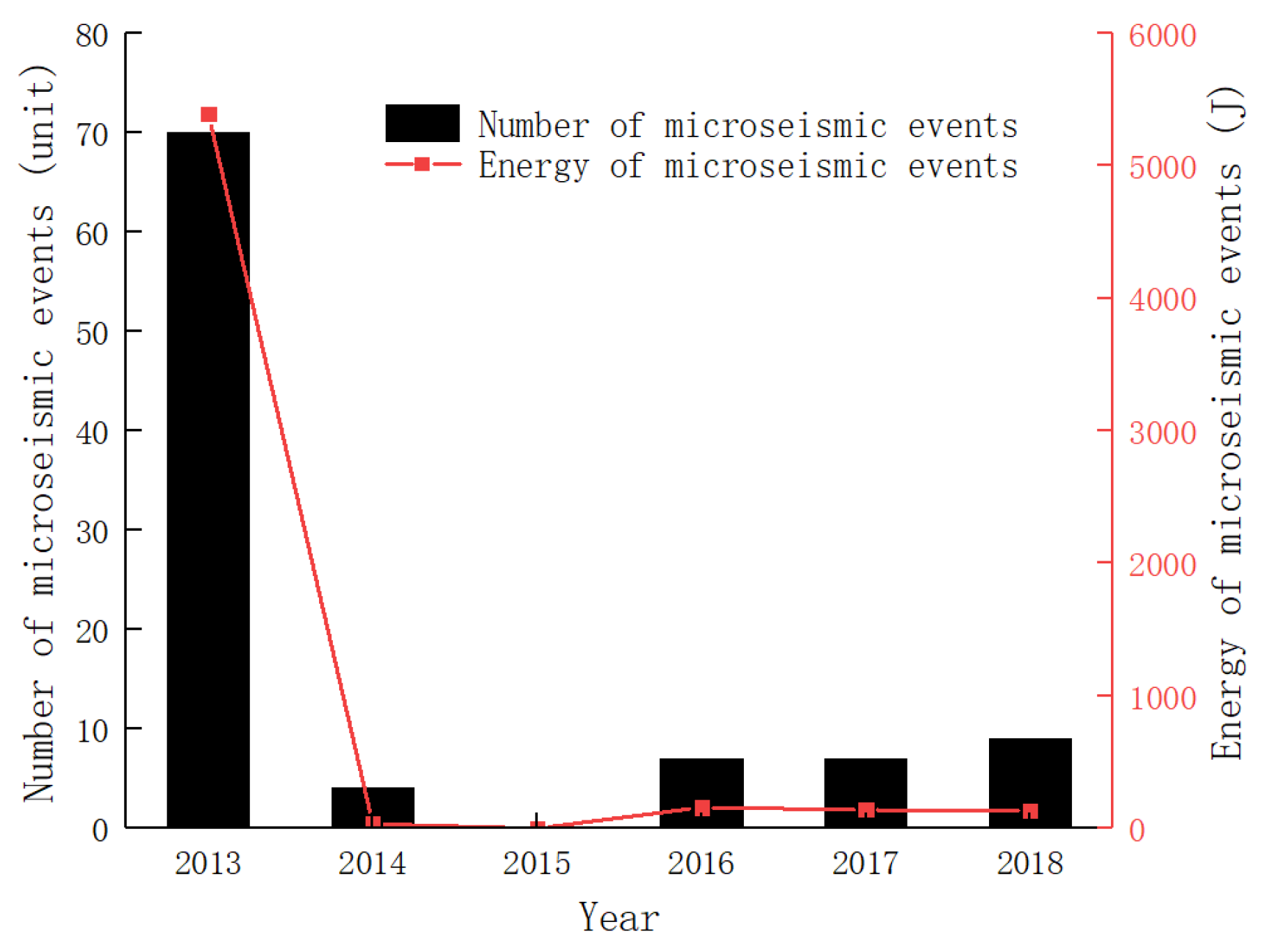
- Field application involved reinforcing 42 critical pillars in a tungsten mine using C25 reinforced concrete encapsulation with a minimum thickness of 3 m. Following the completion of pillar reinforcement in key areas, the underground microseismic activity decreased markedly without further large-scale ground pressure manifestations. The overall underground ground pressure has been effectively controlled. The field demonstration confirms that concrete-encapsulated pillar reinforcement effectively manages mine-wide ground pressure.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guo, Q.; Yu, H.; Dan, Z.; Li, S. Mining Method Optimization of Gently Inclined and Soft Broken Complex Ore Body Based on AHP and TOPSIS: Taking Miao-Ling Gold Mine of China as an Example. Sustainability 2021, 13, 12503. [Google Scholar] [CrossRef]
- Lin, Y. Research on Mining Technology of Steeply Inclined Thin Ore Body in High-grade Content Mine. IOP Conf. Ser. Earth Environ. Sci. 2021, 632, 022038. [Google Scholar] [CrossRef]
- Javanshirgiv, M.; Safari, M. The selection of an underground mining method using the fuzzy topsis method: A case study in the kamar mahdi ii fluorine mine. Min. Sci. 2017, 24, 161. [Google Scholar]
- Liang, W.Z.; Dai, B.; Zhao, G.Y.; Wu, H. Assessing the Performance of Green Mines via a Hesitant Fuzzy ORESTE–QUALIFLEX Method. Mathematics 2019, 7, 788. [Google Scholar] [CrossRef]
- Ghasemi, E.; Ataei, M.; Shahriar, K. Prediction of global stability in room and pillar coal mines. Nat. Hazards 2014, 72, 405–422. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Li, M.; Xu, X.D.; Li, X.T.; Ma, Y.D.; Ma, Z. Research on catastrophic pillar instability in room and pillar gypsum mining. Sustainability 2018, 10, 3773. [Google Scholar] [CrossRef]
- Li, T.; Cai, M.F.; Zhang, S.Q. Mining-induced seismicity in China. Seismol. Res. North. Chin. 2005, 21, 1–26. [Google Scholar]
- Tong, Q.; Tong, Y.S.; Kang, C.X. Feature categorization of mining induced tremor in Hunan Province. Seismol. Geomagn. Obs. Res. 2023, 44, 41–47. [Google Scholar]
- Wang, G.B. Study on Rock Burst Induced by Roof Falling and Its Control Methods in Gypsum Mine. Master’s Thesis, Wuhan University of Technology, Wuhan, China, 2006. [Google Scholar]
- Wen, J.; Gou, X.B.; Zhao, J.Y. The gestation process and the caution of the Xingtai gypsum mine subsidence. Seismol. Geom. Obs. Res. 2007, 28, 36–40. [Google Scholar]
- Yao, Q. Research on the Treatment Methods of Goaf Areas in Xingtai Gypsum Mining Area. Min. Technol. 2012, 3, 59–61. [Google Scholar]
- Hunan Earthquake Administration. Analysis Report on the Xiang’an Tungsten Industry Mine Earthquake; Hunan Earthquake Administration: Changsha, China, 2022.
- Watson, B.; Maphosa, T.; Theron, W.; Fernandes, N.; Stacey, T.; Morgan, A.; Carpede, A.; Betz, G. Establishing a UG2 pillar strength formula in south african platinum mines. Minerals 2024, 14, 1161. [Google Scholar] [CrossRef]
- Liang, W.Z.; Luo, S.Z.; Zhao, G.Y.; Wu, H. Predicting Hard Rock Pillar Stability Using GBDT, XGBoost, and LightGBM Algorithms. Mathematics 2020, 8, 765. [Google Scholar] [CrossRef]
- Zhou, J.; Li, X.; Mitri, H.S. Comparative performance of six supervised learning methods for the development of models of hard rock pillar stability prediction. Nat. Hazards 2015, 79, 291–316. [Google Scholar] [CrossRef]
- Mortazavi, A.; Hassani, F.P.; Shabani, M. A numerical investigation of rock pillar failure mechanism in underground openings. Comput. Geotech. 2009, 36, 691–697. [Google Scholar] [CrossRef]
- Griffiths, D.V.; Fenton, G.A.; Lemons, C.B. Probabilistic analysis of underground pillar stability. Int. J. Numer. Anal. Met. 2002, 26, 775–791. [Google Scholar] [CrossRef]
- Tawadrous, A.S.; Katsabanis, P.D. Prediction of surface crown pillar stability using artificial neural networks. Int. J. Numer. Anal. Met. 2007, 31, 917–931. [Google Scholar] [CrossRef]
- Wattimena, R.K. Predicting the stability of hard rock pillars using multinomial logistic regression. Int. J. Rock Mech. Min. 2014, 71, 33–40. [Google Scholar] [CrossRef]
- Ding, H.X.; Li, G.H.; Dong, X.; Lin, Y. Prediction of pillar stability for underground mines using the stochastic gradient boosting technique. IEEE Access 2018, 6, 69253–69264. [Google Scholar] [CrossRef]
- Grgic, D.; Homand, F.; Hoxha, D. A short-and long-term rheological model to understand the collapses of iron mines in Lorraine France. Comput. Geotech. 2003, 30, 557–570. [Google Scholar] [CrossRef]
- AI Heib, M.; Duval, C.; Theoleyre, F. Analysis of the historical collapse of an abandoned underground chalk mine in 1961 in Clamart (Paris France). Bull. Eng. Geol. Environ. 2015, 74, 1001–1018. [Google Scholar] [CrossRef]
- Salmi, E.F.; Nazem, M.; Karakus, M. The effect of rock mass gradual deterioration on the mechanism of post-mining subsidence over shallow abandoned coal mine. Int. J. Rock Mech. Min. 2017, 91, 59–71. [Google Scholar] [CrossRef]
- Zhou, Z.L.; Chen, L.; Zhao, Y. Experimental study on failure mechanism and bearing characteristic of double-pillar system. Chin. J. Rock Mech. Eng. 2017, 36, 420–428. [Google Scholar]
- Guan, Y.W.; Wei, Y.Q.; Yang, Z.J. Failure mechanism of the key strata-pillar system in room and pillar goaf based ona numerieal simulation. Chin. J. Geol. Hazard Control 2017, 28, 59–63. [Google Scholar]
- Liu, J.X.; Tang, C.A.; Zhu, W.C. Rock-coal model for studying the rockburst. Chin. J. Geotech. Eng. 2004, 26, 276–280. [Google Scholar]
- Zhu, D.F.; Tu, S.H.; Wang, F.T. Stability evaluation on pillar system of room and pillar mining in goaf at shallow depth seam. J. Chin. Coal Soc. 2018, 43, 390–397. [Google Scholar]
- Feng, G.R.; Bai, J.W.; Shi, X.D. Key pillar theory in the chain failure of residual coal pillars and its application prospect. J. Chin. Coal Soc. 2021, 46, 164–179. [Google Scholar]
- Tesarik, D.R.; Seymour, J.B.; Yanske, T.R. Longterm stability of a backfilled room-and-pillar test section at the buick mine missouri. Int. J. Rock Mech. Min. Sci. 2009, 46, 1182–1196. [Google Scholar] [CrossRef]
- Tan, Y.Y.; Zhang, K.; Yu, X.; Song, W.D.; Wang, J.; Hai, C.L. The mechanical and microstructural properties of composite structures made of a cement-tailing backfill and rock core. Minerals 2020, 10, 159. [Google Scholar] [CrossRef]
- Zhang, C.; Jin, Z.; Feng, G.; Tai, Y.; Gao, R.; Li, C. Joint load-bearing behaviors and interface failure mechanism of encased coal samples under uniaxial compression. Compos. Struct. 2024, 10, 118480. [Google Scholar] [CrossRef]
- Li, J.; Bai, J.W.; Feng, G.R.; Wang, S.Y. Compressive performance of innovative reinforced pillars in closed/abandoned mines. J. Cent. South Univ. 2024, 31, 2780–2793. [Google Scholar] [CrossRef]
- Zhao, H.C.; Ren, T.; Remennikov, A. Behaviour of FRP-confined coal reject concrete columns under axial compression. Compos. Struct. 2021, 262, 113621. [Google Scholar] [CrossRef]
- Ren, T.; Zhao, H.C.; Remennikov, A. Fibre-reinforced polymer confined-coal rejects concrete: Compressive behaviour. Compos. Struct. 2022, 299, 116063. [Google Scholar] [CrossRef]
- Song, W.D.; Cao, S.; Fu, J.X. Sensitivity analysis of impact factors of pillar stability and its application. Rock Soil Mech. 2014, 35, 271–277. [Google Scholar]
- Yin, S.H.; Wu, A.X.; Li, X.W. Orthogonal polar difference analysis for sensitivity of the factors influencing the ore pillar stability. J. Chin. Coal Soc. 2012, 37, 48–52. [Google Scholar]
- Dong, J.Y.; Yang, J.H.; Yang, G.X. Research on similar material proportioning test of model test based on orthogonal design. J. Chin. Coal Soc. 2012, 37, 44–49. [Google Scholar]
- Lu, Y.D.; Ge, X.R.; Jiang, Y. Study on conventional triaxial compression test of complete process for marble and its constitutive equation. Chin. J. Rock Mech. Eng. 2004, 23, 2489–2493. [Google Scholar]
- He, M.C.; Xie, H.P.; Peng, S.P.; Jiang, Y.D. Study on rock mechanics in deep mining engineering. Chin. J. Rock Mech. Eng. 2005, 16, 2803–2813. [Google Scholar]
- Zhang, L.; Wang, B.X.; Yang, T. Research of rock triaxial compression test with multilevel confining pressure. Site Investig. Sci. Technol. 2007, 3, 6–8. [Google Scholar]
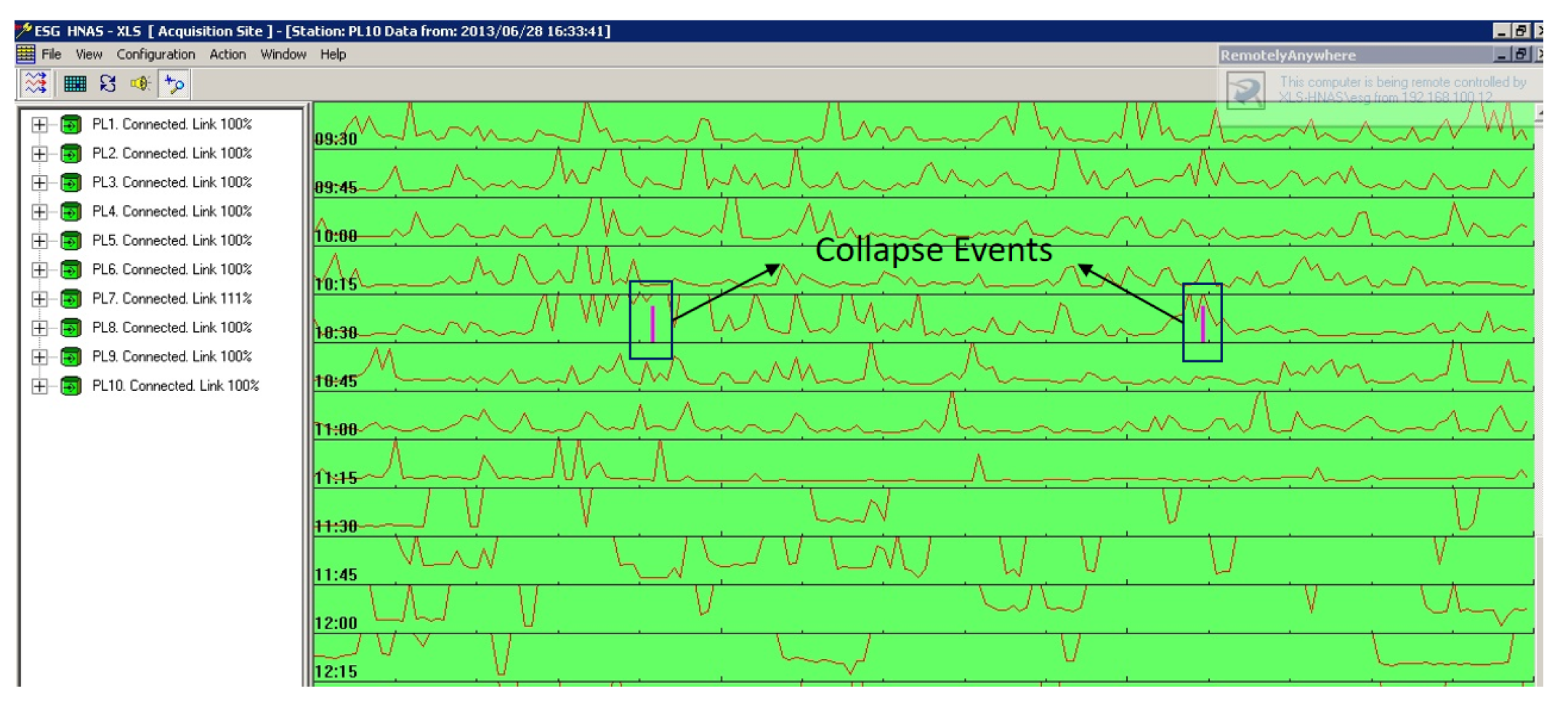
- Hu, J.Y.; Lin, F.; Peng, F.H. Research on application of microseismic monitoring technology on ground pressure hazard of residual are in Xianglushan tungsten mine. Chin. J. Geol. Hazard Control 2010, 21, 109–115. [Google Scholar]
- Peng, F.H.; Li, S.L.; Leng, X.N. Study of influence of rainfall permeation on shallow stope stability by microseismic Monitoring. Chin. J. Rock Mech. Eng. 2016, 35, 4154–4163. [Google Scholar]











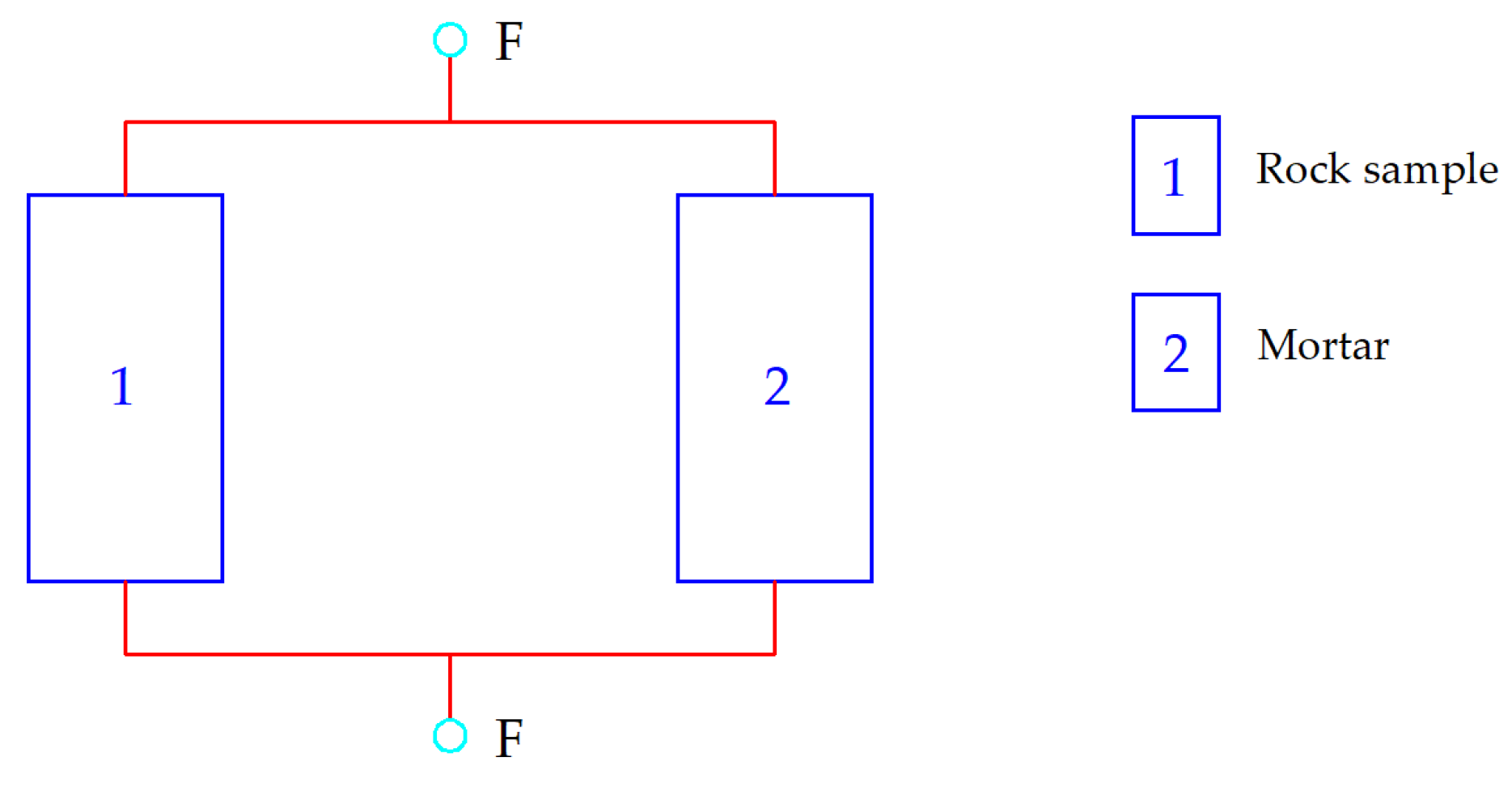





| Material | Quality Mix Ratio | Mold | Curing | Grinding |
|---|---|---|---|---|
| ordinary Portland cement 42.5, dry fine sand (0.25 mm–0.35 mm), water | cement–sand–water ratio = 1:4.5:1.1 (M10) cement–sand–water ratio = 1:6.0:1.2 (M5) | PVC pipes with internal diameters of 70 mm, 100 mm, and 150 mm | after being demolded at 24 h, the specimens are cured in a chamber at 20 °C and 90% relative humidity for 28 days | the specimen shall be ground at both ends to achieve a height tolerance of ±0.5 mm |
| Rock Sample | H (mm) | d (mm) | (KN) | (KN) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| H-16 | 50 | 50 | 31.61 | 0.0172 | 126.47 | 0.0896 | 4.00 | 4.08 | 5.21 | 3.87 |
| H-17 | 50 | 50 | 31.61 | 0.0172 | 136.11 | 0.0692 | 4.31 | 4.02 | ||
| H-18 | 50 | 50 | 31.61 | 0.0172 | 123.95 | 0.0409 | 3.92 | 2.38 | ||
| H-1 | 100 | 50 | 44.49 | 0.0107 | 136.31 | 0.0135 | 3.06 | 2.99 | 1.26 | 1.32 |
| H-2 | 100 | 50 | 44.49 | 0.0107 | 132.41 | 0.0147 | 2.98 | 1.37 | ||
| H-3 | 100 | 50 | 44.49 | 0.0107 | 130.74 | 0.0141 | 2.94 | 1.32 | ||
| H-13 | 150 | 50 | 43.35 | 0.0074 | 118.87 | 0.0100 | 2.74 | 2.52 | 1.35 | 1.93 |
| H-14 | 150 | 50 | 43.35 | 0.0074 | 103.75 | 0.0155 | 2.39 | 2.09 | ||
| H-15 | 150 | 50 | 43.35 | 0.0074 | 105.08 | 0.0175 | 2.42 | 2.36 | ||
| H-22 | 200 | 50 | 36.52 | 0.0058 | 78.07 | 0.0076 | 2.14 | 2.16 | 1.31 | 1.77 |
| H-23 | 200 | 50 | 36.52 | 0.0058 | 79.56 | 0.0144 | 2.18 | 2.48 | ||
| H-24 | 200 | 50 | 36.52 | 0.0058 | 78.47 | 0.0089 | 2.15 | 1.53 | ||
| Rock Sample | Encasing Thicknesses (mm) | (KN) | (KN) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| H-10 | 10 | 44.49 | 0.0107 | 64.17 | 0.0111 | 1.44 | 1.67 | 1.04 | 1.02 |
| H-11 | 10 | 44.49 | 0.0107 | 81.92 | 0.0106 | 1.84 | 0.99 | ||
| H-12 | 10 | 44.49 | 0.0107 | 76.36 | 0.0109 | 1.72 | 1.02 | ||
| H-1 | 25 | 44.49 | 0.0107 | 136.31 | 0.0135 | 3.06 | 2.99 | 1.26 | 1.32 |
| H-2 | 25 | 44.49 | 0.0107 | 132.41 | 0.0147 | 2.98 | 1.37 | ||
| H-3 | 25 | 44.49 | 0.0107 | 130.74 | 0.0141 | 2.94 | 1.32 | ||
| H-19 | 50 | 44.49 | 0.0107 | 233.73 | 0.0346 | 5.25 | 5.31 | 3.23 | 3.27 |
| H-20 | 50 | 44.49 | 0.0107 | 247.94 | 0.0363 | 5.57 | 3.39 | ||
| H-21 | 50 | 44.49 | 0.0107 | 227.35 | 0.0341 | 5.11 | 3.19 | ||
| Rock Sample | Peak Bearing Capacity | Peak Strain | Failure Mode | |
|---|---|---|---|---|
| Category | Characteristic Description | |||
| H-16 | 126.47 | 0.0896 | Large fragmented blocks | Forming large rock blocks and a large amount of debris after failure |
| H-17 | 136.11 | 0.0692 | ||
| H-18 | 123.95 | 0.0409 | ||
| H-1 | 136.31 | 0.0135 | Large blocks | Forming several large rock blocks after failure |
| H-2 | 132.41 | 0.0147 | ||
| H-3 | 130.74 | 0.0141 | ||
| H-13 | 118.87 | 0.0100 | Splitting pattern | Producing a single main fracture surface and splitting into two large blocks |
| H-14 | 103.75 | 0.0155 | ||
| H-15 | 105.08 | 0.0175 | ||
| H-22 | 78.07 | 0.0076 | Large blocks | Forming several large rock blocks after end failure |
| H-23 | 79.56 | 0.0144 | ||
| H-24 | 78.47 | 0.0089 | ||
| Q-1 | 225.28 | 0.0200 | Splitting pattern | Producing a single main fracture surface and splitting into two large blocks |
| Q-2 | 234.18 | 0.0155 | ||
| Q-3 | 237.54 | 0.0159 | ||
| B-1 | 252.30 | 0.0160 | Splitting pattern | Producing a single main fracture surface and splitting into two large blocks |
| B-2 | 272.12 | 0.0214 | ||
| B-3 | 294.59 | 0.0159 | ||
| H-4 | 106.87 | 0.0111 | Large blocks | Forming several large rock blocks after failure |
| H-5 | 74.00 | 0.0149 | ||
| H-6 | 78.71 | 0.0166 | ||
| H-7 | 133.02 | 0.0177 | Large blocks | Forming large rock blocks and a large amount of debris after the outer layer of mortar fails, with the rock remaining relatively intact |
| H-8 | 140.07 | 0.0150 | ||
| H-9 | 124.89 | 0.0168 | ||
| H-10 | 64.17 | 0.0111 | Large blocks | Forming several large rock blocks after failure |
| H-11 | 81.92 | 0.0106 | ||
| H-12 | 76.36 | 0.0109 | ||
| H-19 | 233.73 | 0.0346 | Small fragmented blocks | Forming small blocks and a large amount of debris after failure |
| H-20 | 247.94 | 0.0363 | ||
| H-21 | 227.35 | 0.0341 | ||
| Influencing Factors | Level 1 | Level 2 | Level 3 | Level 4 |
|---|---|---|---|---|
| height-to-diameter ratio | 1 | 2 | 3 | 4 |
| rock strength (KN) | 45 | 92.79 | 118.03 | / |
| encasing material | M5 | M10 | M10 mortar with steel wire | / |
| encasing thickness (mm) | 10 | 25 | 50 | / |
| Test Number | Height-to-Diameter Ratio | Rock Strength (KN) | Encasing Material | Encasing Thickness (mm) | Peak Stress Enhancement Ratio |
|---|---|---|---|---|---|
| 1 | 1 | 45 | M10 | 25 | 4.08 |
| 2 | 2 | 45 | M10 | 25 | 2.99 |
| 3 | 3 | 45 | M10 | 25 | 2.52 |
| 4 | 4 | 45 | M10 | 25 | 2.16 |
| 5 | 2 | 45 | M10 | 25 | 2.99 |
| 6 | 2 | 92.79 | M10 | 25 | 2.50 |
| 7 | 2 | 118.03 | M10 | 25 | 2.32 |
| 8 | 2 | 45 | M5 | 25 | 1.94 |
| 9 | 2 | 45 | M10 | 25 | 2.99 |
| 10 | 2 | 45 | M10 with steel wire | 25 | 2.98 |
| 11 | 2 | 45 | M10 | 10 | 1.67 |
| 12 | 2 | 45 | M10 | 25 | 2.99 |
| 13 | 2 | 45 | M10 | 50 | 5.31 |
| K1 | 4.08 | 2.99 | 2.52 | 2.16 | |
| K2 | 2.99 | 2.50 | 2.32 | ||
| K3 | 1.94 | 2.99 | 2.98 | ||
| K4 | 1.67 | 2.99 | 5.31 | ||
| the range | R1 = 1.92 | R2 = 0.67 | R3 = 1.05 | R4 = 3.64 | |
| Order of Factor Significance | encasing thickness > height-to-diameter ratio > encasing material > rock strength | ||||
| Rock Sample | Encasing Thickness (mm) | (KN) | F (KN) | ||||
|---|---|---|---|---|---|---|---|
| H-10 | 10 | 18.84 | 64.17 | 45.33 | 44.49 | 1.02 | 1.24 |
| H-11 | 10 | 18.84 | 81.92 | 63.08 | 44.49 | 1.42 | |
| H-12 | 10 | 18.84 | 76.36 | 57.52 | 44.49 | 1.29 | |
| H-1 | 25 | 58.88 | 136.31 | 77.44 | 44.49 | 1.74 | 1.67 |
| H-2 | 25 | 58.88 | 132.41 | 73.54 | 44.49 | 1.65 | |
| H-3 | 25 | 58.88 | 130.74 | 71.87 | 44.49 | 1.62 | |
| H-19 | 50 | 157.00 | 233.73 | 76.73 | 44.49 | 1.72 | 1.78 |
| H-20 | 50 | 157.00 | 247.94 | 90.94 | 44.49 | 2.04 | |
| H-21 | 50 | 157.00 | 227.35 | 70.35 | 44.49 | 1.58 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, F.; Wang, W. Experimental Study and Engineering Application of Concrete-Encased Reinforcement for Mine Pillars. Appl. Sci. 2025, 15, 10615. https://doi.org/10.3390/app151910615
Peng F, Wang W. Experimental Study and Engineering Application of Concrete-Encased Reinforcement for Mine Pillars. Applied Sciences. 2025; 15(19):10615. https://doi.org/10.3390/app151910615
Chicago/Turabian StylePeng, Fuhua, and Weijun Wang. 2025. "Experimental Study and Engineering Application of Concrete-Encased Reinforcement for Mine Pillars" Applied Sciences 15, no. 19: 10615. https://doi.org/10.3390/app151910615
APA StylePeng, F., & Wang, W. (2025). Experimental Study and Engineering Application of Concrete-Encased Reinforcement for Mine Pillars. Applied Sciences, 15(19), 10615. https://doi.org/10.3390/app151910615




