Fusing Historical Records and Physics-Informed Priors for Urban Waterlogging Susceptibility Assessment: A Framework Integrating Machine Learning, Fuzzy Evaluation, and Decision Analysis

Featured Application

What are the main findings?

• This study proposes a dual-source sample enhancement strategy that integrates Physics-Informed Priors (PI-PRIORS) with HWR, incorporating extreme rainfall scenarios and applying a joint filtering mechanism based on membership, credibility, and impact degrees. This approach systematically extracts high-quality samples and embeds extreme-scenario information into the modeling process.
• To address the heterogeneity of polygon-based waterlogging risk distributions, a dimension-reduction sampling framework is introduced based on TWD theory. It integrates an MCCM and the CRITIC-TOPSIS method, which integrates the CRITIC (Criteria Importance Through Intercriteria Correlation) method and the TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) method, to quantify membership degrees of overlapping risk levels, while also assessing credibility and social influence scores to support robust point-based sampling in spatially complex environments.
• A MaxEnt (Maximum Entropy) modeling framework—a statistical learning approach rooted in information entropy theory—is developed by integrating variables from natural conditions, social capital, infrastructure, and the built environment. The contributions and directional effects of each factor are quantified, achieving a balance between interpretability and scalability. This framework offers a transferable tool for diverse urban settings and targeted flood mitigation planning.

Abstract

Urban Waterlogging Susceptibility Assessment (UWSA) is vital for resilient urban planning and disaster preparedness. Conventional methods depend heavily on Historical Waterlogging Records (HWR), which are limited by their reliance on extreme rainfall events and prone to human omissions, resulting in spatial bias and incomplete coverage. While hydrodynamic models can simulate waterlogging scenarios, their large-scale application is restricted by the lack of accessible underground drainage data. Recently released flood control plans and risk maps provide valuable physics-informed priors (PI-Priors) that can supplement HWR for susceptibility modeling. This study introduces a dual-source integration framework that fuses HWR with PI-Priors to improve UWSA performance. PI-Priors rasters were vectorized to delineate two-dimensional waterlogging zones, and based on the Three-Way Decision (TWD) theory, a Multi-dimensional Connection Cloud Model (MCCM) with CRITIC-TOPSIS was employed to build an index system incorporating membership degree, credibility, and impact scores. High-quality samples were extracted and combined with HWR to create an enhanced dataset. A Maximum Entropy (MaxEnt) model was then applied with 20 variables spanning natural conditions, social capital, infrastructure, and built environment. The results demonstrate that this framework increases sample adequacy, reduces spatial bias, and substantially improves the accuracy and generalizability of UWSA under extreme rainfall.

1. Introduction

With the accelerating pace of urbanization and the increasing frequency of extreme rainfall events driven by climate change, urban flooding has emerged as one of the most frequent and destructive types of urban disasters worldwide. It poses direct threats to public safety and critical infrastructure, while also severely disrupting urban functionality and causing substantial economic losses. Among urban water-related hazards, fluvial flooding and urban pluvial flooding (waterlogging) are often interrelated in their mechanisms and spatial distribution [1]. However, they differ significantly in terms of driving factors, triggering processes, spatial extent, and management strategies [2]. Fluvial floods arise from watershed-scale runoff and manifest as river overflow or levee breaches, with wide spatial impact, long duration, and severe regional consequences [3]. In contrast, urban waterlogging is localized and sudden. It is caused by short-term heavy rainfall exceeding the design threshold of the drainage system and thus surpassing the local drainage capacity, or by the accumulation of water in low-lying areas through slope differences and the convergence effect [4]. Although typically short-lived, such events can paralyze transportation, disrupt infrastructure, and endanger residents [5]. Waterlogging is also highly sensitive to micro-topography, land use, and drainage networks [6], resulting in fragmented distribution and requiring fine-scale spatial analysis for accurate risk assessment.

In China, waterlogging has become a major meteorological-hydrological hazard due to rapid urban growth and more frequent extreme weather [7]. The Global Natural Disaster Assessment Report identifies China among the countries most severely affected [8], particularly in the Yangtze River Basin and South China, where short-duration, high-intensity rainfall frequently overwhelms drainage systems [9]. The Zhengzhou rainstorm of 20 July 2021 exemplified this threat, causing 398 deaths and economic losses of over 120 billion RMB, and ranking among the most severe global urban water disasters [10]. Similar events in Guangzhou (2020) [11], Beijing (2023), and cities such as Nanjing, Shenzhen, and Wuhan [12] highlight systemic vulnerabilities and the limits of emergency response. These cases underscore the urgent need for fine-scale susceptibility mapping and proactive risk governance to enhance resilience.

It is important to clarify that this study focuses specifically on waterlogging susceptibility, defined as the inherent tendency of a spatial unit to experience water accumulation under specific physical, meteorological, and anthropogenic conditions. Unlike vulnerability or exposure, susceptibility pertains to the likelihood of hazard occurrence without necessarily involving damage or population presence [13,14]. Vulnerability relates to the potential for harm within a system [15], while exposure concerns the value or sensitivity of elements in hazard-prone areas [16]. These concepts, though often conflated, serve distinct roles within disaster risk analysis and must be clearly distinguished to ensure conceptual clarity and analytical precision. The UWSA conducted here represents a critical component of the broader risk evaluation chain, providing spatially explicit insights that support drainage system optimization, urban resilience planning, and anticipatory risk management. Current UWSA approaches can be broadly categorized into four types, each offering unique advantages and limitations in data requirements, spatial resolution, interpretability, and modeling accuracy, and they hold strong potential for integrated application.

A widely adopted approach to UWSA is statistical analysis based on HWR data [17]. Drawing from field surveys, public reports, or remote sensing, these methods utilize spatial regression, weighted overlays, or geostatistical techniques [18]. Their strengths include easy data acquisition and straightforward implementation, making them effective for detecting large-scale patterns and conducting preliminary zoning. At the same time, they can offer direct evidence of historical events. However, their heavy reliance on HWR limits their applicability in newly developed urban areas or under climate change scenarios. For example, certain regions have consistently encountered significant precipitation events, whereas others have remained largely unaffected, which may lead to the lack or irrelevance of past data. At the same time, under extreme rainfall, HWR may encounter situations where it is unable to capture areas prone to waterlogging due to hidden physical loopholes (such as overly small drainage pipes and concave vertical Bridges). Models based only on historical samples thus lack robustness for anticipating intensified rainfall.

Another mainstream method is Physics-based Hydrodynamic Simulation (PB-HydroSim), which combines one-dimensional drainage networks with two-dimensional surface runoff models (e.g., InfoWorks ICM, MIKE URBAN) to replicate interactions such as pipe surcharging, overflow, and overland flow [19]. These models are physically grounded and widely used for high-resolution analysis at the site or sub-district level [20]. Nevertheless, they face notable challenges: their sensitivity to detailed input parameters, including pipe diameter, slope, and node configuration, and the limited availability of drainage infrastructure data, which are often confidential and inaccessible in many cities.

To address these limitations, integrated multi-source modeling approaches have emerged. By incorporating topography, land use, socio-economic factors, and infrastructure data, and employing algorithms such as Analytic Hierarchy Process [21], fuzzy comprehensive evaluation [22], Maximum Entropy [23], random forests [24], and support vector machines [25], these methods offer flexibility and adaptability in data-scarce environments. They enable susceptibility mapping even without detailed inundation records or drainage maps. Integrating such outputs with HWR improves training quality and model stability. However, their effectiveness depends on the representativeness and completeness of training data, which is often very sensitive and costly, and some models lack physical interpretability, which may affect their credibility and stability.

With advances in artificial intelligence, deep learning models have recently entered urban waterlogging research [26]. Architectures such as Convolutional Neural Networks [27], Recurrent Neural Networks [28], and U-Net [29], integrate high-dimensional inputs from remote sensing, street-level imagery, radar precipitation, and ground observations. These models excel in feature extraction and non-linear pattern recognition, particularly in image and time-series analysis. However, they require large volumes of high-quality, multimodal datasets—including rainfall–flood time series, in situ waterlogging photos, and surveillance videos—which are often difficult to obtain, scattered across departments, and restricted by privacy or security concerns. Consequently, their application remains largely experimental and limited to small-scale pilots.

In summary, all the above three types of UWSA methods have limitations, yet their complementary strengths in data applicability, precision, and interpretability highlight the potential for methodological integration. Tailoring or combining approaches according to local conditions and data availability can improve risk identification and urban water management. In addition, leveraging more abundant multi-source data for systematic processing and in-depth analysis can further enhance the effectiveness of the integration method.

Recently, municipal agencies have begun releasing risk maps to enhance public awareness and preparedness. For example, in 2024, Beijing agencies issued a waterlogging risk map integrating HWR, remote sensing, and topography [30]. Developed through international and domestic models under multiple scenarios, the map identified representative risk zones for planning and preparedness. Despite increasing availability, the scientific use of these maps remains limited. Beyond communication, they can serve as supplementary data for susceptibility modeling by supporting training, validating outputs, and aiding data fusion. Yet their polygon-based representation introduces spatial heterogeneity and boundary uncertainty, complicating point-level sampling and classification.

Addressing these issues requires the development of a framework that can account for the coexistence of multiple risk levels and resolve local spatial heterogeneity in a consistent and quantifiable way. To this end, the present study proposes an integrated strategy that combines HWR data, PB-HydroSim outputs, and multi-source data-driven evaluation methods. By incorporating uncertainty analysis and the MaxEnt machine learning algorithm, the research conducts a spatial UWSA framework in Hefei’s central area. The resulting framework is designed to be transferable and adaptive, leveraging the empirical accuracy of HWR data, the scenario flexibility of PB-HydroSim, and the comprehensive spatial coverage of multi-dimensional indicators. The key contributions of this study are as follows:

(1) This study proposes a dual-source sample enhancement strategy that integrates PI-Priors with HWR, incorporating extreme rainfall scenarios and applying a joint filtering mechanism based on membership, credibility, and impact degrees. This approach systematically extracts high-quality samples and embeds extreme-scenario information into the modeling process.

(2) To address the heterogeneity of polygon-based waterlogging risk distributions, a dimension-reduction sampling framework is introduced based on TWD theory. It integrates an MCCM and the CRITIC-TOPSIS method to quantify membership degrees of overlapping risk levels, while also assessing credibility and social influence scores to support robust point-based sampling in spatially complex environments.

(3) A MaxEnt modeling framework is developed by integrating variables from natural conditions, social capital, infrastructure, and the built environment. The contributions and directional effects of each factor are quantified, achieving a balance between interpretability and scalability. This framework offers a transferable tool for diverse urban settings and targeted flood mitigation planning.

2. Research Area and Data Collection

2.1. Overview of the Study Area

Hefei, the capital of Anhui Province in eastern China, is the province’s political, economic, and cultural center. Its central urban area comprises four core districts—Yaohai, Luyang, Shushan, and Baohe—and extends into parts of surrounding counties such as Changfeng, Feidong, and Feixi (Figure 1).

This zone has high population density, concentrated economic activity, and well-developed infrastructure. Urban expansion has blurred the boundaries between core districts and neighboring counties, with suburban towns like Taohua and Shangpai in Feixi now highly urbanized and functionally integrated with central Hefei. Major industrial zones, including the Hefei Economic and Technological Development Zone, also straddle Feixi and Changfeng, reinforcing spatial and economic connectivity.

These areas share drainage networks and public infrastructure, with strong interdependence in transportation, industry, and commuting. Accordingly, this study defines Hefei’s central urban area as including both the four districts and adjacent rapidly urbanized zones (Figure 1). The widespread replacement of natural surfaces by impervious materials has substantially heightened the risk of waterlogging under extreme rainfall.

2.2. UWSA Indicator System

Previous studies have identified a wide range of natural and anthropogenic indicators for assessing urban waterlogging, consistently showing strong links with natural conditions, social capital, infrastructure, and the built environment. Commonly used variables include rainfall intensity, elevation, slope, surface roughness, terrain undulation, population density, and GDP. Infrastructure factors, however, are often simplified, with transportation typically represented by basic measures such as road density [31], distance to overpasses [23], or distance to major roads [32].

Yet transportation infrastructure is highly vulnerable during waterlogging, and disruptions can severely affect mobility, safety, and economic activity. To address these gaps, this study develops an indicator system (

Table 1. Index system for UWSA.

Dimension	Indicator	Reference	Data Source
Natural condition	Elevation ($N_1$)	[33,34]	https://www.rivermap.cn/home/mapdata.html (accessed on 15 July 2025)
	Roughness ($N_2$)	[35,36]	/
	Relief ($N_3$)	[37,38]	/
	Slope ($N_4$)	[39,40]	/
	Precipitation ($N_5$)	[19,41]	https://gre.geodata.cn/ (accessed on 21 June 2025)
Social capital	Population density ($S_1$)	[42,43]	https://landscan.ornl.gov/ (accessed on 23 June 2025)
	GDP ($S_2$)	[44,45]	https://www.resdc.cn/doi/doi.aspx?DOIid=33 (accessed on 25 June 2025)
Infrastructure	Distance to overpass ($I_1$)	[46,47]	Gaode map
	Distance to concave-down overpass ($I_2$)	[48,49]	Plan 2020
	Distance to underpass ($I_3$)	[50]	Plan 2020
	* Distance to main stormwater pipe ($I_4$)	[51,52]	Plan 2020
	* Density of main stormwater pipe ($I_5$)	[51,52]	Plan 2020
	Road density ($I_6$)	[53,54]	https://www.rivermap.cn/home/mapdata.html (accessed on 8 July 2025)
Built environment	Distance to surface water system ($B_1$)	[55,56]	/
	Building density ($B_2$)	[22,57]	https://www.rivermap.cn/home/mapdata.html (accessed on 8 July 2025)
	Building height ($B_3$)	[58,59]	https://www.rivermap.cn/home/mapdata.html (accessed on 8 July 2025)
	Impervious surface ($B_4$)	[60,61]	https://zenodo.org/records/12779975 (accessed on 9 July 2025)
	Water density ($B_5$)	[62,63]	https://zenodo.org/records/12779975 (accessed on 10 July 2025)
	Green space ($B_6$)	[64,65]	https://doi.org/10.57760/sciencedb.07049 (accessed on 12 July 2025) [66]
	Land use ($B_7$)	[67,68]	https://zenodo.org/records/12779975 (accessed on 8 July 2025)

* Note: It should be noted that due to historical construction practices, the old urban areas of Hefei have adopted a combined sewer system in which both stormwater and wastewater share the same drainage infrastructure. As a result, the statistics on stormwater pipelines in these areas also include a portion of the wastewater pipes. Additionally, all density and length-related indicators are expressed in units of (m/km²) and (m²/km²), respectively.

) that incorporates additional transportation-related variables, including distance to underpasses, concave-down overpasses, and major stormwater pipes. These indicators provide a more detailed representation of exposure mechanisms and improve the precision of susceptibility assessment.

2.3. Indicator Data Collection

Data for all indicators in Table 1 were collected from multi-source datasets and standardized to a 100 m × 100 m grid resolution in ArcGIS Pro. Zonal statistics were used to generate spatial distributions (Figure 2). In addition, 139 waterlogging-prone locations were obtained from the Comprehensive Urban Drainage and Waterlogging Prevention Plan of Hefei (2013–2020), hereafter “Plan 2020,” and used as labeled samples for susceptibility assessment.

For natural condition variables, $N_2-N_4$ were derived from $N_1$ through spatial analysis in ArcGIS Pro. In the built environment dimension, $B_1$ was extracted from the Annual Land Cover Dataset of China [69] and processed using nearest-neighbor analysis. Infrastructure indicators $I_1$-$I_4$ were also generated through nearest-neighbor analysis.

PI-Priors from Plan 2020 were further incorporated (Figure 3). Raster outputs of PB-HydroSim simulations for Hefei’s seven drainage zones were vectorized through a semi-automated process, with manual correction to address overlapping pixel colors. The simulations were conducted with MIKE FLOOD, which couples a 1D drainage network with a 2D hydrodynamic model. A risk index $R$ was then calculated as

$$\begin{array}{c}R=d\times \left(v+0.5\right)+\rho \end{array}$$

(1)

where $d \left(\mathrm{m}\right)$ is water depth, $v (\mathrm{m}/\mathrm{s})$ is flow velocity, and $\rho$ is the depth-related hazard coefficient. Specifically, when $d < 0.15 \mathrm{m}$, $\rho$ is set to 0.5. When $d \ge 0.15 \mathrm{m}$, $\rho$ is set to 1.0. Based on $R$, waterlogging risk was categorized into three levels: High risk $(R\ge 1.25)$, Medium risk $\left(0.75\le R\le 1.25\right)$, and Low risk $(R\le 0.75)$.

3. Materials and Methods

In the previous sections, we introduced the datasets and acquisition process for UWSA. Building on this foundation, the proposed framework integrates HWR and PI-Priors through four core modules: indicator selection and analysis, construction of the supplementary dataset from PI-Priors, UWSA model development, and generation and interpretation of susceptibility probability maps (Figure 4).

3.1. Dominant Factor Identification and Correlation Analysis

Given the large number of UWSA indicators, this section applied multiple diagnostic techniques to detect multicollinearity, as shown in Figure 5. Figure 5a presents the Variance Inflation Factors (VIF) and Condition Indices for all variables. Typically, VIF values above 10 or Condition Indices above 30 indicate severe multicollinearity. Indicators $B_5$ and $B_7$ exceed these thresholds, suggesting redundancy and the risk of biased estimates. Figure 5b displays a scree plot of eigenvalues derived from the standardized covariance matrix. The sharp decline followed by a plateau, along with several eigenvalues below 1, suggests underlying dimensional dependencies and shared variance among variables.

Figure 5c shows the Pearson correlation heatmap for the UWSA indicators. A coefficient above 0.8 generally indicates a strong correlation. While most variables exhibit low to moderate correlations, a high correlation is evident between $B_5$ and $B_7.$ This is because the density of water bodies, including rivers and lakes, expressed by B5 has an extremely high degree of overlap with the land, including the total area that human beings can be involved in production activities expressed by B7. Consequently, the land use variable was excluded, yielding a final set of 19 UWSA indicators.

3.2. Supplementary Waterlogging Dataset Construction Using PI-Priors

Constructing a supplementary dataset from PI-Priors is a key step linking simulation outputs with probabilistic modeling. The main challenge is extracting representative and spatially balanced samples from continuous risk surfaces. HWR data are sparse and temporally constrained, while PB-HydroSim outputs provide broader spatial coverage but are prone to oversampling and mixed classification within the same unit. Integrating these outputs into a representative dataset is, therefore, essential for enhancing model generalizability and spatial robustness.

Three-Way Decision (TWD) theory [70] offers a rigorous framework for resolving these problems. Originating in rough-set research, TWD partitions any decision space into an acceptance region, a rejection region, and a deferment region. Each region is defined by two thresholds that balance evidence in favor of, against, or undecided about a given hypothesis. In the context of PI-Priors, these thresholds translate naturally into three evaluation dimensions:

• Membership measures the probability that a grid cell truly belongs to a high-risk class.
• Impact captures the potential consequences should waterlogging occur, derived from socio-economic and infrastructural exposure.
• Credibility quantifies the internal consistency of simulation output within a cell, reflecting model stability.

Applying TWD lets us treat membership, impact, and credibility as orthogonal evidential sources. Cells that exceed upper thresholds on all three metrics enter the acceptance region and become definitive training points. Those that fall below lower thresholds enter the rejection region and are discarded. Cells with conflicting signals form a deferment region; for these, we apply CRITIC–TOPSIS weighting to decide whether their overall evidential profile justifies inclusion.

The procedure can be understood as a dimensionality reduction process that transforms a two-dimensional continuous surface into a set of discrete representative points, while preserving essential spatial meaning and physical interpretability. By applying the TWD framework to PI-Priors, we are able to derive a well-balanced sample set that integrates high-risk relevance, spatial representativeness, and simulation credibility. To this end, this study follows the workflow illustrated in Figure 6 to construct an enhanced dataset based on PI-Priors. The following sections will provide a detailed explanation of the theoretical foundations and technical procedures involved in this process.

3.2.1. Membership Degree Quantification Based on the 2-D Connection Cloud Model

As shown in Figure 7, during the construction of the enhanced dataset based on PI-Priors, a single fishnet grid cell may contain multiple coexisting waterlogging risk levels. These risk levels differ in their proportional area coverage, and their boundaries often exhibit a degree of spatial ambiguity. Traditional hard classification methods, such as the maximum area method or the average area method, fail to capture this transitional and uncertain nature effectively.

To address this issue, this study applies the Connection Cloud Model (CCM) to quantify the waterlogging membership within each grid cell. CCM [71] extends the Normal Cloud Model (NCM) [72] by integrating set pair analysis and connection number theory [73]. Unlike NCM, which assumes normally distributed inputs and struggles to represent boundary ambiguity between classification levels [71], CCM offers greater flexibility in handling real-world indicator distributions and better captures the continuity and compatibility between adjacent risk levels. These advantages make it particularly suitable for complex systems where level boundaries are inherently fuzzy, and it has been widely applied in various uncertainty analysis and decision-making tasks [74,75,76].

In this study, CCM converts the proportion of each risk level within a grid cell into a conceptual membership degree. This approach preserves categorical distinctions while accounting for spatial heterogeneity and uncertainty, offering a more realistic representation of urban waterlogging patterns. The resulting membership degree serves as a more physically meaningful input for subsequent sample selection and model training. To handle multiple indicators simultaneously, MCCM generalizes CCM to higher dimensions. It reduces computational complexity and improves precision. Its definition is as follows: Suppose the task involves $m$ levels and $n$ indicators. For the $j-th$ indicator at level $i$, the MCCM is composed of two clusters of cloud droplets with an expected value of $E{x}_{ij}$. Let $\mathbf{C}$ be a qualitative concept in an n-dimensional quantitative space $\mathbf{Q}$, and let $\mathbf{x}\in \mathbf{Q}$ be a random realization of $\mathbf{C}$. If $\mathbf{x}$ follows a normal distribution $\mathbf{x}~\mathcal{N}(\mathbf{E}\mathbf{x},{\mathit{\sigma }}^2)$, and $\mathit{\sigma }~\mathcal{N}\left(\mathbf{E}\mathbf{n},\mathbf{H}{\mathbf{e}}^2\right)$, then the overall quantitative characteristics of $\mathbf{C}$ are defined as follows:

$$\begin{array}{c}{\mu }_i\left(\mathbf{x}\right)=\exp \left(-{\displaystyle \frac{9}{2}}{\displaystyle {\displaystyle \sum _{j=1}^n}}{\left|{\displaystyle \frac{x_{ij}-E{x}_{ij}}{3{\sigma }_{ij}}}\right|}^{{\lambda }_{ij}}\right)\end{array}$$

(2)

where ${\mu }_i\left(\mathbf{x}\right)$ denotes the membership degree between sample $\mathbf{x}$ and level $i$. For indicator $j$ at level $i$, the parameters $E{x}_{ij}$, ${En}_{ij}$, ${He}_{ij}$, ${\lambda }_{ij}$, and ${\sigma }_{ij}~\mathcal{N}\left(E{n}_{ij},H{e}_{ij}^2\right)$ correspond to expected value, entropy, hyper-entropy, cloud order, and a random variable, respectively.

A sample $\mathbf{x}(x_1,x_2,...,x_n)$ in an n-dimensional space, paired with its membership degree ${\mu }_i\left(\mathbf{x}\right)$, forms a single cloud droplet. Repeating this process across all indicators and levels yields an n-dimensional CCM $\left(\mathbf{x},\mathit{\mu }\right)$. In previous studies, the calculation of $E{x}_{ij}$, ${En}_{ij}$, ${He}_{ij}$, and ${\lambda }_{ij}$ relies on predefined evaluation criteria for each indicator. Therefore, establishing a well-defined evaluation criterion for determining whether a grid cell is waterlogging-prone is a necessary first step.

Numerous studies suggest that road surface water exceeding 0.25 to 0.35 m can impair vehicle control. For instance, Yin recommends avoiding roads submerged beyond this depth, which matches typical exhaust pipe height [77]. Similarly, Coles et al. and Green et al. proposed a 0.25 m threshold for emergency vehicle access in the UK [78,79]. Moreover, the Chinese Code for Design of Urban Road Engineering (CJJ37-2012) stipulates that curbstone heights range from 0.1 to 0.2 m. When water depth is below this range, waterlogging is generally confined to the roadway without affecting sidewalks or green belts. As shown in Equation (1), when a grid cell is classified as low or no risk $(R\le 0.75)$, the water depth $d$ remains below 0.15 m. Accordingly, we adopts 0.15 m as the threshold to distinguish between waterlogging-prone and safe areas.

Table 2. The initial urban waterlogging risk assessment criterion based on PI-Priors.

State	Safety Factor ${\mathit{S}}_{\mathit{k}}={\mathit{P}}_{\mathit{k}}^{\mathit{N}}+{\mathit{P}}_{\mathit{k}}^{\mathit{L}}$	Hazard Factor ${\mathit{H}}_{\mathit{k}}={\mathit{P}}_{\mathit{k}}^{\mathit{M}}+{\mathit{P}}_{\mathit{k}}^{\mathit{H}}$
Waterlogging-prone area	$0\le { S}_k \le \xi$	$1-\xi <H_k \le 1$
Waterlogging-safe area	$\xi <{ S}_k \le$1	$0<H_k \le 1-\xi$

summarizes the initial classification criteria based on PI-Priors.

Table 2 defines $\xi$ as the Safety-Hazard Demarcation Index. For the $k-\mathrm{t}\mathrm{h}$ analysis grid, the Safety Factor $S_k$ is computed based on the proportion of No-risk $\left(P_k^N\right)$ and Low-risk $\left(P_k^L\right)$ areas, while the Hazard Factor $H_k$ is derived from the proportion of Medium-risk $\left(P_k^M\right)$ and High-risk $\left(P_k^H\right)$ areas. When computing $S_k\left(P_k^N,P_k^L\right)$ and $H_k\left(P_k^M,P_k^H\right)$, it is essential to recognize that different risk levels contribute unequally to waterlogging susceptibility. A simple sum of area proportions cannot accurately reflect their relative significance. For example, although both cases $P_k^N=1,{ P}_k^L=0$ and $P_k^N=0,{ P}_k^L=1$ yield the same total $S_k=1$, the former clearly indicates a lower risk likelihood. To account for such differences, weighting factors should be introduced to modify the contribution of each risk level. The modified Safety Factor ${\widehat{S}}_k$ and Hazard Factor ${\widehat{H}}_k$ are calculated as follows:

$$\begin{array}{c}\left\{\begin{array}{c}{\widehat{S}}_k=w_N{P}_k^N+w_L{P}_k^L,0<w_L<w_N<1\\ {\widehat{H}}_k=w_M{P}_k^M+w_H{P}_k^H,0<w_M<w_H<1\end{array}\right.\end{array}$$

(3)

where $w_N + w_L = 1$ and $w_M + w_H = 1$. These weights ensure that higher risk levels exert greater influence in the hazard computation. The introduction of weights also changes the value ranges of ${\widehat{S}}_k$ and ${\widehat{H}}_k$, which can be determined through basic linear programming (Figure 8) based on the conditions listed in Table 2.

Figure 8c illustrates the modified ranges of ${\widehat{S}}_k$ and ${\widehat{H}}_k$. These ranges intersect, creating an ambiguous and fuzzy zone in which grid-cell membership cannot be assigned with confidence. Therefore, it is necessary to revise the classification criteria defined in Table 2, and the updated version is presented in

Table 3. A modified urban waterlogging risk assessment criterion based on PI-Priors.

State	Modified Safety Factor ${\widehat{\mathit{S}}}_{\mathit{k}}$	Modified Hazard Factor ${\widehat{\mathit{H}}}_{\mathit{k}}$
Waterlogging-prone area	$0 \le { \widehat{S}}_k<{ w}_L·\xi$	$w_H·\left(1-\xi \right)\le {\widehat{H}}_k\le w_H$
Waterlogging-fuzzy area	$w_L·\xi \le {\widehat{S}}_k<w_N·\xi$	$w_M·\left(1-\xi \right) \le {\widehat{H}}_k<w_H·\left(1-\xi \right)$
Waterlogging-safe area	$w_N·\xi \le {\widehat{S}}_k \le w_N$	$0 \le {\widehat{H}}_k<w_M·\left(1-\xi \right)$

.

Based on Table 3, the numerical characteristics $(E{x}_{ij},E{n}_{ij},H{e}_{ij},{\lambda }_{ij})$ required to construct the MCCM can be calculated. As shown in Figure 8c, the expected value for the waterlogging-prone area, denoted as $\mathbf{E}{\mathbf{x}}_{\mathrm{W}-\mathrm{P}}$, is clearly $\left(0,w_H\right)$ because in this case ${\widehat{S}}_k$ reaches its minimum, while ${\widehat{H}}_k$ reaches its maximum. Similarly, the expected value for the waterlogging-safe area, $\mathbf{E}{\mathbf{x}}_{\mathrm{W}-\mathrm{S}}$ is $\left(w_N,0\right)$. For the fuzzy area, the center point represents the most ambiguous classification, and its expected value is calculated as $\mathbf{E}{\mathbf{x}}_{\mathrm{W}-\mathrm{F}}=\left({\displaystyle \frac{(w_N+w_L)\xi }{2}},{\displaystyle \frac{(w_M+w_H)(1-\xi )}{2}}\right)$. The remaining parameters are calculated as follows:

$$\begin{array}{c}E{n}_{ij}={\displaystyle \frac{a_{ij}}{3}}\end{array}$$

(4)

$$\begin{array}{c}H{e}_{ij}=\beta \cdot E{n}_{ij}\end{array}$$

(5)

$$\begin{array}{c}{\lambda }_{ij}={\displaystyle \frac{\mathrm{l}\mathrm{n}\left(\frac{\mathrm{l}\mathrm{n} 4}{9}\right)}{\mathrm{l}\mathrm{n}\left|\frac{I_{ij}-E{x}_{ij}}{3E{n}_{ij}}\right|}}\end{array}$$

(6)

where $\beta$ is the MCCM fuzziness coefficient, fixed at 0.01 in this study. $I_{ij}$ denotes the upper $\left(I_{ij}^{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$ or lower $\left(I_{ij}^{\mathrm{m}\mathrm{i}\mathrm{n}}\right)$ bound of indicator $j$ in level $i$. The width $a_{ij}$ of each cloud is defined by the left $\left(a_{ij}^{\mathrm{L}}\right)$ and right $\left(a_{ij}^{\mathrm{R}}\right)$ half-widths. In this study, it is calculated as follows:

$$\begin{array}{c}\left\{\begin{array}{c}{a}_{ij}^{\mathrm{L}}=E{x}_{ij}-I_{\left(i-1\right)j}^{\mathrm{m}\mathrm{i}\mathrm{n}}\\ a_{ij}^{\mathrm{R}}=I_{\left(i+1\right)j}^{\mathrm{m}\mathrm{a}\mathrm{x}}-E{x}_{ij}\end{array}\right.\end{array}$$

(7)

Once the parameters $(w_N,w_L,w_M,w_H,\xi )$ are specified, all numerical characteristics can be determined based on Equations (4)–(7), and used to construct the MCCM. For each sample $\mathbf{x}$, the corresponding membership vector $\mathit{\mu }\left(\mathbf{x}\right)=\left[{\mu }^{\mathrm{w}\mathrm{p}},{\mu }^{\mathrm{w}\mathrm{f}},{\mu }^{\mathrm{w}\mathrm{s}}\right]$ is calculated, and each grid cell is finally labeled by the maximum-membership rule.

3.2.2. Impact and Credibility Score Quantification Based on the CRITIC-TOPSIS Method

Based on the MCCM, the membership matrix $\mathbf{U}\in {\mathbb{R}}^{\mathrm{K}\times 3}$ can be computed for the initial sample set $\mathbf{X}$, enabling a preliminary classification of the PI-Priors spatial outputs. Using TWD theory, each sample $i$ is routed to an acceptance, rejection, or fuzzy region. Samples with $\mathrm{m}\mathrm{a}\mathrm{x}\left({\mathbf{U}}_i\right)={\mu }_i^{\mathrm{w}\mathrm{p}}$ enter the acceptance region, those with $\mathrm{m}\mathrm{a}\mathrm{x}\left({\mathbf{U}}_i\right)={\mu }_i^{\mathrm{w}\mathrm{s}}$ enter the rejection region, and ambiguous cases fall into the fuzzy region for further screening. To extract the most representative waterlogging-prone points with strong potential relevance and physical plausibility, we analyze a filtered subset ${\mathbf{X}}_{\mathrm{s}\mathrm{e}\mathrm{l}}$ drawn from the acceptance and fuzzy regions. The CRITIC-TOPSIS procedure then ranks these samples by two complementary criteria:

• The Impact matrix ${\mathbf{X}}_{\mathrm{i}\mathrm{m}\mathrm{p}}$ includes four indicators: population density, GDP, building density, and road density (see Table 1). These indicators reflect the potential urban exposure and losses if waterlogging occurs in the area.
• The Credibility matrix ${\mathbf{X}}_{\mathrm{c}\mathrm{r}\mathrm{e}}$ includes four spatial proximity indicators: distance to water system, distance to underpass, distance to concave-down overpasses, and distance to HWR points. These indicators assess the spatial and physical reliability of the PI-Priors by estimating how likely the identified risk is to exist in reality.

The following procedures are then applied to both the impact matrix ${\mathbf{X}}_{\mathrm{i}\mathrm{m}\mathrm{p}}$ and the credibility matrix ${\mathbf{X}}_{\mathrm{c}\mathrm{r}\mathrm{e}}$.

Step 1. Indicator Direction Alignment and Normalization Mapping 

Let the indicator matrix be denoted as $\mathbf{X}={ \left[x_{ij}\right]}_{m\times n}$, where $x_{ij}$ represents the value of the $j-\mathrm{t}\mathrm{h}$ indicator for the $i-\mathrm{t}\mathrm{h}$ sample $(i = 1,2,\dots ,m; j=1,2,\dots ,n)$. To harmonize indicator direction and scale, we first apply Z-score standardization and then map the standardized values through the standard normal cumulative distribution function $\mathrm{\Phi }$, producing the normalized matrix $\widehat{\mathbf{X}}={\left[{\widehat{x}}_{ij}\right]}_{m\times n}$:

$$\begin{array}{c}{\widehat{x}}_{ij}=\left\{\begin{array}{c}\mathrm{\Phi }\left({\displaystyle \frac{x_{ij}-\mathbb{E}\left[x_j\right]}{\sqrt{\mathrm{V}\mathrm{a}\mathrm{r}\left[x_j\right]}}}\right), \mathrm{if} x_j \mathrm{is} \mathrm{a} \mathrm{benefit}-\mathrm{type} \mathrm{indicator}\\ \mathrm{\Phi }\left(-{\displaystyle \frac{x_{ij}-\mathbb{E}\left[x_j\right]}{\sqrt{\mathrm{V}\mathrm{a}\mathrm{r}\left[x_j\right]}}}\right), \mathrm{if} x_j \mathrm{is} \mathrm{a} \mathrm{cost}-\mathrm{type} \mathrm{indicator}\end{array}\right.\end{array}$$

(8)

where $\mathbb{E}\left[x_j\right]$ and $\mathrm{V}\mathrm{a}\mathrm{r}$[$x_j$] denote the mean and variance of the $j-\mathrm{t}\mathrm{h}$ indicator, respectively. The normalized value ${\widehat{x}}_{ij}\in \left[0,1\right]$ with values closer to 1 indicating higher importance or contribution to risk.

Step 2. Indicator Weight Calculation Based on the CRITIC Method 

To assign objective weights to each indicator, we adopt the CRITIC (Criteria Importance Through Intercriteria Correlation) method [80]. CRITIC balances an indicator’s discriminative power, captured by its standard deviation, with its redundancy, captured by Pearson correlations, thereby eliminating subjective bias in weighting. For the normalized matrix $\widehat{\mathbf{X}}$, the standard deviation of each indicator is calculated as ${\sigma }_j = \mathrm{S}\mathrm{t}\mathrm{d}\left[{\widehat{x}}_j\right]$, and the Pearson correlation matrix $\mathit{\rho }$ is constructed as follows:

$$\begin{array}{c}\mathit{\rho }=\left[\begin{array}{cccc}{\rho }_{11}& {\rho }_{12}& \dots & {\rho }_{1n}\\ {\rho }_{21}& {\rho }_{22}& \dots & {\rho }_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\rho }_{n1}& {\rho }_{n2}& \dots & {\rho }_{nn}\end{array}\right], {\rho }_{jk}={\displaystyle \frac{{\sum }_{i=1}^m\left({\widehat{x}}_{ij}-{\overline{x}}_j\right)\left({\widehat{x}}_{ik}-{\overline{x}}_k\right)}{\sqrt{{\sum }_{i=1}^m{\left({\widehat{x}}_{ij}-{\overline{x}}_j\right)}^2}\cdot \sqrt{{\sum }_{i=1}^m{\left({\widehat{x}}_{ik}-{\overline{x}}_k\right)}^2}}}\end{array}$$

(9)

Finally, the information content of indicator $j$ denoted as $R_j$, is computed based on its variability and correlation with other indicators. The weight $w_j$ is then derived by normalizing the information content across all indicators:

$$\begin{array}{c}\left\{\begin{array}{c}{R}_j={\sigma }_j{\displaystyle {\displaystyle \sum _{k=1}^n}}\left(1-\left|{\rho }_{ik}\right|\right), j=1,...,n\\ w_j={\displaystyle \frac{R_j}{{\sum }_{j=1}^n{R}_j}}, \mathbf{w}=\left[w_1,w_2,...,w_n\right]\end{array}\right.\end{array}$$

(10)

Step 3. Composite Scoring Using the TOPSIS Method 

After obtaining the indicator weights $\mathbf{w}$, the TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) method [81] is applied to evaluate and rank each sample based on a composite score. This method calculates the relative closeness of each sample to the ideal solution by comparing its distance to both the positive ideal solution and the negative ideal solution [82]. To implement this process, the first step is to determine the positive ideal solution ${\mathbf{A}}^{+}$ and the negative ideal solution ${\mathbf{A}}^{-}$ for each indicator:

$$\begin{array}{c}\left\{\begin{array}{c}{A}_j^{+}=\underset{1⩽i⩽m}{\mathrm{m}\mathrm{a}\mathrm{x}}{\widehat{x}}_{ij},{\mathbf{A}}^{+}={\left[A_j^{+}\right]}_{1\times n}\\ A_j^{-}=\underset{1⩽i⩽m}{\mathrm{m}\mathrm{i}\mathrm{n}}{\widehat{x}}_{ij},{\mathbf{A}}^{-}={\left[A_j^{-}\right]}_{1\times n}\end{array}\right.\end{array}$$

(11)

Next, for each sample, the Euclidean distances to ${\mathbf{A}}^{+}$ and ${\mathbf{A}}^{-}$ in the weighted indicator space are computed as follows:

$$\begin{array}{c}\left\{\begin{array}{c}{D}_i^{+}=\sqrt{{\displaystyle {\displaystyle \sum _{j=1}^n}}{w}_j{\left({\widehat{x}}_{ij}-A_j^{+}\right)}^2}\\ D_i^{-}=\sqrt{{\displaystyle {\displaystyle \sum _{j=1}^n}}{w}_j{\left({\widehat{x}}_{ij}-A_j^{-}\right)}^2}\end{array}\right.\end{array}$$

(12)

Finally, the TOPSIS composite score $S_i$ for sample $i$ is calculated as

$$\begin{array}{c}{S}_i={\displaystyle \frac{D_i^{-}}{D_i^{+}+D_i^{-}}}\end{array}$$

(13)

where $S_i\in \left[0,1\right]$, with higher values indicating closer proximity to the ideal high-risk condition. In this study, TOPSIS scores are calculated separately for two dimensions: $S_i^{\left({\mathbf{X}}_{\mathrm{i}\mathrm{m}\mathrm{p}}\right)}$ for impact (potential social consequences) and $S_i^{\left({\mathbf{X}}_{\mathrm{c}\mathrm{r}\mathrm{e}}\right)}$ for credibility (spatial and physical reliability). These scores are then used to identify and prioritize high-risk potential waterlogging locations.

3.2.3. Selection of Supplementary Waterlogging Points Based on TWD Theory

Applying MCCM together with CRITIC–TOPSIS yields, for every grid cell, (i) a membership vector ${\mathit{\mu }}_i$ and (ii) two composite scores: impact $S_i^{\left({\mathbf{X}}_{\mathrm{i}\mathrm{m}\mathrm{p}}\right)}$ and credibility $S_i^{\left({\mathbf{X}}_{\mathrm{c}\mathrm{r}\mathrm{e}}\right)}$. We use TWD to route cells into acceptance, rejection, or fuzzy regions (Figure 9). Cells with strong evidence (high membership) enter the acceptance region; weak-evidence cases remain fuzzy; and clearly negative cases go to rejection.

To reflect gradual transitions, the acceptance region is split into strong-acceptance and weak-acceptance; the fuzzy region is split into positive-leaning and negative-leaning. Strong-acceptance cells are directly added to the qualified supplementary set ${\mathbf{\Psi }}^{+}$. Weak-acceptance and positive-leaning fuzzy cells are retained only if both composite scores exceed their thresholds ($S_i^{\left({\mathbf{X}}_{\mathrm{i}\mathrm{m}\mathrm{p}}\right) }\ge { \epsilon }_I^{+}$ and $S_i^{\left({\mathbf{X}}_{\mathrm{c}\mathrm{r}\mathrm{e}}\right)} \ge {\epsilon }_C^{+}$). For fuzzy cases, the thresholds are set more strictly. Negative-leaning fuzzy and rejection cells are discarded. This rule preserves informative transitional samples while controlling false positives, producing a balanced, credible set of supplementary waterlogging points for downstream modeling.

3.3. MaxEnt-Based Modeling for UWSA

After completing indicator selection and supplementary-dataset construction (Section 3.1 and Section 3.2), this section develops a spatial UWSA model using MaxEnt. Rooted in information-entropy theory, MaxEnt originated in statistical mechanics and was later adapted for ecological niche modeling [83]. It excels at spatial prediction when data are incomplete because it infers the probability distribution with the highest entropy, producing the least-biased estimates consistent with observed information. MaxEnt does not require negative samples and can accommodate diverse predictor types, which makes it particularly suitable for environmental-hazard analyses such as urban waterlogging.

3.3.1. MaxEnt Principles and Methods

Mathematically, let $x$ denote the input vector and $y_1,y_2,\dots ,y_n$ the output classes. MaxEnt defines the conditional probability of output $y$ given input $x$ as

$$\begin{array}{c}p\left(y\mid x\right)={\displaystyle \frac{1}{Z\left(x\right)}}\exp \left({\displaystyle {\displaystyle \sum _{i=1}^k}}{w}_i{f}_i\left(x,y\right)\right)\end{array}$$

(14)

where $f_i\left(x,y\right)$ is the $i-\mathrm{t}\mathrm{h}$ feature function, $w_i$ its learned weight, and $Z\left(x\right)$ a normalization constant ensuring probabilities sum to one. This modeling approach allows prior knowledge to be effectively integrated with spatial features. The objective of MaxEnt is to maximize the regularized log-likelihood function over the training set $D$, expressed as

$$\begin{array}{c}{\displaystyle \underset{w}{\mathrm{m}\mathrm{a}\mathrm{x}}}{\displaystyle \sum _{\left(x,y\right)\in D}}\mathrm{l}\mathrm{o}\mathrm{g} p\left(y|x\right)-C\cdot R\left(w\right)\end{array}$$

(15)

with $C$ the regularization coefficient, and $R\left(w\right)$ the penalty term that controls overfitting.

3.3.2. Parameter Setting and Model Construction of MaxEnt

Previous studies confirm that MaxEnt can deliver objective spatial predictions and quantify each indicator’s contribution [84]. In this work, we use the MaxEnt v3.4.4 software released by Columbia University to estimate waterlogging susceptibility. The HWR dataset is combined with ${\mathbf{\Psi }}^{+}$ to form the merged sample set. Geographic coordinates are entered as species-occurrence points, and the UWSA indicators serve as environmental variables. The merged samples are randomly split into training and testing datasets at a ratio of 75% to 25%. Indicator importance is examined with the built-in jackknife test [85], while all other parameters remain at their default values. Model stability is assessed through ten bootstrap replicates [86].

Model performance is evaluated with the Receiver Operating Characteristic (ROC) curve. The area under this curve (AUC) ranges from 0 to 1, where 0.5 denotes random prediction, values below 0.6 indicate poor performance, 0.6~0.8 moderate, 0.8~0.9 good, and above 0.9 excellent [87]. Outputs are exported in ASCII format and visualized in ArcGIS Pro using the Jenks natural-breaks method [88] to map waterlogging susceptibility levels distribution across the central urban area of Hefei.

3.4. Spatial Autocorrelation Analysis Method

To evaluate whether supplementary waterlogging points show spatial dependence, this study applies spatial autocorrelation analysis after model construction. Spatial autocorrelation measures the clustering or dispersion of susceptibility across space and serves both as a validation of model outputs and as support for spatial decision-making. In this study, both global and local indices are used. The global Moran’s I index assesses the overall spatial association across the study area, computed as follows:

$$\begin{array}{c}I={\displaystyle \frac{n{\displaystyle {\displaystyle \sum _{i=1}^n}}{\displaystyle {\displaystyle \sum _{j=1}^n}}{\alpha }_{ij}\left(x_i-\overline{x}\right)\left(x_j-\overline{x}\right)}{{\displaystyle {\displaystyle \sum _{i=1}^n}}{\displaystyle {\displaystyle \sum _{j=1}^n}}{\alpha }_{ij}\left({\displaystyle \sum _{i=1}^n}{\left(x_i-\overline{x}\right)}^2\right)}}\end{array}$$

(16)

where $n$ is the total number of spatial grid cells, $x_i$ represents the attribute value of cell $i$, $\overline{x}$ is the mean attribute value, and ${\alpha }_{ij}$ is the spatial weight based on distance. The value of Moran’s I ranges from $-1$ to $+1$, where positive values indicate positive spatial correlation (that is, clustering), negative values indicate negative spatial correlation (that is, dispersion), and values close to zero suggest a random spatial pattern.

To identify local clusters and outliers in waterlogging susceptibility, the Local Indicators of Spatial Association (LISA), specifically the local Moran’s I index, is further applied as follows:

$$\begin{array}{c}{I}_i=\left(x_i-\overline{x}\right){\displaystyle {\displaystyle \sum _{j=1}^n}}{w}_{ij}\left(x_j-\overline{x}\right)\end{array}$$

(17)

LISA can reveal patterns such as high-high clusters (hotspots), low-low clusters (coldspots), and spatial outliers (high-low or low-high). The statistical significance of these local patterns is evaluated using Monte Carlo randomization and pseudo p-value estimation.

4. Results

4.1. Results of the Supplementary Dataset Based on PI-Priors

According to the procedure described in Section 3.2, the MCCM for waterlogging risk is constructed using the parameter set $(w_N,w_L,w_M,w_H,\xi ) = (0.6,0.4,0.2,0.8,0.75)$ as illustrated in Figure 10. By inputting all grid cell samples into the MCCM-CRITIC-TOPSIS framework, the membership vector ${\mathit{\mu }}_i$, the impact score $S_i^{\left({\mathbf{X}}_{\mathrm{i}\mathrm{m}\mathrm{p}}\right)}$, and the credibility score $S_i^{\left({\mathbf{X}}_{\mathrm{c}\mathrm{r}\mathrm{e}}\right)}$ are calculated for each grid cell ${\mathbf{x}}_i$. Then, based on the sample selection logic presented in Figure 9, thresholds are set to identify qualified supplementary waterlogging points using the PI-Priors.

For the threshold parameters $({\tau }_{\mu }^{+},{\tau }_{\mu }^0,{\epsilon }_I^{+},{\epsilon }_C^{+},{\epsilon }_I^0,{\epsilon }_C^0)$ shown in Figure 9, this study adopts an empirical and conservative approach. Specifically, ${\tau }_{\mu }^0$ is set to 2, ${\epsilon }_I^{+} = {\epsilon }_C^{+} = 0.3$, and ${\epsilon }_I^0 = {\epsilon }_C^0 = 0.6$. The value of ${\tau }_{\mu }^0$ reflects the assumption that samples in the positive-leaning fuzzy region ${\mathbf{\Omega }}_{+}^0$, although classified within the fuzzy region ${\mathbf{\Omega }}^0$, exhibit a stronger tendency toward the acceptance region ${\mathbf{\Omega }}^{+}$. The inequalities ${\epsilon }_I^{+} < {\epsilon }_I^0$ and ${\epsilon }_C^{+} < {\epsilon }_C^0$ indicate that samples in the positive-leaning fuzzy region ${\mathbf{\Omega }}_{+}^0$ must satisfy stricter criteria for both impact and credibility than those in the weak-acceptance region ${\mathbf{\Omega }}_{-}^{+}$ in order to be classified as qualified supplementary waterlogging points. Compared with the empirical selection of the above thresholds, a more general strategy is recommended for setting the parameter ${\tau }_{\mu }^{+}$. This approach is described as follows:

$$\begin{array}{c}{\tau }_{\mu }^{+}=\underset{\mathbf{x}\in {\mathbf{\Omega }}^{+}}{\mathrm{m}\mathrm{a}\mathrm{x}}\left\{{\mu }^{\mathrm{f}}\left(\mathbf{x}\right)\right\}\end{array}$$

(18)

Based on Equation (18), the parameter ${\tau }_{\mu }^{+}=0.5959$ was obtained. Following the logic rule outlined in Figure 9, a qualified supplementary waterlogging dataset ${\mathbf{\Psi }}^{+}$ comprising 984 additional waterlogging points was generated (Figure 11a). Among them, qualified supplementary waterlogging points are concentrated in low-lying and hydrologically vulnerable areas, while non-qualified supplementary waterlogging points are more scattered, illustrating how terrain and drainage infrastructure filter valid waterlogging events. Due to the limited spatial coverage, HWR data (Figure 11b) were mainly concentrated in the central urban area and relatively sparse elsewhere. In contrast, ${\mathbf{\Psi }}^{+}$ offers higher spatial resolution and broader geographic coverage. It is particularly valuable in peripheral zones or regions lacking HWR data, especially extending to peri-urban regions, where it effectively identifies additional areas of potential risk.

4.2. Results of Model Accuracy Validation and Dominant Factor Analysis

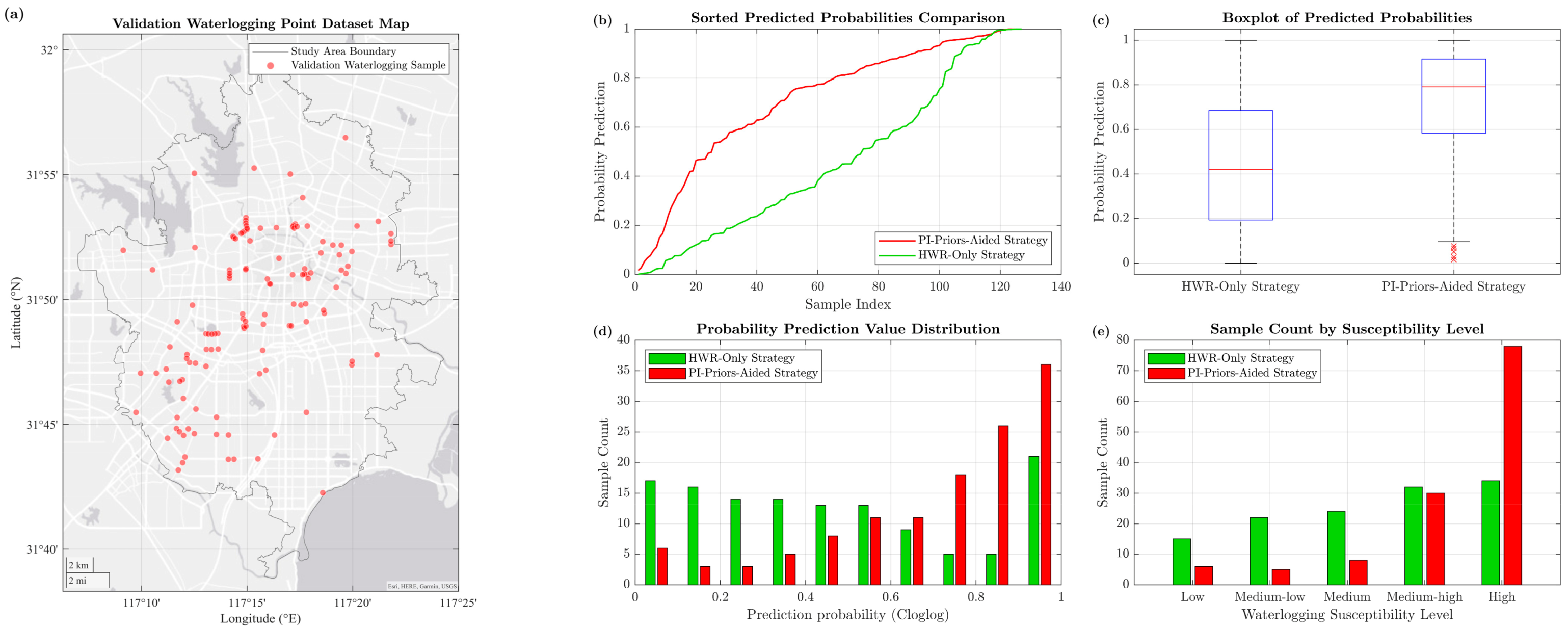
4.2.1. Model Accuracy Validation

In the MaxEnt modeling process, the inputs include species occurrence points and environmental variables. In this study, the environmental variables refer to the 19 UWSA evaluation indicators, while the species occurrence points correspond to the union of HWR and ${\mathbf{\Psi }}^{+}$ shown in Figure 11. The key parameter settings for the MaxEnt are listed in

Table 4. MaxEnt model parameter settings.

Random Seed	Random Test Percentage	Replicates	Maximum Iterations	Replicated Run Type	Output Format
True	25%	10	1000	Bootstrap	Cloglog

. After multiple rounds of experimental iteration, the ROC curve and omission curve for the waterlogging susceptibility prediction were obtained, as shown in Figure 12.

As presented in Figure 12a, the average AUC values for the training and testing datasets over 10 runs are 0.884 and 0.864, respectively, both significantly higher than the simulated value of 0.5 that represents a random distribution. Furthermore, Figure 12b demonstrates a high level of agreement between the predicted omission rate and the omission rates of both the testing and training samples. Taken together, these MaxEnt performance indicators suggest that the model has strong accuracy. It effectively explains the spatial distribution of current waterlogging points and provides reliable predictions for potential waterlogging-prone areas within the city.

4.2.2. Dominant Factor Analysis

To examine variable contributions to waterlogging susceptibility, Figure 13 shows response curves from ten MaxEnt runs. Most indicators ($N_1$, $S_1$, $I_2$, $I_3$, $I_5$, $I_6$, $B_1$, $B_2$, $B_3$, $B_4$, $B_6$) display limited variations, indicating stable and reliable predictions of waterlogging-prone areas. The curves also reveal both positive and negative effects. Roughness, slope, distance to stormwater pipes, and road density are positively correlated with waterlogging probability, while elevation, population density, and distances to concave-down overpasses and underpasses are negatively correlated. These patterns align with hydrological mechanisms, as areas near concave-down overpasses and underpasses are more prone to water accumulation ($I_2$, $I_3$). Other indicators, including precipitation, green space, impervious surface, and GDP, show no consistent directional trends.

To further quantify the contribution of each variable,

Table 5. Analysis of each index contributions.

Dimension	Index	Percent Contribution (%)	Permutation Importance (%)
Natural condition	Elevation ($N_1$)	3.2	12.2
	Roughness ($N_2$)	0.4	0.8
	Relief ($N_3$)	2.9	2.8
	Slope ($N_4$)	1.9	1.6
	Precipitation ($N_5$)	6.6	12.0
Social capital	Population density ($S_1$)	9.5	5.1
	GDP ($S_2$)	4.7	5.1
Infrastructure	Distance to overpass ($I_1$)	1.5	2.5
	Distance to concave-down overpass ($I_2$)	1.1	2.5
	Distance to underpass ($I_3$)	4.2	22.2
	Distance to stormwater drainage pipe ($I_4$)	13.5	7.6
	Density of stormwater drainage pipe ($I_5$)	8.7	0.7
	Road density ($I_6$)	18.9	11.3
Built environment	Distance to surface water system ($B_1$)	2.7	3.5
	Building density ($B_2$)	2.2	2.3
	Building height ($B_3$)	2.3	1.5
	Impervious surface ($B_4$)	13.9	2.6
	Water density ($B_5$)	0.5	1
	Green space ($B_6$)	1.3	2.8

and Figure 14 present the percentage contributions and jackknife test results of regularized training gain, respectively. According to Table 5, the top five contributing indicators are $I_6$ (18.9%), $B_4$ (13.9%), $I_4$ (13.5%), $S_1$ (9.5%), and $I_5$ (8.7%), totaling 64.5%. This highlights the dominant role of built environment and drainage infrastructure variables.

Permutation importance further reveals model sensitivity to each variable. The top five variables by permutation importance are $I_3$ (22.2%), $N_1$ (12.2%), $N_5$ (12.0%), $I_6$ (11.3%), and $I_4$ (7.6%). Compared with contribution rates, permutation importance emphasizes how strongly the model responds to changes in each variable. It highlights variables that may not contribute significantly during model training but have a substantial influence on the final prediction results. For instance, although elevation contributes only 3.2%, its permutation importance reaches 12.2%, suggesting it may have a significant effect through interactions with other variables. Similarly, distance to the underpass contributes only 4.2% but ranks first in permutation importance, indicating its high sensitivity in prediction and underscoring the need for special attention in future urban drainage planning and risk monitoring. By jointly considering both contribution rate and permutation importance, we gain a more comprehensive understanding of the role each variable plays in the model. This dual perspective helps identify key intervention points for urban waterlogging mitigation and supports data-informed decision-making in planning and risk management.

In addition, Figure 14 presents jackknife test results, confirming that most variables show low training gain when used alone ($\mathrm{G}\mathrm{a}\mathrm{i}{\mathrm{n}}^{\mathrm{o}}$), indicating the model primarily relies on variable combinations. However, variables like $S_1$, $I_4$, $I_5$, and $I_6$ demonstrate strong independent predictive power, each with individual training gains above 0.2. Among them, $I_4$ produces the highest gain as a single variable (0.374), but its removal results in only a small gain reduction ($\mathsf{\Delta }\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}=\mathrm{G}\mathrm{a}\mathrm{i}{\mathrm{n}}^{\mathrm{a}}-\mathrm{G}\mathrm{a}\mathrm{i}{\mathrm{n}}^{\mathrm{w}} = 0.047$). Similar patterns are observed for $S_1$ and $I_5$. These results highlight the strong independent explanatory power of these variables and underscore the direct influence of drainage infrastructure distribution, pipe density, and population clustering on urban waterlogging risk. It is also worth noting that some variables exhibit substantial gain reduction ($\mathsf{\Delta }\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}$) when excluded, notably $I_6$, $N_1$, and $I_3$. For example, the removal of road density ($I_6$) causes a substantial decline in model performance, and its $\mathrm{G}\mathrm{a}\mathrm{i}{\mathrm{n}}^{\mathrm{o}}$ is also relatively high. This suggests that the road network not only explains spatial variation in waterlogging independently but also interacts strongly with other variables. Therefore, it can be considered a key factor.

Moreover, elevation and precipitation show only moderate gain when used individually, but cause notable model degradation when excluded. This implies that these two variables influence susceptibility primarily through interactions with urbanization-related indicators. Additionally, while $I_3$ does not perform prominently in the only variable scenario, it ranks among the top three in terms of $\mathsf{\Delta }\mathrm{G}\mathrm{a}\mathrm{i}\mathrm{n}$, revealing a “low-contribution, high-sensitivity” profile. This suggests that underpasses should receive particular attention in the design of urban drainage systems.

4.3. Results of Susceptibility Assessment and Identification of Waterlogging Prone Areas

Based on the .asc files from ten MaxEnt runs and visualization in ArcGIS Pro, both continuous and classified susceptibility maps are shown in Figure 15. To assess the effect of incorporating PI-Priors, Figure 15 also compares results from the HWR-only strategy. Jenks’ classified maps (Figure 15b,d) were derived from continuous outputs (Figure 15a,c) using the Jenks natural breaks method with five susceptibility levels.

HWR-only predictions (Figure 15a,b) highlight high-risk zones concentrated in the old urban core, with peripheral areas showing near-zero susceptibility. In contrast, incorporating PI-Priors (Figure 15c,d) significantly changes the spatial distribution, identifying additional high-risk areas in newly developed zones, major road corridors, and dense residential districts. This effect is especially evident in the southwestern quadrant $(117.15~117.25° \mathrm{E},31.70~31.80° \mathrm{N})$, where medium-to-high-susceptibility zones expand beyond locations near HWR, indicating potential future risks.

To further validate the feasibility and effectiveness of incorporating PI-Priors, 127 verified real-waterlogging points from recent Hefei drainage planning documents (2021–2035) and official media reports of extreme rainfall events from 2020 to 2024, including the 18 July 2020 rainstorm event (Figure 16a). Their distribution in Figure 15b,d enables comparative evaluation of HWR-only and PI-Priors-aided predictions (Figure 16b–e).

For validation points, prediction probabilities closer to 1 indicate better outcomes. As shown in Figure 16b,c, the PI-Priors-Aided MaxEnt outperforms the HWR-Only model, with a median probability of 0.7914. Figure 16d further shows that 102 of 127 validation samples fall within the [0.5, 1.0] range, nearly twice the number (53) under the HWR-Only strategy. Using Jenks’ classification, samples in the Medium-high and High levels are considered priority sites for monitoring and intervention. Under this criterion, the PI-Priors-Aided strategy correctly classified 108 of 127 validation samples, achieving an accuracy of 85.04%, compared with 51.97% for the HWR-Only model (Figure 16e). These results confirm that PI-Priors substantially enhance the accuracy and robustness of UWSA.

Urban waterlogging typically shows strong spatial and temporal patterns. While meteorological triggers vary, long-term distribution is shaped by stable factors such as elevation, depressions, drainage density, and land use. Repeated accumulation at specific sites reflects structural vulnerabilities embedded in the urban landscape. The superior performance of PI-Priors-Aided modeling stems from its capacity to capture this spatial determinism. Although rainfall events are uncertain in timing and intensity, susceptibility patterns are historically formed and structurally persistent. Thus, disasters are not random occurrences but manifestations of enduring vulnerabilities. Incorporating PI-Priors, therefore, not only improves prediction accuracy but also aligns with a theoretical understanding of disaster formation as a product of urban spatial inertia and structural rigidity.

4.4. Results of Spatial Autocorrelation Analysis

Building on the identification of high-susceptibility zones in Section 4.3, this section examines whether these patterns show spatial autocorrelation. Global Moran’s I was first calculated to test overall spatial dependence. As shown in Figure 17, the Moran’s I values are 0.68 and 0.74 for the HWR-Only and PI-Priors-Aided strategies, respectively, with p-values < 0.01. These results indicate strong, non-random clustering of waterlogging susceptibility. The higher Moran’s I under the PI-Priors-Aided strategy suggests greater spatial coherence, further supported by the denser alignment of sample points in the Moran scatterplot. This provides empirical evidence that physically based variables enhance spatial explanatory power and robustness of susceptibility mapping.

To complement the global analysis, Local Indicators of Spatial Association (LISA) were applied to reveal fine-scale clustering (High-High, Low-Low, High-Low, Low-High). In Figure 18a (HWR-Only), High-High clusters are concentrated in the urban core along the Nanfei River, while Low-Low clusters dominate peripheral areas. After incorporating PI-Priors (Figure 18b), clusters become more continuous, with new High-High zones emerging in the southwestern industrial area. Notably, risks near rivers and lakes are underestimated by the HWR-Only model, as historical records are concentrated on roadways and residential sites. During events such as the 18 July 2020 Hefei rainstorm, however, rapid overflow of the Nanfei River inundated nearby low-lying areas—dynamics better captured by the PI-Priors-Aided model.

Overall, LISA analysis supports the global Moran’s I results and highlights the spatial heterogeneity of waterlogging risks. Incorporating PI-Priors improves detection of clusters near rivers and lakes, compensating for HWR limitations and providing a more physically grounded basis for urban waterlogging susceptibility modeling.

To make these patterns actionable, each output can be read as a decision cue. The continuous susceptibility surface and its class map indicate where the city is structurally prone; agencies can start with high-probability, high-credibility cells for pre-season desilting, additional inlets, and pump staging. LISA clusters move priorities from cells to corridors and neighborhoods, helping to keep lifeline routes open and plan detours. The TWD triage (accept/defer/reject) mirrors municipal practice under uncertainty: accepted cells enter maintenance and pre-deployment lists; deferred cells receive field checks or a few temporary sensors; rejected cells are archived unless corroborated. Finally, factor importance and response curves point to where pipe upsizing, local storage, and small nature-based retrofits yield the greatest marginal benefit. Read together, these elements turn the susceptibility layer into a practical order of work rather than a static map.

5. Conclusions

This study proposed a MaxEnt-based framework that integrates HWR with PI-Priors under TWD theory to assess urban waterlogging susceptibility in Hefei. The framework vectorized raster-based simulations, applied MCCM with CRITIC-TOPSIS to calculate membership, impact, and credibility, and designed a sample selection mechanism that fuses HWR with PI-Priors for enhanced modeling. Comparative analysis then identified key contributing factors and evaluated model performance under HWR-Only and PI-Priors-Aided strategies. The main conclusions are as follows:

(1) An automated procedure was developed for extracting representative waterlogging points from physically simulated rasters using TWD. Empirical validation in Hefei showed that this approach captures physically plausible, high-risk samples that complement historical records and expand spatial coverage.

(2) The MaxEnt model identified road density (18.9%), impervious surface (13.9%), distance to stormwater drainage pipes (13.5%), population density (9.5%), and drainage pipe density (8.7%) as the five most influential factors. Susceptibility was positively associated with roughness, slope, distance to drainage pipes, and road density, while areas near concave-down overpasses and underpasses were especially vulnerable.

(3) The PI-Priors-Aided strategy markedly improved model performance, achieving 85.04% prediction accuracy on the validation dataset versus 51.97% for HWR-Only. It also enhanced the detection of waterlogging clusters near rivers and lakes, aligning predictions more closely with hydrological processes.

While the proposed framework improves accuracy and spatial robustness, it relies primarily on structured inputs such as historical records and physical simulations. Future work will incorporate big data techniques to leverage unstructured sources, including social media, online news, and other urban data streams, combined with remote sensing and geospatial layers. Coupling these crowdsourced observations with general AI models and Multi-Context Processing (MCP) will enable richer, continuously updated datasets and more generalizable susceptibility frameworks. This direction may support intelligent, real-time waterlogging risk identification and provide stronger evidence for drainage planning and emergency response.