A Rapid Modeling Method for Sound Radiation of China’s Locomotive Traction Drive Systems in Railways
Abstract
1. Introduction
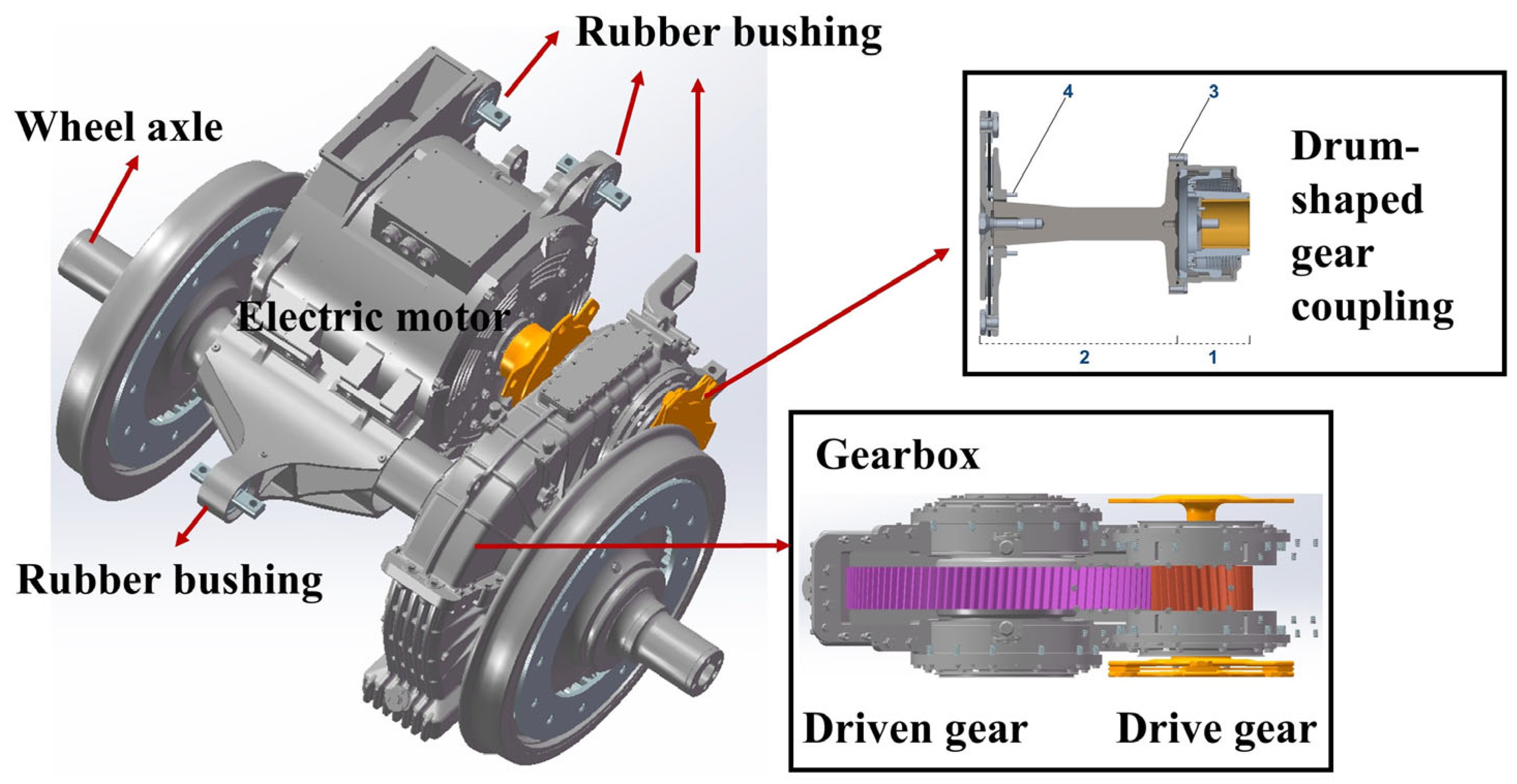
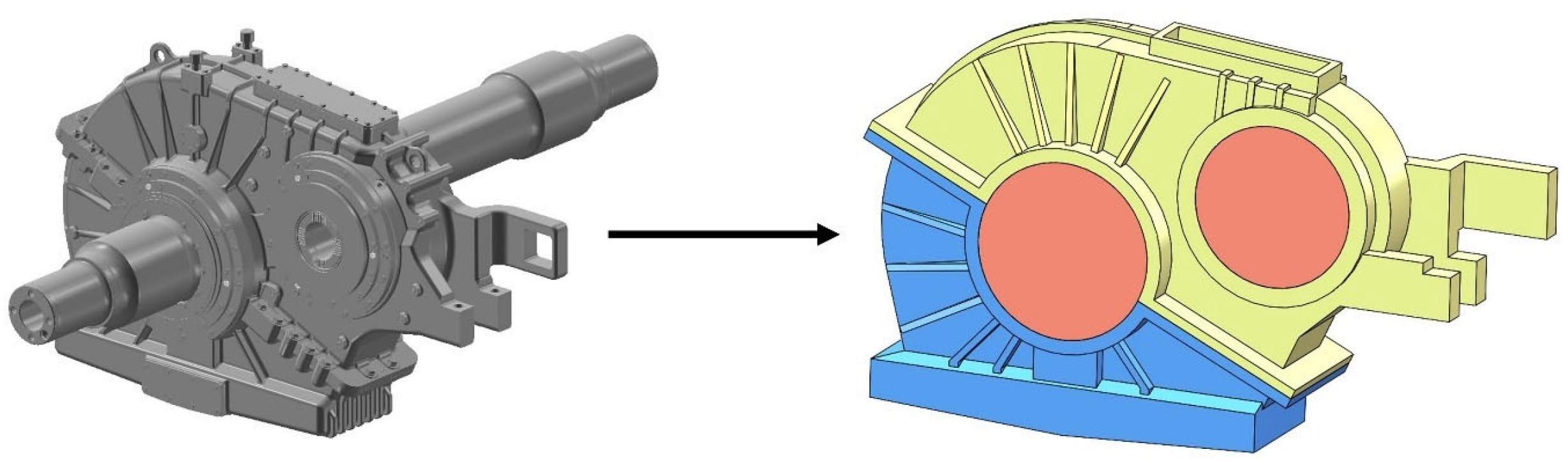
2. Configuration of Locomotive Traction Drive Systems
3. Vibro-Acoustic Test and Analysis
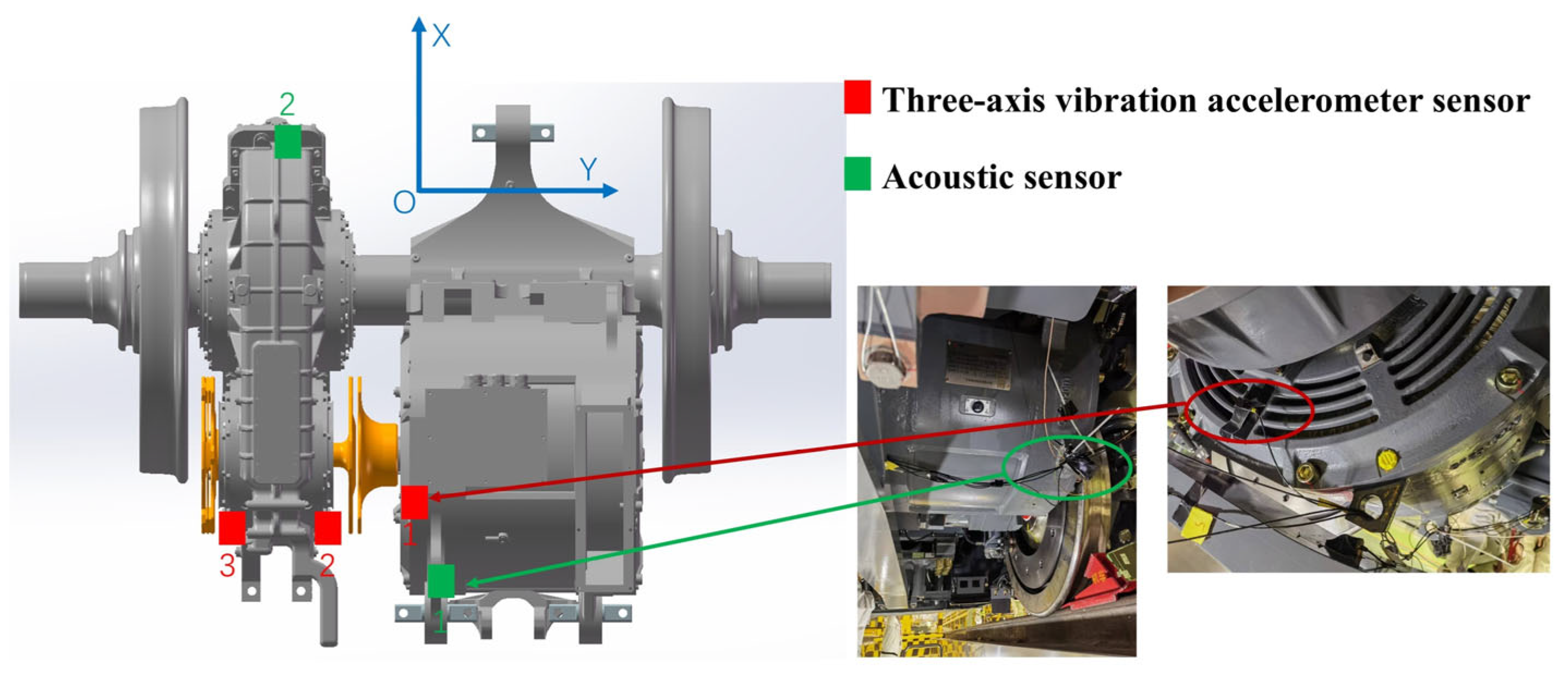
3.1. Sensor Arrangement and Main Test Conditions
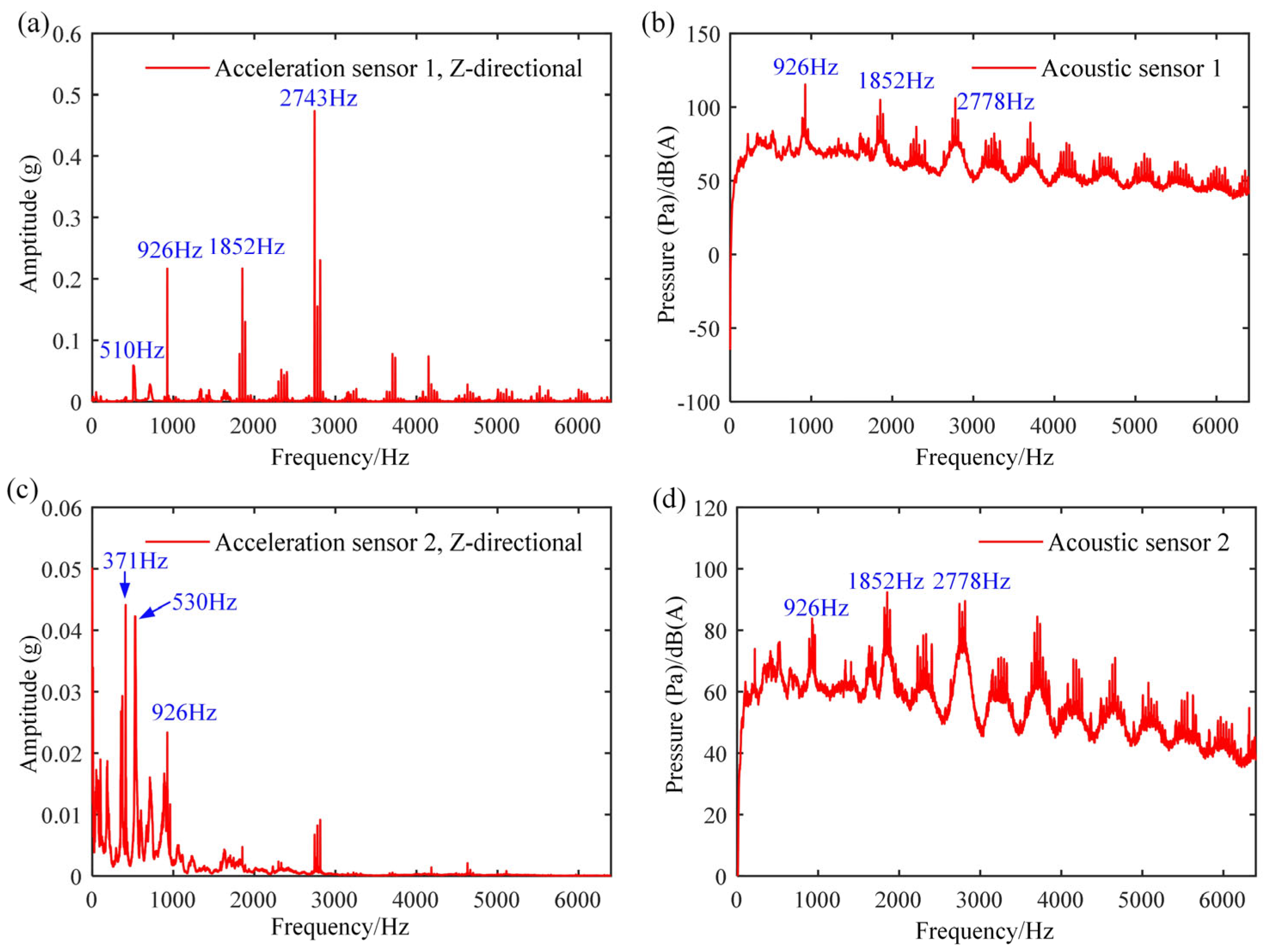
3.2. Analysis of Testing Results
4. Rapid Modeling of Acoustic Radiation
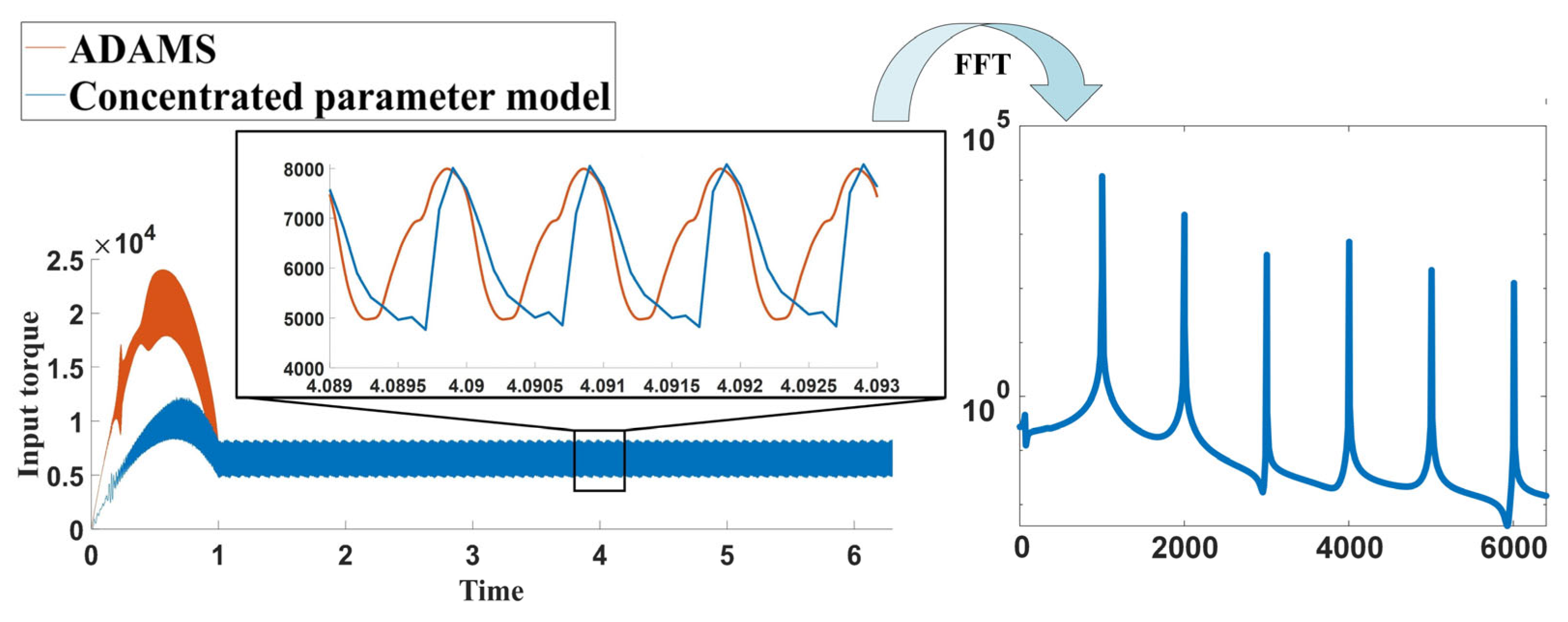
4.1. Parametric Modeling and Verification of Gear System
4.2. Dynamic Force Excitation Calculation for Gearbox Housing
4.3. Meshing Noise Excitation Calculation
4.4. Motor Noise Excitation Calculation
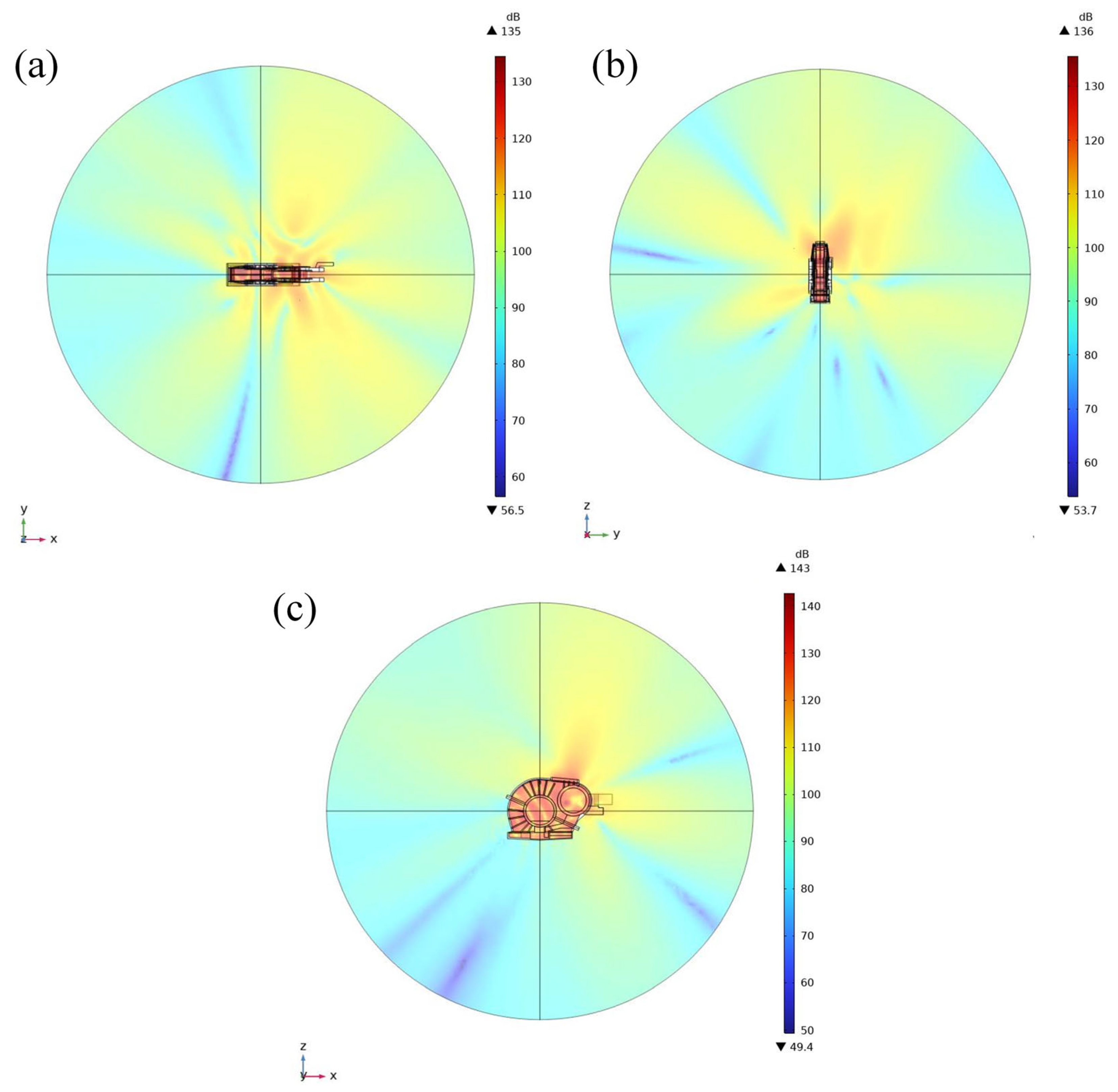
4.5. Sound Radiation Simulation of Total Traction Drive System
5. Parametric Impact Analysis of Acoustic Radiation
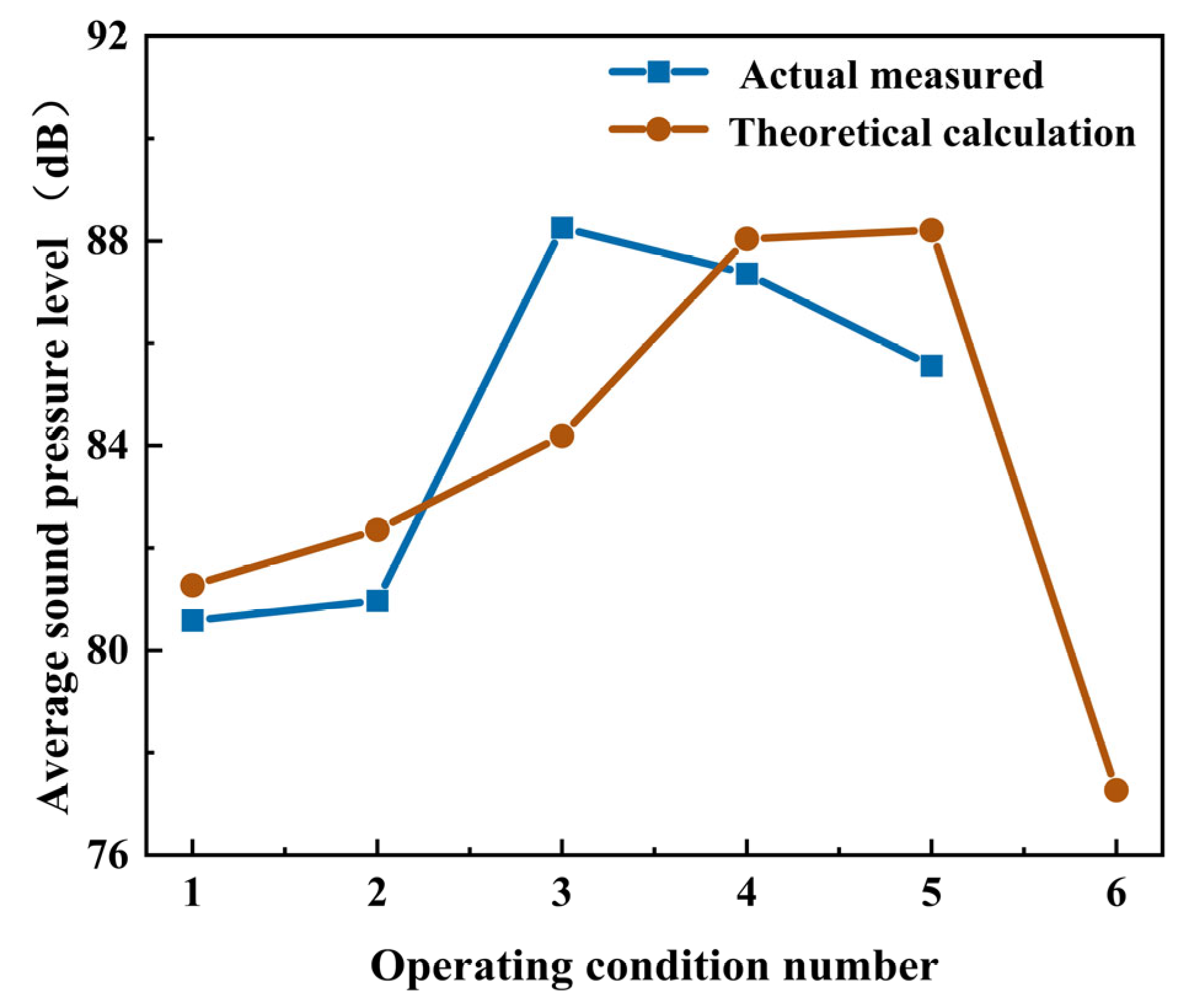
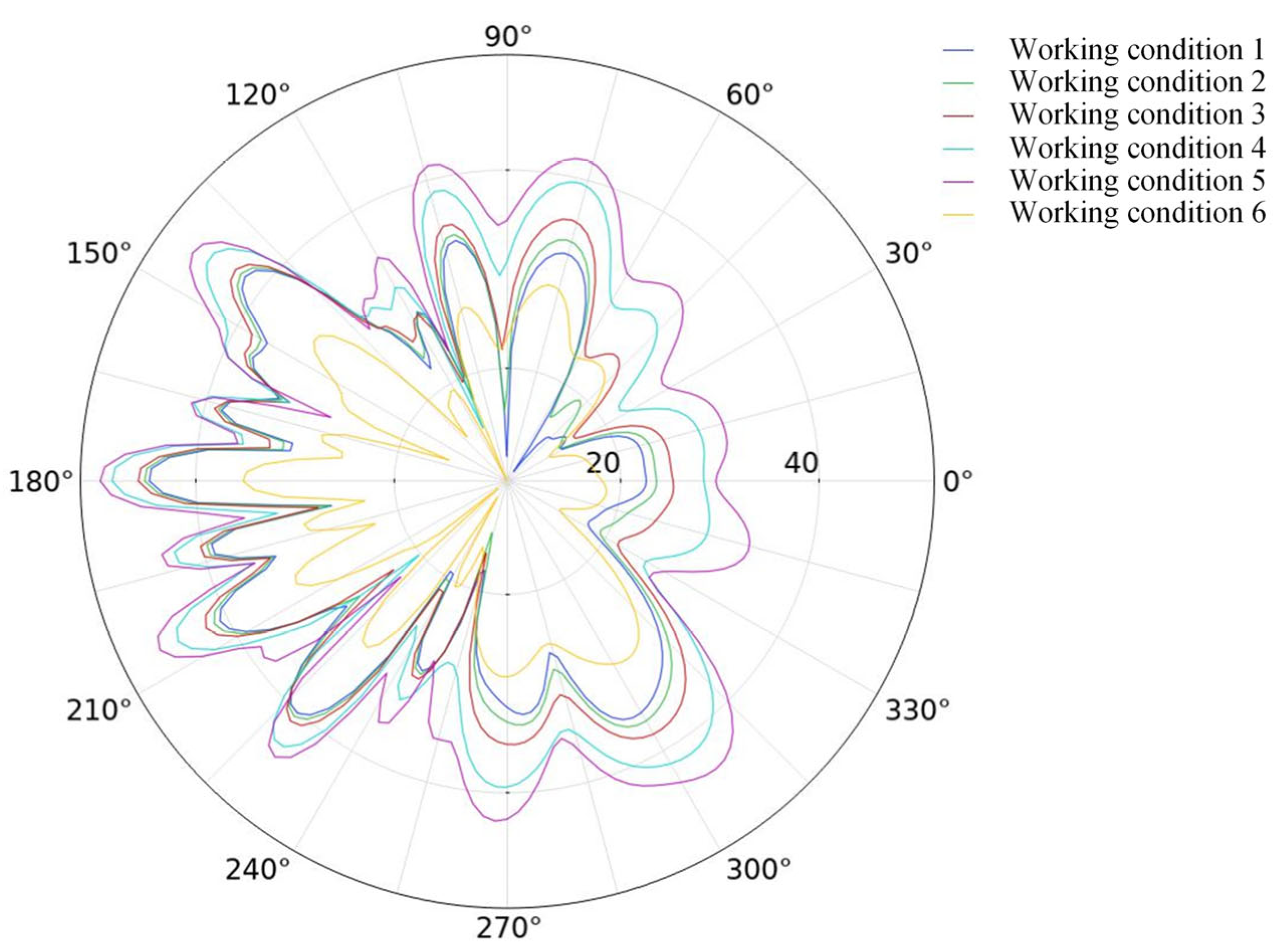
5.1. The Effect of Operating Condition (Speed) on Acoustic Radiation
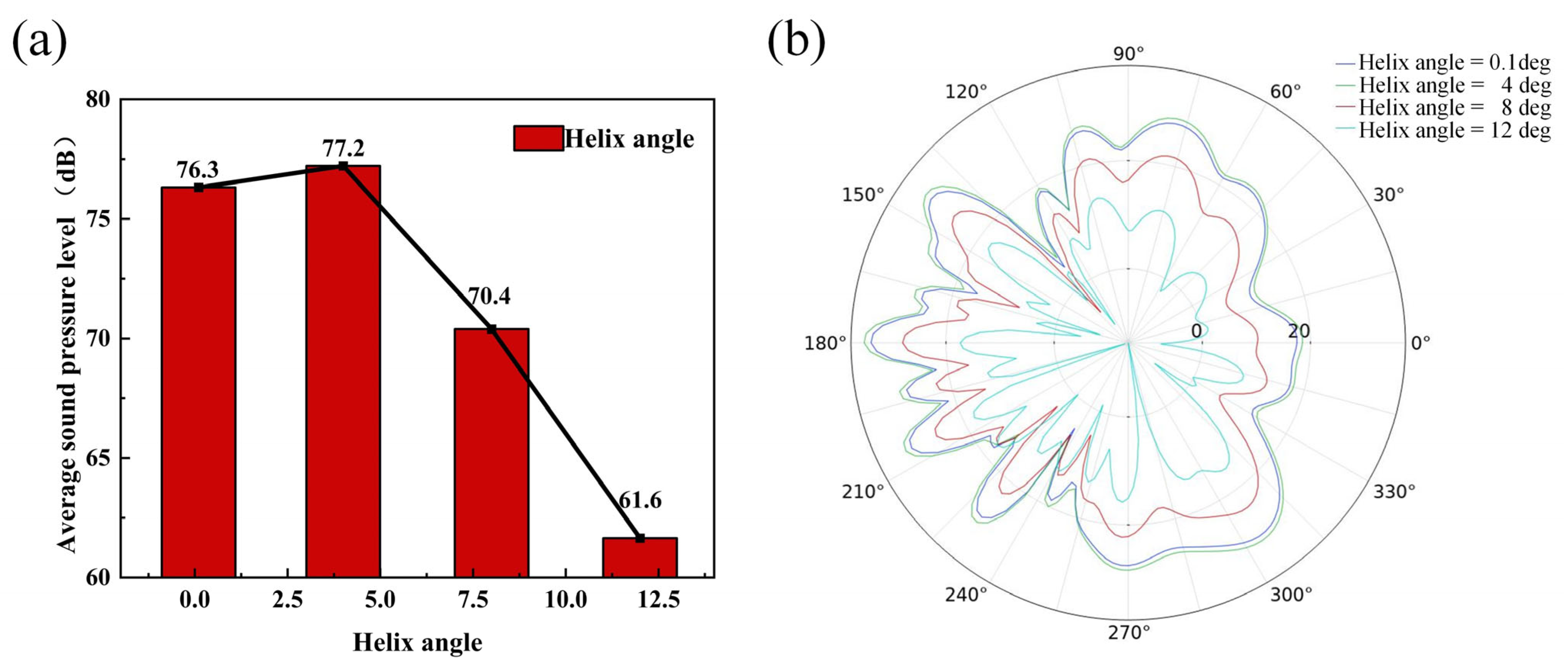
5.2. The Effect of Helix Angle on Acoustic Radiation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, J.; Luo, C.; Qiu, L.; Liu, X.; Xu, B.; Shou, J.; Fang, Y. Recent advances in traction drive technology for rail transit. J. Zhejiang Univ. A 2023, 24, 177–188. [Google Scholar] [CrossRef]
- Polater, N.; Tricoli, P. Technical Review of Traction Drive Systems for Light Railways. Energies 2022, 15, 3187. [Google Scholar] [CrossRef]
- Morgado, T.; Branco, C.; Infante, V. A failure study of housing of the gearboxes of series 2600 locomotives of the Portuguese Railway Company. Eng. Fail. Anal. 2008, 15, 154–164. [Google Scholar] [CrossRef]
- Ye, Z.; Chen, Z.; Zhou, Z.; Zhai, W. Dynamic modelling of locomotive with direct drive traction system considering electromechanical coupling effect. Veh. Syst. Dyn. 2024, 62, 1756–1779. [Google Scholar] [CrossRef]
- Poliakov, N.; Arbuzina, A.; Arkharova, M. Four Quadrant AC-DC Converter Control System Prototype for AC Locomotive Traction Drive. In Proceedings of the 2023 IEEE 24th International Conference of Young Professionals in Electron Devices and Materials (EDM), Novosibirsk, Russia, 29 June–3 July 2023; pp. 1670–1675. [Google Scholar]
- Burkov, A.T.; Valinsky, O.S.; Evstaf’eV, A.M.; Maznev, A.S.; Tretyakov, A.V. Modern Locomotive Traction Drive Control Systems. Russ. Electr. Eng. 2019, 90, 692–695. [Google Scholar] [CrossRef]
- Lu, B.; Song, Y.; Liu, Z.; Tao, G.; Wang, X.; Zhang, Q.; Li, Z. Evolution analysis of wheel polygon wear considering the effect of interharmonics in electrical traction drive system. Mech. Mach. Theory 2024, 191, 105470. [Google Scholar] [CrossRef]
- Bao, J.; Tian, Y.; Zheng, L.; He, W. Dynamic simulation and fatigue life prediction of locomotive traction drive system. J. Comput. Methods Sci. Eng. 2024, 24, 4128–4142. [Google Scholar] [CrossRef]
- Buynosov, A.; Sergeev, B.; Kalinichenko, A.; Antropov, S. Development of an Automatic Locomotive Traction Drive Control System to Reduce the Amount of Wheel Slippage on the Rail. In Proceedings of the VIII International Scientific Siberian Transport Forum, Novosibirsk, Russia, 22–27 May 2019; Springer Science and Business Media Deutschland GmbH: Cham, Switzerland, 2020. [Google Scholar]
- Antipin, D.Y.; Vorobiyov, I.; Izmerov, O.V.; Shorokhov, S.G.; Bondarenko, D.A. Friction Self-Oscillation Decrease in Nonlinear System of Locomotive Traction Drive; IOP Publishing Ltd.: Tomsk, Russia, 2017. [Google Scholar]
- Antipin, D.Y.; Izmerov, O.V.; Kopyilov, O.S. Influence of Locomotive Traction Drive Design on Main Forms of Self-Oscillations During Spinning; IOP Publishing Ltd.: Saint-Petersburg, Russia, 2017. [Google Scholar]
- Zhou, Z.; Chen, Z.; Spiryagin, M.; Wolfs, P.; Wu, Q.; Zhai, W.; Cole, C. Dynamic performance of locomotive electric drive system under excitation from gear transmission and wheel-rail interaction. Veh. Syst. Dyn. 2022, 60, 1806–1828. [Google Scholar] [CrossRef]
- Wu, G.; Shen, L.; Yao, Y.; Song, W.; Huang, J. Determination of the dynamic characteristics of locomotive drive systems under re-adhesion conditions using wheel slip controller. J. Zhejiang Univ. A 2023, 24, 722–734. [Google Scholar] [CrossRef]
- Ren, B.; Liu, P.; Yang, S.; Song, W. Locomotive Drive System Fault Diagnosis Based on Dynamic Self-Adaptive Blind Source Separation. In Proceedings of the First International Conference on Rail Transportation, Chengdu, China, 10–12 July 2017; pp. 736–744. [Google Scholar]
- Zhao, Y.; Li, Q.; Yang, J.; Liu, C.; Wang, J. A Lagrangian approach for the railway vehicle with gear system coupled model considering wheel polygonal faults under traction conditions. J. Vib. Control. 2024, 30, 1339–1352. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, Z.; Zhai, W.; Wang, K. Establishment and validation of a locomotive–track coupled spatial dynamics model considering dynamic effect of gear transmissions. Mech. Syst. Signal Process. 2019, 119, 328–345. [Google Scholar] [CrossRef]
- Wu, P.; Song, C.; Wang, X.; Qu, S.; Wu, H. Vibration Analysis of Traction Drive System Components Based on the Field Test for High-Speed Train. J. Adv. Transp. 2023, 2023, 1–10. [Google Scholar] [CrossRef]
- Zhang, K.; Yang, J.; Liu, C.; Wang, J.; Yao, D. Dynamic Characteristics of a Traction Drive System in High-Speed Train Based on Electromechanical Coupling Modeling under Variable Conditions. Energies 2022, 15, 1202. [Google Scholar] [CrossRef]
- Wang, X.; Qu, S.; Wu, P.; Zeng, J. Influence of beat frequency excitation on the traction drive system in high-speed train under electromechanical coupling. J. Vib. Control. 2025, 1–14. [Google Scholar] [CrossRef]
- Thompson, D. Chapter 14—Vehicle Interior Noise. In Railway Noise and Vibration, 2nd ed.; Thompson, D., Ed.; Elsevier: Amsterdam, The Netherlands, 2024; pp. 643–684. [Google Scholar]
- Soeta, Y.; Shimokura, R. Survey of interior noise characteristics in various types of trains. Appl. Acoust. 2013, 74, 1160–1166. [Google Scholar] [CrossRef]
- Sapena, J.; Tabbal, A.; Jove, J.; Guerville, F. Interior noise prediction in high-speed rolling stock driver’s cab: Focus on structure-borne paths (mechanical and aero sources). In Noise and Vibration Mitigation for Rail Transportation Systems, Proceedings of the 10th International Workshop on Railway Noise, Nagahama, Japan, 18–22 October 2010; Maeda, T., Gautier, P., Hanson, C.E., Hemsworth, B., Nelson, J.T., Schulte-Werning, B., de Vos, P., Eds.; Springer: Tokyo, Japan, 2012; pp. 445–452. [Google Scholar]
- Huang, S.; Aydin, M.; Lipo, T.A. Electromagnetic vibration and noise assessment for surface mounted PM machines. In Proceedings of the 2001 Power Engineering Society Summer Meeting, Conference Proceedings (Cat. No.01CH37262), Vancouver, BC, Canada, 15–19 July 2001; pp. 1417–1426. [Google Scholar]
- Blum, J.; Merwerth, J.; Herzog, H.-G. Investigation of the segment order in step-skewed synchronous machines on noise and vibration. In Proceedings of the 2014 4th International Electric Drives Production Conference (EDPC), Nuremberg, Germany, 30 September–1 October 2014; pp. 1–6. [Google Scholar]
- Torregrossa, D.; Peyraut, F.; Cirrincione, M.; Espanet, C.; Cassat, A.; Miraoui, A. A New Passive Methodology for Reducing the Noise in Electrical Machines: Impact of Some Parameters on the Modal Analysis. IEEE Trans. Ind. Appl. 2010, 46, 1899–1907. [Google Scholar] [CrossRef]
- Yuan, B.; Chang, L.; Liu, G.; Chang, S.; Liu, L.; Shen, Y. An efficient three-dimensional dynamic contact model for cylindrical gear pairs with distributed tooth flank errors. Mech. Mach. Theory 2020, 152, 103930. [Google Scholar] [CrossRef]
- Li, F.; Jiao, H.; Zhang, J.; Fu, Q. Dynamic Modeling and Output Characteristics Analysis of the Hub-Drive Reduction System. Appl. Sci. 2025, 15, 1680. [Google Scholar] [CrossRef]
- Adams, version 2020. Software for Multibody Dynamics Simulation. MSC Software Corporation: Newport Beach, CA, USA, 2020.
- MATLAB, version R2023b. Software for Numerical Computing. The MathWorks, Inc.: Natick, MA, USA, 2023.
- Wu, H.; Wu, P.; Li, F.; Shi, H.; Xu, K. Fatigue analysis of the gearbox housing in high-speed trains under wheel polygonization using a multibody dynamics algorithm. Eng. Fail. Anal. 2019, 100, 351–364. [Google Scholar] [CrossRef]
- Fernandez-Del-Rincon, A.; Diez-Ibarbia, A.; Theodossiades, S. Gear transmission rattle: Assessment of meshing forces under hydrodynamic lubrication. Appl. Acoust. 2019, 144, 85–95. [Google Scholar] [CrossRef]
- Theodossiades, S.; De la Cruz, M.; Rahnejat, H. Prediction of airborne radiated noise from lightly loaded lubricated meshing gear teeth. Appl. Acoust. 2015, 100, 79–86. [Google Scholar] [CrossRef]
- Masuda, T.; Abe, T.; Hattori, K. Prediction Method of Gear Noise Considering the Influence of the Tooth Flank Finishing Method. J. Vib. Acoust. Trans. ASME 1986, 108, 95–100. [Google Scholar] [CrossRef]
- COMSOL Multiphysics, version 6.2. Software for Multiphysics Simulation. COMSOL AB: Stockholm, Sweden, 2023.




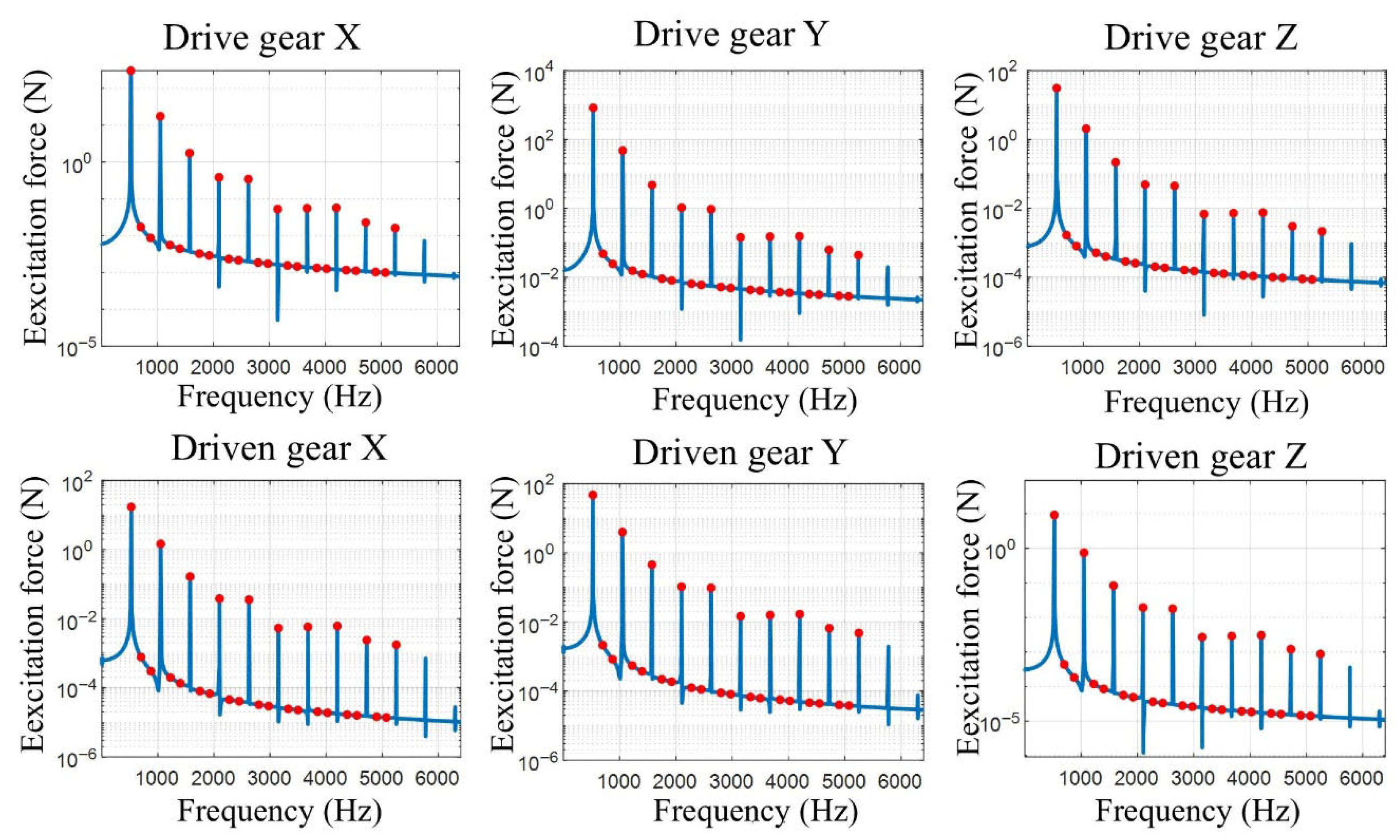
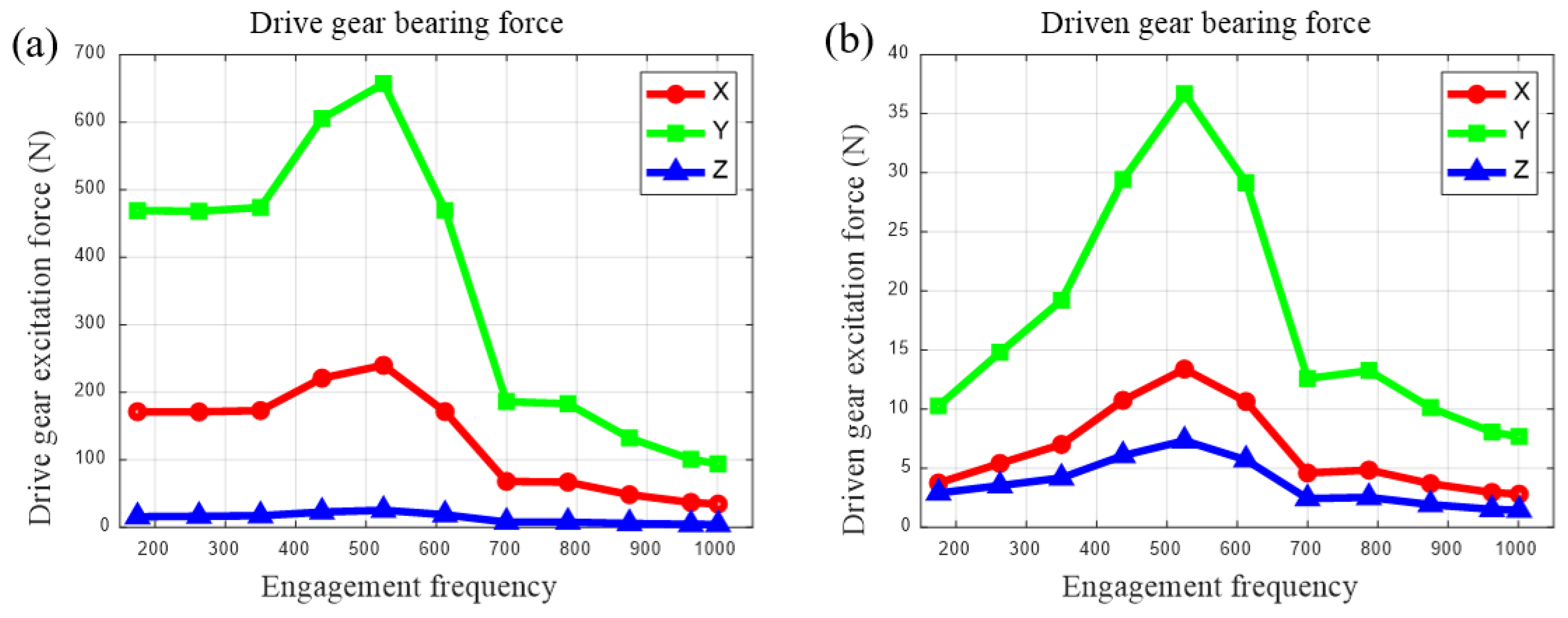
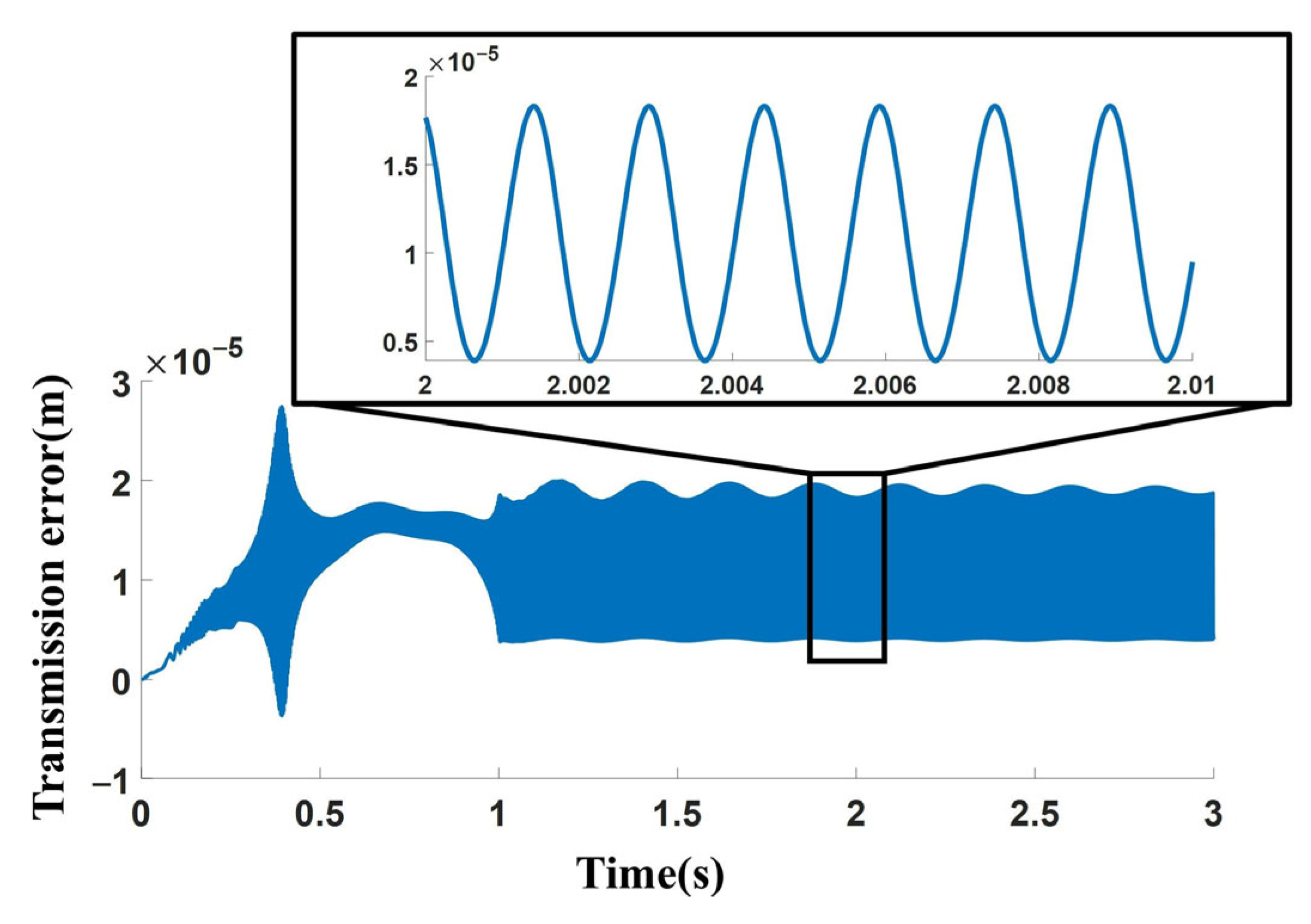
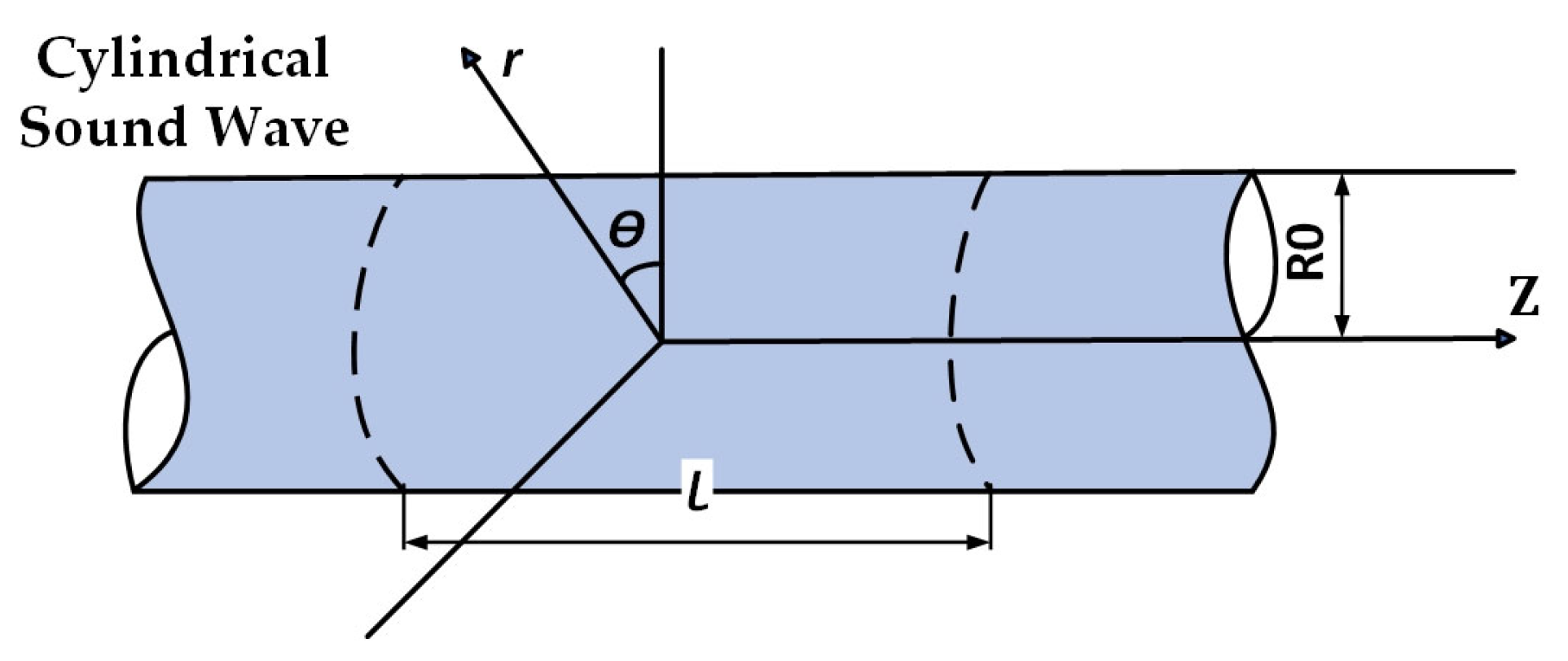

| Working Conditions | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Travel speed | 20 km/h | 30 km/h | 40 km/h | 50 km/h | 60 km/h |
| Theoretical motor speed | 338.65 rpm | 507.97 rpm | 677.30 rpm | 846.61 rpm | 1015.90 rpm |
| Calculated meshing frequency | 174.97 Hz | 262.45 Hz | 349.94 Hz | 437.42 Hz | 524.90 Hz |
| Working Conditions | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Motor vibration frequency (Hz) | 510 926 1852 2743 | 933 1857 2780 | 705 1207 2453 | 1131 2468 | 705 1032 |
| Gearbox vibration frequency (Hz) | 371 530 926 | 266 520 933 | 350 705 | 462 918 1387 | 527 1031 |
| Noise characteristic frequency (Hz) | 926 1852 2778 | 933 1857 2780 | 1207 2453 | 463 918 1132 1387 | 527 1032 1594 2112 |
| Parameters | Driving Wheel | Driven Wheel |
|---|---|---|
| Module | 7.35 | |
| Number of teeth | 31 | 104 |
| Tooth profile angle | 20° | |
| Tooth top height coefficient | 1.2 | |
| Top clearance coefficient | 0.35 | |
| Normal displacement coefficient | 0.27807 | −0.59026 |
| Helix angle | 4° | |
| Center distance | 495 | |
| Operating Conditions | Train Speed (km/h) | Meshing Frequency (Hz) |
|---|---|---|
| 1 | 20 | 174.97 |
| 2 | 30 | 262.45 |
| 3 | 40 | 349.94 |
| 4 | 50 | 437.42 |
| 5 | 60 | 524.9 |
| 6 | 114 | 1001 |
| Working Conditions | Train Speed (km/h) | Excitation Frequency (Hz) | Sound Pressure Level (dB) |
|---|---|---|---|
| 1 | 20 | 174.97 | 70.7811 |
| 2 | 30 | 262.45 | 85.5865 |
| 3 | 40 | 349.94 | 84.9987 |
| 4 | 50 | 437.42 | 92.8384 |
| 5 | 60 | 524.9 | 93.6556 |
| 6 | 114 | 1001 | 88.5417 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, C.; Liu, X.; Yu, K.; Yang, Z.; Zhang, J.; Li, P. A Rapid Modeling Method for Sound Radiation of China’s Locomotive Traction Drive Systems in Railways. Appl. Sci. 2025, 15, 10597. https://doi.org/10.3390/app151910597
Li C, Liu X, Yu K, Yang Z, Zhang J, Li P. A Rapid Modeling Method for Sound Radiation of China’s Locomotive Traction Drive Systems in Railways. Applied Sciences. 2025; 15(19):10597. https://doi.org/10.3390/app151910597
Chicago/Turabian StyleLi, Chao, Xiaobo Liu, Kangfan Yu, Zhiwen Yang, Jianrun Zhang, and Pu Li. 2025. "A Rapid Modeling Method for Sound Radiation of China’s Locomotive Traction Drive Systems in Railways" Applied Sciences 15, no. 19: 10597. https://doi.org/10.3390/app151910597
APA StyleLi, C., Liu, X., Yu, K., Yang, Z., Zhang, J., & Li, P. (2025). A Rapid Modeling Method for Sound Radiation of China’s Locomotive Traction Drive Systems in Railways. Applied Sciences, 15(19), 10597. https://doi.org/10.3390/app151910597






