Research on High-Resolution Image Harmonization Method Based on Multi-Scale and Global Feature Guidance

Abstract

During the image compositing process, there may be inconsistencies in tone and illumination between the foreground and background, leading to poor visual quality and low realism in the composite images. To address these issues, image harmonization techniques can be employed. This paper proposes an image harmonization method based on multi-scale and global feature guidance (MSGF). In general, images captured in different scenes may exhibit inconsistencies in lighting after composition. The goal of image harmonization is to adjust the foreground illumination to match that of the background. Traditional methods often attempt to blend pixels directly, which can result in unrealistic outcomes. The proposed approach combines multi-scale feature extraction with global feature guidance, forming the MSGF framework. The experiment was conducted on the iHarmony4 dataset. Comparative experiments showed that MSGF achieved the best performance on three subset indicators, including HCOCO. Ablation studies demonstrated the effectiveness of the proposed module. Efficiency evaluation results indicated that it took 0.01s and had 20.9 million parameters, outperforming comparative methods and effectively achieving high-quality image harmonization.

1. Introduction

Image harmonization refers to the process in computer vision and image processing where one or more image elements (such as objects, textures, or colors) are integrated into another image to make the overall image appear more natural and consistent, as shown in Figure 1. This process typically involves adjusting the color, lighting, shadows, and texture of the newly added image elements to match the visual characteristics of the target image. The goal of image harmonization is to address issues such as mismatches in color, brightness, contrast, and texture that may arise when directly compositing images, thereby creating a seamlessly synthesized image that looks like it was taken in the same scene. This technique has widespread applications in digital image editing, film post-production, virtual reality, and augmented reality. Traditional image harmonization methods mainly rely on handcrafted statistical features of images, such as illumination, color temperature, contrast, saturation, etc., to determine color-to-color transformations, ensuring that the foreground tones match those of the background. In recent years, image harmonization methods based on deep learning have emerged continuously and achieved significant progress.

The framework of traditional image harmonization primarily involves transferring the appearance characteristics of the background to the foreground using handcrafted statistical methods. Sunkavalli et al. introduced a multi-scale image harmonization framework [1]. This framework achieves seamless image stitching by decomposing images and noise into pyramids, adjusting the source images and noise at different scales, and then reconstructing the blended image using the modified pyramid coefficients. It incorporates methods based on alpha channels and seamless boundary constraints to ultimately achieve harmonization of the images. This framework demonstrates how realistic composites can be generated across various scenarios with minimal user interaction. Luan et al. [2] achieved the transfer of statistical properties from the background image to the pasted image by utilizing a VGG neural network, preserving the correlations between neural responses across different layers to enhance the quality of the output image. Their process involves two steps: first, achieving coarse harmonization at a single scale, followed by fine-scale refinement based on the initial pass. However, a downside of traditional image harmonization methods is their inefficiency when dealing with large-scale images and their lack of robustness when there are significant differences between images, often relying heavily on specific image features. Xue et al. [3] finally realized the transfer of features from the background image to the foreground image by matching the histogram and adjusting the brightness, hue, and other factors of the image.

In response to the traditional image harmonization methods mentioned above, recent advancements in deep learning and artificial intelligence have provided new solutions for image registration. Neural networks can now automatically learn image features and achieve more efficient and robust registration. However, these approaches also present challenges, such as the need for extensive training data and issues with model generalization.

Deep learning-based image harmonization methods have commonly leveraged the advantages of autoencoders in semantic feature extraction to achieve a consistent and harmonious appearance between the foreground and background. Through this approach, the models can more accurately adjust both local and global visual styles of the image, thereby enhancing the realism and naturalness of the composite image. Sofiiuk et al. [4] proposed a novel architecture that utilizes high-level feature spaces learned by pre-trained classification networks. The model was validated on public datasets and demonstrated promising results. Ke et al. [5] addressed the problem of image harmonization for high-resolution images by transforming the task into an image-level regression problem through filter parameter adjustment. They proposed a framework combining global guidance with detailed awareness for image harmonization. Unlike previous black-box autoencoder-based methods, Harmonizer includes a neural network for filter parameter prediction and several white-box filters for image harmonization. This method is not only applicable to images but also extends to videos. It offers more stable performance, clearer results, and higher efficiency.

In summary, despite their notable successes, these methods still face three key challenges. First, they perform inadequately in handling fine-scale edges (e.g., hair, semi-transparent regions, and object boundaries), often altering the original image content. Second, they incur high computational overhead when processing high-resolution images. Third, these methods struggle in cases where there are specific color mismatches or differing illumination conditions between each synthetic element and the background.

Our contributions are summarized as follows:

(1)

We propose a method that combines multi-scale processing with global feature guidance. Using multi-scale methods, we handle image details at different scales to achieve seamless integration. By introducing global features, we enable transformations of foreground features.

(2)

We introduce a lightweight refinement module to effectively integrate different methods, providing a delicate approach for image harmonization tasks.

(3)

Extensive experiments conducted on the benchmark iHarmony4 dataset demonstrate that our method performs well across all metrics, achieving significant improvements in time while reducing the number of parameters.

2. Related Work

2.1. Image Harmonization

In addition to processing appearance features, traditional methods have also proposed supervised learning-based approaches, achieving significant success in image harmonization by learning from synthetic training pairs (e.g., the iHarmony dataset [6]). DovNet [6] is a novel deep image harmonization method that introduces a new domain verification discriminator. Recently, CNN-based models have been developed for end-to-end image harmonization. Guo et al. [7] introduced the Transformer architecture into the image harmonization task, leveraging the Transformer’s strong capability in modeling long-range contextual dependencies to address the problem of image harmonization. We propose the design of our harmonization Transformer framework without disentanglement, along with comprehensive experiments and ablation studies, demonstrating the power of Transformers and providing insights into their visual behavior in image harmonization. Wang et al. [8] proposed a novel semi-supervised training strategy to address the problem of image harmonization. According to user studies, this method outperforms previous works on established benchmarks and real-world composites, and can interactively process high-resolution images. Meng et al. [9] introduced an adaptive interval color transformation technique, which forecasts pixel-level color transformations and dynamically adjusts the sampling intervals. This approach enables the modeling of local nonlinearities in color transformation at high resolutions. The Poisson blending method proposed by Perez et al. [10] achieves smooth transitions between images by optimizing in the gradient domain, effectively suppressing stitching artifacts, and has been widely applied in image fusion tasks; however, it exhibits limited adaptability to scenes with inconsistent illumination. To improve image harmonization, Tian et al. [11] developed a self-supervised image harmonization framework that enables semantic-aware local style adjustment and global illumination transfer. Usama et al. [12] formulated image harmonization and denoising as an image-to-image translation task, leveraging a generative adversarial network to simultaneously enhance texture consistency and reduce noise. Mwubahimana et al. [13] further introduced a hybrid architecture combining Transformer and CNN, which, under a weakly supervised setting, fully exploits global contextual information to significantly improve harmonization performance in complex scenes. Additionally, Oriti et al. [14] designed an immersive gaming platform to evaluate the integration of virtual and augmented reality, effectively enhancing users’ sense of immersion in virtual environments.

Although the aforementioned methods can achieve image harmonization, they are not ideal in terms of computational efficiency and implementation effectiveness, especially because low-resolution images consume more resources, leading to poorer performance and slower inference speed at high resolutions. In contrast, our method incorporates a multi-scale strategy to effectively and efficiently allocate resources. We formulate the image harmonization task, and our proposed multi-scale and global feature-guided image harmonization approach can address this task at high resolutions with a consistent inference speed, while maintaining performance with negligible degradation.

2.2. Multi-Scale Image Harmonization

Multi-scale image harmonization refers to the process of processing images at different scales to ensure visual harmony across all parts of the image. This technique is commonly used in the fields of image editing and composition, aiming to make the synthesized image appear more natural and reduce visible artifacts caused by manual editing. In image harmonization, “multi-scale” means considering different resolutions or levels of detail within the image. For example, in a high-resolution image, it may be necessary to adjust large-scale features such as overall color and lighting variations, while also paying attention to small-scale elements such as fine objects or textures. By optimizing these characteristics at different scales simultaneously, a more realistic and visually harmonious result can be achieved. Sunkavalli [1] proposed an image multi-scale pyramid method to achieve effective image composition, matching the texture, noise, and other aspects, while requiring minimal user interaction. Duan et al. [15] proposed a multi-scale region correlation-driven strategy to deeply explore the content relevance between the foreground and background, enabling the foreground object to blend more naturally and seamlessly into the background semantics.

This paper primarily employs multi-scale representation methods, such as the Laplacian pyramid, for image harmonization. It is well known that the image pyramid approach allows for the processing of image features at different levels. In multi-scale image processing, the image is first decomposed into a multi-scale pyramid, and then each layer of the pyramid is analyzed or processed in detail at different levels to achieve the desired result. In Heeger and Bergen’s work, pyramids were ingeniously applied to texture synthesis. They demonstrated that by precisely matching the subband coefficients histograms of the noise pyramid with those of the given texture, realistic random textures can be generated. This technique not only preserves the fine details of the original texture but also allows flexible adjustment of the complexity and directionality of the texture, thus finding wide application in the image editing, computer vision, and virtual reality fields. This method effectively captures the key characteristics of textures across multiple scales, thereby enabling realistic texture synthesis.

2.3. Image Harmonization Global Features

The global features of an image become especially important in order to achieve a better and more effective fusion of foreground elements and background. Cong et al. [16] proposed a high-resolution image harmonization network based on Collaborative Dual Transformations (CDTNet). This approach consists of three main components: a low-resolution generator for pixel-level translation, an RGB transformation module for color space mapping, and a refinement module that leverages the results from both, thereby enhancing the overall harmonization of the image. Niu et al. [17], targeting situations where the lighting of the foreground image is inconsistent with that of the background image, introduced a novel method called GiftNet. This approach utilizes global information to guide the transformation of foreground features, leading to significant improvements. Yuan et al. [18] proposed a multi-color curve network that captures richer color information by processing images across multiple color spaces. The network employs an encoder based on modified Transformer blocks to perform multi-stage curve learning in different color spaces. Meanwhile, a multi-color integration module is introduced to effectively fuse feature information extracted from various color spaces, and a lightweight fine-grained refinement module is further incorporated to enhance the output quality, achieving superior image color adjustment performance.

We extract bottleneck features from the encoder as global features to guide the transformation of foreground features in each feature map. Regarding the method of transformation, we opted for using modulated convolution kernels; however, other transformation methods are also applicable. Specifically, we utilize global features to derive modulated convolution kernels and apply these to the foreground features. Our approach shares similarities with CDTNet, which uses global features to predict color transformations. In contrast, our method primarily employs global features to predict feature transformations.

3. Method

We denote the composite image as ${\mathrm{I}}_c$, which is composed of a foreground ${\mathrm{I}}_f$ and a background ${\mathrm{I}}_b$, with the ground-truth image being ${\mathrm{I}}^{gt}$. The objective of the image harmonization task is to adjust the composited foreground ${\mathrm{I}}_f$, so that the resulting harmonized image closely resembles ${\mathrm{I}}^{gt}$. Our approach is built upon a UNet-based network, which includes three modules: a multi-scale module, a global feature guidance module, and a lightweight refinement module. We apply the designed multi-scale and global feature (MSGF) guided module to image harmonization. The main framework of this module will be detailed in Section 3.1. Then, we provide an in-depth explanation of the multi-scale module in Section 3.2. In Section 3.3, we describe the global feature module, and in Section 3.4, we detail the design of the lightweight refinement module.

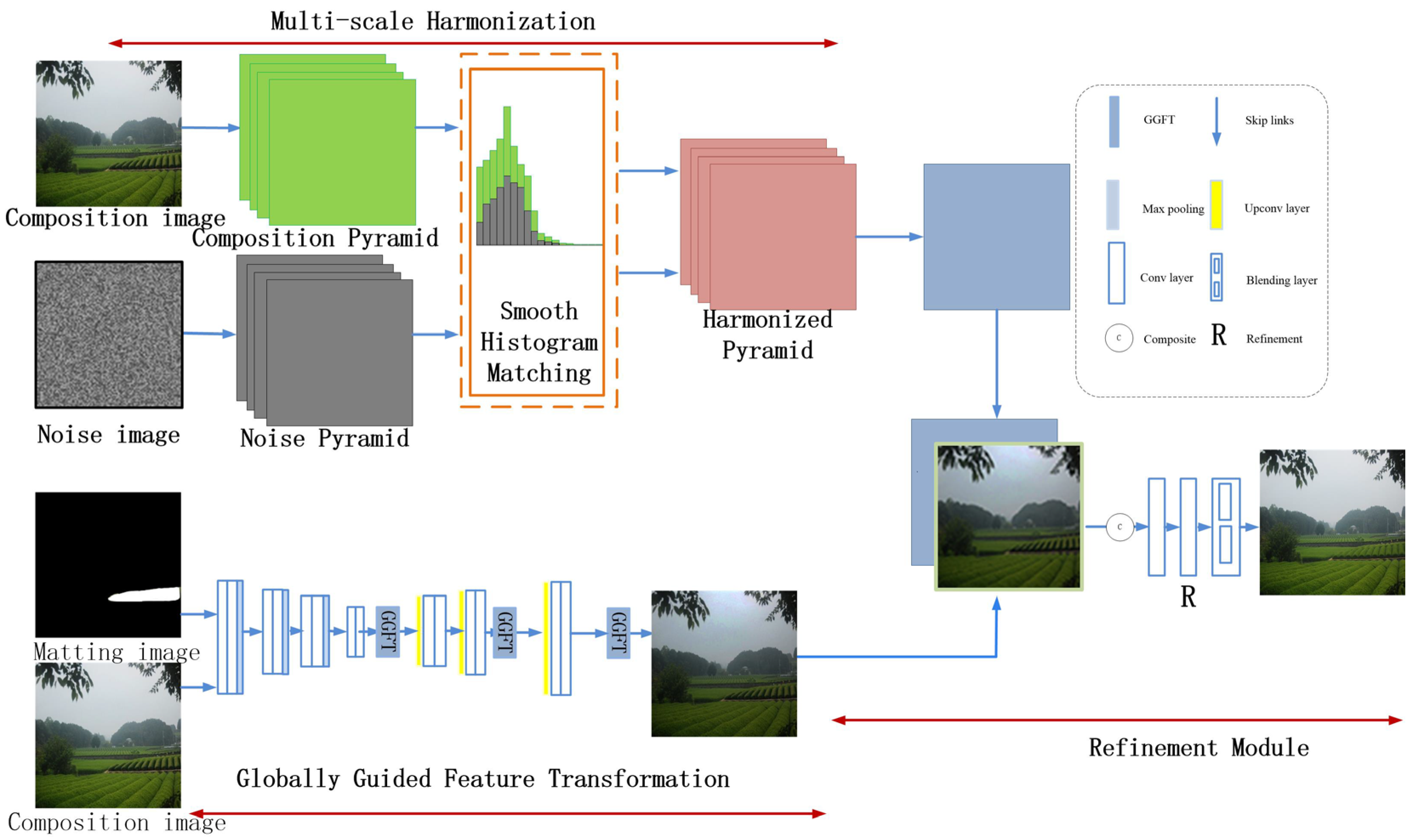
3.1. Design of the Main Framework for Image Harmonization Based on Multi-Scale and Global Feature Guidance

Our network consists of multi-scale harmonization, globally guided feature transformation and lightweight refinement module as shown in Figure 2. The multi-scale branch fuses the synthetic image and random noise through the histogram matching technique, thus making the synthetic image more natural and realistic both in color and lighting. In the global feature guidance branch, we employ a UNET structure to perform feature transformation on the global features through the global feature branch. We use the global features to predict a scale vector $\mathrm{s}$, and then obtain the modulated convolution weights $\overline{W}$, which are subsequently applied to the foreground feature maps. This process ultimately achieves harmonization of the composite image. The image obtained from the multi-scale module and the features obtained from the global feature module are effectively fused by a lightweight refinement module to obtain a more harmonized image.

3.2. Multi-Scale Modular Design

In the module, our main work is to combine synthetic and random noise images using a linear pyramid approach. First, the input synthetic and random noise images are decomposed into pyramids, and the synthetic and noise pyramids are iteratively shaped to match the target pyramid using a smooth histogram matching technique. Histogram matching is used in image harmonization (IH) to make the synthesized image look more natural. When an object needs to be extracted from one image and inserted into another background image, it usually encounters inconsistencies in color, lighting, and texture, which make the composite effect look abrupt. With the histogram matching technique, we can adjust the color distribution of the foreground object so that it is closer to the color distribution of the background image, thus achieving better visual integration. Specifically, it can be considered in terms of color harmonization and lighting condition matching. When the colors of the foreground and background may not be consistent, by histogram matching, the color distribution of the foreground objects can be made to match the background, which reduces the color difference and makes the composite look more harmonious. If the foreground object was acquired from different lighting conditions, it may not look like the background. Histogram matching can help adjust brightness and contrast to better simulate the lighting conditions of the original scene. Simple histogram matching may result in artifacts.

3.3. Module Design for Global Feature Guidance

In the global feature guidance module, we introduce the globally guided instance feature transformation (GGFT) mechanism, which is an improvement on the GiftNet proposed by Niu et al. [17]. The mechanism uses global features to predict scale vectors and generates modulated convolutional weights accordingly, aiming to optimize the representation of the foreground feature map without changing the background feature map. In the GGFT itself, the mechanism contains an encoder and a decoder; the encoder contains four modules; the decoder contains three modules into which the GGFT is inserted. In our innovative application, we insert the GGFT modules into each encoder and decoder after the foreground feature map is extracted for each convolution and the global feature vector is extracted.

This architecture contains a total of four encoder blocks. We extract the corresponding foreground features. $T_e^1$ through each encoder denotes the feature map obtained by the first $l$ encoder, and through average pooling, the feature map will be extracted from the corresponding feature vector $t_e^1$. This feature vector contains the important global features of the foreground image, which provides an important basis for the later image and coordination. After obtaining the feature vectors, the feature vectors are used to guide the feature transformation during the feature mapping process. The specific method is to apply the modulated convolutional weights to the foreground feature map. In the task of image harmonization, the global feature $t_e^1$ is used to guide the modulation of the convolutional weights, which provides global guidance for the feature transformation. In order to achieve harmony between the foreground and background within the image, our method implements transformations only for the foreground feature maps, ensuring that the compatibility between foreground elements and the background environment is optimized. The basic convolutional weight $\overline{W}$ used here refers to the spatial position weight of the $x$ th input, the $y$ th output, at the $z$ th position. The size of $\overline{W}$ is adjusted by the obtained scale vectors. The features are augmented by the normalization method. By modulating the foreground feature mapping, similarity to the background feature mapping is achieved.

3.4. Lightweight Refined Module Design

In the lightweight refinement module, we introduce lightweight models that can help us to process the results obtained through the module and the global feature module to optimize the synthesized images.

After the pixel-to-pixel transformation in the transformation, we can get the result ${\hat{\mathrm{I}}}_{msh}\in {ℝ}^{\mathrm{H}\times \mathrm{W}\times 3}$ after the transformation, and the result ${\hat{\mathrm{I}}}_{ggft}\in {ℝ}^{\mathrm{H}\times \mathrm{W}\times 3}$ from the global feature guidance module. ${\hat{\mathrm{I}}}_{msh}$ has high resolution and can realize fine etching in detail, but lacks global feature processing. ${\hat{\mathrm{I}}}_{ggft}$ has rich global features, so they are complementary to each other. In order to better fuse the two obtained results, we therefore designed a lightweight refinement module $\mathrm{R}$ to produce better high-resolution results.

In the lightweight refinement module, we first connect the result ${\hat{\mathrm{I}}}_{msh}\in {ℝ}^{\mathrm{H}\times \mathrm{W}\times 3}$ of the transformation and the result ${\hat{\mathrm{I}}}_{ggft}\in {ℝ}^{\mathrm{H}\times \mathrm{W}\times 3}$ obtained from the global feature bootstrap module as inputs to the channel. The refinement module $\mathrm{R}$ contains two convolutional layers. As a result, the refinement module $\mathrm{R}$ receives inputs from ${\hat{\mathrm{I}}}_{msh}$ and ${\hat{\mathrm{I}}}_{ggft}$ and produces a finer high-resolution output ${\hat{\mathrm{I}}}^h$. We force ${\hat{\mathrm{I}}}^h$ to be close to a high-resolution ground-truth image of ${\mathrm{I}}^{gt}$, denoted ${\mathfrak{L}}_{ref}={‖{\widehat{I}}^h-{\mathrm{I}}^{gt}‖}_{\lambda }$, by imposing a reconstruction loss.

3.5. Loss Function Setting

The overall loss function of our MSGF is ${\mathfrak{L}}_f$:

$${\mathfrak{L}}_f={\mathfrak{L}}_{msh}+{\mathfrak{L}}_{ggft}+{\mathfrak{L}}_{ref}$$

(1)

where ${\mathfrak{L}}_{msh}$ denotes the loss function of the multi-scale module, ${\mathfrak{L}}_{ggft}$ denotes the loss function of the global feature module, and ${\mathfrak{L}}_{ref}$ denotes the loss function of the lightweight refinement module. Although the refinement module has a simple structure, it performs better in fusing the multi-scale results and global feature-guided results due to the presence of the information input and the hybrid layer.

4. Experimentation and Analysis

In this paper, we trained and tested the algorithm in a medium implementation on the NVIDIA TITAN X GPU platform. We used four objective evaluation metrics to evaluate the experimental results. In the comparative study, we chose the state-of-the-art image harmonization method to compare with our method. First, the dataset and evaluation metrics are presented; then, the experimental results are analyzed; finally, the quantitative analysis leads to the conclusions in this section.

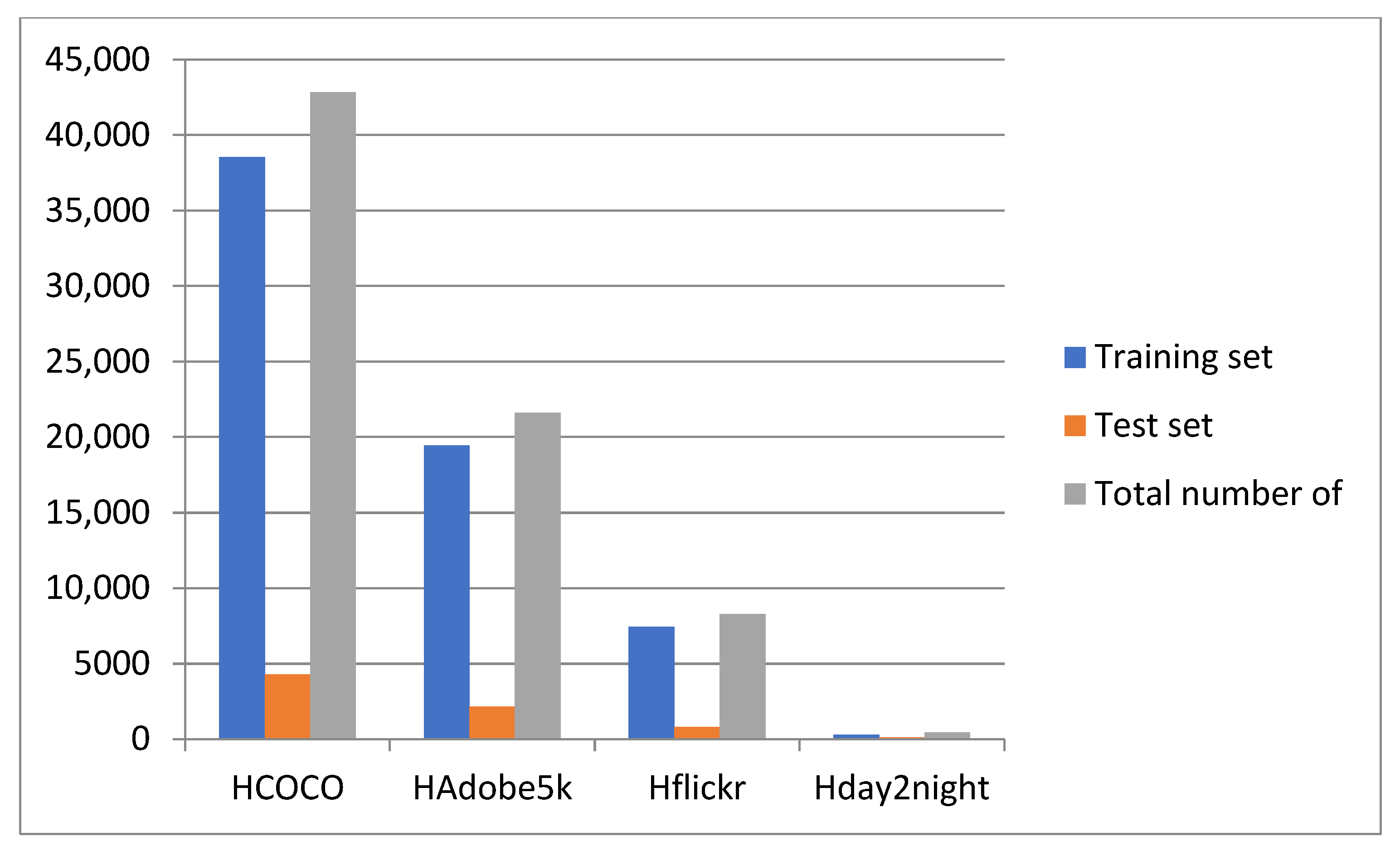
4.1. Experimental Dataset

The following datasets are widely used for image harmonization: iHarmony4 [19] dataset, RHHarmony dataset, RealHM dataset, HVIDIT dataset, and ccHarmony dataset. In this study, we selected the iHarmony4 dataset as the training and testing dataset. iHarmony4 is a comprehensive and recently proposed benchmark dataset that integrates multiple types of synthetic images, including real synthetic images, globally adjusted synthetic images, synthetic images with local operations, and synthetic images generated through deep learning-based hybrid methods. This diversity ensures comprehensive evaluation across various realistic and challenging scenarios. In recent years, numerous studies in the field of image harmonization have adopted iHarmony4 as the standard benchmark, facilitating fair comparisons with state-of-the-art methods. Each of iHarmony4 contains a wealth of resources inside as shown in Figure 3, which can be used for deep learning training and testing. Our experiments are conducted on the iHarmony4 dataset. iHarmony4 consists of four datasets, namely HCOCO [20], HFlickr [21], HAdobe5K [22], and Hday2night [23]. We used the complete iHarmony4 dataset in our experiments.

4.2. Experimental Test Program

In the comparative experiments, we selected three representative image harmonization methods for performance evaluation. The selection criteria are as follows. (1) The method is highly representative and has demonstrated strong experimental performance in existing studies. (2) It has significant academic influence in the relevant field and has been widely cited. (3) Its source code is publicly available on platforms such as GitHub, facilitating reproducibility and experimental validation. (4) The method exhibits good generalization ability and can be applied to various scenarios or tasks. We conducted experiments on four publicly available datasets from iHarmony4: the HCOCO, HFlickr, HAdobe5K, and Hday2night datasets, which we used as training and to test the visualization results. These methods include the iS2AM [18] (https://github.com/SamsungLabs/, accessed on 12 January 2025) method. Unlike previous methods that train encoder–decoder networks from scratch, this method utilizes the high-level feature space learned by pre-trained classification networks to enhance the ability of neural networks to learn high-level representations of objects. The CDTNet [8] (https://github.com/bcmi/, accessed on 12 January 2025) method’s core innovation lies in proposing a dual-transformation mechanism that performs spatial and color transformations on the foreground and background, respectively, and ensures the visual consistency of the two through co-optimization. Specifically, the spatial transformation module adjusts the shape and position of the foreground objects through an adaptive convolutional network, while the color transformation module accurately matches the color distributions of the foreground and background through a multi-scale feature fusion technique. In addition, the study introduces an efficient generative adversarial network (GAN) framework, which further enhances the realism of the generated images. Harmonizer [4] (https://github.com/ZHKKKe/Harmonizer, accessed on 12 January 2025), using a cascaded regressor and dynamic loss strategy, makes the learning process of filter parameters more stable and accurate. Since the network only generates image-level parameters and the filters used have efficient computational characteristics, this method significantly reduces computational overhead while maintaining performance, thereby improving processing speed.

Comprehensive experiments show that MSGF is obviously superior to the existing methods, which is beneficial to the fusion of fine images at the edges as well as the harmonization of global images through multi-scale and global feature guidance, especially in the high-resolution input.

4.3. Evaluation Criteria

We use mean square error (MSE), foreground mean square error (fMSE), and peak signal-to-noise ratio (PSNR) as evaluation metrics to measure the performance of image harmonization. Specifically, fMSE calculates the mean square error for the foreground region only, not the entire image, because the image harmonization process does not alter the appearance of the background.

4.4. Comparative Experiments and Analysis

In order to better investigate high-resolution image harmonization, we conducted quantitative and qualitative experiments to verify its effectiveness. We compare four methods of image harmonization and give the test results in four more subsets, which are obtained from the models copied or published in the original paper. With

Table 1. Quantitative analysis: test values for each method in the comparison experiment. (↓ indicates smaller values are better, ↑ indicates larger values are better. Bold indicates the optimal value.)

Method	HCOCO			HFlickr			HAdobe5k			Hday2night
	MSE ↓	fMSE ↓	PSNR ↑	MSE ↓	fMSE ↓	PSNR ↑	MSE ↓	fMSE ↓	PSNR ↑	MSE ↓	fMSE ↓	PSNR ↑
iS2AM	16.48	266.14	39.29	69.68	443.63	33.56	22.59	166.19	37.24	40.59	591.07	37.72
CDTNet	16.25	261.29	39.15	68.61	423.03	33.55	20.62	149.88	38.24	36.72	549.47	37.95
Harmo nizer	17.34	298.42	38.77	64.81	434.06	33.63	21.89	170.05	37.64	33.14	542.07	37.56
Ours	16.02	260.67	39.69	60.42	350.56	33.42	18.43	130.96	39.78	33.01	480.67	37.98

we can see the considerable performance of the various harmonization methods in different subsets. For each metric, the values indicating optimal performance are shown in bold. For the three test sets, HCOCO, HAdobe5k, and Hday2night, our method outperforms the SOTA method to a large extent. For example, in the HCOCO test set, there is a relative improvement of 2.7% over iS2AM, 1.4% over CDTNet, and 7.67% over Harmonizer on the MSE metric. On the fMSE metric, there was a 2% relative improvement over iS2AM, a 0.2% improvement over CDTNet, and a 12.6% relative improvement over Harmonizer. On the PSNRA metric, there was a 1% relative improvement over iS2AM, a 1.3% improvement over CDTNet, and a 2.3% relative improvement over Harmonizer. Our method achieved the best results on HCOCO, HAdobe5k, and Hday2night. Our method did not achieve fully optimal results on HFlickr, and the PSNR metrics were lower than the other methods. The experimental results are as follows, and Figure 4 shows the experimental results of the selected methods on the iHarmony4 dataset.

As shown in Figure 4, the actual results of iS2AM, CDTNet, Harmonizer and our method for a specific dataset iHarmony4 are demonstrated from a horizontal perspective. From a general point of view, several existing methods are able to achieve the harmonization function, but through comparison, we are still able to see that our method will be closer to ground-truth both in terms of the synthesis effect of the synthesized edges and the fusion with the background image. From the leftmost synthesized image, we can see that the synthesized edges of the effect are rather abrupt, which can be effectively prompted to be harmonized by our method.

In order to better validate the advantages of MSGF in real image coordination, it was tested by means of a user study. We use the real synthesized images published in [17] with a total of 99 images. The harmonized images generated by the method involved in Figure 4 plus the synthetic images form a set of five images in total, and we ranked each set of images by inviting 50 participants. In

Table 2. B–T scores of 100 real synthetic images by different methods.(↑ indicates larger values are better. Bold indicates the optimal value).

Method	Input Composite	iS2AM	CDTNet	HIM	Ours
B–T score↑	0.387	0.465	0.893	0.851	1.328

, to better validate the effectiveness of our harmonization method, we use the Bradley–Terry model (B–T model) [19] for ranking. MSGF achieves the highest B–T score, which demonstrates the validity of the proposed approach.

4.5. Computational Efficiency Assessment

To evaluate the efficiency of the proposed method in this chapter, we conduct experiments on the iHarmony4 dataset using the iS2AM, CDTNet, Harmonizer, and our method. We record the inference time and model parameter count for each method, with the results presented in

Table 3. Time loss in image harmonization by different methods on the iHarmony4 dataset (Bolding indicates the best ranked value).

Method	Time (s)	Model Parameters (in Millions)
iS2AM	14.7	68
CDTNet	10.8	216
HIM	0.02	21.7
Ours	0.01	20.9

. As shown in Table 3, the MSGF method has the shortest inference time, attributed to its lightweight refinement module. Fast inference speed is essential for real-time applications, while a small model size and low memory requirements are beneficial for deployment on mobile devices. Quantitative results demonstrate that MSGF is faster, lighter, and more memory-efficient than the other methods. Notably, on an NVIDIA GeForce RTX 4090 GPU, MSGF runs twice as fast as the previously fastest method, Harmonizer, and over 100 times faster than iS2AM and CDTNet. Furthermore, as observed from the table, MSGF achieves faster computation and fewer parameters by integrating an image pyramid approach with a lightweight refinement fusion module.

4.6. Analysis of Ablation Experiments

In order to better validate the effectiveness of the multi-scale module and the global feature bootstrap module for the MSGF model, valuable experience has been gained in a wide range of techniques to be able to validate our modules more effectively. In

Table 4. Objective evaluation metrics of different modules for image harmonization on the iHarmony4 dataset. (↓ indicates smaller values are better, ↑ indicates larger values are better. Bold indicates the optimal value).

Method	HCOCO			HFlickr			HAdobe5k			Hday2night
	MSE ↓	fMSE ↓	PSNR ↑	MSE ↓	fMSE ↓	PSNR ↑	MSE ↓	fMSE ↓	PSNR ↑	MSE ↓	fMSE ↓	PSNR ↑
Baseline	16.48	266.14	39.29	69.68	443.63	33.56	22.59	166.19	37.24	40.59	591.07	37.72
MSHG	16.22	262.02	37.25	64.79	432.75	31.78	21.06	152.67	38.92	35.39	580.62	36.21
GFTR	16.10	261.78	38.83	62.43	398.52	32.41	19.87	143.66	39.41	34.87	503.41	37.54
Ours	16.02	260.67	39.69	60.42	350.56	33.42	18.43	130.96	39.78	33.01	480.67	37.98

, we provide a complete analysis and insights on all the individual modules and demonstrate the validity of the methodology presented in this section. The same metrics are used as in Section 4.3 and the design of the ablation experiments in the same database is shown as follows: (1) baseline model: CDTNet is used as the baseline, and the method proposed in this chapter is an improvement based on the CDTNet model; (2) harmonization of images using only the multi-scale module and the lightweight refinement module is called MSHR; (3) harmonization of images using only the global feature bootstrap and the lightweight refinement module is called GFTR; (4) the method proposed in this chapter. In Figure 5 the harmonization effects of the different modules are demonstrated and visualized for the following images: (a) synthesized image, (b) real image, (c) “MSHR” harmonization result, (d) “GFTR” harmonization result, (e) synthesized result by MSGF method.

From the qualitative results in Figure 5, it can be seen that the method in this chapter, MSGF, has the best harmonization effect, and the MSHG method, although the multi-scale pyramid method was used for image harmonization, is slightly better than the Baseline methods, but it is obvious in the first line that the detailed hair part still shows the phenomenon of hair lumps, and it can be clearly seen that in the unnatural image, the GFTR effect is slightly better than that of MSHG, and it is achieved by global feature feature transformation to achieve image harmonization, but not as good as MSHG in terms of color contrast. Our method combines the advantages of the two methods to achieve a better harmonization effect. In the quantitative analysis results in Table 4, we can see that overall, these three methods have their advantages relative to other methods, but the MSGF method is especially outstanding in all indicators, and can achieve better image harmonization through the effective combination of the multi-scale pyramid method and global feature guidance.

5. Conclusions

In this paper, we investigate the process of image harmonization on synthetic images. For better realism, we consider the approach and global features in a unified way and try to optimize the synthetic images with a lightweight refinement module, which inspired us to design and implement the MSGF method. The method efficiently processes images from two aspects, and thanks to our new architecture and the effective combination of the two methods, MSGF is lighter and faster than previous methods while achieving new state-of-the-art performance. However, our method does have limitations. It does not give good results in dealing with the problem of harmonization of video images. In future work, we hope to develop more suitable image harmonization methods to solve this problem.