Vision-Based Adaptive Control of Robotic Arm Using MN-MD3+BC

Abstract

Aiming at the problems of traditional calibrated visual servo systems relying on precise model calibration and the high training cost and low efficiency of online reinforcement learning, this paper proposes a Multi-Network Mean Delayed Deep Deterministic Policy Gradient Algorithm with Behavior Cloning (MN-MD3+BC) for uncalibrated visual adaptive control of robotic arms. The algorithm improves upon the Twin Delayed Deep Deterministic Policy Gradient (TD3) network framework by adopting an architecture with one actor network and three critic networks, along with corresponding target networks. By constructing a multi-critic network integration mechanism, the mean output of the networks is used as the final Q-value estimate, effectively reducing the estimation bias of a single critic network. Meanwhile, a behavior cloning regularization term is introduced to address the common distribution shift problem in offline reinforcement learning. Furthermore, to obtain a high-quality dataset, an innovative data recombination-driven dataset creation method is proposed, which reduces training costs and avoids the risks of real-world exploration. The trained policy network is embedded into the actual system as an adaptive controller, driving the robotic arm to gradually approach the target position through closed-loop control. The algorithm is applied to uncalibrated multi-degree-of-freedom robotic arm visual servo tasks, providing an adaptive and low-dependency solution for dynamic and complex scenarios. MATLAB simulations and experiments on the WPR1 platform demonstrate that, compared to traditional Jacobian matrix-based model-free methods, the proposed approach exhibits advantages in tracking accuracy, error convergence speed, and system stability.

1. Introduction

With the continuous advancement of science and technology, robotics is developing at an astonishing rate and is widely used in numerous fields, undertaking critical missions. Robots can replace highly repetitive and complex production tasks previously performed by humans, significantly improving production efficiency while ensuring consistent product quality. Moreover, robots can be deployed in hazardous environments, effectively enhancing operational safety [1]. Due to their outstanding advantages in production, robots are now extensively applied in agriculture [2], healthcare [3], nuclear industry [4], aerospace [5], and many other fields.

Traditional calibrated systems refer to those where the system parameters (e.g., camera intrinsic and extrinsic parameters, distortion coefficients) are precisely calibrated using specific methods before processing image or sensor data. For visual systems, it is also necessary to calibrate the camera parameters and the hand–eye coordinate transformation. The accuracy of these parameters directly affects overall performance, imposing significant limitations in practical applications [6]. To overcome the limitations of calibrated visual servoing, researchers have proposed uncalibrated visual servoing systems [7,8,9,10]. Uncalibrated visual servoing systems do not require parameter calibration but can accurately control robots by analyzing real-time image features, combining the robot’s current state information, and using advanced control algorithms to compute the system’s control input for the next time step. Compared to traditional calibrated systems, uncalibrated systems eliminate the need for precise geometric or kinematic model calibration, reducing system complexity and improving adaptability in practical applications.

With the deepening of research on uncalibrated visual servoing, Model-Free Adaptive Control (MFAC) has gradually gained attention due to its independence from system models. Model-Free Adaptive Control, as an advanced control methodology that does not rely on precise mathematical models of controlled objects, is fundamentally characterized by dynamically adjusting control strategies through online acquisition of system input–output data, rather than depending on a priori mechanistic models for control law design. Based on methodological differences, existing MFAC approaches can be primarily classified into two implementation paradigms. The first category encompasses dynamic linearization-based methods, which construct time-varying linear approximation models through online estimation techniques of pseudo-gradient or pseudo-Jacobian matrices. While these methods retain the structural assumption of local system linearization, they completely eliminate dependence on global model information. The second category comprises fully data-driven model-free methods. These approaches directly establish nonlinear mapping relationships based on input–output data or employ intelligent algorithms (such as neural networks, fuzzy logic systems, etc.) to generate control laws, thereby fundamentally circumventing the modeling process inherent in traditional control methodologies. For the quintessential nonlinear control problem of robotic motion control, scholars in the control field have proposed various specialized model-free adaptive control methods.

In [11], a hybrid adaptive disturbance rejection control (HADRC) algorithm was proposed, which integrates dynamic linearization, disturbance observers, and fuzzy logic control to significantly improve the control performance of inflatable robotic arms. Dynamic linearization is suitable for multiple scenarios, disturbance observers enhance anti-disturbance capabilities, and fuzzy logic control effectively handles highly nonlinear and uncertain systems. In [12], a neural network-based model-free control method was proposed, which uses neural network approximation techniques and position measurements to estimate uncertain Jacobian matrices, significantly improving the adaptability and accuracy of continuum robots in complex environments. Additionally, for the dynamic uncertainty and saturation constraints of rehabilitation exoskeleton robots, [13] proposed a data-driven model-free adaptive containment control (MFACC) strategy, which linearizes the dynamic system into an equivalent data model and designs an improved model-free controller to enhance control performance in complex environments. For the nonlinear dynamics of NAO robots in robust walking, [14] proposed a model-free method based on time-delay estimation (TDE) and fixed-time sliding mode control, which uses TDE to estimate system dynamics in real-time and combines a fixed-time observer with an improved exponential reaching law (MERL) to enhance the stability and trajectory tracking accuracy of the control system.

Although model-free control methods do not rely on precise system models and have shown significant advantages in handling complex dynamic systems, their overall performance still has limitations. First, these methods have limited adaptability to environmental changes, especially in highly nonlinear, uncertain, or strongly disturbed scenarios, where control accuracy and stability may be affected. Second, the design of model-free control often relies on empirical criteria and the selection of algorithm parameters, which poses certain limitations for complex control tasks in high-dimensional spaces. Additionally, traditional model-free control methods struggle to fully utilize large amounts of online data, limiting their potential for dynamic optimization and long-term performance improvement.

Reinforcement Learning (RL), with its core mechanism of autonomously learning optimal policies through interaction with the environment, provides a novel approach to overcome traditional challenges in robotic arm visual servoing [15,16,17,18,19]. Its key advantages lie in eliminating the need for precise robot kinematics/dynamics models or cumbersome camera calibration, significantly reducing system complexity, as well as its exceptional capability in high-dimensional policy generation—enabling direct learning of complex control strategies from high-dimensional visual inputs (e.g., camera images). These strengths have led to the widespread application of RL in robotic arm visual servoing tasks, such as target localization, grasping, trajectory tracking, and obstacle avoidance [20,21,22,23,24].

To address diverse task requirements, the RL algorithm framework has continued to evolve. Early value-based methods (e.g., Deep Q-Network (DQN) [25]) successfully tackle simple tasks with discrete action spaces, such as image-based target localization, but struggle to handle the continuous action spaces required for robotic arm control, often resulting in non-smooth motions. To overcome these limitations, policy gradient-based Actor–Critic methods (e.g., Deep Deterministic Policy Gradient (DDPG) [26,27], Soft Actor–Critic (SAC) [28]) have emerged as the dominant approach. These methods directly output continuous actions and demonstrate superior performance in complex dynamic environments, including high-DoF precise positioning, smooth trajectory tracking, and multi-task learning. However, such methods heavily rely on online environment interaction for extensive trial-and-error learning, posing significant safety risks and high training costs when deployed on real robotic arms. Additionally, the sim-to-real transfer challenge further limits their practical efficiency.

To overcome the bottlenecks in data collection efficiency and security associated with online interaction, offline reinforcement learning (Offline RL) has emerged accordingly. Its core idea is to utilize a pre-collected static experience dataset for training, thereby completely avoiding the risks and costs of online interaction. Among various Offline RL solutions, the Twin Delayed Deep Deterministic Policy Gradient Algorithm with Behavior Cloning (TD3+BC) [29] represents a simple yet effective representative approach. This method introduces a behavior cloning (BC) regularization term into the Twin Delayed Deep Deterministic Policy Gradient Algorithm (TD3) [30] framework, which explicitly encourages the agent’s policy to imitate behaviors present in the dataset. This constrains the policy from deviating excessively from the dataset distribution, thereby effectively suppressing overestimation of Out-of-Distribution (OOD) actions.

However, the TD3+BC method has critical limitations that constrain its performance ceiling. First, it inherits the clipped double Q-learning mechanism from TD3, which uses the minimum value of the outputs from two critic networks as the final Q-value estimate. Although this mechanism effectively mitigates the overestimation bias caused by a single network, it tends to yield overly conservative Q-value estimates in offline settings. This leads to timid policy updates, ultimately slowing convergence and potentially resulting in suboptimal solutions. Second, the strength of its BC regularization term depends on the scale of Q-values. This adaptive weighting can be unstable in certain scenarios, leading to either excessive or insufficient constraints.

To address the conservatism issue of TD3+BC, several improvements have been proposed in the literature. For instance, Conservative Q-Learning (CQL) [31] introduces an explicit regularization term in the learning objective to directly penalize high Q-values for OOD actions, thereby learning a conservative lower bound of the Q-function. However, this approach itself may cause severe underestimation. Implicit Q-Learning (IQL) [32], on the other hand, takes a different path by entirely avoiding value function queries for OOD actions. Instead, it employs a technique called expectile regression to implicitly infer the Q-values of optimal actions, thereby achieving a better balance between mitigating extrapolation error and avoiding excessive conservatism. These methods collectively suggest that an ideal Offline RL algorithm must strike a more delicate balance between preventing overestimation and avoiding over-conservatism.

This study proposes an uncalibrated visual servoing control method for robotic manipulators based on improved offline reinforcement learning. The core innovation lies in the novel Multi-Network Mean Delayed Deep Deterministic Policy Gradient Algorithm with Behavior Cloning (MN-MD3+BC). This approach establishes multiple innovative mechanisms to achieve high-performance visual servoing control without system calibration.

The main contributions of this work are as follows:

1.

A multi-critic network integration architecture is adopted, which uses the mean output of multiple critic networks as the final Q-value estimate. This effectively reduces the estimation bias inherent in single-critic methods and improves the accuracy and stability of value function estimation, providing a more reliable foundation for policy optimization.

2.

A behavior cloning regularization term is incorporated into the policy gradient update, forming a dual-driven optimization mechanism combined with traditional Q-value maximization objectives. This approach constrains policy deviations from the dataset distribution while balancing the conservatism of behavior cloning through Q-optimization objectives, thereby enhancing policy optimization potential without compromising safety.

3.

A data recombination technology-based offline pretraining framework is proposed, which enhances experience reuse efficiency by reorganizing and utilizing pre-constructed high-quality datasets. This technology maximizes the utility of limited datasets while improving training efficiency, providing sufficient data support for end-to-end control policy learning.

4.

An end-to-end direct mapping strategy from visual features to joint control commands is designed, completely eliminating the dependence on complex camera parameter calibration and hand–eye calibration processes required in conventional methods. This significantly reduces the system’s requirement for precise calibration and environmental prior knowledge, providing a new solution for visual servoing control in complex scenarios.

Compared with existing approaches, this solution maintains control precision while significantly reducing the system’s dependence on precise calibration and environmental prior knowledge, offering a novel and effective approach for visual servoing control of robotic manipulators in complex scenarios.

The remainder of this paper is organized as follows: Section 2 describes the experimental platform and outlines theoretical foundations. Section 3 details the proposed offline reinforcement learning adaptive controller and the MN-MD3+BC algorithm architecture. Section 4 presents validation results through both MATLAB (version R2023a) simulations and WPR1 robotic arm experiments. Finally, Section 5 provides concluding remarks on the research findings.

2. Related Work

This section introduces the Programmable Universal Machine for Assembly (PUMA560) simulation platform and the WPR1 robotic arm experimental platform, and briefly outlines the theoretical foundations of robotic arm control.

2.1. Experimental Platforms

2.1.1. PUMA560 Simulation Platform

The PUMA560 (Programmable Universal Machine for Assembly) is a classic six-degree-of-freedom industrial robotic arm introduced by Unimation in the 1970s (Danbury, CT, USA). Known for its flexibility, high precision, and modular design, the PUMA560 has been widely used in both industrial and research fields. It supports complex trajectory planning and manipulation tasks, offering a large workspace and excellent load capacity. In academic research, the PUMA560 is often used to validate robotic control algorithms, such as inverse kinematics, trajectory planning, and visual servoing, due to its standardized kinematic and dynamic models. Its model is integrated into tools such as the MATLAB Robotics Toolbox and ROS, making it a classic platform for robotic control and simulation research.

In this paper, the built-in PUMA560 model from the Robotics Toolbox is used. The first three joints of the PUMA560 control the end-effector position, while the last three joints control the end-effector spatial attitude. Since this study focuses on target position tracking, the end-effector spatial attitude is ignored, reducing the problem to a three-degree-of-freedom control task.

2.1.2. WPR1 Robotic Arm Experimental Platform

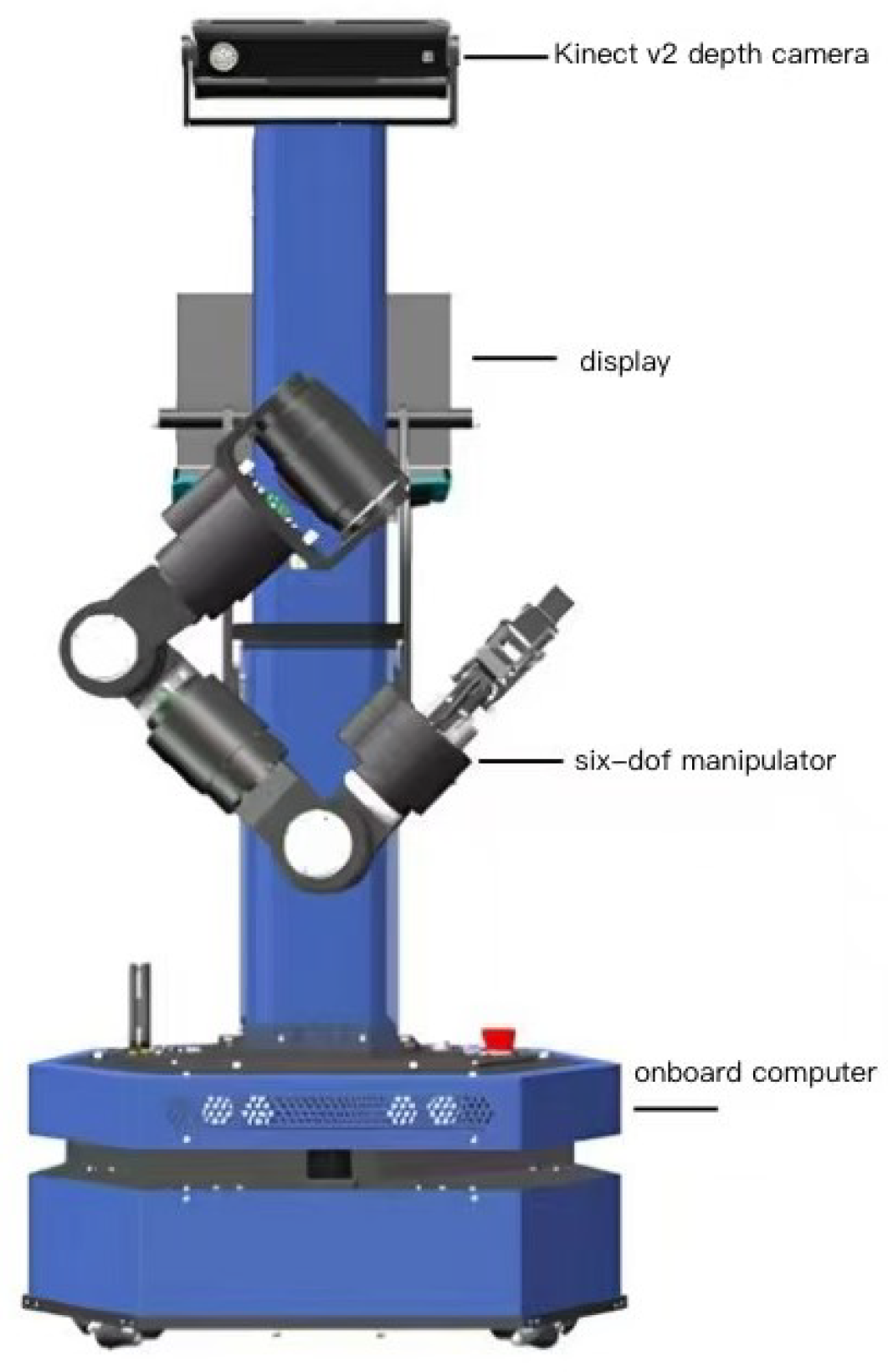
The WPR1 is a robotic arm platform designed for service-oriented applications, developed by Beijing Liubu Workshop Technology Co., Ltd. (Beijing, China) Its main components include an onboard computer, a display, a high-precision six-degree-of-freedom robotic arm, and a wide-angle Kinect v2 depth camera (Microsoft Corporation, Redmond, WA, USA). The robot features a safety-redundant design, ensuring high reliability while maintaining functional diversity. The WPR1 experimental platform is shown in Figure 1.

The Kinect v2 depth camera is mounted at the top of the WPR1’s main body, providing a fixed-position setup. The six-degree-of-freedom robotic arm is installed in the middle of the main body, enabling an eye-to-hand visual servoing system. Additionally, the WPR1 is equipped with an onboard computer at the base and a micro-display at the top, allowing it to operate independently when powered on. The joint limits of the WPR1 robotic arm are listed in

Table 1. Joint limits of the WPR1 robotic arm.

Joint Number	Range of Motion
1	$-{180}^{\circ }$ to ${180}^{\circ }$
2	$-{90}^{\circ }$ to ${90}^{\circ }$
3	$-{180}^{\circ }$ to ${180}^{\circ }$
4	$-{120}^{\circ }$ to ${120}^{\circ }$
5	$-{180}^{\circ }$ to ${180}^{\circ }$
6	$-{120}^{\circ }$ to ${120}^{\circ }$

.

2.2. D-H Parameter Method

The Denavit–Hartenberg (D-H) parameter method [33] is a universal approach for modeling robotic arms. A robotic arm consists of a series of consecutive joints and links, and the D-H method standardizes the establishment of link coordinate systems by assigning a coordinate system to each link to describe its motion. The motion of the robotic arm in the workspace can be described using four parameters related to the x and z axes. This method simplifies the description of the transformation relationship between links using the following four parameters:

(a)

Joint angle (${\mathit{q}}_{\mathit{i}}$): The rotation angle of joint $\mathit{i}$ about the ${\mathit{z}}_{\mathit{i}-\mathbf{1}}$-axis, defined as the joint angle. Rotating by ${\mathit{q}}_{\mathit{i}}$ makes the ${\mathit{x}}_{\mathit{i}-\mathbf{1}}$-axis and ${\mathit{x}}_{\mathit{i}}$-axis parallel.

(b)

Link offset (${\mathit{d}}_{\mathit{i}}$): The offset of joint $\mathit{i}$ along the ${\mathit{z}}_{\mathit{i}-\mathbf{1}}$-axis, describing the displacement from the origin of frame $\mathit{i}-\mathbf{1}$ to the origin of frame $\mathit{i}$ along the ${\mathit{z}}_{\mathit{i}-\mathbf{1}}$-axis. Translating by ${\mathit{d}}_{\mathit{i}}$ makes the ${\mathit{z}}_{\mathit{i}-\mathbf{1}}$-axis and ${\mathit{z}}_{\mathit{i}}$-axis collinear.

(c)

Link length (${\mathit{l}}_{\mathit{i}}$): The length of link $\mathit{i}$ along the ${\mathit{x}}_{\mathit{i}}$-axis, describing the distance between the ${\mathit{x}}_{\mathit{i}-\mathbf{1}}$-axis and ${\mathit{x}}_{\mathit{i}}$-axis. Translating by ${\mathit{l}}_{\mathit{i}}$ makes the origins of the ${\mathit{z}}_{\mathit{i}-\mathbf{1}}$-axis and ${\mathit{z}}_{\mathit{i}}$-axis coincide.

(d)

Link twist (${\mathit{\alpha }}_{\mathit{i}}$): The rotation angle of joint $\mathit{i}$ about the ${\mathit{x}}_{\mathit{i}}$-axis, describing the rotation from frame $\mathit{i}-\mathbf{1}$ to frame $\mathit{i}$. Rotating the ${\mathit{z}}_{\mathit{i}-\mathbf{1}}$-axis about the ${\mathit{x}}_{\mathit{i}}$-axis by ${\mathit{\alpha }}_{\mathit{i}}$ aligns it with the ${\mathit{z}}_{\mathit{i}}$-axis.

For prismatic joints, the link offset (d) is the variable, while for revolute joints, the joint angle (q) is the variable. In this paper, the MATLAB simulation is conducted specifically for the Puma560 model. Therefore, only the D-H parameters and joint motion ranges of the Puma560 are provided, as shown in the

Table 2. D-H parameters of the PUMA560 model.

Link	d (m)	a (m)	$\mathit{q}{(}^{\circ })$	$\mathit{\alpha }{(}^{\circ })$	Limits
1	0	0	$q_1$	90	$-{160}^{\circ }$ to ${160}^{\circ }$
2	0	$0.4318$	$q_2$	0	$-{45}^{\circ }$ to ${255}^{\circ }$
3	$0.15$	$0.0203$	$q_3$	$-90$	$-{255}^{\circ }$ to ${45}^{\circ }$
4	$0.4318$	0	$q_4$	90	$-{110}^{\circ }$ to ${170}^{\circ }$
5	0	0	$q_5$	$-90$	$-{100}^{\circ }$ to ${100}^{\circ }$
6	0	0	$q_6$	0	$-{266}^{\circ }$ to ${266}^{\circ }$

.

2.3. Kinematic Analysis

Based on the D-H parameter method described in the previous section, the relationship between two consecutive links can be described using four parameters, which define the transformation matrix between link $i-1$ and link i. The transformation from coordinate frame $i-1$ to coordinate frame i is achieved through the following four standard steps: first, rotate by the joint angle $q_i$ about the $z_{i-1}$-axis; second, translate by the distance $d_i$ along the $z_{i-1}$-axis; then, translate by the distance $l_i$ along the $x_i$-axis; and, finally, rotate by the angle ${\alpha }_i$ about the $x_i$-axis.

Following this procedure, the transformation matrix between two consecutive link frames, $i-1$ and i, can be established through a series of rotations and translations. The transformation matrix is given by Equation (1):

$$T_i^{i-1}=\left[\begin{array}{cccc}cos{q}_i& -sin{q}_{i}cos{\alpha }_i& sin{q}_{i}sin{\alpha }_i& l_{i}cos{q}_i\\ sin{q}_i& cos{q}_{i}cos{\alpha }_i& -cos{q}_{i}sin{\alpha }_i& l_{i}sin{q}_i\\ 0& sin{\alpha }_i& cos{\alpha }_i& d_i\\ 0& 0& 0& 1\end{array}\right]$$

(1)

From Equation (1), the transformation matrix between two consecutive links can be accurately described. For a robotic arm with M consecutive links, the end-effector pose relative to the base frame can be obtained by multiplying the transformation matrices of all links:

$$T_M^0=T_1^0·T_2^1·\dots ·T_M^{M-1}$$

(2)

The transformation matrix in Equation (2) contains M joint variables. The actual values of these variables are obtained from joint sensors, and the transformation matrix for each link is calculated using Equation (1). By multiplying these matrices, the pose of the end-effector frame relative to the base frame can be expressed as:

$$T_M^0=\left[\begin{array}{cc}R& P\\ 0& 1\end{array}\right]$$

(3)

In Equation (3), R is the rotation matrix describing the orientation of the end-effector, and P is the translation vector describing the position of the end-effector in space.

Based on the above conclusions, the homogeneous transformation matrix of the monocular camera relative to the base coordinate frame of the Puma560 in this paper is as follows:

$$T=\left[\begin{array}{cccc}0.9397& 0& 0.3420& 0\\ 0& -1& 0& 0\\ 0.3420& 0& -0.9397& 0.9\\ 0& 0& 0& 1\end{array}\right]$$

(4)

2.4. Robotic Arm Visual Servoing Task

Robotic arm servoing tasks involve controlling the motion of the robotic arm to achieve precise manipulation of target objects, with applications in manufacturing, healthcare, and service industries. Kinematic modeling is a critical aspect of servoing tasks, as it describes the mapping between joint space and task space to achieve accurate end-effector positioning and spatial attitude control.

Using the D-H parameter method, the forward kinematics model can be established to compute the end-effector’s position and spatial attitude in task space based on joint angles. Conversely, inverse kinematics solves for the joint angles required to achieve a specific task, often requiring numerical methods due to the complexity of the robotic arm’s geometry.

In robotic arm servoing control, two main approaches are used: position-based servoing and vision-based servoing. Position-based servoing relies on precise geometric modeling and system calibration, using inverse kinematics to compute target joint angles and controllers to achieve desired trajectories. However, traditional methods are sensitive to model accuracy and calibration errors, limiting their performance in dynamic environments.

To address these limitations, vision-based servoing methods have been developed. Vision-based servoing uses real-time images from cameras to extract visual features and compare them with target features, adjusting the robotic arm’s motion based on the computed error. The integration of robot kinematics and vision-based servoing provides theoretical and technical support for complex tasks. However, in dynamic environments, traditional servoing methods may be affected by calibration errors, task complexity, and modeling limitations. As a result, data-driven methods such as reinforcement learning have gained attention, enabling robotic arms to learn control strategies directly from visual input, further improving the precision and adaptability of servoing tasks.

3. Methodology

For robotic arm visual servoing tasks, this paper proposes a visual servo control system framework based on the Multi-Network Mean Delayed Deep Deterministic Policy Gradient Algorithm with Behavior Cloning (MN-MD3+BC), designed to achieve efficient and precise control of complex tasks. The system fully leverages the advantages of offline reinforcement learning by employing offline policy optimization to reduce the risks and costs associated with direct training in real-world environments, while effectively addressing control challenges arising from the system’s nonlinear characteristics and environmental disturbances in robotic arm manipulation. This section will comprehensively present the algorithmic architecture of MN-MD3+BC and its implementation in robotic arm visual servoing tasks. Detailed explanations will focus on the core modules of the MN-MD3+BC algorithm, including (1) the neural network architecture design, (2) definitions of state space and action space, and (3) construction of the reward function.

3.1. MN-MD3+BC Algorithm Architecture Framework

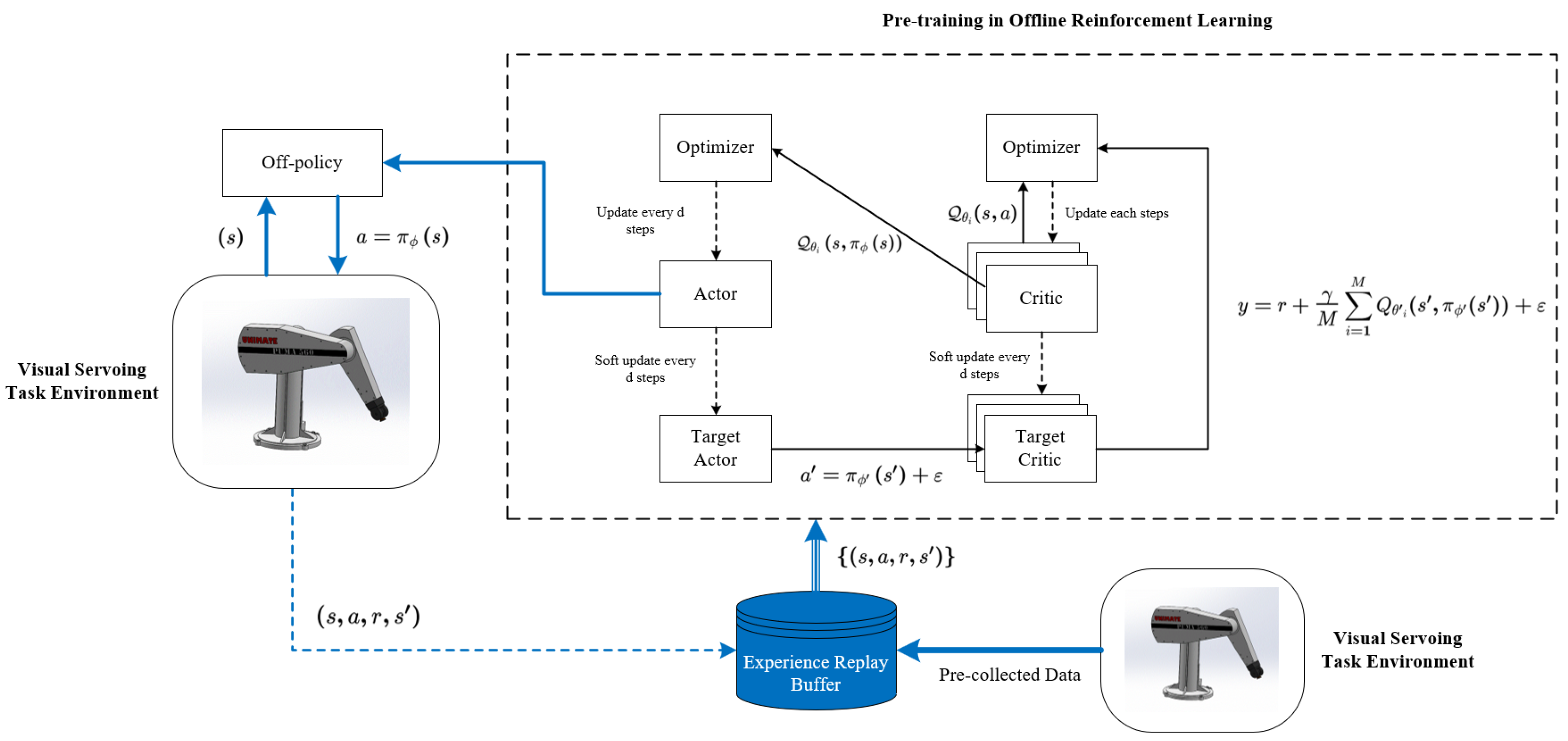
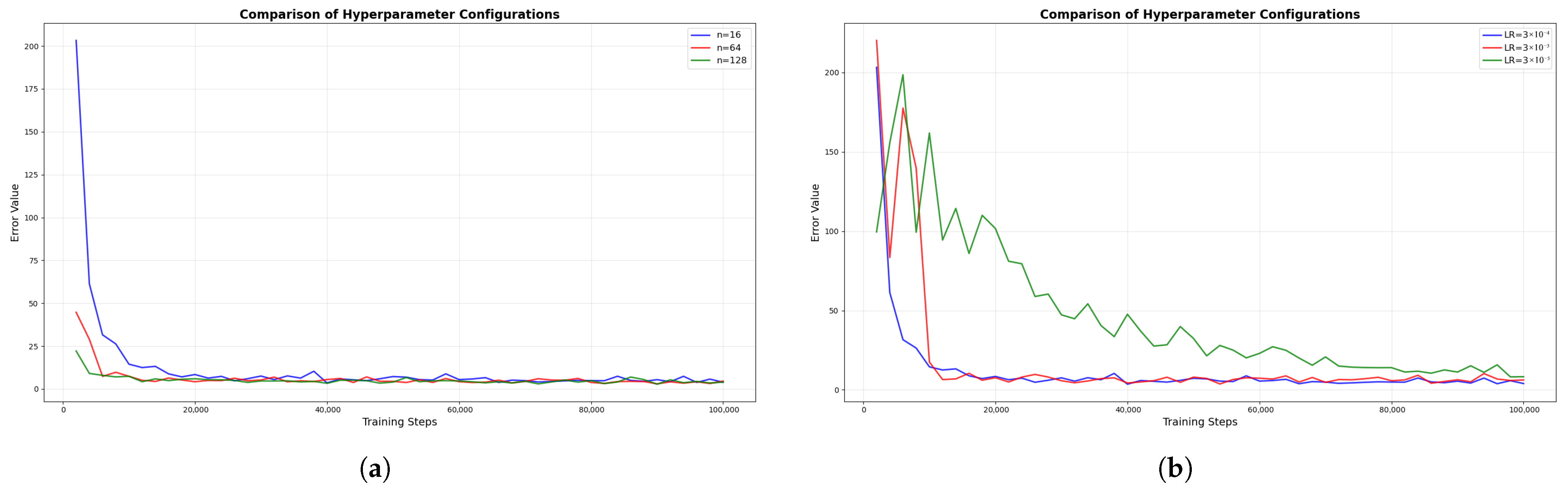
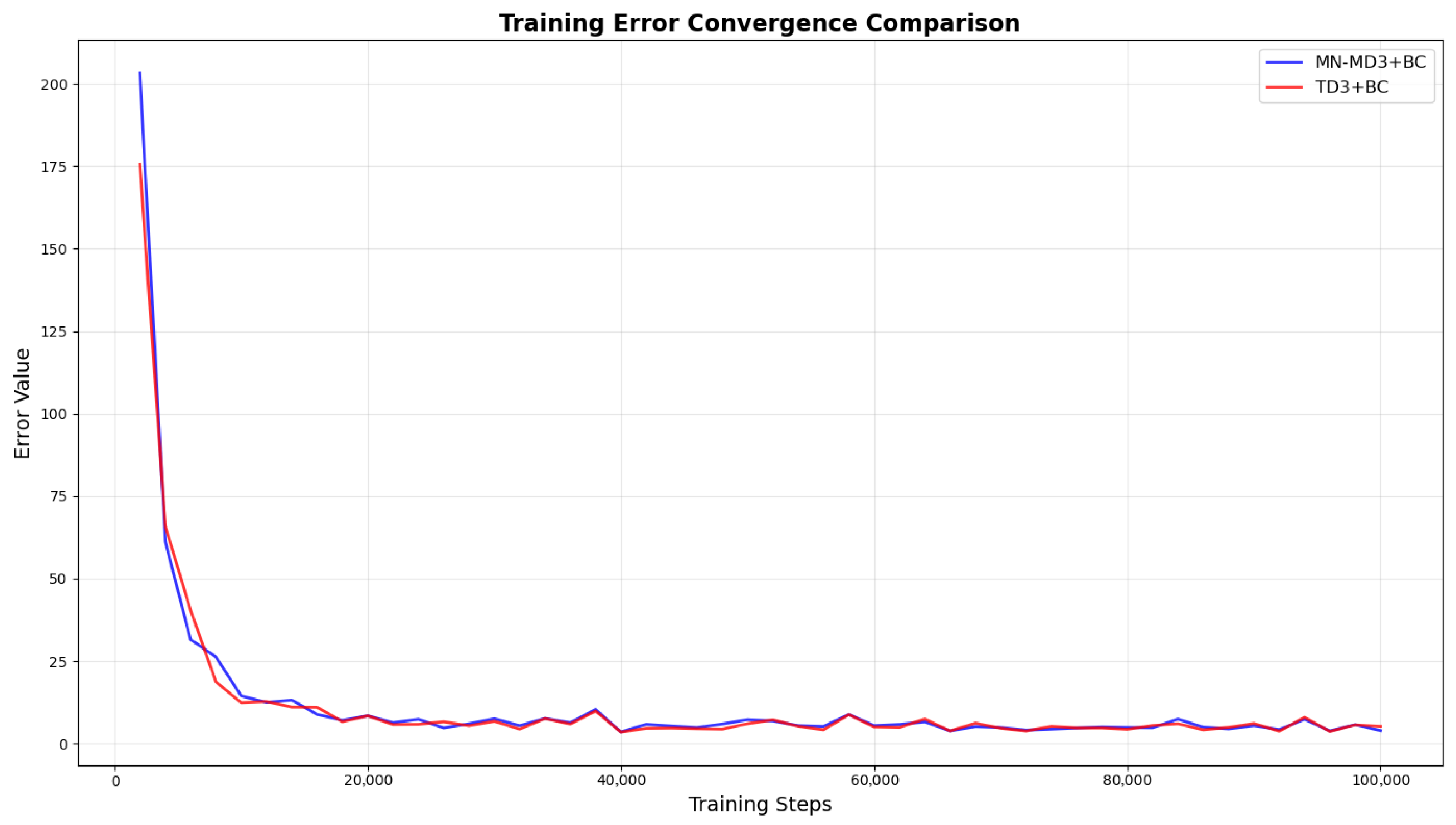
The MN-MD3+BC algorithm, building upon the TD3 framework, innovatively employs three Critic networks to enhance decision-making reliability (as shown in Figure 2). The choice of three—rather than more—networks reflects a critical trade-off between performance and efficiency. Averaging across three networks effectively balances estimation bias and variance, providing sufficiently robust evaluation. Adding a fourth or more networks would yield negligible performance improvements, while significantly increasing computational costs and the risk of overfitting. Therefore, “three” represents the optimal number that maximizes robustness without compromising real-time performance.This architecture employs three independent critic networks to evaluate policies from multiple perspectives, utilizing mean value computation for target Q-value estimation, which effectively mitigates potential estimation biases inherent in single-critic approaches. The algorithm implements a dual-objective optimization mechanism that dynamically weights behavior cloning loss against Q-value maximization objectives. This design ensures policy constraints remain within dataset-supported boundaries while preserving exploration capabilities in high-performance regions. In practical control processes, this balance manifests as the decision network’s dual capability: it reliably tracks effective actions from demonstration data while autonomously optimizing more precise motion trajectories.

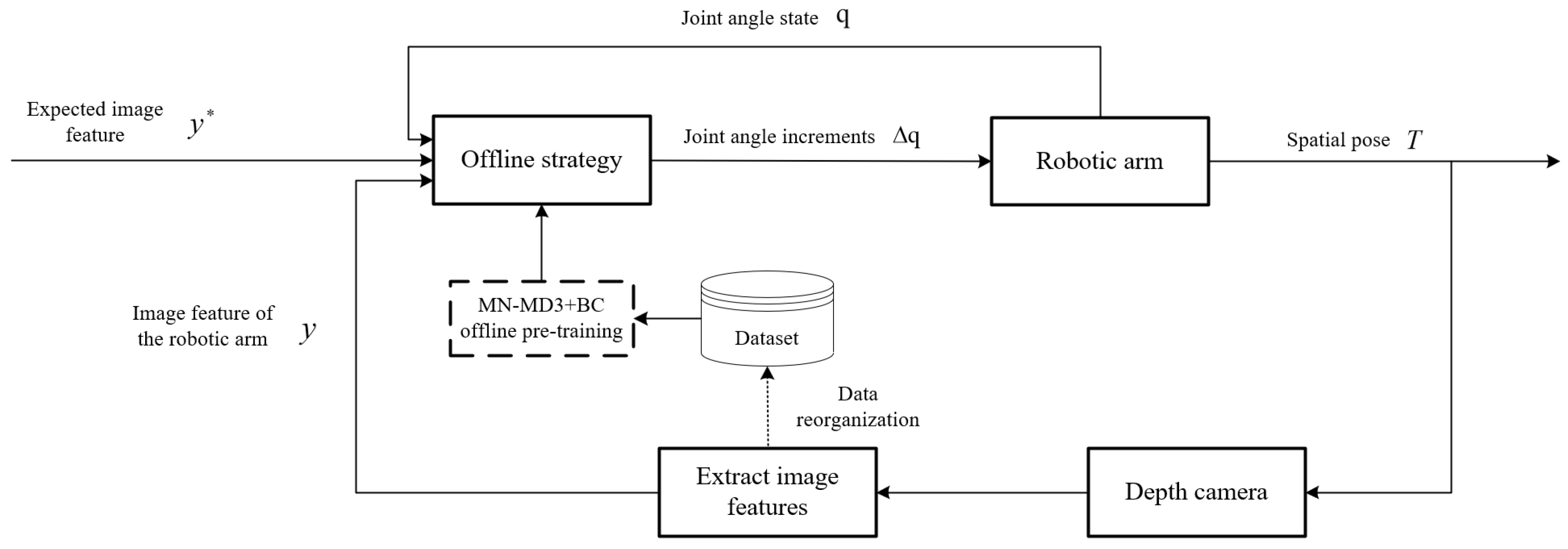
In the robotic arm visual servoing control process (as shown in Figure 3), the system first extracts image features from camera-captured images. These extracted image features, combined with desired image features and current joint angles, form the state information that is fed into the policy network. The policy network then computes the joint angle variations based on the trained offline policy. These computed joint angle variations are subsequently executed by the robotic arm to perform the required movement. Following the arm’s motion, the system captures new image features again and repeats the aforementioned steps. This cyclic process continues iteratively until the visual servoing control task is successfully completed.

3.2. Network Structure Design

The network architecture of the Twin Delayed Deep Deterministic Policy Gradient (TD3) algorithm [30] consists of one policy network (Actor), two independent value networks (Critic), and their corresponding target networks. The policy network takes the current environmental state as input and outputs optimal continuous actions for environmental interaction. The Critic networks receive both state and action as inputs to independently estimate the Q-value of actions.

In conventional Actor–Critic frameworks, the Actor and Critic networks typically employ relatively consistent architectures, where the Critic network serves as an approximation of the state-action value function to evaluate actions generated by the Actor policy network. However, to address the overestimation bias inherent in traditional methods, TD3 adopts the Double Q-learning approach by utilizing two separate Critic networks to independently estimate Q-values and using their minimum for target updates. Although this design effectively mitigates overestimation bias, it may result in persistently low value estimation of actions output by the Actor network, thereby affecting the algorithm’s convergence speed and the conservativeness of the policy.

To address this limitation, we extend the TD3 framework by introducing M Critic networks with corresponding target networks. Instead of taking the minimum Q-value, we compute the mean across all Critic networks:

$$y=r+\gamma ·{\displaystyle \frac{1}{M}}\sum _{i=1}^M{Q}_{{\theta }_i^{\prime }}(s^{\prime },{\pi }_{{\varphi }^{\prime }}\left(s^{\prime }\right))$$

(5)

where M denotes the number of Critic networks, r denotes the reward value corresponding to the current action, $\gamma$ denotes the discount factor, and $s^{\prime }$ denotes next state after taking the action. In this and the following equations, $\theta$ and $\varphi$ denote the parameters of the Actor and Critic networks, respectively, while ${\theta }^{\prime }$ and ${\varphi }^{\prime }$ represent the parameters of their corresponding target networks.

Furthermore, for target policy regularization, noise is incorporated into the target policy:

$$y=r+\gamma ·{\displaystyle \frac{1}{M}}\sum _{i=1}^M{Q}_{{\theta }_i^{\prime }}(s^{\prime },{\pi }_{{\varphi }^{\prime }}\left(s^{\prime }\right)+ϵ)$$

(6)

where $ϵ\sim \mathcal{N}(0,\sigma )$ represents target policy regularization noise.

The Critic network parameters ${\theta }_i$ are updated by minimizing the following loss function:

$${\mathcal{L}}_{\mathrm{critic}}={\displaystyle \frac{1}{N}}\sum _{(s,a,r,s^{\prime })\in \mathcal{B}}\sum _{i=1}^M{\left(Q_{{\theta }_i}(s,a)-y\right)}^2$$

(7)

where $\mathcal{B}$ denotes a mini-batch of size N sampled from the experience replay buffer.

Although the TD3 algorithm has demonstrated excellent performance in online reinforcement learning, its core design relies on continuous interaction with the environment, which makes it unsuitable for direct application in offline reinforcement learning. In offline scenarios, the TD3 algorithm requires generating new actions during policy updates. However, these generated actions may deviate from the distribution of the offline dataset, leading to the distributional shift problem. Specifically, this shift can cause the value function to erroneously overestimate the policy’s performance, resulting in performance degradation or even policy collapse. To address the distributional shift issue in offline reinforcement learning, we have introduced Behavioral Cloning (BC) into the policy update process. The BC loss constrains the learned policy to remain close to the behavioral policy that generated the dataset:

$${\mathcal{L}}_{\mathrm{bc}}={\displaystyle \frac{1}{N}}\sum _{(s,a)\in \mathcal{B}}{∥{\pi }_{\varphi }\left(s\right)-a∥}^2$$

(8)

The combined policy loss becomes a multi-objective optimization problem:

$${\mathcal{L}}_{\mathrm{actor}}=-\lambda ·{\mathbb{E}}_{s\sim \mathcal{B}}\left[{\displaystyle \frac{1}{M}}\sum _{i=1}^M{Q}_{{\theta }_i}(s,{\pi }_{\varphi }\left(s\right))\right]+(1-\lambda )·{\mathcal{L}}_{\mathrm{bc}}$$

(9)

where $\lambda ={\displaystyle \frac{c}{{\mathbb{E}}_{s\sim \mathcal{B}}\left[\right|Q_{{\theta }_i}(s,{\pi }_{\varphi }\left(s\right))\left|\right]}}$ is a weighting factor that controls the relative importance of the behavior cloning term. The value of c is set to 2.5 in this paper.

The target networks undergo soft updates as follows:

$$\begin{array}{cc}\hfill {\varphi }^{\prime }& \leftarrow \tau \varphi +(1-\tau ){\varphi }^{\prime }\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill {\theta }_i^{\prime }& \leftarrow \tau {\theta }_i+(1-\tau ){\theta }_i^{\prime }\mathrm{for}i=1,\dots ,M\hfill \end{array}$$

(11)

where $\tau$ is the learning rate for target network updates.

3.3. State Space Definition

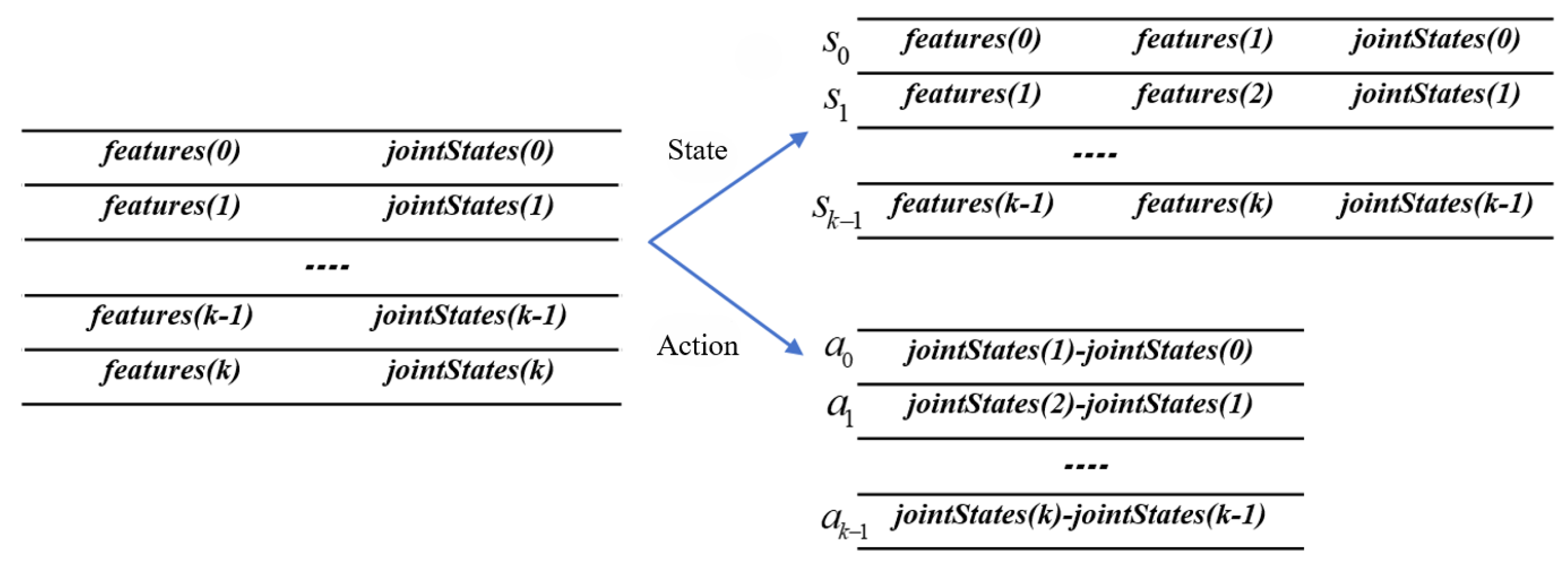
The state space of a robotic arm refers to the observed state information during its operation, encompassing both environmental states and the robotic arm’s own states. In the context of robotic arm control problems, the state space may include the robotic arm’s joint angles, the position of the end-effector, the position of the target point, and so forth. These elements serve as input variables that enable the robotic arm to acquire state information, based on which, along with the current policy, it selects appropriate actions to execute and subsequently obtains corresponding reward values.

For the calibration-free visual servoing task investigated in this study, environmental state perception primarily relies on visual sensor information. Specifically, the system employs a depth camera as the visual sensor, with acquired image features including the pixel’s horizontal coordinate u, the pixel’s vertical coordinate v, and the pixel’s depth value $depth$. These features collectively constitute the state space representation of the system. The robotic arm’s own state refers to the changing state of its structure, specifically the angle values of each joint. Due to the issue of degrees of freedom in robotic arms, a high degree of freedom robotic arm can have multiple inverse solutions for the same end-effector position. Therefore, the current joint angle values are necessary to seek the optimal policy that enables reaching the next position with minimal movement.

Since this paper focuses on the problem of tracking the target position of the robotic arm’s end-effector, the issue of the end-effector’s orientation is temporarily disregarded. The tracking of the robotic arm’s target position is a stochastic and continuous process, and the sole introduction of the current target position is not applicable to all tracking tasks. Consequently, this paper introduces the expected image feature of the target at the next moment into the state space. This feature value can be calculated through pre-set parameters or an independent target prediction algorithm, satisfying the requirements of positioning and tracking tasks. The state space is defined as:

$$s_t=\left[f_t,f_t^{*},q_t\right]$$

(12)

where:

• $f_t=(u_t,v_t,dept{h}_t)$ denotes the current image features with pixel coordinates $(u_t,v_t)$ and depth $dept{h}_t$ from the depth camera;
• $f_t^{*}=(u_t^{*},v_t^{*},dept{h}_t^{*})$ represents the expected target image features;
• $q_t={(q_1,\dots ,q_n)}^{\top }$ is the joint angle vector with n degrees of freedom.

3.4. Action Space Definition

To accomplish the robotic arm target tracking task, it is necessary to ensure that the end-effector of the robotic arm follows the movement of the target. The required state information, including environmental data and the joint angles of the robotic arm, has already been acquired. The action space should aim to minimize the distance between the end-effector position and the target position by providing the required joint angle changes for the next time step. These changes are then accumulated to the current joint angles, enabling the robotic arm to continuously adjust its angles and, consequently, the position of the end-effector. The action space defines the joint angle increments for trajectory tracking:

$$a_t=\Delta {\mathit{q}}_t={(\Delta q_1,\dots ,\Delta q_n)}^T$$

(13)

where each $\Delta q_i$ is bounded by the mechanical constraints $\Delta q_i\in [\Delta q_{min},\Delta q_{max}]$.

3.5. Reward Function Design

The key to robotic arm target tracking lies in the acquisition of reward values, which represent the objective of the task and drive the learning strategy of the robotic arm. Without proper rewards, the arm would engage in endless, aimless movements. Therefore, designing an appropriate reward function is one of the critical elements in solving reinforcement learning problems.

In this section, with the task background of uncalibrated visual target tracking by a robotic arm, the reward function design must be based on the relative distance between the end-effector features and target features in the visual sensor’s frame, while also considering the magnitude of actions. Consequently, the proposed reward function consists of two components: distance reward and action reward, as expressed in the following equation:

$$r_t=\underset{\mathrm{Distance}\mathrm{reward}}{\underbrace{-\alpha \parallel {\mathit{f}}_{t+1}-{\mathit{f}}_t^{*}{\parallel }_2}}+\underset{\mathrm{Action}\mathrm{reward}}{\underbrace{-\beta \parallel \Delta {\mathit{q}}_t{\parallel }_2^2}}$$

(14)

with feature distance computed as:

$$\parallel {\mathit{f}}_{t+1}-{\mathit{f}}_t^{*}{\parallel }_2=\sqrt{{(u_{t+1}-u_t^{*})}^2+{(v_{t+1}-v_t^{*})}^2+{(dept{h}_{t+1}-dept{h}_t^{*})}^2}$$

(15)

where

• The values of $\alpha$ and $\beta$, set to 10 and 1, respectively, are weighting coefficients that prioritize tracking precision.
• $\Delta {\mathit{q}}_t$ is the joint angle change vector.

3.6. Algorithm Training Process

In order to more clearly understand the implementation process, we propose the following pseudo code (Algorithm 1) for the training process of the MN-MD3+BC algorithm.

Algorithm 1 MN-MD3+BC training procedure

Initialize:    Actor network parameters $\varphi$ and target ${\varphi }^{\prime }$    M Critic networks ${\theta }_1,\dots ,{\theta }_M$ and targets ${\theta }_1^{\prime },\dots ,{\theta }_M^{\prime }$    Experience replay buffer $\mathcal{D}$ with normalized dataset for step $=0$ to ${\mathrm{steps}}_{max}$ do     Sample mini-batch $(s,a,r,s^{\prime })\sim \mathcal{D}$     Update Critic networks by minimizing Equation (7)     if step $modd==0$ then         Update Actor network via Equation (9)         Soft update target networks:            ${\varphi }^{\prime }\leftarrow \tau \varphi +(1-\tau ){\varphi }^{\prime }$            ${\theta }_i^{\prime }\leftarrow \tau {\theta }_i+(1-\tau ){\theta }_i^{\prime },\forall i=1,\dots ,M$     end if end for

4. Experiments

To evaluate the performance of the MN-MD3+BC uncalibrated robotic arm visual adaptive control algorithm, this study conducts comprehensive testing and verification on both the Matlab simulation platform and the WPR1 experimental platform. The evaluation process focuses on analyzing the algorithm’s accuracy in executing visual servoing tasks, thereby validating its adaptability across different platforms and task completion effectiveness.

4.1. Dataset Construction for Offline Pretraining

To enable effective pretraining of the MN-MD3+BC offline reinforcement learning algorithm proposed in Section 3, a tailored pretraining dataset must be constructed. The quality of this dataset critically influences the convergence of algorithm training and the performance of the learned policy, which subsequently impacts the effectiveness of the uncalibrated visual servoing control task. This section details a data-splicing-based dataset construction methodology aligned with visual servoing objectives.

4.1.1. Data Collection Phase

A robotic arm visual servoing system serves as the data source. The joint angles of the robotic arm are randomly initialized within their permissible limits. The arm executes random motions with varying joint velocity rates, where the action magnitude is constrained to the range $(-0.05,0.05)$. Joint angle limits are enforced throughout the motion. During motion execution, joint angle states and corresponding end-effector image features are recorded at each timestep. Data collection terminates if the end-effector image features are lost or when the maximum timestep threshold (2000 steps) is reached. The data collection phase is repeated until 16 episodes are attained.

After discarding episodes prematurely terminated due to feature loss, approximately 30,000 valid data entries are collected.

4.1.2. Data Reorganization Phase

The raw dataset requires restructuring to align with reinforcement learning frameworks, where each experience replay buffer entry contains (state, action, reward, next-state) components:

(a)

State Representation:

$$s_t=\left[f_t,f_t^{*},q_t\right]$$

(16)

where $f_t$ denotes current image features, $f_t^{*}$ is derived by offsetting subsequent features from the raw dataset, and $q_t$ represents joint angles.

(b)

Action Derivation:

$$a_t=\Delta {\mathit{q}}_t=q_{t+1}-q_t$$

(17)

(c)

Reward Calculation:

The reward function is set as Equation (14).

The data reorganization process is illustrated in Figure 4; k represents the index of the original data sequence. For example, through iterative processing of the original sequential data containing image features $f_1$, $f_2$, $f_3$, $f_4$ and joint angles $q_1$, $q_2$, $q_3$, $q_4$, we successfully construct three complete training instances: at timestep $t=1$, the state $s_1$ is composed of the current image feature $f_1$, target feature $f_1^{*}=f_2$, and joint angle $q_1$, and the executing action $a_1=q_2-q_1$ yields reward $r_1$ and transitions to the next state $s_2$; at timestep $t=2$, taking action $a_2=q_3-q_2$ from state $s_2$ results in reward $r_2$ and leads to state $s_3$; at timestep $t=3$, executing action $a_3=q_4-q_3$ from state $s_3$ with reward $r_3$ leads to state $s_4$, ultimately generating three experience tuples $(s_1,a_1,r_1,s_2)$, $(s_2,a_2,r_2,s_3)$, and $(s_3,a_3,r_3,s_4)$, with the cyclic processing of the entire raw dataset producing the final pretraining dataset for the experience replay buffer, ensuring full compatibility with the previously defined state space, action space, and reward function.

During the dataset construction process, a certain level of diversity in the initial data is ensured through random initialization and large-range joint motions. Nevertheless, potential limitations of the dataset should be noted. First, the target features are derived from the actual next-frame image, which may not be optimal for the servoing task and only serve as a pseudo-supervision signal. Second, the distribution of image features is constrained by the robotic arm’s range of motion. If the task workspace is large, the collected data may not fully cover it. Finally, the action distribution generated by the random motion strategy may not be sufficiently uniform, posing a risk of learning bias. In the future, the coverage and diversity of the dataset could be further improved by incorporating multiple motion patterns, adding noise injection, or combining task-oriented sampling strategies, thereby enhancing the robustness and generalization capability of the learned policy.

4.2. Matlab Simulation Platform Experiments

The simulation environment is built using Robotics Toolbox and Machine Vision Toolbox in MATLAB. We compare MN-MD3+BC with TD3+BC and Model-Free Adaptive Control (MFAC).

In the simulated PUMA560 visual servoing system, the visual measurements consist of the pixel coordinates of target points and their depth values $[u_t,v_t,dept{h}_t]$. Considering that the first three joints of the PUMA560 control the end-effector’s positional degrees of freedom (DOFs) in Cartesian space while the last three joints govern spatial attitude, this study focuses solely on end-effector position tracking. By neglecting spatial attitude control, the problem is simplified to a 3-DOF robotic arm control task. The control inputs are defined as the first three joint angles (in radians):

$${\mathbf{q}}_c={[q_1,q_2,q_3]}^T$$

(18)

To evaluate the performance of different algorithms across various motion trajectories, this paper conducts a comparative experiment between the final policy networks obtained from the MN-MD3+BC and TD3+BC algorithms (trained for $1\times {10}^5$ steps) and the MFAC algorithm. The hyperparameter settings used in the experiments are listed in

Table 3. Hyperparameter configuration.

Parameter	Reinforcement Learning		MFAC
	MN-MD3+BC	TD3+BC
Max timesteps	$1\times {10}^5$	$1\times {10}^5$	-
Batch size	16	16	-
Discount factor ($\gamma$)	0.99	0.99	-
Target update rate ($\tau$)	0.005	0.005	-
Policy noise	0.2	0.2	-
Noise clip	0.5	0.5	-
Critic networks	3	2	-
$\rho$	-	-	0.05
$\eta$	-	-	1.096
$\mu$	-	-	0.92
$\lambda$	-	-	1.56

. To further investigate the impact of hyperparameters on training effectiveness, a sensitivity analysis is performed. The results (as shown in the Figure 5) indicate that increasing the batch size accelerates convergence but significantly extends per-epoch training time. In the later stages of training, the performance error across different batch sizes converges. In the learning rate comparison experiment, the value of 3 × 10⁻⁴ yields the best performance. After balancing convergence efficiency and stability, the batch size is set to 16 and the learning rate to 3 × 10⁻⁴. The remaining common parameters follow the widely validated default settings proposed by Fujimoto et al. [30] in the TD3 algorithm. The parameters of the MFAC algorithm are configured according to its theoretical framework [34]. All parameters are verified through preliminary experiments to ensure stability and reproducibility of the learning process.

In both the MN-MD3+BC and TD3+BC algorithms, the final policy networks obtained after training for $1\times {10}^5$ steps are used for experimental evaluation. To ensure the reliability of the experimental results, each algorithm is independently trained three times, and the average tracking error is used to plot the curves. The error variation curves during the training process of the policy networks are shown in the Figure 6. It can be observed that after $1\times {10}^5$ training steps, the errors of both algorithms have converged, indicating that their performance meets the basic task requirements.

• Experiment 1: Spiral Trajectory Tracking

The target spiral trajectory is defined as:

$$\left\{\begin{array}{c}x\left(t\right)=0.5cos\left(0.5\pi t\right)\hfill \\ y\left(t\right)=0.5sin\left(0.5\pi t\right)\hfill \\ z\left(t\right)=0.1t\hfill \end{array}\right.,t\in [0,10]$$

(19)

The motion trajectory $\left[x\right(t),y(t),z(t\left)\right]$ needs to be converted into image pixel coordinates $(u,v)$ and a depth value $\mathit{depth}$ to serve as observational inputs for the algorithm. This conversion is based on the pinhole camera model, where the pixel coordinates $(u,v)$ represent the perspective projection of a 3D spatial point onto a two-dimensional imaging plane. The depth observation $\mathit{depth}$ corresponds to the component along the optical axis of the straight-line distance from the target to the camera’s optical center, calculated based on geometric principles. Finally, the observation vector $\left[u\right(t),v(t),depth(t\left)\right]$ is used as the input feature for the algorithm.

The trajectory tracking performance of the three algorithms is illustrated in Figure 7.

The experimental results from Figure 7 clearly demonstrate that compared with the MFAC algorithm, the MN-MD3+BC algorithm and the TD3+BC algorithm perform better in terms of error convergence, and can converge the error to zero more quickly. This indicates that the robotic arm visual servo control method combined with reinforcement learning outperforms the traditional model-free control method based on the Jacobian matrix in terms of response speed, and the convergence speed of the MN-MD3+BC algorithm is slightly faster than that of the TD3+BC algorithm. During the subsequent tracking process, all three algorithms exhibit error fluctuations to varying degrees. Among them, the error fluctuations of the TD3+BC algorithm and the MFAC algorithm are relatively obvious, with large fluctuations occurring in the middle and late stages of the tracking task, respectively. In contrast, the error curve of the MN-MD3+BC algorithm is relatively stable, with a smaller fluctuation range, demonstrating better tracking stability and precision.

• Experiment 2: Circular Trajectory Tracking

The target circular trajectory is defined as:

$$\left\{\begin{array}{c}x\left(t\right)=0.4cos\left(0.8\pi t\right)\hfill \\ y\left(t\right)=0.4sin\left(0.8\pi t\right)\hfill \\ z\left(t\right)=0.3\hfill \end{array}\right.,t\in [0,5]$$

(20)

The trajectory tracking performance of the three algorithms is illustrated in Figure 8.

As shown in the Figure 8, during the process of approaching the target trajectory, the MN-MD3+BC algorithm and the TD3+BC algorithm exhibit almost the same trajectory, with only a slight separation of the trajectories occurring at the moment of approaching the target trajectory. In contrast, the MFAC algorithm approaches the target trajectory gradually along a more tortuous path. During the tracking period, there is a noticeable gap between the motion trajectories of the TD3+BC algorithm and the MFAC algorithm and the target trajectory, indicating a certain deviation. However, the tracking trajectory of the MN-MD3+BC algorithm basically coincides with the target trajectory, demonstrating higher tracking accuracy. The MN-MD3+BC algorithm still has a faster convergence speed, being able to converge the error to zero more quickly, and the error fluctuation range during the tracking process is also relatively small, indicating that the MN-MD3+BC algorithm has higher stability.

To further compare the performance of the three algorithms, we calculate both the mean and variance of image feature tracking errors for Experiment 1 and Experiment 2. The mean feature error reflects the algorithm’s accuracy, while the variance of feature error indicates the fluctuation degree of errors. The detailed data are presented in

Table 4. Error analysis.

Exp. No.	Algorithm	Mean Error	Variance
1	MFAC	10.443	1.348
	TD3+BC	6.353	1.157
	MN-MD3+BC	4.871	0.315
2	MFAC	8.447	0.882
	TD3+BC	3.203	0.276
	MN-MD3+BC	3.107	0.247

.

As evidenced by Table 4, in Experiment 1, the MN-MD3+BC algorithm achieves the lowest mean feature error along with significantly smaller error variance compared to the other two algorithms, demonstrating its superior tracking performance. This advantage remains consistent in Experiment 2, where MN-MD3+BC maintains both lower mean feature error and reduced error variance, confirming its overall outstanding performance across different test conditions.

In conclusion, compared with the traditional model-free method based on the Jacobian matrix, the robotic arm visual servo control method combined with reinforcement learning has a faster response and smaller errors. In addition, the MN-MD3+BC algorithm proposed in this paper shows excellent tracking performance in the experiments, demonstrating further advantages over the TD3+BC algorithm.

4.3. WPR1 Experimental Platform Validation

To further verify the effectiveness of the proposed algorithm, based on the analysis of the hardware and software environmental parameters of the WPR1 robotic arm experimental platform presented in Section 2, a depth camera-based WPR1 robotic arm visual servoing system is constructed on this experimental platform. The proposed MN-MD3+BC algorithm is compared with the Model-Free Adaptive Control algorithm (MFAC algorithm) and the TD3+BC algorithm in real visual servoing tasks. In this section, the visual servoing measurements include the pixel coordinates and depth values of the target points in the image. Different from Section 4.2, the control outputs in this section are the radian values of the six joint angles.

4.3.1. Static Target Positioning Experiment

The initial image features of the robotic arm are denoted as (440, 254, 870). The target object is placed at 10 different locations, and positioning experiments are conducted for each location. The positioning results of the two algorithms are derived based on the motion of the robotic arm. Due to inherent errors in the visual servoing system of the robotic arm, the positioning phase may be continuously affected by disturbances, causing slight movements without reaching a complete static. As a result, it is challenging to obtain a definitive final positioning result.

To compare the positioning errors of the algorithms, the observed feature values at the 50th timestep during the motion are selected as the positioning results for the end-effector image features. The experimental results are summarized in

Table 5. Positioning results on WPR1 platform (feature coordinates).

Exp. No.	Target Feature	MFAC	TD3+BC	MN-MD3+BC
1	(410, 235, 840)	(410, 236, 839)	(410, 235, 838)	(410, 235, 837)
2	(530, 213, 818)	(530, 215, 820)	(529, 215, 819)	(529,214,818)
3	(450, 250, 850)	(451, 250, 852)	(450, 249, 851)	(450,248,851)
4	(510, 220, 890)	(511, 222, 887)	(510, 220, 888)	(510,218,890)
5	(500, 200, 900)	(500, 204, 902)	(501, 201, 900)	(502,198,899)
6	(515, 232, 795)	(515, 230, 795)	(515, 230, 796)	(515,230,797)
7	(520, 180, 780)	(520, 182, 778)	(520, 180, 776)	(518,179,780)
8	(480, 270, 820)	(479, 269, 823)	(479, 271, 824)	(480,272,823)
9	(390, 300, 800)	(390, 300, 802)	(390, 300, 800)	(391,299,799)
10	(460, 300, 790)	(460, 299, 789)	(459, 299, 789)	(457, 298, 790)
MAE		2.625	2.597	2.566

Note: Feature coordinates represent (u, v, depth) in pixel-space.

.

As shown in Table 5, in all 10 experimental trials, none of the three algorithms experiences image feature loss, and the WPR1 robotic arm successfully positions itself near the target point in each case. The three algorithms demonstrate similar average feature errors, with no significant differences observed in positioning accuracy.

To further analyze the positioning performance of these algorithms, we select one set of data from these 10 experiments for detailed examination. This section focuses specifically on the data from Experiment 2 to conduct a more in-depth comparison and evaluation of their positioning effectiveness. The comparative results are illustrated in Figure 9.

As shown in Figure 9, although all three algorithms can position near the target point, compared with the other two algorithms, the MN-MD3+BC algorithm can more directly position near the target point, demonstrating superior convergence performance by achieving faster convergence to steady state while maintaining errors at a smaller level. In contrast, the MFAC algorithm shows significantly slower convergence speed than MN-MD3+BC, and its positioning error remains consistently larger than that of MN-MD3+BC throughout the entire process. While the TD3+BC algorithm’s convergence speed is only slightly slower than MN-MD3+BC, its error fluctuations are noticeably greater than those of the MN-MD3+BC algorithm.

In summary, for visual servoing tasks involving static target positioning, the MN-MD3+BC algorithm proposed in this paper demonstrates significantly better overall performance compared to both the traditional Jacobian matrix-based Model-Free Adaptive Control algorithm and the TD3+BC algorithm, exhibiting faster response speed and smaller positioning errors.

4.3.2. Dynamic Target Tracking Experiments

This section conducts target tracking experiments on the object using the previously proposed MFAC algorithm, TD3+BC algorithm, and MN-MD3+BC algorithm, respectively, to further compare the performance of the three algorithms.

To ensure the fairness of the comparative experiments, it is necessary to guarantee that the dynamic targets tracked by the three algorithms follow identical motion processes. Therefore, the target motion in this section is pre-recorded by having the experimenter manually move a red ball along a predetermined trajectory. All three algorithms receive the target image features at the same frequency and control the WPR1 robotic arm accordingly. Since the target ball’s velocity is manually controlled by the experimenter, precise speed regulation is impossible, but an approximate velocity of 0.05 m/s is maintained as consistently as possible.

Multiple types of target motion trajectories are collected in this section, from which two representative trajectories are selected for algorithm analysis. By comparing the tracking trajectories and tracking errors of the three algorithms, their relative strengths and weaknesses can be evaluated. The comparative results are illustrated in Figure 10 and Figure 11.

The evaluation of trajectory tracking performance reveals distinct differences among the three control algorithms (as shown in Figure 10). Experimental results indicate that the MFAC algorithm exhibits noticeable trajectory jitter when approaching the target path, while both the TD3+BC and MN-MD3+BC algorithms demonstrate smoother tracking trajectories. It is worth noting that in the later stages of the tracking task, all three algorithms achieve good alignment with the target trajectory, confirming their fundamental capability to complete the tracking task.

Through in-depth analysis of error characteristics, it is found that the MFAC algorithm shows significant tracking errors during the initial tracking phase, revealing deficiencies in its control computation process. To further compare the control performance of different algorithms, this study conducts a magnified analysis of tracking errors during the system’s stable phase. The results demonstrate that compared to the MN-MD3+BC algorithm, the TD3+BC algorithm exhibits more pronounced error fluctuations, with this difference being particularly evident in the vertical (v) direction error metrics.

Overall, the MN-MD3+BC algorithm demonstrates optimal robustness with the smallest error fluctuation amplitude, indicating that it possesses more stable control performance and higher tracking accuracy in trajectory tracking tasks.

The experimental results show that the three control algorithms exhibit significant differences in complex trajectory tracking tasks (as shown in Figure 11). The test trajectory contains various motion characteristics including curves, straight lines, and sharp turns, providing comprehensive verification for algorithm performance evaluation. Although the three algorithms show similar temporal characteristics when approaching the target trajectory, there are obvious differences in trajectory accuracy and stability.

Specifically, the MN-MD3+BC algorithm demonstrates the best comprehensive performance, with its generated tracking trajectories not only showing optimal smoothness but also maintaining high consistency with the reference trajectory. In comparison, the MFAC algorithm exhibits obvious trajectory deviation during turning segments, indicating inherent limitations of traditional Jacobian matrix-based model-free methods in complex motion tracking. While the TD3+BC algorithm shows improvement over MFAC, it still displays relatively large trajectory fluctuations, especially at sharp “V”-shaped turns.

The error comparison plots reveal deeper performance differences. The MFAC algorithm performs worst, showing the largest tracking errors in the initial phase that are significantly greater than the other two algorithms. Although the converged tracking error of TD3+BC is only slightly worse than MN-MD3+BC, the enlarged plots clearly show that TD3+BC has greater fluctuations.

In terms of control components, all three algorithms maintain similarly low steady-state errors in the u and depth directions. However, in the v component, the MFAC algorithm shows significant fluctuations in the initial phase, while the TD3+BC algorithm still exhibits additional fluctuations compared to MN-MD3+BC. These differences are particularly evident in trajectory segments containing sharp turns. These experimental results further confirm that the MN-MD3+BC algorithm has advantages in both control stability and precision.

The comprehensive experimental results demonstrate that in complex visual servoing tasks, the MN-MD3+BC algorithm not only significantly outperforms traditional model-free methods but also shows performance improvements over the TD3+BC algorithm, verifying its advantages in control accuracy, stability, and robustness.

4.3.3. Comprehensive Performance Comparison

To ensure the reliability and generalization of the experimental conclusions, this study conducts systematic evaluation of algorithm performance through multiple repeated experiments (including ten static target positioning experiments and twenty dynamic target tracking experiments).

Table 6. Comparative analysis of comprehensive positioning performance in fixed-point experiments.

Metric	MFAC	TD3+BC	MN-MD3+BC
Mean Feature Error	12.622	8.967	6.473
Mean Convergence Steps (step)	30.56	12.84	9.23

and

Table 7. Comparative analysis of comprehensive performance in trajectory tracking experiments.

Metric	MFAC	TD3+BC	MN-MD3+BC
Mean Feature Error	29.425	10.175	9.475
Mean Convergence Steps (step)	27.32	21.92	20.18
Feature Error Variance	218.63	34.551	22.82

, respectively, present the key performance metrics of the three algorithms in point-to-point positioning experiments and trajectory tracking experiments: mean feature error, average convergence steps, and feature error variance. Here, the mean feature error quantifies positioning accuracy (smaller values indicate higher precision), average convergence steps reflect dynamic convergence speed (fewer steps indicate faster convergence), and feature error variance characterizes steady-state stability (smaller variance indicates better stability).

The results indicate that the MN-MD3+BC algorithm consistently achieves the best average performance across all evaluation metrics. Specifically, in the trajectory tracking task, statistical tests show that the mean feature error of the MFAC controller is significantly higher than those of both TD3+BC (p < 0.0001) and MN-MD3+BC (p < 0.0001). Although the average error of MN-MD3+BC (9.475) is lower than that of TD3+BC (10.175), the difference between them does not reach statistical significance (p = 0.612). However, this does not imply equivalent performance: in all 20 independent trials, the error of MN-MD3+BC is consistently lower than that of TD3+BC. Moreover, the error variance of MN-MD3+BC (22.82) is significantly reduced compared to that of TD3+BC (34.55). These findings suggest that although MN-MD3+BC does not demonstrate a statistically significant advantage in mean error, it exhibits superior stability and reliability—a practically important improvement.

In the fixed-point positioning task, a fully consistent trend is observed: MN-MD3+BC achieves the lowest mean feature error and the fewest average convergence steps.

In summary, the performance of the MFAC controller is significantly worse than both reinforcement learning-based algorithms (TD3+BC and MN-MD3+BC), as reflected in its substantially higher mean error and variance, which is confirmed by statistical tests. The proposed MN-MD3+BC algorithm outperforms all others in every tested scenario, demonstrating advantages in terms of lower average error, faster convergence, and significantly reduced variance indicating exceptional stability. Compared to TD3+BC, MN-MD3+BC exhibits a clear performance improvement trend. Although the reduction in mean error is not statistically significant, the notable decrease in variance represents an important practical advantage, confirming that the proposed algorithm offers stronger robustness and reliability.

These quantitative results fully validate the comprehensive advantages of the MN-MD3+BC algorithm in visual servoing control tasks. Particularly in application scenarios requiring high-precision positioning and fast response, the algorithm’s excellent performance demonstrates significant practical value. The consistency of experimental data indicates that the proposed improved algorithm not only possesses theoretical innovation but also shows reliable performance enhancement in practical applications.

5. Conclusions

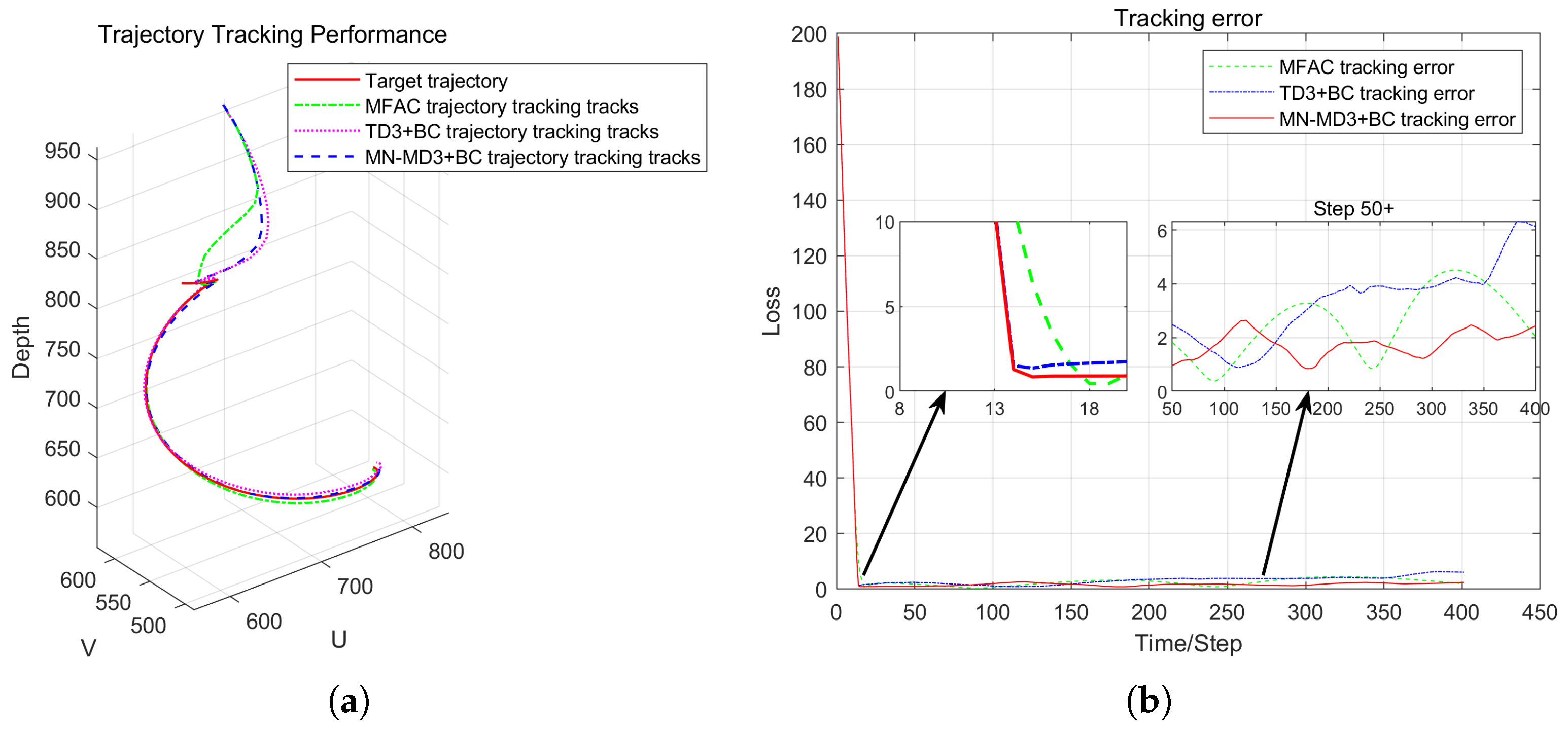
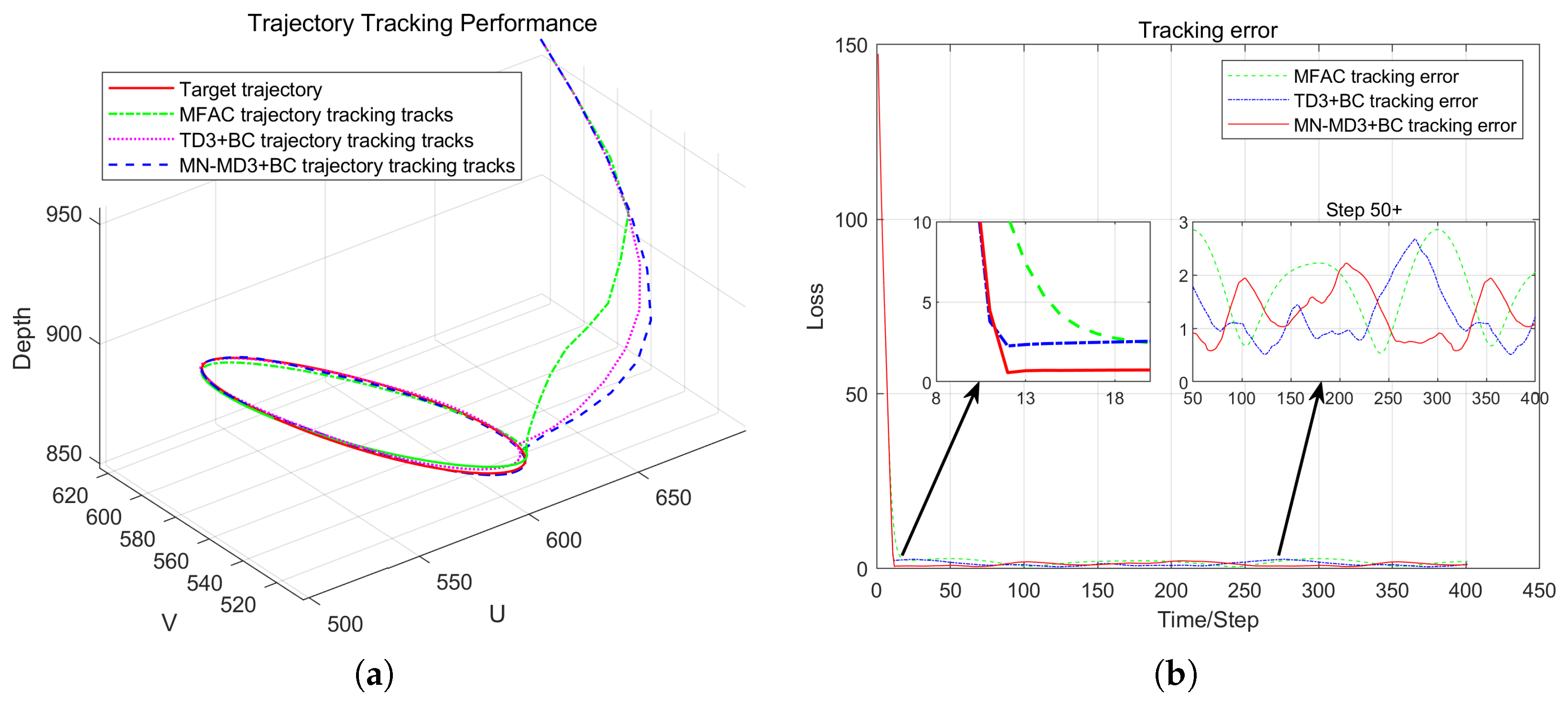
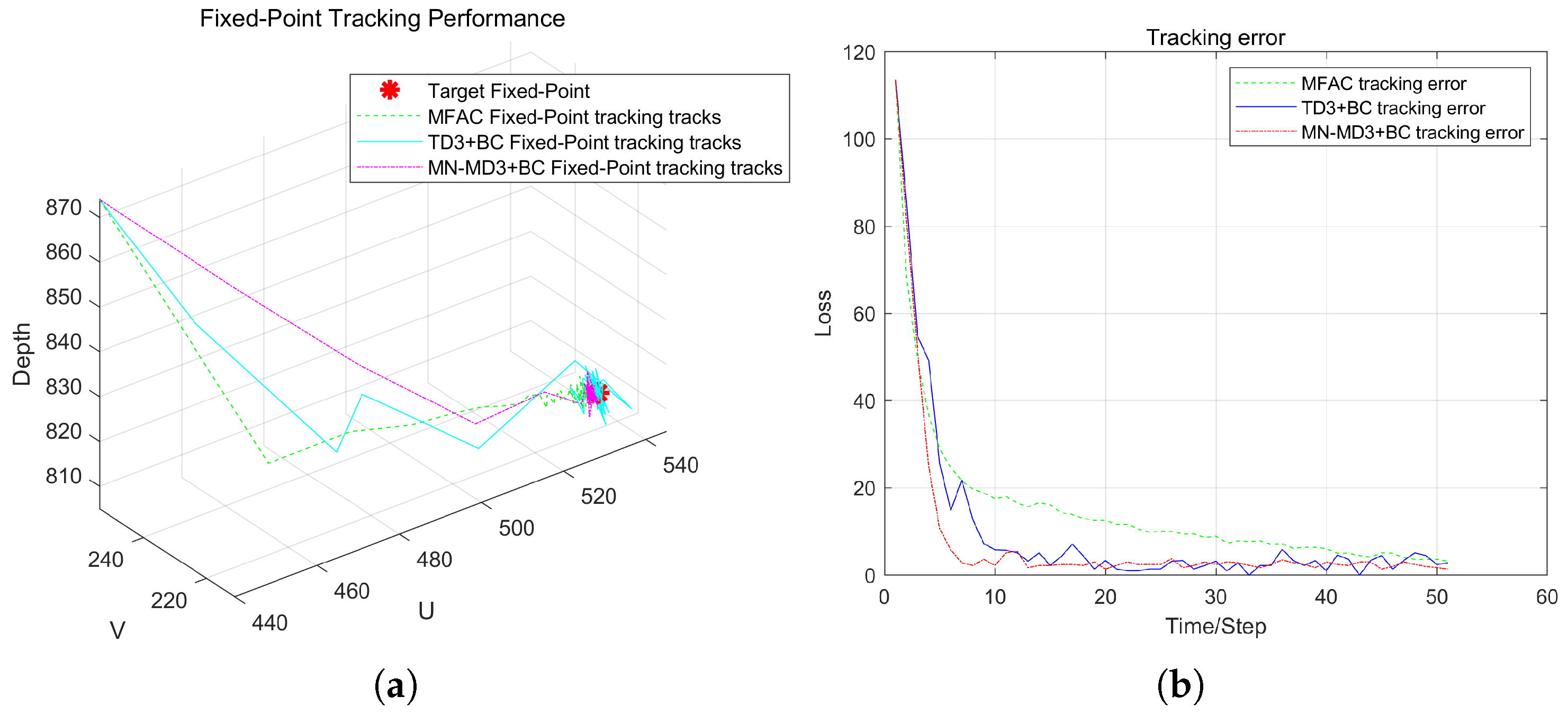
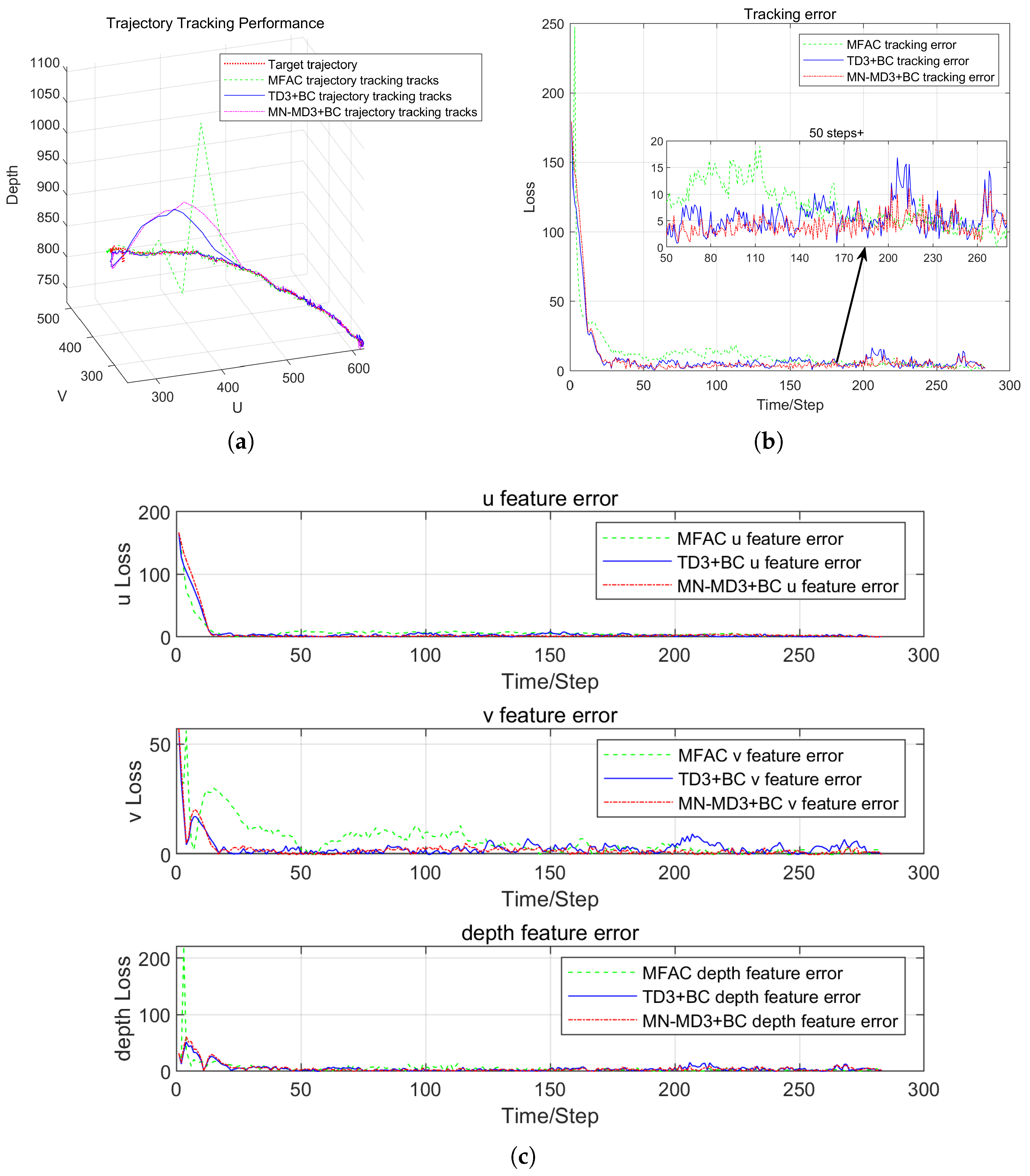
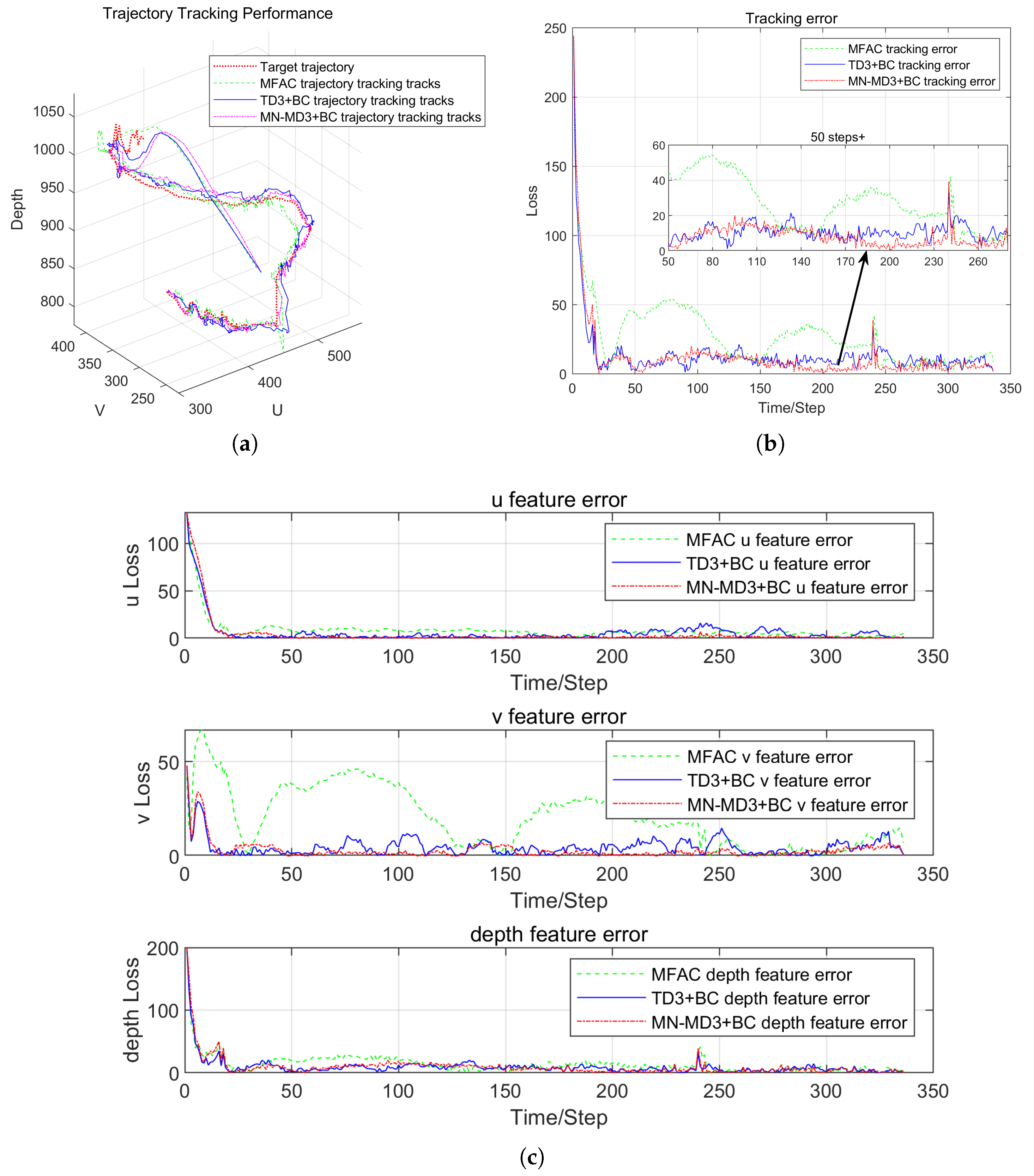
Different from the existing methods for designing robotic arm vision controllers based on online reinforcement learning, this paper proposed a deterministic policy gradient offline reinforcement learning algorithm based on multi-evaluation network averaging (MN-MD3+BC algorithm) from the perspective of real-world applications, in response to the problems of training inefficiency and underutilized data faced by online reinforcement learning in a high-dimensional state space. The algorithm made targeted improvements on the basis of the TD3+BC offline reinforcement learning algorithm, especially achieving breakthroughs in performance optimization in the uncalibrated visual servoing task. The MN-MD3+BC algorithm improves the accuracy of the value evaluation by means of multi-evaluating network averaging, and at the same time enhances the robustness of the strategy, effectively avoiding the common overestimation bias problem of traditional reinforcement learning algorithms in the process of strategy convergence. Compared with online reinforcement learning, the algorithm substantially reduces the dependence on real-time environment interaction during the training process by pre-training the policy network offline, which enhances the practicality in real robotic arm control tasks.

In order to verify the performance of the proposed algorithm, comparative experiments were conducted in Matlab custom simulation environment and on the actual WPR1 robotic arm experimental platform. The experimental results showed that the MN-MD3+BC algorithm exhibits significant advantages in terms of tracking accuracy, error convergence speed, and system stability compared with the traditional model-free control method. Especially when dealing with visual servo tasks such as complex trajectories and sharp turns, the MN-MD3+BC algorithm is able to converge to the target trajectory more quickly and with smaller error fluctuations, showing better robustness and control performance.

The proposed MN-MD3+BC algorithm not only overcomes the limitations of traditional calibration-based methods but also effectively addresses challenges faced by online reinforcement learning in real-time control tasks, offering an efficient and practical offline reinforcement learning solution. Through simulations and physical experiments, the research outcomes provide new insights and references for future studies in the field of visual servoing control for robotic manipulators, demonstrating significant theoretical value and application potential. However, several challenges remain before the method can be deployed in real industrial settings. First, although offline reinforcement learning reduces dependence on environmental interaction, its performance is highly reliant on the diversity and coverage of the training data, which may lead to limited generalization capability when encountering unseen working conditions. Furthermore, since behavior cloning strategies may cause policy updates to rely excessively on historical data, the exploratory ability of the policy in unfamiliar environments could be constrained. In particular, the scalability of the algorithm under more challenging multi-target scenarios and dynamically changing lighting conditions requires further validation. Although the experimental setup already includes motion-induced jitter noise and the algorithm exhibits inherent robustness to some extent, its target recognition and decision-making mechanisms may need adjustments when handling multiple targets with different shapes and priorities simultaneously. Significant illumination variations may also affect the stability of visual feature extraction. While the training data incorporated a certain degree of lighting diversity, the algorithm’s performance under extreme illumination conditions still warrants systematic evaluation. Therefore, future research will focus on enhancing the algorithm’s generalization in complex scenarios—particularly its adaptability and robustness in multi-target collaboration and dynamically changing lighting conditions—while optimizing the exploration–exploitation trade-off to achieve a more efficient and reliable visual servoing control system.