SRNet-Trans: A Singal-Image Guided Depth Completion Regression Network for Transparent Object

Abstract

Transparent objects are prevalent in various everyday scenarios. However, their reflective and refractive optical properties present significant challenges for conventional optical sensors. This difficulty makes the task of generating dense depth maps from sparse depth maps and high-resolution RGB images a critical area of research. In this paper, we introduce SRNet-Trans, a novel two-stage depth completion framework specifically designed for transparent objects. The approach is structured into two stages, each primarily focused on leveraging semantic and depth information, respectively. In the first stage, RGB images and sparse depth maps are used to predict a relatively dense depth map. The second stage then takes the predicted depth from the first stage, along with the sparse depth map, to generate a final dense depth map. The depth information produced by the two stages is complementary, allowing for effective fusion of both outputs. To enhance the depth estimation process, we integrate a self-attention mechanism in the first stage to better capture semantic features and introduce geometric convolutional layers in the second stage to improve depth encoding accuracy. Additionally, we incorporate a global consistency-based fine depth recovery technique to further refine the final depth map. Extensive experiments on the large-scale real-world TransCG dataset demonstrate that SRNet-Trans outperforms current state-of-the-art methods in terms of depth estimation accuracy.

1. Introduction

With the rapid advancement of unmanned systems, including aerial drones, ground robots, and service platforms, intelligent perception has become a cornerstone for enabling autonomous navigation, accurate positioning, and reliable task execution. In such contexts, robots must be capable of perceiving and interpreting diverse objects in their environment to ensure safety and efficiency. However, transparent objects—such as glass, plastics, and laboratory containers—pose unique challenges due to their refractive and reflective optical properties, which often disrupt conventional vision and depth-sensing mechanisms. The inability to perceive transparent objects may result in navigation errors, manipulation failures, or even safety risks. Therefore, enhancing the perception capabilities of unmanned systems toward transparent objects is of critical importance, as it directly supports applications such as collision-free navigation in cluttered scenes, robotic grasping and manipulation of fragile transparent items, and high-precision localization in safety-critical domains.

Transparent objects are ubiquitous in everyday life, with materials such as glass, plastic, and glass lids being commonly encountered. Similarly, industrial glassware such as beakers, test tubes, and petri dishes are integral to laboratory settings. With the increasing integration of robotics into daily activities, it is essential for robots to be capable of obtaining accurate pose information for transparent objects in their environment [1]. Depth sensing technologies, such as RGB-D cameras, play a pivotal role in achieving this. Depth maps produced by these cameras have found extensive applications in fields like 3D reconstruction and robotics, offering improved insight into the complex geometric details of dense scenes and fine geometric features of targets when compared to RGB images. However, transparent objects, due to their refractive and reflective properties, present a significant challenge for conventional depth sensors. These optical characteristics disrupt the geometric light path assumptions that depth sensing relies on, complicating the task of acquiring reliable depth data for such objects [2]. As a result, a hybrid approach that combines the scene geometry captured by RGB images with the sparse depth information provided by depth sensors is necessary to reconstruct a more accurate, higher-density depth map.

Depth completion for transparent objects has emerged as a challenging problem in computer vision in recent years. Given the inherent material properties of transparent objects, hardware-based solutions often struggle to address the complexities of depth recovery in general scenarios [3]. However, with the rapid advancements in neural networks and large language models, new methodologies for transparent object depth completion have emerged. Currently, approaches in this domain can be broadly classified into two categories: multi-view and single-view methods [4]. While multi-view approaches offer more comprehensive reconstruction and enhanced perception of transparent objects, they introduce additional challenges in practical scenarios. Specifically, the instability of multi-camera setups during deployment can lead to uncertainties in algorithmic results. Moreover, multi-view methods fail to leverage valuable information present in the original depth map, which may limit their adaptability, particularly in dynamic environments.

Single-view depth completion, in contrast, faces three primary challenges [5]. First, many current methods rely on the encoder–decoder structure, which is common in visual tasks, to restore depth information. However, this approach often overlooks the difficulties associated with the lack of texture features in transparent objects. Second, there is a tendency to neglect the cross-modal interaction between the shallow feature details of transparent objects and RGB-D data, leading to a loss of local details and unclear object contours in the predicted depth map. Finally, not all areas of a depth image require completion. Depth completion should be applied selectively, focusing only on regions where depth information is missing or erroneous. However, many existing methods employ full convolutional networks, treating all regions equally, which is inefficient and can result in suboptimal performance.

To address the limitations of existing approaches, this paper proposes an end-to-end deep regression network designed to achieve efficient and high-precision depth completion for transparent objects. Our method introduces a two-stage network architecture, consisting of a semantic clue-dominated stage and a depth information-dominated stage. In more detail, the semantic clue-dominated stage primarily focuses on understanding semantic information that is crucial for depth prediction. This stage emphasizes semantic cues, making the predicted depth particularly reliable around the edges of transparent objects. However, it is more sensitive to variations in color and texture. The depth information-dominated stage, on the other hand, takes both the sparse depth data and the depth predictions from the first stage as input to generate a dense depth map. While this stage typically produces more reliable depth estimates, the input sparse depth data can introduce significant noise, especially along the edges of transparent objects. Since the depth maps produced by these two stages are complementary, we perform a deep fusion of their results to achieve a more accurate final output. Additionally, we refine the fused dense depth map using a fine depth recovery process that ensures global consistency across the entire map.

The main contributions of this paper are as follows:

• Two-Stage Network Architecture for Transparent Object Depth Completion: To fully extract features from RGB-D images of transparent objects, we propose a two-stage depth completion network tailored for semantic scenes. This architecture integrates a semantic information-guided stage and a depth information-driven stage to perform dense depth prediction, effectively leveraging and combining the cross-modal features of RGB-D data.
• Introduction of Self-Attention for Transparent Object Depth Completion: This paper is the first to incorporate a self-attention mechanism into transparent object depth completion. The self-attention mechanism enables comprehensive encoding of surface normal information and edge details, significantly enhancing the performance of depth completion tasks for transparent objects.
• Global Consistency via Scale Factor-Based Refinement: We introduce a scale factor approach to refine depth completion in the scale space, improving the global consistency of the depth map. This refinement process greatly enhances the accuracy and quality of the predicted depth map.

2. Related Work

Transparent object perception has long been a challenging problem in computer vision. Early methods often relied on physical priors, such as surface shape measurement techniques based on polarization imaging. These methods reconstruct surface normals by analyzing the polarization characteristics of reflected and transmitted light from transparent objects. However, they typically require high-precision sensors and specific environmental lighting conditions. Stereo vision-based methods, like KeyPose [6], utilize stereo cameras to predict 3D keypoints of transparent objects, avoiding explicit depth computation. Despite maintaining good generalization performance even with unseen object categories, these methods are dependent on high-quality stereo images and sensitive to feature matching accuracy.

With the development of deep learning, data-driven methods have gradually become mainstream. For example, ClearGrasp uses synthetic data to train a network for depth completion of transparent objects, thereby enhancing the stability of robotic grasping. The introduction of the Trans2Seg and Trans10K datasets has significantly advanced research in transparent object semantic segmentation. However, due to the difficulty of obtaining ground truth depth data for transparent regions, research on depth completion in real-world scenarios remains in its early stages. Recently, light field imaging techniques have been introduced for transparent object detection, utilizing multi-view information and angular constraints to achieve fast detection. For instance, a self-adaptive density clustering method proposed by Zhang et al. [7] combines feature saliency and motion consistency constraints based on light field data, achieving a fivefold improvement in computational speed without sacrificing accuracy. A 2024 study from the Wuhan Textile University team proposed a depth completion method based on a dual-cross attention network, where the U-Net structure was improved with dual-cross attention modules and spectral residual blocks. This effectively reduced the semantic gap between RGB images and depth maps, enhancing the stability of depth completion. In low-light conditions, a team from MIT [8] explored deep neural network-based methods for transparent object imaging, achieving successful reconstruction of transparent objects in near-dark environments. Additionally, the Prior Depth Anything framework [9], developed by Zhejiang University and the University of Hong Kong, supports zero-shot depth completion, super-resolution, and repair tasks. By fusing sparse depth sensor data with geometric priors from RGB images, it has demonstrated outstanding performance across various real-world datasets.

Depth completion aims to generate dense depth maps from sparse or noisy depth measurements, guided by RGB images. Early works mainly used convolutional neural networks (CNNs) or encoder–decoder architectures, such as Eigen et al.’s multi-scale depth prediction network. Recently, Transformer models have been introduced into this field due to their powerful global context modeling capabilities. For example, Dense Prediction Transformer (DPT) [10] captures long-range dependencies using Vision Transformers [11], significantly improving edge-preserving abilities in depth maps. However, most methods assume opaque object surfaces, overlooking depth uncertainties caused by refraction and reflection in transparent regions.

Recent studies have begun to explore dedicated depth completion methods for transparent objects. For example, methods based on compressed sensing and super-resolution convolutional neural networks (SRCNNs) [12] have been used for transparent object imaging, reconstructing surface details at low sampling rates through single-pixel detection and total variation minimization. A 2025 study introduced a multi-frequency time-domain iterative strategy based on stripe modulation, effectively eliminating interference from parasitic reflections on transparent objects’ rear surfaces in defect detection. Additionally, self-supervised learning paradigms such as Monodepth2 [13] and ManyDepth2 [14] use photometric consistency constraints from stereo image pairs or video sequences to reduce reliance on ground truth depth annotations. GeoDepth [15] further models 3D scenes as sets of planes and uses normal and offset parameterization for self-supervised monocular depth estimation, improving depth discontinuity in indoor and outdoor scenes [9]. The Prior Depth Anything framework adopts a coarse-to-fine approach, performing pixel-level metric alignment before refining the results with conditional monocular depth estimation models, demonstrating robust adaptation to various sparse priors in a zero-shot setting.

Liu et al. [16] proposed the DualTransNet network that uses segmentation features for transparent depth completion. In our DualTransNet, it feed segmentation features from an extra module to the main network for better depth completion quality. This demonstrates the effectiveness of segmentation features for depth estimation of transparent objects. Zhai et al. [17] introduced TCRNet, a transparent object depth completion network based on a cascaded refinement structure that effectively balances accuracy and real-time performance. The network utilizes a cascaded refinement mechanism during the decoding stage to iteratively refine features, thereby enhancing the accuracy of the depth information. Additionally, an attention module is incorporated to focus on the depth-related features of the transparent object regions, further improving performance. Gao et al. [18] presented a method for transparent object depth estimation based on a single RGB-D input, using a U-Net architecture with an efficient channel attention module. Despite employing a minimal number of parameters, the network significantly boosts performance. Li et al. [19] proposed a voxel-based deep learning approach for transparent object depth completion. This method leverages image features from the RGB input and valid points in the intersecting voxels derived from the point cloud. A multi-layer perceptron is used to predict the missing depth values, optimizing them under the constraint of surface normal consistency.

Jing et al. [20] proposed a novel simulation-to-real transferable model, CAGT, which incorporates interactive embedding aggregation and geometric perception capabilities for reconstructing severely sparse depth maps of transparent objects. Pathak et al. [21] introduced the Context Encoders model, utilizing a conditional GAN architecture to enhance the visual realism of generated completion images through adversarial training. This approach effectively improves completion quality by maximizing the similarity between the generated image and the real image. The “Generative Inpainting” model, proposed by Yu et al. [22], further advances the realism of completion images by combining GANs with local context information. The adversarial training strategy within this model leads to more natural and visually coherent restoration results. Li et al. [23] investigated the effect of transparency variations on detection accuracy and proposed a detection method based on visual-tactile fusion. Their research highlighted the influence of lighting changes and the diversity of transparent object shapes on the accuracy of detection outcomes.

3. Method

3.1. Problem Formulation

The depth completion task aims to fill in missing regions of depth measurements using the scene geometry cues provided by the corresponding RGB image. The core challenge of this task lies in efficiently fusing the geometric relationships of the monocular scene with the sparse depth data from the depth sensor—two distinct modalities—to achieve accurate depth reconstruction.

Mathematically, given a set of matched data samples, the goal is to learn a mapping function F such that Y = F (X _RGB, X _Depth), where X _RGB ∈ R ^3*H*W represents the three-channel RGB image, X _Depth ∈ R ^H*W represents the one-channel sparse depth map, and Y ∈ R ^H*W denotes the ground truth depth map.

To address this, we propose a high-performance depth completion network with a novel design that enables effective depth completion from a single RGB-D image of a transparent object. Specifically, this paper introduces a two-stage semantic scene-based depth completion algorithm tailored for transparent objects.

3.2. Network Architecture

We propose an end-to-end depth completion learning framework tailored for semantic scenes. As illustrated in the figure, the framework consists of two distinct stages: the scene geometry understanding stage, guided by semantic segmentation features, and the depth completion stage, which is primarily driven by depth information. In the backbone network, the first stage focuses on semantic information and predominantly utilizes color cues to predict relatively dense depth maps. The second stage, on the other hand, is driven by depth information, leveraging depth cues to produce even denser depth maps. The depth maps generated by these two stages are highly complementary, and we further enhance their accuracy by fusing them using confidence-based weighting. Finally, the fused depth map undergoes refinement through depth enhancement based on global consistency. The architecture of this network is designed to fully exploit and integrate the cross-modal features of RGB-D images, ensuring improved depth completion performance. The full network architecture is shown in Figure 1.

3.2.1. Semantic Information Guidance Phase Based on the Self-Attention Mechanism

Each residual block in both stages follows the classic bottleneck design, composed of three convolutional layers (1 × 1, 3 × 3, 1 × 1) with batch normalization and ReLU activations. Skip connections are employed to facilitate gradient propagation.

The confidence maps (C1 and C2) are generated by feeding the intermediate feature maps from the two stages into parallel 1 × 1 convolution layers followed by a sigmoid activation, representing the reliability of each stage’s depth prediction. These maps are used in the fusion equation as follows:

D = (C1·D1 + C2·D2)/ (C1 + C2 + ε)

where ε prevents division by zero.

The proposed cost function integrates three terms, including scale-invariant depth error (L_si), SSIM loss (L_ssim), and smoothness regularization (L_sm), as follows:

L = L_si + λ1·L_ssim + λ2·L_sm

where λ1 = 0.1 and λ2 = 0.01. This design aligns with our two-stage proposal and jointly optimizes global accuracy and local structure.

The first stage is the semantic scene branch, which highlights the transparent object regions based on the semantic segmentation results of the transparent object RGB-D image. This stage extracts boundary occlusion and surface normal information for depth prediction, ultimately generating a relatively dense depth map. To enhance effectiveness, the aligned sparse depth map is also incorporated for depth calibration, improving the overall depth estimation.

In this stage, the network follows an encoder–decoder architecture with a symmetrical structure: the encoder consists of one convolutional layer followed by ten residual blocks, while the decoder includes five deconvolutional layers and one convolutional layer. Depth completion involves filling in the missing gaps in a relatively sparse depth map, which can be framed as a regression problem. However, depth regression typically learns to simply copy or interpolate depth values as output. This tendency may cause the network to fall into a local minimum, where it merely copies or interpolates rather than predicting accurate depth values. To address this, we introduce a self-attention mechanism to each convolutional layer, allowing the network to focus on precise feature values at each convolution stage and output more relevant information.

To implement this, gated convolution is employed in our network. Specifically, we define the input of a convolution block as X, the feature extraction convolution block as Convf, and the gating convolution block as Convg. The self-attention model can then be defined as follows:

$$\begin{array}{l}Gating=sigmoid(\mathit{normalization}(Con{v}_{\mathit{g}}(X)))\\ Feature=sigmoid(\mathit{normalization}(Con{v}_{\mathit{f}}(X)))\\ \mathit{Output}=\mathit{Gating}\odot Feature\end{array}$$

The normalization function normalization (*) is used for spectral normalization, and ⊙ represents element-wise pixel multiplication. The gating operation unique to the self-attention mechanism enables the network to dynamically select the most effective features, highlighting the semantic information within the image. As a result, the model can retain useful feature regions in the output. This convolutional network, aided by self-attention, focuses on finer image details and generates more accurate depth values.

For the self-attention network, surface normals and occlusion boundaries provide essential surface properties and texture features for transparent objects. We combine these two representations with the original sparse depth map to generate the first-stage predicted depth map, which then serves as part of the input for the second-stage network.

3.2.2. Depth Guidance Phase Based on Geometric Convolution

The primary goal of the second stage is to predict a dense depth map by upsampling the sparse depth map. This branch also follows a similar encoder–decoder architecture. Additionally, we employ a decoder–encoder fusion strategy to integrate the semantic information-dominated features into this branch. Specifically, the decoder features from the semantic information-dominated stage are concatenated with the corresponding encoder features in the depth information-dominated branch. Furthermore, the depth prediction results from the first stage are also fed into this branch. This approach enables the fusion of color and depth modalities across multiple stages.

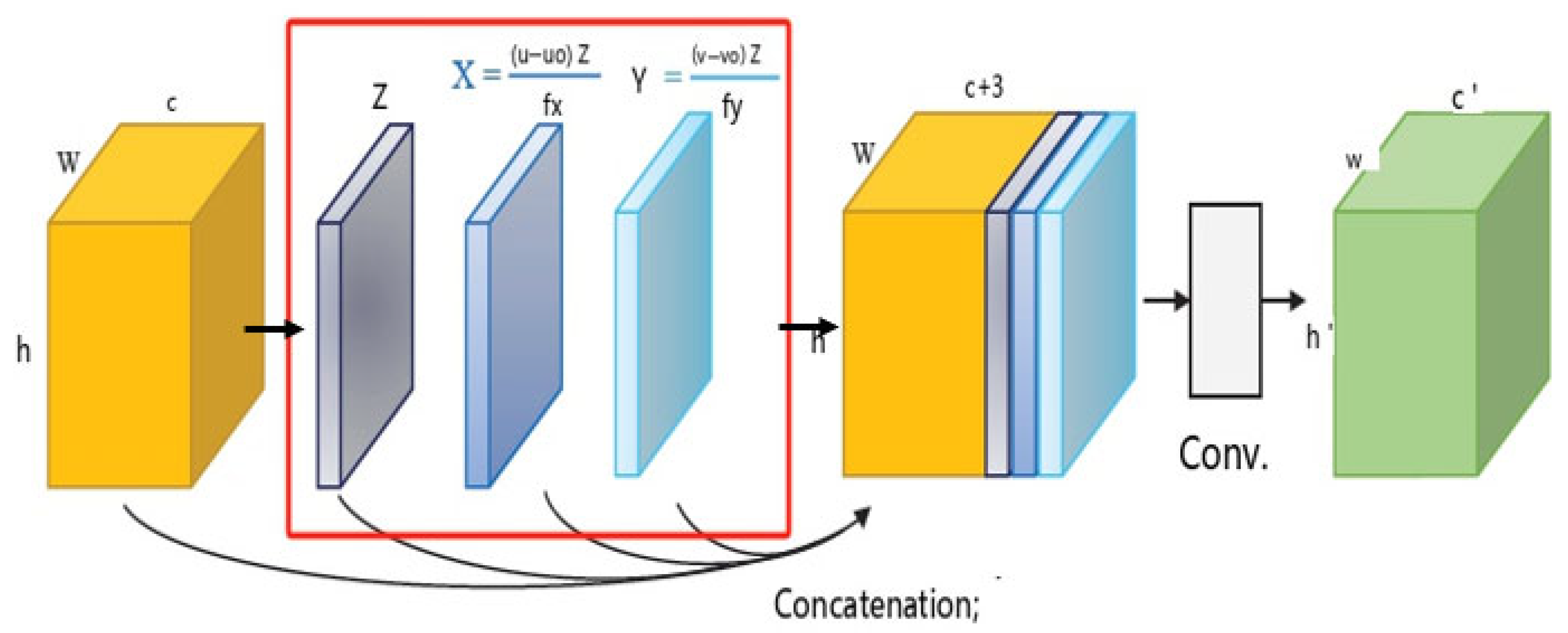
From a network implementation perspective, the second stage emphasizes 3D geometric cues. Building on the concept of Learning Joint 2D–3D Representations for Depth Completion, we introduce geometric convolutional layers into the encoder of this stage, replacing the conventional convolutional layers in each ResBlock to encode 3D geometric information. To enhance the convolutional layers, we incorporate the 3D position map (X, Y, Z) as additional input. The 3D position map is derived using the following formulas: $X=(u-u_0)Z/f_x$, $Y=(v-v_0)Z/f_y$, $Z=D$ where (u,v) are the pixel coordinates and (u0,v0,fx,fy) are the camera intrinsic parameters.

Additionally, to better encode 3D geometric information into the depth information-dominated branch, the sparse depth map undergoes a minimum pooling operation to reduce the value of Z sufficiently.

When predicting two dense depth maps, we perform depth fusion using the following strategy:

$${\widehat{Y}}_f(u,v)={\displaystyle \frac{e^{C_{RGB}(u,v)}·{\widehat{Y}}_{RGB}(u,v)+e^{C_{Depth}(u,v)}·{\widehat{Y}}_{Depth}(u,v)}{e^{C_{RGB}(u,v)}+e^{C_{Depth}(u,v)}}}$$

Here, ${\widehat{Y}}_{RGB}(u,v)$ and ${\widehat{Y}}_{Depth}(u,v)$ represent the depth completion results from the first and second stages, respectively, while $e^{C_{RGB}(u,v)}$ and $e^{C_{Depth}(u,v)}$ are the confidence maps corresponding to each stage.

3.2.3. Fine-Grained Depth Recovery Based on Global Consistency

Leveraging a multi-scale network based on a logarithmic space scale-independent loss function, initially proposed by Eigen, the network employs a coarse-to-fine approach for depth estimation. We make a simple assumption: adjacent pixels with similar intensities in the semantic scene segmentation image should also exhibit similar depths. This process is achieved by optimizing a weighted quadratic cost function, as described in Section 3.2.1:

$$Cost(U)={\displaystyle \sum _r(U(r)-{\displaystyle \sum _{s\in N(r)}{w}_{rs}U(s){)}^2}}$$

Here, U represents the sparse depth to be completed, r and s refer to spatially adjacent pixels, wrs is the weight, and N(r) is defined as follows:

$$w_{rs}\propto 1+{\displaystyle \frac{1}{{\sigma }_r^2}}({\mathit{X}}_{\mathit{RGB}}(r)-{\mu }_r)({\mathit{X}}_{\mathit{RGB}}(s)-{\mu }_r)$$

where ${\sigma }_r$ and ${\mu }_r$ are the mean and variance of the depth values within the r-domain window. The algorithm in this paper uses a 3 × 3 domain window. Additionally, the corresponding RGB image is denoted as ${\mathit{X}}_{\mathit{RGB}}$.

To enhance structural information for the depth completion task, we introduce a structure-related loss term Ls, which is based on the Structural Similarity Index (SSIM). SSIM evaluates the degradation of structural information, and in our task, a higher SSIM index indicates a stronger structural consistency in the completed depth map. By incorporating SSIM, we aim to guide the network to generate depth maps with better structural integrity, resulting in more refined depth completion across different scales while preserving the underlying spatial geometric structure.

3.2.4. Encoder–Decoder Architecture Details

The encoder consists of one convolutional layer followed by ten residual blocks. Each residual block follows the bottleneck design with three convolutional layers (1 × 1, 3 × 3, 1 × 1), batch normalization, and ReLU activations. The decoder consists of five deconvolutional layers and one convolutional layer. Skip connections are used to facilitate gradient propagation. The self-attention mechanism is integrated into each convolutional layer in the first stage, as detailed in Section 3.2.1 and Figure 2. The geometric convolution layer, used in the second stage, is illustrated in Figure 3.

3.3. Loss Function

The previous discussion demonstrated that effective depth cues can be inferred from a single transparent object image. Now, we will focus on two key aspects: the global scale of the unknown scene and the multi-scale challenges between different pixels.

To address these issues, this paper proposes an error function based on scale invariance to evaluate the accuracy of predicted depth:

$$E(Y,\widehat{Y})={\displaystyle \frac{1}{\mathit{n}}}{{\displaystyle \sum _{\mathit{i}=1}^{\mathit{n}}\left(\frac{{\displaystyle \sum _{\mathit{i}}{Y}_{\mathit{i}}{\widehat{Y}}_i}}{{\displaystyle \sum _{\mathit{i}}{Y}_{\mathit{i}}^2}}·Y_{\mathit{i}}-\widehat{Y}\right)}}^2$$

where n denotes the total number of valid pixels in the depth map, and all operations (multiplication, division, and summation) are performed element-wise over the depth map pixels. Y is the predicted depth, and $\widehat{Y}$ is the true depth. Based on this formulation, we observe that multiplying Y by any non-zero scalar α results in the same error:

$$E(\alpha ·Y,\widehat{Y})={\displaystyle \frac{1}{\mathit{n}}}{{\displaystyle \sum _{\mathit{i}=1}^{\mathit{n}}\left(\frac{{\displaystyle \sum _{\mathit{i}}(\alpha ·Y_{\mathit{i}}){\widehat{Y}}_{\mathit{i}}}}{{\displaystyle \sum _{\mathit{i}}{(\alpha ·Y_{\mathit{i}})}^2}}·(\alpha ·Y_{\mathit{i}})-\widehat{Y}\right)}}^2=E(Y,\widehat{Y})$$

Thus, the error function proposed in this paper is inherently based on global scale invariance.

To simplify the calculation, we discard the terms that are independent of the predicted depth Y from the above formula ${\displaystyle \frac{1}{\mathit{n}}}{{\displaystyle \sum _{\mathit{i}=1}^{\mathit{n}}\left(\widehat{Y}\right)}}^2$. The loss function can therefore be optimized as follows:

$$\mathit{L}=1-{\displaystyle \frac{{\left({\displaystyle \sum _{\mathit{i}=1}^{\mathit{n}}{Y}_{\mathit{i}}{\widehat{Y}}_{\mathit{i}}}\right)}^2}{\left({\displaystyle \sum _{\mathit{i}=1}^{\mathit{n}}{Y}_{\mathit{i}}^2}\right)\left({\displaystyle \sum _{\mathit{i}=1}^{\mathit{n}}{\widehat{Y}}_{\mathit{i}}^2}\right)}}$$

4. Experiment

4.1. Dataset

The TransCG dataset [24] consists of 57,715 RGB images and their corresponding depth maps. It includes 51 transparent objects and approximately 200 opaque objects. All images in the dataset are captured from various real-world scenes, encompassing a total of 130 unique scenes. The objects in the dataset are randomly placed in both simple and cluttered environments, simulating real-world robot grasping scenarios. To maintain consistency with the original dataset’s division, we use the same data split, which includes 34,191 images.

4.2. Evaluation Metrics

In this paper, we continue to utilize the evaluation metrics from previous works [25,26], employing them to compare the performance of the networks.

(1) Root Mean Squared Error (RMSE): We calculate RMSE to evaluate the error between the predicted depth and the ground truth. It can be calculated as follows:

$$\mathit{RMSE}=\sqrt{{\displaystyle \frac{1}{\mathit{N}}}{\displaystyle \sum _{i=1}^N{‖{\mathit{y}}_{\mathit{i}}-{\hat{\mathit{y}}}_{\mathit{i}}‖}^2}}$$

where N is the total number of pixels in the depth map, y represents a pixel in the predicted depth map Y, and $\hat{\mathit{y}}$ represents the corresponding pixel in the ground truth depth map $\hat{\mathit{Y}}$.

(2) Absolute Relative Difference (REL): We calculate REL to indicate the mean absolute relative difference, which can be calculated as follows:

$$\mathit{REL}={\displaystyle \frac{1}{\mathit{N}}}{\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}\frac{\left|{\mathit{y}}_{\mathit{i}}-{\hat{\mathit{y}}}_{\mathit{i}}\right|}{{\hat{\mathit{y}}}_{\mathit{i}}}}$$

where N is the total number of pixels in the depth map, y is a pixel in the predicted depth map, and $\hat{\mathit{y}}$ is the corresponding pixel in the ground truth depth map.

(3) Mean Absolute Error (MAE): We use MAE to calculate the mean absolute error between estimated depth and ground truth, which can be calculated as follows:

$$\mathit{MAE}={\displaystyle \frac{1}{\mathit{N}}}{\displaystyle \sum _{\mathit{i}=1}^N\left|\mathit{y}-\hat{\mathit{y}}\right|}$$

where N is the total number of pixels in the depth map, y is a pixel in the predicted depth map, and $\hat{\mathit{y}}$ is the corresponding pixel in the ground truth depth map.

(4) Threshold: We use the threshold to calculate the percentage of pixels with predicted depths, which can be calculated as follows:

$$threshold={\displaystyle \frac{1}{\mathit{N}}}{\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}{\displaystyle \prod (\frac{{\widehat{y}}_i}{y_i}\prec threshold)}}$$

In this paper, we set the threshold with 1.05, 1.10, and 1.25.

In the above formulas, N is the total number of pixels in the depth map, y represents a pixel in the predicted depth map Y, and $\hat{\mathit{y}}$ represents the corresponding pixel in the ground truth depth map $\hat{\mathit{Y}}$.

4.3. Ablation Experiment

We first conducted a series of experiments to validate the effectiveness of the specialized design components proposed in this paper, including the two-stage backbone architecture, the incorporation of a self-attention mechanism, and deep refinement based on scale factors.

Effectiveness of the Two-Stage Backbone Structure: We propose four variants of the backbone, differentiated by whether the sparse depth map is input into the semantic guidance stage and whether the first-stage depth prediction is used as input for the depth-dominant branch. The performance of these variants, labeled M1 to M4, is shown in

Table 1. Ablation test results of the effectiveness of the two-stage backbone structure.

Models	Configuration	Sg-Input Sparse Depth	DD-Input Relative Depth	Guidance Map	Self-Attention	Refined	RMSE ↓	MAE ↓	REL ↓
M1	RGB only						0.0302	0.0176	0.0731
M2	RGB + self-attention	√					0.0299	0.0172	0.0532
M3	Sparse depth only		√				0.0295	0.0157	0.0517
M4	RGB + sparse depth + self-attention	√	√				0.0291	0.0153	0.0515
M5	M4 + extra guidance map	√	√	√			0.0291	0.0155	0.0619
M4 + SA	M4 with self-attention	√	√		√		0.0190	0.0113	0.0254
M4 + SA + C1	M4 + SA with confidence fusion	√	√		√	√	0.0138	0.0107	0.0155

. The results indicate a significant performance improvement when the relative depth input (SG-Input relative depth) benefits from semantic guidance assistance and depth-dominant support. Additionally, we explore another backbone variant (M5), inspired by FusionNet and DeepLiDAR, which generates an additional guidance map from the first stage to assist the second stage. The results suggest that this extra guidance map is unnecessary and even slightly detrimental to performance. Figure 4 illustrates some typical examples.

Effectiveness of the Self-Attention Mechanism: As shown in Table 1, the inclusion of the self-attention convolutional layer significantly improves the performance of the backbone network, particularly in terms of RMSE. When the deep refinement module (Re) is added, the final model (M4 + SA + Re) achieves superior detection accuracy, as indicated in the last row of the table.

Figure 5 presents a typical example to illustrate the differences between the models. The model with the self-attention convolutional layer demonstrates superior depth inference, particularly when the color features of foreground transparent objects are obscured by the background color. The first two rows of

Table 2. SSIM loss function effectiveness ablation experiment results.

Model	RMSE ↓	Mean ↓	SSIM ↑	1.05 ↑	1.10 ↑	1.25 ↑
SA	0.1095	0.400	0.673	79.13	93.60	98.57
SA + SSIM	0.1096	0.407	0.776	88.47	92.45	95.49
SA + SSIM + GC	0.0138	0.392	0.799	90.41	97.11	99.72

examine the impact of the self-attention mechanism on full-depth results. Indeed, the self-attention mechanism provides a significant performance boost over the FCN model. For comparison, we use ResNet18, which has similar parameters to the classic FCN. The results indicate that this improvement stems from the network’s ability to attend to convolutional features, allowing the model to focus on critical areas and key features. In this context, the self-attention mechanism enhances the model’s ability to learn and retain geometric information.

SSIM Loss Function Based on Global Consistency: By introducing a smaller weight for the SSIM loss during optimization, the self-attention network learns to balance structural information without significantly affecting RMSE and delta percentage. After incorporating the SSIM loss, the SSIM score increased by 15.3%, demonstrating that the network successfully generates more accurate depth map values.

4.4. Comparison with SOTA

Table 3. Experimental results compared with SOTA.

Model	RMSE ↓	MAE ↓	REL ↓	1.05 ↑	1.10 ↑	1.25 ↑	Params (M)	FPS
ClearGrasp [27]	0.0540	0.0370	0.0831	50.48	68.68	95.28	42.5	21.6
LIDF-Refine [28]	0.0393	0.0150	0.0340	78.22	94.26	99.80	28.7	31.2
TranspareNet [29]	0.0361	0.0134	0.0231	88.45	96.28	99.42	30.3	27.4
TransCG [24]	0.0182	0.0123	0.0270	83.76	95.67	99.71	26.1	33.0
TODE-Trans [30]	0.0271	0.0216	0.0487	64.24	86.98	99.51	29.1	29.4
TCRNet [17]	0.0170	0.0109	0.0200	88.96	96.94	99.87	34.5	22.8
Ours	0.0138	0.0107	0.0155	90.41	97.11	99.72	23.8	28.3

presents the full quantitative performance of our model, along with comparisons to the top five published or archived papers. The experiments were conducted using Python 3.8, PyTorch 2.1.2, Ubuntu 20.04, and a single 4090 GPU. The results reveal significant improvements in RMSE, which is the primary evaluation metric.

4.5. Generalization Experiment

To further assess the generalizability of the proposed method beyond the TransCG dataset, we conducted additional evaluations on the TOD-10K dataset, a large-scale synthetic dataset for transparent object depth estimation. As shown in

Table 4. Experimental results on the TOD-10K dataset.

Model	RMSE ↓	MAE ↓	REL ↓	1.05 ↑	1.10 ↑	1.25 ↑
ClearGrasp [17]	0.0615	0.0421	0.0952	45.31	63.87	92.15
LIDF-Refine [18]	0.0442	0.0173	0.0395	73.58	91.44	96.25
TranspareNet [19]	0.0418	0.0159	0.0283	84.71	93.89	94.84
TransCG [14]	0.0210	0.0142	0.0321	80.15	93.24	96.75
TODE-Trans [20]	0.0317	0.0251	0.0561	60.47	83.12	98.09
TCRNet [11]	0.0205	0.0125	0.0283	85.34	94.82	97.81
Ours	0.0162	0.0121	0.0189	88.05	94.33	98.78

, our method consistently outperforms other state-of-the-art approaches across most metrics, demonstrating its robustness and strong generalization capability. The results indicate that the design of our two-stage network and the incorporation of the self-attention mechanism are effective not only on real-world data but also in synthetic environments.

4.6. Implementation Details

Our model was implemented using PyTorch 2.1.2 and trained on an NVIDIA GeForce RTX 4090 GPU. We used the Adam optimizer with a learning rate of 1 × 10⁻⁴ and a batch size of 8. The input RGB and depth images were resized to 320 × 240 pixels. The model was trained for 50 epochs.

5. Discussion

The quantitative results presented in Table 3 demonstrate that our method achieves state-of-the-art performance on the TransCG dataset. Specifically, SRNet-Trans attains the lowest RMSE (0.0138), MAE (0.0107), and REL (0.0155), outperforming existing approaches such as TCRNet and TransCG. The significant improvement in these metrics indicates that our model produces more accurate and reliable depth estimates, which is critical for enhancing the performance of downstream robotic tasks such as transparent object grasping and navigation in cluttered environments.

The superior performance can be attributed to the novel two-stage architecture that effectively combines semantic guidance and geometric depth refinement. The first stage, enhanced with the self-attention mechanism, successfully captures fine-grained surface normal and boundary information of transparent objects, which is often challenging due to their lack of texture and high reflectivity. The second stage, equipped with geometric convolutional layers, further improves the spatial accuracy of depth values by explicitly incorporating 3D geometric cues. The complementary nature of the two stages allows for effective fusion, resulting in a dense and consistent depth map.

When compared to existing methods, our approach shows particular strength in recovering detailed edges and thin structures, as visually supported in Figure 6. For instance, methods like ClearGrasp and TranspareNet often fail to accurately reconstruct highly reflective or curved regions, whereas our model maintains structural integrity owing to the global consistency loss and multi-scale refinement.

Despite these advancements, the computational cost of SRNet-Trans remains non-negligible. The two-stage design and self-attention modules increase inference time, which may hinder deployment in real-time robotic systems. Future work may explore model distillation or lightweight attention variants to improve efficiency.

In summary, while SRNet-Trans sets a new benchmark in transparent object depth completion, achieving real-time performance and broader generalization under challenging physical conditions will be essential for real-world deployment.

6. Conclusions

This paper introduces a novel approach to depth completion for transparent object RGB-D images. We designed a two-stage depth completion network: the semantic information-guided stage and the depth information-dominant stage, which effectively realizes the cross-modal fusion of RGB-D images for accurate depth completion. Additionally, we are the first to apply the self-attention mechanism to depth completion of transparent objects, further enhancing the network’s performance. Finally, we implemented refined depth completion processing, leading to substantial improvements in the predicted depth map. The effectiveness and superiority of our approach were validated through extensive comparison with state-of-the-art (SOTA) methods.

7. Future Work

Moreover, our method exhibits certain limitations. The two-stage architecture and self-attention modules lead to increased computational costs, which could impede deployment on resource-constrained robotic systems. The network also encounters challenges when processing transparent objects with highly curved or complex non-planar geometries, where strong refraction effects occur, as well as highly reflective surfaces and very thin structures (e.g., glass edges), due to severe light distortion and insufficient depth cues. Future work will prioritize developing lightweight attention mechanisms to reduce model complexity, investigating geometry-aware data augmentation to improve generalization across varied transparent shapes and materials, and validating the approach on additional datasets and real robotic platforms to enhance practical applicability.