Analysis of the Influence of RTK Observations on the Accuracy of UAV Images
Abstract
1. Introduction
1.1. Direct Georeferencing of UAV Images
1.2. Influence of GCP Distribution and Flight Geometry
1.3. Aim of the Article
2. Materials and Methods
2.1. Test Area and UAVs
2.2. GCP Location and Flight Mission Planning
2.3. Data Processing
3. Results
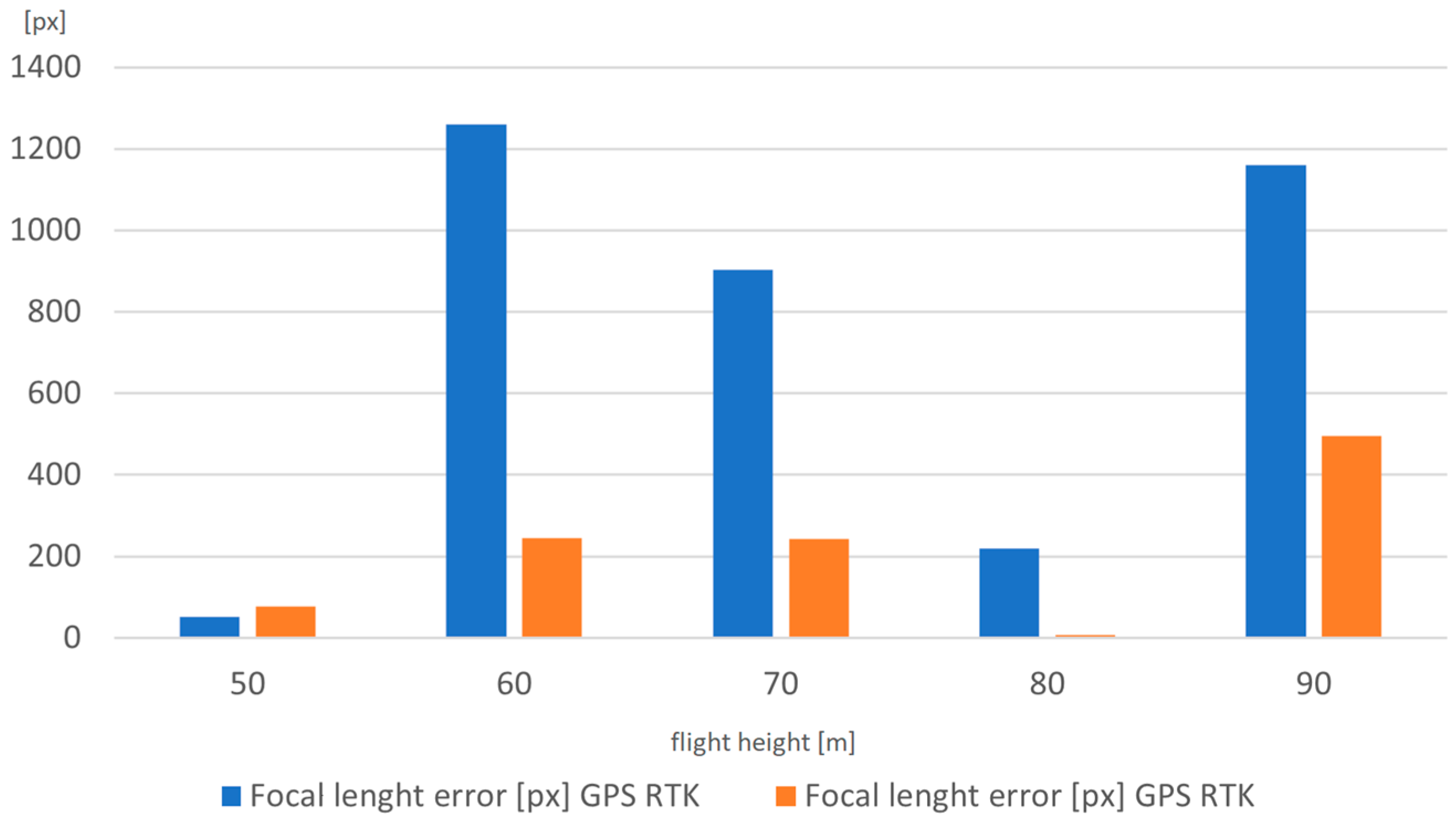
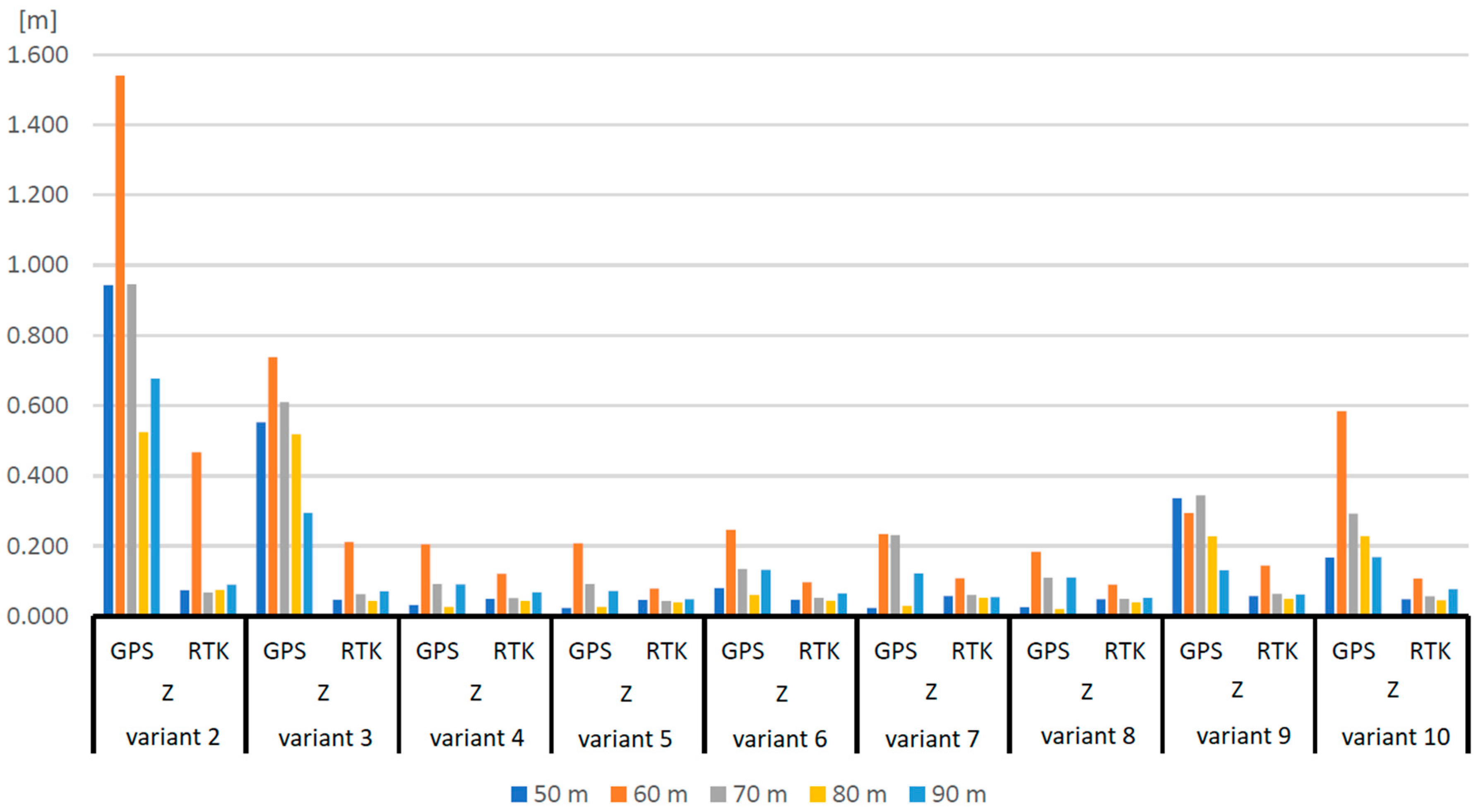
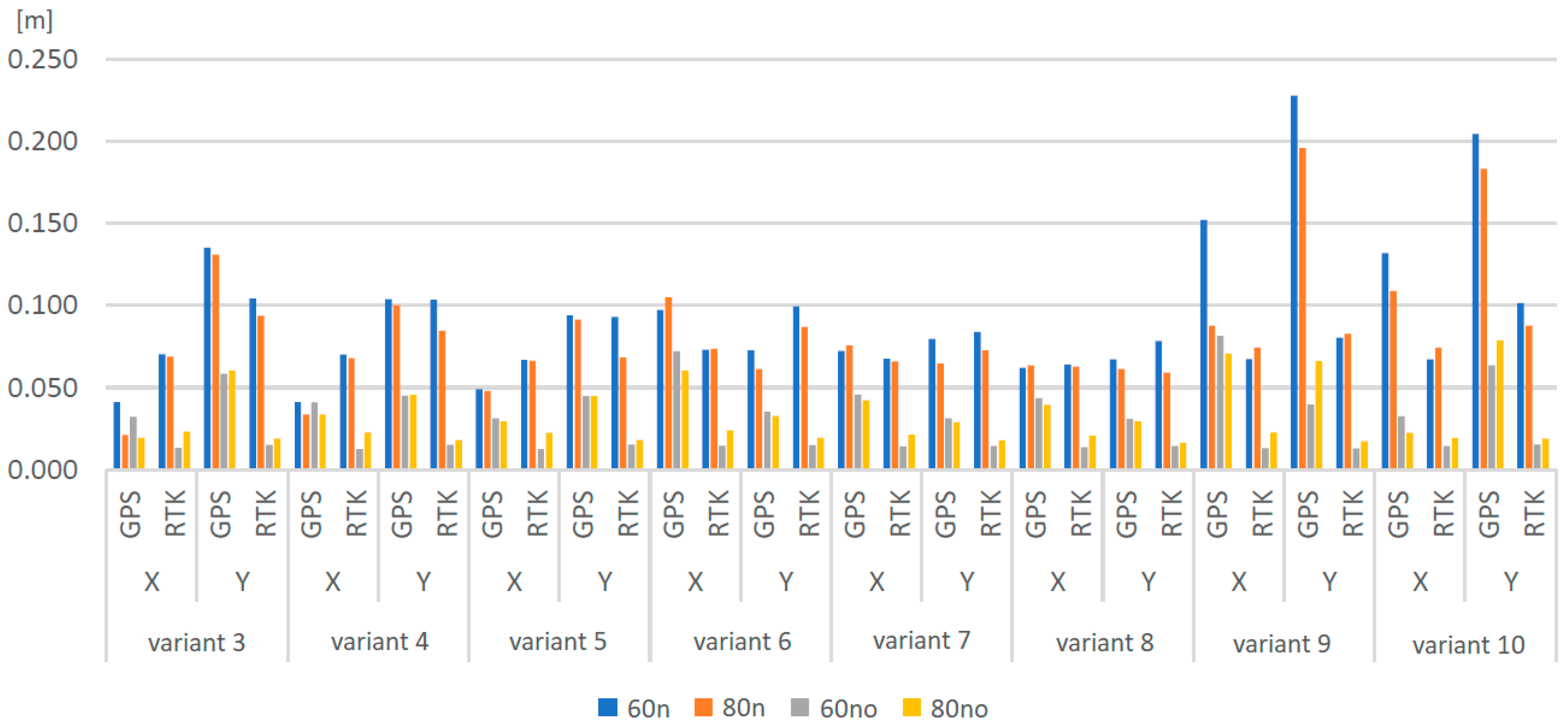
3.1. Nadir Images and Influence of RTK Observations on Aerial Triangulation Results
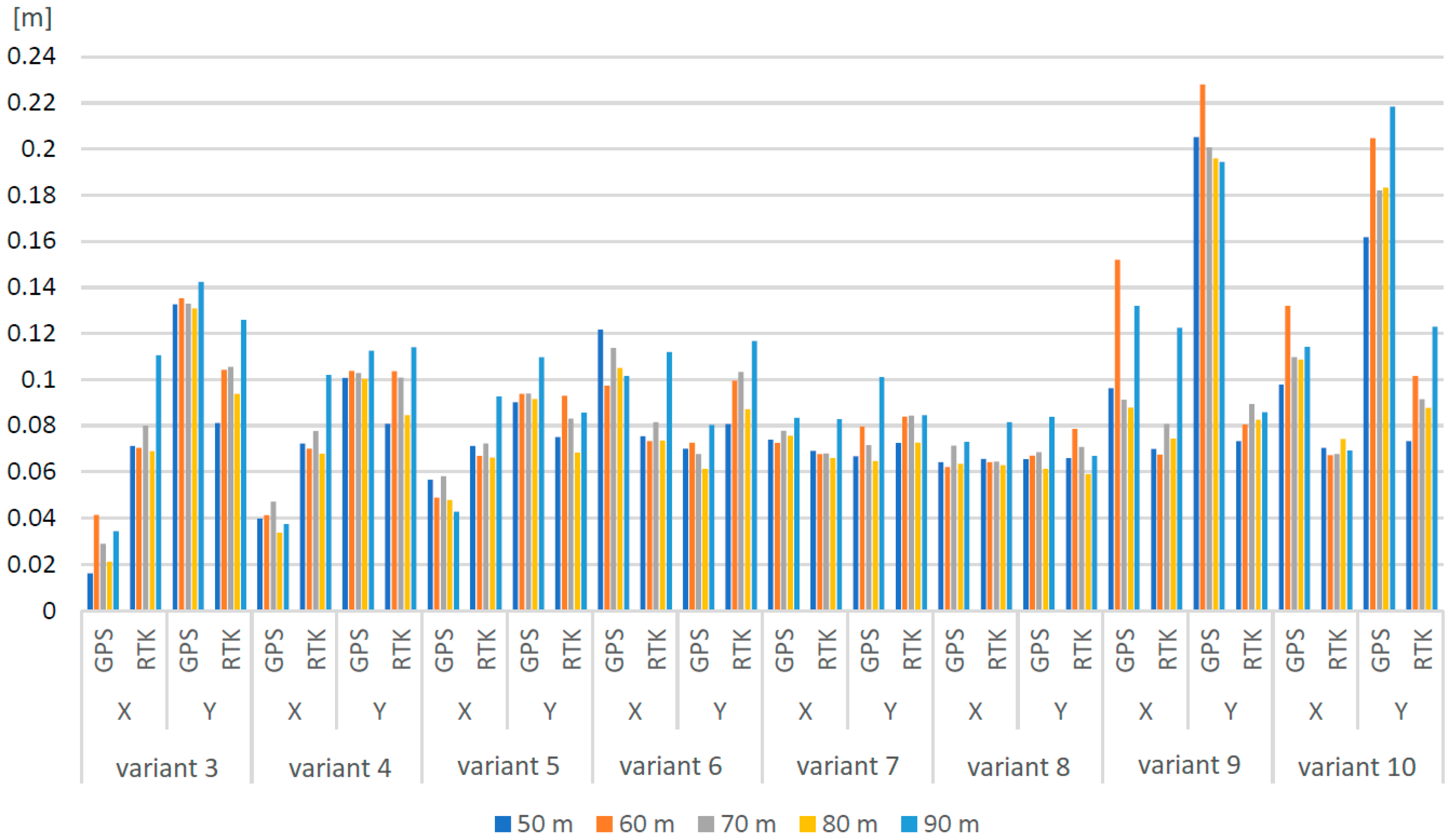
3.2. Role of Oblique Images in Aerial Triangulation Results
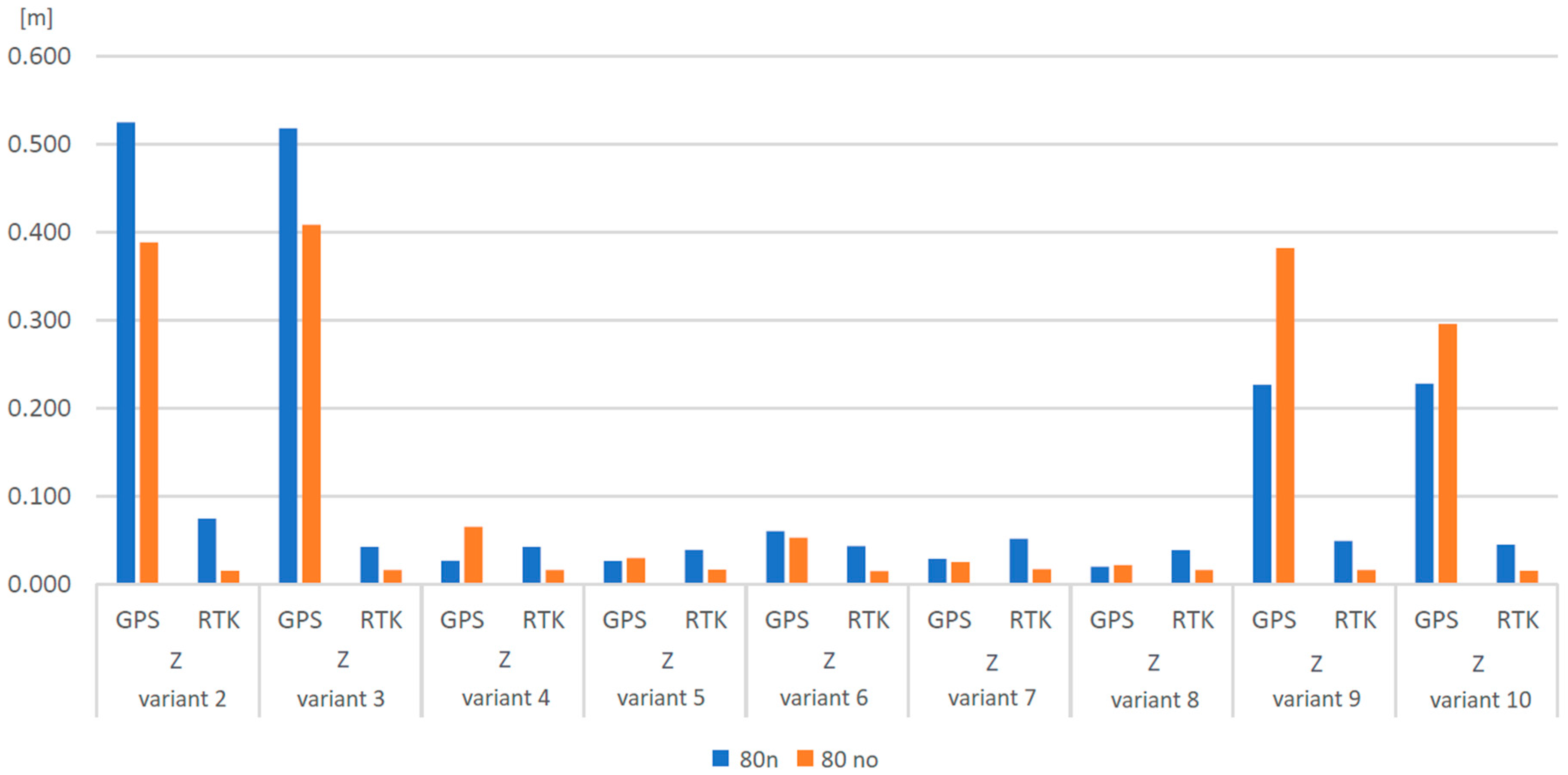
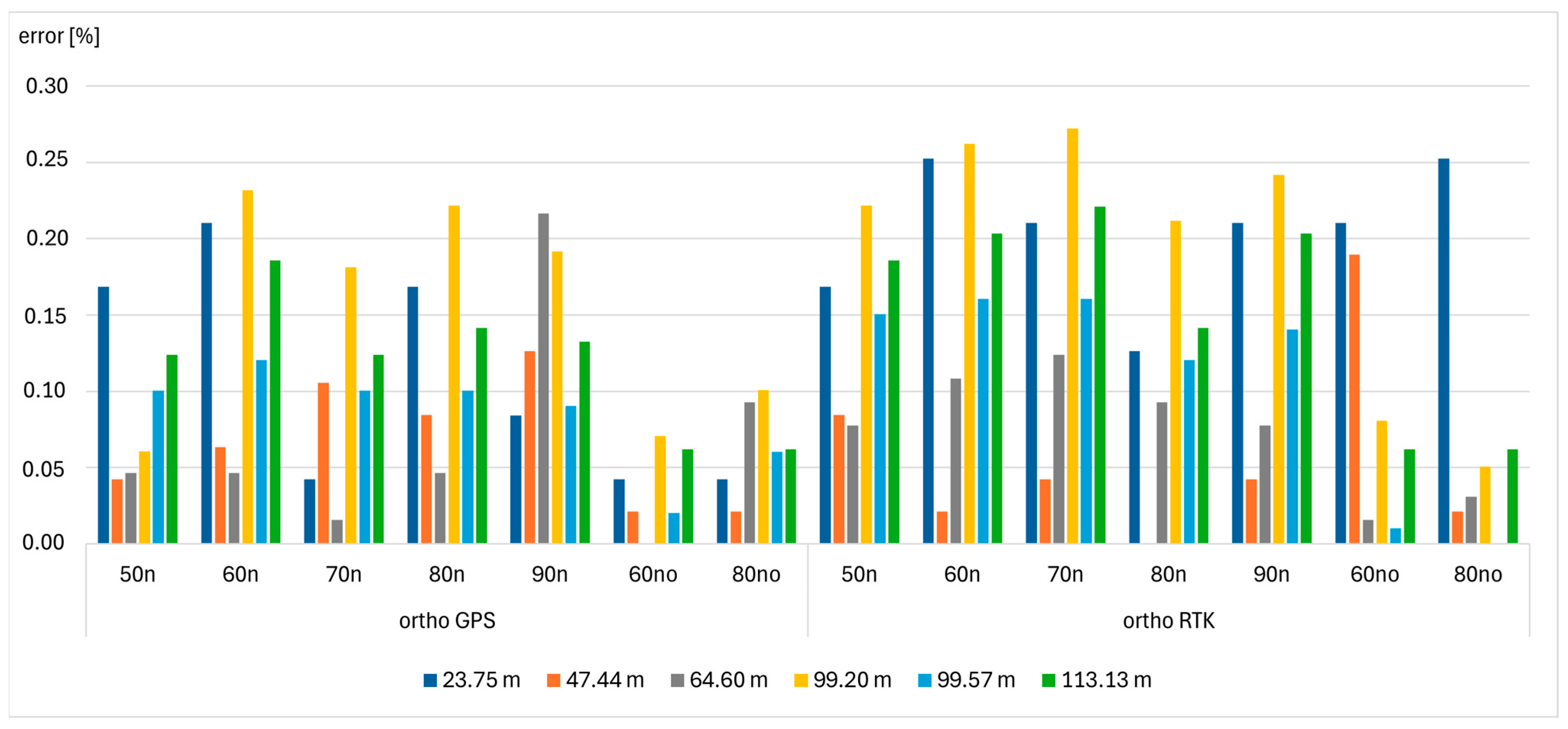
3.3. Orthomosaic Quality Check Based on the Check Distances
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| 50 GPS | 50 RTK | 60 GPS | 60 RTK | 70 GPS | 70 RTK | 80 GPS | 80 RTK | 90 GPS | 90 RTK | 60 GPS no | 60 RTK no | 80 GPS no | 80 RTK no | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z | Z | Z | Z | Z | Z | Z | Z | Z | Z | Z | Z | Z | Z | ||
| variant 1 | Mean | 1.16 | −0.23 | −19.82 | 4.92 | 17.06 | 5.73 | −3.55 | 1.19 | −24.21 | 13.26 | 1.50 | 0.02 | 0.51 | 0.01 |
| STD | 0.21 | 0.05 | 0.29 | 0.07 | 0.33 | 0.07 | 1.05 | 0.05 | 0.39 | 0.13 | 0.26 | 0.02 | 0.15 | 0.01 | |
| RMS | 1.18 | 0.24 | 19.82 | 4.92 | 17.06 | 5.73 | 3.70 | 1.19 | 24.21 | 13.26 | 1.53 | 0.02 | 0.53 | 0.02 | |
| Moran | 0.46 | 0.24 | 0.20 | 0.17 | 0.26 | 0.34 | 0.64 | 0.32 | 0.37 | 0.31 | 0.72 | 0.16 | 0.56 | 0.06 | |
| variant 2 | Mean | 0.26 | −0.06 | −1.24 | 0.46 | −0.20 | −0.03 | −0.01 | −0.06 | 0.68 | −0.03 | 0.13 | 0.02 | 0.05 | 0.01 |
| STD | 0.92 | 0.05 | 0.93 | 0.06 | 0.94 | 0.06 | 0.53 | 0.05 | −0.49 | 0.09 | 0.27 | 0.02 | 0.39 | 0.01 | |
| RMS | 0.94 | 0.07 | 1.54 | 0.47 | 0.95 | 0.07 | 0.52 | 0.07 | 0.47 | 0.09 | 0.30 | 0.02 | 0.39 | 0.02 | |
| Moran | 0.65 | 0.24 | 0.45 | 0.35 | 0.62 | 0.52 | 0.55 | 0.28 | 0.50 | 0.59 | 0.56 | 0.24 | 0.53 | 0.08 | |
| variant 3 | Mean | 0.02 | 0.00 | −0.02 | 0.20 | 0.05 | 0.04 | 0.02 | 0.00 | 0.00 | 0.03 | 0.05 | 0.02 | 0.02 | 0.01 |
| STD | 0.56 | 0.05 | 0.75 | 0.06 | 0.62 | 0.05 | 0.53 | 0.04 | 0.30 | 0.07 | 0.28 | 0.02 | 0.02 | 0.01 | |
| RMS | 0.55 | 0.05 | 0.74 | 0.21 | 0.61 | 0.06 | 0.52 | 0.04 | 0.29 | 0.07 | 0.29 | 0.02 | 0.02 | 0.02 | |
| Moran | 0.56 | 0.24 | 0.54 | 0.29 | 0.54 | 0.46 | 0.55 | 0.24 | 0.52 | 0.51 | 0.56 | 0.10 | 0.10 | 0.00 | |
| variant 4 | Mean | 0.00 | −0.01 | 0.01 | 0.11 | 0.00 | 0.02 | 0.00 | −0.01 | 0.01 | 0.03 | 0.01 | 0.02 | 0.00 | 0.01 |
| STD | 0.03 | 0.05 | 0.21 | 0.05 | 0.09 | 0.05 | 0.03 | 0.04 | 0.09 | 0.06 | 0.05 | 0.02 | 0.07 | 0.01 | |
| RMS | 0.03 | 0.05 | 0.20 | 0.12 | 0.09 | 0.05 | 0.03 | 0.04 | 0.09 | 0.07 | 0.05 | 0.02 | 0.07 | 0.02 | |
| Moran | 0.44 | 0.23 | 0.19 | 0.30 | 0.22 | 0.45 | 0.15 | 0.23 | 0.01 | 0.55 | 0.52 | 0.08 | 0.52 | −0.01 | |
| variant 5 | Mean | 0.00 | 0.00 | 0.08 | 0.06 | −0.03 | 0.01 | 0.01 | 0.00 | −0.01 | 0.02 | 0.01 | 0.02 | 0.01 | 0.01 |
| STD | 0.02 | 0.05 | 0.20 | 0.05 | 0.09 | 0.04 | 0.02 | 0.04 | 0.07 | 0.04 | 0.03 | 0.02 | 0.03 | 0.01 | |
| RMS | 0.02 | 0.05 | 0.21 | 0.08 | 0.09 | 0.04 | 0.03 | 0.04 | 0.07 | 0.05 | 0.03 | 0.02 | 0.03 | 0.02 | |
| Moran | 0.19 | 0.03 | 0.16 | 0.06 | 0.18 | 0.26 | 0.19 | −0.02 | −0.25 | 0.30 | 0.32 | 0.04 | 0.27 | −0.07 | |
| variant 6 | Mean | 0.05 | −0.01 | 0.12 | 0.08 | −0.07 | −0.01 | 0.04 | −0.01 | 0.07 | 0.02 | 0.03 | 0.01 | 0.02 | 0.01 |
| STD | 0.06 | 0.05 | 0.22 | 0.06 | 0.12 | 0.05 | 0.05 | 0.04 | 0.11 | 0.06 | 0.04 | 0.02 | 0.05 | 0.01 | |
| RMS | 0.09 | 0.05 | 0.27 | 0.11 | 0.15 | 0.06 | 0.07 | 0.05 | 0.15 | 0.07 | 0.06 | 0.02 | 0.06 | 0.02 | |
| Moran | 0.33 | 0.20 | 0.09 | 0.25 | 0.20 | 0.49 | 0.19 | 0.22 | 0.07 | 0.61 | 0.49 | 0.08 | 0.48 | 0.00 | |
| variant 7 | Mean | 0.01 | 0.04 | −0.09 | 0.09 | 0.18 | 0.04 | 0.02 | 0.04 | −0.01 | −0.01 | 0.03 | 0.02 | 0.01 | 0.01 |
| STD | 0.02 | 0.04 | 0.22 | 0.06 | 0.14 | 0.04 | 0.02 | 0.03 | 0.12 | 0.06 | 0.02 | 0.01 | 0.02 | 0.01 | |
| RMS | 0.02 | 0.06 | 0.23 | 0.11 | 0.23 | 0.06 | 0.03 | 0.05 | 0.12 | 0.05 | 0.03 | 0.02 | 0.03 | 0.02 | |
| Moran | 0.26 | 0.27 | 0.10 | 0.47 | 0.19 | 0.48 | −0.13 | 0.20 | 0.29 | 0.40 | 0.19 | 0.08 | 0.30 | −0.03 | |
| variant 8 | Mean | −0.01 | 0.03 | −0.02 | 0.07 | 0.06 | 0.03 | 0.01 | 0.02 | 0.00 | 0.00 | 0.02 | 0.02 | 0.01 | 0.01 |
| STD | 0.02 | 0.04 | 0.19 | 0.05 | 0.09 | 0.04 | 0.02 | 0.03 | 0.11 | 0.05 | 0.02 | 0.01 | 0.02 | 0.01 | |
| RMS | 0.02 | 0.05 | 0.18 | 0.09 | 0.11 | 0.05 | 0.02 | 0.04 | 0.11 | 0.05 | 0.03 | 0.02 | 0.02 | 0.02 | |
| Moran | 0.38 | 0.18 | −0.11 | 0.52 | 0.14 | 0.48 | −0.19 | 0.07 | 0.22 | 0.30 | 0.26 | 0.12 | 0.17 | 0.02 | |
| variant 9 | Mean | 0.27 | 0.04 | −0.16 | 0.14 | 0.28 | 0.05 | 0.19 | 0.02 | −0.01 | 0.03 | 0.40 | 0.02 | 0.33 | 0.01 |
| STD | 0.21 | 0.05 | 0.25 | 0.05 | 0.20 | 0.04 | 0.12 | 0.05 | 0.13 | 0.06 | 0.23 | 0.01 | 0.20 | 0.01 | |
| RMS | 0.34 | 0.06 | 0.29 | 0.14 | 0.34 | 0.06 | 0.23 | 0.05 | 0.13 | 0.06 | 0.46 | 0.02 | 0.38 | 0.02 | |
| Moran | 0.63 | 0.25 | 0.36 | 0.45 | 0.55 | 0.41 | 0.60 | 0.30 | 0.26 | 0.35 | 0.60 | 0.18 | 0.59 | 0.04 | |
| variant 10 | Mean | −0.15 | 0.02 | −0.48 | 0.09 | −0.25 | −0.02 | −0.19 | 0.01 | −0.13 | −0.03 | −0.05 | 0.01 | −0.26 | 0.01 |
| STD | 0.08 | 0.04 | 0.33 | 0.06 | 0.16 | 0.05 | 0.12 | 0.05 | 0.11 | 0.07 | 0.04 | 0.02 | 0.15 | 0.01 | |
| RMS | 0.17 | 0.05 | 0.58 | 0.11 | 0.29 | 0.06 | 0.23 | 0.05 | 0.17 | 0.08 | 0.06 | 0.02 | 0.30 | 0.02 | |
| Moran | 0.44 | 0.26 | 0.35 | 0.34 | 0.40 | 0.55 | 0.47 | 0.41 | 0.12 | 0.67 | 0.50 | 0.21 | 0.49 | 0.04 |
| 50 GPS | 50 RTK | 60 GPS | 60 RTK | 70 GPS | 70 RTK | 80 GPS | |||||||||
| X | Y | X | Y | X | Y | X | Y | X | Y | X | Y | X | Y | ||
| variant 1 | Mean | 0.86 | 0.81 | 0.00 | −0.01 | 0.80 | 0.63 | −0.01 | −0.02 | 0.96 | 0.80 | 0.01 | −0.01 | −0.09 | −0.89 |
| STD | 0.19 | 0.16 | 0.07 | 0.08 | 0.31 | 0.49 | 0.07 | 0.09 | 0.25 | 0.42 | 0.07 | 0.10 | 0.02 | 0.14 | |
| RMS | 0.88 | 0.83 | 0.07 | 0.08 | 0.86 | 0.79 | 0.07 | 0.09 | 0.99 | 0.90 | 0.06 | 0.10 | 0.09 | 0.90 | |
| Moran | 0.67 | 0.72 | 0.67 | 0.63 | 0.55 | 0.69 | 0.67 | 0.60 | 0.52 | 0.70 | 0.61 | 0.61 | 0.42 | 0.52 | |
| variant 2 | Mean | 0.02 | 0.01 | 0.00 | 0.00 | 0.20 | 0.28 | 0.00 | −0.03 | 0.01 | 0.01 | 0.02 | −0.01 | 0.02 | 0.03 |
| STD | 0.22 | 0.15 | 0.08 | 0.08 | 2.23 | 3.26 | 0.07 | 0.10 | 0.10 | 0.13 | 0.09 | 0.12 | 0.12 | 0.22 | |
| RMS | 0.21 | 0.15 | 0.07 | 0.08 | 2.21 | 3.22 | 0.07 | 0.10 | 0.10 | 0.13 | 0.09 | 0.12 | 0.12 | 0.22 | |
| Moran | 0.71 | 0.73 | 0.68 | 0.63 | 0.57 | 0.73 | 0.65 | 0.62 | 0.63 | 0.65 | 0.59 | 0.67 | 0.57 | 0.62 | |
| variant 3 | Mean | 0.01 | 0.03 | 0.00 | 0.00 | 0.01 | 0.02 | 0.00 | −0.03 | 0.01 | 0.02 | 0.02 | −0.01 | 0.01 | 0.01 |
| STD | 0.01 | 0.13 | 0.07 | 0.08 | 0.04 | 0.14 | 0.07 | 0.10 | 0.03 | 0.13 | 0.08 | 0.11 | 0.02 | 0.13 | |
| RMS | 0.02 | 0.13 | 0.07 | 0.08 | 0.04 | 0.14 | 0.07 | 0.10 | 0.03 | 0.13 | 0.08 | 0.10 | 0.02 | 0.13 | |
| Moran | 0.18 | 0.56 | 0.68 | 0.64 | 0.49 | 0.56 | 0.65 | 0.62 | −0.14 | 0.55 | 0.59 | 0.65 | 0.44 | 0.55 | |
| variant 4 | Mean | 0.01 | 0.01 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | −0.03 | 0.01 | 0.00 | 0.02 | −0.01 | 0.01 | 0.00 |
| STD | 0.04 | 0.10 | 0.07 | 0.08 | 0.04 | 0.10 | 0.07 | 0.10 | 0.05 | 0.10 | 0.08 | 0.10 | 0.03 | 0.10 | |
| RMS | 0.04 | 0.10 | 0.07 | 0.08 | 0.04 | 0.10 | 0.07 | 0.10 | 0.05 | 0.10 | 0.08 | 0.10 | 0.03 | 0.10 | |
| Moran | 0.70 | 0.57 | 0.70 | 0.67 | 0.70 | 0.56 | 0.68 | 0.62 | 0.53 | 0.56 | 0.66 | 0.67 | 0.70 | 0.55 | |
| variant 5 | Mean | −0.02 | 0.00 | 0.00 | 0.00 | 0.00 | 0.03 | 0.00 | −0.02 | 0.00 | 0.02 | 0.01 | 0.00 | 0.00 | 0.02 |
| STD | 0.06 | 0.09 | 0.07 | 0.08 | 0.05 | 0.09 | 0.07 | 0.09 | 0.06 | 0.09 | 0.07 | 0.08 | 0.05 | 0.09 | |
| RMS | 0.06 | 0.09 | 0.07 | 0.08 | 0.05 | 0.09 | 0.07 | 0.09 | 0.06 | 0.09 | 0.07 | 0.08 | 0.05 | 0.09 | |
| Moran | 0.72 | 0.54 | 0.63 | 0.58 | 0.74 | 0.51 | 0.62 | 0.50 | 0.58 | 0.50 | 0.60 | 0.55 | 0.73 | 0.51 | |
| variant 6 | Mean | −0.04 | 0.01 | 0.00 | 0.00 | 0.01 | 0.04 | 0.00 | −0.02 | −0.01 | 0.03 | 0.02 | 0.00 | 0.00 | 0.03 |
| STD | 0.12 | 0.07 | 0.08 | 0.08 | 0.10 | 0.06 | 0.07 | 0.10 | 0.12 | 0.06 | 0.08 | 0.10 | 0.11 | 0.06 | |
| RMS | 0.12 | 0.08 | 0.08 | 0.09 | 0.11 | 0.08 | 0.08 | 0.11 | 0.13 | 0.08 | 0.09 | 0.11 | 0.12 | 0.07 | |
| Moran | 0.74 | 0.64 | 0.67 | 0.59 | 0.74 | 0.44 | 0.63 | 0.57 | 0.75 | 0.50 | 0.59 | 0.62 | 0.75 | 0.51 | |
| variant 7 | Mean | −0.01 | 0.00 | −0.01 | −0.01 | −0.02 | −0.02 | 0.00 | −0.03 | 0.00 | 0.00 | 0.01 | −0.02 | −0.02 | −0.02 |
| STD | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | 0.08 | 0.07 | 0.09 | 0.08 | 0.07 | 0.07 | 0.08 | 0.07 | 0.06 | |
| RMS | 0.07 | 0.07 | 0.07 | 0.07 | 0.07 | 0.08 | 0.07 | 0.09 | 0.08 | 0.07 | 0.07 | 0.08 | 0.08 | 0.06 | |
| Moran | 0.70 | 0.51 | 0.69 | 0.61 | 0.71 | 0.55 | 0.64 | 0.62 | 0.69 | 0.51 | 0.67 | 0.62 | 0.71 | 0.50 | |
| variant 8 | Mean | 0.01 | 0.01 | 0.00 | 0.00 | 0.01 | 0.01 | 0.00 | −0.02 | 0.02 | 0.01 | 0.01 | −0.01 | 0.00 | 0.00 |
| STD | 0.06 | 0.07 | 0.07 | 0.07 | 0.06 | 0.07 | 0.07 | 0.08 | 0.07 | 0.07 | 0.06 | 0.07 | 0.06 | 0.06 | |
| RMS | 0.06 | 0.07 | 0.07 | 0.07 | 0.06 | 0.07 | 0.06 | 0.08 | 0.07 | 0.07 | 0.06 | 0.07 | 0.06 | 0.06 | |
| Moran | 0.65 | 0.46 | 0.66 | 0.56 | 0.67 | 0.46 | 0.63 | 0.55 | 0.63 | 0.42 | 0.66 | 0.54 | 0.65 | 0.44 | |
| variant 9 | Mean | 0.08 | 0.17 | 0.01 | 0.02 | 0.13 | 0.18 | 0.02 | 0.00 | 0.08 | 0.17 | 0.04 | 0.02 | 0.08 | 0.16 |
| STD | 0.05 | 0.11 | 0.07 | 0.07 | 0.08 | 0.15 | 0.07 | 0.08 | 0.05 | 0.11 | 0.07 | 0.09 | 0.05 | 0.11 | |
| RMS | 0.10 | 0.21 | 0.07 | 0.07 | 0.15 | 0.23 | 0.07 | 0.08 | 0.09 | 0.20 | 0.08 | 0.09 | 0.09 | 0.20 | |
| Moran | 0.61 | 0.58 | 0.69 | 0.60 | 0.57 | 0.63 | 0.67 | 0.60 | 0.48 | 0.56 | 0.63 | 0.61 | 0.60 | 0.56 | |
| variant 10 | Mean | −0.07 | −0.14 | −0.02 | −0.03 | −0.11 | −0.18 | −0.02 | −0.05 | −0.09 | −0.16 | −0.02 | −0.05 | −0.09 | −0.16 |
| STD | 0.06 | 0.08 | 0.07 | 0.07 | 0.07 | 0.11 | 0.07 | 0.09 | 0.07 | 0.09 | 0.06 | 0.08 | 0.06 | 0.09 | |
| RMS | 0.10 | 0.16 | 0.07 | 0.07 | 0.13 | 0.20 | 0.07 | 0.10 | 0.11 | 0.18 | 0.07 | 0.09 | 0.11 | 0.18 | |
| Moran | 0.64 | 0.47 | 0.64 | 0.52 | 0.54 | 0.52 | 0.58 | 0.53 | 0.62 | 0.51 | 0.60 | 0.56 | 0.61 | 0.50 | |
| 80 RTK | 90 GPS | 90 RTK | 60 GPS no | 60 RTK no | 80 GPS no | 80 RTK no | |||||||||
| X | Y | X | Y | X | Y | X | Y | X | Y | X | Y | X | Y | ||
| variant 1 | Mean | 0.01 | −0.01 | 1.71 | 0.72 | 0.07 | 0.01 | 0.64 | −0.24 | 0.00 | 0.00 | 1.21 | 0.17 | 0.02 | 0.00 |
| STD | 0.08 | 0.12 | 0.70 | 0.88 | 0.07 | 0.12 | 0.09 | 0.04 | 0.01 | 0.02 | 0.09 | 0.03 | 0.02 | 0.02 | |
| RMS | 0.08 | 0.12 | 1.85 | 1.12 | 0.09 | 0.12 | 0.65 | 0.24 | 0.01 | 0.02 | 1.21 | 0.17 | 0.02 | 0.02 | |
| Moran | 0.62 | 0.65 | 0.61 | 0.68 | 0.53 | 0.60 | 0.72 | 0.65 | 0.34 | 0.35 | 0.72 | 0.70 | 0.46 | 0.48 | |
| variant 2 | Mean | 0.01 | −0.01 | 1.38 | 1.90 | 0.08 | −0.06 | 0.06 | −0.04 | 0.00 | 0.00 | 0.04 | 0.00 | 0.02 | 0.00 |
| STD | 0.08 | 0.12 | 0.12 | 0.18 | 0.11 | 0.17 | 0.16 | 0.11 | 0.01 | 0.02 | 0.12 | 0.08 | 0.02 | 0.02 | |
| RMS | 0.08 | 0.12 | 1.40 | 1.92 | 0.13 | 0.18 | 0.17 | 0.12 | 0.01 | 0.02 | 0.12 | 0.08 | 0.02 | 0.02 | |
| Moran | 0.62 | 0.67 | 0.59 | 0.72 | 0.56 | 0.68 | 0.72 | 0.72 | 0.35 | 0.36 | 0.73 | 0.74 | 0.46 | 0.50 | |
| variant 3 | Mean | 0.01 | −0.01 | 0.02 | 0.02 | 0.07 | −0.05 | 0.03 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.02 | 0.00 |
| STD | 0.07 | 0.09 | 0.03 | 0.14 | 0.09 | 0.12 | 0.01 | 0.06 | 0.01 | 0.02 | 0.01 | 0.02 | 0.02 | 0.02 | |
| RMS | 0.07 | 0.09 | 0.03 | 0.14 | 0.11 | 0.13 | 0.03 | 0.06 | 0.01 | 0.02 | 0.01 | 0.02 | 0.02 | 0.02 | |
| Moran | 0.67 | 0.64 | 0.10 | 0.49 | 0.61 | 0.65 | 0.48 | 0.58 | 0.36 | 0.28 | 0.36 | 0.28 | 0.45 | 0.44 | |
| variant 4 | Mean | 0.00 | −0.01 | 0.00 | 0.01 | 0.06 | −0.04 | 0.03 | 0.00 | 0.00 | 0.00 | 0.02 | 0.01 | 0.02 | 0.00 |
| STD | 0.07 | 0.09 | 0.04 | 0.11 | 0.09 | 0.11 | 0.03 | 0.05 | 0.01 | 0.02 | 0.02 | 0.05 | 0.02 | 0.02 | |
| RMS | 0.07 | 0.08 | 0.04 | 0.11 | 0.10 | 0.11 | 0.04 | 0.04 | 0.01 | 0.02 | 0.03 | 0.05 | 0.02 | 0.02 | |
| Moran | 0.71 | 0.66 | 0.58 | 0.46 | 0.66 | 0.65 | 0.69 | 0.56 | 0.42 | 0.25 | 0.70 | 0.55 | 0.48 | 0.46 | |
| variant 5 | Mean | 0.00 | 0.00 | 0.00 | 0.05 | 0.05 | −0.02 | 0.01 | 0.01 | 0.00 | 0.00 | 0.01 | 0.02 | 0.02 | 0.00 |
| STD | 0.07 | 0.07 | 0.04 | 0.10 | 0.08 | 0.09 | 0.03 | 0.04 | 0.01 | 0.02 | 0.03 | 0.04 | 0.02 | 0.02 | |
| RMS | 0.07 | 0.07 | 0.04 | 0.11 | 0.09 | 0.09 | 0.03 | 0.04 | 0.01 | 0.02 | 0.03 | 0.04 | 0.02 | 0.02 | |
| Moran | 0.67 | 0.55 | 0.68 | 0.52 | 0.63 | 0.52 | 0.71 | 0.58 | 0.32 | 0.27 | 0.71 | 0.56 | 0.41 | 0.45 | |
| variant 6 | Mean | 0.01 | 0.00 | −0.01 | 0.03 | 0.07 | −0.03 | 0.02 | 0.01 | 0.00 | 0.00 | 0.02 | 0.02 | 0.02 | 0.00 |
| STD | 0.07 | 0.09 | 0.10 | 0.07 | 0.09 | 0.11 | 0.07 | 0.03 | 0.01 | 0.02 | 0.06 | 0.03 | 0.02 | 0.02 | |
| RMS | 0.08 | 0.10 | 0.11 | 0.09 | 0.12 | 0.13 | 0.08 | 0.04 | 0.02 | 0.02 | 0.07 | 0.04 | 0.03 | 0.02 | |
| Moran | 0.67 | 0.59 | 0.77 | 0.28 | 0.60 | 0.60 | 0.76 | 0.71 | 0.30 | 0.35 | 0.77 | 0.62 | 0.41 | 0.46 | |
| variant 7 | Mean | −0.01 | −0.01 | −0.01 | −0.05 | 0.04 | −0.04 | 0.02 | −0.01 | 0.00 | 0.00 | 0.01 | 0.00 | 0.02 | 0.00 |
| STD | 0.07 | 0.07 | 0.08 | 0.09 | 0.07 | 0.08 | 0.04 | 0.03 | 0.01 | 0.01 | 0.04 | 0.03 | 0.01 | 0.02 | |
| RMS | 0.07 | 0.07 | 0.08 | 0.10 | 0.08 | 0.08 | 0.05 | 0.03 | 0.01 | 0.01 | 0.04 | 0.03 | 0.02 | 0.02 | |
| Moran | 0.69 | 0.60 | 0.70 | 0.49 | 0.67 | 0.56 | 0.70 | 0.48 | 0.37 | 0.27 | 0.71 | 0.47 | 0.48 | 0.40 | |
| variant 8 | Mean | 0.00 | 0.00 | 0.01 | −0.02 | 0.04 | −0.02 | 0.02 | 0.00 | 0.00 | 0.00 | 0.01 | 0.00 | 0.02 | 0.00 |
| STD | 0.06 | 0.06 | 0.07 | 0.08 | 0.07 | 0.06 | 0.04 | 0.03 | 0.01 | 0.01 | 0.04 | 0.03 | 0.01 | 0.02 | |
| RMS | 0.06 | 0.06 | 0.07 | 0.08 | 0.08 | 0.07 | 0.04 | 0.03 | 0.01 | 0.01 | 0.04 | 0.03 | 0.02 | 0.02 | |
| Moran | 0.66 | 0.53 | 0.68 | 0.35 | 0.64 | 0.45 | 0.66 | 0.44 | 0.41 | 0.18 | 0.66 | 0.43 | 0.50 | 0.30 | |
| variant 9 | Mean | 0.03 | 0.03 | 0.11 | 0.14 | 0.10 | 0.01 | 0.07 | 0.02 | 0.01 | 0.00 | 0.06 | 0.05 | 0.02 | 0.00 |
| STD | 0.07 | 0.08 | 0.08 | 0.13 | 0.08 | 0.09 | 0.05 | 0.03 | 0.01 | 0.01 | 0.04 | 0.04 | 0.01 | 0.02 | |
| RMS | 0.07 | 0.08 | 0.13 | 0.19 | 0.12 | 0.09 | 0.08 | 0.04 | 0.01 | 0.01 | 0.07 | 0.07 | 0.02 | 0.02 | |
| Moran | 0.70 | 0.60 | 0.60 | 0.57 | 0.62 | 0.58 | 0.72 | 0.51 | 0.41 | 0.23 | 0.72 | 0.51 | 0.51 | 0.41 | |
| variant 10 | Mean | −0.03 | −0.05 | −0.10 | −0.19 | 0.01 | −0.10 | 0.01 | −0.05 | 0.00 | 0.00 | −0.01 | −0.07 | 0.01 | 0.00 |
| STD | 0.07 | 0.07 | 0.06 | 0.11 | 0.07 | 0.08 | 0.03 | 0.04 | 0.01 | 0.02 | 0.02 | 0.04 | 0.02 | 0.02 | |
| RMS | 0.07 | 0.09 | 0.11 | 0.22 | 0.07 | 0.12 | 0.03 | 0.06 | 0.01 | 0.02 | 0.02 | 0.08 | 0.02 | 0.02 | |
| Moran | 0.64 | 0.52 | 0.48 | 0.46 | 0.64 | 0.54 | 0.69 | 0.54 | 0.24 | 0.27 | 0.64 | 0.42 | 0.33 | 0.41 | |
References
- Kovanič, Ľ.; Topitzer, B.; Pet’ovský, P.; Blišt’an, P.; Bindzárová Gergel’ová, M.; Blišt’anová, M. Review of Photogrammetric and Lidar Applications of UAV. Appl. Sci. 2023, 13, 6732. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Noor, F.; Ullah, I.; Alsharif, M.H. Towards the Unmanned Aerial Vehicles (UAVs): A Comprehensive Review. Drones 2022, 6, 147. [Google Scholar] [CrossRef]
- DJI—Official Website. Available online: https://www.dji.com/ (accessed on 5 September 2025).
- Zhao, B.; Li, J.; Wang, L.; Shi, Y. Positioning Accuracy Assessment of a Commercial RTK UAS. In Autonomous Air and Ground Sensing Systems for Agricultural Optimization and Phenotyping V; SPIE-Intl Soc Optical Eng: Bellingham, WA, USA, 2020; p. 8. [Google Scholar]
- Ekaso, D.; Nex, F.; Kerle, N. Accuracy Assessment of Real-Time Kinematics (RTK) Measurements on Unmanned Aerial Vehicles (UAV) for Direct Geo-Referencing. Geo-Spat. Inf. Sci. 2020, 23, 165–181. [Google Scholar] [CrossRef]
- Dinkov, D. Accuracy Assessment of High-Resolution Terrain Data Produced from UAV Images Georeferenced with on-Board PPK Positioning. J. Bulg. Geogr. Soc. 2023, 2023, 43–53. [Google Scholar] [CrossRef]
- Eker, R.; Alkan, E.; Aydın, A. A Comparative Analysis of UAV-RTK and UAV-PPK Methods in Mapping Different Surface Types. Eur. J. For. Eng. 2021, 7, 12–25. [Google Scholar] [CrossRef]
- Stott, E.; Williams, R.D.; Hoey, T.B. Ground Control Point Distribution for Accurate Kilometre-Scale Topographic Mapping Using an RTK-GNSS Unmanned Aerial Vehicle and SfM Photogrammetry. Drones 2020, 4, 55. [Google Scholar] [CrossRef]
- Teppati Losè, L.; Chiabrando, F.; Giulio Tonolo, F. Are Measured Ground Control Points Still Required in UAV Based Large Scale Mapping? Assessing the Positional Accuracy of an RTK Multi-Rotor Platform. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2020, 43, 507–514. [Google Scholar] [CrossRef]
- Liu, Y.; Han, K.; Rasdorf, W. Assessment and Prediction of Impact of Flight Configuration Factors on UAS-Based Photogrammetric Survey Accuracy. Remote Sens. 2022, 14, 4119. [Google Scholar] [CrossRef]
- Liu, X.; Lian, X.; Yang, W.; Wang, F.; Han, Y.; Zhang, Y. Accuracy Assessment of a UAV Direct Georeferencing Method and Impact of the Configuration of Ground Control Points. Drones 2022, 6, 30. [Google Scholar] [CrossRef]
- Dai, W.; Zheng, G.; Antoniazza, G.; Zhao, F.; Chen, K.; Lu, W.; Lane, S.N. Improving UAV-SfM Photogrammetry for Modelling High-Relief Terrain: Image Collection Strategies and Ground Control Quantity. Earth Surf. Process. Landforms 2023, 48, 2884–2899. [Google Scholar] [CrossRef]
- Mesas-Carrascosa, F.J.; García, M.D.N.; De Larriva, J.E.M.; García-Ferrer, A. An Analysis of the Influence of Flight Parameters in the Generation of Unmanned Aerial Vehicle (UAV) Orthomosaicks to Survey Archaeological Areas. Sensors 2016, 16, 1838. [Google Scholar] [CrossRef]
- Villanueva, J.K.S.; Blanco, A.C. Optimization of Ground Control Point (GCP) Configuration for Unmanned Aerial Vehicle (UAV) Survey Using Structure from Motion (SFM). Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2019, 42, 167–174. [Google Scholar] [CrossRef]
- Zhang, K.; Okazawa, H.; Hayashi, K.; Hayashi, T.; Fiwa, L.; Maskey, S. Optimization of Ground Control Point Distribution for Unmanned Aerial Vehicle Photogrammetry for Inaccessible Fields. Sustainability 2022, 14, 9505. [Google Scholar] [CrossRef]
- Llabani, A.; Abazaj, F. Evaluating UAV RTK Photogrammetry Mapping Accuracy in Urban Areas without Ground Control Points. Int. Res. J. Innov. Eng. Technol. 2024, 8, 82–87. [Google Scholar] [CrossRef]
- Mulakala, J. Measurement Accuracy of the DJI Phantom 4 RTK & Photogrammetry; DroneDeploy: San Francisco, CA, USA, 2019. [Google Scholar]
- Stöcker, C.; Nex, F.; Koeva, M.; Gerke, M. High-Quality UAV-Based Orthophotos for Cadastral Mapping: Guidance for Optimal Flight Configurations. Remote Sens. 2020, 12, 3625. [Google Scholar] [CrossRef]
- Cramer, M.; Zhang, S.; Meißner, H.; Reulke, R. Quality Assessment of High-Resolution UAV Imagery and Products. In Proceedings of the 40. Wissenschaftlich-Technische Jahrestagung der DGPF in Stuttgart, Stuttgart, Germany, 4–6 March 2020; pp. 33–46. [Google Scholar]
- Gerke, M.; Przybilla, H.J. Accuracy Analysis of Photogrammetric UAV Image Blocks: Influence of Onboard RTK-GNSS and Cross Flight Patterns. Photogramm. Fernerkund. Geoinf. 2016, 2016, 17–30. [Google Scholar] [CrossRef]
- Zhou, Y.; Rupnik, E.; Meynard, C.; Thom, C.; Pierrot-Deseilligny, M. Simulation and Analysis of Photogrammetric UAV Image Blocks-Influence of Camera Calibration Error. Remote Sens. 2020, 12, 22. [Google Scholar] [CrossRef]
- Nesbit, P.R.; Hugenholtz, C.H. Enhancing UAV-SfM 3D Model Accuracy in High-Relief Landscapes by Incorporating Oblique Images. Remote Sens. 2019, 11, 239. [Google Scholar] [CrossRef]
- Niu, Z.; Xia, H.; Tao, P.; Ke, T. Accuracy Assessment of UAV Photogrammetry System with RTK Measurements for Direct Georeferencing. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, 10, 169–176. [Google Scholar] [CrossRef]
- Peppa, M.V.; Hall, J.; Goodyear, J.; Mills, J.P. Photogrammetric Assessment and Comparison of DJI Phantom 4 Pro and Phantom 4 RTK Small Unmanned Aircraft Systems. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2019, 42, 503–509. [Google Scholar] [CrossRef]
- Przybilla, H.J.; Bäumker, M.; Luhmann, T.; Hastedt, H.; Eilers, M. Interaction between Direct Georeferencing, Control Point Configuration and Camera Self-Calibration for RTK-Based UAV Photogrammetry. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2020, 43, 485–492. [Google Scholar] [CrossRef]
- Oniga, V.-E.; Breaban, A.-I.; Statescu, F. Determining the Optimum Number of Ground Control Points for Obtaining High Precision Results Based on UAS Images. Proceedings 2018, 2, 352. [Google Scholar] [CrossRef]
- Sanz-Ablanedo, E.; Chandler, J.H.; Rodríguez-Pérez, J.R.; Ordóñez, C. Accuracy of Unmanned Aerial Vehicle (UAV) and SfM Photogrammetry Survey as a Function of the Number and Location of Ground Control Points Used. Remote Sens. 2018, 10, 1606. [Google Scholar] [CrossRef]
- Ferrer-González, E.; Agüera-Vega, F.; Carvajal-Ramírez, F.; Martínez-Carricondo, P. UAV Photogrammetry Accuracy Assessment for Corridor Mapping Based on the Number and Distribution of Ground Control Points. Remote Sens. 2020, 12, 2447. [Google Scholar] [CrossRef]
- Garcia, M.V.Y.; Oliveira, H.C. The Influence of Ground Control Points Configuration and Camera Calibration for DTM and Orthomosaic Generation Using Imagery Obtained from A Low-Cost UAV. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, 5, 239–244. [Google Scholar] [CrossRef]
- Kersten, T.; Wolf, J.; Lindstaedt, M. Investigations into the accuracy of the UAV system DJI Matrice 300 RTK with the sensors Zenmuse P1 and L1 in the Hamburg test field. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2022, 43, 339–346. [Google Scholar] [CrossRef]
- Przybilla, H.J.; Gerke, M.; DIkhoff, I.; Ghassoun, Y. Investigations on the Geometric Quality of Cameras for UAV Applications Using the High Precision UAV Test Field Zollern Colliery. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2019, 42, 531–538. [Google Scholar] [CrossRef]
- Wiącek, P.; Pyka, K. The Test Field for UAV Accuracy Assessments. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2019, 42, 67–73. [Google Scholar] [CrossRef]
- Leica GS07 Website. Available online: https://leica-geosystems.com/products/gnss-systems/smart-antennas/leica-gs07-made-for-you (accessed on 5 September 2025).
- Leica TS16: Robotic Total Station Website. Available online: https://leica-geosystems.com/products/total-stations/robotic-total-stations/leica-ts16 (accessed on 5 September 2025).
- DJI Ground Station Pro Website. Available online: https://www.dji.com/pl/ground-station-pro (accessed on 5 August 2025).
- Agisoft Metashape Website. Available online: https://www.agisoftmetashape.com/ (accessed on 5 September 2025).




| Parameter | Phantom 4 Pro V2.0/Phantom 4 RTK |
|---|---|
| Lens | 8.8 mm/24 mm (35 mm format equivalent) f/2.8–f/11 |
| Image resolution | 13.2 × 8.8 mm, 5472 × 3648 px |
| Pixel size | 2.41 μm |
| Effective pixels | 20 Mpx |
| Sensor | 1-inch CMOS |
| Field of view (FOV) | 84° |
| Shutter speed | Mechanical: 8-1/2000 s, electronic: 8-1/8000 s |
| Max f-stop | 1:2.8 |
| Flight Altitude (AGL) [m] | Nadir Images | Oblique Images |
|---|---|---|
| 50 | X | |
| 60 | X | X |
| 70 | X | |
| 80 | X | X |
| 90 | X |
| Variant | Description | No. of GCPs | No. of Checkpoints |
|---|---|---|---|
| 1 | No GCPs in aerial triangulation | 0 | 38 |
| 2 | 1 GCP in the middle | 1 | 37 |
| 3 | 3 evenly distributed GCPs | 3 | 35 |
| 4 | 6 evenly distributed GCPs | 6 | 32 |
| 5 | 12 evenly distributed GCPs | 12 | 26 |
| 6 | Without GCPs in corners (GCPs in the middle part of the area) | 6 | 32 |
| 7 | GCPs only in corners | 6 | 32 |
| 8 | GCPs in the corners and on the edges | 11 | 27 |
| 9 | GCPs on the right side of the block | 6 | 32 |
| 10 | GCPs on the left side of the block | 6 | 32 |
| Check Distance (Start and End GCP) | Length of the Distance [m] |
|---|---|
| 38–39 | 23.75 |
| 37–12 | 47.44 |
| 12–33 | 64.60 |
| 12–30 | 99.20 |
| 11–34 | 99.57 |
| 30–37 | 113.13 |
| Flight Height [m] | Variant 1 (Adjusted f) | Variant 1 (Fixed f) | Variant 2 (Adjusted f) | Variant 2 (Fixed f) | ||||
|---|---|---|---|---|---|---|---|---|
| Z Error [m] | ||||||||
| GPS | RTK | GPS | RTK | GPS | RTK | GPS | RTK | |
| 50 | 1.18 | 0.24 | 0.53 | 0.81 | 0.94 | 0.07 | 0.95 | 0.72 |
| 60 | 19.82 | 4.92 | 0.97 | 1.12 | 1.54 | 0.47 | 1.13 | 0.86 |
| 70 | 17.06 | 5.73 | 1.34 | 1.19 | 0.95 | 0.07 | 1.04 | 0.76 |
| 80 | 3.70 | 1.19 | 1.33 | 1.33 | 0.53 | 0.08 | 0.67 | 0.70 |
| 90 | 24.21 | 13.26 | 1.48 | 1.51 | 0.68 | 0.09 | 0.81 | 0.59 |
| Flight Height [m] | Variant 1 (Adjusted f) | Variant 2 (Adjusted f) | ||||||
|---|---|---|---|---|---|---|---|---|
| X Error [m] | Y Error [m] | X Error [m] | Y Error [m] | |||||
| GPS | RTK | GPS | RTK | GPS | RTK | GPS | RTK | |
| 50 | 0.88 | 0.07 | 0.83 | 0.08 | 0.22 | 0.08 | 0.15 | 0.08 |
| 60 | 0.86 | 0.07 | 0.79 | 0.09 | 2.21 | 0.07 | 3.23 | 0.11 |
| 70 | 0.99 | 0.07 | 0.90 | 0.10 | 0.10 | 0.09 | 0.13 | 0.12 |
| 80 | 0.09 | 0.08 | 0.90 | 0.12 | 0.12 | 0.08 | 0.22 | 0.12 |
| 90 | 1.85 | 0.09 | 1.13 | 0.12 | 1.38 | 0.13 | 1.90 | 0.18 |
| Flight Height [m] | Flight Variant | Z Error [m] | |
|---|---|---|---|
| GPS | RTK | ||
| 60 | n | 19.821 | 4.923 |
| 80 | o | 3.700 | 1.192 |
| 60 | no | 1.526 | 0.022 |
| 80 | no | 0.533 | 0.016 |
| Flight Variant | GCP Variant | GCP Variant 2 | ||||||
|---|---|---|---|---|---|---|---|---|
| X Error [m] | Y Error [m] | X Error [m] | Y Error [m] | |||||
| GPS | RTK | GPS | RTK | GPS | RTK | GPS | RTK | |
| 60n | 0.86 | 0.07 | 0.79 | 0.09 | 2.21 | 0.07 | 3.23 | 0.11 |
| 80n | 0.09 | 0.08 | 0.90 | 0.12 | 0.12 | 0.08 | 0.22 | 0.12 |
| 60no | 0.65 | 0.02 | 0.24 | 0.02 | 0.17 | 0.02 | 0.12 | 0.02 |
| 80no | 1.21 | 0.02 | 0.17 | 0.02 | 0.12 | 0.02 | 0.08 | 0.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pilarska-Mazurek, M.; Łoza, D. Analysis of the Influence of RTK Observations on the Accuracy of UAV Images. Appl. Sci. 2025, 15, 10559. https://doi.org/10.3390/app151910559
Pilarska-Mazurek M, Łoza D. Analysis of the Influence of RTK Observations on the Accuracy of UAV Images. Applied Sciences. 2025; 15(19):10559. https://doi.org/10.3390/app151910559
Chicago/Turabian StylePilarska-Mazurek, Magdalena, and Dawid Łoza. 2025. "Analysis of the Influence of RTK Observations on the Accuracy of UAV Images" Applied Sciences 15, no. 19: 10559. https://doi.org/10.3390/app151910559
APA StylePilarska-Mazurek, M., & Łoza, D. (2025). Analysis of the Influence of RTK Observations on the Accuracy of UAV Images. Applied Sciences, 15(19), 10559. https://doi.org/10.3390/app151910559






