P-HNSW: Crash-Consistent HNSW for Vector Databases on Persistent Memory

Abstract

The rapid growth of Large Language Models (LLMs) has generated massive amounts of high-dimensional feature vectors extracted from diverse datasets. Efficient storage and retrieval of such data are critical for enabling accurate and fast query responses. Vector databases (Vector DBs) provide efficient storage and retrieval for high-dimensional vectors. These systems rely on Approximate Nearest Neighbor Search (ANNS) indexes, such as HNSW, to handle large-scale data efficiently. However, the original HNSW is implemented on DRAM, which is both costly and vulnerable to crashes. Therefore, we propose P-HNSW, a crash-consistent HNSW on persistent memory. To guarantee crash consistency, P-HNSW introduces two logs, NLog and NlistLog. We describe the logging process during the operation and the recovery process in the event of system crashes. Our experimental results demonstrate that the overhead of the proposed logging mechanism is negligible, while P-HNSW achieves superior performance compared with SSD-based recovery mechanisms.

1. Introduction

As Large Language Models (LLMs) are increasingly used in various applications  [1,2,3], the importance of vector databases (Vector DBs) for enhancing the quality of LLM responses has grown. Vector databases provide efficient storage and retrieval of high-dimensional feature vectors extracted from various datasets. To provide prompt query responses, vector databases employ Approximate Nearest Neighbor Search (ANNS) instead of k-Nearest Neighbor Search (k-NN) [4]. This is because high-dimensional vector data make exact nearest neighbor search computationally expensive, and using k-NN incurs significant overhead [5]. There are various ANNS indexes, such as Annoy [6], LSH [7], DiskANN [8], and HNSW [9]. Annoy, developed by Spotify, is a tree-based ANNS library that builds multiple random projection trees to partition vectors and then searches them by traversing trees. Once constructed, the index is stored on disk as a file and loaded into memory via memory mapping when needed. Annoy does not support dynamic updates, requiring a complete rebuild of the index for any modifications. LSH places similar vectors into the same buckets using randomized hash functions so that queries only need to access the corresponding bucket. It achieves relatively fast query performance with low memory consumption, but the accuracy is limited. DiskANN, developed by Microsoft, is a graph-based ANNS index that stores and manages the entire graph on SSD. Since only a small portion of the index is kept in memory, it achieves low memory usage. DiskANN also supports dynamic updates, but frequent SSD accesses result in significantly higher query latency. In particular, the Hierarchical Navigable Small World (HNSW) is a representative method that achieves high search performance and high recall by leveraging a hierarchical graph structure. This structure organizes vectors across multiple layers, where the sparse layers (upper layers) handle broad search traversal, and the dense layers (lower layers) focus on precise neighbor searches, resulting in logarithmic search complexity in practice. However, HNSW implementations are typically based on in-memory data structures that store the entire graph index on DRAM, which does not provide persistence.

Persistent memory technologies, such as NVDIMM-N (Non-Volatile Dual In-line Memory Module-N) [10] and CXL-SSD (e.g., Samsung’s CMM-H [11]), can significantly mitigate the index-rebuilding overhead after a system crash. In addition to providing persistence, they also provide byte-addressability, enabling memory semantics and efficient random access. However, since CPU caches are not part of the persistence domain even when using persistent memory, the index can still be left in an inconsistent state after a crash. Therefore, a proper crash consistency scheme is required to ensure the consistency of an index stored in persistent memory.

Crash consistency refers to the guarantee that data structures remain in a recoverable and logically consistent state after unexpected failures, such as power loss or system crashes. If crash consistency is not guaranteed, an interruption during index updates may lead to partial or corrupted data in persistent memory, resulting in inaccurate query results or even system errors after recovery.

Prior studies on persistent memory indexes primarily focused on traditional structures, such as B+-Trees and hash tables, and their logging and crash consistency mechanisms. However, since these studies mainly targeted OLTP workloads, they are not well suited to vector database applications. In this work, we focus on the HNSW index for ANNS, and we design P-HNSW, which considers the structural characteristics of an HNSW to ensure persistence and consistency in persistent memory environments with minimal overhead. To the best of our knowledge, no prior work has implemented HNSW on persistent memory while explicitly addressing crash consistency.

In this study, we propose P-HNSW, a persistent HNSW implementation optimized for persistent memory. To guarantee the crash consistency of the HNSW, we introduce a logging and recovery mechanism based on two logs, which are called NLog and NlistLog. We conduct extensive experiments and find that our proposed logging techniques do not incur significant overhead.

The contributions of this study are as follows:

• We design P-HNSW, a persistent HNSW on persistent memory that employs a logging mechanism. Our logging mechanism employs two logs, called NLog and NlistLog, which leverage the byte-addressability and persistence of persistent memory.
• We provide a detailed analysis of failure scenarios and show how our logging mechanism ensures crash consistency and enables reliable recovery of P-HNSW.
• We conduct extensive experiments that include an SSD-based crash consistency mechanism. Our experimental results show that the overhead of the logging mechanism is negligible, while P-HNSW guarantees both robustness and persistence.

The rest of this paper is organized as follows. Section 2 introduces ANNS algorithms, including HNSW, persistent memory, and the recovery mechanism in current vector databases. Section 3 presents an overview of P-HNSW. Section 4 explains how the logging technique of P-HNSW works using NLog and NlistLog, and Section 5 describes how P-HNSW recovers from a system crash. Section 6 presents the experimental results. Section 7 reviews the related work, and Section 8 concludes this paper.

2. Background

2.1. Approximate Nearest Neighbor Search (ANNS)

As the demand for services that leverage vector data continues to grow rapidly, the importance of efficient vector data search methods is increasing. The primary objective of these services is to search for the top-k nearest vectors for a given query vector. The most straightforward approach is to find the nearest data by calculating the similarity between the entire dataset and the given query vector and then selecting the top-k results. This method is commonly referred to as k-Nearest Neighbor Search (k-NN). However, as real-world services often handle billions of high-dimensional vectors [12], calculating the similarity between the query and the entire dataset is extremely challenging.

Approximate Nearest Neighbor Search (ANNS) is a search algorithm designed to efficiently retrieve the top-k vectors most similar to a given query vector in large and high-dimensional datasets. Since ANNS searches for nearest neighbors approximately, its accuracy is typically slightly lower than that of k-NN. Nevertheless, ANNS significantly reduces the computational cost and provides a good trade-off between accuracy and efficiency. The search quality of ANNS is typically measured using recall, which indicates how often the true nearest neighbors are retrieved. ANNS is widely used in industries, such as in recommender systems, large language models (LLMs), and image retrieval, where high-throughput similarity computation is required in real time [13].

ANNS can be categorized based on hashing, graph, or tree structures. Hashing-based ANNS (e.g., LSH) [7,14,15,16] is designed to probabilistically place similar data into the same bucket using hash functions designed to preserve the similarity of high-dimensional vectors. Graph-based ANNS (e.g., HNSW, DiskANN) [8,9,17,18] represents vectors as nodes and establishes connections based on their similarity. These methods offer high flexibility and search efficiency, but they involve higher maintenance overhead and algorithmic complexity. Tree-based ANNS (e.g., KD-tree) [6,19,20,21] uses less memory and performs efficiently in low-dimensional spaces but is unsuitable for high-dimensional vectors. Graph-based ANNS has recently gained significant attention due to its balance between efficiency and accuracy. In particular, the Hierarchical Navigable Small World (HNSW) [9] is one of the most widely adopted approaches, and we focus on it in the following subsection.

2.2. Hierarchical Navigable Small World (HNSW)

Hierarchical Navigable Small World (HNSW) [9] is a widely used graph-based index for ANNS in high-dimensional vector spaces. It provides both high recall and high efficiency, making it popular across many industries. Vector databases, such as Milvus [22], offer HNSW as an index option, and Facebook’s FAISS [23] library also supports HNSW. Applications such as Pinterest [24] and Spotify [25] employ search engines based on HNSW.

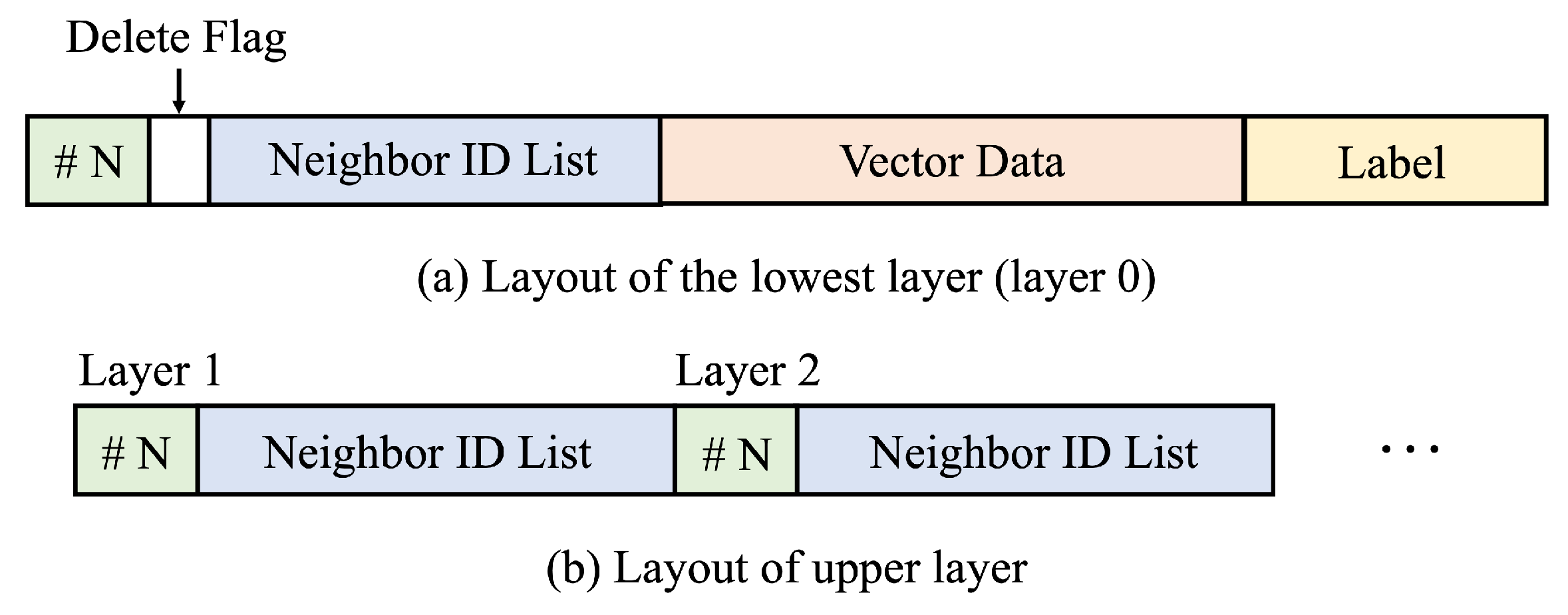
HNSW comprises multiple layers of graphs, similar to a skiplist, as shown in Figure 1. The bottom layer (layer 0) contains all vector data, while higher layers have progressively sparser graphs. In HNSW, each node represents a vector and is connected based on its vector similarity. This hierarchical design enables efficient top-down traversal, which narrows the search space from a coarse to a fine resolution. HNSW pre-allocates space for the maximum number of nodes at index creation. When a new vector is inserted, HNSW assigns it an internal node ID and adds it to the label-to-node mapping table with the user-provided external label. The new vector is then placed in the pre-allocated space corresponding to its node ID. If a vector is deleted, its node ID and vector space can later be reassigned to future insertions after reinitializing the space via memset.

When a query arrives, HNSW starts traversal from the top layer and moves downward. At each higher layer, it finds the closest node to the query and uses it as the entry point for the next lower layer. Once it reaches the bottom layer, HNSW performs a beam search to identify the nearest neighbors and returns the top-k results. Recent studies have proposed improvements to HNSW to further enhance its efficiency and robustness. For example, HNSW++ [26] introduces dual search branches and leverages Local Intrinsic Dimensionality (LID) values to mitigate the effect of local minima and improve connectivity between clusters. Dynamic HNSW (DHNSW) [27] employs a data-adaptive parameter-tuning framework at the node level, aiming to reduce build time and memory consumption. Previous studies have focused on improving the efficiency of HNSW in terms of build time and memory usage. However, since HNSW was originally designed as an in-memory vector index, a system failure results in the loss of both vector data and the index, requiring a complete rebuild that incurs significant time and computational overhead.

2.3. Recovery in Vector DB

Large-scale vector databases must be able to recover quickly and accurately even after a system failure. Applications such as recommender systems and search engines, which rely heavily on vector databases, handle real-time user requests and large-scale searches. Therefore, it is critical to ensure data reliability and enable fast, consistent recovery. To address these requirements, modern vector databases employ various recovery mechanisms.

DRAM-based HNSW offers low search latency and supports dynamic updates, but all data and index structures are lost if the system crashes. To address this problem, major vector database systems employ a combination of recovery mechanisms, including write-ahead logging (WAL), snapshots, and replication. For example, Milvus [22] records every insertion and deletion in the WAL before updating the index. Additionally, it updates its recovery point by taking periodic snapshots. In the case of Weaviate [28], it supports crash recovery of HNSW by utilizing an incremental disk write mechanism, which writes only the modified parts to disk. However, HNSW’s hierarchical graph structure and frequent dynamic updates cause the edge information in each layer to change constantly. This requires snapshots and WALs to be generated frequently, which leads to significant performance overhead. Furthermore, the complexity of the graph makes it difficult to maintain consistency between snapshots and WALs. Since unflushed data cannot be recovered, failures may still result in data loss.

Storing the index on SSD can be an alternative solution to tolerate a system failure, and SSD-based vector databases have also been proposed to address the limited capacity of DRAM. Although SSDs offer slower access performance than that of DRAM, they offer the advantage of vast and non-volatile storage capacity. FreshDiskANN [29] is a graph-based vector index optimized for SSD, where the entire graph index is stored and managed on SSD. It maintains a temporary in-memory graph consisting of newly inserted nodes, which is periodically snapshotted to SSD. A list of deleted nodes is also stored in memory. To ensure recoverability in case of a system failure, all update operations are also recorded in a persistent redo log. Inserted and deleted nodes in memory are periodically reflected in the SSD-resident index. To maintain graph consistency during this process, a copy of the existing graph is created, and updates are merged into this copy asynchronously. Once the merge is complete, the original graph is atomically replaced with the updated version. However, data that have not yet been flushed to the SSD can still be lost, and frequent flush operations may degrade performance. In large-scale vector databases where real-time processing is crucial, such performance degradation can directly affect service quality.

In summary, both DRAM- and SSD-based approaches exhibit fundamental trade-offs between performance and persistence. DRAM offers low latency and high throughput, but it loses all data upon failure, whereas SSD ensures persistence but suffers from slower performance and high flush overhead.

2.4. Persistent Memory

While SSDs provide persistence, their relatively high latency and I/O overhead still limit performance, especially for fine-grained data access. To address these limitations, next-generation memory technologies, such as Persistent Memory (PM) and CXL-SSD, are being rapidly developed. NVDIMM-N is a persistent memory technology; it is essentially DRAM equipped with its own battery. It provides persistence, ensuring data integrity even after power loss. Meanwhile, CXL-SSD [11] achieves byte-addressability and lower latency compared with conventional SSDs by using the CXL interconnect [30] while offering higher capacity than typical memory-bus-based solutions.

Since both technologies provide common features, such as persistence and byte-addressability, this study focuses on these two characteristics. Considering these characteristics, applying next-generation memory technologies to vector indexes enhances system persistence and availability. Modern vector databases often manage billions of vectors, and in DRAM-based systems, a failure results in the complete loss of the HNSW index, requiring a costly full rebuild. By storing HNSW in persistent memory, both vector data and index structures can be preserved across failures, enabling rapid recovery and high-quality restoration.

However, even when using persistent memory, we need to consider the ordering of memory instructions and their persistence. Persistent memory can be classified into two persistence domains: Asynchronous DRAM Refresh (ADR) and extended Asynchronous DRAM Refresh (eADR). In ADR, since CPU caches are not in the persistence domain, explicit cache line flushes and memory ordering instructions, such as clwb and sfence, are required to guarantee instruction ordering and durability. In eADR, CPU caches are also included in the persistence domain, so only memory ordering instructions, such as sfence, are needed. In the ARM architecture, the DCCVAP [31] and DSB [31] instructions are used for cache line flushing and memory ordering, respectively. In CXL-based memory-semantic SSDs, a cache line flush instruction, such as clwb, is required. After issuing the cache line flush instruction, a subsequent read request to the same cache line is needed to guarantee the completion of the PCIe transaction [32]. Moreover, the atomic granularity of both the system and persistent memory is critical for guaranteeing the consistency of both graph structures and vector data. In this study, we assume the x86 architecture, so the atomic granularity is 8 bytes.

This study aims to make HNSW persistent and recoverable by leveraging the persistence of NVDIMM-N. Since NVDIMM-N provides byte-addressability and low latency, it enables reliable management of HNSW without incurring significant performance overhead.

3. Design Overview

HNSW has a hierarchical graph structure, where the upper layers comprise a sparse subset of nodes, while the lowest layer (layer 0) stores all nodes. As shown in Figure 2a, each node contains the following information: a vector label, vector data, the number of neighbor nodes, a neighbor node list, and a delete flag. In contrast, the purpose of layers above layer 0 is solely to guide the search process toward lower layers. Therefore, they store only the neighbor node information without the actual vector data (Figure 2b). Since the HNSW index resides in DRAM, all insert and update operations can be performed quickly. However, the entire index is lost upon system shutdown, requiring a full reconstruction that incurs significant time and computational overhead.

To address the limitations of DRAM-based HNSW, such as volatility and recovery challenges, we introduce P-HNSW, a persistent version of HNSW that stores the entire index in persistent memory. Persistent memory offers byte-addressability and non-volatility, thereby combining DRAM-like latency with SSD-like persistence. To ensure persistence, the index structure must be stored in a persistent storage medium. Since a system crash may occur at any time, both the index structure and label-to-node mapping table must remain crash-consistent. In particular, because HNSW has a hierarchical structure, each insertion requires updates across all levels of the graph, and dynamic updates occur frequently. As a result, maintaining the consistency of the graph becomes challenging, and even the corruption of a few nodes can significantly degrade the functionality of the index or the search performance.

To address these challenges, we introduce two types of logs: the Node Log (NLog) and the Neighbor List Log (NlistLog). To enable efficient logging at each stage of the insert operation, we divide the original inserts algorithm into three phases: neighbor search, neighbor information storage, and neighbor-of-neighbor search/store. The NLog is a redo log that guarantees the atomicity of new data insertions. It records the state of the operation along with its associated metadata, enabling P-HNSW to figure out how far the insert operation is reflected in persistent memory and to apply an appropriate recovery strategy. In contrast, the NlistLog serves as an undo log to prevent data inconsistencies in a node’s neighbor information. It stores the previous neighbor data, and if the new neighbor information has not yet been fully stored, P-HNSW restores the neighbor information by overwriting it. Since graph inconsistencies can significantly affect the index operations, the recovery process first restores the integrity of the graph using the NlistLog and then resolves the interrupted operations using the NLog. With these logs, the graph can be reconstructed to its original structure after recovery.

The label-to-node mapping table can be reconstructed during the recovery by traversing all nodes in the lowest layer, but this traversal incurs high overhead. To avoid this, we store it in persistent memory using a persistent hash table called Cacheline-Conscious Extendible Hashing (CCEH) [33]. Since CCEH provides its own crash consistency, there exists a performance trade-off between insert operations and recovery efficiency. While the crash consistency mechanism introduces a slight insertion overhead, our preliminary results show that the cost of maintaining crash consistency in the persistent hash table is minimal.

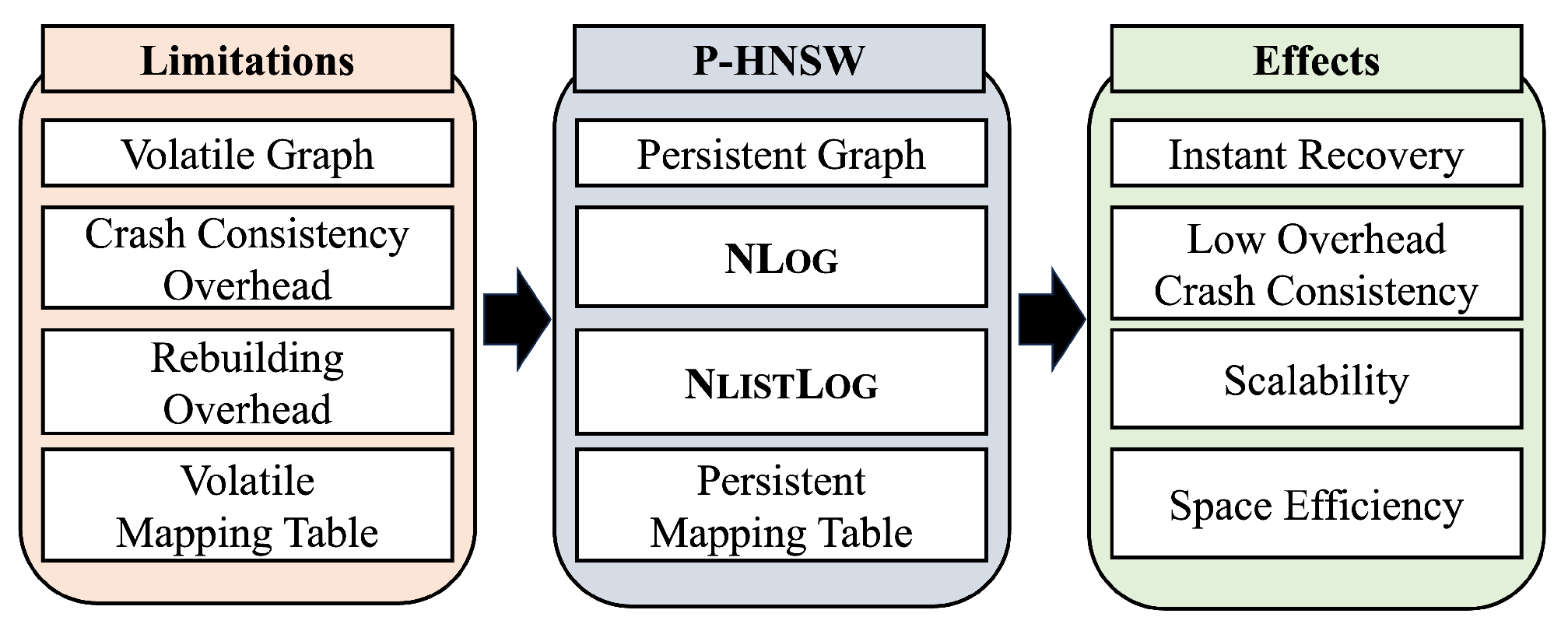
Figure 3 provides an overview of P-HNSW, summarizing the limitations of DRAM-based HNSW, our proposed contributions, and the resulting effects of the techniques.

4. Logging for P-HNSW

In this section, we explain how the logging mechanism works using NLog and NlistLog.

Storing HNSW in persistent memory enables the graph to be managed persistently. This allows the system to access the graph immediately after a system crash, without requiring lengthy reconstruction. However, if the system crashes during an operation, the data stored in persistent memory may remain in an inconsistent state. Such partial updates can be broadly categorized into structural inconsistency and semantic inconsistency.

Structural inconsistency refers to a logically contradictory state of the graph caused by interruptions during data updates, which can lead to critical failures in index operations. For example, if a system crash occurs during the insert operation, a node might exist only in an upper layer but not in lower layers, as HNSW inserts the node in a top-down manner. Additionally, a mismatch can occur between the actual number of neighbor nodes and the count recorded in the index.

Semantic inconsistency, on the other hand, indicates a state where the graph remains consistent, but some information is missing. Although the index may still operate normally, such inconsistencies can lead to a degradation in search performance if not resolved. For example, this can happen when only a subset of the total neighbor nodes is recorded, or when all out-edges are established but some corresponding in-edges are missing.

P-HNSW addresses such inconsistencies by using NLog and NlistLog to maintain the consistency of the graph in the event of system crashes. With these logs, incomplete parts of the graph can be recovered during the recovery process, thereby maintaining the accuracy and performance of the index even after a crash. Additionally, the logs in P-HNSW record only the unique node ID instead of the original vector data to improve space efficiency. Since the full vector data reside in Layer 0, which is stored permanently in persistent memory, storing only the node ID in the logs is sufficient.

The log spaces for NLog and NlistLog are pre-allocated in persistent memory with a fixed number of entries, which are managed in a circular manner. Each log entry maintains a state that indicates both its availability and the progress of the insertion. The log states are as follows: NONE, LOGGING, LOGGED, and N_COMPLETE. Log entries in NONE are available for use. When an insertion operation begins, P-HNSW atomically changes the state from NONE to LOGGING using a Compare_And_Swap (CAS) instruction to ensure safe selection in a multi-threaded environment. When P-HNSW changes the state of a log entry, it is persisted in the state using instructions such as clwb and sfence. Once the log entry is fully written and all its contents are persisted, its state is updated to LOGGED. The update of the log entry to the LOGGED state is also explicitly persisted to guarantee the crash consistency. Once the entire operation is completed and permanently recorded in the index, the log state is atomically reset to NONE and persisted, making the entry reusable. Specifically, N_COMPLETE is used only in the NLog, representing a state where the log entry has been successfully written and the new node has been connected to its out-edges. However, the in-edges from the neighbor nodes have not yet been established.

Note that P-HNSW employs the locking protocol inherited from the original HNSW. In addition, since the locks are stored in DRAM, P-HNSW reinitializes them when the recovery process begins.

4.1. Node Log (NLog)

The Node Log (NLog) is a redo log used to ensure the atomicity and crash consistency of new node insertions. Even if a crash occurs during the insert operation, the node and its connections can be fully and consistently recovered using the NLog. Each log entry corresponds to a single node insertion and contains neighbor information for all layers where the new node exists. The NLog plays a critical role in resolving semantic inconsistencies. For example, a system crash might occur when a node has been inserted only into the upper layer or when a new node has been connected to its neighbors (out-edges), but the corresponding back-links (in-edges) are missing. These situations indicate that the insert operation was not fully completed. To resolve such cases, NLog leverages its state to choose an appropriate recovery strategy, minimizing data loss and ensuring recovery that closely reflects the original graph.

Before an insert operation begins, P-HNSW first selects a log entry in the NONE state and updates its state to LOGGING. It then records the ID and level of the new node and searches for its neighbors in each layer to establish out-edges. The selected neighbor information is stored in the NLog, after which the state of the NLog entry is updated to LOGGED. From this point, even if a system crash occurs, the new node can be recovered using the recorded log. Once the neighbor information in the log has been persistently written to persistent memory, P-HNSW changes the NLog entry’s state to N_COMPLETE. This state indicates that the new node has been connected to its neighbors with out-edges across relevant layers. To complete the insertion, P-HNSW then establishes the in-edges. It traverses neighbor nodes in all layers and adds the new node to each neighbor’s neighbor list. If the neighbor list is already full, it creates a new list by combining the existing neighbors with the new node and removing the farthest one; otherwise, it simply adds the new node. After this step is fully persisted to the index, the entire insert operation is considered complete, and the NLog entry’s state is reset to NONE.

4.2. Neighbor List Log (NlistLog)

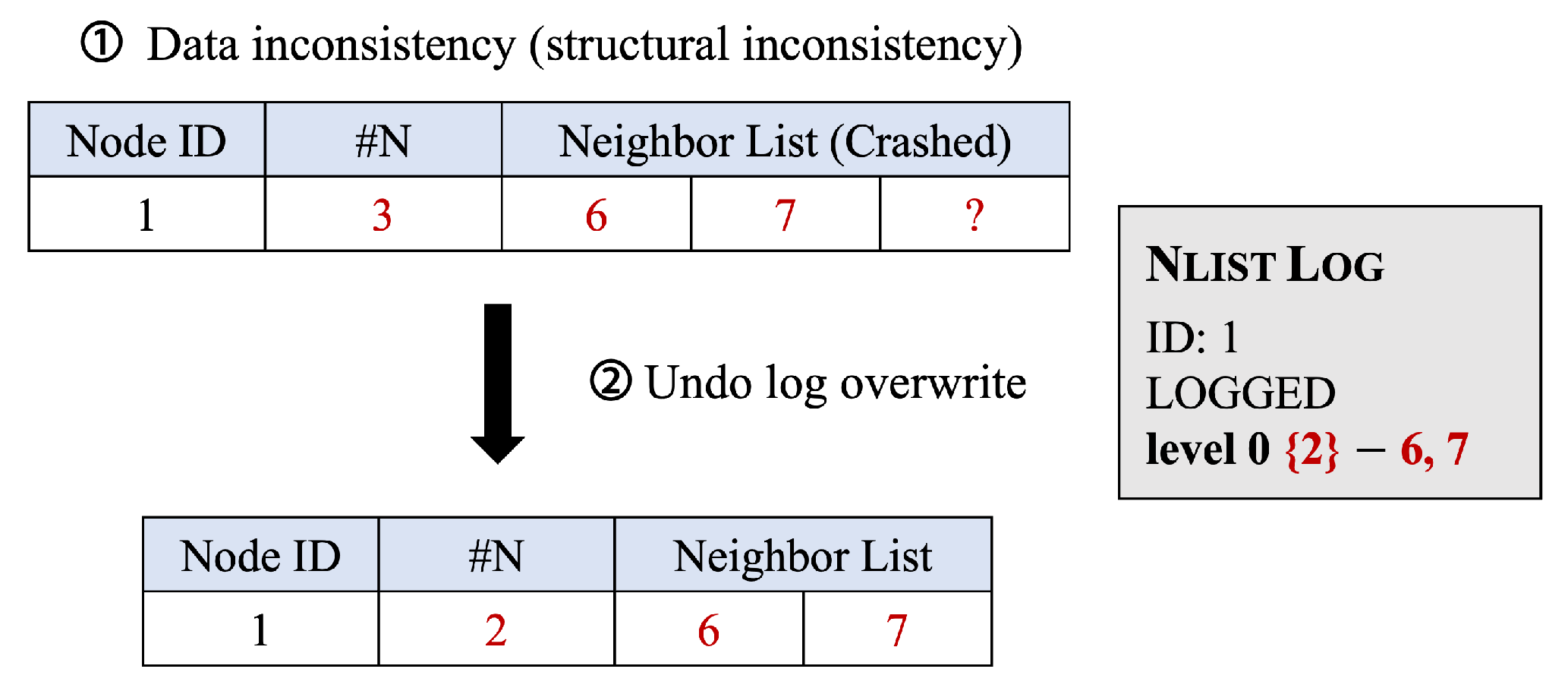
The Neighbor List Log (NlistLog) is an undo log designed to resolve structural inconsistencies when a system crash occurs during the modification of a node’s neighbor list. This log is primarily used when modifying the neighbor lists to establish a new node’s in-edges. Structural inconsistencies may arise if a system crash occurs after a neighbor count has been updated in persistent memory, but before the corresponding neighbor entries have been fully written. For example, if the number of neighbors is increased from 3 to 4, and the system crashes before the fourth neighbor is recorded, the system may attempt to access a non-existent entry, resulting in an out-of-bounds error.

To prevent this, P-HNSW selects a free log entry in the NONE state and atomically changes its state to LOGGING. It then records the original neighbor information and sets the state to LOGGED. By recording this information before the update, P-HNSW can restore the original state if the update is only partially completed. Once the updated neighbor information has been fully persisted, the log’s state is reset to NONE.

4.3. Logging Procedure During an Insert Operation

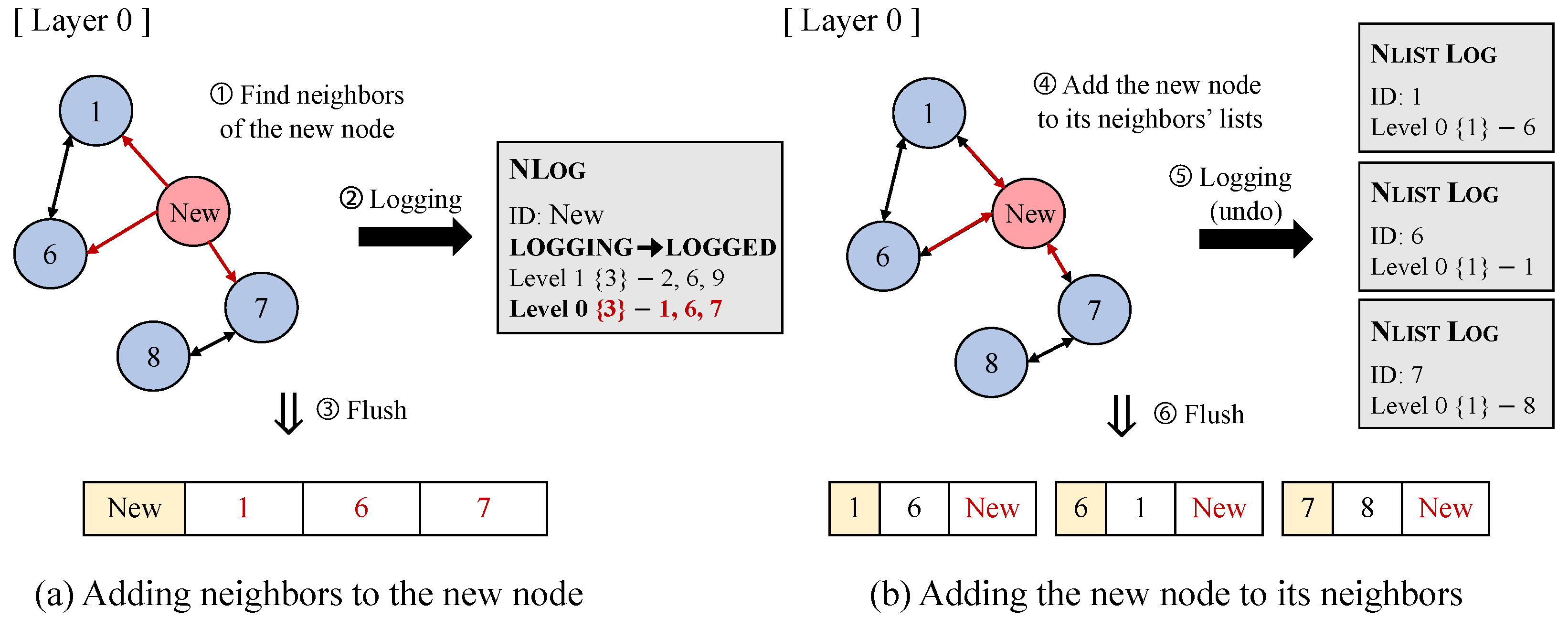
This section describes the logging procedure during insertion with the NLog and the NlistLog. The insertion process consists of two stages; Figure 4a depicts adding neighbors to the new node, and Figure 4b depicts adding the new node to its neighbors.

First, upon insertion, the new node is assigned a level and a node ID, and both the node ID and its vector data are stored in persistent memory. Next, P-HNSW searches for the appropriate insertion point by traversing from the highest layer down to the assigned level. At this point, P-HNSW finds a free NLog entry, atomically sets its state to LOGGING, and records the node ID and level in the log.

Then, starting from the assigned level down to layer 0, P-HNSW repeatedly searches for neighbors of the new node to connect out-edges (①). P-HNSW then stores the neighbor lists and the number of neighbors in the log entry (②). Once the log entry is fully written and persisted, its state is updated to LOGGED. From this point on, the new node becomes recoverable, so it is added to the label-to-node mapping table. Afterward, P-HNSW flushes the neighbor lists for each layer to the index (③) and sets the log state to N_COMPLETE, indicating that all out-edge connections have been successfully completed.

In the next stage, P-HNSW establishes the new node’s in-edges by adding it to the neighbor lists in each layer. During this process, the NlistLog is used to resolve neighbor data inconsistencies. To add the new node to its neighbors, each neighbor node generates an updated neighbor list by comparing the new node with its existing neighbors (④). Before the updated list is applied to the index, P-HNSW sets an NlistLog entry to LOGGING and records its old neighbor list (⑤). Once this logging is complete, the state of the log entry is updated to LOGGED. Afterward, P-HNSW flushes the new neighbor list (⑥), and the log entry’s state is reset to NONE to make it available for reuse. Once all neighbors across all layers complete this process, the NLog state is also reset to NONE, indicating that the entire insert operation has been atomically completed.

By leveraging these two types of logs, P-HNSW effectively minimizes data loss and ensures the crash consistency of the graph, even if a system crash occurs during an insert operation. In addition, by recording the state at each step, P-HNSW can quickly apply an appropriate recovery process.

4.4. Failure Model and Assumptions

In this section, we discuss the failure model and assumptions of P-HNSW. The crash consistency mechanism in P-HNSW relies on the 8-byte atomicity guarantee of the x86 architecture. Each log entry state is stored in an 8-byte memory region and updated using atomic 8-byte writes. In addition, because CPU caches are volatile, any cache line that has not been explicitly flushed may be lost after a crash. Based on these assumptions, P-HNSW ensures that recovery is always possible.

• NLog: Figure 5a illustrates the logging process of NLog in P-HNSW. When a crash occurs in the LOGGING state, the log entry is ignored during recovery, and thus, the graph structure remains unaffected. In the LOGGED state, all neighbor information of the new node has already been written and persisted in the log. Importantly, the neighbor information is persisted before the log entry state is changed to LOGGED, ensuring that the out-edges of the new node can be reconstructed during recovery. In the N_COMPLETE state, the out-edges have been fully persisted. To ensure that the in-edges are also correct, P-HNSW leverages NlistLog.
• NlistLog: Figure 5b illustrates the logging process of NlistLog. Similarly to NLog, a log entry is ignored during recovery if its state is LOGGING. When the state is LOGGED, the corresponding in-edges can be reconstructed during recovery.

5. Recovery

In this section, we explain how the recovery mechanism of P-HNSW works with NLog and NlistLog.

The recovery process is performed in two steps. First, structural inconsistencies that occur during updates to neighbor lists are restored using NlistLog. Next, the insertion operation of the new node is completed using NLog, addressing semantic inconsistencies. This recovery order is intended to prevent errors while reading neighbor information during the NLog-based recovery. By restoring neighbor information first, the subsequent NLog-based recovery can be performed more effectively.

During recovery, the method to be applied is determined by the state of each log entry. Log entries with LOGGING are skipped, as this indicates that the log was not fully written to the persistent memory. In this case, since the node has not yet been added to the graph, it can be safely ignored. For other states, the graph in persistent memory has likely been modified, and an appropriate recovery method is applied based on the log’s state to restore the graph’s consistency. Once the recovery process is complete, the log entry’s state is atomically reset to NONE, making it available for reuse.

5.1. Crash Before Storing the New Node’s Information in NLog

If the state of an NLog entry is LOGGING, it means that the log has not been fully written. In other words, the insert operation began but was interrupted before completion, leaving the log itself only partially recorded—corresponding to an interruption during step ② in Figure 4. The recovery process ignores the log’s insert operation and resets the state to NONE, since the operation has not affected other nodes, and the recorded information is insufficient for recovery. Even if some of the node’s information was partially written to the index, it is not accessible because the node has not yet been added to the label-to-node mapping table and will eventually be overwritten by a subsequently inserted node.

5.2. Crash During the Update of a New Node’s Out-Edges

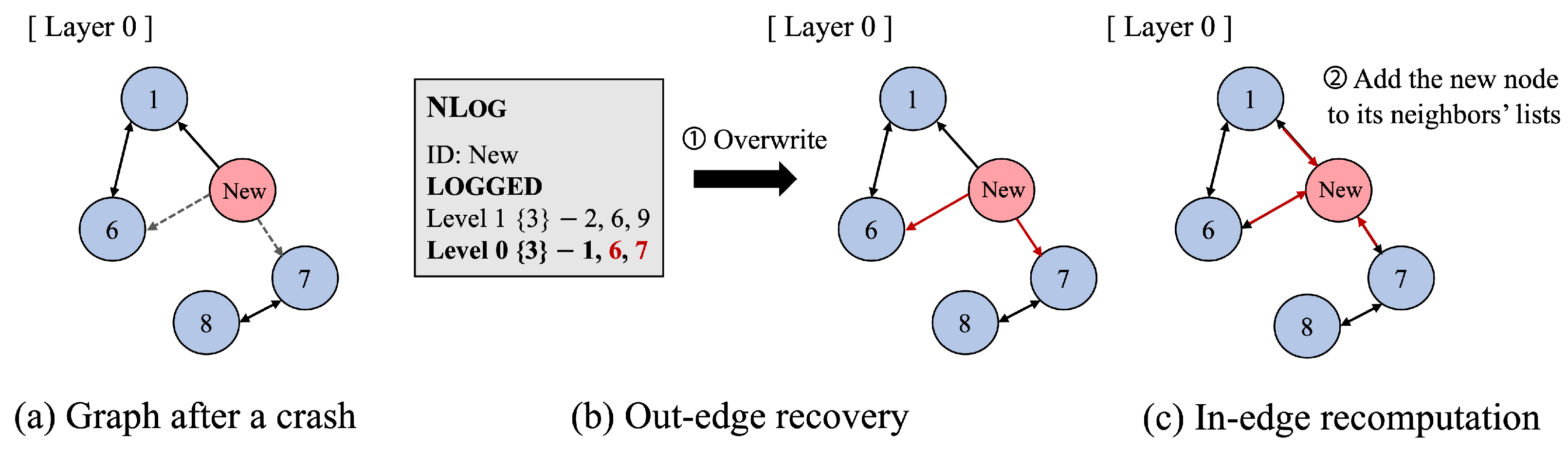
This case corresponds to an interruption during step ③ in Figure 4, where the process of writing neighbor information to the index is interrupted. At this point, its state is LOGGED, since the neighbor information has already been stored in NLog. Because the insertion of the new node was interrupted, the graph may have semantic inconsistencies (e.g., missing connection information and having no out-edges).

During the recovery process, P-HNSW must restore both the new node’s out-edge and in-edge connections. First, as shown in Figure 6b, P-HNSW persistently stores the neighbor information of each layer from the NLog to establish out-edges. This step overwrites any partial modifications to the index that occurred before the crash. Next, to connect the in-edges, P-HNSW traverses the neighbors and recomputes their neighbor lists to update the index (Figure 6c). This process follows the insertion algorithm. Once this process is complete, the log state is reset to NONE.

5.3. Crash During the Update of the New Node’s In-Edges

This case occurs when all out-edges of the new node have been stored in the index, but the process of updating the neighbor lists of those neighbors is interrupted. This corresponds to a crash during the step in Figure 4b. The state of the NLog is N_COMPLETE. In this case, the new node has out-edges but is missing in-edges, making it inaccessible during a search.

Before performing NLog recovery, NlistLog recovery must be conducted first. This is because if a neighbor’s neighbor information was being modified just before the crash, only a partial change causes a structural inconsistency, which may cause errors during NLog recovery. If the state of the NlistLog is LOGGED, it means that the updated neighbor information was not fully stored in the index, so P-HNSW overwrites the index with previous information recorded in the NlistLog, as illustrated in Figure 7. This process is solely for error prevention; since neighbor information will be recalculated during NLog recovery, it does not affect index accuracy. Once NlistLog recovery is complete, the insertion operation is finished by connecting the new node’s in-edges. P-HNSW traverses the relevant neighbor nodes and reconstructs their neighbor lists. After all updates are complete, the log state is reset to NONE.

5.4. Crash During Recovery

During recovery, both NLog and NlistLog are used to record the procedure and update their states according to the progress of the operation. Therefore, if a crash occurs during recovery, the same procedure can be applied again to complete the recovery successfully.

6. Evaluation

6.1. Experimental Environment

• System configuration: We conducted our experiments on a machine equipped with an Intel Xeon w5-3433 processor with 16 physical cores and 32 threads using the x86_64 architecture. The server was equipped with 256 GB of DDR5 DRAM and a PM9A1 NVMe Samsung 512 GB SSD.
• Dataset: We used the first 10 million vectors from the SIFT1B base set of the BigANN benchmark [34], which is commonly used for approximate nearest neighbor search. Each vector was 128-dimensional and represented as 4-byte floating-point numbers. For higher-dimensional evaluation, we used the GIST1M [35] dataset, which consists of 1 million 960-dimensional vectors. Similarly to SIFT, each vector was stored as 4-byte floating-point numbers.
• Software: The server ran the Linux 5.15 kernel. We built upon the C++ hnswlib [36] and implemented P-HNSW by porting it to persistent memory, integrating a logging mechanism, and modifying parts of the algorithm to support crash consistency. To exploit persistent memory, we used the PMDK (Persistent Memory Development Kit) library (libpmem 1.12.1). We emulated persistent memory by allocating a portion of DRAM via Linux’s memmap kernel parameter and the ndctl utility, configured in fsdax mode with DAX support. Since NVDIMM-N provides performance characteristics close to those of DRAM while offering persistence, DRAM-based emulation is widely adopted and faithfully represents the behavior of real NVDIMM-N devices. We implemented P-HNSW in C++ and compiled it using GCC 11.4.0 with the -Ofast optimization flag. We also report log usage statistics, where NLog and NlistLog occupied at most 51,200 bytes and 12,800 bytes, respectively. For index construction, we set the HNSW parameters to M = 16 and efConstruction = 100. We used the L2 (Euclidean) distance as the similarity metric.
• Baselines: For comparison, we used the original HNSW (the unmodified version of hnswlib) and implemented both a snapshot-enabled HNSW (HNSW_SNAP) and a WAL-enabled HNSW (HNSW_WAL). Note that both HNSW_SNAP and HNSW_WAL are implemented on an SSD rather than persistent memory. While this comparison is not entirely equivalent to our PM-based approach, we include them as baselines because no prior crash-consistent HNSW has been proposed for persistent memory. HNSW_SNAP periodically captures the full-index state and stores it to SSD using the saveIndex() function provided by hnswlib, while HNSW_WAL records node information during insertion. The logs are first buffered in memory and then flushed to SSD once the buffer is full. Note that the baselines in these experiments did not provide the same crash consistency guarantees as P-HNSW. Providing the same crash consistency guarantees would require invoking fdatasync() after every operation, but this approach incurs a prohibitive overhead and was, therefore, excluded from our experimental results.

6.2. Single-Thread Performance

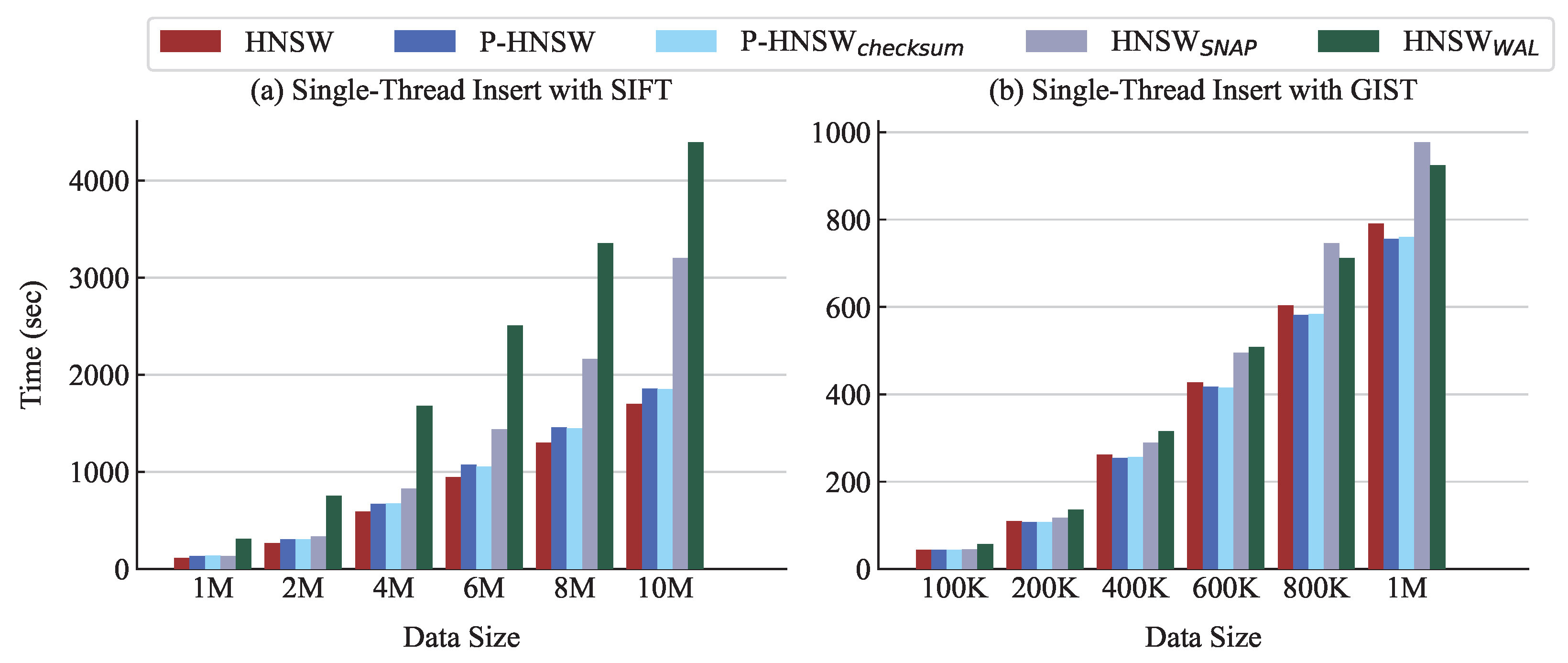
Figure 8 shows the single-thread insertion performance for varying data sizes. In particular, Figure 8a demonstrates that P-HNSW incurs only a slight overhead compared with HNSW across all data sizes. At 10M data points, P-HNSW takes only 1.1× the execution time of HNSW, whereas HNSW_SNAP takes nearly 1.9×. For reference, we also implement a checksum-added version, P-HNSW_CHECKSUM, whose performance is comparable with that of P-HNSW.

As the dataset size increases, the snapshot size also increases, leading to higher execution time. Consequently, HNSW_SNAP shows a dramatic increase in execution time due to the cost of saving the entire index. In contrast, P-HNSW records updates through fine-grained, per-operation logging, thereby avoiding the overhead of full-index writes. As a result, its insertion time increases only marginally relative to data size. HNSW_WAL incurs longer execution times than the other approaches, as it flushes data to the SSD more frequently. While the size of each log entry is smaller than that of HNSW_SNAP, the number of fdatasync calls is greater.

Similarly, Figure 8b shows that on the GIST dataset, P-HNSW and P-HNSW_CHECKSUM perform even faster than HNSW, while HNSW_SNAP incurs significantly larger overhead. The performance gain of P-HNSW primarily comes from decomposing the insert operation to guarantee crash consistency, which, in turn, optimizes the efficiency of vector computations and neighbor searches. Since GIST has 960 dimensions, the overhead of vector operations is substantial, and thus, these optimizations have an even greater impact, enabling P-HNSW to outperform HNSW. When the data size exceeds 800K, HNSW_SNAP becomes slower than HNSW_WAL. Because a snapshot captures the entire graph, its storage cost increases with the dimensionality. Moreover, since the snapshot also includes the vector data, it incurs higher latency than HNSW_WAL.

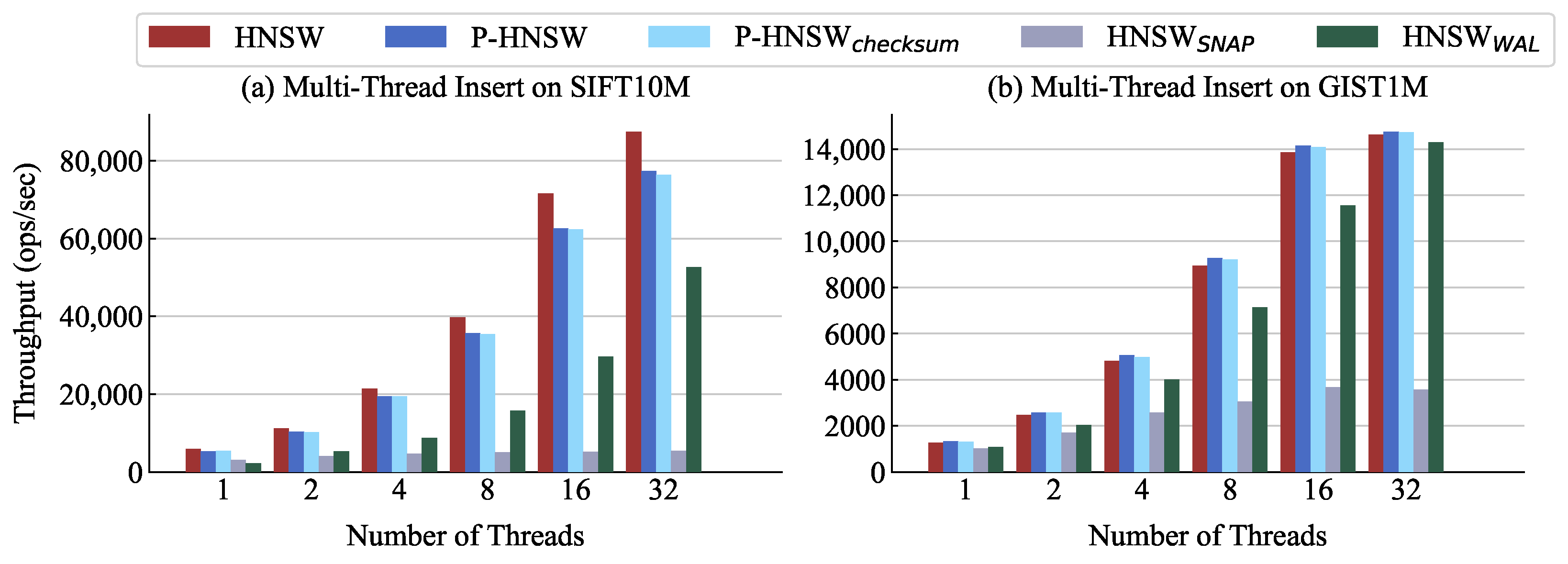
6.3. Multi-Thread Performance

Figure 9a shows the multi-thread insertion throughput on SIFT10M. As the number of threads increases, the original HNSW, P-HNSW, P-HNSW_CHECKSUM, and HNSW_WAL exhibit significant improvements in throughput, with the original HNSW achieving slightly higher performance. The throughput of the original HNSW increases by about 14.8× from 1 to 32 threads, while P-HNSW improves by about 14.4×. P-HNSW_CHECKSUM also shows similar performance to P-HNSW. In contrast, HNSW_SNAP shows limited performance gains with increasing threads, with the throughput improving by only 1.7× from 1 to 32 threads. This is because the full-index recording process is executed in a single thread to ensure data consistency, which introduces significant overhead. HNSW_WAL buffers logs and flushes them without blocking during logging, unlike HNSW_SNAP. As a result, it achieves better performance and good scalability, though its throughput remains lower than that of HNSW and P-HNSW.

As shown in Figure 9b, for the GIST dataset, the original HNSW, P-HNSW, P-HNSW_CHECKSUM, and HNSW_WAL demonstrate strong scalability. The throughput of the original HNSW increases by about 11.6× from 1 to 32 threads, while P-HNSW improves by about 11.1×. P-HNSW_CHECKSUM shows comparable performance to that of P-HNSW. Across all thread counts, however, P-HNSW achieves higher throughput than the original HNSW. As discussed in Section 6.2, this improvement results from our optimization for crash consistency. In contrast, HNSW_SNAP suffers from scalability limitations due to the high latency of SSD. Meanwhile, HNSW_WAL effectively benefits from multi-threading, showing strong scalability.

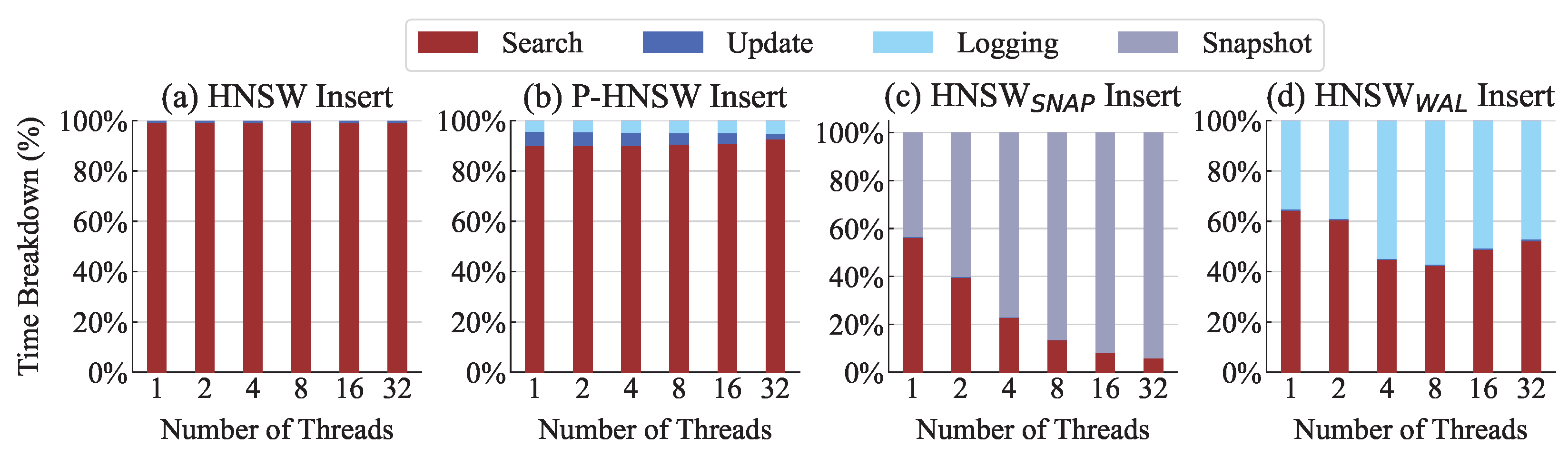
6.4. Performance Breakdown

Figure 10 shows the time distribution in a multi-thread environment. The Search includes the process of finding the insertion position and identifying the neighbors, while the Update involves modifying the index structure and persisting vector data. P-HNSW and HNSW_WAL have an additional Logging, which records data in the log. The Snapshot is the time required to store the entire index. Note that the crash consistency mechanisms in these experiments guarantee only the consistency of the index structure.

In Figure 10a, the original HNSW spends most of its time in the Search, showing a similar distribution across all thread counts, with the Update occupying less than 1%. In Figure 10b, P-HNSW spends slightly more time on the Update compared with the original HNSW, but this still accounts for only about 5.71% of the total execution time. The Logging accounts for only about 4.37%, indicating that its overhead has little impact on overall performance. P-HNSW slightly increases the proportion of Logging as the thread count grows from 4.37% at 1 thread to 5.2% at 32 threads. This is because it maintains a fixed number of log entries and reuses them, which leads to longer times spent searching for empty logs. P-HNSW shows a slight decrease in the Update proportion at 32 threads, as the Search no longer benefits from parallelization at that scale. In contrast, Figure 10c shows that the HNSW_SNAP spends most of its time on snapshot saving regardless of thread count. The snapshot portion grows from 43.42% at 1 thread to 94.1% at 32 threads. Since this snapshot saving is performed in a single thread to ensure data consistency, there is almost no performance gain from parallel processing. Consequently, even in multi-thread environments, the HNSW_SNAP exhibits bottlenecks, whereas P-HNSW provides more stable scalability. As shown in Figure 10d, HNSW_WAL demonstrates better scalability under multi-threaded workloads than HNSW_SNAP. When the buffer becomes full, one thread is responsible for creating a copy of the buffer and flushing it to SSD, while the remaining threads continue to insert using the original buffer.

Figure 11 shows the performance breakdown of insert operations on the high-dimensional GIST dataset. Because GIST vectors are 960-dimensional, the proportion of time spent on the Search is higher than in SIFT. In Figure 11b, even as the number of threads grows, the logging overhead in P-HNSW remains nearly constant, indicating that the mechanism is lightweight and scales well to high-dimensional workloads. Specifically, with 1 thread, logging accounts for only about 0.7% of total execution time, and with 32 threads, it remains nearly the same at 0.6%. In contrast, as shown in Figure 11c, HNSW_SNAP exhibits the same bottleneck behavior as in SIFT. The Snapshot dominates the execution time as the thread count increases, growing from about 19.5% at 1 thread to over 75.6% at 32 threads. For HNSW_WAL, the time spent on Search is also large, and thus, the proportion of Logging is small.

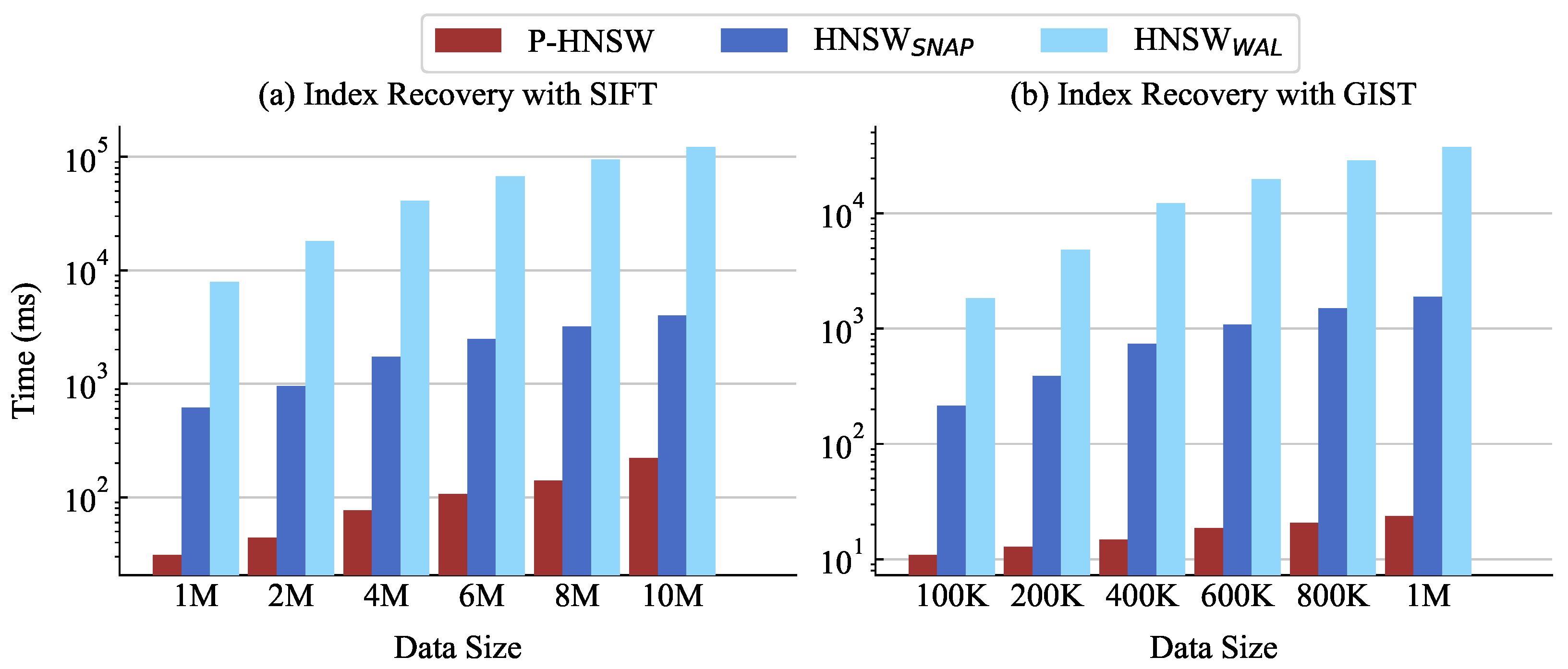
6.5. Recovery Time

Figure 12 compares the recovery time of the crash consistency mechanism for different data sizes. To evaluate the recovery performance, we measure the reconstruction time of the indexes after program termination. HNSW_SNAP reads the entire stored index from storage and loads it into memory, causing the recovery time to increase linearly with the dataset size. As shown in Figure 12a, at 10M data points, HNSW_SNAP is about 18× slower than P-HNSW, and even at 1M, it is approximately 19.7× slower. For 10M data points, the recovery time is over 4 seconds, resulting in severe delays in large-scale datasets. In contrast, P-HNSW stores all indexes and information in persistent memory, enabling direct access upon restart. As a result, it only needs to sequentially read two types of logs and perform the recovery process, allowing for significantly faster recovery times.

We also present the recovery time of the indexes for the GIST dataset across different data sizes, as shown in Figure 12b. At 100K data points, HNSW_SNAP is about 19.5× slower than P-HNSW, and the gap becomes nearly 80× at 1M data points. Because GIST has much higher dimensionality than SIFT, HNSW_SNAP requires 2.76× more time for recovery in GIST1M (1880.99 ms) compared with SIFT1M (681.367 ms). In contrast, in P-HNSW, the recovery times are similar, with SIFT1M taking 30.19 ms and GIST1M taking 23.6 ms. This is because all data in P-HNSW are already stored in persistent memory, making the recovery time largely independent of dataset dimensionality.

HNSW_WAL requires replaying each log entry to reconstruct the graph, making it considerably slower than HNSW_SNAP. While the logs in HNSW_WAL are smaller and more space-efficient, the overhead of index reconstruction results in long recovery times across both datasets.

7. Related Works

7.1. Vector Database

Vector databases are optimized for processing high-dimensional vector data. Unlike traditional relational databases, they are suitable for handling unstructured data, such as images, documents, and videos. They also support the retrieval of similar data based on a query vector.

Milvus [22] is a vector database that leverages graph- and quantization-based indexes. It utilizes hardware accelerators such as GPUs to improve search performance and stores data in a distributed manner across multiple nodes for large-scale data management. Qdrant [37] and Chroma [38] are open-source vector databases based on HNSW, and they are integrated with frameworks such as LangChain [39] to facilitate RAG service deployment. Vespa [40] employs a hybrid index combining HNSW and an inverted file index (IVF) to support both keyword search and filtered search. Meanwhile, Pinecone [41] is a vector database offered as Software-as-a-Service (SaaS), which leverages an independently implemented index to manage data.

Generally, vector databases utilize SSD to store large-scale vector data and employ methods to minimize performance degradation caused by the high latency of SSD. Therefore, utilizing persistent memory can provide DRAM-like performance for managing large-scale vector data and enhance the vector database performance.

7.2. Persistent Indexes

Indexes are optimized for storage devices. Existing persistent indexes aim to eliminate the additional overhead of the crash consistency mechanism. They leverage atomic instructions such as CAS, FAA (Fetch-And-Add), and 8-byte atomic writes supported by the x86 architecture. There have been several previous studies on persistent tree structures for persistent memory. ZBTree [42] is an index that stores inner nodes and compacted leaf nodes on DRAM and stores per-core data segments with a PLeaf-list. PACTree [43] stores the entire index in persistent memory and separates the search layer from the data layer to mitigate the limited bandwidth of Intel DCPMM. ROART [44] presents a persistent version of the Adaptive Radix Tree (ART) with merged leaf nodes to enable efficient range queries.

Persistent hash tables have also been proposed. CCEH [33] is an extensible hash table that introduces an additional level called a segment. DASH [45] presents extendable hashing and linear hashing schemes designed to address the limited bandwidth of persistent memory. HALO [46] proposes a persistent hash index design that uses DRAM for hash tables while storing pages and snapshots in persistent memory.

A number of persistent indexes have been proposed. However, to the best of our knowledge, there are no persistent vector indexes that have been introduced. Previous studies are limited to traditional indexes such as B⁺-tree and hash tables that are optimized for OLTP workloads.

8. Conclusions

In this paper, we present P-HNSW, a crash-consistent variant of HNSW on persistent memory. P-HNSW introduces a lightweight logging mechanism consisting of two logs, NLog and NlistLog. We describe how these logs guarantee crash consistency during insert operations and enable reliable recovery after system crashes. Our evaluation demonstrates that P-HNSW incurs negligible logging overhead and outperforms SSD-based recovery mechanisms, highlighting the potential of persistent memory for building reliable and efficient vector indexes.

Although our work shows promising results, it also has limitations. First, our approach focuses on HNSW, and its applicability to other ANN indexes, such as DiskANN or Annoy, remains an open question. Second, our evaluation was conducted on x86-based platforms with emulated persistent memory, so the behavior of P-HNSW on other hardware environments, such as ARM-based processors or eADR-enabled systems, may differ. These limitations open up opportunities for future research.

In particular, we plan to extend our crash consistency techniques to a broader range of ANN indexes and evaluate them on diverse persistent memory hardware platforms.