Probabilistic Analysis of Wedge Failures and Stability of Underground Workings with Combined Support Under Thrust Faulting Conditions
Abstract
1. Introduction
2. Materials and Methods
2.1. Observations of Rock Pressure Manifestations and Maintenance of Excavation Stability
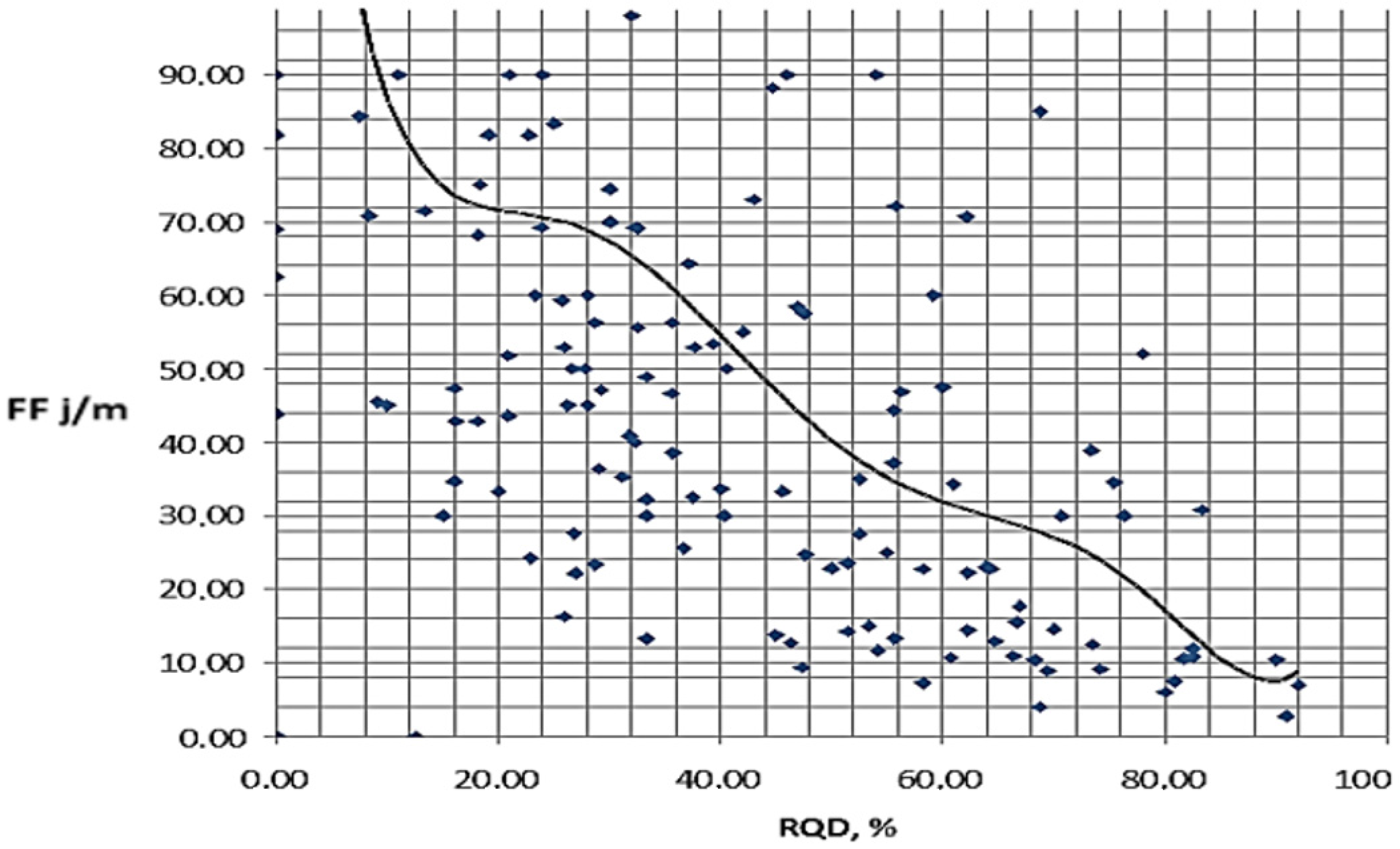
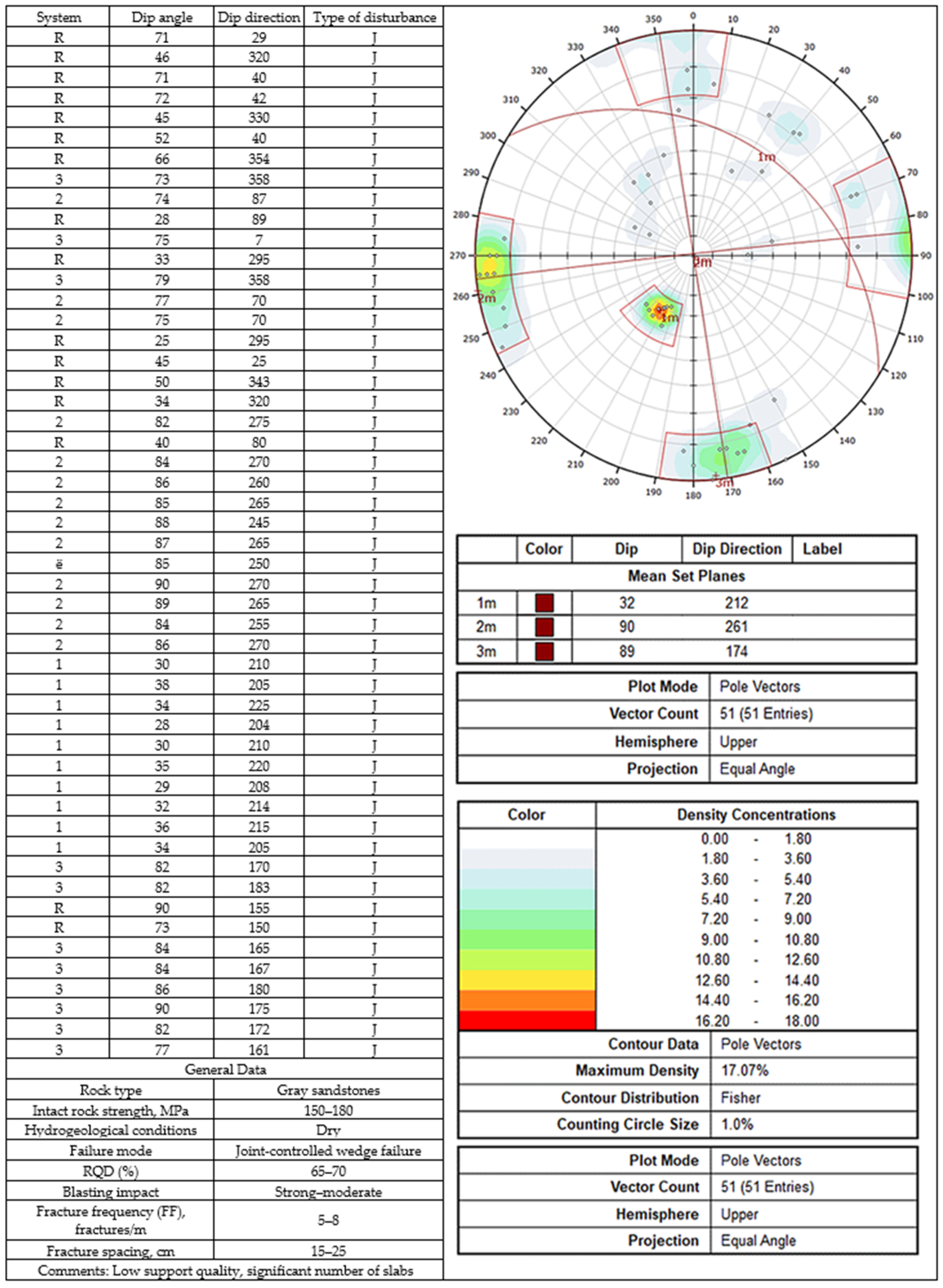
2.2. Methods for Assessing Rock Mass Fracturing and Determining the Factor of Safety of Wedges
2.3. Intelligent Monitoring (Concept and Integration with Modeling)
3. Results
3.1. Assessment of Mining–Geological Conditions and Rock Mass Fracturing
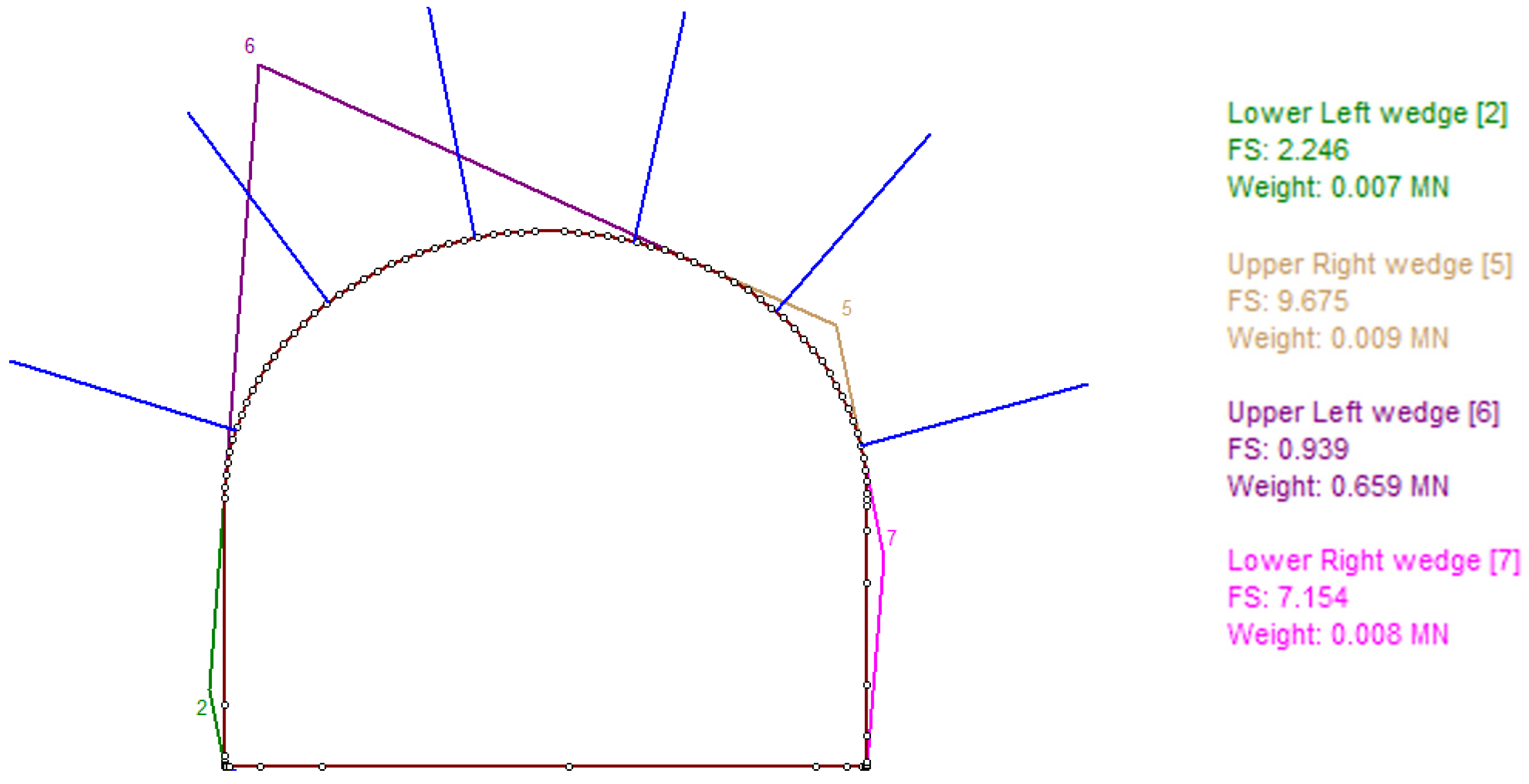
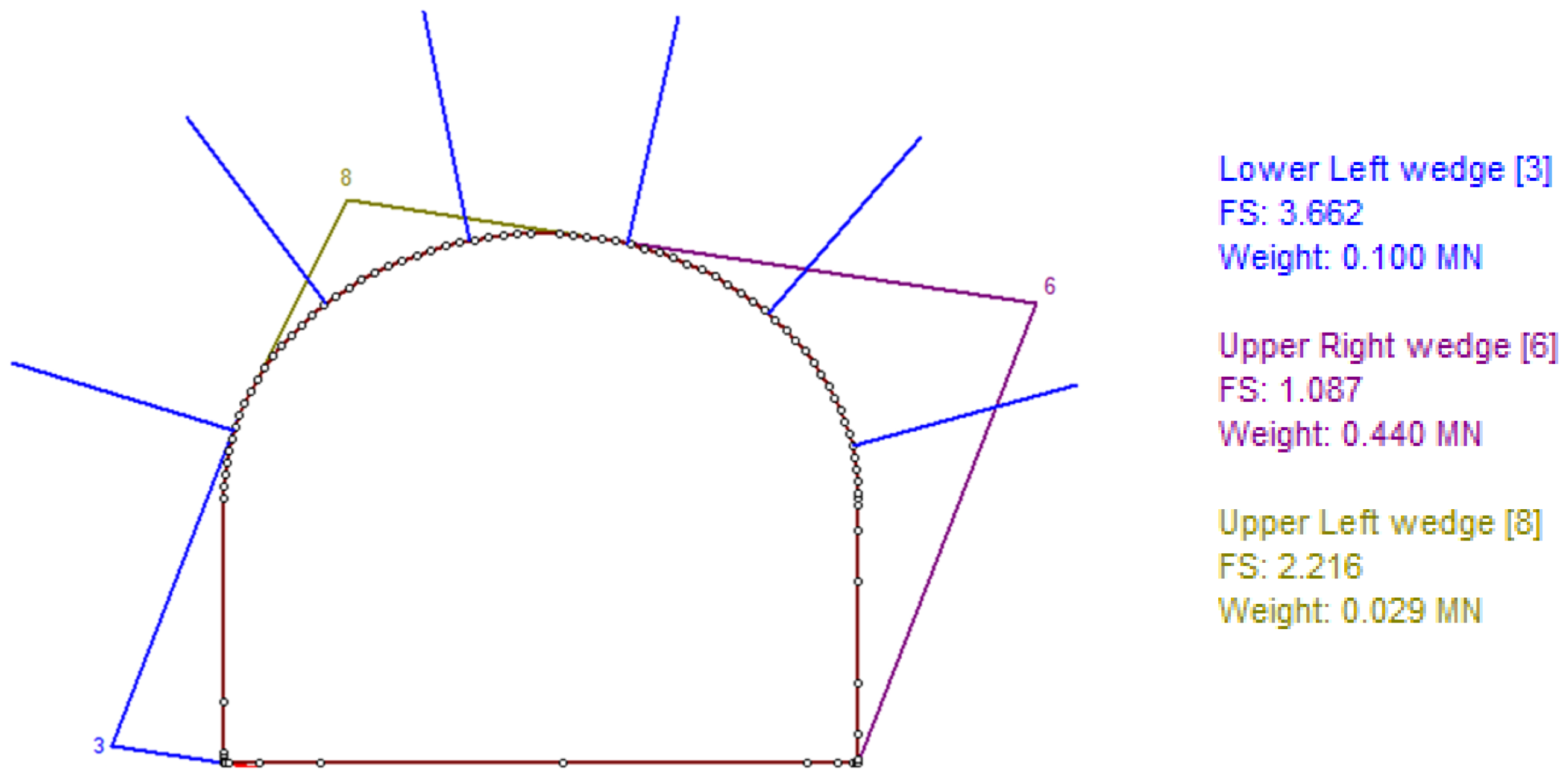
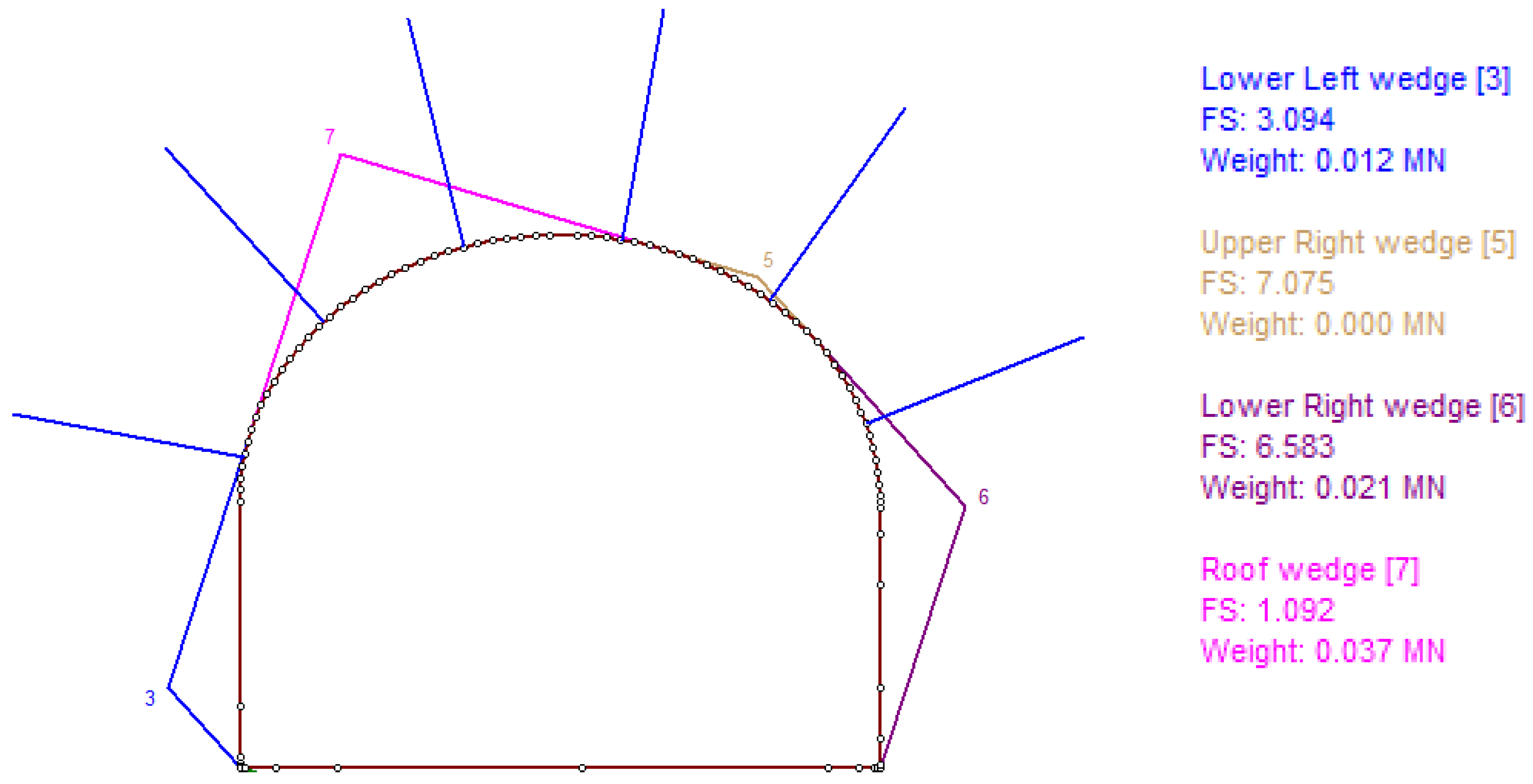
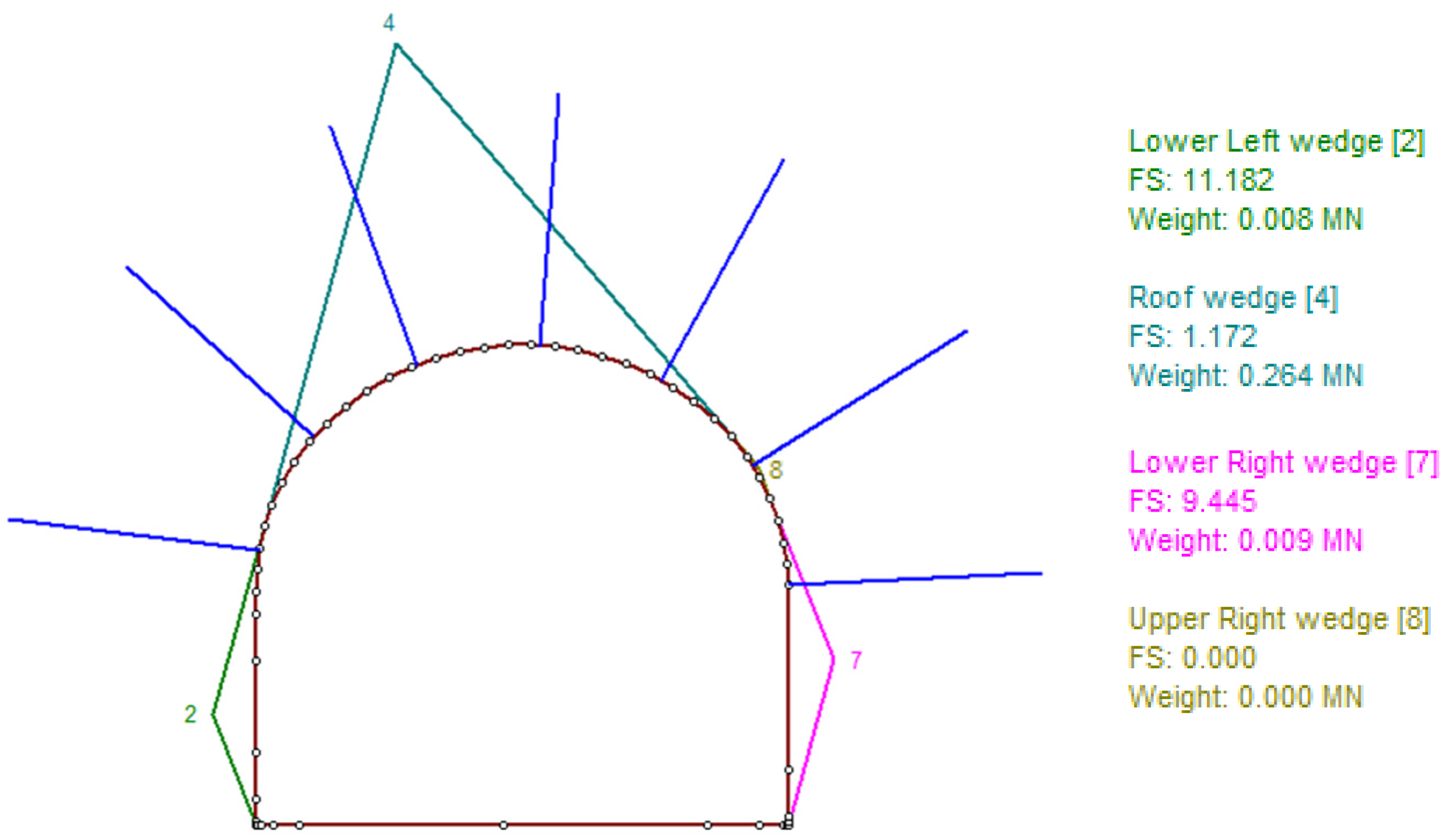
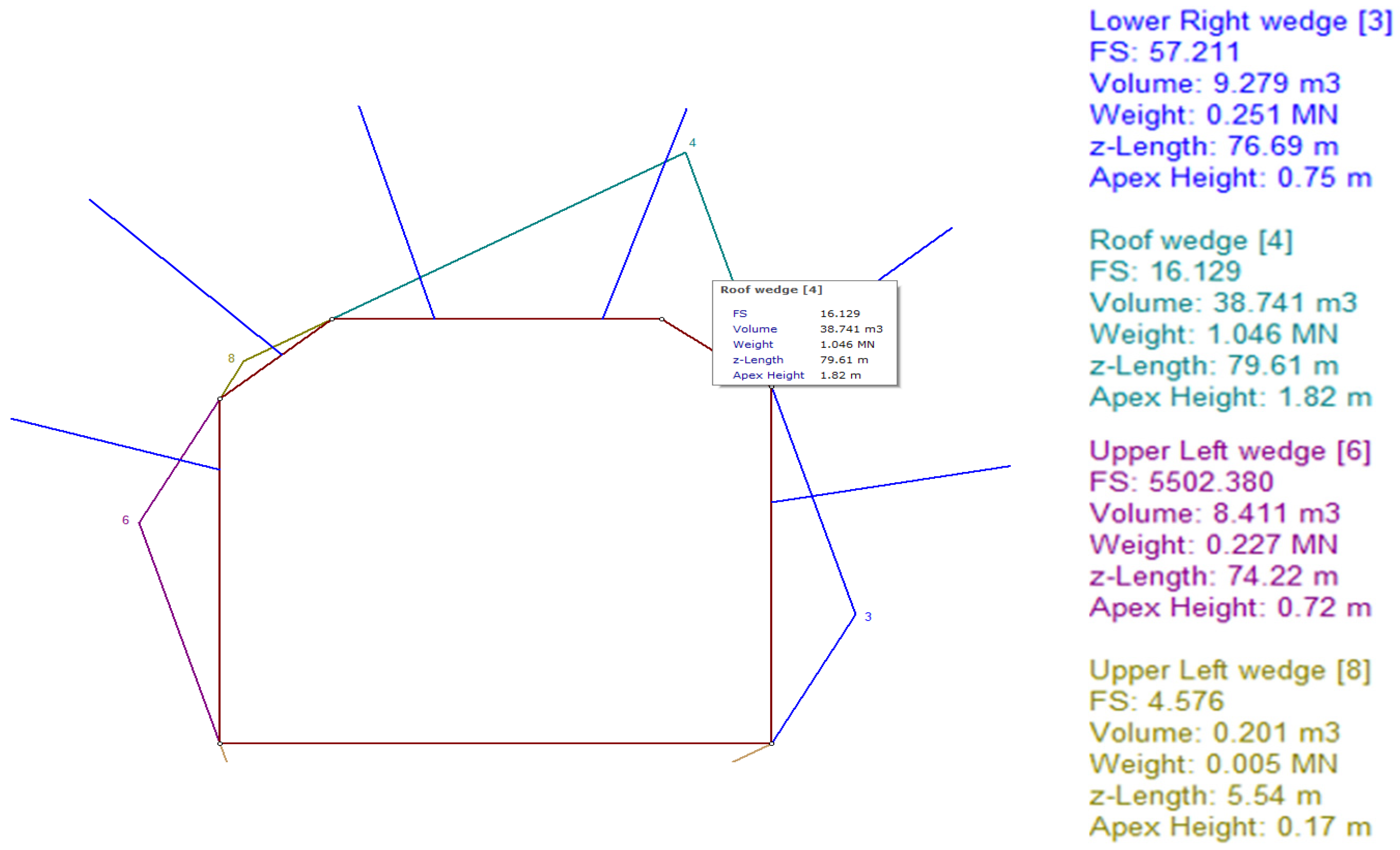
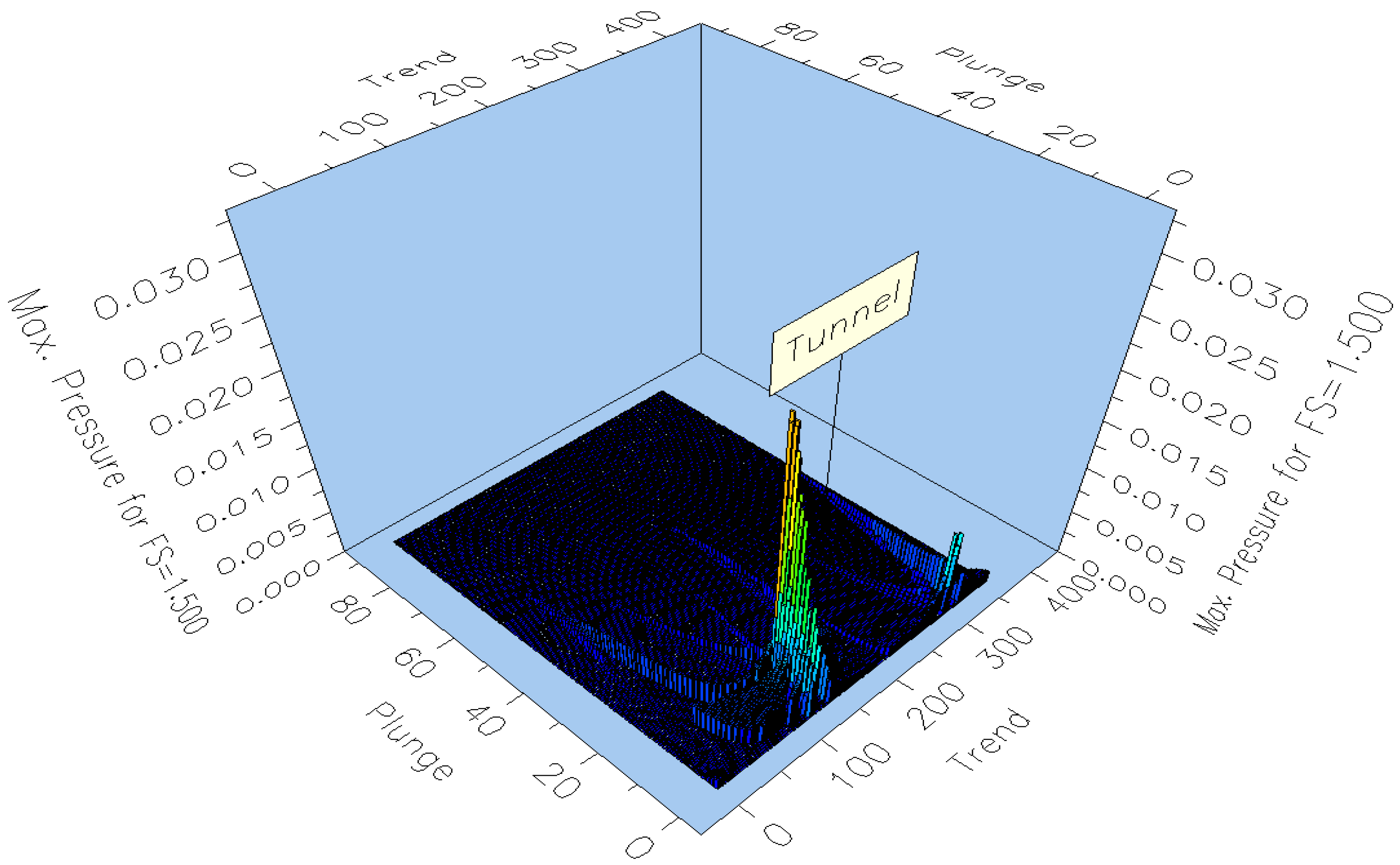
3.2. Probabilistic Analysis of Wedge Stability in the Rock Mass
4. Discussion
4.1. Comparison with Existing Methods
4.2. Advantages of the Proposed Approach
4.3. Limitations and Model Sensitivity
4.4. Multi-Field Sensitivity
4.5. Guidelines for Support and Orientation (Design-Ready)
4.6. Practical Value and Prospects for Development
5. Conclusions
- At the deposit, a thrust-faulting regime was established (σ1 > σ2 > σv). With increasing depth from 100 to 310 m, stress components also increase (σ1: 6 → 18 MPa; σ2: 4 → 11 MPa; σv: 2.7 → 8.3 MPa). The rock mass is characterized by RQD = 65–70%, FF = 5–8, and fracture spacing of 15–25 cm, indicating medium rock quality and a predisposition to wedge failures.
- Probabilistic analysis showed that with bolt-only support, FS = 0.939–1.172 (< 1.2), whereas combined support (bolts + shotcrete ≥ 0.05 m) increases FS to 2.389–3.461, thereby ensuring normative stability of the surrounding rock mass. Under the studied conditions, the combined support scheme is therefore recommended.
- Critical excavation orientations correspond to azimuths of 120° and 141°, where wedges of maximum size are formed. A “safe orientation window” of 70° ± 10° was identified, within which wedge volumes are minimal.
- The obtained quantitative benchmarks (stress parameters, fracture indices, FS ranges, and azimuth ranges), together with the framework integrating results with intelligent monitoring, can be applied to practical support design and excavation alignment aimed at reducing the risk of wedge failures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- LLP R&D Center “GeoMark”. Instruktsiya po Krepleniyu Gornykh Vyrabotok na Rudnike “Zhomart”; GeoMark: Zhezkazgan, Kazakhstan, 2020; p. 149. (In Russian) [Google Scholar]
- Industrial Safety Rules for Hazardous Facilities Conducting Mining and Geological Exploration; Ministry for Investment and Development of the Republic of Kazakhstan: Astana, Kazakhstan, 2015; 147p. (In Russian)
- Makarov, A.B. Prakticheskaya Geomekhanika: Posobie dlya Gornykh Inzhenerov; Gornaya Kniga: Moscow, Russia, 2006; p. 391. (In Russian) [Google Scholar]
- Shaposhnik, Y.N.; Neverov, S.A.; Neverov, A.A.; Konurin, A.I. Reitingovaya otsenka massiva gornykh porod Veduginskogo mestorozhdeniya. Fundam. Appl. Min. Sci. 2020, 7, 202–208. (In Russian) [Google Scholar] [CrossRef]
- Onuprienko, V.S.; Eremenko, A.A.; Shaposhnik, Y.N.; Kopytov, A.I. Vybor tipov i parametrov krepei v usloviyakh podzemnoi otrabotki apatit-nefelinovykh. Bull. Kuzbass State Tech. Univ. 2023, 2, 56–70. (In Russian) [Google Scholar] [CrossRef]
- Bjureland, W. Reliability aspects of rock tunnel design with the observational method. Int. J. Rock Mech. Min. Sci. 2017, 98, 102–110. [Google Scholar] [CrossRef]
- Bjureland, W.; Johansson, F.; Sjölander, A.; Spross, J.; Larsson, S. Probability distributions of shotcrete parameters for reliability-based analyses of rock tunnel support. Tunn. Undergr. Space Technol. 2019, 87, 15–26. [Google Scholar] [CrossRef]
- Spross, J.; Gasch, T.; Johansson, F. Implementation of reliability-based thresholds to excavation of shotcrete-supported rock tunnels. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2023, 17, 361–375. [Google Scholar] [CrossRef]
- Do, D.P.; Guo, X.; Dias, D. Probabilistic stability analysis of deep rock tunnel excavated by mechanized tunneling considering anisotropic initial stresses. Appl. Sci. 2022, 12, 7479. [Google Scholar] [CrossRef]
- Villaescusa, E.; Thompson, A.; Windsor, C. Probabilistic estimate of rock mass static and dynamic demands for underground excavation stabilisation. J. Rock Mech. Geotech. Eng. 2019, 11, 481–493. [Google Scholar] [CrossRef]
- Tiwari, G.; Pandit, B.; Latha, G.M.; Babu, G.L.S. Probabilistic analysis of tunnels considering uncertainty in peak and post-peak strength parameters. Tunn. Undergr. Space Technol. 2017, 70, 375–387. [Google Scholar] [CrossRef]
- Qin, W.; Chen, E.J.; Wang, F.; Zhou, C. Data-driven models in reliability analysis for tunnel structure: A systematic review. Tunn. Undergr. Space Technol. 2024, 152, 105928. [Google Scholar] [CrossRef]
- Li, M.; Wang, G.; Ma, Z.; Kang, F.; Li, J. Reliability analysis of tunnels considering the rock-support interaction using a metamodel-based reliability method. Comput. Geotech. 2024, 170, 106325. [Google Scholar] [CrossRef]
- Low, B.K.; Boon, C.W. Probability-based design of reinforced rock slopes using coupled FORM and Monte Carlo methods. Rock Mech. Rock Eng. 2024, 57, 1195–1217. [Google Scholar] [CrossRef]
- Zhou, M.; Jiang, A.; Zhou, X.; Qiu, H.; Jiang, W. Probabilistic analysis of tunnel roof deflection under sequential excavation using ANN-based Monte Carlo simulation and simplified reliability approach. J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 2021, 7, 04021030. [Google Scholar] [CrossRef]
- Wu, B.; Zhu, R.; Wang, W.; Zeng, J.; Liu, C. Quantitative analysis of construction risks in shallowly buried biased tunnel portal section. Sci. Rep. 2024, 14, 21974. [Google Scholar] [CrossRef]
- Terrón-Almenara, J.; Skretting, E.; Holter, K.G.; Høien, A.H. Design of rock support in hard and layered rock masses using a hybrid method: A study based on the construction of the New Skarvberg Tunnel, Norway. Rock Mech. Rock Eng. 2024, 57, 10491–10532. [Google Scholar] [CrossRef]
- Narimani, S.; Davarpanah, S.M.; Bar, N.; Vásárhelyi, B. Analyzing drill core logging using Rock Quality Designation—60 years’ experience from modifications to applications. Appl. Sci. 2025, 15, 1309. [Google Scholar] [CrossRef]
- Salmi, E.F.; Sellers, E.J.; Esmaieli, K.; Evans, A.M. A review of the methods to incorporate the geological and geotechnical characteristics of rock masses in blastability assessments for selective blast design. Eng. Geol. 2021, 281, 105970. [Google Scholar] [CrossRef]
- Morawietz, S.; Heidbach, O.; Reiter, K.; Ziegler, M.; Rajabi, M.; Zimmermann, G.; Müller, B.; Tingay, M. An open-access stress magnitude database for Germany and adjacent regions. Geotherm. Energy 2020, 8, 25. [Google Scholar] [CrossRef]
- Ferrill, D.A.; Smart, K.J.; Cawood, A.J.; Morris, A.P. The fold-thrust belt stress cycle: Superposition of normal, strike-slip, and thrust faulting deformation regimes. J. Struct. Geol. 2021, 148, 104362. [Google Scholar] [CrossRef]
- Escuder-Viruete, J.; Fernández, F.J.; Pérez Valera, F.; McDermott, F. Active tectonics, Quaternary stress regime evolution and seismotectonic faults in southern central Hispaniola: Implications for the quantitative seismic hazard assessment. Geochem. Geophys. Geosyst. 2024, 25, e2023GC011003. [Google Scholar] [CrossRef]
- Berisavljević, Z.; Bajić, D.; Jovičić, V. Development and application of methodology for quantification of overbreaks in hard rock tunnel construction. Appl. Sci. 2023, 13, 1379. [Google Scholar] [CrossRef]
- Hekmatnejad, A.; Crespin, B.; Vallejos, J.A.; Opazo, A.; Adoko, A.C. A hybrid predictive model of unstable rock blocks around a tunnel based on estimated volumetric fracture intensity and circular variance from borehole data sets. Tunn. Undergr. Space Technol. 2021, 111, 103865. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, S.; Zhang, M.; Wu, B. Identification of key blocks considering finiteness of discontinuities in tunnel engineering. Front. Earth Sci. 2022, 10, 794936. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, M.; Wang, S.; Zha, W. A parametric method for maximum key block on tunnels excavation and its verification. Tunn. Undergr. Space Technol. 2025, 163, 106608. [Google Scholar] [CrossRef]
- Ma, G.; Li, M.; Wang, H.; Chen, Y. Equivalent discrete fracture network method for numerical estimation of deformability in complexly fractured rock masses. Eng. Geol. 2020, 277, 105784. [Google Scholar] [CrossRef]
- Wang, H.; Wang, W.; Yang, J.; Wu, Y. A deterministic–stochastic DFN–DEM numerical modeling method with application in stability of fractured rock slope in BDa hydropower station. Eng. Geol. 2025, 353, 108111. [Google Scholar] [CrossRef]
- Wang, D.-J.; Zhang, Y.-H.; Cheng, Z.-Y.; Wang, Y.-L. Probabilistic failure assessment of bolt-stabilized pro-dip slopes considering shear effect. Sci. Rep. 2025, 15, 18288. [Google Scholar] [CrossRef]
- Hamdi, P.; Ufrecht, S.; Achtziger-Zupančič, P.; Bröker, K.; Ma, X.; Amann, F. Understanding the regional stress in active tectonic regime using 3D numerical modeling: Case study of BedrettoLab, Switzerland. Rock Mech. Rock Eng. 2025, 1–20. [Google Scholar] [CrossRef]
- Rocscience Inc. Dips, Version 8.0; Rocscience Inc.: Toronto, ON, Canada, 2022. Available online: https://www.rocscience.com/software/dips (accessed on 15 August 2025).
- Rocscience Inc. UnWedge, Version 6.0; Rocscience Inc.: Toronto, ON, Canada, 2022. Available online: https://www.rocscience.com/software/unwedge (accessed on 15 August 2025).
- Expert PRO LLC. Razrabotka Resursosberegayushchei Tekhnologii Krepleniya Gorno-Podgotovitel’nykh Vyrabotok v Geomekhanicheskikh Usloviyakh Mestorozhdeniya “Zhilandy”: Otchet NIR (Promezhutochnyi Etap III); Expert PRO LLC: Ust’-Kamenogorsk, Kazakhstan, 2023; p. 321. (In Russian) [Google Scholar]
- International Society for Rock Mechanics (ISRM). Suggested Methods for the Quantitative Description of Discontinuities in Rock Masses. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1978, 15, 319–368. [Google Scholar] [CrossRef]
- Priest, S.D.; Hudson, J.A. Estimation of Discontinuity Spacing and Trace Length Using Scanline Surveys. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1981, 18, 183–197. [Google Scholar] [CrossRef]
- Rocscience Inc. Dips, Version 8.029; Rocscience Inc.: Toronto, ON, Canada, 2025. Available online: https://www.rocscience.com/software/dips (accessed on 15 August 2025).
- Goodman, R.E.; Shi, G. Block Theory and Its Application to Rock Engineering; Prentice-Hall: Englewood Cliffs, NJ, USA, 1985. [Google Scholar]






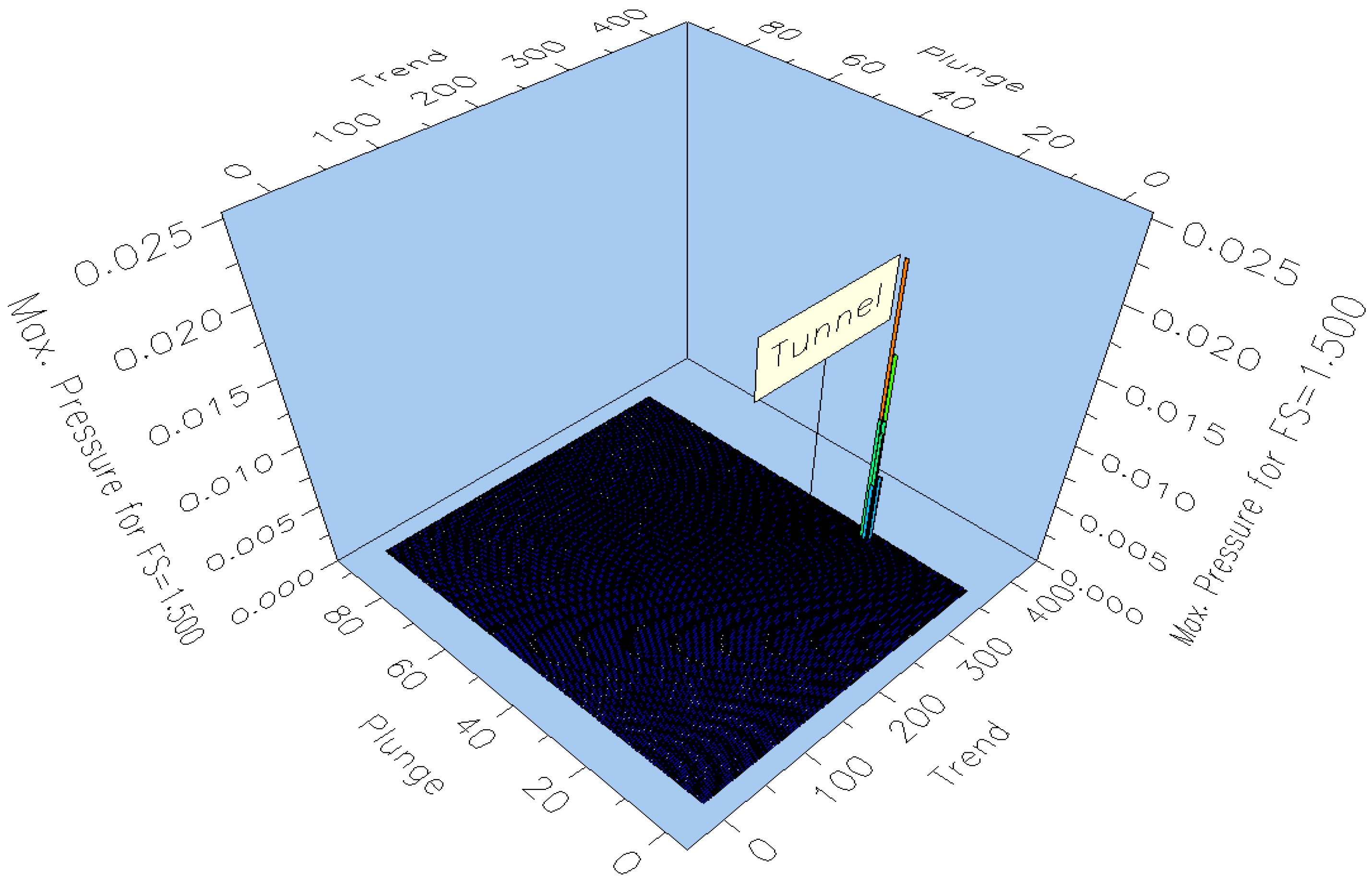
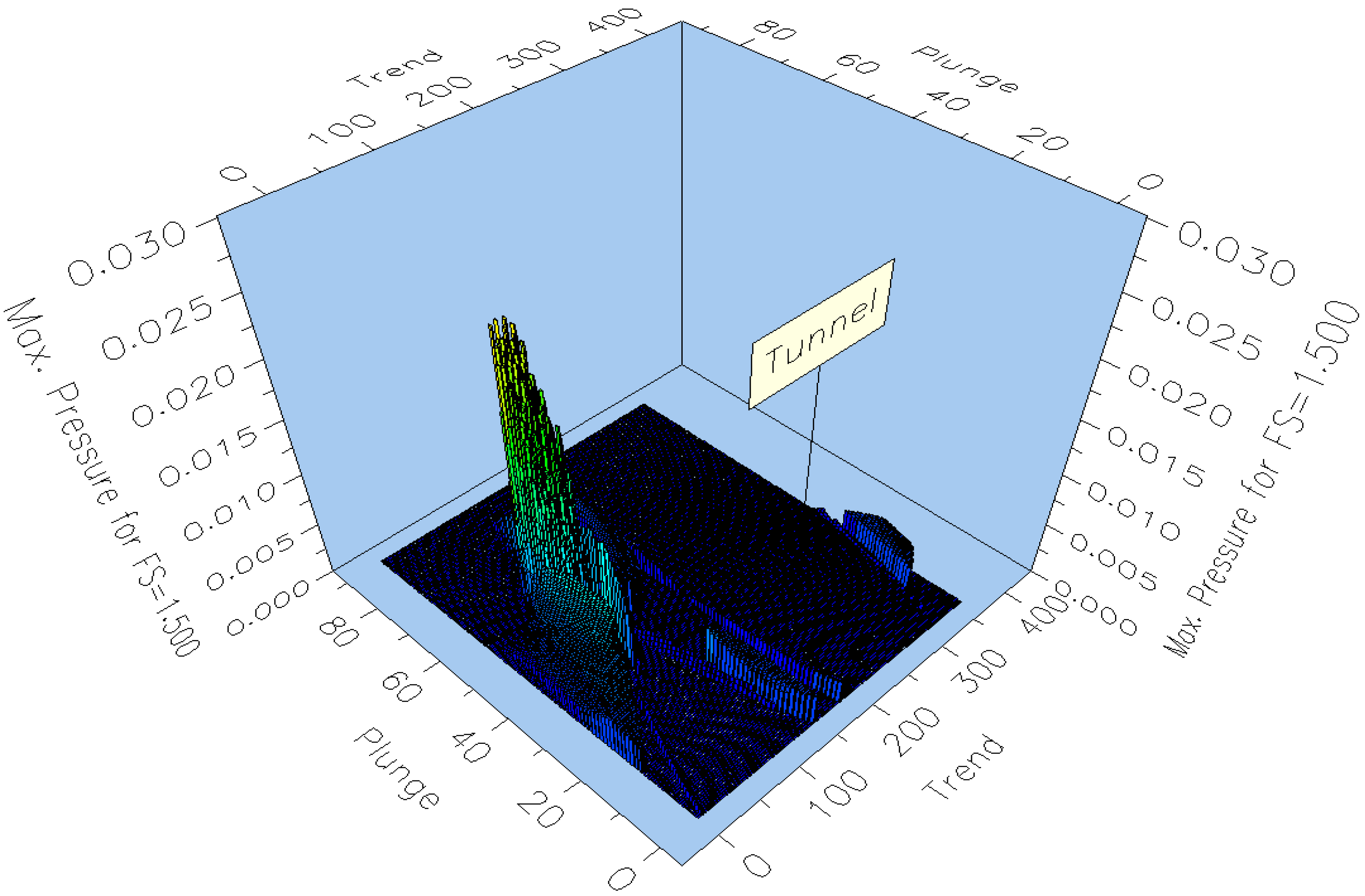

| Name | FS (Rock Bolts) | FS (Rock Bolts + Shotcrete Support) |
|---|---|---|
| 300 m horizon, panel 1 | 0.939 ± 0.05 | 3.117 ± 0.10 |
| Panel 1, chamber 25, pillar 43–44 | 1.087 ± 0.05 | 2.908 ± 0.10 |
| 300 m horizon, panel 2 | 1.092 ± 0.05 | 2.389 ± 0.10 |
| Panel 7, pillar 190–191 | 1.02 ± 0.05 | 2.529 ± 0.10 |
| 270 m horizon | 1.172 ± 0.05 | 3.461 ± 0.10 |
| Depth, m | σ1, MPa | σ2, MPa | σ3, MPa 1 |
|---|---|---|---|
| 100 | 6.0 ± 0.3 | 4.0 ± 0.2 | 2.7 ± 0.2 |
| 310 | 18.0 ± 0.9 | 11.0 ± 0.6 | 8.3 ± 0.4 |
| Condition | Orientation | Support Scheme | Notes/Risks |
|---|---|---|---|
| “Safe window” | 70° ± 10° | Rock bolts + shotcrete ≥ 0.05 m | Low risk; baseline configuration |
| Critical orientations | 120°; 141° | Rock bolts + shotcrete ≥ 0.05 m | High risk without reinforcement; increase bolt density/length; apply mesh/reinforcement frames |
| Water-bearing fractures | — | Combined support; increase shotcrete class/thickness | Reduced friction and cohesion expected; monitor for inflows |
| Elevated stresses | — | Combined support; check bolt spacing/length | Scale σ with depth; recheck FS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demin, V.; Kalinin, A.; Tomilova, N.; Tomilov, A.; Mutovina, N.; Akpanbayeva, A.; Demina, T. Probabilistic Analysis of Wedge Failures and Stability of Underground Workings with Combined Support Under Thrust Faulting Conditions. Appl. Sci. 2025, 15, 10533. https://doi.org/10.3390/app151910533
Demin V, Kalinin A, Tomilova N, Tomilov A, Mutovina N, Akpanbayeva A, Demina T. Probabilistic Analysis of Wedge Failures and Stability of Underground Workings with Combined Support Under Thrust Faulting Conditions. Applied Sciences. 2025; 15(19):10533. https://doi.org/10.3390/app151910533
Chicago/Turabian StyleDemin, Vladimir, Alexey Kalinin, Nadezhda Tomilova, Aleksandr Tomilov, Natalya Mutovina, Assem Akpanbayeva, and Tatiana Demina. 2025. "Probabilistic Analysis of Wedge Failures and Stability of Underground Workings with Combined Support Under Thrust Faulting Conditions" Applied Sciences 15, no. 19: 10533. https://doi.org/10.3390/app151910533
APA StyleDemin, V., Kalinin, A., Tomilova, N., Tomilov, A., Mutovina, N., Akpanbayeva, A., & Demina, T. (2025). Probabilistic Analysis of Wedge Failures and Stability of Underground Workings with Combined Support Under Thrust Faulting Conditions. Applied Sciences, 15(19), 10533. https://doi.org/10.3390/app151910533






