Recent Advances on the VAN Method
Abstract
1. Introduction
2. Materials and Methods
2.1. Brief Description of the VAN Method
2.2. Description of the VAN Telemetric Network
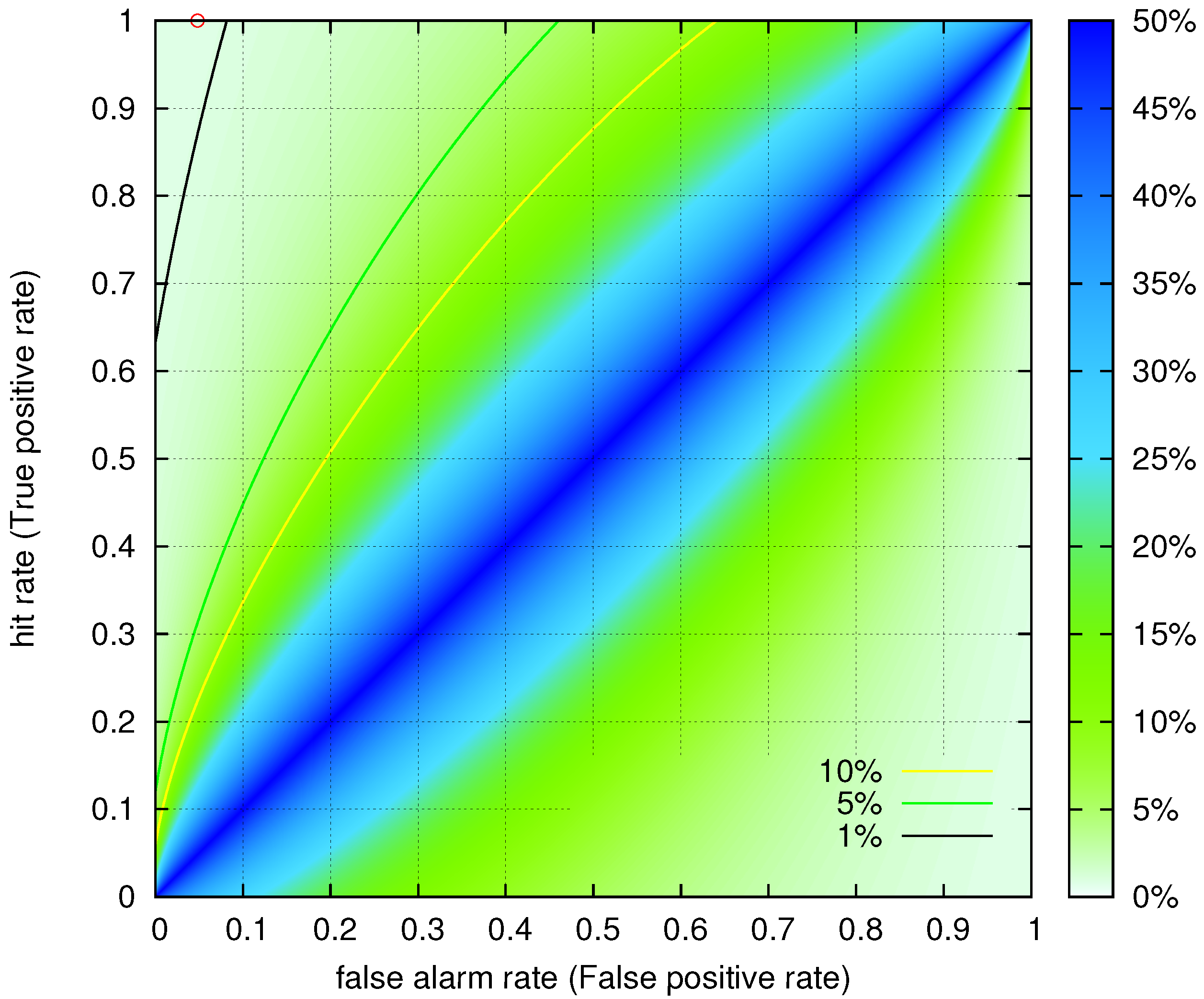
2.3. Receiver Operating Characteristics
2.4. Physical Mechanisms for the Generation of SES
3. Results
3.1. SES Recorded at KER Geoelectric Field Station
3.2. SES Recorded at PIR Geoelectric Field Station
3.3. SES Recorded at ASS Geoelectric Field Station
4. Discussion
5. Conclusions
- The VAN method is statistically significant, leading to a false alarm rate of 4.8%;
- The study of the AUC in the ROC diagrams points to the characterization of the method as outstanding;
- The continuation of experimentation on the VAN method in Greece will improve the accuracy of the related predictions.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ASS | Assiros geoelectric field station |
| AUC | Area under the curve |
| ATH | Athens |
| CH | Channel |
| EQ | Earthquake |
| FN | False negative |
| FP | False positive |
| GI-NOA | Institute of geodynamics of the national observatory of Athens |
| GMT | Generic mapping tools |
| GSM | Global system for mobile communications |
| IOA | Ioannina geoelectric field station |
| KER | Keratea geoelectric field station |
| LAM | Lamia geoelectric field station |
| LOU | Loutraki geoelectric field station |
| M | magnitude |
| MAR | March |
| ML(ATH) | Local magnitude reported by GI-NOA |
| PAT | Patras geoelectric field station |
| PIR | Pirgos geoelectric field station |
| PSPC | Pressure stimulated polarization currents |
| ROC | Receiver operating characteristics |
| SES | Seismic electric signals |
| TN | True negative |
| TP | True positive |
| VAN | Varotsos, Alexopoulos, and Nomicos |
| VOL | Volos geoelectric field station |
| USGS | United States geological survey |
References
- Sobolev, G.A. Application of electric method to the tentative short-term forecast of Kamchatka earthquakes. Pure Appl. Geophys. 1975, 113, 229–235. [Google Scholar] [CrossRef]
- Rikitake, T. Current Research in Earthquake Prediction; D. Reidler Publishing Company: Dordrecht, The Netherlands, 1981. [Google Scholar]
- Varotsos, P.; Alexopoulos, K.; Nomicos, K.; Lazaridou, M. Earthquake prediction and electric signals. Nature 1986, 322, 120. [Google Scholar] [CrossRef]
- Fraser-Smith, A.C.; Bernardi, A.; McGill, P.R.; Ladd, M.E.; Helliwell, R.A.; Villard, O.G. Low-frequency magnetic-field measurements near the epicenter of the Ms-7.1 Loma-Prieta earthquake. Geophys. Res. Lett. 1990, 17, 1465. [Google Scholar] [CrossRef]
- Varotsos, P.; Lazaridou, M. Latest aspects of earthquake prediction in Greece based on Seismic Electric Signals. Tectonophysics 1991, 188, 321–347. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K.; Lazaridou-Varotsou, M.; Nagao, T. Earthquake predictions issued in Greece by seismic electric signals since 6 February 1990. Tectonophysics 1993, 224, 269–288. [Google Scholar] [CrossRef]
- Monastersky, R. Electric Signals may herald earthquakes. Sci. News 1995, 148, 260. [Google Scholar] [CrossRef]
- Igarashi, G.; Saeki, S.; Takahata, N.; Sumikawa, K.; Tasaka, S.; Sasaki, Y.; Takahashi, M.; Sano, Y. Ground-Water Radon Anomaly Before the Kobe Earthquake in Japan. Science 1995, 269, 60–61. [Google Scholar] [CrossRef] [PubMed]
- Uyeda, S. Introduction to the VAN method of earthquake prediction. In A Critical Review of VAN: Earthquake Prediction from Seismic Electric Signals; Lighthill, S.J., Ed.; World Scientific: Singapore, 1996; Volume 16, pp. 3–28. [Google Scholar] [CrossRef]
- Molchan, G.M. Earthquake prediction as a decision-making problem. Pure Appl. Geophys. 1997, 149, 233–247. [Google Scholar] [CrossRef]
- Uyeda, S. VAN Method of Short-term Earthquake Prediction Shows Promise. Eos Trans. AGU 1998, 79, 573–580. [Google Scholar] [CrossRef]
- Freund, F. Earthquake prediction is worthy of study. Eos Trans. AGU 1999, 80, 230–232. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Spatio-Temporal complexity aspects on the interrelation between Seismic Electric Signals and Seismicity. Pract. Athens Acad. 2001, 76, 294–321. Available online: http://physlab.phys.uoa.gr/org/pdf/p3.pdf (accessed on 24 September 2025).
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Electric Fields that “arrive” before the time derivative of the magnetic field prior to major earthquakes. Phys. Rev. Lett. 2003, 91, 148501. [Google Scholar] [CrossRef]
- Ghosh, D.; Deb, A.; Sengupta, R. Anomalous radon emission as precursor of earthquake. J. Appl. Geophys. 2009, 69, 67–81. [Google Scholar] [CrossRef]
- Uyeda, S.; Nagao, T.; Kamogawa, M. Short-term earthquake prediction: Current status of seismo-electromagnetics. Tectonophysics 2009, 470, 205–213. [Google Scholar] [CrossRef]
- Hattori, K.; Serita, A.; Gotoh, K.; Yoshino, C.; Harada, M.; Isezaki, N.; Hayakawa, M. ULF geomagnetic anomaly associated with 2000 Izu Islands earthquake swarm, Japan. Phys. Chem. Earth Parts A/B/C 2004, 29, 425–435. [Google Scholar] [CrossRef]
- Tramutoli, V.; Cuomo, V.; Filizzola, C.; Pergola, N.; Pietrapertosa, C. Assessing the potential of thermal infrared satellite surveys for monitoring seismically active areas: The case of Kocaeli (İzmit) earthquake, 17 August 1999. Remote Sens. Environ. 2005, 96, 409–426. [Google Scholar] [CrossRef]
- Uyeda, S.; Nagao, T.; Kamogawa, M. Earthquake Precursors and Prediction. In Encyclopedia of Solid Earth Geophysics; Springer: Dordrecht, The Netherlands, 2011; pp. 168–178. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere—Ionosphere Coupling (LAIC) model – An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Freund, F. Pre-earthquake signals: Underlying physical processes. J. Asian Earth Sci. 2011, 41, 383–400. [Google Scholar] [CrossRef]
- Lazaridou-Varotsos, M.S. Earthquake Prediction by Seismic Electric Signals. The Success of the VAN Method Over Thirty Years; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Xu, G.; Han, P.; Huang, Q.; Hattori, K.; Febriani, F.; Yamaguchi, H. Anomalous behaviors of geomagnetic diurnal variations prior to the 2011 off the Pacific coast of Tohoku earthquake (Mw9.0). J. Asian Earth Sci. 2013, 77, 59–65. [Google Scholar] [CrossRef]
- Rozhnoi, A.; Solovieva, M.; Hayakawa, M. VLF/LF signals method for searching of electromagnetic earthquake precursors. In Earthquake Prediction Studies: Seismo Electromagnetics; Hayakawa, M., Ed.; TERRAPUB: Tokyo, Japan, 2013; pp. 31–48. [Google Scholar]
- Chen, C.H.; Wen, S.; Liu, J.Y.; Hattori, K.; Han, P.; Hobara, Y.; Wang, C.H.; Yeh, T.K.; Yen, H.Y. Surface displacements in Japan before the 11 March 2011 M9.0 Tohoku-Oki earthquake. J. Asian Earth Sci. 2014, 80, 165–171. [Google Scholar] [CrossRef]
- Orihara, Y.; Kamogawa, M.; Nagao, T. Preseismic Changes of the Level and Temperature of Confined Groundwater related to the 2011 Tohoku Earthquake. Sci. Rep. 2014, 4, 6907. [Google Scholar] [CrossRef] [PubMed]
- Han, P.; Hattori, K.; Xu, G.; Ashida, R.; Chen, C.H.; Febriani, F.; Yamaguchi, H. Further investigations of geomagnetic diurnal variations associated with the 2011 off the Pacific coast of Tohoku earthquake (Mw 9.0). J. Asian Earth Sci. 2015, 114, 321–326. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Huang, Q.; Hirooka, S.; Yoshino, C. Spatiotemporal characteristics of the geomagnetic diurnal variation anomalies prior to the 2011 Tohoku earthquake (Mw 9.0) and the possible coupling of multiple pre-earthquake phenomena. J. Asian Earth Sci. 2016, 129, 13–21. [Google Scholar] [CrossRef]
- Hayakawa, T.; Asano, T.; Rozhnoi, A.; Solovieva, M. VLF/LF sounding of ionospheric perturbations and possible association with earthquakes. In Pre-Earthquake Processes: A Multidisciplinary Approach to Earthquake Prediction Studies; Ouzounov, D., Pulinets, S., Hattori, K., Taylor, P., Eds.; Geophysical Monograph Series; American Geophysical Union: Hoboken, WA, USA, 2018; pp. 277–304. [Google Scholar]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Phenomena preceding major earthquakes interconnected through a physical model. Ann. Geophys. 2019, 37, 315–324. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, X.; Yuan, S.; Wang, L.; Cao, J.; Huang, J.; Zhu, X.; Piergiorgio, P.; Dai, J. The state-of-the-art of the China Seismo-Electromagnetic Satellite mission. Sci.-China-Technol. Sci. 2018, 61, 634–642. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S. Study in Natural Time of Geoelectric Field and Seismicity Changes Preceding the Mw6.8 Earthquake on 25 October 2018 in Greece. Entropy 2018, 20, 882. [Google Scholar] [CrossRef]
- Gitis, V.; Derendyaev, A. From monitoring of seismic fields to the automatic forecasting of earthquakes. Int. J. Web Inf. Syst. 2019, 15, 535–549. [Google Scholar] [CrossRef]
- Cianchini, G.; De Santis, A.; Di Giovambattista, R.; Abbattista, C.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; Cesaroni, C.; De Santis, A.; Marchetti, D.; et al. Revised Accelerated Moment Release Under Test: Fourteen Worldwide Real Case Studies in 2014–2018 and Simulations. Pure Appl. Geophys. 2020, 177, 4057–4087. [Google Scholar] [CrossRef]
- Chen, C.H.; Yeh, T.K.; Wen, S.; Meng, G.; Han, P.; Tang, C.C.; Liu, J.Y.; Wang, C.H. Unique Pre-Earthquake Deformation Patterns in the Spatial Domains from GPS in Taiwan. Remote Sens. 2020, 12, 366. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Schekotov, A.; Contoyiannis, Y.; Balasis, G.; Koulouras, G.E.; Melis, N.S.; Boutsi, A.Z.; Hayakawa, M.; Eftaxias, K.; Nomicos, C. On Possible Electromagnetic Precursors to a Significant Earthquake (Mw = 6.3) Occurred in Lesvos (Greece) on 12 June 2017. Entropy 2019, 21, 241. [Google Scholar] [CrossRef]
- Potirakis, S.M.; Contoyiannis, Y.; Schekotov, A.; Eftaxias, K.; Hayakawa, M. Evidence of critical dynamics in various electromagnetic precursors. Eur. Phys. J. Spec. Top. 2021, 230, 151–177. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Order Parameter and Entropy of Seismicity in Natural Time before Major Earthquakes: Recent Results. Geosciences 2022, 12, 225. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The New View of Time, Part II. Advances in Disaster Prediction Using Complex Systems; Springer Nature Switzerland AG: Cham, Switzerland, 2023. [Google Scholar] [CrossRef]
- Wibowo, A.; Purnama, S.R.; Pratama, C.; Heliani, L.S.; Sahara, D.P.; Wibowo, S.T. Anomaly detection on displacement rates and deformation pattern features using tree-based algorithm in Japan and Indonesia. Geod. Geodyn. 2023, 14, 150–162. [Google Scholar] [CrossRef]
- Chi, C.; Li, C.; Han, Y.; Yu, Z.; Li, X.; Zhang, D. Pre-earthquake anomaly extraction from borehole strain data based on machine learning. Sci. Rep. 2023, 13, 20095. [Google Scholar] [CrossRef]
- Ouzounov, D.; Khachikyan, G. Studying the Impact of the Geospace Environment on Solar Lithosphere Coupling and Earthquake Activity. Remote Sens. 2024, 16, 24. [Google Scholar] [CrossRef]
- Rosca, C.M.; Stancu, A. Earthquake Prediction and Alert System Using IoT Infrastructure and Cloud-Based Environmental Data Analysis. Appl. Sci. 2024, 14, 10169. [Google Scholar] [CrossRef]
- Mukherjee, B.; Shaw, R.L.; Sharma, M.L.; Sain, K. Earthquake prediction using machine learning perspectives in Himalayan seismic belt and its surroundings. J. Asian Earth Sci. 2025, 293, 106764. [Google Scholar] [CrossRef]
- Neha; Chuang, R.Y.; Nishimura, T.; Lee, Z.; Gao, J.C. Balancing of geodetic and seismic moment rates and its implications for probabilistic seismic hazard analysis in Taiwan. Earth Planets Space 2025, 77, 125. [Google Scholar] [CrossRef]
- Graciosa, J.C.; Corbi, F.; Capitanio, F.A. Uncovering Deformation Prior to Analogue Megathrust Earthquakes With Explainable Artificial Intelligence. Geophys. Res. Lett. 2025, 52, e2024GL114428. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K.; Nomicos, K. Seismic Electric Currents. Pract. Athens Acad. 1981, 56, 277–286. [Google Scholar]
- Varotsos, P.; Alexopoulos, K.; Nomicos, K. Seven-hour precursors to earthqaukes determined from telluric currents. Pract. Athens Acad. 1981, 56, 417–433. [Google Scholar]
- Varotsos, P.; Alexopoulos, K.; Lazaridou, M. Latest aspects of earthquake prediction in Greece based on Seismic Electric Signals, II. Tectonophysics 1993, 224, 1–37. [Google Scholar] [CrossRef]
- Varotsos, P. The Physics of Seismic Electric Signals; TERRAPUB: Tokyo, Japan, 2005; p. 338. [Google Scholar]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S. Natural Time Analysis: The New View of Time. Precursory Seismic Electric Signals, Earthquakes and Other Complex Time-Series; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K. Thermodynamics of Point Defects and Their Relation with Bulk Properties; North Holland: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Varotsos, P.; Sarlis, N.; Lazaridou, M.; Kapiris, P. Transmission of stress induced electric signals in dielectric media. J. Appl. Phys. 1998, 83, 60–70. [Google Scholar] [CrossRef]
- Sarlis, N.; Lazaridou, M.; Kapiris, P.; Varotsos, P. Numerical Model of the Selectivity Effect and ΔV/L criterion. Geophys. Res. Lett. 1999, 26, 3245–3248. [Google Scholar] [CrossRef]
- United States Geological Survey, Earthquake Hazards Program. Search Earthquake Catalog. Available online: https://earthquake.usgs.gov/earthquakes/search/ (accessed on 31 August 2025).
- Kanamori, H. Quantification of Earthquakes. Nature 1978, 271, 411–414. [Google Scholar] [CrossRef]
- Hanks, T.C.; Kanamori, H. A moment magnitude scale. J. Geophys. Res. 1979, 84, 2348–2350. [Google Scholar] [CrossRef]
- United States Geological Survey, Earthquake Hazards Program. M6.9—Southern Greece, Greece. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/usp000fyw4/executive (accessed on 31 August 2025).
- Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S.; Varotsos, P.A. Investigation of seismicity after the initiation of a Seismic Electric Signal activity until the main shock. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2008, 84, 331–343. [Google Scholar] [CrossRef]
- Uyeda, S.; Kamogawa, M. The Prediction of Two Large Earthquakes in Greece. Eos Trans. AGU 2008, 89, 363. [Google Scholar] [CrossRef]
- Uyeda, S.; Kamogawa, M. Comment on ‘The Prediction of Two Large Earthquakes in Greece’. Eos Trans. AGU 2010, 91, 163. [Google Scholar] [CrossRef]
- USGS, See the United States Geological Survey (USGS) Earthquake SearchWeb Page for the Relevant Seismic Catalogues. 2010. Available online: https://earthquake.usgs.gov/earthquakes/map/ (accessed on 31 August 2025).
- United States Geological Survey, Earthquake Hazards Program. M7.0—26 km SW of Lixoúri, Greece. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/usp0001sa1/executive (accessed on 31 August 2025).
- Sarlis, N.V. Statistical Significance of Earth’s Electric and Magnetic Field Variations Preceding Earthquakes in Greece and Japan Revisited. Entropy 2018, 20, 561. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Lazaridou, M. Reply to “Rebuttal to Reply by Varotsos and Lazaridou: Towards plainly successful prediction,” by Paul W. Burton. Geophys. Res. Lett. 1996, 23, 1389–1390. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou-Varotsos, M.S. Identifying the occurrence time of an impending mainshock: A very recent case. arXiv 2025, arXiv:1908.00279. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Geoelectric field and seismicity changes preceding the 2018 Mw6.8 earthquake and the subsequent activity in Greece. arXiv 2024, arXiv:901.06658. [Google Scholar] [CrossRef]
- United States Geological Survey, Earthquake Hazards Program. M 4.9—4 km SSW of Níkiti, Greece. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us6000jm7j/executive (accessed on 31 August 2025).
- United States Geological Survey, Earthquake Hazards Program. M5.3—56 km SW of Palaióchora, Greece. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us7000n0l7/executive (accessed on 31 August 2025).
- Uyeda, S.; Kamogawa, M.; Tanaka, H. Analysis of electrical activity and seismicity in the natural time domain for the volcanic-seismic swarm activity in 2000 in the Izu Island region, Japan. J. Geophys. Res. Solid Earth 2009, 114, B02310. [Google Scholar] [CrossRef]
- Uyeda, S.; Nagao, T.; Orihara, Y.; Yamaguchi, T.; Takahashi, I. Geoelectric potential changes: Possible precursors to earthquakes in Japan. Proc. Natl. Acad. Sci. USA 2000, 97, 4561–4566. [Google Scholar] [CrossRef] [PubMed]
- Uyeda, S.; Hayakawa, M.; Nagao, T.; Molchanov, O.; Hattori, K.; Orihara, Y.; Gotoh, K.; Akinaga, Y.; Tanaka, H. Electric and magnetic phenomena observed before the volcano-seismic activity in 2000 in the Izu Island Region, Japan. Proc. Natl. Acad. Sci. USA 2002, 99, 7352–7355. [Google Scholar] [CrossRef] [PubMed]
- Orihara, Y.; Kamogawa, M.; Nagao, T.; Uyeda, S. Preseismic anomalous telluric current signals observed in Kozu-shima Island, Japan. Proc. Natl. Acad. Sci. USA 2012, 109, 19125–19128. [Google Scholar] [CrossRef]
- Zlotnicki, J.; Kossobokov, V.; Le Mouël, J.L. Frequency spectral properties of an ULF electromagnetic signal around the 21 July 1995, M=5.7, Yong Deng (China) earthquake. Tectonophysics 2001, 334, 259–270. [Google Scholar] [CrossRef]
- Fan, Y.Y.; Du, X.B.; Zlotnicki, J.; Tan, D.C.; An, Z.H.; Chen, J.Y.; Zheng, G.L.; Liu, J.; Xie, T. The Electromagnetic Phenomena Before the Ms8.0 Wenchuan Earthquake. Chinese J. Geophys. 2010, 53, 997–1010. [Google Scholar] [CrossRef]
- Huang, Q. Retrospective investigation of geophysical data possibly associated with the Ms8.0 Wenchuan earthquake in Sichuan, China. J. Asian Earth Sci. 2011, 41, 421–427. [Google Scholar] [CrossRef]
- Ramírez-Rojas, A.; Flores-Márquez, E.L.; Guzmán-Vargas, L.; Gálvez-Coyt, G.; Telesca, L.; Angulo-Brown, F. Statistical features of seismoelectric signals prior to M7.4 Guerrero-Oaxaca earthquake (México). Nat. Hazards Earth Syst. Sci. 2008, 8, 1001–1007. [Google Scholar] [CrossRef]
- Ramírez-Rojas, A.; Telesca, L.; Angulo-Brown, F. Entropy of geoelectrical time series in the natural time domain. Nat. Hazards Earth Syst. Sci. 2011, 11, 219–225. [Google Scholar] [CrossRef]
- Papadopoulou, K.; Skordas, E.; Zlotnicki, J.; Nagao, T.; Rybin, A. Study of Geo-Electric Data Collected by the Joint EMSEV-Bishkek RS-RAS Cooperation: Possible Earthquake Precursors. Entropy 2018, 20, 614. [Google Scholar] [CrossRef]
- Sarlis, N.; Varotsos, P. Magnetic field near the outcrop of an almost horizontal conductive sheet. J. Geodyn. 2002, 33, 463–476. [Google Scholar] [CrossRef]
- Uyeda, S.; Al-Damegh, E.; Dologlou, E.; Nagao, T. Some relationship between VAN seismic electric signals (SES) and earthquake parameters. Tectonophysics 1999, 304, 41–55. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications, Vol. II; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Lesche, B. Instabilities of Renyi entropies. J. Stat. Phys. 1982, 27, 419. [Google Scholar] [CrossRef]
- Lesche, B. Renyi entropies and observables. Phys. Rev. E 2004, 70, 017102. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, P.; Alexopoulos, K. Physical Properties of the variations of the electric field of the Earth preceding earthquakes, I. Tectonophysics 1984, 110, 73–98. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K. Physical Properties of the variations of the electric field of the Earth preceding earthquakes, II. Tectonophysics 1984, 110, 99–125. [Google Scholar] [CrossRef]
- Nomicos, K.; Chatzidiakos, P. A telemetric system for measuring electrotelluric variations in Greece and its application to Earthquake prediction. Tectonophysics 1993, 224, 39–46. [Google Scholar] [CrossRef]
- Nomicos, K.; Makris, J.; Kefalas, M. The telemetric system of VAN group. In The Critical Review of VAN: Earthquake Prediction from Seismic Electric Signals; Lighthill, S.J., Ed.; World Scientific: Singapore, 1996; pp. 77–88. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recogn. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Mason, S.J.; Graham, N.E. Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation. Q. J. R. Meteor. Soc. 2002, 128, 2145–2166. [Google Scholar] [CrossRef]
- Mann, H.B.; Whitney, D.R. On a Test of Whether one of Two Random Variables is Stochastically Larger than the Other. Ann. Math. Statist. 1947, 18, 50–60. [Google Scholar] [CrossRef]
- Sarlis, N.V.; Christopoulos, S.R.G. Visualization of the significance of Receiver Operating Characteristics based on confidence ellipses. Comput. Phys. Commun. 2014, 185, 1172–1176. [Google Scholar] [CrossRef]
- Christopoulos, S.R.G.; Tsagiannis, G.I.; Papadopoulou, K.A.; Sarlis, N.V. VISROC 2.0: Updated Software for the Visualization of the significance of Receiver Operating Characteristics based on confidence ellipses. Comput. Phys. Commun. 2022, 280, 108492. [Google Scholar] [CrossRef]
- Steyerberg, E.W.; Vickers, A.J.; Cook, N.R.; Gerds, T.; Gonen, M.; Obuchowski, N.; Pencina, M.J.; Kattan, M.W. Assessing the Performance of Prediction Models A Framework for Traditional and Novel Measures. Epidemiology 2010, 21, 128–138. [Google Scholar] [CrossRef]
- Mandrekar, J.N. Receiver Operating Characteristic Curve in Diagnostic Test Assessment. J. Thorac. Oncol. 2010, 5, 1315–1316. [Google Scholar] [CrossRef] [PubMed]
- Hosmer, D.W.; Lemeshow, S. Applied Logistic Regression; John Wiley & Sons, Ltd.: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Fitterman, D.V. Theory of electrokinetic and magnetic anomalies associated with dilatant regions in a layered Earth. J. Geophys. Res. Solid Earth 1978, 83, 5923–5928. [Google Scholar] [CrossRef]
- Fitterman, D.V. Calculation of self-potential anomalies near vertical contacts. Geophys 1979, 44, 195–205. [Google Scholar] [CrossRef]
- Gershenzon, N.; Gokhberg, M. On the origin of electrotelluric disturbances prior to an earthquake in Kalamata, Greece. Tectonophysics 1993, 224, 169–174. [Google Scholar] [CrossRef]
- Ishido, T.; Mizutani, H. Experimental and theoretical basis of electrokinetic phenomena in rock-water systems and its applications to geophysics. J. Geophys. Res. Solid Earth 1981, 86, 1763–1775. [Google Scholar] [CrossRef]
- Jouniaux, L.; Pozzi, J.P. Streaming potential and permeability of saturated sandstones under triaxial stress: Consequences for electrotelluric anomalies prior to earthquakes. J. Geophys. Res. Solid Earth 1995, 100, 10197–10209. [Google Scholar] [CrossRef]
- Jouniaux, L.; Pozzi, J.P. Laboratory measurements anomalous 0.1–0.5 Hz streaming potential under geochemical changes: Implications for electrotelluric precursors to earthquakes. J. Geophys. Res. Solid Earth 1997, 102, 15335–15343. [Google Scholar] [CrossRef]
- Mizutani, H.; Ishido, T. A new interpretation of magnetic field variation associated with Matsushiro earthquakes. J. Geomagn. Geoelectr. 1976, 28, 179–188. [Google Scholar] [CrossRef]
- Mizutani, H.; Ishido, T.; Yokokura, T.; Ohnishi, S. Electrokinetic phenomena associated with earthquakes. Geophys. Res. Lett. 1976, 3, 365–368. [Google Scholar] [CrossRef]
- Morgan, D. A model for the explanation of SES-generation based on electrokinetic effect. In Proceedings of the International Conference on Measurements and Theoretical Models of the Earth’s Field Variations Related to Earthquakes, Athens, Greece, 6–8 February 1990; p. 57. [Google Scholar]
- Morgan, F.D. Electrodynamics of the earthquake source. In Proceedings of the Eos, Transactions, American Geophysical Union Supply—AGU 1995 Fall Meeting, San Francisco, CA, USA, 11–15 December 1995. F173. [Google Scholar]
- Sornette, A.; Sornette, D. Earthquake rupture as a critical point: Consequences for telluric precursors. Tectonophysics 1990, 179, 327–334. [Google Scholar] [CrossRef]
- Slifkin, L. Seismic electric signals displacement of charged dislocations. Tectonophysics 1993, 224, 149–152. [Google Scholar] [CrossRef]
- Slifkin, L. A dislocation model for seismic electric signals. In Critical Review of VAN: Earthquake Prediction from Seismic Electric Signals; Lighthill, S.J., Ed.; World Scientific: Singapore, 1996; pp. 97–104. [Google Scholar] [CrossRef]
- Lazarus, D. Short term earthquake prediction in Greece by Seismic Electric Signals. In Proceedings of the Critical Review of VAN: Earthquake Prediction from Seismic Electric Signals; Lighthill, S.J., Ed.; World Scientific: Singapore, 1996; pp. 91–96. [Google Scholar] [CrossRef]
- Varotsos, P.; Alexopoulos, K. Physical properties of the variations in the electric field of the earth preceding earthquakes, III. Tectonophysics 1987, 136, 335–339. [Google Scholar] [CrossRef]
- United States Geological Survey, Earthquake Hazards Program. M6.0—1 km ENE of Paralía Vérgas, Greece. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/usp0002y1v/executive (accessed on 31 August 2025).
- Anagnostopolous, S.A.; Rinaldis, D.; Lekidis, V.A.; Margaris, V.N.; Theodulidis, N.P. The Kalamata, Greece, Earthquake of 13 September 1986. Earthq. Spectra 1987, 3, 365–402. [Google Scholar] [CrossRef]
- National Observatory of Athens, Institute of Geodynamics. Earthquake Catalogues. Available online: https://www.gein.noa.gr/en/services-products/recent-seismicity/ (accessed on 31 August 2025).
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Christopoulos, S.R.G.; Lazaridou-Varotsos, M.S. Identifying the occurrence time of an impending mainshock: A very recent case. Earthq. Sci. 2015, 28, 215–222. [Google Scholar] [CrossRef]
- Varotsos, P.; Sarlis, N.; Skordas, E. A note on the spatial extent of the Volos SES sensitive site. Acta Geophys. Pol. 2001, 49, 425–435. [Google Scholar]
- Lazaridou-Varotsos, M.S. Disastrous Athens earthquake, 1999. In Earthquake Prediction by Seismic Electric Signals: The Success of the VAN Method over Thirty Years; Springer: Berlin/Heidelberg, Germany, 2013; pp. 155–158. [Google Scholar] [CrossRef]
- Varotsos, P.A.; Sarlis, N.V.; Skordas, E.S.; Lazaridou, M.S. Fluctuations, under time reversal, of the natural time and the entropy distinguish similar looking electric signals of different dynamics. J. Appl. Phys. 2008, 103, 014906. [Google Scholar] [CrossRef]
- United States Geological Survey, Earthquake Hazards Program. M5.5—5 km NNW of Flórina, Greece. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us7000gaex/executive (accessed on 31 August 2025).
- United States Geological Survey, Earthquake Hazards Program. M5.5—25 km SSE of Karyes, Greece. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us7000gcfq/executive (accessed on 31 August 2025).
- United States Geological Survey, Earthquake Hazards Program. M5.5—45 km SW of Lixoúri, Greece. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us6000ii2v/executive (accessed on 31 August 2025).
- United States Geological Survey, Earthquake Hazards Program. M5.5—Crete, Greece. Available online: https://earthquake.usgs.gov/earthquakes/eventpage/us7000ir86/executive (accessed on 31 August 2025).
- Sarlis, N.V. On the recent seismic activity in North-Eastern Aegean Sea including the Mw 5.8 earthquake on 8 January 2013. Proc. Jpn. Acad. Ser. B Phys. Biol. Sci. 2013, 89, 438–445. [Google Scholar] [CrossRef] [PubMed]
- Kanarachos, S.; Christopoulos, S.R.G.; Chroneos, A.; Fitzpatrick, M.E. Detecting anomalies in time series data via a deep learning algorithm combining wavelets, neural networks and Hilbert transform. Expert Syst. Appl. 2017, 85, 292–304. [Google Scholar] [CrossRef]
- Xue, J.; Huang, Q.; Wu, S.; Nagao, T. LSTM-Autoencoder Network for the Detection of Seismic Electric Signals. IEEE Trans. Geosci. Remote. Sens. 2022, 60, 5917012. [Google Scholar] [CrossRef]
- Xue, J.; Wu, S.; Huang, Q.; Zhao, L.; Sarlis, N.V.; Varotsos, P.A. RASE: A Real-Time Automatic Search Engine for Anomalous Seismic Electric Signals in Geoelectric Data. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5905911. [Google Scholar] [CrossRef]
- Williams, T.; Kelley, C. Gnuplot 4.6: An Interactive Plotting Program. 2014. Available online: http://www.gnuplot.info (accessed on 28 February 2014).
- Wessel, P.; Luis, J.F.; Uieda, L.; Scharroo, R.; Wobbe, F.; Smith, W.H.F.; Tian, D. The Generic Mapping Tools Version 6. Geochem. Geophys. Geosystems 2019, 20, 5556–5564. [Google Scholar] [CrossRef]


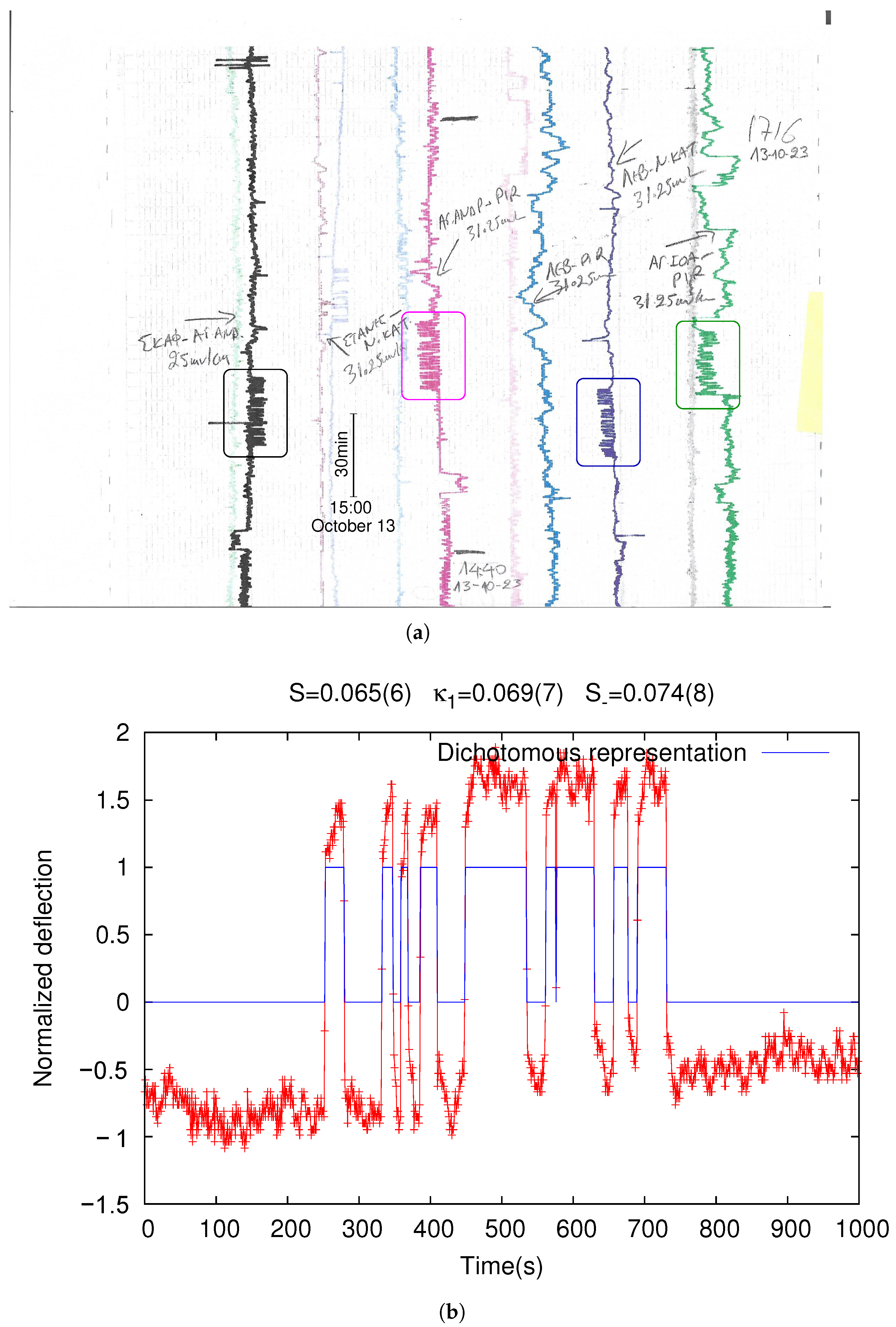
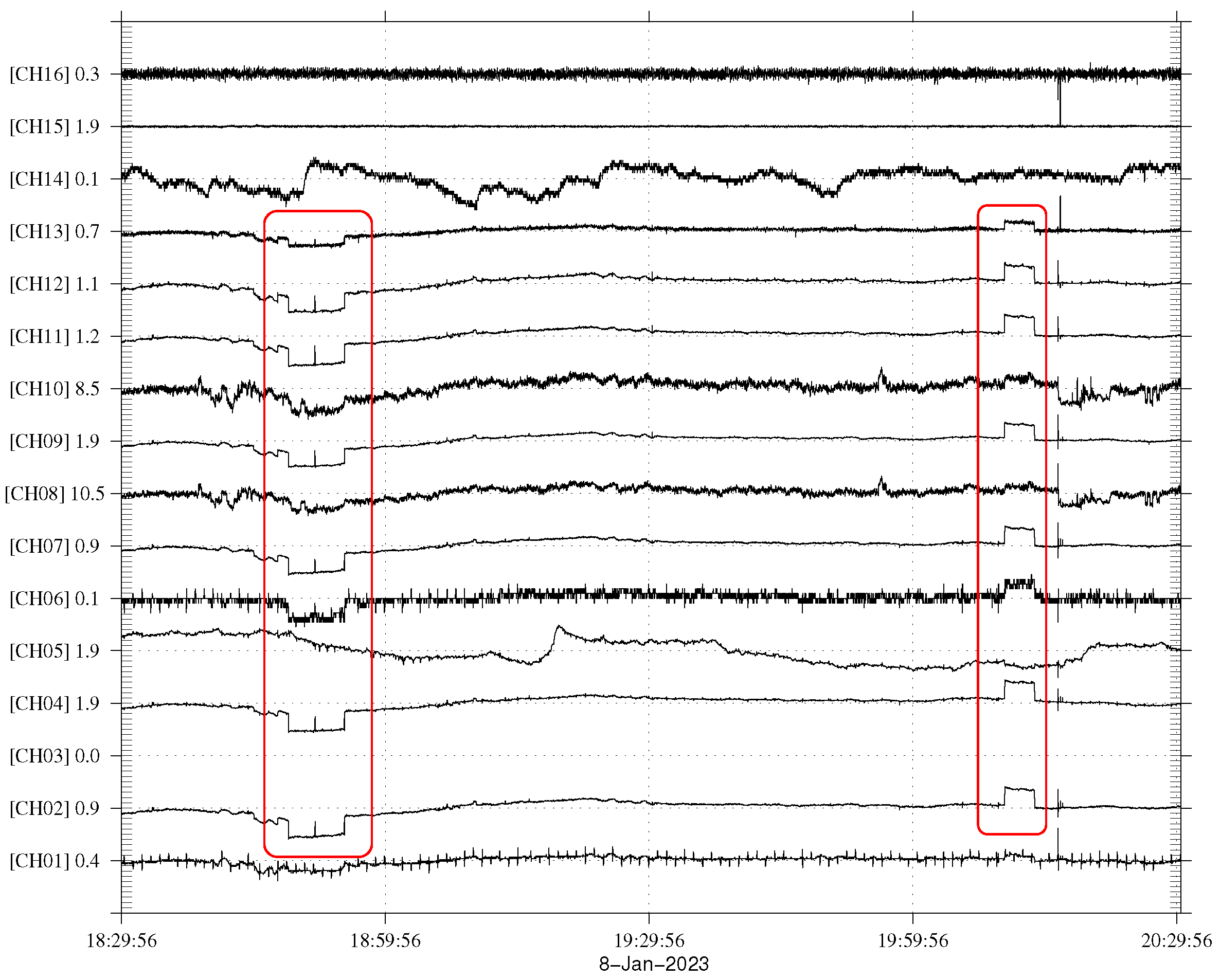
| Date of SES | Station Name | Related Seismic Activity | Label |
|---|---|---|---|
| 8 January 2023 1 | ASS | 4.9 on 7 February 2023 2 | ASS1 |
| 13 October 2023 3 | PIR | on 29 March 2024 | PIR1 |
| 30 May 2024 1 | KER | Drastic increase of ML(ATH) EQs | KER1 |
| 6 July 2024 3 | PIR | on 21 July 2024 4 | PIR2 |
| 20 April 2025 1 | KER | 6.0 and 6.2 on 13 and 22 May 2025 | KER2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarlis, N.V.; Skordas, E.S.; Varotsos, P.A. Recent Advances on the VAN Method. Appl. Sci. 2025, 15, 10516. https://doi.org/10.3390/app151910516
Sarlis NV, Skordas ES, Varotsos PA. Recent Advances on the VAN Method. Applied Sciences. 2025; 15(19):10516. https://doi.org/10.3390/app151910516
Chicago/Turabian StyleSarlis, Nicholas V., Efthimios S. Skordas, and Panayiotis A. Varotsos. 2025. "Recent Advances on the VAN Method" Applied Sciences 15, no. 19: 10516. https://doi.org/10.3390/app151910516
APA StyleSarlis, N. V., Skordas, E. S., & Varotsos, P. A. (2025). Recent Advances on the VAN Method. Applied Sciences, 15(19), 10516. https://doi.org/10.3390/app151910516







