Denoising of Partial Discharge Signal in Stator Using Wavelet Transform with Improved Thresholding Function
Abstract
1. Introduction
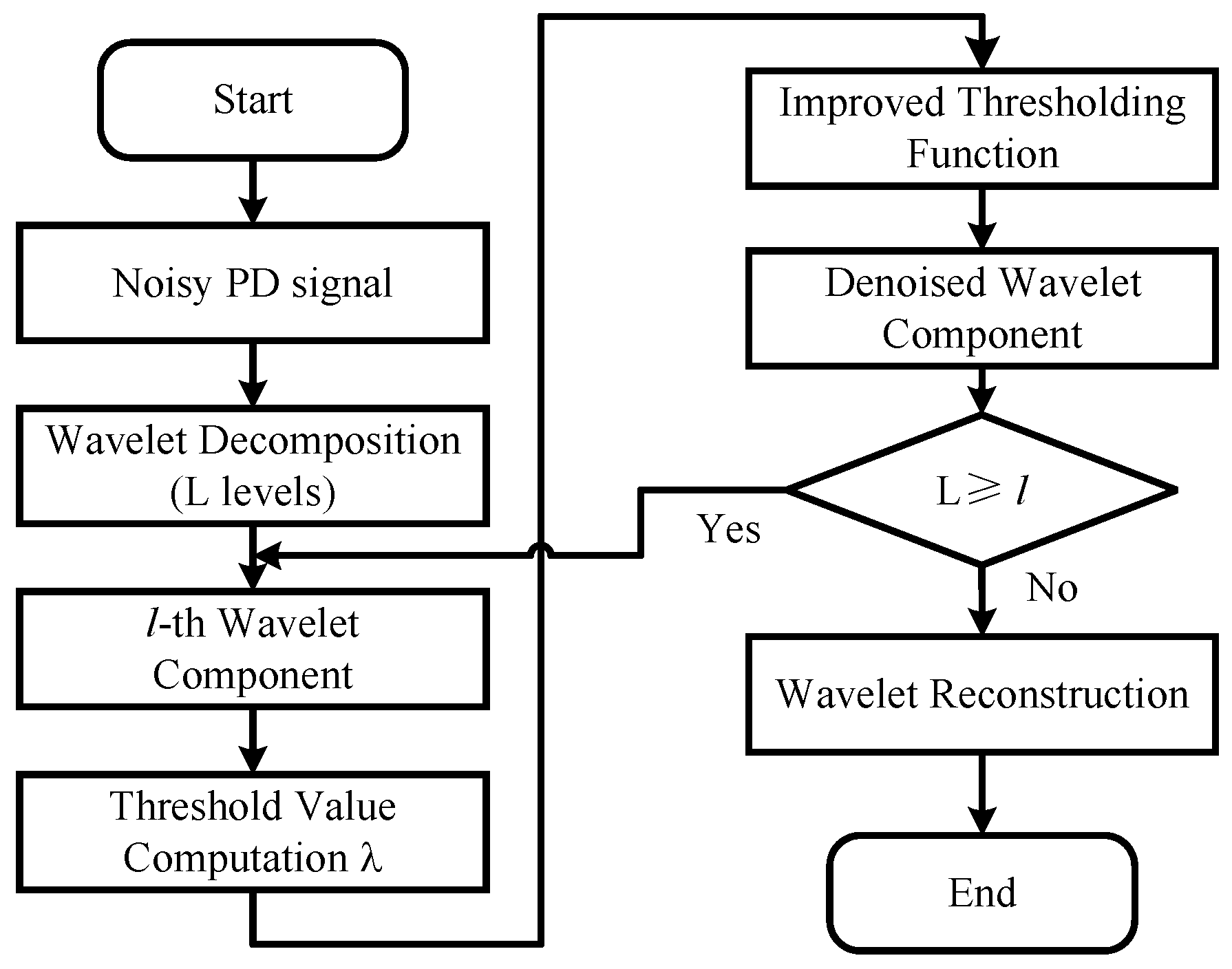
2. Wavelet Threshold Denoising Technique
2.1. Wavelet Decomposition
2.2. Threshold Processing
2.3. Wavelet Reconstruction
3. PD Denoising Algorithm with Proposed Improved Threshold Function
3.1. Improved Wavelet Threshold Function
3.2. Selection of Wavelet Basis Function
3.3. Adaptive Threshold Value Calculation
3.4. Denoising Procedure
- Input noised PD signal S, the selected wavelet basis , and decomposition level L;
- Decompose the PD signal by applying wavelet transform;
- Calculate the threshold value according to (9) at different decomposition levels;
- Utilize the improved wavelet thresholding function in (5) to perform denoising at each decomposition level;
- Reconstruct the denoised signal by applying the inverse wavelet transform.
3.5. Evaluation Criteria
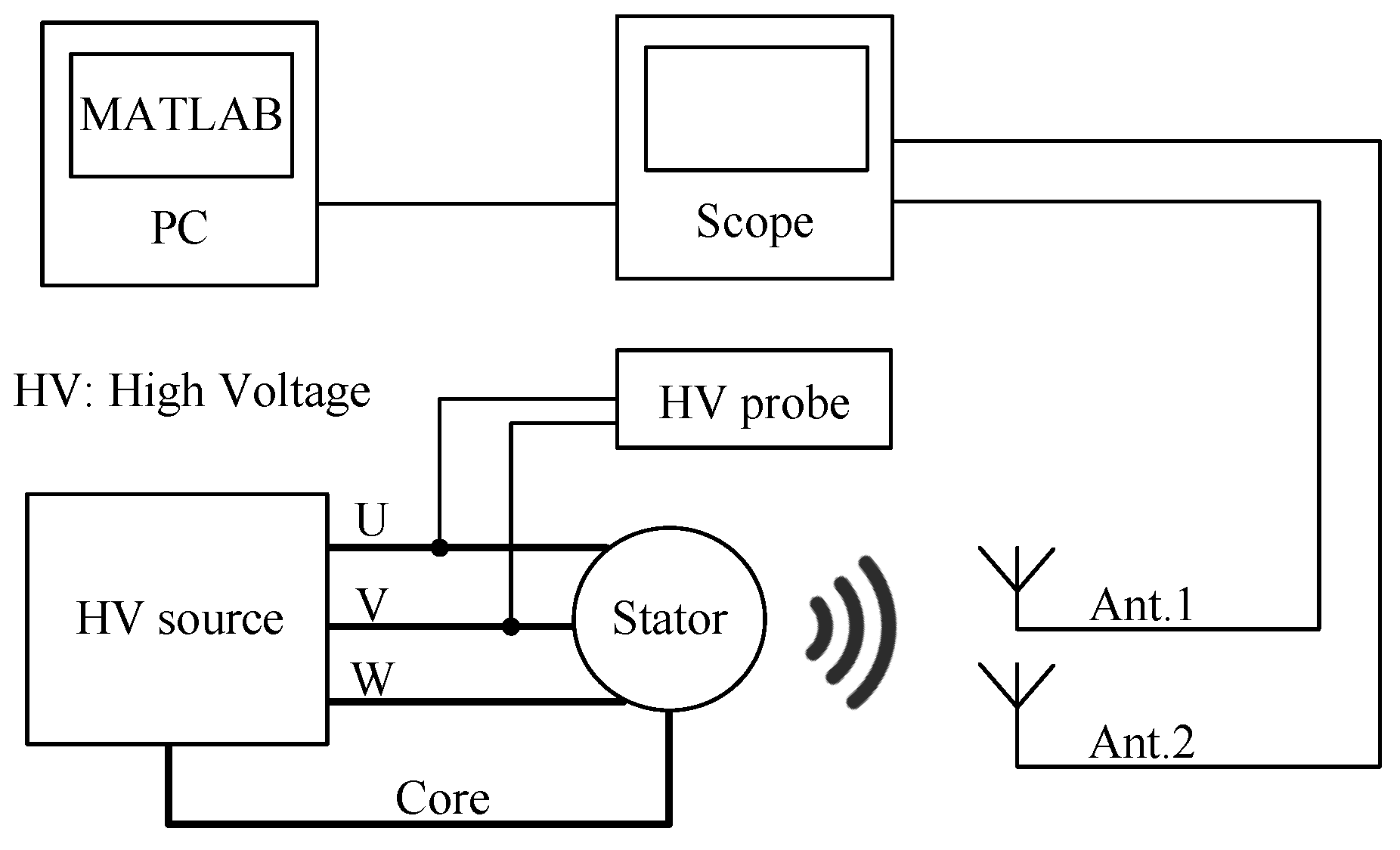
4. Experiments and Results
4.1. Simulation Experimental Results
4.1.1. Wavelet Basis Selection
4.1.2. Influence of Threshold Value on Proposed Improved Threshold Function
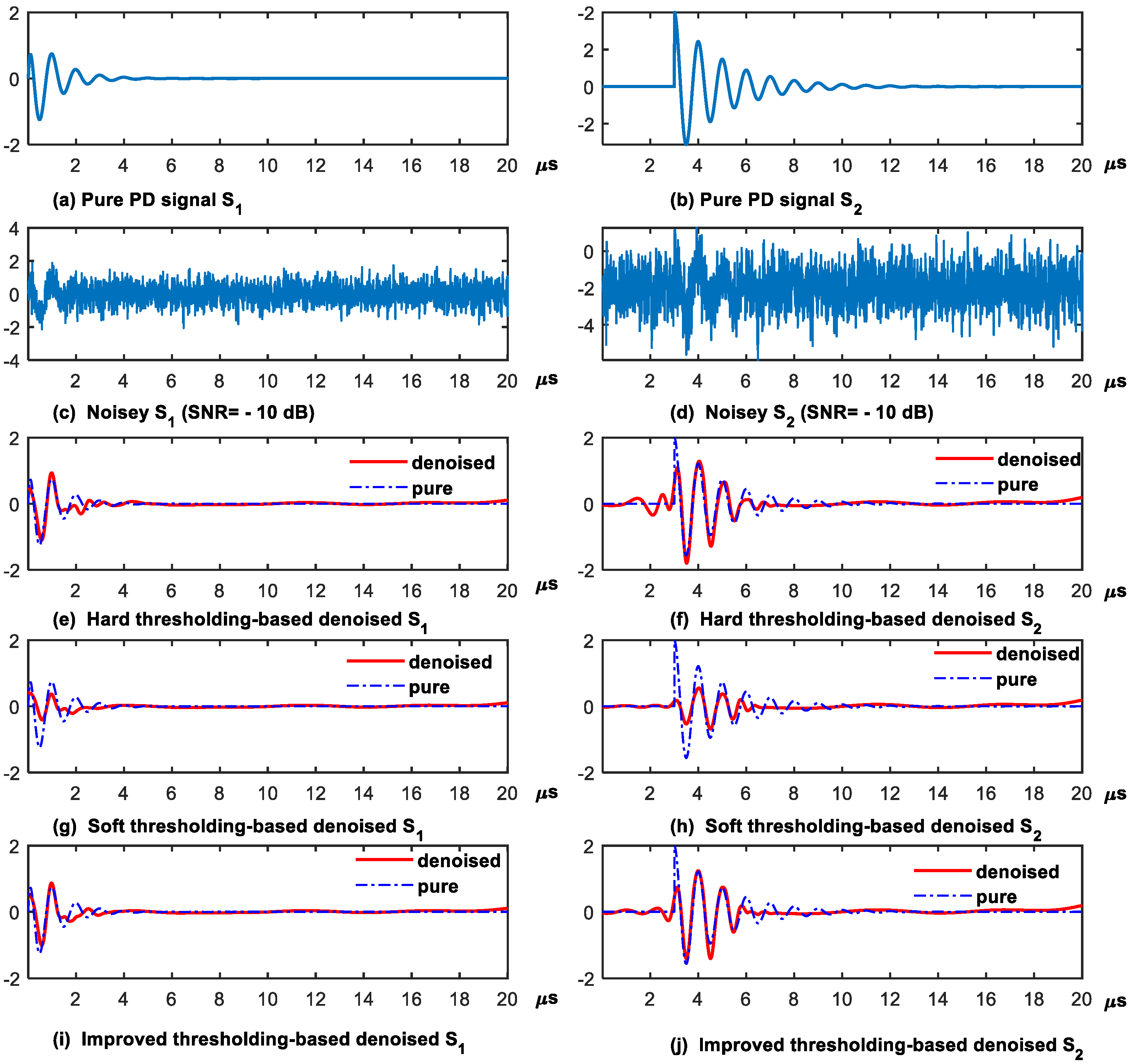
4.1.3. Effectiveness of the Proposed Improved Thresholding Function
4.1.4. Comparison with Other Denoising Approaches
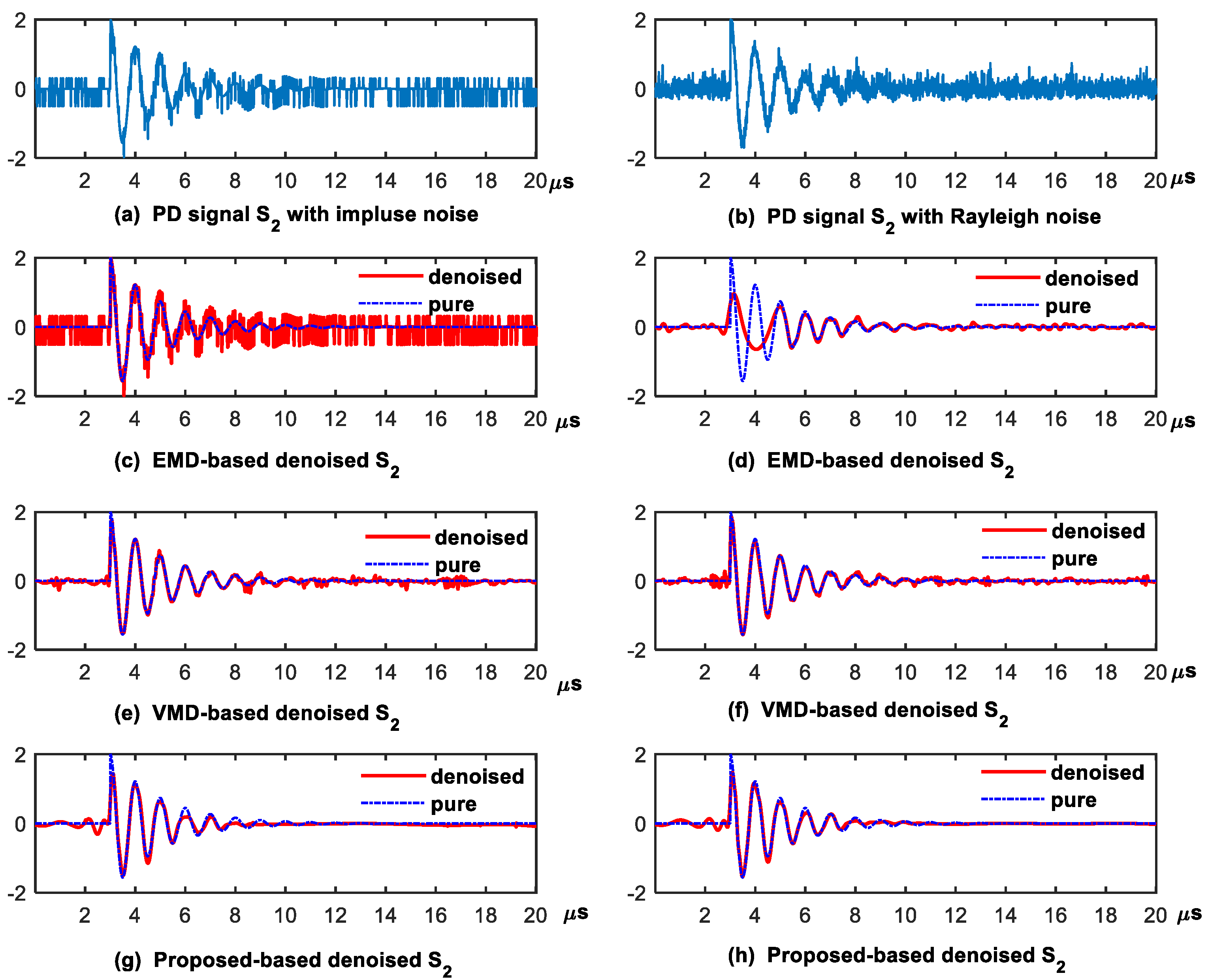
4.1.5. Comparison Under Different Noise Types
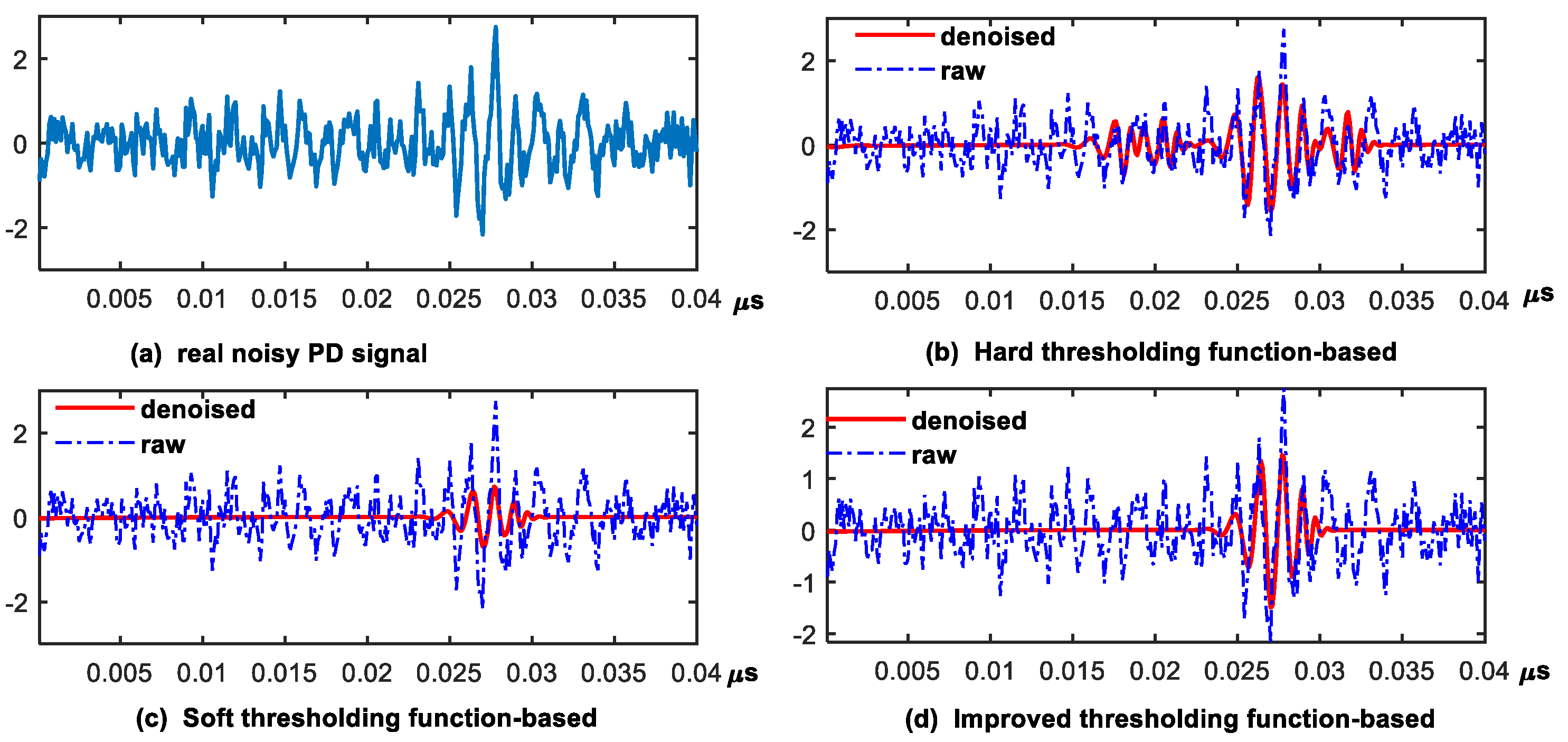
4.2. Application on Real Signal
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, R.; Li, H.; Hu, B.; Guo, Q. Groundwall insulation damage localization of large generator stator bar using an active Lamb waves method. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 1860–1869. [Google Scholar] [CrossRef]
- Habib, B.; Al Zaabi, O.; Harid, N.; Al Hosani, K.; Alkhatib, M. Condition Monitoring Based on Partial Discharge Diagnostics Using UHF Sensors: A Comprehensive State-of-the-Art Review. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 2860–2873. [Google Scholar] [CrossRef]
- Ilkhechi, H.D.; Samimi, M.H. Applications of the Acoustic Method in Partial Discharge Measurement: A Review. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 42–51. [Google Scholar] [CrossRef]
- Yusoff, N.A.; Isa, M.; Hamid, H.; Adzman, M.R.; Rohani, M.N.K.H.; Chai, C.Y.; Ayop, N.N. Denoising technique for partial discharge signal: A comparison performance between artificial neural network, fast fourier transform and discrete wavelet transform. In Proceedings of the 2016 IEEE International Conference on Power and Energy (PECon), Melaka, Malaysia, 28–29 November 2016; pp. 311–316. [Google Scholar] [CrossRef]
- Friebe, K.; Jenau, F. Evaluation Study on Wavelet Denoising of Antenna-Based PD Measurements in Strong Interference Environments Considering a New Reliability Score of Pulse Detection. IEEE Trans. Dielectr. Electr. Insul. 2024, 31, 2887–2896. [Google Scholar] [CrossRef]
- Chan, J.C.; Ma, H.; Saha, T.K.; Ekanayake, C. Self-adaptive partial discharge signal de-noising based on ensemble empirical mode decomposition and automatic morphological thresholding. IEEE Trans. Dielectr. Electr. Insul. 2014, 21, 294–303. [Google Scholar] [CrossRef]
- Wang, X.; Wang, X.; Gao, J.; Tian, Y.; Kang, Q.; Zhang, F.; Liu, W. A Denoising Method for Cable Partial Discharge Signals Based on Image Information Entropy and Multivariate Variational Mode Decomposition. IEEE Trans. Instrum. Meas. 2024, 73, 3500415. [Google Scholar] [CrossRef]
- Cao, J.; Wang, Y.; Zhu, W.; Zhang, Y. A Noise Reduction Algorithm for White Noise and Periodic Narrowband Interference Noise in Partial Discharge Signals. Appl. Sci. 2025, 15, 1760. [Google Scholar] [CrossRef]
- Raymond, W.J.K.; Xin, C.W.; Kin, L.W.; Illias, H.A. Noise invariant partial discharge classification based on convolutional neural network. Measurement 2021, 177, 109220. [Google Scholar] [CrossRef]
- Soltani, A.A. Employing Artificial Neural Network as a Novel Method for De-noising of Partial Discharge Signals. In Proceedings of the 2019 International Power System Conference (PSC), Tehran, Iran, 9–11 December 2019; pp. 269–274. [Google Scholar] [CrossRef]
- Barrios, S.; Buldain, D.; Comech, M.P.; Gilbert, I. Partial Discharge Identification in MV Switchgear Using Scalogram Representations and Convolutional AutoEncoder. IEEE Trans. Power Deliv. 2021, 36, 3448–3455. [Google Scholar] [CrossRef]
- Chaudhuri, S.; Ghosh, S.; Dey, D.; Munshi, S.; Chatterjee, B.; Dalai, S. Denoising of partial discharge signal using a hybrid framework of total variation denoising-autoencoder. Measurement 2023, 223, 113674. [Google Scholar] [CrossRef]
- Zhong, J.; Liu, Z.; Bi, X. Partial Discharge Signal Denoising Algorithm Based on Aquila Optimizer—Variational Mode Decomposition and K-Singular Value Decomposition. Appl. Sci. 2024, 14, 2755. [Google Scholar] [CrossRef]
- Hassan, F.; Rahim, L.A.; Mahmood, A.K.; Abed, S.A. A Hybrid Particle Swarm Optimization-Based Wavelet Threshold Denoising Algorithm for Acoustic Emission Signals. Symmetry 2022, 14, 1253. [Google Scholar] [CrossRef]
- Liu, Z.; Li, J.; Zhang, T.; Chen, S.; Xin, D.; Liu, K.; Chen, K.; Liu, Y.C.; Sun, C.; Gao, G.; et al. Accurate Identification of Partial Discharge Signals in Cable Terminations of High-Speed Electric Multiple Unit Using Wavelet Transform and Deep Belief Network. Appl. Sci. 2024, 14, 4743. [Google Scholar] [CrossRef]
- Kumar, C.; Ganguly, B.; Dey, D.; Chatterjee, S. Recent trends and open challenges in acoustic partial discharge signal denoising techniques: A review. Electr. Power Syst. Res. 2025, 248, 111931. [Google Scholar] [CrossRef]
- Jiang, X.; Lang, Q.; Jing, Q.; Wang, H.; Chen, J.; Ai, Q. An Improved Wavelet Threshold Denoising Method for Health Monitoring Data: A Case Study of the Hong Kong-Zhuhai-Macao Bridge Immersed Tunnel. Appl. Sci. 2022, 12, 6743. [Google Scholar] [CrossRef]
- Carvalho, A.T.; Lima, A.C.; Cunha, C.F.; Petraglia, M. Identification of partial discharges immersed in noise in large hydro-generators based on improved wavelet selection methods. Measurement 2015, 75, 122–133. [Google Scholar] [CrossRef]
- Wang, G.; Kim, S.J.; Kil, G.S.; Kim, S.W. Optimization of wavelet and thresholding for partial discharge detection under HVDC. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 200–208. [Google Scholar] [CrossRef]
- Ma, X.; Zhou, C.; Kemp, I. Automated wavelet selection and thresholding for PD detection. IEEE Electr. Insul. Mag. 2002, 18, 37–45. [Google Scholar] [CrossRef]
- Hussein, R.; Shaban, K.B.; El-Hag, A.H. Wavelet Transform With Histogram-Based Threshold Estimation for Online Partial Discharge Signal Denoising. IEEE Trans. Instrum. Meas. 2015, 64, 3601–3614. [Google Scholar] [CrossRef]
- Li, H.; Shi, J.; Li, L.; Tuo, X.; Qu, K.; Rong, W. Novel Wavelet Threshold Denoising Method to Highlight the First Break of Noisy Microseismic Recordings. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5910110. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Zhao, X.Y. Noise Smoothing for Structural Vibration Test Signals Using an Improved Wavelet Thresholding Technique. Sensors 2012, 12, 11205–11220. [Google Scholar] [CrossRef]
- Li, S.; Liu, S.; Wang, J.; Yan, S.; Liu, J.; Du, Z. Adaptive-Wavelet-Threshold-Function-Based M2M Gaussian Noise Removal Method. IEEE Internet Things J. 2024, 11, 33177–33192. [Google Scholar] [CrossRef]
- Sun, Z.; Lu, J. An Ultrasonic Signal Denoising Method for EMU Wheel Trackside Fault Diagnosis System Based on Improved Threshold Function. IEEE Access 2021, 9, 96244–96256. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M. Ideal Spatial Adaptation by Wavelet Shrinkage. Biometrika 1994, 81, 425–455. [Google Scholar] [CrossRef]
- Jing-Yi, L.; Hong, L.; Dong, Y.; Yan-Sheng, Z. A New Wavelet Threshold Function and Denoising Application. Math. Probl. Eng. 2016, 2016, 3195492. [Google Scholar] [CrossRef]
- Cunha, C.F.; Carvalho, A.T.; Petraglia, M.R.; Lima, A.C. A new wavelet selection method for partial discharge denoising. Electr. Power Syst. Res. 2015, 125, 184–195. [Google Scholar] [CrossRef]
- Haider, N.S. Respiratory sound denoising using Empirical Mode Decomposition, Hurst analysis and Spectral Subtraction. Biomed. Signal Process. Control 2021, 64, 102313. [Google Scholar] [CrossRef]
- Naveed, K.; Akhtar, M.T.; Siddiqui, M.F.; ur Rehman, N. A statistical approach to signal denoising based on data-driven multiscale representation. Digit. Signal Process. 2021, 108, 102896. [Google Scholar] [CrossRef]
- Rauscher, A.; Kaiser, J.; Devaraju, M.; Endisch, C. Deep learning and data augmentation for partial discharge detection in electrical machines. Eng. Appl. Artif. Intell. 2024, 133, 108074. [Google Scholar] [CrossRef]
- Rauscher, A. Dataset of Partial Discharge and Noise Signals. Figshare. Available online: https://figshare.com/articles/dataset/Dataset_of_partial_discharge_and_noise_signals/24033225/1 (accessed on 16 November 2023).


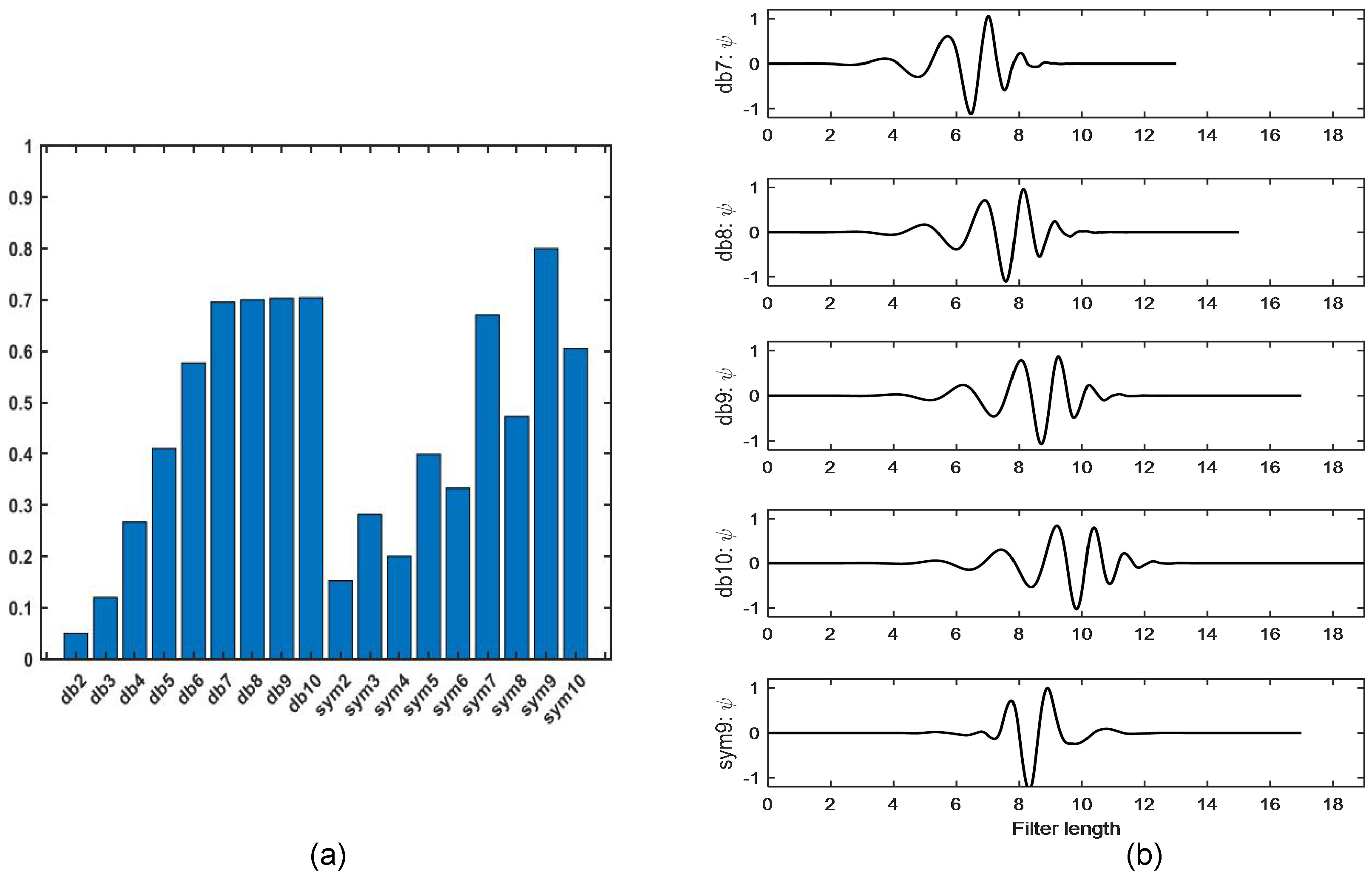

| Wavelet Basis | PD Signal in (14) (Mean ± Std) | PD Signal in (15) (Mean ± Std) | ||||
|---|---|---|---|---|---|---|
| (dB) | CC | MSE | (dB) | CC | MSE | |
| db2 | 6.0182 ± 1.2096 | 0.8720 ± 0.0370 | 0.3056 ± 0.0856 | 3.7604 ± 0.5850 | 0.7717 ± 0.0322 | 0.0431 ± 0.0058 |
| db3 | 5.8308 ± 1.1324 | 0.8667 ± 0.034 | 0.3173 ± 0.0801 | 4.2894 ± 0.8913 | 0.8007 ± 0.0416 | 0.0386 ± 0.0078 |
| db4 | 5.6425 ± 0.9514 | 0.8587 ± 0.0316 | 0.3286 ± 0.0745 | 4.7276 ± 0.6725 | 0.8210 ± 0.0300 | 0.0346 ± 0.0052 |
| db5 | 7.2287 ± 1.3358 | 0.9029 ± 0.0294 | 0.2336 ± 0.0770 | 5.4934 ± 0.6821 | 0.8517 ± 0.0241 | 0.0290 ± 0.0045 |
| db6 | 6.2959 ± 1.0510 | 0.8840 ± 0.0301 | 0.2843 ± 0.0721 | 5.0290 ± 0.8023 | 0.8326 ± 0.0325 | 0.0324 ± 0.0059 |
| db7 | 4.8637 ± 1.0145 | 0.8313 ± 0.0384 | 0.3940 ± 0.0897 | 4.1013 ± 0.8369 | 0.7871 ± 0.0465 | 0.0402 ± 0.0079 |
| db8 | 5.8423 ± 1.1083 | 0.8672 ± 0.0341 | 0.3165 ± 0.0824 | 5.0521 ± 0.8256 | 0.8355 ± 0.0363 | 0.0323 ± 0.0064 |
| db9 | 7.5603 ± 1.6169 | 0.9097 ± 0.0341 | 0.2211 ± 0.0853 | 5.4571 ± 0.5975 | 0.8512 ± 0.0218 | 0.0292 ± 0.0041 |
| db10 | 5.2929 ± 0.9447 | 0.8529 ± 0.0314 | 0.3558 ± 0.0772 | 4.8264 ± 0.7662 | 0.8248 ± 0.0352 | 0.0340 ± 0.0060 |
| sym2 | 5.8177 ± 1.1254 | 0.8674 ± 0.0329 | 0.3184 ± 0.0817 | 3.6741 ± 0.6304 | 0.7689 ± 0.0348 | 0.0440 ± 0.0063 |
| sym3 | 5.7901 ± 1.2779 | 0.8626 ± 0.0434 | 0.3237 ± 0.0984 | 4.4950 ± 0.8354 | 0.8096 ± 0.0376 | 0.0367 ± 0.0067 |
| sym4 | 6.5722 ± 1.3190 | 0.8850 ± 0.0378 | 0.2709 ± 0.0821 | 5.3185 ± 0.9629 | 0.8461 ± 0.0378 | 0.0306 ± 0.0068 |
| sym5 | 6.3388 ± 1.1059 | 0.8810 ± 0.0327 | 0.2823 ± 0.0736 | 5.4483 ± 0.7592 | 0.8508 ± 0.0284 | 0.0294 ± 0.0053 |
| sym6 | 6.3283 ± 1.2789 | 0.8781 ± 0.0364 | 0.2858 ± 0.0843 | 5.3936 ± 1.0286 | 0.8467 ± 0.0398 | 0.0301 ± 0.0070 |
| sym7 | 6.9338 ± 1.1729 | 0.8973 ± 0.0257 | 0.2472 ± 0.0700 | 5.6208 ± 0.6990 | 0.8571 ± 0.0243 | 0.0282 ± 0.0046 |
| sym8 | 6.7236 ± 1.3681 | 0.8881 ± 0.0367 | 0.2624 ± 0.0817 | 5.2626 ± 0.8675 | 0.8438 ± 0.0347 | 0.0309 ± 0.0064 |
| sym9 | 7.0519 ± 1.4886 | 0.8961 ± 0.0379 | 0.2461 ± 0.0889 | 6.6908 ± 1.0597 | 0.8889 ± 0.0276 | 0.0224 ± 0.0052 |
| sym10 | 6.4015 ± 1.3635 | 0.8780 ± 0.0418 | 0.2827 ± 0.0892 | 5.2229 ± 0.9478 | 0.8404 ± 0.0393 | 0.0312 ± 0.0067 |
| Threshold Value Selection Approaches | PD Signal in (14) (Mean ± Std) | PD Signal in (15) (Mean ± Std) | ||||
|---|---|---|---|---|---|---|
| CC | MSE | (dB) | CC | MSE | ||
| Rigrsure | 3.3704 ± 1.9453 | 0.8074 ± 0.0688 | 0.0239 ± 0.0112 | 1.3284 ± 1.7562 | 0.7245 ± 0.0678 | 0.0810 ± 0.0325 |
| Heursure | 7.6367 ± 1.3352 | 0.9082 ± 0.0309 | 0.0085 ± 0.0027 | 5.4219 ± 0.7099 | 0.8503 ± 0.0244 | 0.0295 ± 0.0050 |
| Sqtwolog | 6.4464 ± 1.3210 | 0.8768 ± 0.0469 | 0.0112 ± 0.0037 | 5.0308 ± 0.6282 | 0.8303 ± 0.0342 | 0.0323 ± 0.0055 |
| Minimaxi | 5.6296 ± 1.1192 | 0.8625 ± 0.0388 | 0.0133 ± 0.0034 | 3.4378 ± 0.8205 | 0.7835 ± 0.0349 | 0.0468 ± 0.0087 |
| Equation (9) | 7.8754 ± 1.3431 | 0.9133 ± 0.0289 | 0.0080 ± 0.0025 | 5.4789 ± 0.6250 | 0.8510 ± 0.0230 | 0.0291 ± 0.0042 |
| Noisy | Thresholding | PD Signal in (14) (Mean ± Std) | PD Signal in (15) (Mean ± Std) | ||||
|---|---|---|---|---|---|---|---|
| Function | (dB) | CC | RSE | (dB) | CC | RSE | |
| Hard | 2.2368 ± 1.9562 | 0.7120 ± 0.1179 | 0.0310 ± 0.0138 | 1.0807 ± 1.6075 | 0.6535 ± 0.1193 | 0.0848 ± 0.0328 | |
| −15 dB | Soft | 1.6573 ± 0.8465 | 0.5553 ± 0.1151 | 0.0327 ± 0.0063 | 1.1120 ± 0.8518 | 0.4708 ± 0.1481 | 0.0801 ± 0.0159 |
| Improved | 3.1572 ± 1.4255 | 0.7231 ± 0.1110 | 0.0239 ± 0.0077 | 2.1482 ± 1.3022 | 0.6744 ± 0.1286 | 0.0649 ± 0.0211 | |
| Hard | 6.5267 ± 1.7792 | 0.8857 ± 0.0437 | 0.0113 ± 0.0043 | 4.7661 ± 1.0737 | 0.8337 ± 0.0377 | 0.0349 ± 0.0086 | |
| −10 dB | Soft | 5.0642 ± 0.9552 | 0.8548 ± 0.0409 | 0.0150 ± 0.0032 | 4.0329 ± 0.5987 | 0.8059 ± 0.0393 | 0.0405 ± 0.0057 |
| Improved | 7.7268 ± 1.2927 | 0.9109 ± 0.0274 | 0.0083 ± 0.0024 | 5.5267 ± 0.6776 | 0.8532 ± 0.0237 | 0.028 ± 0.0045 | |
| Hard | 10.5002 ± 1.2989 | 0.9543 ± 0.0136 | 0.0044 ± 0.0013 | 8.0284 ± 0.8943 | 0.9213 ± 0.0160 | 0.0163 ± 0.0033 | |
| −5 dB | Soft | 8.9286 ± 0.8530 | 0.9534 ± 0.0121 | 0.0061 ± 0.0012 | 6.6922 ± 0.5317 | 0.9061 ± 0.0129 | 0.0219 ± 0.0026 |
| Improved | 11.7572 ± 0.9553 | 0.9662 ± 0.0082 | 0.0032 ± 0.0007 | 8.2108 ± 0.5782 | 0.9220 ± 0.0108 | 0.0155 ± 0.0020 | |
| Hard | 14.4275 ± 1.2036 | 0.9815 ± 0.0053 | 0.0018 ± 0.0005 | 11.8330 ± 0.7584 | 0.9669 ± 0.0060 | 0.0068 ± 0.0012 | |
| 0 dB | Soft | 12.6548 ± 0.6468 | 0.9815 ± 0.0030 | 0.0026 ± 0.0004 | 9.5486 ± 0.4154 | 0.9539 ± 0.0056 | 0.0113 ± 0.0011 |
| Improved | 14.5107 ± 0.6323 | 0.9824 ± 0.0026 | 0.0017 ± 0.0002 | 11.0006 ± 0.5162 | 0.9595 ± 0.0050 | 0.0081 ± 0.0010 | |
| Hard | 18.7930 ± 0.9320 | 0.9933 ± 0.0015 | 0.0006 ± 0.0001 | 16.3392 ± 0.7337 | 0.9883 ± 0.0021 | 0.0024 ± 0.0004 | |
| 5 dB | Soft | 16.0659 ± 0.5810 | 0.9910 ± 0.0014 | 0.0012 ± 0.0002 | 12.7499 ± 0.4274 | 0.9783 ± 0.0025 | 0.0054 ± 0.0005 |
| Improved | 16.4360 ± 0.4898 | 0.9888 ± 0.0013 | 0.0011 ± 0.0001 | 13.5302 ± 0.4454 | 0.9778 ± 0.0024 | 0.0045 ± 0.0005 | |
| Proposed | EMD-Based | VMD-Based | |
|---|---|---|---|
| Computational Complexity | O() | O() | O() |
| Memory Complexity | O(N) | O() | O() |
| Practical Speed | Fast | Moderate | Slow |
| Noisy | Approaches | PD Signal in (14) (Mean ± Std) | PD Signal in (15) (Mean ± Std) | ||||
|---|---|---|---|---|---|---|---|
| (dB) | CC | RSE | (dB) | CC | RSE | ||
| EMD | −3.0127 ± 1.3608 | 0.5076 ± 0.1375 | 0.0711 ± 0.0241 | −3.1075 ± 1.2793 | 0.5199 ± 0.0998 | 0.2174 ± 0.0711 | |
| −15 dB | VMD | −4.1515 ± 0.6356 | 0.5038 ± 0.0557 | 0.0888 ± 0.0127 | −4.1953 ± 0.5788 | 0.4889 ± 0.0626 | 0.2692 ± 0.0359 |
| Proposed | 3.1572 ± 1.4255 | 0.7231 ± 0.1110 | 0.0239 ± 0.0077 | 2.1482 ± 1.3022 | 0.6744 ± 0.1286 | 0.0649 ± 0.0211 | |
| EMD | 1.3751 ± 1.3611 | 0.6937 ± 0.1775 | 0.0260 ± 0.0093 | 1.3697 ± 1.2750 | 0.7296 ± 0.0934 | 0.0776 ± 0.0258 | |
| −10 dB | VMD | 0.8282 ± 0.5852 | 0.7289 ± 0.0350 | 0.0282 ± 0.0039 | 0.7870 ± 0.6570 | 0.7223 ± 0.0369 | 0.0857 ± 0.0133 |
| Proposed | 7.7268 ± 1.2927 | 0.9109 ± 0.0274 | 0.0083 ± 0.0024 | 5.5267 ± 0.6776 | 0.8532 ±0.0237 | 0.028 ± 0.0045 | |
| EMD | 4.4849 ± 2.7644 | 0.7389 ± 0.2609 | 0.0150 ± 0.0109 | 5.3738 ± 1.7046 | 0.8360 ± 0.1706 | 0.0327 ± 0.0206 | |
| −5 dB | VMD | 5.7132 ± 0.6081 | 0.8844 ± 0.0152 | 0.0092 ± 0.0013 | 5.6707 ± 0.5904 | 0.8801 ± 0.0145 | 0.0278 ± 0.0038 |
| Proposed | 11.7572± 0.9553 | 0.9662 ± 0.0082 | 0.0032 ± 0.0007 | 8.2108 ± 0.5782 | 0.9220 ± 0.0108 | 0.0155 ± 0.0020 | |
| EMD | 6.4090± 4.0645 | 0.7733 ± 0.2544 | 0.0121 ± 0.0114 | 8.3309 ±2.5963 | 0.8857 ± 0.1846 | 0.0199 ± 0.0239 | |
| 0 dB | VMD | 10.4991± 0.5353 | 0.9564 ± 0.0053 | 0.0030 ± 0.0004 | 10.3454 ± 0.5928 | 0.9545 ± 0.0058 | 0.0095 ± 0.0013 |
| Proposed | 14.5107 ± 0.6323 | 0.9824 ± 0.0026 | 0.0017 ± 0.0002 | 11.0006 ± 0.5162 | 0.9595 ± 0.0050 | 0.0081 ± 0.0010 | |
| EMD | 9.2040 ± 6.0582 | 0.7804 ± 0.3016 | 0.0105 ± 0.0131 | 10.9485 ± 3.6104 | 0.9140 ± 0.1719 | 0.0149 ± 0.0262 | |
| 5 dB | VMD | 14.0686 ± 0.3758 | 0.9803 ± 0.0017 | 0.0013 ± 0.0001 | 14.7777 ± 0.5774 | 0.9832 ± 0.0022 | 0.0034 ± 0.0004 |
| Proposed | 16.4360 ± 0.4898 | 0.9888 ± 0.0013 | 0.0011 ± 0.0001 | 13.5302 ± 0.4454 | 0.9778 ± 0.0024 | 0.0045 ± 0.0005 | |
| Noisy | Approaches | Impulse Noise (Mean ± Std) | Rayleigh Noise (Mean ± Std) | ||||
|---|---|---|---|---|---|---|---|
| (dB) | CC | RSE | (dB) | CC | RSE | ||
| EMD | −13.4047 ± 0.6747 | 0.0858 ± 0.0637 | 2.2498 ± 0.3239 | −3.1848 ± 1.4427 | 0.5536 ± 0.0916 | 0.2231 ± 0.0758 | |
| −15 dB | VMD | −10.3635 ± 2.7936 | 0.3414 ± 0.1273 | 1.4449 ± 1.4287 | −4.1022 ± 0.6774 | 0.5053 ± 0.0705 | 0.2644 ± 0.0417 |
| Proposed | −9.3244 ± 0.5746 | 0.3930 ± 0.0641 | 0.8767 ± 0.1112 | 0.7690 ± 1.3836 | 0.4610 ± 0.2476 | 0.0891 ± 0.0257 | |
| EMD | −5.9532 ± 0.6810 | 0.3935 ± 0.1067 | 0.4048 ± 0.0615 | 0.9747 ± 1.2578 | 0.6928 ± 0.1600 | 0.0847 ± 0.0262 | |
| −10 dB | VMD | −4.6431 ± 2.6923 | 0.5344 ± 0.1590 | 0.3891 ± 0.4161 | 0.7284 ± 0.5672 | 0.7208 ± 0.0314 | 0.0866 ± 0.0113 |
| Proposed | −3.4910 ± 0.4849 | 0.6421 ± 0.0418 | 0.2283 ± 0.0245 | 4.8177 ± 1.1403 | 0.8195 ± 0.0638 | 0.0348 ± 0.0108 | |
| EMD | −0.0575± 3.3718 | 0.6894 ± 0.1902 | 0.1479 ± 0.1497 | 5.1037 ± 1.6754 | 0.8356 ± 0.1479 | 0.0343 ± 0.0189 | |
| −5 dB | VMD | 2.5433 ± 0.5257 | 0.8323 ± 0.0280 | 0.0570 ± 0.0070 | 5.5328 ± 0.6960 | 0.8777 ± 0.0167 | 0.0288 ± 0.0045 |
| Proposed | 2.7333 ± 0.6555 | 0.8469 ± 0.0235 | 0.0548 ± 0.0086 | 6.8865 ± 0.7260 | 0.8918 ± 0.0183 | 0.0211 ± 0.0034 | |
| EMD | 1.9693 ± 3.1396 | 0.7577 ± 0.1318 | 0.0795 ± 0.0414 | 7.9319 ± 2.6825 | 0.8725 ± 0.2006 | 0.0220 ± 0.0258 | |
| 0 dB | VMD | 9.5146 ± 0.5030 | 0.9512 ± 0.0061 | 0.0114 ± 0.0014 | 10.2021 ± 0.5237 | 0.9534 ± 0.0059 | 0.0098 ± 0.0012 |
| Proposed | 8.5846 ± 0.6961 | 0.9378 ± 0.0117 | 0.0142 ± 0.0023 | 9.4609 ± 0.6512 | 0.9418 ± 0.0096 | 0.0116 ± 0.0018 | |
| EMD | 5.3695 ± 1.8558 | 0.8652 ± 0.1028 | 0.0319 ± 0.0129 | 8.9506 ± 5.3528 | 0.8051 ± 0.2888 | 0.0311 ± 0.0432 | |
| 5 dB | VMD | 14.3526± 0.5913 | 0.9826 ± 0.0026 | 0.0038 ± 0.0005 | 14.7831 ± 0.5674 | 0.9833 ± 0.0022 | 0.0034 ± 0.0004 |
| Proposed | 11.6736 ± 0.5912 | 0.9673 ± 0.0047 | 0.0070 ± 0.0010 | 11.9500 ± 0.6688 | 0.9676 ± 0.0052 | 0.0066 ± 0.0010 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, D.; Song, K.; Yi, R.; Xiong, H.; Yang, X. Denoising of Partial Discharge Signal in Stator Using Wavelet Transform with Improved Thresholding Function. Appl. Sci. 2025, 15, 10509. https://doi.org/10.3390/app151910509
Yang D, Song K, Yi R, Xiong H, Yang X. Denoising of Partial Discharge Signal in Stator Using Wavelet Transform with Improved Thresholding Function. Applied Sciences. 2025; 15(19):10509. https://doi.org/10.3390/app151910509
Chicago/Turabian StyleYang, Dong, Kunlong Song, Ruijie Yi, Haonan Xiong, and Xiaomei Yang. 2025. "Denoising of Partial Discharge Signal in Stator Using Wavelet Transform with Improved Thresholding Function" Applied Sciences 15, no. 19: 10509. https://doi.org/10.3390/app151910509
APA StyleYang, D., Song, K., Yi, R., Xiong, H., & Yang, X. (2025). Denoising of Partial Discharge Signal in Stator Using Wavelet Transform with Improved Thresholding Function. Applied Sciences, 15(19), 10509. https://doi.org/10.3390/app151910509







