Loop Modeling of the Reciprocal Inhibition Between HPA and HPG Endocrine Axes Reveals Transitions to Bistability and Critical Bifurcation Parameters
Abstract
Featured Application
Abstract
1. Introduction
2. Methods
2.1. Literature Survey
2.2. Mathematical Model
3. Results
3.1. Model Construction
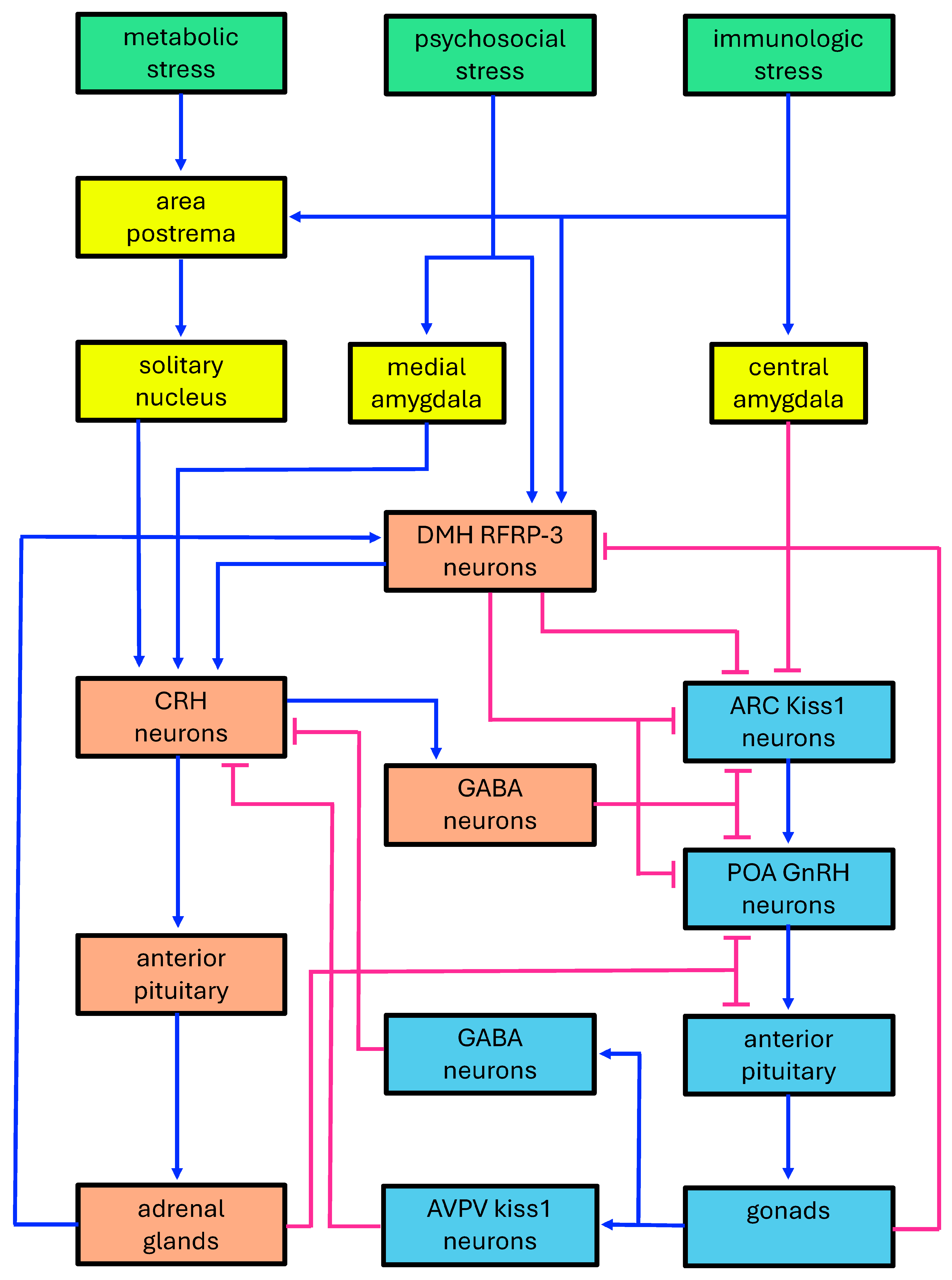
3.1.1. Neuroendocrine Mechanisms of the HPA-HPG Inhibition
3.1.2. Increasingly Expanded Interaction Maps
3.1.3. Mathematical Modeling
3.2. Computational Analysis of Phase Portraits and Bifurcation Patterns
4. Discussion
4.1. Interpretation of the Results and Their Possible Application
4.2. Limitation of the Study
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Blanchini, F.; EI-Samad, H.; Giordano, G.; Sontag, E.D. Control-theoretic methods for biological networks. In Proceedings of the 2018 IEEE Conference on Decision and Control (CDC), Miami, FL, USA, 17–19 December 2018; pp. 466–483. [Google Scholar]
- Burlando, B. Loopomics: A new functional approach to life. J. Appl. Physiol. 2017, 123, 1011–1013. [Google Scholar] [CrossRef]
- El-Samad, H. Biological feedback control-Respect the loops. Cell Syst. 2021, 12, 477–487. [Google Scholar] [CrossRef]
- Munoz-Culla, M.; Irizar, H.; Gorostidi, A.; Alberro, A.; Osorio-Querejeta, I.; Ruiz-Martinez, J.; Olascoaga, J.; Lopez de Munain, A.; Otaegui, D. Progressive changes in non-coding RNA profile in leucocytes with age. Aging 2017, 9, 1202–1218. [Google Scholar] [CrossRef]
- Saxton, R.A.; Sabatini, D.M. mTOR Signaling in Growth, Metabolism, and Disease. Cell 2017, 168, 960–976. [Google Scholar] [CrossRef]
- Agorastos, A.; Chrousos, G.P. The neuroendocrinology of stress: The stress-related continuum of chronic disease development. Mol. Psychiatry 2022, 27, 502–513. [Google Scholar] [CrossRef]
- Peper, J.S.; Brouwer, R.M.; van Leeuwen, M.; Schnack, H.G.; Boomsma, D.I.; Kahn, R.S.; Hulshoff Pol, H.E. HPG-axis hormones during puberty: A study on the association with hypothalamic and pituitary volumes. Psychoneuroendocrinology 2010, 35, 133–140. [Google Scholar] [CrossRef]
- Mastorakos, G.; Pavlatou, M.G.; Mizamtsidi, M. The hypothalamic-pituitary-adrenal and the hypothalamic-pituitary-gonadal axes interplay. Pediatr. Endocrinol. Rev. 2006, 3, 172–181. [Google Scholar]
- Caufriez, A.; Leproult, R.; Copinschi, G. Circadian profiles of progesterone, gonadotropins, cortisol and corticotropin in cycling and postmenopausal women. Chronobiol. Int. 2018, 35, 72–79. [Google Scholar] [CrossRef]
- Rahman, S.A.; Grant, L.K.; Gooley, J.J.; Rajaratnam, S.M.W.; Czeisler, C.A.; Lockley, S.W. Endogenous Circadian Regulation of Female Reproductive Hormones. J. Clin. Endocrinol. Metab. 2019, 104, 6049–6059. [Google Scholar] [CrossRef]
- Demori, I.; Losacco, S.; Giordano, G.; Mucci, V.; Blanchini, F.; Burlando, B. Fibromyalgia pathogenesis explained by a neuroendocrine multistable model. PLoS ONE 2024, 19, e0303573. [Google Scholar] [CrossRef]
- Kottler, M.L.; Coussieu, C.; Valensi, P.; Levi, F.; Degrelle, H. Ultradian, circadian and seasonal variations of plasma progesterone and LH concentrations during the luteal phase. Chronobiol. Int. 1989, 6, 267–277. [Google Scholar] [CrossRef]
- Elsner, C.W.; Buster, J.E.; Preston, D.L.; Killam, A.P. Interrelationships of circulating maternal steroid concentrations in third trimester pregnancies. III. Effect of intravenous cortisol infusion on maternal concentrations of estriol, 16 alpha-hydroxyprogesterone, 17 alpha-hydroxyprogesterone, progesterone, 20 alpha-dihydroprogesterone, delta 5-pregnenolone, delta5-pregnenolone sulfate, dehydroepiandrosterone sulfate, and cortisol. J. Clin. Endocrinol. Metab. 1979, 49, 30–33. [Google Scholar] [CrossRef]
- Saketos, M.; Sharma, N.; Santoro, N.F. Suppression of the hypothalamic-pituitary-ovarian axis in normal women by glucocorticoids. Biol. Reprod. 1993, 49, 1270–1276. [Google Scholar] [CrossRef]
- Segebladh, B.; Bannbers, E.; Moby, L.; Nyberg, S.; Bixo, M.; Backstrom, T.; Sundstrom Poromaa, I. Allopregnanolone serum concentrations and diurnal cortisol secretion in women with premenstrual dysphoric disorder. Arch. Womens Ment. Health 2013, 16, 131–137. [Google Scholar] [CrossRef]
- Brownlee, K.K.; Moore, A.W.; Hackney, A.C. Relationship between circulating cortisol and testosterone: Influence of physical exercise. J. Sports Sci. Med. 2005, 4, 76–83. [Google Scholar]
- Anderson, T.; Lane, A.R.; Hackney, A.C. Cortisol and testosterone dynamics following exhaustive endurance exercise. Eur. J. Appl. Physiol. 2016, 116, 1503–1509. [Google Scholar] [CrossRef]
- Rubinow, D.R.; Roca, C.A.; Schmidt, P.J.; Danaceau, M.A.; Putnam, K.; Cizza, G.; Chrousos, G.; Nieman, L. Testosterone suppression of CRH-stimulated cortisol in men. Neuropsychopharmacology 2005, 30, 1906–1912. [Google Scholar] [CrossRef]
- Oyola, M.G.; Handa, R.J. Hypothalamic-pituitary-adrenal and hypothalamic-pituitary-gonadal axes: Sex differences in regulation of stress responsivity. Stress 2017, 20, 476–494. [Google Scholar] [CrossRef]
- Lehman, M.N.; Hileman, S.M.; Goodman, R.L. Neuroanatomy of the kisspeptin signaling system in mammals: Comparative and developmental aspects. Adv. Exp. Med. Biol. 2013, 784, 27–62. [Google Scholar] [CrossRef]
- Goodman, R.L.; Lehman, M.N. Kisspeptin neurons from mice to men: Similarities and differences. Endocrinology 2012, 153, 5105–5118. [Google Scholar] [CrossRef]
- Cravo, R.M.; Margatho, L.O.; Osborne-Lawrence, S.; Donato, J., Jr.; Atkin, S.; Bookout, A.L.; Rovinsky, S.; Frazao, R.; Lee, C.E.; Gautron, L.; et al. Characterization of Kiss1 neurons using transgenic mouse models. Neuroscience 2011, 173, 37–56. [Google Scholar] [CrossRef]
- Miller, B.H.; Gore, A.C. N-Methyl-D-aspartate receptor subunit expression in GnRH neurons changes during reproductive senescence in the female rat. Endocrinology 2002, 143, 3568–3574. [Google Scholar] [CrossRef]
- Ivanova, D.; O’Byrne, K.T. Optogenetics studies of kisspeptin neurons. Peptides 2023, 162, 170961. [Google Scholar] [CrossRef]
- Ottem, E.N.; Godwin, J.G.; Krishnan, S.; Petersen, S.L. Dual-phenotype GABA/glutamate neurons in adult preoptic area: Sexual dimorphism and function. J. Neurosci. 2004, 24, 8097–8105. [Google Scholar] [CrossRef]
- Putteeraj, M.; Soga, T.; Ubuka, T.; Parhar, I.S. A "Timed" Kiss Is Essential for Reproduction: Lessons from Mammalian Studies. Front. Endocrinol. 2016, 7, 121. [Google Scholar] [CrossRef]
- Watanabe, M.; Fukuda, A.; Nabekura, J. The role of GABA in the regulation of GnRH neurons. Front. Neurosci. 2014, 8, 387. [Google Scholar] [CrossRef]
- Maffucci, J.A.; Gore, A.C. Chapter 2: Hypothalamic neural systems controlling the female reproductive life cycle gonadotropin-releasing hormone, glutamate, and GABA. Int. Rev. Cell Mol. Biol. 2009, 274, 69–127. [Google Scholar] [CrossRef]
- Di Giorgio, N.P.; Bizzozzero-Hiriart, M.; Libertun, C.; Lux-Lantos, V. Unraveling the connection between GABA and kisspeptin in the control of reproduction. Reproduction 2019, 157, R225–R233. [Google Scholar] [CrossRef]
- Li, X.F.; Bowe, J.E.; Kinsey-Jones, J.S.; Brain, S.D.; Lightman, S.L.; O’Byrne, K.T. Differential role of corticotrophin-releasing factor receptor types 1 and 2 in stress-induced suppression of pulsatile luteinising hormone secretion in the female rat. J. Neuroendocr. 2006, 18, 602–610. [Google Scholar] [CrossRef]
- Breen, K.M.; Karsch, F.J. New insights regarding glucocorticoids, stress and gonadotropin suppression. Front. Neuroendocr. 2006, 27, 233–245. [Google Scholar] [CrossRef]
- Phumsatitpong, C.; Wagenmaker, E.R.; Moenter, S.M. Neuroendocrine interactions of the stress and reproductive axes. Front. Neuroendocr. 2021, 63, 100928. [Google Scholar] [CrossRef]
- Herman, J.P.; Mueller, N.K.; Figueiredo, H. Role of GABA and glutamate circuitry in hypothalamo-pituitary-adrenocortical stress integration. Ann. N. Y. Acad. Sci. 2004, 1018, 35–45. [Google Scholar] [CrossRef]
- Rasiah, N.P.; Loewen, S.P.; Bains, J.S. Windows into stress: A glimpse at emerging roles for CRH(PVN) neurons. Physiol. Rev. 2023, 103, 1667–1691. [Google Scholar] [CrossRef]
- Maguire, J. The relationship between GABA and stress: ‘It’s complicated’. J. Physiol. 2018, 596, 1781–1782. [Google Scholar] [CrossRef]
- Levy, B.H.; Tasker, J.G. Synaptic regulation of the hypothalamic-pituitary-adrenal axis and its modulation by glucocorticoids and stress. Front. Cell Neurosci. 2012, 6, 24. [Google Scholar] [CrossRef]
- Aguilera, G.; Liu, Y. The molecular physiology of CRH neurons. Front. Neuroendocr. 2012, 33, 67–84. [Google Scholar] [CrossRef]
- Gunn, B.G.; Cunningham, L.; Mitchell, S.G.; Swinny, J.D.; Lambert, J.J.; Belelli, D. GABAA receptor-acting neurosteroids: A role in the development and regulation of the stress response. Front. Neuroendocr. 2015, 36, 28–48. [Google Scholar] [CrossRef]
- Marraudino, M.; Miceli, D.; Farinetti, A.; Ponti, G.; Panzica, G.; Gotti, S. Kisspeptin innervation of the hypothalamic paraventricular nucleus: Sexual dimorphism and effect of estrous cycle in female mice. J. Anat. 2017, 230, 775–786. [Google Scholar] [CrossRef]
- Rao, Y.S.; Mott, N.N.; Pak, T.R. Effects of kisspeptin on parameters of the HPA axis. Endocrine 2011, 39, 220–228. [Google Scholar] [CrossRef]
- Angelopoulou, E.; Quignon, C.; Kriegsfeld, L.J.; Simonneaux, V. Functional Implications of RFRP-3 in the Central Control of Daily and Seasonal Rhythms in Reproduction. Front. Endocrinol. 2019, 10, 183. [Google Scholar] [CrossRef]
- Ullah, R.; Batool, A.; Wazir, M.; Naz, R.; Rahman, T.U.; Wahab, F.; Shahab, M.; Fu, J. Gonadotropin inhibitory hormone and RF9 stimulate hypothalamic-pituitary-adrenal axis in adult male rhesus monkeys. Neuropeptides 2017, 66, 1–7. [Google Scholar] [CrossRef]
- Iwasa, T.; Matsuzaki, T.; Yano, K.; Irahara, M. Gonadotropin-Inhibitory Hormone Plays Roles in Stress-Induced Reproductive Dysfunction. Front. Endocrinol. 2017, 8, 62. [Google Scholar] [CrossRef]
- Molnar, C.S.; Kallo, I.; Liposits, Z.; Hrabovszky, E. Estradiol down-regulates RF-amide-related peptide (RFRP) expression in the mouse hypothalamus. Endocrinology 2011, 152, 1684–1690. [Google Scholar] [CrossRef]
- Poling, M.C.; Kim, J.; Dhamija, S.; Kauffman, A.S. Development, sex steroid regulation, and phenotypic characterization of RFamide-related peptide (Rfrp) gene expression and RFamide receptors in the mouse hypothalamus. Endocrinology 2012, 153, 1827–1840. [Google Scholar] [CrossRef]
- Angelopoulou, E.; Inquimbert, P.; Klosen, P.; Anderson, G.; Kalsbeek, A.; Simonneaux, V. Daily and Estral Regulation of RFRP-3 Neurons in the Female Mice. J. Circadian Rhythm. 2021, 19, 4. [Google Scholar] [CrossRef]
- Ronnekleiv, O.K.; Qiu, J.; Kelly, M.J. Hypothalamic Kisspeptin Neurons and the Control of Homeostasis. Endocrinology 2022, 163, bqab253. [Google Scholar] [CrossRef]
- Blanchini, F.; Cuba Samaniego, C.; Franco, E.; Giordano, G. Aggregates of Monotonic Step Response Systems: A Structural Classification. IEEE Trans. Control. Netw. Syst. 2018, 5, 782–792. [Google Scholar]
- Jones, J.R.; Chaturvedi, S.; Granados-Fuentes, D.; Herzog, E.D. Circadian neurons in the paraventricular nucleus entrain and sustain daily rhythms in glucocorticoids. Nat. Commun. 2021, 12, 5763. [Google Scholar] [CrossRef]
- Skinner, D.C.; Evans, N.P.; Delaleu, B.; Goodman, R.L.; Bouchard, P.; Caraty, A. The negative feedback actions of progesterone on gonadotropin-releasing hormone secretion are transduced by the classical progesterone receptor. Proc. Natl. Acad. Sci. USA 1998, 95, 10978–10983. [Google Scholar] [CrossRef]
- Alon, U. An Introduction to Systems Biology: Design Principles of Biological Circuits; Chapman and Hall/CRC: Boca Raton, FL, USA, 2019; p. 320. [Google Scholar]
- Demori, I.; Giordano, G.; Mucci, V.; Losacco, S.; Marinelli, L.; Massobrio, P.; Blanchini, F.; Burlando, B. Thalamocortical bistable switch as a theoretical model of fibromyalgia pathogenesis inferred from a literature survey. J. Comput. Neurosci. 2022, 50, 471–484. [Google Scholar] [CrossRef]
- Klipp, E.; Liebermeister, W.; Wierling, C.; Kowald, A. Systems Biology: A Textbook; Wiley-Blackwell: Hoboken, NJ, USA, 2016; p. 504. [Google Scholar]
- Ferrell, J.E., Jr. Self-perpetuating states in signal transduction: Positive feedback, double-negative feedback and bistability. Curr. Opin. Cell Biol. 2002, 14, 140–148. [Google Scholar] [CrossRef]
- Bintu, L.; Buchler, N.E.; Garcia, H.G.; Gerland, U.; Hwa, T.; Kondev, J.; Phillips, R. Transcriptional regulation by the numbers: Models. Curr. Opin. Genet. Dev. 2005, 15, 116–124. [Google Scholar] [CrossRef]
- Russell, G.; Lightman, S. The human stress response. Nat. Rev. Endocrinol. 2019, 15, 525–534. [Google Scholar] [CrossRef]
- Mucci, V.; Demori, I.; Browne, C.J.; Deblieck, C.; Burlando, B. Fibromyalgia in Pregnancy: Neuro-Endocrine Fluctuations Provide Insight into Pathophysiology and Neuromodulation Treatment. Biomedicines 2023, 11, 615. [Google Scholar] [CrossRef]
- Burlando, B. A general hypothesis of multistable systems in pathophysiology. F1000Res 2022, 11, 906. [Google Scholar] [CrossRef]
- Desroches, M.; Guckenheimer, J.; Krauskopf, B.; Kuehn, C.; Osinga, H.M.; Wechselberger, M. Mixed-Mode Oscillations with Multiple Time Scales. SIAM Rev. 2012, 54, 211–288. [Google Scholar]
- Koseska, A.; Volkov, E.; Kurths, J. Oscillation quenching mechanisms: Amplitude vs. oscillation death. Phys. Rep. 2013, 531, 173–199. [Google Scholar] [CrossRef]
- Tolin, D.F.; Foa, E.B. Sex differences in trauma and posttraumatic stress disorder: A quantitative review of 25 years of research. Psychol. Bull. 2006, 132, 959–992. [Google Scholar] [CrossRef]
- Albert, P.R. Why is depression more prevalent in women? J. Psychiatry Neurosci. 2015, 40, 219–221. [Google Scholar] [CrossRef]
- de Kloet, E.R.; Joels, M.; Holsboer, F. Stress and the brain: From adaptation to disease. Nat. Rev. Neurosci. 2005, 6, 463–475. [Google Scholar] [CrossRef]
- Anacker, C.; Zunszain, P.A.; Carvalho, L.A.; Pariante, C.M. The glucocorticoid receptor: Pivot of depression and of antidepressant treatment? Psychoneuroendocrinology 2011, 36, 415–425. [Google Scholar] [CrossRef]
- Gjerstad, J.K.; Lightman, S.L.; Spiga, F. Role of glucocorticoid negative feedback in the regulation of HPA axis pulsatility. Stress 2018, 21, 403–416. [Google Scholar] [CrossRef]
- Turner, B.B. Sex difference in glucocorticoid binding in rat pituitary is estrogen dependent. Life Sci. 1990, 46, 1399–1406. [Google Scholar] [CrossRef]
- Agba, O.B.; Lausser, L.; Huse, K.; Bergmeier, C.; Jahn, N.; Groth, M.; Bens, M.; Sahm, A.; Gall, M.; Witte, O.W.; et al. Tissue-, sex-, and age-specific DNA methylation of rat glucocorticoid receptor gene promoter and insulin-like growth factor 2 imprinting control region. Physiol. Genom. 2017, 49, 690–702. [Google Scholar] [CrossRef]
- Vandevyver, S.; Dejager, L.; Libert, C. On the trail of the glucocorticoid receptor: Into the nucleus and back. Traffic 2012, 13, 364–374. [Google Scholar] [CrossRef]
- Arango-Lievano, M.; Lambert, W.M.; Bath, K.G.; Garabedian, M.J.; Chao, M.V.; Jeanneteau, F. Neurotrophic-priming of glucocorticoid receptor signaling is essential for neuronal plasticity to stress and antidepressant treatment. Proc. Natl. Acad. Sci. USA 2015, 112, 15737–15742. [Google Scholar] [CrossRef]
- Van Moortel, L.; Gevaert, K.; De Bosscher, K. Improved Glucocorticoid Receptor Ligands: Fantastic Beasts, but How to Find Them? Front. Endocrinol. 2020, 11, 559673. [Google Scholar] [CrossRef]
- Meltzer-Brody, S.; Colquhoun, H.; Riesenberg, R.; Epperson, C.N.; Deligiannidis, K.M.; Rubinow, D.R.; Li, H.; Sankoh, A.J.; Clemson, C.; Schacterle, A.; et al. Brexanolone injection in post-partum depression: Two multicentre, double-blind, randomised, placebo-controlled, phase 3 trials. Lancet 2018, 392, 1058–1070. [Google Scholar] [CrossRef]
- Deligiannidis, K.M.; Meltzer-Brody, S.; Maximos, B.; Peeper, E.Q.; Freeman, M.; Lasser, R.; Bullock, A.; Kotecha, M.; Li, S.; Forrestal, F.; et al. Zuranolone for the Treatment of Postpartum Depression. Am. J. Psychiatry 2023, 180, 668–675. [Google Scholar] [CrossRef]
- Caparros-Gonzalez, R.A.; Romero-Gonzalez, B.; Strivens-Vilchez, H.; Gonzalez-Perez, R.; Martinez-Augustin, O.; Peralta-Ramirez, M.I. Hair cortisol levels, psychological stress and psychopathological symptoms as predictors of postpartum depression. PLoS ONE 2017, 12, e0182817. [Google Scholar] [CrossRef]
- Iliadis, S.I.; Comasco, E.; Sylven, S.; Hellgren, C.; Sundstrom Poromaa, I.; Skalkidou, A. Prenatal and Postpartum Evening Salivary Cortisol Levels in Association with Peripartum Depressive Symptoms. PLoS ONE 2015, 10, e0135471. [Google Scholar] [CrossRef]
- Burlando, B.; Demori, I. Neurosteroids as a possible new horizon in the treatment of fibromyalgia. Med. Hypotheses 2024, 191, 111444. [Google Scholar]




| Symbol | Assigned Range/Value | Quantity | Ref. | |
|---|---|---|---|---|
| Variables | Scaled to | (see Box 1) | ||
| Variables of the harmonic oscillator generating a sinusoid trend | ||||
| Parameters | 2.5 | Hill coefficient of neuronal effects | [11] | |
| 6 | Hill coefficient of endocrine effects | [11] | ||
| 0.2 | half-saturation constant of neuronal effects measuring the threshold of inducing a significant response of | [11] | ||
| 0.3 | half-saturation constant of endocrine effects (see above) | [11] | ||
| 1 | weight of the self-limiting effect in neuronal elements | |||
| 1 | weight of the self-limiting effect in endocrine elements | |||
| 0.1, 0.2 | amplitude of oscillation | [57] | ||
| frequency of oscillation |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demori, I.; Siriya, S.; Burlando, B. Loop Modeling of the Reciprocal Inhibition Between HPA and HPG Endocrine Axes Reveals Transitions to Bistability and Critical Bifurcation Parameters. Appl. Sci. 2025, 15, 10483. https://doi.org/10.3390/app151910483
Demori I, Siriya S, Burlando B. Loop Modeling of the Reciprocal Inhibition Between HPA and HPG Endocrine Axes Reveals Transitions to Bistability and Critical Bifurcation Parameters. Applied Sciences. 2025; 15(19):10483. https://doi.org/10.3390/app151910483
Chicago/Turabian StyleDemori, Ilaria, Seth Siriya, and Bruno Burlando. 2025. "Loop Modeling of the Reciprocal Inhibition Between HPA and HPG Endocrine Axes Reveals Transitions to Bistability and Critical Bifurcation Parameters" Applied Sciences 15, no. 19: 10483. https://doi.org/10.3390/app151910483
APA StyleDemori, I., Siriya, S., & Burlando, B. (2025). Loop Modeling of the Reciprocal Inhibition Between HPA and HPG Endocrine Axes Reveals Transitions to Bistability and Critical Bifurcation Parameters. Applied Sciences, 15(19), 10483. https://doi.org/10.3390/app151910483






