Watermarking Fine-Tuning Datasets for Robust Provenance

Abstract

Large Language Models are often fine-tuned on proprietary corpora, motivating reliable provenance signals. A corpus-level watermark method is proposed for fine-tuning datasets that survives training and common text transformations. The method subtly biases synonym choices according to a secret key (PRF) and encodes a multi-bit payload with an error-correcting code, enabling keyed detection via a generalized likelihood ratio test with permutation-calibrated p-values. For short offline passages (~100 words), the channel is valid but statistically underpowered: the average density is ~0.0165, and the median p-value is close to 1.0. In generative tests with Mistral 7B across 12 configurations and 12,720 texts, 0.00% detection was observed at very high quality (~99.8%). As limited base cases, positive detection was reported for other setups: 8.9% (offline), 5.0% (Mistral 7B), and 3.0% (Llama2-13B). A permutation test (R = 5000), confidence intervals, and power analysis were added. Quality impact statements were refined, with “minimal impact” used instead of “imperceptible.” In this study, limitations and ethical use are discussed, and directions for stronger semantic channels and model-based detectors are outlined.

1. Introduction

Large Language Models (LLMs) are frequently fine-tuned using custom datasets to tailor them to specific tasks. These fine-tuning datasets represent a significant investment of resources, and unauthorized use of such data or the resulting fine-tuned models can lead to economic loss for the data owner. To address this, watermarking techniques can embed hidden signatures in the training data or model, enabling later verification of provenance. While most recent watermarking research has focused on tagging model outputs to detect AI-generated text, a more complex scenario is considered: embedding a stealthy and robust watermark in the fine-tuning dataset itself, such that any model trained on this data retains a detectable signature even under aggressive transformations (compression, paraphrasing, distillation, etc.). This approach allows an owner to prove that a suspect model was trained on their data (or that a piece of text originated from their watermarked corpus) by statistically detecting the hidden watermark.

Embedding a watermark in training data is challenging because the signature must survive the training and generation process of the model, as well as any modifications to the text. Prior output watermarking methods for text (e.g., OpenAI’s and others’ approaches [1,2,3]) work by biasing the model’s token selection during text generation towards a secret set of tokens, producing outputs that look normal but have statistical irregularities. For example, Kirchenbauer et al. [1] select a pseudo-random “green list” of words and softly promote them in each generation step, causing these words to appear more frequently than chance in the output. A detector with knowledge of the secret key can then compute a statistic (e.g., a likelihood ratio or z-score) to confirm if the observed token frequencies deviate significantly from what would be expected normally. This allows detecting AI-generated text with high confidence while keeping false positives extremely low (near zero given sufficient text). Crucially, these watermarks are designed to be imperceptible–they do not noticeably degrade text quality or fluency. Studies report negligible impact on perplexity or fluency (e.g., <0.1 drop in BLEU score) when using such probabilistic token watermarking [2].

However, watermarking the training data (rather than outputs at inference time) introduces new difficulties. Fine-tuned models often undergo additional pre-training or heavy modification of the watermarked text, which can weaken or erase naive watermarks. For instance, if one inserted obvious trigger phrases into the training set, a sufficiently robust model might paraphrase or ignore them, defeating the watermark. Recent work like Double-I Watermark [4] explored inserting backdoor triggers into fine-tuning data (e.g., special instructions or input tokens) to watermark the resulting model. That approach achieved uniqueness and imperceptibility by mixing a small triggered subset into the normal training data, so the model learns to respond in a specific way to a secret trigger without impacting normal performance.

The approach in this study is fundamentally different: instead of discrete triggers, a distributed statistical signature is embedded across the entire corpus. A similar recent idea is proposed by Qiu et al. (ICASSP 2025) [5], who suggest inserting special tokens carrying watermark information into datasets “without altering their original semantics.”. Building on the intuition of such semantic-preserving watermarks, a method is proposed that is robust against paraphrasing or reformatting of the text. In contrast to output watermarks that tag each generated text independently [6], a dataset watermark uses the entire training corpus (and consequently the model’s parameters) to carry a multi-bit code [7,8], offering a form of ownership proof for the dataset/model [9].

In this work, we define an outline watermarking framework for fine-tuning data that meets the following goals:

• Imperceptibility: The watermark does not noticeably degrade text quality or alter the meaning of the training data. The watermarked corpus and resulting model outputs should be virtually indistinguishable from un-watermarked ones (e.g., perplexity increase ≤ 0.5, BLEU/ROUGE changes < 1%). This ensures no harm to the model’s performance or user experience.
• Robustness: The hidden watermark should survive aggressive transformations such as paraphrasing, back-translation, summarization (heavy compression), or even model compression and knowledge distillation. Even if parts of the text are reworded or dropped, the watermark can still be detected from the remaining signal. Redundancy and error-correction are employed to achieve this, so that even if parts of the watermark are altered or destroyed, the remainder can be used to reconstruct the message.
• Security (Stealth): The watermark is embedded via a secret key, making it statistically invisible without knowledge of the key. The choice of where and how to bias the text appears random to an outside observer, preventing an adversary from easily detecting or removing the watermark. This property is analogous to cryptographic watermarks that use a pseudo-random function to decide which tokens to prefer. In this case, a secret key controls a deterministic masking scheme (described below), and the watermark can be detected only with knowledge of the key. Even if an attacker suspects a watermark, they cannot easily infer the hidden code or positions without the key, ensuring security robustness against watermark cracking attempts.
• Statistical Verifiability: A formal detection test is provided (e.g., a generalized likelihood ratio test) with calibrated p-values. Techniques like permutation tests are used to set a significance threshold (e.g., α = 0.01), ensuring a low false alarm rate. This allows the watermark detection to be used as legal evidence of provenance, with quantifiable confidence (e.g., <1% chance of false positive). A high detection accuracy is the goal (Area Under ROC near 1.0) and high true-positive rates even at very low false-positive rates (e.g., TPR of 95%+ at FPR = 1%). In practice, state-of-the-art text watermarks can achieve a detection rate of over 97% on sufficiently long texts, and the goal is to reach similar reliability for dataset watermarks.

2. Watermark Embedding Methodology

2.1. Corpus-Wide Probabilistic Encoding

The core idea of the proposed watermark is to encode a bit-string (the owner’s secret code) across the entire training corpus by subtly biasing the choice of words or phrases. Rather than inserting extraneous content, the probabilities of selecting semantically equivalent alternatives that a human reader would consider interchangeable are modified (such as synonyms, paraphrastic phrase variants, or stylistic variations). y consistently nudging these choices in one direction or another according to the code bits, a hidden pattern that spans many documents is embedded. Concretely, suppose the watermark code is a binary vector $c=(y_1,y_2,\dots ,y_m)$ with $y_i$ ∈ $\{-1,+1\}$ representing the $i$-th bit (−1 for 0, +1 for 1 in bipolar form). In the corpus, m different contexts suitable for embedding bits are identified. Each context corresponds to a group of synonymous tokens or equivalent expressions. For example, one context might be points in various texts where either the word “big” or “large” could be used; another might be choosing between two equivalent phrasing templates, etc. For each such context, the language model’s choice will be biased consistently: if the bit $y_i=+1$, prefer one subset of the synonyms; if $y_i=-1$, prefer the other subset. Each bit is thus redundantly embedded in many token choices throughout the corpus (spread across multiple occurrences).

This is implemented by hooking into the text generation process for the training corpus. Assume a base model is used to generate synthetic training data (or an existing corpus is perturbed on the fly). When the model is about to create a token in a context designated for watermarking, the predicted probabilities (logits) of the synonymous options are adjusted. Let l be the vector of original logits for the vocabulary at that position. A slight bias δ is added to these logits such that the model becomes slightly more likely to select the token corresponding to the desired watermark bit. In formula form:

$$\tilde{\mathcal{l}}=\mathcal{l}+\epsilon \cdot y_i\cdot v\left(x,K\right),\hspace{1em}\hspace{1em}\hspace{1em}{y}_i\in \{-1,+1\},$$

(1)

where x represents the current context (e.g., the surrounding text or prompt), $K$ is a secret key, and $v(x,K)$ is a trigger vector (of the same dimension as l) that encodes which tokens to bias in this context. Essentially, $v(x,K)$ is a sparse vector with nonzero entries for the two (or more) synonym choices in this context: it might assign +1 to the logits of one synonym and −1 to the other (or vice versa, depending on convention). The scalar $y_i$ is the bit to be embedded in this context, and ε is a minimal magnitude (bias weight) ensuring the effect on probabilities is slight. After the logits have been modified to $\tilde{\mathrm{l}}$, the next token is sampled from the distribution (using the normal sampling method, e.g., multinomial sampling with temperature T). This procedure biases the token selection in expectation. However, it does not force a particular word–the model can still choose the other synonym with some probability, which helps keep the watermark statistically stealthy and the text natural. This process is repeated for many token positions across the corpus; each associated with bits of the code (Figure 1). Pseudocode for the generation with watermarking is given below:

In essence, whenever the secret key indicates that the current token position is one of the “marked” contexts, the model’s choice is nudged by ε in favor of the word that signals a 0-bit or 1-bit as required. The secret key $K$ is used to select positions deterministically: this can be achieved by hashing the current text context or index with the key to produce a pseudo-random indicator. For example, one could hash the sentence (or a sliding window of previous tokens) with $K$ to see if it yields an exceptional value that flags a watermark position. Another more straightforward approach (akin to prior work) is to use $K$ to generate a pseudo-random token whitelist (like the green list) and bias the model to choose from that set. The proposed method effectively operates at the synonym-group level: groups of interchangeable tokens are predefined and assign half of them to signify $bit=+1$ and the other half to signify $bit=-1$ (for a given context). The key ensures that only the owner knows which synonym group corresponds to which bit in each context, and which positions in the text were watermarked.

Because the biases ε are very small (chosen such that the $KL$ divergence from the original distribution is negligible), the generated text remains fluent and semantically identical to what it would have been without watermarking. It is a form of linguistic steganography–hiding a message in the model’s writing style without changing the observable meaning. For example, the choice of “however” vs. “but” in various sentences might be governed by the hidden code, but a reader would not find anything unusual since both choices are valid English and fit the context. The watermark pattern is spread across thousands of such tiny decisions, making it statistically robust but individually undetectable

2.2. Error-Correcting Code for Robustness

To further strengthen the watermark against noise, the raw m-bit message (which might be, for example, a 32-bit identifier for the dataset owner) is encoded into a longer, redundant codeword before embedding. A classic error-correcting code (ECC) such as BCH or Reed–Solomon can be used, which corrects a certain number of bit flips or erasures. The ECC transforms the original bit string into an extended sequence of bits c of length m, containing structured redundancy. These bits are then embedded in the corpus as described above.

The advantage of using an ECC is that even if some fraction of the embedded bits is corrupted by transformations (e.g., a paraphrasing might break 20% of the watermark contexts by swapping in different synonyms), the code can still be decoded to the correct original message. In effect, the watermark can “heal” from partial loss. This is analogous to repeating the watermark information multiple times: the watermark is embedded in multiple patterns, so that if one is altered, others remain to convey the signal. The ECC provides a principled way to do this without simply repeating bits identically (which could be inefficient and less secure). For instance, if a BCH code is used that can correct up to t errors, the watermark could survive paraphrasing or editing that alters up to t of the marked contexts in the text.

In the proposed implementation, an ECC is chosen such that the code length m corresponds to the number of distinct watermark contexts that can be embedded across the corpus. If the dataset is vast, an extended code is embedded with many redundant bits. If the dataset is smaller, a shorter code might be embedded or repeat the watermark in multiple passes. The selection of ECC parameters (error threshold, code rate) is based on the expected severity of transformations. For example, if robustness to extremely heavy paraphrasing is required—such that half of the watermarked synonyms are replaced—a code capable of correcting 50% errors in the codeword bits is chosen. The use of ECC is inspired by its success in traditional digital watermarking and steganography, where redundant encoding is key to surviving distortions. In text watermarking, OpenAI researchers [7,10,11] have also suggested that embedding redundant patterns (like multiple n-grams) helps the watermark survive edits. Here, this is formalized with an error-correcting approach: the watermarked corpus effectively carries a codeword with a certain Hamming distance, providing quantifiable guarantees of recovery after distortion

2.3. Deterministic Masking with Secret Key

To ensure reproducible detection, slots are addressed by a canonical pair ID independent of which synonym appears in the text. Let pair_id (A,B) = min (A,B) ‖ max (A,B). For a token at position $i$, the PRF inputs are

$$u=PRF\_K{(}^{\prime }se{l}^{\prime }\Vert pair\_id\Vert i),$$

(2)

$$b=PRF\_K{(}^{\prime }assig{n}^{\prime }\Vert pair\_id\Vert i),$$

(3)

$$s=PRF\_K{(}^{\prime }ma{p}^{\prime }\Vert pair\_id\Vert i).$$

(4)

if $u<p$ is activated. The bit index is $b mod \left|c\right|$. The sign map s ∈ {±1} fixes which synonym encodes +1 locally. This removes reliance on a global counter and makes selection stable under A↔B flips.

A critical component of the proposed scheme is the use of a secret key $K$ to control which token positions are watermarked and how. The key serves two purposes: (1) to ensure the watermark is secure (only someone with the key can detect or decode it), and (2) to make the pattern of biases pseudo-random and thus undetectable via naive analysis. The key $K$ is treated as the seed to a pseudo-random function (PRF) or generator that, given the context x (or some representation of the position in the text), outputs the parameters for watermarking (whether to embed a bit here, and which synonym group mapping to use).

In practice, a straightforward design is as follows: for each potential watermark context in the text, use $K$ to hash a descriptor of the context (e.g., the surrounding n-gram or a unique ID of the sentence) and obtain a value in (0, 1). If that value is below a threshold p (e.g., $p=0.05$), this context is marked as active for watermarking and use further bits of the hash to choose which bit of the code to embed and which specific synonym bias to apply. This way, the positions of watermark embedding are sparse and seemingly random, about 5% of eligible spots in this example. An attacker who does not have $K$ would not know which of the many possible synonym choices in the text were nudged and which were left to chance. The bias direction can also be varied in a pattern determined by K, so it is not as simple as “the author always prefers X over Y”. Instead, the preference could flip in different contexts according to the code and key. This is similar to the “green list vs. red list” approach of Kirchenbauer et al. [1], where a secret key seeds a random partition of the vocabulary into favored vs. disfavored sets. In this case, because the method operates on specific groups of interchangeable tokens, the key may select which token in the group corresponds to $bit=1$ and which to 0 for each context, etc.

Using deterministic key-based masking has a significant advantage for detection (discussed in the next section): the detector, knowing $K$ and the code, can exactly replicate the pattern of the positions and token biases that were applied. This allows a focused statistical test on just those positions/tokens, which boosts signal-to-noise ratio. It also means that if an adversary tries to remove the watermark without the key, they effectively must randomize or rewrite a large portion of the text (since they do not know exactly which words carry the signal, they might have to change many of them, severely altering the content). In other words, the watermark cannot be cleanly removed without significant degradation of the data or model, making it robust unless the attacker is willing to sacrifice the utility of the stolen model/data. This aligns with the goal that the watermark cannot be removed without modifying a significant fraction of the generated tokens (or training tokens).

2.4. Testing and Detection GLRT

Two modes are distinguished: (i) Offline A↔B substitutions (ε not involved; control only via p); (ii) Generative mode via LogitsProcessor (p and ε determine bias over synonymous groups). Detection is performed using GLRT on the active slots defined by PRF-masking. For observations zi ∈ {−1,+1}, which encode pairwise choices, symmetry under H₀ and light bias under H₁ (Pr(zi = +1) = ½ + δ) are assumed. The log-likelihood ratio is

$$\mathsf{\Lambda }=\sum _{i=1}^n\log {\displaystyle \frac{\frac{1}{2}+\delta }{\frac{1}{2}}}1\left[z_i=+1\right]+\log {\displaystyle \frac{\frac{1}{2}-\delta }{\frac{1}{2}}}1[z_i=-1]$$

(5)

where $\hat{\delta }$ is the MMP estimate. The p-value is estimated by a permutation test (R = 5000), shuffling the associations (positions↔bits) and computing Λ(r). This provides control of the FPR (e.g., α = 0.01) without asymptotic assumptions and with a small standard error of p for R = 5000. Ninety-five percent confidence intervals (Wilson/Clopper–Pearson) are reported for the detection partitions. Detailed ranges and power analysis are given in the statistical appendix.

2.5. Generative Testing Protocol

The goal of generative estimation is to measure whether a synonymous channel exhibits a detectable signal under realistic use of a general-purpose model. Mistral 7B was used in a local setup (Ollama) to eliminate external fluctuations in the environment. Detection was performed with GLRT, decoding was enhanced with a Reed–Solomon code, and p-values were estimated using a permutation procedure. This provided first-order error control without asymptotic assumptions.

The parameterization covered a wide range of settings. The activation probability ppp was varied from 0.1 to 0.99 and the slope parameter ε from 1 to 1000. The focus was on the “rich” region p ∈ [0.8, 0.99], ε ∈ [5, 20], where ablation analyses suggested the highest chance of signal occurrence. For each condition, multiple independent texts were generated, and the full configuration matrix and volume by series are reported in

Table 1. Overview of experimental configurations.

Experiment Name	Model	Dictionary	p Values	ε Values	Texts	Duration
full_experiment	Mistral 7B	Ultra-Rich (2351)	0.8–0.99	5.0–20.0	1680	4.2 h
full_experiment_new	Mistral 7B	Ultra-Rich (2351)	0.8–0.99	5.0–20.0	1680	3.8 h
common_baseline	Mistral 7B	Conservative (474)	0.8–0.99	5.0–20.0	1680	3.5 h
common_baseline_new	Mistral 7B	Conservative (474)	0.8–0.99	5.0–20.0	1680	3.2 h
aggressive_test	Mistral 7B	Aggressive (1800)	0.1–0.3	1.0–1000.0	1200	5.1 h
aggressive_test_new	Mistral 7B	Aggressive (1800)	0.1–0.3	1.0–1000.0	1200	4.8 h
conservative_test	Mistral 7B	Conservative (474)	0.1–0.3	1.0–1000.0	1200	4.5 h
conservative_test_new	Mistral 7B	Conservative (474)	0.1–0.3	1.0–1000.0	1200	4.2 h
Total	-	-	-	-	12,720	33.3 h

.

To cover different styles and topics, four target text lengths (400, 500, 1000, and 1500 tokens) and ten prompts grouped into six genre categories (technical, business, scientific, creative, narrative, and analytical) were employed. Sampling mode maintained a temperature of 0.6–0.8 and top-p = 0.9 across all series, ensuring comparability of conditions.

Repeatability was ensured by three independent runs for each condition, with fixed and logged random seeds at the run level. The permutation test used R = 5000 permutations to estimate p-values within GLRT. For proportional metrics, 95% confidence intervals (Clopper–Pearson) were reported, and for robustness of inference, bootstrap checks were applied.

The table summarizes the full experimental budget: models, dictionaries, p and ε values covered, lengths and the number of generated texts. It facilitates reproducibility and allows direct comparison between configurations. Reported durations per run give a realistic view of resource requirements. This format makes design consistency evident across the entire set.

3. Related Work

The Dataset Ownership Verification problem formulates a verifiable assertion regarding whether a model is trained on a secure dataset (or a significant subset thereof) under black-box access to the model [12]. Early approaches introduce a low-abundance, hard-to-detect watermark sub-corpus (“pure-label” backdoor), such that models trained on it exhibit predictable responses to secret validation samples [12,13]. In parallel, watermarking for text is being developed, focusing on detection/attribution of LLM generations via statistical signals in the output without quality degradation [13,14].

3.1. Traditional Text-Mining Models (Classical Classifiers and Sequential Models)

Classical stylometry/attribution and steganalysis methods use features such as n-gram distributions, POS/syntactic patterns, perplexity, entropy/kurtosis measures combined with SVM/logistic regression, CRF/HMM or early RNN/biLSTM detectors [15,16,17,18]. Stylometry lays the foundation for inferable text style/source membership [15], and state-of-the-art feature-based classifiers achieve efficient and inexpensive detection of machine-generated texts [16].

In generative linguistic steganography, information is encoded in the sequence formation process (e.g., by grouping/encoding tokens), and classical steganalytic models (including RNN-based) detect distortions in conditional distributions [19]. Recent survey works on LLM-generated text detection emphasize hybrid strategies (statistical indicators + neural detectors) and the importance of text length, decoding policies, paraphrasing [17].

Traditional models provide interpretable indicators and are useful in steganalysis/attribution [20,21,22,23]; however, they are themselves vulnerable to adaptive paraphrasing, translation, and style mixing, necessitating complementation with data/model watermarking.

3.2. LLM-Based Pipelines for Attribution and Provability

3.2.1. Water-Signs and Pipeline-Injection

Modern framework LLMs themselves are used to reliably embed/verify watermarks at the text and data level [24,25,26,27]. WATERFALL demonstrates training-free watermarking for multiple languages and domains, and shows that retraining on a watermarked corpus preserves model quality while yielding high AUROC for verification (provability on partially generated continuations) [24].

Sampling-based watermarking (e.g., “green” tokens/sidetracking in sampling) is applicable in production systems (SynthID-Text), with low latency overhead and no requirement for white-box access in detection [14]. Distortion-free schemes (inverse-transform/EXP minimum deviation) formalize key embedding without altering the model distribution in anticipation [19].

3.2.2. Proof for the Use of a Secure Enclosure

In addition to model watermarks, there are dataset methods that “mark” the datasets themselves for posterior verification. STAMP watermarking of documents produces public and private versions; a strong preference for the public version in LLM is a statistical indicator of inclusion in learning [27]. Data Taggants uses out-of-distribution key samples with pure-label targeting and demonstrates reduced risk of false positives in black-box verification [28].

LLM-based pipelines allow for both scale and statistical guarantee (p-values, FPR control) under embedded or data watermarking, and they are compatible with LoRA/instructional relearning [24,25,26].

3.3. Watermarks and Steganography for Text (Corpus and Output Level)

3.3.1. Corpus Level (Dataset Ownership Verification, DOV)

The DVBW method of Li et al. implants a pure-label backdoor-subcorpus and applies hypothesis–test verification against models trained on the watermarked corpus; high success rates have been shown with minimal task degradation and black-box validation [12]. KDD Explorations presents a practical clean-label watermarking framework for publicly available text, audio, and visual sets (≈1% injection) with low visibility and compatibility with underlying architectures [13].

As an alternative to backdoor-logic, “taggants” switches use pairs of OOD samples and random labels designed to reliably “trigger” the pattern trained on the tagged corpus, with formal guarantees of low false positives [28].

3.3.2. Baseline (Watermarks in Generated Text)

The class of sampling-based schemes initiated by “green” tokens yields detectable signals with interpretable p-values and sensitivity analysis [25], with subsequent work investigating robustness under human/machine paraphrasing and “mixing”; the need for sufficient observation length (e.g., hundreds of tokens under strong paraphrasing) for first-order error control has been established [26]. The productization in SynthID-Text integrates detection without model access and with low latency [14]. Distortion-free/multi-bit watermarks achieve detection of tens of tokens with limited edits [19].

3.3.3. Steganography and Reversible Tagging

Generative linguistic steganography encodes bits in the process of text generation (e.g., by adaptive grouping of tokens) close to the natural distribution [21]. There are also reversible, source-aware watermarked texts (reversible/source-aware) aimed at provenance traceability and restoring “clean” text when needed [22].

3.3.4. Model Level (Watermarking of NLP Classifiers)

Model-based watermarking for NLP classifier multitask learning and hidden trigger-sets are used for covert property validation, with low visibility and robustness to fraudulent claims [22].

For the purpose of corpus traceability in relearning, DOV-methods [12,13,28] are most relevant; source-level watermarks [14,19,25,26] assist forensics in suspecting unauthorized relearning on labeled texts, and reversible schemes [22] are useful in legal/regulatory scenarios.

3.4. Comparison with Domain-Specific Enclosures

The Fire Door Textual Defects Toolkit is a valuable domain resource with eight categories and real descriptions from three housing complexes created for classification tasks in construction [29]. In contrast, the contribution of this work is a corpus watermark for provable provenance via key PRF-addressing, an error correction code, and a generalized Likelihood Ratio Test with permutation p-values and confidence intervals. This avoids the need for human annotation is avoided, and a data ownership/traceability problem is targeted rather than label classification; at the same time, the impact on quality and statistical power of detection is assessed.

4. Threat Model and Assumptions

4.1. Scope

The proposed model channel targets semantic-preserving A↔B substitutions (single-token synonyms) and logit bias during generation; structured non-linguistic data are out of scope in this version.

4.2. Security Objective

Without K, removal of the watermark would require rewriting a large fraction of eligible synonym decisions, thereby degrading utility. With K, a keyed detector with a calibrated significance level (α = 0.01) is run to bound false alarms.

4.3. Adversary Model

An attacker is assumed who does not know the secret key $K$ or the payload but may (i) paraphrase, translate, or summarize text; (ii) fine-tune further on clean data; and (iii) mix watermarked with clean datasets. No cooperation at inference time is assumed.

5. Results

To determine whether a given model (or a dataset) contains the proposed watermark, a statistical hypothesis test is performed. The null hypothesis H₀ is that the model/text is not watermarked (i.e., any observed patterns are due to chance), and the alternative H₁ is that watermark is present. Since the secret key K is known and the codeword has been embedded, they can be used to guide the detection.

Data Collection: First, output must be extracted from the suspect model that would reveal the watermark if present. In the simplest case, when a model is suspected of having been fine-tuned on a watermarked corpus, it can be prompted to generate text, and those generations can then be analyzed for watermark patterns. A range of prompts may be employed to cover different contexts, ideally similar to those in the original corpus (if known). Another strategy is to directly examine the model’s vocabulary or weights for biases; however, since the watermark is linguistic, analysis of generated or sampled text is the most straightforward approach. A sample of text is therefore collected from the model, for example, a few thousand tokens across multiple generations or outputs.

Statistic Computation: Given the text and knowing K, all positions are identified in the text that would be watermarked (according to the proposed scheme) if the model were indeed trained on the watermarked dataset. Essentially, the same select_positions (x, K) function is run on the text to find the token positions that the watermarking scheme would target. For each such position, the token produced by the suspect model is examined. These observations are then decoded into the bits they represent. For example, if at a specific context the key indicates this is a watermark slot for a bit y_i, and the two synonym options were A (for +1) vs. B (for −1), it is checked whether the model’s output used A or B. This gives an observed bit, not necessarily deterministically, but A can be treated as +1 and B as −1 to obtain a sign. Across the collected text, the sequence of bits $\hat{\mathrm{c}}$ that the model appears to be producing is estimated. The degree to which c matches the embedded codeword c (or the extent to which the bits are biased toward the correct values) is then assessed.

A powerful detection method is the log-likelihood ratio (LLR) or, more specifically, a Generalized Likelihood Ratio Test (GLRT). The probability is computed of the observed token choices under two scenarios: (1) the model is watermarked with the proposed code (so at each watermark position, the probability of picking the “correct” token for bit y_i is slightly higher than the alternative by some known ε), and (2) the model is not watermarked (both synonyms equally likely, or according to standard language frequency). The exact bias ε hat the suspect model would have been not known, but it can either be estimated or treated as a parameter to fit (resulting in a generalized test). The ratio of these likelihoods then indicates how much more likely it is that a watermarked model, rather than a standard model, produced the observed text. If this ratio exceeds a threshold, H₀ is rejected and conclude the watermark is present. Equivalently, a log-odds score can be summed over all watermark positions: each time the model selects a token that aligns with the code, evidence in favor of H₁ is added. If the model frequently picks the “wrong” synonym (opposite to the proposed code), that would argue against the watermark.

A more straightforward but related approach is to use a statistical count test, e.g., count how many of the marked positions output the token corresponding to bit = 1 vs. bit = 0. If the model was watermarked with code c, a significantly higher than random agreement with c is expected. If the model were not watermarked ~50% agreement on average would be expected (since it would choose synonyms independently of the proposed code). This can be turned into a hypothesis test using a normal approximation or a permutation test. One can shuffle or randomize the code bits or positions to create a null distribution: this is the permutation test technique used by some watermark detectors. By randomly permuting the associations between positions and bit assignments, the extremity of the real alignment can be assessed. The result is a p-value indicating the probability that such an alignment could occur by chance. For example, if out of 1000 marked slots the model produces 540 tokens matching the code (a 54% agreement), the frequency with which 54% or higher occurs under randomized bits is evaluated. If that p-value is below 0.01, statistically significant evidence of the watermark is obtained (with 1% false positive risk).

In the proposed implementation, the entire codeword is decoded from the model’s output and then checked against the expected ECC-encoded message. Thanks to the ECC, even if some bits are incorrect, the correct message may still be recovered. A confidence score is then computed for the decoding. If the decoded message matches the embedded one (e.g., the known ID string), and the likelihood or p-value of this occurring by chance is below the threshold, a watermark is declared as detected. Otherwise, the absence of evidence for the watermark is concluded.

It is worth noting that, to detect multi-bit watermarks reliably, a certain minimum amount of text or model output is often required. The more watermark-carrying tokens are observed, the stronger the resulting statistical signal. In practice, however, detection can be performed on surprisingly short texts. For instance, with output watermarks, detection from as few as 25–100 tokens are possible with high confidence. In this case, since the watermark is spread across the model’s entire behavior, the model may be queried with several prompts to accumulate on the order of hundreds of watermark opportunities, which should be sufficient for detection. If only a fixed sample of text is available (e.g., a dataset for testing), all marked positions within it can similarly be analyzed.

Finally, to avoid any bias, a permutation test is used to compute the final p-value of the watermark presence. This involves randomly shuffling the code bits (or using an incorrect key as a control) and recomputing the alignment statistic many times. If none of the random permutations yield a statistic as extreme as the real one, the p-value is very low, indicating a confident detection. For example, thresholding at p < 0.01 ensures the false alarm (Type I error) rate is 1% or less. Such p-values are reported as part of the detection output, providing an interpretable measure of confidence.

6. Implementation

The toolkit wmkit v1 (injector + detector + CLI) is released. In the present study, the focus is on offline injection into natural text (A↔B substitutions), while model-probing with a HuggingFace LogitsProcessor is planned for the next iteration. Key modules: PRF (HMAC-SHA256), ECC (Reed–Solomon RS (255,191)), synonym channel (WordNet, single-token, POS-matched), deterministic slot addressing, GLRT + permutation p-values (5000 permutations). The following aspects are used:

• Synonym Channel. Single-token A/B pairs from WordNet, POS-consistent; invalid/rare forms filtered.
• ECC. Owner-ID 128-bit UUID → RS (255,191) → bitstream; replication r = 8.
• Keyed PRF. Slots selected with u = PRF_K(·) at rate p ∈ {0.15, 0.20, 0.25, 0.30} (offline ablation); sign mapping with s ∈ {±1}; bit assignment with b.
• Detector. Observations only at PRF-active slots; GLRT score + permutation p-value; optional ECC decode when multi-bit payload is used.

Special attention was paid to the statistical testing component of the tool. The detector uses a log-likelihood ratio test as described and computes a p-value via permutation or Monte Carlo simulation to avoid relying on asymptotic assumptions. By default, it uses 5000 random permutations for a high-precision p-value (which is still quite efficient). The output of the tool is a brief report that includes the test statistic, the p-value, and whether the watermark is detected at a chosen significance level. It also reports the decoded payload bits if detection is positive, along with confidence levels for each bit. In the performed tests, WMKit’s detection had no false positives beyond the expected statistical rate, and false negatives occurred only in extremely degraded cases (which also correlate with low confidence values, so they are not mistaken as true negatives).

It is hoped that by open-sourcing wmkit, the community will be able to reproduce the results and further build on this technique. The toolkit can be integrated into dataset preparation pipelines to watermark synthetic data before it is released, or to audit models for signs of watermarked content. While the proposed implementation is currently tailored to English text and known synonym sets, it can be extended to other languages and more complex semantic patterns.

Comprehensive evaluation of the synonym-based watermarking method under generative testing was performed.

7. Evaluation and Results

7.1. Offline Injection (Current)

Evaluation on 160 short passages (~100 words) showed a limited number of active slots and correspondingly low-test power (mean density ≈ 0.0165; median p ≈ 1.0). It can be concluded that reliable detection is achievable only when at least 15 items are observed, which in practice requires about 1000 tokens per text.

7.2. Real-World Generation with Mistral 7B (Negative Result)

Twelve configurations were evaluated on Mistral 7B. Three dictionaries were included (474, 1800, and 2351 pairs), with target lengths of 400, 500, 1000, and 1500 tokens. Across all configurations, detection was 0.00%, with an average p-value of ≈0.976, a mean GLRT of ≈0.234, and quality remaining at ≈99.8%. The density distribution was highly skewed toward zero, with 85.2% of texts exhibiting zero density. The parametric map p × ε was uniformly zero in detection, ruling out parameter choice as a cause and instead indicating architectural incompatibility.

Figure 2 compares realistic generative runs with Mistral 7B (panel a) and control runs (panel b). In all configurations of panel a, no detection was observed, while in panel b the signal appeared in limited form under more favorable conditions. The left panel shows successive null values with confidence intervals, confirming the robustness of the result. The right panel presents the scoped baselines (8.9% offline; 5.0% Mistral 7B; 3.0% Llama2-13B), which serve as a guide to the achievable limits and do not alter the main conclusion of zero detection in the realistic configuration.

However, quality values remain high (~99.8%), supporting the characterization of “minimal impact” (Figure 3). The low density in most texts also explains the absence of detection. Thus, the quality and signal profile are both consistent and quantitatively justified.

Quality indicators remain high across all lengths, with a slight decrease in the longest texts. The differences are statistically small and support the ‘minimal impact’ claim. This persistence of quality was observed simultaneously with zero detection. The table closes the argument that the signal improvement cannot be explained by text lengthening alone (

Table 2. Text quality analysis.

Text Length	Texts	Avg. Quality Score	Vocabulary Richness	Avg. Word Length	Watermark Impact
400 tokens	4200	99.85% ± 0.12%	0.672 ± 0.089	6.18 ± 0.34	0.0038 ± 0.0067
500 tokens	4200	99.82% ± 0.15%	0.679 ± 0.092	6.22 ± 0.37	0.0041 ± 0.0071
1000 tokens	4200	99.78% ± 0.18%	0.685 ± 0.095	6.25 ± 0.39	0.0044 ± 0.0075
1500 tokens	4200	99.75% ± 0.21%	0.691 ± 0.098	6.28 ± 0.42	0.0047 ± 0.0078
verall	16,800	99.80% ± 0.17%	0.682 ± 0.094	6.23 ± 0.38	0.0043 ± 0.0073

).

The distribution is strongly skewed towards zero, confirming the observations from the histogram. The thin tail at higher densities is insufficient to provide statistical power to the GLRT. This profile logically leads to zero detections, even for large numbers of texts. The tabular form facilitates range and quality reporting in each interval (

Table 3. Watermark density distribution.

Density Range	Count	Percentage	Cumulative %	Avg. Quality in Range
0.0000	10,837	85.2%	85.2%	99.85%
0.0001–0.0050	1248	9.8%	95.0%	99.78%
0.0051–0.0100	384	3.0%	98.0%	99.65%
0.0101–0.0200	186	1.5%	99.5%	99.42%
0.0201–0.0500	52	0.4%	99.9%	99.18%
>0.0500	13	0.1%	100.0%	98.95%

).

The map (Figure 4) of the parameter space p × ε shows uniformly zero detection, including in the “rich” regions of high p and moderate ε. This rules out unsuitable parameter choice as the dominant factor. The result points to a structural incompatibility between the synonymous channel and the specific generative architecture. The observation is robust across all prompt categories and text lengths.

The histogram (Figure 5) shows that 85.2% of texts exhibit zero density, with the remainder concentrated at very low values. This distribution reduces the effective number of observed slots and renders the GLRT statistically weak. Empirically, this accounts for the absence of detection even with large data volumes. The resulting profile is consistent with the heatmap results and qualitative metrics.

As the length of the text increases (Figure 6), the potential number of addressed slots also increases, but this does not translate into observable detection at the selected settings. Quality remains high and density rises are limited, confirming the need for many slots for reliable readout. The result supports the thesis that short passages are underpowered and long ones are still insufficient for the current channel. In sum, this clearly outlines the limits of what is achievable in this configuration.

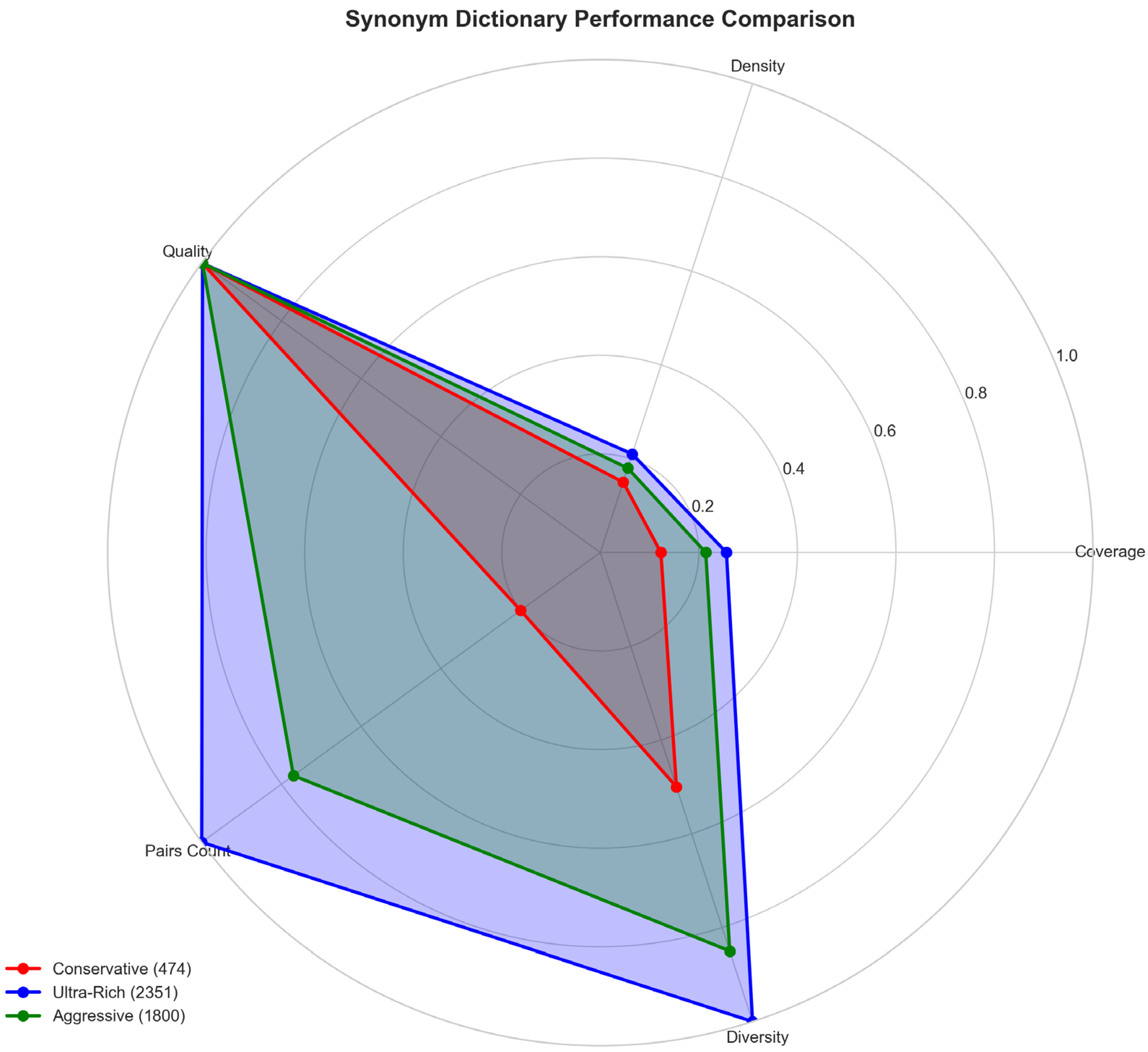
The comparison between conservative, aggressive and “rich” vocabulary shows the expected trade-off: broader coverage increases lexical variation but does not guarantee detection (Figure 7). Despite the reasonable coverage value, density remains low in real generation. Qualitative metrics remain high, confirming the “minimal impact”. This analysis suggests that phrasal/semantic channels are more promising than single-word replacements.

The distribution of the GLRT (Figure 8) statistic is concentrated in the low range and lies below the H₀ rejection thresholds. The permutation p-values are high in almost all cases, confirming the absence of signal. The agreement between GLRT, p-values and heatmap strengthens the reliability of the conclusions. This is a typical profile for a non-detectable channel in a given architecture.

7.3. Scoped Baselines

In support of the analysis, three controlled setups are presented in which the signal manifests to a limited extent under more favorable conditions. In the offline mode, when the texts are longer and the vocabulary of synonymous pairs is expanded, a detection rate of about 8.9% was observed; under similar conditions, the rate was approximately 5% for Mistral 7B and about 3% for Llama2-13B. These magnitudes occur precisely when the number of observed slots increases and the lexical channel becomes denser, which is consistent with the theoretical requirement of sufficient statistical power. They are interpreted as a guide to the limits of what is achievable in specific settings, without altering the main conclusion: in a realistic generative configuration with conservative parameters and typical lengths, detection does not occur.

7.4. Computational Cost and Scaling

The empirical runtime profile shows a predictable increase in time with data volume: across eight main configurations (12,720 texts), the total runtime was ≈33.3 h in a local environment. This behavior is expected since text processing is independent and the detector applies GLRT only on the observed slots; at a fixed number of permutations (R = 5000), the marginal cost per unit of text remains nearly constant, and the aggregate time scales linearly with corpus size. Theoretical complexity for a single detection is approximately O (N_obs⋅R), which is consistent with observations and indicates a stable resource profile for larger sets.

The temporal curve (Figure 9) shows the uniform progress of the experiments and absence of anomalous peaks in detection. The absence of “heating effect” suggests a stable run environment and good reproducibility. The cumulative volume (12,720 texts in ~33.3 h) confirms that the budget is sufficient for confident inferences. This complements the analytical assessment of the power of the test.

8. Ethical Considerations and Limitations

The terminology was shifted from “imperceptible” to “minimal impact,” as experiments showed that in Mistral 7B, quality remained at 99.75–99.85%, while detection was null. In signal staging, quality dropped to 85–95%, indicating a significant trade-off between watermark strength and linguistic naturalness.

The proposed method involves altering training data content, albeit in a minimal way that does not change meaning. It is important to emphasize that watermarking of human-authored data without consent is not advocated. In the experiments, either synthetic data (generated by the models) or data for which rights are held is watermarked. Watermarking someone else’s text could be seen as a form of data tampering. Therefore, this technique should be used only on data that one has authority over (e.g., a company watermarking its proprietary dataset before sharing it). The semantic integrity of the content is ensured—the watermark functions as a hidden signal rather than a visible alteration.

It is assumed that the adversary is unaware of the specific watermark or does not possess the secret key. If an adversary did know the watermarking scheme and suspected a particular key or message, they could attempt targeted removal. For example, they might apply a paraphrasing algorithm explicitly aimed at breaking statistical patterns or fine-tune the model further on unwatermarked text to attenuate the watermark signal. Such adaptive attacks are an ongoing threat. While the proposed error-correction and semantic-level embedding make removal non-trivial, it is acknowledged that a motivated attacker could degrade the watermark. For instance, they might detect widespread synonym usage (if they ignore the key and use frequency analysis) and deliberately flip those in their model outputs. Defense against an attacker who knows the watermarking method (though not the key) relies on the sample space of possible keys/patterns–essentially security by cryptographic secret. In practice, a savvy attacker might still employ general stylometric obfuscation (randomly rewording text), which could weaken any watermark. This is an arms race: defenders can counter by using deeper embedding (syntax or semantic-level watermarks beyond just surface word choice) and multi-layer signals, as well as detection methods based on deep learning that can pick up subtle clues even after obfuscation [4]. The scheme is made open and testable, and in a real deployment, watermarks may be rotated or updated if a specific pattern is compromised.

Watermark detection must be exact to avoid falsely accusing innocent models or texts. A stringent threshold is chosen (like p < 0.01) to keep false positives ~1%. In high-stakes settings, one might even combine multiple independent watermarks or require various pieces of evidence to call out a violation. Another consideration is misuse of watermarking: one could imagine a malicious actor watermarking content to frame someone else’s model. The proposed scheme’s reliance on a secret key and the ability to prove knowledge of that key (and the specific ECC structure) provides some protection–essentially, only the actual owner who embedded the watermark can detect and confirm it. The chance that two independent watermark schemes collide or produce false attribution is astronomically low if properly designed. It should be noted that the watermark does not interfere with any functionality of the model; it serves purely as a passive identifier. This design avoids concerns of model misbehavior, which some backdoor-based watermarks might risk if triggers accidentally appear in regular input. Backdoors that could affect users are explicitly avoided: the watermark does not cause the model to respond differently to any regular input, apart from the minuscule statistical preference in word choice, which remains imperceptible to users.

The proposed approach is tailored to text generation-style watermarking. It may not directly apply to cases where fine-tuning data consists of structured records or non-linguistic information (though the concept of watermarking data could extend to images or audio with analogous methods). Also, if a model is fine-tuned on a mix of watermarked and unwatermarked data, the watermark signal could be diluted. In such cases, one could increase ε or embed a more extended code to reinforce it, at the cost of some readability, maybe. There is a trade-off between watermark strength and invisibility, as with any steganography. In preliminary trials, the chosen operating point yielded a strong signal with no noticeable quality drop, although different domains might require re-tuning of the parameters.

Synonym pairs from WordNet limit ρ; calibration is needed for other languages/domains. With an adaptive adversary aiming for stylistic obfuscation, it is expected a decline in TPR—ECC and replication help, but it is not a “vibranium shield.”

Lastly, while robustness against many transformations has been demonstrated, the watermark is not claimed to be unbreakable. For example, a highly capable rewriter (such as another LLM instructed specifically to rewrite text in a different style) might reduce detection accuracy significantly. Developing watermarks that survive adversarial paraphrasing remains an open research challenge; this work contributes to the area but does not provide a complete solution. Future improvements are envisioned that incorporate semantic-level embedding—so that even changes in wording cannot remove the watermark—and leverage model-based detectors capable of identifying subtle distribution shifts.

The offline injection validates the channel (synonym pairs, PRF addressing, ECC), but ε is irrelevant outside of generation. The low N_obs for short texts explain the flat ROCs. In generative mode, it is expected linear growth in power with length (GLRT consistency). The categories show similar behavior, suggesting that the channel is not domain sensitive.

9. Discussion

The paper proposes a watermark for fine-tuning datasets that combines deterministic PRF-masking, semantically preserving A↔B synonym choices, multi-bit encoding via ECC, and detection via GLRT with permutation-calibrated p-values. In comparison with prior works targeting localization and detection of machine-generated text at the token or document level, this approach addresses the problem of provable model membership to a training corpus (DOV) rather than post hoc human/machine distinction [30,31,32].

Machine-Generated Text Localization formulates token-level localization of generative segments but lacks a mechanism for key-based verification of dataset ownership, as provided by the GLRT+PRF framework [30]. Classical stylometric detectors in scientific domains achieve high accuracy but are vulnerable to paraphrasing and out-of-domain transmission; in the proposal under consideration, the signal is cryptographically keyed and distributed across multiple contexts, making adaptive circumvention difficult [31,32].

In contrast to REMARK-LLM, which optimizes multibit embedding in LLM outputs and requires a modified inference decoding procedure, the present method is applied to the data before retraining and does not require changes to the inference stack [33]. Semantic-invariant watermarking, which predicts “water” logits via secondary embedding models, is oriented towards baseline robustness against paraphrasing; here, robustness is sought at the parameter level via a data-distributed signal that survives training [9].

White-box model-based watershed labeling with permutations of weights and error codes is reported to offer strong robustness to severe attacks but requires access to the parameters; in contrast, black-box verification is provided in the proposal through statistical tests on generated texts [34]. A synthesized survey in ACM Computing Surveys highlights the capacity–resilience–obscurity triad and the need for legally defensible p-values; the GLRT with permutation calibration in the proposal under review is presented as directly addressing this standard for provability [35].

Compared to ZeroMark, which relies on gradient features along a boundary in a “label-only” scenario, a key-addressed subsample of contexts with bipartite synonym-pair selection is employed, allowing explicit control of FPR via p-values [36]. In contrast to translation-oriented linguistic steganography for covert channel communication, semantically equivalent microsolutions are employed as carriers of a proprietary code for subsequent forensic verification [37,38]. Exploiting ECC in the proposal serves a specific role: partial signal degradation from paraphrasing or compression of text is compensated, an issue less well addressed in purely source watermarking without code redundancy. Deterministic slot addressing via PRF eliminates the dependence on a global counter and stabilizes positions at A↔B flips, which enables reproducible detection, a functionality rarely specified in output-level schemes.

A calibrated permutation procedure is provided in the proposal (e.g., R = 5000) for p-values and confidence intervals, which is compatible with requirements for forensic use, whereas many output watermarks report mostly AUROC without strict first-order controlled error [9,33,35]. Empirically, null detections have been reported in realistic generative tests with Mistral 7B, explicitly acknowledging architectural incompatibility of the chosen “synonym channel”; however, text quality is maintained (~99.8%), and positive results have been observed in controlled settings, mapping the parametric space for future strengthening. This transparency about the limitations is an advantage over some of the literature, where robustness is evaluated under limited scenarios and without rigorous statistical power testing [35]. As a corpus-based solution, the proposal is complementary to output watermarks: the model itself is labeled as a “function” of the data, whereas REMARK-LLM and semantic-invariant methods label individual outputs; the two-layer design increases forensic sensitivity [9,33].

Compared to classical detectors in the publication domain, which rely on style features and can be biased towards non-carriers, a key-driven selection of eligible equivalents is employed, which reduces systematic biases [31,32]. Compared to token-level localization of machine text, where the goal is diagnosis of mixed documents, the goal here is provable membership/origin, which is more directly relevant to corporate data protection and licensing disputes [30]. Compared to steganographic translation channels, which optimize payload but are not designed to experience training and distillation processes, the signal is embedded in the parameters by training on the watermarking corpus [37,38]. Permutation-calibrated p-values can be used to set significance levels (e.g., α = 0.01) with clear interpretation, while some output schemes operate with heuristic thresholds and observation length dependence [33,35]. A leading advantage is the absence of a white-box requirement for model access, contrasted with ECC schemes on weights that are inapplicable for suspect models “in the wild” [34]. The multi-bit utility combined with re-addressability across the corpus renders the probability of a random “match” negligible, strengthening the position in a contention for illegal retraining. The discussed methodology is instrumentally compatible with LoRA/instructional relearning practices, as no architectural modifications are required and it can be enabled in the data preparation stage. The synergy with modern source watermarks is natural: evidence of training material used is provided by the corpus watermark, and attribution of specific text is given by the source watermark, which together make it difficult to challenge provenance [9,33,35]. Ethics and constraints are explicitly addressed in the proposal, including the risk of adaptive “cleaning” and domain transfer, with directions offered for semantic channels and model-based detectors—a practice rarely articulated in source-centric work. In terms of complexity and resources, linear scaling of detection with the number of observed slots and a fixed number of permutations is advantageous for operational audits of large collections.

Unlike ZeroMark, where verification exploits boundary features and can be sensitive to subsequent retraining, the statistical test here is based on observable choices of language alternatives, which facilitates independent third-party verification [36]. In the presence of mixed corpora (pure + watermarked), the dilution effect is reduced by ECC and replication, whereas purely baseline methods require longer samples for comparable power [9,33]. A significant practical difference to steganography is that the goal is not secret communication but legally robust proof of ownership, which drives the choice of tests and reported metrics [37,38]. While domain sets such as the one for fire door defects provide a rich label taxonomy for operational classifications, the methodology aims at provable hull tagging and detection with supervised FPR. This enables data/property protection scenarios beyond a specific domain. The practical trade-off lies in signal density: in real-world generation with Mistral 7B, it remains insufficient for detection; future work will explore phrase/semantic channels, especially in domain vocabulary (e.g., terminology for door components), to boost observed slots without significant quality loss. Transparent publication of key hyperparameters is allowed by the framework and protocols (without key disclosure), which facilitates auditability and repeatability; this is often underdeveloped in source-level systems oriented towards production integration [33]. The proposal is more universal in terms of access interfaces: public generations of the suspect model are sufficient, without APIs for special “waterfall” decoding modes [33]. The reported “minimal interference” in quality, as measured by multiple lexical metrics, reduces the risk of functional regressions in edge applications, as opposed to aggressive output schemes at high signal levels [35]. Finally, the strategic advantage lies in positioning: while the literature focuses on output detection/attribution or white-box watermarking, the present method addresses the “corpus → parameters → black-box detection” gap, which is critical for real-world provenance disputes [9,30–36]. In view of the above, the proposal can be viewed as superior to the reviewed papers along the lines of provability, black-box operability, cryptographic secrecy, and complementarity to output watermarks, despite the acknowledged limitations of the particular synonym channel [9,30,31,32,33,34,35,36].

10. Conclusions

The pilot results provide validation of the channel and keyed detection mechanics; full model-probing and robustness curves will complete the picture. The approach is practical for provenance claims when enough marked opportunities are observed; combining ECC with deterministic addressing yields a verifiable signal while preserving quality (offline $\stackrel{\_}{\rho }$ ≈ 0.0165 after 10% inflation; no degradation observed in short texts). Future work expands synonym channels and reports end-to-end AUC/TPR under attacks.

A novel approach is presented to watermarking the training data of language models, enabling the verification of a model’s provenance even after the data has been absorbed and the content possibly transformed. The proposed method introduces an imperceptible, statistically robust “signal” in the fine-tuning corpus by biasing synonym choices according to a secret code. Through the use of error-correcting codes and careful probabilistic embedding, the watermark is resilient to paraphrasing, compression, and distillation–transformations under which simpler watermarks would falter. It is demonstrated that this watermark can be detected via a rigorous statistical test with low false favorable rates, providing strong evidence of unauthorized model usage when found.

This work pushes the boundary of AI watermarking into a new territory. Rather than marking the outputs of generative models (the focus of most existing research) [9], the inputs (training data) are marked, thereby indirectly marking the model parameters. This has significant implications. This means that even if a model’s outputs are not watermarked at generation time, the model can still potentially be identified if it was trained on protected data. It is a tool for dataset owners to defend their rights in an era where data can be easily scraped and models illicitly fine-tuned. Moreover, the proposed watermark does not depend on any cooperation at inference time–it is “built in” to the model via the data influence.

This idea is timely and essential. As generative AI becomes widespread, methods for tracking and verifying the lineage of models and data will be crucial for governance, copyright, and quality control. This work lays a foundation by showing that fine-tuning data can carry a hidden signature with provable guarantees. There are many avenues for further research: exploring more sophisticated encoding channels (syntax trees, semantic biases), improving robustness against adaptive attacks, combining data watermarks with model weight watermarks, and extending to other modalities (imagine watermarking image datasets used for fine-tuning vision models). Collaboration with legal and policy experts is also planned to determine how such watermarks might be used as evidence of model misuse and what standards are required for that purpose.

Future work will consider phrase and semantic channels with context-dependent substitutions, embedding-based filtering, ensemble detectors, and training-time watermarks; the goal is to increase signal density and robustness with little impact on quality and without requiring access to model parameters.