GPU-Driven Acceleration of Wavelet-Based Autofocus for Practical Applications in Digital Imaging
Abstract
1. Introduction
2. Materials and Methods
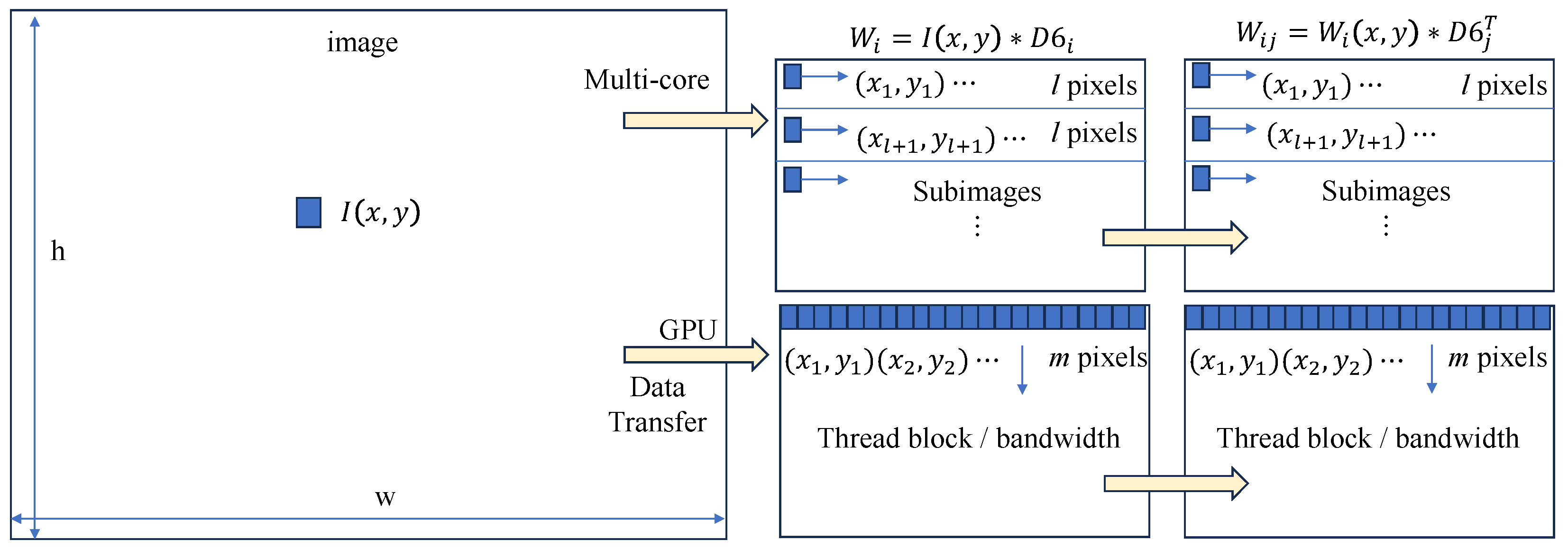
2.1. Parallelizing 2D Wavelets
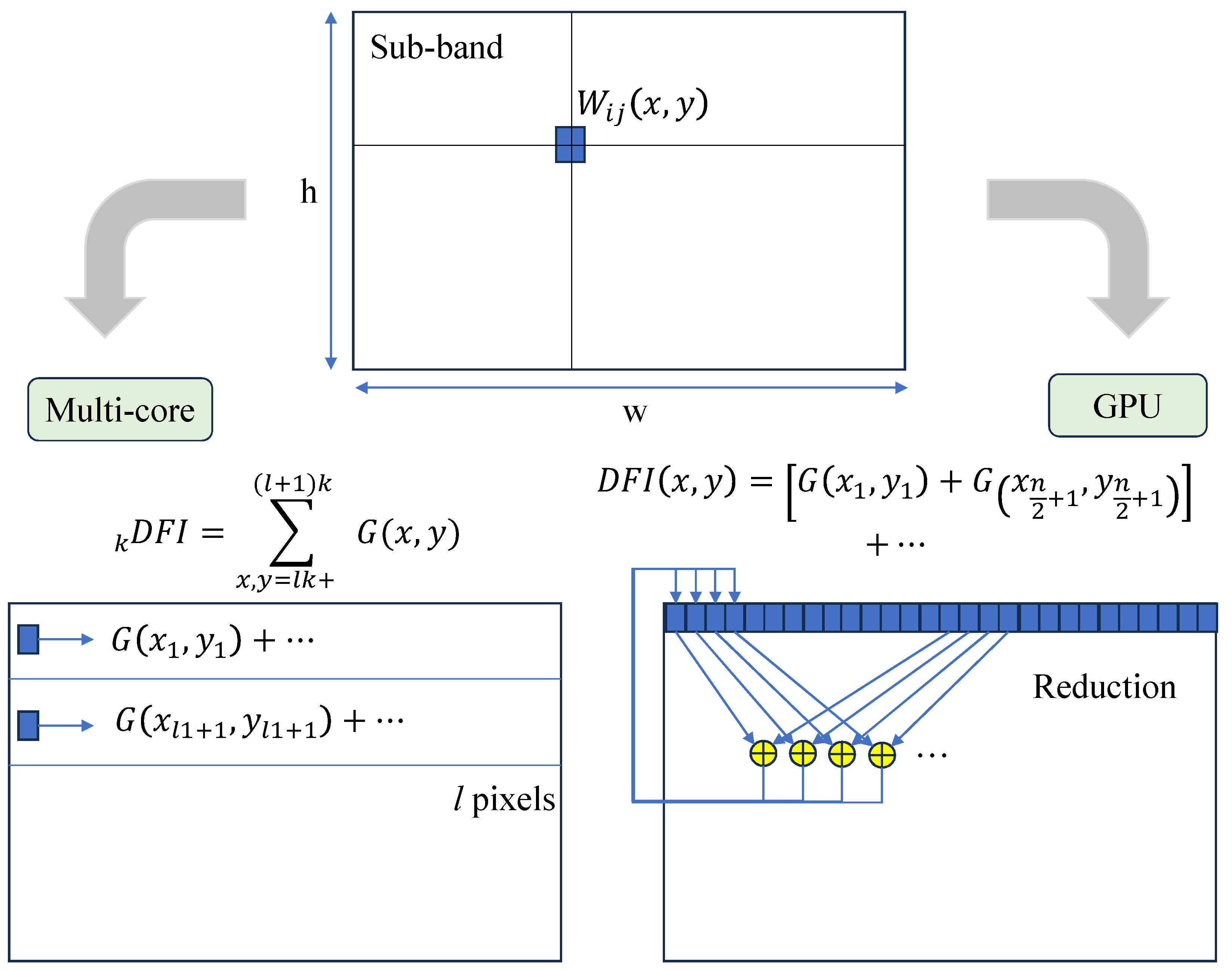
2.2. Wavelet Sum
2.3. Wavelet Variance
2.4. Versatile Wavelets
2.5. Experiments
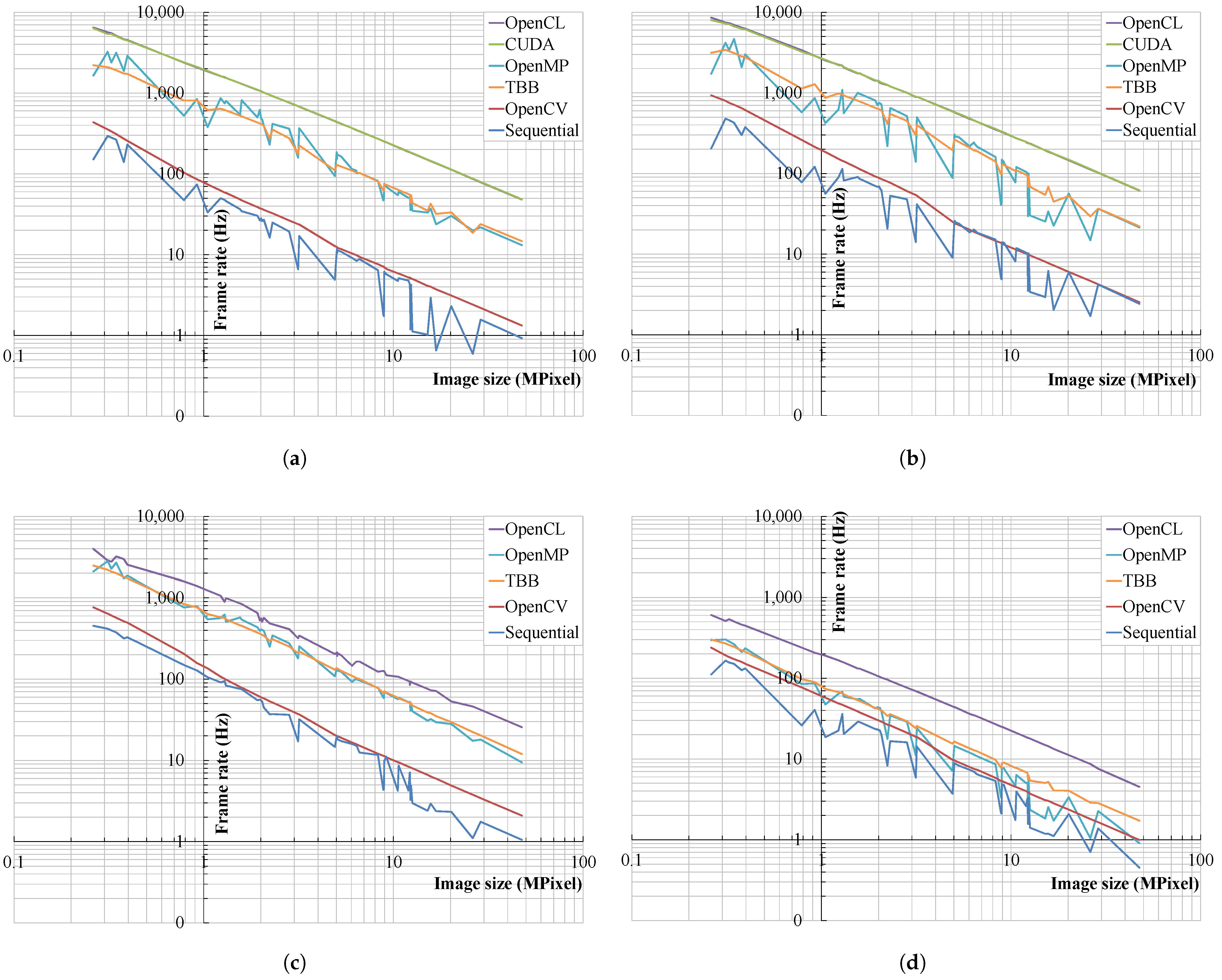
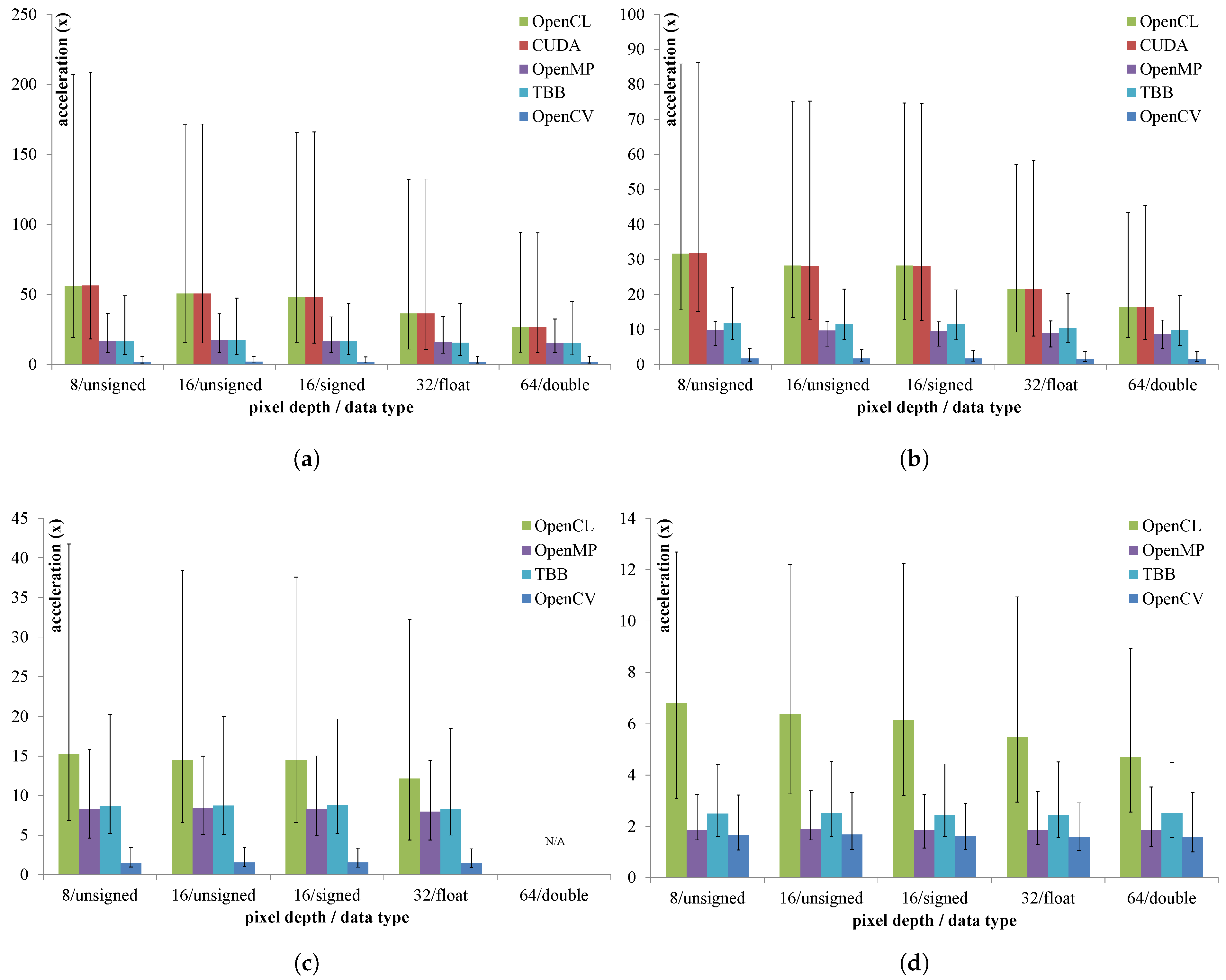
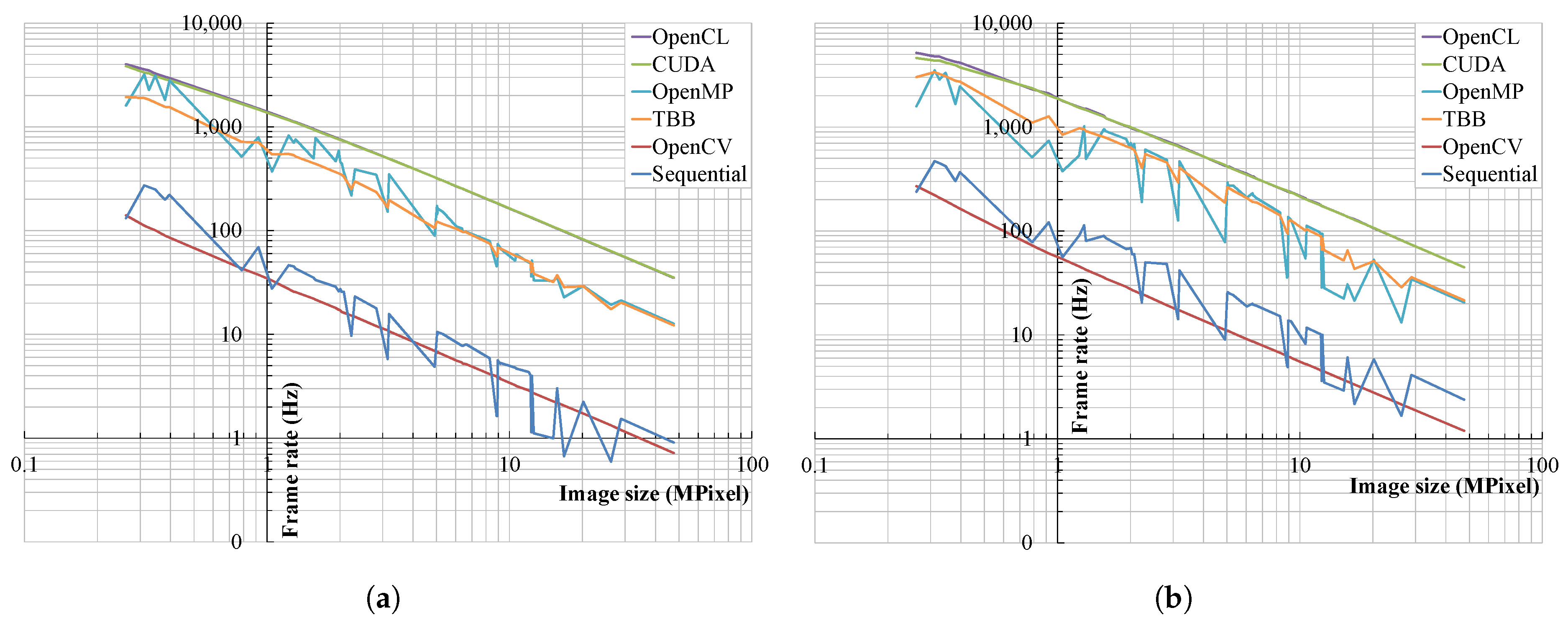
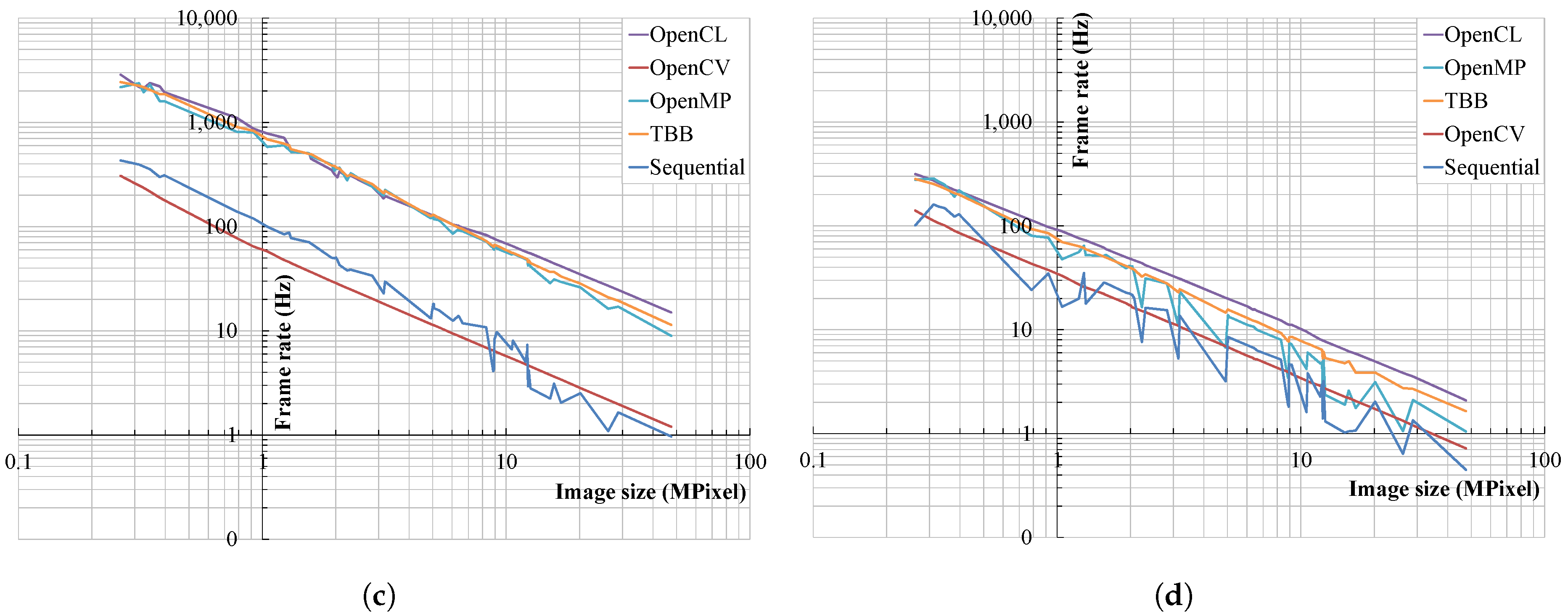
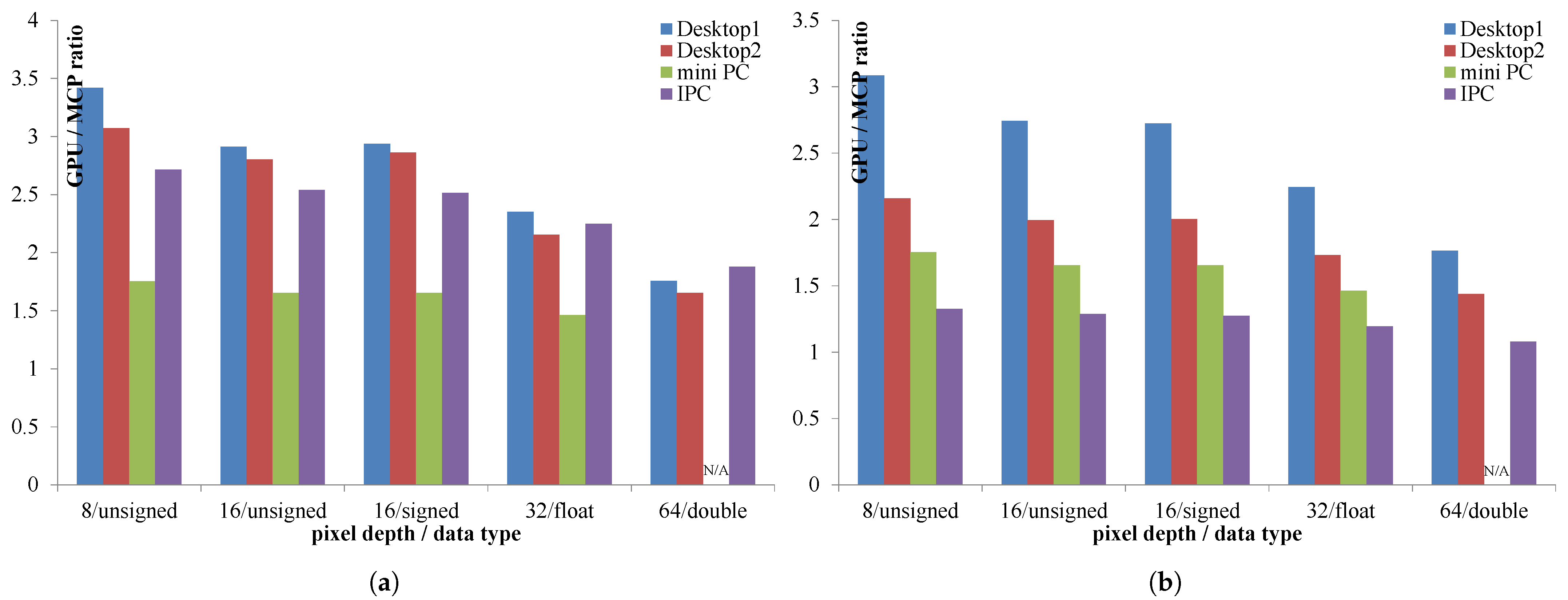
3. Results
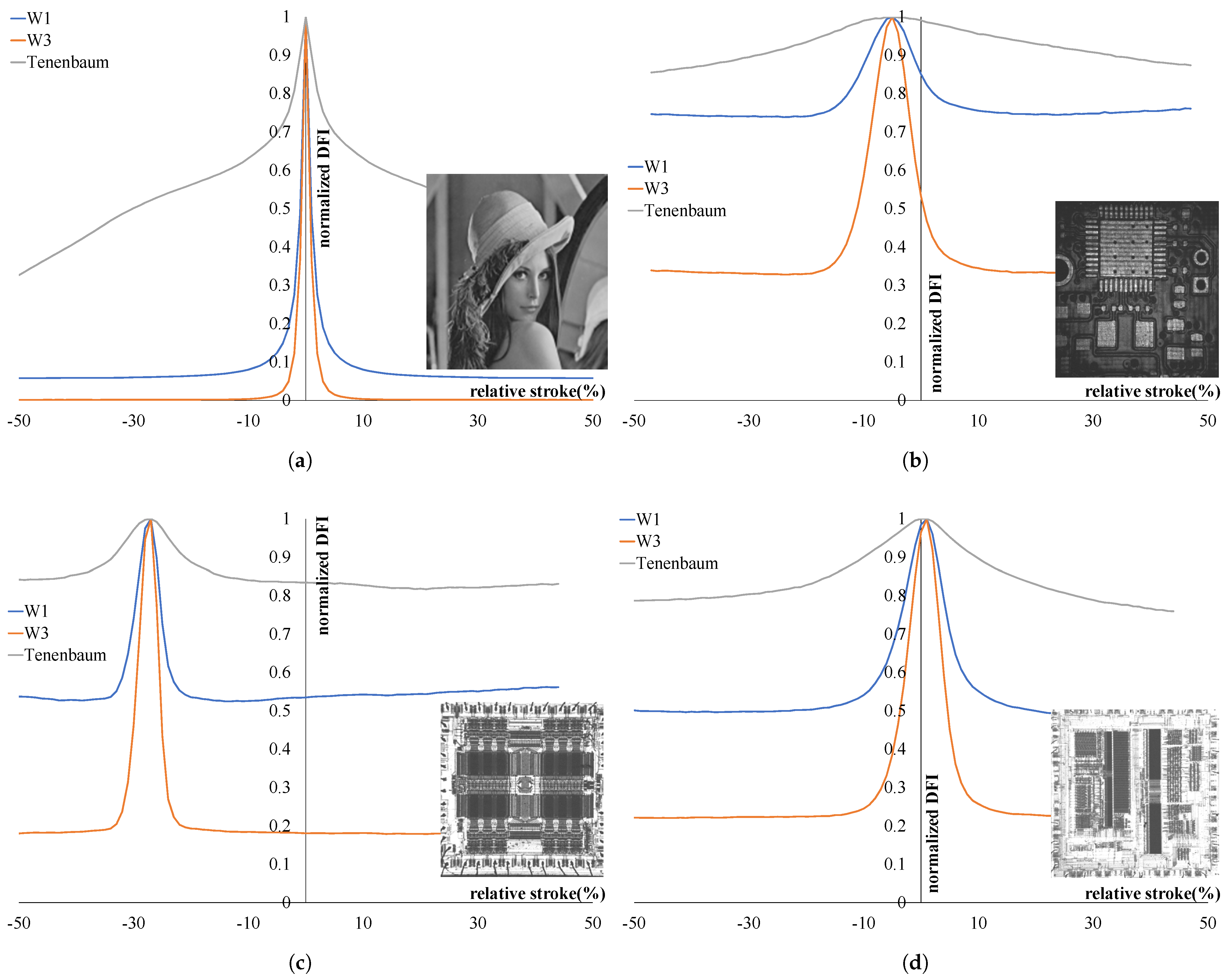
3.1. Focus Evaluation
3.2. Wavelet Sum
3.3. Wavelet Variance
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ALU | Arithmetic Unit |
| API | Application Program Interface |
| DB6 | Daubechies 6 |
| DFI | Digital Focus Index |
| DWT | Discrete Wavelet Transformation |
| FBA | Filter Bank Algorithm |
| GPU | General Processing Unit |
| IPC | Industrial Process Controller |
| MCP | Multicore Processor |
| PC | Personal Computer |
| UIS | Unsupervised Image Segmentation |
| WBA | Wavelet-Based Autofocus |
| WDFI | Wavelet-Based Digital Focus Index |
References
- Jang, J.; Lee, S.; Hwang, S.; Lee, J. A Study on Denoising Autoencoder Noise Selection for Improving the Fault Diagnosis Rate of Vibration Time Series Data. Appl. Sci. 2025, 15, 6523. [Google Scholar] [CrossRef]
- Arunachalaperumal, C.; Dhilipkumar, S. An Efficient Image Quality Enhancement using Wavelet Transform. Mat. Today Proc. 2020, 24, 2004–2010. [Google Scholar] [CrossRef]
- Kumar, G.S.; Rani, M.L.P. Image Compression Using Discrete Wavelet Transform and Convolution Neural Networks. J. Electr. Eng. Technol. 2024, 19, 3713–3721. [Google Scholar] [CrossRef]
- Jiang, X.; Ma, K.; Wu, J.; Li, Z. Bridge Damage Identification Based on Variational Modal Decomposition and Continuous Wavelet Transform Method. Appl. Sci. 2025, 15, 6682. [Google Scholar] [CrossRef]
- Ramamonjisoa, M.; Firman, M.; Watson, J.; Lepetit, V.; Turmukhambetov, D. Single Image Depth Prediction with Wavelet Decomposition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 11084–11093. [Google Scholar]
- Widjaja, J.; Jutamulia, S. Use of wavelet analysis for improving autofocusing capability. Opt. Commun. 1998, 151, 12–14. [Google Scholar] [CrossRef]
- Um, G.; Hur, N.; Kim, H.; Cho, J.; Lee, J. Control Parameter Extraction using Wavelet Transform for Auto-Focus Control of Stereo Camera. J. Brod. Eng. 2000, 5, 239–246. [Google Scholar]
- Acharya, T.; Metz, W. Auto-Focusing Algorithm Using Discrete Wavelet Transform. U.S. Patent 6151415A, 21 November 2000. [Google Scholar]
- Yang, G.; Nelson, B.J. Micromanipulation Contact Transition Control by Selective Focusing and Microforce Control. In Proceedings of the IEEE International Conference on Robotics and Automation, Taipei, Taiwan, 14–19 September 2003; pp. 3200–3206. [Google Scholar]
- Nguyen, K.; Do, K.; Vu, T.; Than, K. Unsupervised image segmentation with robust virtual class contrast. Pattern Recognit. Lett. 2023, 173, 10–16. [Google Scholar] [CrossRef]
- Niu, D.; Wang, X.; Han, X.; Lian, L.; Herzig, R.; Darrell, T. Unsupervised Universal Image Segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognitio, Seattle, WA, USA, 16–22 June 2024; pp. 22744–22754. [Google Scholar]
- Forster, B.; Van De Ville, D.; Berent, J.; Sage, D.; Unser, M. Extended depth-of-focus for multi-channel microscopy images: A complex wavelet approach. In Proceedings of the IEEE International Symposium on Biomedical Imaging: Nano to Macro, Arlington, VA, USA, 18 April 2004; pp. 660–663. [Google Scholar]
- Tsai, D.; Wang, H. Segmenting focused objects in complex visual images. Pattern Recognit. Lett. 1998, 19, 929–940. [Google Scholar] [CrossRef]
- Wang, J.Z.; Li, J.; Gray, R.M.; Wiederhold, G. Unsupervised multiresolution segmentation for images with low depth of field. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 85–90. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, J.; Wang, C.; Song, L.; Yang, G. XNet: Wavelet-Based Low and High Frequency Fusion Networks for Fully- and Semi-Supervised Semantic Segmentation of Biomedical Images. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Paris, France, 1–6 October 2023; pp. 21028–21039. [Google Scholar]
- Qian, X.; Lu, W.; Zhang, Y. Adaptive wavelet-VNet for single-sample test time adaptation in medical image segmentation. Med. Phys. 2024, 51, 8865–8881. [Google Scholar] [CrossRef]
- Wang, Z. Unsupervised Wavelet-Feature Correlation Ratio Markov Clustering Algorithm for Remotely Sensed Images. Appl. Sci. 2024, 14, 767. [Google Scholar] [CrossRef]
- Mertens, F.; Lobanov, A. Wavelet-based decomposition and analysis of structural patterns in astronomical images. Astron. Astrophys. 2015, 574, A67. [Google Scholar] [CrossRef]
- Kautsky, J.; Flusser, J.; Zitová, B.; Šimberová, S. A new wavelet-based measure of image focus. Pattern Recognit. Lett. 2002, 23, 1785–1794. [Google Scholar] [CrossRef]
- Yang, G.; Nelson, B.J. Wavelet-based autofocusing and unsupervised segmentation of microscopic images. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, 27–31 October 2003; pp. 2143–2148. [Google Scholar]
- Zong, G.; Sun, M.; Bi, S.; Dong, D. Research on Wavelet Based Autofocus Evaluation in Micro-vision. Chin. J. Aeronaut. 2006, 19, 239–246. [Google Scholar] [CrossRef]
- Xie, H.; Rong, W.; Sun, L. Construction and evaluation of a wavelet-based focus measure for microscopy imaging. Microsc. Res. Tech. 2007, 70, 987–995. [Google Scholar] [CrossRef]
- Makkapati, V.V. Improved wavelet-based microscope autofocusing for blood smears by using segmentation. In Proceedings of the IEEE International Conference on Automation Science and Engineering, Bangalore, India, 22–25 August 2009; pp. 208–211. [Google Scholar]
- Akiyama, A.; Kobayashi, N.; Mutoh, E.; Kumagai, H.; Yamada, H.; Ishii, H. Infrared image guidance for ground vehicle based on fast wavelet image focusing and tracking. SPIE Opt. Eng. Appl. 2009, 7429, 742906. [Google Scholar]
- Wang, Z.; He, X.; Wu, X. An autofocusing technology for core image system based on lifting wavelet transform. J. Sichuan Univ. Nat. Sci. Ed. 2008, 45, 838–841. [Google Scholar]
- Fan, Z.; Chen, S.; Hu, H.; Chang, H.; Fu, Q. Autofocus algorithm based on Wavelet Packet Transform for infrared microscopy. In Proceedings of the IEEE International Congress on Image and Signal Processing, Yantai, China, 16–18 October 2010; pp. 2510–2514. [Google Scholar]
- Mendapara, P.; Baradarani, A.; Wu, Q.M.J. An efficient depth map estimation technique using complex wavelets. In Proceedings of the IEEE International Conference on Multimedia and Expo, Singapore, 19–23 July 2010; pp. 1409–1414. [Google Scholar]
- Śliwiński, P. Autofocusing with the help of orthogonal series transforms. Int. J. Electron. Telecommun. 2010, 56, 33–42. [Google Scholar] [CrossRef]
- Abele, R.; Fronte, D.; Liardet, P.Y.; Boi, J.M.; Damoiseaux, J.L.; Merad, D. Autofocus in infrared microscopy. In Proceedings of the IEEE International Conference on Emerging Technologies and Factory Automation, Turin, Italy, 4–7 September 2018; pp. 631–637. [Google Scholar]
- Yin, A.; Chen, B.; Zhang, Y. Focusing evaluation method based on wavelet transform and adaptive genetic algorithm. Opt. Eng. 2012, 51, 023201. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, H.; Yu, H.; Hu, R.; Zhang, G.; Hu, J.; He, T. A Method for Medical Microscopic Images’ Sharpness Evaluation Based on NSST and Variance by Combining Time and Frequency Domains. Sensors 2022, 22, 7607. [Google Scholar] [CrossRef]
- Surh, J.; Jeon, H.; Park, Y.; Im, S.; Ha, H.; Kweon, I.S. Noise Robust Depth from Focus Using a Ring Difference Filter. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2444–2453. [Google Scholar]
- Herrmann, C.; Bowen, R.S.; Wadhwa, N.; Garg, R.; He, Q.; Barron, J.T.; Zabih, R. Learning to Autofocus. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 2227–2236. [Google Scholar]
- Piao, W.; Han, Y.; Hu, L.; Wang, C. Quantitative Evaluation of Focus Measure Operators in Optical Microscopy. Sensors 2025, 25, 3144. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wu, C.; Gao, Y.; Liu, H. Deep Learning-Based Dynamic Region of Interest Autofocus Method for Grayscale Image. Sensors 2024, 24, 4336. [Google Scholar] [CrossRef]
- Chen, T.; Li, H. Segmenting focused objects based on the Amplitude Decomposition Model. Pattern Recognit. Lett. 2012, 33, 1536–1542. [Google Scholar] [CrossRef]
- Liu, S.; Liu, M.; Yang, Z. An image auto-focusing algorithm for industrial image measurement. EURASIP J. Adv. Signal Process. 2016, 2016, 70. [Google Scholar] [CrossRef]
- Ahn, S.; Lee, S.; Kang, M.G. Lightweight Super-Resolution for Real-World Burst Images Captured by Handheld Camera Sensors Based on Partial Differential Equations. IEEE Sens. J. 2025, 25, 25241–25251. [Google Scholar] [CrossRef]
- Kim, H.; Kim, Y.H.; Moon, S.; Kim, H.; Yoo, B.; Park, J.; Kim, S.; Koo, J.M.; Seo, S.; Shin, H.J.; et al. A 0.64 µm 4-Photodiode 1.28 µm 50Mpixel CMOS Image Sensor with 0.98e- Temporal Noise and 20Ke- Full-Well Capacity Employing Quarter-Ring Source-Follower. In Proceedings of the IEEE International Solid-State Circuits Conference, San Francisco, CA, USA, 19–23 February 2023; pp. 1–3. [Google Scholar]
- Castillo-Secilla, J.M.; Saval-Calvo, M.; Medina-Valdès, L.; Cuenca-Asensi, S.; Martínez-Álvarez, A.; Sánchez, C.; Cristóbal, G. Autofocus method for automated microscopy using embedded GPUs. Biomed. Opt. Express 2017, 8, 1731–1740. [Google Scholar] [CrossRef]
- Kim, H.; Lee, D.; Choi, D.; Kang, J.; Lee, D. Parallel Implementations of Digital Focus Indices Based on Minimax Search Using Multi-Core Processors. KSII Trans. Internet Inf. Syst. 2023, 17, 542–558. [Google Scholar] [CrossRef]
- Tenllado, C.; Setoain, J.; Prieto, M.; Piñuel, L.; Tirado, F. Parallel Implementation of the 2D Discrete Wavelet Transform on Graphics Processing Units: Filter Bank versus Lifting. IEEE Trans. Parallel Distrib. Syst. 2008, 19, 299–310. [Google Scholar] [CrossRef]
- Rodriguez-Martinez, E.; Benavides-Alvarez, C.; Aviles-Cruz, C.; Lopez-Saca, F.; Ferreyra-Ramirez, A. Improved Parallel Implementation of 1D Discrete Wavelet Transform Using CPU-GPU. Electronics 2023, 12, 3400. [Google Scholar] [CrossRef]
- Puchala, D.; Stokfiszewski, K. Highly Effective GPU Realization of Discrete Wavelet Transform for Big-Data Problems. In Proceedings of the International Conference on Computational Science, Krakow, Poland, 16–18 June 2021; pp. 213–227. [Google Scholar]
- Kolomenskiy, D.; Onishi, R.; Uehara, H. WaveRange: Wavelet-based data compression for three-dimensional numerical simulations on regular grids. J. Vis. 2022, 25, 543–573. [Google Scholar] [CrossRef]
- de Cea-Dominguez, C.; Moure, J.C.; Bartrina-Rapesta, J.; Aulí-Llinàs, F. GPU Architecture for Wavelet-Based Video Coding Acceleration. Adv. Parallel Comput. 2020, 36, 83–92. [Google Scholar]
- Wu, H.; Wang, X.; Zhao, X.; Qiao, X.; Wang, X.J.; Qiu, X.J.; Fu, Z.; Xiong, C. Parallel Acceleration Algorithm for Wavelet Denoising of UAVAGS Data Based on CUDA. Nucl. Eng. Technol. 2025, 57, 103811. [Google Scholar] [CrossRef]
- Sun, Y.; Duthaler, S.; Nelson, B.J. Autofocusing in computer microscopy: Selecting the optimal focus algorithm. Microsc. Res. Tech. 2004, 65, 139–149. [Google Scholar] [CrossRef] [PubMed]
- Shahbahrami, A. Algorithms and architectures for 2D discrete wavelet transform. J. Supercomput. 2012, 62, 1045–1064. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, Y.; Zhao, Y.; Liang, J.; Sun, B.; Chu, S. Algorithm Research on Detail and Contrast Enhancement of High Dynamic Infrared Images. Appl. Sci. 2023, 13, 12649. [Google Scholar] [CrossRef]
- Lindfield, G.; Penny, J. Chapter 8—Analyzing Data Using Discrete Transforms. In Numerical Methods Using MATLAB, 4th ed.; Academic Press: London, UK, 2019; pp. 383–431. [Google Scholar]
- Chaver, D.; Tenllado, C.; Piñuel, L.; Prieto, M.; Tirado, F. Wavelet Transform for Large Scale Image Processing on Modern Microprocessors. Lect. Notes Comput. Sci. 2003, 2565, 549–562. [Google Scholar]
- Kim, H.; Song, J.; Seo, J.; Ko, C.; Seo, G.; Han, S.K. Digitalized Thermal Inspection Method of the Low-Frequency Stimulation Pads for Preventing Low-Temperature Burn in Sensitive Skin. Bioengineering 2025, 12, 560. [Google Scholar] [CrossRef] [PubMed]
- Jradi, W.A.R.; do Nascimento, H.A.D.; Martins, W.S. A GPU-Based Parallel Reduction Implementation. Commun. Comput. Inf. Sci. 2020, 1171, 168–182. [Google Scholar]
- Pertuz, S.; Puig, D.; Garcia, M.A. Analysis of focus measure operators for shape-from-focus. Pattern Recognit. 2013, 46, 1415–1432. [Google Scholar] [CrossRef]
- Ingwersen, C.K.; Danielak, A.H.; Eiríksson, E.R.; Nielsen, A.A.; Pedersen, D.B. Computer vision for focus calibration of photo-polymerization systems. In Proceedings of the ASPE and euspen Summer Topical Meeting, Berkeley, CA, USA, 22–25 July 2018; pp. 89–91. [Google Scholar]
- Hutchinson, J. Culture, Communication, and an Information Age Madonna. IEEE Prof. Commun. Soc. Newsl. 2001, 45, 1–6. [Google Scholar]
- Zhang, H.; Yao, J. Automatic Focusing Method of Microscopes Based on Image Processing. Math. Probl. Eng. 2021, 2021, 8243072. [Google Scholar] [CrossRef]
- Mao, Z.; Li, X.; Hu, S.; Gopalakrishnan, G.; Li, A. A GPU accelerated mixed-precision Smoothed Particle Hydrodynamics framework with cell-based relative coordinates. Eng. Anal. Bound. Elem. 2024, 161, 113–125. [Google Scholar] [CrossRef]
- Luis, C.; Garcia-Feal, O.; Nord, G.; Piton, G.; Legoût, C. Implementation of a GPU-enhanced multiclass soil erosion model based on the 2D shallow water equations in the software Iber. Environ. Model. Softw. 2024, 179, 106098. [Google Scholar] [CrossRef]
- Cabazos-Marín, A.R.; Álvarez-Borrego, J. Automatic focus and fusion image algorithm using nonlinear correlation: Image quality evaluation. Optik 2018, 164, 224–242. [Google Scholar] [CrossRef]
- Valdiviezo-N, J.C.; Hernandez-Lopez, F.J.; Toxqui-Quitl, C. Parallel implementations to accelerate the autofocus process in microscopy applications. J. Med. Imaging 2020, 7, 014001. [Google Scholar]
- Lun, D.P.K.; Hsung, T. Image denoising using wavelet transform modulus sum. In Proceedings of the IEEE International Conference on Signal Processing, Beijing, China, 12–16 October 1998; pp. 1112–1116. [Google Scholar]
- Hur, Y.; Zheng, F. Coset Sum: An Alternative to the Tensor Product in Wavelet Construction. IEEE Trans. Inf. Theory 2013, 59, 3554–3571. [Google Scholar] [CrossRef]
- Jeong, B.; Eom, I. Demosaicking Using Weighted Sum in Wavelet domain. In Proceedings of the IEEK Conference, Yongpyong, Republic of Korea, 18–20 June 2008; pp. 821–822. [Google Scholar]
- Ahalpara, D.P.; Verma, A.; Parikh, J.C.; Panigrahi, P.K. Characterizing and modelling cyclic behaviour in non-stationary time series through multi-resolution analysis. Pramana J. Phys. 2008, 71, 459–485. [Google Scholar] [CrossRef]
- Lemire, D. Wavelet-based relative prefix sum methods for range sum queries in data cubes. In Proceedings of the Conference of the Centre for Advanced Studies on Collaborative Research, Toronto, ON, Canada, 30 September–3 October 2002. [Google Scholar]

| WDFI | OpenCV | API |
|---|---|---|
| W1 | cv::Mat Src, L, H, LH, HL, HH; Src = cv::imread(FileName); cv::filter2D(Src, L, CV_64F, DB6L); cv::filter2D(Src, H, CV_64F, DB6H); cv::filter2D(L, LH, CV_64F, DB6HT); cv::filter2D(H, HL, CV_64F, DB6LT); cv::filter2D(H, HH, CV_64F, DB6HT); double lh = cv::norm(LH,cv::NORM_L1); double hl = cv::norm(HL,cv::NORM_L1); double hh = cv::norm(HH,cv::NORM_L1); W1 = lh + hl + hh; | cv::Mat Src = cv::imread(FileName); W1 = IndexWavelet1(Src); W1 = ompWavelet1(Src); W1 = tbbWavelet1(Src); W1 = cuWavelet1(Src); W1 = clWavelet1(Src); |
| W3 | cv::Mat Src, L, H, LH, HL, HH; Src = cv::imread(FileName); cv::filter2D(Src, L, CV_64F, DB6L); cv::filter2D(Src, H, CV_64F, DB6H); cv::filter2D(L, LH, CV_64F, DB6HT); cv::filter2D(H, HL, CV_64F, DB6LT); cv::filter2D(H, HH, CV_64F, DB6HT); cv::Mat aLH = cv::abs(LH); cv::Scalar mLH,sLH; cv::meanStdDev(aLH, mLH, sLH); … W3 = sLH × sLH + sHL × sHL + sHH × sHH; | cv::Mat Src = cv::imread(FileName); W3 = IndexWavelet3(Src); W3 = ompWavelet3(Src); W3 = tbbWavelet3(Src); W3 = cuWavelet3(Src); W3 = clWavelet3(Src); |
| GPU Grade | Advanced-User | Budget | ||
|---|---|---|---|---|
| Hardware | Desktop1 | Desktop2 | Mini PC | IPC |
| PC Vendor | Custom | Coolzen | ASRock | Crevis |
| CPU | Ryzen 3950X | Ryzen 7900X | i9-12900K | i7-6600U |
| CPU cores | 16 | 12 | 16 | 2 |
| CPU Vendor | AMD (Santa Clara, CA, USA) | AMD | Intel (Santa Clara, CA, USA) | Intel |
| RAM | 64 GB | 64 GB | 64 GB | 4 GB |
| GPU | RTX2070 | RTX4090 | UHD 770 | HD 520 |
| GPU Vendor | NVIDIA (Santa Clara, CA, USA) | NVIDIA | Intel | Intel |
| Interface | PCIe | PCIe | CPU-resident | CPU-resident |
| OS | Ubuntu 20.04 | Ubuntu 24.04 | Ubuntu 24.04 | Ubuntu 22.04 |
| MCP Tools | OpenMP 1, TBB (Santa Clara, CA, USA) | OpenMP, TBB | OpenMP, TBB | OpenMP, TBB |
| GPU Tools | CUDA (Santa Clara, CA, USA), OpenCL 2 | CUDA, OpenCL | OpenCL | OpenCL |
| Precision | FP64 | FP64 | FP32 | FP64 |
| Applications | office desktop | software development | commercial kiosk | industrial machine vision |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, H.; Lee, D.-Y.; Choi, D.; Lee, D.-W. GPU-Driven Acceleration of Wavelet-Based Autofocus for Practical Applications in Digital Imaging. Appl. Sci. 2025, 15, 10455. https://doi.org/10.3390/app151910455
Kim H, Lee D-Y, Choi D, Lee D-W. GPU-Driven Acceleration of Wavelet-Based Autofocus for Practical Applications in Digital Imaging. Applied Sciences. 2025; 15(19):10455. https://doi.org/10.3390/app151910455
Chicago/Turabian StyleKim, HyungTae, Duk-Yeon Lee, Dongwoon Choi, and Dong-Wook Lee. 2025. "GPU-Driven Acceleration of Wavelet-Based Autofocus for Practical Applications in Digital Imaging" Applied Sciences 15, no. 19: 10455. https://doi.org/10.3390/app151910455
APA StyleKim, H., Lee, D.-Y., Choi, D., & Lee, D.-W. (2025). GPU-Driven Acceleration of Wavelet-Based Autofocus for Practical Applications in Digital Imaging. Applied Sciences, 15(19), 10455. https://doi.org/10.3390/app151910455







