Visual Hull-Based Approach for Coronary Vessel Three-Dimensional Reconstruction
Abstract
1. Introduction
1.1. Justification
1.2. Related Works
- Traditional methods generally follow a sequence encompassing segmentation, registration, and surface reconstruction. Segmentation involves delineating medical images into distinct regions corresponding to specific anatomical structures, while registration aligns multiple images to establish a coherent and spatially consistent 3D representation. Surface reconstruction subsequently generates a geometric model of the organ or tissue from the acquired data. Within this framework, Active Contour Models (ACMs) and Statistical Shape Models (SSMs) are frequently employed to enhance the precision and reliability of both segmentation and reconstruction.
- Recent advances have increasingly incorporated machine learning (ML) techniques, integrating deep neural networks at various stages of the reconstruction pipeline to improve automation and accuracy. Convolutional neural network (CNN) architectures, including U-Net, Mask R-CNN, and Mesh R-CNN, are widely applied for segmentation tasks. Generative Adversarial Networks (GANs) facilitate the generation of realistic 3D organ models, particularly when imaging data are incomplete or of suboptimal quality. Point-cloud-based reconstruction approaches further enable the direct creation of 3D surfaces from imaging-derived point clouds, providing high-fidelity geometric representations.
1.2.1. 3D Reconstruction
1.2.2. Calibration
1.2.3. Segmentation
1.3. Aim of This Work
2. Materials and Methods
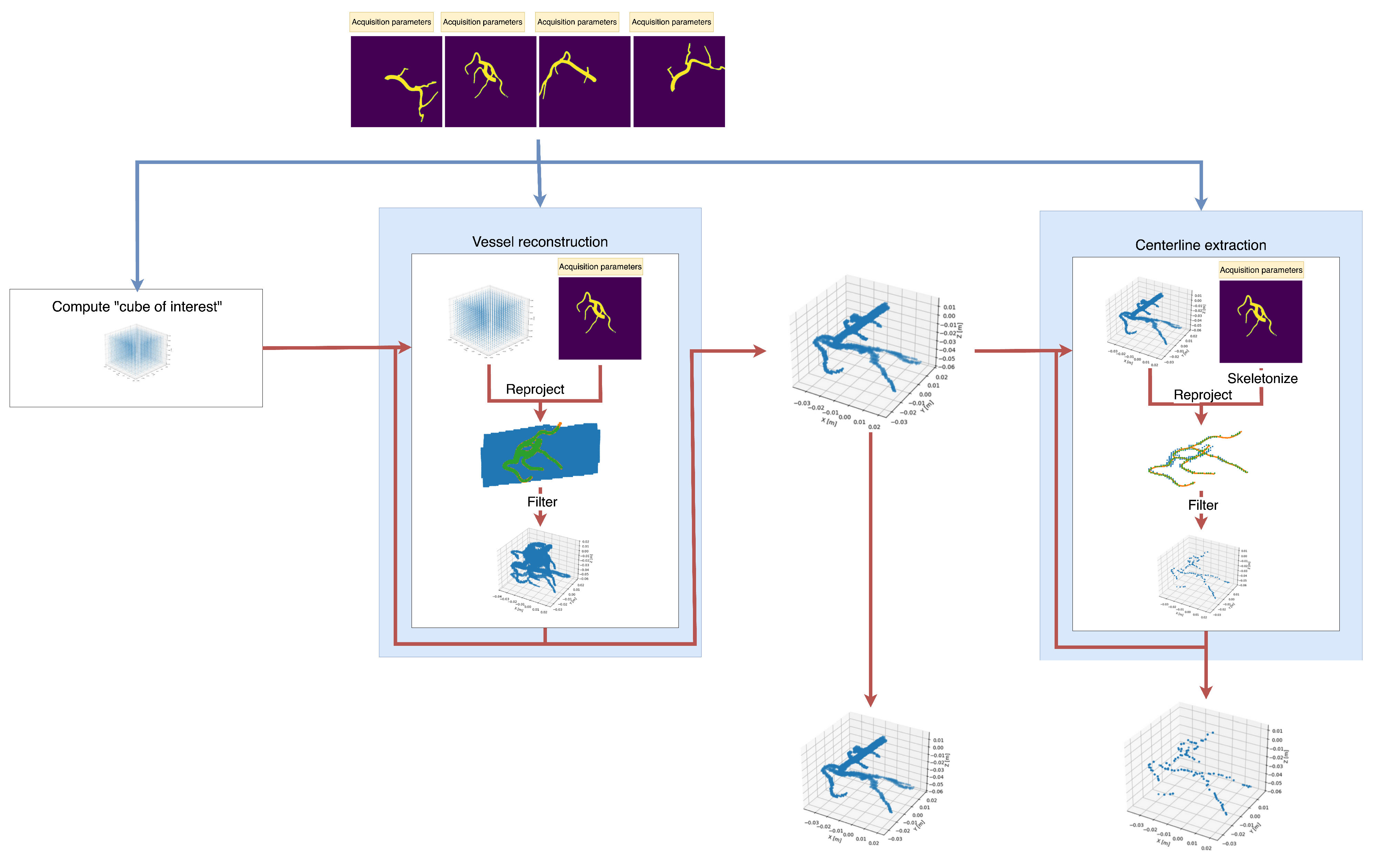
2.1. Proposed Method
2.1.1. Overview
| Algorithm 1 Method pseudocode. |
|
2.1.2. First Step: Segmentation
2.1.3. Second Step: Initial “Cube of Interest” Construction
2.1.4. Third Step: Point Cloud Filtering
| Algorithm 2 Filtering. |
|
2.1.5. Fourth Step (Optional): Centerline Extraction
| Algorithm 3 Filtering variant for centerline extraction. |
|
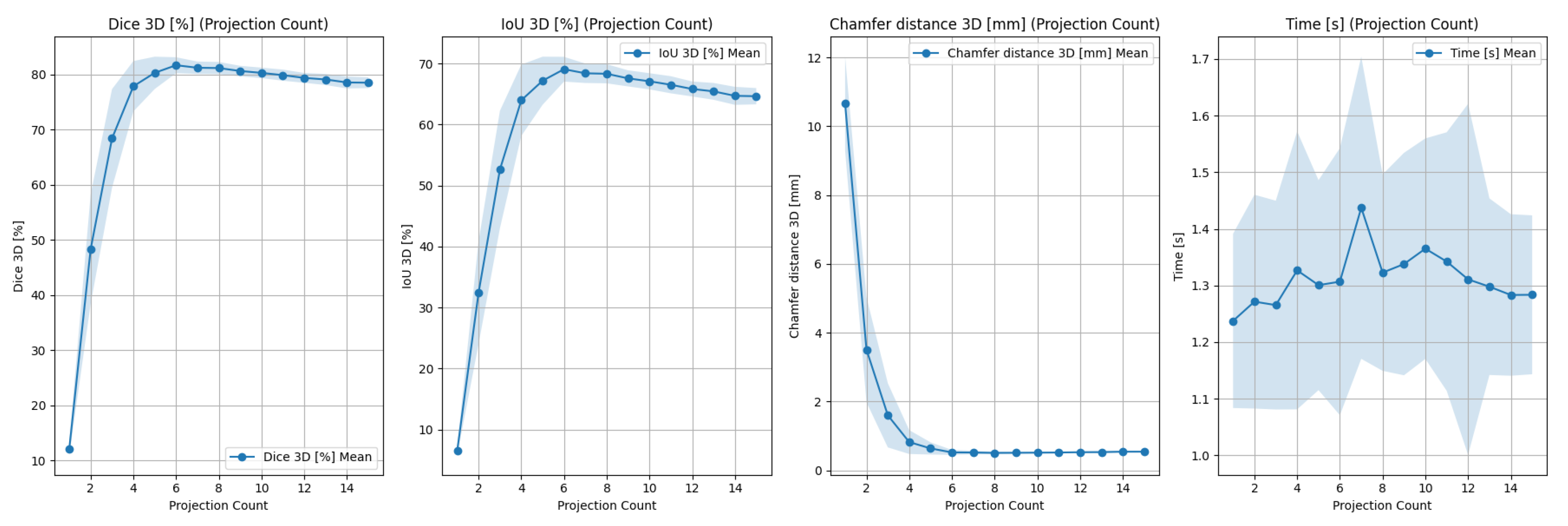
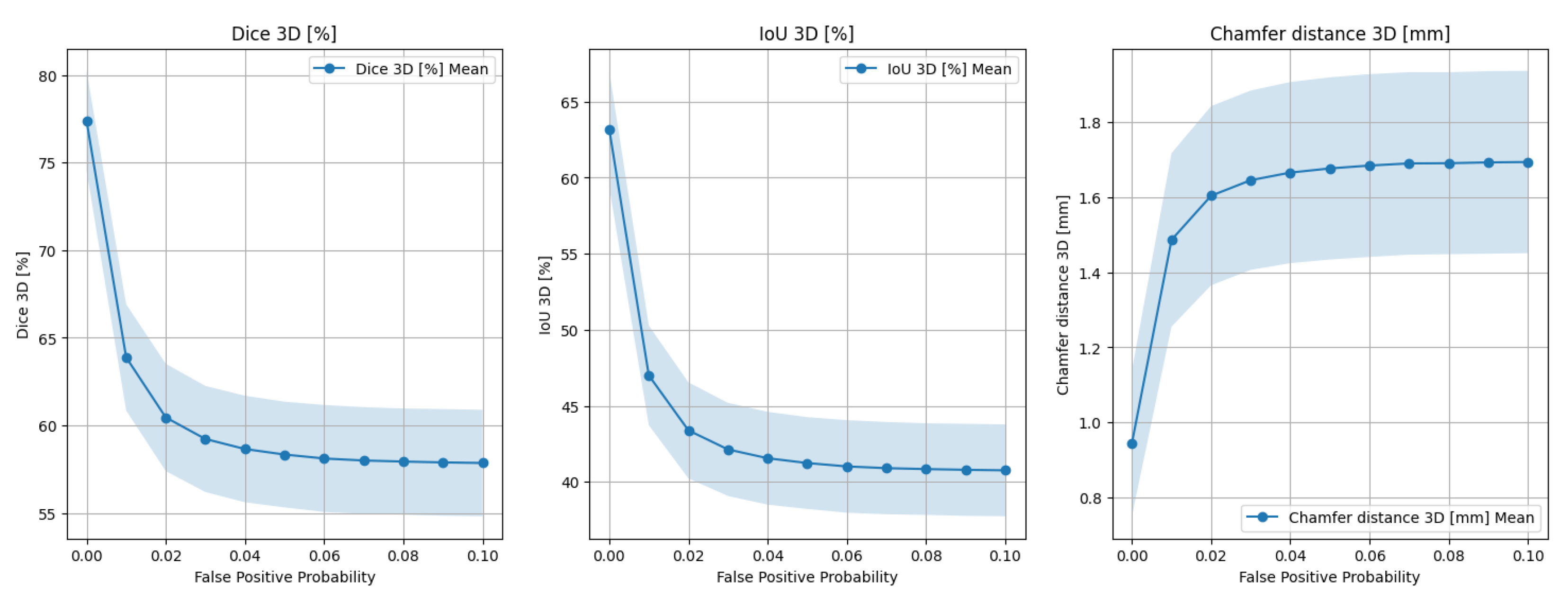
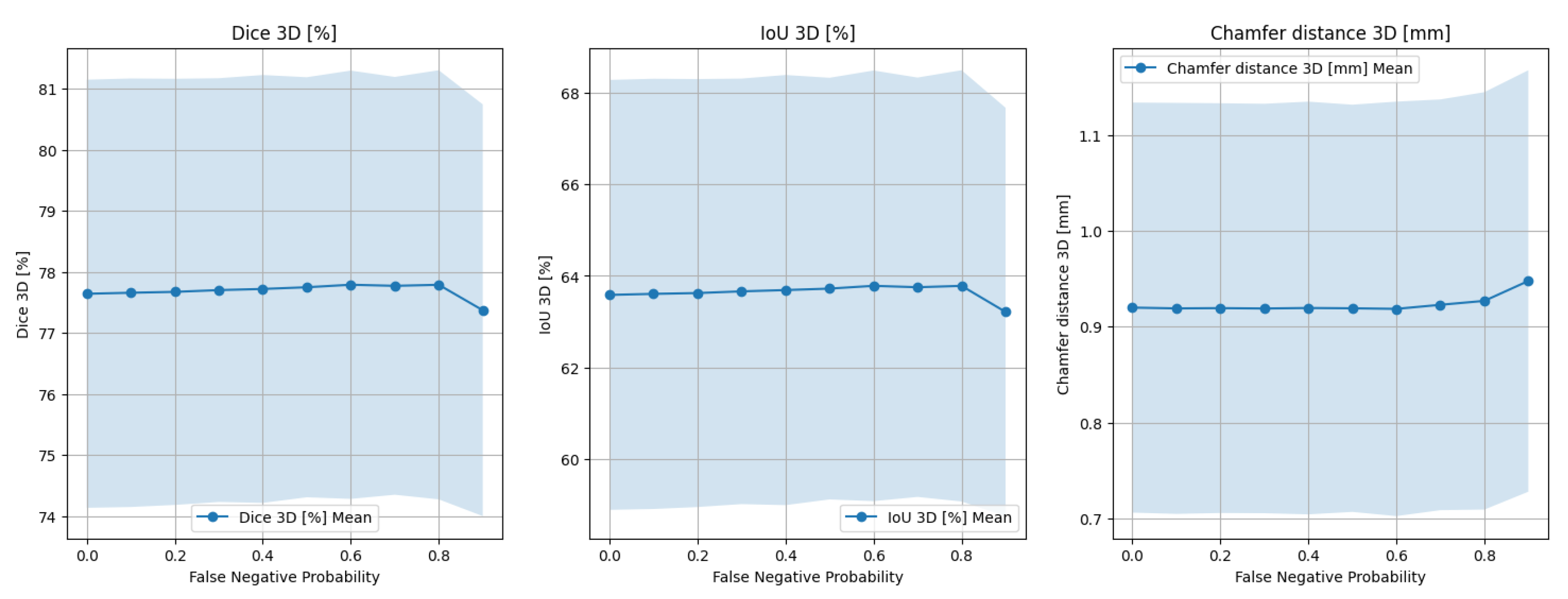
2.2. Experiments
2.2.1. Design
- Mean Dice coefficient () between reprojected point cloud and each input projection;
- Execution time ().
- Dice coefficient in 3D () between the reconstructed and target point clouds;
- IoU metric in 3D ();
- Chamfer distance in 3D ().
- Number of input images;
- Patient and heart motion;
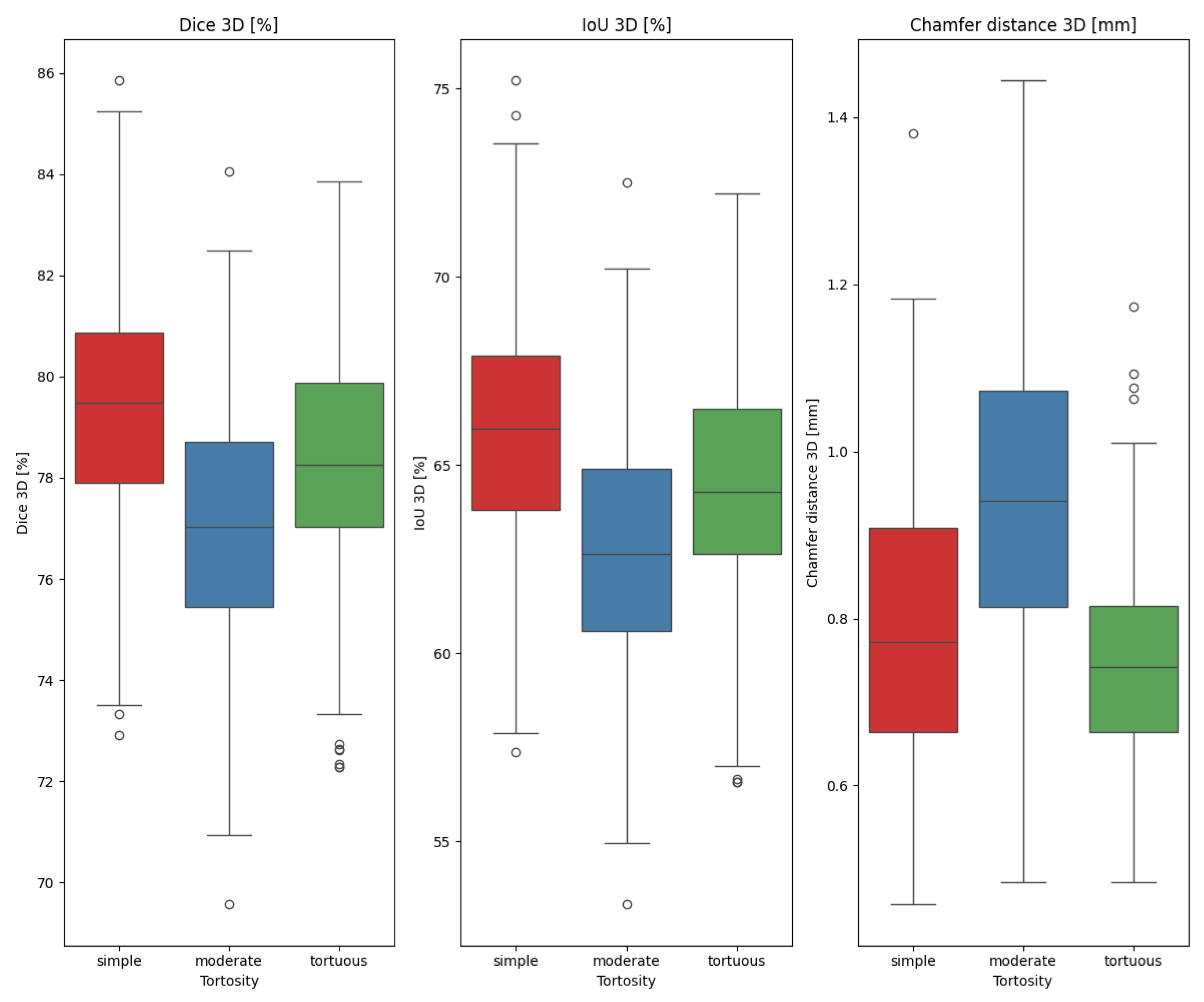
- Vessel tortuousness;
- Segmentation artifacts.
2.2.2. Datasets
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SID | source–image distance (distance between X-ray sources and the absorbing screen) |
| SOD | source–object distance |
| ICD | International Classification of Diseases |
| IHD | Ischemic Heart Disease |
References
- ec.europa.eu. Cardiovascular Diseases Statistics. Available online: https://ec.europa.eu/eurostat/statistics-explained/index.php?title=Cardiovascular_diseases_statistics (accessed on 10 September 2025).
- Martin, S.S.; Aday, A.W.; Almarzooq, Z.I.; Anderson, C.A.; Arora, P.; Avery, C.L.; Baker-Smith, C.M.; Barone Gibbs, B.; Beaton, A.Z.; Boehme, A.K.; et al. 2024 Heart Disease and Stroke Statistics: A Report of US and Global Data From the American Heart Association. Circulation 2024, 149, e347–e913. [Google Scholar] [CrossRef]
- Cimen, S.; Gooya, A.; Grass, M.; Frangi, A.F. Reconstruction of coronary arteries from X-ray angiography: A review. Med. Image Anal. 2016, 32, 46–68. [Google Scholar] [CrossRef]
- Sarmah, M.; Neelima, A.; Singh, H.R. Survey of methods and principles in three-dimensional reconstruction from two-dimensional medical images. Vis. Comput. Ind. Biomed. Art 2023, 6, 15. [Google Scholar] [CrossRef] [PubMed]
- Vukicevic, A.M.; Çimen, S.; Jagic, N.; Jovicic, G.; Frangi, A.F.; Filipovic, N. Three-dimensional reconstruction and NURBS-based structured meshing of coronary arteries from the conventional X-ray angiography projection images. Sci. Rep. 2018, 8, 1711. [Google Scholar] [CrossRef] [PubMed]
- Galassi, F.; Alkhalil, M.; Lee, R.; Martindale, P.; Kharbanda, R.K.; Channon, K.M.; Grau, V.; Choudhury, R.P. 3D reconstruction of coronary arteries from 2D angiographic projections using non-uniform rational basis splines (NURBS) for accurate modelling of coronary stenoses. PLoS ONE 2018, 13, e0190650. [Google Scholar] [CrossRef] [PubMed]
- Lorenz, C.; von Berg, J. A comprehensive shape model of the heart. Med. Image Anal. 2006, 10, 657–670. [Google Scholar] [CrossRef]
- Frangi, A.; Niessen, W.; Hoogeveen, R.; van Walsum, T.; Viergever, M. Model-based quantitation of 3-D magnetic resonance angiographic images. IEEE Trans. Med. Imaging 1999, 18, 946–956. [Google Scholar] [CrossRef]
- Bappy, D.; Hong, A.; Choi, E.; Park, J.O.; Kim, C.S. Automated three-dimensional vessel reconstruction based on deep segmentation and bi-plane angiographic projections. Comput. Med. Imaging Graph. 2021, 92, 101956. [Google Scholar] [CrossRef]
- Hwang, M.; Hwang, S.B.; Yu, H.; Kim, J.; Kim, D.; Hong, W.; Ryu, A.J.; Cho, H.Y.; Zhang, J.; Koo, B.K.; et al. A Simple Method for Automatic 3D Reconstruction of Coronary Arteries From X-Ray Angiography. Front. Physiol. 2021, 12, 724216. [Google Scholar] [CrossRef]
- Bransby, K.M.; Tufaro, V.; Cap, M.; Slabaugh, G.; Bourantas, C.; Zhang, Q. 3D Coronary Vessel Reconstruction from Bi-Plane Angiography using Graph Convolutional Networks. arXiv 2023, arXiv:2302.14795. [Google Scholar] [CrossRef]
- Wang, Y.; Banerjee, A.; Choudhury, R.P.; Grau, V. DeepCA: Deep Learning-Based 3D Coronary Artery Tree Reconstruction from Two 2D Non-Simultaneous X-Ray Angiography Projections. In Proceedings of the 2025 IEEE/CVF Winter Conference on Applications of Computer Vision (WACV), Tucson, AZ, USA, 26 February–6 March 2025; IEEE: New York, NY, USA, 2025; pp. 337–346. [Google Scholar] [CrossRef]
- Fu, X.; Li, Y.; Tang, F.; Li, J.; Zhao, M.; Teng, G.J.; Zhou, S.K. 3DGR-CAR: Coronary artery reconstruction from ultra-sparse 2D X-ray views with a 3D Gaussians representation. arXiv 2024, arXiv:2410.00404. [Google Scholar] [CrossRef]
- Wang, Y.; Banerjee, A.; Grau, V. NeCA: 3D Coronary Artery Tree Reconstruction from Two 2D Projections via Neural Implicit Representation. Bioengineering 2024, 11, 1227. [Google Scholar] [CrossRef] [PubMed]
- Atlı, I.; Gedik, O.S. 3D reconstruction of coronary arteries using deep networks from synthetic X-ray angiogram data. Commun. Fac. Sci. Univ. Ank. Ser. A2-A3 Phys. Sci. Eng. 2022, 64, 1–20. [Google Scholar] [CrossRef]
- Zeng, A.; Wu, C.; Lin, G.; Xie, W.; Hong, J.; Huang, M.; Zhuang, J.; Bi, S.; Pan, D.; Ullah, N.; et al. ImageCAS: A large-scale dataset and benchmark for coronary artery segmentation based on computed tomography angiography images. Comput. Med. Imaging Graph. 2023, 109, 102287. [Google Scholar] [CrossRef]
- Murphy, A.; Dabirifar, S.; Feger, J. Cardiac Gating (CT). 2021. Available online: https://radiopaedia.org/articles/88788 (accessed on 14 September 2025).
- Shechter, G.; Shechter, B.; Resar, J.; Beyar, R. Prospective motion correction of X-ray images for coronary interventions. IEEE Trans. Med. Imaging 2005, 24, 441–450. [Google Scholar] [CrossRef]
- Tu, S.; Hao, P.; Koning, G.; Wei, X.; Song, X.; Chen, A.; Reiber, J.H. In vivo assessment of optimal viewing angles from X-ray coronary angiography. EuroIntervention 2011, 7, 112–120. [Google Scholar] [CrossRef]
- Kalmykova, M.; Poyda, A.; Ilyin, V. An approach to point-to-point reconstruction of 3D structure of coronary arteries from 2D X-ray angiography, based on epipolar constraints. Procedia Comput. Sci. 2018, 136, 380–389. [Google Scholar] [CrossRef]
- Jun, T.J.; Kweon, J.; Kim, Y.H.; Kim, D. T-Net: Nested encoder–decoder architecture for the main vessel segmentation in coronary angiography. Neural Netw. 2020, 128, 216–233. [Google Scholar] [CrossRef]
- Chang, S.S.; Lin, C.T.; Wang, W.C.; Hsu, K.C.; Wu, Y.L.; Liu, C.H.; Fann, Y.C. Optimizing ensemble U-Net architectures for robust coronary vessel segmentation in angiographic images. Sci. Rep. 2024, 14, 6640. [Google Scholar] [CrossRef]
- Xu, J.; Pan, Y.; Pan, X.; Hoi, S.; Yi, Z.; Xu, Z. RegNet: Self-Regulated Network for Image Classification. arXiv 2021, arXiv:2101.00590. [Google Scholar] [CrossRef]
- Zhu, X.; Cheng, Z.; Wang, S.; Chen, X.; Lu, G. Coronary angiography image segmentation based on PSPNet. Comput. Methods Programs Biomed. 2021, 200, 105897. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Esposito, M.; Xu, Z.; Zhou, W. HAGMN-UQ: Hyper association graph matching network with uncertainty quantification for coronary artery semantic labeling. Med. Image Anal. 2025, 99, 103374. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Xu, Z.; Jiang, J.; Esposito, M.; Pienta, D.; Hung, G.U.; Zhou, W. AGMN: Association graph-based graph matching network for coronary artery semantic labeling on invasive coronary angiograms. Pattern Recognit. 2023, 143, 109789. [Google Scholar] [CrossRef]
- Molenaar, M.A.; Selder, J.L.; Nicolas, J.; Claessen, B.E.; Mehran, R.; Bescós, J.O.; Schuuring, M.J.; Bouma, B.J.; Verouden, N.J.; Chamuleau, S.A.J. Current State and Future Perspectives of Artificial Intelligence for Automated Coronary Angiography Imaging Analysis in Patients with Ischemic Heart Disease. Curr. Cardiol. Rep. 2022, 24, 365–376. [Google Scholar] [CrossRef]
- Kaur, A.; Dong, G.; Basu, A. GradXcepUNet: Explainable AI Based Medical Image Segmentation. In Smart Multimedia; Berretti, S., Su, G.M., Eds.; Springer: Cham, Switzerland, 2022; pp. 174–188. [Google Scholar] [CrossRef]
- NEMA PS3/ISO 12052:2017; Digital Imaging and Communications in Medicine (DICOM). National Electrical Manufacturers Association (NEMA): Rosslyn, VA, USA, 2025.
- Banerjee, A.; Galassi, F.; Zacur, E.; De Maria, G.L.; Choudhury, R.P.; Grau, V. Point-Cloud Method for Automated 3D Coronary Tree Reconstruction From Multiple Non-Simultaneous Angiographic Projections. IEEE Trans. Med. Imaging 2020, 39, 1278–1290. [Google Scholar] [CrossRef]
- Guo, Z.; Hall, R.W. Parallel thinning with two-subiteration algorithms. Commun. ACM 1989, 32, 359–373. [Google Scholar] [CrossRef]
- Tsompou, P.I.; Andrikos, I.O.; Karanasiou, G.S.; Sakellarios, A.I.; Tsigkas, N.; Kigka, V.I.; Kyriakidis, S.; Michalis, L.K.; Fotiadis, D.I.; Author, S.B. Validation study of a novel method for the 3D reconstruction of coronary bifurcations. In Proceedings of the 2020 42nd Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Montreal, QC, Canada, 20–24 July 2020; pp. 1576–1579. [Google Scholar] [CrossRef]
- Martin, R.; Vachon, E.; Miro, J.; Duong, L. 3D reconstruction of vascular structures using graph-based voxel coloring. In Proceedings of the 2017 IEEE 14th International Symposium on Biomedical Imaging (ISBI 2017), Melbourne, VIC, Australia, 18–21 April 2017; IEEE: New York, NY, USA, 2017; pp. 1032–1035. [Google Scholar] [CrossRef]
- Muneeb, M.; Nuzhat, N.; Khan Niazi, A.; Khan, A.H.; Chatha, Z.; Kazmi, T.; Farhat, S. Assessment of the Dimensions of Coronary Arteries for the Manifestation of Coronary Artery Disease. Cureus 2023, 15, e46606. [Google Scholar] [CrossRef]
- Green, P.; Frobisher, P.; Ramcharitar, S. Optimal angiographic views for invasive coronary angiography: A guide for trainees. Br. J. Cardiol. 2016, 23, 110–113. [Google Scholar] [CrossRef]
- Iyer, K.; Nallamothu, B.K.; Figueroa, C.A.; Nadakuditi, R.R. A multi-stage neural network approach for coronary 3D reconstruction from uncalibrated X-ray angiography images. Sci. Rep. 2023, 13, 17603. [Google Scholar] [CrossRef]
- Popov, M.; Amanturdieva, A.; Zhaksylyk, N.; Alkanov, A.; Saniyazbekov, A.; Aimyshev, T.; Ismailov, E.; Bulegenov, A.; Kuzhukeyev, A.; Kulanbayeva, A.; et al. Dataset for Automatic Region-based Coronary Artery Disease Diagnostics Using X-Ray Angiography Images. Sci. Data 2024, 11, 20. [Google Scholar] [CrossRef]
- Andrikos, I.O.; Sakellarios, A.I.; Siogkas, P.K.; Rigas, G.; Exarchos, T.P.; Athanasiou, L.S.; Karanasos, A.; Toutouzas, K.; Tousoulis, D.; Michalis, L.K.; et al. A novel hybrid approach for reconstruction of coronary bifurcations using angiography and OCT. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Republic of Korea, 11–15 July 2017; IEEE: New York, NY, USA, 2017; pp. 588–591. [Google Scholar] [CrossRef]
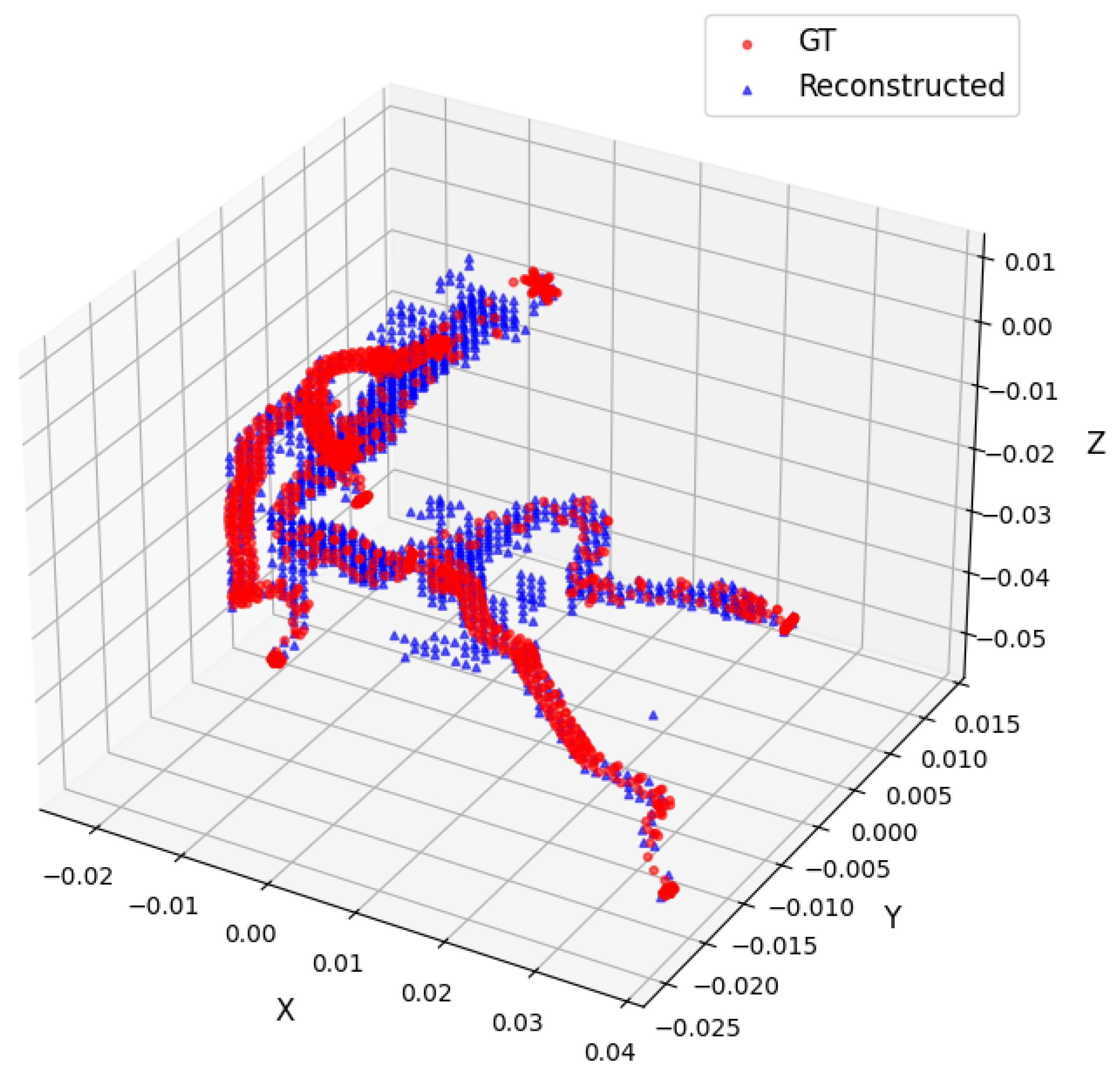

| [%] | [%] | [mm] | [%] | |
|---|---|---|---|---|
| 78.17 | 64.24 | 0.8307 | 78.61 | |
| 2.660 | 3.573 | 0.1863 | 1.095 | |
| (77.96, 78.38) | (63.95, 64.53) | (0.8157, 0.8456) | (78.53, 78.70) |
| [%] | [%] | [mm] | [%] | |
|---|---|---|---|---|
| 75.25 | 60.39 | 0.9992 | 73.66 | |
| 2.626 | 3.375 | 0.2151 | 1.177 | |
| (75.04, 75.46) | (60.12, 60.66) | (0.9820, 1.016) | (73.56, 73.75) |
| X | Y | p-Value |
|---|---|---|
| tortuous | simple | 0.01130 |
| tortuous | moderate | × |
| simple | moderate | × |
| Method | Result | Number of Projections | Architecture/Approach | Comment |
|---|---|---|---|---|
| ours | see Table 1 and Table 2 | 3 | Sequential reprojection and filtering of the outlier points. | - |
| [11] | 87.59 [%] | 2 | Segmentation-based initialization, GCN-driven surface refinement, and branch stitching for bifurcations | Is not fully automatic (segment of interest needs to be specified). Bi-plane |
| [13] | 70.03 [%] | 2 | U-Net to predict vessel depth from X-rays, which are then used in 3D Gaussian models. | Tested on ImageCAS dataset. |
| [14] | 90.43 [%] | 2 | Based on neural implicit representation using the multiresolution hash encoder and differentiable cone-beam forward projector layer. | Tested on ImageCAS dataset. |
| [12] | 83.31 [%], [mm] | 2 | Wasserstein conditional generative adversarial network with gradient penalty, latent convolutional transformer layers, and a dynamic snake convolutional critic. | Tested on ImageCAS dataset. |
| [33] | 86.71 [%] (pulmonary), 95.85 [%] (aorta) | 1 | Random walks algorithm on a graph-based representation of a discretized visual hull. | Only selected main vessels, no fine details taken into account. |
| [36] | [mm] (centerlines) | 3 | Feature extraction network (ResNet101) and a regular MLP (black box). | Reported MSE is close to Chamfer Distance as correspondence between points is known beforehand. |
| [38] | 85.00 [%] (main), 78.00 [%] (side) | 2 | Combining OCT-detected lumen borders with vessel centerlines derived by an expert. | The second part of the algorithm is not fully automatic. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lau, D.B.; Dziubich, T. Visual Hull-Based Approach for Coronary Vessel Three-Dimensional Reconstruction. Appl. Sci. 2025, 15, 10450. https://doi.org/10.3390/app151910450
Lau DB, Dziubich T. Visual Hull-Based Approach for Coronary Vessel Three-Dimensional Reconstruction. Applied Sciences. 2025; 15(19):10450. https://doi.org/10.3390/app151910450
Chicago/Turabian StyleLau, Dominik Bernard, and Tomasz Dziubich. 2025. "Visual Hull-Based Approach for Coronary Vessel Three-Dimensional Reconstruction" Applied Sciences 15, no. 19: 10450. https://doi.org/10.3390/app151910450
APA StyleLau, D. B., & Dziubich, T. (2025). Visual Hull-Based Approach for Coronary Vessel Three-Dimensional Reconstruction. Applied Sciences, 15(19), 10450. https://doi.org/10.3390/app151910450






