Waveform Self-Referencing Algorithm for Low-Repetition-Rate Laser Coherent Combination

Abstract

Indirect detection phase control algorithms, such as the dithering algorithm and the stochastic parallel gradient descent algorithm (SPGD), have simple system structures and are applicable to filled-aperture coherent combinations with high efficiency. The performances of these algorithms are limited when applied to a coherent combination of pulsed fiber lasers with a low repetition rate (≤5 kHz). Firstly, due to the overlap of the phase noise frequency and repetition rate, conventional algorithms cannot effectively distinguish the phase noise from the pulse fluctuation, and directly applying filtering will result in the phase information being filtered out. Secondly, if the pulse fluctuation is ignored and only the continuous part of the phase information is utilized, it relies on the presetting of conditions to separate the pulse from the continuous part and loses the phase information of the pulse part. In this article, we propose a waveform self-referencing algorithm (WSRA) based on a two-channel near-infrared laser coherent combination system to overcome the above challenges. Firstly, by modelling a self-referencing waveform, a nonlinear scaling operation is performed on the combined signal to generate a pseudo-continuous signal, which removes the intrinsic pulse fluctuation while preserving the phase noise information. Secondly, the phase control signal is calculated based on the pseudo-continuous signals after parallel perturbation. Finally, the phase noise is corrected by optimization. The results show that our method effectively suppresses the waveform fluctuation at a 5 kHz repetition rate, the light intensity reaches an ideal value (0.9939 $I_{\max }$), and the root-mean-square (RMS) phase error is only 0.0130 $\lambda$. This method does not require the presetting of pulse detection thresholds or conditions, and solves the challenge of coherent combination at a low repetition rate, with adaptability to different pulse waveforms.

1. Introduction

Low-repetition-rate pulsed fiber lasers can accumulate higher single pulse energies compared to high-repetition-rate lasers at the same average power. Therefore, they have been widely applied in fields requiring huge single pulse energy and peak power, such as lidar, advanced manufacturing, and health care [1,2,3]. The improvement of pulsed fiber laser power faces the difficulties of nonlinear effects and damage thresholds [4,5,6,7]. Fiber laser coherent combination technology can significantly increase output power while maintaining high beam quality [8]. An international research team has launched the International Coherent Amplification Network (ICAN) project to achieve ultra-high peak power pulse output through the coherent combination of thousands of optical fibers [9]. The core of coherent combination lies in high-precision phase control algorithms, and the performance of the algorithm directly determines the combination efficiency. To date, the existing phase control methods for coherent combination can be classified into two categories: passive control methods and active control methods. Compared with passive control methods, active control methods can achieve a higher combination efficiency [10]. Active control methods can be further divided into two types: direct detection methods and indirect detection methods. Direct detection methods obtain the phase errors between laser beams through methods such as the heterodyne method [11], the Hansch–Couillaud (HC) polarization detection method [12], shearing interferometry [13], and homodyne interferometry [14,15]. However, the structure of their error detection system is relatively complex. In contrast, indirect detection methods extract the energy of the main lobe in the far-field spot of the combined beam using a photodetector, and then conducts optimization iterations with methods such as the SPGD [16,17,18,19] and the dithering algorithm [20,21] to maximize the energy, which have the advantage of simple system structures. Machine learning methods [22,23,24,25] usually rely on complex calculations and analyses of far-field spot images [26,27,28]. In a filled-aperture coherent beam combination system, the combined spot does not contain spatial information such as modulation fringes that can be used to calculate the phase of each channel. Therefore, most machine learning methods can only be used in tiled-aperture systems. Limited by the energy loss of the side lobes, the combining efficiency is relatively low. Zhou et al. recently proposed a machine learning method for filled-aperture coherent beam combination. This is the first time that machine learning has been made feasible in filled-aperture coherent beam combination systems [29]. However, the training of this algorithm requires a large amount of sample data, and the size of the dataset increases rapidly with the expansion of the number of channels. It is often difficult to collect sufficient data with the ground truth in actual systems. If simulation data are used, there is a problem with the difference between simulation and reality. In contrast, the indirect detection method does not rely on image processing or a large dataset, and is naturally suitable for filled-aperture systems that can achieve higher combination efficiency. Therefore, it is considered an effective method to improve laser brightness.

Indirect detection methods are generally based on the combined light intensity as the phase-locking criterion. Due to the intrinsic light intensity fluctuation of the pulsed laser’s intensity profile, indirect detection methods struggle to distinguish the intrinsic light intensity fluctuation of the pulse from that caused by the phase noise. Thus, the combination effect is adversely affected. The filtering method offers a solution to the coherent combination of pulsed fiber lasers. It filters out intrinsic pulse fluctuation by adding a low-pass filter with an appropriate cutoff frequency behind the photodetector and then performs phase control according to indirect detection methods. Wang et al. achieved stable coherent combination with a 20 kHz repetition rate by introducing a low-pass filter to eliminate the fluctuation of the metric function caused by the pulsed laser and using the SPGD for active phase control [30]. However, this method is only effective at a relatively high repetition rate. In fiber laser systems, the main sources of the phase noise are thermal effects and external environmental vibrations, with a typical cutoff frequency of 5 kHz [31]. We define a low repetition rate as less than 5 kHz. At a low repetition rate, the phase noise spectrum overlaps with the repetition rate, and the filtering process removes the critical phase noise information, resulting in misalignment of the phase control signal.

To solve the problem of the low-repetition-rate coherent combination, Zhang et al. proposed an adaptive window filtering algorithm, which effectively filters out the pulse fluctuation by automatically adapting to the changes in the pulse noise amplitude and the spreading. It replaces the pulse points by interpolation without changing the continuous signal points, and achieves phase-locking using a multi-dithering method [32]. Active phase control can also be achieved by using the continuous part as a probe when the repetition rate is lower than the phase noise cutoff frequency [33,34,35,36]. The continuous light probe method uses acousto-optic modulators or other devices to chop the pulse, retaining only the continuous part between pulses, and using the phase information contained in the continuous part to correct the phase error of the pulse part. Lombard et al. achieved coherent combination at a 10 kHz repetition rate using signal leakage between 100 ns pulses, with a combination efficiency of 95% and an RMS phase error of $\lambda$/27 without significant beam quality degradation [33]. Palese et al. achieved a combination efficiency of 79% for two channels with a 25 kHz repetition rate and a pulse width of 1 ns by utilizing the continuous part between the pulses for phase control [34]. Su et al. utilized the signal leakage between pulses for phase-locking, and the combination efficiency of two pulsed lasers with a pulse width of 500 ns and a repetition rate of 5 kHz was 89% [35]. Zou et al. utilized the continuous part as the effective signal and coherently combined two lasers with a repetition rate of 15 kHz and a pulse width of 100 ns by the SPGD, and the beam combining efficiency was 95% [36]. However, the above methods need to preset pulse detection thresholds or conditions to separate the continuous part from the pulse part, and it may be difficult to realize effective pulse part detection if the waveform has a long tail, which leads to poor adaptability to complex laser waveforms. In addition, these methods ignore the phase information of the pulse part, and the information available in the continuous part is drastically reduced in the case of a high duty cycle.

In this paper, we propose a waveform self-referencing algorithm (WSRA) for low-repetition-rate near-infrared laser phase control, which constructs a self-referencing waveform by extracting a single-channel pulsed intensity signal, performs nonlinear scaling on the combined signal, effectively eliminates the pulse fluctuation and retains the phase noise information completely, generates a pseudo-continuous signal that characterizes the real phase deviation, and uses the pseudo-continuous signal as the input to the SPGD for phase-locking. This method avoids the presetting of chopping conditions and the loss of phase information, adaptively suppresses pulse fluctuation, and can realize stable phase control under different low repetition rates and pulse waveforms. The simulation results show that after applying the WSRA to coherently combine two lasers with a repetition rate of 5 kHz and a pulse width of 600 ns, the combined light intensity reaches 0.9939 $I_{\max }$, and the RMS phase error is 0.0130 $\lambda$, which shows the superior performance of the laser coherent combination with a low repetition rate.

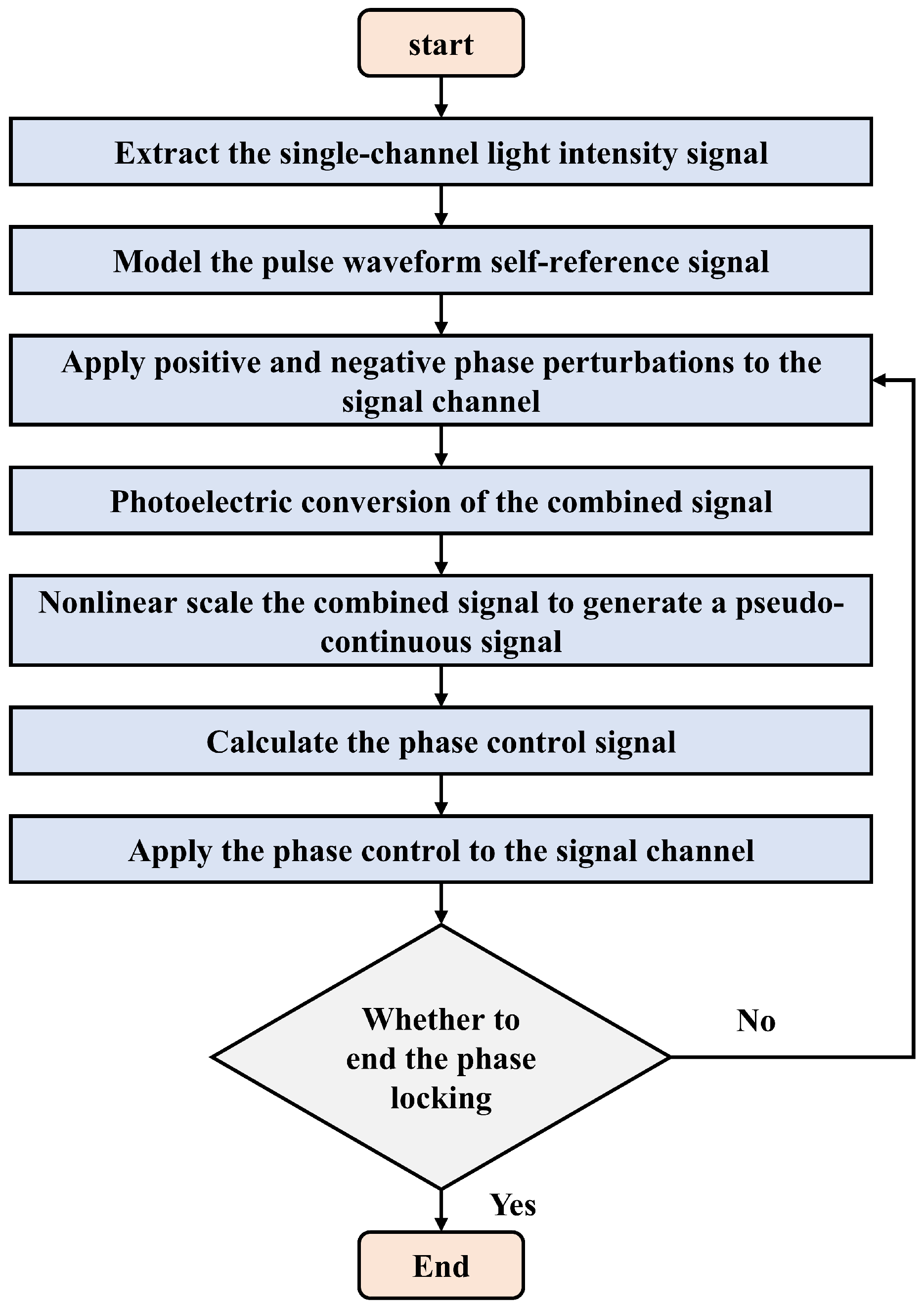
2. Theoretical Foundation and Methodology

The light intensity fluctuation signal of a single channel is captured by the photodetector, and the self-referencing waveform is constructed based on this signal. By blocking one of the channels, only the laser of a single channel is incident on the photodetector. After the analog-to-digital converter (ADC), a period of the voltage value of the N sampling points is acquired, capturing the light intensity fluctuation characteristics of the laser pulse for the subsequent establishment of the self-referencing waveform. The voltage value of the N sampling points is given by

$$V_{\mathrm{ref}}\left(n\right),n=1,2,\dots ,N$$

(1)

The acquired voltage values $V_{\mathrm{ref}}\left(n\right)$ of N sampling points are combined into a discrete sequence $S_{\mathrm{ref}}\left(n\right)$ in time order, constructing a self-referencing waveform without presetting pulse detection thresholds or conditions, which varies with different pulse shapes and is used for the subsequent scaling process of the coherent combination system. The discrete sequence of the self-referencing signal is expressed as

$$S_{\mathrm{ref}}\left(n\right)=[V_{\mathrm{ref}}\left(1\right),V_{\mathrm{ref}}\left(2\right),\dots V_{\mathrm{ref}}\left(n\right)]$$

(2)

One channel without a phase modulator is used as the reference one, and another channel with a phase modulator is used as the signal one. Positive and negative phase perturbations are applied to the signal channel by the phase modulator. The time domains of the signal channel with the added positive and negative phase perturbations are expressed, respectively, as

$$E_{\mathrm{k}}\left(t\right)={\mathsf{\Gamma }}_{\mathrm{k}}\left(t\right){\mathrm{e}}^{-i\left[\omega t+{\phi }_{\mathrm{k}}+{\phi }_{\mathrm{kn}}\left(t\right)+{\phi }_{\delta }\right]},t=1,2,\dots ,mN$$

(3)

$$E_{\mathrm{k}}\left(t+1\right)={\mathsf{\Gamma }}_{\mathrm{k}}\left(t+1\right){\mathrm{e}}^{-i\left[\omega \left(t+1\right)+{\phi }_{\mathrm{k}}+{\phi }_{\mathrm{kn}}\left(t+1\right)-{\phi }_{\delta }\right]}$$

(4)

where ${\mathsf{\Gamma }}_{\mathrm{k}}\left(t\right)$ is the envelope amplitude of the signal channel, $\omega$ is the laser angular frequency, ${\phi }_{\mathrm{k}}$ is the initial phase, ${\phi }_{\mathrm{kn}}\left(t\right)$ is the phase noise of the signal channel, ${\phi }_{\delta }$ is the applied phase perturbation, and m is the number of pulse periods sustained by the phase control.

The photodetector converts the output beam of the combined lasers. The time domain of the two-channel combined signal before phase-locking is given by

$$E_{\mathrm{c}}\left(t\right)=E_{\mathrm{r}}\left(t\right)+E_{\mathrm{k}}\left(t\right)={\mathsf{\Gamma }}_{\mathrm{r}}\left(t\right)e^{-i\left[\omega t+{\phi }_{\mathrm{r}}+{\phi }_{\mathrm{rn}}\left(t\right)\right]}+{\mathsf{\Gamma }}_{\mathrm{k}}\left(t\right)e^{-i\left[\omega t+{\phi }_{\mathrm{k}}+{\phi }_{\mathrm{kn}}\left(t\right)+{\phi }_{\delta }\right]}$$

(5)

The electrical signal output by the photoelectric conversion is proportional to the square of the amplitude in the time domain, and after analog-to-digital conversion, the discrete sequence of the combined signal is denoted as

$$V_{\mathrm{c}}\left(t\right)\propto E_{\mathrm{c}}{\left(t\right)}^2={\mathsf{\Gamma }}_{\mathrm{r}}{\left(t\right)}^2+{\mathsf{\Gamma }}_{\mathrm{k}}{\left(t\right)}^2+2{\mathsf{\Gamma }}_{\mathrm{r}}\left(t\right){\mathsf{\Gamma }}_{\mathrm{k}}\left(t\right)e^{-i\left[2\omega t+{\phi }_{\mathrm{r}}+{\phi }_{\mathrm{rn}}\left(t\right)+{\phi }_{\mathrm{k}}+{\phi }_{\mathrm{kn}}\left(t\right)+{\phi }_{\delta }\right]}$$

(6)

If the ratio of the two channels in the coherent combination system is 1:X, i.e., ${\mathsf{\Gamma }}_{\mathrm{k}}\left(t\right)=X{\mathsf{\Gamma }}_{\mathrm{r}}\left(t\right)$, the above equation simplifies as

$$V_{\mathrm{c}}\left(t\right)\propto E_{\mathrm{c}}{\left(t\right)}^2=(1+X^2){\mathsf{\Gamma }}_{\mathrm{r}}{\left(t\right)}^2+2X{\mathsf{\Gamma }}_{\mathrm{r}}{\left(t\right)}^2{e}^{-i\left[2\omega t+{\phi }_{\mathrm{r}}+{\phi }_{\mathrm{rn}}\left(t\right)+{\phi }_{\mathrm{k}}+{\phi }_{\mathrm{kn}}\left(t\right)+{\phi }_{\delta }\right]}$$

(7)

Based on the established discrete sequence of the self-referencing signal $S_{\mathrm{ref}}\left(n\right)$, the discrete sequence of the pseudo-continuous signal $V_{\mathrm{p}}\left(t\right)$ is generated by performing the sample-by-sample scaling operation on the discrete sequence of the combined signal $V_{\mathrm{c}}\left(t\right)$, retaining the fluctuation characteristics caused by the phase noise while eliminating the intrinsic pulse fluctuation. The discrete sequence of the pseudo-continuous signal is given by

$$V_{\mathrm{p}}\left(t\right)={\displaystyle \frac{V_{\mathrm{c}}\left(t\right)}{S_{\mathrm{ref}}\left\{\left[\left(t-1\right)\mathrm{mod}N\right]+1\right\}}}$$

(8)

The phase control signal is calculated from the discrete sequence of the pseudo-continuous signal, and the difference between the scaled signal obtained at the moment t of the positive phase perturbation and that obtained at the moment t + 1 of the negative phase perturbation is written as

$$\Delta J=V_{\mathrm{p}}\left(t+1\right)-V_{\mathrm{p}}\left(t\right)$$

(9)

The difference is scaled to obtain a phase control signal, which is given by

$${\phi }_{\mathrm{feedback}}=G\times \Delta J$$

(10)

where G is the signal gain.

The calculated phase control signal is applied to the signal channel through the phase modulator to compensate for the phase error and finally enhance the power of the coherently combined output beam. The time domain of the signal channel to which the phase control signal is applied is as follows

$$E_{\mathrm{k}}\left(t+2\right)={\mathsf{\Gamma }}_{\mathrm{k}}\left(t+2\right)e^{-i\left[\omega (t+2)+{\phi }_{\mathrm{k}}+{\phi }_{\mathrm{kn}}\left(t+2\right)+{\phi }_{\delta }+{\phi }_{\mathrm{feedback}}\right]}$$

(11)

To express the calculation process of the WSRA more clearly, the algorithm is represented in the form of the flow chart, as shown in Figure 1.

3. Simulation and Result Analysis

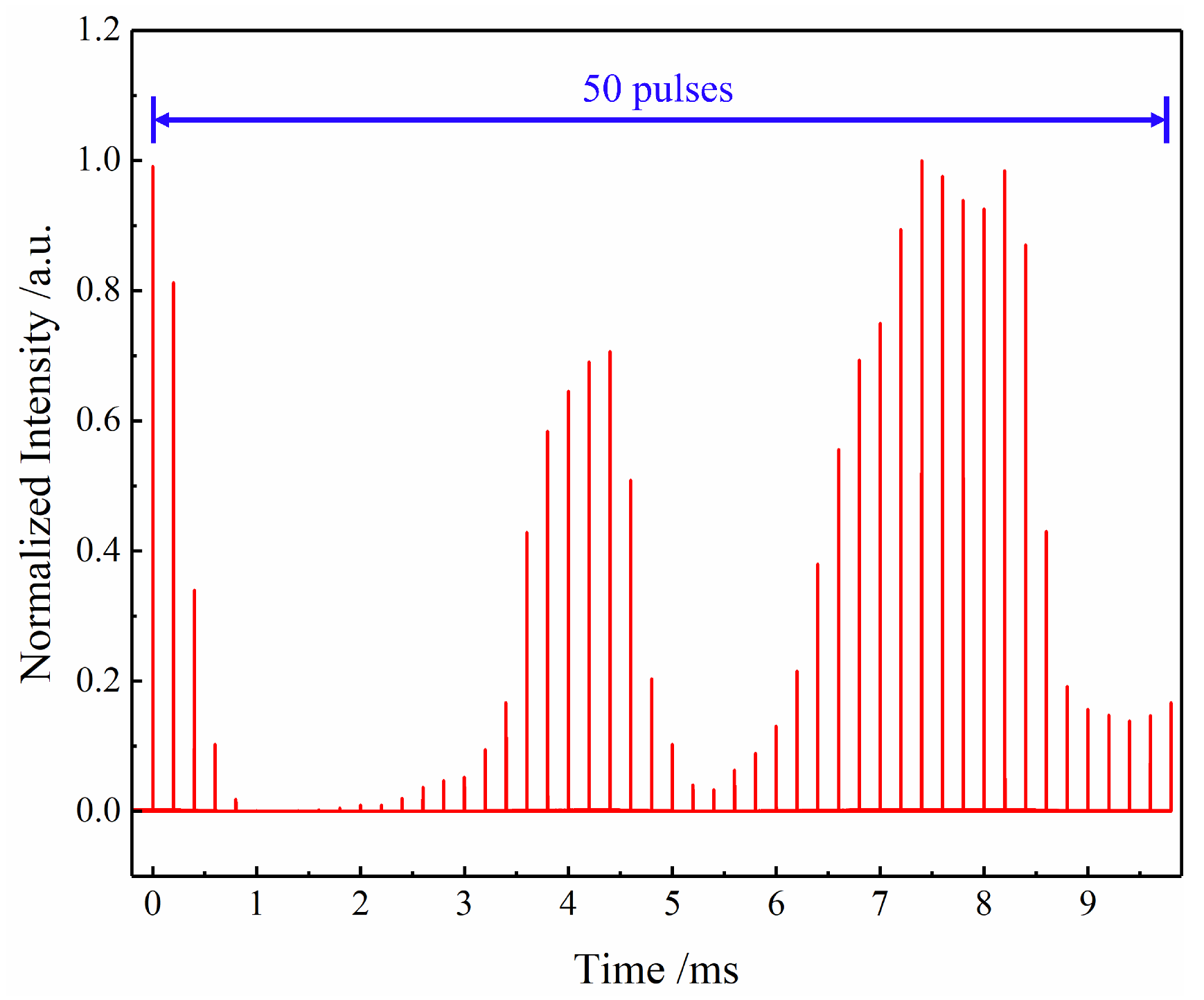
3.1. Two-Channel Combination Before Phase-Locking

The simulation system is based on a near-infrared two-channel fiber laser coherent combination architecture, and analyzes the coupling effect of the environmental noise and the intrinsic pulse fluctuation under the low-repetition-rate condition to obtain the performance of the two-channel low-repetition-rate pulsed laser coherent combination. The wavelength is 1550 nm. The waveform is set as a periodic Gaussian pulse with a pulse half-height width of 600 ns and a pulse repetition rate of 5 kHz, which is at the same frequency order as the phase noise (the phase noise is mainly concentrated within 5 kHz [31]). The single execution delay is 300 ns. Therefore, the total time for positive and negative disturbances and feedback is 900 ns. The intensity ratio of the two channels is set to 50:50.

The phase noise consists of two parts: the low-frequency part and the high-frequency part, where the low-frequency part is simulated by the superposition of sinusoids, and the high-frequency part is simulated by the random white noise, which is generated directly by the software. The overall expression of the phase noise is defined as

$$N_{noise}=\sum _{i=1}^h{A}_{i}sin({\omega }_{i}t+{\phi }_i)+n_{noise}$$

(12)

where $A_i$ is the amplitude of the sinusoid, ${\omega }_i$ is the angular frequency, ${\phi }_i$ is the initial phase, and h is the number of sinusoidal frequencies divided within the specified frequency range. The larger h is, the finer the phase noise bandwidth is. $n_{noise}$ is the random white noise.

Figure 2a shows the time domain intensity of the phase noise, which is randomly distributed in the positive and negative intervals. Figure 2b shows the power spectral density of the phase noise at 0–500 kHz, and the inset of Figure 2b shows the power spectral density of the phase noise at 0–10 kHz. As shown in Figure 2b, the phase noise is concentrated within 5 kHz. The high-frequency part shows an amplitude greater than −70 dB, which is reflected in Figure 2a as high-frequency vibration generated on the low-frequency line.

Before phase-locking, the time-domain intensity of the combined signal of the two low-repetition-rate lasers is shown in Figure 3. In addition to the intrinsic light intensity fluctuation of the pulse waveform, there is an unstable light intensity fluctuation in the pulse part due to the phase noise.

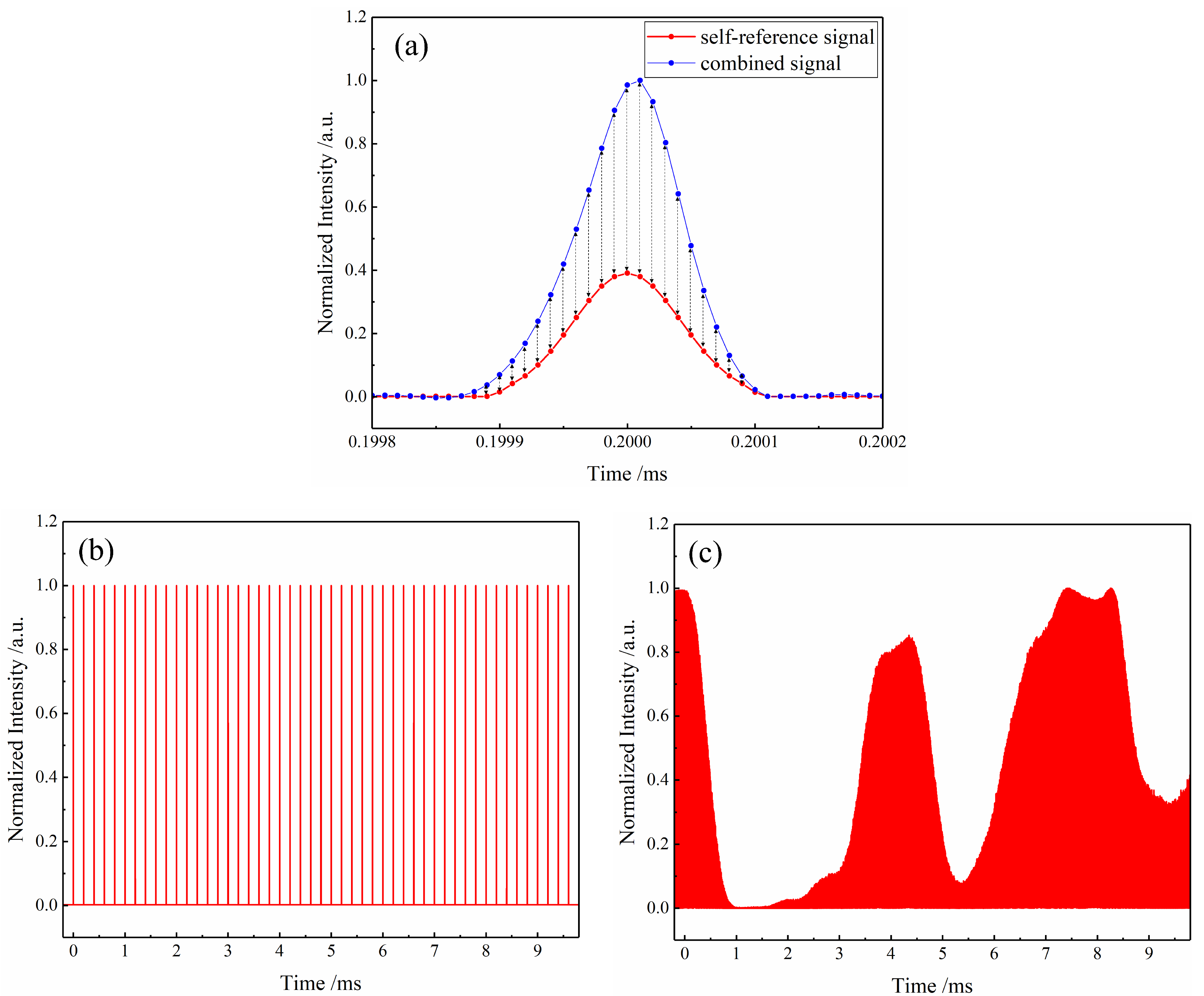
3.2. Self-Referencing Waveform Construction

A self-referencing waveform that characterizes the intrinsic pulse fluctuation is constructed by directly capturing the envelope intensity signal of a single channel. By directly capturing the fluctuation characteristics of the pulse intensity, we generate a reference model that matches the shape of a single-channel waveform, thus providing a baseline for subsequent nonlinear scaling.

The nonlinear scaling process of one pulse is shown in Figure 4a. The red line is one period of the self-referencing waveform, the blue line is one period of the combined signal, and the black arrows represent nonlinear scaling operations. The full self-referencing waveform constructed by extracting the single-channel light intensity is shown in Figure 4b, which reflects the intrinsic light intensity fluctuation present in the single-channel laser. For a two-channel laser coherent combination system with a spectral ratio of 50:50, the pulse envelope intensities of the two channels are the same, and the intrinsic pulse intensity fluctuation information is included in their combined signals, as shown in Equation (7), which is proportional to the light intensity of a single channel (${\mathsf{\Gamma }}_{\mathrm{r}}\left(t\right)$). Based on the constructed self-referencing waveform, the combined signal is nonlinearly scaled sample-by-sample to generate a pseudo-continuous signal, which eliminates the unfavorable effect on the phase control due to the intrinsic pulse fluctuation. As shown in Figure 4c, the intrinsic light intensity fluctuation is eliminated, and the light intensity fluctuation of the pseudo-continuous signal is only caused by the phase noise. This process does not require setting pulse detection thresholds or conditions, and no additional noise is introduced.

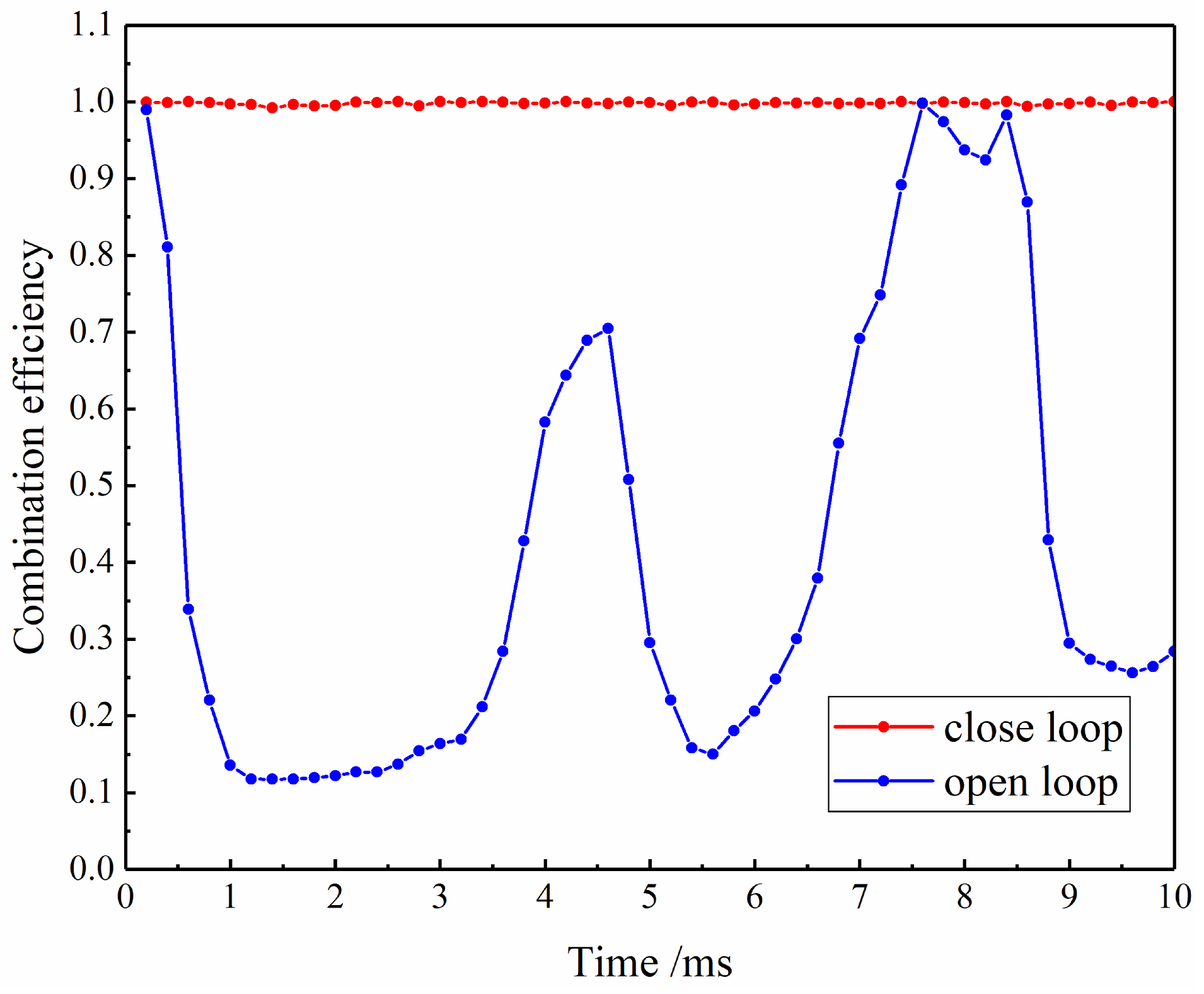
3.3. Two-Channel Coherent Combination After Phase-Locking

After constructing the self-referencing waveform and performing nonlinear scaling, the phase control signal is calculated based on the generated pseudo-continuous signals, and the two combined signals are phase-locked to verify the effectiveness of the WSRA in the low-repetition-rate condition. Under the same condition, the phase-locking performance of the WSRA is compared with that of the conventional SPGD to reflect the core advantages of the waveform self-referencing mechanism in the low-repetition-rate condition.

The coherent combination performance is evaluated using two metrics, combination efficiency and RMS phase error, where combination efficiency is defined as the ratio of the pulsed peak light intensity to the ideal peak light intensity. The RMS phase error [37] is calculated as

$$\Delta {\phi }_{\mathrm{rms}}=2\sqrt{{\displaystyle \frac{\Delta V_{\mathrm{rms}}}{V_{\max }}}}$$

(13)

where $\Delta V_{\mathrm{rms}}$ represents the RMS error of the photoconverted output voltage and $V_{\max }$ represents the maximum value of the photoconverted output voltage.

The variation in the combination efficiency of the two low-repetition-rate lasers before and after phase-locking is shown in Figure 5. It shows that the combination efficiency fluctuates a lot before the phase-locking is turned on. When the phase-locking is turned on, the combination efficiency reaches close to 1 (0.9939 $I_{\max }$), indicating that the phase noise is compensated for. The RMS phase error is 0.0130 $\lambda$.

After phase-locking, the time-domain intensity of the two low-repetition-rate laser coherently combined signals is shown in Figure 6. It can be seen that after phase-locking by the WSRA, the peak light intensity of the pulse part reaches close to 1, and a stable 5 kHz low-repetition-rate coherently combined pulsed laser is outputted.

To further reflect the advantages of the WSRA in the coherent combination of low-repetition-rate pulsed lasers, we compare the WSRA with the conventional SPGD under the same condition, and the comparison result of the combination efficiency is shown in Figure 7. It can be seen that the combination efficiency of the conventional SPGD is 0.2242 and the RMS phase error is 0.2138 $\lambda$ when it is applied to the low-repetition-rate laser coherent combination, whereas the combination efficiency of the WSRA is 0.9939, and the RMS phase error is 0.0130 $\lambda$, which is superior to that of the conventional SPGD. The reason for this result is that the conventional SPGD directly applied to the coherent combination of low-repetition-rate lasers will mistakenly consider the pulse intrinsic fluctuation as a result of the perturbation, and thus will make an error in the calculation of the phase control signal. The WSRA, on the other hand, eliminates this effect of pulse fluctuations by nonlinearly scaling the combined signal. Since there is no need to preset pulse detection thresholds or conditions, it can theoretically be applied to arbitrary waveforms, and the generated pseudo-continuous signals can easily be solved by the optimization algorithm to produce the correct phase control signal.

4. Discussion

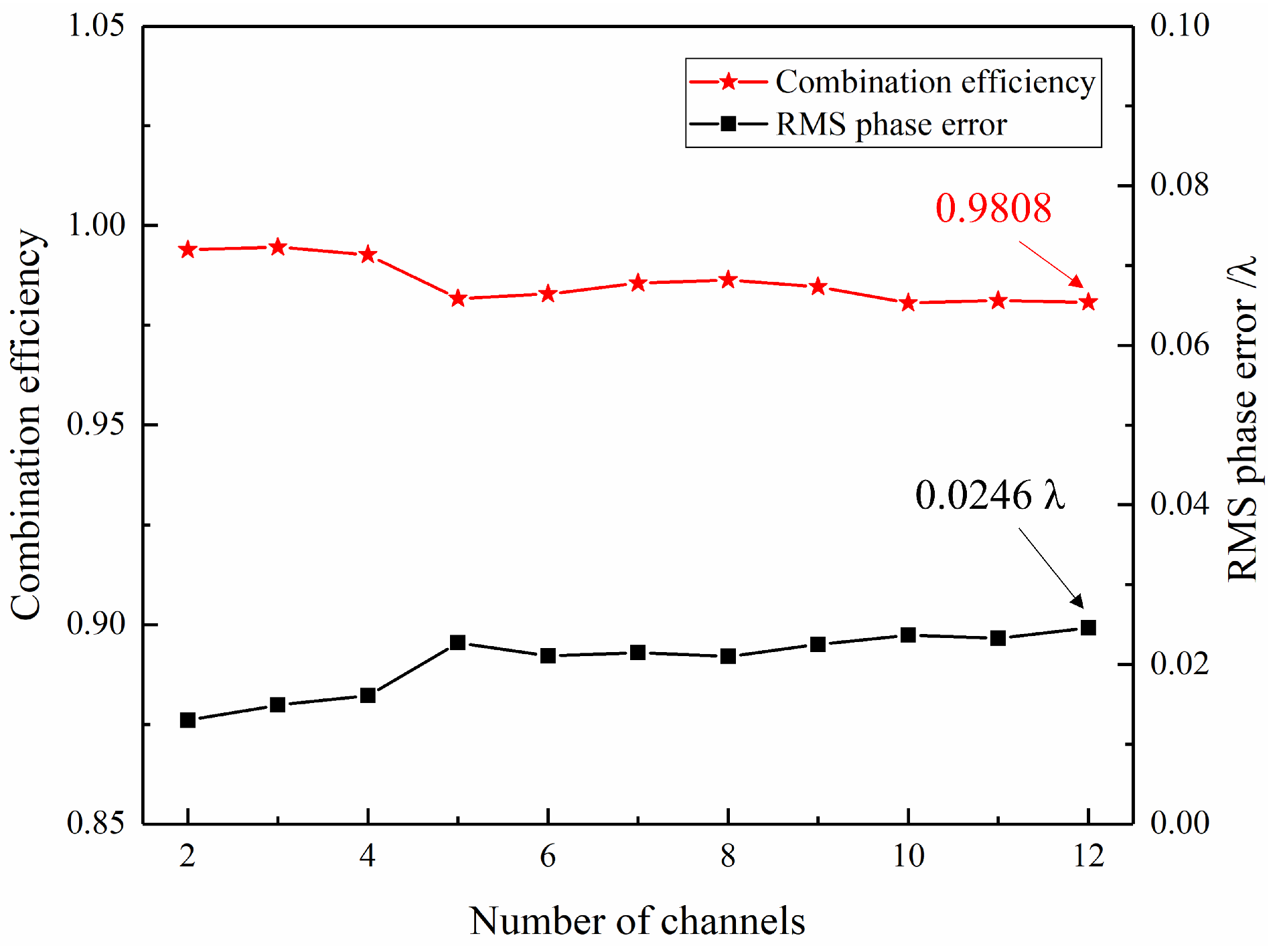
4.1. The Performance of the WSRA Under Extended Conditions

To verify the robustness of the WSRA, an experiment in a strong noise environment is carried out. As shown in

Table 1. The performance of the WSRA under different phase noise levels.

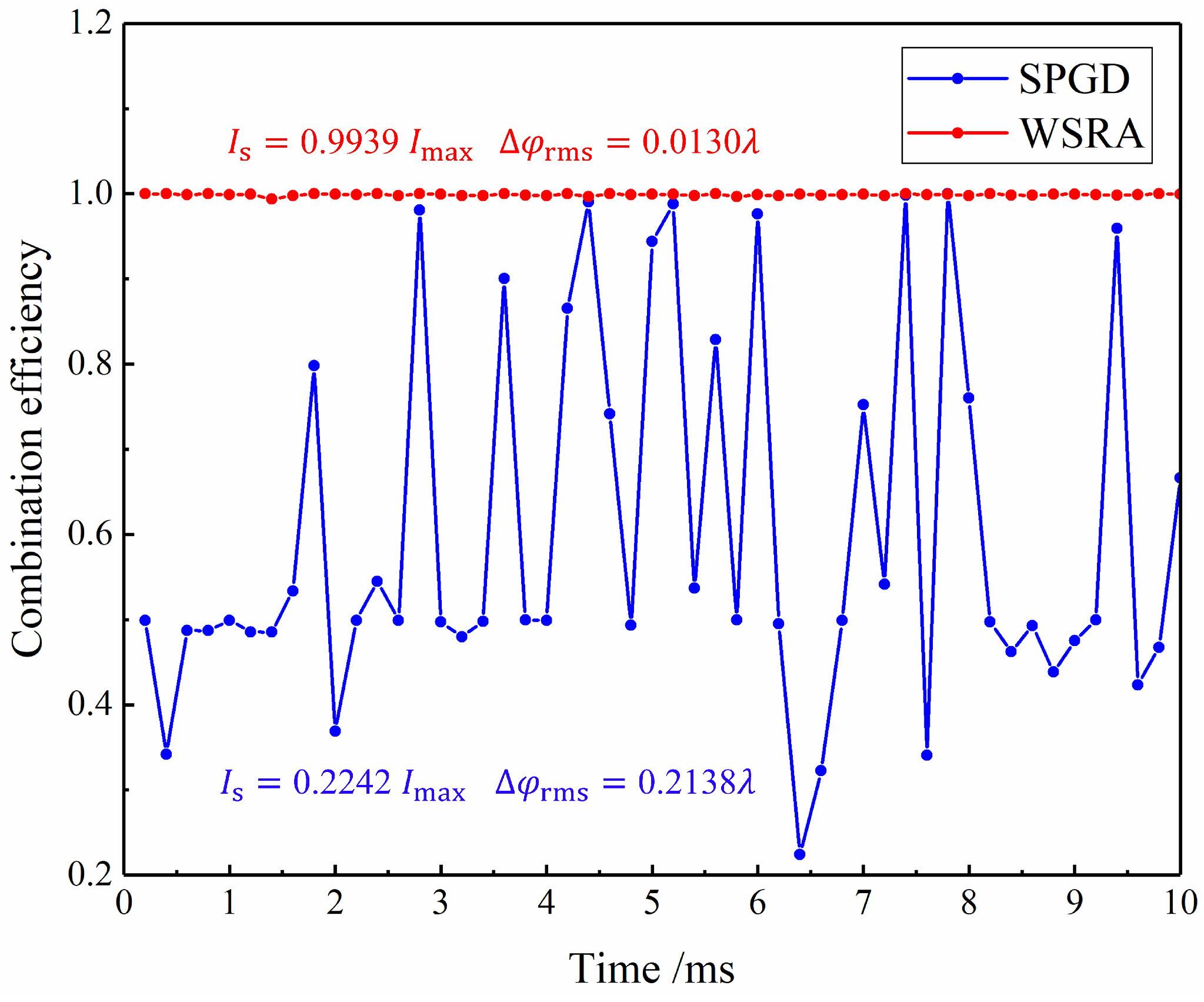
Maximum Noise Amplitude	Combination Efficiency	RMS Phase Error
1$\pi$	0.9939	0.0130 $\lambda$
2$\pi$	0.9895	0.0150 $\lambda$
3$\pi$	0.9823	0.0130 $\lambda$
4$\pi$	0.9712	0.0231 $\lambda$
5$\pi$	0.9551	0.0284 $\lambda$

, when the maximum phase noise amplitude increases from $\pi$ to 5$\pi$, the combination efficiency decreases from 0.9939 to 0.9551, and the RMS phase error rises from 0.0130 $\lambda$ to 0.0284 $\lambda$. The reason for these results is that since the phase noise amplitude can be equivalent within the range of 0–2$\pi$, increasing the amplitude will increase the frequency of crossing 0–2$\pi$ within the same time. Therefore, the fluctuation frequency of the combined light intensity increases under the influence of noise, making it difficult for the phase control system with a fixed feedback rate to track high-frequency phase change, thus leading to performance degradation. This result indicates that although the noise level has a certain impact, the WSRA can still maintain good performance (with a combination efficiency of 0.9551) under noise as strong as 5$\pi$. If the feedback rate of the hardware system is improved, it can handle stronger phase noise.

We analyze the sensitivity of the WSRA to the channel imbalance and waveform asymmetry. The performance under the condition of an unbalanced splitting ratio ranging from 3:1 to 1:3 is shown in

Table 2. The performance of the WSRA under different channel light intensity ratios.

Channel Intensity Ratio	Combination Efficiency	RMS Phase Error
3:1	0.9959	0.0111 $\lambda$
2:1	0.9948	0.0122 $\lambda$
1:1	0.9939	0.0130 $\lambda$
1:2	0.9948	0.0122 $\lambda$
1:3	0.9959	0.0111 $\lambda$

. The result shows that both the combination efficiency and the RMS phase error can be maintained at a relatively high level, indicating that the WSRA has good adaptability to different channel intensity ratios. The reason for this result is that even if the intensities of each channel are not equal, the combined signal is still proportional to the envelope intensity of a single channel (Equation (7)). Therefore, the intrinsic pulse fluctuations can still be eliminated through nonlinear scaling based on the self-referencing waveform. The performance under the condition of waveform asymmetry is shown in

Table 3. The performance of the WSRA under different degrees of waveform asymmetry.

Waveform Pulse Width Deviation	Combination Efficiency	RMS Phase Error
−20 ns	0.9409	0.0473 $\lambda$
−10 ns	0.9843	0.0216 $\lambda$
0 ns	0.9939	0.0130 $\lambda$
10 ns	0.9625	0.0391 $\lambda$
20 ns	0.9038	0.0681 $\lambda$

. We create waveform differences by changing the pulse width of one channel, ranging from −20 ns to 20 ns, to simulate the possible waveform asymmetry in the actual system. The result shows that as the degree of waveform asymmetry increases, the combination efficiency decreases, and the RMS phase error increases. The reason for this result is that since the self-referencing waveform cannot fully match the combined signal, there are residual intensity fluctuations in the pulse part after nonlinear scaling. However, the WSRA can still effectively eliminate the huge intensity fluctuations between the pulse and the continuous part, which is the key interference source affecting phase control. Therefore, the combination efficiency remains above 0.9 under a large waveform asymmetry of ±20 ns.

To verify the adaptability of the WSRA for arbitrary waveforms, experiments under various waveforms are carried out. The performance of the WSRA under Gaussian, long-tail, oscillatory deformation, and triangle pulse waveforms is shown in Figure 8. The result shows that the combined efficiency after phase-locking stably remains above 0.99 (RMS phase error ≤ 0.02 $\lambda$). The reason for this result is that the envelope term ${\mathsf{\Gamma }}_{\mathrm{r}}{\left(t\right)}^2$ of the combined signal $V_{\mathrm{c}}\left(t\right)$ has strict mathematical homology with the self-referencing signal $S_{\mathrm{ref}}$ (i.e., the discrete sequence of the single-channel envelope ${\mathsf{\Gamma }}_{\mathrm{r}}{\left(t\right)}^2$). This causes the envelope of any waveform to be eliminated during the nonlinear scaling operation, and this mechanism is visually presented in Figure 4a. Therefore, the WSRA can adapt to any envelope function without the presetting of pulse detection conditions, which confirms its adaptability from a mathematical principle and is also reflected in Figure 8.

To verify its performance under multi-channel expansion, we experiment on the coherent combination of 12 channels. The experimental result is shown in Figure 9. The WSRA successfully achieved phase-locking of multiple beams, with the beam combination efficiency reaching 0.9808, and the RMS phase error being 0.0246 $\lambda$ when the number of channels was expanded to 12, demonstrating good feasibility and robustness. This provides an experimental basis for the application of large-scale arrays.

4.2. Analysis of the WSRA Under Real Laboratory Conditions

The WSRA mainly focuses on correcting the piston phase error. In real laboratory conditions, its performance will be affected by various factors. In addition to the piston phase error, there are also the group delay caused by the optical path mismatch and thermal drift and the beam overlap offset caused by the tilt error. The group delay will cause the mismatch of sampling positions during the sample-by-sample nonlinear scaling process, and the tilt error will lead to weak combination light intensity. They jointly affect the combination efficiency. To correct these errors, it is necessary to integrate existing technical means at the system level, such as precision delay lines for timing synchronization and adaptive fiber collimators or fast steering mirrors for spatial calibration, to construct a complete error control system.

The planned experimental setup adopts a hierarchical control architecture. The combined beam is incident on three detectors through three low-reflectivity optical windows to process different errors (the piston phase error, the tilt error, and the group delay), respectively. Firstly, a temperature control module and a vibration isolation platform are integrated to minimize the disturbances of thermal drift and environmental vibration, providing a stable physical foundation for piston phase control. Secondly, a precision delay line is used to compensate for group delays between channels, ensuring precise time synchronization. A pointing control unit (such as an adaptive fiber collimator) is used to correct the tilt error, ensuring the precise overlap of the beam spots. Finally, the WSRA will serve as the core to perform closed-loop compensation of the piston phase error. By physically blocking the laser in the signal channel, only the laser in the reference channel is incident on the detector used for piston phase error correction. After being converted by the ADC, the discrete sequence of the self-referencing signal is obtained and stored in the FPGA. Then the blocking is cancelled, and the combined signal of multi-channel lasers is converted by the ADC to obtain the discrete sequence of the combined signal, which enters the FPGA for nonlinear scaling and phase control signal calculation. The acquisition of the discrete sequence of the self-referencing signal is completed before feedback. Thus, it does not affect the feedback rate. Except for the step of obtaining the discrete sequence of the self-referencing signal, the experimental system is the same as the conventional pulsed coherent combination system. Therefore, it is experimentally feasible.

We further analyze the real-time feedback capability of the WSRA by considering the time delay of hardware devices. The WSRA introduces self-referencing waveform construction and nonlinear scaling operations. The self-referencing waveform is pre-generated and does not participate in the real-time calculation process. The computation time for the nonlinear scaling process is 25 ns. According to [38], the time delay of each component is as follows: 59 ns for the photodetector, 13 ns for the ADC module, 14 ns for FPGA signal processing, 10 ns for the DAC module, 170 ns for the amplifier, and 5 ns for the phase modulator. The single execution delay is approximately 296 ns. Thus, a conservative value of 300 ns is taken. The simulation results show that under this feedback speed, the WSRA can achieve effective phase-locking. The combination efficiency reaches 0.9939 and the RMS phase error is 0.0130 $\lambda$. This fully demonstrates that the WSRA has the feasibility of being applied to high-speed active phase control scenarios.

5. Conclusions

In this paper, an innovative WSRA is proposed for low-repetition-rate pulsed fiber laser coherent combinations. The algorithm accurately models the pulse self-referencing waveform by collecting a single-channel intensity signal, then it performs a sample-by-sample nonlinear scaling operation on the combined signals to generate a pseudo-continuous signal, which effectively removes the intrinsic pulse intensity fluctuation while preserving the phase noise information completely. On this basis, the pseudo-continuous signal is input into the SPGD to calculate the phase control signal, and the phase-locking is stabilized by closed-loop feedback. Simulation results show that the method successfully suppresses the waveform fluctuation at a repetition rate of 5 kHz, which is in the same order of frequency as the phase noise, and the peak light intensity is stabilized near the ideal value (0.9939 $I_{\max }$) after phase-locking, with the RMS phase error as low as 0.0130 $\lambda$. The WSRA outperforms the direct application of the conventional SPGD. Compared with the filtering method and the continuous light probe method, the core advantage of this method is that there is no need to preset pulse detection thresholds or conditions, and it makes full use of the phase information contained in the whole pulse waveform, which solves the problem of phase control in low-repetition-rate coherent combinations, and it has adaptability to different pulse waveforms.

The waveform self-referencing mechanism proposed in this study provides a new solution for the phase control of the low-repetition-rate pulsed laser. The method is not only applicable to the Gaussian waveform simulated in this paper, but its adaptive self-referencing waveform construction mechanism is also theoretically compatible with arbitrary complex pulse waveforms, including any with a low repetition rate, which broadens the application scope of coherent combination technology. Future work will focus on building an experimental platform to verify the performance and reliability of this method in actual engineering applications, and to promote the development of high-energy, low-repetition-rate pulsed fiber laser coherent combination systems.