GPU-Accelerated High-Efficiency PSO with Initialization and Thread Self-Adaptation

Abstract

Particle Swarm Optimization (PSO) is a widely used heuristic algorithm valued for its simplicity and robustness in solving diverse optimization problems. However, its high computational cost often limits large-scale applications. With the rapid development of parallel computing and Graphics Processing Units (GPUs), researchers have increasingly leveraged these technologies to enhance PSO efficiency. This paper introduces a High-Efficiency PSO (HEPSO) algorithm designed for GPU-based architectures. HEPSO improves computational performance through two key strategies: (1) transferring data initialization from the CPU to the GPU to reduce I/O overhead caused by repeated data migration, and (2) incorporating a self-adaptive thread management mechanism to enhance execution efficiency. Experiments conducted on nine benchmark optimization functions demonstrate that HEPSO achieves more than a sixfold speedup compared to conventional GPU-PSO. Moreover, in terms of convergence time, HEPSO requires only about one-third of the runtime in most cases.

1. Introduction

Particle Swarm Optimization (PSO) is a stochastic optimization algorithm based on swarm intelligence, first proposed by J. Kennedy and R. C. Eberhart in 1995 [1]. PSO is characterized by its simple implementation, few adjustable parameters, rapid convergence rate, and robust performance [2].

However, the traditional PSO algorithm suffers from inherent limitations, such as being prone to local optima and exhibiting premature convergence speed. To address these issues, researchers have attempted to optimize PSO performance by modifying the algorithm itself, altering relevant parameters [3,4], topology structure [5,6], optimizing particle learning strategies [7,8], and combining PSO with other algorithms [9,10]. These methods all have achieved positive results, which efficiently improved the convergence speed and accuracy of PSO. Nevertheless, when encountering large-scale and highly complex cyclic optimization problems, a large number of iterations only adds to the computational complexity in obtaining a quality solution as the number of particles increases [11].

Considering the interdependence and cooperation of particles in the PSO algorithm, researchers have explored parallelism to accelerate PSO effectively. There are three main parallel computation strategies for PSO: (1) hardware environment-based parallel PSO algorithms, typically implemented using hardware architectures [12,13] such as controllers [14] and Field Programmable Gate Array (FPGA) [15]; (2) CPU-based parallel PSO algorithms, utilizing multi-threading techniques [16,17] or multi-core processors [18,19] to express particle independence and exploit parallelism; (3) GPU-based parallel PSO algorithms, leveraging GPU architecture to synchronize parallel optimization processes for particles [20,21,22,23]. Each approach presents strengths and limitations. Hardware-based methods are relatively straightforward to implement but rely heavily on cluster scale. CPU-based strategies can be deployed on standard PCs but are constrained by processor architecture and the overhead of inter-process communication. In contrast, GPUs offer a favorable balance of cost and computational power, making them especially attractive for PSO parallelization.

With the steady improvement of GPU performance and the availability of programming frameworks such as CUDA, GPU-based PSO has been applied to optimization problems of growing scale and complexity. Nevertheless, two issues remain: (1) repeated data migration between CPU and GPU introduces additional I/O overhead, and (2) thread management strategies are often not fully efficient in practice.

To address these limitations, this work develops a High-Efficiency Particle Swarm Optimization (HEPSO) algorithm that performs data initialization directly on the GPU and applies a self-adaptive thread management strategy to improve execution efficiency. It should be noted that the acronym “HEPSO” has also been used in the literature to denote High Exploration Particle Swarm Optimization [24], which aims to enhance the exploration ability of particles to avoid local optima. In contrast, our HEPSO focuses on parallelization and efficiency improvements through GPU-based acceleration. Although both share the same acronym, their objectives and methodologies are distinct.

Object and Innovation

With the growing complexity of optimization problems, it becomes crucial to integrate the inherent independence of particle behaviors with the parallel architecture of CUDA in order to improve the efficiency of PSO. Building on this motivation, the proposed HEPSO leverages GPU-based initialization and thread adaptation to improve efficiency. Inspired by the asynchronous update model of PSO [25], HEPSO treats each particle’s loop iteration behavior as an independent optimization process, employing a coarse-grained parallel method to map particles to threads one-to-one. At the same time, the GPU-based PSO algorithm is optimized in two directions: (1) reducing unnecessary data transfers by improving memory usage and data throughput, and (2) enhancing parallel execution by employing a thread scheduling strategy that better utilizes GPU resources. These optimizations are consistent with general recommendations for CUDA programming and are adapted here to the specific requirements of PSO. The main contributions of the paper are as follows.

(1)

A GPU-based PSO framework (HEPSO) is presented, in which the algorithm structure is adapted to the independence of particles and the iterative update process of PSO.

(2)

The workflow of PSO is modified so that data initialization and updates are performed on the GPU, and adaptive thread scheduling and multiplexing strategies are applied according to the mapping between particles and dimensions, reducing I/O operations and improving resource utilization.

(3)

Benchmark experiments are carried out to evaluate the proposed framework. The results show up to 580× acceleration compared with CPU-PSO, about 6× improvement over a standard GPU-PSO implementation, and more than 3× average improvement relative to GPU-PSO.

The remainder of this paper is organized as follows. Section 2 provides background on various PSO algorithms and the CUDA computing architecture. Section 3 details of the proposed HEPSO algorithm, emphasizing its innovations. In Section 4, we design and implement experiments using nine benchmark functions to test HEPSO’s efficiency improvements. Finally, Section 5 summarizes and discusses our work.

2. Background

2.1. Standard PSO

The PSO is a stochastic optimization algorithm inspired by swarm intelligence and group foraging activities [26]. It generates a swarm of particles of a specific size, representing potential solutions in the problem space, and iteratively searches for the optimal result [27]. Each particle has its own velocity and position, with the function value corresponding to the particle’s position representing the solution it has found [28]. During iterative updates, the individual’s historical optimal solution and the swarm’s global optimal solution are used to calculate the initial velocity and position for the next iteration. The particle continues searching in the space until finding the global optimal solution or a satisfactory feasible solution. The equations for updating the particle’s velocity and position are as follows.

$$V_i^{d+1}=\omega V_i^d+c_1{r}_1\left(P_i^d-X_i^d\right)+c_2{r}_2\left(P_g^d-X_i^d\right)$$

(1)

$$X_i^{d+1}=X_i^d+\alpha V_i^{d+1}$$

(2)

In which, i = 1, 2…, M, d = 1, 2…, N. $\omega$ is a non-negative inertia factor influencing the algorithm’s convergence effect. The larger its value, the wider the particle’s leap range. $P_i$ is the local optimal position and $P_g$ is the global optimal position. The learning factors $c_1$ and $c_2$ are non-negative constants, which are parameters for adjusting the weights of local and global optimal values. In practice, the most appropriate parameter values are determined through multiple experimental adjustments. $r_1$ and $r_2$ are random numbers in the range of [0, 1]. $\alpha$ is a constraint factor controlling the velocity’s weight. In standard PSO implementations, the entire algorithm calculation is completed on CPUs. Note that $X_i^{d+1}$ and $V_i^{d+1}$ are the current position and velocity, respectively, while $X_i^d$ and $V_i^d$ are the previous position and velocity, respectively.

2.2. Traditional GPU-Based PSO

In recent years, researchers have made significant efforts to enhance PSO efficiency by utilizing GPU architecture parallelism, yielding many achievements. However, improving the efficiency of GPU-based PSO algorithms remains a continuous challenge.

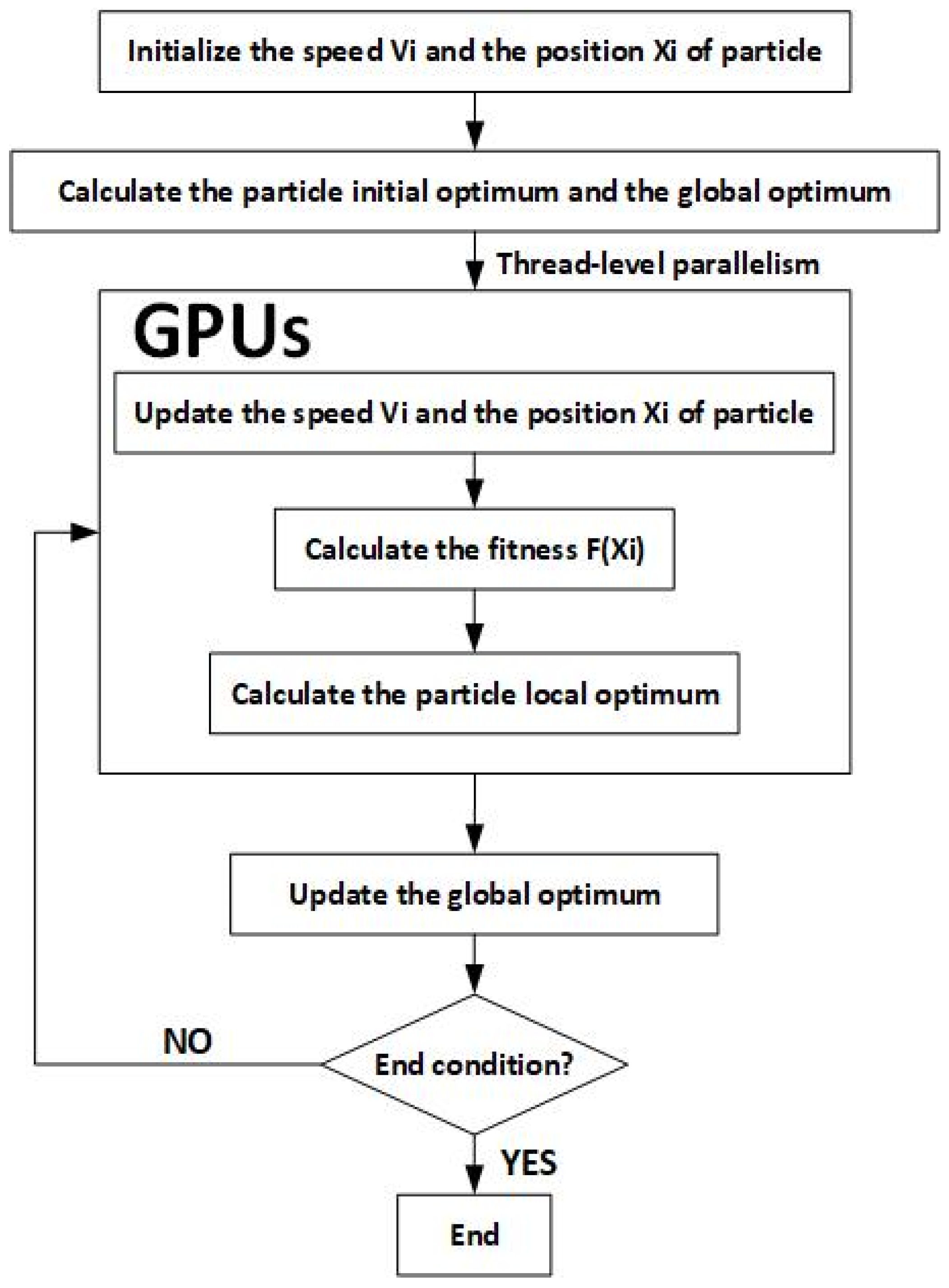
Figure 1 illustrates the typical workflow of a traditional GPU-PSO algorithm. After initializing particle positions and velocities, the algorithm computes both the individual best and the global best solutions. Particle updates are then executed in parallel at the thread level on the GPU, where each thread is responsible for updating one particle’s state. The fitness of each particle is evaluated, personal bests are updated accordingly, and the global best is recalculated after each iteration until the termination condition is satisfied.

R. M. Calazan et al. [20] proposed the Parallel Dimension PSO (PDPSO) algorithm, which massively parallelizes PSO programs on the GPU architecture. Each particle is implemented as a block, and each dimension is mapped to a distinct thread. Their experimental results demonstrated a speedup of up to 85 times compared to the serial implementation on a CPU. You Zhou et al. [21] proposed a variational PSO algorithm that accelerates convergence speed by evolving particles in a beneficial direction. Using several benchmark functions, they demonstrated that their variant PSO algorithm has an improved running speed, achieving a speedup of at least 25 times after GPU acceleration with larger population sizes. Cai Yong et al. [22] designed a coarse-grained synchronous parallel PSO algorithm, which employs a one-to-one correspondence between threads and particles, based on coarse-grained parallelism. This method creates numerous threads to parallelize the particle search process and fully utilizes CUDA’s mathematical function calculation libraries, ensuring PSO reliability and usability. Through experiments with three optimization functions, they demonstrated that, compared to traditional CPU-PSO, their algorithm can achieve a computational speedup of up to 90 times while maintaining function convergence. Xicheng Fu et al. [23] proposed a local PSOA based on medical image registration GPU. Their method has distinct advantages in optimizing high-dimensional objective functions, with the maximum acceleration ratio reaching 95 times. The total average difference in the number of iterations when the serial implementation and parallel implementation of the algorithm stop running under the premise of satisfying the accuracy is 17 times.

2.3. Thread Allocation Strategy Based on CUDA Parallel Architecture

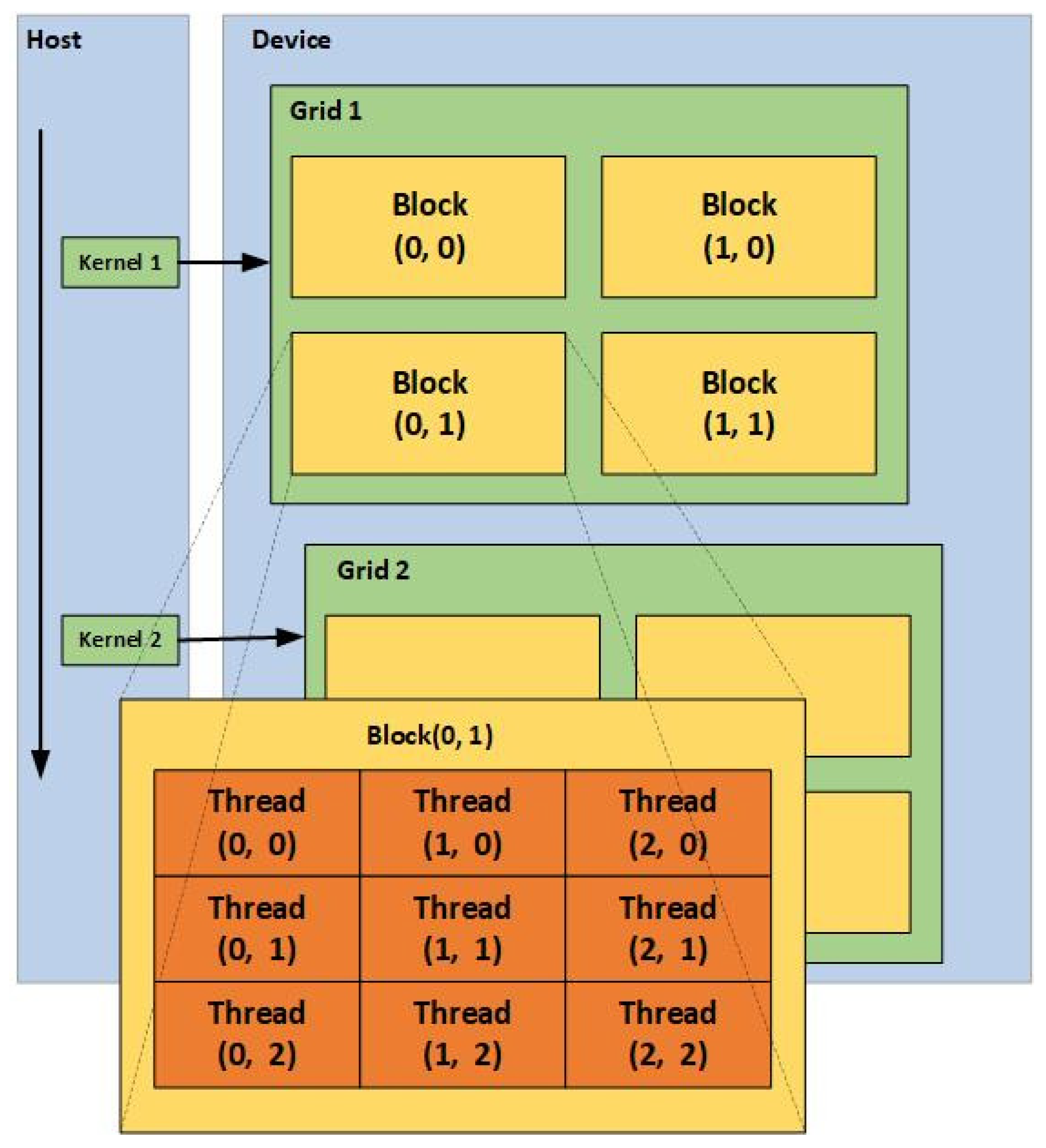
As in Figure 2, CUDA’s parallel computing model adopts a multi-level memory architecture divided into three levels: Thread, Block, and Grid. Each block contains multiple threads, and each grid contains multiple blocks. In practice, a block is divided into smaller thread bundles (Warp), which serve as the basic unit of scheduling and execution for Streaming Multiprocessor (SM).

Currently, there are three main thread allocation schemes suitable for the CUDA parallel architecture model [29]: (1) coarse-grained parallelism, where particles correspond to threads one by one [22], (2) fine-grained parallelism, where particles correspond to blocks one by one and the dimensions of the particles correspond to threads one by one [20,23], (3) adaptive thread bundle parallelism, where particles correspond to one or more warps, the dimensions of the particles correspond to threads one by one, and one or more particles correspond to a block [29]. In a concrete implementation, the number of threads in each block can be maximized, and the block size can be set to a multiple of warp. This ensures task balance among SMs and improves the running efficiency of the algorithm.

3. Methodology

3.1. Algorithm Flow

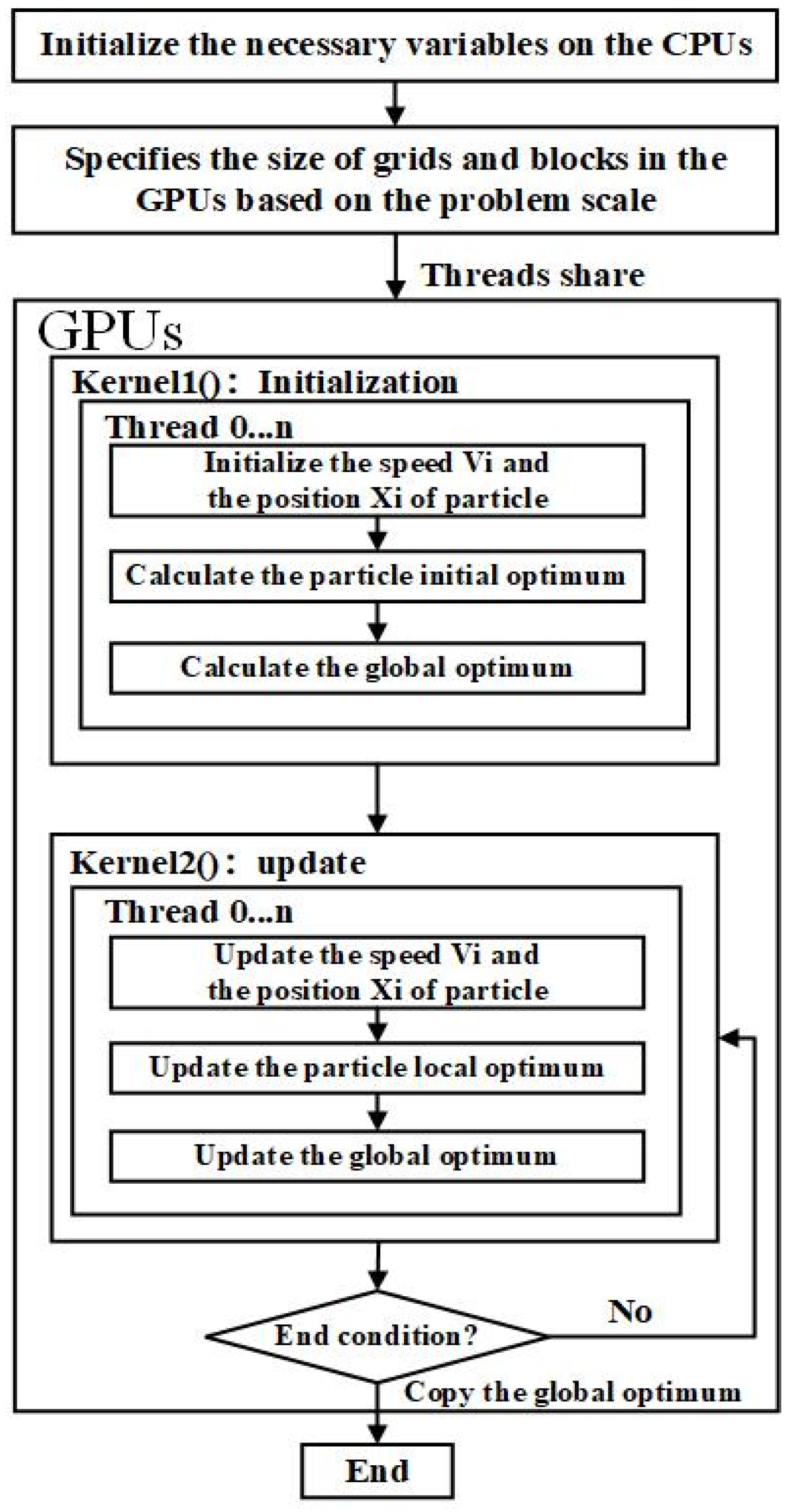
The algorithm flow of HEPSO is shown in Figure 3.

The steps of HEPSO are as follows.

(1)

The CPUs initialize the relevant variables and copy them to the GPUs using the function cuda.to_device();

(2)

Based on the problem scale and swarm size, the CPUs adaptively specify the execution configuration [GridDim, BlockDim];

(3)

The CPUs invoke the kernel1() to initialize the particle swarm on the GPUs, obtaining initial velocity and position to calculate the particle’s local optimum and the swarm’s global optimum;

(4)

The CPUs invoke the kernel2() to cyclically update velocity and position on the GPUs, calculating the fitness value of the particle while obtaining the particle’s local optimum and global swarm optimum through comparison;

(5)

The GPU loops through step 4 until the end condition is met (reaching the target accuracy or the specified number of iterations);

(6)

The GPUs terminate the loop and copy the solution of the global swarm optimum to CPUs using the function cuda.copy_to_host().

Among the above steps, steps 3 and 4 are the core of the HEPSO algorithm, with the pseudo-code provided.

In Algorithm 1, the initialization stage of the swarm is performed. Each GPU thread is mapped to one particle, and the position vector X[i][j] and velocity vector V[i][j] of particle iii are initialized dimension by dimension. After initialization, the fitness value F[i] of each particle is computed, and the corresponding personal best value PF[i] and position PFX[i] are recorded. Once all particles have been processed, a reduction step is applied to determine the global best fitness PB and the corresponding position PBX of the swarm. This stage ensures that both personal best and global best values are available before entering the iterative search. The complete procedure is summarized in Algorithm 1.

Algorithm 1 kernel1(): Initialization

Map all the threads to S particles one-to-one

//Do operations to thread i (i = 1,…,S) synchronously:

for i = 1 to S do

for j = 1 to N do

initialize the position X[i][j] and velocity V[i][j]

end for

compute the fitness F[i]

set PF[i] ← F[i], PFX[i] ← X[i][:]

end for

compute the global optimum PB[i] of Swarm

In Algorithm 2, the update phase of PSO is executed iteratively until the termination condition is met. Each thread again corresponds to one particle. For every particle, the velocity and position vectors are updated across all dimensions according to the PSO update rules. The fitness F[i] of each particle is then evaluated. If the new fitness outperforms its personal best PF[i], both PF[i] and the associated best position PFX[i] are updated. After all particles have been updated in one iteration, a global reduction is performed to update the global best PB and its position PBX. This iterative procedure continues until the stopping criterion is satisfied, after which the global best solution is returned. The process is presented in Algorithm 2.

Algorithm 2 kernel2(): Update

Map all the threads to S particles one-to-one

//Do operations to thread i (i = 1,…,S) synchronously:

Repeat

for i = 1 to S do

for j = 1 to N do

update position X[i][j] and velocity V[i][j]

end for

compute fitness F[i]

if F[i] better-than PF[i] then

PF[i] ← F[i]

PFX[i] ← X[i][:]

end if

end for

update the global optimum (PB, PBX) of the swarm

Until reaching the stop conditions

Return PB[i] and PBX[i]

During the execution of Algorithm 2, a large number of random numbers are required for velocity updates. To support efficient and parallel random number generation on the GPU, we employ the function numba.cuda.random.create_xoroshiro128p_states(), which provides independent random number streams for each thread.

3.2. GPU Initialization

Traditional data initialization involves initializing operations on CPUs and then copying the data to GPUs for further computation. However, this conventional IO process can waste significant time.

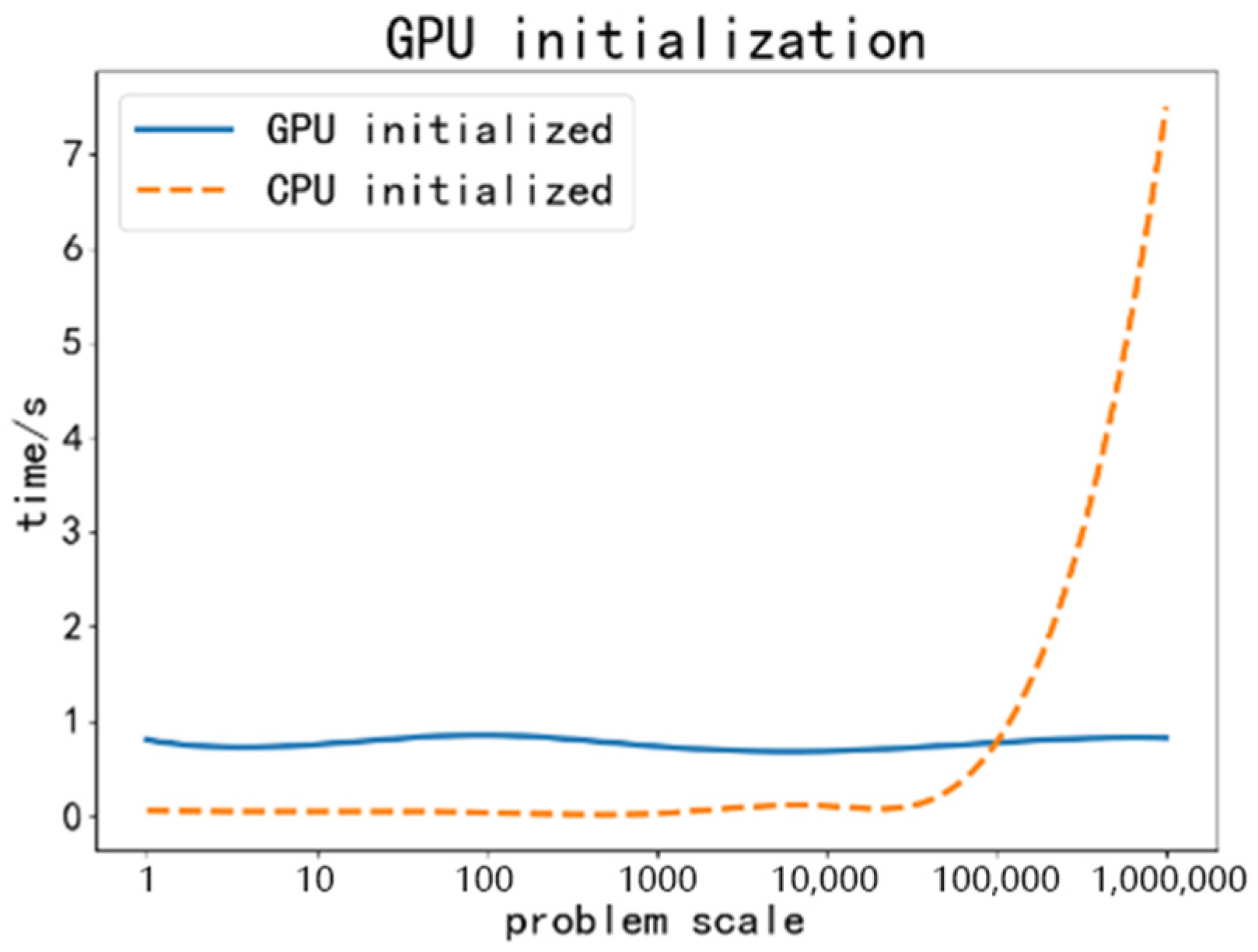
Based on the experimental environment shown in

Table 1. Experimental computing environment.

Name	Version
CPU	Intel(R) Core (TM) i7-6700 CPU @ 3.40 GHz 3.41 GHz
GPU	NVIDIA Tesla T4
Operating System	Centos7
Development Environment	Anaconda 3, CUDA 10.2

, we test the time consumption of data initialization on both CPUs and the GPUs. The experimental results as shown in Figure 4.

We can notice that when the problem scale reaches the million level, one IO operation causes an average time loss of 6 s, which greatly limiting the algorithm’s execution efficiency. HEPSO we proposed only performs necessary initialization on CPUs, such as population dimension and particle number. Meanwhile, all the rest of data initialization, such as velocity, position, and fitness by creating some empty arrays to take over, and the initialization of concrete assignments are performed by GPUs. This approach allows most of the initializations, all subsequent iterations, and data comparisons to be fully performed by the GPU core without consuming IO resources.

3.3. Thread Self-Adaptive Strategy

The execution configuration of the kernel function (Kernel<<<GridDim, BlockDim>>>) is determined at CUDA call time after debugging sessions. In the Single-Instruction Multiple-Thread (SIMT) architecture used by the streaming multiprocessor (SM), a warp is the smallest unit of scheduling and execution. If the number of threads in a block is not set properly, some inactive threads may remain in underutilized warps, thereby consuming SM resources. To avoid wasting memory resources, it is generally recommended to set the number of threads in a block as an integer multiple of the warp size.

In our experiments, we propose a thread-adaptive coarse-grained parallel algorithm that fully utilizes shared memory and maximizes parallel execution. This algorithm automatically adjusts parameters according to the number of particles and the problem dimensions when calling the kernel function, ensuring that particles correspond to threads one by one. In Equation (3), the two parameter groups inside the square brackets represent the grid configuration $\left[S/(N·BlockDim),N\right]$ and the block configuration $\left[n,\mathit{WarpSize}\right]$, respectively. The revised notation clearly distinguishes function calls from grouped parameters, thereby avoiding ambiguity. The self-adaptive formula is shown in Equation (3).

$$\mathit{Kernel}\left[\mathit{GridDim}, \mathit{BlockDim}\right]=\mathit{Kernel}[S/(N·\mathit{BlockDim}), N; n, \mathit{WarpSize}]$$

(3)

In this formula, GridDim is the size of a grid, representing the number of blocks contained in it; BlockDim is the size of a block, representing the number of threads contained in it. We set the maximum size of BlockDim to 512. WarpSize represents the size of a warp, which is normally calculated by the GPU in HalfWarp units, so WarpSize is defined as 16. This self-adaptive strategy allows the kernel function to expand the number of threads in each block as much as possible and set the BlockDim to a multiple of warp [29]. It dynamically adjusts the number of threads to match both the problem scale and particle size to avoid the waste of memory resources and improve program performance.

3.4. Thread Multiplexing

There is overhead in the creation and destruction of threads in the GPU using CUDA. To process a large amount of data, CUDA needs to create more threads than the number of calculations. If each thread only performs an operation once and is then destroyed, the more data there is, the greater the cost will be. To save this overhead, we adopt the grid stride method, which adds a loop for each thread to achieve thread multiplexing, allowing a created thread to be used repeatedly. The grid stride is shown in Figure 5.

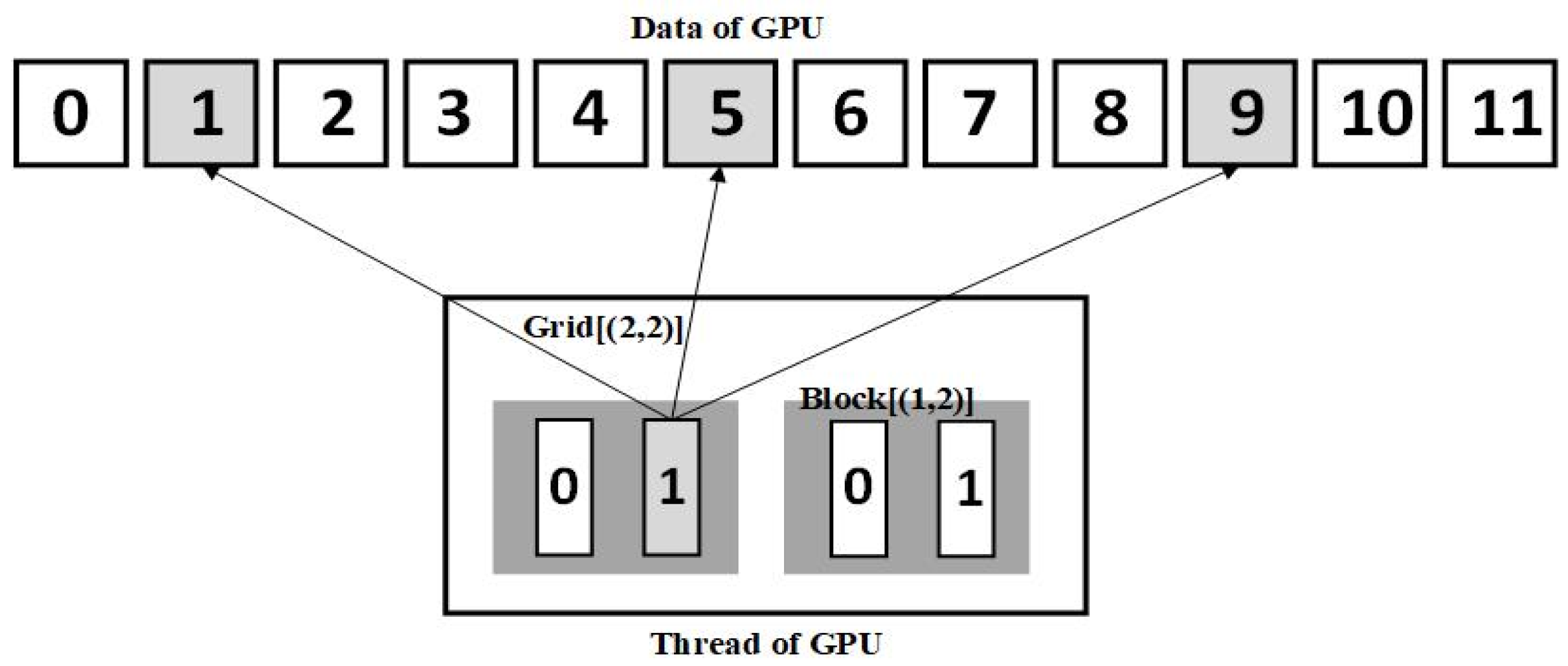
In Figure 5, the data size to process in parallel is 12. We create a grid that can start 4<<<2,2>>> threads in parallel and set the stride size to 4 after adding a loop. That means, the 1st, 5th, and 9th data can share thread 1. This procedure allows each thread to be utilized multiple times, reducing the thread overhead of repeatedly starting and destroying and enabling CUDA to parallelly handle large-scale problems.

4. Experiment

4.1. Experimental Environment

The computing environment for our experiments is shown in Table 1.

4.2. Optimization Function

In practice, the performance of optimization algorithms is usually determined by the function evaluation value. In this paper, performance comparisons were conducted based on nine benchmark test functions listed in

Table 2. Benchmark functions.

F(x)	Domain	Optimum Solution
$f1\left(X_i\right)={\displaystyle \sum _{i=1}^{n-1}}{(100\left(X_{i+1} - X_i^2\right)}^2+{(X_i - 1)}^2)$	$[-10, 10]$	$f_{\mathit{min}}=f (1, 1,\dots ,1)=0$
$f2\left(X_i\right)={\displaystyle \sum _{i=1}^n}{X}_i^2$	$[-100, 100]$	$f_{\mathit{min}}=f (0, 0,\dots ,0)=0$
$f3\left(X_i\right)={\displaystyle \sum _{i=1}^n}{\left(⌊X_i+0.5⌋\right)}^2$	$[-100, 100]$	$f_{\mathit{min}}=f (0, 0,\dots ,0)=0$
$f4\left(X_i\right)=10n+{\displaystyle \sum _{i=1}^n}(X_i^2- 10\cos (2\pi X_i\left)\right)$	$[-5.12, 5.12]$	$f_{\mathit{min}}=f (0, 0,\dots ,0)=0$
$f5\left(X_i\right) ={\displaystyle \sum _{i=1}^n}{\displaystyle \frac{X_i^2}{4000}} - {\displaystyle \prod _{i=1}^n}\cos \left({\displaystyle \frac{X_i}{\sqrt{i}}}\right)+1$	$[-600, 600]$	$f_{\mathit{min}}=f (0, 0,\dots ,0)=0$
$f6\left(X_i\right) ={\displaystyle \sum _{i=1}^n}\left(X_i \times \sin \left({\left|X_i\right|}^{0.5}\right)\right)$	$[-500, 500]$	$f_{\mathit{min}}=f (420.9687,\dots ,420.9687)$ = −418.9829*n
$f7\left(X\right)=4 \times {X_1}^2-2.1 \times {X_1}^4+{\displaystyle \frac{1}{3}} \times {X_1}^6+X_1 \times X_2-4 \times {X_2}^2+4 \times {X_2}^4$	$[-5, 5]$	$f_{\mathit{min}}=f(0.08983, -0.7126)$ $=f(-0.08983, 0.7126)$ $=-1.0316285$
$f8\left(X\right)={\left(X_2-{\displaystyle \frac{5.1}{4{\pi }^2}} \times {X_1}^2+{\displaystyle \frac{5}{\pi }} \times X_1-6\right)}^2$ $+10 \times \left(1-{\displaystyle \frac{1}{8\pi }}\right)\cos \left(X_1\right)+10$	$[-5, 15]$	$f_{\mathit{min}}=f(-3.142, 12.275)$ $=f(3.142, 2.275)$ $=f(9.425, 2.425)$ $=0.398$
$f9\left(X\right)=\left[1+{\left(X_1+X_2+1\right)}^2 \times \left(19-14 \times X_1+3 \times {X_1}^2-14 \times X_2+6 \times X_1\times X_2+3 \times {X_2}^2\right)\right]$ $*\left[30+{\left(2 \times X_1-3 \times X_2\right)}^2\left(18-32 \times X_1+12 \times {X_1}^2+48 \times X_2-36 \times X_1 \times X_2+27 \times {X_2}^2\right)\right]$	$[-2, 2]$	$f_{\mathit{min}}=f(0, -1)$ $=3$

The inertia weight ω was set to 0.32, the learning factors C1 and C2 were both set to 2.0, and the constraint factor α was set to 0.5.

. In which, functions f1–f6 are high-dimensional problems, and functions f7–f9 are low-dimensional functions which have only a few local minima [30].

4.3. Evaluation Assessment

To quantitatively access the performance of different algorithms, an evaluation index is required. In this subsection, we introduce two index computing methods. They are based on the time cost but with different finish conditions.

4.3.1. The Assessment of Time-Ratio to Stop Iterating

The first method is the time ratio to stop iterating, which indicates the time difference between different algorithms under the same iteration conditions. It can evaluate the pure computational capability of an algorithm.

Under the condition that the number of particles and iterations are specified to be the same, we define “${ \mathit{T}}_{\mathit{Ref}}$” and “${\mathit{T}}_{\mathit{Obj}}$” as the running time of the reference and object algorithm programs, respectively. The time ratio to stop iteration index “S_iteration” is set as follows.

$$S_{\mathit{iteration}}={\displaystyle \frac{{\mathit{T}}_{\mathit{Ref}}}{{\mathit{T}}_{\mathit{Obj}}}}$$

(4)

4.3.2. The Assessment of Time-Ratio After Functions Convergence

On the other hand, the above assessment index ignores the convergence difference within the optimization solver, which may result in one party stopping iterating while the other party continues running. As a result, we consider testing the overall average difference in execution time after functions convergence between different algorithms.

We define “$\mathit{min}\left({\mathit{T}}_{\mathit{Ref}}\right)$” and “${\mathit{min}(\mathit{T}}_{\mathit{Obj}})$” as the minimum running time under the condition of function convergence to a particular precision of reference and object algorithm, respectively. This index “${\mathrm{S}}_{\mathrm{convergence}}$” is set as follows.

$$S_{\mathit{convergence}}={\displaystyle \frac{\mathit{min}(T_{\mathit{Ref}})}{{\mathit{min}(T}_{\mathit{Obj}})}}$$

(5)

4.4. Experimental Results

4.4.1. Statistical Tests

ANOVA was applied to the results of 20 experiments with GPU-PSO and HEPSO to examine whether differences between the two implementations were statistically significant. The test outcomes are summarized in

Table 3. Statistical tests results.

Functions	f_Value	p_Value
f1	125.2339476	3.64 × 10−6
f2	75.68779983	2.38 × 10−5
f3	25.4401375	0.000996877
f4	12.97296013	0.006964076
f5	51.8643667	9.23 × 10−5
f6	8290.714833	2.36 × 10−13
f7	4239.765082	3.44 × 10−12
f8	726.6323232	3.86 × 10−9
f9	2514.573137	2.77 × 10−11

.

As shown in Table 3, p_value for the nine benchmark test functions (f1–f9) were much smaller than 0.01. Therefore, we can conclude that there is a significant difference in the average performance of GPU-PSO and HEPSO. Next, we will further calculate and analyze these differences.

4.4.2. Time-Ratio to Stop Iterating

The initial number of particles and iterations were set to 128 and 10,000, respectively. Meanwhile the dimension N of benchmark functions f1–f6 was 16, and f7–f9 was 2. In the experiments, we increased the number of particles and dynamically decreased the number of iterations to reduce the execution time on CPUs. The number of particles and iterations ranges from 128 to 131,072 and from 10,000 to 200. Each experiment was run until the maximum number of iterations was reached. The optimizations were repeated 20 times with different seeds. The average results are shown in Figure 6 and Figure 7 and

Table A1. Execution time and “S_iteration” of f1.

Swarmsize	Iterations	Execution Time/s			Siteration
		CPU	GPU	HEPSO	CPU/HEPSO	GPU/HEPSO
128	10,000	49.951	16.988	4.547	10.99	3.74
256	9000	93.823	15.789	4.674	20.07	3.38
512	7500	154.924	14.183	4.625	33.49	3.07
1024	6000	245.898	12.409	4.003	61.43	3.10
2048	5000	414.184	12.149	4.150	99.80	2.93
4096	3000	501.445	10.190	3.757	133.48	2.71
8192	2000	640.905	9.168	4.073	157.37	2.25
16,384	1200	792.098	8.093	2.860	276.92	2.83
32,768	700	899.922	7.989	2.096	429.27	3.81
65,536	380	998.583	8.903	2.023	493.72	4.40
131,072	200	1018.983	11.666	1.746	583.66	6.68

,

Table A2. Execution time and “S_iteration” of f2.

Swarmsize	Iterations	Execution Time/s			Siteration
		CPU	GPU	HEPSO	CPU/HEPSO	GPU/HEPSO
128	10,000	16.726	16.771	4.122	4.06	4.07
256	9000	29.223	15.371	4.022	7.27	3.82
512	7500	49.287	13.509	3.862	12.76	3.50
1024	6000	76.568	11.722	3.725	20.55	3.15
2048	5000	127.971	11.284	3.482	36.75	3.24
4096	3000	154.396	9.116	2.788	55.38	3.27
8192	2000	204.227	8.777	2.671	76.47	3.29
16,384	1200	249.169	7.555	2.025	123.03	3.73
32,768	700	287.210	6.548	1.533	187.35	4.27
65,536	380	317.406	6.584	1.537	206.49	4.28
131,072	200	334.853	7.511	1.485	225.44	5.06

,

Table A3. Execution time and “S_iteration” of f3.

Swarmsize	Iterations	Execution Time/s			Siteration
		CPU	GPU	HEPSO	CPU/HEPSO	GPU/HEPSO
128	10,000	15.443	16.587	4.028	3.83	4.12
256	9000	25.203	15.384	4.07	6.19	3.78
512	7500	41.445	13.346	4.018	10.31	3.32
1024	6000	59.178	11.715	3.708	15.96	3.16
2048	5000	96.056	11.317	3.337	28.79	3.39
4096	3000	112.762	8.899	2.842	39.68	3.13
8192	2000	150.006	8.255	2.935	51.11	2.81
16,384	1200	179.813	6.674	2.102	85.54	3.18
32,768	700	213.07	6.251	1.544	138.00	4.05
65,536	380	235.396	6.28	1.405	167.54	4.47
131,072	200	255.484	7.239	1.261	202.60	5.74

,

Table A4. Execution time and “S_iteration” of f4.

Swarmsize	Iterations	Execution Time/s			Siteration
		CPU	GPU	HEPSO	CPU/HEPSO	GPU/HEPSO
128	10,000	21.692	16.958	5.615	3.86	3.02
256	9000	38.740	15.977	5.374	7.21	2.97
512	7500	62.691	14.707	5.278	11.88	2.79
1024	6000	100.296	13.686	5.899	17.00	2.32
2048	5000	169.697	14.410	7.718	21.99	1.87
4096	3000	200.803	10.991	8.142	24.66	1.35
8192	2000	268.514	9.401	10.024	26.79	0.94
16,384	1200	322.508	9.465	6.443	50.05	1.47
32,768	700	379.388	9.337	4.107	92.38	2.27
65,536	380	420.789	10.006	2.768	152.00	3.61
131,072	200	444.381	10.892	2.807	158.30	3.88

,

Table A5. Execution time and “S_iteration” of f5.

Swarmsize	Iterations	Execution Time/s			Siteration
		CPU	GPU	HEPSO	CPU/HEPSO	GPU/HEPSO
128	10,000	32.419	17.266	5.906	5.49	2.92
256	9000	56.345	16.707	6.261	8.99	2.67
512	7500	93.533	15.741	7.373	12.69	2.13
1024	6000	151.712	15.508	9.803	15.48	1.58
2048	5000	253.252	15.085	14.304	17.70	1.05
4096	3000	300.272	10.960	15.499	19.37	0.71
8192	2000	387.161	11.188	19.817	19.54	0.56
16,384	1200	470.528	11.740	11.640	40.42	1.01
32,768	700	549.339	12.207	7.097	77.40	1.72
65,536	380	614.538	13.327	4.360	140.94	3.06
131,072	200	649.055	15.094	4.408	147.25	3.42

,

Table A6. Execution time and “S_iteration” of f6.

Swarmsize	Iterations	Execution Time/s			Siteration
		CPU	GPU	HEPSO	CPU/HEPSO	GPU/HEPSO
128	10,000	17.487	17.314	5.963	2.93	2.90
256	9000	29.706	16.57	5.613	5.29	2.95
512	7500	48.858	15.215	5.782	8.45	2.63
1024	6000	77.648	14.36	6.903	11.25	2.08
2048	5000	129	14.931	9.419	13.70	1.59
4096	3000	153.565	10.28	10.189	15.07	1.01
8192	2000	205.231	9.482	12.265	16.73	0.77
16,384	1200	245.526	9.254	7.742	31.71	1.20
32,768	700	286.483	9.513	4.977	57.56	1.91
65,536	380	313.899	9.837	3.184	98.59	3.09
131,072	200	333.375	11.063	3.233	103.12	3.42

,

Table A7. Execution time and “S_iteration” of f7.

Swarmsize	Iterations	Execution Time/s			Siteration
		CPU	GPU	HEPSO	CPU/HEPSO	GPU/HEPSO
128	10,000	12.548	17.101	4.106	3.05	4.16
256	9000	23.397	15.521	3.860	6.06	4.02
512	7500	39.551	13.373	3.504	11.30	3.82
1024	6000	54.743	10.99	3.170	17.27	3.47
2048	5000	95.507	9.82	2.887	33.05	3.40
4096	3000	101.747	6.748	2.142	47.55	3.15
8192	2000	141.135	5.471	1.776	79.29	3.07
16,384	1200	172.146	4.524	1.486	115.53	3.04
32,768	700	202.314	3.495	1.305	154.44	2.67
65,536	380	214.964	3.172	1.241	173.36	2.56
131,072	200	230.049	3.613	1.095	209.14	3.28

,

Table A8. Execution time and “S_iteration” of f8.

Swarmsize	Iterations	Execution Time/s			Siteration
		CPU	GPU	HEPSO	CPU/HEPSO	GPU/HEPSO
128	10,000	12.326	16.704	4.153	2.97	4.02
256	9000	20.57	15.304	3.923	5.24	3.90
512	7500	32.75	12.98	3.619	9.05	3.59
1024	6000	51.413	10.912	3.309	15.54	3.30
2048	5000	85.434	9.772	2.976	28.71	3.28
4096	3000	103.653	6.764	2.198	47.16	3.08
8192	2000	136.697	5.692	1.821	75.07	3.13
16,384	1200	179.828	4.543	1.529	117.61	2.97
32,768	700	197.844	3.615	1.332	148.53	2.71
65,536	380	231.25	3.268	1.175	196.81	2.78
131,072	200	219.536	3.719	1.209	181.58	3.08

and

Table A9. Execution time and “S_iteration” of f9.

Swarmsize	Iterations	Execution Time/s			Siteration
		CPU	GPU	HEPSO	CPU/HEPSO	GPU/HEPSO
128	10,000	14.168	16.954	4.175	3.39	4.06
256	9000	23.943	15.212	3.954	6.06	3.85
512	7500	38.962	13.198	3.653	10.67	3.61
1024	6000	61.225	10.973	3.358	18.23	3.27
2048	5000	100.948	9.71	2.979	33.89	3.26
4096	3000	120.07	6.76	2.219	54.11	3.05
8192	2000	158.451	5.722	1.85	85.65	3.09
16,384	1200	192.721	4.626	1.539	125.22	3.01
32,768	700	224.919	3.613	1.359	165.50	2.66
65,536	380	244.377	3.517	1.283	190.47	2.74
131,072	200	258.903	4.021	1.226	211.18	3.28

, respectively.

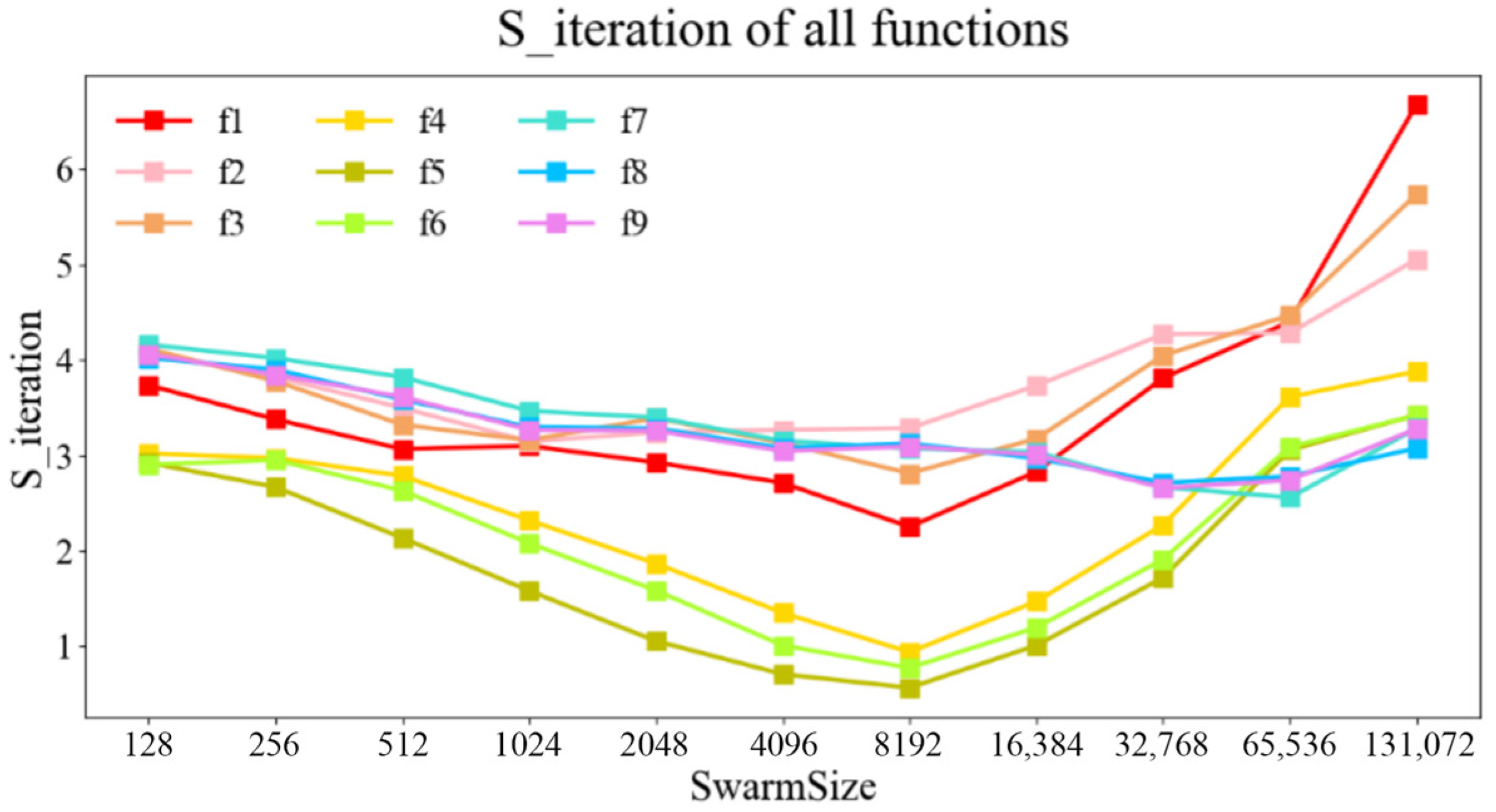
The “$S_{\mathit{iteration}}$” of the 9 benchmark functions is shown in Figure 7.

Analysis of the experimental results in Figure 6 and Figure 7 and Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8 and Table A9 shows that the HEPSO algorithm on nine benchmark functions achieved the maximum “${\mathrm{S}}_{\mathrm{iteration}}$” of 583.6, 225.4, 202.6, 158.3, 147.2, 103.1, 209.1, 181.6, and 211.2 compared to CPU-PSO. Meanwhile, for HEPSO compared to GPU-PSO in Figure 7, it achieved the maximum “${\mathrm{S}}_{\mathrm{iteration}}$” of 6.68, 5.06, 5.74, 3.88, 3.42, 3.42, 3.28, 3.08, and 3.28.

Several conclusions can be drawn as follows.

(1)

From the experiments, we can conclude that PSO executed on the CPU is suitable only for simple functions optimization problems (the number of particles is small, usually below 300). When facing more complex and higher dimensional problem requiring a larger number of particles, the CPU load expands accordingly, and the optimization time increases significantly.

(2)

Overall, the execution time of HEPSO is less than GPU-PSO. When the number of particles is greater than 32,768, the time consumption difference exhibits a rapidly widening trend. With the support of the parallel ability of the GPU, the computation time is shorter with a larger number of particles. This means that more particles can be deployed to accelerate the optimization search process.

(3)

For more complex high-dimensional functions f1–f6, when the number of particles is less than 8192, the execution time of GPU-PSO keeps decreasing while the execution time of HEPSO keeps increasing. This is because the advantage of local parallelism outweighs the time required for thread synchronization. When the number of particles increases to more than 8192, the benefits brought by local parallelism gradually fail to offset the large IO loss, causing a significant decrease in GPU-PSO efficiency to about 1/2. This indicates that the HEPSO we proposed needs to generate a large number of particles to accelerate the optimization process with more complicated functions.

(4)

For simple low-dimensional functions f7–f9, overall, the increasing number of particles does not make the “${\mathrm{S}}_{\mathrm{iteration}}$” rise, instead showing a decreasing trend. It is worth mentioning that when the number of particles is larger than 65,536, too many particles greatly increase the burden on the CPU, causing the spurious phenomenon of “${\mathrm{S}}_{\mathrm{iteration}}$” rising. Therefore, HEPSO we proposed does not show its advantages on simple low-dimensional functions.

(5)

Among the test functions, HEPSO achieved the best speedup for f1. It achieved 580 times “${\mathrm{S}}_{\mathrm{iteration}}$” compared with CPU-PSO and 6 times “${\mathrm{S}}_{\mathrm{iteration}}$ ” compared with GPU-PSO. Therefore, HEPSO can be proven to be suitable for solving large-scale optimization problems with complex functions.

4.4.3. Time-Ratio After Functions Convergence

To address the concern in Section 4.3.2, we conducted an additional experiment with the termination criterion set to a convergence error of 10⁻⁴. The optimization was repeated 50 times with different random seeds. To ensure a fair comparison, the swarm size was fixed at 65,536 for all functions and for both implementations (GPU-PSO and HEPSO). The average results are summarized in

Table 4. Results under unified swarm size (65,536) and time ratio = GPU-time/HEPSO-time.

F(x)	Accuracy (GPU)	Accuracy (HEPSO)	Iterations (GPU)	Iterations (HEPSO)	GPU-Time (s)	HEPSO-Time (s)	Time Ratio (GPU/HEPSO)
f1	8.73 × 10−5	9.11 × 10−5	395	398	9.26	2.05	4.51
f2	5.22 × 10−5	4.23 × 10−5	335	326	5.81	1.32	4.40
f3	0	0	298	298	4.93	1.10	4.48
f4	9.88 × 10−5	7.32 × 10−5	550	563	14.48	3.92	3.70
f5	3.87 × 10−5	2.88 × 10−5	425	415	14.91	4.76	3.13
f6	9.21 × 10−5	8.65 × 10−5	490	482	12.69	4.04	3.14
f7	8.50 × 10−5	8.50 × 10−5	312	319	2.61	1.02	2.56
f8	7.20 × 10−5	0	100	97	0.86	0.30	2.87
f9	9.10 × 10−5	9.10 × 10−5	105	109	0.97	0.35	2.77

, where the time ratio is defined as GPU-time/HEPSO-time.

The results in Table 4 show that the time ratio ranges from 2.77 to 4.51 across the nine benchmark functions under the unified swarm size, indicating consistent acceleration of HEPSO relative to GPU-PSO while achieving comparable accuracy.

5. Conclusions

This study presents the High-Efficiency Particle Swarm Optimization (HEPSO) algorithm, which refines standard PSO by incorporating GPU-based initialization and adaptive threading strategies. By transferring particle initialization from the CPU to the GPU, the algorithm reduces I/O overhead and improves computational efficiency. Furthermore, adaptive thread scheduling and multiplexing enhance parallel execution and resource utilization.

HEPSO was evaluated on nine benchmark functions using two sets of performance indices. The results indicate that with particle numbers up to 131,072, HEPSO achieves up to a 580-fold speedup compared with CPU-PSO and more than a sixfold speedup compared with GPU-PSO. In terms of convergence efficiency, HEPSO consistently required less computation time, typically about one-third of that needed by GPU-PSO.

These findings suggest that HEPSO provides a practical and scalable framework for improving the computational efficiency of PSO, particularly in large-scale optimization tasks. The motivation for this study stems from industrial time-series decision problems, where optimization runs often extend to several days on CPUs, making GPU acceleration essential to achieve feasible turnaround times. As a future direction, we plan to extend this work to industrial case studies, in order to demonstrate how GPU-accelerated PSO can be applied to real-world large-scale decision-making processes in engineering practice.