Modelling Magnetisation and Transport AC Loss of HTS Tapes near Ferromagnetic Materials Using an Integral Equation Method
Abstract
1. Introduction
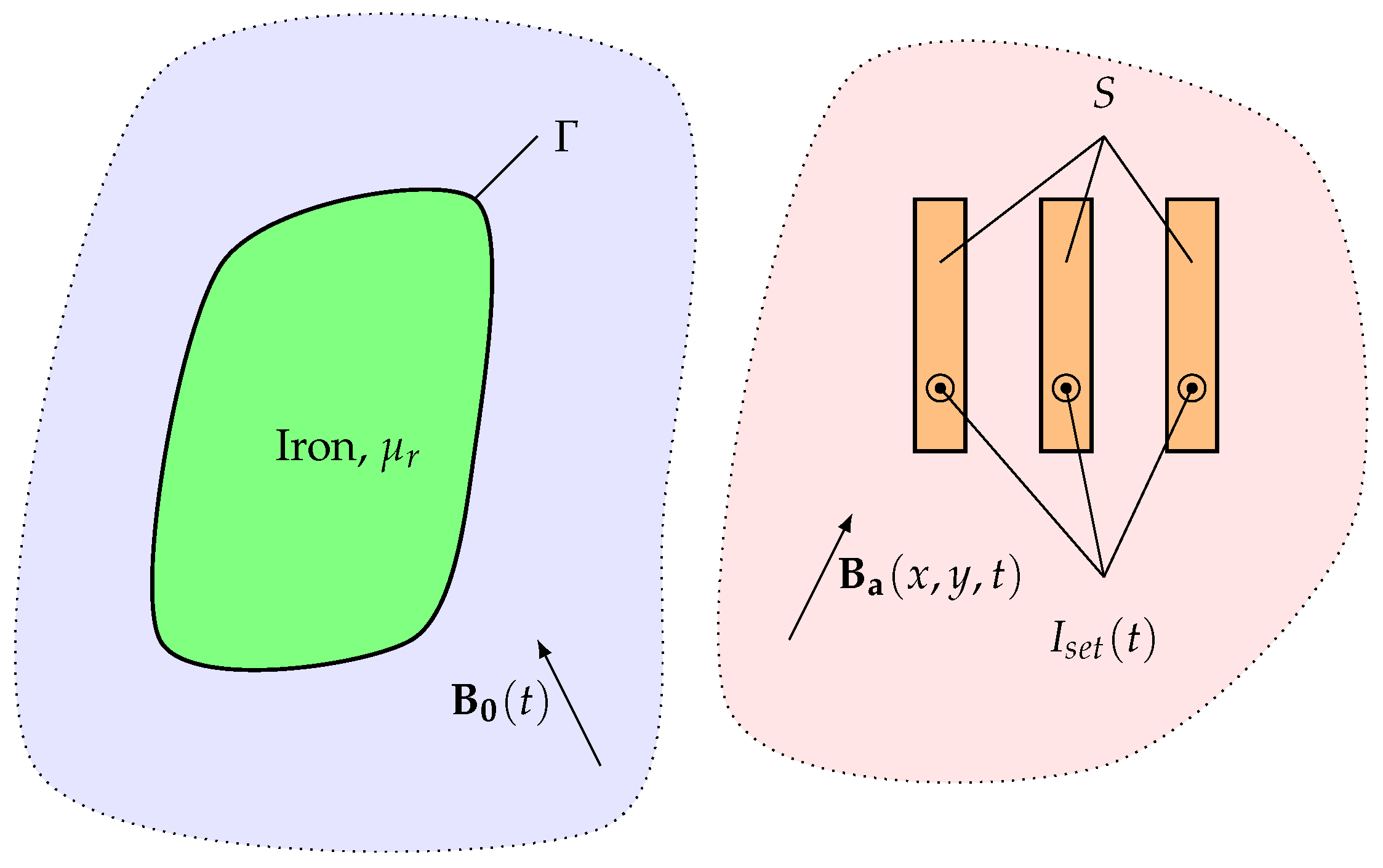
2. Problem Set-Up
3. Formulation
3.1. Representation of Iron Domain as Surface Current Density
3.2. Equations for Superconducting Domain S
3.3. Expression for k
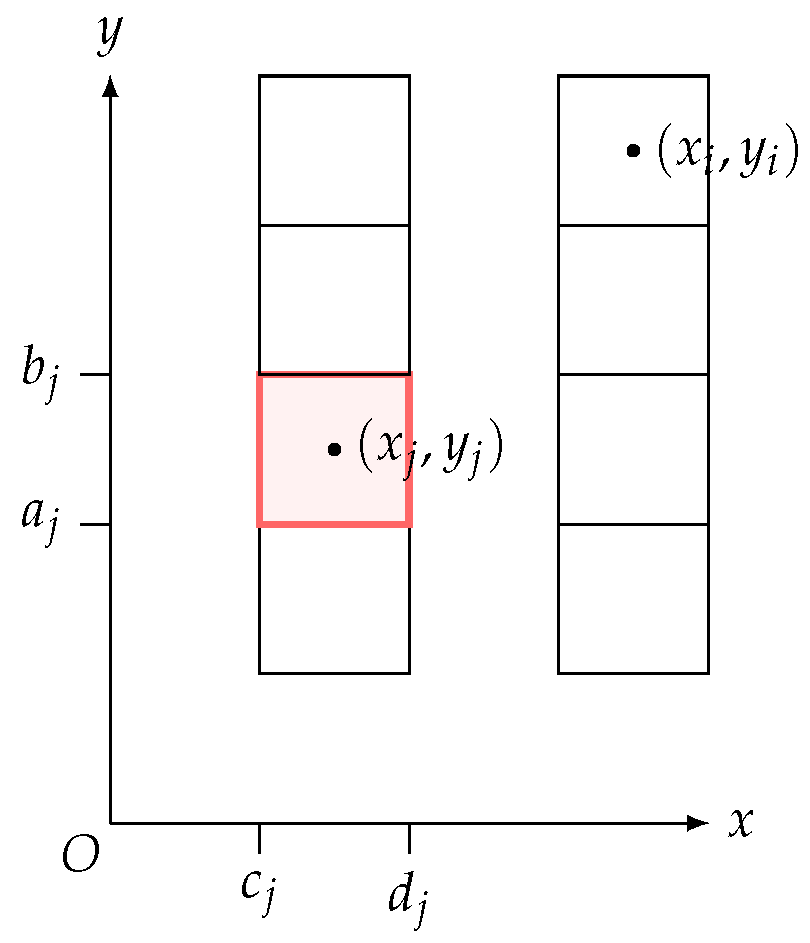
3.4. Further Discretization
3.5. Overall Ordinary Differential Equation
4. Results
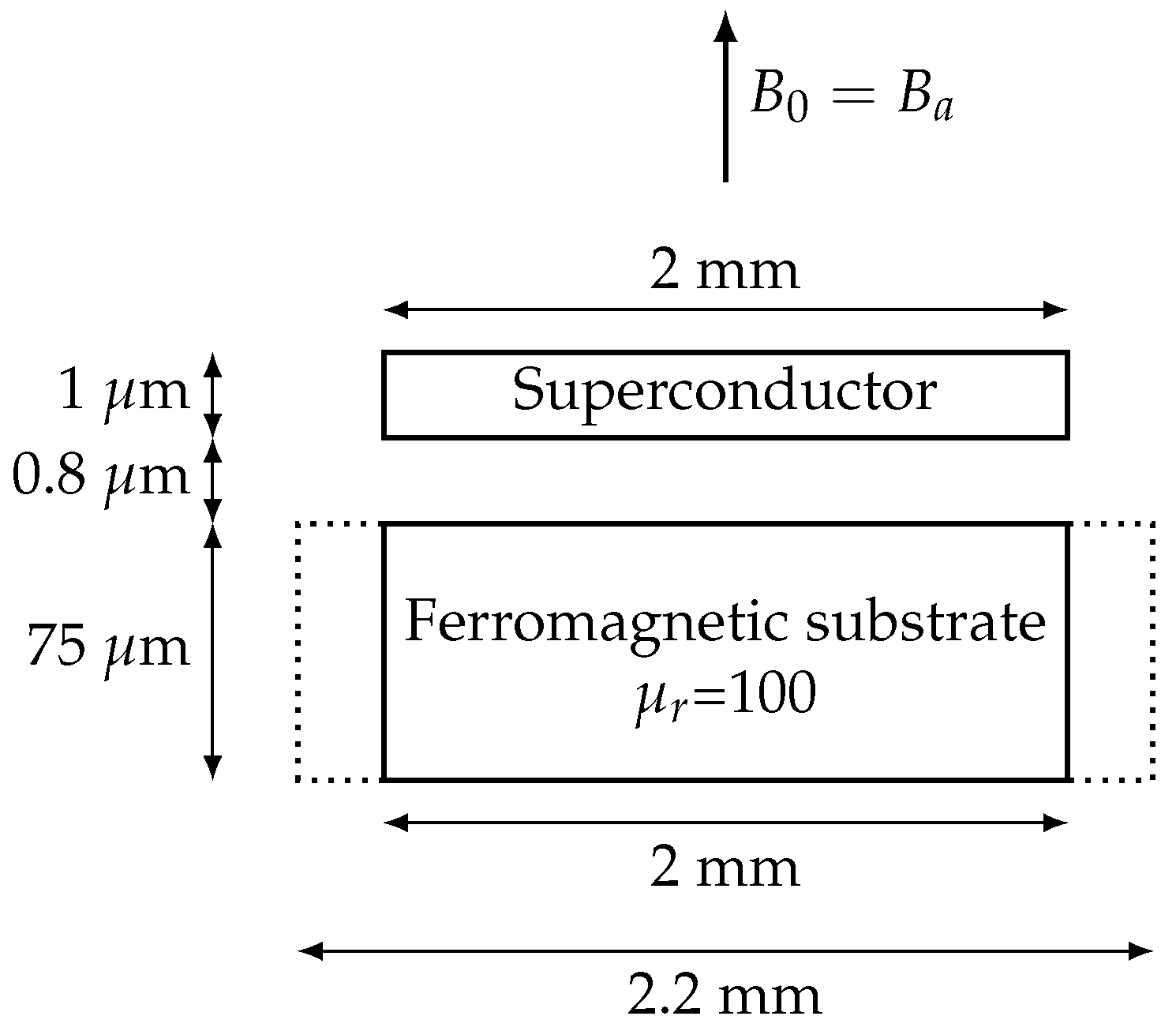
4.1. Benchmark #2
4.2. Tapes near Stator Iron
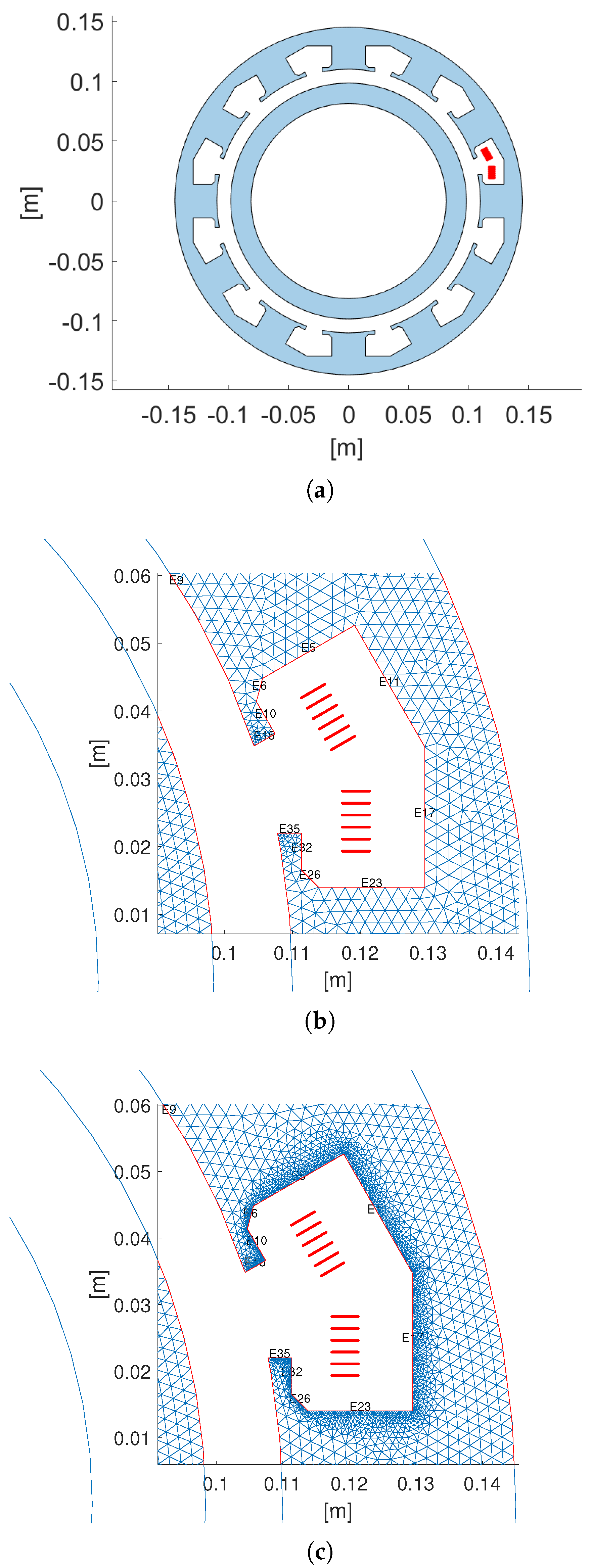
4.3. Machine Environment
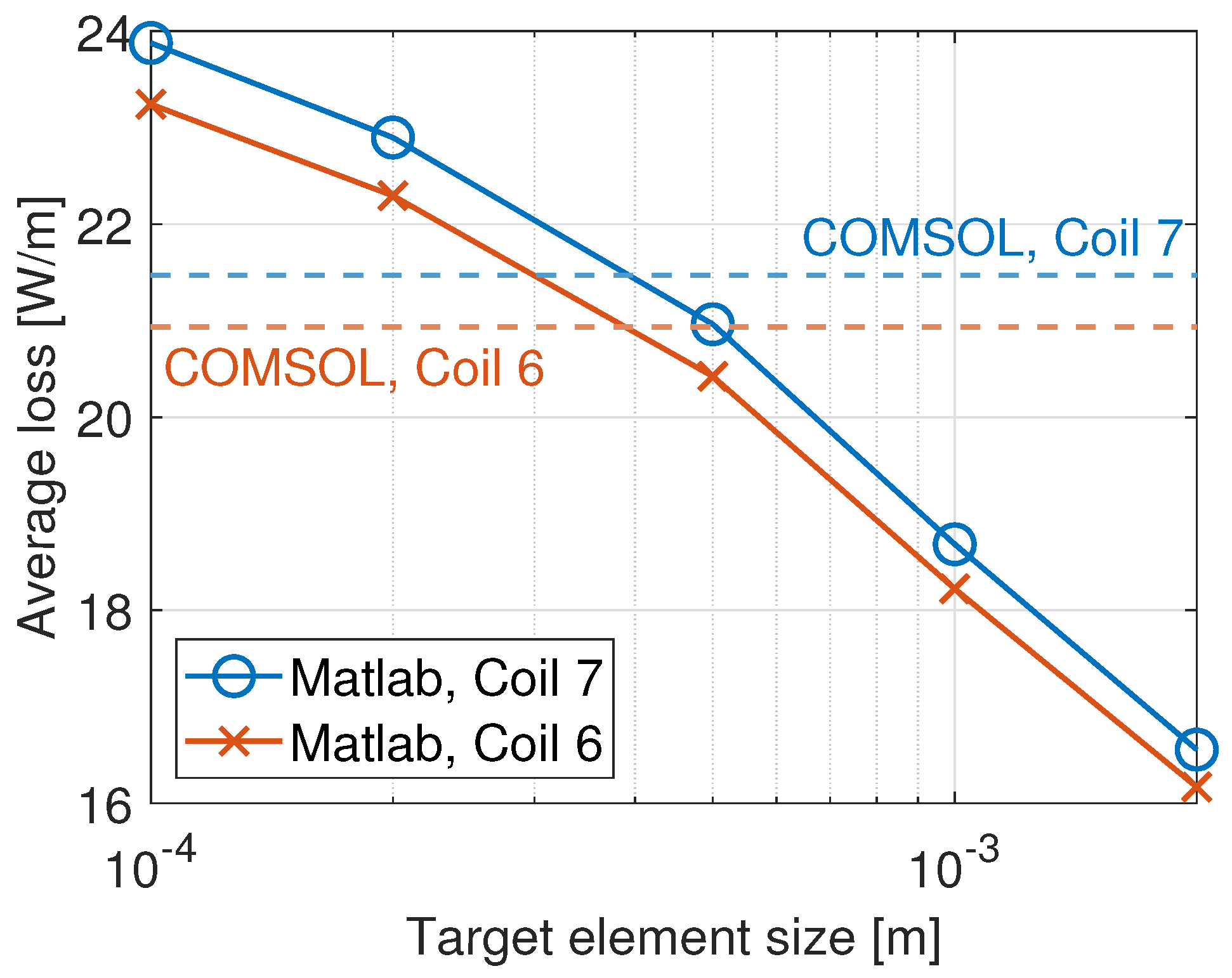
4.3.1. COMSOL Reference Model
4.3.2. Modified Brandt Method Model with Stator and Rotor Iron
4.3.3. Modified Brandt Method Model Without Iron
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| FEM | finite element method |
| HTS | high-temperature superconducting |
| MEC | magnetic equivalent circuit |
| PM | permanent magnet |
Appendix A. Closed Forms for Line and Area Integrals in Matrices
Appendix A.1. Line Integrals
Appendix A.2. Area Integrals
References
- Coombs, T.A.; Wang, Q.; Shah, A.; Hu, J.; Hao, L.; Patel, I.; Wei, H.; Wu, Y.; Coombs, T.; Wang, W. High-temperature superconductors and their large-scale applications. Nat. Rev. Electr. Eng. 2024, 1, 788–801. [Google Scholar] [CrossRef]
- Paidpilli, M.; Selvamanickam, V. Development of RE-Ba-Cu-O superconductors in the U.S. for ultra-high field magnets. Supercond. Sci. Technol. 2022, 35, 043001. [Google Scholar] [CrossRef]
- Yanagisawa, Y.; Hamada, M.; Hashi, K.; Maeda, H. Review of recent developments in ultra-high field (UHF) NMR magnets in the Asia region. Supercond. Sci. Technol. 2022, 35, 044006. [Google Scholar] [CrossRef]
- Chow, C.C.T.; Ainslie, M.D.; Chau, K.T. High temperature superconducting rotating electrical machines: An overview. Energy Rep. 2023, 9, 1124–1156. [Google Scholar] [CrossRef]
- Mitchell, N.; Zheng, J.; Vorpahl, C.; Corato, V.; Sanabria, C.; Segal, M.; Sorbom, B.; Slade, R.; Brittles, G.; Bateman, R.; et al. Superconductors for fusion: A roadmap. Supercond. Sci. Technol. 2021, 34, 103001. [Google Scholar] [CrossRef]
- Ferracin, P.; Ambrosio, G.; Arbelaez, D.; Brouwer, L.; Barzi, E.; Cooley, L.; Garcia Fajardo, L.; Gupta, R.; Juchno, M.; Kashikhin, V.; et al. Towards 20 T hybrid accelerator dipole magnets. IEEE Trans. Appl. Supercond. 2022, 32, 4000906. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, H.; Qiu, Q.; Zhang, Z.; Xiao, L.; Lin, L. Recent progress of superconducting fault current limiter in China. Supercond. Sci. Technol. 2020, 34, 013001. [Google Scholar] [CrossRef]
- Yazdani-Asrami, M.; Seyyedbarzegar, S.; Sadeghi, A.; de Sousa, W.T.B.; Kottonau, D. High temperature superconducting cables and their performance against short circuit faults: Current development, challenges, solutions, and future trends. Supercond. Sci. Technol. 2022, 35, 083002. [Google Scholar] [CrossRef]
- Diyun, W.; Chau, K.T.; Chunhua, L.; Shuang, G.; Fuhua, L. Transient stability analysis of SMES for smart grid with vehicle-to-grid operation. IEEE Trans. Appl. Supercond. 2012, 22, 5701105. [Google Scholar] [CrossRef]
- Kajikawa, K.; Hayashi, T.; Yoshida, R.; Iwakuma, M.; Funaki, K. Numerical evaluation of ac losses in HTS wires with 2D FEM formulated by self magnetic field. IEEE Trans. Appl. Supercond. 2003, 13, 3630–3633. [Google Scholar] [CrossRef]
- Pecher, R.; McCulloch, M.; Chapman, S.J.; Prigozhin, L.; Elliott, C.M. 3D-modelling of bulk type-II superconductors using unconstrained H-formulation. Inst. Phys. Conf. Ser. 2003, 181, 1418. [Google Scholar]
- Shen, B.; Grilli, F.; Coombs, T. Review of the ac loss computation for HTS using H formulation. Supercond. Sci. Technol. 2020, 33, 033002. [Google Scholar] [CrossRef]
- Liang, F.; Venuturumilli, S.; Zhang, H.; Zhang, M.; Kvitkovic, J.; Pamidi, S.; Wang, Y.; Yuan, W. A finite element model for simulating second generation high temperature superconducting coils/stacks with large number of turns. J. Appl. Phys. 2017, 122, 043903. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, M.; Yuan, W. An efficient 3D finite element method model based on the T–A formulation for superconducting coated conductors. Supercond. Sci. Technol. 2017, 30, 024005. [Google Scholar] [CrossRef]
- Huber, F.; Song, W.; Zhang, M.; Grilli, F. The T-A formulation: An efficient approach to model the macroscopic electromagnetic behaviour of HTS coated conductor applications. Supercond. Sci. Technol. 2022, 35, 043003. [Google Scholar] [CrossRef]
- Brandt, E.H. Superconductors of finite thickness in a perpendicular magnetic field: Strips and slabs. Phys. Rev. B 1996, 54, 4246–4264. [Google Scholar] [CrossRef]
- Rhyner, J. Calculation of AC losses in HTSC wires with arbitrary current voltage characteristics. Phys. C 1998, 310, 42–47. [Google Scholar] [CrossRef]
- Yang, Y.; Martinez, E.; Beduz, C. Numerical modeling of the critical state and calculation of ac losses and current profiles in multi-filamentary Bi-2223 tapes. Inst. Phys. Conf. Ser. 1999, 167, 855–858. [Google Scholar]
- Klinčok, B.; Gömöry, F.; Pardo, E. The voltage signal on a superconducting wire in ac transport. Supercond. Sci. Technol. 2005, 18, 694–700. [Google Scholar] [CrossRef]
- Vojenčiak, M.; Šouc, J.; Ceballos, J.M.; Klinčok, B.; Gömöry, F.; Pardo, E.; Grilli, F. Losses in Bi-2223/Ag tape at simultaneous action of ac transport and ac magnetic field shifted in phase. J. Phys. Conf. Ser. 2006, 43, 63–66. [Google Scholar] [CrossRef]
- Klinčok, B.; Gömöry, F. Influence of gaps in monolayer superconducting cable on ac losses. J. Phys. Conf. Ser. 2006, 43, 897–900. [Google Scholar] [CrossRef]
- Yazawa, T.; Rabbers, J.J.; ten Haken, B.; ten Kate, H.H.J.; Maeda, H. AC loss analysis on high-temperature superconductors with finite thickness and arbitrary magnetic field dependent voltage–current relation. J. Appl. Phys. 1998, 84, 5652–5656. [Google Scholar] [CrossRef]
- Nguyen, D.N.; Sastry, P.V.P.S.S.; Knoll, D.C.; Zhang, G.; Schwartz, J. Experimental and numerical studies of the effect of phase difference between transport current and perpendicular applied magnetic field on total ac loss in Ag-sheathed (Bi,Pb)2Sr2Ca2Cu3Ox tape. J. Appl. Phys. 2005, 98, 073902. [Google Scholar] [CrossRef]
- Nguyen, D.N.; Sastry, P.V.P.S.S.; Schwartz, J. Numerical calculations of the total ac loss of Cu-stabilized YBa2Cu3O7-δ coated conductor with a ferromagnetic substrate. J. Appl. Phys. 2007, 101, 053905. [Google Scholar] [CrossRef]
- Zhong, J.; Zou, S.; Lai, L.; Chen, P.; Deng, S. Fast evaluation of the critical current of high-temperature superconducting coils based on the integral method. J. Appl. Phys. 2022, 132, 163901. [Google Scholar] [CrossRef]
- Lucchini, F.; Torchio, R.; Morandi, A.; Dughiero, F. A Fast Integral Equation J-φ Formulation for Superconducting Structures. IEEE Trans. Appl. Supercond. 2024, 34, 5901808. [Google Scholar] [CrossRef]
- Zhang, H.; Kang, X.; Song, P.; Guan, M.; Qu, T.; Wang, X. An advanced computational approach for evaluating screening-current-induced strain in REBCO HTS coils considering electromagnetic-mechanical coupling. IEEE Trans. Appl. Supercond. 2024, 34, 4601105. [Google Scholar] [CrossRef]
- Kang, X.; Zhang, H.; Tong, Y.; Wang, X. Bidirectionally coupled electromagnetic modeling of inductive behavior and screening currents in HTS no-insulation coils. Supercond. Sci. Technol. 2025, 38, 075019. [Google Scholar] [CrossRef]
- Elbaa, M.; Berger, K.; Douine, B.; Halit, M.; Ailam, E.H.; Bentridi, S.E. Analytical modeling of an inductor in a magnetic circuit for pulsed field magnetization of HTS bulks. IEEE Trans. Appl. Supercond. 2018, 28, 8201306. [Google Scholar] [CrossRef]
- Otten, S.; Grilli, F. Simple and fast method for computing induced currents in superconductors using freely available solvers for ordinary differential equations. IEEE Trans. Appl. Supercond. 2019, 29, 8202008. [Google Scholar] [CrossRef]
- Otten, S.; Kario, A.; Demenčik, E.; Nast, R.; Grilli, F. Anisotropic monoblock model for computing ac loss in partially coupled Roebel cables. Supercond. Sci. Technol. 2020, 33, 094013. [Google Scholar] [CrossRef]
- Musso, A.; Breschi, M.; Ribani, P.L.; Grilli, F. Analysis of ac loss contributions from different layers of HTS tapes using the A–V formulation model. IEEE Trans. Appl. Supercond. 2021, 31, 5900411. [Google Scholar] [CrossRef]
- Lai, L.; Gu, C. AC loss calculation in REBCO coils or stacks by solving the equation of motion for current using an integration approach. Supercond. Sci. Technol. 2021, 34, 015003. [Google Scholar] [CrossRef]
- Lai, L.; Gu, C. J model for studying ac magnetization loss in 3D cable structures. Supercond. Sci. Technol. 2022, 35, 045008. [Google Scholar] [CrossRef]
- Kang, X.; Wang, X. A homogenised anisotropic J-model for accelerating computations of screening current profile in large-scale HTS magnets. Supercond. Sci. Technol. 2023, 36, 035011. [Google Scholar] [CrossRef]
- Chow, C.C.T.; Grilli, F.; Chau, K.T. Numerical modelling of HTS tapes under arbitrary external field and transport current via integral method: Review and application to electrical machines. Supercond. Sci. Technol. 2023, 36, 115027. [Google Scholar] [CrossRef]
- Chow, C.C.T.; Zhang, M.; Chau, K.T.; Grilli, F. Modeling HTS coils with different coupling scenarios via integral method. IEEE Trans. Appl. Supercond. 2024, 34, 4606809. [Google Scholar] [CrossRef]
- Gottardi, E.; Krop, D.C.J.; Lomonova, E.A. A hybrid model for studying ac losses in HTS tapes of a linear machine. J. Phys. Conf. Ser. 2025, 3054, 012011. [Google Scholar] [CrossRef]
- Kalsi, S. Influence of magnetic iron teeth in motors employing superconductors for field excitation and ac stator windings. IEEE Trans. Appl. Supercond. 2021, 31, 5201607. [Google Scholar] [CrossRef]
- Patel, A.; Climente-Alarcon, V.; Baskys, A.; Glowacki, B.A.; Reis, T. Design considerations for fully superconducting synchronous motors aimed at future electric aircraft. In Proceedings of the 2018 IEEE International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Nottingham, UK, 7–9 November 2018. [Google Scholar] [CrossRef]
- Lee, C.H.T.; Chau, K.T.; Liu, C.; Ching, T.W.; Chen, M. A new magnetless flux-reversal HTS machine for direct-drive application. IEEE Trans. Appl. Supercond. 2015, 25, 5203105. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, J.; Zou, Z.; Wang, Z.; Chau, K.T. Design and analysis of a HTS flux-switching machine for wind energy conversion. IEEE Trans. Appl. Supercond. 2013, 23, 5000904. [Google Scholar] [CrossRef]
- Jian, L.; Chau, K.T.; Li, W.; Li, J. A novel coaxial magnetic gear using bulk HTS for industrial applications. IEEE Trans. Appl. Supercond. 2010, 20, 981–984. [Google Scholar] [CrossRef]
- Zhu, H.; Ma, J.; Feng, B.; Zhang, Z.; Mellor, P. J-Φ coupled model based on integral methods and magnetic networks for superconductor. Supercond. Sci. Technol. 2025, 38, 055017. [Google Scholar] [CrossRef]
- Statra, Y.; Menana, H.; Douine, B. Semianalytical modeling of ac Losses in HTS stacks near ferromagnetic parts. IEEE Trans. Appl. Supercond. 2021, 31, 5900306. [Google Scholar] [CrossRef]
- Statra, Y.; Menana, H.; Douine, B. Integral modeling of ac losses in HTS tapes with magnetic substrates. IEEE Trans. Appl. Supercond. 2022, 32, 5900407. [Google Scholar] [CrossRef]
- Benchmark #2. Available online: https://htsmodelling.com/benchmark-2 (accessed on 22 August 2025).
- Sirois, F.; Roy, F. Computation of 2-D current distribution in superconductors of arbitrary shapes using a new semi-analytical method. IEEE Trans. Appl. Supercond. 2007, 17, 3836–3845. [Google Scholar] [CrossRef]
- Sirois, F.; Roy, F.; Dutoit, B. Assessment of the computational performances of the semi-analytical method (SAM) for computing 2-D current distributions in superconductors. IEEE Trans. Appl. Supercond. 2009, 19, 3600–3604. [Google Scholar] [CrossRef]
- Sadiku, M.N.O. Elements of Electromagnetics, 6th ed.; Oxford University Press: Oxford, UK, 2015; pp. 358–359. [Google Scholar]
- Benkel, T.; Lao, M.; Liu, Y.; Pardo, E.; Wolfstadter, S.; Reis, T.; Grilli, F. T-A-formulation to model electrical machines with HTS coated conductor coils. IEEE Trans. Appl. Supercond. 2020, 30, 5205807. [Google Scholar] [CrossRef]
- Pardo, E.; Grilli, F.; Liu, Y.; Wolftadler, S.; Reis, T. AC loss modeling in superconducting coils and motors with parallel tapes as conductor. IEEE Trans. Appl. Supercond. 2019, 29, 5202505. [Google Scholar] [CrossRef]
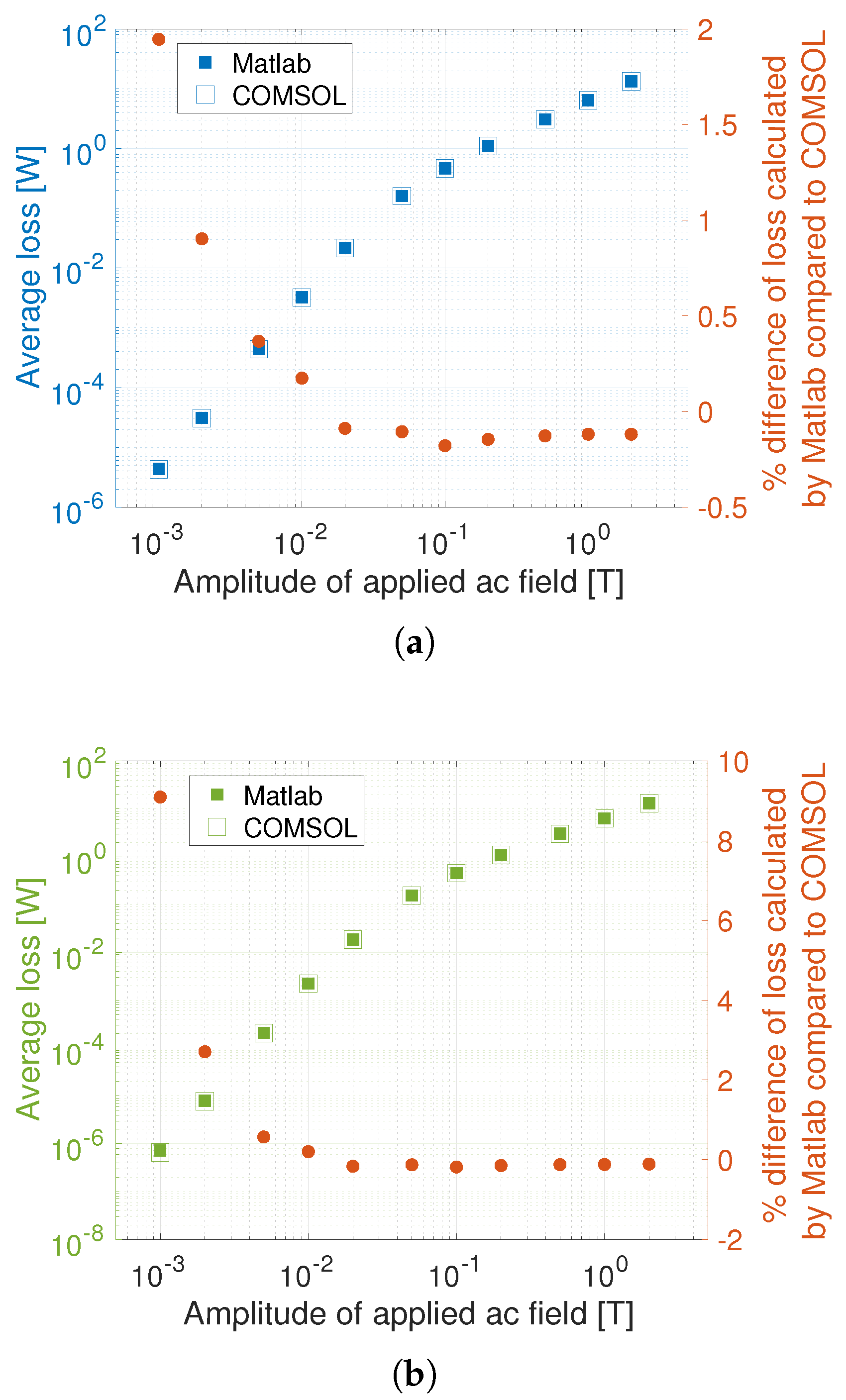
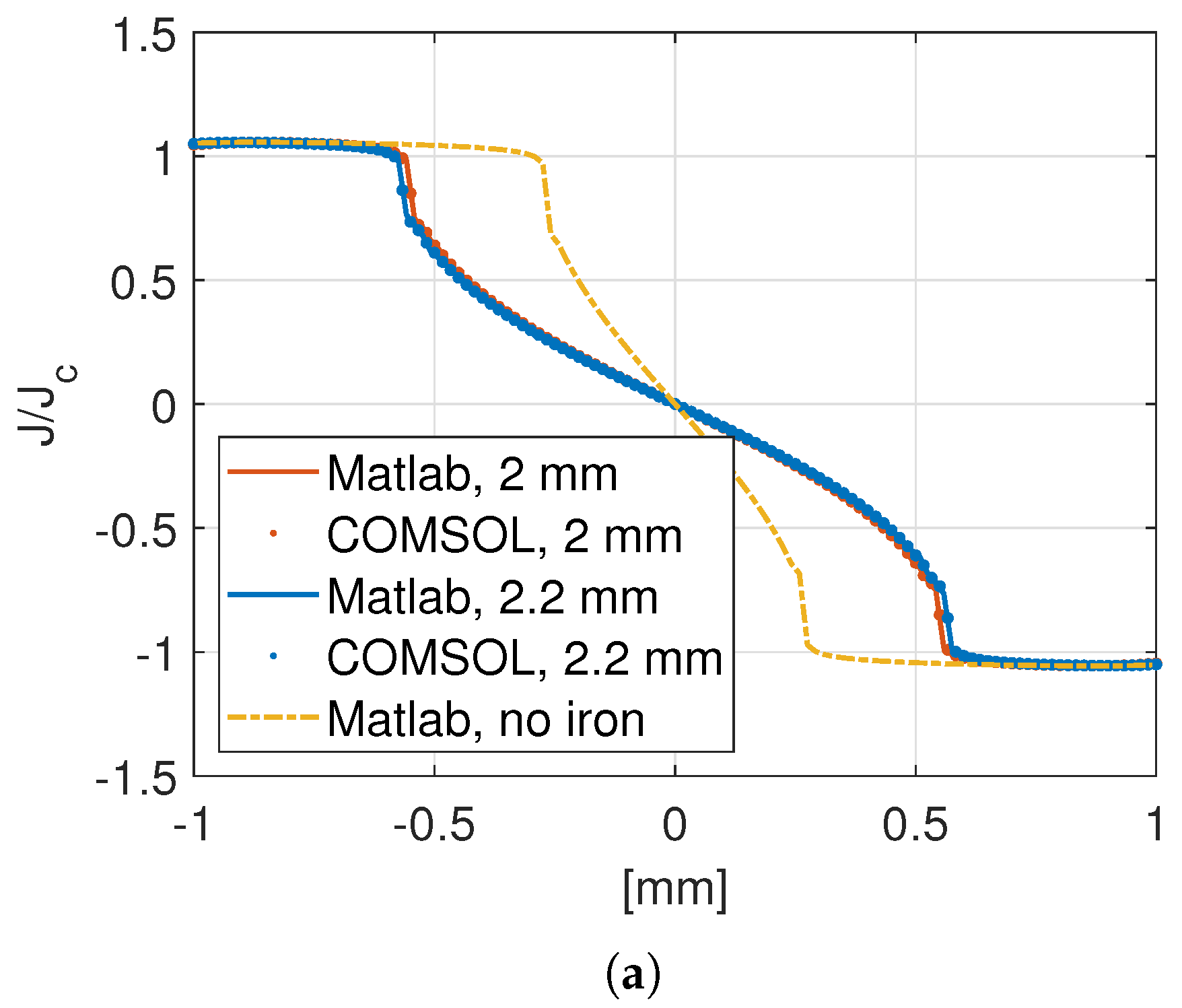
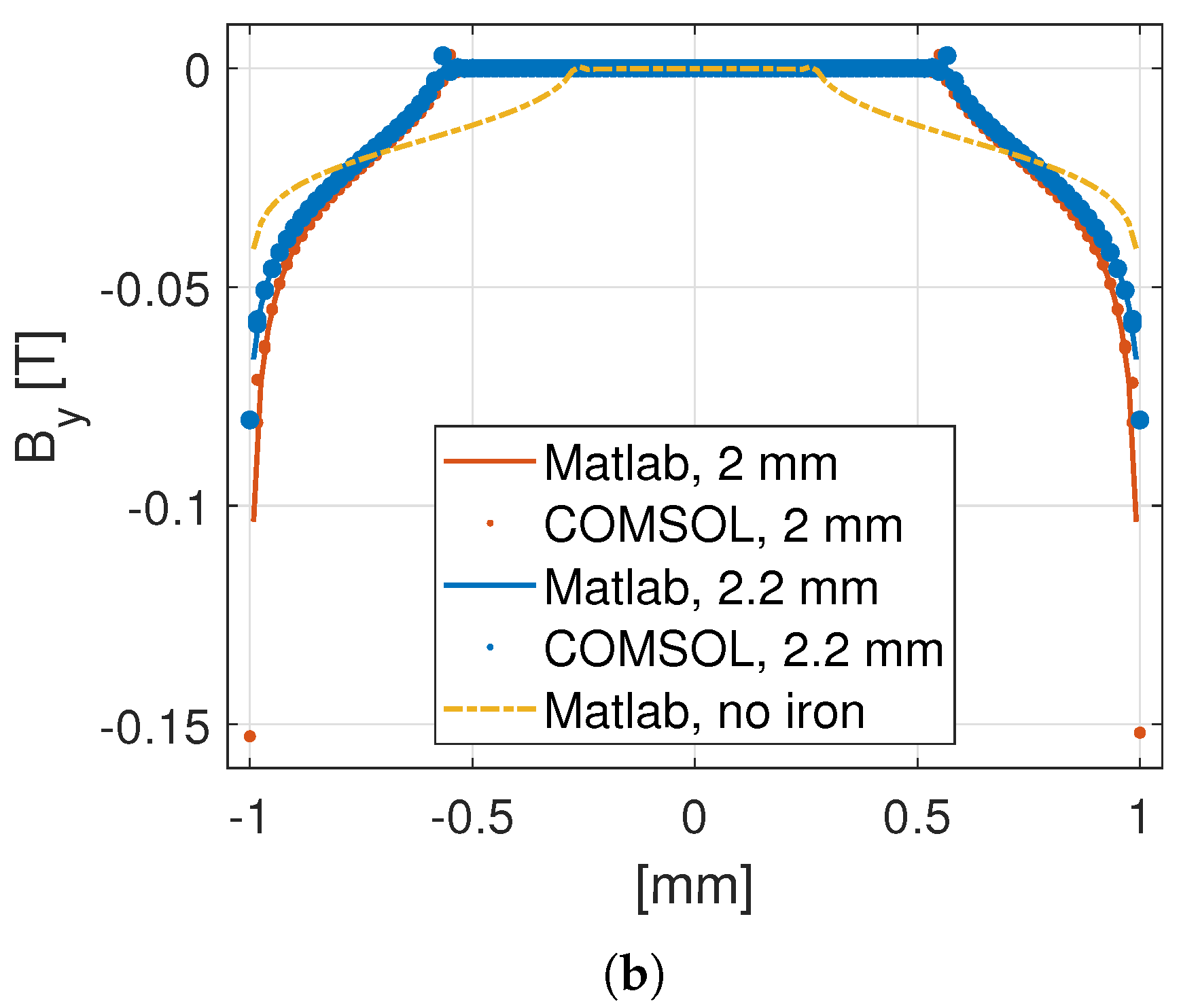
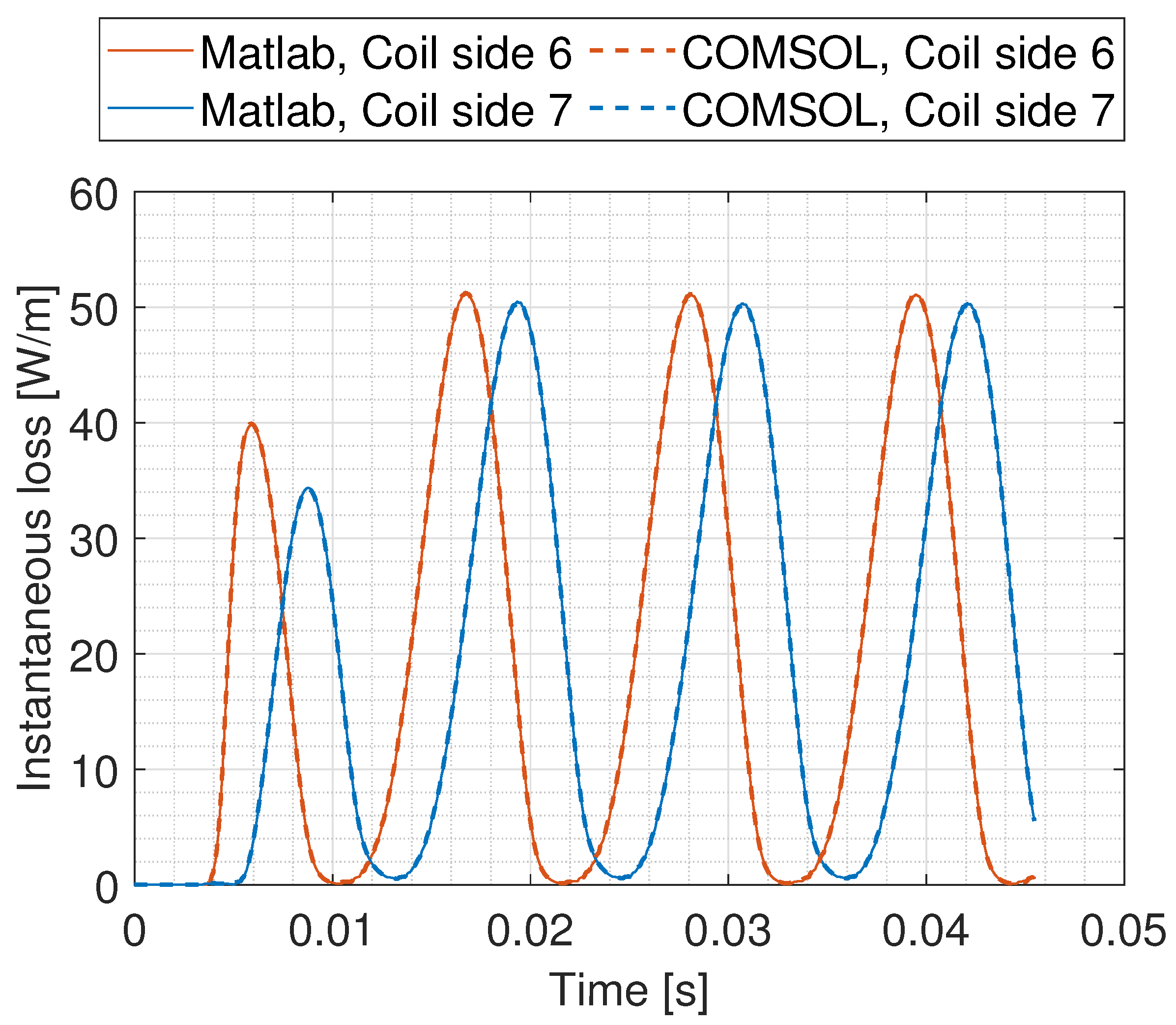
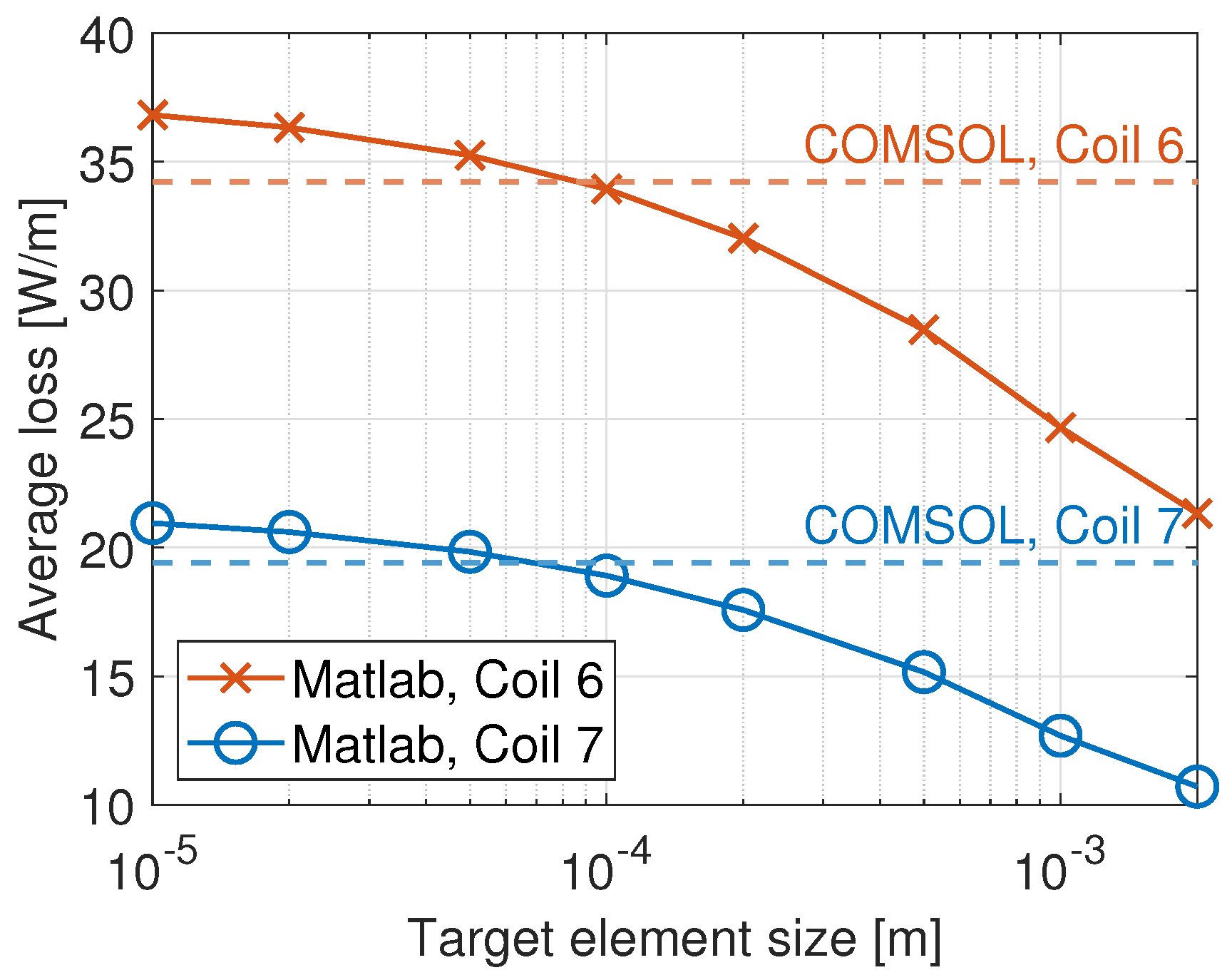
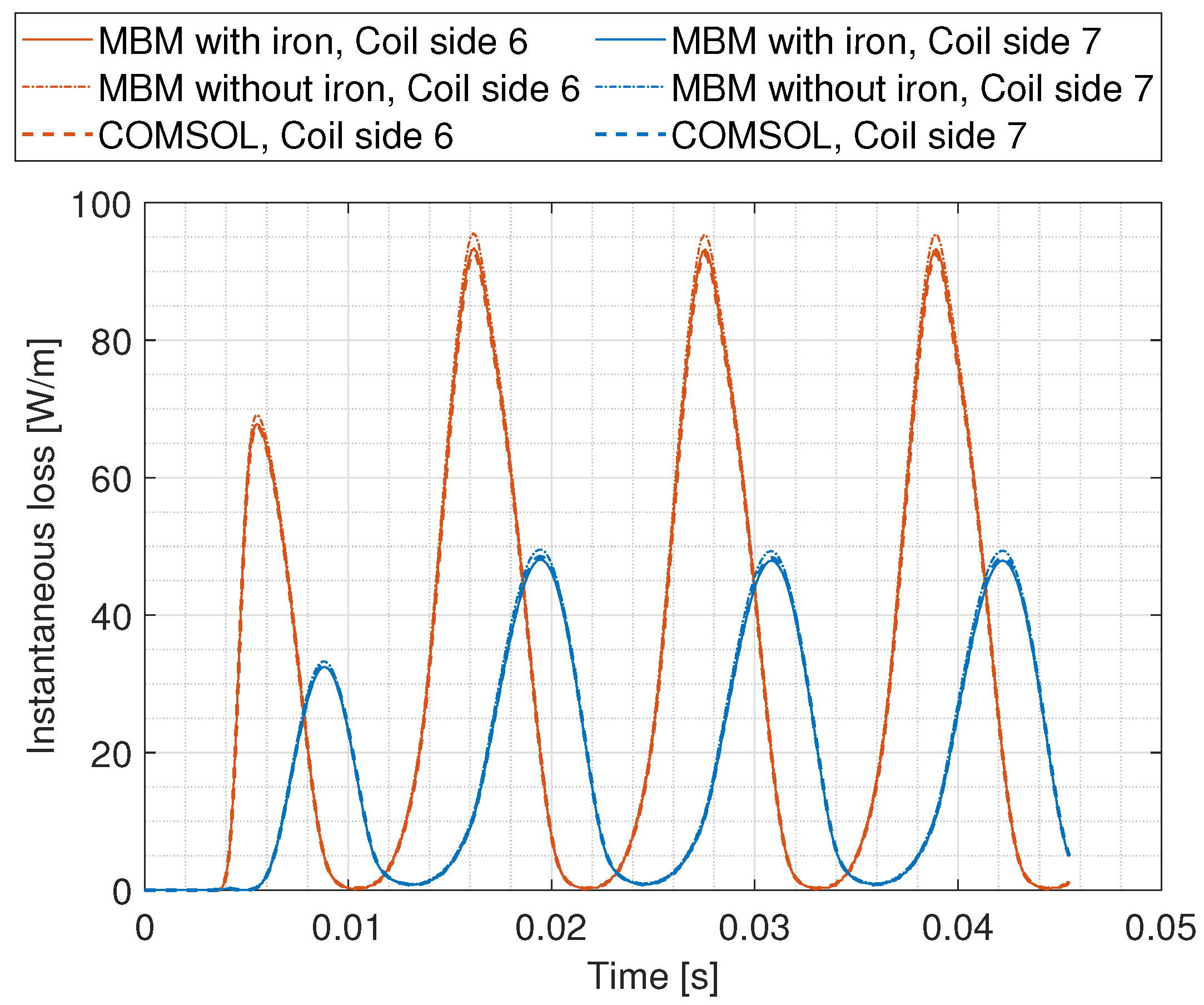
| 2 mm Substrate | 2.2 mm Substrate | |||||||
|---|---|---|---|---|---|---|---|---|
| Target Element Size [m] | 0.002 T | 0.02 T | 0.2 T | 2 T | 0.002 T | 0.02 T | 0.2 T | 2 T |
| 2.00 | n/a | 0.021673 | 1.1057 | 13.3625 | n/a | 0.018429 | 1.0917 | 13.2740 |
| 1.00 | n/a | 0.021685 | 1.1039 | 13.3579 | n/a | 0.018287 | 1.0905 | 13.2693 |
| 5.00 | n/a | 0.021842 | 1.1017 | 13.3298 | n/a | 0.019004 | 1.0898 | 13.2478 |
| 2.00 | 2.96 | 0.021580 | 1.0976 | 13.2883 | 1.50 | 0.018864 | 1.0866 | 13.2149 |
| 1.00 | 3.07 | 0.021539 | 1.0967 | 13.2784 | 7.14 | 0.018598 | 1.0854 | 13.2064 |
| 5.00 | 3.10 | 0.021515 | 1.0962 | 13.2737 | 8.35 | 0.018645 | 1.0851 | 13.2026 |
| 2.00 | 3.13 | 0.021511 | 1.0961 | 13.2720 | 7.89 | 0.018621 | 1.0850 | 13.2011 |
| 1.00 | 3.14 | 0.021507 | 1.0960 | 13.2714 | 7.88 | 0.018618 | 1.0849 | 13.2006 |
| 5.00 | 1.32 | n/a | n/a | n/a | 4.66 | n/a | n/a | n/a |
| 2.00 | 9.13 | n/a | n/a | n/a | 1.25 | n/a | n/a | n/a |
| 1.00 | 8.27 | n/a | n/a | n/a | 1.04 | n/a | n/a | n/a |
| Normal | Dense | |
|---|---|---|
| Max element size on edges 1 [mm] | 0.6 | 0.3 |
| Number of edge elements on edges close to tapes 1 | 164 | 328 |
| Number of triangles in stator iron | 15,778 | 26,057 |
| Average loss 2 coil side 6 [W/m] | 20.914 | 20.918 |
| Average loss 2 coil side 7 [W/m] | 21.452 | 21.456 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chow, C.C.T.; Chau, K.T.; Grilli, F. Modelling Magnetisation and Transport AC Loss of HTS Tapes near Ferromagnetic Materials Using an Integral Equation Method. Appl. Sci. 2025, 15, 10411. https://doi.org/10.3390/app151910411
Chow CCT, Chau KT, Grilli F. Modelling Magnetisation and Transport AC Loss of HTS Tapes near Ferromagnetic Materials Using an Integral Equation Method. Applied Sciences. 2025; 15(19):10411. https://doi.org/10.3390/app151910411
Chicago/Turabian StyleChow, Calvin C. T., K. T. Chau, and Francesco Grilli. 2025. "Modelling Magnetisation and Transport AC Loss of HTS Tapes near Ferromagnetic Materials Using an Integral Equation Method" Applied Sciences 15, no. 19: 10411. https://doi.org/10.3390/app151910411
APA StyleChow, C. C. T., Chau, K. T., & Grilli, F. (2025). Modelling Magnetisation and Transport AC Loss of HTS Tapes near Ferromagnetic Materials Using an Integral Equation Method. Applied Sciences, 15(19), 10411. https://doi.org/10.3390/app151910411







