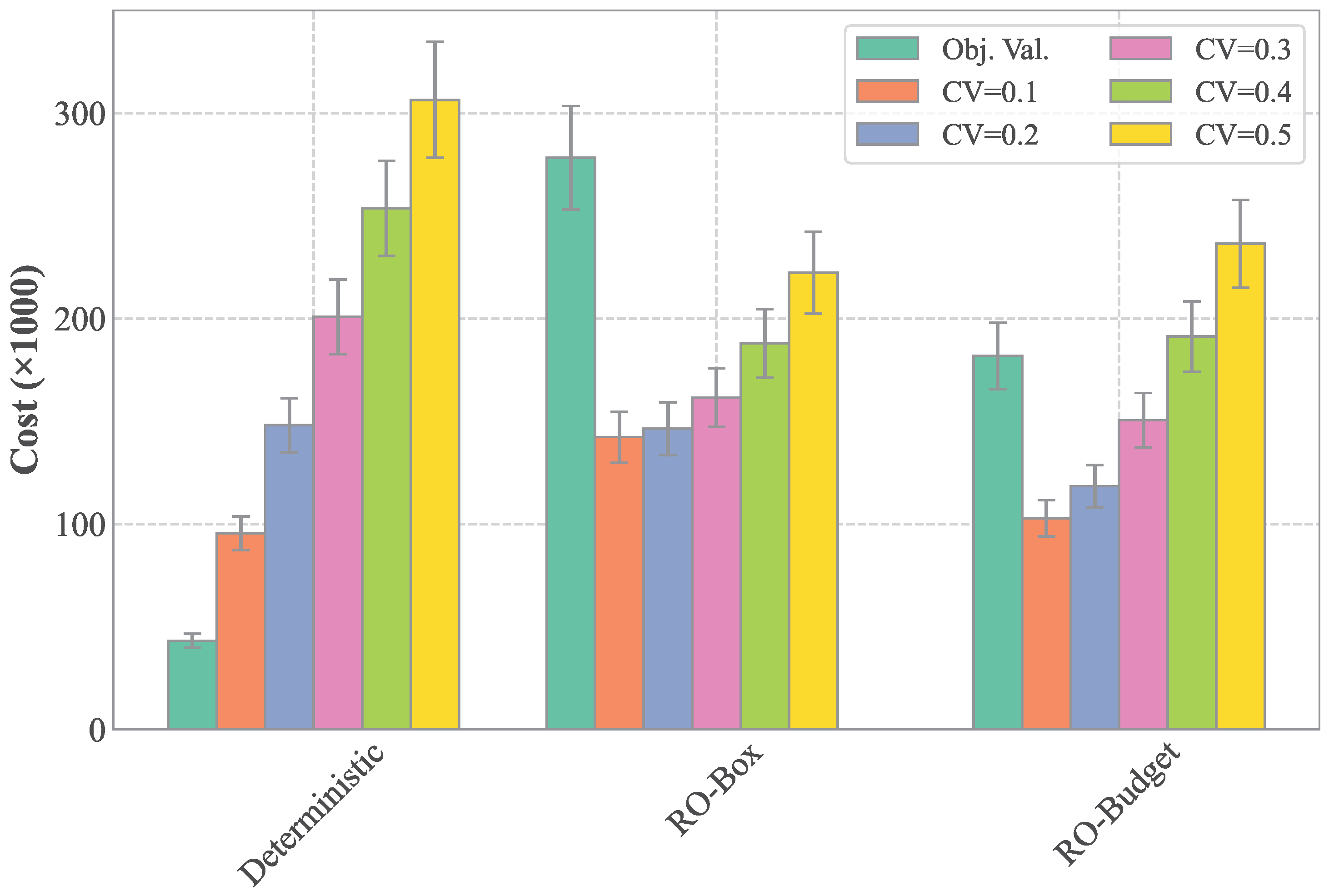A Robust Optimization Approach for the Multi-Period Strip Cutting Problem with Multi-Cutter Slitting Machines

Abstract

This paper studies a multi-period strip cutting problem motivated by the paper industry. The focus is on multi-cutter slitting machines, which allow the simultaneous production of items with different lengths and provide higher cutting flexibility compared to conventional single-cutter machines. We propose a pattern-based mixed-integer programming formulation to evaluate the benefits of multi-cutter machines and compare it with heuristic strategies and a single-cutter benchmark. To address demand uncertainty, we extend the model using robust optimization with budgeted uncertainty sets and derive a tractable reformulation. Computational experiments with real-world data show that multi-cutter machines can substantially reduce raw material usage costs compared to the single-cutter setting. Under demand uncertainty, the budgeted robust model provides lower realized costs and smaller variability than both deterministic and box-type robust models.

1. Introduction

In paper industries, a wide range of products that differ in dimensions and demand volumes are produced. To fulfill customer demands, large paper rolls (jumbo rolls) must be cut into smaller sheets or items. This process is typically carried out by slitter cutting machines, which are also widely used in the steel, plastic film, and textile industries [1,2,3,4].

The cutting process inherently generates trim loss, as the widths of items rarely match the jumbo roll exactly. Trim loss not only increases raw material consumption and production costs but also has negative environmental impacts due to waste generation. With growing attention to sustainability, reducing trim loss and improving cutting efficiency have become key challenges for the paper industry [5]. Particularly, given the large production volumes in this industry, even marginal improvements in material utilization can lead to substantial cost savings.

This industrial challenge has motivated extensive research within the frameworks of the cutting stock problem (CSP), strip packing problem (SPP), strip cutting problem (SCP), and their variants [6,7,8,9,10]. In this study, we focus on the two-dimensional case, particularly the two-dimensional SCP and SPP, where item dimensions are determined by both width and length. In the two-dimensional SCP and SPP, the strip width is fixed and the length is assumed to be effectively infinite, with the objective of minimizing the total strip length used. In contrast, the CSP assumes the stock pieces have both a fixed width and length, aiming to minimize the number of stock pieces required. While the two-dimensional SCP and SPP share similar structural characteristics, the term SPP is typically used when each item type has a unitary demand, whereas the SCP usually refers to cases where items have arbitrary, possibly large, demand quantities [11,12].

The conventional single-cutter machines commonly used in the paper industry employ guillotine cuts, in which the strip is sliced parallel to its horizontal side, running from one edge to the opposite one in a straight line [13]. Recently, multi-cutter machines have been introduced. Unlike single-cutter machines, a multi-cutter machine is equipped with multiple horizontal cutters that can operate at different speeds. This allows for the simultaneous production of items with different lengths, significantly enhancing cutting flexibility and improving raw material utilization. As a result, multi-cutter machines can reduce trim loss and production costs compared to the single-cutter machine.

It should be noted that the multi-cutter machines considered in this study are distinct from the non-guillotine cuts [14,15]. While both provide greater flexibility than guillotine cuts, multi-cutter machines achieve this by enabling multiple horizontal cutters to operate independently and simultaneously, allowing items of different lengths to be produced at once. In contrast, non-guillotine cuts allow any partial cuts within the strip.

These differences are illustrated in Figure 1. Figure 1a shows a guillotine cutting pattern, where the strip is sliced horizontally from one side to the other in a single straight line. Figure 1b illustrates the multi-cutter setting, in which several cutters operate independently and are not restricted to full-width cuts. Figure 1c depicts the non-guillotine cuts, where partial cuts can be made within the strip. Such cuts are not possible in other settings.

Lodi et al. [16] studied a two-dimensional (2D) SPP, in which items must be packed by levels. The authors devised a polynomial-sized formulation with variables representing the levels and the item-to-level assignments. For a similar problem setting, Mrad [11] proposed an arc-flow formulation that represents each cutting pattern as a network flow on a graph. Subsequently, Bezerra et al. [12] introduced a class of valid inequalities for the formulation of [16] and compared the computational performance of the different formulations.

Cintra et al. [13] investigated the 2D-SPP with guillotine cuts and developed solution approaches based on column generation. Rinaldi and Franz [17] addressed a 2D-SCP arising in corrugated cardboard manufacturing, incorporating buffer restrictions and sequencing constraints. They proposed two heuristics, one based on linear programming (LP) and the other on a matching-based approach. Kenmochi et al. [7] addressed the 2D-SPP with and without item rotation and proposed exact branch-and-bound algorithms along with bounding schemes based on dynamic programming and LP.

The above studies primarily focus on single-period problems, where all demands are fulfilled within a single planning horizon. These problems have been extended to multi-period settings, where demand occurs over several periods and production decisions must be coordinated accordingly. In particular, the integration of cutting or packing with lot-sizing decisions, such as inventory management and backlogging, has been a popular research direction. This line of research has led to problem variants such as the integrated lot-sizing and cutting stock problem [18,19] and the integrated lot-sizing and bin packing problem [20,21]. In our study, the adoption of a multi-period structure is further motivated by real-world data collected from our industrial partner. In practice, customer orders exhibit variation over time, and a single-period formulation cannot adequately capture the temporal dynamics involved in demand fulfillment, inventory accumulation, and backlog decisions.

Most of these studies have assumed deterministic demand. In practice, however, demand is often uncertain due to urgent orders or order cancellations. This variability can lead to significant mismatches between supply and demand, resulting in excessive inventory costs, backlog penalties, and lost sales. Robust optimization (RO) provides an effective framework to address this challenge [22,23,24]. Rather than relying on probability distributions as in stochastic programming, the RO approach seeks solutions that remain feasible for all possible demand realizations within a predefined uncertainty set.

Several related studies have applied RO in integrated cutting and lot-sizing contexts. For example, Alem and Morabito [25] developed an RO model for an integrated lot-sizing and cutting stock problem in furniture manufacturing to address uncertain demands and production costs. Curcio et al. [26] proposed both stochastic programming and RO models incorporating demand uncertainty, and introduced a rolling-horizon approach that allows production plans to be adjusted in each period. Ide et al. [27] devised an RO model for a wood cutting problem under uncertain raw material quality. While these works demonstrate the applicability of RO to various cutting and packing problems integrated with lot-sizing decisions, their settings differ from ours in several aspects. In particular, none of them consider the multi-cutter machine configuration, which fundamentally changes the cutting pattern generation process and makes direct application to our problem challenging.

To the best of our knowledge, the only study that explicitly considered a multi-cutter setting is [28], where the authors addressed a cutting machine selection problem to minimize paper loss. They developed heuristic algorithms for cutting pattern generation and proposed a mixed integer programming model. While their work shares some similarities with ours, we extend the scope by addressing a multi-period setting and incorporating an RO framework to account for demand uncertainty. Because their formulation is limited to a single-period deterministic context, a direct numerical comparison with our multi-period robust model is not feasible. While ref. [28] demonstrates the feasibility of multi-cutter machines in a static setting, our work highlights how multi-cutter configurations can be effectively integrated into a dynamic and uncertain environment that better reflects industrial practice.

In this study, we address a multi-period strip cutting problem involving a multi-cutter slitting machine. We first propose a pattern-based optimization model that explicitly incorporates the multi-cutter configuration and evaluate its performance against heuristic strategies and the conventional single-cutter configuration. We then extend this model into a robust optimization framework to account for demand uncertainty. The proposed approaches are validated through computational experiments using real-world test instances.

The main contributions of this study are threefold. First, we address a multi-period strip cutting problem that incorporates a multi-cutter slitting machine, which provides greater cutting flexibility and sustainability benefits compared to traditional single-cutter systems. This problem setting, motivated by real industrial practice, has received limited attention in the literature. This may be attributed to the relatively low adoption of such machines in the past. However, with recent advances in machinery and increasing industrial focus on minimizing material waste, multi-cutter configurations are becoming more relevant in modern manufacturing environments. Second, we propose a pattern-based optimization model that captures the multi-cutter configuration and demonstrate its superiority over single-cutter machines and various heuristic strategies. Finally, to address demand uncertainty, we develop a robust optimization approach based on budgeted uncertainty sets. The proposed robust optimization model achieves a balanced trade-off between robustness and cost efficiency. The effectiveness of this approach is demonstrated through extensive computational experiments using real-world data.

The remainder of this paper is organized as follows. Section 2 introduces the problem setting for the multi-cutter machine and defines cutting patterns. It also presents a pattern-based optimization model for the single-period case together with two heuristic algorithms. In Section 3, we present a deterministic formulation and a robust optimization model for the multi-period problem. In Section 4, we provide the results of computational experiments to demonstrate the effectiveness of the proposed approaches. Finally, in Section 5, we provide concluding remarks and discuss future research directions.

2. Problem Description

In this section, we describe the configuration of the multi-cutter slitting machine and introduce the terminology and notation used in this study. The raw material is supplied in the form of large jumbo rolls with a fixed width W. As in typical 2D-SCPs or 2D-SPPs, the length of the roll is assumed to be effectively infinite. This assumption is reasonable in short-term planning horizons where the available roll length far exceeds the production requirements. If this condition does not hold, additional modeling of roll length constraints would be required, in which case a cutting-stock style formulation would be more appropriate.

The rolls are processed into items by the machine illustrated in Figure 2. It is equipped with multiple slitters (knives) that divide the roll vertically into narrower strips. The spacing between slitters is adjustable, allowing the production of items with different widths. The maximum number of vertical cuts is equal to the number of slitters, denoted by $NS$.

The roll is then cut horizontally by cutters. By adjusting the speed of the cutter, the lengths of the resulting items can be varied. In conventional machines, only one cutter is used, meaning that all items produced in a single cut have the same length. In contrast, the machine considered in this study has multiple cutters that can operate independently, enabling the simultaneous production of items with different lengths. We denote the number of cutters by $NC$. Figure 2 illustrates an example with $NS=4$ and $NC=3$.

2.1. Pattern-Based Formulation for the Single-Period Problem

We first define the notion of a cutting pattern. For variants of cutting and packing problems, pattern-based formulations have been the dominant approach since earlier seminal works of [29,30,31]. For ease of explanation, we introduce cutting patterns together with the formulation of the single-period problem.

A cutting pattern is defined as a combination of items that can be cut within the roll width limit W. Let $\mathcal{I}$ denote the set of items, where each item $i\in \mathcal{I}=\{1,\dots ,NI\}$ has width and length $(w_i,l_i)$ and demand $d_i$. The j-th pattern is represented by $a_j=(a_{1j},a_{2j},\cdots ,a_{NI,j})$, where $a_{ij}$ indicates the number of copies of item i contained in pattern j. Each pattern j is feasible only if the total width does not exceed the roll width, that is, ${\sum }_{i\in \mathcal{I}}{w}_i{a}_{ij}\le W$.

To illustrate, consider the example in Figure 3a with roll width $W=80$ and three items of sizes $(18,30)$, $(25,20)$, and $(15,11)$. Examples of feasible cutting patterns for this instance are shown in Figure 3b, each of which satisfies the width constraint. Many other feasible patterns are also possible, and we let $\mathcal{J}$ be the set of all feasible patterns.

When generating patterns, we apply an index-based ordering rule to avoid redundant symmetric representations. For example, pattern 2 in Figure 3b, which contains three copies of item A and one copy of item B, could equivalently be represented as [A, A, A, B], [A, A, B, A], or [B, A, A, A]. By construction, only one canonical representation is retained, defined by listing items in increasing index order (i.e., [A, A, A, B], as illustrated in the figure), and symmetric variants are excluded. This ensures that equivalent permutations are not redundantly included in the formulation.

Furthermore, we consider only maximal patterns, where a pattern is called maximal if no additional item can be inserted without exceeding the roll width W. In other words, if one more unit of any item were inserted, the width constraint would be violated. Non-maximal and dominated patterns are thus excluded by construction, ensuring that the pattern set remains compact and meaningful for optimization.

When a pattern is used, it is necessary to determine the roll length allocated to that pattern. Let $y_j$ denote the continuous variable representing the length of the roll assigned to pattern j, and let $x_{ij}$ denote the integer variable indicating how many times item i is produced vertically within $y_j$. For example, in Figure 2, pattern 1 in Figure 3b with $a_1=(1,1,2)$ is used for a total roll length of $y_1=60$. Within this length, items 1, 2, and 3 are cut 2, 3, and 5 times, respectively, which corresponds to $x_{11}=2$, $x_{21}=3$, and $x_{31}=5$. The relationship between $x_{ij}$ and $y_j$ is constrained by the item lengths, and must satisfy $l_i{x}_{ij}\le y_j$. Based on these definitions, the single-period problem can be formulated as follows.

$$\begin{array}{}\hfill \mathrm{(1)}& \hfill \min & {\displaystyle \sum _{j\in \mathcal{J}}}{y}_j\hfill & \hfill \mathrm{(2)}& \hfill \mathrm{s}.\mathrm{t}.& {\displaystyle \sum _{j\in \mathcal{J}}}{a}_{ij}{x}_{ij}\ge d_i,\hfill & \hfill \forall i\in \mathcal{I},\hfill \mathrm{(3)}& & l_i{x}_{ij}\le y_j,\hfill & \hfill \forall i\in \mathcal{I},j\in \mathcal{J},\hfill \mathrm{(4)}& & x_{ij}\in {\mathbb{Z}}_{+},\hfill & \hfill \forall i\in \mathcal{I},j\in \mathcal{J},\hfill \mathrm{(5)}& & y_j\ge 0,\hfill & \hfill \forall j\in \mathcal{J}.\end{array}$$

The objective function (1) is to minimize the total strip length. Constraints (2) guarantee that the production of each item i satisfies its demand $d_i$. Note that, in this formulation, the demand is considered only for a single period. Constraints (3) establish the relationship between the variables $x_{ij}$ and $y_j$. Finally, constraints (4) and (5) define the domains of the decision variables.

2.2. Ordering Heuristics for Single-Period Problem

We present an ordering heuristic algorithm for the single-period problem in Algorithm 1. The ordering heuristic generates cutting patterns sequentially based on a predefined item sorting criterion. The sorting criterion can be, for example, the width, length, demand, or area of the item. The sorted list determines the priority in which items are considered for inclusion in each pattern. For instance, sorting items by demand prioritizes items that account for a large proportion of the total demand. Similarly, by sorting items by width, wider items are incorporated into patterns at earlier stages.

Algorithm 1 Ordering-Based Multi-Cutter Heuristic

Require:  W, $(w_i,l_i,d_i)$ for $i\in \mathcal{I}$, sorting criteria Ensure:  Total roll length used, set of cutting patterns   1: Sort items in $\mathcal{I}$ based on CRITERIA   2: $\mathtt{TotLen}\leftarrow 0$, $\mathtt{PatternList}\leftarrow \left[\right]$   3: Set $\mathtt{RemainDem}\left[i\right]\leftarrow d_i$, $\forall i\in \mathcal{I}$   4: while any $\mathtt{RemainDem}\left[i\right]>0$ do   5:     Set $W_{remain}\leftarrow W$, $ns\leftarrow 0$, $nc\leftarrow 0$, pattern ${\mathbf{a}}_j\leftarrow \mathbf{0}$   6:     for $i\in \mathcal{I}$ in sorted order do   7:         while $w_i\le W_{remain}$, $\mathtt{RemainDem}\left[i\right]>0$, $ns<NS$, $nc<NC$ do   8:            $a_{ij}\leftarrow a_{ij}+1$, $W_{remain}\leftarrow W_{remain}-w_i$, $ns+=1$   9:            if $a_{ij}=1$ then 10:                $nc\leftarrow nc+1$ 11:            end if 12:         end while 13:     end for 14:     $M_j\leftarrow min\left\{⌈{\displaystyle \frac{\mathtt{RemainDem}\left[i\right]}{a_{ij}}}⌉·l_i|a_{ij}>0\right\}$ 15:     Update $\mathtt{RemainDem}\left[i\right]\leftarrow max\{0,\mathtt{RemainDem}\left[i\right]-\lfloor M_j/l_i\rfloor ·a_{ij}\}$ 16:     $\mathtt{TotLen}\leftarrow \mathtt{TotLen}+M_j$ 17:     $\mathtt{PatternList}$.append(${\mathbf{a}}_j$) 18: end while 19: return  $\mathtt{TotLen},\mathtt{PatternList}$

The algorithm iteratively selects the largest feasible set of items that satisfies the machine’s operational constraints, such as the maximum number of slitters and cutters (lines 6–12). After each pattern is generated, it is used consecutively until the demand for at least one item included in that pattern is fully satisfied. Once this occurs, the remaining demands are updated (lines 13–14), and the next pattern is generated. This procedure is repeated until the demands of all items are satisfied. Since at least one item’s demand is fulfilled in each iteration, the number of patterns generated by the ordering heuristic is at most equal to the number of items.

The main advantage of the ordering heuristic lies in its simplicity and speed. By relying on a straightforward sorting and selection process, it can generate reasonably good patterns without the computational burden of solving an optimization model at each step. Its performance is influenced by the choice of sorting criterion. In Section 4, we compare the results obtained using various criteria, including width, length, demand, and area.

The proposed heuristics are constructive procedures adapted from classical ordering-based strategies, tailored to the multi-cutter setting. They always terminate in a finite number of steps and produce only patterns that satisfy the roll-width constraint. These heuristics are not intended to provide theoretical performance guarantees; rather, they serve as practical methods to generate feasible patterns efficiently and to act as benchmarks for evaluating the optimization model.

2.3. Knapsack Heuristics for Single-Period Problem

We present a knapsack heuristic algorithm for the single-period problem in Algorithm 2. This algorithm generates cutting patterns by explicitly solving a knapsack-type subproblem at each iteration. In contrast to the ordering heuristic, which determines patterns based solely on a predefined sorting criterion, this approach selects items so that the available width is utilized as efficiently as possible while satisfying the operational constraints of the machine.

Algorithm 2 Knapsack-Based Multi-Cutter Heuristic

Require:  W, $(w_i,l_i,d_i)$ for $i\in \mathcal{I}$ Ensure:  Total roll length used, set of cutting patterns   1: $\mathtt{TotLen}\leftarrow 0$, $\mathtt{PatternList}\leftarrow \left[\right]$, ${\mathcal{I}}^{\prime }\leftarrow \mathcal{I}$   2: Set $\mathtt{RemainDem}\left[i\right]\leftarrow d_i$, $\forall i\in {\mathcal{I}}^{\prime }$   3: while any $\mathtt{RemainDem}\left[i\right]>0$ do   4:     Solve KP$({\mathcal{I}}^{\prime }$)   5:     Obtain pattern $a_{ij}\leftarrow q_i$ from solution   6:     $M_j\leftarrow min\left\{⌈{\displaystyle \frac{\mathtt{RemainDem}\left[i\right]}{a_{ij}}}⌉·l_i|a_{ij}>0\right\}$   7:     Update $\mathtt{RemainDem}\left[i\right]\leftarrow max\{0,\mathtt{RemainDem}\left[i\right]-\lfloor M_j/l_i\rfloor ·a_{ij}\}$   8:     $\mathtt{TotLen}\leftarrow \mathtt{TotLen}+M_j$   9:     $\mathtt{PatternList}$.append(${\mathbf{a}}_j$) 10:     Update ${\mathcal{I}}^{\prime }$ 11: end while 12: return  $\mathtt{TotLen},\mathtt{PatternList}$

Specifically, in each iteration, the algorithm solves the following problem $\mathtt{KP}\left({\mathcal{I}}^{\prime }\right)$, where the set ${\mathcal{I}}^{\prime }\subseteq \mathcal{I}$ contains items that are available to form a pattern. In the problem, the binary variable $p_i$ indicates whether the item i is included in the generated pattern. The integer variable $q_i$ denotes the number of times item i is cut by the slitters.

$$\begin{array}{}\hfill \mathrm{(6)}& \hfill \mathtt{KP}\left({\mathcal{I}}^{\prime }\right)\max & {\displaystyle \sum _{i\in {\mathcal{I}}^{\prime }}}{w}_i{q}_i\hfill & \hfill \mathrm{(7)}& \hfill \mathrm{s}.\mathrm{t}.& {\displaystyle \sum _{i\in {\mathcal{I}}^{\prime }}}{w}_i{q}_i\le W,\hfill & \hfill \mathrm{(8)}& & {\displaystyle \sum _{i\in {\mathcal{I}}^{\prime }}}{p}_i\le NC,\hfill & \hfill \mathrm{(9)}& & {\displaystyle \sum _{i\in {\mathcal{I}}^{\prime }}}{q}_i\le NS,\hfill & \hfill \mathrm{(10)}& & q_i\le NS·p_i,\hfill & \forall i\in {\mathcal{I}}^{\prime },\hfill \mathrm{(11)}& & q_i\in {\mathbb{Z}}_{+},p_i\in \{0,1\},\hfill & \forall i\in {\mathcal{I}}^{\prime }.\end{array}$$

The objective function (6) is to maximize the total utilized width of the jumbo roll. Constraint (7) ensures the maximum width constraint. The constraints (8) and (9) ensure the maximum number of slitters and cutters, respectively. Constraints (10) represent the relationship between the variables $q_i$ and $p_i$.

After solving the problem, the corresponding pattern is constructed and processed consecutively until the demand for at least one item is fully satisfied. The remaining demands are then updated, and a new optimization problem is solved to generate the next pattern. This process continues until the demands for all items are fulfilled. The knapsack heuristic offers greater flexibility in pattern generation compared to the ordering heuristic, as it adaptively determines the set of items in each iteration. This often leads to improved utilization of the jumbo roll and reduced trim loss. In Section 4, we compare the performance of the knapsack heuristic with that of the ordering heuristic and other approaches.

3. Robust Optimization Model for Multi-Period Problem

3.1. Deterministic Model

Before developing the RO model that accounts for demand uncertainty, we introduce the deterministic formulation for the multi-period problem. This formulation extends the single-period model presented in Section 2.

Firstly, to present the multi-period model, we let $\mathcal{T}=\{1,\dots ,NT\}$ be the set of time periods. For $i\in \mathcal{I}$ and $t\in \mathcal{T}$, let $h_{it}$ and $k_{it}$ denote the inventory holding cost and backlog penalty cost of item i in period t, respectively. The variable cost per unit length of the roll used in period t is denoted by $c_t$. The load balancing cost, denoted by l, is incurred based on the difference in roll usage between the most and least utilized periods.

Variables $I_{it}$ and $B_{it}$ denote the inventory and backlog of item i at the end of period t, respectively. In the proposed model, inventory levels are constrained to be nonnegative, and any unmet demand is captured using a backlog variable. The backlog penalty cost is modeled as a soft constraint and is applied proportionally to the amount of unmet demand. In particular, the penalty is charged per unit of backlog and is accumulated across periods until the demand is eventually fulfilled. As a result, the total backlog cost increases with the duration of the fulfillment delay. The variable $y_{jt}$ indicates the length of pattern j used in period t, while $x_{ijt}$ specifies the number of times item i is produced vertically. Finally, $L^{min}$ and $L^{max}$ represent the minimum and maximum daily roll usage across the entire planning horizon. Based on these definitions, the deterministic mixed-integer programming (MIP) model is formulated as follows:

$$\begin{array}{}\hfill \mathrm{(12)}& \hfill \min & {\displaystyle \sum _{j\in \mathcal{J}}}{\displaystyle \sum _{t\in \mathcal{T}}}{c}_t{y}_{jt}+{\displaystyle \sum _{i\in \mathcal{I}}}{\displaystyle \sum _{t\in \mathcal{T}}}\left(h_{it}{I}_{it}+k_{it}{B}_{it}\right)+l(L^{max}-L^{min})\hfill & \hfill \mathrm{(13)}& \hfill \mathrm{s}.\mathrm{t}.& I_{i,t-1}-B_{i,t-1}+{\displaystyle \sum _{j\in \mathcal{J}}}{a}_{ij}{x}_{ijt}=I_{it}-B_{it}+d_{it},\hfill & \hfill \forall i\in \mathcal{I},t\in \mathcal{T},\hfill \mathrm{(14)}& & l_i{x}_{ijt}\le y_{jt},\hfill & \hfill \forall i\in \mathcal{I},j\in \mathcal{J},t\in \mathcal{T},\hfill \mathrm{(15)}& & {\displaystyle \sum _{j\in \mathcal{J}}}{y}_{jt}\le L^{max},\hfill & \hfill \forall t\in \mathcal{T},\hfill \mathrm{(16)}& & {\displaystyle \sum _{j\in \mathcal{J}}}{y}_{jt}\ge L^{min},\hfill & \hfill \forall t\in \mathcal{T},\hfill \mathrm{(17)}& & x_{ijt}\in {\mathbb{Z}}_{+},\hfill & \hfill \forall i\in \mathcal{I},j\in \mathcal{J},t\in \mathcal{T},\hfill \mathrm{(18)}& & y_{jt}\ge 0,\hfill & \hfill \forall j\in \mathcal{J},t\in \mathcal{T},\hfill \mathrm{(19)}& & L^{max},L^{min}\ge 0.\hfill & \end{array}$$

The objective function (12) minimizes the total cost, which is the sum of the variable cost for using rolls, inventory holding, backlogging costs, and the penalty costs for load balancing. Constraints (13) represent the inventory balance equations for each item and period. Constraints (14) ensure the length of pattern j used in period t. Constraints (15) and (16) ensure that variables $L^{max}$ and $L^{min}$ have proper values. Constraints (17)–(19) define the domains of variables, ensuring integer and nonnegativity conditions, respectively.

3.2. Uncertainty Sets

In our RO model, customer demand $d_{it}$ is not treated as a fixed parameter but as an uncertain quantity that is subject to variation. For each item i and period t, demand is assumed to lie within an interval centered at the forecast value ${\overline{d}}_{it}$ with maximum deviation ${\widehat{d}}_{it}$, that is, $d_i\in [{\overline{d}}_{it}-{\widehat{d}}_{it},{\overline{d}}_{it}+{\widehat{d}}_{it}]$. To normalize the deviation, we define the scaled deviation variable $v_{it}:=(d_{it}-{\overline{d}}_{it})/{\widehat{d}}_{it}$, which takes values between $-1$ and 1. Collecting these into a vector ${\mathbf{v}}_i:=(v_{i1},v_{i2},\cdots ,v_{i,NT})$ yields all possible deviation patterns for item i. If we simply require $-1\le v_{it}\le 1$ for every period, the resulting support set corresponds to the well-known box uncertainty set [32].

While the box set provides maximum protection, it also enforces feasibility against the simultaneous worst-case of all deviations. This typically leads to highly conservative decisions. To moderate this, we introduce the widely used concept of a budget of uncertainty [23], which restricts how many deviations can occur simultaneously. Specifically, for each item i and period t, the cumulative deviation is bounded by ${\sum }_{k=1}^t\left|v_{ik}\right|\le {\Gamma }_{it}$. Following [33], the budget parameter satisfies ${\Gamma }_{it}\in [0,t]$ and ${\Gamma }_{i1}\le {\Gamma }_{i2}\le \cdots \le {\Gamma }_{i,NT}$. The corresponding budgeted uncertainty set is defined as

$${\mathcal{V}}_i=\{{\mathbf{v}}_i|-1\le v_{it}\le 1,\sum _{k=1}^t\left|v_{ik}\right|\le {\Gamma }_{it},\forall t\in \mathcal{T}\}.$$

(20)

This set allows the model to calibrate the degree of conservatism. A small ${\Gamma }_{it}$ leads to less protection but lower costs, while a large ${\Gamma }_{it}$ yields solutions that are more resilient but possibly over-conservatism. Two extreme cases help illustrate the role of the budget parameter. When ${\Gamma }_{it}=0$, all deviations vanish ($v_{i1}=\cdots =v_{i,NT}=0$), so the model reduces to the deterministic case. At the other extreme, if ${\Gamma }_{it}=t$, all deviations may simultaneously reach their worst-case values, in which case, ${\mathcal{V}}_i$ coincides with the box uncertainty set [32].

Note that the model is intended for short-term operational planning, where seasonal or long-term trend effects are assumed to have been captured in the nominal demand forecasts. The uncertainty set is designed to reflect short-term deviations from these forecasts, with each demand parameter allowed to vary within a bounded range. A budget constraint is applied to prevent extreme scenarios in which all demands simultaneously deviate in the worst possible direction.

3.3. Robust Optimization Model

In the RO model, the demand balance constraints (13) cannot be satisfied for all possible realizations of $d_{it}$ as they are equality constraints. Therefore, these constraints should be reformulated as inequalities. To do this, we use a closed form expression of the net inventory level $I_{it}-B_{it}$:

$$I_{it}-B_{it}=I_{i0}-B_{i0}+\sum _{k=1}^t\left(\sum _{j\in \mathcal{J}}{a}_{ij}{x}_{ijk}-d_{ik}\right)\forall i\in \mathcal{I},t\in \mathcal{T}.$$

(21)

which represents the net inventory of item i at period t as the sum of initial inventory level $I_{i0}-B_{i0}$ and the cumulative production amount of item i up to period t.

Following the approach proposed by [33], we define auxiliary variables $q_{it}$ representing the maximum value of the inventory holding or backlog penalty cost for item i in period t. Incorporating $d_{ik}={\overline{d}}_{ik}+v_{ik}{\widehat{d}}_{ik}$, the demand constraints (13) are replaced with two sets of inequalities:

$$\begin{array}{}\hfill \mathrm{(22)}& q_{it}\ge h_{it}\left(I_{i0}-B_{i0}+{\displaystyle \sum _{k=1}^t}({\displaystyle \sum _{j\in \mathcal{J}}}{a}_{ij}{x}_{ijk}-({\overline{d}}_{ik}+v_{ik}{\widehat{d}}_{ik}))\right)\hfill & \hfill \forall i\in \mathcal{I},t\in \mathcal{T},{\mathbf{v}}_i\in {\mathcal{V}}_i,\hfill \mathrm{(23)}& q_{it}\ge -k_{it}\left(I_{i0}-B_{i0}+{\displaystyle \sum _{k=1}^t}({\displaystyle \sum _{j\in \mathcal{J}}}{a}_{ij}{x}_{ijk}-({\overline{d}}_{ik}+v_{ik}{\widehat{d}}_{ik}))\right)\hfill & \hfill \forall i\in \mathcal{I},t\in \mathcal{T},{\mathbf{v}}_i\in {\mathcal{V}}_i.\end{array}$$

In addition, the variable $q_{it}$ replaces the terms for inventory holding and backlog penalty costs. Therefore, the RO model can be formulated by replacing constraints (13) with constraints (22) and (23) as follows:

$$\begin{array}{cc}\hfill \left(RO\right):=\{min& \sum _{j\in \mathcal{J}}\sum _{t\in \mathcal{T}}{c}_t{y}_{jt}+\sum _{i\in \mathcal{I}}\sum _{t\in \mathcal{T}}{q}_{it}+l(L^{max}-L^{min}):\mathrm{s}.\mathrm{t}.\left(14\right)\text{–}\left(19\right),\left(22\right),\left(23\right)\}.\hfill \end{array}$$

(24)

3.4. Tractable Reformulation of Robust Counterparts

In the $\left(RO\right)$ model, each demand parameter is allowed to vary within the uncertainty set ${\mathcal{V}}_i$, which would generate infinitely many constraints (22) and (23) if considered explicitly. To obtain a tractable model, we reformulate these constraints using the linear programming duality theorem, a standard approach in robust optimization [23,33].

The feasibility of constraint (22) for all ${\mathbf{v}}_i\in {\mathcal{V}}_i$ can be guaranteed by replacing the uncertain right-hand side with its worst-case value, which corresponds to minimizing ${\sum }_{k=1}^t{v}_{ik}{\widehat{d}}_{ik}$ over ${\mathcal{V}}_i$. For constraint (23), feasibility requires considering the maximum of the same term. Due to the symmetry of the uncertainty set ${\mathcal{V}}_i$, both conditions can be unified as solving a maximization problem of ${\sum }_{k=1}^t{\widehat{d}}_{ik}{v}_{ik}$ over ${\mathcal{V}}_i$.

Since all deviations ${\widehat{d}}_{ik}$ are nonnegative, it suffices to restrict $v_{ik}$ to nonnegative values. Accordingly, the constraints $-1\le v_{ik}\le 1$ and ${\sum }_{k=1}^t\left|v_{ik}\right|\le {\Gamma }_{it}$ can be replaced by $0\le v_{ik}\le 1$ and ${\sum }_{k=1}^t{v}_{ik}\le {\Gamma }_{it}$. The resulting inner maximization problem, denoted as $P(i,t)$ for $i\in \mathcal{I}$ and $t\in \mathcal{T}$, can thus be expressed as follows:

$$\begin{array}{}\hfill \mathrm{(25)}& \hfill P(i,t)=\max & {\displaystyle \sum _{k=1}^t}{\widehat{d}}_{ik}{v}_{ik}\hfill & \hfill \mathrm{(26)}& \hfill \mathrm{s}.\mathrm{t}.& {\displaystyle \sum _{k=1}^t}{v}_{ik}\le {\Gamma }_{it},\hfill & \hfill \mathrm{(27)}& & 0\le v_{ik}\le 1,\hfill & \hfill \forall k=1,\dots ,t.\end{array}$$

By applying the LP duality theorem, the inner maximization problem $P(i,t)$ over the uncertainty set is replaced by its dual $D(i,t)$, resulting in a finite set of linear constraints that capture all possible realizations of the uncertain demand. This guarantees that the reformulated model remains equivalent to the original robust counterpart while being computationally tractable. Let ${\lambda }_{it}$ and ${\mu }_{itk}$ be the dual variables associated with constraints (26) and (27), respectively. Then, the resulting dual formulation $D(i,t)$ is expressed as follows:

$$\begin{array}{}\hfill \mathrm{(28)}& \hfill D(i,t)=min& {\lambda }_{it}{\Gamma }_{it}+{\displaystyle \sum _{k=1}^t}{\mu }_{itk}\hfill & \hfill \mathrm{(29)}& \hfill \mathrm{s}.\mathrm{t}.& {\lambda }_{it}+{\mu }_{itk}\ge {\widehat{d}}_{ik},\hfill & \hfill \forall k=1,\dots ,t,\hfill \mathrm{(30)}& & {\lambda }_{it}\ge 0,\hfill & \hfill \mathrm{(31)}& & {\mu }_{itk}\ge 0,\hfill & \hfill \forall k=1,\dots ,t.\end{array}$$

Because $P(i,t)$ is a feasible and bounded linear program, the strong duality ensures that the optimal objective values of $P(i,t)$ and $D(i,t)$ coincide. This equivalence allows the uncertain terms in constraints (22) and (23) to be replaced by their dual representation $D(i,t)$. Incorporating these dual forms into the $\left(RO\right)$ model leads to the MIP reformulation (32)–(42).

$$\begin{array}{}\hfill \mathrm{(32)}& \hfill \min & {\displaystyle \sum _{j\in \mathcal{J}}}{\displaystyle \sum _{t\in \mathcal{T}}}{c}_t{y}_{jt}+{\displaystyle \sum _{i\in \mathcal{I}}}{\displaystyle \sum _{t\in \mathcal{T}}}{q}_{it}+l(L^{max}-L^{min})\hfill & \hfill \mathrm{(33)}& \hfill \mathrm{s}.\mathrm{t}.& q_{it}\ge h_{it}\left((I_{i0}-B_{i0})+{\displaystyle \sum _{k=1}^t}({\displaystyle \sum _{j\in \mathcal{J}}}{a}_{ij}{x}_{ijk}-{\overline{d}}_{ik}+{\mu }_{itk})+{\lambda }_{it}{\Gamma }_{it}\right)\hfill & \hfill \forall i\in \mathcal{I},t\in \mathcal{T},\hfill \mathrm{(34)}& & q_{it}\ge -k_{it}\left(I_{i0}-B_{i0}+{\displaystyle \sum _{k=1}^t}({\displaystyle \sum _{j\in \mathcal{J}}}{a}_{ij}{x}_{ijk}-{\overline{d}}_{ik}-{\mu }_{itk})-{\lambda }_{it}{\Gamma }_{it}\right)\hfill & \hfill \forall i\in \mathcal{I},t\in \mathcal{T},\hfill \mathrm{(35)}& & l_i{x}_{ijt}\le y_{jt},\hfill & \hfill \forall i\in \mathcal{I},j\in \mathcal{J},t\in \mathcal{T},\hfill \mathrm{(36)}& & {\displaystyle \sum _{j\in \mathcal{J}}}{y}_{jt}\le L^{max},\hfill & \hfill \forall t\in \mathcal{T},\hfill \mathrm{(37)}& & {\displaystyle \sum _{j\in \mathcal{J}}}{y}_{jt}\ge L^{min},\hfill & \hfill \forall t\in \mathcal{T},\hfill \mathrm{(38)}& & {\lambda }_{it}+{\mu }_{itk}\ge {\widehat{d}}_{ik},\hfill & \hfill \forall i\in \mathcal{I},t\in \mathcal{T},k=1,\dots ,t,\hfill \mathrm{(39)}& & x_{ijt}\in {\mathbb{Z}}_{+},\hfill & \hfill \forall i\in \mathcal{I},j\in \mathcal{J},t\in \mathcal{T},\hfill \mathrm{(40)}& & y_{jt}\ge 0,\hfill & \hfill \forall j\in \mathcal{J},t\in \mathcal{T},\hfill \mathrm{(41)}& & L^{min},L^{max}\ge 0,\hfill & \hfill \mathrm{(42)}& & {\lambda }_{it},{\mu }_{itk}\ge 0,\hfill & \hfill \forall i\in \mathcal{I},t\in \mathcal{T},k=1,\dots ,t.\end{array}$$

Although the reformulated problem (32)–(42) introduces $\mathcal{O}(NI·N{T}^2)$ additional variables and constraints compared with the deterministic case, it remains a mixed-integer linear program, so the theoretical complexity does not increase. Thus, the problem can still be solved efficiently using standard commercial optimization software such as Gurobi or CPLEX.

In summary, the overall modeling process can be viewed as a sequence of steps that link industrial inputs to optimization outputs. The demand forecasts, roll dimensions, and machine parameters first serve as inputs to the heuristic procedures that generate feasible cutting patterns. These patterns can then be used to construct the deterministic MIP formulation, which establishes the baseline solution framework. Alternatively, the MIP can also be built using the complete set of maximal patterns, although this substantially increases the problem size. Finally, the model is extended with a robust optimization counterpart to incorporate demand uncertainty. The outputs of this process are cutting patterns and performance measures, including material utilization, costs, and variability.

4. Computational Experiments

In this section, we report the results of the computational experiments. We begin by describing the experimental instances and parameter settings in Section 4.1. We then examine the single-period cases in Section 4.2 to highlight the benefits of the multi-cutter configuration compared with the conventional single-cutter and to assess the relative performance of the heuristics and MIP formulations. Next, we turn to the multi-period cases in Section 4.3, where demand uncertainty is incorporated. Here, the proposed budgeted RO model is evaluated against both the deterministic model and the box-type RO model. In Section 4.4, we conduct out-of-sample validation to investigate how performance changes with increasing variability. Finally, we analyze the sensitivity of the budget parameter, which governs the level of protection in the budgeted RO model in Section 4.5.

4.1. Experiment Settings

We conducted the computational experiments using real-world data obtained from a company in the paper industry. Based on the collected data, we examined the impact of introducing the multi-cutter machine. We set the strip width $W=2800$ (mm), and the machine is configured with $NS=7$ slitters and $NC=3$ cutters, in accordance with the actual operating environment. To test instances of varying numbers of items, we constructed an instance set with the number of items ranging from 11 to 60. The instances were divided into five classes according to the number of items $NI$, with each class containing 10 instances. Specifically, Class 1 includes instances with 11–20 items, Class 2 includes instances with 21–30 items, Class 3 has instances with 31–40 items, Class 4 has instances with 41–50 items, and Class 5 has instances with 51–60 items.

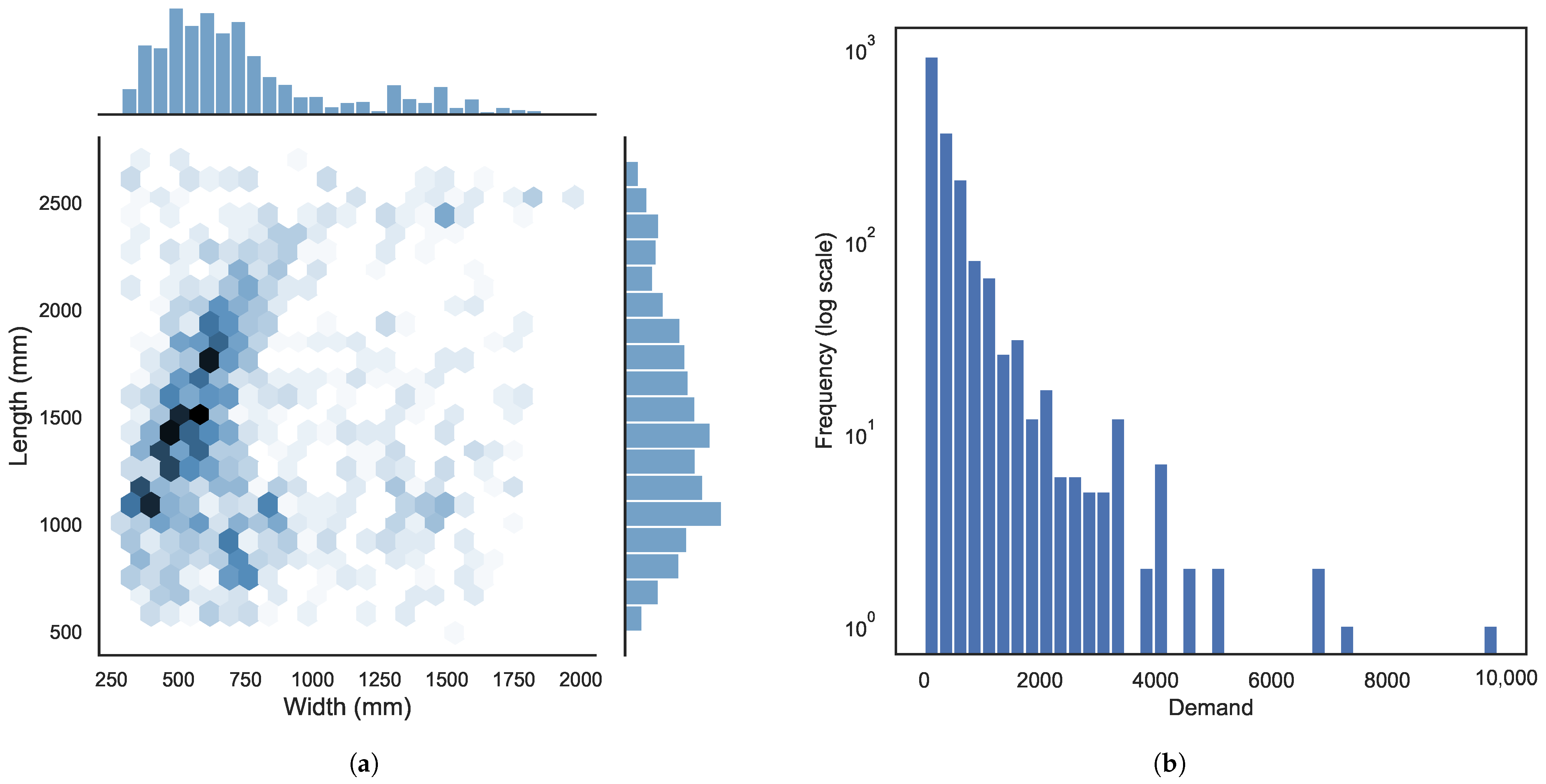
The distributions of item width, length, and demand are independent from the classes, and their distributions are illustrated in Figure 4. Figure 4a presents the joint distribution of item width and length through a two-dimensional density plot. Each cell in the plot corresponds to a range of width and length values, and darker cells indicate areas with higher density. Histograms displayed along the axes show the marginal distributions of width and length, respectively. Figure 4b presents the histogram of item demand on a logarithmic scale. As shown in the figure, while most items exhibit moderate demand, a small number of items show exceptionally high values. The item data used in our experiments has the following characteristics: an average width of 754 mm (standard deviation: 350), an average length of 1474 mm (standard deviation: 512), and an average demand of 455 units (standard deviation: 711). Although the data is drawn from the paper industry, similar slitting and cutting operations are also found in sectors such as film and metal processing, supporting the broader applicability of our model.

For the multi-period case, we considered a one-week planning horizon consisting of seven periods, that is, $NT=7$. Similar to the single-period setting, instances with 10 to 60 items were generated and tested. For these instances, the cost parameters were determined in line with industrial practice. To avoid company-specific disclosure issues, all costs were expressed in unit terms rather than actual monetary values. The unit inventory holding cost was normalized to 1, while the backlog cost was set at five times this value to reflect the higher penalty associated with unmet demand. The variable cost of paper consumption was set to 0.1 per unit length. A balance of cost parameter penalizing deviations in the total paper usage across different days was set as 1000. These settings were designed to capture the underlying trade-off structure of different cost components.

All optimization models and algorithms were implemented in Python 3.10 and solved with Gurobi 10.0.1, using a time limit of 600 s and an optimality tolerance of 0.1% (measured by the relative gap between lower and upper bounds). The experiments were carried out on a macOS 15.1 machine with an Apple M1 Max chip (Apple Inc., Cupertino, CA, USA) and 64 GB of RAM.

4.2. Experiment Results on Single-Period Instances

In this section, we present the results on the single-period instances. The purpose of this experiment is twofold. First, we evaluate the effectiveness of introducing a multi-cutter machine by comparing its performance with that of the conventional single-cutter machine. Second, we assess the performance of the proposed MIP formulation in comparison with various heuristic approaches. We refer to the ordering heuristics based on area, demand, length, and width as A-Order, D-Order, L-Order, and W-Order, respectively, while the knapsack heuristic is denoted as KP-Heur. For the MIP formulations, we consider two variants: MIP-FP, which fully incorporates all maximal patterns, and MIP-HP, which incorporates only the patterns generated by the five heuristics introduced above.

For each instance, the solution obtained with the single-cutter setting was normalized to 100, and the relative solution value of the other algorithms was computed and averaged over all instances in each class. The results are reported in

Table 1. Comparison of algorithm performance for single-period instances.

Instance		Single-Cutter	Multi-Cutter Algorithms
			A-Order	D-Order	L-Order	W-Order	KP-Heur	MIP-HP	MIP-FP
Class 1		100	92.01	93.26	93.60	91.07	91.34	88.40	87.93
Class 2		100	89.36	89.68	90.43	87.88	86.88	84.86	84.43
Class 3		100	83.68	85.85	84.60	81.86	83.78	79.54	78.94
Class 4		100	86.86	88.40	87.05	85.20	84.13	82.30	81.97
Class 5		100	88.52	89.23	89.15	87.31	86.00	83.98	83.63
Statistics	Average	100	88.09	89.28	88.97	86.67	86.43	83.82	83.38
	Min	100	75.11	76.25	70.09	67.60	74.27	67.53	67.51
	Q1	100	85.09	85.40	86.05	83.83	83.87	80.69	80.31
	Median	100	88.26	89.82	89.91	87.33	85.77	84.10	83.98
	Q3	100	92.66	93.38	92.90	91.51	89.92	88.74	88.11
	Max	100	97.36	99.65	98.05	97.01	95.08	94.85	94.04

, which reports the average relative solution values together with additional statistics such as minimum, maximum, median, Q1, and Q3 values. As shown, the use of multi-cutter machines yields a substantial gain compared to the single-cutter setting. In particular, the exact MIP-FP approach for the multi-cutter setting was able to satisfy the same demand while consuming only about 83% of the paper required by the single-cutter. This level of improvement is particularly significant in a large-scale industrial environment, where a 17% reduction in paper usage directly translates into substantial cost savings.

The heuristic methods developed for the multi-cutter setting also consistently outperformed the single-cutter. Among the four ordering heuristics, the width-based ordering W-Order exhibited the best performance, which uses about 86.7% of the paper on average. This can be explained by the fact that ordering items by width tends to generate patterns that more tightly utilize the roll width, thereby reducing trim loss compared to other ordering rules. The knapsack heuristic achieved slightly better results than the ordering heuristics. These trends were observed consistently across all instance classes, providing strong evidence of the effectiveness of introducing multi-cutter machines.

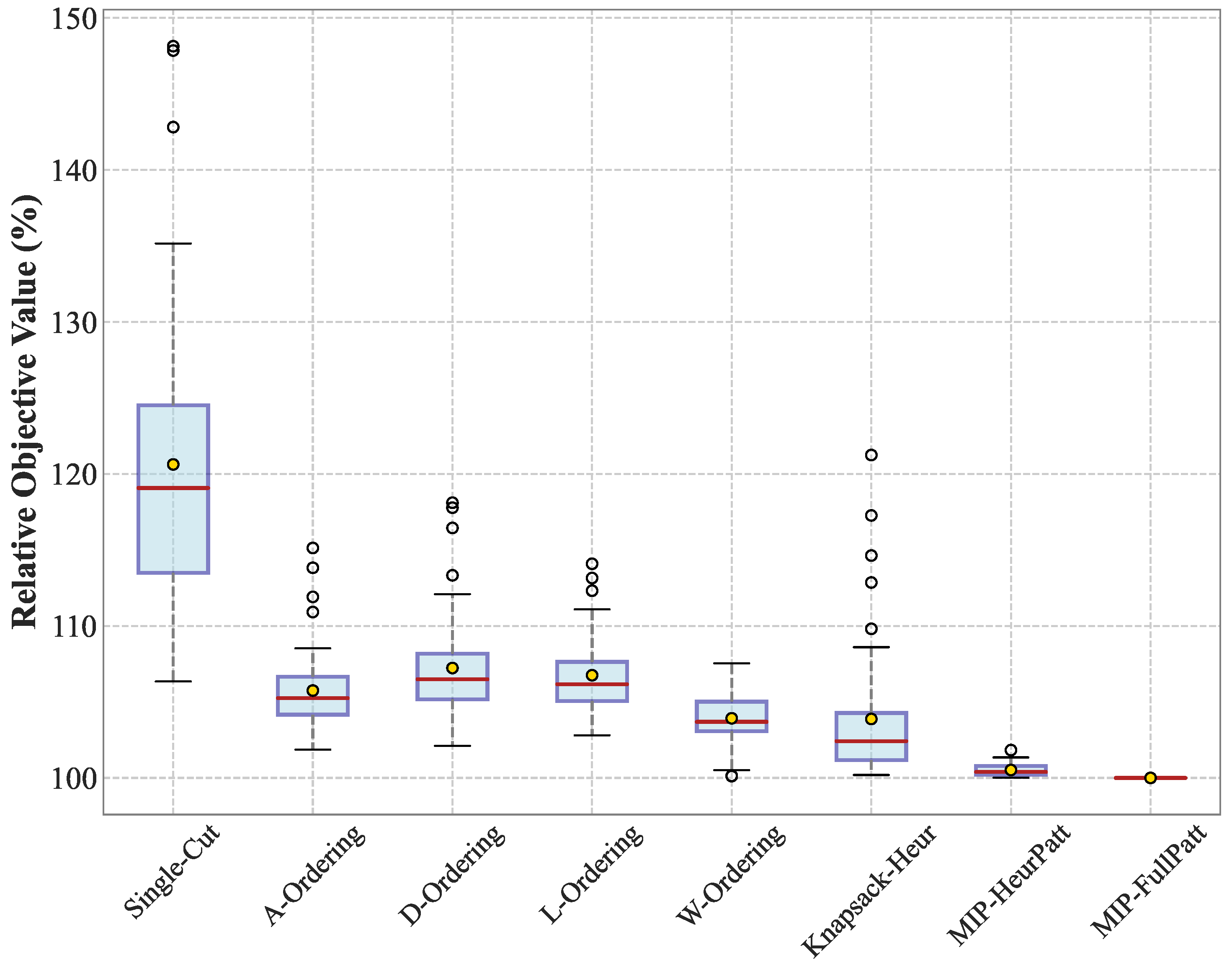
To further examine the consistency of the results, we evaluated the relative solution quality of 50 instances using box plots, as shown in Figure 5. In this analysis, the performance of each algorithm is expressed relative to the MIP-FP, whose objective value is normalized to 100. The results show that the single-cutter not only yields substantially larger solution values on average, but also exhibits much greater variability. In the most extreme cases, the solution quality approaches about 150% of the MIP-FP. Among the ordering heuristics and the knapsack heuristic, the W-Order demonstrated the smallest deviation, whereas the KP-Heur, despite having a slightly low average, occasionally produced solutions exceeding 120%, indicating higher variability.

While the average performance of heuristic methods was relatively good, Figure 5 shows that some heuristic runs resulted in substantially inferior solutions. In contrast, the MIP model provided more stable and consistently high-quality solutions. Furthermore, the MIP formulation plays a critical role not only in the single-period setting but also as the foundation for the robust optimization model in the multi-period case, where inventory decisions, backlog, and demand uncertainty must be jointly addressed. These elements are difficult to handle using heuristics alone, which makes the MIP-based approach essential for extending the model to more realistic and dynamic planning environments.

It is noteworthy that the MIP-HP, which uses only the patterns generated by the heuristics, achieved results that were almost indistinguishable from the full-pattern MIP-FP, with small deviations. To provide a more detailed comparison between the two models,

Table 2. Comparison of MIP models for single-period instances.

Instance		Rel. Obj. Val. (%)		# Patterns		Time (s)		Gap (%)		# Opt.
		MIP-HP	MIP-FP	MIP-HP	MIP-FP	MIP-HP	MIP-FP	MIP-HP	MIP-FP	MIP-HP	MIP-FP
Class 1		100.52	100	42.4	1663.8	0.3	87.2	0.00	0.02	10	9
Class 2		100.51	100	75.6	7886.6	125.6	375.9	0.02	0.10	8	4
Class 3		100.74	100	119.2	10,258.1	186.4	404.2	0.05	0.11	7	4
Class 4		100.40	100	159.1	40,345.6	241.0	443.6	0.07	0.14	6	3
Class 5		100.43	100	190.5	73,166.0	344.0	600.0	0.07	0.19	5	0
Statistics	Average	100.52	100	117.4	26,664.0	179.4	382.2	0.04	0.11	-	-
	Min	100.01	100	25.0	660.0	0.0	0.1	0.00	0.00	-	-
	Q1	100.22	100	65.8	3055.8	0.1	22.6	0.00	0.00	-	-
	Median	100.39	100	111.5	10,283.5	2.8	600.0	0.00	0.13	-	-
	Q3	100.79	100	169.8	43,967.3	600.0	600.0	0.10	0.17	-	-
	Max	101.83	100	236.0	147,621.0	600.0	600.0	0.40	0.54	-	-

reports the objective values, the number of patterns used, computation times and optimality gaps, as well as the number of instances for which the optimal solution was found.

As shown in the table, using only heuristic-generated patterns resulted in an average performance gap of merely 0.5% compared to the case where all maximal patterns were generated. In contrast, the number of patterns employed differed drastically. On average, MIP-HP used about 120 patterns, whereas the MIP-FP used more than 26,000 patterns, which corresponds to nearly a 200-fold increase. The difference became more pronounced in larger instances, with the full-pattern model in Class 5 using almost 380 times as many patterns. These results clearly demonstrate the effectiveness of heuristic-generated patterns, showing that generating all maximal patterns is unnecessary.

Since the MIP model grows larger as more patterns are used, computation times and optimality gaps tend to increase. This is also reflected in the smaller number of instances where MIP-FP was able to find an optimal solution. For instance, in Class 5, none of the instances solved by MIP-FP reached proven optimality within the time limit, although the final gaps were relatively small (0.19% on average). In contrast, MIP-HP generally achieved smaller gaps and more frequent convergence to optimality, demonstrating better computational efficiency overall. These findings indicate that heuristic-generated patterns provide a viable alternative to the full-pattern approach. Accordingly, we employ heuristic-generated patterns rather than full pattern enumeration in the subsequent multi-period experiments. One thing to note is that, while the observed performance of MIP-HP was consistently strong across all instances, obtaining near-optimal solutions may be more difficult in other problem settings, particularly those involving more complex or tightly constrained items.

4.3. Experiment Results on Multi-Period Instances

We examine the multi-period instances, where demand uncertainty is explicitly considered. The focus is on evaluating the proposed RO model with a budgeted uncertainty set, denoted as $R{O}_{budget}$. The uncertainty budget is defined as ${\Gamma }_{it}=\gamma \times t$, with $\gamma =0.5$ used as the baseline setting. The sensitivity to alternative values of $\gamma$ is analyzed later in Section 4.5. For benchmarking, results are compared against both the deterministic model ($Det$) and the box-type RO model ($R{O}_{box}$). The $R{O}_{box}$ model corresponds to the case ${\Gamma }_{it}=t$ for all i and t.

The evaluation follows a simulation-based procedure. For each instance, solutions obtained from $Det$, $R{O}_{box}$, and $R{O}_{budget}$ were tested under 500 demand scenarios. These scenarios were generated by sampling demands uniformly from their respective intervals $[{\overline{d}}_{it}-{\widehat{d}}_{it},{\overline{d}}_{it}+{\widehat{d}}_{it}]$, where the deviation parameter was set as ${\widehat{d}}_{it}=CV·{\overline{d}}_{it}$ with $CV=0.3$. The uniform distribution reflects the RO framework, in which all realizations within the uncertainty set are equally possible. For each solution, realized costs were computed across scenarios and averaged to assess performance. Additional out-of-sample test results based on normally distributed scenarios are reported in Section 4.4.

Table 3. Comparison of performance of optimization models.

Instance	Objective Value ($\mathbf{\times }{10}^3$)			Realized Cost ($\mathbf{\times }{10}^3$)			Gap (%)			Time (s)
	$\mathit{Det}$	${\mathit{RO}}_{\mathit{box}}$	${\mathit{RO}}_{\mathit{budget}}$	$\mathit{Det}$	${\mathit{RO}}_{\mathit{box}}$	${\mathit{RO}}_{\mathit{budget}}$	$\mathit{Det}$	${\mathit{RO}}_{\mathit{box}}$	${\mathit{RO}}_{\mathit{budget}}$	$\mathit{Det}$	${\mathit{RO}}_{\mathit{box}}$	${\mathit{RO}}_{\mathit{budget}}$
Class 1	25.78	159.53	104.42	77.94	83.61	65.60	0.03	0.00	0.00	122.5	0.5	0.6
Class 2	30.94	196.98	128.89	96.83	102.37	80.35	0.12	0.00	0.00	423.0	1.4	4.7
Class 3	35.87	205.66	136.15	103.36	109.03	86.42	0.16	0.00	0.01	540.8	3.7	74.4
Class 4	60.80	400.36	261.11	196.38	206.19	161.48	0.14	0.00	0.01	503.8	4.9	64.6
Class 5	62.66	428.67	278.58	209.70	218.80	170.64	0.15	0.00	0.00	561.9	8.1	21.4
Average	43.21	278.24	181.83	136.84	144.00	112.90	0.12	0.00	0.00	430.4	3.7	33.1

reports the objective values, realized costs from the simulation, optimality gaps, and computation times. As expected, the objective values follow the order of $Det<R{O}_{budget}<R{O}_{box}$. This is natural because the deterministic model ignores demand uncertainty and optimizes only for the nominal values, whereas the RO models adopt more conservative solutions to protect against uncertainty. In particular, $R{O}_{box}$ considers the largest uncertainty set, which leads to even more conservative results than $R{O}_{budget}$.

The simulation results, however, yield a different result. As indicated in the ‘Realized Cost’ column, $R{O}_{budget}$ consistently achieves the lowest costs. In contrast, the $Det$ model suffers from substantially higher realized costs than its nominal objectives, reflecting its inability to hedge against demand variability. Conversely, the realized costs of $R{O}_{box}$ are significantly lower than its nominal objectives, since minimizing worst-case costs inherently leads to conservative solutions that perform better under most realizations. These results highlight that the $R{O}_{budget}$ model provides a favorable balance between robustness and cost efficiency.

This pattern is also clearly illustrated in Figure 6. As shown in Figure 6a, the deterministic model consistently achieves the lowest objective values across all instance classes. However, Figure 6b reveals that its realized costs are substantially higher than those nominal values. In contrast, the $R{O}_{box}$ model shows the opposite behavior. In these charts, the error bars indicate the deviations across instances within groups, highlighting the variability of objective values and realized costs, respectively. Overall, these results highlight the superior performance of $R{O}_{budget}$, which achieves the lowest realized costs.

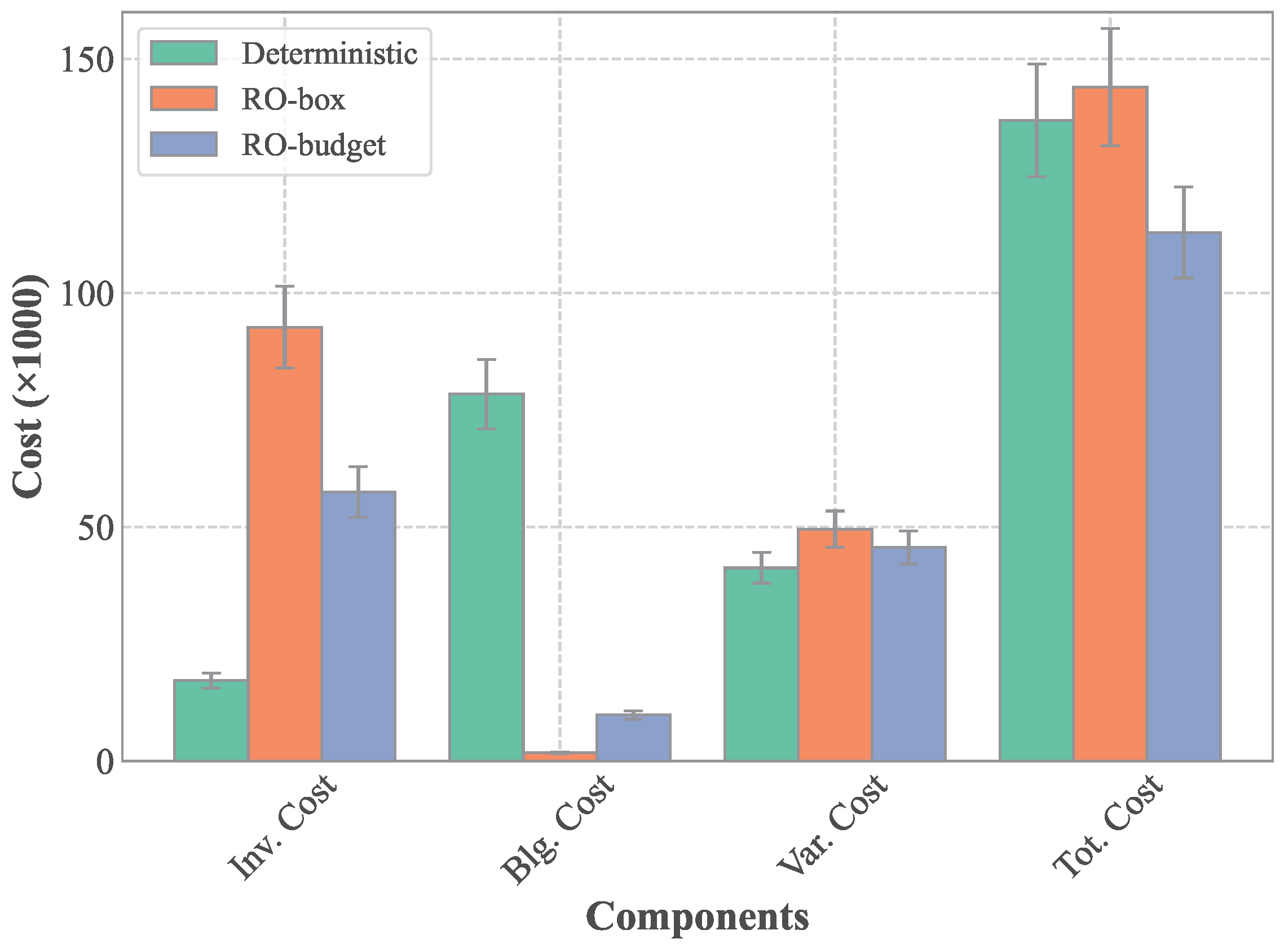
To further investigate, the average total costs are decomposed into inventory, backlog, and variable cost components, as shown in Figure 7. The results reveal clear differences across models. For inventory costs, the deterministic model incurred relatively low values, whereas the RO models, which anticipate higher demand realizations, resulted in higher inventory levels, with $R{O}_{box}$ being the most conservative. This, in turn, led to almost no backlog costs for $R{O}_{box}$, while the deterministic model exhibited substantially higher backlog costs. Regarding variable costs, which are proportional to the length of paper used, $R{O}_{box}$ consumed the most, followed by $R{O}_{budget}$ and then the deterministic model. Overall, $R{O}_{budget}$ provides the most balanced trade-off among overproduction, underproduction, and raw material usage, resulting in the lowest total costs.

Finally, Figure 8 examines not only average costs but also their variability for an instance with $NI=55$. While $Det$ and $R{O}_{box}$ models yield similar mean costs, the $Det$ model exhibits considerably larger deviations, making $R{O}_{box}$ a more reliable option from a planning perspective. In addition, the $R{O}_{budget}$ model outperforms both alternatives, achieving not only lower average costs but also reduced variability across scenarios.

4.4. Out-of-Sample Validation Results

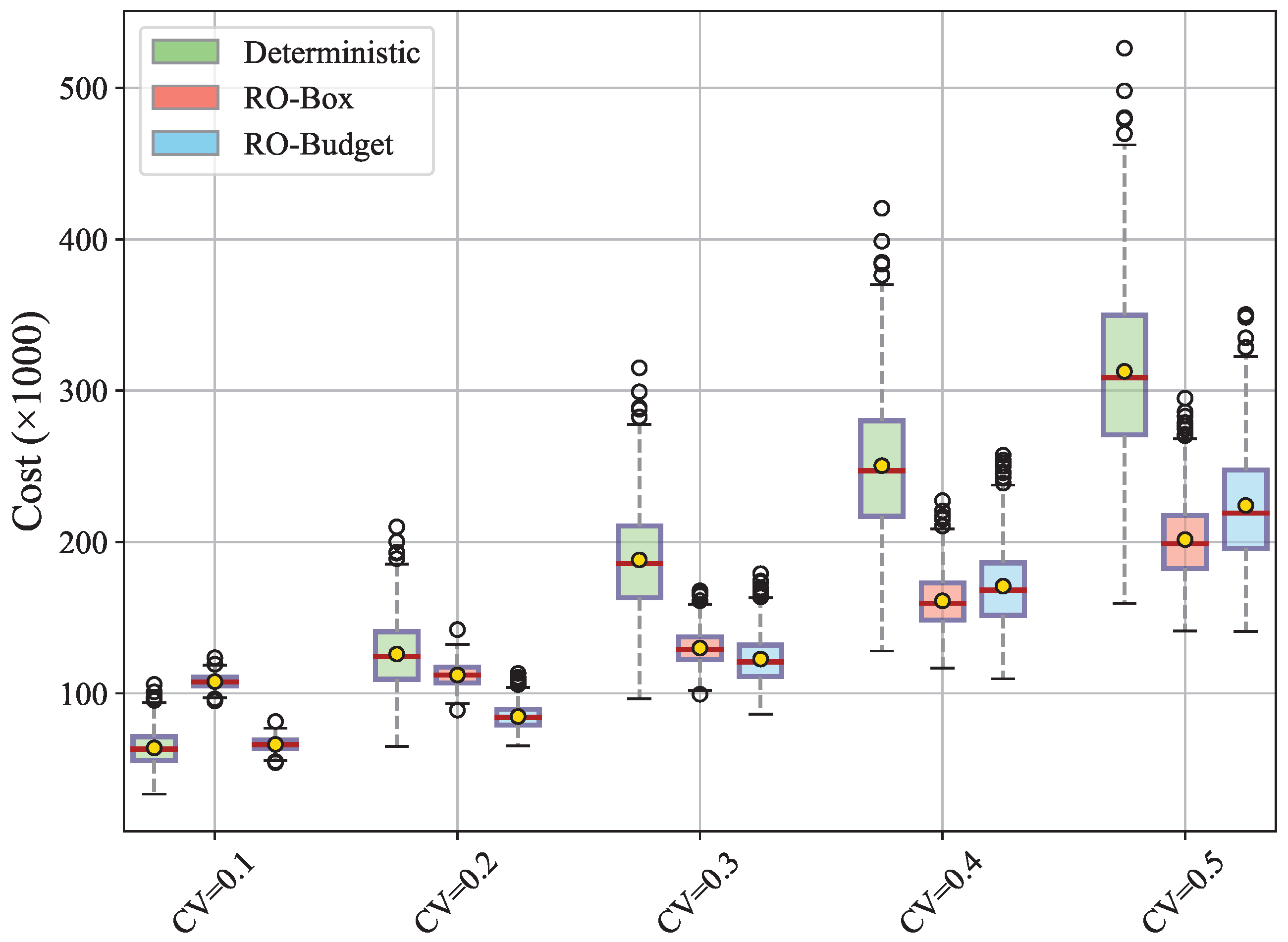
In this section, we present the out-of-sample validation results to assess the effectiveness of the models. In contrast to the previous analysis, where simulation scenarios were generated from within the originally assumed uncertainty sets, we now draw each $d_{it}$ from a normal distribution $N({\overline{d}}_{it},{\widehat{d}}_{it}^2)$, where ${\widehat{d}}_{it}$ is defined as $CV\times {\overline{d}}_{it}$. To test the impact of different levels of demand variability, the $CV$ values are varied between 0.1 and 0.5. Note that the uncertainty set used in the RO model corresponds to $CV=0.3$.

The results are presented in Figure 9. For each of the three models, the leftmost bar shows the nominal objective value, and the subsequent bars corresponds to out-of-sample costs with $CV$ ranging from 0.1 to 0.5. As in the earlier results, the $Det$ model yields the lowest objective value, whereas the $R{O}_{box}$ model yields the highest. However, when uncertainty is introduced, the realized costs of the $Det$ model increase sharply. Even in the case of $CV=0.1$, where variability is relatively small, its realized cost nearly doubles compared to its objective value. By contrast, the RO models explicitly account for uncertainty and therefore achieve lower realized costs. The increasing trend of realized costs with larger variability is evident across all models, illustrating the negative effect of demand fluctuations.

For the $R{O}_{box}$ model, the realized costs remain below the objective value even as variability grows. Although this demonstrates robustness, the considerable gap between the objective value and realized cost at $CV=0.3$ highlights its excessive conservatism, which may limit its practical applicability. The $R{O}_{budget}$ model, on the other hand, achieves a more favorable balance between robustness and cost efficiency, showing the best performance at $CV=0.3$. Nevertheless, when variability becomes much greater than the level assumed in the uncertainty set (e.g., $CV=0.5$), the realized cost of $R{O}_{budget}$ can exceed that of $R{O}_{box}$. This underscores the importance of constructing an uncertainty set that accurately captures the actual level of variability.

To examine not only average costs but also their variability, we analyzed the out-of-sample validation results for the instance with $NI=55$ across 500 scenarios, as illustrated in Figure 10. As the $CV$ increases, the overall variability of costs also tends to grow. The increase is particularly pronounced for the $Det$ model, whereas the RO models exhibit more moderate variability. The relative performance of the models also changes with the level of variability. When $CV=0.1$, the realized costs of the $Det$ model remain the lowest due to the limited fluctuations. For $CV=0.2$ and $0.3$, the $R{O}_{budget}$ model delivers the best results, while for larger variability levels, the $R{O}_{box}$ model becomes more favorable. This indicates that more conservative models perform better as variability grows, whereas under the originally assumed $CV=0.3$, the $R{O}_{budget}$ model remains the preferred option. This finding suggests that properly calibrating the uncertainty set to the actual variability level is essential for achieving reliable and cost-effective solutions in practice.

It should also be noted that the robustness of the model depends on how accurately the uncertainty set reflects actual demand variability. If the set fails to cover certain extreme realizations, performance may deteriorate under those conditions, while an overly conservative set may lead to unnecessarily high costs. This sensitivity becomes particularly relevant when variability is very large, in which case the advantage of the budgeted robust model may decrease. These observations highlight the importance of carefully calibrating the uncertainty set to available data and suggest that future research could benefit from data-driven calibration methods or the adoption of distributionally robust optimization approaches.

4.5. Impact of Budget Parameters

We next examine the sensitivity of $R{O}_{budget}$ to the budget parameter $\gamma$, which determines ${\Gamma }_{it}=\gamma ·t$ and thereby controls the degree of conservatism. Larger values of $\gamma$ expand the uncertainty set, forcing the model to guard against a wider range of demand realizations. The corresponding results are presented in Figure 11.

The outcomes reveal two distinct trends. First, the objective value consistently increases as $\gamma$ grows. This occurs because a larger uncertainty set requires the model to hedge against more scenarios, which results in a more conservative solution with a higher cost. Second, the realized costs do not follow the same pattern. The lowest realized cost is observed at $\gamma =0.3$. This suggests that the effectiveness of the model depends on calibrating $\gamma$ to the actual level of demand variability. If $\gamma$ is set too high, the model becomes excessively conservative and generates unnecessarily high costs. If it is set too low, the model underestimates uncertainty and produces solutions that are not sufficiently robust. Overall, these findings highlight the importance of carefully tuning the budget parameter in order to balance robustness and cost efficiency in the $R{O}_{budget}$ model.

In practice, the budget parameter $\gamma$ can be set based on historical demand variability. Given demand records over a certain period, statistical measures such as variance or the coefficient of variation can be computed to quantify the level of uncertainty. When demand variability is high, a larger value of $\gamma$ should be used to enhance robustness, whereas lower variability justifies a smaller value of $\gamma$. This provides a data-driven guideline for selecting $\gamma$ in industrial applications.

5. Conclusions

In this paper, we addressed a multi-period strip cutting problem for multi-cutter slitting machines in the paper industry. The problem aims to reduce trim loss, improve raw material utilization, and manage demand uncertainty. To tackle this problem, we proposed a pattern-based MIP formulation that explicitly captures the multi-cutter configuration and compared its performance with the conventional single-cutter setting as well as several heuristic strategies. Further, to account for demand uncertainty, we extended the model to a robust optimization framework with budgeted uncertainty sets, allowing for a balanced trade-off between cost efficiency and robustness against demand uncertainty.

Computational experiments using real-world data demonstrated that adopting a multi-cutter machine can significantly reduce paper usage compared to the single-cutter setting. The experiments also showed that heuristic-generated patterns, when integrated into the MIP model, achieved solutions that were close to optimal while requiring substantially fewer pattern variables than full-pattern enumeration. Under demand uncertainty, the budgeted RO model consistently outperformed both the deterministic model and the box-type RO model in terms of realized costs and exhibited smaller variability across scenarios. Sensitivity analyses highlighted the importance of properly setting the budget parameter to reflect actual variability. Although the numerical differences between the budgeted and box-type robust models are sometimes moderate, they remain meaningful in practice. In large-scale paper production, even small percentage improvements can translate into substantial cost savings and waste reduction, while the budgeted model also provides a more balanced trade-off between robustness and efficiency.

For practical implementation, the proposed model can be applied using daily or weekly planning data, including item specifications, demand forecasts, and current inventory levels. The optimization models and heuristics were implemented in Python and solved using commercial solvers such as Gurobi. Given the moderate computational times reported in Section 4, the model is suitable for integration into daily re-optimization routines, particularly in environments where demand or production constraints evolve frequently. This practical applicability makes the approach relevant for large-scale production systems seeking to reduce trim loss and improve scheduling efficiency.

This work can be extended in several directions. One promising direction is to adopt a distributionally robust optimization (DRO) approach. While the budgeted RO model protects against all scenarios within a predefined uncertainty set, DRO seeks solutions that perform well against the worst-case probability distribution within an ambiguity set estimated from data. This allows the model to capture both variability and statistical estimation errors, producing solutions that are less conservative than RO while still maintaining protection against poor performance under rare but plausible demand realizations. By tailoring the ambiguity set to historical demand data, the resulting plans could achieve better average performance without sacrificing robustness.

Another promising extension is to develop adaptive or multi-stage RO models, where production plans are revised dynamically as updated demand information becomes available during the planning horizon. Unlike the static RO approach adopted in this study, which fixes a cutting plan for the entire horizon, an adaptive framework can adjust decisions in later periods based on actual demand realizations in earlier periods. This flexibility can reduce unnecessary conservatism while better aligning production with changing demand patterns.

Finally, integrating the problem into broader supply chain planning frameworks would be valuable. In practice, cutting schedules often interact with upstream processes such as inventory replenishment and raw material procurement, as well as downstream activities including transportation and order fulfillment. Extending the model to incorporate these interactions would allow decision makers to coordinate resources across multiple stages of the supply chain. This integration could lead to better synchronization between processes, leading to improved overall efficiency and service levels.