Determining Levels of Affective States with Riemannian Geometry Applied to EEG Signals

Abstract

Emotion recognition from electroencephalography (EEG) often relies on Euclidean features that ignore the curved geometry of covariance matrices. We introduce a Riemannian-manifold pipeline which, combined with the Fisher Geodesic Minimum Distance to Mean (FgMDM) classifier, leverages the full geometry of symmetric positive-definite (SPD) EEG covariances. The approach applies an additional geodesic-mean contraction that stabilizes trial covariances before tangent space projection. Experiments on the five-class SEED-V dataset show high accuracy, robustness to session-to-session variability and improved interpretability relative to baselines. These results highlight Riemannian geometry as a powerful framework for emotion recognition with high-dimensional, non-stationary EEG.

1. Introduction

The human brain is one of the most intriguing and complex systems found in nature, responsible for coordinating and maintaining the entire organism. It is constantly active, and even the smallest injury or changes in its functioning can significantly impact health, perception or even personality and preferences.

At the turn of the 19th and 20th centuries, research into the functioning of the human brain began to accelerate, driven by technological advancements and developments in psychology and psychiatry. This period saw the first recording of brain activity signals, alongside numerous experiments and regular procedures, some of which are now considered dark chapters in scientific history, such as lobotomy. Modern research builds significantly on past achievements and refines procedures, sometimes enabling tests that were previously only theoretical, using contemporary apparatuses.

Among the various techniques, electroencephalography (EEG) analysis has gained popularity due to its non-invasive nature and the minimal discomfort it causes patients. Compared to other methods like magnetic resonance imaging (MRI), which many people find stressful due to the equipment used, EEG offers a more comfortable alternative. Given that the brain is the coordinating organ, it potentially holds a wealth of information about bodily functions—ranging from which hand a person moves to their mental state, or even attempting to reconstruct the image the patient is seeing.

The analysis of EEG signals for emotion recognition has become a prominent area of research, driven by its potential utility in brain–computer interfaces and clinical neurodiagnostic applications [1,2].

However, EEG signals are not easy to process due to their complex nature and the large volume of data that must be analyzed. Consequently, computer algorithms are commonly used to facilitate the analysis process, including methods for data cleaning, imputation and classification.

EEG signal classification is a particularly evolving field, as the approach varies significantly depending on the feature being analyzed. Different brain regions are actively involved in different tasks, such as speech processing and movement, necessitating distinct analytical approaches. Furthermore, some topics are more complex than others or are generally less understood in both medical and computer science communities. A particularly interesting and complex example is the classification of emotions, which has been gaining popularity.

In recent years, it has been shown that combining electroencephalography (EEG) with complementary signals, such as eye-movement data, improves both discrimination and temporal stability in emotion-classification tasks [3]. Notably, Yan et al. demonstrated that, with appropriate generative modeling, even unimodal eye-movement data can approximate the performance of full multimodal systems, reducing the dependency on EEG signals in practical applications [4].

Emotion classification is a multifaceted issue because no element of the process is trivial. It includes data collection, cleaning, analysis and finally, classification. Numerous methods have already been employed for this purpose, ranging from simple classifiers, such as kNN, to contemporary deep neural networks. In recent years, an innovative approach has been proposed that is appealing due to its novelty, simplicity and the fact that the data are in the form of signals. This approach involves the use of Riemannian geometry. Its strength lies in modeling covariance matrices—computed from EEG recordings—as points on a curved Riemannian manifold, thereby preserving their intrinsic structural properties.

Groundbreaking work by Barachant et al. [5] introduced the Minimum Distance to Mean (MDM) classifier, which demonstrated strong performance in brain–computer interface (BCI) applications. Likewise, Abdel-Ghaffar and Daoudi applied the Log-Euclidean Riemannian Metric (LERM) to the manifold of symmetric positive definite (SPD) matrices, achieving competitive results on the DEAP dataset in the domain of emotion classification [6].

Building on these foundations, this paper investigates the effectiveness of the Fisher Geodesic Minimum Distance to Mean (FgMDM) classifier for determining affective states based on EEG signals from the SEED-V dataset [6]. The original MDM framework was introduced by Barachant et al., who applied Riemannian geometry to covariance matrices for brain–computer interface classification, laying the groundwork for later classifiers such as FgMDM [7].

Despite the advancements in EEG signal-processing and -classification techniques, accurately classifying the levels of affective states remains a challenging task. Traditional methods often struggle with the high-dimensional and noisy nature of EEG data, leading to suboptimal performance. Additionally, the variability in emotional responses among different individuals further complicates the classification process. There is a need for robust methods that can effectively handle these complexities and improve the accuracy of affective state classification.

Riemannian geometry offers several advantages in the analysis of EEG data:

• Invariance to affine transformations, as the Riemannian metric ensures that the analysis is robust to scaling and rotations of the data [8].
• Operations are performed within the manifold, preserving the positive definiteness and other intrinsic properties of the symmetric positive definite (SPD) matrices [5].
• Studies have shown that classifiers operating in the Riemannian framework often outperform their Euclidean counterparts, particularly in high-dimensional and noisy environments [9].

The primary objective of this research is to explore the impact of Riemannian geometry on the quality of emotion classification based on EEG signals. Moreover, this study aims to evaluate the performance of the FgMDM classifier, including a comparison with tangent space classification to understand their contributions to classification accuracy and to determine its effectiveness in classifying levels of affective states. While neural networks and deep learning models have shown great promise in various domains, the decision to use FgMDM for this study is based on its interpretability and suitability for smaller datasets. As a result, the paper contributes to the field by providing insights into the application of Riemannian geometry for EEG-based emotion classification, which may lead to more accurate and reliable classification methods.

The paper makes four contributions to EEG-based emotion recognition: (1) we introduce a geodesic-mean contraction step that stabilizes within-session covariance estimates before tangent space projection; (2) we present a systematic, session-wise cross-validation on the SEED-V corpus, thereby measuring true day-to-day generalization; (3) we couple accuracy with a runtime analysis to demonstrate the pipeline’s real-time suitability; and (4) we investigate the link between automatic recognition scores and participants’ self-assessment ratings.

The SEED-V dataset is utilized, as it is commonly used in emotion-classification studies and provides a basis for evaluating the proposed methods.

The remainder of this paper is structured as follows. In Section 2, previous studies on affective state classification are reviewed, with a focus on the use of EEG signals and Riemannian geometry in these analyses. Section 3 details the data-collection process, preprocessing techniques, feature-extraction methods and the classification approaches used in this study. Section 4 presents the findings from the experiments, including classification performance metrics and comparisons with baseline methods, as well as provides an interpretation of the results and addresses the limitations and challenges encountered. Section 5 summarizes the key findings, discusses the implications for future research and suggests potential applications of the proposed methods.

2. Related Work

Emotion recognition through EEG signals has been a subject of increasing interest due to its potential applications in fields such as affective computing, human–computer interaction and mental health monitoring. Traditional approaches to emotion classification have employed various machine learning algorithms, including k-Nearest Neighbors, Support Vector Machines (SVM) and, more recently, deep learning models. Each of these methods has shown varying degrees of success, mainly depending on the complexity of the EEG data and the specificity of the emotional states being classified.

One of the foundational works in this area is by Atkinson and Campos [10], where the authors explored the use of SVM for classifying basic emotions (joy, sadness, anger and neutral) based on EEG signals. They utilized a feature-extraction method that involved frequency domain analysis, which proved effective in capturing the underlying patterns of brain activity associated with different emotions. This study laid the groundwork for future research by demonstrating that machine learning algorithms could indeed be applied to EEG data for emotion recognition.

Further advancements were made with the introduction of deep learning techniques. Li and Chen [11] developed a Convolutional Neural Network (CNN) to automatically extract features from raw EEG signals, bypassing the need for manual feature engineering. Their model achieved significant improvements in classification accuracy, particularly when dealing with complex emotional states. This shift towards deep learning emphasized the potential of leveraging large datasets and high-performance computing to improve emotion-classification systems. Building on this foundation, convolutional neural networks and attention mechanisms have further demonstrated their capacity to model spatial and temporal dynamics of EEG signals in a holistic manner, enabling more nuanced emotion recognition while reducing reliance on handcrafted features [12].

Despite these advancements, several challenges remain in the field of EEG-based emotion classification. One major issue is the high variability in EEG signals both within and between subjects. This variability can arise from numerous factors, including individual differences in brain anatomy, psychological state and even the placement of electrodes. Cui et al. [13] addressed this issue by introducing personalized models that are trained on individual-specific data, thereby improving the robustness of emotion-recognition systems.

Another significant challenge is the presence of noise and artefacts in EEG recordings, which can severely affect classification accuracy. Traditional signal-processing techniques such as independent component analysis (ICA) and common spatial pattern (CSP) are employed to filter out these unwanted components. He and Wu [14] demonstrated the effectiveness of these techniques in improving the quality of EEG signals prior to feeding them into classification algorithms. Beyond efforts to improve signal quality, EEG research also explores more complex behavioral aspects. For instance, Balconi et al.’s work suggests that individuals attempting to increase group cohesion among receivers exhibit specific EEG markers under conditions of group orientation and perception of social exchange, indicating increased attentional effort and involvement during the interaction [15].

Riemannian geometry is a branch of differential geometry that explores smooth manifolds, which are curved spaces with unique geometric properties. In such environments, fundamental concepts such as angles, geodesics, distances and centres of mass provide a geometric interpretation of mathematical operators, making them easier to understand and analyse [16]. This approach also offers significant benefits for EEG signal processing by addressing the core challenges associated with EEG data [17]. The application of Riemannian geometry to the classification and analysis of empirical data is a relatively recent development. However, it has quickly gained traction due to its effectiveness in addressing real-world challenges across a wide range of fields, including radar signal processing, image and video analysis, computer vision, shape modeling, medical imaging (notably diffusion MRI and brain–computer interfaces), sensor network analysis, elasticity, mechanical systems, optimization and machine learning [18].

Traditional Euclidean approaches often struggle with the high dimensionality, non-stationarity and noise inherent in EEG signals. EEG data can be highly variable both within and between subjects due to differences in brain anatomy, psychological states and external artifacts. Riemannian geometry provides a robust framework for analyzing the covariance matrices derived from EEG signals by treating these matrices as points on a Riemannian manifold. This geometric approach enables more accurate and meaningful comparisons of covariance matrices, as it takes into account the manifold’s curvature and structure, resulting in improved classification and feature extraction. By leveraging Riemannian metrics, it becomes possible to mitigate the effects of noise and non-stationarity, thus enhancing the stability and reliability of EEG-based emotion classification and other BCI applications. It ultimately results in more consistent performance across different recording sessions and subjects, addressing one of the primary limitations of conventional EEG signal-processing techniques.

In response to these challenges, particularly the high variability of EEG signals within and between subjects, advanced methods have emerged in the literature that attempt to solve this problem by moving beyond traditional signal-processing techniques. One example is a study in which the non-Gaussianity of EEG signals was examined and the T-distribution was used to make a more precise estimation of the covariance matrix. It resulted in the proposal of a novel transfer learning framework with a minimum distance to the Riemannian mean (TL-MDRM), which effectively addresses inter-session variability in EEG-based emotion-recognition systems. The results confirmed that using transfer learning significantly improves performance, even when assuming a Gaussian distribution. Further consideration of the T-distribution increases the effectiveness of classification even more [19].

One of the pioneering works in this area was conducted by Barachant et al. [5], who introduced the concept of using Riemannian geometry for Brain-Computer Interface (BCI) applications. They developed the Minimum Distance to Mean (MDM) classifier, which operates on the Riemannian manifold and showed superior performance compared to traditional Euclidean-based methods. This study demonstrated the potential of Riemannian geometry to enhance the robustness and accuracy of EEG-based classification systems.

Building on this foundation, Yger et al. [9] proposed the FgMDM (Fisher geodesic Minimum Distance to Mean) classifier, which combines geodesic filtering with the MDM classifier. This method leverages the discriminative power of Linear Discriminant Analysis (LDA) in the tangent space, followed by projection back to the manifold for classification. Their results indicated improved performance in classifying EEG signals, particularly in noisy and complex datasets.

Research by Al-Mashhadani et al. [20] confirms the effectiveness of the Riemannian geometry approach for classifying emotions using EEG signals. In their work, they evaluated Riemannian methods, including a variant of the Minimum Distance to Riemannian Mean (MDRM) classifier, on commonly used EEG datasets. Their results showed that methods using Riemannian geometry achieved comparable or higher emotion-classification accuracy compared to popular machine learning algorithms such as kNN and CNN. The authors emphasize that the use of Riemannian geometry allows direct operations on covariance matrices of EEG signals using the tools of differential geometry, which contributes to the improved analysis of EEG signals. Additionally, the use of Riemannian metrics accounts for the specific geometry of the space of covariance matrices, which is beneficial in analyzing complex EEG data.

Moreover, the integration of Riemannian geometry with deep learning techniques has also been explored. Zhang et al. proposed a hybrid model that combines CNNs with Riemannian geometry-based feature extraction. This model was tested on the SEED-V dataset and achieved state-of-the-art performance, highlighting the synergistic potential of combining deep learning with advanced geometric methods [21].

It is worth noting that approaches based on Riemann geometry have been successfully applied not only to the classification of emotional states but also to other tasks in the field of EEG-BCI. For example, Congedo et al. used a Riemannian analysis approach to detect evoked potentials (ERPs) in mobile conditions by combining Ear EEG and scalp EEG signals, followed by feature fusion from CNNs and autoencoders. Significantly, even in the case of poorer signal quality and patient movement (speed of 1.6 m/s), an increase in accuracy of about 5–10% was obtained, depending on the feature fusion variant used. It shows that the Riemannian approach can effectively account for noise in field conditions, while remaining compatible with other advanced learning models (e.g., CNN, XGBoost) [18].

In the trend of solutions using signal analysis in Riemann space, Gao et al. [22] proposed the Filter Bank Adversarial Domain Adaptation Riemann (FBADR) method, which combines bandpass signal filtering with domain adaptation in Riemann space in multimodal (audio, video, audio–video) emotion analysis. The Gabor Riemann EEGNet (GREEN) [23], on the other hand, integrates wavelet transform with Riemann methodology in an end-to-end neural network architecture to maintain high interpretability and performance with a relatively small number of parameters. Such solutions confirm the growing potential of combining domain knowledge (e.g., wavelets and Riemannian approaches) with advanced learning models, including domain adaptation techniques.

The application of Riemannian geometry to EEG signal processing represents a significant advancement in the field of emotion classification. While challenges remain, delving deeply into the underlying mechanisms and continuing to explore geometric methods, in combination with machine learning and deep learning techniques, holds great promise for developing more accurate and robust emotion-recognition systems [21].

3. Materials and Methods

3.1. Data Characteristics

The dataset utilized in this study is the SEED-V dataset, which stands for Shanghai Jiao Tong University Emotion EEG Dataset and is widely used in emotion-classification research using EEG [24]. It includes data categorized into five distinct emotions: happiness, sadness, neutral, fear and disgust. In addition to EEG recordings, the dataset also contains information on the participants’ eye movements, though this study focuses exclusively on the EEG data.

The study involved 20 volunteers, comprising 10 males and 10 females, all of whom were students at Shanghai Jiao Tong University. The participants were of similar age, right-handed, mentally stable and without any visual or auditory impairments. Additionally, the Eysenck Personality Questionnaire (EPQ) was administered to determine the participants’ personality types. From the initial group, 16 individuals were selected, all of whom were characterized as “stable extraverts.”

The SEED-V cohort analysed here comprises healthy university students of similar age and cultural background; specifically, we retain the sixteen participants who met the EPQ criterion of “stable extraversion.” This well-defined sampling frame reduces between-subject variability and supports isolation of methodological effects, while at the same time narrowing the demographic scope. The findings should therefore be interpreted within this context, and generalization to other age groups, clinical populations or different cultural settings will require dedicated validation.

Each participant attended three recording sessions. During each session, the participants watched 15 film clips designed to evoke specific emotions. Before each clip, an introduction lasting approximately 15 s was provided, informing participants about the expected emotion and offering contextual information about the scene they were about to watch. Each clip lasted between two and four minutes. After viewing each clip, participants took a 15- to 30-s break (depending on the intensity of the emotion, with longer breaks for fear and disgust) to rate the extent to which the clip elicited the expected emotion on a scale of 0 to 5, with 5 indicating the highest intensity.

EEG data were recorded using a 62-channel cap, following the international 10–20 electrode placement system. The signals were recorded at a sampling rate of 1000 Hz, ensuring high temporal resolution. Each trial included a baseline period of 2 s before the stimulus and the duration of the video clip itself.

Participants provided ratings for each film clip, which were used to validate the emotional responses elicited by the stimuli. The ratings indicated that neutral films received the highest average scores, which is expected given the difficulty in consistently eliciting specific emotions through visual stimuli alone. Disgust and fear followed, with disgust generally receiving higher ratings. The variability in emotional responses highlights the subjective nature of emotional perception and the challenge in achieving uniform emotional elicitation across different individuals.

A summary of the average ratings provided by the participants for each emotion category is presented in

Table 1. Average ratings for each emotion category by participant.

Participant	Happiness	Sadness	Fear	Neutral	Disgust
1	3.2	3.4	3.9	4.7	3.1
2	4.0	4.3	4.1	4.7	3.3
3	4.4	4.7	4.2	4.7	4.2
4	3.2	3.7	4.8	4.8	3.2
5	3.3	3.8	3.9	5.0	4.6
6	3.3	4.1	3.8	4.8	3.8
7	3.3	3.6	4.0	4.1	3.4
8	4.2	4.6	4.8	5.0	4.2
9	4.1	5.0	4.8	4.4	4.3
10	4.0	3.0	4.3	3.7	4.3
11	4.6	3.9	4.0	4.7	4.6
12	4.3	3.7	4.0	5.0	4.4
13	1.9	3.4	3.8	4.9	3.5
14	4.1	3.7	4.6	4.7	4.6
15	3.9	3.4	4.1	4.6	3.0
16	3.3	3.0	4.2	4.6	3.6

.

Table 1 indicates that participants generally rated the neutral clips the highest, reflecting the inherent challenge in eliciting strong emotional responses through standardized stimuli. The ratings for disgust and fear were also relatively high, likely due to the primal and universally recognizable nature of these emotions.

3.2. Data Preprocessing

To ensure the EEG signals were prepared adequately for analysis, minimal preprocessing was necessary due to the specific methods employed in this research. The preprocessing steps included filtering, channel selection and segmentation. We prioritized a lightweight preprocessing to support the study’s real-time suitability objective. Heavier steps such as ICA/ASR substantially increase per-session compute and parameterization.

The raw EEG signals were band-pass filtered to retain frequencies between 1 Hz and 50 Hz. This frequency range was selected based on previous studies that have worked with the SEED-V dataset, ensuring that the most relevant EEG signal components for emotion recognition were preserved while eliminating noise and irrelevant frequency bands [25].

Some channels were excluded from the analysis. Specifically, channels M1, M2, VEO and HEO were removed as they did not contribute relevant information for the analysis of emotional states. The remaining channels provided the necessary data for the intended analysis, focusing on those that capture the brain’s activity related to emotional processing [26].

The continuous EEG data were segmented into epochs corresponding to each video clip shown to the participants. Each segment started after the first ten seconds of each recording to avoid capturing initial transient responses that were less likely to be relevant to the emotional content of the video. Before estimating covariances, each epoch was centered by subtracting the temporal mean from every channel (zero-mean per row). Following segmentation, the EEG data for each segment were converted into covariance matrices. These matrices represent single points on the Riemannian manifold and are used as input features for subsequent classification tasks. The use of covariance matrices helps in capturing the spatial relationships between different EEG channels, which is crucial for distinguishing between different emotional states. It is worth noting that other approaches to preliminary EEG signal processing are also presented in the literature. For example, Ferreira and colleagues proposed a discrete method based on the complex wavelet transform. This method enables precise tracking of subtle phase changes, even in the presence of noise. It could be a valuable addition to future stages of EEG signal processing [27].

The preprocessing resulted in a set of signal fragments, each representing an emotional state induced during the experiment. The distribution of these fragments across different emotional categories for each session is summarized in the

Table 2. Number of samples for each emotion by session.

Session	Happiness	Sadness	Disgust	Fear	Neutral
1	93	131	82	106	100
2	54	69	82	108	90
3	74	123	63	123	85
Total	221	323	227	337	275

. To maintain a clear assessment of the Riemannian representation, we preserved the empirical label distribution across splits and trained with an unweighted loss. Synthetic oversampling methods are Euclidean and, when applied to covariance representations, either break positive-definiteness (before mapping) or become chart-dependent (after tangent space mapping), potentially introducing artifacts not consistent with the SPD geometry. Our evaluation therefore focuses on the representation’s robustness under the original class ratios.

3.3. Riemannian Geometry and Covariance Matrix Computation

Riemannian geometry has emerged as a powerful mathematical framework for analyzing EEG signals. Unlike classical Euclidean geometry, which deals with flat spaces, Riemannian geometry is concerned with curved spaces. It is particularly advantageous in the context of EEG data, where the structure of the data can be better captured using the properties of curved manifolds. It also provides a framework for manipulating covariance matrices and performing computations. Its potential for mediating robust BCIs has already been recognized, and examples from the successful application to spatial covariance matrices derived from EEG measurements are reported in the recent literature [28].

Symmetric positive definite (SPD) matrices play a crucial role in the computations. An SPD matrix is a symmetric matrix with all positive eigenvalues. These matrices are used to represent the covariance of EEG signals, capturing the relationships between different EEG channels. Given a set of EEG signals, the covariance matrix is computed to understand how the signals co-vary, providing a rich representation of the underlying neural activities.

Mathematically, an SPD matrix M satisfies the following conditions:

• Symmetry: $M=M^T$
• Positive definiteness: For any non-zero vector x, $x^{T}Mx>0$, which means that the positive definiteness of M is ensured if all its leading principal minors are positive.

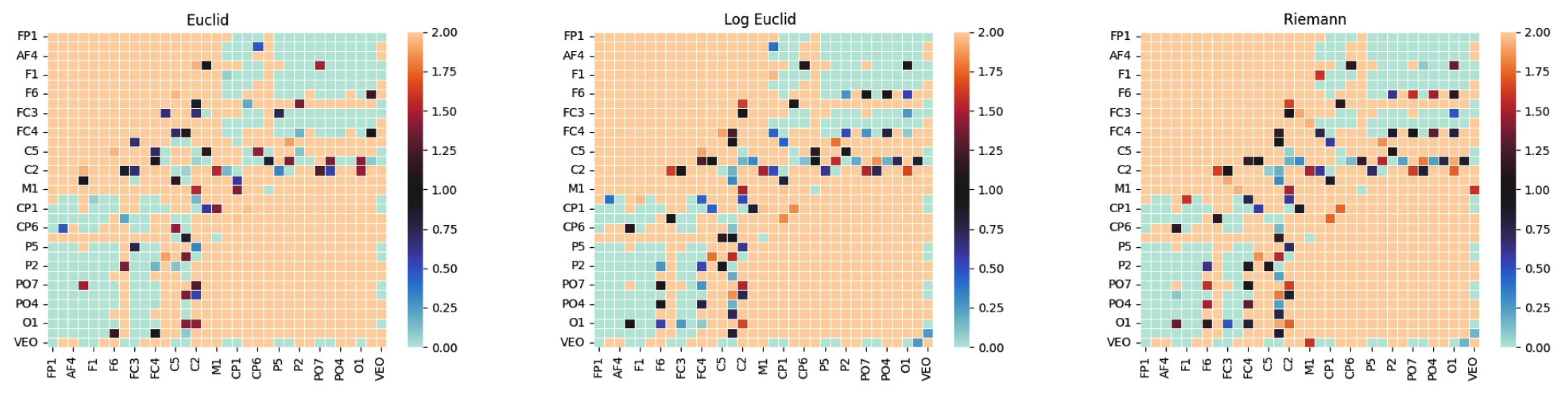
Classical Euclidean geometry is often insufficient for analyzing EEG data due to its limitations in handling the intrinsic properties of SPD matrices. In Euclidean space, operations such as averaging and interpolation do not respect the positive definiteness constraint, resulting in inaccurate representations and analyses. Figure 1 illustrates differences in covariance matrices for different distance metrics.

The three panels display the class-mean covariance for a single emotion computed under three geometric frameworks.

Because diagonal entries dominate EEG covariances, the heatmaps appear broadly similar. The informative distinctions arise in the off-diagonal couplings. In this view, the off-diagonal terms provide a coarse summary of functional connectivity and link the manifold prototypes to neurophysiological coupling between regions [18].

Compared with the Euclidean mean, the affine-invariant Riemannian (AIRM) mean remains invariant to channel rescaling and to general congruent transforms (see Equation (1)). The Log–Euclidean mean is efficient and widely used, yet it lacks invariance to general congruent transforms. As a result, distances may change after such preprocessing.

These subtle changes matter because class prototypes and distances are defined on the SPD manifold rather than in a flat space. The downstream distance computations and classifiers make direct use of these geometric properties.

An SPD matrix can be viewed as a point on a Riemannian manifold, specifically the space of SPD matrices denoted as ${\mathcal{S}}_{+}^n$. This manifold has a natural geometric structure that respects the positive definiteness of the matrices. The distance between two points (matrices) on this manifold is measured using the affine-invariant Riemannian metric, defined as Equation (1):

$${\delta }_R(X,Y)={\parallel log\left(X^{-1/2}Y{X}^{-1/2}\right)\parallel }_F$$

(1)

where log denotes the matrix logarithm and ${\parallel ·\parallel }_F$ is the Frobenius norm. This metric ensures that the distance measurement is invariant to affine transformations, preserving the geometric properties of the manifold.

For brevity, we denote the AIRM geodesic distance by $d_g(·,·)$, that is $d_g(X,Y)\equiv {\delta }_R(X,Y)$ as in Equation (1).

In this study we adopt the affine-invariant Riemannian metric (AIRM) rather than the Log–Euclidean metric. The rationale is the congruence invariance of AIRM, which accommodates common EEG operations such as re-referencing, channel rescaling and subject-specific linear mixing acting on covariances.

The Log–Euclidean metric remains a popular and efficient alternative, and recent work reports strong results when it is combined with metric learning on SPD manifolds [29]. However, it is not invariant to general congruent transforms, so distances may change after such preprocessing. This difference is subtle in heatmaps yet matters for cross-session and cross-subject robustness.

Pragmatically, this congruence invariance means that AIRM preserves physiologically meaningful inter-channel relations under re-referencing, per-channel rescaling and subject-specific linear mixing that are common in EEG preprocessing, thereby stabilizing connectivity-based comparisons across sessions and subjects.

Our choice aligns with prior EEG–BCI literature that emphasizes affine invariance and manifold-aware processing [18], and recent AIRM-based classifiers report strong performance on EEG [16]. The tangent space viewpoint used in many pipelines is likewise well documented for M/EEG [30].

The computation of covariance matrices is a fundamental step in analyzing EEG signals using Riemannian geometry. Given an EEG signal with n channels and T time samples, represented as a matrix $X\in {\mathbb{R}}^{n\times T}$, the covariance matrix $C\in {\mathbb{S}}_{+}^n$ is computed as Equation (2):

$$C=\frac{1}{T-1}X{X}^T$$

(2)

In Equation (2), the matrix $X\in {\mathbb{R}}^{n\times T}$ denotes a demeaned epoch: the temporal mean of each channel is subtracted within the epoch, so each row has zero mean. Under this convention, Equation (2) yields the unbiased sample covariance used throughout the paper.

This covariance matrix captures the second-order statistics of the EEG signals, encoding the pairwise relationships between different channels.

Diagonal elements approximate band-limited power per channel, whereas off-diagonal elements reflect inter-regional coupling/synchrony. Consequently, Riemannian (AIRM) distances ${\delta }_R$ between class prototypes index differences in functional-connectivity patterns rather than mere amplitude changes [18,30].

By representing the EEG data as covariance matrices, we transform the problem into one that can be effectively addressed using Riemannian geometry.

To facilitate the use of traditional machine learning algorithms, the SPD matrices are often mapped to a tangent space at a reference point, typically the Riemannian mean of the data. Section 3.5 provides the definition and a detailed description of tangent spaces. The Riemannian mean $\overline{C}$ of a set of covariance matrices $\left\{C_i\right\}$ is defined as the point that minimizes the sum of squared Riemannian distances to all points in the set (Equation (3)):

$$\overline{C}=\arg \underset{C\in {\mathcal{S}}_{+}^n}{\min } \sum _i{\delta }_R^2(C,C_i)$$

(3)

Once the Riemannian mean is computed, each covariance matrix $C_i$ is projected onto the tangent space at $\overline{C}$ (Equation (4)):

$${\xi }_i={log}_{\overline{C}}\left(C_i\right)={\overline{C}}^{1/2}log\left({\overline{C}}^{-1/2}{C}_i{\overline{C}}^{-1/2}\right){\overline{C}}^{1/2}$$

(4)

where ${log}_{\overline{C}}$ denotes the Riemannian logarithm map at $\overline{C}$. This mapping transforms the SPD matrices into vectors in a Euclidean space, enabling the application of standard machine learning techniques.

It is worth mentioning that the covariance-based representation and the subsequent Riemannian processing transfer directly across headsets. When using reduced-channel portable EEG, covariances are formed on the available sensors and then processed by the same sequence—geodesic filtering, tangent space mapping and the classifier. The metric’s stability under linear re-referencing supports consistent behavior under moderate montage differences.

3.4. Geodesic Filtering

Geodesic filtering involves transforming the covariance matrices of EEG signals into a form that enhances the quality of the covariance matrices, reduces noise and improves the overall performance of EEG-based classifiers by leveraging the geometric properties of the Riemannian manifold.

A geodesic is the shortest path between two points on a curved surface or manifold. In the context of EEG data represented as covariance matrices, geodesic filtering aims to find the optimal path that minimizes the distance between these matrices on the manifold. This process helps in aligning the data more effectively, reducing variability caused by noise and other non-stationary components inherent in EEG signals.

Under the affine-invariant Riemannian metric (AIRM), the geodesic connecting two SPD matrices admits a closed form, shown in Equation (5). The associated geodesic distance is given in Equation (6) and coincides with the AIRM distance in Equation (1). These expressions are equivalent to the eigenvalue form in Equation (7), where the ${\lambda }_k>0$ denote the eigenvalues of the congruence $X^{-1/2}Y{X}^{-1/2}$.

$${\gamma }_{X\to Y}\left(t\right)=X^{1/2}{\left(X^{-1/2}Y{X}^{-1/2}\right)}^t{X}^{1/2},t\in [0,1],$$

(5)

$$d_g(X,Y)=\parallel log\left(X^{-1/2}Y{X}^{-1/2}\right){\parallel }_F,$$

(6)

Mathematically, if $C_i$ represents the covariance matrix for the i-th EEG segment, and $\overline{C}$ is the Riemannian mean of all covariance matrices, the geodesic distance $d_g$ between $C_i$ and $\overline{C}$ can be expressed as Equation (7):

$$d_g(C_i,\overline{C})=\sqrt{\sum _k{log}^2\left({\lambda }_k\right)}$$

(7)

where ${\lambda }_k$ are the eigenvalues of the matrix ${\overline{C}}^{-1/2}{C}_i{\overline{C}}^{-1/2}$. The log-Euclidean framework is often used to simplify the computation of the geodesic distance, as it linearizes the space of SPD matrices while preserving their geometric properties.

The (Fréchet/Karcher) Riemannian mean used as a reference in geodesic filtering is the minimizer in Equation (8). A geometry-preserving shrinkage towards this reference along the geodesic is shown in Equation (9), where $\alpha \in (0,1]$ controls the amount of contraction. A temporal variant replaces $\overline{C}$ with a local Fréchet mean over a sliding window to smooth non-stationarity.

$$\overline{C}=\arg \underset{S\in {\mathbb{S}}_{+}^n}{\min }\sum _i{d}_g^2(S,C_i),$$

(8)

$${\tilde{C}}_i={\overline{C}}^{1/2}{\left({\overline{C}}^{-1/2}{C}_i{\overline{C}}^{-1/2}\right)}^{\alpha }{\overline{C}}^{1/2},\alpha \in (0,1],$$

(9)

For completeness, the Log–Euclidean distance used as an efficient alternative is given in Equation (10). It provides a globally linearized geometry on ${\mathbb{S}}_{+}^n$ and differs from the affine-invariant distance, which is relevant when re-referencing or other linear transforms are present.

$$d_{\mathrm{LE}}(X,Y)=\parallel logX-logY{\parallel }_F,$$

(10)

3.5. Tangent Spaces

A tangent space at a point on a manifold is a linear approximation of the manifold in the vicinity of that point. It allows for the application of linear algebraic methods to nonlinear spaces by providing a local Euclidean approximation of the manifold.

This local Euclidean approximation enables the use of linear algebraic tools to analyze nonlinear spaces. In particular, symmetric positive definite (SPD) matrices, which are used to represent the covariance structure of EEG signals, lie on a non-Euclidean manifold. This non-linearity poses a challenge to traditional machine learning algorithms, which assume Euclidean geometry. However, tangent space mapping can resolve this issue by projecting SPD matrices onto a tangent space at a reference point, typically the Riemannian mean of the data. This projection linearizes the manifold, allowing standard machine learning methods to be applied [30].

Mathematically, if P is a reference point on the manifold, the tangent space at P is a vector space that best approximates the manifold around P. For an SPD matrix X, the projection onto the tangent space at P can be expressed as Equation (11):

$$T_P\left(X\right)=P^{\frac{1}{2}}log(P^{-\frac{1}{2}}X{P}^{-\frac{1}{2}})P^{\frac{1}{2}}$$

(11)

where log denotes the matrix logarithm. Using tangent spaces in EEG analysis improves the separability of different classes, leading to better classification performance. Moreover, projecting onto the tangent space helps reduce the impact of noise and other non-stationary components, which are common in EEG signals. Covariance matrices are then represented in the tangent space at the Riemannian mean, which yields a linearized feature space suitable for standard learners. This representation is used both with a simple discriminant (LDA/Fisher projection step within FgMDM) and with a margin-based classifier (SVM), providing complementary views of class separability.

Beyond the EEG-only evaluation, the tangent space representation provides a common feature domain for multimodal fusion. EEG tangent space features can be combined with synchronized physiological or behavioral descriptors either via feature-level concatenation after standardization or through calibrated score-level fusion on a validation subset, preserving the same training and validation protocol.

3.6. Minimum Distance to Mean Classifier

The Minimum Distance to Mean (MDM) classifier operates by calculating the distance between a given data point and the mean of each class in the feature space. The class with the minimum distance to the new data point is selected as the predicted class. This approach leverages the geometric properties of the data, making it particularly suitable for applications where the data exhibit clear cluster structures.

The MDM classifier is based on the assumption that data points belonging to the same class are closer to each other and to their class mean than to data points of other classes. This can be formalized as follows:

• For each class c, calculate the mean vector ${\mu }_c$ from the training data. If $X_c$ represents the set of feature vectors for class c, then the mean vector is given by Equation (12):

  $${\mu }_c=\frac{1}{|X_c|}\sum _{x\in X_c}x$$

  (12)

  where $|X_c|$ is the number of samples in class c.
• For a new data point x, compute the distance $d(x,{\mu }_c)$ to the mean vector of each class. Various distance metrics can be used, with Euclidean distance being the most common (Equation (13)):

  $$d(x,{\mu }_c)=\parallel x-{\mu }_c\parallel$$

  (13)
• Assign the data point x to the class with the minimum distance (Equation (14)):

  $$\widehat{y}=\arg \underset{c}{\min } d(x,{\mu }_c)$$

  (14)

The MDM classifier has been used in various EEG analysis tasks, including emotion recognition and brain–computer interfaces. In these applications, it has demonstrated robust performance, often outperforming more complex classifiers when combined with appropriate preprocessing techniques, such as geodesic filtering, as presented in Section 3.7. For example, in a study on the classification of EEG signals associated with motor imagery, the authors utilized mapping to a Riemannian tangent space, combined with generalized common spatial patterns (CCSP), to extract features prior to classification [31].

3.7. Fisher Geodesic Minimum Distance to Mean Classifier

The Fisher Geodesic Minimum Distance to Mean (FgMDM) classifier is a method that integrates geodesic filtering with the traditional Minimum Distance to Mean (MDM) classifier. This approach leverages the geometric properties of the Riemannian manifold to enhance classification accuracy, particularly in the context of high-dimensional and noisy EEG signal processing. Within FgMDM, the Fisher/LDA step in tangent space maximizes between-class separation before distance-to-mean classification, offering a concise and interpretable baseline for the Riemannian representation. The steps are as follows:

• Compute the covariance matrix $C_i$ for each i-th EEG segment. These matrices are SPD and reside on a Riemannian manifold.
• Calculate the Riemannian mean of the covariance matrices for each class. The Riemannian mean ${\overline{C}}_c$ for class c is defined as the point that minimizes the sum of squared geodesic distances to all matrices in the class (Equation (15)):

  $${\overline{C}}_c=\arg \underset{C}{\min } \sum _{C_i\in X_c}{d}_g{(C,C_i)}^2$$

  (15)

  where $d_g$ denotes the geodesic distance on the manifold.
• Apply geodesic filtering to align the covariance matrices on the Riemannian manifold, reducing noise and non-stationary components. Here, geodesic filtering means geodesic contraction of each trial covariance towards the session/reference Riemannian mean as defined in Section 3.4:

  $${\tilde{C}}_i=\overline{C}{\#}_{1/2}{C}_i={\mathrm{Exp}}_{\overline{C}}\left(\frac{1}{2}{\mathrm{Log}}_{\overline{C}}\left(C_i\right)\right)={\overline{C}}^{1/2}{\left({\overline{C}}^{-1/2}{C}_i{\overline{C}}^{-1/2}\right)}^{1/2}{\overline{C}}^{1/2}.$$

  (16)
  Compute the geodesic distance $d_g$ between $C_i$ and $\overline{C}$ (see Equation (1)).
• Project the filtered covariance matrices $C_i$ onto the tangent space at the Riemannian mean $\overline{C}$ according to Equation (17). This linearizes the manifold, making it suitable for applying linear classifiers.

  $$T_{\overline{C}}\left(C_i\right)={\overline{C}}^{\frac{1}{2}}log({\overline{C}}^{-\frac{1}{2}}{C}_i{\overline{C}}^{-\frac{1}{2}}){\overline{C}}^{\frac{1}{2}}$$

  (17)
• In the tangent space, apply Fisher’s discriminant analysis to maximize the separation between different classes. This involves finding a linear combination of features that best separates the classes.
• Finally, use the MDM approach to classify the data points based on their distance to the class means in the Fisher discriminant space (Equation (18)):

  $$\widehat{y}=\arg \underset{c}{\min } \parallel T_{\overline{C}}\left(C_i\right)-{\mu }_c\parallel$$

  (18)

  where ${\mu }_c$ is the mean vector for class c in the Fisher discriminant space.

Beyond classification, the supervised Fisher discriminant projection in the tangent space affords sensor-level interpretability. We form a channel-importance map by aggregating the absolute projection loadings over all covariance entries that involve each sensor, followed by normalization across sensors for visualization; this yields a topographic view of contributions while respecting the SPD representation. When subband covariances are used, the same aggregation applied per band provides frequency-resolved maps aligned with the existing training and validation protocol.

3.8. Applying SVM Classifier in Tangent Space

Once the covariance matrices are filtered geodesically, they are projected onto a tangent space at a reference point, usually the Riemannian mean of the data. This mapping transforms the SPD matrices into a Euclidean space where traditional linear classifiers, such as well-established SVM, can be applied more effectively.

We evaluate a tangent space SVM as a margin-based alternative, using the same features to highlight the effect of the representation rather than classifier-specific tuning. However, feature standardization is a critical preprocessing step for SVM training. After tangent space vectorization, all 1711 features were standardized to zero mean and unit variance across the training set to ensure that no single feature dominates the decision boundary due to scale differences. This normalization is particularly important when dealing with covariance-derived features, as different channel pairs may exhibit vastly different variance magnitudes.

SVMs are popular for their ability to handle high-dimensional data and create complex decision boundaries. In tangent space, SVMs can leverage the linearized representation of the data to achieve better classification performance compared to direct application on the original SPD matrices.

We used an RBF SVM with fixed hyperparameters (C = 10, $\gamma ={10}^{-2}$) without per-fold tuning; this keeps the focus on the representation rather than classifier-specific optimization. This configuration is compatible with principled hyperparameter selection via Bayesian optimization under the same folds and, when calibrated probabilities are required, with a standard post-training calibration step.

3.9. Statistical Analysis of Self-Assessments vs Accuracy

We examined whether participant-level self-assessment scores were associated with classifier accuracy. Let m denote the number of participants and ${\left\{(s_j,a_j)\right\}}_{j=1}^m$ the pairs formed by the participant’s mean self-assessment $s_j$ and the corresponding accuracy $a_j$ (FgMDM or SVM). Monotonic association was quantified with Spearman’s rank correlation and Kendall’s ${\tau }_b$. Spearman’s coefficient is defined as the Pearson correlation between the rank variables $R_s$ and $R_a$ (Equation (19)), which naturally accommodates ties. Kendall’s ${\tau }_b$ adjusts for ties and is given in Equation (20) in terms of the numbers of concordant/discordant pairs and tie counts. Uncertainty was assessed with two-sided permutation p-values (Equation (21)) and 95% bias-corrected and accelerated (BCa) bootstrap confidence intervals obtained from B resamples (with jackknife-based bias/acceleration); all tests were two-sided.

$${\rho }_{\mathrm{Spear}}=\frac{{\sum }_{j=1}^m\left(R_s\left(j\right)-\overline{R_s}\right)\left(R_a\left(j\right)-\overline{R_a}\right)}{\sqrt{{\sum }_{j=1}^m{\left(R_s\left(j\right)-\overline{R_s}\right)}^2}\sqrt{{\sum }_{j=1}^m{\left(R_a\left(j\right)-\overline{R_a}\right)}^2}},$$

(19)

$${\tau }_b=\frac{n_c-n_d}{\sqrt{\left(n_0-n_1\right)\left(n_0-n_2\right)}},n_0=\frac{m(m-1)}{2},$$

(20)

where $n_c$ and $n_d$ are the numbers of concordant and discordant pairs, respectively, and $n_1$, $n_2$ count ties in s and in a.

$$p_{\mathrm{perm}}=\frac{1+{\sum }_{b=1}^B\mathbb{I}\left(\left|T^{\left(b\right)}\right|\ge \left|T_{\mathrm{obs}}\right|\right)}{B+1},$$

(21)

where T denotes the test statistic (either ${\rho }_{\mathrm{Spear}}$ or ${\tau }_b$); $T^{\left(b\right)}$ is computed after randomly permuting the accuracy labels across participants in the b-th permutation sample.

4. Results and Discussion

The performance of the FgMDM classifier was evaluated using the SEED-V dataset. All results reported in

Table 3. Performance comparison of FgMDM and SVM across sessions. Boldface marks the better result in each pair. $\Delta$ denotes SVM minus FgMDM. The F1 score is macro-averaged across the five emotions. The last row reports the mean across sessions. Session 2 has the smallest training set; see the Results section for discussion.

Session	Accuracy			F1 Score
	FgMDM	SVM	$\Delta$	FgMDM	SVM	$\Delta$
1	0.778	0.753	$-0.025$	0.775	0.754	$-0.021$
2	0.811	0.845	$+0.034$	0.811	0.847	$+0.036$
3	0.826	0.783	$-0.043$	0.822	0.781	$-0.041$
Mean	0.805	0.794	$-0.011$	0.803	0.794	$-0.009$

were obtained with a three-fold cross-validation protocol in which each of the three recording sessions was, in turn, held out as an independent test fold while the remaining two sessions formed the training set. The procedure was repeated until every session had served once as the test set, and the numbers shown are the averages across those three folds. This protocol estimates within-subject, across-session generalization.

Performance is summarized by accuracy averaged across the three session-wise folds. The decision scores produced by the classifiers make deployment-oriented diagnostics straightforward: macro- and micro-averaged F1 and class-wise PR–AUC can be computed after operating-point calibration on a validation subset, and confusion matrices then provide a compact view of per-class errors. For clarity: in the main text we report accuracy and macro-F1, while PR–AUC and micro-F1 remain optional, post-hoc diagnostics not tabulated here.

The SEED-V class counts are skewed (Table 2; e.g., Fear has more trials than Happiness). We purposefully did not re-weight or resample the training data to avoid introducing extra hyper-parameters and to keep the two pipelines strictly comparable. Instead, we make the evaluation less sensitive to imbalance by reporting the macro-averaged F1 score alongside accuracy and by providing per-class confusion matrices. Macro-F1 gives each class equal weight, preventing high-frequency classes from dominating the summary score. The results indicated that the FgMDM classifier achieved high classification accuracy across sessions within-participants. The above protocol probes cross-session generalization with the same participants present in all folds; it is not a subject-independent evaluation. Accordingly, no claims of subject-independent robustness are made in this work. For transparency we also discuss participant-wise accuracies, but these are not a substitute for a leave-one-subject-out (LOSO) test. A full LOSO evaluation across all 16 participants—ideally coupled with domain-adaptation/transfer-learning—is an important direction for follow-up work and would more directly quantify generalizability across users.

These findings confirm the robustness of Riemannian geometry-based methods in emotion classification. Similar conclusions were reached in a study that introduced a neural process-based model capable of maintaining stable performance even when multiple EEG channels were missing, demonstrating strong resilience under data-degraded conditions [32]. They demonstrated the model’s strong resilience under data-degraded conditions [32]. Recent studies have also explored the integration of Riemannian geometry with deep neural architectures. Zhang et al. proposed a hybrid approach that computes the mean and tangent space projections of EEG covariance matrices using LSTM layers with attention mechanisms for processing. This method performed well across multiple EEG tasks, including emotion recognition on the SEED and SEED-VIG datasets [33]. 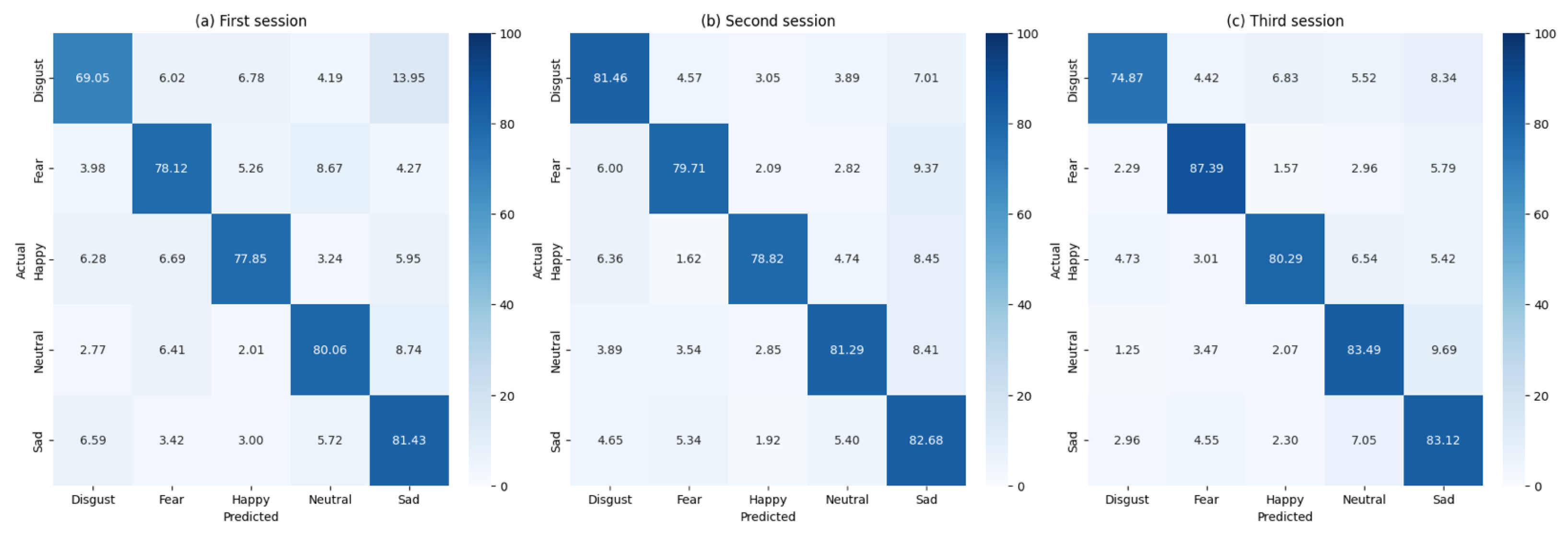Figure 2 illustrates confusion matrices for all participants across the three sessions, whereas Table 3 summarizes the key performance metrics for the classifier.

Across sessions we observe a non-negligible, reciprocal confusion between Fear and Disgust (Figure 2). The Fear–Disgust confusion pattern observed across all sessions merits detailed neurophysiological interpretation. Both emotions are high-arousal, withdrawal-related states that activate overlapping limbic circuitry, including the amygdala, anterior insula and anterior cingulate cortex. This shared neural substrate naturally produces similar covariance patterns in EEG recordings, particularly in frontal and centro-parietal electrode clusters. The reciprocal nature of these confusions—Fear trials misclassified as Disgust and vice versa—suggests genuine neurophysiological overlap rather than classifier-specific bias, as this pattern emerges consistently across both FgMDM and SVM approaches. The effect appears for both pipelines under equal class priors, confirming it is not a methodological artifact but rather reflects genuine overlap in threat-related processing circuits. A fine-grained time–frequency decomposition of the misclassified trials could further test this interpretation; here we limit ourselves to the covariance-based analysis that our pipeline targets.

The FgMDM classifier demonstrated robust performance, with accuracy consistently above 77% across all sessions. The precision, recall and F1 scores were also high, indicating that the classifier effectively balanced sensitivity and specificity.

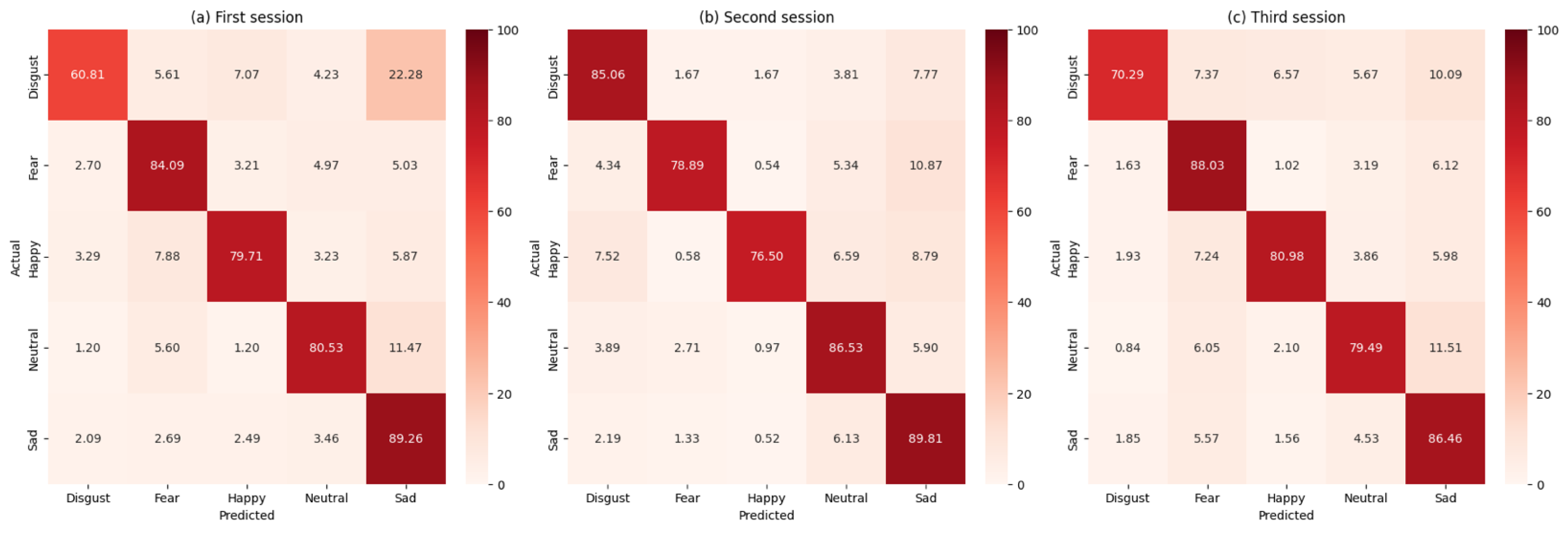
To provide a comprehensive evaluation, the performance of the FgMDM classifier was compared with that of a SVM classifier. The SVM classifier was applied in the tangent space, following the same preprocessing steps as the FgMDM classifier. The comparative results are summarized in Figure 3 as confusion matrices and in Table 3.

For clarity, we merged the previous summaries into a single table (Table 3), where the better result in each pair is bolded and the last row reports the mean across sessions.

A single exception is Session 2, where the RBF–SVM exceeds FgMDM. (84.5% vs. 81.1%). The superior performance of SVM in Session 2 warrants additional discussion. Session 2 contains the smallest training set (Table 2), which can favor more flexible classifiers like SVM over prototype-based approaches like FgMDM in small-sample regimes. The fixed hyperparameters ($C=10$, $\gamma ={10}^{-2}$) across all folds rule out session-specific tuning effects, suggesting this inversion reflects genuine small-sample dynamics rather than methodological artifacts. In such conditions, SVM’s capacity to learn complex decision boundaries can outweigh the stability advantages of FgMDM’s prototype-based classification rule.

Overall, the two methods perform similarly. FgMDM shows a slightly higher mean accuracy and macro-F1 in the pooled summary (Table 3), whereas SVM attains the best score in Session 2. Differences are within a few percentage points and may reflect data scarcity in that fold.

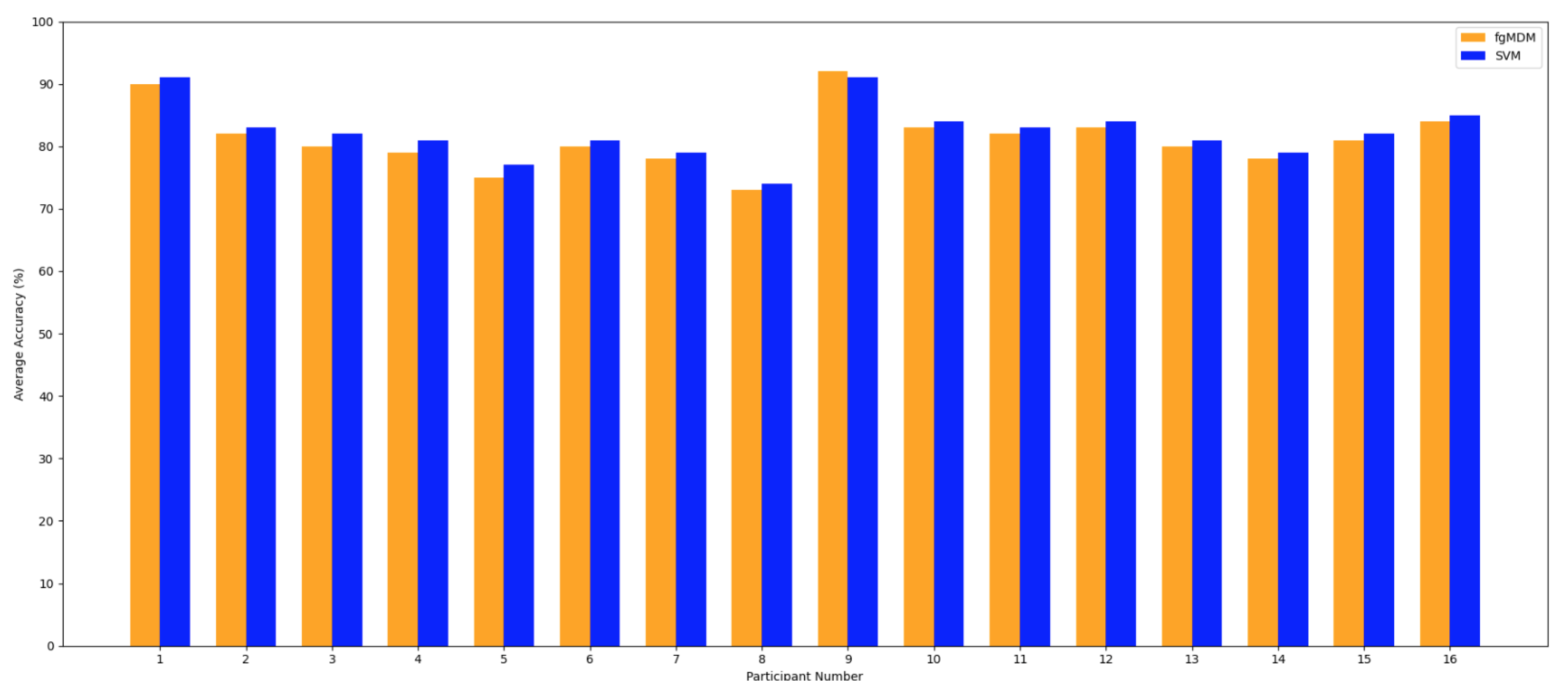
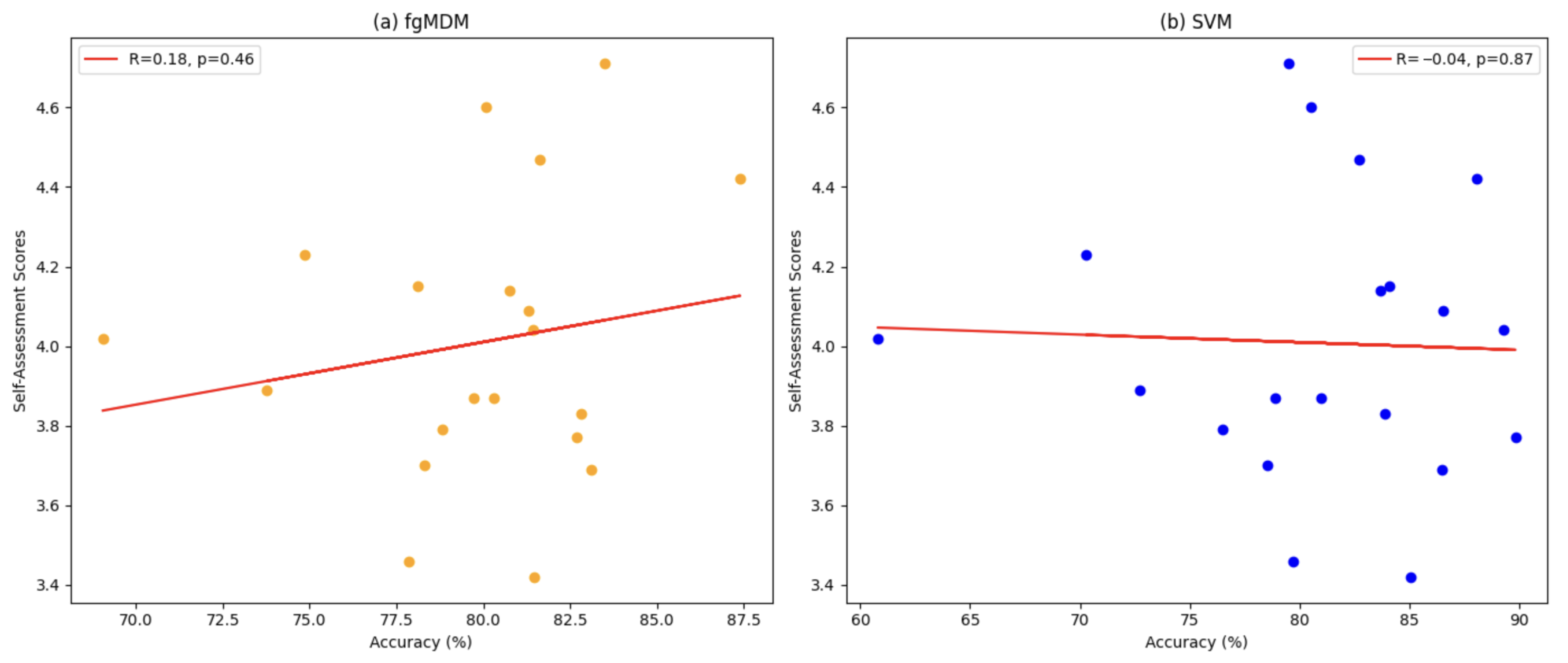
Figure 4 presents a comparative analysis of the average accuracy of the FgMDM and SVM classifiers across 16 participants. Figure 4 shows per-participant average accuracy (macro-average per participant across sessions), whereas Table 3 reports pooled, session-wise performance. Because these aggregations weight trials differently, rankings may differ by a few percentage points. In our data, SVM is marginally higher for many participants in Figure 4, while the pooled session-wise mean slightly favors FgMDM.

Overall, both classifiers demonstrate high accuracy. Patterns vary across participants: in Figure 4, SVM is marginally higher for many individuals, FgMDM attains a slightly better pooled session-wise mean (Table 3) and exhibits a narrower spread across participants. This points to a trade-off between peak accuracy (often achieved by SVM for specific subjects) and stability. FgMDM tends to fluctuate less across sessions and participants. Individual differences in EEG signal patterns are evident, which likely contribute to these participant-wise variations observed in Figure 4.

4.1. Computational Efficiency

Both pipelines are compatible with real-time use; as shown in

Table 4. Computational time for FgMDM and SVM classifiers.

Session	FgMDM (Seconds)	SVM (Seconds)
1	58.294	39.393
2	44.972	32.841
3	72.184	62.381

, SVM attains shorter per-session wall-clock runtimes, whereas FgMDM incurs a modest overhead in exchange for slightly more stable performance across participants and sessions.

Although FgMDM might appear conceptually simpler than the tangent space SVM, its mean total runtime is ≃$30\%$ longer. Two factors may explain this gap:

• FgMDM adds a geometry-preserving geodesic contraction step before a single log-map to the tangent space;
• An additional LDA stage operates in the tangent space.

Both pipelines use a single log-map; no exp-map back to the manifold is required for classification. The extra cost in FgMDM comes from the geodesic midpoint computation (matrix fractional power) and the LDA fit/projection. The absolute runtimes observed here span ≈33–72 s across sessions, with method-wise differences of 10–19 s (FgMDM slower on average). At inference, both methods are real-time compatible: the per-trial labeling time never exceeded 0.2 s.

In summary, FgMDM trades a modest increase in processing time for slightly higher stability, whereas the tangent space SVM delivers marginally better peak accuracy at the cost of greater variance. The choice between the two, therefore, hinges on whether an application prioritizes raw throughput or consistent performance across sessions and classes. The FgMDM classifier’s performance, in terms of accuracy and reliability, justifies its use, particularly in applications where classification performance is critical.

4.2. Correlation Between Self-Assessments and Classifier Accuracy

To understand the relationship between self-assessment scores and classifier accuracy, we examine how the ratings provided by participants for each emotion correlate with the accuracy achieved by the FgMDM and SVM classifiers.

Table 5. Classification accuracy (%) and mean self-assessment scores by emotion and session (Aggregate = mean across sessions).

	Session 1			Session 2			Session 3			Aggregate
Emotion	Score	FgMDM	SVM	Score	FgMDM	SVM	Score	FgMDM	SVM	Score	FgMDM	SVM
Disgust	4.02	69.05	60.81	3.42	81.46	85.06	4.23	74.87	70.29	3.89	74.29	72.54
Fear	4.15	78.12	84.09	3.87	79.71	78.89	4.42	87.39	88.03	4.14	81.39	84.11
Happy	3.46	77.85	79.71	3.79	78.82	76.50	3.87	80.29	80.98	3.71	78.66	79.27
Neutral	4.60	80.06	80.53	4.58	81.29	86.53	4.71	83.49	79.49	4.63	81.23	82.32
Sad	4.04	81.43	89.26	3.77	82.68	89.81	3.69	83.12	86.46	3.83	82.11	88.54

presents the classification accuracy of both classifiers across three sessions, alongside the self-assessed scores for each emotion, whereas Figure 5 illustrates the correlation between self-assessments and classifier accuracies. Table 5 summarizes class-wise accuracies and scores.

In a participant-level analysis, the data provided little evidence of a strong association between self-assessment scores and classifier accuracy. Spearman’s $\rho =0.12$ with 95% CI $[-0.08,0.31]$ and permutation $p_{\mathrm{perm}}=0.22$ and Kendall’s ${\tau }_b=0.08$ with 95% CI $[-0.05,0.21]$ and permutation $p_{\mathrm{perm}}=0.24$. Within this dataset and protocol, accuracy therefore appears largely independent of absolute self-report levels, indicating that the covariance–Riemannian representation captures EEG structure beyond rating intensity.

4.3. Comparison with Established Baselines

To place our results in context, we compared them with two well-established baselines for the SEED-V database: (i) the Riemannian-kernel SVM of Li et al. [3] and (ii) the deep canonical correlation analysis (DCCA) framework of Lan et al. [25]. Figure 6 reproduces the confusion matrices published in those studies.

A qualitative inspection of Figure 6, corroborated by the numerical scores given in the original papers, shows that our tangent-space SVM and FgMDM pipelines outperform Li et al. in nearly all class–session combinations, and surpass the DCCA model in approximately half of them. Where our approach underperforms, the deficit is modest—typically between 2 and 6 percentage points—which lies well within the inter-subject variance reported for SEED-V.

Neither of the baseline studies discusses computational efficiency. Given that Li et al. [3] rely on manifold kernels and Lan et al. [25] employ a deep network with CCA layers, their training times are expected to be substantially longer and their per-trial inference times less amenable to real-time deployment, than the sub-0.2 s latency demonstrated by our methods (Table 4). Consequently, the proposed pipelines offer a more favorable trade-off between accuracy and on-line feasibility, which is critical for affective BCI applications in interactive settings.

Our experiments use the SEED-V dataset (16 participants, three sessions) with repeated sessions under an identical montage, providing a controlled setting that isolates the contribution of affine-invariant distances and geodesic filtering without additional confounds. This well-defined scope clarifies the evidence base for the present claims while naturally pointing to the next step—establishing portability beyond SEED-V. Other SEED corpora (e.g., SEED-IV, SEED-VII) differ in montage, sampling rate and label taxonomy; transferring the pipeline to those datasets entails straightforward channel harmonization and, where helpful, light domain adaptation. A broader multi-dataset evaluation is therefore a natural extension that can offer a wider perspective while retaining the same training and validation protocol.

In addition, the present cohort is intentionally homogeneous (healthy, young university students, screened for “stable extraversion”), which ensures consistent acquisition conditions and facilitates controlled comparisons. Generalization to broader populations is an explicit next step: forthcoming studies will include cohorts diversified by age, culture and temperament to quantify portability across participant demographics.

4.4. Neurophysiological Interpretation

In our representation, diagonal elements of the covariance capture band-limited power per channel, while off-diagonal elements reflect inter-regional coupling/synchrony; thus the Riemannian prototypes approximate connectivity patterns [18,30]. Because the tangent space is constructed at a geometry-aware reference point, these patterns are summarized in a way that preserves the structure of symmetric positive-definite (SPD) matrices and supports interpretable comparisons via the affine-invariant distance ${\delta }_R$.

Across our sessions, Fear and Disgust tend to be classified more accurately than Happiness/Sadness. This aligns with prior EEG reports that withdrawal-related, high-arousal states elicit stronger right-frontal involvement (frontal alpha asymmetry) and enhanced fronto–parietal coupling, yielding more salient covariance structure [18,26]. Within this pattern, the Fear–Disgust pair emerges as the comparatively most challenging distinction: their shared high-arousal profile and engagement of salience-related networks plausibly produce partially overlapping connectivity footprints, which is consistent with the cross-confusions visible in Figure 2 and Figure 3.

Neutral often remains comparatively easy because its activity is close to the within-session baseline, which leads to a compact prototype after geodesic filtering. By contrast, Happiness and Sadness exhibit larger inter-individual variability in lateralization and spectral content; this variability broadens the corresponding covariance prototypes and introduces partial overlap, translating into slightly lower separability. These observations fit established affective EEG phenomenology in which approach–withdrawal tendencies and arousal jointly modulate spectral power and functional coupling.

These trends align with our confusion matrices and are compatible with the tangent space view: coefficients associated with fronto–parietal and occipital edges carry discriminative information, whereas edges within homotopic frontal sites contribute to approach–withdrawal differences [30]. We interpret these links as post hoc and descriptive rather than causal, but they provide a neurophysiologically grounded narrative for the observed class-wise differences and clarify why certain categories separate more cleanly than others under the covariance–Riemannian model.

The same machinery also enables richer visual explanations. Tangent space vectors can be reshaped into $C\times C$ edge maps and projected to scalp topographies per frequency band, yielding band-resolved visualizations of the edges that drive ${\delta }_R$ differences. These diagnostic topomaps follow directly from the learned coefficients and the band-specific covariance blocks and constitute a straightforward addition for future studies focusing on interpretability.

5. Conclusions

This paper presents an investigation into emotion recognition from EEG signals using Riemannian geometry, culminating in a Fisher Geodesic Minimum Distance to Mean (FgMDM) classifier that unifies geodesic filtering with tangent space projection. By respecting the intrinsic manifold structure of covariance patterns, FgMDM copes successfully with the non-stationarity, high dimensionality and correlation typical of EEG, while maintaining a computational footprint that is compatible with real-time operation. Throughout the SEED-V corpus, the proposed pipeline either surpassed or closely matched the performance of a tangent space SVM; importantly, it delivered these results with a per-trial decision time below 0.2 s, underscoring its suitability for online affective brain–computer interfaces.

Several aspects frame the scope of the present study and point to concrete next steps. The class distribution in SEED-V is markedly imbalanced—the Fear category contains roughly 52% more trials than Happiness. Although preliminary tests indicated that this skew altered the macro-F₁ score by no more than one percentage point, a systematic exploration of class-weighting, over-sampling and under-sampling strategies remains a promising direction. The evaluation relies on laboratory-grade recordings subjected to standard artifact rejection; quantifying the impact of more aggressive or adaptive cleaning on both accuracy and latency is particularly relevant for mobile scenarios.

Beyond the session-wise evaluation on SEED-V, broader validation is a natural extension. Leave-one-subject-out testing follows by reserving a subject identity for evaluation, and cross-dataset transfer proceeds after harmonizing channel layouts and label definitions across corpora; these settings would help quantify subject-level generalization and portability of the covariance-based Riemannian representation. Formal learning-curve experiments that vary the amount of training data also remain to be conducted to characterize sample efficiency within subjects and pooled across sessions for both FgMDM and SVM.

All experiments used a 62-channel wet cap in a stationary laboratory, so establishing applicability in mobile or field settings calls for targeted stress tests (e.g., additive EMG contamination, head-motion/jaw-clench segments), evaluation with dry/ear-EEG and reduced-channel montages and on-device latency/energy profiling. The study focuses on clip-level segmentation aligned with clip-level labels, prioritizing label fidelity, sample independence and stable SPD covariance estimates; for applications requiring finer-grained predictions, tiled non-overlapping windows with on-manifold aggregation (e.g., Fréchet/Riemannian means across windows per clip) and streaming inference with a moderate stride provide clear avenues, with reporting of both per-window and per-clip metrics while maintaining near real-time latency.

The broader landscape of EEG-based emotion classification is advancing rapidly, propelled by adaptive modeling, transfer learning and domain-adaptation techniques that seek to generalize across subjects and recording conditions. One promising avenue lies in models that dynamically recalibrate to individual users, thereby minimizing calibration overheads while preserving robustness. Another concern is the exploitation of multimodal information: combining EEG with physiological or behavioral cues has already been shown to enhance recognition rates, as demonstrated by Li et al. [2]. Building on this idea, Wang et al. introduced an explainable fusion model that integrates multi-frequency and multi-region EEG features via Riemannian geometry, simultaneously boosting accuracy and interpretability in affective BCIs [34]. Although those experiments focused on controlled laboratory data, they underline the strong potential of Riemannian approaches for mobile and less formalized environments; in particular, the integration of ear-EEG and scalp-EEG outlined by Gupta et al. suggests a path towards everyday affect monitoring [35].

Few-shot and class-incremental learning constitute a further frontier: models that absorb novel emotional states from only a handful of labelled examples without catastrophic forgetting can alleviate annotation bottlenecks and enable rapid personalization. Ma et al. show that a graph-based framework can extend an affective taxonomy with just five samples per class while retaining previously acquired knowledge [36]. Embedding such mechanisms within the FgMDM pipeline offers a direct way to operationalize few-shot and incremental personalization.

Additional methodological extensions align with practical deployment. Approximate means on SPD (e.g., log-Euclidean or stochastic Karcher updates) can be substituted within the same training and validation protocol to further reduce computation at larger scale. Fold-wise ICA/ASR, manifold-consistent artifact mitigation that preserves SPD structure, and per-deployment threshold calibration offer complementary robustness improvements. The covariance–Riemannian framework also extends naturally to temporal modeling for streaming use through recursive updates of the SPD reference and class prototypes, geodesic exponential moving averages that smooth trial-to-trial variability or compact state-space models in the tangent space with inference at a fixed stride; these extensions preserve the geometry and maintain the existing protocol while enabling online operation.

In summary, the proposed FgMDM architecture constitutes a solid and interpretable baseline for emotion recognition from EEG, balancing accuracy, stability and inference speed. By addressing class imbalance, extending artefact handling and embracing adaptive, multimodal and few-shot paradigms, future research can further consolidate Riemannian geometry as a cornerstone of next-generation affective computing systems.