Enhancing Secure Multi-Party Computation with Damgård–Jurik and NIZK Proofs: A Lightweight Protocol for Scalable Aggregation

Abstract

Privacy-preserving secure multi-party computation protocols are known to face scalability and efficiency challenges in environments where participants hold distinct attributes of the same records (vertical partitioning) or controls a subset of complete records (horizontal partitioning), as in cross-institutional health data analysis or federated IoT analytics, mostly because of communication overhead and the need to address adaptability to large scale or heterogeneous settings. This work introduces a novel MPC protocol based on the Damgård–Jurik cryptosystem and Schnorr zero-knowledge proofs (ZKP), designed to securely aggregate private data distributed across a number of parties. By combining homomorphic encryption with non-interactive ZKP’s, the protocol ensures privacy, correctness, and scalability, aligning with the principles of privacy-enhancing technologies (PETs). Our approach minimizes data exposure, allowing participants to audit results, and achieves linear $O\left(N\right)$ communication complexity, thus making it suitable for large-scale applications in secure data analytics and collaborative computing.

1. Introduction

Secure multi-party computation (SMPC) enables multiple entities to collaboratively perform distributed computations without compromising the confidentiality of their private data. However, in scenarios involving vertical partitioning (where different participants control distinct attributes of the same set of records) and horizontal partitioning (where each participant controls a subset of complete records), traditional protocols suffer from a lack of scalability and high communication overhead [1]. This need arises in applications such as collaborative health analysis between hospitals (vertical) or federated computing of IoT device usage metrics (horizontal), where the volume of data and the heterogeneity of participants demand more efficient solutions [2,3,4,5]. Fully homomorphic encryption (FHE) (see for example [6]), or somewhat homomorphic encryption [7], introduce orders-of-magnitude higher computational overhead than additive homomorphic encryption (like Damgård–Jurik), making it impractical for the high-throughput aggregation tasks we target. In this context, the Damgård–Jurik cryptosystem [8], a homomorphic generalization of the Paillier scheme [9], emerges as an efficient alternative for secure aggregation operations, overcoming limitations of traditional asymmetric protocols such as RSA [10] or ElGamal [11,12]. Its ability to perform summations and scalar multiplications over encrypted data makes it an ideal candidate for decentralized multi-party environments. Various alternative SMPC frameworks, including MOTION [13], GMW (Goldreich-Micali-Wigderson) [14], or SPDZ protocols [15], are prevalent in multi-party secure computation. However, these frameworks are not considered in our current study because we focus here on the most straightforward summation protocol designed for diverse distributed environments.

The protocol proposed by Mehnaz et al. [16], based on ElGamal, offers resistance to collusion between up to $N-2$ parties but introduces quadratic complexity $O\left(N^2\right)$ and relies heavily on a trusted server, which limits its scalability. Furthermore, its layered encryption strategy introduces significant computational and communication overhead, particularly in the key-sharing phase, a step omitted in the original analysis. These limitations motivate the exploration of additive homomorphic schemes that simplify the architecture and reduce trust assumptions.

In this work, we present an adaptation of the Mehnaz protocol that uses the Damgård–Jurik cryptosystem, integrating Schnorr’s noninteractive zero-knowledge proofs (NIZK) [17] to verify the integrity of the results without revealing intermediate inputs. Our core contributions demonstrate that

(i)

The additive homomorphic structure of Damgård–Jurik enables direct aggregation of encrypted values without intermediate decryption operations, thereby reducing the overall computational complexity to $O\left(N\right)$, [18,19]. By encrypting inputs end-to-end and performing computations on ciphertexts, the protocol ensures that no party—including the trusted server—learns individual contributions, adhering to PETs’ principle of data minimization and thus, making it suitable for large-scale applications such as federated learning, secure voting, or collaborative analytics.

(ii)

Removing redundant encryption layers mitigates partial collusion risks, since no multi-party cooperation is needed for decryption. This strengthens the model’s security guarantees against semi-honest adversaries [20,21].

(iii)

The use of NIZK’s to validate the total sum of encrypted values sent by the last participating node to the mediator node eliminates the need for additional verification rounds, thereby reducing communication overhead without compromising the validity of the final result. The proofs are compactly attached to the last shared ciphertext, enabling efficient verification, [22]. This mechanism empowers parties to audit the trusted server’s output independently, ensuring transparency and trust in the computation—a critical aspect of PETs that balances accountability with privacy.

(iv)

By assuming a semi-honest trusted server and validating outputs via ZKPs, our design mitigates risks of tampering while maintaining practicality. This trust model reflects PETs’ emphasis on reducing single points of failure and enhancing system resilience, enabling privacy-by-design data aggregation, directly supporting use cases like medical research, financial auditing, and IoT sensor networks, domains in which it is critical to minimize personal data exposure while preserving functionality.

We implemented our protocol through a proof-of-concept that processes data under both vertical and horizontal partitioning schemes, evidencing linear execution times and efficient handling of large data volumes. The results show a significant contrast to those reported for ElGamal in [23], where the quadratic complexity constrains its practical applicability.

The article is organized as follows: Section 2 presents the theoretical foundations of Damgård–Jurik and Mehnaz’s protocol, alongside our proposed implementation. Section 4 highlights the advantages of scalability achieved through reduced communication and computational complexity. Section 5 discusses the results obtained from the local experimental implementation. Finally, Section 6 provides concluding remarks and explores practical implications, offering recommendations for future improvements such as key generation optimization and decentralized coordination strategies.

2. Theoretical Framework

In this section, we present the foundational concepts and cryptographic mechanisms that underpin the design and implementation of the proposed secure summation protocol. The framework is structured to offer a comparative analysis between existing approaches and the protocol introduced in this work, highlighting both theoretical robustness and practical applicability. We begin by reviewing the protocol proposed by Mehnaz et al., which uses the ElGamal cryptosystem to enable secure multi-party aggregation. Despite its notable resistance to collusion, this approach suffers from scalability limitations due to its quadratic complexity and reliance on a central trusted server. To address these limitations, we explore the principles of homomorphic encryption, with particular attention to the Damgård–Jurik cryptosystem, an extension of the Paillier scheme offering enhanced additive homomorphic capabilities. Additionally, we incorporate Schnorr’s noninteractive zero-knowledge proofs (NIZK) to ensure result verifiability without compromising input privacy. The theoretical exposition provided here laid the foundations for the protocol proposed in this study and justifies the architectural decisions taken to improve efficiency, scalability, and security in distributed settings.

2.1. Protocol Proposed by Mehnaz et al

The protocol introduced by Mehnaz et al. [16] is based on the ElGamal cryptosystem and supports secure summation among multiple parties, resisting collusion by up to $N-2$ participants. Each data element must be encrypted in successive layers using the public keys of all participants, resulting in a computational complexity of $𝒪\left(N^2\right)$ and a communication overhead estimated at $3N+1$ messages. However, this estimate excludes the key-sharing phase, which imposes additional costs.

Furthermore, the model assumes the presence of a trusted server under the “honest-but-curious” paradigm, acting as a “trusted third party” whose role is to collect encrypted data and disseminate the aggregated results to the involved participants. This intermediary entity adheres to the protocol but endeavors to extract as much information as possible from the data transactions.

However, a notably desirable feature in any secure multi-party summation protocol is the elimination of such intermediaries. The reliance on a central coordinator inherently limits the applicability of this scheme in decentralized settings. See [23] for evidence that illustrates how quadratic complexities can significantly affect the performance of the protocol.

2.2. Homomorphic Encryption

Homomorphic encryption enables computations on encrypted data without the need to decrypt it beforehand. This property is fundamental to secure multi-party computation, as it facilitates the processing of sensitive information without exposing its content [24].

2.3. Damgård–Jurik Cryptosystem

The Damgård–Jurik cryptosystem is a generalization of the Paillier cryptosystem, offering enhanced homomorphic properties. It operates on the ring ${\mathbb{Z}}_{n^{s+1}}$, where n is an RSA modulus and s is a positive integer, making the operational ring adaptable to different scenarios.

It extends the Paillier cryptosystem, offering improved homomorphic characteristics that permit the addition and scalar multiplication of encrypted data without decrypting intermediate results. This makes it particularly suitable for secure aggregation tasks in multi-party environments, ensuring confidentiality.

Let $E:\mathcal{M}\to \mathcal{C}$ denote the encryption function from the message space to the cipher space, which we assume are scalars, such that the following operations hold. For any two ciphertexts $E\left(m_1\right),E\left(m_2\right)\in \mathcal{C}$:

$$E\left(m_1\right)·E\left(m_2\right)\equiv E(m_1+m_2)$$

(1)

where the product is performed in $\mathcal{C}$ and the sum in $\mathcal{M}$. This follows directly from the Paillier-like structure of the cryptosystem. As a consequence,

It also supports the multiplication of an encrypted message by a scalar:

$$E{\left(m\right)}^k=E\left(m\right)·E\left(m\right)·····E\left(m\right)=E(m+\cdots +m)=E(k·m)$$

(2)

where k is a scalar and m is the message.

These properties enable efficient computation on encrypted data sets without decryption [25].

The following describes the key generation, encryption, and decryption algorithms of the Damgård–Jurik cryptosystem.

• Key Generation

• Input:  Security parameter $s\ge 1$
• Output: Public key $(n,s,g)$, private key $(\lambda ,\mu )$
• Select large primes p and q such that $p\ne q$
• Compute $n=pq$ and define $n^s$
• Compute $\lambda =lcm(p-1,q-1)$
• Select a generator $g\in {\mathbb{Z}}_{n^{s+1}}^{*}$ that belongs to the subgroup of elements congruent to 1 modulo n
• Define auxiliary function $L\left(x\right)={\displaystyle \frac{x-1}{n}}$
• Compute $\mu ={\left(L\left(g^{\lambda }mod{n}^{s+1}\right)\right)}^{-1}modn$
• Return: Public key $(n,s,g)$, private key $(\lambda ,\mu )$

It should be noted that in order to avoid attacks by, say, continued fractions in the Damgård–Jurik cryptosystem, the primes p and q should be large, of similar bit size, and chosen so that the private exponent is not too small, as small exponent or small differences between p and q can make the system vulnerable [26,27]. One question that might arise when analyzing this algorithm (specifically, the key generation step) concerns the computability of the function $L\left(x\right)={\displaystyle \frac{x-1}{n}}$. In particular, how is it ensured that the division within this expression is always feasible and well defined?

To answer this, recall that Carmichael’s function $\lambda =\lambda \left(n\right)$ is defined as the smallest possible integer satisfying $a^{\lambda }\equiv 1modn$ for all a coprime with n. If $n=pq$, it can be shown that $\lambda \left(n\right)=\lambda \left(pq\right)=lcm(p-1,q-1)$, certainly only if p and q are different. As a consequence, since $g^{\lambda }\equiv 1modn$, it lies in the subgroup of elements congruent to 1 modulo n—a crucial property for the homomorphic properties. From here, since $g=1+an$, for some a, by the binomial expansion $g^{\lambda }={(1+an)}^{\lambda }=1+\lambda an+\left({\displaystyle \genfrac{}{}{0pt}{}{\lambda }{2}}\right){\left(an\right)}^2+\cdots \equiv 1+\lambda anmod{n}^{(s+1)}$, for $s\ge 1$. Hence the expression $g^{\lambda }mod{n}^{(s+1)}$ will always yield a result of the form:

$$g^{\lambda }mod{n}^{(s+1)}=1+kn(\mathrm{for}\mathrm{some}\mathrm{integer}k),$$

(3)

so that

$$L(g^{\lambda }mod{n}^{(s+1)})={\displaystyle \frac{g^{\lambda }mod{n}^{(s+1)}-1}{n}}={\displaystyle \frac{1+kn-1}{n}}={\displaystyle \frac{kn}{n}}=k.$$

(4)

It is evident that the result is always an integer k, with no risk of division being undefined or invalid.

• Encryption

• Input: Message $m\in {\mathbb{Z}}_{n^s}$, public key $(n,s,g)$
• Output: Ciphertext c
• Select random $r\in {\mathbb{Z}}_{n^{(s+1)}}^{\ast }$
• Compute $c=g^m·r^{n^s}mod{n}^{(s+1)}$
• Return: c

Notice that the random value r is not stored explicitly but is embedded within the ciphertext structure and is protected by the hardness of computing the discrete logarithm modulo $n^{s+1}$ and its value is preserved through the multiplicative structure of the ciphertext. In fact, because r belongs to ${\mathbb{Z}}_{n^{(s+1)}}^{*}$ and $\lambda$ is the Carmichael function for n, it follows that $r^{\lambda }$ is congruent to 1 mod n, thereby disappearing in the decryption process.

• Decryption

• Input: Ciphertext c, private key $(\lambda ,\mu )$
• Output: Message m
• Compute $x=L\left(c^{\lambda }mod{n}^{(s+1)}\right)$
• Retrieve $m=x·\mu mod{n}^s$
• Return: m

Notice that the function L plays a key role in decryption, by mapping a value in ${\mathbb{Z}}_{n^{(s+1)}}^{*}$ back to the plain text space ${\mathbb{Z}}_{n^s}$. Indeed, the decryption process in the Damgård–Jurik cryptosystem begins by raising the ciphertext c to the power of $\lambda =\mathrm{lcm}(p-1,q-1)$ modulo $n^{s+1}$. This operation exploits the fact that for a valid ciphertext $c=g^m·r^{n^s}mod{n}^{s+1}$, raising c to the power $\lambda$ eliminates the randomness introduced by $r^{n^s}$, because:

$$c^{\lambda }\equiv g^{\lambda m}mod{n}^{s+1}.$$

(5)

At this stage, the function $L\left(x\right)={\displaystyle \frac{x-1}{n}}$ is applied to $c^{\lambda }$, which maps the result from the multiplicative group ${\mathbb{Z}}_{n^{s+1}}^{*}$ into the additive space ${\mathbb{Z}}_{n^s}$. Specifically:

$$L\left(c^{\lambda }\right)={\displaystyle \frac{c^{\lambda }-1}{n}},\mathrm{and}m=\mu ·L\left(c^{\lambda }\right)mod{n}^s,$$

(6)

where $\mu ={\left(L\left(g^{\lambda }\right)\right)}^{-1}modn$ is part of the private key.

This works because $g^{\lambda }\equiv 1+knmod{n}^{s+1}$ for some integer k, and so $L\left(g^{\lambda }\right)\equiv kmodn$, allowing inversion to recover the message. The security of the scheme relies on the difficulty of computing $\lambda \left(n\right)=\mathrm{lcm}(p-1,q-1)$ without knowledge of the factorization of n, which is required to compute $\lambda$ and hence perform decryption.

Instead, decryption leverages group-theoretic properties of the chosen generator g, the Carmichael function $\lambda \left(n\right)$, and the special function L to efficiently extract the plaintext while preserving the homomorphic structure of the system.

The security of this scheme is underpinned by the decisional composite residuosity (DCR) assumption; This implies that decrypting a message requires solving a mathematical problem closely tied to the structure of n (the product of two primes). The theorem affirms that only those who possess the secret prime factors of n can “unravel” the operation ${(1+n)}^x{r}^{n^s}mod{n}^{s+1}$ to systematically recover both the original message x and the random component r. Without this knowledge, distinguishing between encrypted and random ciphertexts is as hard as solving the DCR problem, thereby ensuring cryptographic security.

2.4. Non-Interactive Zero-Knowledge Proof of Schnorr

The Schnorr NIZK (non-interactive zero-knowledge) proof is a non-interactive adaptation of the original three-step Schnorr identification scheme, made non-interactive through the Fiat–Shamir heuristic. It enables a prover to demonstrate knowledge of a discrete logarithm without disclosing any information about its value [17].

The protocol operates within a cyclic group G of prime order q, with a generator g. The prover’s public key is $y=g^x$, where x is the private key. The Schnorr NIZK proof proceeds as follows:

• The prover selects a random $r\in {\mathbb{Z}}_q$ and computes $R=g^r$.
• The prover computes the challenge $c=H(g \Vert y \Vert R)$, where H denotes a cryptographic hash function.
• The prover computes the response $s=r+cxmodq$.
• The proof consists of the tuple $(R,s)$.
• The verifier accepts the proof if and only if $g^s=R·y^c$.

As highlighted by Agal et al. in [28], noninteractive zero-knowledge proofs offer significant advantages in authentication systems. In our SMPC context, these benefits extend to ensuring the correctness of computations while preserving the privacy of individual inputs.

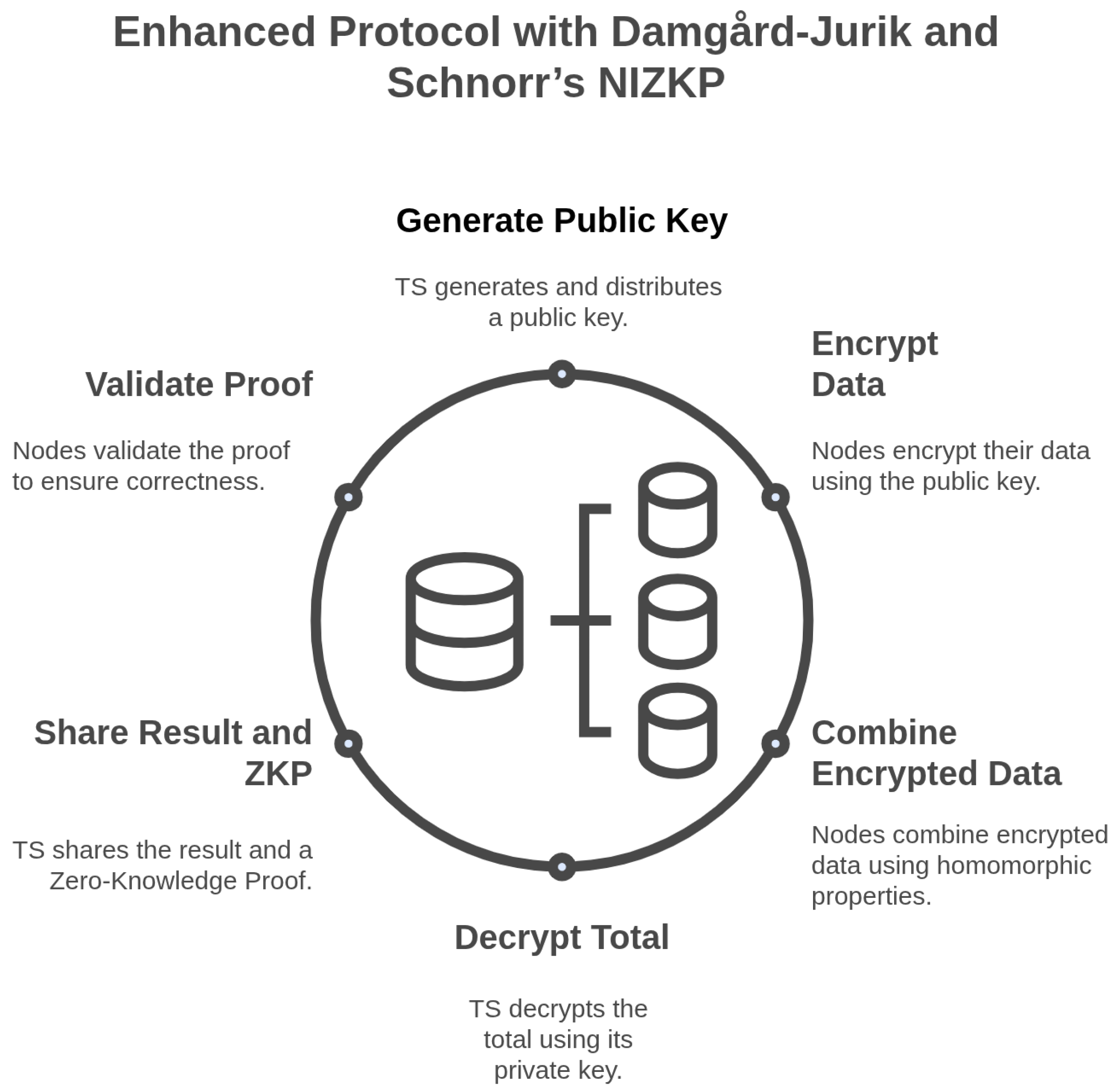
3. An Enhanced Protocol with Damgård–Jurik and Schnorr’s NIZKP

The SMPC protocol built on Damgård–Jurik encryption ensures privacy against collusion involving up to $N-2$ parties. As long as at least two parties remain honest, their individual values cannot be determined, as the additive homomorphism conceals the data within the encrypted sum.

The security of Schnorr’s NIZK is based on the discrete logarithm assumption and the random oracle model (for the hash function). Although these assumptions are widely trusted in current cryptographic practice, it is important to note that they are not secure in post-quantum contexts.

Table 1. Cyberattack resistance analysis of the Damgård–Jurik scheme.

Attack Type	Resistance Level
Interception attack (MITM, Sniffing)	Secure (encrypted values traverse the network and cannot be decrypted without the mediator’s private key).
Forced decryption attack (ciphertext cryptanalysis)	Secure (Damgård–Jurik is asymmetric and RSA-based, offering resistance to factorization attacks).
Partial sum attack (deduction attack)	Partially vulnerable if $N-2$ parties collude (they may reconstruct the remaining participant’s value).
Brute force attacks	Secure, provided large key sizes are used (typically 2048 bits or higher).
Compromised private key attack	Vulnerable if the mediator’s private key is stolen (all encrypted values could be decrypted).

. summarizes the resistance level of the Damgård–Jurik scheme to a number of known threats and cyberattacks; In order to achieve a balance between computational efficiency, proof conciseness, and the robust security properties required for privacy-preserving multi-party computations, we propose now to include Schnorr’s NIZKP to the scheme, as follows (see Figure 1).

We consider a minimum configuration of three parties ($P_1$, $P_2$, and $P_3$), together with a trusted server or mediator, hereafter referred to as the trusted server ($TS$), while the extension to $N>3$ parties is straightforward.

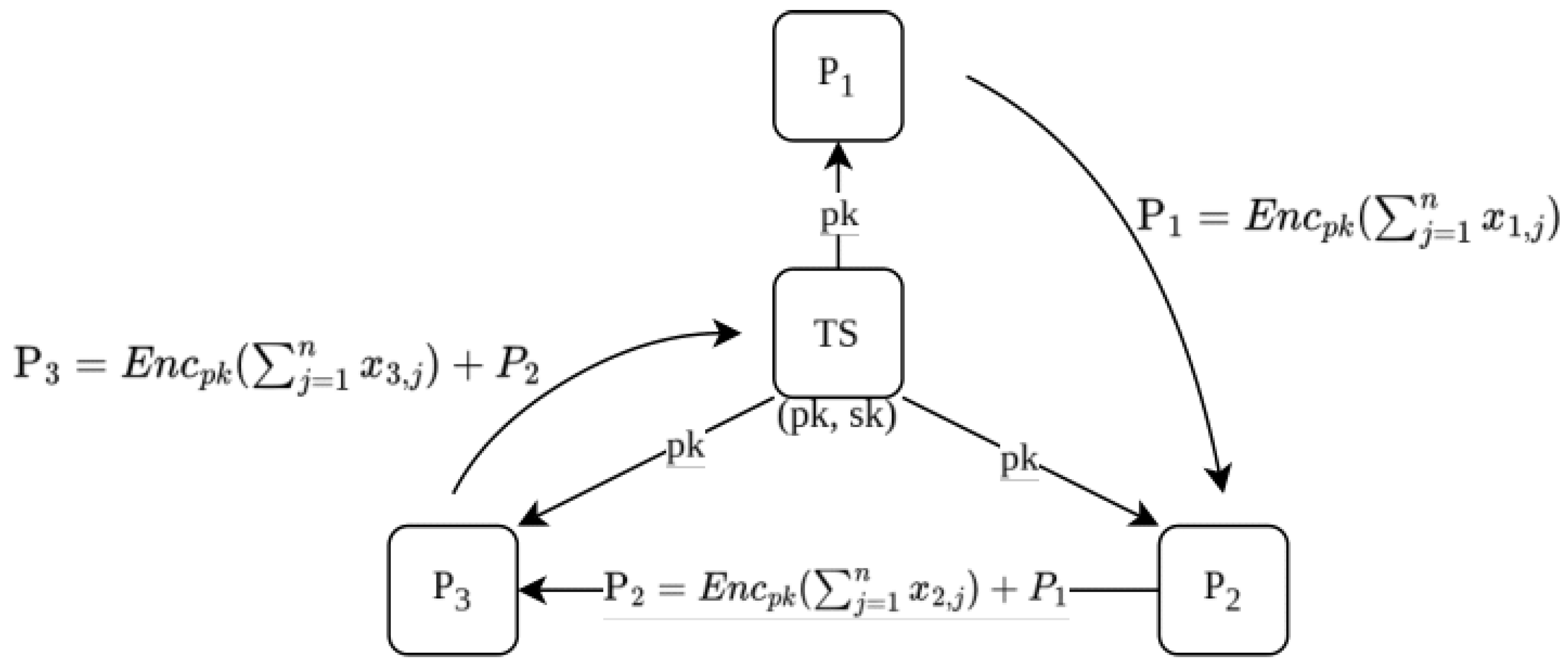
3.1. Initialization, Encryption, and Homomorphic Addition

The mediator generates a public-private key pair, distributes the public key among all parties, and each party uses it to encrypt their local data. These encrypted values are then homomorphically summed, and the aggregated result is returned to the mediator; see Figure 2 and the accompanying Algorithm 1: The initial diagram illustrates the trusted server (TS) generating and distributing a public key $p_k$. Participating Node 1 uses this key to encrypt the sum of its data and sends the encrypted result to Participating Node 2. Subsequently, Participating Node 2 encrypts the sum of its own data, combines it with the value received from Node 1 using the homomorphic property upon the encrypted values, and forwards the aggregated result to Participating Node 3. Node 3 performs a similar encryption with its own data, adds it to the combined sum, and transmits the final encrypted value to the TS.

Algorithm 1 Initialization, data encryption, and generalized homomorphic summation

1: Input: Public key $(n,g)$, private key $\lambda$   2: Output: Homomorphic sum y sent to the mediator   3: Initialization:   4: The mediator generates the Public Key $(n,g)$ and Private Key $\lambda$   5: The mediator distributes the public key $(n,g)$ to all parties $P_i$, for $i=1,2,\cdots ,n$   6: Local Computation and Encryption:   7: for each party $P_i$ ($i=1,\cdots ,n$) do   8:    $P_i$ computes its local sum: $${\mathrm{local\_sum}}_i=\sum _{j=1}^m{x}_{i,j}(\mathrm{The}\mathrm{sum}\mathrm{of}\mathrm{its}\mathrm{private}\mathrm{entries})$$   9:    $P_i$ encrypts its local sum using the public key: $$c_i=\mathrm{Enc}\left({\mathrm{local\_sum}}_i\right)$$ 10: end for 11: Homomorphic Summation: 12: Initialize the encrypted accumulated result $y=1$. (Identity element for multiplication) 13: for each party $P_i$ ($i=1,\dots ,n$) do 14:    $P_i$ multiplies its encrypted value $c_i$ with the current accumulator: $$y=y·c_{i}mod{n}^{s+1}$$ 15: end for 16: Result Transmission to Mediator: 17: The final party $P_n$ sends y to the mediator

Notice that in step 14 of the algorithm, the homomorphic property ensures that the local sums are sequentially added while preserving privacy.

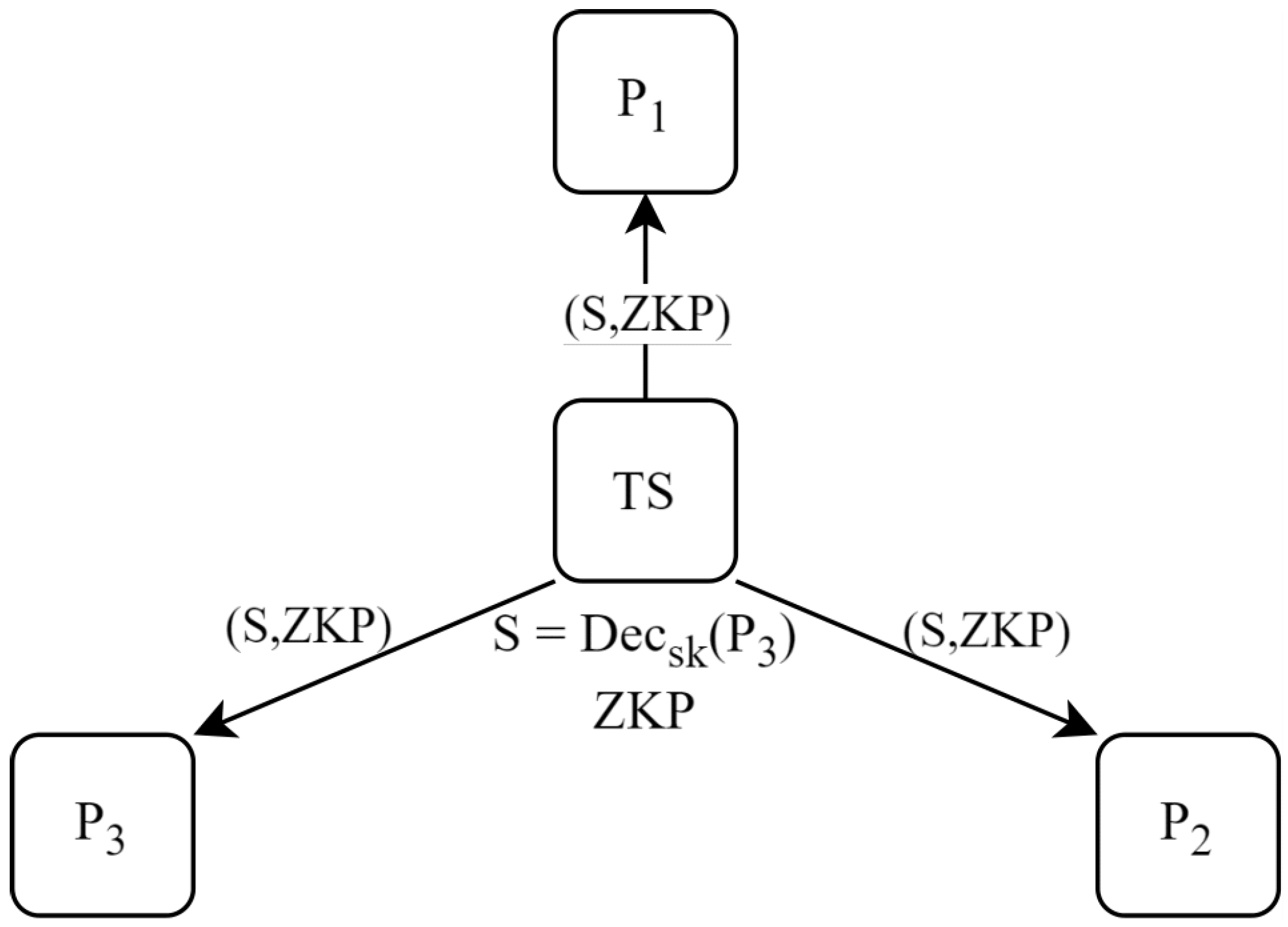
3.2. Decryption and Verification

The mediator decrypts the total sum and generates a Schnorr-type zero-knowledge proof to verify the integrity of the result; see [28].

Diagram in Figure 3, corresponding to Algorithm 2, explains the decryption of the total sum and the verification of its integrity using a zero-knowledge proof (ZKP). The trusted server (TS) decrypts the total amount using its private key, then shares the result along with a zero-knowledge proof (ZKP) based on the Schnorr protocol. The participating nodes then validate the proof to ensure the result’s correctness. A failed validation may indicate possible result tampering. These procedures ensure that the result remains unchanged, fostering trust in the system without compromising individual data.

Algorithm 2 Decryption and verification using Schnorr proof

1: Input: Homomorphically encrypted sum $y_3$, private key $\lambda$   2: Requirements: g and n   3: Output: Decrypted sum and verification via Schnorr proof   4: The mediator decrypts $y_3$: $\mathrm{sum}=\mathrm{Dec}(y_3,\lambda )$   5: The mediator generates $(y,c,z)$ such that:   6: $r\in {\mathbb{Z}}_n$ is randomly chosen   7: $y\leftarrow g^{r}mod{n}^2$   8: $c\leftarrow H\left(y\right)modn$   9: $z\leftarrow r+c·\mathrm{sum}modn$ 10: The mediator sends $(y,c,z)$ to all parties $P_i$ 11: for each party $P_i$ do 12:    Party $P_i$ verifies whether $g^z\stackrel{?}{=}y·g^{c·\mathrm{sum}}mod{n}^2$ 13:     if equality holds then 14:         The proof is valid 15:     else 16:          The proof is invalid 17:     end if 18: end for

4. Comparative Evaluation of Communication and Computational Complexity

In the design and analysis of cryptographic protocols, two fundamental dimensions determine their efficiency and practical feasibility: communication- and computational complexity. These metrics enable performance evaluation both in terms of the volume of exchanged data and the computational effort required for secure execution.

Communication complexity refers to the amount of data that must be exchanged between the parties involved (N) to perform a cryptographic computation. It can also be interpreted as the total number of messages transmitted. This factor is crucial in techniques such as secure multi-party computation (SMPC) and homomorphic encryption (HE), where it directly impacts network latency and resource consumption.

The most relevant models of communication complexity include:

• Linear complexity: Denoted by $𝒪\left(N\right)$, where the number of messages grows proportionally to the number of participants. Each entity exchanges a constant number of messages, thereby enhancing scalability.
• Quadratic complexity: Represented by $𝒪\left(N^2\right)$, arises when each participant must communicate with every other, as in protocols requiring exhaustive interaction to preserve security in distributed computations.
• Logarithmic and sublinear complexity: Denoted by $𝒪(logN)$ and $𝒪\left(\sqrt{N}\right)$, respectively, these complexities emerge in optimized protocols that employ hierarchical structures or efficient networks to reduce inter-party communication.

Evaluating communication complexity is essential to ensure that a protocol can scale efficiently in settings with many participants and large data volumes.

On the other hand, computational complexity refers to the processing resources required to execute a cryptographic protocol, including CPU time, arithmetic operations, and memory usage, among others [29].

• Processing: Includes operations such as encryption, decryption, key generation, digital signing, and verification. These processes may be intensive, depending on the underlying algorithm.
• Resources: Protocols with high computational complexity require more processing power and memory capacity, posing challenges in resource-constrained devices such as sensors, mobile platforms, or IoT devices.

Together, communication and computational complexity define the operational cost of cryptographic protocols. Analyzing both dimensions allows for optimal trade-offs between security, efficiency, and scalability, critical for the development of practical and secure cryptographic solutions.

4.1. Communication Complexity of the Proposed Protocol as a Function of N

When extending the protocol for $N>3$, it can be generalized as follows:

• The mediator shares the public key with the N parties: N messages.
• Each pair of consecutive parties exchanges encrypted data: $N-1$ messages.
• The last party sends the aggregate to the mediator: 1 message.
• The mediator sends the result and the noninteractive challenge to all parties: N messages.

Thus, the generalized communication cost is:

$$C_{protocol}=N+(N-1)+1+N=3N$$

(7)

Regarding the communication complexity of the protocol proposed by Mehnaz et al., their article specifies a general complexity of $3N+1$, with N representing the number of participants.

A relevant observation is that this expression does not fully account for all the phases of the protocol, notably omitting the key-sharing stage conducted by both the trusted server and the participating nodes. This omission introduces additional communication costs that must be considered for a realistic analysis of the efficiency of the protocol.

Two alternative approaches are proposed below to model the key-sharing phase and incorporate these additional costs into the communication complexity analysis.

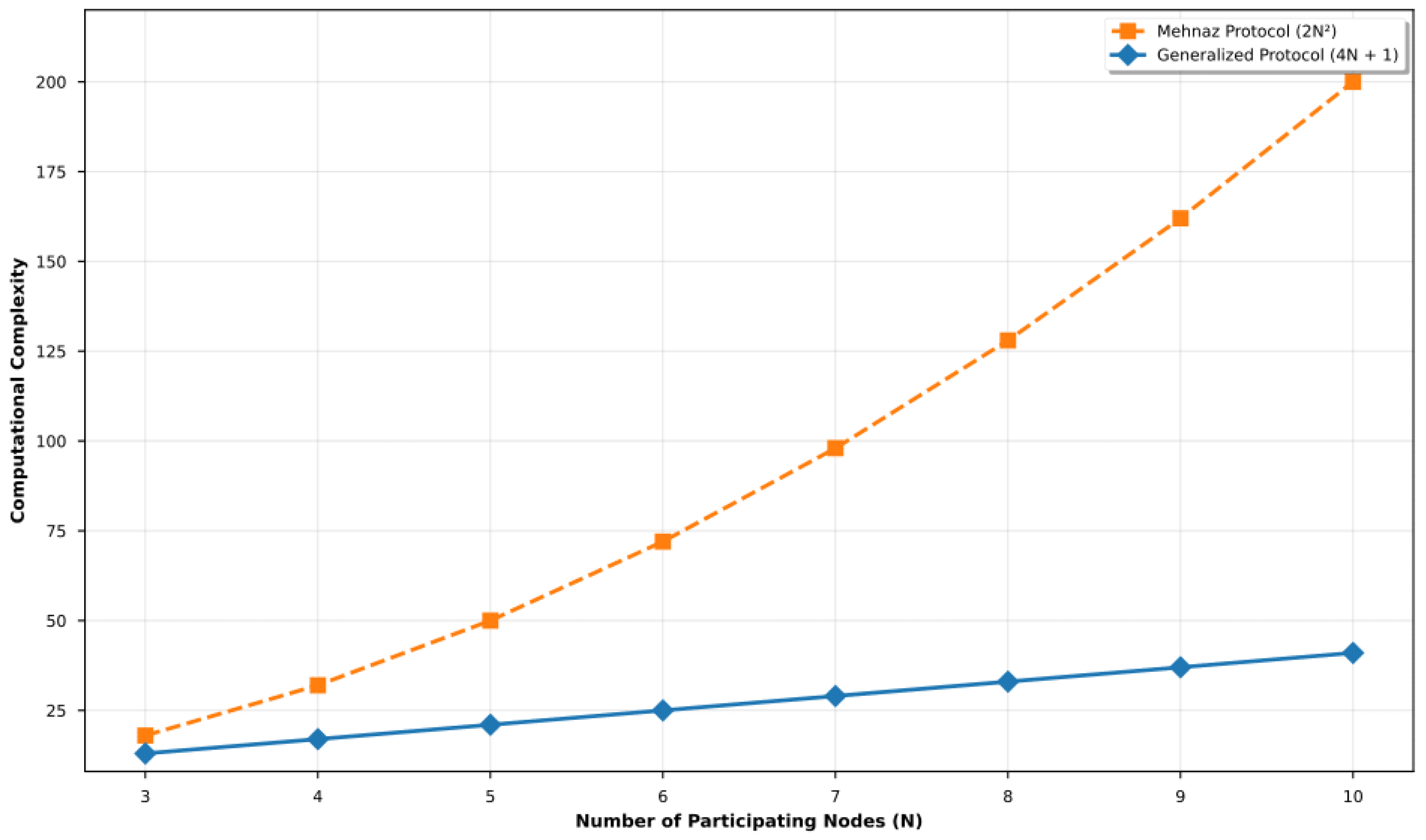
• Direct-sharing method: In this scheme, each participant, including the mediator, communicates directly with each other to share keys. This results in $N(N-1)$ exchanges, added to the $3N+1$ initially considered. The total complexity becomes $N(N-1)+3N+1=N^2+2N+1$, indicating a quadratic growth with additional linear and constant terms, which negatively affects scalability.
• Publish-subscribe (Pub-Sub) model: In this approach, each participant publishes their key on a shared channel accessible to all others, requiring N write operations. Subsequently, each participant reads the keys of the others, generating N additional reads. This introduces $2N$ exchanges for key sharing, which added to the initial $3N+1$ results in $5N+1$, producing linear complexity with an additional constant term. This model improves communication efficiency and enhances the scalability of the protocol.

Figure 4 presents the communication complexity curves for both proposed methods, alongside that of the generalized protocol proposed here. This comparison provides a visual perspective on the real impact of architectural decisions on the total communication cost of the system.

Figure 4 clearly shows that omitting the key exchange stage conceals the true complexity of the communication system, leading to an underestimation in the analysis of communication costs.

4.2. Computational Complexity of the Proposed Protocol as a Function of N

From a computational standpoint, the efficiency of multi-party cryptographic protocols is evaluated based on the number of operations involved in each phase. The growth of these operations as a function of the number of participants (N) allows classification into linear $𝒪\left(N\right)$, quadratic $𝒪\left(N^2\right)$, or higher-order complexity. Formally, the total cost of the protocol is expressed as follows.

$$C_{\mathrm{Total}}=\sum _{i=1}^n(E_i+D_i+T_i),$$

(8)

where:

• $E_i$ denotes encryption operations.
• $D_i$ denotes decryption operations.
• $T_i$ denotes homomorphic transformations.

Proposed protocol based on Damgård–Jurik

This protocol follows a five-stage structure:

• Key generation: performed by the mediator (1 operation).
• Individual encryption: each participant performs one encryption (n operations).
• Sequential aggregation: requires $N-1$ homomorphic operations.
• Final decryption: performed by the trusted entity (1 operation).
• Non-interactive verification: each participant conducts verification checks (n operations).

The total computational cost is

$$C_{\mathrm{total}}=\underset{\underset{\mathrm{keygen}}{︸}}{1}+\underset{\mathrm{enc}}{\underbrace{N}}+\underset{\mathrm{hom}}{\underbrace{(N-1)}}+\underset{\mathrm{dec}}{\underbrace{1}}+\underset{\mathrm{verify}}{\underbrace{2N}}=4N+1$$

(9)

The unidirectional aggregation structure ensures that the protocol exhibits linear computational complexity $𝒪\left(N\right)$.

Mehnaz et al.’s protocol based on ElGamal

The Mehnaz et al. scheme is built on ElGamal and comprises three main stages:

• Distributed key generation: each participant generates a public-private key pair (N operations).
• Parallel encryption: $N^2$ operations are executed.
• Multiple re-encryptions: $N(N-1)$ transformations are required.

The total computational complexity is:

$$C_{\mathrm{total}}=\underset{\mathrm{keygen}}{\underbrace{N}}+\underset{\mathrm{enc}}{\underbrace{N^2}}+\underset{\mathrm{reenc}}{\underbrace{N(N-1)}}=2N^2$$

(10)

The graphical analysis in Figure 5 illustrates that the protocol of Mehnaz et al. exhibits quadratic complexity $𝒪\left(N^2\right)$ in both variations, limiting its scalability in resource-constrained environments, as also noted in [23].

In contrast, the proposed Damgård–Jurik-based protocol maintains linear complexity $𝒪\left(N\right)$, due to its sequential structure and efficient use of homomorphic operations. This makes it suitable for distributed systems with computational constraints, ensuring enhanced scalability and efficiency in multi-party cryptographic schemes.

Table 2. Comparison of communication and computational complexity in protocols.

Protocol	Communication Complexity		Computational Complexity
	Broker Communication	Direct Communication
Mehnaz protocol	$𝒪\left(N\right)$	$𝒪\left(N^2\right)$	$𝒪\left(N^2\right)$
Proposed protocol (Damgård–Jurik Based)	—	$𝒪\left(N\right)$	$𝒪\left(N\right)$

provides a summary of the communication and computational complexity orders for the protocols under analysis, namely the scheme proposed by Mehnaz et al. and the protocol introduced in this article based on the Damgård–Jurik cryptosystem.

5. Proof of Concept in a Local Environment

To empirically validate the feasibility and efficiency of the proposed secure summation protocol, this section presents a proof-of-concept implementation conducted in a controlled local environment. The goal is to evaluate the performance of the protocol under realistic computational constraints and varying data distributions. To this end, a set of virtual machines was configured to emulate a decentralized setting with multiple participating entities and a trusted mediator. The implementation evaluates two distinct data partitioning strategies—vertical and horizontal—that simulate different real-world data ownership and distribution scenarios. By analyzing execution times across varying data set sizes, this proof-of-concept provides critical insights into the scalability and operational practicality of the protocol in secure multi-party computations.

5.1. Experimental Setup

To evaluate the protocol, a local environment consisting of six virtual machines was configured with the following specifications:

• Operating system: Ubuntu Server 24.04 LTS
• CPU: Each machine utilized a Ryzen 5 3500U processor.
• RAM: 2 GB per machine.
• Storage: 10 GB per machine.

Five of the machines served as participating nodes in the protocol, while the sixth acted as the mediator node. The system was implemented using Python 3.12.3, with ZeroMQ (https://zeromq.org/languages/python/ accessed on 24 June 2025) enabling inter-party communication, see [30]. A Python script executing the Damgård–Jurik cryptographic algorithm [8] handled the encryption, with keys set at 2048 Bits. The related code can be accessed publicly in https://doi.org/10.5281/zenodo.15491909 (accessed on 22 June 2025).

The study used five data sets, generated specifically to evaluate the protocol experimentally, each containing nine attributes. Experimental validation used five multidimensional data sets (9 attributes per case), with sizes progressively ranging from ${10}^4$ to $5\times {10}^6$ records. Data sets, segmented using hybrid vertical–horizontal partitioning, allowing an evaluation of the efficiency of the protocol under both data distribution frameworks can be found in https://doi.org/10.5281/zenodo.15491909 (accessed on 22 June 2025).

For each experiment, the data sets were evenly distributed among 3, 4, and 5 participating nodes. In cases of inexact partitions (where the number of records or attributes was not divisible among the participants), the additional row or column was assigned to one of the nodes, minimizing the imbalance and ensuring a fairly balanced distribution.

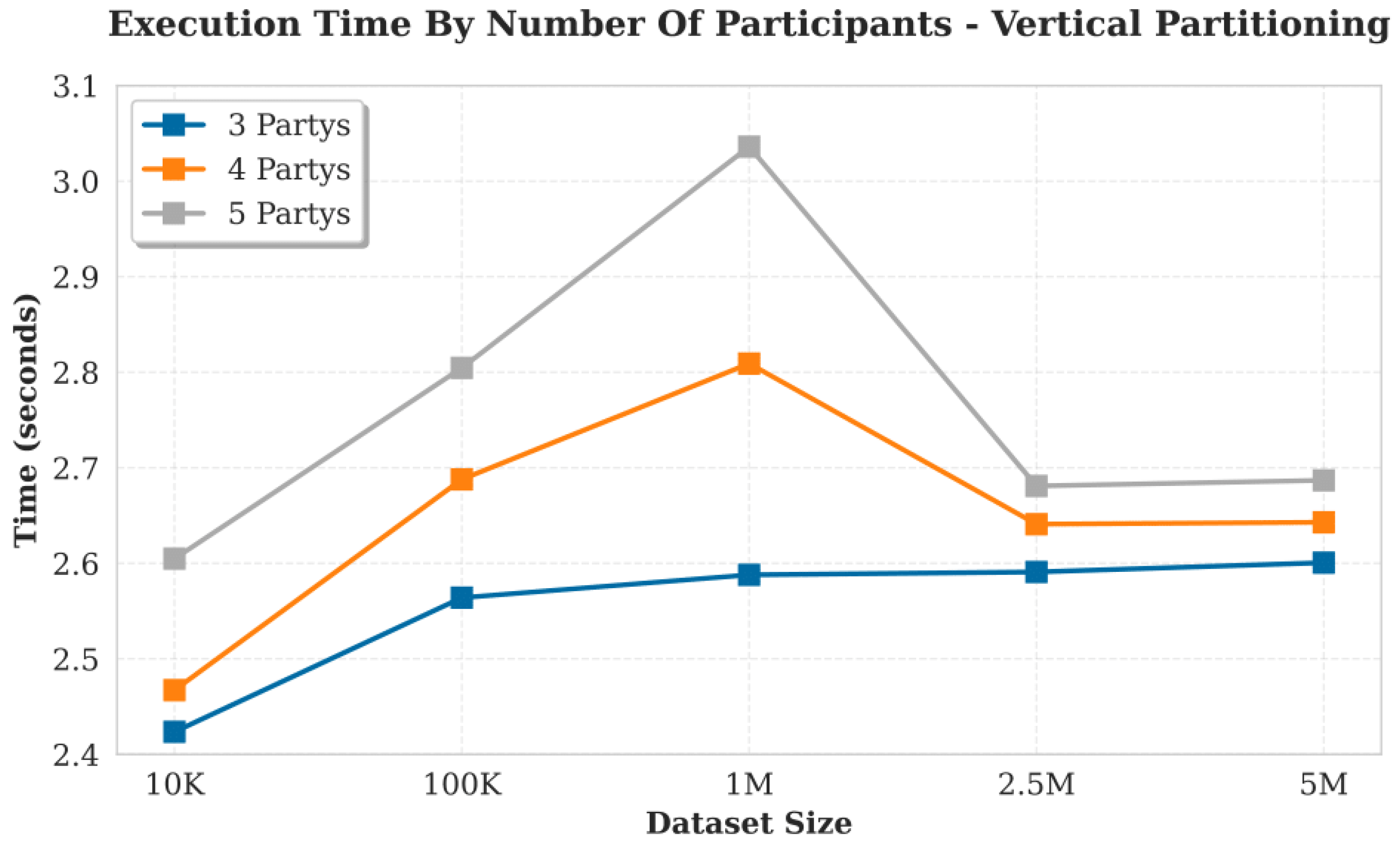
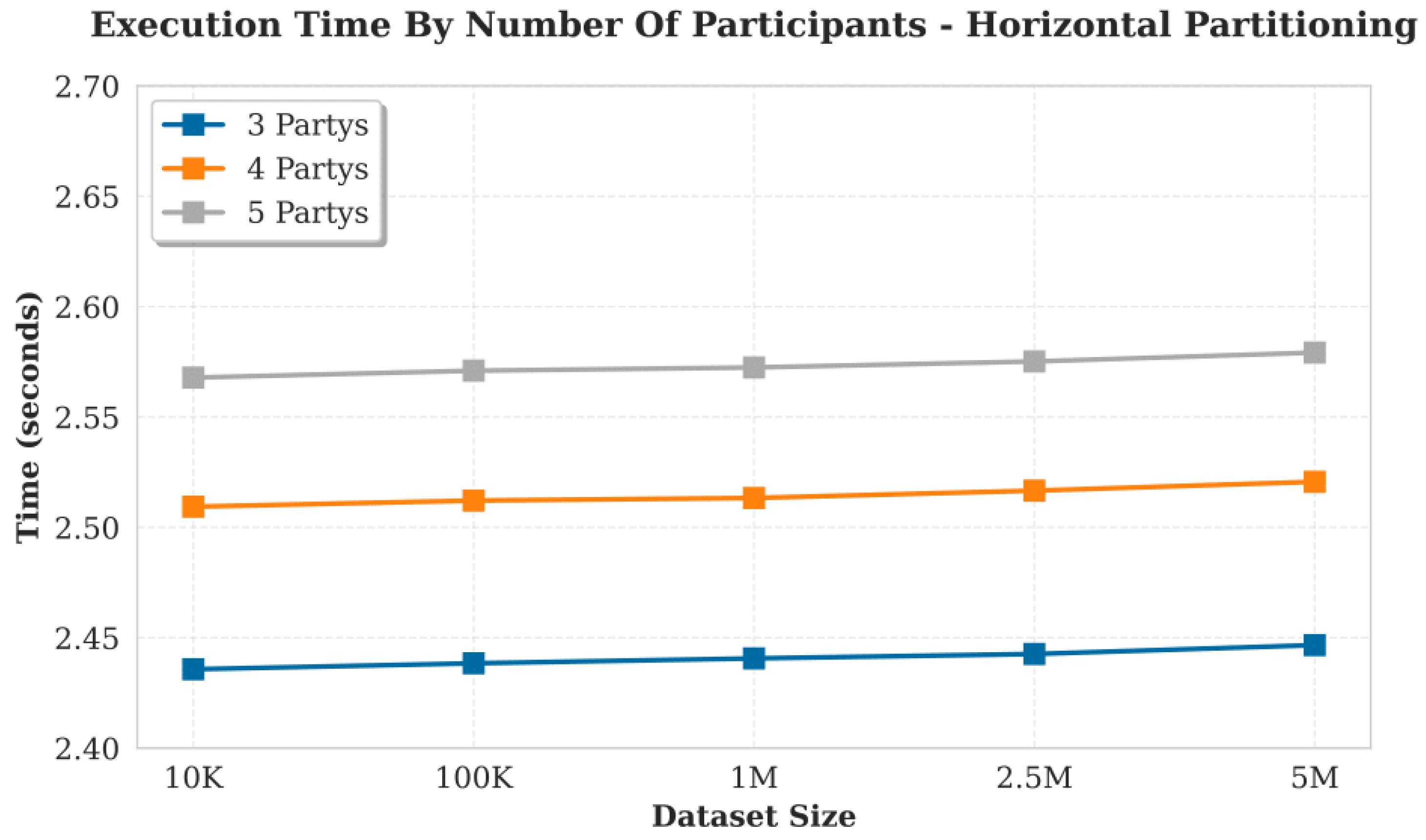
5.2. Performance of the Proof of Concept

This section examines the two proposed partitioning schemes (vertical and horizontal, as in

Table 3. Vertical (above) and Horizontal (below) partitioning schemes used in the experiment. Each color represents a partition.

Attribute 1	Attribute 2	Attribute 3	Attribute 4
80	110	40	60
92	120	60	86
78	100	90	73
Attribute 1	Attribute 2	Attribute 3	Attribute 4
80	110	40	60
92	120	60	86
78	100	90	73

.) used in the proof-of-concept. It presents graphs that illustrate the execution times for each case, accompanied by a detailed analysis explaining the observed behaviors and implications of each method.

Figure 6 displays the execution times for various data sets in vertical partitioning. The x-axis indicates the size of the data set (in rows). The figure shows an ascending trend; however, beginning with the 2.5 M rows data set, execution times seem to stabilize. This behavior may be attributed to a balanced data distribution between nodes: larger data sets allow data loads to be distributed more uniformly and efficiently among participating nodes. As a result, the numerical values to be encrypted become more uniform in length, reducing biases in computational effort among participants.

Notice that additional supporting metrics, such as load distribution or network utilization, were not analyzed in this proof-of-concept.

Figure 7 presents the execution times for various data sets in a horizontal partitioning scheme. Again, the x-axis represents the number of rows in the data sets. The curves show a nearly linear behavior, attributed to the consistent digit lengths of encrypted values throughout the encryption phases. In this scheme, since the data set is uniformly distributed, each participant receives a partition with a similar structure and characteristics. This leads to input values of approximately constant length for encryption, resulting in uniform processing loads and execution times that scale linearly with data set size.

5.3. Result of the Proof of Concept

Table 4. Key gen, encryption, and decryption execution times—vertical partitioning.

Protocol	Nodes	Key Gen (s)	SD	Key Dist (s)	SD	Enc (s)	SD	Dec (s)	SD
Proposed	4	0.89128	0.2041	0.9645	0.5619	0.3019	0.0526	0.3398	0.0434
Mehnaz	4	13.4363	7.4428	20.2525	6.3362	2.9850	0.5626	1.5040	0.8516
Proposed	5	0.9778	0.3400	0.9721	0.5357	0.3541	0.0854	0.3642	0.0611
Mehnaz	5	15.0448	6.9638	23.2300	7.0628	2.7923	0.4032	1.2717	0.7915

and

Table 5. Schnorr NIZKP and total execution times—vertical partitioning.

Protocol	Nodes	ZKP Val. (s)	SD	Total (s)	SD
Proposed	4	0.2171	0.0807	3.3177	0.1882
Mehnaz	4	0.0000	0.0000	55.4722	2.9796
Proposed	5	0.2133	0.0590	3.4906	0.3806
Mehnaz	5	0.0000	0.0000	82.6498	11.4219

display the execution times for key generation, encryption, decryption, Schnorr’s zero knowledge proof, and the overall elapsed time, measured in seconds. The results indicate improved performance, as our protocol replaces the iterative encryption and decryption steps in Mehnaz’s protocol with a single encryption round. Note that the total time (in seconds) also accounts for additional processes not detailed in the table, but these can be accessed on the provided Github.

The protocol demonstrated its ability to efficiently handle large data sets, provided that the summation is performed locally. This local aggregation results in a single value per party, which is then encrypted using homomorphic addition. This technique enables the combination of multiple encrypted values without the need for decryption. Although this implementation was tested only as a proof-of-concept, it was observed that the generation of public and private keys is the most time-intensive task, primarily due to key bit length. For this reason, this process is not reflected in Figure 6 and Figure 7, as its duration depends on the hardware and is usually performed in advance.

6. Conclusions

This paper presents a secure summation protocol based on the Damgård–Jurik cryptosystem, generalizing and improving upon prior work for both vertically and horizontally partitioned environments [16]. Using additive homomorphism and local preaggregation, the protocol reduces communication and computational complexity from quadratic to linear order while maintaining privacy through encryption and integrity through NIZKs. Experimental validation confirms its practicality for large-scale deployments, although challenges such as key distribution overhead persist. Future work should include comprehensive performance comparisons with a wider range of existing protocols (including FHE-based and secret-sharing approaches), optimization of key management procedures, and extension to dynamic multi-party settings with adaptive security guarantees. These advancements would further solidify the position of the protocol as a versatile solution for secure decentralized computation.