Group Attention Aware Coordination Graph

Abstract

Cooperative Multi-Agent Reinforcement Learning (MARL) relies on effective coordination among agents to maximize team performance in complex environments. However, existing coordination graph-based approaches often overlook dynamic group structures and struggle to accurately capture fine-grained inter-agent dependencies. In this paper, we introduce a novel method called the Group Attention Aware Coordination Graph (G2ACG), which builds upon the group modeling capabilities of the Group-Aware Coordination Graph (GACG). G2ACG incorporates a dynamic attention mechanism to dynamically compute edge weights in the coordination graph, enabling a more flexible and fine-grained representation of agent interactions. These learned edge weights guide a Graph Attention Network (GAT) to perform message passing and representation learning, and the resulting features are integrated into a global policy via QMIX for cooperative decision-making. Experimental results on the StarCraft II Multi-Agent Challenge (SMAC) benchmark show that G2ACG consistently outperforms strong baselines, including QMIX, DICG, and GACG, across various scenarios with diverse agent types and population sizes. Ablation studies further confirm the effectiveness of the proposed attention mechanism, demonstrating that both the number of attention heads and the number of GAT layers significantly affect performance, with a two-layer GAT and multi-head attention configuration yielding the best results.

1. Introduction

Cooperative Multi-Agent Reinforcement Learning (MARL) aims to enable a group of agents to collaboratively solve complex tasks in a shared environment through collaboration and coordination [1]. Compared to single-agent reinforcement learning, the introduction of multiple agents brings additional challenges, particularly when dealing with vast state and action spaces, where traditional reinforcement learning algorithms prove inefficient [2]. A straightforward approach is to decompose the global training objective into individual tasks for each agent, solving for the maximization of the overall return by maximizing the action–value function of each single agent, as seen in algorithms like VDN [3] and QMIX [4]. However, real-world tasks are often hard to decompose into simple individual subtasks. This limitation motivates the need to model inter-agent relationships explicitly, often represented by coordination graphs (CGs), where nodes denote agents and edges capture their dependencies.

Recent advances in MARL have explored coordination graphs to model agent interactions, leading to three main branches: directly linking all nodes to create complete graphs [2], weighting edges of fully connected graphs with attention mechanisms [5], and introducing group relationships to construct sparse graphs [2,6]. However, these algorithms fail to effectively balance capturing group dynamics and the accurate acquisition of weights between agents, resulting in sub-par performance. Moreover, they often overlook the need to adaptively model fine-grained inter-agent differences in complex environments. Take StarCraft II (StarCraft and StarCraft II are trademarks of Blizzard Enterainment) games as an example. Some maps, such as 2 Stalkers & 3 Zealots, feature diverse types of agents. This demands not only the efficient division of labor between their groups but also the real-time and precise construction of weight relationships between nodes.

Motivated by these limitations, we aim to enhance coordination graph expressiveness by introducing dynamic edge reasoning while preserving group structure modeling. To address the limitation of the current GACG algorithm, where the sampled graph lacks subsequent edge weight computation, resulting in weaker capability to capture node differences, we propose a novel improved algorithm: Group Attention Aware Coordination Graph (G2ACG). This algorithm builds upon the GACG framework while preserving its group relationship modeling capabilities, and introduces one of the latest dynamic attention mechanisms [7] to enable the more precise capture of inter-agent relationships. Specifically, it integrates a multi-head attention module to dynamically generate edge weights, which are then used in a Graph Attention Networks (GATs) for message propagation and policy learning. The integration of these components significantly enhances multi-agent coordination efficiency in more complex environments. Recent studies have introduced various attention mechanisms to enhance multi-agent learning performance, such as the DAGMIX [8] and GA-Comm [9] algorithms. However, these methods still face challenges in complex, heterogeneous scenarios.

In order to validate the superiority of the G2ACG algorithm, we conducted tests on decentralized micromanagement tasks in the StarCraft II Multi-Agent Challenge (SMAC) environment [10]. Through experimental evaluation, we not only verified the algorithm’s superior performance but also investigated the contributions of its individual components.

The contributions of this paper are summarized as follows:

• We provide a systematic categorization of existing coordination graph-based MARL algorithms, analyzing their construction paradigms and limitations to guide future research.
• Building upon the GACG framework, we integrate its group relationship modeling while introducing a novel dynamic attention mechanism that breaks the weight-sharing constraint in traditional GAT networks [11]. This design enables agents to flexibly assign attention weights to different neighbors, enhancing the model’s expressiveness in representing diverse inter-agent interactions.
• Through conducting experiments on the StarCraft II (SMAC) environment [10], we demonstrate that our proposed G2ACG algorithm outperforms other baseline methods, showcasing the advantages of combining group relationships with dynamic attention mechanisms. Additionally, ablation studies validate the effectiveness of key components, highlighting the importance of multi-head attention and GAT layer depth.

2. Related Work

In the field of MARL, coordination graph-based approaches provide effective solutions for enabling cooperation among agents [5,12]. These methods aim to represent agent interactions as structured graphs, allowing information exchange, policy decomposition, and coordination to be more interpretable and efficient. To adapt to environmental changes and task requirements, current algorithms need to monitor environmental dynamics and agent states in real time and dynamically adjust coordination relationships [13]. The following are some major algorithms and their characteristics.

DCG [5] is one of the earliest proposed algorithms. It factors the joint value function according to a coordination graph into pairwise payoffs, and employs parameter sharing and low-rank approximations to manage complexity. However, its static graph structure limits its ability to adapt to changing agent behaviors. DICG [14] uses attention mechanisms and attempts to dynamically learn coordination relationships among agents through a deep network structure. GCS [15] proposes decomposing the joint team policy into a graph generator and a graph-based coordination policy, enabling the graph structure to evolve during training. GACG [2] leverages group-level behavior similarities and represents edges in the coordination graph as Gaussian distributions, combining agent–pair interaction and group-level dependencies. LTS-CG [16] calculates a probability matrix for agent pairs based on historical observation data and samples sparse coordination graphs for efficient information propagation. DMCG [6] extends traditional coordination graphs by introducing dynamic edge types to capture higher-order and indirect relationships among agents. GA-Comm [9] proposes a two-stage attention mechanism for multi-agent game abstraction, using hard attention to prune edges and soft attention to weight interactions. Co-GNN [17] treats nodes as agents that dynamically choose actions, enabling adaptive graph rewiring via jointly trained policy and environment networks. The corresponding algorithm can be found in

Table 1. Comparison of coordination graph-based methods.

Approach	Core Methodology	Graph Type
DCG	Full connectivity of all nodes	Complete graph
DICG	Attention-weighted edges	Dynamic dense graph
GCS	Two-stage policy	Sparse graph
GACG	Group-wise Gaussian edges	Hierarchical graph
LTS-CG	History-based edge pruning	Sparse temporal graph
DMCG	Typed edge modeling	Multi-relational graph
GA-Comm	Two-stage attention	Dynamic sparse graph
Co-GNN	Node-level action selection	Adaptive directed graph

.

While these approaches demonstrate promising progress in coordination modeling, they also exhibit key limitations. Many existing algorithms either overlook higher-order group structures or fail to capture fine-grained inter-agent variations in edge weights, which are essential for dynamic coordination. Consequently, they struggle to complete the adjustment and optimization of coordination relationships within short timeframes [18]. This limitation affects the overall performance and adaptability of multi-agent systems and results in insufficient capability when facing complex and uncertain environments.

3. Background

We consider a classical Decentralized Partially Observable Markov Decision Process (Dec-POMDP) [19], described with a tuple $\langle N,S,{\left\{A_i\right\}}_{i=1}^n,P,{\left\{O_i\right\}}_{i=1}^n,{\left\{{\pi }_i\right\}}_{i=1}^n,R,\gamma \rangle$. Let $N=\{N_1,N_2,\dots ,N_n\}$ denote the set of n agents. The true state of the environment is represented by $s\in S$. At each time step t, agent $N_i$ receives an observation $o_i^t\in O^t$ and takes an action ${\mathbf{a}}_i^t\in A^t$ according to its policy ${\pi }_i$. The environment then transitions to the next state $s^{\prime }$ based on the state transition function $P\left(s^{\prime }\right|s,\mathbf{a})$. All agents share a common reward function $R(s,\mathbf{a})$, and $\gamma \in [0,1]$ is the discount factor. In a T-length scenario, the agents collaborate to maximize the joint action–value function at moment t:

$$Q_{\mathrm{tot}}(s^t,{\mathbf{a}}^t)={\mathbb{E}}_{s^{t+r},{\mathbf{a}}^{t+r}}\left[\sum _{i=0}^T{\gamma }^{i}R(s^{t+i},{\mathbf{a}}^{t+i})|s^t,{\mathbf{a}}^t\right]$$

(1)

4. Methods

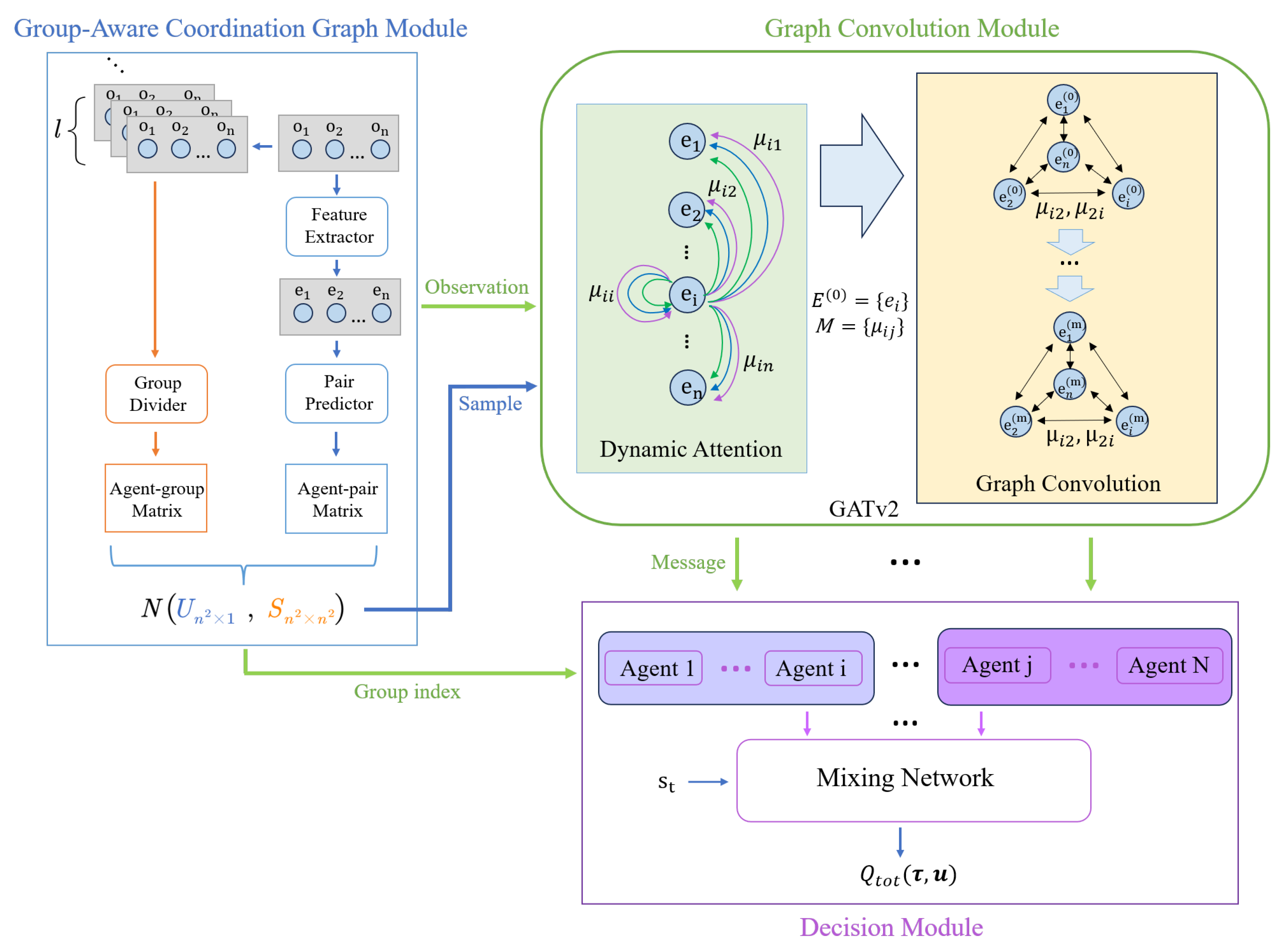
We adopt the GACG framework to generate a coordination graph. By incorporating a dynamic attention mechanism, we design the G2ACG algorithm, as illustrated in Figure 1. The algorithm can be broadly divided into three components:

• Group-Aware Coordination Graph Module (Blue Box). This module employs the group relationship capturing method from GACG [2]. It utilizes group relationships to derive a Gaussian distribution, which is then used to sample the edges of the coordination graph.
• Graph Convolution Module (Green Box). We introduce a dynamic attention mechanism [7] to dynamically compute the attention weights of nodes in the sampled coordination graph. Through multi-layer GCN (Graph Convolutional Network) [20] convolutions, the features of node messages in the coordination graph are extracted.
• Action Decision Module (Purple Box). Each group of agents determines the optimal Q-values based on their current observations and action inputs. These Q-values are then aggregated using the QMIX network [4] to derive the optimal value of the joint action–value function.

Below is an introduction to its implementation principles.

Figure 1. The framework of G2ACG, consisting of three main components: a Group-Aware Coordination Graph module (blue), a Graph Convolution Module (green), and an action decision module (purple). We use GATv2 network to generate the weight of edges dynamically.

Figure 1. The framework of G2ACG, consisting of three main components: a Group-Aware Coordination Graph module (blue), a Graph Convolution Module (green), and an action decision module (purple). We use GATv2 network to generate the weight of edges dynamically.

4.1. Group-Aware CG

Our approach adopts the group relationship capturing method from GACG. For the observations of agents at time step t: $\{o_1^t,o_2^t,\dots ,o_n^t\}$, a feature extractor $f_{\mathrm{ext}}(·)$ extracts their hidden features $\{{\mathit{e}}_1,{\mathit{e}}_2,\dots ,{\mathit{e}}_n\}$, which is realized via a multi-layer perceptron (MLP). Then, pair predictor $f_{\mathrm{pre}}(·)$, an attention network, computes the weights between agent nodes at the current timestep. The weight relations can be represented as an adjacency matrix, which is denoted as the agent–pair matrix:

$$\begin{array}{cc}\hfill {\mathit{e}}_i& =f_{\mathrm{ext}}\left({\mathit{o}}_i\right)\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill u_{ij}& =f_{\mathrm{pre}}({\mathit{e}}_i,{\mathit{e}}_j)\hfill \end{array}$$

(3)

To facilitate the representation of edge weights, the matrix is reshaped into a column vector:

$${\mathit{U}}_{ij}=vec\left(u_{ij}\right)$$

(4)

On the other hand, we record observation trajectories over a fixed window length l (set to 10 in this experiment). Under the premise that agents with similar observations within a specific time period are likely to exhibit similar behaviors [2], the group divider partitions the agents into m distinct groups, yielding group relationships:

$$G=f_{\mathrm{div}}\left({\mathit{O}}^{t-l:t}\right)$$

(5)

Here, $f_g(·)$ maps the set of agents N to the set of groups G, and ${\mathit{O}}^{t-l:t}$ represents the observation trajectories of agents from timestep $t-l$ to t. Based on the agent grouping, the agent-group matrix $\mathit{S}$ is constructed:

$$s_{ij}^t=\left\{\begin{array}{cc}1\hfill & a_i,a_j\in g_m\mathrm{at}\mathrm{moment}t\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(6)

This matrix indicates whether agents $a_i$ and $a_j$ belong to the same group at timestep t. The group relationships between agents can then be transformed into group relationships between edges in the coordination graph using the following method:

$$S_{L_1{L}_2}^t=vec\left(s_{ab}^t\right)·vec{\left(s_{cd}^t\right)}^T$$

(7)

$S_{L_1{L}_2}^t=1$ signifies that the four nodes $a,b,c,$ and d on edges $L_1$ and $L_2$ are all in the same group at the current timestep; otherwise, the value is 0.

The weights between agents reflect their connectivity, while the group relationships reflect their dispersion [2]. Using these two matrices, the relationships between edges in the coordination graph can be represented as a two-dimensional Gaussian distribution, i.e.,

$$({\mathit{e}}_{ab},{\mathit{e}}_{cd})\sim \mathcal{N}\left(\left(\begin{array}{c}{U}_{ab},U_{cd}\end{array}\right),\left[\begin{array}{cc}{S}_{L_1{L}_1}& S_{L_1{L}_2}\\ S_{L_2{L}_1}& S_{L_2{L}_2}\end{array}\right]\right)$$

(8)

4.2. Group Attention Aware Cooperative for MARL

Utilizing the Gaussian distribution defined in Equation (8), we sample the edges of the Group-Aware Coordination Graph at each timestep, reshaping them into matrix form ${\mathit{C}}^t$.

Definition 1

(Dynamic attention). For a query node set Q and key node set K, if there exists a family of scoring functions $f\in \mathcal{F}$, such that, for every query $i\in \left[v\right]$ and non-target key $j_{\ne \phi \left(i\right)}\in \left[w\right]$, it satisfies

$$f(q_i,k_{\phi \left(i\right)})>f(q_i,k_j)$$

(9)

then f is called a dynamic attention function, where $\phi :\left[v\right]\to \left[w\right]$. This mechanism effectively addresses the limitation of static attention coefficients where the sorting is independent of the query nodes [7].

For the sampled sparse graph, we employ a dynamic attention mechanism [7] to compute weights between nodes. Compared to the standard Graph Attention Network (GAT) [11], GATv2 modifies the internal operation sequence: it applies the $\mathit{a}$ layer (a single-layer feedforward network) after the nonlinearity $\mathit{LeakyReLU}$ (with negative input slope 0.2), and applies the $\mathit{W}$ layer after feature concatenation [7]. This yields the attention coefficients

$$z_{ij}={\mathit{a}}^T\mathit{LeakyReLU}\left(\mathit{W}·[{\mathit{e}}_i\parallel {\mathit{e}}_j]\right)$$

(10)

where $\mathit{e}=\{{\mathit{e}}_1,{\mathit{e}}_2,\dots ,{\mathit{e}}_n\}$ denotes features extracted in the preceding stage, $\mathit{a}$ is the weight vector of the $\mathit{a}$ layer, and $\mathit{W}$ is the weight matrix. Cross-node normalization is achieved via softmax to obtain weights between feature nodes:

$${\mu }_{ij}={softmax}_j\left(z_{ij}\right)={\displaystyle \frac{exp\left(z_{ij}\right)}{{\sum }_{k\in {\mathcal{N}}_i}exp\left(z_{ik}\right)}}$$

(11)

The dynamic attention values ${\mu }_{ij}$ are integrated into the Graph Convolutional Network (GCN) [20] to generate the final message. The features $E^{\left(0\right)}=\left\{e_i\right\}$ serve as the original input, and the features of the l-th layer are obtained through the following iteration:

$$E^{\left(l\right)}=\mathrm{ReLU}\left({\tilde{D}}^{-{\displaystyle \frac{1}{2}}}M{\tilde{D}}^{-{\displaystyle \frac{1}{2}}}{E}^{(l-1)}{W}_c^{(l-1)}\right)$$

(12)

where ${\tilde{D}}_{ii}={\sum }_j{\mu }_{ij}$, and $W_c^{\left(l\right)}$ is the trainable weight matrix of the l-th layer. The features $E^{\left(m\right)}$ obtained from the final convolution serve as the messages $\left\{m^t\right\}$, which, together with the agent’s observation $\left\{o_i^t\right\}$ and the previous action $\left\{a_i^{t-1}\right\}$, are fed into the QMIX network. The mixing network then outputs the global optimal Q-value, based on which the next action $a^t$ is determined.

5. Experiments and Results

In this section, we design experiments to investigate the following: (1) How does G2ACG perform in complex cooperative multi-agent tasks compared to other CG-based methods? (2) How do different numbers of GCN layers affect G2ACG’s performance? (3) How does increasing the number of dynamic attention heads impact the final results? For the experiments in this study, we test our algorithm on decentralized micromanagement problems in the SMAC environment. We consider combat scenarios where two identical groups of units are symmetrically positioned on the map, with each scenario containing at least five agents. The environment difficulty level is set to 7. To ensure the robustness and reliability of our experimental methodology, all tests are conducted with five random seeds.

5.1. Compared with Other CG-Based Methods

We use QMIX [4], DICG [14], and GACG [2] as baseline algorithms for comparison (the characteristics of each method are summarized in Table 2):

• QMIX decomposes the global value function into a monotonic mixing of individual value functions through monotonicity constraints. It is suitable for multi-agent tasks in simple situations.
• DICG dynamically infers the coordination graph structure through a self-attention mechanism, enabling the method to be applied to more abstract multi-agent domains.
• GACG introduces higher-order group relationships and encourages behavioral specialization between groups through group-aware coordination, making it suitable for scenarios that emphasize group collaboration among diverse types of agents.

Table 2. Comparison of characteristics among different baseline algorithms (h denotes the number of attention heads, and l is the trajectory length).

Approach	Graph	Attention	Group	GC Time Complexity
QMIX	✕	✕	✕	✕
DICG	✓	Static	✕	$O\left(h{N}^2\right)$
GACG	✓	✕	✓	$O\left(l{N}^2\right)$
G2ACG	✓	Dynamic	✓	$O\left(hl{N}^2\right)$

✓ indicates that the algorithm incorporates the structure/component, whereas ✕ means it does not.

Table 2. Comparison of characteristics among different baseline algorithms (h denotes the number of attention heads, and l is the trajectory length).

Approach	Graph	Attention	Group	GC Time Complexity
QMIX	✕	✕	✕	✕
DICG	✓	Static	✕	$O\left(h{N}^2\right)$
GACG	✓	✕	✓	$O\left(l{N}^2\right)$
G2ACG	✓	Dynamic	✓	$O\left(hl{N}^2\right)$

✓ indicates that the algorithm incorporates the structure/component, whereas ✕ means it does not.

We conducted comparative experiments in four different map environments: 2s3z, 3s5z, 8m, and 8m_vs_9m. The experimental results are shown in Figure 2 (for intuitive visualization, all data in the results were smoothed with a coefficient of 0.6). Among them, G2ACG demonstrated optimal performance across all scenarios. In the 8m and 8m_vs_9m maps, G2ACG not only achieved significantly higher final win rates than the other three baseline algorithms, but also showed noticeably faster convergence speed. In the 2s3z and 3s5z maps, although the convergence speed was not significantly faster than QMIX and GACG, G2ACG still maintained higher final win rates than the other three baseline algorithms.

The three baseline algorithms each exhibited their respective limitations. The QMIX algorithm, lacking graph structure utilization, demonstrated poor adaptability in maps with larger numbers of agents such as 8m_vs_9m. DICG, which neglects the importance of group relationships, showed significantly weaker learning performance in maps like 2s3z and 3s5z that require clear inter-group specialization among diverse agent types. As for GACG, its failure to incorporate attention mechanisms resulted in inflexible weight calculations between agents, leading to substantially lower win rates compared to G2ACG in maps with numerous agents such as 8m and 8m_vs_9m.

The experimental results clearly demonstrate the advantages of G2ACG’s combination of group relationships and attention mechanisms. The algorithm not only incorporates GACG’s approach to capturing group relationships, but also introduces dynamic attention mechanisms, enabling a more precise modeling of inter-agent relationships and consequently achieving superior performance compared to other algorithms.

5.2. Ablation Study

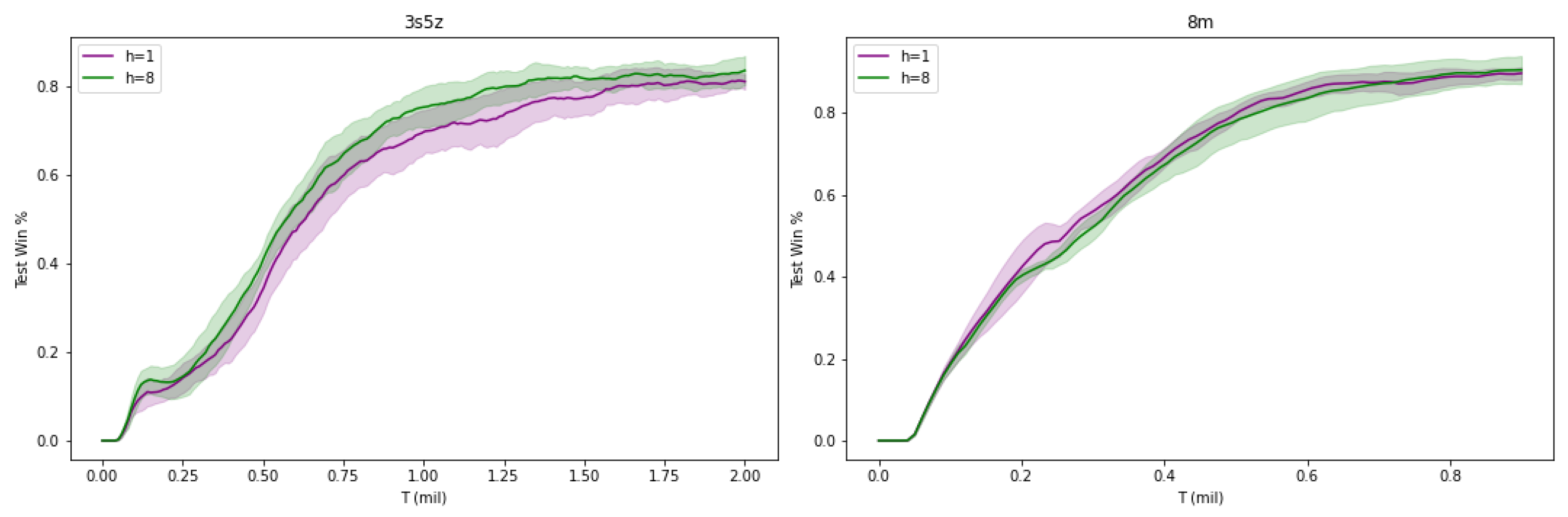
In this section, we conducted ablation experiments to further investigate the roles of various components in the introduced GATv2 network. In the 3s5z and 8m map environments, we examined the impact of different heads of attention on the learning performance of the GACG algorithm. Meanwhile, in the 3s5z and 8m_vs_9m map environments, we studied the performance variations of the G2ACG algorithm when modifying the number of GCN layers.

5.2.1. Heads for Dynamic Attention

To ensure that the output feature dimensions are divisible by the number of heads in our experiments, we uniformly set the message dimension coefficient to 0.5 (the message dimension is the observation dimension multiplied by this coefficient). Under this configuration, the experiment is conducted with h set to $\{1,8\}$, allowing us to systematically investigate the impact of varying head numbers (h) on the algorithm’s performance.

When $h=1$, this indicates the absence of multiple attention mechanisms in the model, meaning that the model relies solely on a single perspective to capture relationships between nodes. Under this configuration, the model may fail to capture subtle interactions that can only be discovered by considering multiple aspects simultaneously. When $h=8$, eight independent weights are employed, which independently compute attention scores and can capture node relationships from multiple different perspectives, thereby achieving a richer representation of the graph structure.

Figure 3 illustrates the impact of attention heads on G2ACG’s performance. The results demonstrate that increasing the number of attention heads can improve the algorithm’s learning effectiveness to some extent, which is particularly evident in the 3s5z map, while showing comparable performance between both agent groups in the 8m map.

5.2.2. Layers of GCNs

In this analysis, to thoroughly investigate the impact of GCN layer numbers (n) on algorithm performance, we explore different values for n, specifically $\{1,2,3,4\}$. When $n=2$, this represents our actually selected G2ACG algorithm configuration.

When $n=1$, the model lacks deep hierarchical graph structure learning, capturing only direct neighborhood information for each node. Conversely, when $n\in \{2,3,4\}$, the presence of multiple GCN layers enables the model to capture deeper-level and more complex structural information.

The result is shown in Figure 4. According to the results, increasing the number of GCN layers within a certain range can improve the final win rate of the algorithm, while an excessively large number of layers leads to a decline in performance. In the scenarios of 3s5z and 8m_vs_9m, the learning performance reaches its optimal level with 2 layers. For an overly large number of GCN layers, on the one hand, as the number of layers increases, the gradient during backpropagation becomes increasingly smaller, causing slow weight updates in the layers closer to the input, i.e., the vanishing gradient problem; on the other hand, information can be lost or overly smoothed during multi-layer propagation, making it difficult for the node feature representations to accurately reflect their intrinsic characteristics and the differences among neighboring nodes.

6. Conclusions

In this paper, we propose G2ACG, which aims to solve the limitation that current multi-agent collaborative reinforcement learning algorithms cannot effectively combine group relationship utilization and node relationship capture, and aims to improve learning efficiency. Compared with previous algorithms, G2ACG not only integrates GACG’s method of capturing group relations by observing behavior patterns on trajectories, but also constructs an edge Gaussian distribution with group relationships, which makes the information exchange efficiency of agents, through graph neural networks, higher in the decision-making process. At the same time, the latest dynamic attention mechanism is introduced to break the weight sharing mechanism in traditional GAT networks [11], so that the network can more flexibly model the varying preferences of nodes toward their neighbors and enhance the ability of the model to deal with complex environments. Through a series of comparative experiments, our approach is evaluated to be superior to the current baseline algorithm overall. In ablation experiments, we further explored the effects of numbers of heads and GCN layers on model performance. The results of this study can improve the accuracy of relationship capture between agents, and help to further improve the efficiency of multi-agent cooperation in more complex environments. Looking ahead, we will enhance G2ACG’s scalability to hundreds of agents via hierarchical sparse graphs and distributed training, and extend it to real-world, communication-limited domains such as multi-robot coordination and autonomous driving fleets.