A Physics-Informed Neural Network Integration Framework for Efficient Dynamic Fracture Simulation in an Explicit Algorithm
Abstract
Featured Application
Abstract
1. Introduction
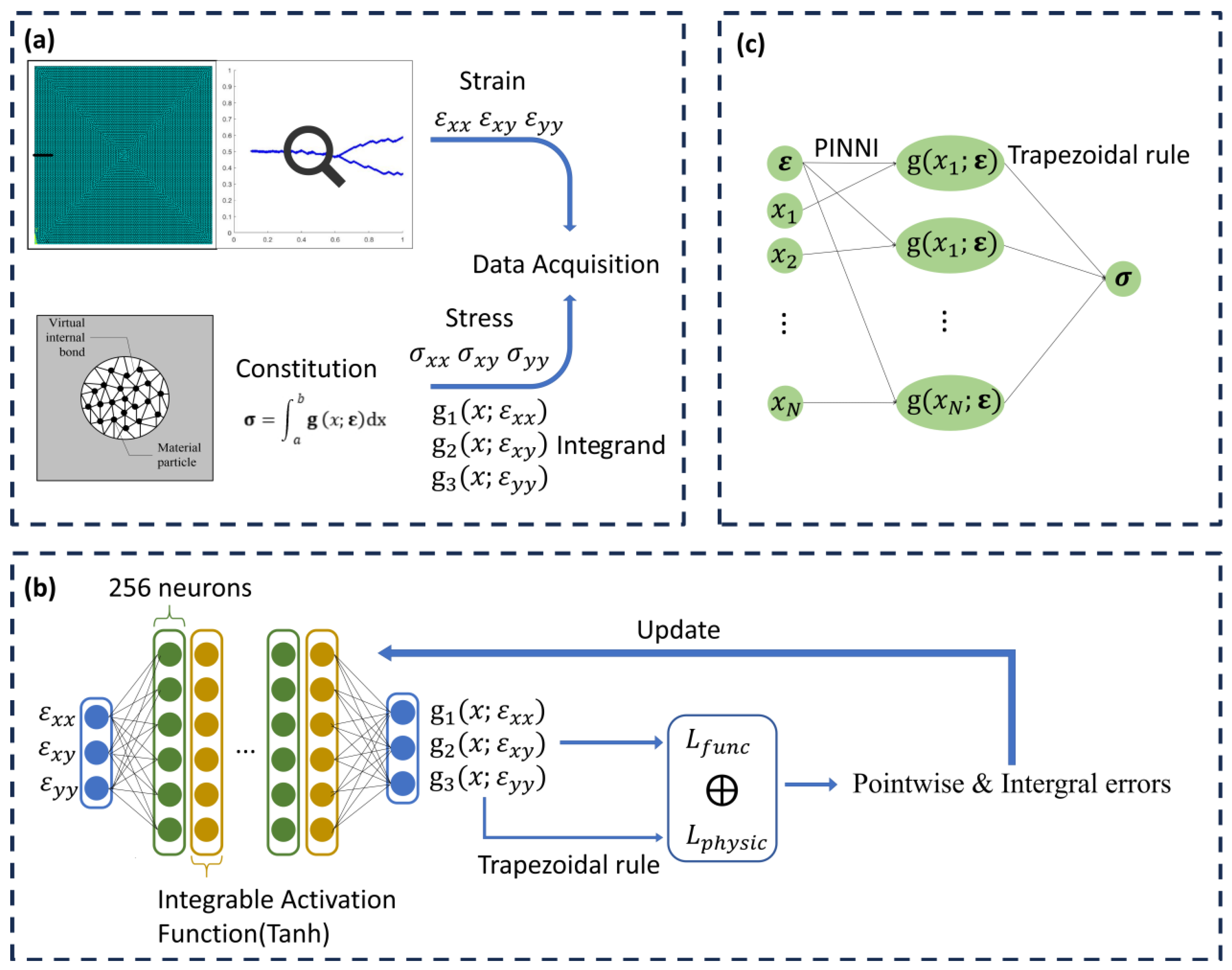
2. Methods
2.1. Physics-Informed Neural Network Integration
2.2. Inference and Integration
- (1)
- A dense vector of points, , is defined over the integration domain.
- (2)
- The trained neural network is queried times, once for each point , while keeping the input features derived from the state constant. This yields a vector of predicted integrand values: .
- (3)
- The integral value, is computed by applying the trapezoidal rule to this vector of integrand values.
- (4)
- The final stress tensor is then calculated from this integral.
2.3. Validation Method
3. PINNI Training and Performance Check
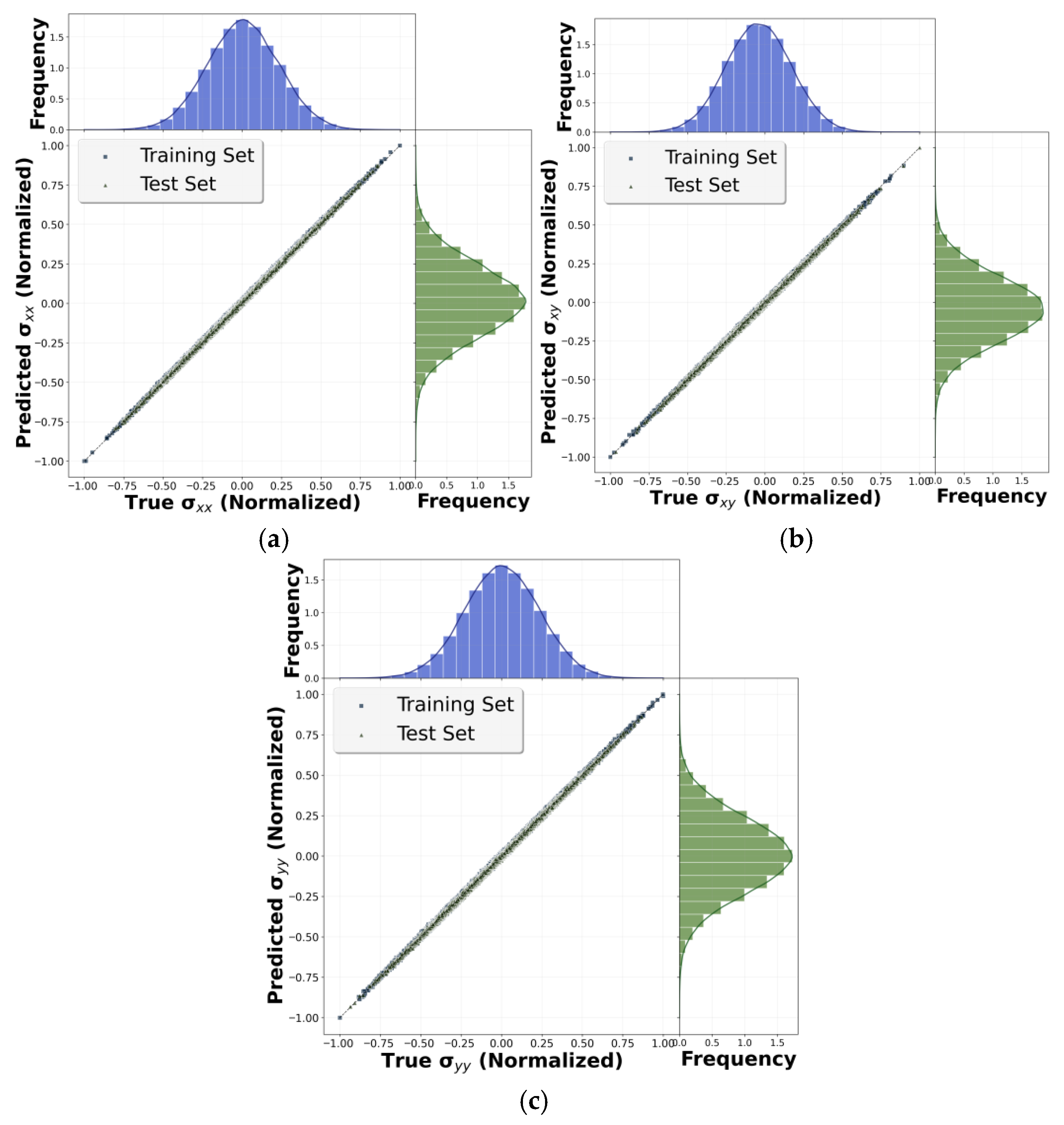
3.1. Linear Case
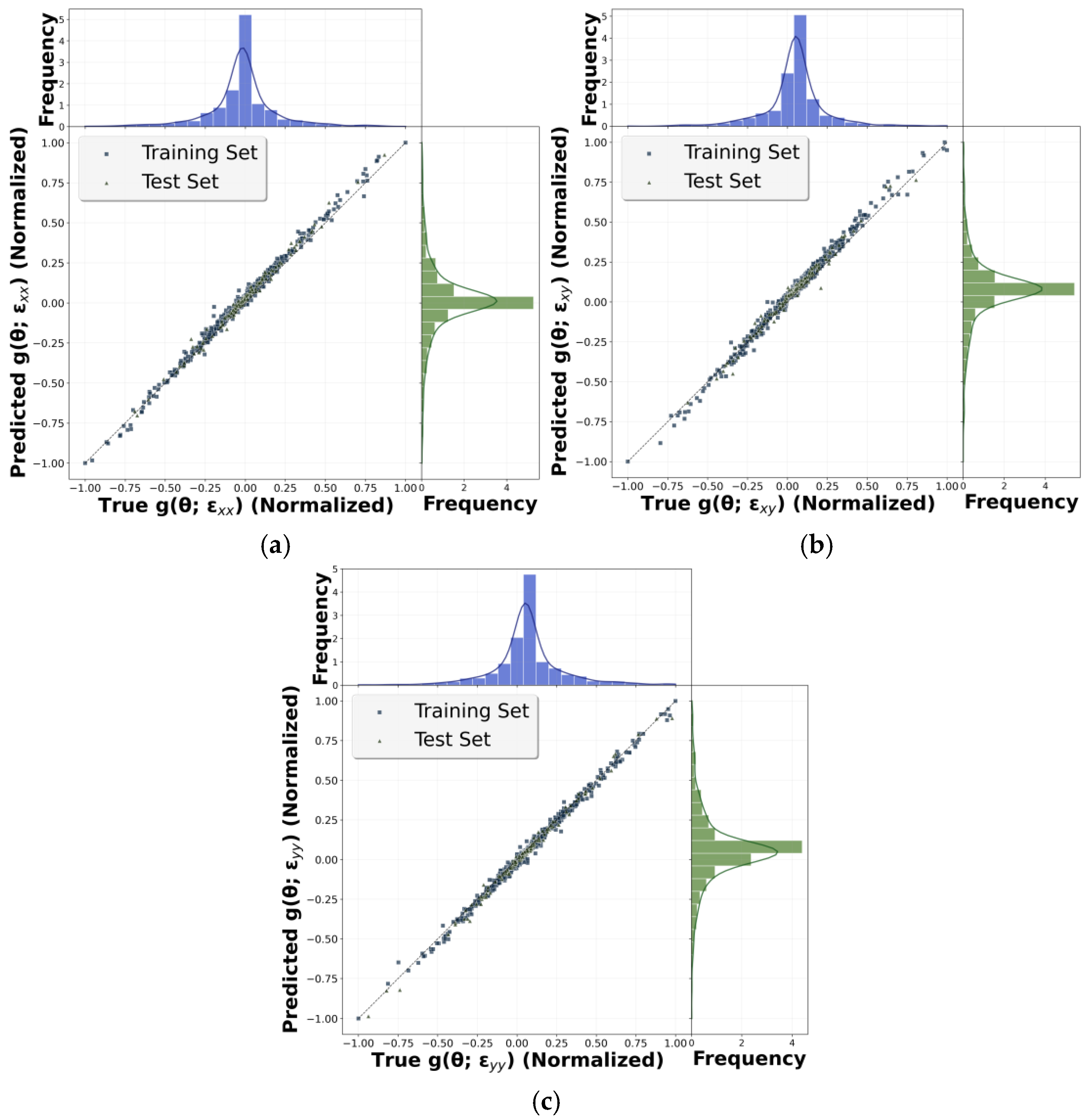
3.2. Nonlinear Case
3.2.1. Nonlinear Hyperelastic Constitutive Model
3.2.2. Training and Accuracy Check
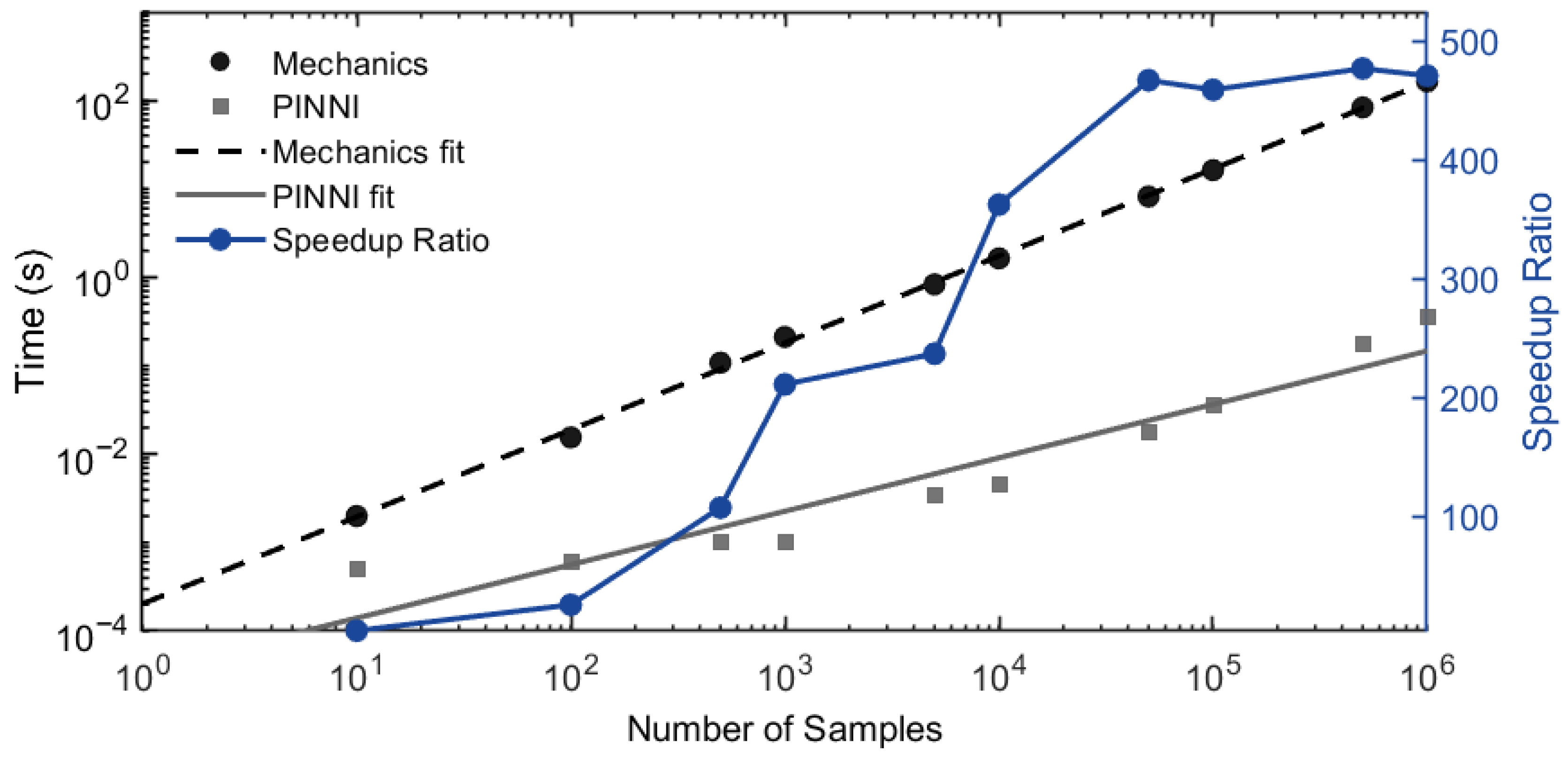
3.2.3. Efficiency Check
3.3. Benchmark Comparison
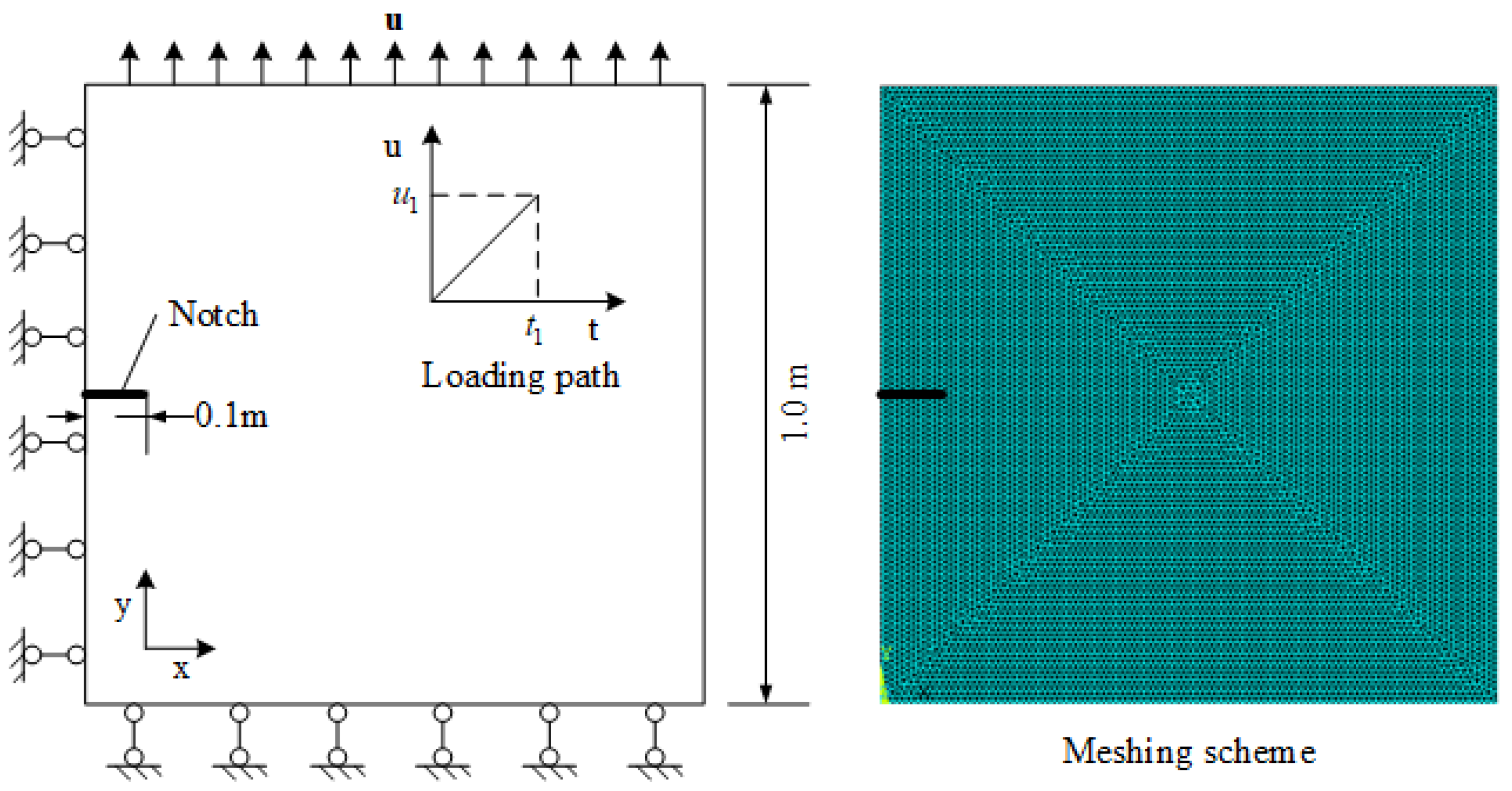
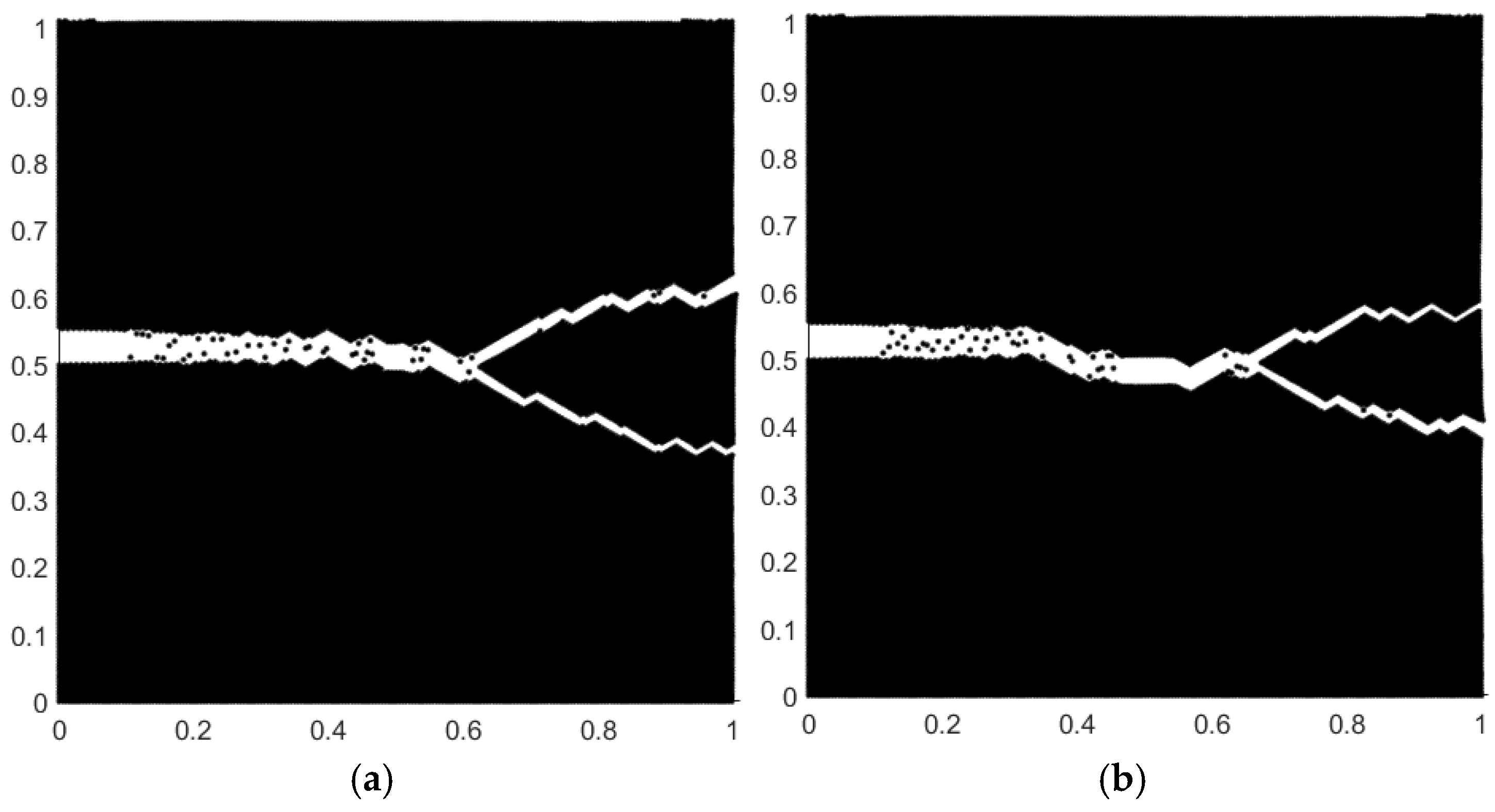
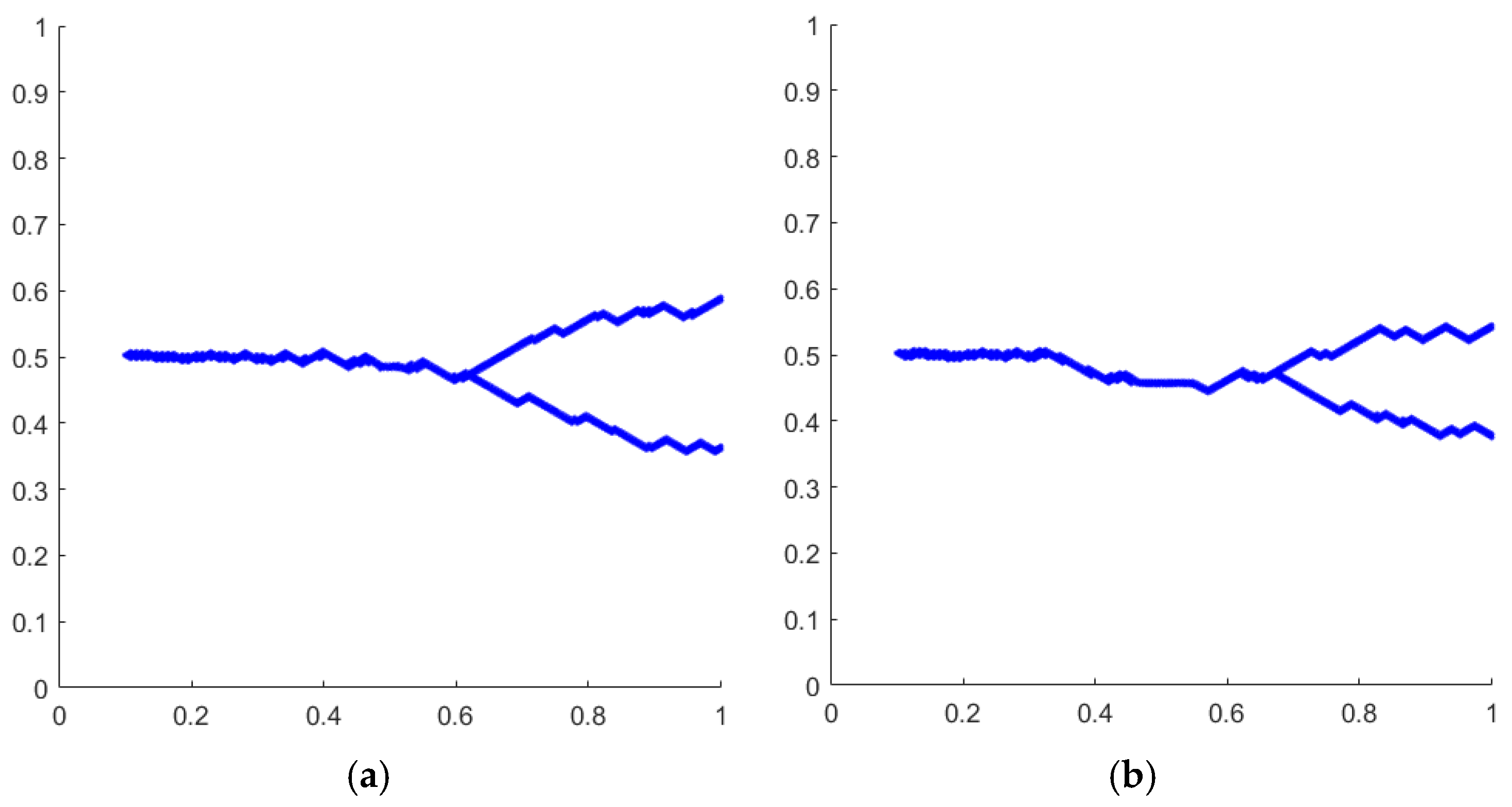
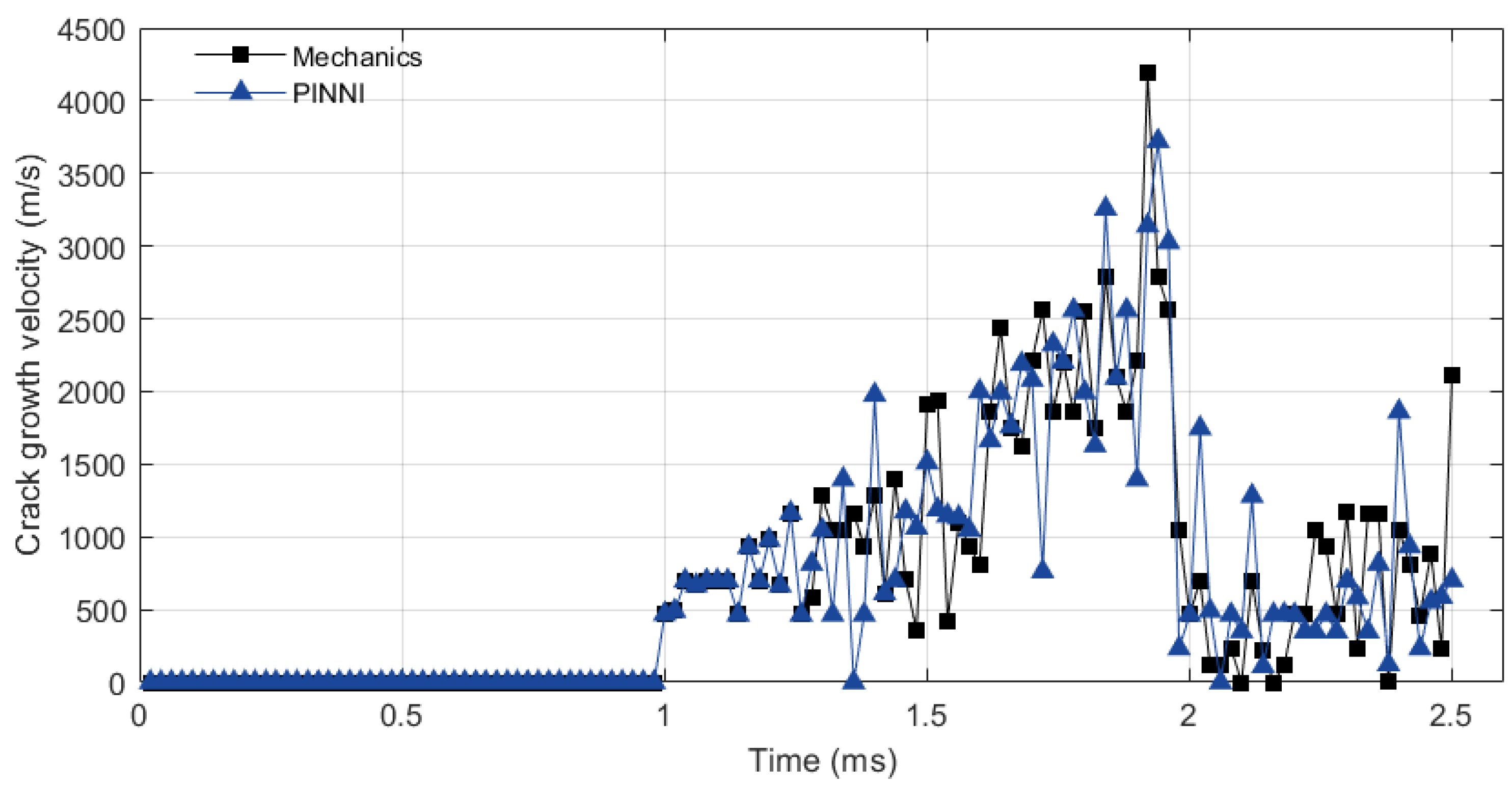
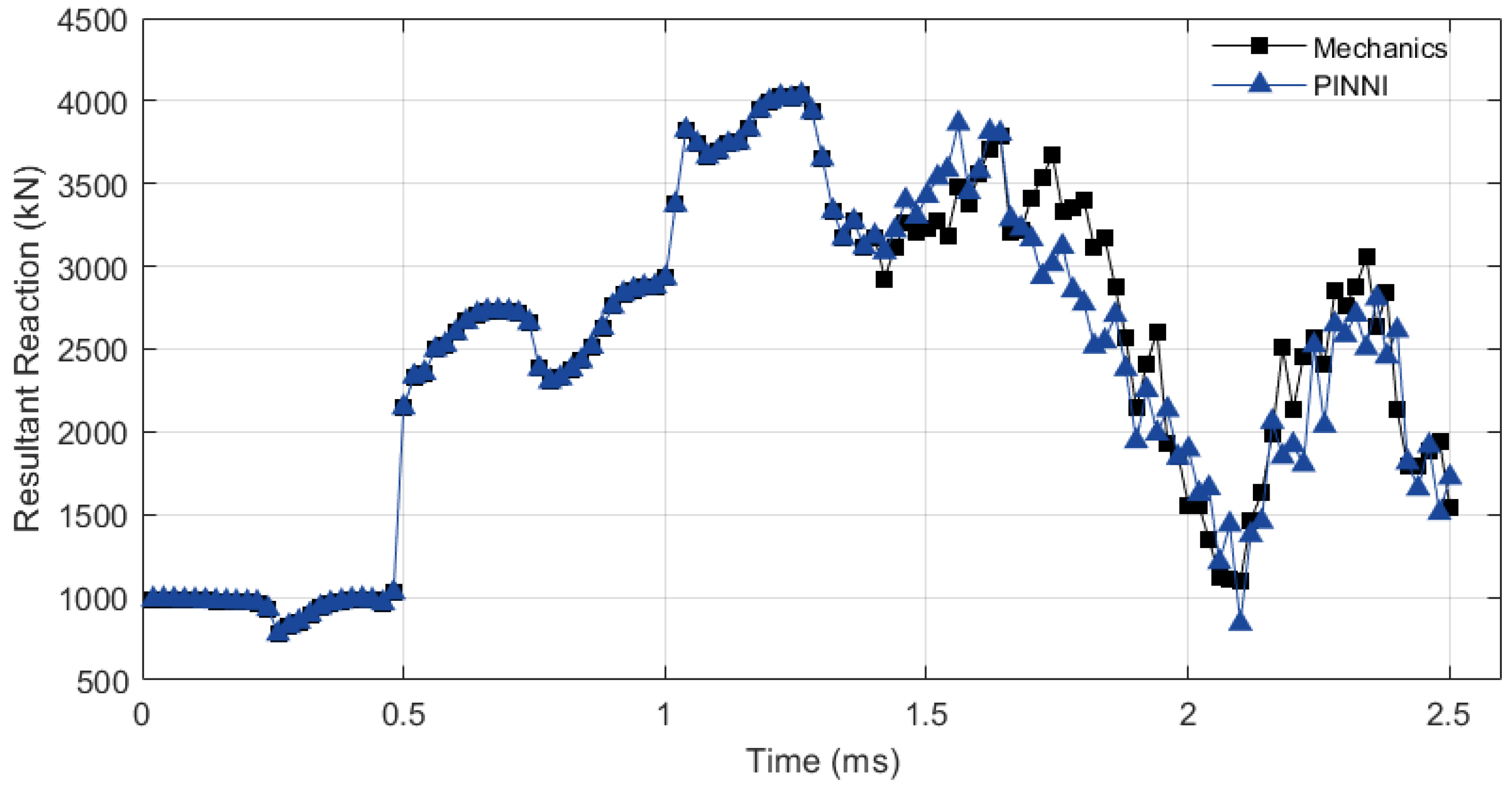
4. Simulation Example
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| PINN | Physics-informed neural network |
| NNI | Neural network integration |
| AVIB | Augmented virtual internal bond |
References
- Sánchez, P.J.; Huespe, A.E.; Oliver, J. On some topics for the numerical simulation of ductile fracture. Int. J. Plast. 2008, 24, 1008–1038. [Google Scholar] [CrossRef]
- Besson, J. Continuum models of ductile fracture: A review. Int. J. Damage Mech. 2010, 19, 3–52. [Google Scholar] [CrossRef]
- Lloyd, S.; Irani, R.A.; Ahmadi, M. Using neural networks for fast numerical integration and optimization. IEEE Access 2020, 8, 84519–84531. [Google Scholar] [CrossRef]
- Hassan, A.; Aljawad, M.S.; Mahmoud, M. An artificial intelligence-based model for performance prediction of acid fracturing in naturally fractured reservoirs. ACS Omega 2021, 6, 13654–13670. [Google Scholar] [CrossRef] [PubMed]
- Noels, L.; Stainier, L.; Ponthot, J.P. Combined implicit/explicit algorithms for crashworthiness analysis. Int. J. Impact Eng. 2004, 30, 1161–1177. [Google Scholar] [CrossRef]
- Martinez, X.; Rastellini, F.; Oller, S.; Flores, F.; Oñate, E. Computationally optimized formulation for the simulation of composite materials and delamination failures. Compos. Part B Eng. 2011, 42, 134–144. [Google Scholar] [CrossRef]
- Kuchnicki, S.N.; Cuitiño, A.M.; Radovitzky, R.A. Efficient and robust constitutive integrators for single-crystal plasticity modeling. Int. J. Plast. 2006, 22, 1988–2011. [Google Scholar] [CrossRef]
- Wang, J.; Lu, L.; Zhu, F. Efficiency analysis of numerical integrations for finite element substructure in real-time hybrid simulation. Earthq. Eng. Eng. Vib. 2018, 17, 73–86. [Google Scholar] [CrossRef]
- Perera, R.; Agrawal, V. Multiscale graph neural networks with adaptive mesh refinement for accelerating mesh-based simulations. Comput. Methods Appl. Mech. Engrg. 2024, 429, 117152. [Google Scholar] [CrossRef]
- Aldakheel, F.; Satari, R.; Wriggers, P. Feed-forward neural networks for failure mechanics problems. Appl. Sci. 2021, 11, 6483. [Google Scholar] [CrossRef]
- Baek, J.; Chen, J.-S. A neural network-based enrichment of reproducing kernel approximation for modeling brittle fracture. Comput. Methods Appl. Mech. Eng. 2024, 419, 116590. [Google Scholar] [CrossRef]
- Goswami, S.; Anitescu, C.; Chakraborty, S.; Rabczuk, T. Transfer learning enhanced physics informed neural network for phase-field modeling of fracture. Theor. Appl. Fract. Mech. 2020, 106, 102447. [Google Scholar] [CrossRef]
- van de Weg, B.P.; Greve, L.; Andres, M.; Eller, T.; Rosic, B. Neural network-based surrogate model for a bifurcating structural fracture response. Eng. Fract. Mech. 2021, 241, 107424. [Google Scholar] [CrossRef]
- Horvat, C.; Roach, L.A. WIFF1.0: A hybrid machine-learning-based parameterization of wave-induced sea ice floe fracture. Geosci. Model Dev. 2022, 15, 803–814. [Google Scholar] [CrossRef]
- Vu-Quoc, L.; Humer, A. Deep learning applied to computational mechanics: A comprehensive review, state of the art, and the classics. CMES Comput. Model. Eng. Sci. 2023, 137, 1070–1343. [Google Scholar] [CrossRef]
- Herrmann, L.; Kollmannsberger, S. Deep learning in computational mechanics: A review. Comput. Mech. 2024, 74, 281–331. [Google Scholar] [CrossRef]
- Zhang, B.; Allegri, G.; Hallett, S.R. Embedding artificial neural networks into twin cohesive zone models for composites fatigue delamination prediction under various stress ratios and mode mixities. Int. J. Solids Struct. 2022, 236-237, 111311. [Google Scholar] [CrossRef]
- Xi, X.; Yin, Z.Q.; Yang, S.T.; Li, C.Q. Using artificial neural network to predict the fracture properties of the interfacial transition zone of concrete at the meso-scale. Eng. Fract. Mech. 2021, 242, 107488. [Google Scholar] [CrossRef]
- Hu, W.F.; Shih, Y.J.; Lin, T.S.; Lai, M.C. A shallow physics-informed neural network for solving partial differential equations on static and evolving surfaces. Comput. Methods Appl. Mech. Eng. 2024, 418, 116486. [Google Scholar] [CrossRef]
- Raissi, M.; Yazdani, A.; Karniadakis, G.E. Hidden fluid mechanics: Learning velocity and pressure fields from flow visualizations. Science 2020, 367, 1026–1030. [Google Scholar] [CrossRef] [PubMed]
- Tran, H.; Gao, Y.F.; Chew, H.B. Numerical and experimental crack-tip cohesive zone laws with physics-informed neural networks. J. Mech. Phys. Solids 2024, 193, 105866. [Google Scholar] [CrossRef]
- Koeppe, A.; Bamer, F.; Selzer, M.; Nestler, B.; Markert, B. Explainable artificial intelligence for mechanics: Physics-explaining neural networks for constitutive models. Front. Mater. 2022, 8, 834946. [Google Scholar] [CrossRef]
- Krizhevsky, A. One weird trick for parallelizing convolutional neural networks. arXiv 2014, arXiv:1404.5997. [Google Scholar] [CrossRef]
- Zhang, Z.N.; Gao, H.J. Simulating fracture propagation in rock and concrete by an augmented virtual internal bond method. Int. J. Numer. Anal. Methods Geomech. 2012, 36, 459–482. [Google Scholar] [CrossRef]
- Gao, H.J.; Klein, P. Numerical simulation of crack growth in an isotropic solid with randomized internal cohesive bond. J. Mech. Phys. Solids 1998, 46, 187–218. [Google Scholar] [CrossRef]
- Xu, X.P.; Needleman, A. Numerical simulations of fast crack growth in brittle solids. J. Mech. Phys. Solids 1994, 42, 1397–1434. [Google Scholar] [CrossRef]
| Training Samples | ||||||
|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.5 | 1 | 2 | ||
| 50 | 2.0 | 1.7 | 1.3 | 1.6 | 2.0 | |
| 100 | 1.1 | 9.0 × 10−1 | 6.5 × 10−1 | 8.2 × 10−1 | 1.1 | |
| 200 | 3.2 × 10−1 | 2.6 × 10−1 | 2.9 × 10−1 | 3.1 × 10−1 | 3.4 × 10−1 | |
| 500 | 1.1 × 10−1 | 9.0 × 10−2 | 8.5 × 10−2 | 9.5 × 10−2 | 1.2 × 10−1 | |
| 1000 | 4.0 × 10−2 | 3.2 × 10−2 | 2.8 × 10−2 | 3.0 × 10−2 | 4.5 × 10−2 | |
| 2000 | 1.5 × 10−2 | 1.2 × 10−2 | 1.0 × 10−2 | 1.1 × 10−2 | 1.8 × 10−2 | |
| 50 | 9.8 × 10−1 | 8.2 × 10−1 | 4.7 × 10−1 | 5.7 × 10−1 | 7.8 × 10−1 | |
| 100 | 5.2 × 10−1 | 4.2 × 10−1 | 1.9 × 10−1 | 2.3 × 10−1 | 3.2 × 10−1 | |
| 200 | 1.8 × 10−1 | 1.4 × 10−1 | 5.0 × 10−2 | 9.0 × 10−2 | 1.2 × 10−1 | |
| 500 | 5.5 × 10−2 | 4.2 × 10−2 | 2.0 × 10−2 | 2.8 × 10−2 | 4.0 × 10−2 | |
| 1000 | 1.8 × 10−2 | 1.4 × 10−2 | 7.0 × 10−3 | 1.0 × 10−2 | 1.5 × 10−2 | |
| 2000 | 6.0 × 10−3 | 4.6 × 10−3 | 2.5 × 10−3 | 3.2 × 10−3 | 5.0 × 10−3 | |
| 50 | 6.2 × 10−1 | 4.8 × 10−1 | 2.3 × 10−1 | 2.5 × 10−1 | 3.9 × 10−1 | |
| 100 | 3.0 × 10−1 | 2.2 × 10−1 | 8.5 × 10−2 | 9.0 × 10−2 | 1.4 × 10−1 | |
| 200 | 1.0 × 10−1 | 7.4 × 10−2 | 3.2 × 10−2 | 3.7 × 10−2 | 5.3 × 10−2 | |
| 500 | 3.0 × 10−2 | 2.2 × 10−2 | 1.2 × 10−2 | 1.4 × 10−2 | 2.0 × 10−2 | |
| 1000 | 1.0 × 10−2 | 7.5 × 10−3 | 4.0 × 10−3 | 4.8 × 10−3 | 7.0 × 10−3 | |
| 2000 | 3.4 × 10−3 | 2.6 × 10−3 | 1.5 × 10−3 | 1.8 × 10−3 | 2.9 × 10−3 | |
| 50 | 3.1 × 10−1 | 2.5 × 10−1 | 2.1 × 10−1 | 2.3 × 10−1 | 2.8 × 10−1 | |
| 100 | 1.5 × 10−1 | 1.3 × 10−1 | 1.2 × 10−1 | 1.2 × 10−1 | 1.4 × 10−1 | |
| 200 | 4.5 × 10−2 | 3.7 × 10−2 | 3.2 × 10−2 | 3.5 × 10−2 | 4.3 × 10−2 | |
| 500 | 1.2 × 10−2 | 9.1 × 10−3 | 7.1 × 10−3 | 8.2 × 10−3 | 1.1 × 10−2 | |
| 1000 | 3.1 × 10−3 | 2.5 × 10−3 | 1.9 × 10−3 | 2.2 × 10−3 | 3.0 × 10−3 | |
| 2000 | 4.0 × 10−4 | 2.8 × 10−4 | 7.8 × 10−5 | 1.1 × 10−4 | 2.3 × 10−4 | |
| Model | Average Relative Error (%) | |
|---|---|---|
| PINNI (Proposed) | 0.9940 | |
| Classical MLP | 0.9082 | |
| Random Forest | 0.9210 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, M.; Pan, Y.; Zhang, Z. A Physics-Informed Neural Network Integration Framework for Efficient Dynamic Fracture Simulation in an Explicit Algorithm. Appl. Sci. 2025, 15, 10336. https://doi.org/10.3390/app151910336
Wan M, Pan Y, Zhang Z. A Physics-Informed Neural Network Integration Framework for Efficient Dynamic Fracture Simulation in an Explicit Algorithm. Applied Sciences. 2025; 15(19):10336. https://doi.org/10.3390/app151910336
Chicago/Turabian StyleWan, Mingyang, Yue Pan, and Zhennan Zhang. 2025. "A Physics-Informed Neural Network Integration Framework for Efficient Dynamic Fracture Simulation in an Explicit Algorithm" Applied Sciences 15, no. 19: 10336. https://doi.org/10.3390/app151910336
APA StyleWan, M., Pan, Y., & Zhang, Z. (2025). A Physics-Informed Neural Network Integration Framework for Efficient Dynamic Fracture Simulation in an Explicit Algorithm. Applied Sciences, 15(19), 10336. https://doi.org/10.3390/app151910336






