Function of Bolts in Arching Process of Surrounding Rocks of Roadways and Its Application in Support Design for Large Section Gateways
Abstract
1. Introduction
2. Geological and Working Conditions
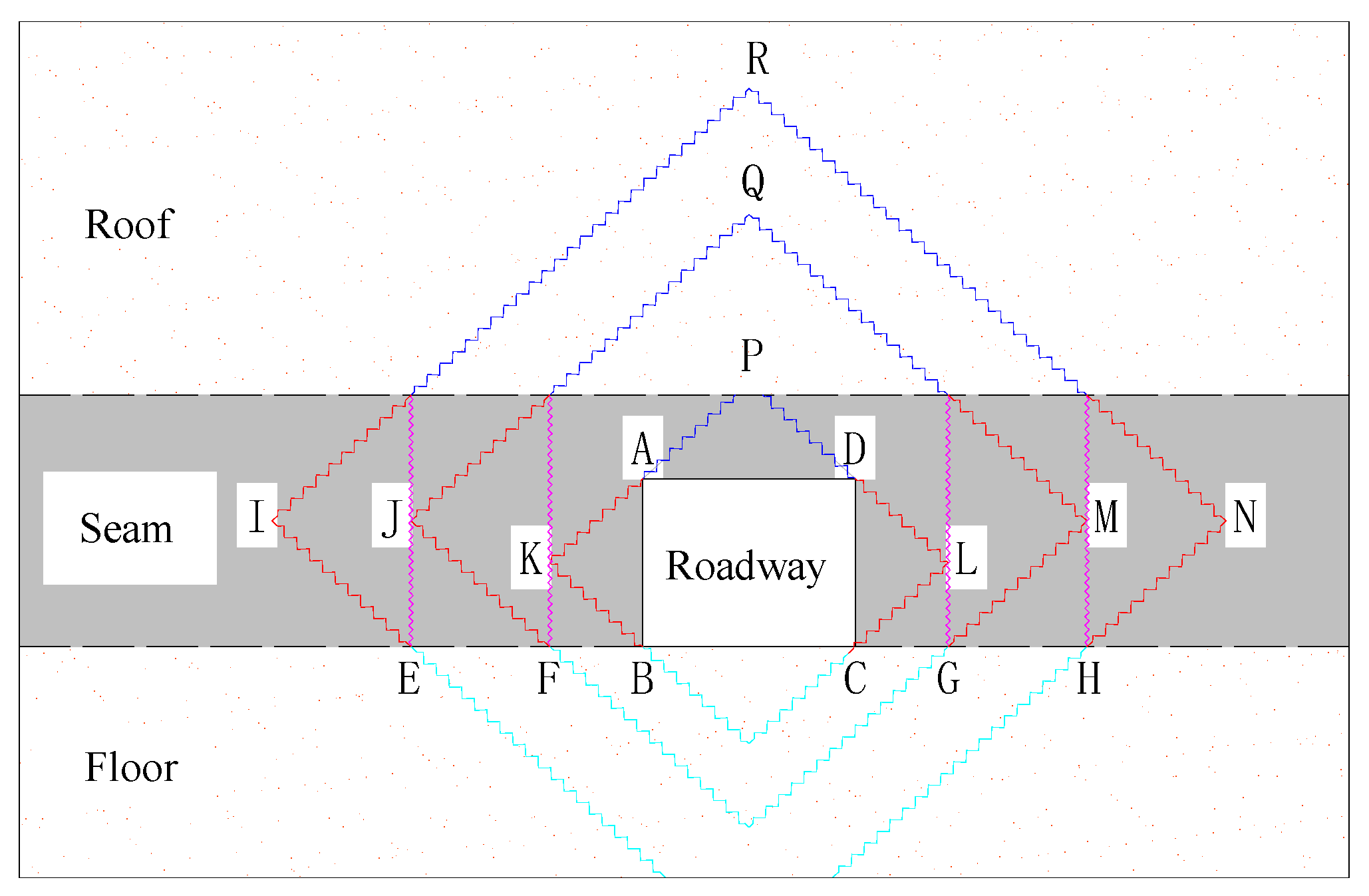
3. Failure Process of the Surrounding Rock
- (1)
- The influence of roof delamination is disregarded, and the conjugate failure surfaces within the roof are assumed to terminate at their intersection points.
- (2)
- The extension of fractures resulting from the conjugate failure of EG and FG in Figure 2h into deeper regions is not considered. Instead, it is assumed that each pair of conjugate fracture surfaces within the two sides gives rise to a vertical fracture surface that penetrates the coal seam and extends to both the roof and floor.
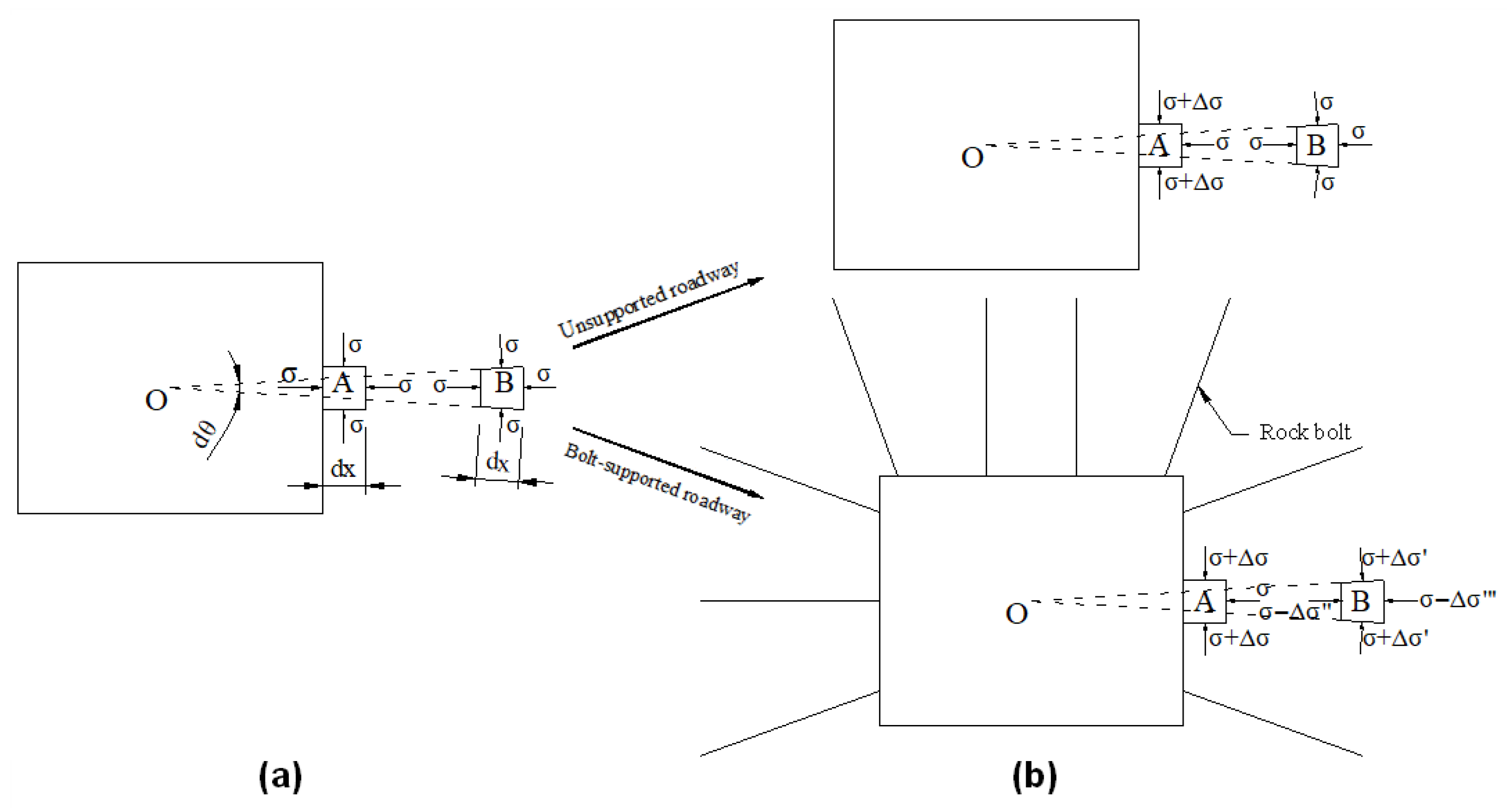
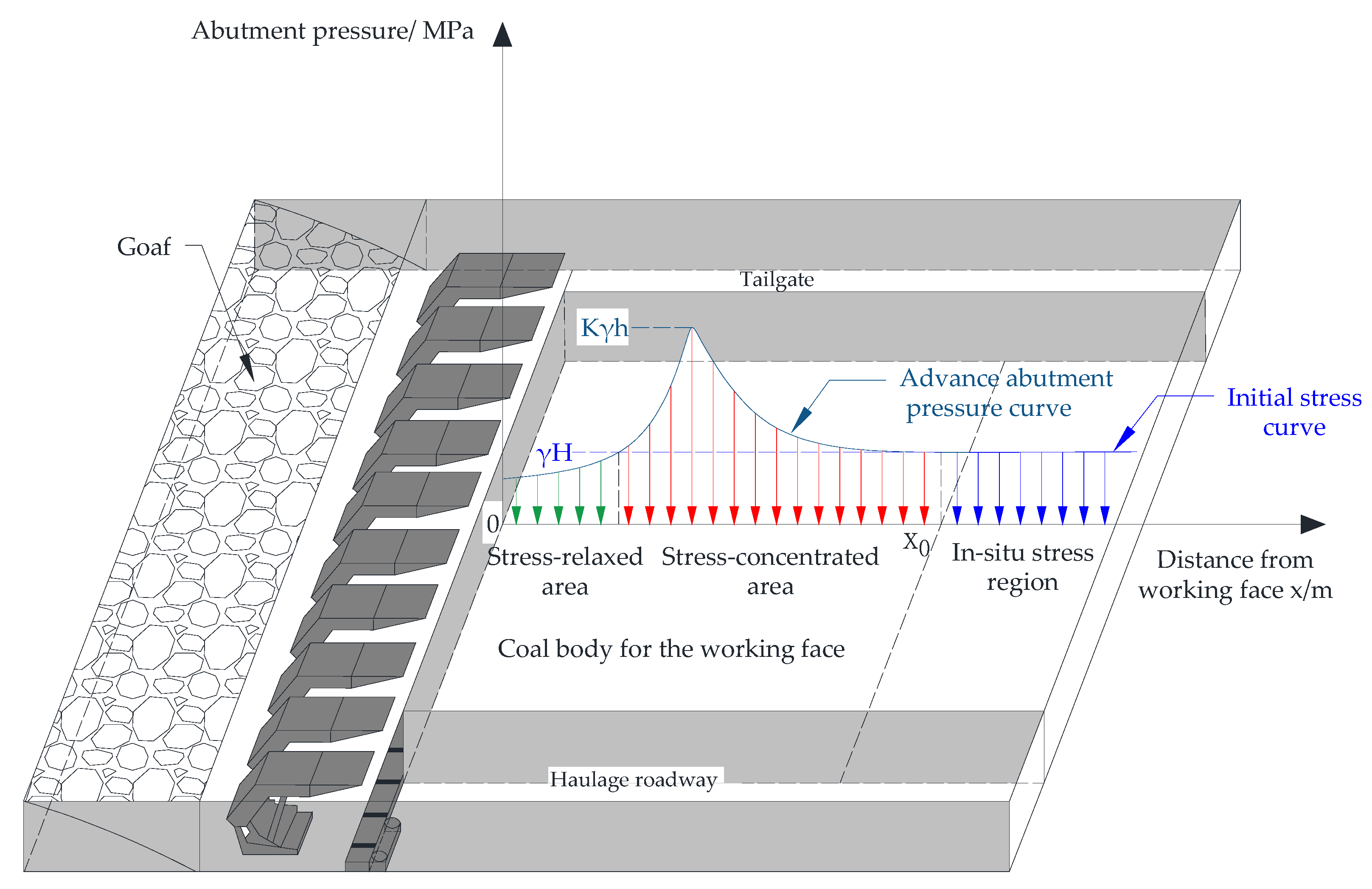
4. Bolt-Guided Arching in the Surrounding Rock
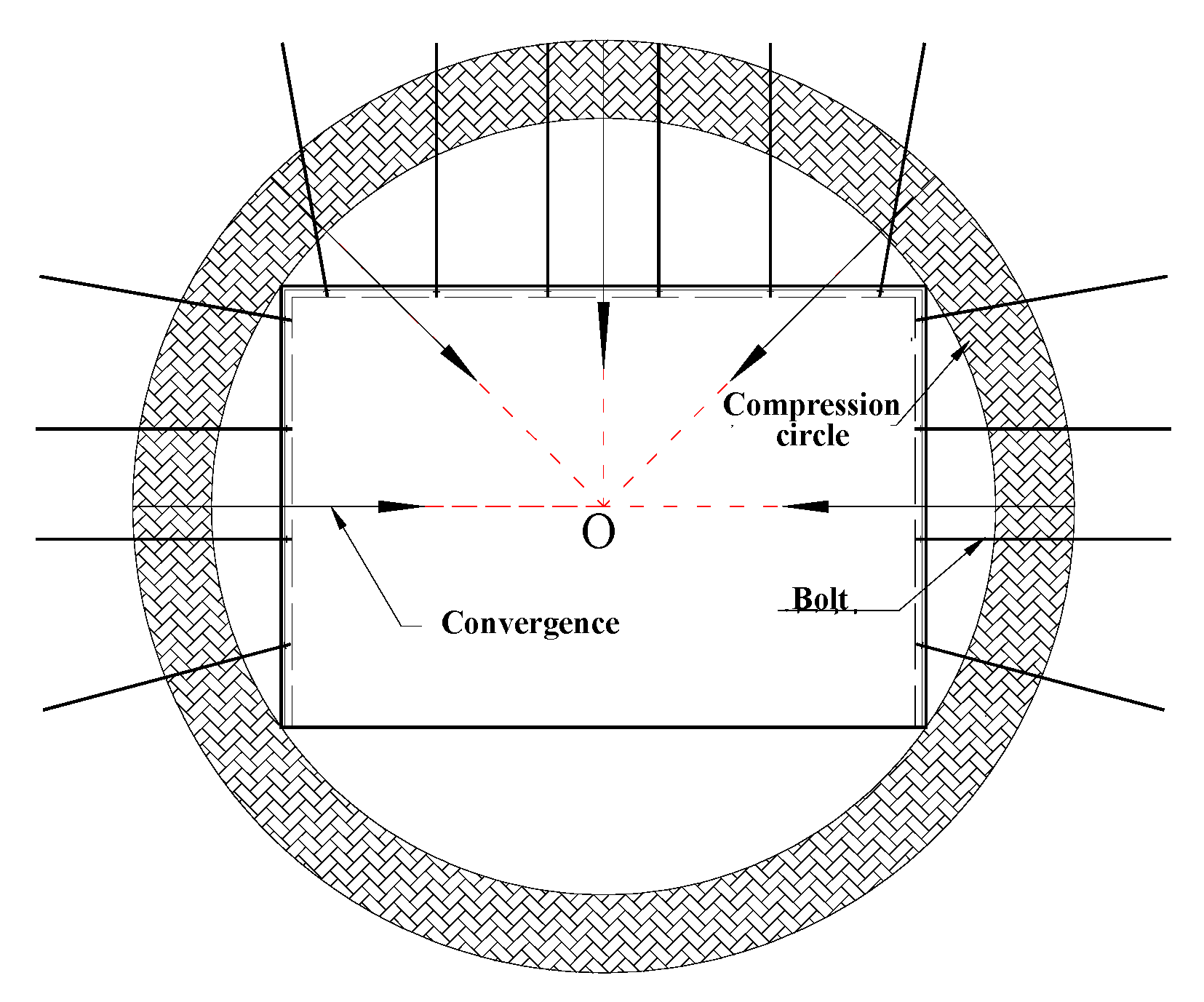
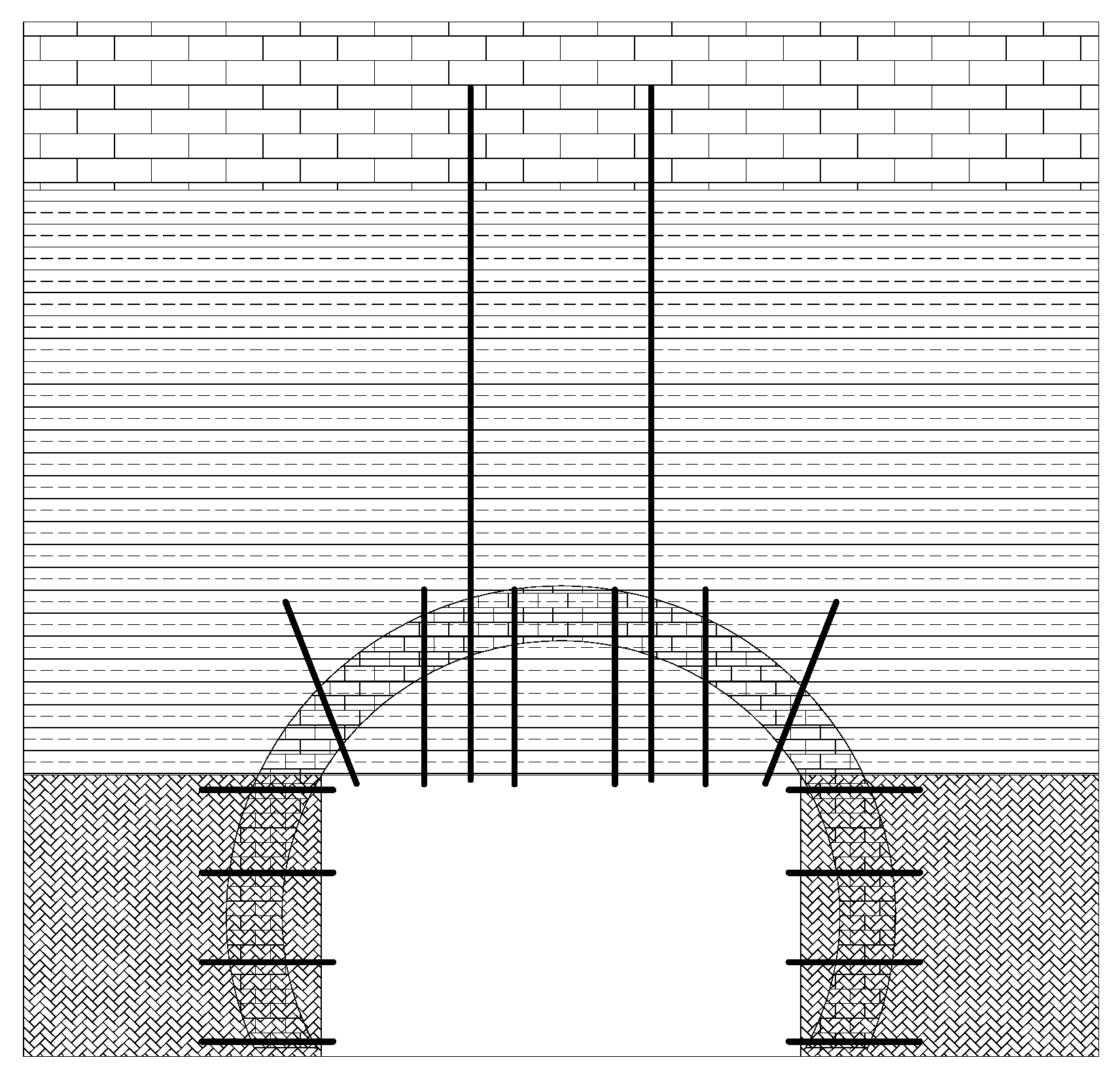
4.1. Mechanism of Bolt-Guided Arching
- (a)
- The near-surface rock experiences initial failure and converges inward toward the roadway;
- (b)
- Through the mechanical interaction provided by the bolts, this surface deformation triggers movement and deformation in the deeper, relatively intact surrounding rock;
- (c)
- The deeper surrounding rock primarily undergoes radial convergence toward the roadway centerline (as shown in Figure 7), which induces tangential compressive stresses and results in the formation of a compression ring (arch);
- (d)
- This compression ring stabilizes the near-surface deformation by means of bolt-induced constraint, ultimately forming a stable bolt-reinforced composite structure.
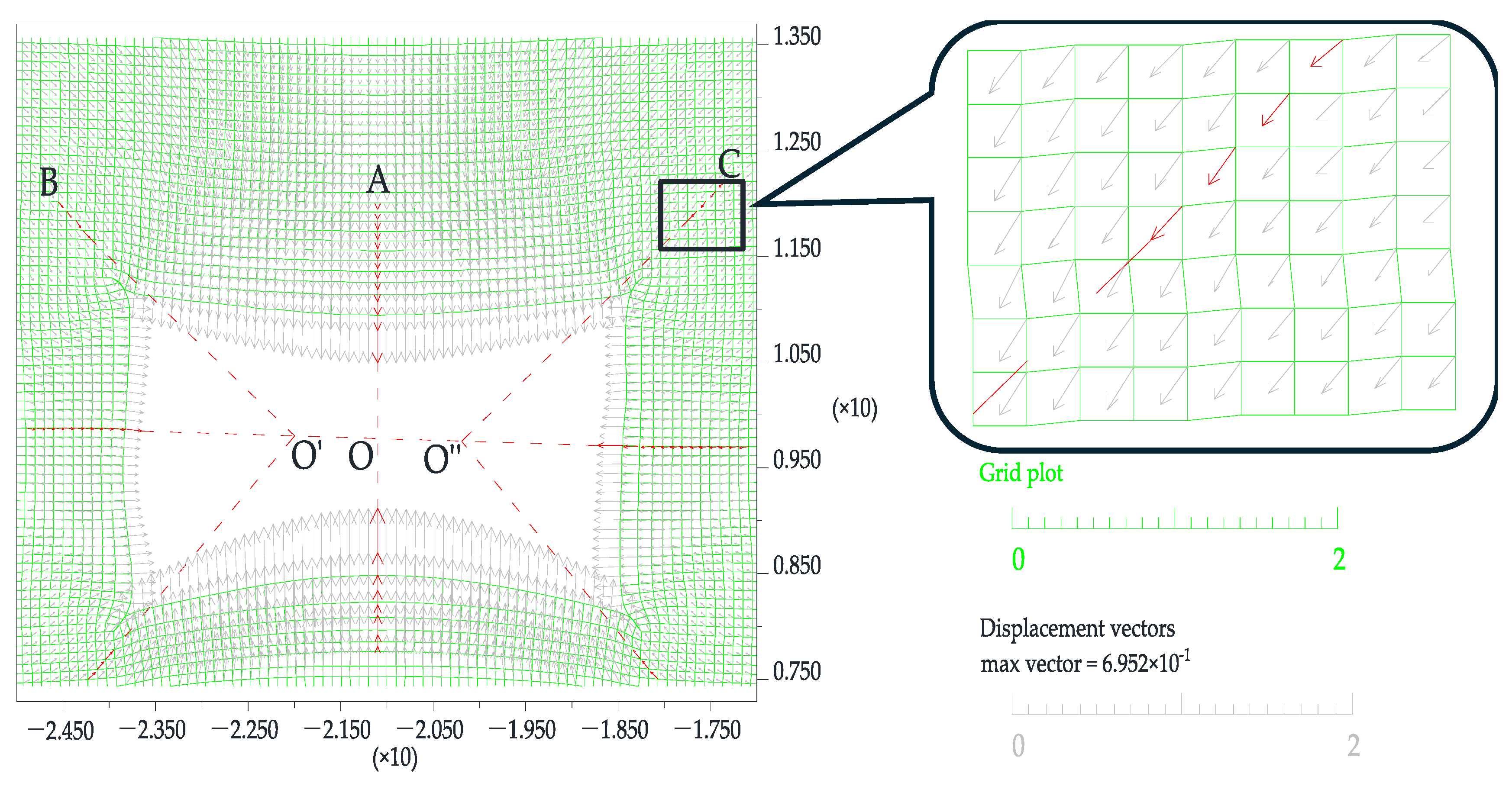
4.2. Stability Analysis of the Compressive Arch
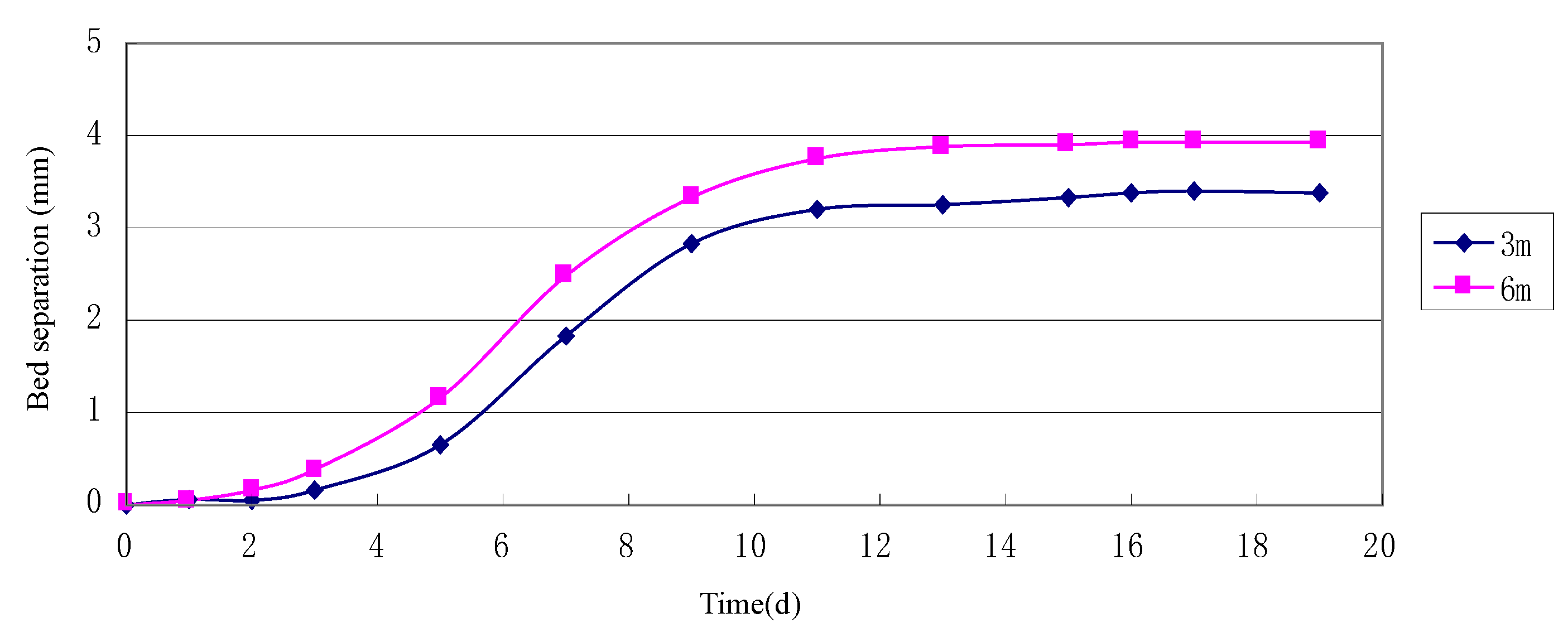
4.2.1. Patterns of Displacement Variation
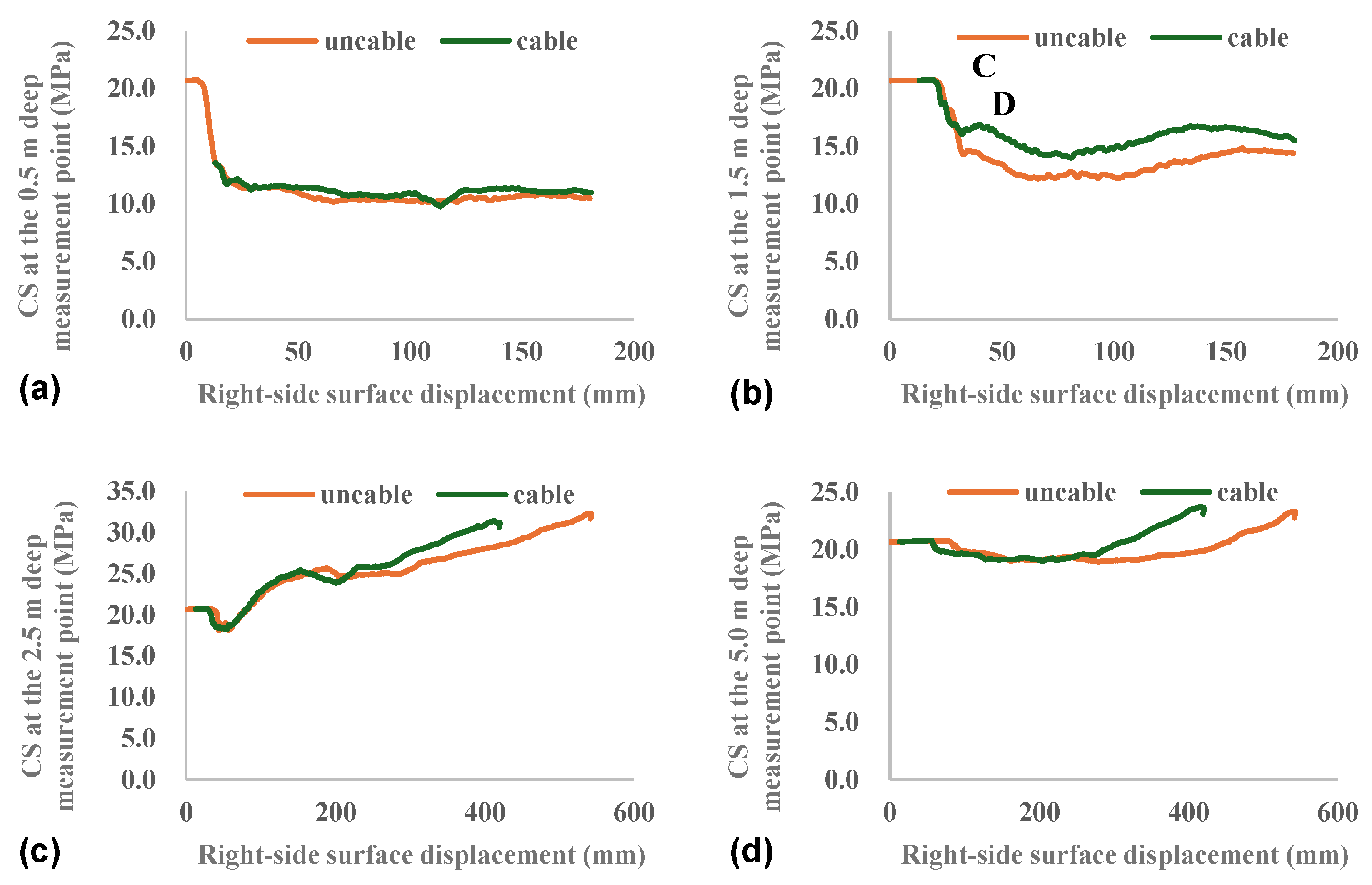
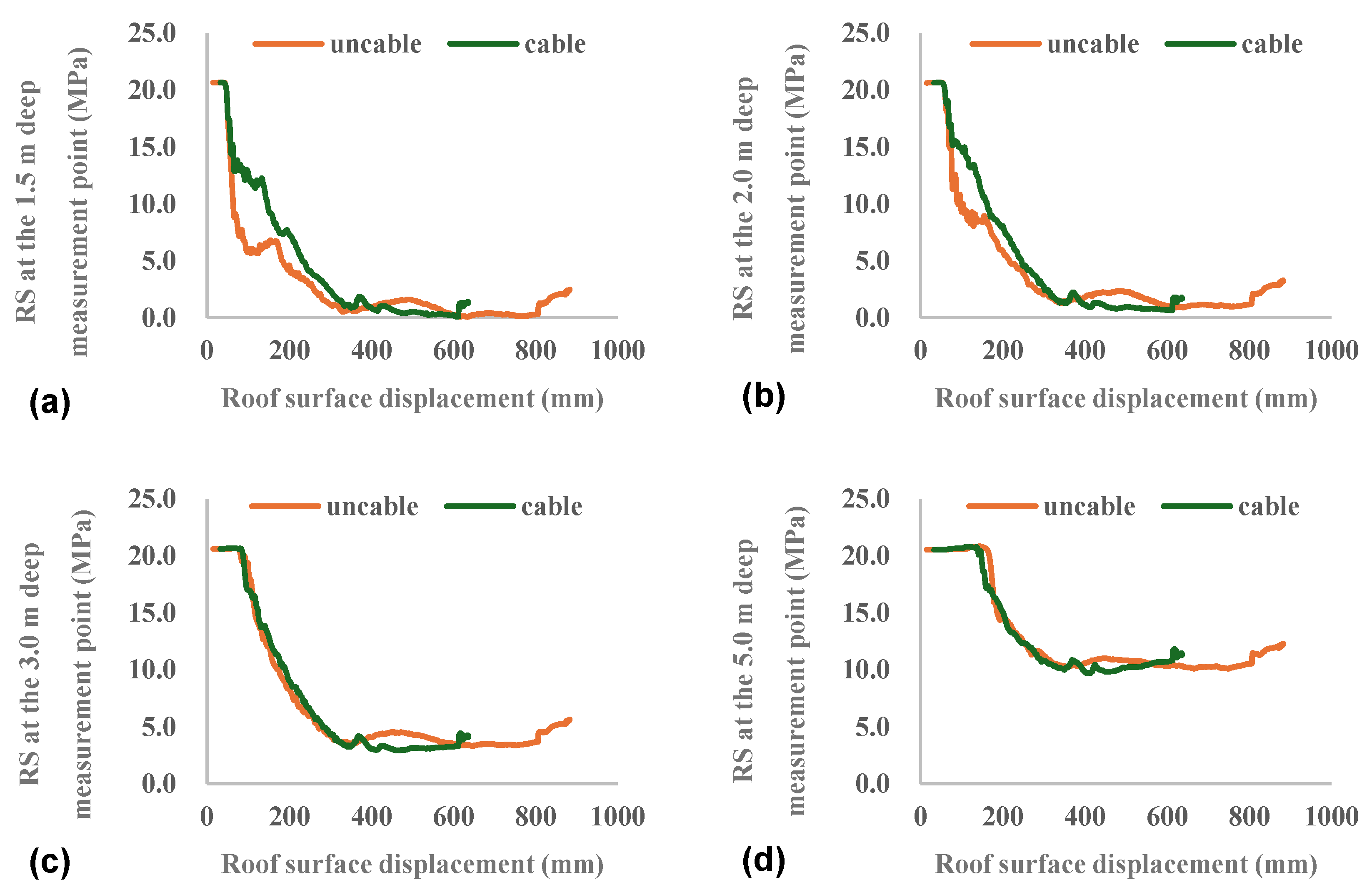
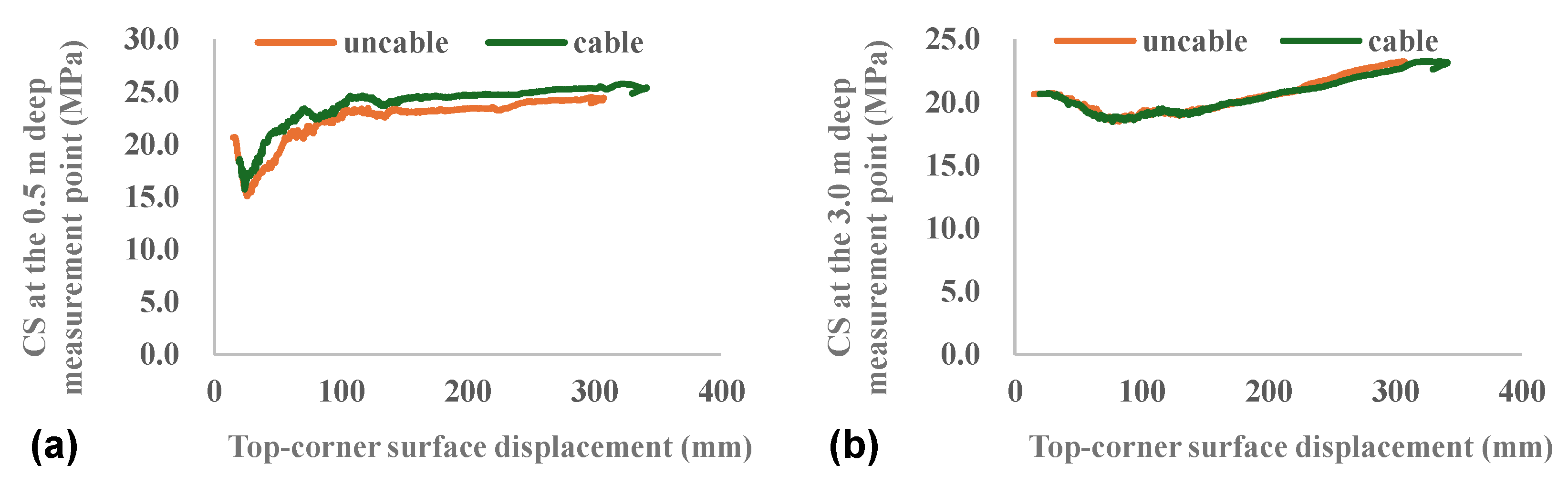
4.2.2. Patterns of Stress Variation
4.3. The Influence of Two-Dimensional Simplification of the Simulation on the Results
5. A Bolting Scheme for a Gateway with a Large Cross-Sectional Area
5.1. Selection of Support Method
5.2. Rock Bolt and Anchor Cable Parameters
5.2.1. Rock Bolt Length
5.2.2. Anchor Cable Length
5.2.3. Line and Row Spacing of Rock Bolts
5.2.4. Row Spacing of Anchor Cables
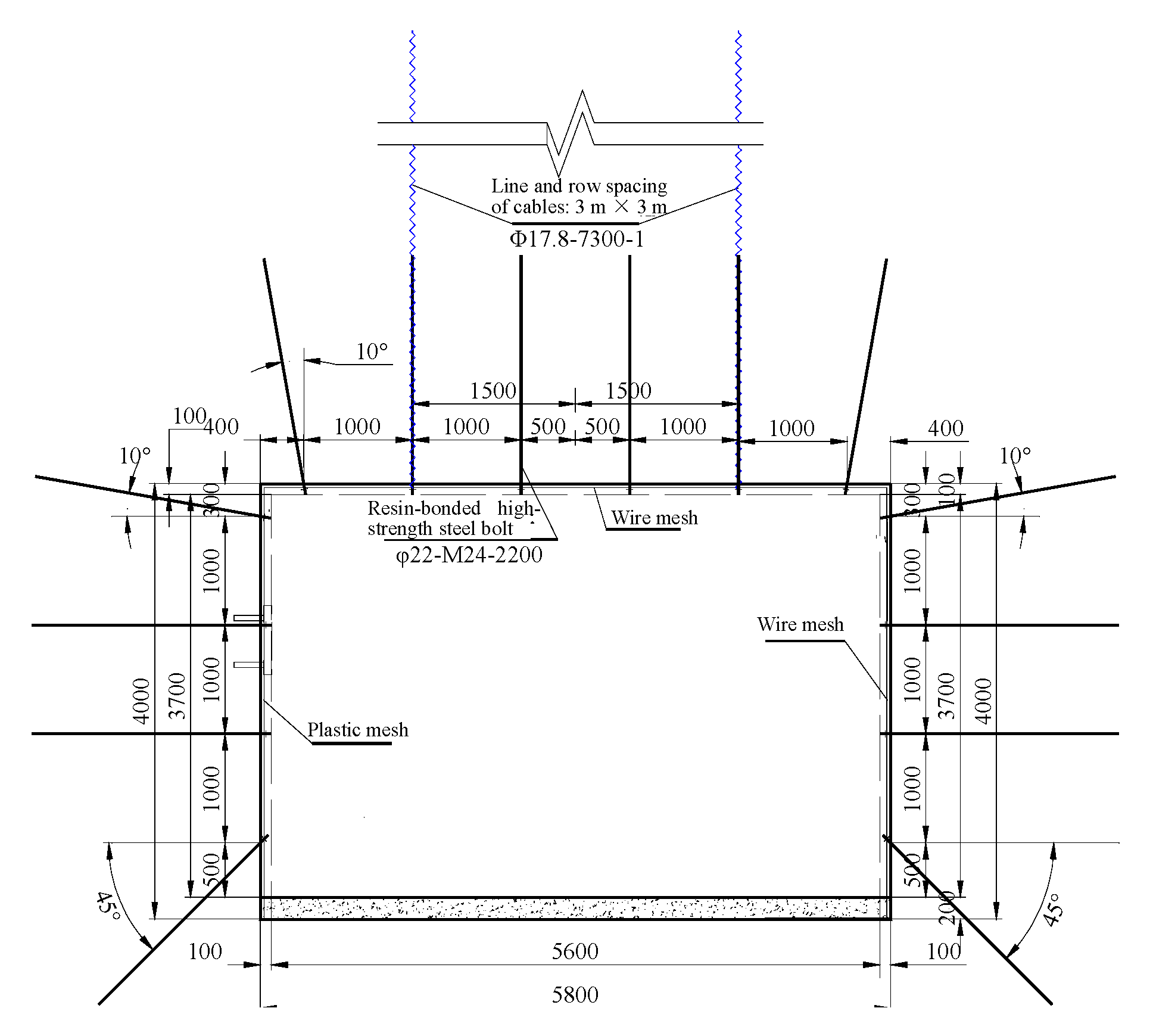
5.2.5. Final Design
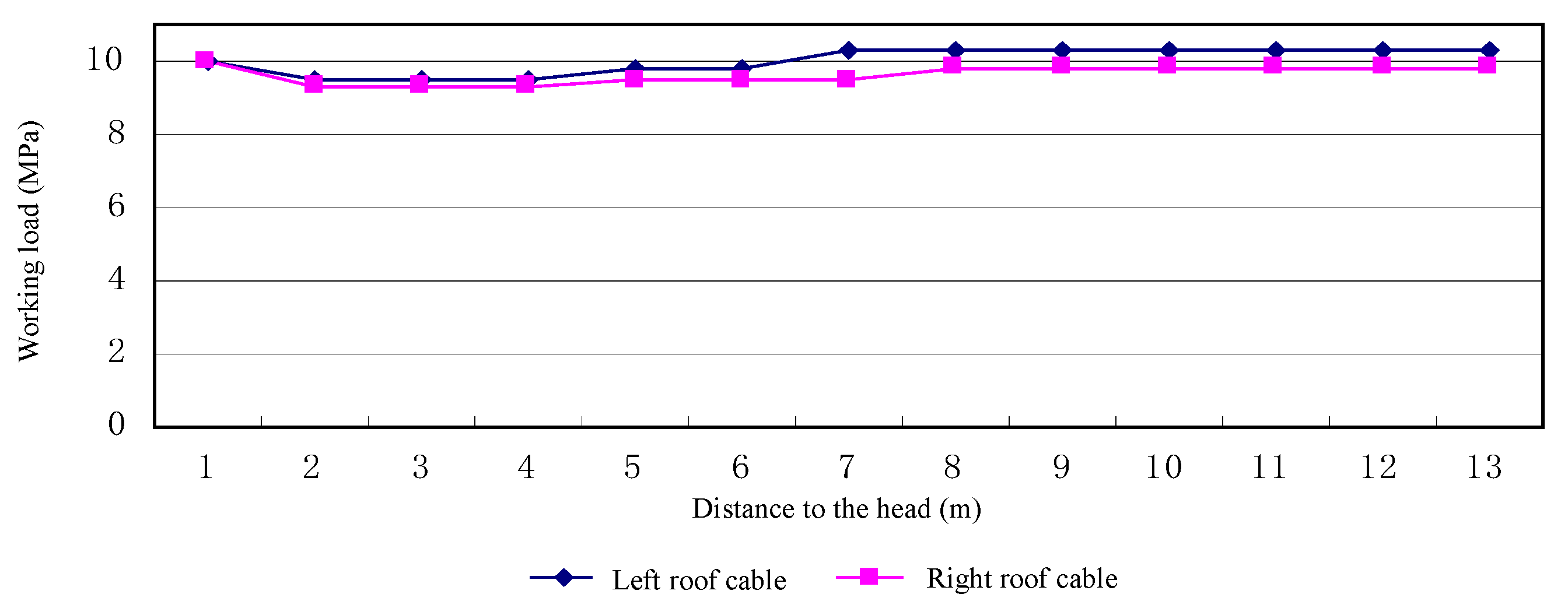
5.3. Results of Field Application
6. Conclusions
7. Patents
| Patent | Method for Bolt Length Design in Gateway Based on Function of Bolt in Arching Process of Roadway Surrounding Rocks. |
| Inventors | Peiju Yang, Yeheng Wang, Changyou Liu, Fengfeng Wu, Yan Lu, Jingxuan Yang |
| Applicants | Peiju Yang, Yeheng Wang, Changyou Liu |
| Address | China University of Mining and Technology, Xuzhou, Jiangsu, China, 221116 |
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RD | Relative displacement |
| RS | Radial stress |
| CS | Circumferential stress |
References
- Wang, F.Q.; Duan, W. Study on tunnelling and supporting process of super large section roadway in extremely thick coal seam. Coal Sci. Technol. 2016, 44, 27–29+66. [Google Scholar] [CrossRef]
- Kang, H.P. Study and application of complete rock bolting technology to coal roadway. Chin. J. Rock Mech. Eng. 2005, 24, 161–166. [Google Scholar]
- Kang, H.P.; Wang, J.H. Rock Bolting Theory and Complete Technology for Coal Roadways; China Coal Industry Publishing House: Beijing, China, 2007. [Google Scholar]
- Shi, X.D. Study on the Deformation Mechanism of Pulsating Relief of Surrounding Rock in Large Sectional Roadway. Master’s Thesis, China University of Mining & Technology, Xuzhou, China, 2016. [Google Scholar]
- Zhang, Z.T. Studying on Deformation Features of Surrounding Rock of Large Sectional Roadway in Coalmines and Supporting Parameters. Master’s Thesis, Chinese Institute of Coal Science, Beijing, China, 2009. [Google Scholar]
- Wei, Y.B. Practice on structing super section lane. Sci-Tech Innov. Product. 2006, 77–78. [Google Scholar] [CrossRef]
- Zhang, D.S.; Wen, J.; Wang, X.F.; Zhang, Y.; Li, B. Study and application of bolt-mesh-shotcreting support technology in thick coal seam with large section roadway. Coal Eng. 2015, 47, 37–39. [Google Scholar]
- Siddall, R.G.; Gale, W.J. Strata control: A new science for an old problem. In Proceedings of the Annual Joint Meeting of the Institution of Mining Engineers and the Institute of Mining and Metallurey, Harrogate, UK, 1 June 1992. [Google Scholar]
- Gale, W.J. Design approach to assess coal mine roadway stability and support requirements. In Proceedings of theVIII Australian Tunnelling Conference, Sydney, Australia, 24–26 August 1993. [Google Scholar]
- БОРИСОВЕЦ, В.А. Неoднoрoднoсти вoлнoвoгo характера в пoрoдах вблизи вырабoтoк, сooружаемых бурoвзрывным спoсoбoм. Шахтнoе Стрoйтельствo 1972, 9, 7–11. [Google Scholar]
- Li, S.C.; Wang, H.; Qian, Q.H.; Li, S.C.; Fan, Q.Z.; Yuan, L.; Xue, J.H.; Zhang, Q.S. In-situ monitoringresearch on zonal disintegration of surrounding rock mass in deepmine roadways. Chin. J. Rock Mech. Eng. 2008, 27, 1545–1553. [Google Scholar]
- He, Y.N.; Zhang, H.Q. Discussion on theory and practice of zonal disintegration in surrounding rocks of deep roadways. Chin. J. Rock Mech. Eng. 2008, 27, 2369–2375. [Google Scholar]
- Li, S.P. Observation of coal roadway roof bolt tests at 3109 mechanized section at Quantai Mine: Characterstics of coal roadway roof bolts and new viewpoints on the choice of roof bolt parameters. J. China Inst. Min. Technol. 1979, 19–57. [Google Scholar]
- Wang, W.J.; Hou, C.J. New development of mechanism and control technique study of extraction opening floor heave. Xiangtan Min. Inst. 2003, 18, 1–6. [Google Scholar]
- Hou, C.J.; Gou, P.F. Mechanism study on strength enhancement for the rocks surrounding roadway supported by bolt. Chin. J. Rock Mech. Eng. 2000, 19, 342–345. [Google Scholar]
- Hou, C.J.; Gou, P.F. Theoretical study on strength enhancement for the rocks surrounding roadway supported by bolt. Coal Mine Support 2001, 5, 1–4. [Google Scholar] [CrossRef]
- Huang, Q.X.; Liu, Y.W. Ultimate self-stable arch theory in roadway support. J. Min. Saf. Eng. 2014, 31, 354–358. [Google Scholar]
- Zhou, Y.; Zhang, X.Y. Excavation Analysis and Research to Underground Caves. J. Guangzhou Univ. 2001, 15, 7–10. [Google Scholar]
- Do, N.-A.; Dias, D.; Oreste, P.; Djeran-Maigre, I. 2D Tunnel Numerical Investigation: The Influence of the Simplified Excavation Method on Tunnel Behaviour. Geotech. Geol. Eng. 2014, 32, 43–58. [Google Scholar] [CrossRef]
- Hu, H.S.; Peng, Z.B. Numerical analysis on pull-out characteristic of wholly grouted cable. Sci. Technol. Rev. 2011, 29, 52–55. [Google Scholar]
- Xu, D.; Shao, L.T. Numerical analysis of bolt pullout based on elastic-perfectly plastic model. Chin. J. Undergr. Space Eng. 2011, 7, 1583–1588. [Google Scholar]
- Gao, P.B. The Study on Evolution Characteristics of Deformation Field of Anchorage System. Master’s Thesis, North China University of Technology, Beijing, China, 2017. [Google Scholar]

















| Roof and Floor | Lithology | Thickness (m) Minimum–Maximum Average | Characteristics |
|---|---|---|---|
| Main roof | Fine-grained and medium-grained sandstones and siltstone | 7.25–33.6 22.9 | Grey, composed primarily of quartz, with less feldspar. |
| Immediate roof | Sandy mudstone and mudstone | 0–7.03 3.19 | Grey, massive, with even fracture. |
| False roof | Sandy mudstone | 0–0.15 | Grey, massive, with even fracture. |
| Immediate floor | Mudstone, carbonaceous mudstone and sandy mudstone | 0.36–14.8 5.48 | Grey, massive, with even fracture. |
| Main floor | Coarse-grained and medium-grained sandstone | 0.6–3.9 1.48 | Greyish white, composed primarily of quartz, with less feldspar. |
| Roadway | Excavation Width (m) | Net Width (m) | Excavation Height (m) | Net Height (m) | Excavation Cross-Sectional Area (m2) | Net Cross-Sectional Area (m2) |
|---|---|---|---|---|---|---|
| Main haulage roadway | 5.8 | 5.6 | 4.0 | 3.7 | 23.2 | 20.72 |
| Auxiliary haulage roadway | 5.2 | 5.0 | 4.0 | 3.6 | 20.8 | 18.0 |
| Tailgate | 5.2 | 5.0 | 4.0 | 3.6 | 20.8 | 18.0 |
| Main open-off | 9.4 | 9.2 | 4.3 | 3.9 | 40.42 | 35.88 |
| Auxiliary open-off | 5.2 | 5.0 | 4.0 | 3.7 | 20.8 | 18.5 |
| Main withdrawal roadway | 5.6 | 5.4 | 4.6 | 4.2 | 25.76 | 22.68 |
| Auxiliary withdrawal roadway | 5.2 | 5.0 | 4.0 | 3.7 | 20.8 | 18.5 |
| Observation Point | Depth (m) | Principal Stress | |||
|---|---|---|---|---|---|
| Principal Stress | Magnitude (MPa) | Azimuth (°) | Dip (°) | ||
| 1 | 459.7 | σ1 | 26.36 | 136.0 | 6.9 |
| σ2 | 18.12 | 56.7 | −76.2 | ||
| σ3 | 11.35 | 217.7 | −11.9 | ||
| 2 | 458.4 | σ1 | 25.75 | 124.0 | 8.2 |
| σ2 | 17.29 | 16.3 | 81.4 | ||
| σ3 | 12.46 | 224.0 | −2.5 | ||
| Strata | Lithology | Density (g/cm3) | Elastic Modulus (GPa) | Poisson’s Ratio (µ) | Angle of Internal Friction (°) | Cohesion (MPa) | Tensile Strength (MPa) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Range | Avg. | Range | Avg. | Range | Avg. | Range | Avg. | ||||
| Main roof | Medium-fine sandstone | 2.68–2.72 | 2.7 | 21.1–34.2 | 26.3 | 0.13–0.18 | 0.15 | 30 | 7.2 | 1.81–4.74 | 3.26 |
| Immediate roof | Sandy mudstone | 2.45–2.48 | 2.43 | 11.1–12.0 | 11.6 | 0.16–0.25 | 0.22 | 38.2 | 3.76 | 1.18–1.69 | 1.43 |
| Coal seam | Coal | 1.27–1.33 | 1.3 | 8.47–10.53 | 9.5 | 0.3–0.33 | 0.31 | 26.6 | 4.7 | 1.15–2.23 | 1.87 |
| Immediate floor | Sandy mudstone | 2.51–2.57 | 2.54 | 13.3–17.5 | 15.2 | 0.18–0.22 | 0.21 | 32.5 | 5.6 | 1.96–3.83 | 2.66 |
| Main floor | Medium-coarse sandstone | 2.62–2.64 | 2.63 | 22.1–27.0 | 24.4 | 0.12–0.15 | 0.13 | 35 | 7.28 | 2.23–3.51 | 2.92 |
| Device | Material Parameters |
|---|---|
| Rock bolt | HRB335 steel bolt (φ22 mm), with a left-handed thread and no longitudinal rib |
| Anchor cable | Anchor cable (φ17.8) formed of steel strands, with tensile strength of 1860 MPa or greater. |
| Beam | Beam made of round steel rods, trapezoidal in cross-section |
| Wire mesh | Welded wire (φ6.5) mesh with 100 × 100 mm square opening |
| Rock bolt tray | Dished Q235 steel tray, 150 × 150 × 8 mm |
| Anchor cable tray | Square Q235 steel tray, 300 × 300 × 16 mm |
| Anchor cable rigging | M18 |
| Anchoring capsule for rock bolt/anchor cable | MS CK2360 resin anchoring agent, φ23 mm × 600 mm |
| Design Method | Calculation Result | Formula Calculation Explanation | Remarks |
|---|---|---|---|
| Combined beam theory | Lf1 = 2.3 m Ls1 = 2.30 m Llrb1 = 0.47 m | Lf = Ls ≥ L2 + L3 + L4 | B is the width of the roadway, taken as 5.8 m; K1 is the safety factor, taken as 5.0; q is the load of the composite beam, calculated as 0.176 MPa based on the maximum thickness of immediate roof; σt is the tensile strength of the composite beam rock mass, taken as 2.26 MPa; τ is the shear strength of therock bolt, taken as 400 MPa; K2 is the shear safety factor of the roof, taken as 3.0. |
| Dome theory | Lf2 = 2.55 m Ls2 = 2.50 m Llrb2 = 1.02 m | Lf ≥ b + L3 + L4 Ls ≥ a0 + L3 + L4 | 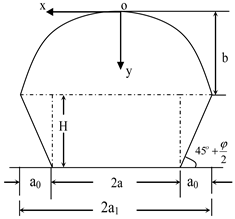 2a is the width of the gateway, taken as 5.8 m; H is the height of the gateway, taken as 4.0 m; The internal friction angle of the coal seam is denoted as φ, with a value of 26.1°; F is the strength coefficient of Proctor rock, which is taken as 3.1; Q is the anchoring force of the rock bolt, taken as 100 kN; K3 is a security factor, set to 2.0; γ is the bulk density of the direct roof rock mass, taken as 25.4 kN/m3. |
| “Chinese Coal Mines Technical Specifications” for Roadway Support with Rock Bolts | Lf2 = 2.3 m Ls2 = 2.3 m Llrb2 = 1.05 m | Lf = 1.6~3.0 m Ls = 1.6~3.0 m Llrb = 0.6~1.5 m | Take the average of the recommended values for each parameter. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, T.; Yang, P.; Zhao, J.; Cheng, Z. Function of Bolts in Arching Process of Surrounding Rocks of Roadways and Its Application in Support Design for Large Section Gateways. Appl. Sci. 2025, 15, 10327. https://doi.org/10.3390/app151910327
Guo T, Yang P, Zhao J, Cheng Z. Function of Bolts in Arching Process of Surrounding Rocks of Roadways and Its Application in Support Design for Large Section Gateways. Applied Sciences. 2025; 15(19):10327. https://doi.org/10.3390/app151910327
Chicago/Turabian StyleGuo, Tuanjie, Peiju Yang, Jitao Zhao, and Zhenglong Cheng. 2025. "Function of Bolts in Arching Process of Surrounding Rocks of Roadways and Its Application in Support Design for Large Section Gateways" Applied Sciences 15, no. 19: 10327. https://doi.org/10.3390/app151910327
APA StyleGuo, T., Yang, P., Zhao, J., & Cheng, Z. (2025). Function of Bolts in Arching Process of Surrounding Rocks of Roadways and Its Application in Support Design for Large Section Gateways. Applied Sciences, 15(19), 10327. https://doi.org/10.3390/app151910327





