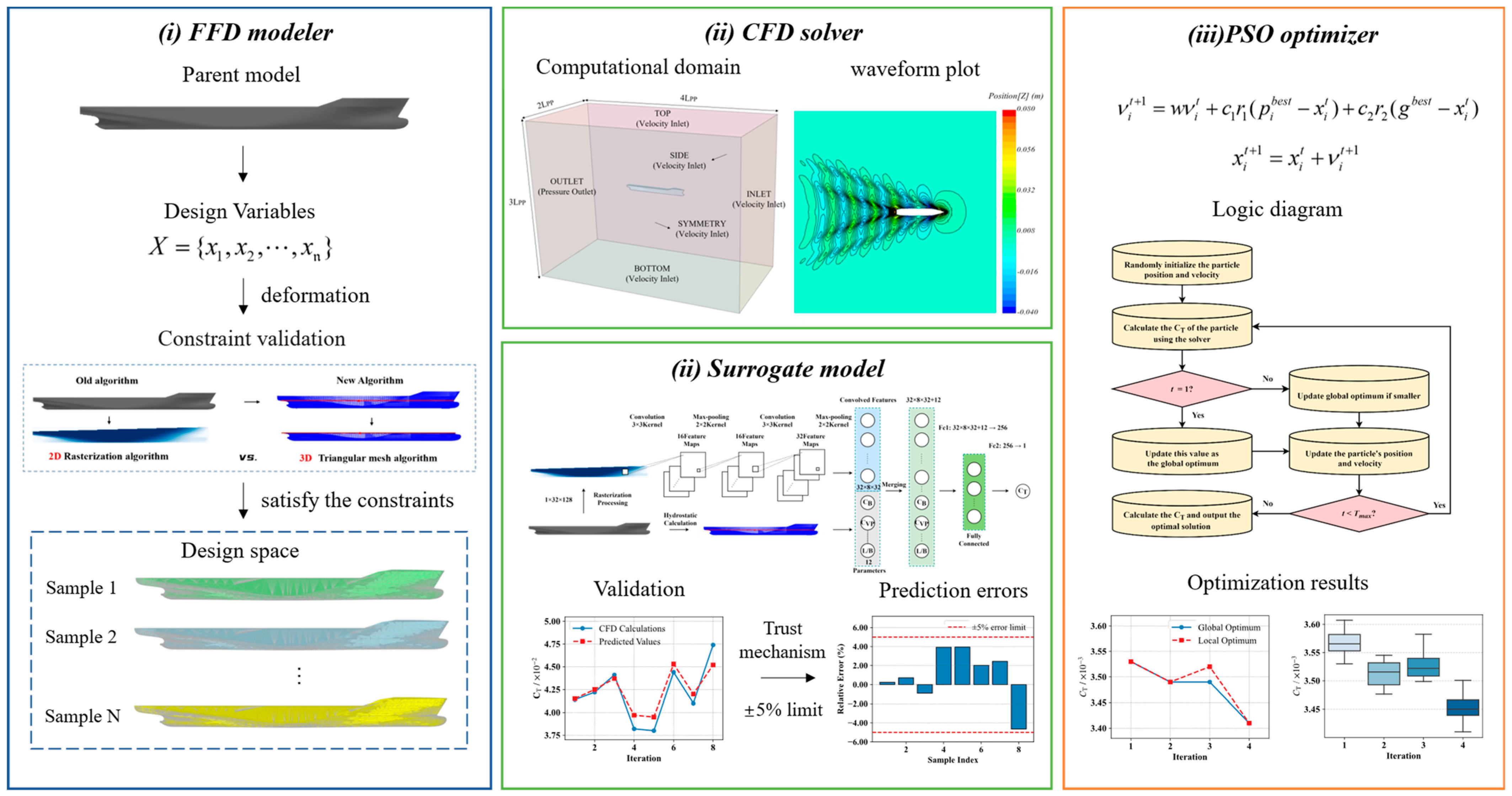
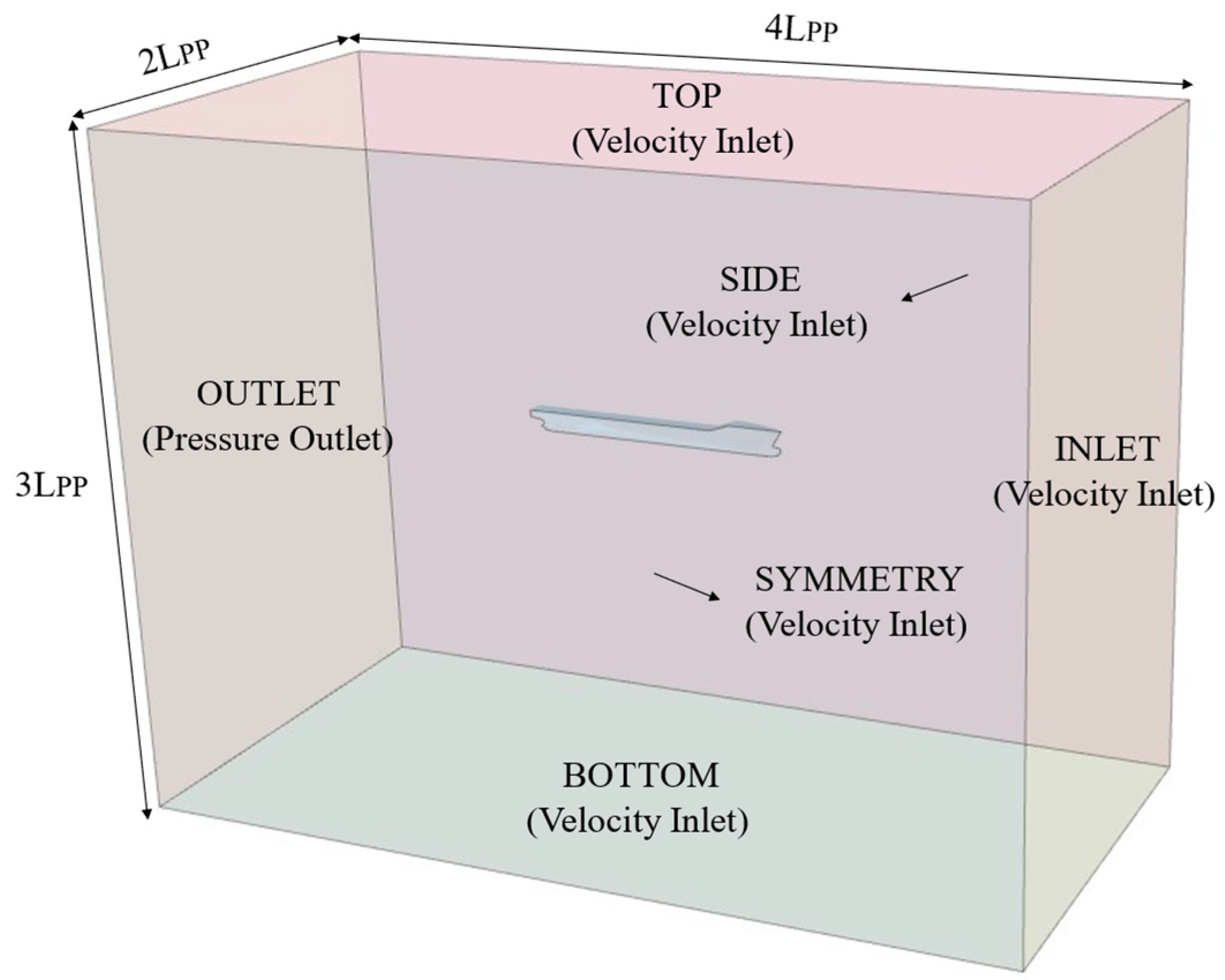
The hull form optimization system developed in this study is built upon the Simulation-Based Design (SBD) framework, integrating key technologies such as optimization algorithms, geometric modeling, and Computational Fluid Dynamics (CFD) into a closed-loop, fully automated optimization process [
26], as illustrated in
Figure 3. The system is designed to refine hull designs and toward the optimal performance through multiple optimization cycles iteratively, thereby enabling efficient and effective ship design. It consists of three modules: the optimizer, the modeler, and the solver, corresponding, respectively, to optimization techniques, automatic hull geometry modification, and CFD simulation.
The optimizer is responsible for sampling and updating the population using optimization algorithms. These algorithms can be broadly classified into two categories. The first category is gradient-based optimization, which includes methods such as the steepest descent method [
27] and Sequential Quadratic Programming (SQP) [
28]. The second category is stochastic search optimization, including Particle Swarm Optimization (PSO) [
29] and Genetic Algorithms (GA) [
30]. In ship design optimization, the optimizer evaluates and refines ship models based on performance-related parameters.
The modeler applies parametric deformation techniques to decode sample data and construct 3D ship models. This process generally falls into two approaches: geometry modification based on ship parameters and geometry modeling–based methods. Parameter-based geometry modification—such as parametric modeling [
31] and the Lackenby deformation method [
32]—reshapes hull geometry quickly by adjusting parameters like
L/
B or block coefficient. Geometry modeling–based methods, such as CAD modeling [
33] and Free-Form Deformation (FFD) [
34], allow not only overall hull deformation but also precise local adjustments, while maintaining control over volume changes before and after deformation.
These three modules work in close coordination: the optimizer generates design samples, the modeler transforms them into hull geometries, and the solver evaluates their performance. The results are then fed back to the optimizer, guiding the next round of refinement. Through this loop, the design progressively converges toward the optimal hull form.
2.2.1. PSO Optimizer
Ship design and performance optimization problems often feature high-dimensional design spaces and nonlinear constraints. Such complexity limits the effectiveness of purely gradient-based optimization methods in finding global optima [
37]. By contrast, swarm intelligence optimization algorithms have become an important tool in engineering optimization, as they do not rely on gradient information, have strong global search capabilities, and are relatively easy to implement [
38]. Among these, Particle Swarm Optimization (PSO) has been widely applied to hull form optimization [
39] and energy efficiency improvement [
40] because of its small number of parameters, fast convergence, and stable performance in various engineering tasks.
Compared with other evolutionary algorithms such as Genetic Algorithms (GA) or NSGA-II, PSO is chosen in this study because it requires fewer control parameters, converges faster in continuous design spaces, and provides reliable performance with relatively low computational overhead. Since the objective of this work is to validate the feasibility of the proposed dual-mode optimization framework rather than to benchmark different optimizers, PSO offers a practical balance between efficiency and robustness under the limited number of expensive CFD-based evaluations [
41].
In PSO, each particle represents a candidate solution, and its motion in the search space is determined by both position and velocity. During the iteration process, particles adjust their trajectories based on their own historical best position (personal best,
pbest) and the best position found by the swarm (global best,
gbest), enabling dynamic evolution of the solutions. The velocity and position are updated using the following equations:
Here, and denote the position and velocity of the particle at iteration, is the inertia weight, and are learning factors, are random numbers that help increase search diversity.
In this study, PSO aims to minimize the total resistance coefficient, with the design variables being the control point parameters of the FFD method. The optimizer first reads the initial positions and velocities of the particle swarm from a historical sample database and evaluates the objective function for each particle. The global best solution is initialized with the state of the first particle, after which the iterative update process begins. In each generation, particle velocities and positions are updated according to Equations (1) and (2), new models are generated, and their performance is evaluated by the solver. The personal and global best values are then updated. When the maximum number of iterations is reached, the current best design is output. The PSO parameter settings used in this study are given in
Table 2. The inertia weight (
w = 0.3) and learning factors (
c1 = 0.35,
c2 = 0.8) follow recommended values in the literature [
42] and have been validated in our previous studies [
17]. The relatively small inertia weight promotes local exploitation, while the asymmetric learning factors (
c2 >
c1) prioritize swarm knowledge over individual memory, which accelerates convergence and reduces the number of costly function evaluations. The position range ([−1, 1]) and velocity range ([0.04, 0.06]) are chosen to constrain the FFD control point displacements within realistic bounds: large enough to ensure effective exploration of the design space, but limited to avoid unphysical hull distortions.
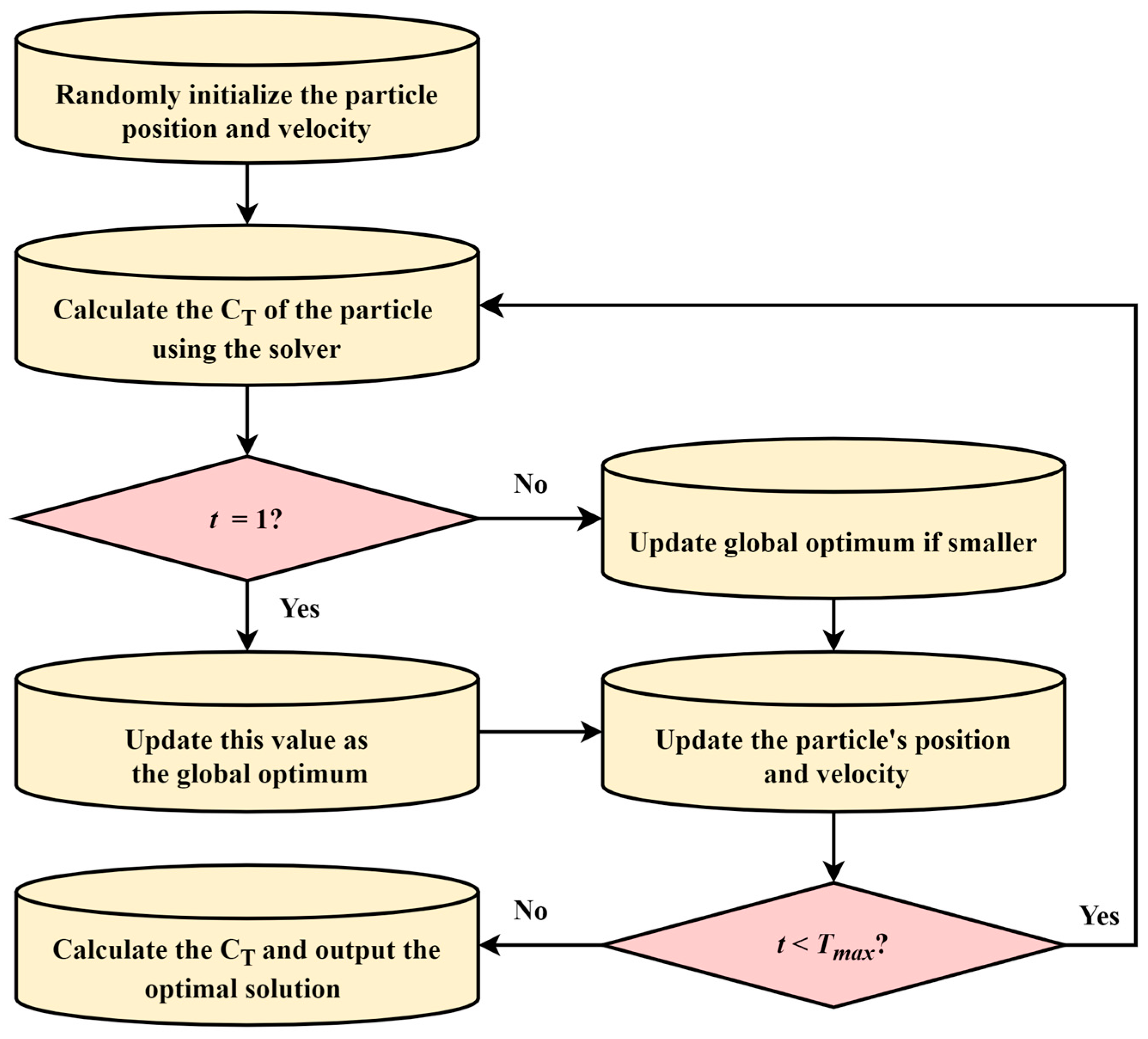
The flow chart of PSO optimizer is illustrated in
Figure 4. The initial population is first converted into 3D geometric models by the modeler. The solver then computes the corresponding total resistance coefficient
CT. Based on this performance feedback, the optimizer dynamically adjusts the particle swarm and continues iterating until the termination condition is met. This optimization module, working in conjunction with the modeler and solver, forms the core optimization engine of the SBD framework in this study.
2.2.2. FFD Modeler
In the previous section, the optimizer module has already produced the design variables that describe hull deformations. This section focuses on the selection and implementation of the geometric modeling method, which transforms these abstract parameters into three-dimensional hull geometries for subsequent hydrodynamic performance evaluation. The choice of geometric modeling approach not only affects the expressiveness of the design variables but also directly determines the exploration capability of the design space and the computational accuracy during optimization.
Some popular techniques such as blending methods, Bezier patches, radial basis interpolation, and the Lackenby transformation each have their strengths but also notable limitations. The blending method depends heavily on the initial set of hull forms, making it difficult to go beyond the original geometry. The Bezier patch approach enables precise local shape adjustments but is less efficient for large-scale deformations. Radial basis interpolation offers a small number of design variables and computational flexibility, yet tends to produce distortions when applied to large surface modifications. The Lackenby transformation involves few parameters and is well-suited to global scale changes, but lacks the ability to finely control local surface features [
43].
To overcome these drawbacks and enable more flexible, fine-grained, and continuous geometric transformations, this study adopts the Free-Form Deformation (FFD) technique. First proposed by Sederberg and Parry in 1986 [
44], FFD has been widely applied in computer graphics, but its systematic application to ship design and optimization has only gained traction in the past decade. The core idea of FFD is to embed the target object in a regular control volume and achieve continuous deformation by moving the positions of control points, thereby allowing both global and local geometry adjustments.
The process begins by establishing a local coordinate system for the control volume enclosing the object. Taking
X0 as the origin and
S,
T, and
U as the three directional vectors, any point
X within the control volume can be expressed in the local coordinates as:
Here, s, t, and u are the coordinates of the point in the local system, ranging from [0, 1].
Once the local coordinates are obtained, polynomial basis functions are used to map the control points, as expressed in Equation (4):
where
represents the position of a parameter point in the deformed space,
is the new position of the
control point, and
is the cubic Bernstein basis function.
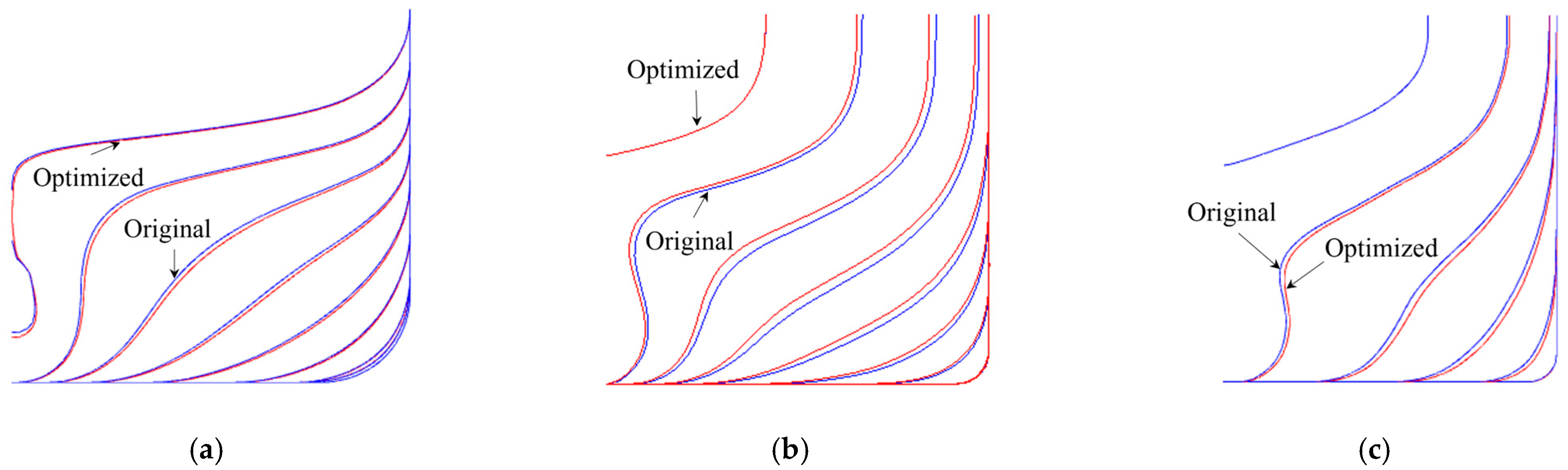
Figure 5 illustrates the application of Free-Form Deformation (FFD) to hull form modification. The initial hull geometry is embedded within a three-dimensional control lattice composed of uniformly distributed control nodes, with local densification around the fore and aft-body region to enable precise shape adjustments. By displacing selected control points in the x, y, or z directions, the surrounding hull surface deforms smoothly through the FFD interpolation function. These displacement values are later treated as design variables for the optimizer, which employs CFD evaluations to guide the iterative hull optimization process.
The selection of control points in the FFD lattice plays a key role in defining the design space and influencing optimization outcomes. In this study, control points were uniformly distributed overall, with local densification around the fore and aft-body regions. This arrangement provides an appropriate balance between computational efficiency and optimization precision.
To prevent excessive geometric distortion or displacement-related errors such as variations in displacement volume, the magnitude of control point shifts in the x, y, and z directions is limited to within 2%. Additionally, a geometry verification algorithm is implemented to ensure modeling accuracy. To provide a clearer explanation for
Figure 6, the verification algorithm works on the deformed STL geometry through a multi-step process: (a) The algorithm first parses the STL file to extract the vertices and normal vectors of all triangular facets. (b) The waterplane contour at a specified draft is precisely determined by calculating the intersection lines between the triangulated surface and the draft plane. (c) These intersection points are sorted and connected to form a closed, non-intersecting polygon representing the waterline. (d) The closed waterplane polygon is then triangulated into a set of simple triangles for which area and centroid calculations are straightforward. (e) Finally, the hydrostatics are computed by integrating the properties of these triangles, ensuring high numerical precision necessary for reliable CFD evaluation.
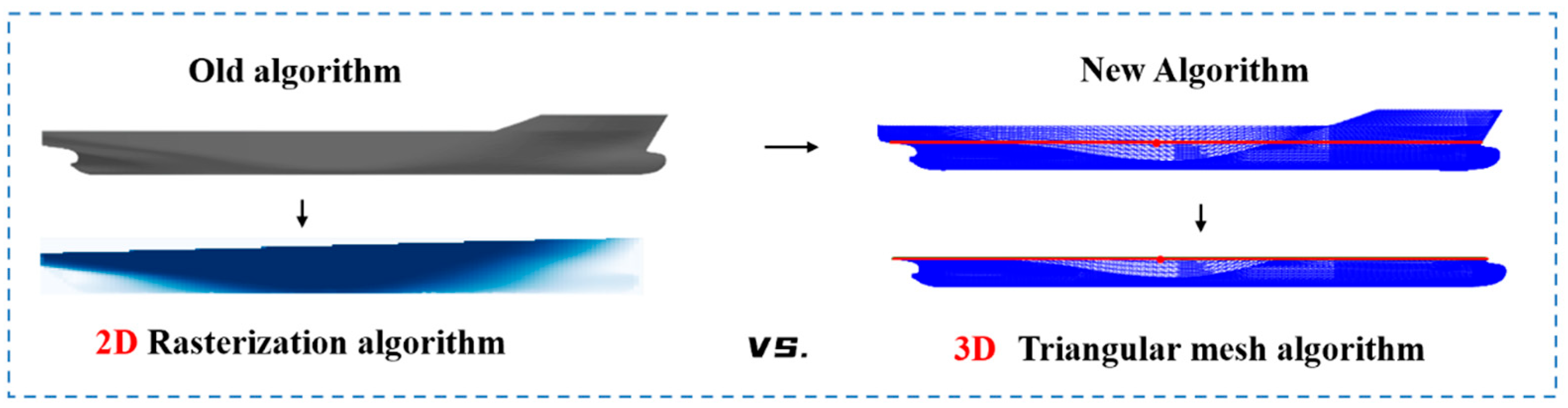
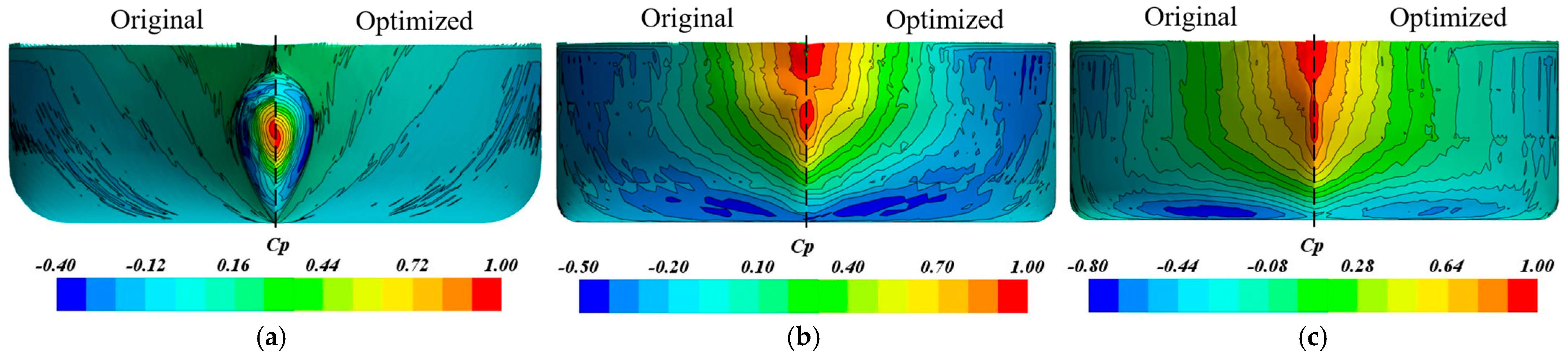
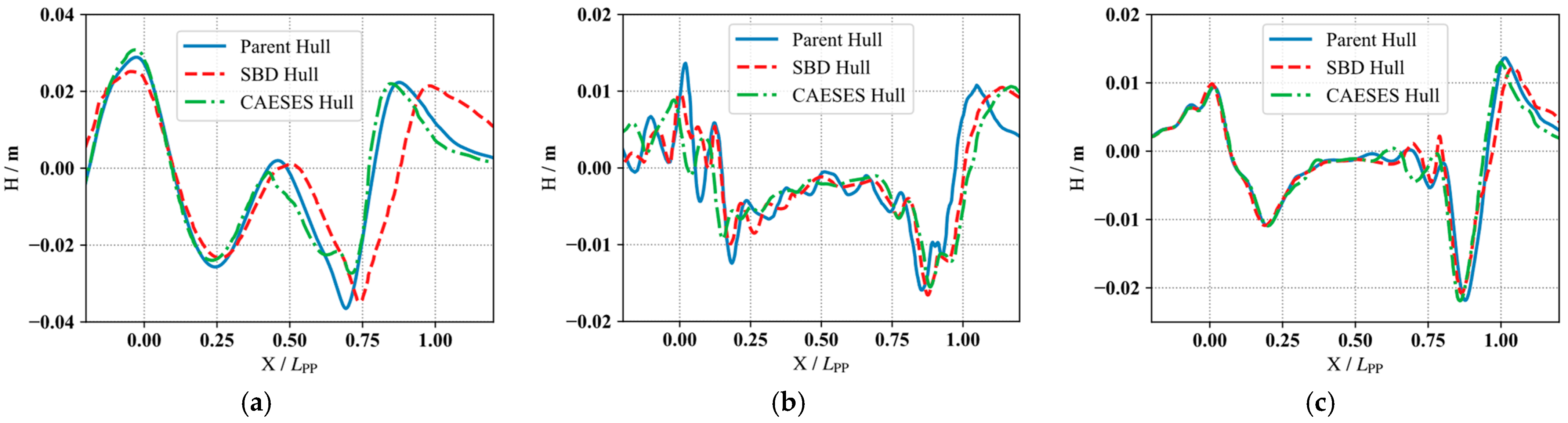
As illustrated in
Figure 7, compared with the 2D rasterization algorithm mapping the 3D surface offset on the central plane and calculating hydrostatics based on projected area, the proposed 3D triangular mesh algorithm, however, preserves the 3D features of the original geometry. As a result, it achieves significantly higher accuracy for parameters closely related to 3D volume and surface area, such as wetted surface area (m
2) and displacement volume (m
3).
To evaluate the accuracy of the algorithms, the KCS benchmark model is used. The reference values (“Reference Data”) for all hull form parameters are obtained from the complete geometry database provided by the official SIMMAN 2008 website, which serves as the benchmark for this study. The evaluation results of both the conventional and proposed algorithms are summarized in
Table 3. The proposed method limits calculation errors against the reference data for all hull form parameters to within 1% (maximum is 0.71% from
CM), with a particularly notable improvement in displacement volume accuracy.
2.2.3. Dual-Mode Solver
In the previous section, the FFD modeler converted the design variables output by the optimizer into computable three-dimensional hull models. To assess the hydrodynamic performance of these designs, a numerical solver is required to simulate the surrounding flow field and predict resistance. The CFD solver is the core tool for this task. Its fundamental principle involves discretizing the governing equations of fluid motion, then solving them iteratively on a computational grid to obtain the velocity field, pressure field, and total resistance around the hull. Widely used in ship design, CFD offers high-accuracy numerical predictions that complement physical experiments, providing a robust physical basis for performance optimization.
However, high-fidelity CFD simulations come at a steep computational cost, particularly in hull form optimization, where numerous candidate designs must be evaluated repeatedly. For example, resistance prediction for a single hull at full scale with a refined mesh can require several hours or more, making large-scale exploration of the design space impractical.
To address this challenge, surrogate models have been increasingly introduced into hydrodynamic performance prediction in recent years. The core idea is to employ data-driven methods to learn the nonlinear mapping between input features and target performance, thereby reducing computational demands while sacrificing only minimal accuracy [
45]. Among these, deep learning approaches, owing to their powerful feature extraction and generalization capabilities, have shown strong performance in tasks such as hull resistance prediction [
46] and ship speed estimation [
47]. In particular, Convolutional Neural Networks (CNNs), which excel at capturing both local and global geometric features, have proven well-suited for hydrodynamic performance prediction [
48].
Building on this foundation, the present study proposes a hydrodynamic performance evaluation framework that integrates a two-dimensional Convolutional Neural Network (2D CNN) with a dual-mode mechanism. The method dynamically switches between CFD simulation and surrogate model prediction during optimization, striking a balance between computational accuracy and efficiency to enable fast yet reliable hull performance assessment.
Here, the 2D CNN serves as the surrogate model, and its logical structure is illustrated in
Figure 8. The 2D CNN effectively captures local spatial features on the hull surface and extracts multi-scale geometric patterns through convolution operations, enhancing both generalization capability and prediction accuracy.
In the data preprocessing stage, the hull surface is projected onto a two-dimensional grid and rasterized at a fixed resolution of 32 × 128, yielding a 2D tensor. The network input consists of two parts: (1) The rasterized 2D hull geometry data. (2) A 12 × 1 vector containing principal dimensions and form coefficients.
The raster data are first processed through the convolutional network to extract features, after which the 12 × 1 parameter vector is concatenated with the flattened convolutional features.
The 2D CNN architecture designed in this study comprises two convolutional layers and two pooling layers. The convolution operations capture multi-scale local geometric features of the hull surface, while pooling operations reduce data dimensionality. Finally, the flattened convolutional features are fused with the 12-dimensional parameters and passed through fully connected layers to perform regression, producing the total resistance coefficient CT as the output.
The model is trained using a dataset of 200 pre-computed CFD samples, split into 80% for training and 20% for validation.
Table 4 summarizes the key hyperparameters and training configuration.
The prediction accuracy of the CNN model is evaluated on the test set. As shown in
Figure 9, the scatter plot of predicted versus true
CT values indicates that most points cluster near the ideal 1:1 line, indicating high predictive accuracy.
In this study, the input dataset is inherently high-dimensional, consisting of 12 principal coefficients together with 4096 rasterized geometric features. Traditional methods such as Kriging and RSM typically struggle to maintain predictive accuracy when applied to such high-dimensional and highly nonlinear data, as their scalability and feature extraction capability are limited. By contrast, CNNs are well-suited to this task because convolutional layers can effectively capture local and global geometric patterns while mitigating the curse of dimensionality.
For a horizontal comparison, reference values for the Kriging model and RSM are taken from relevant studies and are listed together with the CNN results in
Table 5. As can be seen, the proposed CNN achieves a normalized root mean square error (NRMSE) of 0.042 and an R
2 of 0.979, outperforming the RSM (NRMSE = 0.070, R
2 = 0.939) and Kriging (NRMSE = 0.015, R
2 = 0.955) baselines. These results demonstrate that the CNN model provides more accurate resistance prediction in the context of high-dimensional hull-form data.
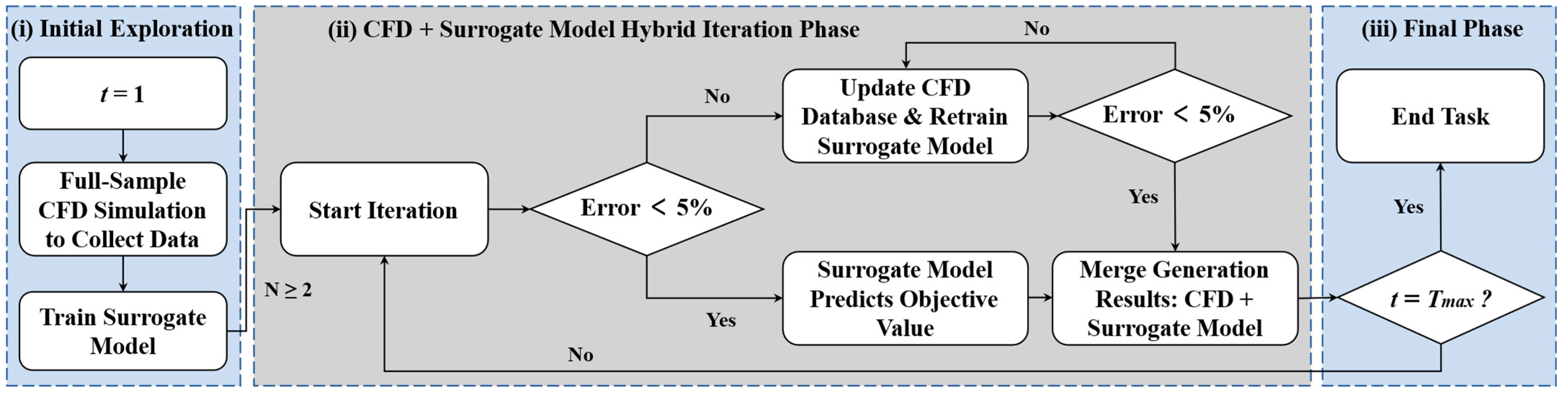
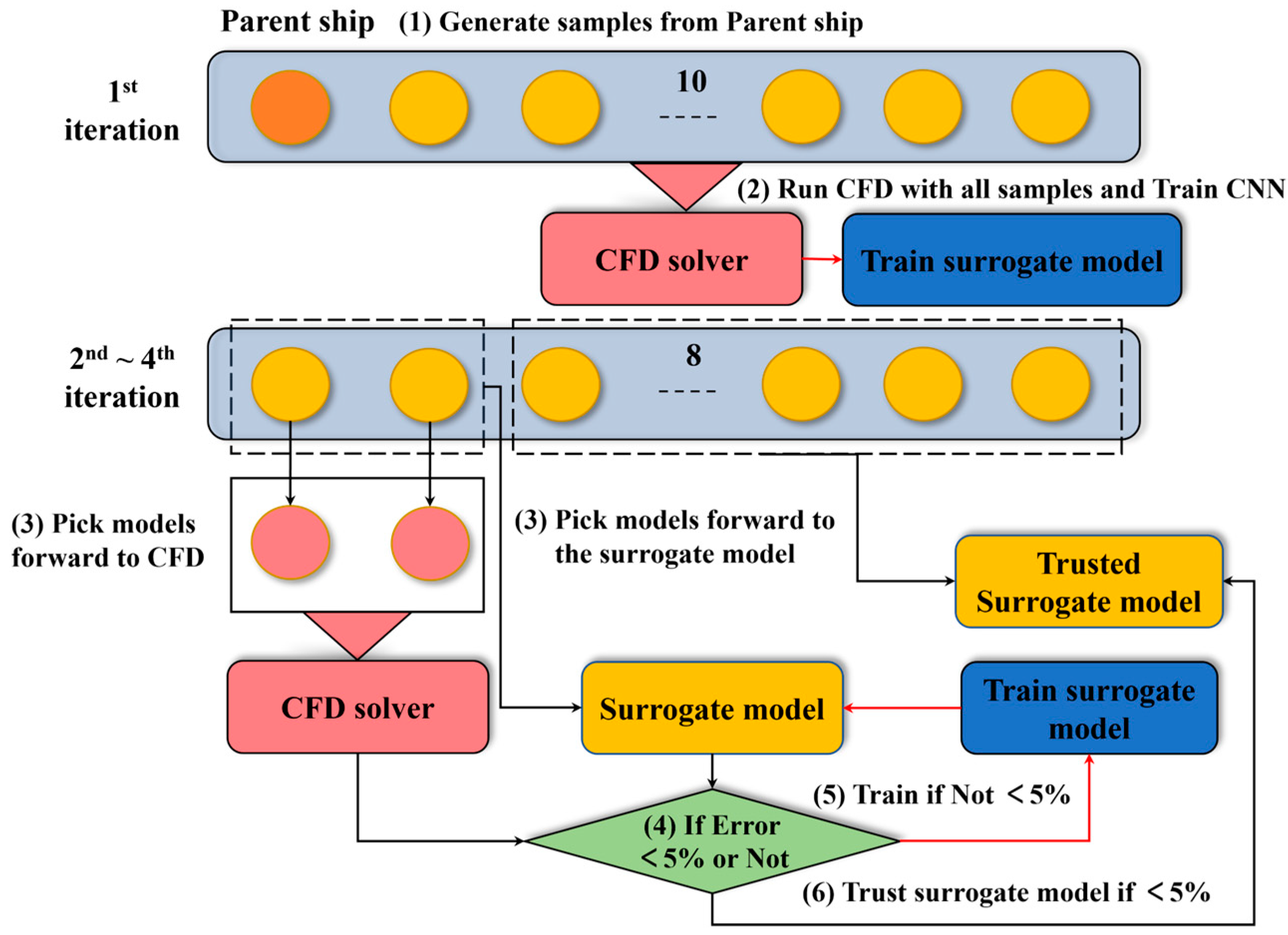
The overall workflow is illustrated in
Figure 10 and can be divided into three main stages:
- 1.
Initial Exploration Stage: At the start of optimization, the CFD solver is applied to all three-dimensional hull samples. The resulting high-fidelity hydrodynamic data are used to train the surrogate model, providing both an accurate performance baseline and guidance for determining promising search directions;
- 2.
Hybrid-Mode Iteration Stage: From the second optimization cycle onward, a hybrid strategy is applied: Only a subset of ship designs is evaluated using CFD, while the surrogate model predicts the remaining designs. The choice of evaluation method depends on the prediction error of the surrogate model:
Case 1: If the surrogate model’s prediction error is below 5%, the model’s output is accepted directly, improving computational efficiency;
Case 2: If the surrogate model’s prediction error exceeds 5%, CFD is used for that sample. The new CFD data are then incorporated into retraining the surrogate model until its error falls below the 5% threshold.
- 3.
Final stage: Once the maximum number of optimization cycles is reached, the final optimized hull form and its performance metrics are output.
Table 6 presents a short-term demonstrative case designed to validate the functionality of the dual-mode solver and to illustrate its working principle in a computationally affordable manner. The simulation duration is limited to 0.3 s, and the number of cycles and samples per cycle are intentionally kept small, allowing a clear demonstration of the stochastic sampling, optimization, and CFD verification procedure, while avoiding excessive computational overhead. The chosen ship speed corresponds to the standard JBC test condition from the Tokyo 2015 CFD Workshop, ensuring representativeness of the setup.
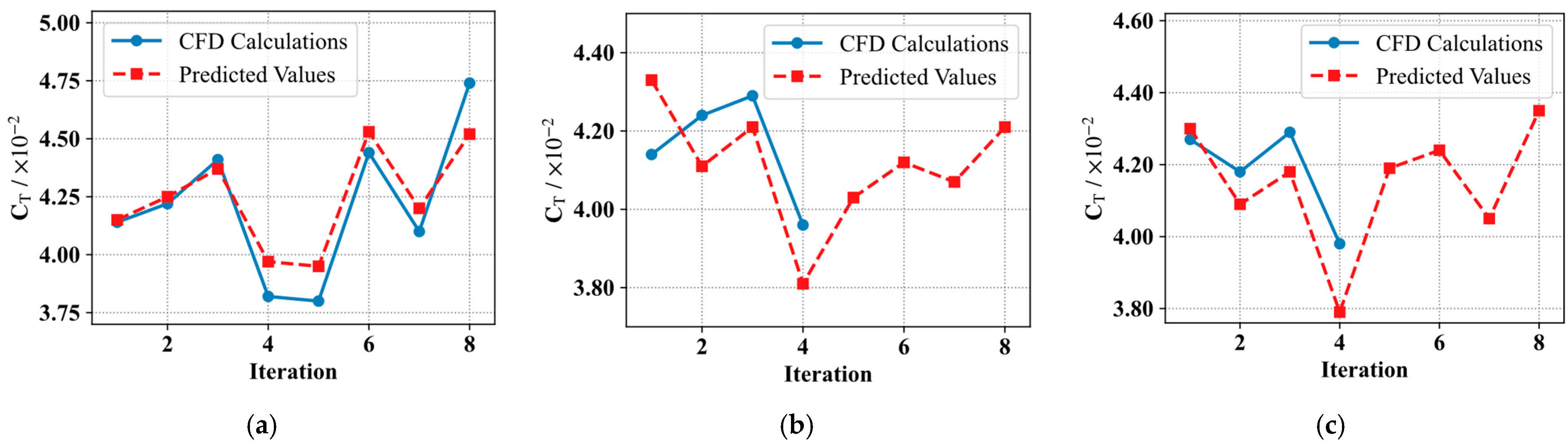
The dual-mode solver’s behavior in this test is shown in
Figure 11:
Figure 11a: First iteration—all samples are evaluated using both CFD and the 2D CNN surrogate model for comparison. Blue solid lines indicate CFD results, and red dashed lines indicate surrogate predictions.
Figure 11b: Second iteration—CFD is applied only to the first 4 samples, with the rest predicted by the surrogate model.
Figure 11c: Third iteration—followed the same computation mode as the second iteration.
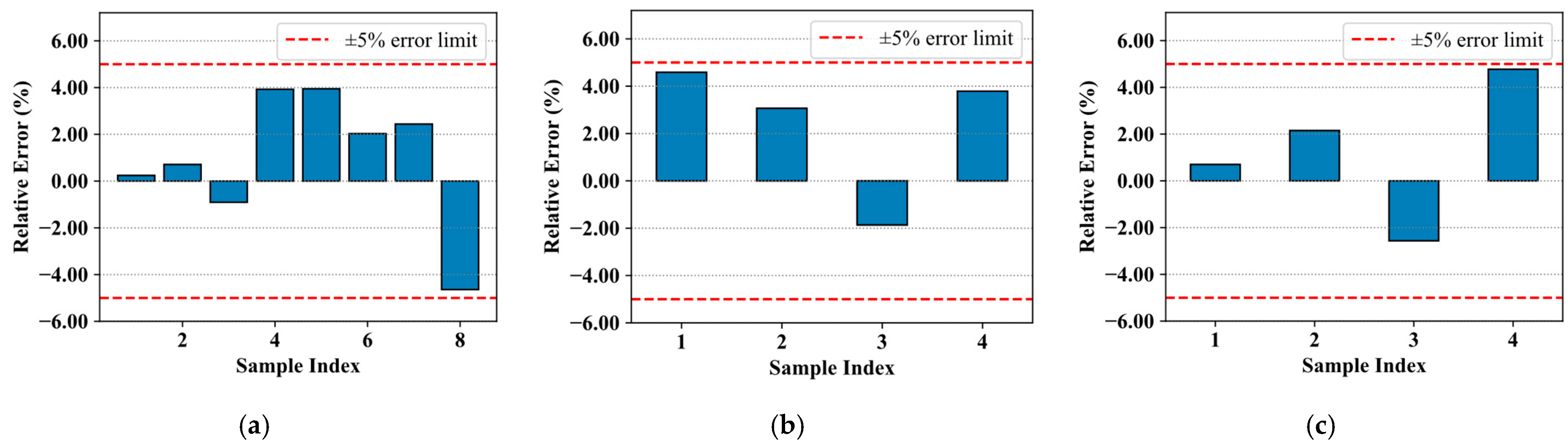
The relative error between surrogate predictions and CFD calculations is computed according to Equation (5). If the error for a given cycle is within 5%, the surrogate model is considered reliable and is used for the remaining samples; otherwise, additional CFD calculations are performed to retrain the model until the error falls below the threshold.
The choice of a 5% error threshold for surrogate model acceptance is supported by empirical studies in naval architecture, such as Chen et al. [
51], who reported surrogate model errors in the range of 3–7% for similar ship resistance prediction tasks. The error evaluation results for the short-term test are presented in
Figure 12. Across all iterations, the surrogate model’s prediction error remained below 5%, confirming its reliability and applicability in the hybrid computation framework.