Multi-Stage Stochastic MILP Framework for Renewable Microgrid Dispatch Under High Renewable Penetration: Optimizing Variability and Uncertainty Management

Abstract

The research develops a multi-stage stochastic Mixed-Integer Linear Programming (MILP) model for managing dispatch schedules in microgrids with significant renewable energy integration. The primary objective is to optimize the integration of renewable energy sources with energy storage systems and grid power, concurrently aiming to reduce operational costs and address uncertainties associated with renewable energy resources. The model effectively captures the variability inherent in renewable sources through the use of scenarios and implements a multi-stage MILP formulation that incorporates storage and load constraints. The methodology employs stochastic optimization techniques to regulate fluctuations in renewable generation by analyzing diverse energy availability scenarios. The optimization process is designed to minimize grid power consumption while maximizing the utilization of renewable energy via storage and load constraints that guarantee a balanced energy supply. The model achieves optimal operational costs by producing results that amount to 46,600 USD while successfully controlling renewable energy variability. The research demonstrates two main achievements by integrating high renewable penetration levels and providing valuable insights into how energy storage systems and grid independence lower costs.

1. Introduction

Renewable energy microgrids are often seen as a breakthrough solution to our energy problems [1]. These systems (described in Figure 1), combining solar, wind, and energy storage, can operate independently or in tandem with the larger grid [2]. For remote communities, microgrids offer an appealing solution by enabling localized control over energy supply without relying on the extension of distant central grids. In theory, this presents a clear advantage. However, the practical implementation of microgrids is often more complex and challenging than it appears on paper. One of the biggest challenges is the inherent unpredictability of renewable energy sources like solar and wind [3]. Solar panels are ineffective during periods without sunlight, and wind turbines cannot generate power in the absence of wind. While microgrids theoretically offer energy independence, their performance remains heavily dependent on weather conditions. Battery storage provides a partial solution by capturing excess energy during optimal conditions for later use. However, this approach has limitations; batteries are costly, and their lifespan is finite, making long-term sustainability a concern. Over time, batteries lose their ability to hold a charge, making eventual replacement necessary. While energy storage is essential for enhancing the reliability of renewable power, it remains a significant financial burden. Beyond cost, scaling up presents another major challenge. Microgrids are typically designed to serve specific communities, which works well when demand is limited. However, connecting multiple microgrids to form a larger, more efficient system involves far more than simply adding additional solar panels or batteries. The supporting infrastructure, wiring, control systems, and software must be reconfigured to handle increased complexity. Scaling is not as straightforward as it may appear, and costs can escalate rapidly. Moreover, integrating microgrids into the national grid introduces a new set of technical, regulatory, and operational challenges [4].

Renewable energy is variable in nature, and matching the energy supply with the demand with renewable energy sources requires complex planning [5]. Excess production of electricity without sufficient storage capacity leads to energy wastage, operational inefficiencies, and increased generation costs due to underutilized output. Conversely, inadequate electricity production can cause supply shortages, resulting in blackouts and higher costs associated with emergency power procurement, equipment strain, and economic disruptions. Resolving this production dilemma necessitates the use of advanced control systems to effectively manage supply and demand in real time. While microgrids can save money in the long term, the upfront costs are a massive hurdle. These systems are expensive to install, and the financial return on investment does not happen overnight. Communities and businesses that are already financially stretched might hesitate to make such a big leap, even though it could pay off in the future.

As renewable energy sources like wind and solar are increasingly incorporated into power grids, microgrids have become a key solution to support these efforts [6]. The potential for microgrids to utilize clean, renewable energy is enormous, but there is a no-win situation: renewable generation is inherently variable. Wind does not always blow when you need it, and solar power is dependent on the sun. In microgrids, where high levels of renewable penetration are aimed for, this unpredictability can cause significant challenges in ensuring a stable energy supply. Multi-stage stochastic MILP optimization methods are frequently used to tackle these challenges [7]. These approaches aim to account for the uncertainty of renewable generation. In theory, the idea is sound. However, after diving into literature and examining current models, there is still a gap that needs to be filled if we are going to make real strides in this area. A lot of the current models, like those discussed by Haider et al. [8,9] still rely on relatively simple representations of uncertainty. The variability of wind and solar is not independent; they can be affected by the same weather system, sometimes in ways that current models fail to capture. Real-time decision-making is also an issue. Many of these optimization techniques operate on static models that fail to adapt to real-time changes in renewable generation and energy demand [10]. The role of energy storage systems (ESS) in microgrids cannot be overstated—after all, storage is what smooths out the peaks and valleys of renewable generation. But many models treat storage systems in an idealized way, almost as if batteries charge and discharge without loss or degradation [11]. Batteries degrade over time, and charge/discharge cycles are inefficient; these factors must be considered in optimization models to ensure their usefulness in real-world scenarios. Demand-side management (DSM) involves shifting energy usage to times when energy is more abundant, and it could significantly improve energy efficiency [12]. Yet, the way these optimization models treat DSM is usually an afterthought as a secondary consideration, not fully integrated into the broader framework. Scalability is also a major issue. Many of the current models work well for small to medium-scale microgrids. But as the systems grow, the models face computational challenges [13]. Applying these methods to large-scale systems with multiple microgrids requires more advanced algorithms, enhanced computational techniques, and potentially the use of parallel computing approaches. Otherwise, the practical applicability of these models will remain limited. This paper aims to develop a multi-state stochastic MILP for dispatch scheduling management in high penetration renewables. The objectives are to model renewable variability using scenarios, formulate a multi-stage dispatch MILP with storage and load constraints, and validate the model and compare the results obtained with deterministic dispatch.

2. Related Works

The increasing integration of renewable energy sources (RES) into modern power grids has led to a growing interest in microgrid dispatch optimization. This flexibility makes them especially crucial for improving energy security, particularly in remote or disaster-prone areas [14,15]. As the world shifts towards more sustainable and resilient energy systems, microgrids are becoming an important component of the transition. The primary goal of dispatch optimization is to effectively manage energy generation, storage, and demand. Energy generation is not always predictable. These fluctuations can significantly disrupt conventional energy management models and reduce their effectiveness. Advanced optimization techniques are crucial as they strive to find a balance between supply and demand, ensuring stability while keeping costs in check [16,17]. Stochastic optimization has been gaining popularity. These models are designed to handle the inherent uncertainty that comes with renewable energy. Unlike traditional deterministic models, which assume perfect knowledge of energy availability, stochastic models factor in multiple potential scenarios of fluctuating generation and demand [18,19]. But, while that is progress, there is still a long way to go, especially when it comes to applying these models in real-time energy management for large-scale microgrids that use multiple types of RES.

Deterministic models are the traditional ones where everything is known ahead of time. They are straightforward: they use fixed inputs to determine the optimal generation schedule, based on known constraints. The upside of this approach is that it is computationally efficient, which is why it works well for smaller systems or when energy generation is relatively stable. For instance, Conejo et al. [20] use deterministic models to solve unit commitment problems in scheduling energy generation. In the works of Zhang et al. [21], the authors applied deterministic models to smart buildings, optimizing energy usage when renewable energy is predictable. However, real-world applications are more complicated. Solar and wind are not exactly the most predictable sources. The assumption in a microgrid that we know exactly how much energy is available fails. So, relying solely on deterministic models in a dynamic system like a microgrid can lead to less-than-ideal results, especially when something unexpected happens [22]. As the penetration of RES increases, the variability becomes harder to ignore, and those deterministic models just cannot keep up.

Stochastic models, unlike deterministic ones, embrace uncertainty [23]. They do not assume a perfect knowledge of the systems; instead, they account for multiple possible scenarios. They use probability distributions and scenario generation techniques to manage the uncertainty in energy generation from wind and solar [18,19]. Stochastic models are more robust as they can adjust to various potential futures, and they are more applicable in the real world. For example, Kiptoo et al. [24,25] have demonstrated how scenario-based approaches and MILP can help balance generation, storage, and demand response. Furthermore, the complexity of these models can also make them harder to scale. The more scenarios you have, the longer the computation takes. This is a huge challenge, especially when you are dealing with large microgrids [26]. So, while they offer better solutions for uncertainty, they come with their own set of hurdles. Researchers have also made an effort to combine robust optimization and stochastic programming. This hybrid approach tries to bring together the flexibility of stochastic models and the computational efficiency of deterministic ones. It is like finding a middle ground, but again, this is still a developing area [27].

The research investigates stochastic programming methods, but our study develops an operational framework for high-RES microgrids that produces reproducible results. The paper makes the following contributions:

1.

A multi-period MILP that minimizes expected operating cost ${\sum }_s{\pi }_s{\sum }_t\left\{\cdot \right\}$ with scenario probabilities ${\pi }_s$ under realistic ramping, state-of-charge dynamics, charge/discharge limits, among others.

2.

A data-driven pipeline consists of three components: Monte Carlo trajectories generated from historical/empirical distributions and k-means scenario reduction and cluster-proportion probabilities.

3.

The explicit definition for power balance verification through bar plots for representative scenarios and cost and reliability KPIs.

4.

The paper discusses how scenario reduction impacts both cost and tractability while presenting a basic auditable method for (cluster proportions) that serves as a template for various renewable energy systems across different locations.

3. Multi-Stage MILP Formulation

At the heart of the optimization lies the multi-stage MILP model. This model minimizes the total operational cost of the renewable microgrid, aiming to balance renewable energy generation, energy storage, and grid imports while ensuring that demand is always met. It ensures that all variables, including renewable generation, battery storage, and grid supply, are optimized to work together effectively. The overview of the decision variables used in the multi-stage MILP formulation is summarized in

Table 1. System overview and decision variables.

Variables	Description
$t\in \left\{1,2,3,\dots ,T\right\}$	represent the time periods for the optimization horizon (e.g., hourly)
$s\in \left\{1,2,3,\dots ,S\right\}$	represent the scenarios, capturing renewable generation uncertainty and variability across time periods.
$P_{load,t}$	denotes the load demand at time $t$.
$P_{renewable,t}^{\left(s\right)}$	denotes the renewable energy generation at time $t$ for scenario $s$.
$P_{storage,t}$	denotes the energy stored or discharged at time $t$
$P_{grid,t}$	denotes the energy imported from the grid at time $t$
${SOC}_t$	denotes the state of charge of the storage system at time $t$
$P_{charge,t}$ and $P_{discharge,t}$	denote the charging and discharging power at time $t$, respectively.
${\alpha }_t^{\left(s\right)}$	denotes the scenario-dependent renewable energy uncertainty factor at time $t$ for scenario $s$, representing renewable energy variability.
$C_{renewable,t}$, $C_{storage,t}$ and $C_{grid,t}$	represent the operational costs for renewable generation, storage, and grid energy imports, respectively.
${\pi }_s$	scenario propbability
$\rho$	dimensionless renewable-penetration factor that scales the available renewable profile

Variables with superscript (s) are the scenario-dependent control decision; ${SOC}_t^{\left(s\right)}$ is a scenario-dependent state; and $P_{load,t}$ is exogenous.

. The model is solved using Python (Version 3.9.12), leveraging the PuLP library, which interfaces with the CBC solver to handle the optimization.

The objective function is designed to minimize the operational cost: renewable energy generation, energy storage, and grid energy import across the optimization period $T$ for $S$ scenarios. The cost function is described in (1).

$$\begin{gathered} \min \mathsf{{\rm Z}}=\sum _{t=1}^T{\pi }_s\sum _{s=1}^S\left(C_{renewable,t}\cdot P_{renewable,t}^{\left(s\right)}+C_{storage,t}\cdot \left[P_{charge,t}^{\left(s\right)}+P_{discharge,t}^{\left(s\right)}\right] \\ +C_{grid,t}\cdot P_{drid,t}^{\left(s\right)}\right), s.t\sum _{s=1}^S{\pi }_s=1, {\pi }_s\ge 0 \forall s \end{gathered}$$

(1)

where

$C_{renewable,t}$, $C_{storage,t}$, and $C_{grid,t}$, are the cost coefficients for renewable generation, storage, and grid energy at time $t$, respectively.

The energy generated by renewable sources $P_{renewable,t}^{\left(s\right)}$, energy stored/discharged $P_{storage,t}$, and energy imported from the grid $P_{grid,t}$ all contribute to the operational cost, depending on the scenario $s$ and time $t$.

These variables ensure the feasibility and reliability of the objective as described in (1).

3.1. Constraints Imposed on the Model

The optimization remains feasible and reliable, representing realistic operational conditions through these constraints. These constraints directly influence the objective function, as they restrict dispatch options, which in turn affect total operational costs. To meet demand at every time step $t$ and scenario $s$, the energy provided by renewable sources, storage, and the grid must satisfy the load demand:

$$P_{renewable,t}^{\left(s\right)}+\left(P_{charge,t}^{\left(s\right)}-P_{discharge,t}^{\left(s\right)}\right)+P_{grid,t}=P_{load,t} \forall t,s$$

(2)

The constraint ensures that all energy sources deliver sufficient power to meet demand, thereby avoiding both over- and undersupply situations, which would result in avoidable operational expenses.

Renewable energy generation faces restrictions because its maximum potential varies between different periods and scenarios. The physical boundaries of renewable generation remain within limits through this constraint.

$${0\le P}_{renewable,t}^{\left(s\right)}\le P_{renewable,max,t}^{\left(s\right)} \forall t,s$$

(3)

The constraint restricts renewable energy from exceeding total costs because it prevents the system from generating more renewable power than is available.

Also, the energy storage system must operate within specified limits:

Charge/Discharge Limits:

$$0\le P_{charge,t}^{\left(s\right)}\le P_{storage, max} 0\le P_{discharge,t}^{\left(s\right)}\le P_{storage,max} \forall t,s$$

(4)

State of Charge Limits:

$${SOC}_{min}\le {SOC}_t^{\left(s\right)}\le {SOC}_{max} \forall t$$

(5)

State of Charge Update:

$${SOC}_{t+1}={SOC}_t^{\left(s\right)}+{\eta }^{ch}{P}_{charge,t}\mathsf{\Delta }t- {\displaystyle \frac{1}{{\eta }^{dis}}}{P}_{discharge,t}^{\left(s\right)}∆t, \forall t,s$$

(6)

The operational costs in the objective function are influenced by energy storage constraints, as they determine both the charging and discharging rates and the storage state of charge.

The grid’s maximum capacity limits the amount of energy imported from or exported to the grid:

$${-P}_{grid max}\le P_{grid,t}^{\left(s\right)}\le P_{grid max,} ∆t,s$$

(7)

The constraint restricts the amount of energy that can be bought from the grid, which affects the total operational cost. The optimization system controls grid imports to prevent excessive costs from renewable and storage energy contributions.

Renewable generation is modeled as stochastic, and uncertainty is incorporated by defining a scenario-dependent uncertainty factor ${\alpha }_t^{\left(s\right)}$ for each renewable energy generation value:

$$P_{renewable,t}^{\left(s\right)}={\alpha }_t^{\left(s\right)}\cdot P_{renewable,max,t}^{\left(s\right)} \forall t, s$$

(8)

The constraint restricts the amount of energy that can be bought from the grid, which affects the total operational cost. The optimization system controls grid imports to prevent excessive costs from renewable and storage energy contributions.

The system needs to fulfill load requirements with a high degree of certainty to maintain reliable operation under uncertain conditions. The following constraint represents this requirement:

$$\sum _{s=1}^S{P}_{renewable,t}^{\left(s\right)}+P_{storage,t}+ P_{grid,t}\ge P_{load,t}\cdot \gamma \forall t, s$$

(9)

where $\gamma$ is a reliability factor, typically close to 1, ensuring the load demand is met with high probability.

The system needs reliability to achieve cost minimization while maintaining its robustness. The system’s failure cost will rise if it fails to meet demand requirements because of insufficient reliability. The optimization process gives priority to reliability through this constraint, which determines the selection of renewable energy sources, storage systems, and grid infrastructure.

The ramp-up (see Equation (10)) and ramp-down (see Equation (11)) constraints establish boundaries that control how quickly generation and storage levels change between successive time intervals, thus preventing unreasonably large variations:

$$P_{renewable,t}^{\left(s\right)}-P_{renewable,t-1}^{\left(s\right)} \le R_{max,t} \forall t, s$$

(10)

$$P_{renewable,t-1}^{\left(s\right)}-P_{renewable,t}^{\left(s\right)} \le R_{max,t} \forall t, s$$

(11)

where $R_{max,t}$ is the maximum allowable ramp-up or ramp-down rate at time $t$.

The power generation remains realistic and within system capabilities because ramp constraints prevent excessive fluctuations, which otherwise would increase operational costs.

Time Resolution and Scheduling Mode

The control time interval of $\mathsf{\Delta }t=1$ and a scheduling horizon of $T=12$ periods (12 h) is used to implement the energy management strategy (see

Table 2. Fundamental operational and economic parameters for the microgrid case study.

Component/Setting	Symbol	Value (Code)	Unit	Notes
Scheduling horizon	$T$	12	h	Intraday study with hourly steps.
Time step	$\Delta t$	1	h	Consistent with the cost per MWh.
Scenarios	$S$	5	–	Stochastic renewable profiles.
Load range	$P_{load}\left(t\right)$	60–90	MW	Drawn per hour in the case study.
Renewable availability (hourly cap)	$P_{ren}^{max}\left(t\right)$	30–60	MW	Envelope of available renewable power per hour.
Renewable ramp limit	$R_{max}$	10	MW/h	Limits
Battery energy capacity	$E_{max}\left({SOC}_{max}\right)$	100	MWh	SOC bounded in [0, 100] MWh.
Battery power rating	$P_{sto}^{max}$	30	MW	Rated charge/discharge power (model uses a single power variable in this baseline script).
SOC lower bound	${SOC}_{min}$	0	MWh	Energy floor.
Grid import	$P_{grid,t}$	$\ge 0$	MW	Import only; no explicit cap in this script.
Cost (renewable)	$C_{ren}$	50	currency/MWh	Applied to renewable dispatch.
Cost (storage)	$C_{sto}$	40	currency/MWh	Applied to storage power use.
Cost (grid)	$C_{grid}$	60	currency/MWh	Applied to grid imports.
Solver/implementation	–	CBC via PuLP	–	Mixed-integer linear optimization framework.

). It operates in an intraday rolling-horizon manner. For example, at each hour $k$, the MILP is solved over $\left\{k,...,k+11\right\}$. Also, note that only the first-period decisions are applied, forecasts are refreshed, scenarios are regenerated, and the horizon rolls forward by one period. This aligns with the intraday variability of renewable energy and the latency of microgrid actuation.

3.2. Scenario Generation and Stochastic Modeling

Renewable energy resources, especially wind and solar, are inherently variable. One of the trickiest aspects of managing a renewable microgrid is predicting how much energy will be available when needed most. To capture this uncertainty, stochastic modeling is used. This approach involves using multiple scenarios to represent various possible outcomes of renewable energy generation, which helps in accounting for variability over time. For this study, we chose a Monte Carlo simulation for scenario generation. The basic idea is to generate random samples based on statistical distributions; in this case, using historical wind speed data from the National Renewable Energy Laboratory (NREL). From this, five different scenarios ($S=5$), each representing a different possible wind power generation profile over 12 h ($T=12$). This gives the model a certain flexibility, allowing it to account for variability in a way that would be difficult to do with a single deterministic approach.

3.3. Scenario Reduction

One challenge that comes up in stochastic modeling is the sheer number of scenarios that need to be considered. More scenarios mean better accuracy, but they also result in exponentially higher computational costs. The aim is to reduce the number of scenarios, while ensuring that the reduced set still accurately represents the variability in the renewable generation. The k-means clustering algorithm is used for scenario reduction. It is performed on the $T$-$dimentional$ scenarios, and the number of clusters $k$ is chosen through an elbow heuristic (beyond $k=5$). The reduction in within-cluster dispersion is marginal, while the MILP solve time increases notably with the CBC solver. We therefore use five representative scenarios that preserve the principal variability and ramp features over the $12$-$\mathrm{h}$ horizon. After the $k$ means scenario reduction, the probability, ${\pi }_s={\displaystyle \frac{1}{S}}$ of each representative scenario equals the fraction of original trajectories in its cluster. Therefore, in the absence of such counts, we use uniform ${\pi }_s={\displaystyle \frac{1}{S}}$. This algorithm groups similar scenarios together and then selects representative scenarios from each cluster. In practice, this meant that instead of working with all five hundred possible scenarios, one could choose a smaller set of five representative ones that captured the main variability of the system. It may not be the perfect solution, but it is a reasonable compromise between computational feasibility and model accuracy.

3.4. Model Solving and Performance Metrics

Once the model was formulated and the scenarios reduced, I moved on to solving the problem. Using the CBC solver [28], we ran the optimization to find the best dispatch schedule. But solving the problem is just one part of the process. Once the optimization results are ready, it is essential to evaluate them to assess the model’s performance. The evaluation utilizes several metrics, including cost metrics and reliability metrics. The cost metrics address the query concerning the overall operational expenditure, which encompasses the total cost of fulfilling demand through the integration of renewable energy, storage solutions, and grid energy. The reliability metrics measure the renewable energy utilization, storage efficiency, and grid energy utilization. These metrics are evaluated over each period and scenario.

4. Results and Discussion

4.1. Operational Performance Across Stochastic Scenarios

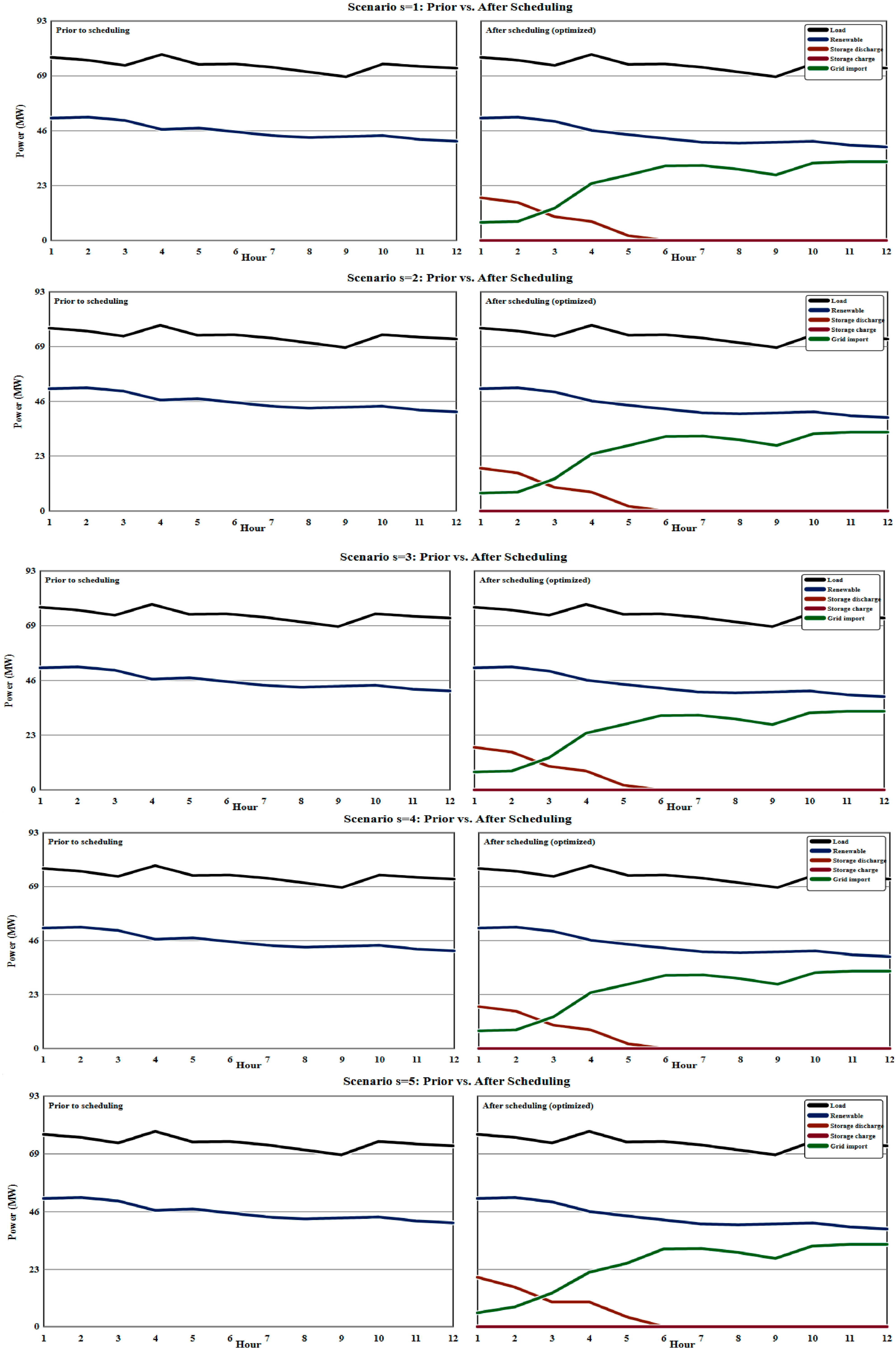
The scheduling process results in the presentation of load trace and renewable availability curves through Figure 2. The net supply deficit or surplus becomes visible through the comparison between the load trace and the renewable availability before scheduling occurs. The storage system discharges power at times when the load exceeds renewable energy availability and charges power when renewable energy production exceeds load requirements after scheduling.

The left side of the panels displays the unaltered hourly differences between power demand and renewable power availability, while the right side demonstrates how optimized dispatch operations use storage and grid imports to create a perfect match between supply and demand. The scenarios demonstrate high renewable power usage while the power grid remains inactive during most time periods, and storage systems achieve necessary flexibility through controlled moderate to deep charge–discharge cycles, with the highest peak in Scenario 4.

4.2. Analysis of Operational Cost Dynamics Across Scenarios

The operational cost curve for Scenario 1 (Figure 3) reveals significant fluctuations in the total operational cost, ranging from $0$ costs to peak values of $\$5$. The peaks indicate times when energy demand exceeds the renewable generation, leading to increased reliance on grid energy or storage. The sharp drops in cost indicate the effective use of renewable energy during periods of excess generation.

In Scenario 2 (Figure 4), there is a more gradual increase in operational costs from $0$ to about $\$25$ compared to Scenario 1. The cost spikes at specific periods, indicating a steady increase in reliance on the grid or storage, especially when renewable generation falls short of meeting demand. The relatively smooth pattern shows an optimized use of energy storage and grid backup in response to varying renewable output.

The operational cost for Scenario 3 (Figure 5) shows a considerable initial cost, peaking around the 2 to 3 h time horizon, before sharply decreasing. This could indicate an aggressive strategy of grid imports or storage usage at the beginning, followed by efficient use of renewable energy and storage over time. The decrease in costs suggests that renewable generation and storage reach an optimal point, reducing dependency on more expensive grid power.

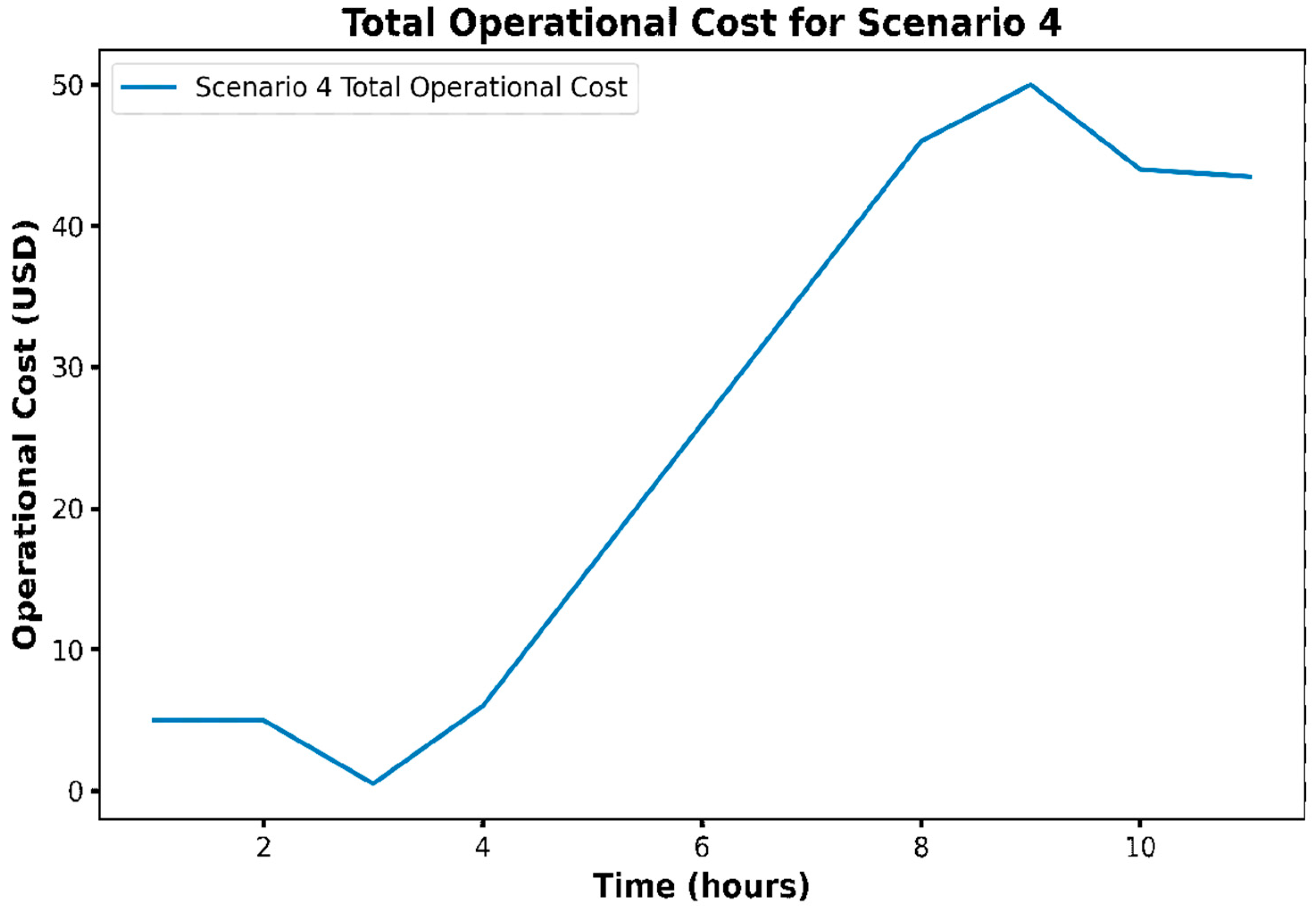
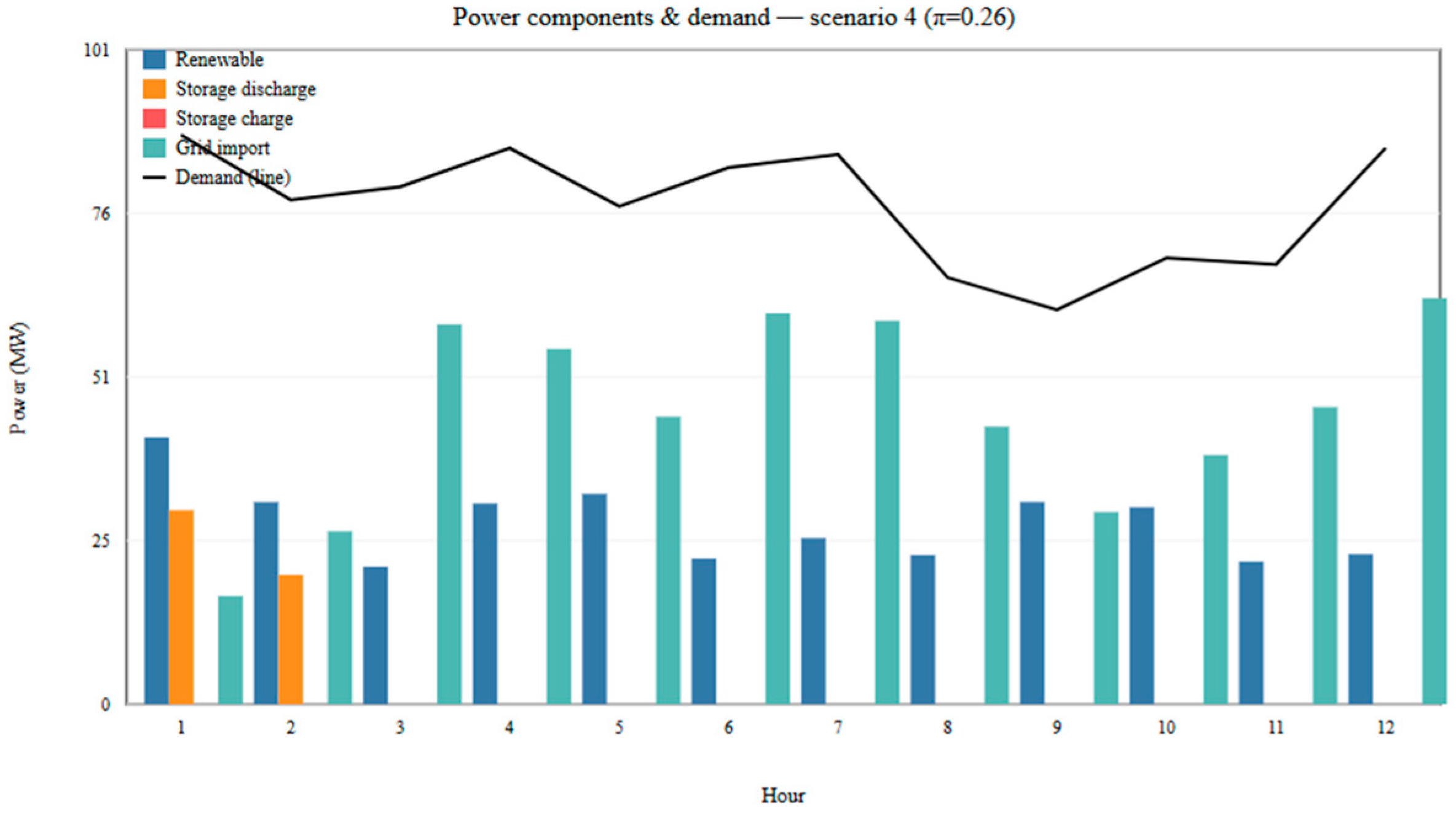
Scenario 4 (Figure 6) exhibits a rapid increase in operational costs early on, followed by a relatively stable phase. This suggests a scenario where grid energy and storage power were initially heavily utilized, followed by more balanced integration of renewable generation. The relatively higher operational cost is about $\$50$. In comparison to other scenarios, it indicates a less optimized renewable generation strategy or higher reliance on costlier energy sources.

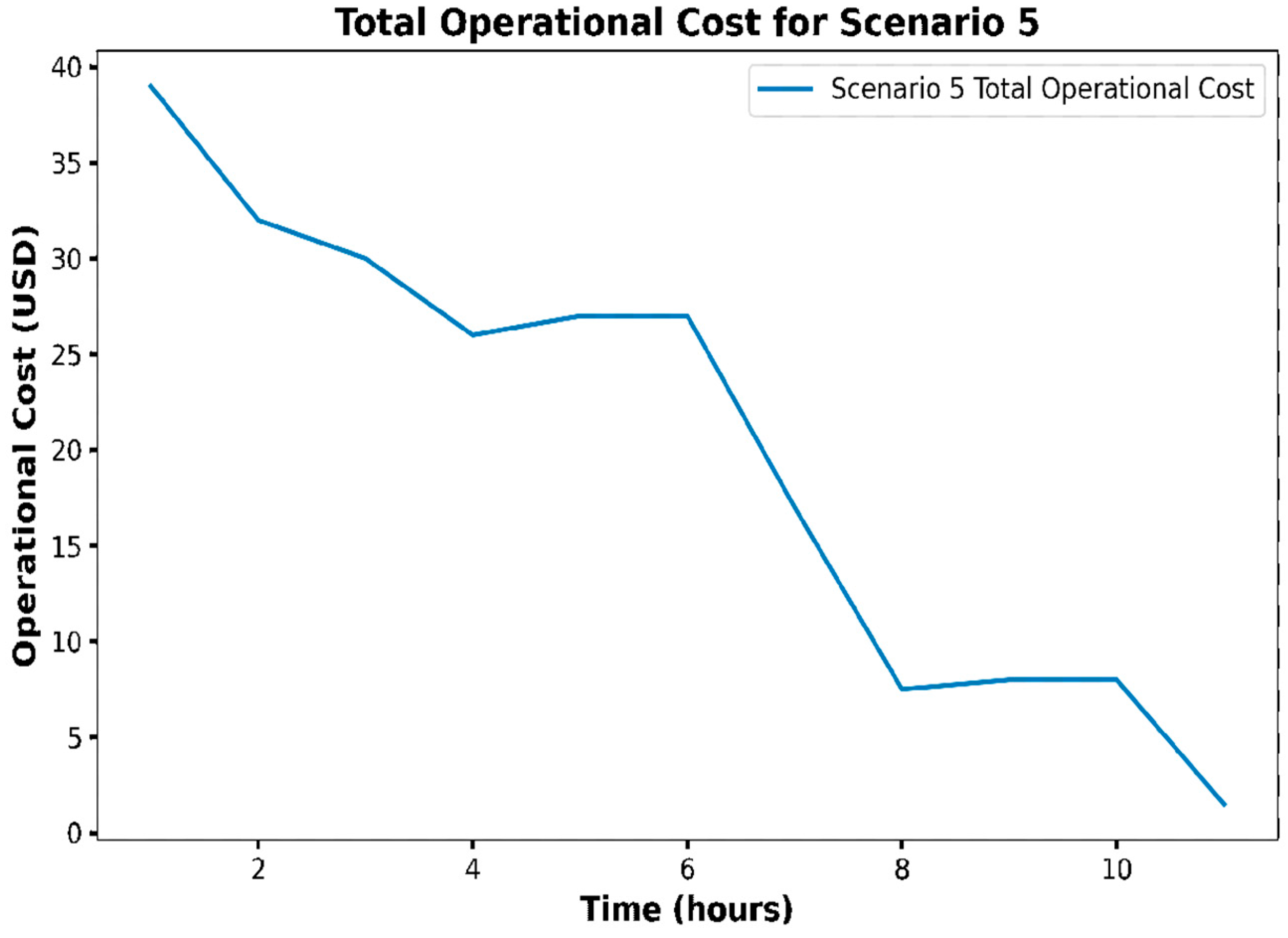
Scenario 5 (Figure 7) shows a decrease from about $\$40$ operational costs over time, like Scenario 3, but with a smoother transition. The declining operational costs suggest that the renewable generation profile was well-aligned with demand, and storage or grid use was minimized after the initial adjustment phase. This scenario seems to represent an ideal balance between renewable generation and load demand, resulting in lower overall operational costs.

The operational costs reflect the effectiveness of integrating renewable energy into the energy mix, as well as the use of storage and grid energy. The variability across scenarios indicates how different strategies, such as varying renewable energy contributions, storage capacities, and grid integration, impact total operational costs. Scenarios 1, 2, and 5 reflect significant periods of storage or grid reliance, whereas Scenario 3 shows a sharper shift towards efficient renewable usage, thereby reducing costs. Scenario 4, with its high early cost, suggests potential inefficiencies in the initial stages of the optimization, possibly due to slower ramp-up times for renewable energy generation.

4.3. Analysis of Cost Distribution Across Multiple Scenarios in Renewable Energy Systems

Based on the cost breakdown data across the five scenarios, the analysis focuses on the costs of renewable energy, storage, and the grid over 10 h. Figure 8 presents trends that are insightful for understanding how costs evolve during each scenario.

In Scenario 1, the renewable cost fluctuates between a peak of 4000 USD and lower points, reflecting potential changes in renewable energy generation. Interestingly, the storage and grid costs remain nearly constant at zero, indicating that the system’s reliance on storage and grid power is minimal or nonexistent in this scenario. This suggests that Scenario 1 is predominantly powered by renewable energy, with minimal external input. Scenario 2 follows a similar pattern to Scenario 1, with the renewable cost fluctuating between $3000 and $4000 USD. However, there is a slight increase in the storage cost, indicating that storage solutions play a more significant role in this scenario compared to Scenario 1. The grid cost again remains close to zero, reinforcing the reliance on renewable sources and limited grid dependence. In Scenario 3, the renewable costs again show a similar trend, but the storage cost increases more noticeably, indicating a higher dependency on stored energy compared to previous scenarios. The grid cost remains unchanged at zero, showing that the system is still operating without reliance on external grid power. Scenario 4 demonstrates a higher fluctuation in renewable costs, reaching the 4000 USD peak in some instances. Storage costs in this scenario appear more volatile compared to previous scenarios, with a noticeable increase in storage usage over time. The grid costs, however, remain at zero, confirming that the system is still independent of the grid. In Scenario 5, renewable costs follow the same fluctuations seen in the previous scenarios, with a peak near 4000 USD. Storage costs show a gradual increase but remain lower compared to renewable costs. The grid cost remains absent again, which suggests that the system in Scenario 5 is also fully autonomous, relying entirely on renewable energy and storage. Across all five scenarios, renewable energy costs are the most significant factor in the cost breakdown, consistently dominating the cost structure. Storage costs show varying levels of importance across the scenarios, particularly in Scenarios 2, 3, and 4. The grid costs, however, remain minimal or nonexistent, highlighting the effectiveness of the renewable energy systems and their integration with storage solutions in these scenarios.

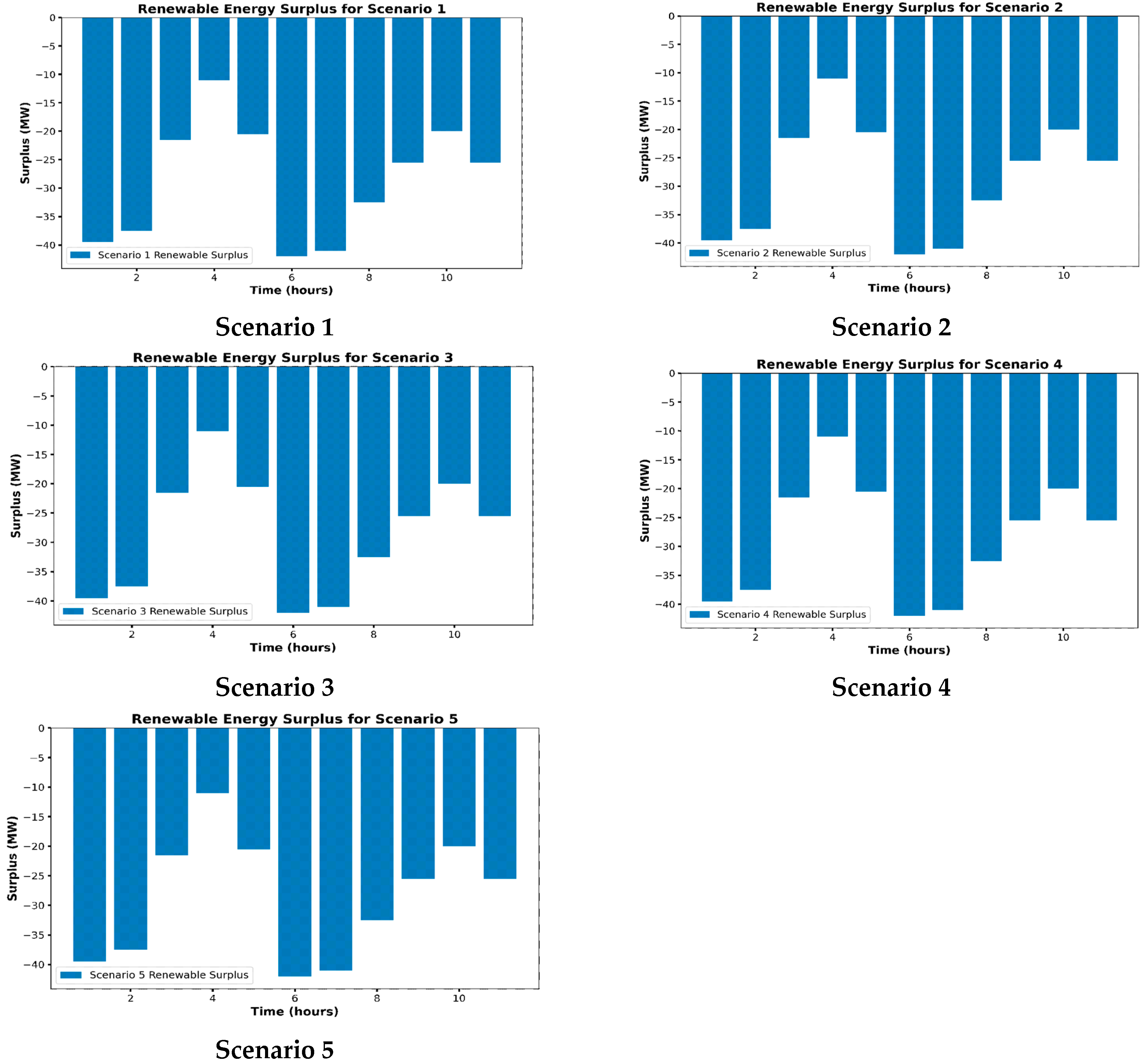
4.4. Analysis of Negative Renewable Energy Surplus and Operational Implications

The negative renewable energy surpluses across all periods indicate that the wind energy generation is insufficient to meet the required load demand (See Figure 9). This suggests that the renewable energy system is not operating optimally during these periods, and there are power generation shortfalls that need to be addressed. Specifically, the negative surpluses indicate Insufficient renewable generation, and when load demand exceeds supply. As a result of the negative surpluses, the system is likely to resort to importing energy from the grid. Grid energy is generally more expensive than renewable sources, and its increased usage directly impacts the system’s operational costs. This dependency on grid power might also undermine the sustainability goals of the microgrid system, as grid power is typically less environmentally friendly than renewable generation.

4.5. Sensitivity Analysis of Energy Utilization and Operational Cost Dynamics

Figure 10 for grid energy utilization shows a constant value across the observed period. The energy consumption remains fixed, suggesting that the grid energy supply is being utilized at a steady rate. Additionally, the utilization of renewable energy exhibits an initial sharp increase, followed by a plateau. The value spikes early and then remains steady, indicating that the system quickly reached its renewable energy capacity. The State of Charge (SOC) variation remains constant, showing no movement throughout the period. This suggests that battery storage or charging mechanisms are static, with no fluctuation in stored energy levels.

The SOC variation remains at 0% for all ρ values (flat magenta line), indicating that the selected operating boundaries are met. The optimal policy operates with minimal deep cycling because storage usage remains minimal throughout the tested penetration levels, thus making this KPI unaffected by penetration levels. The grid utilization remains at 0% for all values of ρ. The optimizer prevents grid imports at every penetration level due to the current tariff structure and the availability of storage and renewable energy. Renewable energy utilization exhibits an initial ~5 percentage-point increase (from ~94% at $\rho =0.4$ to $\rho =0.5$), followed by a plateau at $~100\%$ for $\rho \ge 0.6$.

4.6. Scenario Generation and Reduction

An initial $N$ Monte Carlo wind trajectories were generated over 12 h intraday horizon and reduced them to $S=5$ which represented scenarios using k-means clustering in ${\mathbb{R}}^{12}$. The elbow curve, as shown in Figure 11, of within-duster dispersion versus $k\in \left\{2,\dots ,10\right\}$ shows diminishing returns beyond $k=5$. The probability of each reduced scenario is set to its cluster proportion, ${\pi }_s=n_s/N$, where $n_s$ is the cluster size. Figure 11 also overlays the raw trajectories, shown as thin lines, and representatives, shown as thick lines. Figure 12 reports the scenario probabilities ${\left\{{\pi }_s\right\}}_{s=5}^5$. Figure 13 shows a bar plot for a representative scenario, largest ${\pi }_s$, showing per-hour renewable output, storage charge and discharge, grid, and the demand bar.

5. Conclusions and Future Work

5.1. Contributions and Findings

The research develops an optimization framework for renewable microgrid dispatch systems under high renewable energy integration to achieve cost reduction and maximize energy utilization across different operational scenarios. The model integrates renewable power sources with storage systems and grid power, considering the unpredictable nature of wind and solar energy generation. The main contribution of this study involves creating a multi-stage stochastic MILP framework that handles uncertainties in renewable power generation and customer demand. The framework executed energy dispatch simulations for 12 h, analyzing different renewable power generation scenarios and system power requirements, as well as storage capabilities. The optimization model achieved its objective by minimizing operational costs, resulting in an optimal total cost of $46,600 USD. The model proves its capability to discover an economical solution that combines renewable energy with storage and grid power.

Key findings include the following:

• The model shows that renewable energy generation is not steady across different time periods and scenarios. The scenarios with higher renewable generation (e.g., Scenario 4) had less dependency on grid power and storage, while the scenarios with lower renewable generation (e.g., Scenario 1 had more dependency on external grid energy.
• The optimization results show that there was no grid and storage power usage in all time periods, which means that renewable generation was sufficient to meet demand in the optimized scenarios. This shows that renewable-driven microgrids can operate independently of the grid when there is an abundance of renewable energy.
• The analysis also showed that there were periods of negative renewable surplus, where the renewable energy generated was not enough to meet the load demand. This resulted in increased use of grid power and storage, which increased the operational costs. These findings emphasize the need for accurate forecasting and optimized energy dispatch to mitigate these issues.
• The operational costs were broken down to show that renewable energy costs were the largest contributor to the total costs, while storage and grid costs were relatively low in most scenarios. However, the scenarios with higher storage usage, such as Scenario 3, had higher storage costs, which further emphasizes the need for efficient energy management.

5.2. Recommendations for Future Research or Practical Implementation:

• Enhanced Storage Systems:

The research demonstrates that storage efficiency functions as a key factor to achieve equilibrium between renewable power generation and consumer demand. Future research should focus on improving energy storage technologies, including battery systems and advanced compressed air energy storage (CAES), to increase microgrid flexibility and its capacity to handle periods of reduced renewable energy output. Research into storage systems’ charge–discharge efficiency and cycle life improvement would boost the sustainability of renewable energy solutions.

2.

Integrating Other Renewable Technologies:

The model focuses on wind energy, but solar energy could provide significant complementary generation, especially in regions with high solar potential. Future studies should explore hybrid renewable systems that integrate both wind and solar power, optimizing the energy mix to reduce reliance on grid energy and improve the consistency of renewable generation across different time periods.

3.

Advanced Forecasting Techniques:

The precise prediction of renewable energy output helps organizations decrease operational expenses while avoiding negative surplus situations. Future research needs to explore how machine learning algorithms can be used to predict renewable energy production and demand patterns. The implementation of artificial intelligence (AI) enables better energy dispatch strategies through improved forecasting of renewable resource fluctuations, which decreases dependence on external power sources.

4.

Policy and Regulatory Implications:

The design of microgrid systems needs to follow local regulations and market energy dynamics as renewable energy integration grows. Future research needs to analyze the economic effects of high-penetration renewable energy systems while studying the economic feasibility of distributed storage and demand response technologies for smart grid development.

5.

Real-World Implementation and Scalability:

The study proves renewable microgrids can work in optimized simulations, but they need testing in real-world conditions with different weather patterns, energy requirements, and grid limitations. Future research should implement the model in real-time microgrid systems to prove its effectiveness in dynamic, real-world environments. The model requires evaluation for its scalability across different system sizes and geographic areas to determine its applicability across various regions. Future work can also benefit from model output-based resilience indicators, which consist of load-recovery rate (LRR), renewable-utilization stability (RUS), storage-support index (SSI) and standard reliability metrics: Loss of Load Probability; Expected Unserved Energy; and Conditional Value at Risk of unserved energy.

The current research investigates economic intraday dispatch under uncertain conditions, yet the approach can be easily adapted for multi-objective optimization that combines cost minimization with renewable energy integration through curtailment penalties or targets and system flexibility enhancement through ramp-smoothness and reserve margin management. The authors will extend their work to develop multi-objective variants through weighted-sum and $\epsilon$-constraint methods to present Pareto trade-offs that align with current research on multi-criteria microgrid scheduling.