Improved Commutation Failure Prevention Control for Inter-Phase Short-Circuit Faults
Abstract
1. Introduction
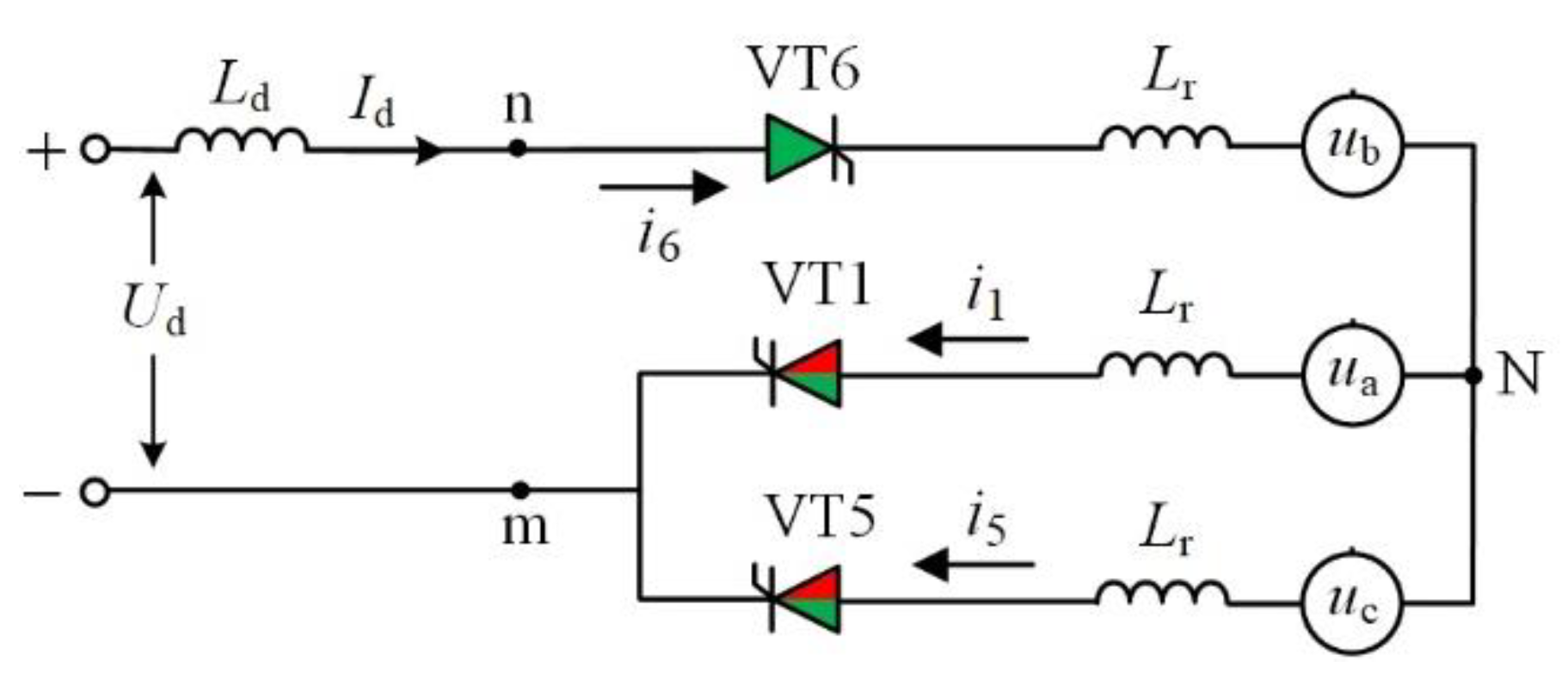
2. Brief Introduction of Commutation Failure and CFPREV Control
2.1. Commutation Failure
2.2. CFPREV Control
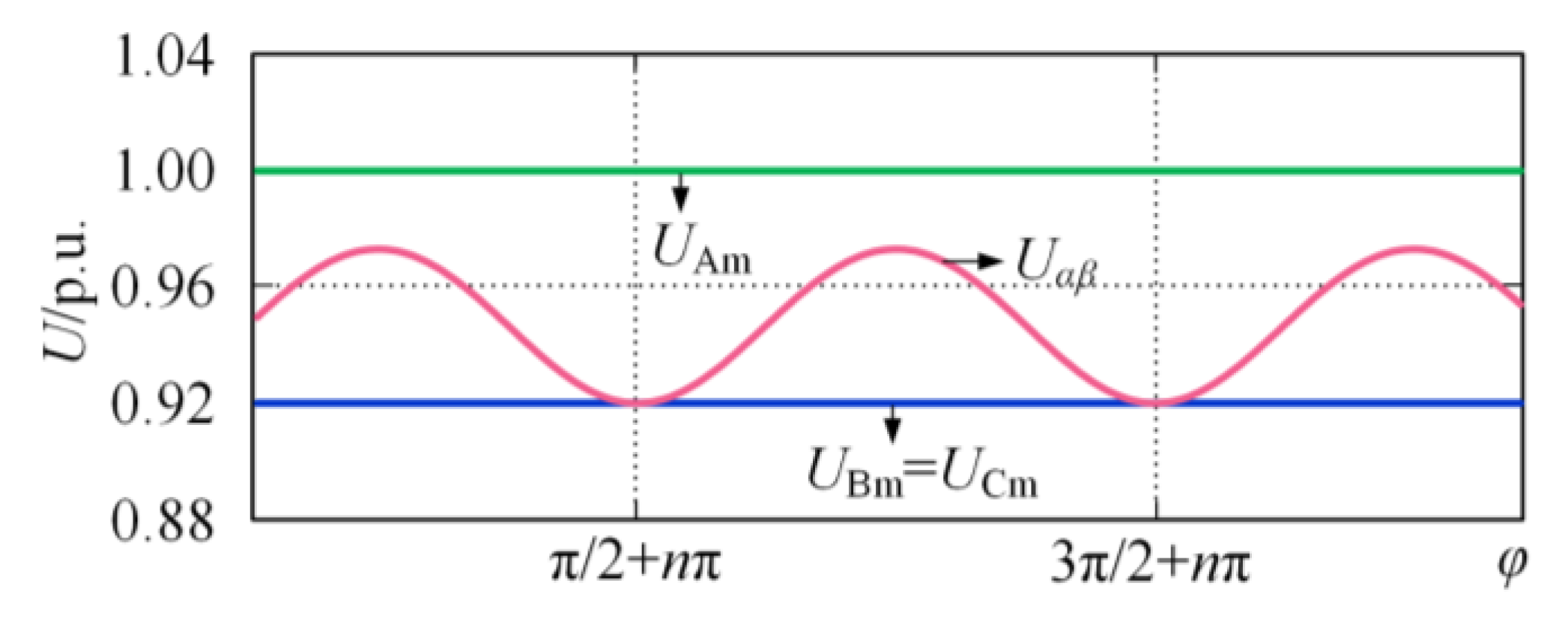
3. Adaptability Analysis of Conventional CFPREV During Interphase Short-Circuit Faults
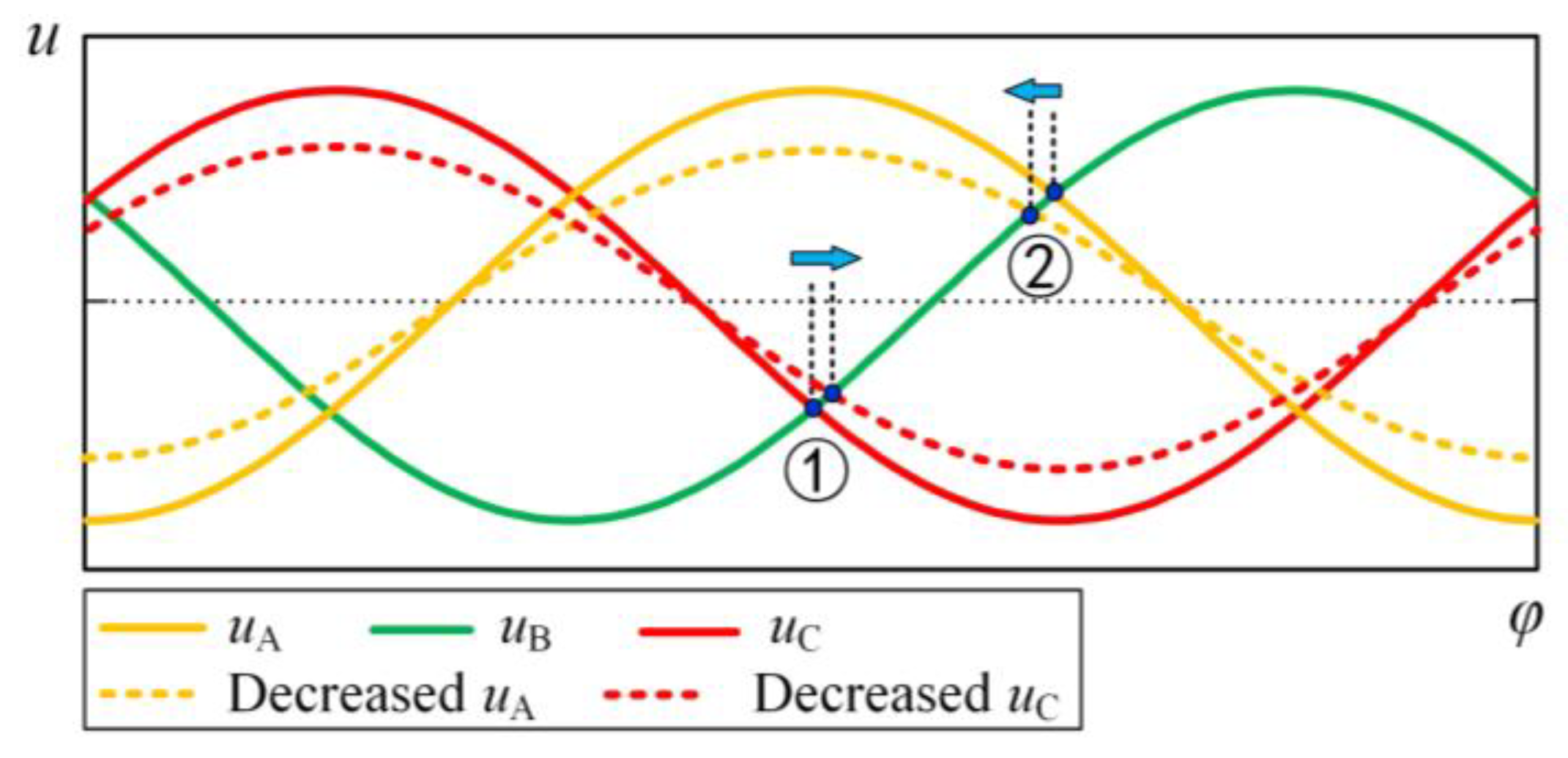
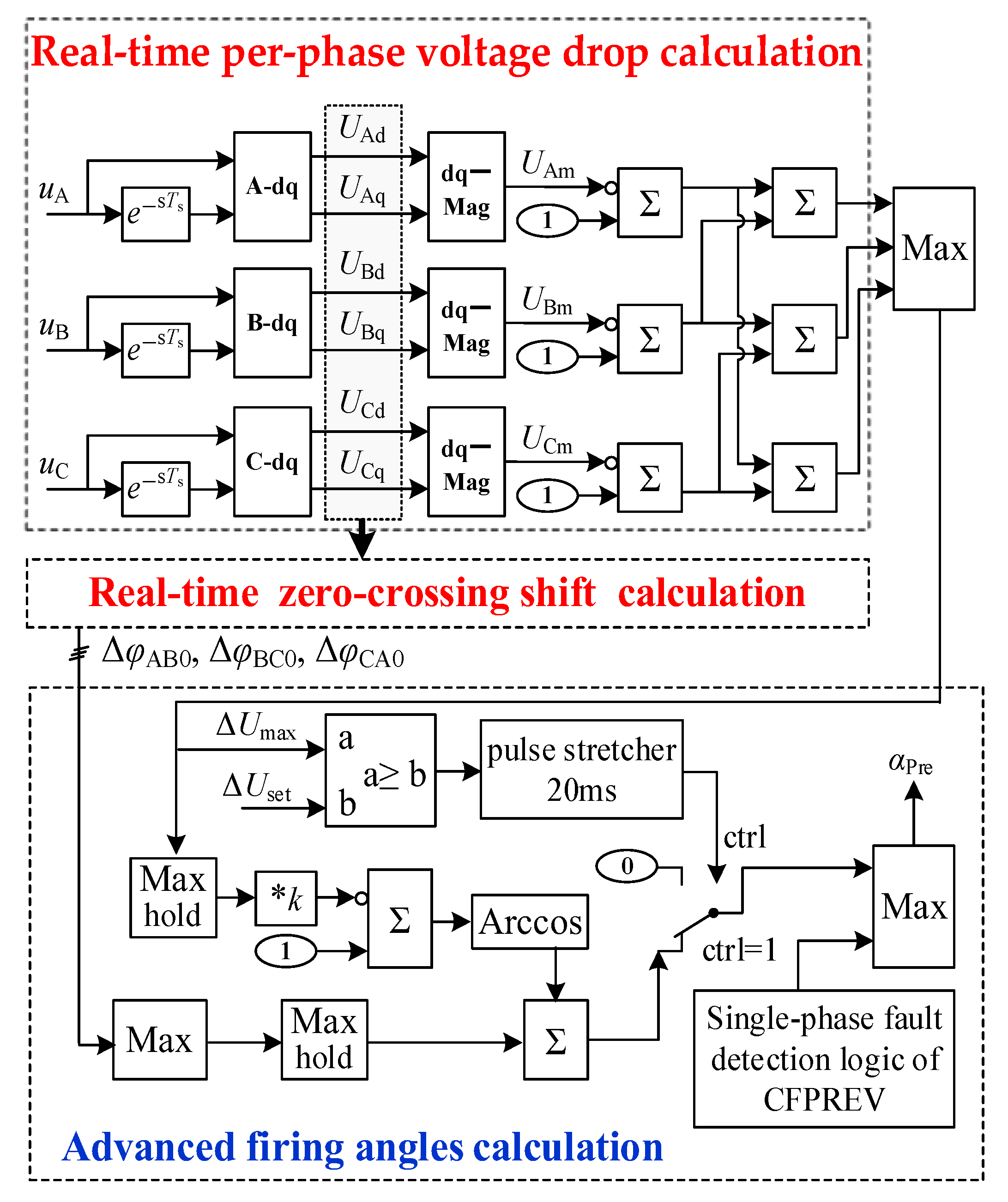
4. Improved Commutation Failure Prevention Control
4.1. Real-Time Per-Phase Voltage Drop Calculation
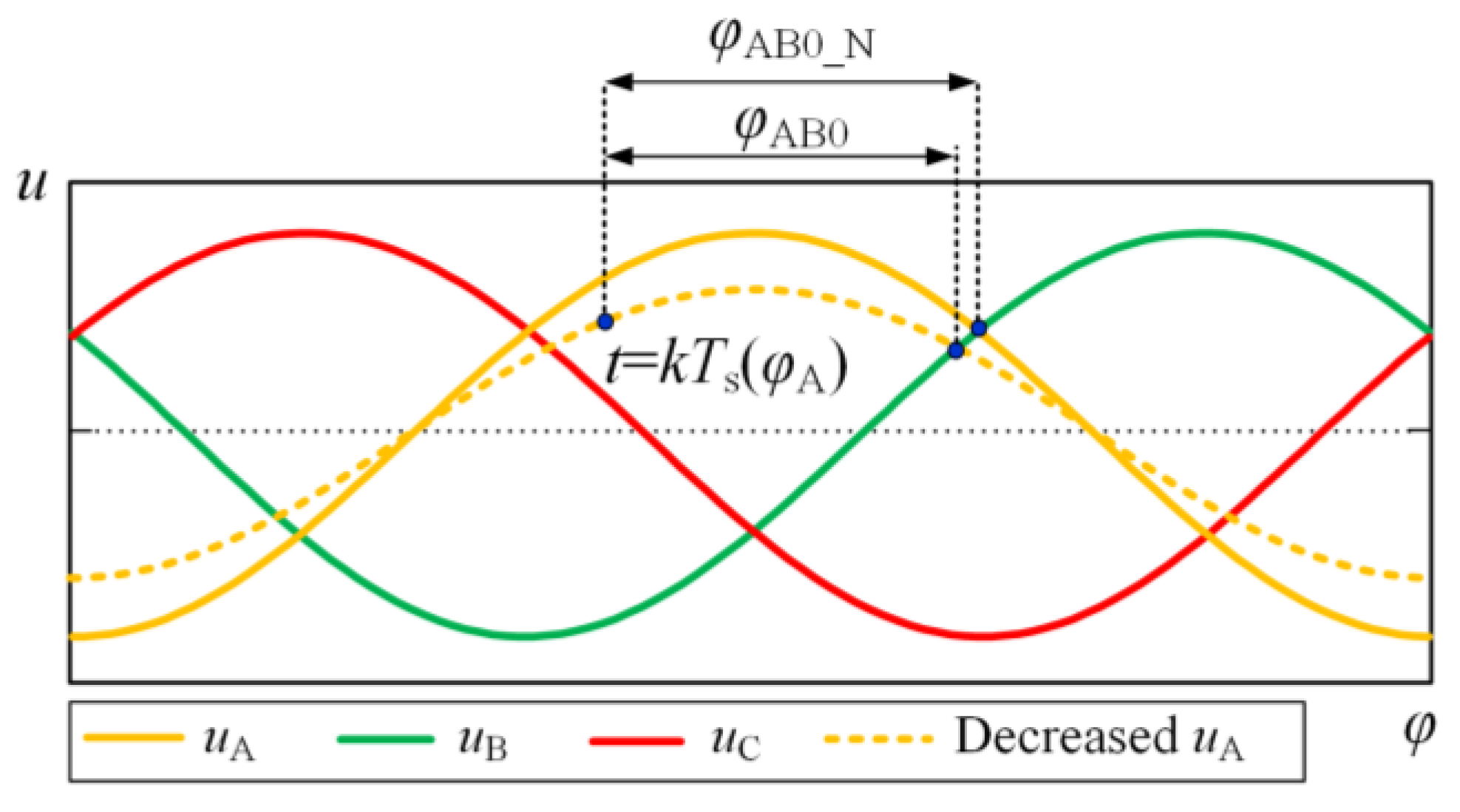
4.2. Real-Time Commutation Voltage Zero-Crossing Shift Prediction
4.3. Improved Commutation Failure Prevention Control for Interphase Short-Circuit Faults
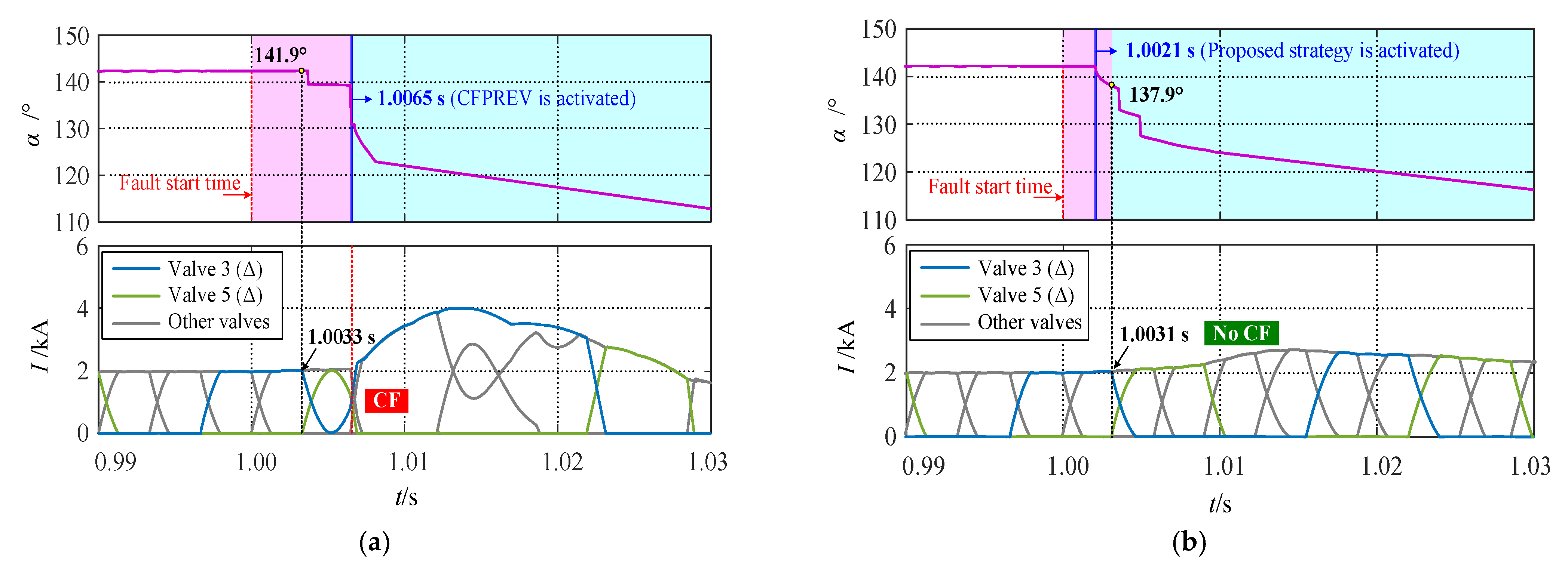
5. Case Study
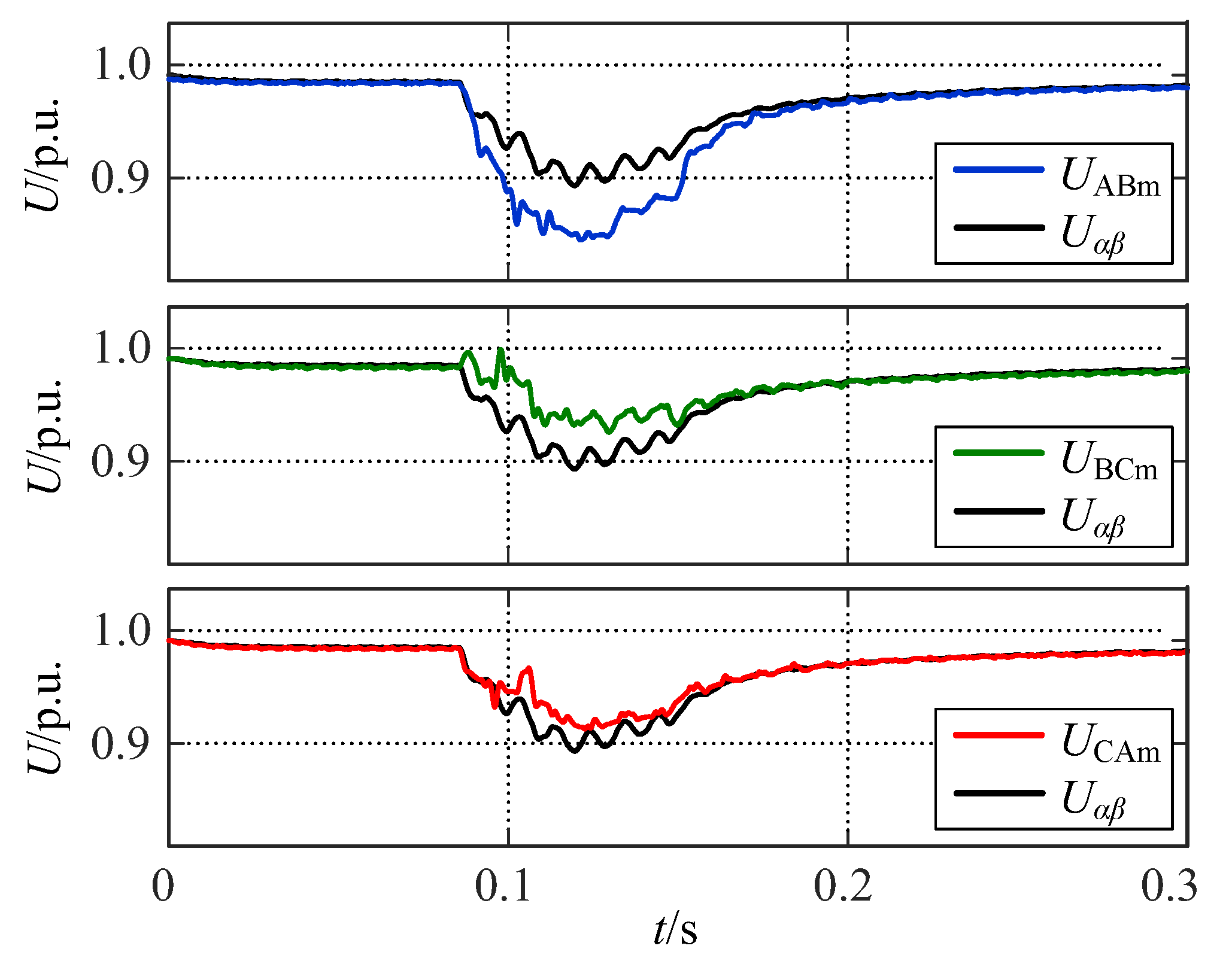
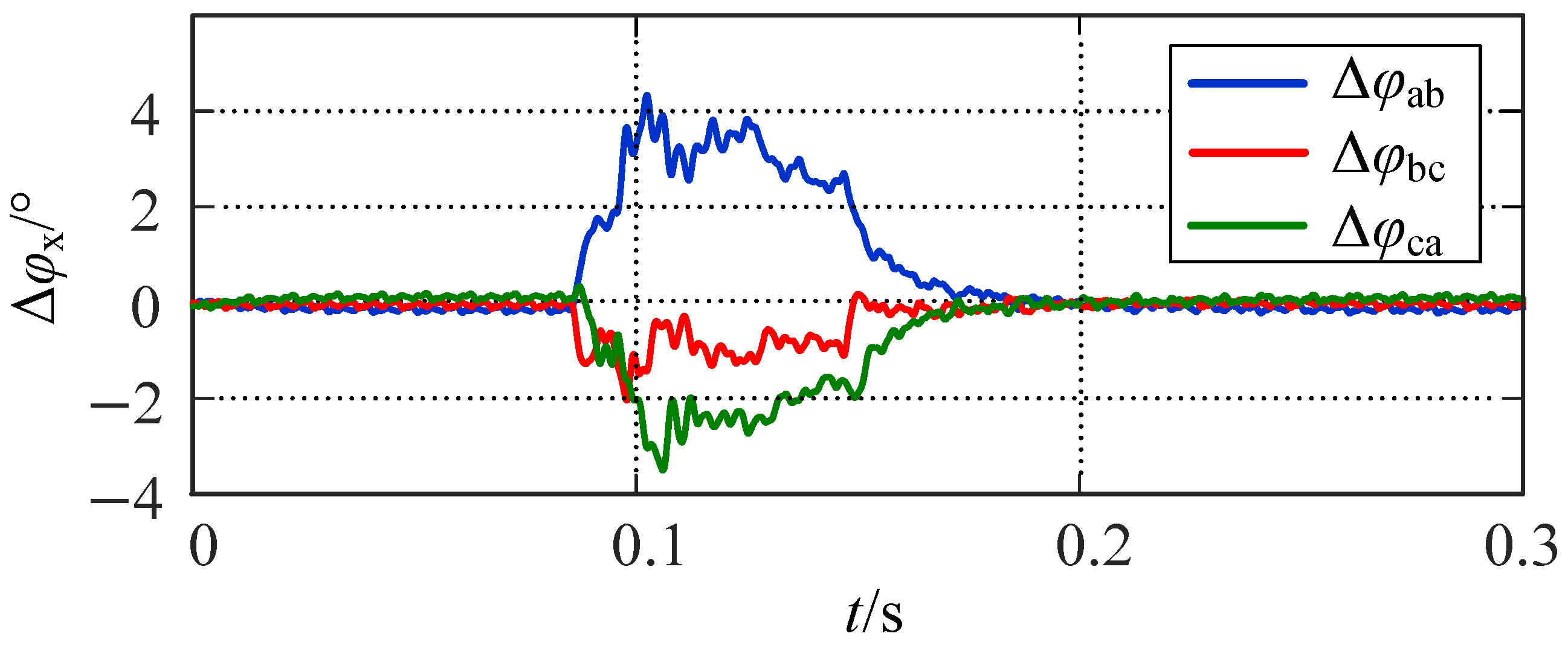
5.1. Verification of Per-Phase Calculation
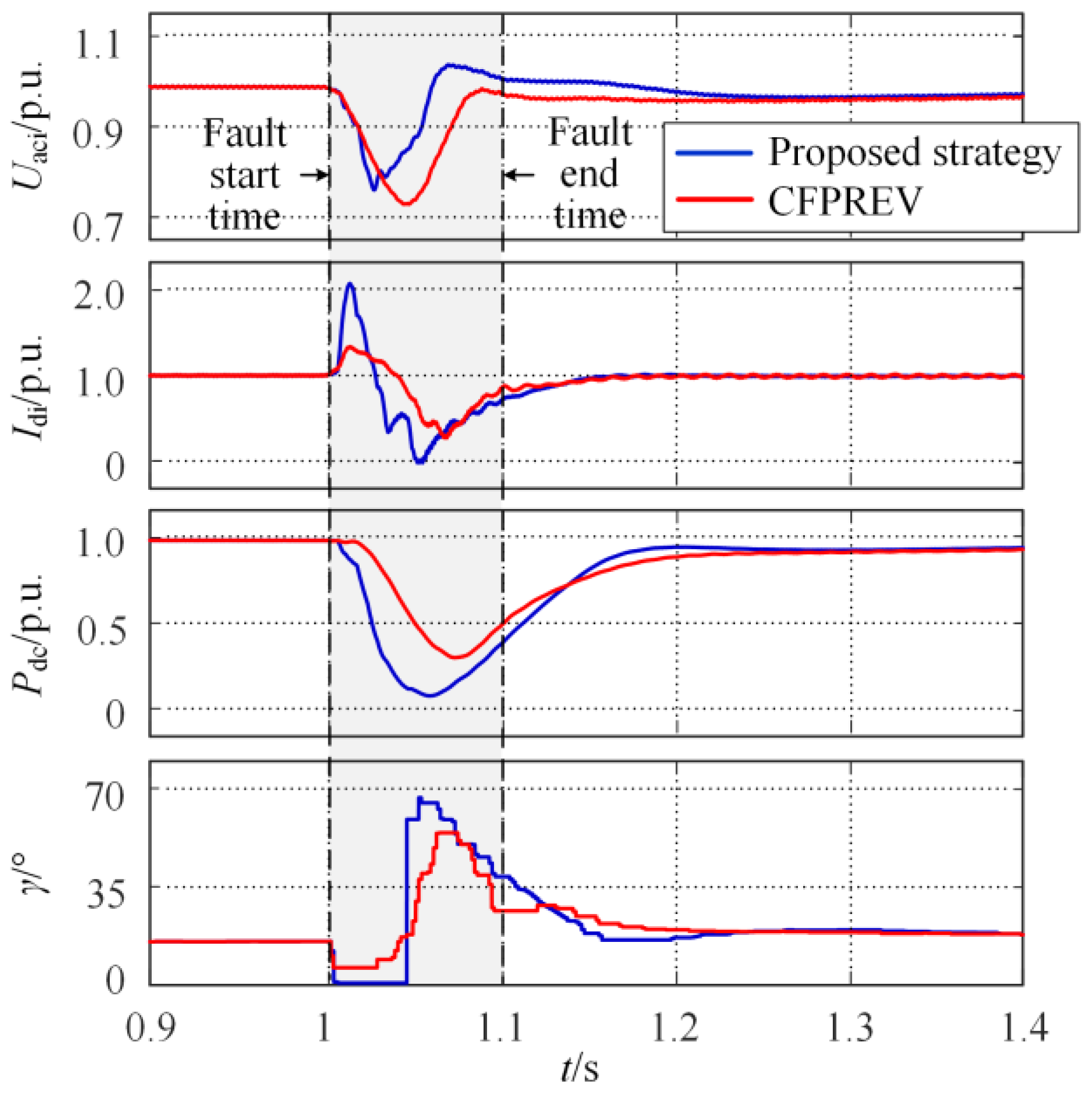
5.2. Simulation Analysis of Commutation Failure Mitigation
6. Discussion
- Under interphase faults, the three-phase criterion of the conventional CFPREV method accurately reflects faulted-phase voltage drops only at specific phase angles, generally underestimating fault severity due to periodic variation;
- Real-time per-phase voltage drop calculation and zero-crossing shift prediction can be achieved using two adjacent voltage samples;
- Case studies and simulations demonstrate the strategy effectively enhances system immunity against commutation failures induced by interphase faults;
- The proposed strategy is essentially built upon the conventional CFPREV framework by incorporating phase-by-phase voltage calculation and phase-specific prediction of commutation voltage zero-crossing shifts. Therefore, no additional primary equipment is required, and the algorithm can be directly implemented within the HVDC control and protection devices, relying on existing hardware units and computational resources to optimize the control functionality. The proposed algorithm involves no complex calculations or iterative processes, making it straightforward to implement, and it shows good potential for integration with existing control and protection functions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lü, P. Research on HVDC Operation Characteristics Under Influence of Hybrid AC/DC Power Grids. Power Syst. Technol. 2022, 46, 503–510. [Google Scholar]
- Li, D.; Gao, Y.; Sun, M. A General Self-Adaptive DC Current Control of LCC-HVDC for Eliminating Subsequent Commutation Failure. IEEE Trans. Power Deliv. 2023, 38, 2232–2235. [Google Scholar] [CrossRef]
- Hong, L.; Zhou, X.; Liu, Y.; Xia, H.; Yin, H.; Chen, Y. Analysis and Improvement of the Multiple Controller Interaction in LCC-HVDC for Mitigating Repetitive Commutation Failure. IEEE Trans. Power Deliv. 2021, 36, 1982–1991. [Google Scholar] [CrossRef]
- Dong, X.; Tang, Y.; Bu, G.; Shen, C.; Song, G.; Wang, Z.; Gan, D.; Hou, J.; Wang, B.; Zhao, B.; et al. Confronting Problem and Challenge of Large Scale AC-DC Hybrid Power Grid Operation. Proc. CSEE 2019, 39, 3107–3118. [Google Scholar]
- Guo, Y.; Tan, Z.; Li, X.; Wang, Y.; Liu, Z.; Cai, Z. A Hierarchical Identification Method of Commutation Failure Risk Areas in Multi-Infeed LCC-HVDC Systems. IEEE Trans. Power Syst. 2024, 39, 2093–2105. [Google Scholar] [CrossRef]
- Zhu, H.; Hao, L.; Huang, F.; Chen, Z.; He, J. Research on the Suppression Strategy of Commutation Failure Caused by AC Fault at the Sending End. IEEE Trans. Power Deliv. 2023, 38, 3900–3911. [Google Scholar] [CrossRef]
- Liu, L.; Lin, S.; Liu, J.; Sun, P.; Li, X.; He, Z. Mechanism Analysis of Subsequent Commutation Failures Caused by Improper Interaction of Controllers. Power Syst. Technol. 2019, 43, 3562–3568. [Google Scholar]
- Liu, L.; Lin, S.; Liu, J.; Sun, P.; Liao, K.; Li, X.; He, Z. Analysis and Prevention of Subsequent Commutation Failures Caused by Improper Inverter Control Interactions in HVDC Systems. IEEE Trans. Power Deliv. 2020, 35, 2841–2852. [Google Scholar] [CrossRef]
- Zhu, R.; Zhou, X.; Xia, H.; Hong, L.; Yin, H.; Deng, L. Commutation Failure Mitigation Method Based on Imaginary Commutation Process. J. Mod. Power Syst. Clean Energy 2022, 10, 1413–1422. [Google Scholar] [CrossRef]
- Li, Z.; Xue, Y.; Tang, Y.; Chen, N.; Yang, C. Adaptive advancement angle compensation for suppressing commutation failures during rectifier-and inverter-fault recovery. IEEE Trans. Power Deliv. 2023, 38, 4287–4301. [Google Scholar] [CrossRef]
- Huang, G.; Tian, X.; Yuan, H.; Dong, X.; Zhou, L.; Wang, Q. Commutation failure predictive control based on fast AC voltage measurement in LCC-HVD. IEEE Access 2023, 11, 53634–53642. [Google Scholar] [CrossRef]
- Yao, W.; Liu, C.; Fang, J.; Ai, X.; Wen, J.; Cheng, S.-J. Probabilistic analysis of commutation failure in LCC-HVDC system considering the CFPREV and the initial fault voltage angle. IEEE Trans. Power Deliv. 2019, 35, 715–724. [Google Scholar] [CrossRef]
- Liu, J.; Liu, L.; Lin, S. An improved commutation failure prevention method based on waveform similarity detection. Autom. Electr. Power Syst. 2021, 45, 132–139. [Google Scholar]
- Zhu, J.; Li, Y.; Duan, X. A Constant Extinction Area Based Control Strategy for Suppressing Commutation Failure in Hybrid Dual-Infeed HVDC System. Power Syst. Technol. 2018, 42, 3735–3743. [Google Scholar]
- Wang, J.; Wang, Z.; Xuan, X.; Fu, C.; Huang, M. Extinction Angle Control Based on Predictive Calculation and Its Improvement. Power Syst. Technol. 2018, 42, 3985–3991. [Google Scholar]
- Wang, J.; Wen, Z.; Wu, Q.; Zheng, R.; Li, X.; Fu, C. Mitigation Methods of HVDC First Commutation Failure During AC Faults. Proc. CSEE 2021, 41, 7314–7325. [Google Scholar]
- Zheng, C.; Tang, Y.; Li, Z. Coordinated control strategy for cascading commutation failure mitigation considering reactive power interaction. IEEE Trans. Power Deliv. 2021, 37, 3225–3234. [Google Scholar] [CrossRef]
- Li, X.; Chen, S.; Pang, G.; Lei, X.; Liu, Y.; Wang, J. Optimization of Commutation Failure Prevention and Automatic Recovery for East China Multi-infeed High-voltage Direct Current System. Autom. Electr. Power Syst. 2015, 39, 134–140. [Google Scholar]
- Wang, Y.; Hou, Y.; Liu, F.; Cao, L.; Li, W.; Xue, F.; Huang, Z. Optimization Method for Startup Threshold of Commutation Failure Prediction Control Considering Coordinated Recovery of Multi-infeed HVDC Systems. Autom. Electr. Power Syst. 2018, 42, 85–90. [Google Scholar] [CrossRef]
- Zheng, C.; Zhou, J.; Li, H.; Wan, L.; Sun, H. Impact of Commutation Failure Prediction Control on Voltage Stability and Its Optimization Measures. Autom. Electr. Power Syst. 2016, 40, 179–183. [Google Scholar]
- Wang, Y.; Zhang, X.; Mu, Q.; Chen, X.; Sun, L.; Zhang, X. Parameter Optimization of Commutation Failure Prevention and Control of UHVDC Hierarchical Connection to AC Grid System. High Volt. Eng. 2018, 44, 329–336. [Google Scholar]
- Lu, J.; Yuan, X.; Zhang, M.; Hu, J. Supplementary Control for Mitigation of Successive Commutation Failures Considering the Influence of PLL Dynamics in LCC-HVDC Systems. CSEE J. Power Energy Syst. 2022, 8, 872–879. [Google Scholar]
- Zhou, H.; Yao, W.; Li, C.; Wen, J. A Predictive Voltage Dependent Current Order Limiter with the Ability to Reduce the Risk of First Commutation Failure of HVDC. High Volt. Eng. 2022, 48, 3179–3189. [Google Scholar]
- Sun, Q.; Liu, S.; Ding, C.; Wang, X.; Sun, Y.; Zhou, X. Suppression Strategy of Commutation Failure in DC Transmission System Based on VDCOL Parameter Optimization. Guangdong Electr. Power 2023, 36, 58–66. [Google Scholar]
- Akhmatov, V. Harmonic Distortion Prediction Methods for Meshed Transmission Grids. Energies 2023, 16, 3965. [Google Scholar] [CrossRef]
- Wang, F.; Liu, T.; Zhou, S.; Li, X.; Qiao, G. Mechanism andquantitative analysis method for HVDC commutation failure resultingfrom harmonics. Proc. CSEE 2015, 35, 4888–4894. [Google Scholar]
- Zhang, G.; Jing, L.; Wang, B.; Liu, M.; Dong, X. Study on HVDC consecutive commutation failures mitigation method caused byharmonic. Power Syst. Prot. Control 2020, 48, 33–41. [Google Scholar]
- Liu, L.; Lin, S.; Liao, K.; Sun, P.; Deng, Y.; Li, X.; He, Z. Extinction angle predictivecontrol strategy for commutation failure mitigation in HVDC systemsconsidering voltage distortion. IET Gener. Transm. Distrib. 2019, 13, 5171–5179. [Google Scholar] [CrossRef]
- Xiao, H.; Li, Y.; Duan, X. Enhanced commutation failure predictive detection method and control strategy in multi-infeed LCC-HVDC systems considering voltage harmonics. IEEE Trans. Power Syst. 2020, 36, 81–96. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Fu, C.; Li, Z.; Huang, M. Individual Phase Control of High Voltage Direct Current Based on Single-phase Locked Loop. Autom. Electr. Power Syst. 2018, 42, 160–165. [Google Scholar]
- Gong, Y.; Wang, J.; Wang, Z.; Fu, C. A Novel Phase-locked Loop for HVDC. Power Syst. Technol. 2019, 43, 4097–4104. [Google Scholar]
- Liu, L.; Li, L.; Tan, B.; Li, X.; Teng, Y.; Zou, Y. Analysis of Bipolar Commutation Failure of HVDC Caused by An Interphase Fault of Transmission Line. Sichuan Electr. Power Technol. 2024, 47, 57–60. [Google Scholar]
- Liu, L.; Li, X.; Teng, Y.; Zhang, C.; Lin, S. An enhanced commutation failure prevention control in LCC based HVDC systems. Int. J. Electr. Power Energy Syst. 2023, 145, 108584. [Google Scholar] [CrossRef]

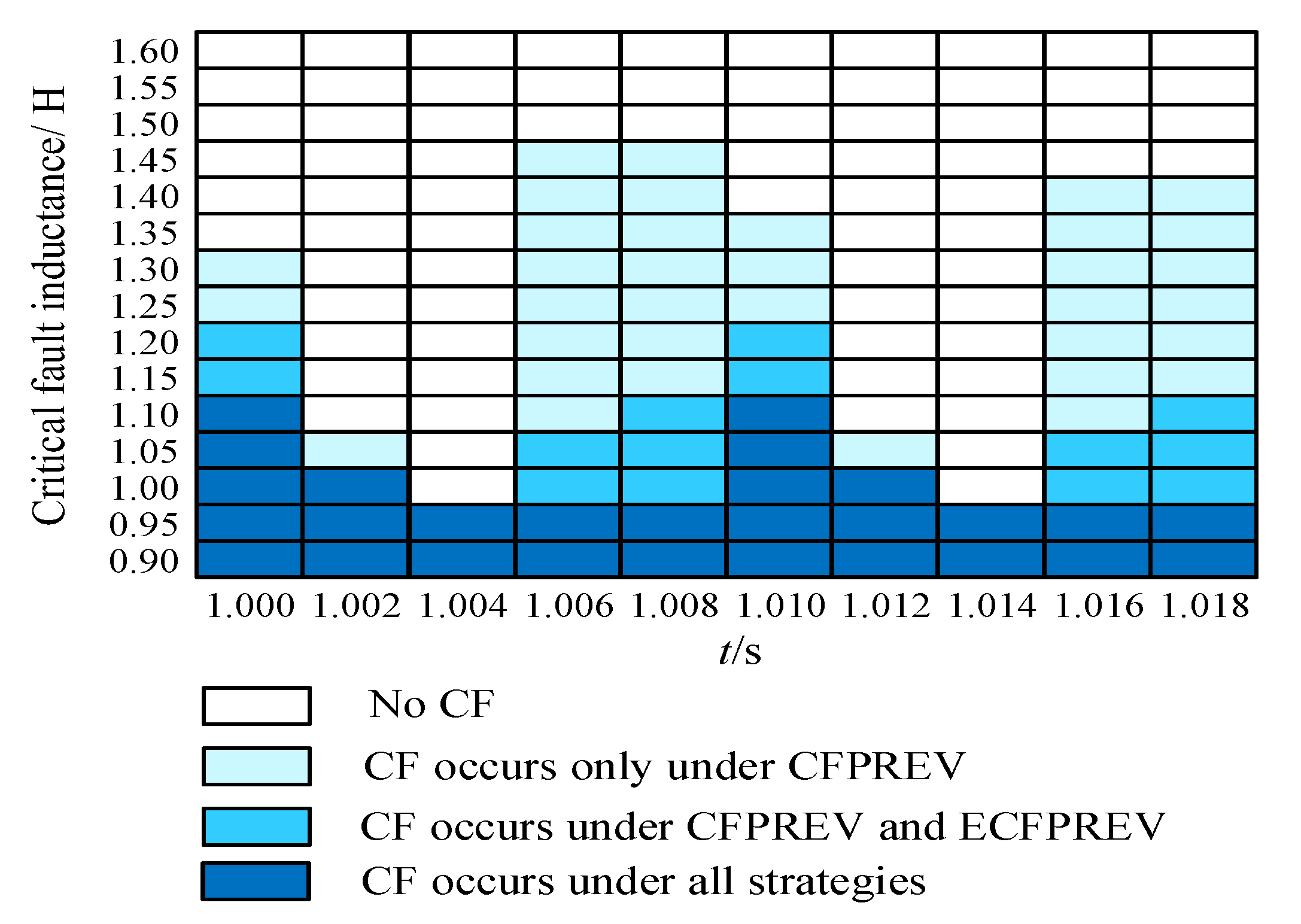
| SCR = 2.0 | SCR = 2.5 | SCR = 3.0 | |
|---|---|---|---|
| Traditional CFPREV strategy | Lc = 1.7 | Lc = 1.45 | Lc = 1.4 |
| Proposed strategy | Lc = 1.25 | Lc = 0.95 | Lc = 0.95 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Li, X.; Teng, Y.; Luo, Y.; Chen, K. Improved Commutation Failure Prevention Control for Inter-Phase Short-Circuit Faults. Appl. Sci. 2025, 15, 9972. https://doi.org/10.3390/app15189972
Liu L, Li X, Teng Y, Luo Y, Chen K. Improved Commutation Failure Prevention Control for Inter-Phase Short-Circuit Faults. Applied Sciences. 2025; 15(18):9972. https://doi.org/10.3390/app15189972
Chicago/Turabian StyleLiu, Lei, Xiaopeng Li, Yufei Teng, Yiping Luo, and Keao Chen. 2025. "Improved Commutation Failure Prevention Control for Inter-Phase Short-Circuit Faults" Applied Sciences 15, no. 18: 9972. https://doi.org/10.3390/app15189972
APA StyleLiu, L., Li, X., Teng, Y., Luo, Y., & Chen, K. (2025). Improved Commutation Failure Prevention Control for Inter-Phase Short-Circuit Faults. Applied Sciences, 15(18), 9972. https://doi.org/10.3390/app15189972






