On Rate Fairness Maximization for the Downlink NOMA with Improper Signaling and Imperfect SIC

Abstract

Non-orthogonal multiple access (NOMA) is a key enabler for 6G networks due to its efficient spectrum utilization, which is garnering significant attention among the Internet of Things (IoT) community. This paper investigates the benefits of the improper Gaussian signaling (IGS) technique on the max–min fairness of the downlink NOMA system under imperfect successive interference cancellation (SIC), where both of the users have the potential to adopt IGS. We first investigate fairness optimization under perfect SIC. In this case, the max–min optimization is solved by the alternate optimization algorithm, where the impropriety degree and power level are iteratively optimized. The closed-form solution for conventional proper Gaussian signaling is also obtained. Then, a deep Q network-based solution is considered for the rate fairness maximization of the downlink NOMA system under IGS and imperfect SIC. The simulations presented for the IGS-aided NOMA system support the analysis, illustrating that IGS can efficiently improve the fairness achievable rate compared to the conventional proper one.

1. Introduction

Non-orthogonal multiple access (NOMA) is a promising technique to achieve massive connectivity and higher spectral efficiency for various kinds of sophisticated applications [1,2,3,4,5,6], such as smart healthcare, remote driving, and virtual reality [7], in beyond 5G and 6G communication networks by allowing different users to access the same time and frequency resources with different power levels [8,9,10,11,12,13,14,15,16]. Typically, the user with weaker channel strength will be allocated more power, and its signal is recovered by directly treating the signals of other users as noise at the receiver end. On the other hand, the signal of the strong channel user is decoded by the successive interference cancellation (SIC) [17,18,19] process, in which the signal of the weak channel user is first detected and then removed from the received signal.

Proper Gaussian signaling (PGS), which is a kind of complex signaling with its in-phase and quadrature components uncorrelated and having equal variance, is a commonly used assumption in various wireless communication systems [20,21]. However, some recent results have proven that improper Gaussian signaling (IGS), where the real and imaginary parts of the signals are correlated or possess unequal variance, can achieve better system throughput and reliability, especially when there exists strong interference between users [22,23,24]. For instance, the achievable rate regions of improper signals were studied in terms of the Pareto boundary and the outer boundary by assuming cooperation between players [25]. However, that work focuses on perfect channel information. For the practical imperfect channel information case, the authors in [26] derived a robust design for the rate-region boundary in closed form, which is independent of the phase of the channels, where only one of the multiple users is allowed to transmit IGS. The above two works only consider the two-user situation. Relatedly, the pioneering work in [27] extends them to the multiuser case, where the precoding matrices of the K-user single-input single-output interference channels were optimized by minimizing the pairwise error probability and symbol error rate. In [28], the rate advantages of IGS were investigated in the interference channel with additive asymmetric hardware distortions by treating interference as noise. The joint design of transmit beamformers and reflecting coefficients of a reconfigurable intelligent surface was considered in [29] in order to maximize the geometric mean of the achievable rates by developing an efficient alternating descent algorithm via generating feasible points for the non-convex problem. To further improve the geometric mean of the data rates, the joint design of widely linear transmit beamformers integrated with programmable reflecting coefficients was also considered. The authors in [30] investigated different optimization frameworks for rate splitting in multiple-input multiple-output reconfigurable intelligent surface-based systems, including weighted sum rate maximization, total transmit power minimization, weighted minimum energy efficiency, and global energy efficiency maximization. Moreover, by integrating simultaneous wireless information and power transfer and hardware impairments with an intelligent reflecting surface [31], fairness maximization was considered by jointly optimizing the reflecting coefficients, beamforming, and power splitting coefficients, subject to the minimum harvested energy requirements and total power budget. A two-layer low-complexity iterative algorithm was proposed in [32] to solve the max–min achievable rate optimization problem, where the transmit beamforming vectors and reflecting phase shifts must be optimized in terms of the transmit power budget constraint.

Despite many reported solutions for IGS-based interference channels and relay networks, this paradigm has just emerged in NOMA systems. Transmit beamforming to maximize users’ minimum throughput under power constraints was investigated [33] in terms of orthogonal multiple access and the NOMA system by using IGS. Moreover, the advantage of IGS over PGS was highlighted in the context of the mixed information superposition technique for the general multi-cell multiuser NOMA network [34]. However, max–min optimization has not been characterized for the IGS-assisted NOMA system under imperfect successive interference cancellation (SIC). In this work, we first formulate the data rates of both users in terms of the impropriety degree under imperfect SIC for the NOMA system. Then, the alternate optimization algorithm is used to optimize the impropriety degrees and power level for the perfect SIC case. We also derive the closed-form solution for the PGS-based NOMA with perfect SIC. Furthermore, by virtue of the deep Q network (DQN), we optimize the impropriety degrees and power levels for the imperfect SIC case. The main contributions of this work are summarized as follows.

• This work is a novel attempt to investigate max–min optimization for the IGS-assisted NOMA system via designing the impropriety degrees and power levels for both users regarding perfect and imperfect SIC. Conversely, [33,34] only considered the perfect SIC case, which is not practical.
• The max–min optimization of the NOMA system employing IGS is formulated under perfect SIC. To solve this problem, the alternate optimization (AO) technique is utilized to iteratively optimize the impropriety degrees and power level.
• The fairness optimization of the IGS-based NOMA system is formulated under imperfect SIC. To address this issue, a DQN-based suboptimal solution is proposed to learn the impropriety degrees and power levels of both users.
• The simulation results confirm the effectiveness of the IGS-aided NOMA system and highlight the improvements introduced by IGS as compared to PGS.

The rest of this paper is organized as follows. Section 2 presents the system model of the IGS-based NOMA system under imperfect SIC. Section 3 optimizes the fairness maximization of the NOMA system with IGS and perfect SIC via the alternate optimization technique. Section 4 provides the DQN solution for the IGS-aided NOMA system under imperfect SIC. The simulation results and discussion are presented in Section 5. Finally, Section 6 concludes the paper.

Notation 1.

Lowercase letters, such as x, are used to denote scalars, and boldface letters, such as x, are used for column vectors. The statistical expectation and absolute value operators are denoted by $E\{·\}$ and $|·|$, respectively.

2. System Model

2.1. Preliminaries for Improper Gaussian Random Variables

A zero-mean complex-valued random variable, x, with variance ${\sigma }_x^2=E\left\{\right|x{|}^2\}$ and complementary variance ${\tilde{\sigma }}_x^2=E\left\{x^2\right\}$ is called proper if ${\tilde{\sigma }}_x^2=0$; otherwise, it is called improper. Furthermore, the variance ${\sigma }_x^2$ and the complementary variance ${\tilde{\sigma }}_x^2$ are a valid pair if and only if ${\sigma }_x^2\ge 0$ and $\left|{\tilde{\sigma }}_x^2\right|\le {\sigma }_x^2$. The impropriety degree of x is defined as

$$\begin{array}{c}\hfill {\kappa }_x={\displaystyle \frac{|{\tilde{\sigma }}_x^2|}{{\sigma }_x^2}}.\end{array}$$

(1)

It is easy to verify that $0\le {\kappa }_x\le 1$ [22,23].

2.2. System Description

This work investigates a two-user downlink NOMA system with a single antenna base station (BS), where a strong channel user (user 1) and a weak channel user (user 2) are served. The channel from the BS to the user i, denoted by $h_i$, $i=1,2,$ is modeled as a complex independent and identically distributed Gaussian random variable with zero mean and variance ${\sigma }_{h_i}^2$, while the zero mean additive white Gaussian noise $n_i$ with variance ${\sigma }_{n_i}^2$ is assumed. We define ${\Gamma }_i=|h_i{|}^2/{\sigma }_{n_i}^2$ as the channel-to-noise ratio (CNR) of the user i, which satisfies ${\Gamma }_1\ge {\Gamma }_2$. The power allocated to user i is $p_i$, which is bounded by $P_i,i=1,2$. According to the protocol of NOMA, the strong channel user is allowed to transmit with a lower power, while the weak channel user is allocated a higher power, i.e., $p_1\le p_2$, and subsequently, $P_1\le P_2$, which operates the efficient SIC decoder. Specifically, the weak user is able to decode its transmitted symbol directly by treating the signal of the strong user as interference due to its limited power. On the other hand, the strong user has to decode the signal of the weak user and then remove it from the received signal by using the SIC technique in order to detect its own symbol. In practice, this SIC procedure is likely to be imperfect, which can be quantified by a factor $\lambda$, where $\lambda =1$ refers to fully invalid SIC, while $\lambda =0$ implies perfect one. In this way, the received signal after SIC of both users can be described as

$$\begin{array}{c}\hfill y_1=\sqrt{p_1}{h}_1{x}_1+\underset{z_1}{\underbrace{\lambda \sqrt{p_2}{h}_2{x}_2+n_1}},\end{array}$$

(2)

and  

$$\begin{array}{c}\hfill y_2=\sqrt{p_2}{h}_2{x}_2+\underset{z_2}{\underbrace{\sqrt{p_1}{h}_2{x}_1+n_2}}\end{array}$$

(3)

where $x_1$ and $x_2$ are the transmitted signals of user 1 and user 2, respectively, subject to potential IGS with impropriety degrees ${\kappa }_1$ and ${\kappa }_2$. The terms $z_1$ and $z_2$ are the interference-plus-noise elements of the strong user and the weak user, respectively. Following the analysis in [23], the achievable rate of user i can be described as

$$\begin{array}{ccc}\hfill R_i& =& {\displaystyle \frac{1}{2}}{log}_2{\displaystyle \frac{{\sigma }_{y_i}^4-|{\tilde{\sigma }}_{y_i}^2{|}^2}{{\sigma }_{z_i}^4-|{\tilde{\sigma }}_{z_i}^2{|}^2}}\hfill \\ & =& \underset{R_{i,\mathrm{Proper}}}{\underbrace{{log}_2{\displaystyle \frac{{\sigma }_{y_i}^2}{{\sigma }_{z_i}^2}}}}+\underset{R_{i,\mathrm{Improper}}}{\underbrace{{\displaystyle \frac{1}{2}}{log}_2{\displaystyle \frac{1-{\sigma }_{y_i}^{-4}{\left|{\tilde{\sigma }}_{y_i}^2\right|}^2}{1-{\sigma }_{z_i}^{-4}{\left|{\tilde{\sigma }}_{z_i}^2\right|}^2}}}},\hfill \end{array}$$

(4)

where ${\sigma }_{y_i}^2\left({\sigma }_{z_i}^2\right)$ and ${\tilde{\sigma }}_{{\mathrm{z}}_{\mathrm{i}}}^2\left({\tilde{\sigma }}_{z_i}^2\right)$ are the variance and complementary variance of $y_i\left(z_i\right)$, respectively, provided by

$$\begin{array}{ccc}\hfill {\sigma }_{y_1}^2& =& E\left\{y_1{y}_1^{*}\right\}=p_1|h_1{|}^2+{\lambda }^2{p}_2{\left|h_1\right|}^2+{\sigma }_{n_1}^2,\hfill \end{array}$$

(5)

$$\begin{array}{ccc}\hfill {\tilde{\sigma }}_{y_1}^2& =& E\left\{y_1^2\right\}=h_1^2{p}_1{\kappa }_1{e}^{j{\varphi }_1}+{\lambda }^2{h}_1^2{p}_2{\kappa }_2{e}^{j{\varphi }_2},\hfill \end{array}$$

(6)

$$\begin{array}{ccc}\hfill {\sigma }_{y_2}^2& =& E\left\{y_2{y}_2^{*}\right\}=p_2|h_2{|}^2+p_1{\left|h_2\right|}^2+{\sigma }_{n_2}^2,\hfill \end{array}$$

(7)

$$\begin{array}{ccc}\hfill {\tilde{\sigma }}_{y_2}^2& =& E\left\{y_2^2\right\}=h_2^2{p}_1{\kappa }_1{e}^{j{\varphi }_1}+h_2^2{p}_2{\kappa }_2{e}^{j{\varphi }_2},\hfill \end{array}$$

(8)

and

$$\begin{array}{ccc}\hfill {\sigma }_{z_1}^2& =& E\left\{z_1{z}_1^{*}\right\}={\lambda }^2{p}_2{\left|h_1\right|}^2+{\sigma }_{n_1}^2,\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill {\tilde{\sigma }}_{z_1}^2& =& E\left\{z_1^2\right\}={\lambda }^2{h}_1^2{p}_2{\kappa }_2{e}^{j{\varphi }_2},\hfill \end{array}$$

(10)

$$\begin{array}{ccc}\hfill {\sigma }_{z_2}^2& =& E\left\{z_2{z}_2^{*}\right\}=p_1{\left|h_2\right|}^2+{\sigma }_{n_2}^2,\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill {\tilde{\sigma }}_{z_2}^2& =& E\left\{z_2^2\right\}=h_2^2{p}_1{\kappa }_1{e}^{j{\varphi }_1},\hfill \end{array}$$

(12)

where ${\varphi }_1$ and ${\varphi }_2$ are the phases of the complementary variance of $x_1$ and $x_2$, respectively. By substituting (5), (6), (9) and (10) into (4), we obtain the achievable rate of user 1 as

$$\begin{array}{ccc}\hfill R_1({\kappa }_1,p_1,{\kappa }_2,p_2,{\varphi }_1,{\varphi }_2)& =& \underset{R_{1,\mathrm{Proper}}}{\underbrace{{log}_2\left(1+{\displaystyle \frac{|h_1{|}^2{p}_1}{{\sigma }_{n_1}^2+{\lambda }^2{\left|h_1\right|}^2{p}_2}}\right)}}+\underset{R_{1,\mathrm{Improper}}}{\underbrace{{\displaystyle \frac{1}{2}}{log}_2{\displaystyle \frac{1-{\sigma }_{y_1}^{-4}{\left|{\tilde{\sigma }}_{y_1}^2\right|}^2}{1-{\sigma }_{z_1}^{-4}{\left|{\tilde{\sigma }}_{z_1}^2\right|}^2}}}},\hfill \\ \hfill & = & {\displaystyle \frac{1}{2}}{log}_2{\displaystyle \frac{{({\Gamma }_1{p}_1+{\Gamma }_1{p}_2{\lambda }^2+1)}^2-{\Gamma }_1^2{|p_1{\kappa }_1+{\lambda }^2{p}_2{\kappa }_2{e}^{j({\varphi }_2-{\varphi }_1)}|}^2}{{({\lambda }^2{\Gamma }_1{p}_2+1)}^2-{\lambda }^4{\Gamma }_1^2{p}_2^2{\kappa }_2^2}}.\hfill \end{array}$$

(13)

Similarly, after some algebraic manipulations, the achievable rate of the weak user can be calculated as

$$\begin{array}{ccc}\hfill R_2({\kappa }_1,p_1,{\kappa }_2,p_2,{\varphi }_1,{\varphi }_2)& =& \underset{R_{2,\mathrm{Proper}}}{\underbrace{{log}_2\left(1+{\displaystyle \frac{|h_2{|}^2{p}_2}{{\sigma }_{n_2}^2+{\left|h_2\right|}^2{p}_1}}\right)}}+\underset{R_{2,\mathrm{Improper}}}{\underbrace{{\displaystyle \frac{1}{2}}{log}_2{\displaystyle \frac{1-{\sigma }_{y_2}^{-4}{\left|{\tilde{\sigma }}_{y_2}^2\right|}^2}{1-{\sigma }_{z_2}^{-4}{\left|{\tilde{\sigma }}_{z_2}^2\right|}^2}}}},\hfill \\ \hfill & = & {\displaystyle \frac{1}{2}}{log}_2{\displaystyle \frac{{({\Gamma }_2{p}_1+{\Gamma }_2{p}_2+1)}^2-{\Gamma }_2^2|p_1{\kappa }_1+p_2{\kappa }_2{e}^{j({\varphi }_2-{\varphi }_1)}{|}^2}{{({\Gamma }_2{p}_1+1)}^2-{\Gamma }_2^2{p}_1^2{\kappa }_1^2}},\hfill \end{array}$$

(14)

Note that, when the transmitted signals of both users adopt the conventional PGS, the data rates in (13) and (14) reduce to the standard one.

3. Fairness Maximization of the NOMA System with IGS Under Perfect SIC

In this section, we investigate the joint impropriety degree and power allocation design to achieve the max–min fairness for the IGS-assisted NOMA system with perfect SIC, which aims to provide fairness for both users. In this case, by setting $\lambda =0$, the achievable data rate of the strong user simplifies to

$$\begin{array}{c}\hfill R_1({\kappa }_1,p_1)={\displaystyle \frac{1}{2}}{log}_2((1-{\kappa }_1^2){\Gamma }_1^2{p}_1^2+2{\Gamma }_1{p}_1+1),\end{array}$$

(15)

and the max–min optimization can be formulated as

$$\begin{array}{c}\hfill \begin{array}{c}\left(\mathrm{P}1\right):\underset{{\kappa }_1,p_1,{\kappa }_2,p_2,{\varphi }_1,{\varphi }_2}{max}min\{R_1({\kappa }_1,p_1),R_2({\kappa }_1,p_1,{\kappa }_2,p_2,{\varphi }_1,{\varphi }_2)\}\hfill \\ \mathrm{s}.\mathrm{t}.\left(\mathrm{C}1\right):0\le p_1\le p_2\le P_2,\hfill \\ \left(\mathrm{C}2\right):0\le {\kappa }_1,{\kappa }_2\le 1,\hfill \\ \left(\mathrm{C}3\right):0\le {\varphi }_1,{\varphi }_2\le \pi ,\hfill \end{array}\end{array}$$

(16)

where $R_1$ and $R_2$ refer to (15) and (14), respectively, (C1) represents the power constraint according to the NOMA principle, (C2) guarantees the validity of the impropriety degree, and (C3) reflects the phase constraints of the complementary variance for the transmitted signals. The constrained optimization in (P1) is obviously non-convex and involves difficulty finding the global solution.

In (14), evidently, the phases of the complementary variance of the transmitted signals of both users, i.e.,  $x_1$ and $x_2$, are independent of the other unknown parameters, i.e.,  $p_i$ and ${\kappa }_i$. Moreover, it is straightforward that $R_2$ in (14) is maximized when the term $|p_1{\kappa }_1+p_2{\kappa }_2{e}^{j({\varphi }_2-{\varphi }_1)}{|}^2$ is minimized. In this way, we have

$$\begin{array}{c}\hfill {\varphi }_2-{\varphi }_1=\pi .\end{array}$$

(17)

Observe, from the data rates in (13) and (14), we are able to find that the transmitted signal of the weak user, $x_2$, does not interfere with the received signal of the strong user, $y_1$. To this end, the optimal transmission strategy for the weak user is to transmit with its maximum power budget, $P_2$.

From the above discussion, the solution to

$$\begin{array}{c}\hfill \underset{p_1\le P_2,0\le {\kappa }_i\le 1,i\in \{1,2\}}{min}|p_1{\kappa }_1+P_2{\kappa }_2{e}^{j\pi }{|}^2,\end{array}$$

(18)

can be calculated as

$$\begin{array}{c}\hfill {\kappa }_2={\displaystyle \frac{{\kappa }_1{p}_1}{P_2}}.\end{array}$$

(19)

Note that the above equation always holds since $p_1\le P_2$ and $0\le {\kappa }_1\le 1$. In this way, by substituting (19) into (14), the achievable rate of the weak user can be reformulated as

$$\begin{array}{c}\hfill R_2({\kappa }_1,p_1)={\displaystyle \frac{1}{2}}{log}_2{\displaystyle \frac{{({\Gamma }_2{p}_1+{\Gamma }_2{P}_2+1)}^2}{{({\Gamma }_2{p}_1+1)}^2-{\Gamma }_2^2{p}_1^2{\kappa }_1^2}}.\end{array}$$

(20)

Now, the max–min fairness in (16) is simplified to

$$\begin{array}{c}\hfill \begin{array}{c}\left(\mathrm{P}2\right):\underset{{\kappa }_1,p_1}{max}min\{R_1({\kappa }_1,p_1),R_2({\kappa }_1,p_1)\}\hfill \\ \mathrm{s}.\mathrm{t}.\left(\mathrm{C}4\right):0\le p_1\le P_2,\hfill \\ \left(\mathrm{C}5\right):0\le {\kappa }_1\le 1.\hfill \end{array}\end{array}$$

(21)

Observe from (13) that it is easy to examine that $R_1({\kappa }_1,p_1)$ is a monotonically decreasing function of ${\kappa }_1$ and a monotonically increasing function of $p_1$, while $R_2({\kappa }_1,p_1)$ is a monotonically increasing function of ${\kappa }_1$ and a monotonically decreasing function of $p_1$. It is difficult to obtain the optimal solution to the optimization in (21). In this work, we proposed an alternate optimization algorithm to solve it by iteratively optimizing the impropriety degree and power allocation of the strong user, i.e., ${\kappa }_1$ and $p_1$.

3.1. Optimal ${\kappa }_1$ Design for IGS-Based NOMA with Perfect SIC

With fixed $p_1$, the max–min fairness in (21) can be reformulated as

$$\begin{array}{c}\hfill \left(\mathrm{P}3\right):\underset{{\kappa }_1}{max}min\{R_1\left({\kappa }_1\right),R_2\left({\kappa }_1\right)\}\mathrm{s}.\mathrm{t}.\left(\mathrm{C}4\right)\end{array}$$

(22)

This optimization also presents difficulty in obtaining the closed-form solution since $R_1\left({\kappa }_1\right)$ is a monotonically decreasing function of ${\kappa }_1$, while $R_2\left({\kappa }_1\right)$ is a monotonically increasing function of ${\kappa }_1$. In this sense, there must exist ${\kappa }_1^{*}$ that satisfies

$$\begin{array}{c}\hfill R_1\left({\kappa }_1^{*}\right)=R_2\left({\kappa }_1^{*}\right),\end{array}$$

(23)

which can be determined by the well-known bisection method, as shown in Algorithm 1.   

Algorithm 1: Bisection-based algorithm for solving (23)

1    Initialization 2    Set ${\kappa }_1^a$ and ${\kappa }_1^b$ with $R_1\left({\kappa }_1^a\right)<R_2\left({\kappa }_1^b\right)$ and the opposite case, respectively. Define the stopping criterion $\epsilon$. 3    Repeat 4    Update ${\kappa }_1^{△}=({\kappa }_1^a+{\kappa }_1^b)/2$ 5    Compute $R_1\left({\kappa }_1^{△}\right)$ and $R_2\left({\kappa }_1^{△}\right)$ 6    If  $R_1\left({\kappa }_1^{△}\right)<R_2\left({\kappa }_1^{△}\right)$ 7    ${\kappa }_1^a={\kappa }_1^{△}$ 8    Else${\kappa }_1^b={\kappa }_1^{△}$ 9    EndIf 10  Until  $|R_1\left({\kappa }_1^a\right)-R_2\left({\kappa }_1^b\right)|<\epsilon$

3.2. Optimal $p_1$ Design for IGS-Based NOMA with Perfect SIC

With the ${\kappa }_1$ in hand, we can rewrite the max–min fairness in (21) as

$$\left(\mathrm{P}4\right):\underset{p_1}{max}min\{R_1\left(p_1\right),R_2\left(p_1\right)\}\mathrm{s}.\mathrm{t}.\left(\mathrm{C}5\right)$$

(24)

Similar to the optimization in (22), it is also not feasible to obtain the closed-form solution. This is because $R_1\left(p_1\right)$ is a monotonically increasing function of $p_1$, while $R_2\left(p_1\right)$ is a monotonically decreasing function of $p_1$. We resort to finding $p_1^{*}$, which satisfies

$$\begin{array}{c}\hfill R_1\left(p_1^{*}\right)=R_2\left(p_1^{*}\right),\end{array}$$

(25)

which can also be solved by the bisection method in Algorithm 1.

The overall AO algorithm to solve the max–min fairness in (21) is summarized in Algorithm 2. It is straightforward that the optimization of the unknown parameters follows the sequence $\cdots ,{\kappa }_1^{△}\left(i\right),p_1^{△}\left(i\right),{\kappa }_1^{△}(i+1),p_1^{△}(i+1),\cdots$, where i and $i+1$ represent the number of iterations. Considering the iteration process, we have  

$$\begin{array}{c}\hfill \underset{p_1^{△}\left(i\right)}{max}min\{R_1\left(p_1^{△}\left(i\right)\right),R_2\left(p_1^{△}\left(i\right)\right)\}\le \underset{{\kappa }_1^{△}\left(i\right)}{max}min\{R_1\left({\kappa }_1^{△}\left(i\right)\right),R_2\left({\kappa }_1^{△}\left(i\right)\right)\}\end{array}$$

(26)

and

$$\begin{array}{c}\hfill \underset{{\kappa }_1^{△}(i+1)}{max}min\{R_1\left({\kappa }_1^{△}(i+1)\right),R_2\left({\kappa }_1^{△}(i+1)\right)\}\le \underset{p_1^{△}\left(i\right)}{max}min\{R_1\left(p_1^{△}\left(i\right)\right),R_2\left(p_1^{△}\left(i\right)\right)\}.\end{array}$$

(27)

Observing Equations (26) and (27), the convergence of Algorithm 2 can be guaranteed.   

Algorithm 2: The overall AO algorithm for solving (21)

1  Initialization 2  Set the total iteration number as $T_i$. 3  Repeat 4  Compute ${\kappa }_1^{△}$ in (23) according to Algorithm 1. 5  Compute $p_1^{△}$ in (25) according to Algorithm 1. 6  Until the maximum iterative number $T_i$. 7  Output: ${\kappa }_1^{△}$ and $p_1^{△}$.

3.3. Optimal Solution for PGS-Based NOMA with Perfect SIC

When ${\kappa }_1={\kappa }_2=0$ and ${\varphi }_1={\varphi }_2=0$, the corresponding achievable rates in (13) and (14) reduce to the standard PGS one, which can be described as

$$\begin{array}{c}\hfill R_1^p\left(p_1\right)={log}_2({\Gamma }_1{p}_1+1),\end{array}$$

(28)

and

$$\begin{array}{c}\hfill \begin{array}{c}{R}_2^p(p_1,p_2)={log}_2{\displaystyle \frac{{\Gamma }_2{p}_1+{\Gamma }_2{p}_2+1}{{\Gamma }_2{p}_1+1}},\hfill \end{array}\end{array}$$

(29)

respectively. In this way, the max–min fairness for the conventional PGS NOMA system becomes

$$\begin{array}{c}\hfill \left(\mathrm{P}5\right):\underset{p_1}{max}min\left\{R_1^p\left(p_1\right)\right),R_2^p(p_1,p_2)\left)\right\}\mathrm{s}.\mathrm{t}.\left(\mathrm{C}1\right)\end{array}$$

(30)

Similar to the analysis above in Equation (18), the optimal transmission strategy for the weak user is to allocate its power budget, $P_2$, and, subsequently, the optimization in (30) simplifies to

$$\begin{array}{c}\hfill \begin{array}{c}\left(\mathrm{P}6\right):\underset{p_1}{max}min\{{\log }_2({\Gamma }_1{p}_1+1),{log}_2({\displaystyle \frac{{\Gamma }_2{p}_1+{\Gamma }_2{P}_2+1}{{\Gamma }_2{p}_1+1}})\}\hfill \\ \mathrm{s}.\mathrm{t}.\left(\mathrm{C}4\right)\hfill \end{array}\end{array}$$

(31)

This optimization is solved according to

$$\begin{array}{c}\hfill {log}_2({\Gamma }_1{p}_1+1)={log}_2({\displaystyle \frac{{\Gamma }_2{p}_1+{\Gamma }_2{P}_2+1}{{\Gamma }_2{p}_1+1}})\end{array}$$

(32)

or equivalently,

$$\begin{array}{c}\hfill {\Gamma }_1{p}_1={\displaystyle \frac{{\Gamma }_2{P}_2}{{\Gamma }_2{p}_1+1}}.\end{array}$$

(33)

After a few mathematical manipulations, the optimal power allocation for user 1 can be obtained as  

$$\begin{array}{c}\hfill p_1^{*}={\displaystyle \frac{-{\Gamma }_1+\sqrt{{\Gamma }_1^2+4{\Gamma }_1{\Gamma }_2^2{P}_2}}{2{\Gamma }_1{\Gamma }_2}}.\end{array}$$

(34)

In this way, the optimal closed-form solution to (30) can be provided by

$$\begin{array}{c}\hfill maxmin\{R_1^p,R_2^p\}={log}_2{\displaystyle \frac{2{\Gamma }_2-{\Gamma }_1+\sqrt{{\Gamma }_1^2+4{\Gamma }_1{\Gamma }_2^2{P}_2}}{2{\Gamma }_2}}.\end{array}$$

(35)

4. Fairness Maximization of the NOMA System with IGS Under Imperfect SIC

In this section, we consider the fairness maximization of the NOMA system with IGS and imperfect SIC. In (13) and (14), $R_i,i=1,2,$ can achieve its maximum when ${\varphi }_2={\varphi }_1+\pi$. In this sense, the resulting data rates can be rewritten as

$$\begin{array}{c}\hfill R_1({\kappa }_1,p_1,{\kappa }_2,p_2)={\displaystyle \frac{1}{2}}{log}_2{\displaystyle \frac{{({\Gamma }_1{p}_1+{\Gamma }_1{p}_2{\lambda }^2+1)}^2-{\Gamma }_1^2{(p_1{\kappa }_1-{\lambda }^2{p}_2{\kappa }_2)}^2}{{({\lambda }^2{\Gamma }_1{p}_2+1)}^2-{\lambda }^4{\Gamma }_1^2{p}_2^2{\kappa }_2^2}},\end{array}$$

(36)

and

$$\begin{array}{c}\hfill R_2({\kappa }_1,p_1,{\kappa }_2,p_2)={\displaystyle \frac{1}{2}}{log}_2{\displaystyle \frac{{({\Gamma }_2{p}_1+{\Gamma }_2{p}_2+1)}^2-{\Gamma }_2^2{(p_1{\kappa }_1-p_2{\kappa }_2)}^2}{{({\Gamma }_2{p}_1+1)}^2-{\Gamma }_2^2{p}_1^2{\kappa }_1^2}}.\end{array}$$

(37)

Then, the objective of joint power allocation and impropriety degree optimization to maximize the minimum data rate can be described as

$$\begin{array}{c}\hfill \begin{array}{c}\underset{{\kappa }_1,p_1,{\kappa }_2,p_2}{max}min\{R_1,R_2\}\hfill \\ \mathrm{s}.\mathrm{t}.0\le p_1\le p_2\le P_2,\hfill \\ 0\le {\kappa }_1,{\kappa }_2\le 1,\hfill \\ R_i\ge R\hfill \end{array}\end{array}$$

(38)

where $R_1$ and $R_2$ refer to (36) and (37), respectively; R is the rate constraint of both users. The above optimization (38) is obviously non-convex and difficult to solve since the optimization variables, ${\kappa }_1,p_1,{\kappa }_2,p_2$, appear in both the nominators and denominators. To address this issue, the deep Q network (DQN) is introduced to solve the joint power allocation and impropriety degree optimization. This is because the max–min optimization can be expressed as a discrete action space, where value-based methods are more suitable and stable than policy gradient approaches. Moreover, DQN achieves higher sample efficiency through experience replay, making it a more practical choice [35].

Q learning is an off-policy and model-free reinforcement learning algorithm, which aims to maximize the action–value (Q) function $Q^{\pi }(s,a)$ under policy $\pi$, and its convergence to optimal can be guaranteed, where s and a represent the finite discrete set of state $\mathcal{A}$ and action $𝒮$, respectively. The optimal Q-function $Q^{★}(s,a)$ can be provided by

$$\begin{array}{ccc}\hfill Q^{★}(s,a)& =& maxE\left\{\sum _{n=1}^{\infty }{\gamma }^{n-1}{r}_{t+n}|s_t=s,a_t=a\right\},\hfill \\ & =& E\{r^{\prime }+\gamma \underset{a^{\prime }}{max}{Q}^{★}(s^{\prime },a^{\prime })|s_t=s,a_t=a\},\hfill \end{array}$$

(39)

where $r^{\prime }$, $s^{\prime }$, and $a^{\prime }$ are the reward, state, and action, respectively, and $\gamma$ is the discount coefficient with $0\le \gamma \le 1$, which determines the importance of future rewards. By means of immediate rewards, the update of the Q-function can be described as  

$$\begin{array}{c}\hfill Q(s,a)=(1-\alpha )Q(s,a)+\alpha [r^{\prime }+\gamma \underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime })],\end{array}$$

(40)

where $\alpha \in (0,1)$ is the learning rate, which determines the balance between the speed of learning and convergence behavior; i.e., a larger $\alpha$ leads to a faster learning procedure yet results in non-convergence of learning procedure, and a smaller $\alpha$ leads to a slower learning procedure. However, the Q table becomes large when the numbers of actions and states are large, which causes great challenges in storage and reading, and the update of Q-function becomes no longer accurate. To overcome these challenges, a deep neural network (DNN) is introduced into Q learning to approximate the Q-function, referred to as DQN. By denoting the DNN parameters as $\mathsf{\theta }$, the DQN structure can be defined as $Q(s,a,\mathsf{\theta })$. The training goal of DQN is to obtain the best values of the weights $\mathsf{\theta }$. Typically, we adopt the hyperbolic tangent function $\tanh (·)$ as the nonlinear activation function, indicated by

$$\begin{array}{c}\hfill \tanh \left(x\right)={\displaystyle \frac{e^x-e^{-x}}{e^x+e^{-x}}}.\end{array}$$

(41)

One key mechanism in DQN is the experience replay strategy, which stores the quadruple $(s,a,r^{\prime },s^{\prime })$ in its memory pool. The neural network is trained by randomly sampling mini-batches of experience data in a first-in-first-out manner from this memory pool. Moreover, to enhance its stability, two NNs, i.e., the quasi-static target network and the local network, are introduced into DQN by updating the weights of target network as ${\mathsf{\theta }}^{\prime }=\mathsf{\theta }$ for every T timeslot, while the weights of the local network $\mathsf{\theta }$ are trained in each timeslot. We use the mean squared error (MSE) loss function in the training phase, indicated by

$$\begin{array}{c}\hfill \mathcal{J}\left(\mathsf{\theta }\right)=\sum _{\mathsf{\Omega }}{(r^{\prime }+\gamma \underset{a^{\prime }}{max}Q(s^{\prime },a^{\prime },{\mathsf{\theta }}^{\prime })-Q(s,a,\mathsf{\theta }))}^2.\end{array}$$

(42)

To solve the fairness maximization for the downlink NOMA system with improper Gaussian signaling and imperfect SIC in (38), the action space, state space, and the reward function are defined as follows.

1.

State space: The state space is defined as

$$\begin{array}{c}\hfill s_t=\{p_1,p_2,{\kappa }_1,{\kappa }_2,r_{t-1}\},\end{array}$$

(43)

where $r_{t-1}$ is the reward obtained in the last timeslot.

2.

Action space: The action space involves different levels of power and impropriety degrees. Let the power and impropriety degree levels uniformly distribute in $[0,P_2]$ and $[0,1]$, respectively. The corresponding quantized intervals are assumed to be ${\Delta }_p$ and ${\Delta }_i$, and thus the power and impropriety degree levels can be calculated as $N_p={\Delta }_p$ and $N_i={\Delta }_i$, respectively. In this way, the action space is defined as

$$\begin{array}{c}\hfill \mathcal{A}=\{{\mathbf{a}}_1,{\mathbf{a}}_2,\dots ,{\mathbf{a}}_u,\dots ,{\mathbf{a}}_{N_1{N}_2}\},\end{array}$$

(44)

where

$$\begin{array}{c}\hfill {\mathbf{a}}_u={[p_{1,n_1},{\kappa }_{l_1},p_{1,n_2},{\kappa }_{l_2}]}^T,\end{array}$$

(45)

in which $n_1,n_2=1,2,\dots ,N_p,l_1,l_2=1,2,\dots ,N_i.$ The adaptive $ϵ$-greedy strategy is used to conduct action selection, provided by

• As time goes on, the action selection strategy becomes less inclined to take a random action from $\mathcal{A}$. In this sense, the decreasing probability ${ϵ}_t$ at timeslot t, defined as 

  $$\begin{array}{c}\hfill {ϵ}_t=max\left\{{ϵ}_{min},{ϵ}_0(1-{\displaystyle \frac{t^{\prime }T+t}{T{T}^{\prime }}})\right\},\end{array}$$

  (46)

  is used in this work, where ${ϵ}_0$, ${ϵ}_{min}$, T, $T^{\prime }$, and $t^{\prime }$ are the initial exploration probability, the minimum exploration probability, the number of training timeslots, the number of training episodes, and the time sample of the current training episode, respectively.
• Take the action that maximizes the Q-value $Q(s,a,\mathsf{\theta })$ with probability $1-{ϵ}_t$.

3.

Reward function: The immediate achieved fairness data rate is defined as the instantaneous reward, provided by

$$\begin{array}{c}\hfill r_{t+1}=\left\{\begin{array}{cc}{R}_1,\hfill & \hfill if{R}_1<R_2\&p_1<p_2\&R_i\ge R\\ R_2,\hfill & \hfill if{R}_1>R_2\&p_1<p_2\&R_i\ge R\\ 0,\hfill & \hfill \mathrm{otherwise}.\end{array}\right.\end{array}$$

(47)

Note that the discount coefficient $\gamma$, the replay memory size $N_r$, the learning rate $\alpha$, the initial value of the adaptive $ϵ$-greedy strategy ${ϵ}_0$, its minimum value ${ϵ}_{min}$, the batch size $N_b$, the weights of the local and the target DNN, $\mathsf{\theta }$ and ${\mathsf{\theta }}^{\prime }$, the copy frequency of the target DNN weights $N_c$, and the total number of training episodes $T_e$ are initialized before training. The total number of action spaces becomes larger when the quantized intervals, i.e., ${\Delta }_p$ and ${\Delta }_i$, become smaller, which makes the design of neural network infeasible. In this sense, the output of neural network is designed to be the movement directions of the unknown parameters. Specifically, the outputs of $-1$ and 1 represent a decrease and an increase for the parameters to be optimized, respectively, while the output of 0 denotes remaining unchanged. The iterative DQN implementation for the fairness maximization of the downlink NOMA sytem with improper signaling and imperfect SIC is summarized in Algorithm 3.   

Algorithm 3: Rate fairness maximization for the downlink NOMA with IGS and imperfect SIC: the DQN solution

1  Initialization 2  Initialize ${ϵ}_0$, ${ϵ}_{min}$, $N_r$, $\gamma$, $N_b$, $\alpha$, the weights of both DNNs as $\mathsf{\theta }={\mathsf{\theta }}^{\prime }$, and $N_c$. 3  for $t^{\prime }=0,1,\dots ,T^{\prime }$ do 4    for $t=0,1,\dots ,T$ do 5      Generate the decreasing probability ${ϵ}_t$ according to (46). 6      Generate a random number $0<\eta <1$. 7      if $\eta <ϵ$ 8        Select a random action ${\mathbf{a}}_t$; 9      else 10        Calculate the action pair ${\mathbf{a}}_t$ based on the output of the DNN. 11      end if 12      Calculate the reward $r_t$ via the chosen action ${\mathbf{a}}_t$, and then store the transition $(s_t,{\mathbf{a}}_t,r_t,s_{t+1})$ in the replay memory. 13      Sample a random mini-batch of size $N_b$ from the replay memory and train the local DQN with the MSE loss function in (42). 14      if $t\%N_c=0$ then 15        Update the weights of the target DNN according to ${\mathsf{\theta }}^{\prime }=\mathsf{\theta }$. 16      end if 17    end for 18  end for

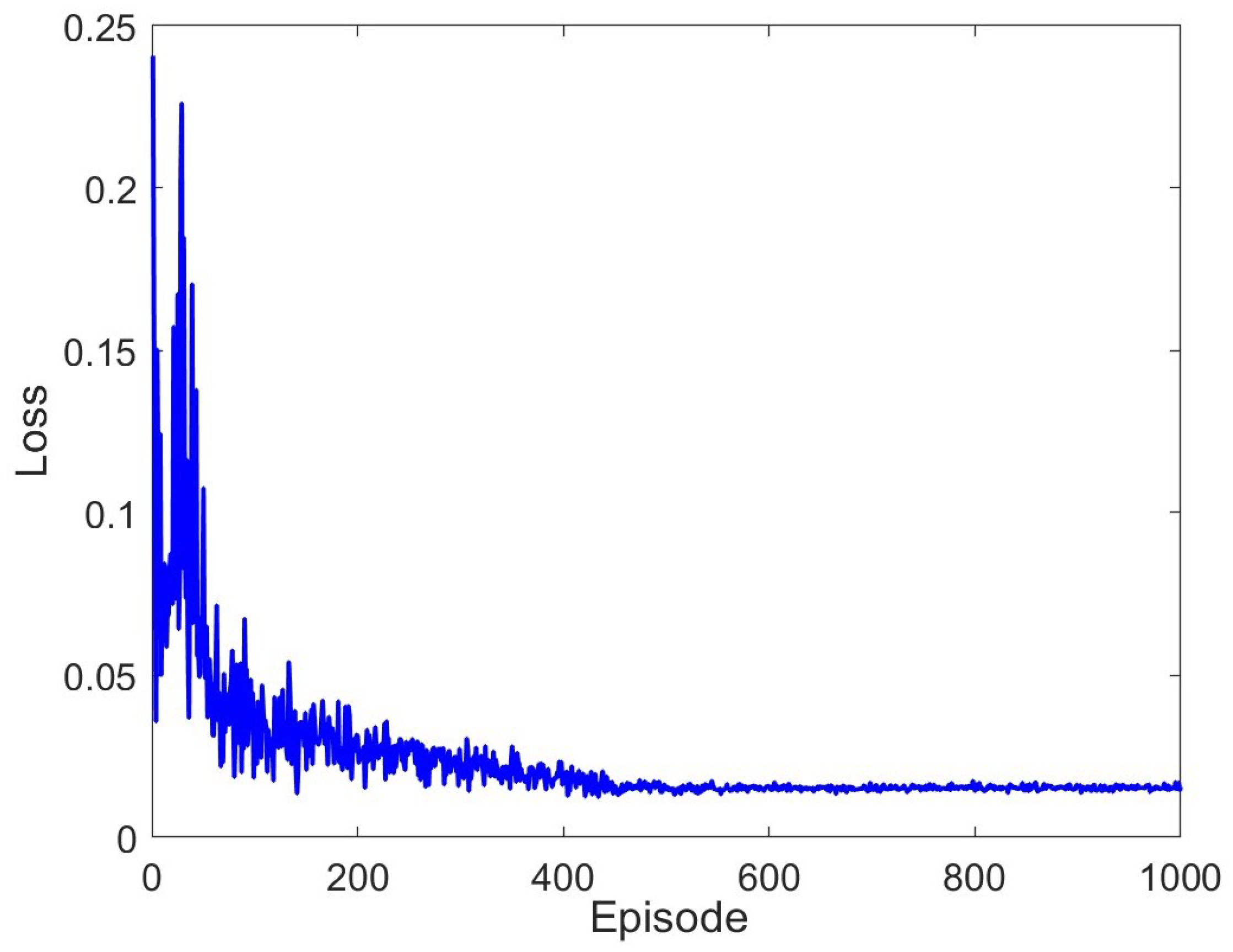
5. Simulation Results

Numerical experiments were performed in order to verify the advantages of the proposed IGS-based signaling scheme for the downlink NOMA system in terms of max–min fairness. The signal-to-noise ratio (SNR) of each user was defined as $p_i/{\sigma }_{n_i}^2,i=1,2$.

5.1. Fairness Rate for the IGS-Based NOMA Under Perfect SIC

This subsection investigates the fairness achievable rate for the IGS-based NOMA system under perfect SIC in the MATLAB 2024b programming environment. We first simulated the fairness achievable rate for the IGS-assisted NOMA system as a function of ${\Gamma }_2$ against different levels of SNR in Figure 1. The fairness achievable rate was computed according to the alternate optimization method, as shown in Algorithm 2. The SNRs of both users were 13 dB and 15 dB, respectively. A considerable rate improvement can be observed from Figure 1 by using IGS instead of PGS. In Figure 1, it is obvious that a higher SNR results in a larger fairness achievable rate since a higher SNR implies a corresponding power budget.

We also investigated the fairness achievable rate for the IGS-assisted NOMA system as a function of SNR against different levels of ${\Gamma }_2$ in Figure 2. The channel-to-noise ratios were 0.5 and 0.8, respectively. As shown in Figure 2, a larger ${\Gamma }_2$ results in a greater fairness achievable rate for the IGS-based NOMA system, and it also highlights the superiority of the advanced IGS technique.

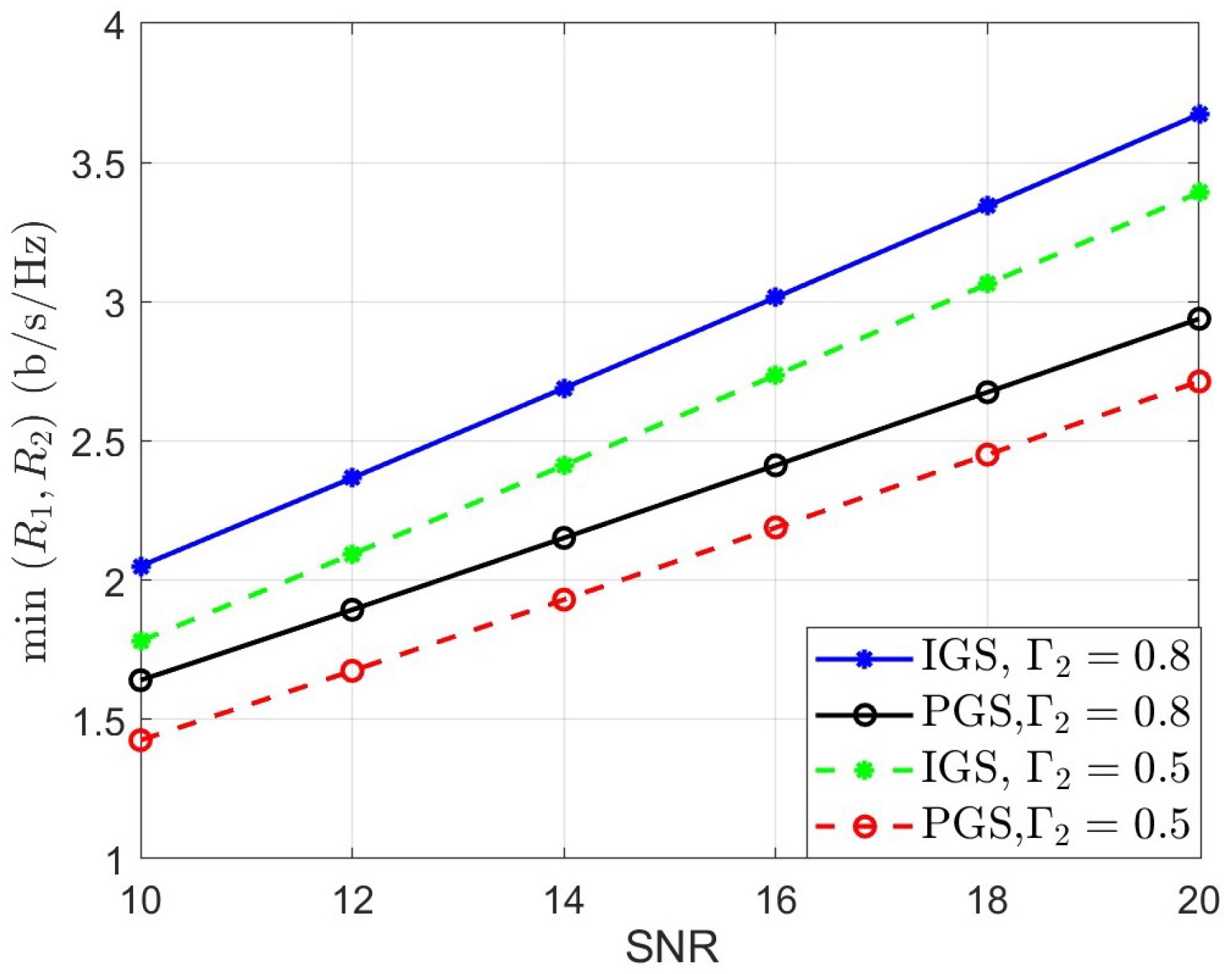
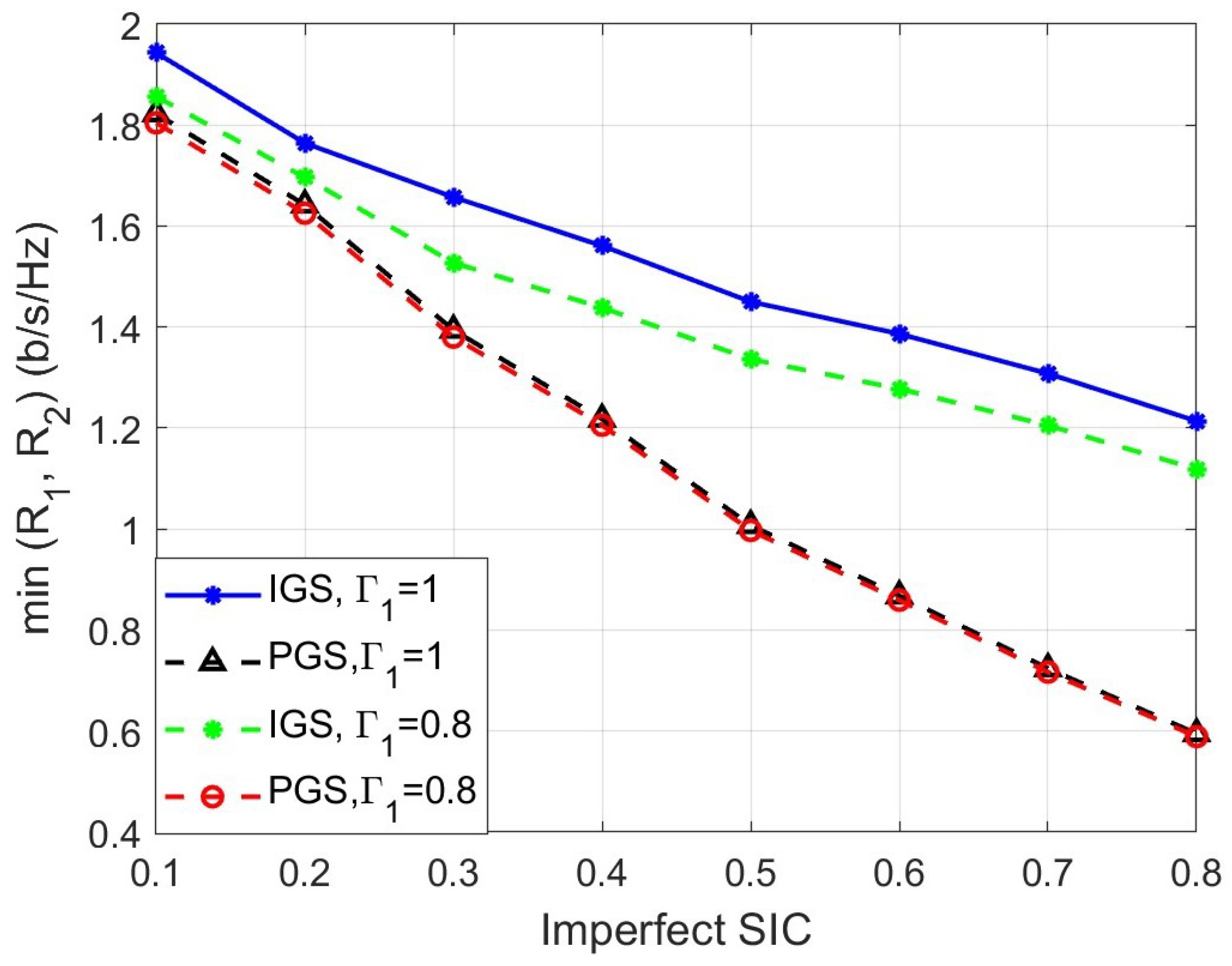
5.2. Fairness Rate for the IGS-Based NOMA Under Imperfect SIC

In this subsection, we investigate the fairness achievable rate for the IGS-based NOMA system under imperfect SIC in Python 3.9.19 with Pytorch 2.2.2 programming environment. The fully connected DNN in DQN consists of two hidden layers, each with 512 neurons. The replay memory size, the discount coefficient, the batch size, and the learning rate are set as $N_r=1000$, $\gamma =0.9$, $N_b=64$, and $\alpha ={10}^{-4}$, respectively. The copy frequency mapping the local DNN weights $\mathsf{\theta }$ to the target DNN weights ${\mathsf{\theta }}^{\prime }$ was set as $N_c=10$. The training parameters are summarized in

Table 1. Training parameters for DQN.

Parameters	Values
Size of each hidden layer	512
Size of mini-batch	64
The discount coefficient	$0.9$
The learning rate	${10}^{-4}$
Optimizer	Adam
Number of hidden layers	2
Activation function	$\tanh (·)$
Size of replay memory	1000

. We first compare the fairness rate for the IGS-based NOMA system with different combinations of ${\Delta }_p$, ${\Delta }_i$, and $\lambda$ and different SNRs in

Table 2. Comparison of the fairness rate for the IGS-based NOMA system with different combinations of ${\Delta }_p$, ${\Delta }_i$, and $\lambda$.

${\mathsf{\Delta }}_{\mathit{p}}$	${\mathsf{\Delta }}_{\mathit{i}}$	$\mathit{\lambda }=0.15$		$\mathit{\lambda }=0.45$
		SNR = 12 dB	SNR = 15 dB	SNR = 12 dB	SNR = 15 dB
$0.1$	$0.1$	1.6922	1.9711	1.3107	1.6433
$0.1$	$0.05$	1.7501	2.0377	1.3693	1.6904
$0.05$	$0.1$	1.7428	2.0254	1.3550	1.6838
$0.05$	$0.05$	1.8376	2.1137	1.4498	1.7751
$0.01$	$0.01$	1.8399	2.1187	1.4532	1.7792

. It is obvious that the achievable rate of ${\Delta }_p={\Delta }_i=0.05$ is almost the same as the case ${\Delta }_p={\Delta }_i=0.01$, while it suffers different levels of rate performance attenuation for other cases. We set ${\Delta }_p={\Delta }_i=0.05$ in the following simulations to find a trade-off between fast convergence and fairness performance. The convergence behavior of the DQN in terms of training loss is illustrated in Figure 3. As indicated in Figure 3, it is suitable to set the number of training episodes as $T_e=500$ in order to balance training cost and fairness performance.

We also investigated the fairness achievable rate for IGS-based NOMA system as a function of $\lambda$ for different SNRs under imperfect SIC in Figure 4. The advantage of the IGS over PGS for the fairness of the NOMA system is obviously observed from Figure 4, where a higher SNR results in a larger achievable rate. Moreover, the rate enhancement is highlighted when the imperfect SIC becomes larger. In the last set of simulations, the fairness achievable rate for IGS-based NOMA system as a function of $\lambda$ for different ${\Gamma }_1$ was considered under imperfect SIC in Figure 5. It is straightforward that a higher value of ${\Gamma }_1$ results in a higher fairness rate. All the simulation results demonstrate that the advanced IGS technique has the potential to enhance the fairness rate performance of the IGS-based NOMA system over the PGS one.

6. Conclusions

In this work, we consider the fairness rate optimization of the downlink NOMA system employing the novel improper signaling technique with both users subjected to a potential IGS. We first formulate the max–min optimization, and then the alternate optimization algorithm is considered by iteratively optimizing the impropriety degrees and power level under perfect SIC. For the PGS case, the closed-form solution is also investigated. Moreover, a DQN-based solution to fairness optimization is applied to verify the effectiveness of the IGS-based downlink NOMA system under imperfect SIC. Numerical experiments show that the proposed IGS-based signaling scheme is able to achieve a higher fairness rate than the traditional PGS-based one.