Spatial–Temporal Physics-Constrained Multilayer Perceptron for Aircraft Trajectory Prediction
Abstract
1. Introduction
- (1)
- A novel spatial–temporal attention-based encoder is applied to find informative features in aircraft trajectories from both time and space dimension. By separately encoding timestamps and spatial coordinates (longitude, latitude and altitude), the model mitigates the feature ambiguity caused by mixed spatiotemporal representations in conventional methods. Simultaneously, by fusing the features of temporal attention and spatial attention, our model can extract degradation information more effectively and improve the prediction accuracy of trajectory points.
- (2)
- HPC-MLP is used to make predictions and capture the hidden physics between the input data and output data. Dynamic equations are integrated as physical constraints to ensure predicted trajectories strictly adhere to aircraft kinematic principles. Furthermore, the loss function is designed to penalize violations of the aircraft’s maximum acceleration and minimum turning radius, thereby preventing physically implausible predictions beyond the aircraft’s maneuverability limits. Benefiting from the physical constraint, the model can make reasonable predictions with improved interpretability and accuracy than pure data-driven methods.
- (3)
- By integrating a spatial–temporal separated encoder based on the attention mechanism and physical constraints derived from aircraft dynamics, the proposed STPC-MLP model exhibits significant advantages in aircraft trajectory prediction, with average RMSE, MAE, and MAPE values of only 0.5158, 0.1891, and 0.0067%, respectively. Compared to the optimal Informer model, it achieves substantial reductions in prediction errors—specifically, 7.13% in RMSE, 40.38% in MAE, and 34.31% in MAPE—highlighting its superior accuracy in capturing complex spatial–temporal dynamic data information. Furthermore, ablation experiments further validate the model’s robustness: removing the HPC-MLP module, attention mechanism, or physical constraint loss term leads to significant increases in prediction errors, confirming the critical role of these components in performance enhancement. Overall, these improvements enable the model to generate more reliable predictions that conform to physical laws, strictly adhering to aircraft kinematic principles (e.g., maximum acceleration and minimum turning radius constraints), thereby enhancing its value in real-world applications where safety and precision are paramount.
2. Related Work
2.1. Kinetics-and-Aerodynamics Models
2.2. State Estimation Models
2.3. Machine Learning Models
3. Methodology
3.1. Problem Formulation
3.2. The Proposed Framework
3.2.1. Encoder
3.2.2. HPC-MLP
4. Experiments
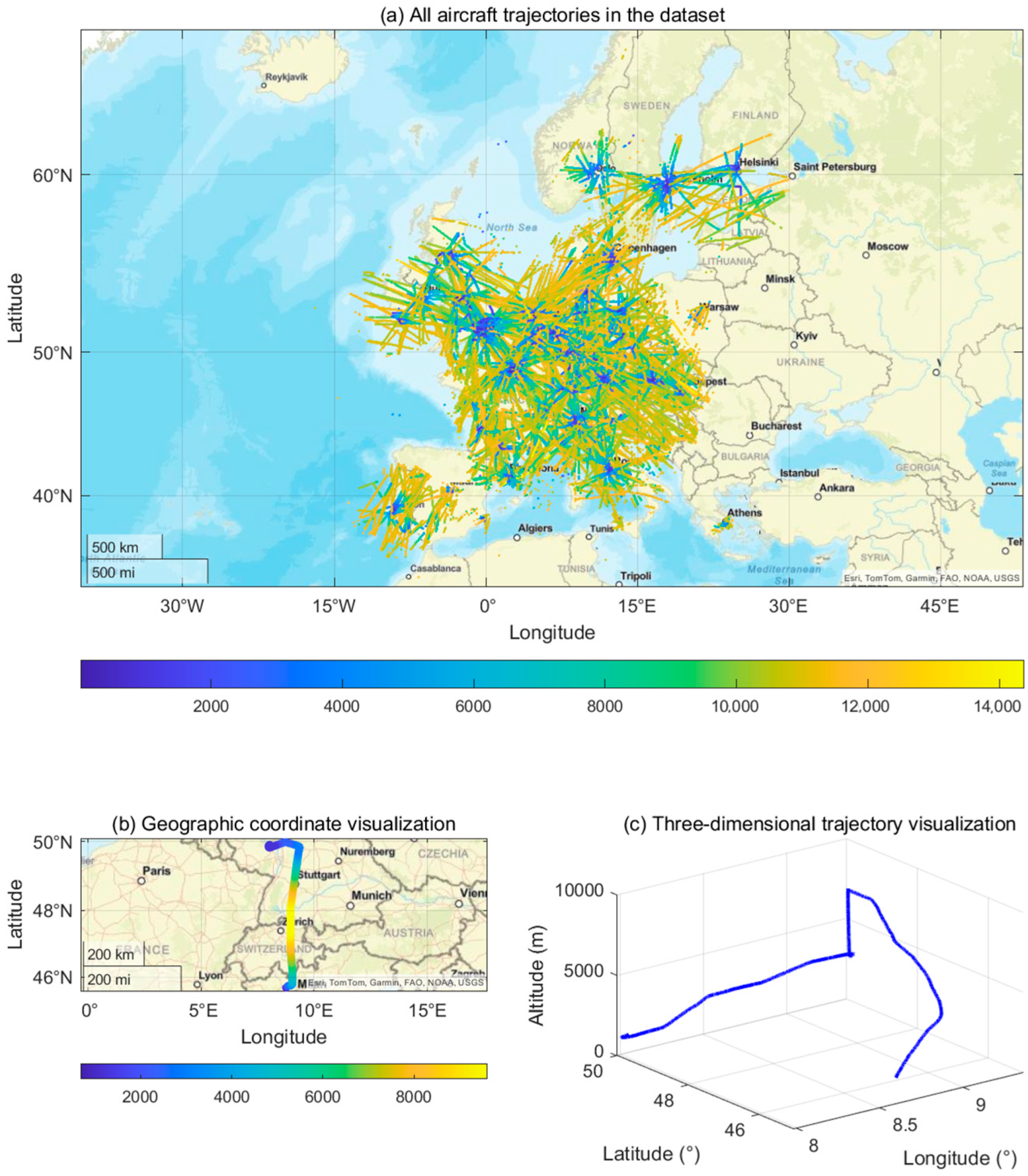
4.1. Data Processing
4.2. Experimental Setting
4.3. Maximum Acceleration and Minimum Turn Radius
4.4. Hyperparameter Configuration
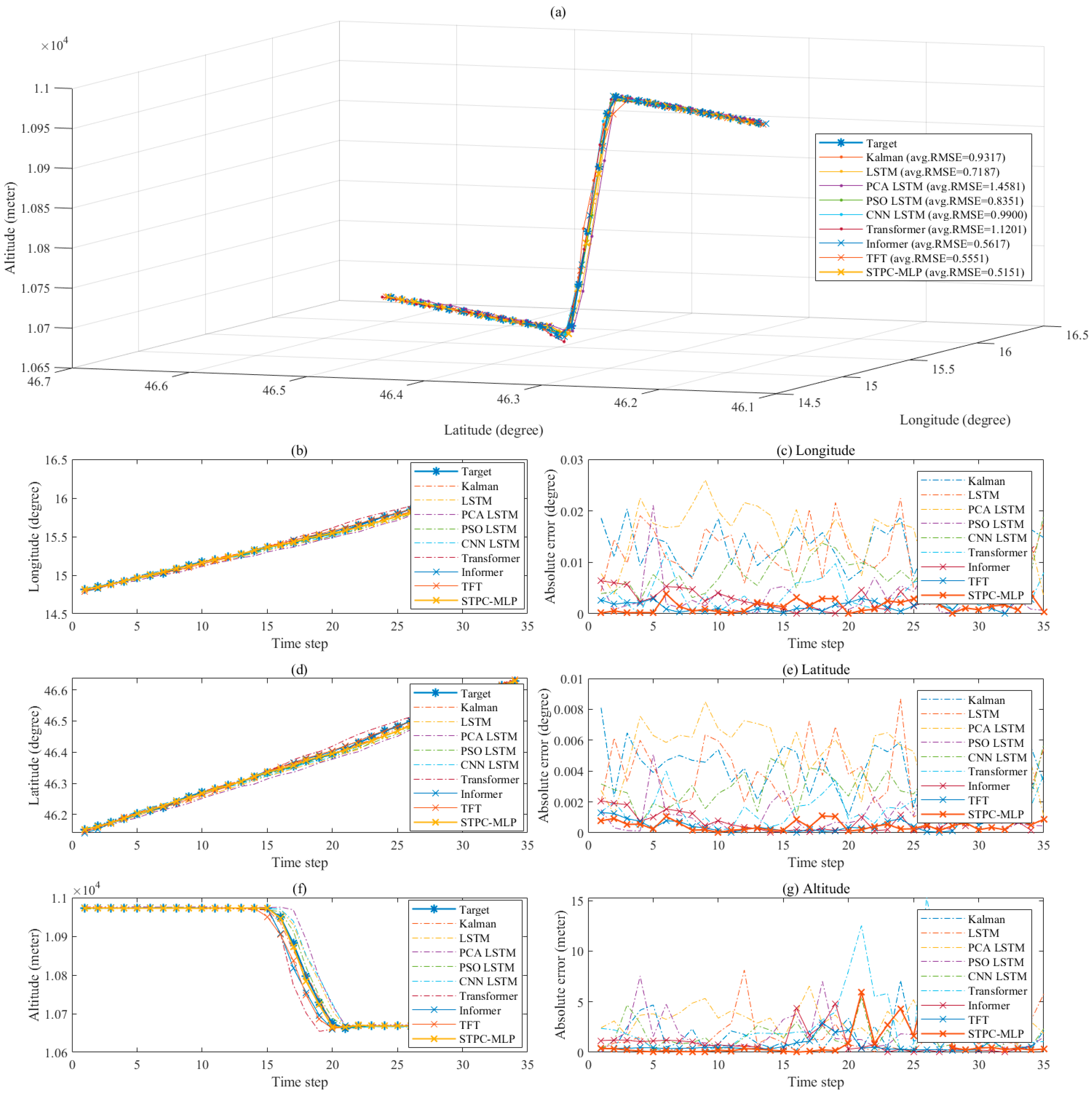
4.5. Result and Comparison with Other Methods
5. Ablation Study
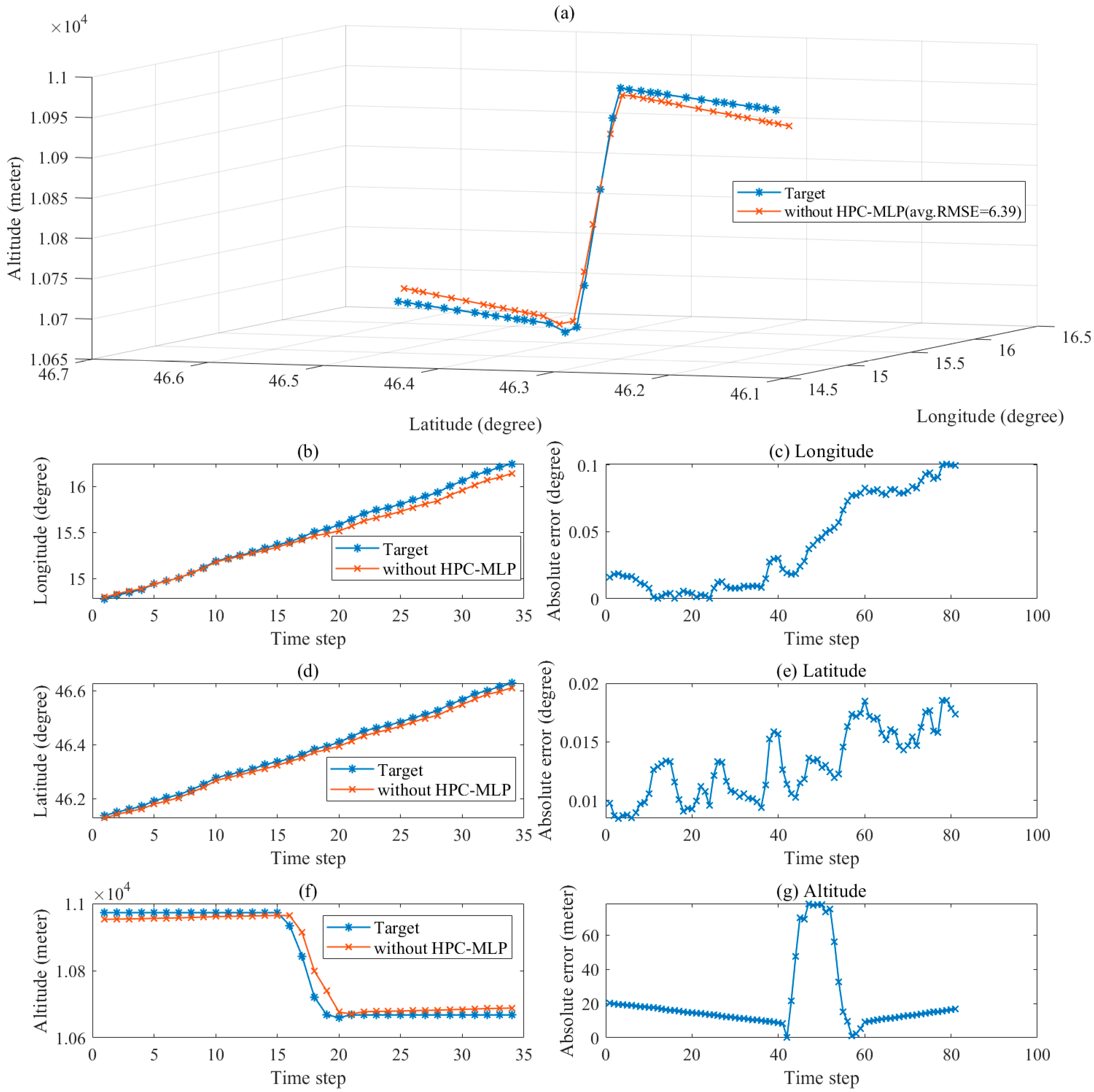
5.1. Ablation of HPC-MLP
5.2. Ablation of Attention Mechanism
5.3. Ablation of Loss Balancing Scheme
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cate, K. Challenges in achieving trajectory-based operations. In Proceedings of the 51st AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Kelly, D.; Efthymiou, M. An analysis of human factors in fifty controlled flight into terrain aviation accidents from 2007 to 2017. J. Saf. Res. 2019, 69, 155–165. [Google Scholar] [CrossRef]
- Guan, X.; Zhang, X.; Wei, J.; Hwang, I.; Zhu, Y.; Cai, K. A strategic conflict avoidance approach based on cooperative coevolutionary with the dynamic grouping strategy. Int. J. Syst. Sci. 2016, 47, 1995–2008. [Google Scholar] [CrossRef]
- Zhang, M.; Chen, S.; Sun, L.; Du, W.; Cao, X. Characterizing flight delay profiles with a tensor factorization framework. Engineering 2021, 7, 465–472. [Google Scholar] [CrossRef]
- Yan, Z.; Yang, H.; Wu, Y.; Lin, Y. A multi-view attention-based spatial-temporal network for airport arrival flow prediction. Transp. Res. Part E Logist. Transp. Rev. 2023, 170, 102997. [Google Scholar] [CrossRef]
- Du, W.B.; Gao, Y.; Liu, C.; Zheng, Z.; Wang, Z. Adequate is better: Particle swarm optimization with limited information. Appl. Math. Comput. 2015, 268, 832–838. [Google Scholar] [CrossRef]
- Guo, D.; Zhang, Z.; Yang, B.; Zhang, J.; Yang, H.; Lin, Y. Integrating spoken instructions into flight trajectory prediction to optimize automation in air traffic control. Nat. Commun. 2025, 15, 9662. [Google Scholar] [CrossRef]
- Singer, R.; Sea, R. New results in optimizing surveillance system tracking and data correlation performance in dense multitarget environments. IEEE Trans. Autom. Control 1973, 18, 571–582. [Google Scholar] [CrossRef]
- Guan, X.; Zhang, X.; Han, D.; Zhu, Y.; Lv, J.; Su, J. A strategic flight conflict avoidance approach based on a memetic algorithm. Chin. J. Aeronaut. 2014, 27, 93–101. [Google Scholar] [CrossRef]
- Zhang, Z.; Guo, D.; Zhou, S.; Zhang, J.; Lin, Y. Flight trajectory prediction enabled by time-frequency wavelet transform. Nat. Commun. 2023, 14, 5258. [Google Scholar] [CrossRef]
- Lee, J.; Lee, S.; Hwang, I. Hybrid System Modeling and Estimation for Arrival Time Prediction in Terminal Airspace. J. Guid. Control Dyn. 2016, 39, 903–910. [Google Scholar] [CrossRef]
- Thipphavong, D.P.; Schultz, C.A.; Lee, A.G.; Chan, S.H. Adaptive Algorithm to Improve Trajectory Prediction Accuracy of Climbing Aircraft. J. Guid. Control Dyn. 2015, 36, 15–24. [Google Scholar] [CrossRef]
- Tang, X.; Zhou, L.; Shen, Z.; Tang, M. 4D trajectory prediction of aircraft taxiing based on fitting velocity profile. In Proceedings of the 2015 Cota International Conference Transportation Professionals, Beijing, China, 25–27 July 2015; Volume 45, pp. 1–12. [Google Scholar] [CrossRef]
- Daigle, M.; Roychoudhury, I.; Spirkovska, L.; Goebel, K.; Sankararaman, S.; Ossenfort, J.; Kulkarni, C.S. Real-time prediction of safety margins in the national airspace. In Proceedings of the 17th AIAA Aviation Technology, Integration, and Operations Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar] [CrossRef]
- Ghasemi Hamed, M.; Gianazza, D.; Serrurier, M.; Durand, N. Statistical prediction of aircraft trajectory: Regression methods vs. point-mass model. In Proceedings of the ATM 2013, 10th USA/Europe Air Traffic Management Research and Development Seminar, Chicago, IL, USA, 10–13 June 2013. [Google Scholar]
- Guo, D.; Wu, E.Q.; Wu, Y.; Zhang, J.; Law, R.; Lin, Y. FlightBERT: Binary Encoding Representation for Flight Trajectory Prediction. IEEE Trans. Intell. Transp. Syst. 2023, 24, 1828–1842. [Google Scholar] [CrossRef]
- Chatterji, G. Short-term trajectory prediction methods. In Proceedings of the Guidance, Navigation, and Control Conference and Exhibit, Portland, OR, USA, 9–11 August 1999. [Google Scholar]
- Mondoloni, S.; Liang, D. Improving trajectory forecasting through adaptive filtering technique. In Proceedings of the 5th USA-Europe ATM Seminar, Budapest, Hungary, 23–27 June 2003. [Google Scholar]
- Chakraborty, S.; Chattaraj, S.; Mukherjee, A. Performance evaluation of particle filter resampling techniques for improved estimation of misalignment and trajectory deviation. Multidimens. Syst. Signal Process. 2018, 29, 821–838. [Google Scholar] [CrossRef]
- Hwang, I.; Hwang, J.; Tomlin, C. Flight-mode-based aircraft conflict detection using a residual-mean interacting multiple model algorithm. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Austin, TX, USA, 11–14 August 2003. [Google Scholar] [CrossRef][Green Version]
- Tastambekov, K.; Puechmorel, S.; Delahaye, D.; Rabut, C. Aircraft trajectory forecasting using local functional regression in sobolev space. Transp. Res. Part C Emerg. Technol. 2024, 39, 1–22. [Google Scholar] [CrossRef]
- Choi, H.C.; Deng, C.; Hwang, I. Hybrid machine learning and estimation-based flight trajectory prediction in terminal airspace. IEEE Access 2021, 9, 151186–151197. [Google Scholar] [CrossRef]
- Alligier, R.; Gianazza, D. Learning aircraft operational factors to improve aircraft climb prediction: A large scale multi-airport study. Transp. Res. Part C Emerg. Technol. 2018, 96, 72–95. [Google Scholar] [CrossRef]
- Kun, W.; Wei, P. A 4-D trajectory prediction model based on radar data. In Proceedings of the 27th Chinese Control Conference, Kunming, China, 16–18 July 2008; pp. 591–594. [Google Scholar][Green Version]
- Wang, T.; Huang, B. Fuzzy Cluster Analysis of 4D Trajectory Based on ADS-B. J. Traffic Inf. Saf. 2013, 31, 38–42. [Google Scholar]
- Wu, Z.J.; Tian, S.; Ma, L. A 4D trajectory prediction model based on the BP neural network. J. Intell. Syst. 2020, 29, 1545–1557. [Google Scholar] [CrossRef]
- Zhang, X.; Mahadevan, S. Bayesian neural networks for flight trajectory prediction and safety assessment. Decis. Support Syst. 2020, 131, 113246. [Google Scholar] [CrossRef]
- Pang, Y.; Zhao, X.; Yan, H.; Liu, Y. Data-driven trajectory prediction with weather uncertainties: A Bayesian deep learning approach. Transp. Res. Part C: Emerg. Technol. 2021, 130, 103326. [Google Scholar] [CrossRef]
- Shi, Z.; Xu, M.; Pan, Q.; Yan, B.; Zhang, H. LSTM-based flight trajectory prediction. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar] [CrossRef]
- Zhang, Z.; Yang, R.; Fang, Y. LSTM Network Based on Antlion Optimization and its Application in Flight Trajectory Prediction. In Proceedings of the 2018 2nd IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Xi’an, China, 25–27 May 2018; pp. 1658–1662. [Google Scholar] [CrossRef]
- Ma, L.; Tian, S. A hybrid CNN-LSTM model for aircraft 4D trajectory prediction. IEEE Access 2020, 8, 134668–134680. [Google Scholar] [CrossRef]
- Shafienya, H.; Regan, A.C. 4D flight trajectory prediction using a hybrid deep learning prediction method based on ads-b technology: A case study of harts field—Jackson Atlanta International Airport (ATL). Transp. Res. Part C Emerg. Technol. 2022, 144, 103878. [Google Scholar] [CrossRef]
- Han, P.; Wang, W.; Shi, Q.; Yue, J. A combined online-learning model with K-means clustering and GRU neural networks for trajectory prediction. Ad Hoc Netw. 2021, 117, 102476. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar] [CrossRef]
- Raissi, M. Deep Hidden Physics Models: Deep Learning of Nonlinear Partial Differential Equations. arXiv 2018, arXiv:1801.06637. [Google Scholar] [CrossRef]
- Nuic, A. User Manual for the Base of Aircraft Data (BADA) Revision 3.10; Eurocontrol: Brussels, Belgium, 2010. [Google Scholar]
- Porretta, M.; Dupuy, M.D.; Schuster, W.; Majumdar, A.; Ochieng, W. Performance evaluation of a novel 4D trajectory prediction model for civil aircraft. J. Navig. 2008, 61, 393–420. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, J.; Zhu, Y.; Liu, W. Simulation study of algorithms for aircraft trajectory prediction based on ads-b technology. In Proceedings of the Asia Simulation Conference-7th International Conference on System Simulation and Scientific Computing, Beijing, China, 10–12 October 2008; pp. 322–327. [Google Scholar] [CrossRef]
- Yan, H.; Huang, G.; Wang, H.; Shu, R. Application of unscented Kalman filter for flying target tracking. In Proceedings of the 2013 International Conference on Information Science and Cloud Computing, Guangzhou, China, 7–8 December 2013. [Google Scholar] [CrossRef]
- Lymperopoulos, I.; Lygeros, J. Adaptive Aircraft Trajectory Prediction using Particle Filters. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V. Survey of maneuvering target tracking. part v. multiple-model methods. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 1255–1321. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, Q.; Jiang, J.; Peng, M.; Zhu, M.; Yang, H.F. Towards explainable traffic flow prediction with large language models. Commun. Transp. Res. 2024, 4, 100150. [Google Scholar] [CrossRef]
- Liao, H.; Shen, H.; Li, Z.; Wang, C.; Li, G.; Bie, Y.; Xu, C. GPT-4 enhanced multimodal grounding for autonomous driving: Leveraging cross-modal attention with large language models. Commun. Transp. Res. 2024, 4, 100116. [Google Scholar] [CrossRef]
- Han, Y.; Wang, M.; Leclercq, L. Leveraging reinforcement learning for dynamic traffic control: A survey and challenges for field implementation. Commun. Transp. Res. 2023, 3, 100104. [Google Scholar] [CrossRef]
- Rodríguez-Sanz, Á.; García, J.M.C.; Ovies-Carro, I.G.; Iglesias, E. A data-driven approach for dynamic and adaptive aircraft trajectory prediction. Transp. Res. Procedia 2021, 58, 5–12. [Google Scholar] [CrossRef]
- Jeung, H.; Shen, H.T.; Zhou, X. Mining trajectory patterns using hidden Markov models. In International Conference on Data Warehousing and Knowledge Discovery; Springer: Berlin/Heidelberg, Germany, 2007; pp. 470–480. [Google Scholar] [CrossRef]
- Jiang, X.-R.; Wen, X.-X.; Wu, M.-G.; Wang, Z.-K.; Qiu, X. A SVM Approach of Aircraft Conflict Detection in Free Flight. J. Adv. Transp. 2018, 2018, 7964641. [Google Scholar] [CrossRef]
- Wiest, J.; Hoffken, M.; Kressel, U.; Dietmayer, K. Probabilistic trajectory prediction with gaussian mixture models. In Proceedings of the 2012 IEEE Intelligent Vehicles Symposium, Madrid, Spain, 3–7 June 2012; pp. 141–146. [Google Scholar] [CrossRef]
- Shi, Z.; Xu, M.; Pan, Q. 4-D flight trajectory prediction with constrained LSTM network. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7242–7255. [Google Scholar] [CrossRef]
- Qi, Y.; Cao, J.; Wu, B. Bidirectional Q-learning for recycling path planning of used appliances under strong and weak constraints. Commun. Transp. Res. 2024, 4, 100153. [Google Scholar] [CrossRef]
- Hashemi, S.M.; Botez, R.M.; Grigorie, T.L. New Reliability Studies of Data-Driven Aircraft Trajectory Prediction. Aerospace 2020, 7, 145. [Google Scholar] [CrossRef]
- Neretin, E.S.; Phuong, N.T.L.; Quan, N.N.H. An Analysis of Human Interaction and Weather Effects on Aircraft Trajectory Prediction via Artificial Intelligence. In Proceedings of the 2022 XIX Technical Scientific Conference on Aviation Dedicated to the Memory of N.E. Zhukovsky (TSCZh), Moscow, Russia, 14–15 April 2022. [Google Scholar] [CrossRef]
- Schafer, M.; Strohmeier, M.; Lenders, V.; Martinovic, I.; Wilhelm, M. Bringing Up OpenSky: A Large-Scale ADS-B Sensor Network for Research. In Proceedings of the 13th IEEE/ACM International Symposium on Information Processing in Sensor Networks (IPSN), Berlin, Germany, 15–17 April 2014; pp. 83–94. [Google Scholar]
- Skinn, D.; Tipps, D.O. Analysis of Boeing 737-400 aircraft operational data. In FAA Report DOT/FAA/AR-95/21; University of Dayton: Dayton, OH, USA, 1996. [Google Scholar]
- Herbst, W.B. Dynamics of air combat. J. Aircr. 1980, 17, 594–598. [Google Scholar] [CrossRef]
- Raymer, D.P. Aircraft Design: A Conceptual Approach, 2nd ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1992. [Google Scholar] [CrossRef]
- Meilinger, P.S. Bomber: The Formation and Early Years of Strategic Air Command; Air University Press: Montgomery, AL, USA, 2010. [Google Scholar]
- Lockheed Martin Corporation. U-2 Dragon Lady: Technical Specifications; Lockheed Martin Corporation: Bethesda, MD, USA, 2015. [Google Scholar]


| Aircraft Type | Representative Aircraft | Min Airspeed (m/s) | Max Load Factor (g) | Max Acceleration (g) | Min Turn Radius (m) |
|---|---|---|---|---|---|
| Civil Aviation | Boeing 737 | 77 | 2.5 | 2.5 | 264 |
| Fighter Jets | F-16 | 67 | 9 | 9 | 51 |
| Bombers | B-52 | 70 | 3 | 3 | 177 |
| Reconnaissance Aircraft | U-2 | 51 | 2.5 | 2.5 | 116 |
| The model adopts values | 10 | 50 | |||
| Learning Rate | Number of Self-Attention Heads | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | |||||||
| RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | RMSE | MAE | ||
| 0.1 | longitude | 0.0137 | 0.0132 | 0.0955 | 0.0776 | 2.8490 | 2.7859 | 0.0250 | 0.0200 | 0.5042 | 0.5033 |
| latitude | 0.0013 | 0.0010 | 0.0352 | 0.0237 | 0.3013 | 0.2969 | 0.0052 | 0.0045 | 0.0118 | 0.0112 | |
| altitude | 1.9363 | 0.8684 | 66.0704 | 40.8829 | 116.3533 | 98.7107 | 67.6720 | 67.2449 | 291.2350 | 275.5930 | |
| 0.01 | longitude | 0.0074 | 0.0060 | 0.0062 | 0.0047 | 0.0054 | 0.0049 | 0.0077 | 0.0067 | 0.0074 | 0.0057 |
| latitude | 0.0056 | 0.0054 | 0.0053 | 0.0050 | 0.0028 | 0.0023 | 0.0020 | 0.0016 | 0.0054 | 0.0050 | |
| altitude | 1.5560 | 0.9227 | 2.5098 | 2.2539 | 3.0472 | 2.6376 | 3.0526 | 2.6909 | 1.7229 | 0.9786 | |
| 0.001 | longitude | 0.0023 | 0.0021 | 0.0047 | 0.0040 | 0.0058 | 0.0052 | 0.0056 | 0.0050 | 0.0055 | 0.0049 |
| latitude | 0.0011 | 0.0008 | 0.0042 | 0.0038 | 0.0040 | 0.0036 | 0.0031 | 0.0025 | 0.0029 | 0.0024 | |
| altitude | 1.5441 | 0.5643 | 1.8980 | 1.4056 | 1.6178 | 1.0255 | 2.5090 | 2.2496 | 3.4439 | 3.2511 | |
| Approach | RMSE | MAE | MAPE (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Long | Lat | Alt | Average | Long | Lat | Alt | Average | Long | Lat | Alt | Average | |
| Kalman Filter | 0.0122 | 0.0038 | 2.7944 | 0.9368 | 0.0111 | 0.0035 | 1.8449 | 0.6198 | 0.0723 | 0.0076 | 0.0169 | 0.0323 |
| Vanilla LSTM | 0.0109 | 0.0036 | 2.1128 | 0.7091 | 0.0098 | 0.0033 | 1.3403 | 0.4511 | 0.0637 | 0.0046 | 0.0124 | 0.0269 |
| PCA LSTM | 0.0180 | 0.0060 | 4.3536 | 1.4592 | 0.0163 | 0.0054 | 3.6384 | 1.2200 | 0.1047 | 0.0117 | 0.0337 | 0.0500 |
| PSO LSTM | 0.0056 | 0.0021 | 2.4918 | 0.8332 | 0.0043 | 0.0017 | 1.7833 | 0.5964 | 0.0280 | 0.0041 | 0.0164 | 0.0162 |
| CNN LSTM | 0.0133 | 0.0045 | 2.9542 | 0.9907 | 0.0118 | 0.0039 | 2.0237 | 0.6798 | 0.0765 | 0.0085 | 0.0188 | 0.0346 |
| Transformer | 0.0093 | 0.0016 | 3.3321 | 1.1143 | 0.0082 | 0.0013 | 3.0632 | 1.0242 | 0.0511 | 0.0028 | 0.0287 | 0.0275 |
| Informer | 0.0037 | 0.0015 | 1.6610 | 0.5554 | 0.0031 | 0.0008 | 0.9478 | 0.3172 | 0.0202 | 0.0018 | 0.0087 | 0.0102 |
| TFT | 0.0040 | 0.0020 | 1.6892 | 0.5651 | 0.0036 | 0.0017 | 0.9818 | 0.3290 | 0.0221 | 0.0037 | 0.0092 | 0.0117 |
| STPC-MLP (Proposed) | 0.0023 | 0.0011 | 1.5441 | 0.5158 | 0.0021 | 0.0008 | 0.5643 | 0.1891 | 0.0131 | 0.0018 | 0.0053 | 0.0067 |
| Approach | RMSE | MAE | ||||||
|---|---|---|---|---|---|---|---|---|
| Long | Lat | Alt | Average | Long | Lat | Alt | Average | |
| M1 | 0.0022 | 0.0013 | 9.9187 | 3.3074 | 0.0022 | 0.0012 | 6.8139 | 2.2722 |
| M2 | 0.0022 | 0.0038 | 30.421 | 10.142 | 0.0022 | 0.0038 | 29.812 | 9.9395 |
| STPC-MLP (Proposed) | 0.0023 | 0.0011 | 1.5441 | 0.5158 | 0.0021 | 0.0008 | 0.5643 | 0.1891 |
| Approach | RMSE | MAE | ||||||
|---|---|---|---|---|---|---|---|---|
| Long | Lat | Alt | Average | Long | Lat | Alt | Average | |
| L1 | 0.0023 | 0.0040 | 31.029 | 10.3452 | 0.0023 | 0.0039 | 30.904 | 10.3037 |
| L2 | 0.0028 | 0.0016 | 12.442 | 4.1488 | 0.0027 | 0.0016 | 12.267 | 4.0907 |
| L3 | 0.0028 | 0.0015 | 11.109 | 3.7044 | 0.0028 | 0.0015 | 11.042 | 3.6822 |
| Loss balancing scheme | 0.0023 | 0.0011 | 1.5441 | 0.5158 | 0.0021 | 0.0008 | 0.5643 | 0.1891 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhang, J.; Lin, Y.; Zhang, K.; Zheng, X.; Xiang, D. Spatial–Temporal Physics-Constrained Multilayer Perceptron for Aircraft Trajectory Prediction. Appl. Sci. 2025, 15, 9895. https://doi.org/10.3390/app15189895
Zhang Z, Zhang J, Lin Y, Zhang K, Zheng X, Xiang D. Spatial–Temporal Physics-Constrained Multilayer Perceptron for Aircraft Trajectory Prediction. Applied Sciences. 2025; 15(18):9895. https://doi.org/10.3390/app15189895
Chicago/Turabian StyleZhang, Zhongnan, Jianwei Zhang, Yi Lin, Kun Zhang, Xuemei Zheng, and Dengmei Xiang. 2025. "Spatial–Temporal Physics-Constrained Multilayer Perceptron for Aircraft Trajectory Prediction" Applied Sciences 15, no. 18: 9895. https://doi.org/10.3390/app15189895
APA StyleZhang, Z., Zhang, J., Lin, Y., Zhang, K., Zheng, X., & Xiang, D. (2025). Spatial–Temporal Physics-Constrained Multilayer Perceptron for Aircraft Trajectory Prediction. Applied Sciences, 15(18), 9895. https://doi.org/10.3390/app15189895







