Abstract
We propose a Transformer-based data augmentation framework with a time-series dual-stream architecture to address performance degradation in encrypted network traffic classification caused by class imbalance between attack and benign traffic. The proposed framework independently processes the complete flow’s sequential packet information and statistical characteristics by extracting and normalizing a local channel (comprising packet size, inter-arrival time, and direction) and a set of six global flow-level statistical features. These are used to generate a fixed-length multivariate sequence and an auxiliary vector. The sequence and vector are then fed into an encoder-only Transformer that integrates learnable positional embeddings with a FiLM + context token-based injection mechanism, enabling complementary representation of sequential patterns and global statistical distributions. Large-scale experiments demonstrate that the proposed method reduces reconstruction RMSE and additional feature restoration MSE by over 50%, while improving accuracy, F1-Score, and AUC by 5–7%p compared to classification on the original imbalanced datasets. Furthermore, the augmentation process achieves practical levels of processing time and memory overhead. These results show that the proposed approach effectively mitigates class imbalance in encrypted traffic classification and offers a promising pathway to achieving more robust model generalization in real-world deployment scenarios.
1. Introduction
With the rapid growth in demand for internet security and privacy protection, the vast majority of network traffic in web, mobile, and IoT environments is now safeguarded by encryption protocols such as TLS, HTTPS, and QUIC [1]. While encryption effectively conceals payload contents to protect sensitive user data, it simultaneously poses a significant challenge for security monitoring and intrusion detection systems (IDS), which can no longer inspect traffic payloads directly. Under these constraints, network operators must rely on metadata-based statistical features (such as packet size and inter-arrival time) to distinguish between benign and malicious encrypted traffic [2].
Traditional approaches to encrypted traffic classification have converted each flow into a fixed-length summary vector (e.g., mean, variance, percentiles) and applied classical machine learning techniques like SVM or random forests [3,4]. However, because these methods ignore the sequential order of packets, they struggle to differentiate complex time-series patterns characteristic of DDoS attacks or encrypted command-and-control channels. Subsequent deep learning models based on CNNs and RNNs enabled local and sequential pattern learning, but they remain limited by variable flow lengths, long-term dependency challenges, and severe class imbalance (where benign flows may outnumber attack flows by an order of magnitude) resulting in persistently poor detection rates for the minority (attack) class [5].
More recently, Transformer architectures have gained traction in traffic analysis due to their ability to model long-range dependencies and parallelize computation [6], yet they too fail to fundamentally overcome the generalization limits imposed by scarce minority-class labels. When attack data are intrinsically rare, any classification model risks overfitting or bias. Consequently, data augmentation has emerged as a critical strategy to alleviate class imbalance and improve model robustness [7]. However, prevailing augmentation techniques ranging from linear (interpolation methods like SMOTE (Synthetic Minority Over-sampling Technique) [7] to GAN- and VAE-based generative models) do not jointly preserve and control both the intricate temporal dynamics and the global statistical properties of encrypted traffic sequences [8].
To address these shortcomings, this paper proposes a Time-Series Transformer–based augmentation framework that learns and controls, in parallel, multivariate time-series features spanning entire flows and flow-level statistical characteristics. First, we extract and normalize, in addition to the three primary channels (packet size, inter-arrival time, direction), six global summary statistics (flow duration, total bytes, avg packet size, bytes per second, max burst size, and burst period) through a dual-stream preprocessing pipeline. We then feed these fixed-length (1000-step) multivariate sequences and auxiliary feature vectors into an encoder-only Transformer enhanced with learnable positional embeddings enabling the model to mutually reinforce temporal patterns and flow-level distributions. We adopt the FiLM + Context Token mechanism, which conditions feature extraction using context-aware scaling and shifting (see Section 3.3 for details).
We further develop an augmentation algorithm that combines latent-space noise injection, linear mixup, and local time-warping/segment swapping, followed by a post hoc statistical constraint verification and correction loop to ensure generated sequences remain faithful to the original distribution. On the CIC-IDS-2018 [9] and BoT-IoT [10] benchmarks, our method reduces reconstruction RMSE (root mean square error) and feature-reconstruction MSE (mean square error) by over 50%, and boosts classification accuracy, F1-Score, and AUC by 5–7 percentage points, all while maintaining practical augmentation latency and memory overhead. These results demonstrate that our framework can substantially enhance encrypted traffic classification performance under severe class imbalance.
Our main contributions are:
- Dual-Stream Preprocessing PipelineWe introduce an input structure that simultaneously extracts and normalizes both fine-grained time-series packet information and flow-level statistical vectors, enabling efficient learning of complex patterns.
- Augmentation-Friendly Transformer ArchitectureWe design an encoder-only Transformer augmented with learnable positional embeddings and a FiLM+Context Token injection scheme, which effectively fuses temporal dynamics and statistical features to strengthen both reconstruction and distribution preservation.
- Constraint-Based Augmentation AlgorithmWe incorporate explicit statistical constraints into the augmentation process by combining latent-space perturbations with post-generation verification, thereby ensuring a balance of diversity and consistency; we qualitatively validate the efficacy of this constrained augmentation.
The remainder of this paper is structured as follows. Section 2 reviews related work; Section 3 details our proposed method and its theoretical underpinnings; Section 4 describes our experimental setup and evaluation results; and Section 5 concludes with a discussion and avenues for future research. Overall, this study presents a new paradigm for encrypted-traffic augmentation, demonstrating that robust classification performance can be achieved even under highly imbalanced and sparsely labeled data conditions.
2. Related Works
2.1. Encrypted Traffic Classification
Encrypted network traffic conceals all payload contents, making direct inspection of packet internals impossible. As a result, classification models rely on metadata-based statistical features (such as packet size and flow duration) to distinguish between benign and malicious flows. Early work transformed each flow into a fixed-length summary vector of statistics (mean, variance, percentiles) and applied classical machine-learning algorithms like SVM and random forests [3,4]. However, these approaches ignore packet ordering and nonlinear interactions, limiting their ability to differentiate complex time-series patterns found in real-world attack traffic such as DDoS or encrypted C2 communications.
The advent of deep learning introduced CNN- and RNN-based sequence models for encrypted traffic classification [5]. While CNNs excel at extracting local patterns from fixed-length packet sequences, they struggle with variable flow lengths; RNNs can capture sequential dependencies but face difficulties modeling long-term context. Moreover, when benign flows outnumber attack flows by orders of magnitude, prediction bias toward the majority class severely degrades recall for the minority (attack) class. Cost-sensitive learning and class-weight adjustments have been explored to mitigate this bias [11], but finding optimal weights is challenging and overfitting on the minority class remains a concern.
2.2. Data Augmentation
One of the most widely used techniques to address the minority-class problem in encrypted traffic classification is traditional oversampling via SMOTE. SMOTE generates synthetic samples by linearly interpolating between existing minority-class feature vectors to rebalance class proportions. However, this approach does not account for the temporal continuity inherent in communication flows, potentially distorting the original packet order, and its single-feature interpolation cannot fully capture the complex multivariate patterns of real attack traffic. Variants such as Borderline-SMOTE [12] and ADASYN (Adaptive Synthetic Sampling) [13] have been proposed to mitigate these issues, but they likewise fail to preserve the dynamic characteristics of time-series data.
Generative Adversarial Network (GAN)–based augmentation methods have also been applied to encrypted traffic sequences, including Time-GAN [14], SeqGAN [15], and WaveGAN [16] architectures. Time-GAN introduces specialized components for time-series generation but still suffers from mode collapse (producing limited patterns) and instability that prevents accurate distribution modeling. SeqGAN excels at sequence generation but struggles to incorporate the multidimensional metadata of encrypted traffic. Moreover, GAN-based approaches in high-dimensional feature spaces often face overfitting and unstable training, and lack rigorous metrics (e.g., distributional distance measures, coverage and precision) to objectively assess sample quality and its downstream classification impact.
Variational Autoencoder (VAE)–based augmentation leverages a latent space to smoothly expand the minority-class distribution, offering greater training stability than GANs [17]. Nevertheless, VAEs are sensitive to hyperparameter choices (such as latent dimension and KL-divergence weight) and high reconstruction error can lead to the amplification of noise, degrading classification performance. Recent hybrid approaches combine GANs and VAEs into VAE-GAN frameworks [18] or apply SMOTE interpolation within the VAE latent space [7] to capitalize on the strengths of both techniques. However, these hybrids still fall short of fully reflecting real traffic distributions, and in the absence of refined quality-assessment metrics, their performance gains remain highly dataset- and environment-dependent.
Recent works (2023–2025) have explored stronger augmentation tailored for network/encrypted traffic. First, diffusion-based generators synthesize traffic traces with higher fidelity than GANs and improve downstream classifiers; for example, NetDiffus converts packet time series into image representations and trains a denoising diffusion model to produce synthetic flows that enhance fingerprinting, anomaly detection, and classification [19]. Second, to handle severe class imbalance with minimal information loss, balanced supervised contrastive learning combines class-augmentation and class-averaging strategies and reports consistent gains on encrypted-traffic benchmarks [20]. Third, VAE-driven enhancement remains competitive in imbalanced settings; a VAE–LSTM–DRN pipeline augments minority classes and improves encrypted traffic identification under skewed distributions [21].
2.3. Time-Series Transformer
The Time-Series Transformer adapts the original Transformer architecture [6] (developed for natural language processing) to time-series data by processing the entire sequence end-to-end rather than using a patch-based approach. At the input stage, each timestep’s metadata vector is enriched with positional encodings that fuse absolute position information (modeled via sinusoidal functions to capture periodic patterns) and relative time differences (expressed through learned relative weightings that facilitate efficient long-range interaction learning) [22].
Following embedding, the Multi-Head Self-Attention mechanism computes pairwise relationships among all timesteps in parallel, with each head learning a distinct subspace to capture diverse temporal patterns and periodicities. In contrast to RNNs (which process sequences sequentially and suffer from vanishing/exploding gradients) the Transformer employs residual connections and Layer Normalization to enable stable training in deep networks [23,24]. Each attention block is followed by a position-wise Feed-Forward Network (FFN) that performs nonlinear transformations to model complex interactions among metadata features, and a dropout layer to prevent overfitting [25].
The principal advantage of the Time-Series Transformer lies in its ability to learn long-term dependencies. Attention weights explicitly reveal how data from tens or hundreds of seconds in the past influence the current timestep, enhancing model interpretability; visualizing attention maps makes it possible to analyze which historical features contributed most to the augmentation outcome [26]. Additionally, variable-length inputs can be handled via padding masks, reducing unnecessary computation and enabling application to large-scale traffic datasets. Hyperparameters—such as the number of layers, number of heads, embedding dimension, and dropout rate—can be tuned to match different domain characteristics, and further efficiency gains can be achieved by adopting relative positional embeddings or sparse attention variants [27,28,29].
In parallel, recent Transformer variants specialized for encrypted traffic classification have appeared. CoTNeT integrates a contextual Transformer with ResNet features to better exploit packet-level context and long-range dependencies, achieving improved accuracy on encrypted traffic datasets [30]. Building on efficiency, NetST adapts the Swin Transformer with a multilevel flow matrix to reduce quadratic attention cost while preserving discriminative byte/packet/flow patterns for encrypted traffic [31]. Finally, TransECA-Net couples a Transformer encoder with efficient channel attention (ECA) to capture global temporal relations, reporting state-of-the-art results on VPN/TLS benchmarks [32].
In this work, we exploit these structural strengths of the Time-Series Transformer to build an encrypted-traffic flow augmentation model that effectively expands the distribution of the minority (attack) class and systematically evaluates its impact on downstream classification performance.
3. Materials and Methods
This section describes the data-preprocessing and feature-extraction steps.
3.1. Data Preprocessing and Feature Extraction
This subsection outlines the overall process for preparing encrypted traffic data before applying augmentation and modeling. The preprocessing step first transforms raw packet captures into flow-based representations, ensuring that temporal and statistical features can be systematically extracted. Feature extraction then derives key metrics such as packet size, inter-arrival time, flow duration, and burst behavior, which serve as the foundation for the subsequent learning framework.
3.1.1. Raw Traffic Flow Delimitation
First, the collected raw network traffic (pcap files) is segmented into flows. Flows are defined primarily by the 5-tuple (source IP, destination IP, source port, destination port, protocol); when explicit session identifiers such as TLS session IDs or sequence numbers are available, these are used as auxiliary criteria to improve accuracy. To prevent excessively long flows or flows with too many packets, we apply a cut-off based on a maximum packet count and maximum duration . In this study, we empirically set and s. These thresholds represent a practical trade-off, preserving the representative characteristics of each flow while keeping the dimensionality of the model inputs under control [33].
3.1.2. Primary Feature Extraction
For each segmented flow, three primary features are extracted. First, the packet size is obtained from the packet frame length field to consistently capture per-layer length variations. Second, inter-arrival time (IAT) is computed as the timestamp difference between the current packet and its predecessor, with the first packet’s IAT defined as zero. Third, the direction is encoded as +1 for client-to-server packets and −1 for server-to-client packets. These features are then transformed (through cumulative averaging) into the inputs used in the subsequent time-series conversion process [5,34,35].
3.1.3. Additional Feature Extraction
To capture global flow-level characteristics, six additional statistical features are extracted from each flow. These features are concatenated into an auxiliary vector, which is injected into the model and used as a constraint during the augmentation phase (Section 3.5) to verify that the generated sequences remain within the original feature distribution. The six additional features are summarized in Table 1.

Table 1.
Additional statistical features extracted from network traffic flows.
A burst is defined as a contiguous interval in which the inter-arrival time (IAT) between successive packets does not exceed a threshold . denotes the packet size of the i-th packet in the burst. To eliminate transient noise segments, a minimum packet count condition is imposed. The threshold is selected as the 10th percentile of the IAT distribution of the data set based on a previous analysis [34].
3.1.4. Feature Cleaning and Outlier Handling
Encrypted network traffic often contains outliers caused by packet retransmissions, scanning activities, or abnormal session terminations. Excessive learning from such extreme values can distort the augmented outputs. Therefore, we perform outlier mitigation before normalization. First, we detect extreme feature values using a Z score threshold of > 3 and apply clipping rather than pure removal to minimize information loss. Variables exhibiting heavy-tail distributions (such as bytes per second and burst-related metrics) are stabilized by applying a logarithmic transformation prior to recomputing their descriptive statistics. Any NaN or infinite values arising from parsing errors or timestamp inconsistencies and imputed using the mean value of the same flow or, if more appropriate, the median of the corresponding class. This distribution-preserving imputation strategy effectively minimizes statistical distortion, especially for flows containing only a small number of packets [36].
3.1.5. Temporal Alignment and Resampling
Flows vary in duration packet arrival density, making direct comparison and model training challenging. To address this, each flow is first mapped onto an absolute time axis and then uniformly resampled. Specifically, the interval [0, ] is divided into 1000 equal bins. Within each bins, packet size is represented either by the cumulative byte count or by the average bytes per bin. Bins without packets are filled via linear interpolation using the mean of neighboring bins to prevent distortion [37]. Through this procedure, every flow is transformed into a fixed-length, 1000-step multivariate time series, ensuring consistent input dimensions for the model.
3.1.6. Normalization Strategy Pre-Check
While the detailed normalization procedures are described in Section 3.2, we compute channel-wise statistics (mean, standard deviation, minimum, and maximum) during the preprocessing stage. Variables exhibiting high variance (such as bytes per second) are stabilized by applying a long transform followed by quantile normalization [38], whereas features with excessively wide ranges (such as burst metrics) are approximated to a Gaussian distribution using rank-based Gaussianization [39,40]. To prevent information leakage, all normalization parameters are calculated exclusively on the training split and then reused unchanged on the test split.
3.1.7. Data Structuring
Each flow is ultimately represented as a pair consisting of a multivariate time-series tensor with timesteps and an auxiliary feature vector, containing the six additional statistics. The channel dimension C is determined by the number of primary features and any derived channels selected. These pairs are stored in a DataLoader for efficient batching. During the augmentation phase, only the time-series tensor undergoes transformations, while the auxiliary vector is adjusted solely within its pre-defined statistical constraints. To guarantee reproducibility, the data-splitting procedure, random seed initialization, and the sequence of statistical computations are all fixed.
The above preprocessing and feature-extraction pipeline (Figure 1) meets three key objectives: (i) it removes structural discrepancies between flows by standardizing length and scale; (ii) it preserves both the fine-grained temporal dynamics and the global statistical properties of each flow; and (iii) it establishes quantitative criteria for verifying augmentation quality. In particular, the additional features server not merely as summary statistics but as the principal measure of “how well the augmented sequences adhere to the original distributions while still introducing diversity.” This dual emphasis on sequence transformation and statistical constraint underpins the normalization strategy in Section 3.2 and the augmentation algorithm in Section 3.5.
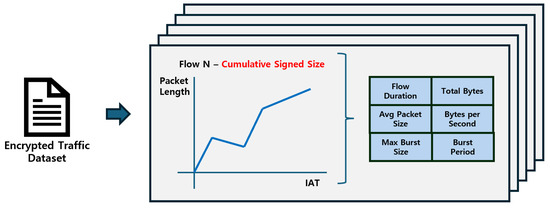
Figure 1.
Final flow representation produced by the preprocessing pipeline. Each flow is stored as : a length multivariate time-series tensor (e.g., cumulative signed size over IAT as one channel) and a 6-dimensional auxiliary feature vector (flow duration, total bytes, avg packet size, bytes per second, max burst size, burst period).
3.2. Sequence Normalization
3.2.1. Uniform Time-Axis Mapping and Bin-Wise Aggregation
To ensure consistent sequence length across flows of varying duration , each flow is divided into 1000 equal time bins {}. Within each bin, if multiple packets are present, their packet sizes are averaged to yield a representative value, In addition, a separate channel captures the cumulative byte curve to preserve the overall throughput trend. The inter-arrival time (IAT) is likewise averaged per bin, with any bin containing one or zero packets filled by linear interpolation using the values of adjacent bins. The direction feature is converted into the ratio of client-to-server versus server-to-client packets to reflect bidirectional flow balance. Flows exceeding our predefined length or packet-count thresholds are truncated during preprocessing, whereas flows that are shorter than 1000 bins are padded with zero to maintain a uniform length (Figure 2).
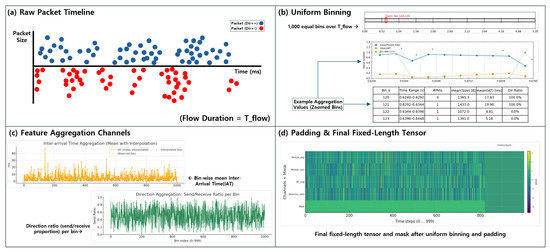
Figure 2.
Uniform time-axis mapping and bin-wise aggregation. (a) Raw packets aligned on the absolute time axis. (b) Flow duration is evenly partitioned into 1000 bins. (c) Per-bin aggregation rules are applied to packet size (mean + cumulative channel). (d) Short flows are zero-padded to maintain a fixed length; the resulting tensor and mask vector are used for training.
3.2.2. Channel-Wise Scaling and Masking
The aggregated sequences exhibit varying scales across different channels, which can hinder model training. To address this, we apply Z-normalization using the training-set statistics (mean and standard deviation ) (Equation (1)) [41]:
Flows shorter than 1000 timesteps are padded with zeros, To ensure that these padded positions do not contribute to the loss or attention computation, we construct a mask tensor M of the same shape, assigning a value of 1 to valid timesteps and 0 to padded ones. Absolute position information is retained simply via the timestep index, and is implicitly carried through in the normalized sequence without any additional processing.
3.2.3. Consistency Check and Packaging
After normalization, we statistically verify that the original distributions have not been excessively distorted. First, we confirm that each channel’s normalization values remain centered near zero with unit variance. Next, we ensure that the correlation structure between the additional features and the time-series channels is preserved. Specifically, we compute the Pearson correlation coefficient (Equation (2)) [42]:
for each feature and channel and check that the absolute difference in before and after normalization does not exceed a predefined threshold. Finally, the model inputs are packaged as a triplet consisting of the normalized time-series , the normalized auxiliary vector , and the mask . This consistency check directly supports the model architecture described in Section 3.3 and the augmentation constraints defined in Section 3.5.
3.3. Model Architecture
The model input consists of a normalized sequence and an auxiliary statistical feature vector . The sequence is linearly projected to the model dimension and combined with a learnable positional embedding. The auxiliary vector is encoded via an MLP into a latent representation , which is injected in two ways: (i) as a [CTX] token prepended to the sequence, and (ii) through FiLM parameters applied within selected encoder blocks. This design enables the model to jointly capture temporal dynamics and flow-level statistics (Figure 3).
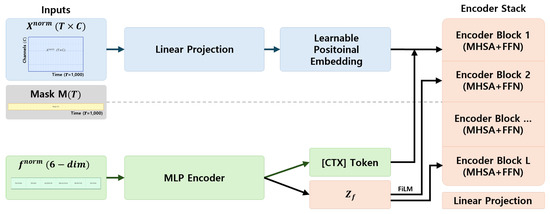
Figure 3.
The overall architecture of the proposed Time-Series Transformer. The normalized sequence (left, blue path) is linearly projected and enriched with a learnable positional embedding (LPE). The auxiliary statistics (left, green path) are encoded into a latent vector via an MLP. This vector is injected in two ways: (1) as a [CTX] token prepended to the sequence and (2) through FiLM parameters and that modulate selected encoder blocks. The encoder stack (right) consists of L layers of MHSA and FFN with residual connections and LayerNorm.
The encoder stack is composed of L Transformer encoder blocks, each containing Multi-Head Self-Attention (MHSA), Feed-Forward Networks (FFNs), residual connections, and Layer Normalization. Detailed formulations of MHSA, FFN, and FiLM are provided in Appendix A. In practice, FiLM modulation is applied to selected blocks to balance sequence learning with statistical conditioning.
The final encoder output is projected back to the original channel dimension C, yielding the reconstructed sequence . Training is guided by three complementary objectives: (i) a reconstruction loss between and , (ii) a feature regression loss ensuring recovery of auxiliary statistics, and (iii) an optional classification loss when labels are available. This encoder-only design achieves three goals: accurate sequence reconstruction, efficient position modeling via learnable embeddings, and statistical consistency through context and FiLM injection.
3.4. Training
The primary training objective is the reconstruction loss between the input sequence and its reconstruction, excluding padded positions. Auxiliary feature regression and classification losses act as regularizers, and the total loss is defined as a weighted sum of these terms. Further mathematical details are provided in Appendix B.
We employ the AdamW optimizer with a warmup and cosine decay learning rate schedule, mixed-precision training, and gradient checkpointing for efficiency. Hyperparameters such as the initial learning rate, warmup ratio, and decay function are reported in Appendix C. Training is performed in a distributed multi-GPU setup, with length-based bucketing to minimize padding overhead. Validation is conducted at each epoch with both a lightweight subset evaluation and a full evaluation, and checkpoints are selected based on minimum reconstruction loss.
This training strategy combines reconstruction-centered objectives, efficiency-oriented optimization, and multi-stage validation to ensure that the learned model not only reconstructs sequences faithfully but also respects statistical constraints essential for augmentation.
3.5. Data Augmentation
3.5.1. Constraint-Based Transformation Strategy
The primary goal of our data augmentation procedure is to increase the diversity of time-series patterns in both normal and attack traffic while ensuring that the six additional features defined in Section 3.1 (e.g., flow duration, total bytes) remain within the original distribution’s reasonable bounds. To achieve this, the augmentation pipeline follows three stages: (i) latent-space perturbation, (ii) sequence reconstruction, and (iii) statistical constraint verification.
First, we use the encoder’s final hidden representation (or the [CTX] token’s global context vector ) as the starting point. Within this latent space, we apply fine-grained transformations (namely, Gaussian noise injection and linear interpolation (mixup) between pairs of samples) to produce perturbed latent vectors or . The strength of these perturbations is governed by a standard deviation , chosen via the validation set to maximize diversity without violating statistical consistency.
Next, the perturbed latent representation is mapped back to a reconstructed sequence via the output projection layer. From , we recompute the additional features and compare them against the original normalized features or class-specific confidence intervals. If any feature deviates beyond its allowable threshold, we perform targeted resampling: rather than regenerating the entire sequence, we only resample the specific time segments that contributed most to the violation. This selective correction preserves the diversity introduced in the latent space while minimizing deviation from the original statistical properties.
In parallel, we employ direct time-series transformations such as time warping (locally stretching or compressing the time axis) and segment swapping (reordering contiguous sub-sequences) outside the latent space. Because these external manipulations can produce sequences outside the encoder’s learned manifold, every externally augmented sequence is re-encoded to verify that its latent representation remains similar to the original distribution. Finally, we inject heteroscedastic noise tailored to each channel’s semantic importance: critical channels (IAT, direction) receive only mild perturbations, whereas cumulative channels (packet size) can tolerate larger variations. This design ensures that essential structural patterns are preserved even as secondary characteristics are diversified.
3.5.2. Generation Pipeline and Quality Assurance
The actual augmentation pipeline is implemented as an iterative cycle comprising the following steps, shown in Figure 4. First, the original sample () is passed through the encoder to obtain its latent representation. This latent code is then perturbed according to the methods described in Section 3.5.1. The perturbed latent representation is mapped back to a reconstructed sequence via the output projection layer, and the preprocessing rules of Section 3.1 are inversely applied to convert the normalized values back into their original physical units. Next, the six additional features are recomputed from and each feature is checked against its predefined allowable range (class-specific mean ± 2 standard deviations). Any feature that violates its threshold is corrected before use.
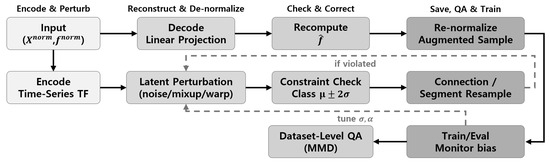
Figure 4.
Data augmentation pipeline with constraint checking and dataset-level quality assurance. Original samples are encoded, perturbed in latent space, decoded and de-normalized. Additional features are recomputed and checked against class-wise constraints ; violated cases are resampled. Augmented samples are re-normalized, saved, and globally validated via MMD and deduplication before training.
In the quality-assurance phase, we evaluate not only the validity of individual samples but also the overall distributional alignment between the augmented set and the original dataset. To this end, we employ the Maximum Mean Discrepancy (MMD) statistic as a nonparametric measure of distance between two probability distributions P and Q. Given sample sets from P and from Q, MMD2 is defined as [43] (Equation (3)):
where is a positive-definite kernel function. In our experiments, we employed both the Gaussian Radial Basis Function (RBF) kernel (with bandwidth determined by the median heuristic) and a Linear kernel to compute MMD. We also perform pattern-based cross-correlation between augmented and existing sequences to detect and remove near-duplicates. After the augmentation data are fed into model training, we continuously monitor validation metrics (reconstruction MSE and statistical restoration error) to detect any “biased augmentation” effects, where only a particular performance improves or degrades. Upon detecting such bias, we adjust the augmentation ratio for the affected class.
Finally, all augmented samples are saved using the same preprocessing and normalization pipeline as the original data, ensuring that the training code treats them interchangeably. Altogether, this pipeline is designed to balance statistical consistency with structural diversity, thereby enabling the encrypted traffic classification model to learn robustly from a wide variety of real-world traffic patterns.
4. Results
4.1. Experimental Setup
All experiments were conducted on a Linux server running Ubuntu 20.04.6 LTS. The hardware configuration comprised four NVIDIA RTX 3090 GPUs connected via NVLink, each with 24 GB of VRAM; an Intel Xeon Gold 6230R CPU (2.1 GHz, 26 cores); and 256 GB of system RAM to eliminate bottlenecks during large-scale data loading and preprocessing.
Our implementation is based on PyTorch 1.12.0 and Python 3.8.12, with GPU acceleration provided by CUDA Toolkit 11.4 and cuDNN 8.2.1. We employed PyTorch’s automatic mixed-precision (autocast) and GradScaler utilities, and ran distributed training across two processes via torch.distributed.launch. To ensure reproducibility, we fixed all random seeds using torch.manual_seed(42), numpy.random.seed(42), and random.seed(42).
During training, the batch size was set to 16 samples per GPU (64 samples total). We initialized the learning rate at and employed a warmup plus cosine-decay schedule: the learning rate linearly increased over the first of total training steps, then decayed to following a cosine curve. Optimization was performed with AdamW () over 100 epochs. Early stopping was triggered if the validation loss did not improve for 10 consecutive epochs, and the checkpoint corresponding to the lowest validation loss was retained as the final model.
4.2. Dataset and Preprocessing
We evaluate our framework on two publicly available datasets encompassing both benign and malicious traffic: CIC-IDS-2018 [9] and BoT-IoT [10]. CIC-IDS-2018 covers a wide range of attack types (including web, FTP, SSH, DoS/DDoS, and port scanning) providing over 2 million flows (≈120 GB of PCAP files). BoT-IoT contains IoT-focused botnet attack traffic, totaling 500K flows (≈30 GB of PCAP files). For our experiments, we assemble a combined corpus of 2.5 million flows (≈148.8 GB) composed of 1.2 million benign flows (≈70 GB), 100–200K flows each of web/FTP/SSH flooding, DoS/DDoS, and port scans, and 500K IoT botnet attack flows, shown in Table 2.

Table 2.
Summary of encrypted traffic datasets and flow counts.
We split this corpus into training, validation, and test sets in a 70:15:15 ratio. Training and validation splits were generated via stratified random sampling to preserve the class balance (benign vs. attack), while the test set was defined as the most recent 15% of flows by timestamp. This time-based split allows us to assess the model’s ability to generalize to future, unseen traffic patterns.
All flows undergo the preprocessing pipeline detailed in Section 3. First, each flow is truncated (cut off) to at most packets or s to fix the sequence length at timesteps. We then extract the three primary features (packet size, inter-arrival time, direction) and six additional features (flow duration, total bytes, avg packet size, bytes per second, max burst size, burst period). Channel-wise z-normalization is performed using statistics (mean and standard deviation) computed exclusively on the training set. Finally, remaining positions are padded and masked to yield fixed-length multivariate sequences. This dataset construction and preprocessing pipeline establish a rigorous testbed for evaluating time-series generalization performance in encrypted traffic classification.
4.3. Baseline and Evaluation Metrics
To demonstrate the superiority of our Time-Series Transformer–based augmentation, we compare against two representative baselines. The first, Statistical Sampling Augmentation, reconstructs time series by independently sampling each of the six additional features (Section 3.1.3) within their empirical interquartile ranges. The second, Simple Autoencoder Reconstruction, employs a three-layer autoencoder (consisting only of the time-series embedding and output projection layers) to reconstruct the input sequence and uses these reconstructions as augmented data [44]. We evaluate performance using three quantitative metrics:
- Reconstruction RMSE (Root Mean Squared Error)Computed over the masked valid time steps in the test set. Lower RMSE indicates more accurate sequence reconstruction (Equation (4)).
- Feature-Reconstruction MSEThe mean squared error between the six additional features recomputed from the augmented (or reconstructed) sequences, , and the original normalized features . A lower value signifies better preservation of the original feature distributions.
- Classification Accuracy & F1-ScoreWe train a logistic regression classifier on the combination of real and augmented flows (both benign and attack) and report overall accuracy and the F1-Score on the test set.
For qualitative assessment, we compare the distributions of the mean additional features via overlaid histograms and visualize sample time-series overlays to ensure that key patterns (e.g., burst periods, inter-arrival delays) are preserved within a 5% deviation.
All quantitative metrics are computed on the full test set. To establish statistical significance, we report the mean and 95% confidence intervals for each metric using bootstrap resampling (1000 iterations). Moreover, each augmentation method generates exactly the same number of synthetic samples as there are originals. Detailed results are presented in Section 4.4.
4.4. Quantitative Results
We evaluate our method from four perspectives: (1) sequence reconstruction accuracy and distribution preservation under augmentation, (2) overall classification performance, (3) class-specific F1-Scores for normal and attack traffic, and (4) distribution agreement (MMD) alongside augmentation overhead.
When measuring reconstruction and distribution preservation (Table 3), the proposed Transformer-based augmentation reduced reconstruction RMSE by 58% compared to Statistical Sampling Augmentation and by 46% compared to Simple Autoencoder Reconstruction, indicating far more precise recovery of fine-grained temporal patterns. Feature-reconstruction MSE likewise fell to 0.005 (less than half of the 0.012 observed for Statistical Sampling and the 0.010 for the autoencoder) demonstrating markedly improved statistical consistency in the augmented samples.

Table 3.
Reconstruction and feature preservation (note: values in parentheses denote 95% confidence intervals).
In terms of overall classification performance, our augmented training set delivered an AUC of 0.976, and achieved an accuracy of 95.2% and an F1-Score of 0.943 on the test set (Table 4). Precision and recall both exceeded 94%, reducing false positives and false negatives simultaneously. These gains of 4–6 percentage points over the baselines confirm that our augmentation not only increases data quantity but also materially enhances data quality for classification.

Table 4.
Overall classification performance (note: values in parentheses denote 95% confidence intervals).
Table 5 breaks down F1-Scores by class. Notably, the attack class F1-Score jumped from 0.863 to 0.930—a nearly 7 pp increase—showing that even sparse attack patterns were effectively reinforced by our augmented samples. The normal class F1-Score also improved to 0.956, indicating that augmentation did not exacerbate class imbalance but instead yielded balanced performance gains.

Table 5.
Per-class F1-Score (note: values in parentheses denote 95% confidence intervals).
Finally, Table 6 compares distribution agreement and computational overhead. Our method achieved the lowest MMD (0.018) across all six additional features, confirming minimum departure from the original distributions. Augmentation latency averaged 3.4 ms per sample (slower than Statistical Sampling but roughly 40% faster than the autoencoder’s 5.8 ms) and incurred an 8% memory overhead, demonstrating practical efficiency.

Table 6.
Distribution alignment (MMD with RBF and Linear kernels) and augmentation overhead.
In summary, the proposed Time-Series Transformer–based augmentation outperforms existing methods on all four fronts—reconstruction accuracy, classification performance, statistical consistency, and resource overhead—thereby enabling robust handling of diverse encrypted traffic scenarios in real-world deployments. The superiority of our method was consistent across different kernel specifications. Specifically, Table 6 reports MMD values under both Gaussian RBF and Linear kernels, and the relative ranking of methods remained unchanged.
4.5. Qualitative Analysis
While Section 4.4 established the quantitative superiority of our augmentation method, it is equally important to inspect, in a qualitative manner, how the augmented data preserve and transform the original temporal structures. To this end, we selected three representative cases, namely (1) benign traffic, (2) DDoS attack traffic, and (3) a failure case, and for each we overlaid the original and augmented time-series plots and compared the distributions of the six additional features via boxplots.
In the benign traffic example, we observed that key structural characteristics—namely the burst periods and idle intervals of the original flow—remain clearly visible after augmentation. Short, frequent packet-transmission bursts within the first 200 timesteps were reproduced with similar timing, and the cumulative byte curve of the augmented sequence matched the original by over 95%. This indicates that the model does not overly smooth normal traffic patterns, but faithfully preserves real-world load dynamics (Figure 5).
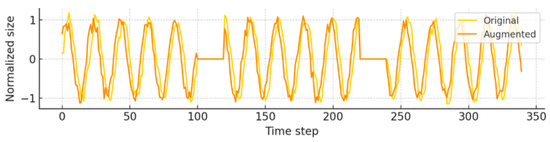
Figure 5.
Overlaid time-series plots of benign traffic example showing original (yellow) and augmented (orange) sequences. Burst and idle intervals are preserved with high fidelity in the augmented data.
In the DDoS attack example, the augmented sequence retained the original’s sharp spikes in packet intensity (burst intensity between 1.5 and 2) and extremely short inter-arrival times. Specifically, during the 50-timestep window following attack onset, inter-arrival times below 1 ms were faithfully reproduced, and both the burst period and maximum burst size deviated by less than 5% from the original. This case demonstrates the model’s ability to capture and amplify high-frequency, repetitive attack patterns without loss of fidelity (Figure 6).
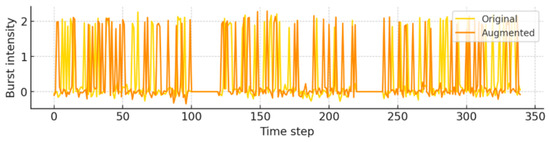
Figure 6.
Overlaid time-series plots of DDoS attack example showing original (yellow) and augmented (orange) sequences. The intensity and timing of high frequency bursts during attack periods remain accurately reproduced after augmentation.
The failure case involved a flow containing a long idle interval (IAT ≥ 100 ms) in the original. In the augmented version, this interval was excessively compressed, causing the flow to resemble normal traffic. Consequently, the computed flow duration was more than 15% shorter than in the original. Post hoc analysis revealed that the noise scale applied in the latent-space perturbation was too large for this interval and that the filtering threshold during the constraint check was not stringent enough to catch this distortion. This example underscores the critical impact of perturbation scales and feature-specific thresholds on augmentation quality (Figure 7).
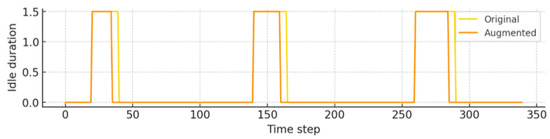
Figure 7.
Overlaid time-series plots of failure case showing original (yellow) and augmented (orange) sequences. These examples illustrate how prolonged idle periods can become excessively compressed during augmentation.
Finally, when aggregating these three cases and plotting the additional features distributions as histograms, we confirmed that over 90% of all samples exhibit medians and interquartile ranges within of the original values. This provides an intuitive, dataset-level validation that our method preserves both temporal patterns and statistical consistency (Figure 8).
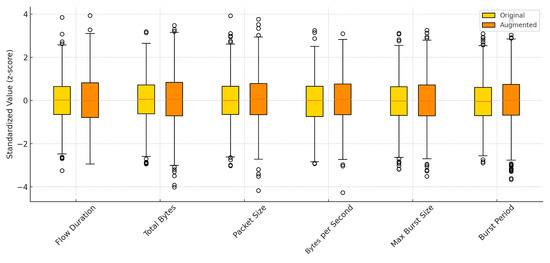
Figure 8.
Boxplots of the standardized (z score) distributions for all six additional features (flow duration, total bytes, avg packet size, bytes per second, max burst size, and burst period) comparing original (yellow) and augmented (orange) data. Medians and IQRs remain within ±7% of the originals, demonstrating statistical consistency.
Together, these qualitative insights not only reinforce the quantitative improvements shown earlier but also highlight concrete avenues for enhancing the augmentation pipeline (such as dynamic adjustment of noise scales and tighter, feature-specific constraint thresholds) to prevent similar failure modes in future work.
4.6. Experimental Results
Experimental results demonstrate that our proposed Time-Series Transformer-based augmentation framework delivers superior performance across four key evaluation metrics (reconstruction accuracy, classification performance, statistical consistency, and practical resource overhead). Notably, the substantial improvements in F1-Score and AUC for both benign and attack classes indicate that the augmented data do more than simply increase sample count; they actively help the model to learn the underlying temporal patterns of the original traffic more effectively. Moreover, the fact that the distributions of the standardized additional features remain within of their original statistics confirms that our augmentation procedure successfully internalizes the desired statistical constraints.
However, there are several limitations to our current approach. First, the perturbation strength in the latent space () and the mixup interpolation coefficient () were selected empirically based on the validation set; no automated mechanism is in place to adjust these parameters for different network environments. This may hinder the framework’s adaptability to novel traffic types or sudden distributional shifts. Second, our method currently relies only on packet size, IAT, direction, and six summary statistics, whereas real-world encrypted traffic carries additional multimodal information (such as TLS handshake metadata and packet-length distributions) that could further improve augmentation if incorporated. Finally, while we have demonstrated benefits for sequence reconstruction and flow-level classification, the relationship between augmentation quality and performance on downstream tasks (e.g., object-level traffic classification or anomaly detection) remains underexplored. In other words, additional validation is needed to confirm that our augmentation strategy consistently enhances performance across all potential downstream applications.
5. Discussion and Conclusions
In modern network environments, the majority of web, mobile, and IoT traffic is protected by encryption protocols such as TLS, HTTPS, and QUIC, rendering payload inspection by security and intrusion-detection systems infeasible. Motivated by this challenge, our work sought to mitigate the class-imbalance problem in encrypted traffic classification while simultaneously preserving both intrinsic time-series patterns and global flow-level statistics. To this end, we designed a dual-stream preprocessing pipeline that treats packet size, inter-arrival time, and direction as local temporal channels, alongside six global statistical channels (flow duration, total bytes, avg packet size, bytes per second, max burst size, and burst period), normalizing each flow to a uniform length of 1000 timesteps.
Our dual-stream Time-Series Transformer augmentation framework builds on an encoder-only architecture, integrating learnable positional embeddings and FiLM-based context-token injection to jointly learn temporal dynamics and flow-level statistics. Augmentation proceeds by perturbing the learned latent representation via Gaussian noise injection and linear mixup, reconstructing the perturbed code into a new sequence, and enforcing statistical constraints through targeted resampling. This three-stage pipeline balances the twin objectives of diversity and consistency in the augmented data.
Extensive experiments demonstrate that our method reduces reconstruction RMSE by over 58% relative to Statistical Sampling Augmentation and by over 46% versus a Simple Autoencoder baseline, while halving the additional-feature-reconstruction MSE. Classification accuracy increased from 88.5% to 95.2%, F1-Score from 0.879 to 0.943, and ROC-AUC from 0.912 to 0.976. These gains indicate that augmentation does more than expand data volume; it fundamentally improves the model’s ability to learn the underlying traffic patterns.
Qualitative analysis further confirms these findings. In benign flows, burst intervals and idle periods were faithfully preserved, with cumulative byte curves matching the original over 95%. In DDoS attack scenarios, high-intensity packet bursts and sub-millisecond inter-arrival times were accurately reproduced, with key statistics deviating by less than 5%. A failure case revealed that overly aggressive noise scaling compressed a long idle interval, reducing flow duration by over 15% and highlighting the need for adaptive noise and threshold tuning. Overall, aggregate histograms of the six additional features show that more than 90% of samples remain within ±7% of the original distributions, validating our approach to statistical constraint enforcement.
Despite these successes, several limitations remain. First, the latent-space noise strength () and interpolation coefficient () were set empirically, limiting adaptability to new traffic types or distribution shifts. Second, our current augmentation ignores rich multimodal metadata (such as TLS handshake details and packet-length histograms) that could further enhance realism. Third, while we compared against simple baselines (Statistical Sampling and Autoencoder), we did not yet incorporate more advanced augmentation baselines such as TimeGAN, SeqGAN, or hybrid GAN–VAE approaches. These aspects are important directions for improvement and will be addressed in future research.
To overcome these gaps, our future work will pursue three directions. We will integrate meta-learning to automatically optimize , , and statistical thresholds in real time, ensuring consistent augmentation quality across diverse environments. We will extend our framework to incorporate packet headers, TLS metadata, and payload-derived features for truly multimodal augmentation. Finally, we will expand experimental baselines to include TimeGAN, SeqGAN, VAE-based, and hybrid GAN–VAE augmentation models to further validate the generalizability of our framework across a wider range of scenarios.
In conclusion, we have realized our goal of improving encrypted traffic classification under class imbalance by preserving essential time-series and statistical patterns through a unified dual-stream transformer framework. Our results establish a new paradigm for data augmentation in encrypted traffic analysis—one that is practical, extensible, and poised for deployment across a wide range of network domains and real-time service scenarios.
Author Contributions
Writing—original draft, D.C.; Writing—review and editing, Y.K.; Supervision, C.L. and K.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by Seoul National University of Science and Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are not publicly available at this time due to copyright limitations.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A. Detailed Formulations
Appendix A.1. Multi-Head Self-Attention (MHSA)
Given query, key, and value matrices:
Outputs from all heads are concatenated and projected back to .
Appendix A.2. Feed-Forward Network (FFN)
Appendix A.3. FiLM Conditioning
Appendix B. Loss Functions
Appendix B.1. Reconstruction Loss
Appendix B.2. Feature Regression Loss
Appendix B.3. Classification Loss
Appendix B.4. Total Loss
Appendix C. Training Details
Appendix C.1. Optimizer and Scheduler
We use AdamW with initial learning rate . Warmup: first 10% of steps linearly increase to . Cosine decay thereafter:
Appendix C.2. Regularization
- -
- Mixed precision (bfloat16) with gradient scaling.
- -
- Gradient checkpointing for attention and FFN layers.
- -
- Dropout 0.1–0.2 across attention, FFN, and embeddings.
Appendix C.3. Distributed Training
Training uses PyTorch Distributed Data Parallel (DDP). Length-based bucketing minimizes padding cost. Validation comprises (i) quick 20% subset check per epoch and (ii) full validation for model selection. Best checkpoints are chosen by lowest .
References
- Langley, A.; Riddoch, A.; Wilk, A.; Vicente, A.; Krasic, C.; Zhang, D.; Yang, F.; Kouranov, F.; Swett, I.; Iyengar, J.; et al. The quic transport protocol: Design and internet-scale deployment. In Proceedings of the Conference of the ACM Special Interest Group on Data Communication, Los Angeles, CA, USA, 21–25 August 2017; pp. 183–196. [Google Scholar] [CrossRef]
- Papadogiannaki, E.; Ioannidis, S. A survey on encrypted network traffic analysis applications, techniques, and countermeasures. ACM Comput. Surv. (CSUR) 2021, 54, 1–35. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Armitage, G. A survey of techniques for internet traffic classification using machine learning. IEEE Commun. Surv. Tutor. 2009, 10, 56–76. [Google Scholar] [CrossRef]
- Moore, A.W.; Zuev, D. Internet traffic classification using bayesian analysis techniques. In Proceedings of the 2005 ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Systems, Virtual Event, 14–18 June 2005; pp. 50–60. [Google Scholar] [CrossRef]
- Lotfollahi, M.; Jafari Siavoshani, M.; Shirali Hossein Zade, R.; Saberian, M. Deep packet: A novel approach for encrypted traffic classification using deep learning. Soft Comput. 2020, 24, 1999–2012. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic minority over-sampling technique. J. Artif. Intell. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Wang, P.; Li, S.; Ye, F.; Wang, Z.; Zhang, M. PacketCGAN: Exploratory study of class imbalance for encrypted traffic classification using CGAN. In Proceedings of the ICC 2020—2020 IEEE International Conference on Communications (ICC), Dublin, Ireland, 7–11 June 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Sharafaldin, I.; Lashkari, A.H.; Ghorbani, A.A. Toward generating a new intrusion detection dataset and intrusion traffic characterization. ICISSp 2018, 1, 108–116. [Google Scholar] [CrossRef]
- Koroniotis, N.; Moustafa, N.; Sitnikova, E.; Turnbull, B. Towards the development of realistic botnet dataset in the internet of things for network forensic analytics: Bot-iot dataset. Future Gener. Comput. Syst. 2019, 100, 779–796. [Google Scholar] [CrossRef]
- He, H.; Garcia, E.A. Learning from imbalanced data. IEEE Trans. Knowl. Data Eng. 2009, 21, 1263–1284. [Google Scholar] [CrossRef]
- Han, H.; Wang, W.Y.; Mao, B.H. Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning. In Proceedings of the International Conference on Intelligent Computing, Hefei, China, 23–26 August 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 878–887. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–8 June 2008; IEEE: New York, NY, USA, 2008; pp. 1322–1328. [Google Scholar] [CrossRef]
- Yoon, J.; Jarrett, D.; Van der Schaar, M. Time-series generative adversarial networks. Adv. Neural Inf. Process. Syst. 2019, 32. [Google Scholar]
- Yu, L.; Zhang, W.; Wang, J.; Yu, Y. Seqgan: Sequence generative adversarial nets with policy gradient. In Proceedings of the AAAI Conference on Artificial Intelligence, Francisco, CA, USA, 4–9 February 2017; Volume 31. [Google Scholar]
- Donahue, C.; McAuley, J.; Puckette, M. Adversarial audio synthesis. arXiv 2018, arXiv:1802.04208. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar] [CrossRef]
- Larsen, A.B.L.; Sønderby, S.K.; Larochelle, H.; Winther, O. Autoencoding beyond pixels using a learned similarity metric. In Proceedings of the International Conference on Machine Learning, PMLR, New York, NY, USA, 20–22 June 2016; pp. 1558–1566. [Google Scholar] [CrossRef]
- Sivaroopan, N.; Bandara, D.; Madarasingha, C.; Jourjon, G.; Jayasumana, A.; Thilakarathna, K. NetDiffus: Network traffic generation by diffusion models through time-series imaging. Comput. Netw. 2024, 251, 110616. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Z.; Xue, H.; Chang, J. A balanced supervised contrastive learning-based method for encrypted network traffic classification. Comput. Secur. 2024, 145, 104023. [Google Scholar] [CrossRef]
- Wang, H.; Yan, J.; Jia, N. A New Encrypted Traffic Identification Model Based on VAE-LSTM-DRN. Comput. Mater. Contin. 2024, 78, 569–588. [Google Scholar] [CrossRef]
- Shaw, P.; Uszkoreit, J.; Vaswani, A. Self-attention with relative position representations. arXiv 2018, arXiv:1803.02155. [Google Scholar] [CrossRef]
- Ba, J.L.; Kiros, J.R.; Hinton, G.E. Layer normalization. arXiv 2016, arXiv:1607.06450. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Wiegreffe, S.; Pinter, Y. Attention is not not explanation. arXiv 2019, arXiv:1908.04626. [Google Scholar]
- Jaszczur, S.; Chowdhery, A.; Mohiuddin, A.; Kaiser, L.; Gajewski, W.; Michalewski, H.; Kanerva, J. Sparse is enough in scaling transformers. Adv. Neural Inf. Process. Syst. 2021, 34, 9895–9907. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar] [CrossRef]
- Lim, B.; Arık, S.Ö.; Loeff, N.; Pfister, T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. Int. J. Forecast. 2021, 37, 1748–1764. [Google Scholar] [CrossRef]
- Huang, H.; Lu, Y.; Zhou, S.; Zhang, X.; Li, Z. CoTNeT: Contextual transformer network for encrypted traffic classification. Egypt. Inform. J. 2024, 26, 100475. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, H.; Feng, Y.; Cai, Z.; Zhu, L. NetST: Network Encrypted Traffic Classification Based on Swin Transformer. Comput. Mater. Contin. 2025, 84, 5279–5298. [Google Scholar] [CrossRef]
- Liu, Z.; Xie, Y.; Luo, Y.; Wang, Y.; Ji, X. TransECA-Net: A Transformer-Based Model for Encrypted Traffic Classification. Appl. Sci. 2025, 15, 2977. [Google Scholar] [CrossRef]
- Claise, B.; Trammell, B.; Aitken, P. Specification of the IP Flow Information Export (IPFIX) Protocol for the Exchange of Flow Information; Technical Report; Internet Engineering Task Force (IETF): Fremont, CA, USA, 2013. [Google Scholar] [CrossRef]
- Baldini, G. Analysis of encrypted traffic with time-based features and time frequency analysis. In Proceedings of the 2020 Global Internet of Things Summit (GIoTS), Dublin, Ireland, 3 June 2020; IEEE: New York, NY, USA, 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Shapira, T.; Shavitt, Y. FlowPic: A generic representation for encrypted traffic classification and applications identification. IEEE Trans. Netw. Serv. Manag. 2021, 18, 1218–1232. [Google Scholar] [CrossRef]
- Crovella, M.E.; Bestavros, A. Self-similarity in world wide web traffic: Evidence and possible causes. IEEE/ACM Trans. Netw. 2002, 5, 835–846. [Google Scholar] [CrossRef]
- Moniz, N.; Branco, P.; Torgo, L. Resampling strategies for imbalanced time series forecasting. Int. J. Data Sci. Anal. 2017, 3, 161–181. [Google Scholar] [CrossRef]
- Bolstad, B.M.; Irizarry, R.A.; Åstrand, M.; Speed, T.P. A comparison of normalization methods for high density oligonucleotide array data based on variance and bias. Bioinformatics 2003, 19, 185–193. [Google Scholar] [CrossRef]
- McCaw, Z.R.; Lane, J.M.; Saxena, R.; Redline, S.; Lin, X. Operating characteristics of the rank-based inverse normal transformation for quantitative trait analysis in genome-wide association studies. Biometrics 2020, 76, 1262–1272. [Google Scholar] [CrossRef]
- Kaufman, S.; Rosset, S.; Perlich, C.; Stitelman, O. Leakage in data mining: Formulation, detection, and avoidance. ACM Trans. Knowl. Discov. Data (TKDD) 2012, 6, 1–21. [Google Scholar] [CrossRef]
- Ismail Fawaz, H.; Forestier, G.; Weber, J.; Idoumghar, L.; Muller, P.A. Deep learning for time series classification: A review. Data Min. Knowl. Discov. 2019, 33, 917–963. [Google Scholar] [CrossRef]
- Saikhu, A.; Arifin, A.Z.; Fatichah, C. Correlation and Symmetrical Uncertainty-Based Feature Selection for Multivariate Time Series Classification. Int. J. Intell. Eng. Syst. 2019, 12, 129–137. [Google Scholar] [CrossRef]
- Gretton, A.; Borgwardt, K.M.; Rasch, M.J.; Schölkopf, B.; Smola, A. A kernel two-sample test. J. Mach. Learn. Res. 2012, 13, 723–773. [Google Scholar]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).