Secure and Scalable File Encryption for Cloud Systems via Distributed Integration of Quantum and Classical Cryptography
Abstract
1. Introduction
- We design a scalable encryption scheme for large-scale file protection, which enhances key security by integrating Kyber-based post-quantum key encapsulation with BB84-based quantum key distribution.
- We design and implement an offset-aware partitioning distributed encryption framework that performs subset-level AES encryption in parallel across multiple slave nodes, while decoupling key generation and transmission through centralized master node coordination.
- We demonstrate that our scheme achieves up to 8.11× faster encryption performance compared to conventional AES, while maintaining stable CPU utilization under real-world workloads.
2. Background
2.1. Post-Quantum Cryptography
2.2. Quantum Key Distribution
2.3. Challenges in Large-Scale File Encryption
3. Design
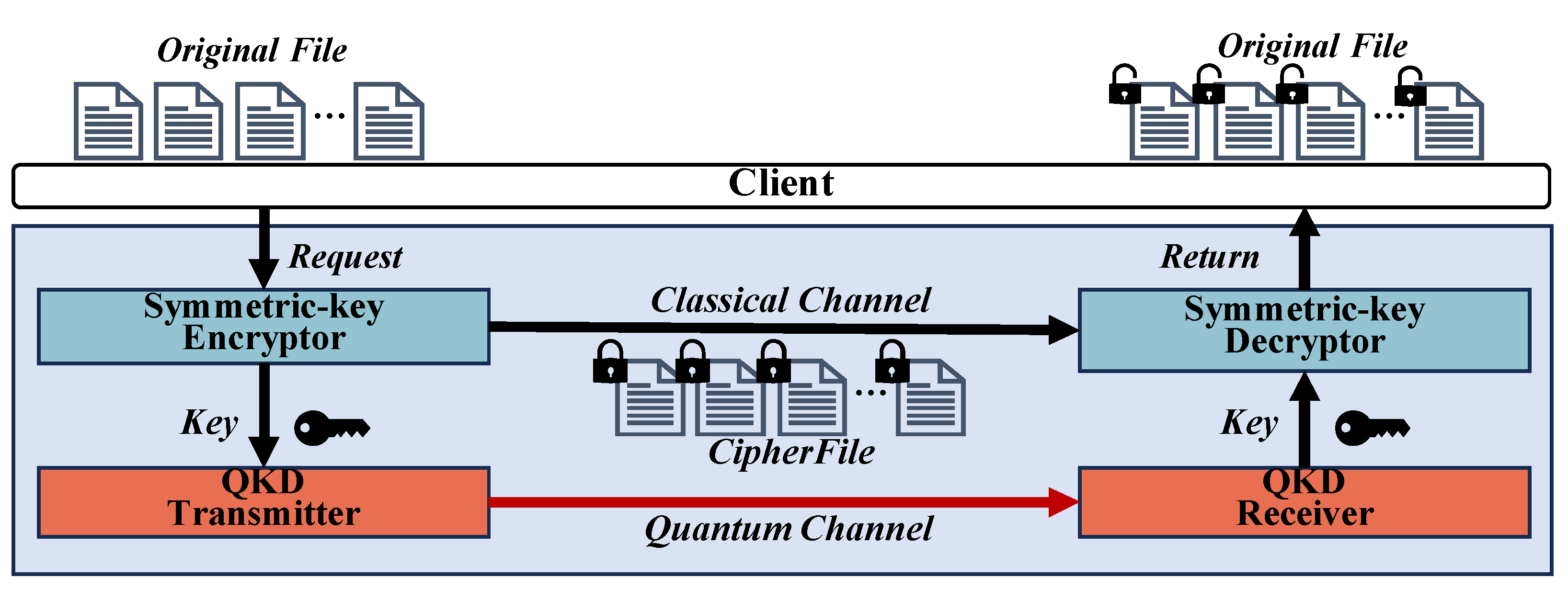
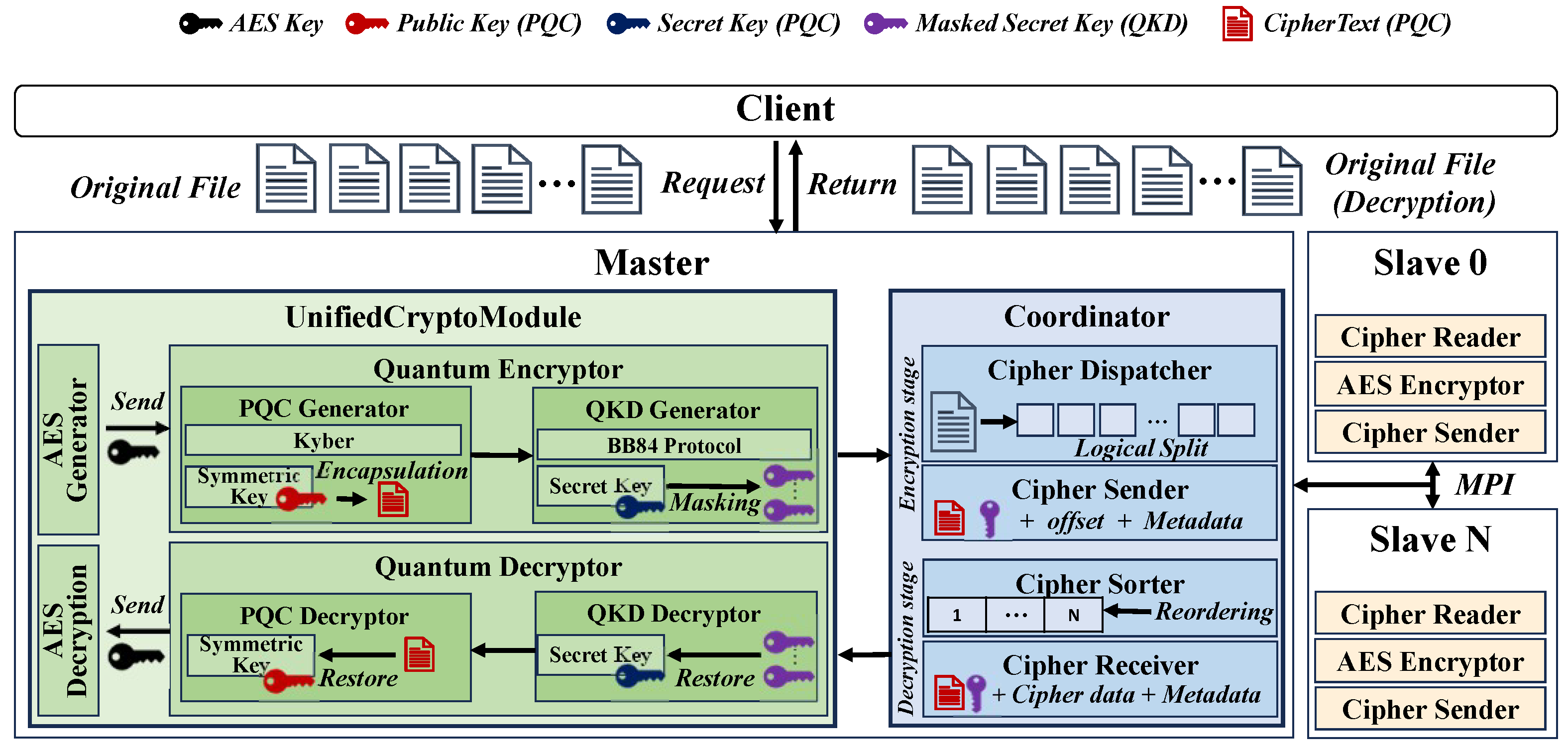
3.1. Overall Architecture
- Security model and threat assumptions: We assume a semi-honest threat model where the master node is trusted to perform key generation and distribution. Our threat model specifically considers an adversary equipped with a quantum computer, capable of breaking classical public-key algorithms such as RSA and ECC. This threat is critical because these algorithms are traditionally used to exchange symmetric keys (e.g., for AES), which could compromise the entire encryption workflow. To address this, our proposed scheme is designed to be resilient against such quantum attacks on the key-exchange mechanism through a layered integration of Kyber-based PQC for key encapsulation and QKD for protecting key transmission.
- Master: The master is responsible for secure key generation, offset partitioning and assignment, and coordination of encryption and decryption across all slaves.
- Slave: Each slave performs streaming encryption of its assigned file into the offset range and asynchronously returns encrypted subsets to the master. Each slave consists of the following components: Cipher Reader, AES Encryptor, and Cipher Sender.
3.2. Layered Key Initialization and Data Partitioning
3.3. Parallel File Encryption in Distributed Architecture
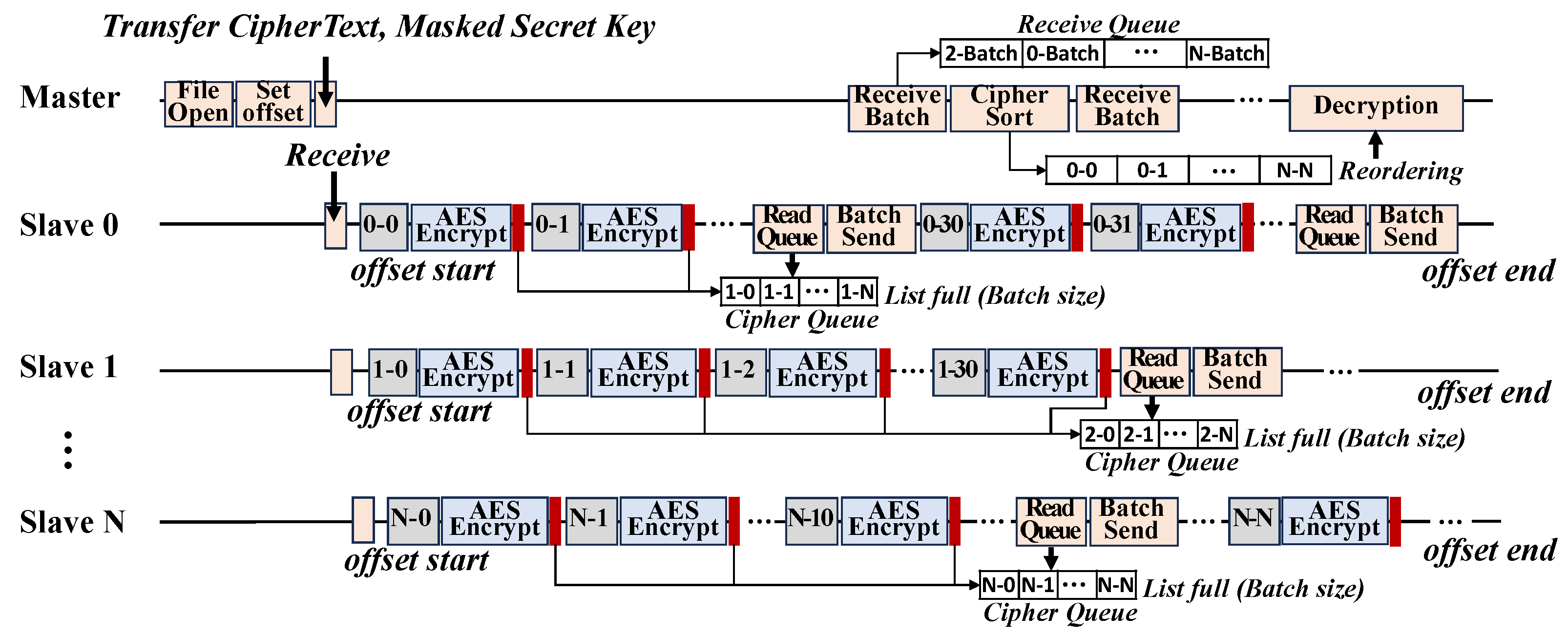
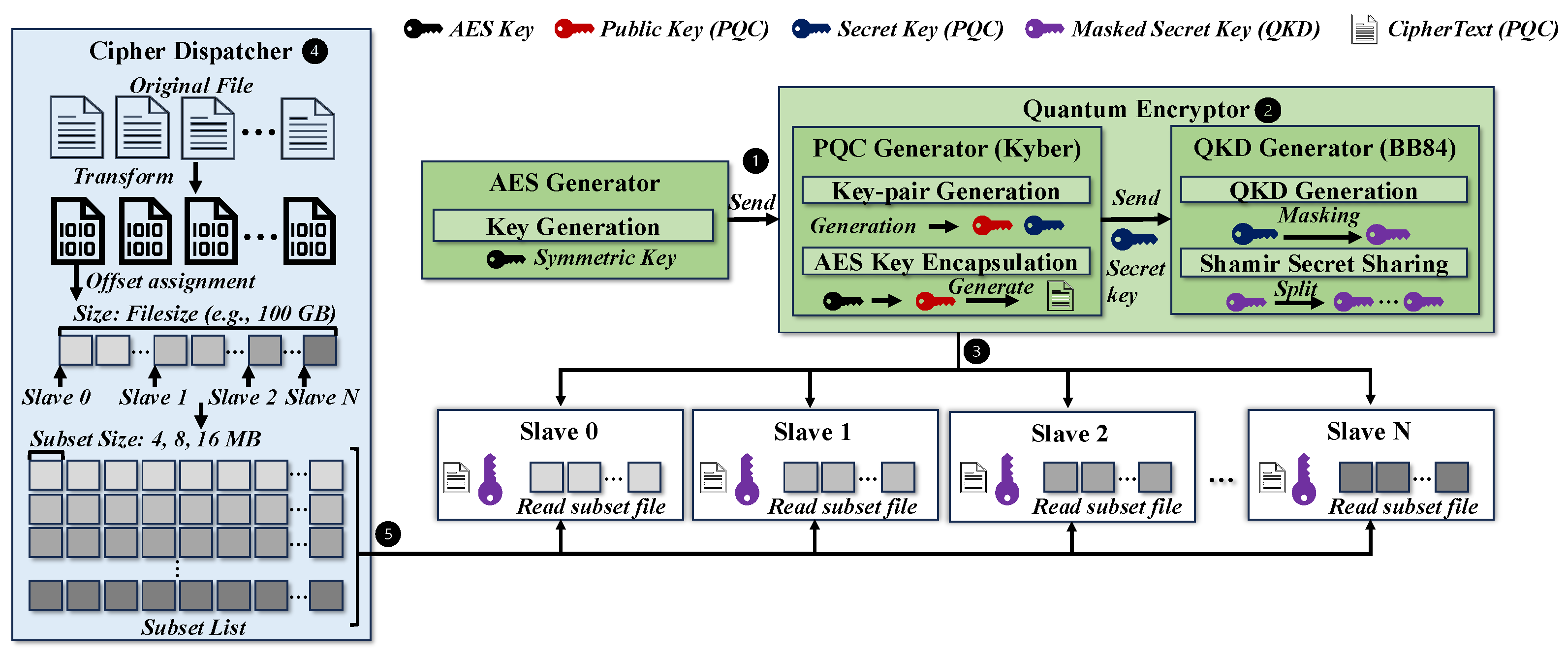
- Procedure: Figure 4 describes how our proposed scheme performs parallel file encryption across distributed slaves. After key transmission, the master calculates the start offset for each slave based on the total file size and the number of participating slaves. Each slave uses this offset information to perform file encryption independently.Figure 4. The procedure of offset-based parallel processing and transmission in distributed AES encryption.Figure 4. The procedure of offset-based parallel processing and transmission in distributed AES encryption.
- Execution model: Algorithm 1 shows the overlapped execution model used by each slave node for AES encryption and subset transmission. Our proposed scheme separates file reading and subset sending into two concurrent paths, enabling encryption and communication to proceed in parallel. This design maximizes I/O throughput by minimizing idle time between subset production and transmission, and supports scalable performance even as the number of nodes or data size increases.
| Algorithm 1 Overlapped AES encryption and subset transfer in slave node. |
|
3.4. Implementation
- Layered Key Initialization: We used the Kyber512 algorithm from the Open Quantum Safe (OQS) library [78] to generate a PQC key pair. The AES key is encapsulated using the PQC public key. The PQC secret key is XOR-masked using a QKD session key simulated with Qiskit Aer [62], and optionally split via Shamir’s secret sharing for fault-tolerant recovery.
- Parallel and Overlapped Subset Encryption: Each slave node performs AES encryption and transmission in parallel by overlapping file reading, encryption, and communication. Encrypted subsets are streamed to the master using non-blocking MPI operations, allowing continuous processing without idle time. This structure improves resource utilization and enables high-throughput distributed encryption.
- Centralized Decryption Pipeline: The master node receives encrypted subsets, reorders them based on subset indices, and reconstructs the AES key by decapsulating the PQC ciphertext and unmasking the PQC secret key. Subsets are decrypted in parallel using a thread pool and merged to restore the original file.
4. Evaluation
4.1. Experimental Setup
4.2. Throughput
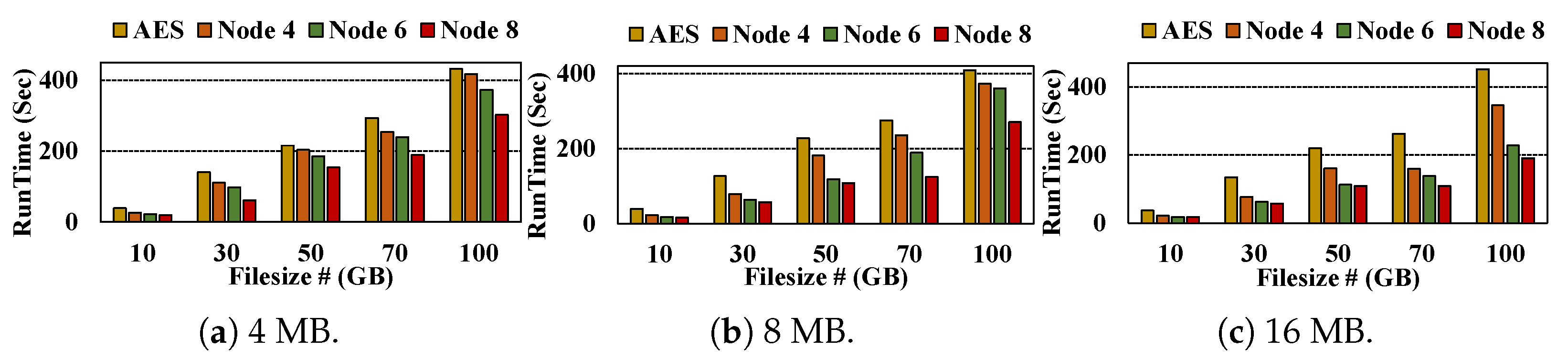
- End-to-End: Figure 5 shows the end-to-end runtime performance of our proposed scheme compared to AES (Original) across different subset sizes (e.g., 4 MB, 8 MB, and 16 MB). The x-axis represents the input file size ranging from 10 GB to 100 GB, and the y-axis represents the total runtime in seconds. The legend distinguishes AES (baseline, single-node execution) and our proposed scheme evaluated on 4, 6, and 8 nodes (e.g., one master and multiple slaves), respectively. The end-to-end runtime for AES includes file read, encryption, decryption, and output generation on a single node. In contrast, our proposed scheme includes file read, quantum-resilient security, which includes PQC-based AES key encapsulation and QKD-based session key masking, parallel AES encryption, inter-node communication, decryption at the master, and the generation of the final output file.Figure 5. End-to-End Performance comparison between AES (Original) and Proposed (PQC + QKD + AES) across multi-node.Figure 5. End-to-End Performance comparison between AES (Original) and Proposed (PQC + QKD + AES) across multi-node.
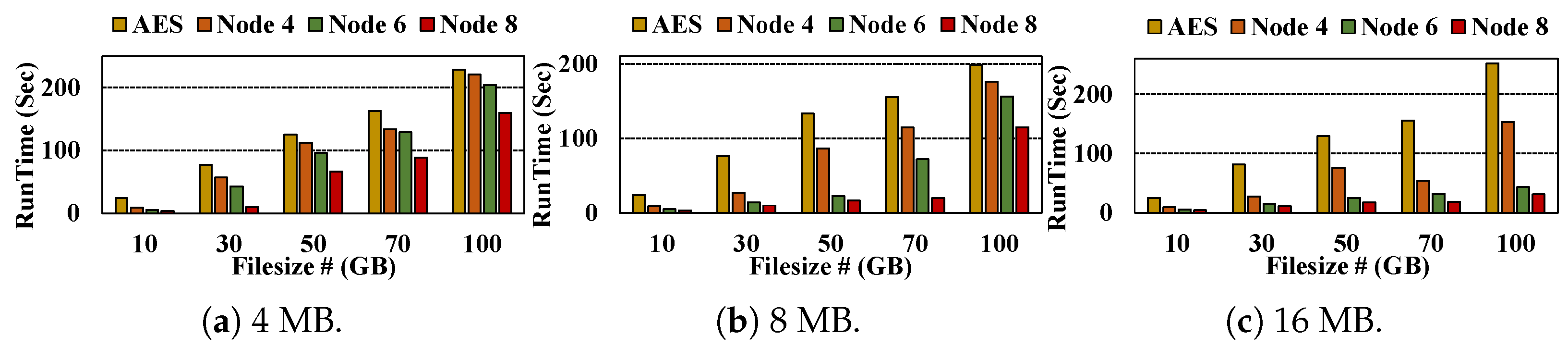
- Encryption: Figure 6 shows the encryption-only runtime performance of our proposed scheme compared to AES (Original) across various subset sizes (e.g., 4, 8, and 16 MB). As shown in the figure, the encryption stage exhibits linear scalability as the number of nodes increases, enabled by offset-aware partitioning that assigns disjoint byte ranges to each slave, allowing AES encryption to proceed independently without inter-node synchronization and centralized bottlenecks. For 70 GB file, encryption is faster as more nodes are used. With 4 MB sizes, the encryption runtime is reduced from 163.34 s (AES) to 133.83, 128.83, and 88.61 s on 4, 6, and 8 nodes, respectively, achieving 1.26× to 1.84× speedups. With 8 MB, it is reduced from 155.16 (AES) to 114.67, 72.09, and 20.09 s, showing improvements of 1.35× to 7.72×. The most significant gain is observed with 16 MB, where the encryption runtime decreases from 155.92 (AES) to 54.25, 31.41, and 17.98 s, yielding 2.87× to 8.67× speedups depending on the number of nodes. A similar trend is observed for the 100 GB file. With 4 MB, runtime is reduced from 228.86 s (AES) to 220.67, 204.36, and 159.74 s on 4, 6, and 8 nodes, resulting in 1.04× to 1.43× speedups. With 8 MB, it is reduced from 198.73 (AES) to 176.16, 156.10, and 114.99 s, showing 1.13× to 1.73× improvements. For 16 MB, the runtime decreases from 252.62 (AES) to 153.41, 43.34, and 31.17 s, achieving 1.65× to 8.11× speedups.Figure 6. Encryption Performance comparison between AES (Original) and Proposed (PQC + QKD + AES) across multi-node.Figure 6. Encryption Performance comparison between AES (Original) and Proposed (PQC + QKD + AES) across multi-node.
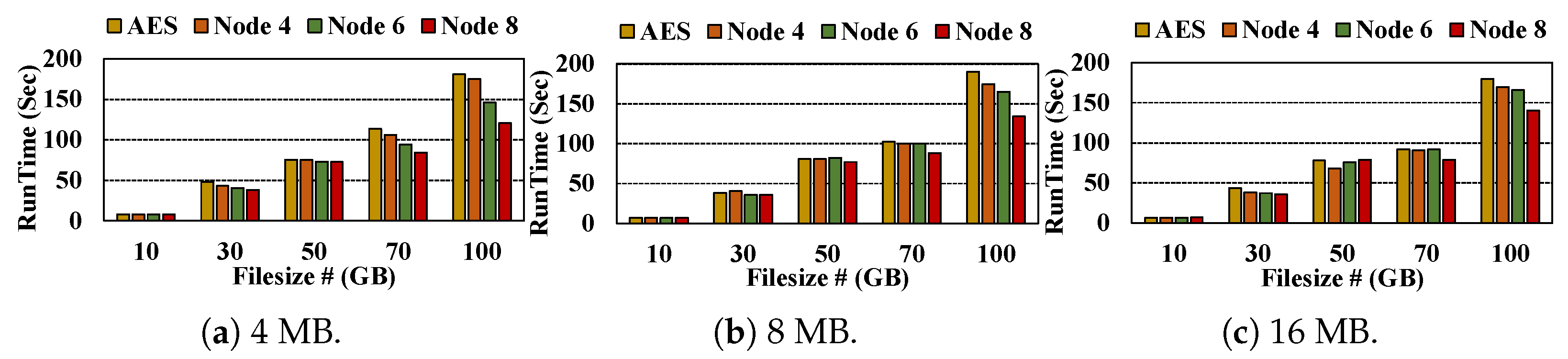
- Decryption: Figure 7 shows the decryption runtime performance of our proposed scheme compared to AES (Original), evaluated with 100 GB input across different subset sizes (e.g., 4, 8, and 16 MB). As decryption is centrally performed at the master node, the decryption runtime is primarily bounded by the master’s local execution, regardless of the number of slave nodes. With 4 MB, AES (Original) requires 180.71 s, while our scheme achieves 174.90, 146.11, and 120.58 s on 4, 6, and 8 nodes, respectively, yielding up to a 1.50× speedup. For 8 MB, the runtime is reduced from 189.93 AES (Original) to 174.50, 164.58, and 134.17 s, achieving up to a 1.41× improvement. With 16 MB, decryption time decreases from 179.52 AES (Original) to 169.65, 165.59, and 139.92 s, resulting in a maximum speedup of 1.28×. Although both the AES (Original) and our proposed scheme perform centralized, thread-based decryption, our scheme shows improved or comparable performance for large files. This is primarily due to structural overlap between communication, memory preparation, and computation. While the master node receives encrypted subsets over the network, it concurrently prepares in-memory buffers and sorts incoming data, allowing decryption to start immediately after reordering. This overlap reduces idle time and enables more efficient use of computational resources. In contrast, AES (Original) performs decryption directly on data loaded from disk, which introduces I/O latency that becomes more pronounced with larger file sizes, such as 70 and 100 GB. In addition, our proposed scheme adopts a streaming-based and offset-aware design to prevent memory exhaustion during decryption. Each decrypted subset is immediately written to the recovered file at the corresponding offset, without aggregating all data in memory. our design maintains stable and efficient memory usage regardless of dataset size and supports large-scale data processing.Figure 7. Decryption Performance comparison between AES (Original) and Proposed (PQC + QKD + AES) across multi-node.Figure 7. Decryption Performance comparison between AES (Original) and Proposed (PQC + QKD + AES) across multi-node.
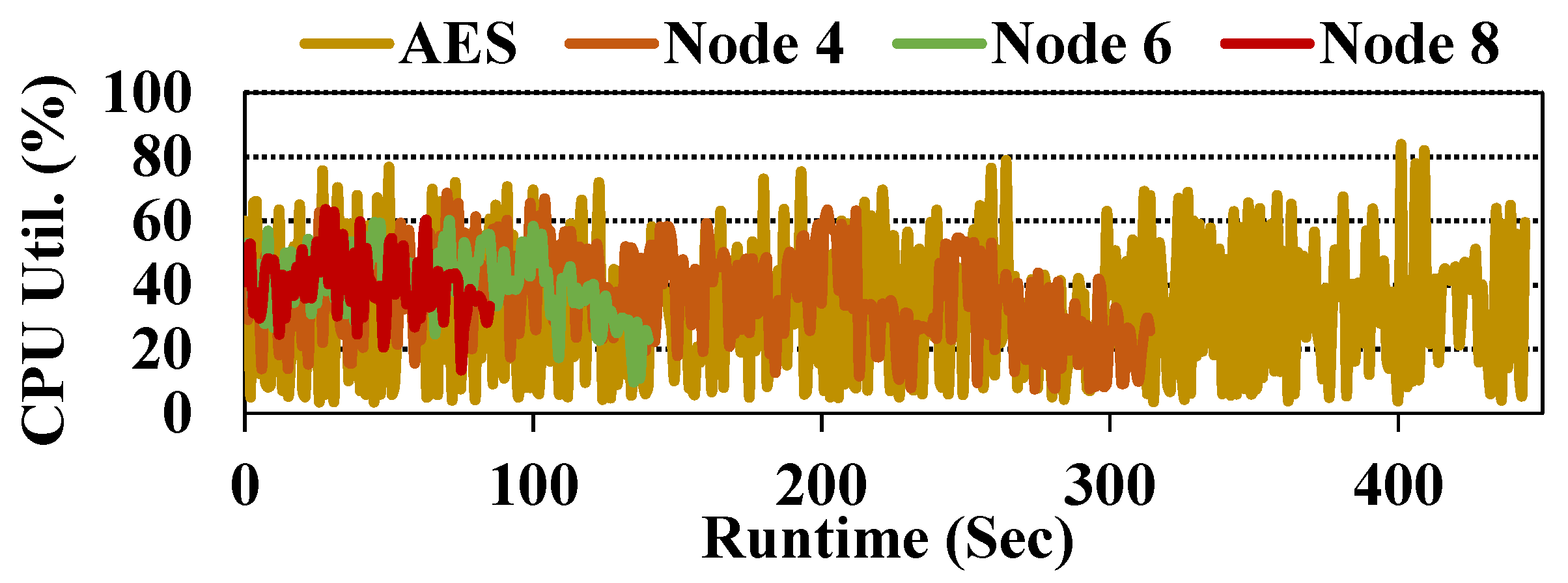
4.3. Node-Level Encryption Performance and Variability
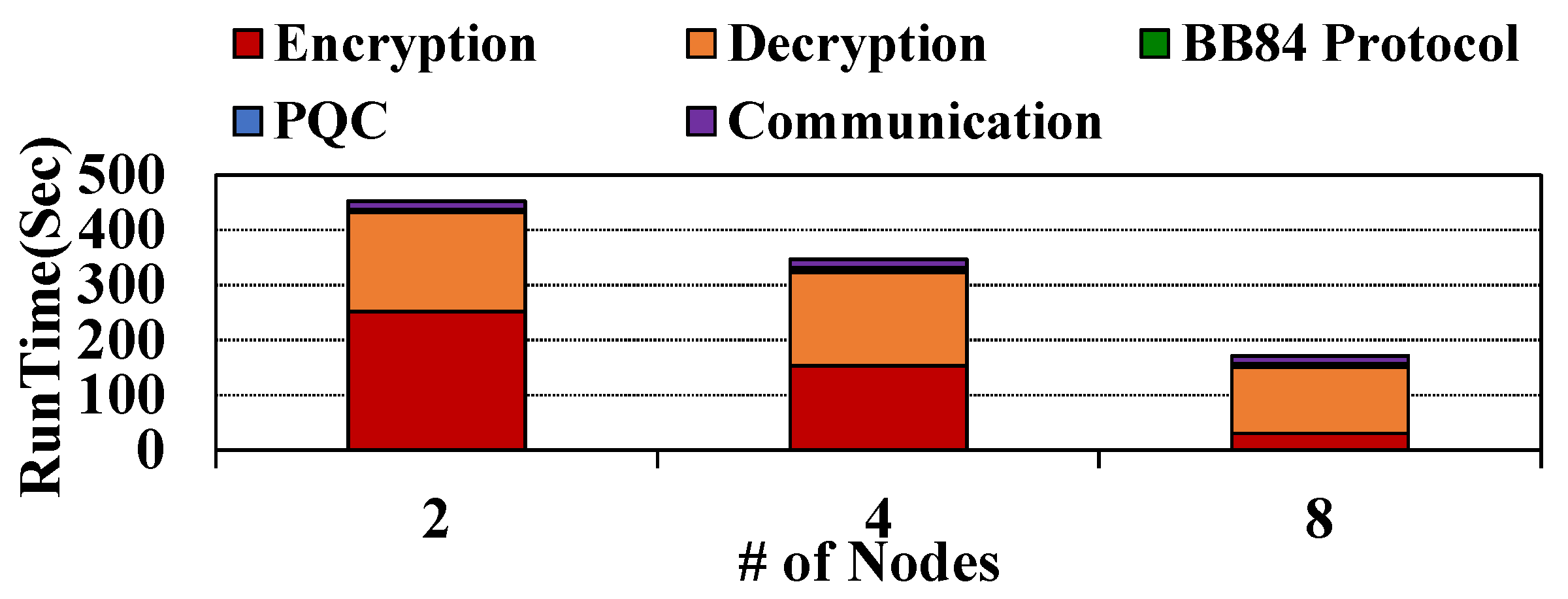
4.4. Communication Cost
4.5. Time Analysis
4.6. QKD Runtime Variability
4.7. Computation Overhead
4.8. CPU Utilization
5. Related Works
5.1. Cryptographic Integration Approaches for Cloud System Security
5.2. Accelerating Security Processing in Cloud Systems with Innovative Cryptographic Methods
5.3. Integrated Cryptographic Approaches for Next-Generation Data Security
6. Limitation and Future Works
- Integrity verification mechanism: Our proposed scheme ensures safe key distribution and secure data delivery through a layered structure that combines Kyber-based key encapsulation, QKD-based masking, and optional Shamir secret sharing. (1) Each AES key is never exposed in plaintext. It is encapsulated via PQC, while the corresponding secret key is QKD-masked and optionally fragmented, making unauthorized key reconstruction infeasible even under partial node compromise. (2) All encrypted subsets are transmitted only after local encryption with securely reconstructed keys, and communication occurs over pre-encrypted data without relying on secure channels, thereby preventing eavesdropping and key leakage in practice. Additionally, each subset is encrypted in CTR mode using a randomly generated nonce, which supports freshness and prevents ciphertext duplication across sessions.
- Non-elastic communication structure in cloud systems: Our proposed scheme adopts MPI-based communication between a master and fixed slave nodes (e.g., number of nodes: 2, 4, 6, 8), which has shown effective in stable, high-throughput performance under controlled cloud workloads such as YCSB (e.g., workload A, B, C, D). (1) This structure enables efficient coordination and predictable communication by leveraging deterministic message passing, resulting in minimal runtime variability across nodes and strong throughput scalability as demonstrated in our evaluation. (2) While this design meets the requirements of large-scale file encryption in a fixed-resource environment, it provides limited elasticity in dynamic cloud-native platforms such as Kubernetes [90], where autoscaling, container migration, and fault-tolerant recovery are essential.
- Centralized decryption and performance-security trade-off: Our decryption strategy is performed at the master node using the AES key recovered through Kyber decapsulation and QKD unmasking, with both operations strictly confined to the master node to minimize key exposure and ensure coordinated trust. Although all slave nodes are capable of reconstructing the AES key from QKD-masked secret shares, only a selected slave nodes retain the key during execution, and the rest discard it immediately after encryption. As a result, decryption cannot be performed by slave nodes alone, which effectively eliminates unauthorized decryption paths and strengthens security against node compromise and replay-based attacks.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kobusińska, A.; Leung, C.; Hsu, C.H.; S., R.; Chang, V. Emerging trends, issues and challenges in Internet of Things, Big Data and cloud computing. Future Gener. Comput. Syst. 2018, 87, 416–419. [Google Scholar] [CrossRef]
- Ramirez, A.H.; Sulieman, L.; Schlueter, D.J.; Halvorson, A.; Qian, J.; Ratsimbazafy, F.; Loperena, R.; Mayo, K.; Basford, M.; Deflaux, N.; et al. The All of Us Research Program: Data quality, utility, and diversity. Patterns 2022, 3, 100570. [Google Scholar] [CrossRef] [PubMed]
- Norori, N.; Hu, Q.; Aellen, F.M.; Faraci, F.D.; Tzovara, A. Addressing bias in big data and AI for health care: A call for open science. Patterns 2021, 2, 100347. [Google Scholar] [CrossRef]
- Boubaker, S.; Liu, Z.; Zhai, L. Big data, news diversity and financial market crash. Technol. Forecast. Soc. Change 2021, 168, 120755. [Google Scholar] [CrossRef]
- Hu, Y.; Kuang, W.; Qin, Z.; Li, K.; Zhang, J.; Gao, Y.; Li, W.; Li, K. Artificial intelligence security: Threats and countermeasures. ACM Comput. Surv. (CSUR) 2021, 55, 20. [Google Scholar] [CrossRef]
- Abouelmehdi, K.; Beni-Hessane, A.; Khaloufi, H. Big healthcare data: Preserving security and privacy. J. Big Data 2018, 5, 1. [Google Scholar] [CrossRef]
- Thomas, K.; Pullman, J.; Yeo, K.; Raghunathan, A.; Kelley, P.G.; Invernizzi, L.; Benko, B.; Pietraszek, T.; Patel, S.; Boneh, D.; et al. Protecting accounts from credential stuffing with password breach alerting. In Proceedings of the 28th USENIX Security Symposium (USENIX Security 19), Santa Clara, CA, USA, 14–16 August 2019; pp. 1556–1571. [Google Scholar]
- Moallem, A. Human behavior in cybersecurity privacy and trust. In Human-Computer Interaction in Intelligent Environments; CRC Press: Boca Raton, FL, USA, 2024; pp. 77–107. [Google Scholar]
- Wu, H.; Dwivedi, A.D.; Srivastava, G. Security and privacy of patient information in medical systems based on blockchain technology. ACM Trans. Multimed. Comput. Commun. Appl. (TOMM) 2021, 17, 60. [Google Scholar] [CrossRef]
- Marjani, M.; Nasaruddin, F.; Gani, A.; Karim, A.; Hashem, I.A.T.; Siddiqa, A.; Yaqoob, I. Big IoT data analytics: Architecture, opportunities, and open research challenges. IEEE Access 2017, 5, 5247–5261. [Google Scholar]
- Alansari, Z.; Soomro, S.; Belgaum, M.R.; Shamshirband, S. The rise of Internet of Things (IoT) in big healthcare data: Review and open research issues. In Progress in Advanced Computing and Intelligent Engineering, Proceedings of ICACIE 2016, Puducherry, India, 15–17 December 2016; Springer: Singapore, 2018; Volume 2, pp. 675–685. [Google Scholar]
- Amazon Web Services (AWS). Available online: https://aws.amazon.com (accessed on 6 July 2025).
- Google Cloud. Available online: https://cloud.google.com/ (accessed on 6 July 2025).
- Microsoft Azure. Available online: https://azure.microsoft.com/ (accessed on 6 July 2025).
- Dierks, T.; Rescorla, E. The Transport Layer Security (TLS) Protocol Version 1.2; Technical Report RFC 5246; Internet Engineering Task Force: Fremont, CA, USA, 2008. [Google Scholar]
- Indu, I.; Anand, P.R.; Bhaskar, V. Identity and access management in cloud environment: Mechanisms and challenges. Eng. Sci. Technol. Int. J. 2018, 21, 574–588. [Google Scholar] [CrossRef]
- Tom, J.J.; Anebo, N.P.; Onyekwelu, B.A.; Wilfred, A.; Eyo, R. Quantum computers and algorithms: A threat to classical cryptographic systems. Int. J. Eng. Adv. Technol 2023, 12, 25–38. [Google Scholar] [CrossRef]
- Azhari, R.; Salsabila, A.N. Analyzing the impact of quantum computing on current encryption techniques. IAIC Trans. Sustain. Digit. Innov. (ITSDI) 2024, 5, 148–157. [Google Scholar] [CrossRef]
- Ajala, O.A.; Arinze, C.A.; Ofodile, O.C.; Okoye, C.C.; Daraojimba, A.I. Exploring and reviewing the potential of quantum computing in enhancing cybersecurity encryption methods. Magna Sci. Adv. Res. Rev 2024, 10, 321–329. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Grover, L.K. A fast quantum mechanical algorithm for database search. In Proceedings of the Twenty-Eighth Annual ACM Symposium on Theory of Computing, Philadelphia, PA, USA, 22–24 May 1996; pp. 212–219. [Google Scholar]
- Daemen, J.; Rijmen, V. AES Proposal: Rijndael. NIST AES Proposal Document. 1999. Available online: https://csrc.nist.gov/csrc/media/projects/cryptographic-standards-and-guidelines/documents/aes-development/rijndael-ammended.pdf (accessed on 6 July 2025).
- Bernstein, D.J.; Lange, T. Post-quantum cryptography. Nature 2017, 549, 188–194. [Google Scholar] [CrossRef]
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dušek, M.; Lütkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301–1350. [Google Scholar] [CrossRef]
- Jenefa, A.; Josh, F.; Taurshia, A.; Kumar, K.R.; Kowsega, S.; Naveen, E. PQC Secure: Strategies for defending against quantum threats. In Proceedings of the 2023 2nd International Conference on Automation, Computing and Renewable Systems (ICACRS), Pudukkottai, India, 13–15 December 2023; pp. 1799–1804. [Google Scholar]
- Joseph, D.; Misoczki, R.; Manzano, M.; Tricot, J.; Pinuaga, F.D.; Lacombe, O.; Leichenauer, S.; Hidary, J.; Venables, P.; Hansen, R. Transitioning organizations to post-quantum cryptography. Nature 2022, 605, 237–243. [Google Scholar] [CrossRef]
- Käppler, S.A.; Schneider, B. Post-quantum cryptography: An introductory overview and implementation challenges of quantum-resistant algorithms. Proc. Soc. 2022, 84, 61–71. [Google Scholar]
- Sharma, P.; Agrawal, A.; Bhatia, V.; Prakash, S.; Mishra, A.K. Quantum key distribution secured optical networks: A survey. IEEE Open J. Commun. Soc. 2021, 2, 2049–2083. [Google Scholar] [CrossRef]
- Zhang, W.; van Leent, T.; Redeker, K.; Garthoff, R.; Schwonnek, R.; Fertig, F.; Eppelt, S.; Rosenfeld, W.; Scarani, V.; Lim, C.C.W.; et al. A device-independent quantum key distribution system for distant users. Nature 2022, 607, 687–691. [Google Scholar] [CrossRef]
- Tsai, C.W.; Yang, C.W.; Lin, J.; Chang, Y.C.; Chang, R.S. Quantum key distribution networks: Challenges and future research issues in security. Appl. Sci. 2021, 11, 3767. [Google Scholar] [CrossRef]
- Sun, S.; Huang, A. A review of security evaluation of practical quantum key distribution system. Entropy 2022, 24, 260. [Google Scholar] [CrossRef]
- Farooq, S.; Altaf, A.; Iqbal, F.; Thompson, E.B.; Vargas, D.L.R.; Díez, I.d.l.T.; Ashraf, I. Resilience optimization of post-quantum cryptography key encapsulation algorithms. Sensors 2023, 23, 5379. [Google Scholar] [CrossRef] [PubMed]
- Hecht, P. PQC: R-Propping of Burmester-Desmedt Conference Key Distribution System. Cryptology ePrint Archive 2021. Available online: https://eprint.iacr.org/2021/024 (accessed on 6 July 2025).
- Campbell, R. The need for cyber resilient enterprise distributed ledger Risk Management Framework. J. Br. Blockchain Assoc. 2020, 3, 9. [Google Scholar] [CrossRef] [PubMed]
- Bouda, J.; Pivoluska, M.; Plesch, M.; Wilmott, C. Weak randomness seriously limits the security of quantum key distribution. Phys. Rev. A Atomic Mol. Opt. Phys. 2012, 86, 062308. [Google Scholar] [CrossRef]
- Jiang, X.L.; Deng, X.Q.; Wang, Y.; Lu, Y.F.; Li, J.J.; Zhou, C.; Bao, W.S. Weak randomness analysis of measurement-device-independent quantum key distribution with finite resources. Photonics 2022, 9, 356. [Google Scholar] [CrossRef]
- Zeng, P.; Bandyopadhyay, D.; Méndez, J.A.M.; Bitner, N.; Kolar, A.; Solomon, M.T.; Ye, Z.; Rozpędek, F.; Zhong, T.; Heremans, F.J.; et al. Practical hybrid PQC-QKD protocols with enhanced security and performance. arXiv 2024, arXiv:2411.01086. [Google Scholar]
- Yang, Z.; Shi, Q.; Cheng, T.; Wang, X.; Zhang, R.; Yu, L. A security-enhanced authentication scheme for quantum-key-distribution (QKD) enabled Internet of vehicles in multi-cloud environment. Veh. Commun. 2024, 48, 100789. [Google Scholar] [CrossRef]
- Zeydan, E.; Baranda, J.; Mangues-Bafalluy, J. Post-quantum blockchain-based secure service orchestration in multi-cloud networks. IEEE Access 2022, 10, 129520–129530. [Google Scholar] [CrossRef]
- Ricci, S.; Dobias, P.; Malina, L.; Hajny, J.; Jedlicka, P. Hybrid keys in practice: Combining classical, quantum and post-quantum cryptography. IEEE Access 2024, 12, 23206–23219. [Google Scholar] [CrossRef]
- Wang, L.J.; Zhang, K.Y.; Wang, J.Y.; Cheng, J.; Yang, Y.H.; Tang, S.B.; Yan, D.; Tang, Y.L.; Liu, Z.; Yu, Y.; et al. Experimental authentication of quantum key distribution with post-quantum cryptography. npj Quantum Inf. 2021, 7, 67. [Google Scholar] [CrossRef]
- Rani, A.; Ai, X.; Gupta, A.; Adhikari, R.S.; Malaney, R. Combined Quantum and Post-Quantum Security for Earth-Satellite Channels. In Proceedings of the 2025 International Conference on Quantum Communications, Networking, and Computing (QCNC), Nara, Japan, 31 March–2 April 2025; pp. 301–308. [Google Scholar]
- Rivest, R.L.; Shamir, A.; Adleman, L. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 1978, 21, 120–126. [Google Scholar] [CrossRef]
- Koblitz, N. Elliptic curve cryptosystems. Math. Comput. 1987, 48, 203–209. [Google Scholar] [CrossRef]
- Faruk, M.J.H.; Tahora, S.; Tasnim, M.; Shahriar, H.; Sakib, N. A review of quantum cybersecurity: Threats, risks and opportunities. In Proceedings of the 2022 1st International Conference on AI in Cybersecurity (ICAIC), Virtual, 21–23 September 2022; pp. 1–8. [Google Scholar]
- Szatmáry, S. Quantum Computers—Security Threats and Solutions. In Proceedings of the IFIP International Conference on Human Choice and Computers, Tokyo, Japan, 8–9 September 2022; pp. 431–441. [Google Scholar]
- Kilber, N.; Kaestle, D.; Wagner, S. Cybersecurity for quantum computing. arXiv 2021, arXiv:2110.14701. [Google Scholar]
- Chawla, D.; Mehra, P.S. A survey on quantum computing for internet of things security. Procedia Comput. Sci. 2023, 218, 2191–2200. [Google Scholar] [CrossRef]
- Kumar, M.; Pattnaik, P. Post quantum cryptography (pqc)-an overview. In Proceedings of the 2020 IEEE High Performance Extreme Computing Conference (HPEC), Virtual, 22–24 September 2020; pp. 1–9. [Google Scholar]
- Soni, D.; Karri, R. Efficient hardware implementation of pqc primitives and pqc algorithms using high-level synthesis. In Proceedings of the 2021 IEEE Computer Society Annual Symposium on VLSI (ISVLSI), Tampa, FL, USA, 7–9 July 2021; pp. 296–301. [Google Scholar]
- Micciancio, D.; Regev, O. Lattice-based cryptography. In Post-Quantum Cryptography; Springer: Berlin/Heidelberg, Germany, 2009; pp. 147–191. [Google Scholar]
- Peikert, C. Public-key cryptosystems from the worst-case shortest vector problem. In Proceedings of the Forty-First Annual ACM Symposium on Theory of Computing, Bethesda, MD, USA, 31 May–2 June 2009; pp. 333–342. [Google Scholar]
- Bos, J.; Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schanck, J.M.; Schwabe, P.; Seiler, G.; Stehlé, D. CRYSTALS-Kyber: A CCA-secure module-lattice-based KEM. In Proceedings of the 2018 IEEE European Symposium on Security and Privacy (EuroS&P), London, UK, 24–26 April 2018; pp. 353–367. [Google Scholar]
- Shor, P.W.; Preskill, J. Simple proof of security of the BB84 quantum key distribution protocol. Phys. Rev. Lett. 2000, 85, 441. [Google Scholar] [CrossRef]
- Boneh, D. The decision diffie-hellman problem. In Proceedings of the International Algorithmic Number Theory Symposium, Leiden, The Netherlands, 2–7 July 2000; pp. 48–63. [Google Scholar]
- Gerhardt, I.; Liu, Q.; Lamas-Linares, A.; Skaar, J.; Kurtsiefer, C.; Makarov, V. Full-field implementation of a perfect eavesdropper on a quantum cryptography system. Nat. Commun. 2011, 2, 349. [Google Scholar] [CrossRef]
- Sibson, P.; Erven, C.; Godfrey, M.; Miki, S.; Yamashita, T.; Fujiwara, M.; Sasaki, M.; Terai, H.; Tanner, M.G.; Natarajan, C.M.; et al. Chip-based quantum key distribution. Nat. Commun. 2017, 8, 13984. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.S.; Bai, Z.L.; Wang, X.Y.; Li, Y.M. FPGA-based implementation of size-adaptive privacy amplification in quantum key distribution. IEEE Photonics J. 2017, 9, 7600308. [Google Scholar] [CrossRef]
- Amiri, R.; Wallden, P.; Kent, A.; Andersson, E. Secure quantum signatures using insecure quantum channels. Phys. Rev. A 2016, 93, 032325. [Google Scholar] [CrossRef]
- Amer, O.; Krawec, W.O. Semiquantum key distribution with high quantum noise tolerance. Phys. Rev. A 2019, 100, 022319. [Google Scholar] [CrossRef]
- Ducas, L.; Kiltz, E.; Lepoint, T.; Lyubashevsky, V.; Schwabe, P.; Seiler, G.; Stehlé, D. Crystals-dilithium: A lattice-based digital signature scheme. IACR Trans. Cryptogr. Hardw. Embed. Syst. 2018, 2018, 238–268. [Google Scholar] [CrossRef]
- IBM Qiskit Aer. Available online: https://github.com/Qiskit/qiskit-aer (accessed on 6 July 2025).
- An, S.; Seo, S.C. Designing a new XTS-AES parallel optimization implementation technique for fast file encryption. IEEE Access 2022, 10, 25349–25357. [Google Scholar] [CrossRef]
- Baladhay, J.S.; Gamido, H.V.; Edjie, M. Large file encryption in a Reduced-Round Permutation-Based AES file management system. Indones. J. Electr. Eng. Comput. Sci. 2024, 34, 2021–2031. [Google Scholar] [CrossRef]
- Xing, B.; Wang, D.; Yang, Y.; Wei, Z.; Wu, J.; He, C. Accelerating DES and AES algorithms for a heterogeneous many-core processor. Int. J. Parallel Program. 2021, 49, 463–486. [Google Scholar] [CrossRef]
- Lipmaa, H.; Rogaway, P.; Wagner, D. CTR-mode encryption. In Proceedings of the First NIST Workshop on Modes of Operation, Gaithersburg, MD, USA, 20–21 October 2000; Volume 39. [Google Scholar]
- Vaidehi, M.; Rabi, B.J. Design and analysis of AES-CBC mode for high security applications. In Proceedings of the Second International Conference on Current Trends In Engineering and Technology-ICCTET 2014, Coimbatore, India, 8–10 July 2014; pp. 499–502. [Google Scholar]
- Lin, C.H.; Hu, G.H.; Chan, C.Y.; Yan, J.J. Chaos-based synchronized dynamic keys and their application to image encryption with an improved AES algorithm. Appl. Sci. 2021, 11, 1329. [Google Scholar] [CrossRef]
- Ashraf, Z.; Sohail, A.; Yousaf, M. Robust and lightweight symmetric key exchange algorithm for next-generation IoE. Internet Things 2023, 22, 100703. [Google Scholar] [CrossRef]
- Bogdanov, A.; Mendel, F.; Regazzoni, F.; Rijmen, V.; Tischhauser, E. ALE: AES-based lightweight authenticated encryption. In Proceedings of the Fast Software Encryption: 20th International Workshop, FSE 2013, Singapore, 11–13 March 2013; pp. 447–466. [Google Scholar]
- Fei, X.; Li, K.; Yang, W.; Li, K. Practical parallel AES algorithms on cloud for massive users and their performance evaluation. Concurr. Comput. Pract. Exp. 2016, 28, 4246–4263. [Google Scholar] [CrossRef]
- Awan, I.A.; Shiraz, M.; Hashmi, M.U.; Shaheen, Q.; Akhtar, R.; Ditta, A. Secure framework enhancing AES algorithm in cloud computing. Secur. Commun. Netw. 2020, 2020, 8863345. [Google Scholar] [CrossRef]
- Liu, B.; Baas, B.M. Parallel AES encryption engines for many-core processor arrays. IEEE Trans. Comput. 2011, 62, 536–547. [Google Scholar] [CrossRef]
- Shamir, A. How to share a secret. Commun. ACM 1979, 22, 612–613. [Google Scholar] [CrossRef]
- Pang, L.J.; Wang, Y.M. A new (t, n) multi-secret sharing scheme based on Shamir’s secret sharing. Appl. Math. Comput. 2005, 167, 840–848. [Google Scholar] [CrossRef]
- Sarah, D.; Peter, C. On the practical cost of Grover for AES key recovery. In Proceedings of the Presentation at the 5th NIST PQC Standardization Conference, Rockville, MD, USA, 10–12 April 2024. [Google Scholar]
- Grassl, M.; Langenberg, B.; Roetteler, M.; Steinwandt, R. Applying Grover’s algorithm to AES: Quantum resource estimates. In Proceedings of the International Workshop on Post-Quantum Cryptography, Fukuoka, Japan, 24–26 February 2016; pp. 29–43. [Google Scholar]
- Open Quantum Safe. Available online: https://openquantumsafe.org/ (accessed on 6 July 2025).
- Ahmed, M.; Byreddy, S.; Nutakki, A.; Sikos, L.F.; Haskell-Dowland, P. ECU-IoHT: A dataset for analyzing cyberattacks in Internet of Health Things. Ad Hoc Netw. 2021, 122, 102621. [Google Scholar] [CrossRef]
- Cooper, B.F.; Silberstein, A.; Tam, E.; Ramakrishnan, R.; Sears, R. Benchmarking cloud serving systems with YCSB. In Proceedings of the 1st ACM Symposium on Cloud Computing, Indianapolis, IN, USA, 10–11 June 2010; pp. 143–154. [Google Scholar]
- Atikah, N.; Ashila, M.R.; Rachmawanto, E.H.; Sari, C.A. AES-RC4 Encryption Technique to Improve File Security. In Proceedings of the 2019 Fourth International Conference on Informatics and Computing (ICIC), Semarang, Indonesia, 16–17 October 2019; pp. 1–5. [Google Scholar]
- Abbas, M.S.; Mahdi, S.S.; Hussien, S.A. Security improvement of cloud data using hybrid cryptography and steganography. In Proceedings of the 2020 international conference on computer science and software engineering (CSASE), Duhok, Iraq, 16–18 February 2020; pp. 123–127. [Google Scholar]
- Velmurugadass, P.; Dhanasekaran, S.; Anand, S.S.; Vasudevan, V. Enhancing Blockchain security in cloud computing with IoT environment using ECIES and cryptography hash algorithm. Mater. Today Proc. 2021, 37, 2653–2659. [Google Scholar] [CrossRef]
- Thabit, F.; Alhomdy, S.; Al-Ahdal, A.H.; Jagtap, S. A new lightweight cryptographic algorithm for enhancing data security in cloud computing. Glob. Transitions Proc. 2021, 2, 91–99. [Google Scholar] [CrossRef]
- Mohammed, S.; Nanthini, S.; Krishna, N.B.; Srinivas, I.V.; Rajagopal, M.; Kumar, M.A. A new lightweight data security system for data security in the cloud computing. Meas. Sens. 2023, 29, 100856. [Google Scholar] [CrossRef]
- Chen, Y.; Tang, C.; Yi, Z. A novel image encryption scheme based on PWLCM and standard map. Complexity 2020, 2020, 3026972. [Google Scholar] [CrossRef]
- Mirzajani, S.; Moafimadani, S.S.; Roohi, M. A New Encryption Algorithm Utilizing DNA Subsequence Operations for Color Images. AppliedMath 2024, 4, 1382–1403. [Google Scholar] [CrossRef]
- Lin, H.; Deng, X.; Yu, F.; Sun, Y. Diversified butterfly attractors of memristive HNN with two memristive systems and application in IoMT for privacy protection. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2024, 44, 304–316. [Google Scholar] [CrossRef]
- Ding, S.; Lin, H.; Deng, X.; Yao, W.; Jin, J. A hidden multiwing memristive neural network and its application in remote sensing data security. Expert Syst. Appl. 2025, 277, 127168. [Google Scholar] [CrossRef]
- Kubernetes. Available online: https://kubernetes.io (accessed on 6 July 2025).
- Google gRPC. Available online: https://cloud.google.com/api-gateway/docs/grpc-overview (accessed on 7 July 2025).

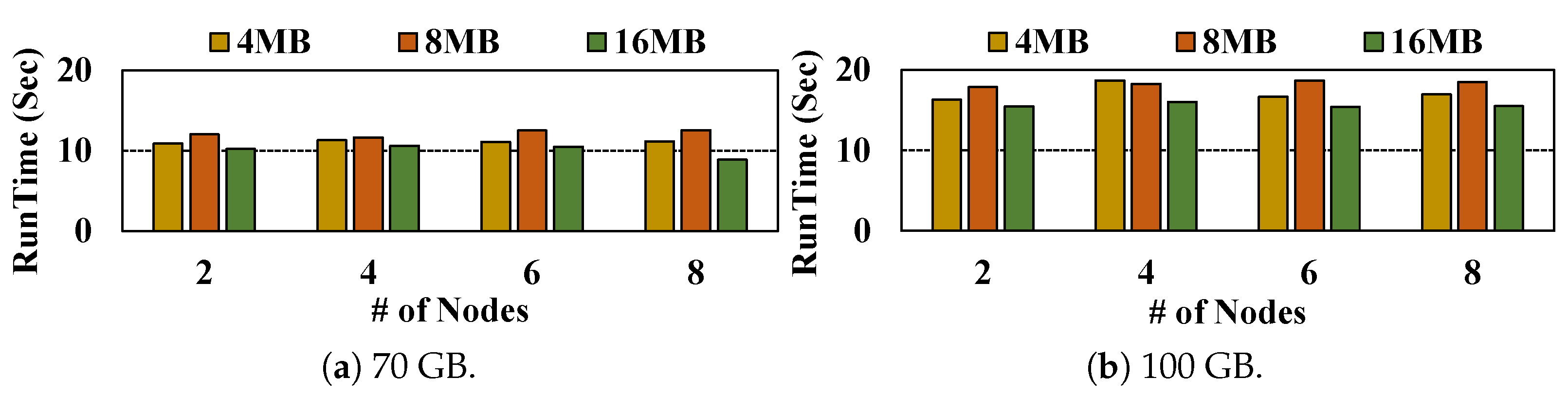

| Paper | Crypto Combination | Target Scope |
|---|---|---|
| Zeng et al. [37] | PQC, QKD | Key Exchange |
| Yang et al. [38] | QKD, Digital Signature | Key Exchange |
| Zeydan et al. [39] | PQC, Digital Signature | Blockchain-based Security |
| Ricci et al. [40] | PQC, QKD | Key Exchange |
| Wang et al. [41] | PQC, QKD | Key Exchange |
| Rani et al. [42] | QKD, AES | File Transmission |
| Our Study | PQC, QKD, AES | File Encryption |
| Workload | Vanilla | AES (Original) | Proposed (PQC + QKD + AES) |
|---|---|---|---|
| workload A | 255.65 | 291.43 | 267.74 |
| workload B | 168.86 | 209.65 | 182.34 |
| workload C | 115.55 | 173.61 | 153.32 |
| workload D | 111.06 | 146.62 | 132.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, C.; Kim, S.; Sohn, K.; Son, Y.; Kumar, M.; Kim, S. Secure and Scalable File Encryption for Cloud Systems via Distributed Integration of Quantum and Classical Cryptography. Appl. Sci. 2025, 15, 7782. https://doi.org/10.3390/app15147782
Kim C, Kim S, Sohn K, Son Y, Kumar M, Kim S. Secure and Scalable File Encryption for Cloud Systems via Distributed Integration of Quantum and Classical Cryptography. Applied Sciences. 2025; 15(14):7782. https://doi.org/10.3390/app15147782
Chicago/Turabian StyleKim, Changjong, Seunghwan Kim, Kiwook Sohn, Yongseok Son, Manish Kumar, and Sunggon Kim. 2025. "Secure and Scalable File Encryption for Cloud Systems via Distributed Integration of Quantum and Classical Cryptography" Applied Sciences 15, no. 14: 7782. https://doi.org/10.3390/app15147782
APA StyleKim, C., Kim, S., Sohn, K., Son, Y., Kumar, M., & Kim, S. (2025). Secure and Scalable File Encryption for Cloud Systems via Distributed Integration of Quantum and Classical Cryptography. Applied Sciences, 15(14), 7782. https://doi.org/10.3390/app15147782